EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A32 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A32
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202348558
Published online 28 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Protoplanetary discs consist of gas and dust that orbit young stars and provide the necessary material for the agglomeration and growth of planetesimals, the building blocks of planets. The dynamical and physical processes occurring within these discs play a crucial role in shaping the characteristics and composition of planetary systems. Among these processes, aeolian erosion of large dust particles might influence the dynamics and evolution of the dust in the inner regions of protoplanetary discs (Blum & Wurm 2000; Wurm et al. 2001). Aeolian erosion is a process whereby dust particles are ejected from a larger object due to the combined action of gas drag and turbulent motions within the disc. It has been studied by Blum & Wurm (2000); Wurm et al. (2001); Paraskov et al. (2006), and more recently by Rozner et al. (2020) and Grishin et al. (2020, hereafter R20 and G20). They showed that large aggregates can be eroded in a short time, typically ranging from a few years to a few thousand years, and reducing in size from several hundred metres down to a couple of centimetres (R20; G20). This process is therefore believed to destroy large boulders very efficiently and impact the evolution of grains in the inner region of the disc. Hence, erosion is another barrier to dust growth from small objects to kilometric ones.

In addition to aeolian erosion, fragmentation of dust particles is a process that can destroy grains in the inner regions of protoplanetary discs. When dust particles collide at high velocities, they may experience catastrophic disruptions, leading to the so-called fragmentation barrier (Weidenschilling & Cuzzi 1993; Dominik & Tielens 1997; Blum & Wurm 2008). Fragmentation thresholds or material properties to model collisions are still not fully understood, with many uncertainties remaining. Moreover, dust experiences radial drift during its growth in the disc due to gas drag. Grains a few centimetres to metres in size drift very efficiently, due to marginal coupling to the gas, and are accreted onto the star (Whipple 1972), which defines the radial drift barrier (Weidenschilling 1977). In order to prevent radial drift and the loss of material onto the star, and help the formation of planetesimals, several solutions have been proposed. Some rely on the capture of dust in pressure maxima; others bypass the barriers to dust growth. For instance, vortices have been explored (Barge & Sommeria 1995; Meheut et al. 2012; Loren-Aguilar & Bate 2015) to trap dust and form clumps directly from gravitational collapse. Snow lines (Kretke & Lin 2007; Brauer et al. 2008; Drazkowska et al. 2014; Vericel & Gonzalez 2020) and self-induced dust traps (Gonzalez et al. 2017; Vericel & Gonzalez 2020; Vericel et al. 2021) form local pressure maxima, stopping the radial drift and helping grain growth by increasing the local dust density. Other properties of dust have also been investigated, like grain porosity (Ormel et al. 2007; Suyama et al. 2008; Okuzumi et al. 2009, 2012; Kataoka et al. 2013; Garcia & Gonzalez 2020), which allows grains to grow faster and to larger sizes, while making them less sensitive to fragmentation. Additionally, other processes related to instabilities have been under investigation in recent years, mostly with the streaming instability (Youdin & Goodman 2005; Youdin & Johansen 2007; Yang et al. 2017; Schäfer et al. 2017; Auffinger & Laibe 2018; Li et al. 2019), which allows dust to directly form boulders from pebbles, bypassing the different barriers that grains might undergo during their evolution. Grishin et al. (2019) looked at a different solution whereby planetesimals can be captured in pro-toplanetary discs early. This had also been shown to occur in earlier stages, such as molecular clouds (Pfalzner & Bannister 2019; Pfalzner et al. 2021).

In this paper, we study the importance of aeolian erosion in relation to fragmentation and its importance in inner disc regions. In a previous paper, we compared the importance of fragmentation and rotational disruption of porous grains (Michoulier & Gonzalez 2022), a new barrier introduced by Tatsuuma & Kataoka (2021). In this paper, however, we will not take into account porosity, as the current aeolian erosion model of R20 and G20 does not take into account the evolution of density. We will therefore limit ourselves to the simpler compact grain formalism.

The paper is built as follows: we first describe our dust growth and fragmentation model and introduce a model that takes aeolian erosion into account in Sect. 2. We then describe the tests that were performed to make sure the implementation of the erosion module was correctly done in Sect. 3. Then, we discuss the results in Sect. 4 using the 1D code PAMDEAS1 (Michoulier & Gonzalez 2022) and the 3D code PHANTOM2 of Price et al. (2018) to show the unimportance of aeolian erosion with respect to fragmentation. Finally, we discuss our results about erosion and the limitations of the codes in Sect. 5, and end with a conclusion in Sect. 6.

2 Methods

To determine the importance of different barriers, we describe in the following how growth, fragmentation, and erosion are taken into account in PAMDEAS. When using PHANTOM (Price et al. 2018), all the details about the implementation of growth and fragmentation are presented in Vericel et al. (2021). The erosion model implemented in PAMDEAS and PHANTOM is the same, and the growth and fragmentation models are identical, but the implementation differs slightly and is code-related.

2.1 Dust grain growth model

In order to model dust growth, we considered a locally uniform mass distribution of grains in which collisions occur exclusively between grains of identical mass. The equation describing the size variation is given by Stepinski & Valageas (1997): 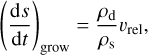(ds dt)grow =ρdρsυrel ,${\left( {{{{\rm{d}}s} \over {{\rm{d}}t}}} \right)_{{\rm{grow }}}} = {{{\rho _{\rm{d}}}} \over {{\rho _{\rm{s}}}}}{v_{{\rm{rel }}}},$(1)

where ρd is the dust local density, ρs is the grain intrinsic density, and υrel, the relative velocity during collision, is 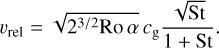υrel =23/2RoαcgSt1+St.${v_{{\rm{rel }}}} = \sqrt {{2^{3/2}}{\mathop{\rm Ro}\nolimits} \alpha } {c_{\rm{g}}}{{\sqrt {{\rm{St}}} } \over {1 + {\rm{St}}}}.$(2)

α is the turbulent viscosity parameter (Shakura & Sunyaev 1973) and cg is the gas sound speed. St is the Stokes number, usually defined as the dimensionless stopping time, ΩKts, where ΩK is the Keplerian frequency and ts the drag stopping time. St quantifies the coupling between gas and dust, which depends on the drag regimes and the grain size (St ∝ s in the Epstein regime). Ro, the Rossby number, is considered to be a constant equal to 3 (Stepinski & Valageas 1997). Full details of the model and its derivation are presented in Laibe et al. (2008); Gonzalez et al. (2015, 2017) or Vericel et al. (2021). Naturally, the growth rate increases as the relative velocity increases, as this enhances the probability of collision occurrence. Moreover, the growth rate exhibits a linear dependence on ρd, indicating that the settling of dust grains or their accumulation in dust traps favour dust growth.

2.2 Fragmentation

When the relative velocity between grains exceeds a critical threshold known as υfrag, instead of growing, the grains undergo fragmentation, as was observed by Tanaka et al. (1996). The impact’s kinetic energy becomes too high for the grain’s structure to absorb, causing the bonds between the constituent monomers of the aggregate to break apart. To quantify the mass variation during fragmentation, we adopted a formulation similar to that proposed by Stepinski & Valageas (1997) for growth. Using a realistic approach developed by Kobayashi & Tanaka (2010) and Garcia (2018) and further used by Vericel et al. (2021), the model introduces a concept of progressive or ‘soft’ fragmentation, taking into account the relative velocity (υrel) compared to υfrag: 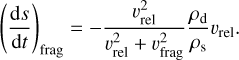(ds dt)frag =−υrel 2υrel 2+υfrag 2ρdρsυrel .${\left( {{{{\rm{d}}s} \over {{\rm{d}}t}}} \right)_{{\rm{frag }}}} = - {{v_{{\rm{rel }}}^2} \over {v_{{\rm{rel }}}^2 + v_{{\rm{frag }}}^2}}{{{\rho _{\rm{d}}}} \over {{\rho _{\rm{s}}}}}{v_{{\rm{rel }}}}.$(3)

When the relative velocity is near the fragmentation threshold, the mass loss becomes less pronounced. Therefore, a fragmenting grain loses approximately half of its initial mass after a collision time3 when υrel = υfrag, or more when υrel > υfrag. When υrel ≫ υfrag, the situation described by Gonzalez et al. (2015) is recovered and the entire grain fragments, losing most of its mass within a collision time.

2.3 Aeolian erosion

R20 and G20 considered aeolian erosion by gas as a mechanism to reduce the size of large aggregates when they are decoupled from the gas. The following section is inspired by those works. During erosion, grains of size sej are ejected from the original aggregate of size s ranging from one metre to one kilometre. If we consider a surrounding gas density, ρg, and a velocity difference between dust and gas, Δυ, the characteristic time for a grain to be ejected is given by 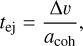tej=Δυacoh,${t_{{\rm{ej}}}} = {{\Delta v} \over {{a_{{\rm{coh}}}}}},$(4)

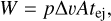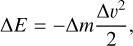where acoh is the cohesive acceleration required for the grain to remain attached. The work exerted by the gas on the aggregate and the energy loss due to erosion are given by R20: W=pΔυAtej,$W = p\Delta vA{t_{{\rm{ej}}}},$(5) ΔE=−ΔmΔυ22,$\Delta E = - \Delta m{{\Delta {v^2}} \over 2},$(6)

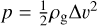where p=12ρgΔυ2$p = {1 \over 2}{\rho _{\rm{g}}}\Delta {v^2}$ is the dynamic pressure and A is the effective shear surface. Since work and energy loss are equal, the mass loss is then 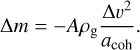Δm=−AρgΔυ2acoh$\Delta m = - A{\rho _{\rm{g}}}{{\Delta {v^2}} \over {{a_{{\rm{coh}}}}}}$(7)

In the case of an infinitesimal time interval, dt < tej, A ≈ s∆υdt, the mass loss becomes 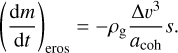(dm dt)eros =−ρgΔυ3acoh s.${\left( {{{{\rm{d}}m} \over {{\rm{d}}t}}} \right)_{{\rm{eros}}}} = - {\rho _{\rm{g}}}{{\Delta {v^3}} \over {{a_{{\rm{coh}}}}}}s.$(8)

Currently, acoh is an unknown but Shao & Lu (2000) showed that the cohesive force could be related to acoh. 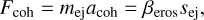Fcoh =mejacoh=βerosSej, ${F_{{\rm{coh}}}} = {m_{{\rm{ej}}}}{a_{{\rm{coh}}}} = {\beta _{{\rm{eros}}}}{S_{{\rm{ej}}}}{\rm{,}}$(9)

where mej is the mass of an ejected grain and βeros is a parameter to define. The experimental measurements of βeros by Heim et al. (1999) and Paraskov et al. (2006) show a strong cohesive force, resulting in a value of βeros = 0.1 kg s−2. With this relation between acoh and βeros, we can finally rewrite Eq. (8) in terms of size loss as (ds dt)eros =−ρg3sej2sΔυ3βeros . ${\left( {{{{\rm{d}}s} \over {{\rm{d}}t}}} \right)_{{\rm{eros}}}} = {{ - {\rho _{\rm{g}}}} \over 3}{{s_{{\rm{ej}}}^2} \over s}{{\Delta {v^3}} \over {{\beta _{{\rm{eros}}}}}}{\rm{.}}$(10)

This equation would be used in the simulations to determine the importance of erosion. However, for erosion to occur, the erosion threshold had first to be reached. This threshold was determined by Shao & Lu (2000) and is expressed as 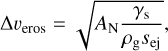Δυeros =ANγsρgsej,$\Delta {v_{{\rm{eros}}}} = \sqrt {{A_{\rm{N}}}{{{\gamma _{\rm{s}}}} \over {{\rho _{\rm{g}}}{s_{{\rm{ej}}}}}}} ,$(11)

where AN = 0.0123 is a numerical constant and γs = 1.65 × 10−4 Jm−2, the surface energy, is the same as in R20. ∆υeros thus depends essentially on sej.

In this work, ∆υ = υd − υg, the velocity difference between dust and gas, is given by 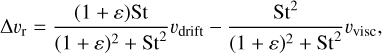Δυr=(1+ε)St(1+ε)2+St2υdrift −St2(1+ε)2+St2υvisc ,$\Delta {v_{\rm{r}}} = {{(1 + \varepsilon ){\rm{St}}} \over {{{(1 + \varepsilon )}^2} + {\rm{S}}{{\rm{t}}^2}}}{v_{{\rm{drift }}}} - {{{\rm{S}}{{\rm{t}}^2}} \over {{{(1 + \varepsilon )}^2} + {\rm{S}}{{\rm{t}}^2}}}{v_{{\rm{visc }}}},$(12) Δυθ=−St2(1+ε)2+St2υdrift 2−(1+ε)St(1+ε)2+St2υvisc 2,$\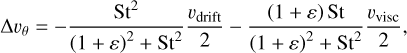Delta {v_\theta } = - {{{\rm{S}}{{\rm{t}}^2}} \over {{{(1 + \varepsilon )}^2} + {\rm{S}}{{\rm{t}}^2}}}{{{v_{{\rm{drift }}}}} \over 2} - {{(1 + \varepsilon ){\rm{St}}} \over {{{(1 + \varepsilon )}^2} + {\rm{S}}{{\rm{t}}^2}}}{{{v_{{\rm{visc }}}}} \over 2},$(13)

where ε is the dust-to-gas ratio, υdrift is the radial drift velocity associated with the gas pressure gradient, and υvisc is the one due to gas motion caused by viscosity (full details on the derivation can be found in Michoulier & Gonzalez 2022). ∆υ is hence given by 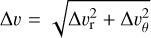Δυ=Δυr2+Δυθ2$\Delta v = \sqrt {\Delta v_{\rm{r}}^2 + \Delta v_\theta ^2} $ and is compared to the erosion threshold, ∆υeros

thumbnail Fig. 1

Validation tests. Left: time evolution of the size, s, of different aggregates as they are eroded. The vertical turnover in the profile gives the characteristic erosion time. The aggregates are kept at a fixed distance of 1 au from the star, and the ejected dust has a size of 100 µm. Dashed lines represent data from R20, which are in excellent agreement with our results. Right: Stokes number at the erosion threshold for aggregates drifting towards the star and four different sizes of ejected grains. Dotted lines represent the analytical solution presented in G20.

3 Tests

To ensure that our implementation of the equations describing erosion worked as intended, we conducted tests to compare our results with those of R20 and G20, as is shown in Fig. 1. To conduct these tests, we used the same disc parameters, which correspond to a minimum-mass solar nebula (MMSN) model (Perets & Murray-Clay 2011; Grishin & Perets 2015). The surface density was Σg = 2 × 104 (r/r0)−1.5 kg m−2, and the temperature Tg = 120 (r/r0)−3/7 K, with r0 = 1 au. This gave an aspect ratio, H/r = 0.022 (r/r0)2/7, and a gas density, ρg ≈ 3 × 10−6 (r/r0)−16/7 kg m−3. The dust-to-gas ratio was small and did not play a role here. Figure 1 on the left demonstrates that our simulations using PAMDEAS perfectly reproduce the data from Fig. 4 of R20. The characteristic erosion timescale for each aggregate size is accurately reproduced. When ∆υeros = ∆υ, as the distance is kept fixed, the erosion threshold corresponds to only one value of St, and hence one size. It should be noted that the size at which the erosion threshold is reached is slightly different (127 cm instead of 200 cm in R20). This difference likely arises from the way ∆υ is computed, which differs between this work and R20 and G20. Although the physical size is different, what determines the relative velocity is the Stokes number, which is the same, as is shown in the right panel.

On the right, Fig. 1 shows the critical Stokes number (St) at the erosion threshold. In this case, the grains to be eroded have an initial size of 10 metres, and are initially placed in the outer disc. Grains then drift toward the star until they cross the erosion threshold. The data are compared with an analytical solution that gives the erosion threshold in terms of the critical Stokes number, a polynomial of degree 5, which takes into account both laminar and turbulent gas flow (see Eq. (8) in G20) around the aggregate. To achieve this, one writes the sum of Δυ for laminar and turbulent gas flow as a function of St, which equals Δυeros at the erosion threshold, and then numerically solves it for St. As the size of the ejected grains increases, erosion becomes easier, as erosion starts at larger distances, r, compared to smaller sej. The simulations also show excellent agreement with the analytical solution. The difference occurs at large St and is due to the fact that a grain evolving in PAMDEAS takes a non-zero time to be eroded and reach the equilibrium.

thumbnail Fig. 2

1D dust evolution. Left: evolution of the size, s, of grains experiencing growth and erosion only, as they grow and drift inwards from different initial distances, r, from the star. The colour represents the Stokes number. The dashed grey line represents the evolution without erosion, while the green, orange, and red lines represent the evolution with growth and fragmentation, using a fragmentation threshold of 20, 40, and 80 m s−1, respectively. The size of the ejected grains is sej = 1 mm, a typical value used by R20 and G20. Right: same as the left panel, but with a pressure maximum that traps dust at 1 au.

4 Results

4.1 Set-up

To be closer to reality than the MMSN model, we used a disc model that reproduces observations, presented in Williams & Best (2014). For PAMDEAS, the masses of the star and of the disc were set to M* = 1 M⊙ and Mdisc = 0.01 M⊙. The inner and outer radii were Rin = 0.1 au and Rout = 300 au, while the disc aspect ratio was H/R0 = 0.0895, with a reference radius R0 = 100 au. The density and temperature profiles exponents were p = 1 and q = 0.5. The turbulent viscosity parameter (Shakura & Sunyaev 1973) was set to α = 5 × 10−3−5 × 10−4. A typical dust-to-gas ratio of 1% was used. We used silicates with ρs = 2.7 kg m−3 and an initial size, s0 = 1 µm, with different fragmentation thresholds, υfrag = 20–40–80 m s−1. For the erosion, we used βeros = 0.1 kg s−2, and the ejected grain size, sej = 1 mm, the largest physical value, to maximise the effect of erosion (R20; G20), as smaller sej would reduce 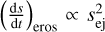(ds dt)eros∝sej2${\left( {{{{\rm{d}}s} \over {{\rm{d}}t}}} \right)_{{\rm{eros}}}} \propto s_{{\rm{ej}}}^2$. In addition, one of the assumptions in the erosion model is that the cohesive force, Fcoh, is proportional to the grain size, which, according to G20 is valid up to 1 mm. Hence, we only use this value in this paper. To model a pressure bump centred on 1 au, we simply added to the initial profile a Gaussian with a width of 0.1 au and a height of 20 times the initial surface at 1 au. The local dust-to-gas ratio in the pressure bump was set to one, a typical value expected in dust traps in which dust is settled and concentrated. As 3D simulations are more expensive, we only modelled the inner disc with PHANTOM, keeping M* and Rin the same but taking Rout = 5 au and R0 = 1 au, which gives Mdisc = 1.64 × 10−4 M⊙, in order to have the same surface density, with α = 5 × 10−3. For all 3D simulations, we used 106 particles. The simulations started with gas only, in order to prevent artefacts due to gas relaxation. After ten orbits at 5 au (~120 yr), the disc was relaxed, dust was added with a uniform dust-to-gas ratio of 1%, and the grain size was initialized at s = 100 µm, with υfrag = 80 m s−1. The other parameters remained the same.

4.2 1D study

In R20 and G20, erosion near the star is presented for certain aggregate sizes. Aggregates of the order of metres can be easily eroded into centimetre-sized aggregates, particularly with large ejected grains. With α = 5 × 10−3, the results are shown in Fig. 2, for grains subject to growth and erosion only. In the left panel, the grains have an initial size of 0.2 µm and grow until they begin to drift towards the star, as their Stokes number approaches 0.1. The grains continue to grow while drifting until erosion occurs at a distance of 0.19 au. Erosion is extremely effective for ejected grains, with sej = 1 mm (R20). The aggregates, with a maximum size of 4 – 6 metres, are rapidly eroded to a few centimetres in size. Then, the grains reach an equilibrium between growth and erosion, and drift slowly from 0.19 au inwards. For comparison, the green, orange, and red lines represent the evolution of a grain considering growth and fragmentation, but no erosion. The fragmentation threshold was set to 20, 40, and 80 m s−1, respectively. Even with a high fragmentation threshold of 80 m s−1 (a value completely unrealistic for most of the disc, resembling pure growth), the fragmentation threshold is reached before the erosion threshold. Therefore, fragmentation is always more effective in destroying dust grains when a realistic value is used.

We also considered what would happen if the dust were trapped and could no longer drift to be accreted onto the star. The answer is shown in the right panel of Fig. 2. Fragmentation is still effective in limiting the grain size. In the case without fragmentation, erosion is unable to balance out growth. There is a small difference around s = 0.1 m due to erosion, which reduces the growth rate without completely countering it, affecting the final grain size somewhat. However, in this case, the final size is of little importance since the grains are trapped, making it possible for them to form larger objects more than one kilometre in size at later stages.

The reason why erosion is almost absent within a dust trap is simple. Erosion depends on Δυ, and in a dust trap the dust-to-gas ratio (ε = 1 in our case) is greater than the typical value of 1%. Taking into account back-reaction, dust tends to make the gas orbit faster and vice versa, reducing Δυ. Additionally, as the dust density, ρd = ερg, increases, the growth rate is multiplied by 100 (Eq. (1)). These two factors work against erosion and prevent it from occurring or at least from having a significant impact.

We then performed the same simulations, but with α = 5 × 10−4 shown in Fig. 3. The results are qualitatively the same. In the left panel, the grains have the same initial size and grow until they begin to drift towards the star. The grains are eroded at the same distance of 0.19 au. Erosion is also effective, but with α = 5 × 10−4, grain growth is less efficient because of lower relative velocities when the viscosity is lower. The aggregates, with a maximum size of 50 centimetres, are eroded to sizes of a few centimetres, reach the equilibrium, and drift inwards. The green line represents the evolution when fragmentation is taken into account, with a threshold set to 20 m s−1. Fragmentation is still more effective in destroying dust grains when such a realistic value is used. Higher thresholds with this α lead to an evolution resembling the pure growth case. Nevertheless, erosion reduces the size of the grains by one order of magnitude, compared to roughly three when α = 5 × 10−3.

Within the dust trap, shown on the right panel, erosion is almost absent. The case with erosion does not differ from the case with pure growth, and only two scenarios are identified. If the threshold is low enough, grains are destroyed by fragmentation. Otherwise, dust grains can grow freely.

We also performed tests considering porosity (see Michoulier & Gonzalez 2022, for its implementation), and we observed no significant change in the appearance of erosion (not shown). We ran a simulation with α = 5 × 10−5, but grain growth is so slow that dust barely reaches sizes of a few centimetres. Erosion still appears, but the dust size is only divided by a factor of two to three. In this case, the limiting factor to the grain size is the very low growth rate.

thumbnail Fig. 3

Same as Fig. 2, but with α = 5 × 10−4 and only one fragmentation threshold.

4.3 3D study

We wanted to check next if we would obtain the same behaviour with 3D simulations. We chose a high velocity threshold of υfrag = 80 m s−1, for which fragmentation is hardly restrictive and which still, according to our 1D simulations, dominates over erosion. Figure 4 shows the radial grain size distribution coloured with the dust-to-gas ratio, ε, for four simulations at time t = 100 yr. The top left panel corresponds to growth only, the top right to growth and fragmentation, the bottom left to growth and erosion, and the bottom right to growth, fragmentation, and erosion. We see that the simulation with growth is able to form large grains up to the decimetre between 0.5 and 2 au. Simulations with fragmentation are identical when erosion is turned on or off (right panels). This means that fragmentation is the dominant mechanism that destroys grains. When comparing the simulation with growth only and the one with erosion, the impact of erosion appears only when sizes are larger than 3 cm, interior to 1 au. This is qualitatively similar to our 1D simulations; however, here grains start to be eroded at larger distances (~0.9 au). This is due to larger volume densities, ρg, in the midplane of the 3D disc compared to the 1D case. Moreover, fragmentation destroys grains at roughly the same size and at the same distance, both in 1D and 3D. Decimetre-sized aggregates are still present, as in the growth-only simulation. For the simulations with fragmentation, the peak in the size profile corresponds to the distance where υrel = υfrag, and the plateau inwards shows an equilibrium between growth and fragmentation (Vericel et al. 2021).

The simulation with growth only is the one where the inner region is the less dust-enriched, with ε < 10−1. One should note that dust has been lost to the star due to radial drift in the very inner region. On the contrary, the ones with fragmentation have ε ~ 2 × 10−1 at 0.6 au. Fragmentation helps grains to stay in the disc because their sizes become smaller the closer they are to the star, which means they will be more coupled to the gas and less prone to drift. With erosion only, the region between 0.6 and 1 au has ε ~ 10−1. Erosion can thus increase the local dust-to-gas ratio in the inner region, but it is not as efficient as fragmentation. Outside 2 au, the size profiles of all simulations are very similar, as neither fragmentation nor erosion affect dust growth.

These simulations support the results from our 1D simulations. Moreover, they show that when accounting for fragmentation, erosion is not present even with υfrag = 80 m s−1, which means it can be ignored during dust evolution and the growth of aggregates.

thumbnail Fig. 4

Comparison between simulations in the (r, s) plane at t = 100 yr with growth only (top left), growth and fragmentation (top right) with υfrag,Si = 80 m s−1, growth and erosion (bottom left), and growth, fragmentation, and erosion (bottom right). The colour gives the dust-to-gas ratio.

5 Discussion

5.1 Caveats

The main limitations arise from our model of dust growth, as we use a 3D code that eliminates most of the approximations done with the 1D Code PAMDEAS. However, since we use the mono-disperse approximation for dust growth, we do not track all the smaller grains ejected from larger bodies due to erosion. This is not very important, as we want to track the evolution of the largest grains, since fragmentation always appears before erosion. In addition, the mono-disperse approximation only considers collisions of equal-sized grains. Unequal-sized grains have relative settling and drifting velocities, acting as additional sources of collisions. The smoothed particle hydrodynamics (SPH) formalism naturally produces a spread in Av, resulting in a spread in υrel as well, similar to the velocity distributions in Windmark et al. (2012b); Garaud et al. (2013). Nevertheless, our approximation cannot account for high-mass-ratio collisions, which have been found to result in net growth even at υrel as high as 70 or 80 m s−1 (Teiser & Wurm 2009; Kothe et al. 2010; Windmark et al. 2012a; Wada et al. 2013; Meisner et al. 2013).

Aeolian erosion is a continuous process and one may wonder whether the discrete nature of particle collision hinders the comparison between both processes. This is not a problem in numerical simulations, in which time is incremented by a finite quantity, the time step. Even when the time between collisions is long, it is still much shorter than a single time step (e.g. Garcia & Gonzalez 2020). Both processes are thus taken into account simultaneously in our simulations.

Another issue is the fact that we do not take into account porosity in the model. This could play a role, as porous grains tend to form larger aggregates, while being less sensitive to fragmentation. A model of erosion taking into account porosity would be more precise in capturing dust evolution. However, we do not think this will change the results significantly because fragmentation will remain the limiting factor.

Lastly, in the erosion model, βeros is still not very well constrained for different kinds of material and more experimental measurements would be needed, although progress has been made in recent work (Demirci et al. 2020; Schönau et al. 2023). The model also assumes that all ejected grains have the same size, while in reality all sizes should be considered.

5.2 Importance of erosion

We see in this paper that fragmentation is always the first process to destroy grains before erosion for υfrag = 20 m s−1. Smaller fragmentation thresholds like 10 or 15 m s−1 only strengthen fragmentation, thus decreasing the effect of erosion, while larger fragmentation thresholds can be considered less realistic, both with α = 5 × 10−3 and α = 5 × 10−4. Moreover, we use the size sej = 1 mm adopted by R20 and G20, which makes erosion more effective. Therefore, we can safely say that erosion can be completely neglected in dust models when α = 5 × 10−3. For α = 5 × 10−4, the only fragmentation considered is υfrag = 20 m s−1, because higher υfrag are extremely similar to pure growth. The difference in sizes just before and after erosion in this case is also smaller, by an order of magnitude, reducing the impact of erosion on dust evolution. Finally, adding a pressure bump at 1 au did not help erosion to appear, despite the fact that grains grow up to one kilometre. Erosion can therefore be neglected in all cases when fragmentation is considered. For a very low-viscosity disc, erosion could still be ignored, as grain growth would be very slow and large sizes wouldn’t be reached. However, it is worth mentioning that if larger boulders or planetesimals are formed or captured, erosion would still be important in grinding them down in the inner disc region, as is discussed by Grishin et al. (2019); Rozner et al. (2020).

6 Summary and conclusion

In this paper, we discuss the importance of erosion in the evolution of dust in the protoplanetary disc. We first present the way we modelled radial drift in a 1D code in order to accurately capture the effect even if the disc is stationary and the gas is not evolving. We then present how erosion has been treated based on R20 and G20, giving the two important equations to implement in the codes. We also present the model that takes into account both growth and fragmentation from Stepinski & Valageas (1997), Laibe et al. (2008), Garcia (2018), Vericel et al. (2021), Michoulier & Gonzalez (2022). We performed some tests to be sure PAMDEAS reproduces some of the key results presented in R20 and G20. We then performed simulations with the same model implemented in both the PAMDEAS and PHANTOM codes. We show that erosion is negligible when fragmentation is taken into account with realistic fragmentation thresholds. Both codes give the same results. When considering a pressure bump, erosion is still not efficient in destroying grains. We then discuss the main caveats of this study and a discussion of the insignificance of erosion. To conclude, erosion can be neglected in models of dust evolution accounting for fragmentation, bouncing, or any other mechanism that limits the dust size to a couple of centimetres in the very inner region of a protoplanetary disc. Usually, such short distances of a fraction of au are not considered when doing simulations and erosion can be safely neglected from a dust evolution perspective.

Acknowledgements

We thank Daniel J. Price for useful discussion and advice and the anonymous referee for their suggestions. The authors acknowledge funding from ANR (Agence Nationale de la Recherche) of France under contract number ANR-16-CE31-0013 (Planet-Forming-Disks) and thank the LABEX Lyon Institute of Origins (ANR-10-LABX-0066) for its financial support within the Plan France 2030 of the French government operated by the ANR. This research was partially supported by the Programme National de Physique Stel-laire and the Programme National de Planétologie of CNRS (Centre National de la Recherche Scientifique)/INSU (Institut National des Sciences de l'Univers), France. We gratefully acknowledge support from the PSMN (Pole Scientifique de Modélisation Numérique) of the ENS de Lyon for the computing resources. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreements No 210021 and No 823823 (DUSTBUSTERS). Figures were made with the Python library matplotlib (Hunter 2007). The data necessary to recreate the PHANTOM simulations and to reproduce Fig. 4 are available in Michoulier et al. (2024).

References

  1. Auffinger, J., & Laibe, G. 2018, MNRAS, 473, 796 [Google Scholar]
  2. Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
  3. Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [Google Scholar]
  5. Brauer, F., Henning, T., & Dullemond, C. P. 2008, A&A, 487, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Demirci, T., Schneider, N., Steinpilz, T., et al. 2020, MNRAS, 493, 5456 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [Google Scholar]
  8. Drazkowska, J., Windmark, F., & Dullemond, C. P. 2014, A&A, 567, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Garaud, P., Meru, F., Galvagni, M., & Olczak, C. 2013, ApJ, 764, 146 [NASA ADS] [CrossRef] [Google Scholar]
  10. Garcia, A. 2018, Ph.D. Thesis, Université de Lyon, France [Google Scholar]
  11. Garcia, A. J. L., & Gonzalez, J.-F. 2020, MNRAS, 493, 1788 [Google Scholar]
  12. Gonzalez, J.-F., Laibe, G., Maddison, S. T., Pinte, C., & Ménard, F. 2015, Planet. Space Sci., 116, 48 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gonzalez, J.-F., Laibe, G., & Maddison, S. T. 2017, MNRAS, 467, 1984 [NASA ADS] [Google Scholar]
  14. Grishin, E., & Perets, H. B. 2015, ApJ, 811, 54 [NASA ADS] [CrossRef] [Google Scholar]
  15. Grishin, E., Perets, H. B., & Avni, Y. 2019, MNRAS, 487, 3324 [NASA ADS] [CrossRef] [Google Scholar]
  16. Grishin, E., Rozner, M., & Perets, H. B. 2020, ApJ, 898, L13 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gunkelmann, N., Ringl, C., & Urbassek, H. M. 2016, A&A, 589, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Heim, L.-O., Blum, J., Preuss, M., & Butt, H.-J. 1999, Phys. Rev. Lett., 83, 3328 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Kobayashi, H., & Tanaka, H. 2010, Icarus, 206, 735 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kothe, S., Güttler, C., & Blum, J. 2010, ApJ, 725, 1242 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kretke, K. A., & Lin, D. N. C. 2007, ApJ, 664, L55 [CrossRef] [Google Scholar]
  24. Laibe, G., Gonzalez, J. F., Fouchet, L., & Maddison, S. T. 2008, A&A, 487, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Li, R., Youdin, A. N., & Simon, J. B. 2019, ApJ, 885, 69 [NASA ADS] [CrossRef] [Google Scholar]
  26. Loren-Aguilar, P., & Bate, M. R. 2015, MNRAS, 453, L78 [CrossRef] [Google Scholar]
  27. Meheut, H., Keppens, R., Casse, F., & Benz, W. 2012, A&A, 542, A9 [Google Scholar]
  28. Meisner, T., Wurm, G., Teiser, J., & Schywek, M. 2013, A&A, 559, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Michoulier, S., & Gonzalez, J.-F. 2022, MNRAS, 517, 3064 [NASA ADS] [CrossRef] [Google Scholar]
  30. Michoulier, S., Gonzalez, J.-F., Grishin, E., & Petetin, C. 2024, https://doi.org/10.5281/zenodo.1079552 [Google Scholar]
  31. Okuzumi, S., Tanaka, H., & Sakagami, M.-a. 2009, ApJ, 707, 1247 [NASA ADS] [CrossRef] [Google Scholar]
  32. Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ormel, C. W., Spaans, M., & Tielens, A. G. G. M. 2007, A&A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Paraskov, G. B., Wurm, G., & Krauss, O. 2006, ApJ, 648, 1219 [NASA ADS] [CrossRef] [Google Scholar]
  35. Perets, H. B., & Murray-Clay, R. A. 2011, ApJ, 733, 56 [Google Scholar]
  36. Pfalzner, S., & Bannister, M. T. 2019, ApJ, 874, L34 [Google Scholar]
  37. Pfalzner, S., Paterson, D., Bannister, M. T., & Portegies Zwart, S. 2021, ApJ, 921, 168 [NASA ADS] [CrossRef] [Google Scholar]
  38. Price, D. J., Wurster, J., Tricco, T. S., et al. 2018, PASA, 35, e031 [Google Scholar]
  39. Ringl, C., Bringa, E. M., Bertoldi, D. S., & Urbassek, H. M. 2012, ApJ, 752, 151 [NASA ADS] [CrossRef] [Google Scholar]
  40. Rozner, M., Grishin, E., & Perets, H. B. 2020, MNRAS, 496, 4827 [NASA ADS] [CrossRef] [Google Scholar]
  41. Schäfer, U., Yang, C.-C., & Johansen, A. 2017, A&A, 597, A69 [Google Scholar]
  42. Schönau, L., Teiser, J., Demirci, T., et al. 2023, A&A, 672, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  44. Shao, Y., & Lu, H. 2000, J. Geophys. Res., 105, 22437 [NASA ADS] [CrossRef] [Google Scholar]
  45. Stepinski, T. F., & Valageas, P. 1997, A&A, 319, 1007 [NASA ADS] [Google Scholar]
  46. Suyama, T., Wada, K., & Tanaka, H. 2008, ApJ, 684, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  47. Tanaka, H., Inaba, S., & Nakazawa, K. 1996, Icarus, 123, 450 [Google Scholar]
  48. Tatsuuma, M., & Kataoka, A. 2021, ApJ, 913, 132 [CrossRef] [Google Scholar]
  49. Teiser, J., & Wurm, G. 2009, MNRAS, 393, 1584 [NASA ADS] [CrossRef] [Google Scholar]
  50. Vericel, A., & Gonzalez, J.-F. 2020, MNRAS, 492, 210 [NASA ADS] [CrossRef] [Google Scholar]
  51. Vericel, A., Gonzalez, J.-F., Price, D. J., Laibe, G., & Pinte, C. 2021, MNRAS, 507, 2318 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wada, K., Tanaka, H., Okuzumi, S., et al. 2013, A&A, 559, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
  54. Weidenschilling, S. J., & Cuzzi, J. N. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine (Tucson: University of Arizona Press), 1031 [Google Scholar]
  55. Whipple, F. L. 1972, in From Plasma to Planet, ed. A. Elvius (New York: Wiley), 211 [Google Scholar]
  56. Williams, J. P., & Best, W. M. J. 2014, ApJ, 788, 59 [Google Scholar]
  57. Windmark, F., Birnstiel, T., Güttler, C., et al. 2012a, A&A, 540, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Windmark, F., Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2012b, A&A, 544, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Wurm, G., Blum, J., & Colwell, J. E. 2001, Phys. Rev. E, 64, 046301 [NASA ADS] [CrossRef] [Google Scholar]
  60. Yang, C.-C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
  62. Youdin, A., & Johansen, A. 2007, ApJ, 662, 613 [Google Scholar]
3

It is worth noting that our definition of fragmentation aligns with the point at which half of the mass is lost. However, it’s important to acknowledge that other definitions exist. For example, Ringl et al. (2012); Gunkelmann et al. (2016) define fragmentation as the moment when at least one monomer is ejected from the main aggregate. We refer to the loss of grain mass when it’s less than half of the initial mass aserosion.

All Figures

thumbnail Fig. 1

Validation tests. Left: time evolution of the size, s, of different aggregates as they are eroded. The vertical turnover in the profile gives the characteristic erosion time. The aggregates are kept at a fixed distance of 1 au from the star, and the ejected dust has a size of 100 µm. Dashed lines represent data from R20, which are in excellent agreement with our results. Right: Stokes number at the erosion threshold for aggregates drifting towards the star and four different sizes of ejected grains. Dotted lines represent the analytical solution presented in G20.
In the text
thumbnail Fig. 2

1D dust evolution. Left: evolution of the size, s, of grains experiencing growth and erosion only, as they grow and drift inwards from different initial distances, r, from the star. The colour represents the Stokes number. The dashed grey line represents the evolution without erosion, while the green, orange, and red lines represent the evolution with growth and fragmentation, using a fragmentation threshold of 20, 40, and 80 m s−1, respectively. The size of the ejected grains is sej = 1 mm, a typical value used by R20 and G20. Right: same as the left panel, but with a pressure maximum that traps dust at 1 au.
In the text
thumbnail Fig. 3

Same as Fig. 2, but with α = 5 × 10−4 and only one fragmentation threshold.
In the text
thumbnail Fig. 4

Comparison between simulations in the (r, s) plane at t = 100 yr with growth only (top left), growth and fragmentation (top right) with υfrag,Si = 80 m s−1, growth and erosion (bottom left), and growth, fragmentation, and erosion (bottom right). The colour gives the dust-to-gas ratio.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.