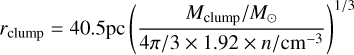| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202348349 | |
| Published online | 04 June 2024 | |
First detection of the [CII] 158 µm line in the intermediate-velocity cloud Draco
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
e-mail: nschneid@ph1.uni-koeln.de
2
Physikalischer Verein, Gesellschaft für Bildung und Wissenschaft,
Robert-Mayer-Str. 2,
60325
Frankfurt,
Germany
3
SOFIA Science Center, NASA Ames Research Center,
Moffett Field,
CA
94 045,
USA
4
Laboratoire d’Astrophysique de Bordeaux, Université de Bordeaux, CNRS,
B18N,
33615
Pessac,
France
5
Max-Planck Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
6
University of Applied Sciences Bonn-Rhein-Sieg,
Grantham-Allee 20,
53757
Sankt Augustin,
Germany
7
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
Received:
23
October
2023
Accepted:
7
March
2024
High-latitude intermediate-velocity clouds (IVCs) are part of the Milky Way’s H I halo and originate from either a galactic fountain process or extragalactic gas infall. They are partly molecular and can most of the time be identified in CO. Some of these regions also exhibit high-velocity cloud gas, which is mostly atomic, and gas at local velocities (LVCs), which is partly atomic and partly molecular. We conducted a study on the IVCs Draco and Spider, both were exposed to a very weak UV field, using the spectroscopic receiver upGREAT on the Stratospheric Observatory for Infrared Astronomy (SOFIA). The 158 µm fine-structure line of ionized carbon ([C II]) was observed, and the results are as follows: In Draco, the [C II] line was detected at intermediate velocities (but not at local or high velocities) in four out of five positions. No [C II] emission was found at any velocity in the two observed positions in Spider. To understand the excitation conditions of the gas in Draco, we analyzed complementary CO and H I data as well as dust column density and temperature maps from Herschel. The observed [C II] intensities suggest the presence of shocks in Draco that heat the gas and subsequently emit in the [C II] cooling line. These shocks are likely caused by the fast cloud’s motion toward the Galactic plane that is accompanied by collisions between H I clouds. The nondetection of [C II] in the Spider IVC and LVC as well as in other low-density clouds at local velocities that we present in this paper (Polaris and Musca) supports the idea that highly dynamic processes are necessary for [C II] excitation in UV-faint low-density regions.
Key words: ISM: clouds / evolution / ISM: general / ISM: molecules / photon-dominated region (PDR) / ISM: structure
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The formation of molecular clouds is commonly defined as the transition of atomic to molecular hydrogen in the interstellar medium (ISM). In steady-state and chemical equilibrium models (Tielens & Hollenbach 1985; van Dishoeck & Black 1988; Sternberg & Dalgarno 1989; Krumholz et al. 2008), the formation of H2 depends mostly on the local radiation field (dissociation of H2 by photons in the Lyman-Werner bands versus H2 formation on dust grains) and H2 shielding efficiencies. In a more dynamic scenario, H2 formation is also governed by turbulent mixing motions in the ISM (Glover & Mac Low 2007; Bialy et al. 2017) that cause large- and small-scale density fluctuations. In these dynamical models of molecular cloud formation, H2 formation happens in shock-compressed layers in converging H I flows in the warm neutral medium (Walder & Folini 1998; Klessen et al. 2000; Heitsch et al. 2006; Vázquez-Semadeni et al. 2006; Dobbs 2008; Clark et al. 2012). This dynamic, turbulent scenario reduces the H2 formation times from a few 10 Myr to a few Megayears (Glover & Mac Low 2007; Valdivia et al. 2016). The flows are driven by the complex interplay between gravity and stellar feedback effects. Additionally, they are influenced by the thermodynamic response of the multiphase ISM.
However, the observation of these large-scale flows presents a challenge due to the selective nature of CO molecule formation. Notably, CO only becomes apparent at the shocked stagnation points within the broader turbulent flow, making the H I and H2 gas “CO-dark”. In a recent study by Schneider et al. (2023), it was demonstrated that the 158 µm line of ionized carbon (see below) can effectively characterize this component and unveil high-velocity H I flows within the Cygnus X region.
The formation of H2 and CO critically depends on the local interstellar radiation field1 and self-shielding efficiencies. In plane-parallel photodissociation region (PDR) models for low-column density2, the transition typically takes place at values of Aeff,V ≈ 0.3 for H2 (Röllig et al. 2007; Glover et al. 2010; Sternberg et al. 2014; Bisbas et al. 2019; Schneider et al. 2022). We note that the model Aeff,V is the local visual extinction at each point in the cloud and not directly comparable to the AV that is an average along the line of sight (Seifried et al. 2022). This is why it is difficult to observationally trace the H I -to-H2 transition, though it has been the subject of a number of observational studies using various tracers (Imara & Burkhart 2016).
The thermal state of the gas is mostly regulated by photoelectric heating and cooling through dust and collisionally excited emission from far-infrared (FIR) molecular and atomic fine-structure lines. Nevertheless, cooling rates exhibit only a weak dependence on temperature for T < 104 K. Consequently, the cooling process driven by atomic fine-structure lines (primarily the [C II] 158 µm line) induces a thermal instability, giving rise to a multiphase ISM (Field et al. 1969; Wolfire et al. 1995). This multiphase ISM includes a volume-filling warm neutral gas (referred to as the H I WNM) characterized by temperatures around T ~ 8000 K and densities of n ~ 1 cm−3 in pressure equilibrium with the cold neutral medium (CNM) exhibiting temperatures of approximately T ~ 30–100 K and densities of n ~ 50–100 cm−3 within the atomic phase. The ISM also encompasses H2 gas with temperatures typically below 30 K and densities n exceeding a few hundred cm−3. Observing gas in these thermally unstable conditions poses a considerable challenge.
One tracer for the gas conditions in very different physical environments is the [C II] 158 µm line. It serves as a cooling line for gas over a large range of temperatures, typically T ~ 100 K, and densities, typically above a few 103 cm−3, in PDRs (Hollenbach et al. 1991; Ossenkopf et al. 2013) and at much lower temperatures (around 20 K) in CO-dark but H2-rich regions (Wolfire et al. 2010; Schneider et al. 2023) and can also arise from the warm ionized medium and from diffuse atomic gas at lower densities (Pineda et al. 2013; Beuther et al. 2014; Kabanovic et al. 2022). The transition from ionized carbon (C+) to CO occurs deeper in the cloud, typically at Aeff,V ~ 1 (Lee et al. 1996; Visser et al. 2009; Glover et al. 2010; Seifried et al. 2020). Here, the photodissociation of CO by FUV photons dominates over the production reaction (Wolfire et al. 2010; Clark et al. 2012; Glover et al. 2015). The [C II] 158 µm line is easy to excite thermally by collisions with electrons and atomic and molecular hydrogen. The critical density, defined by the collisional de-excitation rate being equal to the effective spontaneous decay rate, depends on the temperature. It is 9 cm−3, 3 × 103 cm−3, and 6.1 × 103 cm−3 for collisions with e−, H, and H2, respectively, for gas temperatures ≲ 100 K (Goldsmith et al. 2012). In diffuse gas, the excitation temperature of [C II], which can go down to less than 20 K (Kabanovic et al. 2022), is notably lower than the kinetic temperature because the densities are too low to produce a collisional excitation rate comparable to the spontaneous decay rate (Goldsmith et al. 2012). In addition, the [C II] line can also serve as a cooling line in low to moderate velocity C-type shocks with a low incident UV field (Lesaffre et al. 2013). The authors developed models of low-UV irradiated low and moderate (up to 40 km s−1) C- and J-type shocks and compared the results with observations. They concluded that [C II] is a good tracer for the dissipation of kinetic and magnetic energy in weakly shielded gas where it is the dominant carbon species.
While there is an increasing number of studies focusing on [C II] emission in bright PDRs, [C II] studies of diffuse, translucent, and low-column density clouds3, are relatively scarce. In a work conducted by Goldsmith et al. (2018), a limited number of diffuse interstellar clouds were observed using H I absorption features measured against a background quasar. This approach allowed for the sampling of the entire line of sight through the Galaxy. The researchers concluded that photoelectric heating stands out as the predominant heating mechanism for these clouds, with the [C II] line being the principal cooling line.
In this study, we present novel observational findings pertaining to [C II] and CO emissions within the Draco and Spider high-latitude diffuse clouds. We utilized archival [C II] and CO data concerning the quiescent Polaris cloud and the low-density Musca molecular cloud. All of these clouds are subject to a low-incident UV field, which is, depending on the method used to infer the UV radiation field, between ~1.5 to ~10 Go. The [C II] emission line has been exclusively detected in the intermediate-velocity cloud Draco, with no detection observed at local velocities in the Spider, Polaris, and Musca clouds. A comprehensive comparison of the physical characteristics across these distinct clouds was conducted using models of PDR emission, shocks, and non-LTE (Local Thermodynamic Equilibrium) conditions, leading to an argument in favor of shock excitation as the most plausible rationale for the presence of [C II] within the Draco cloud. This deduction is based on the cloud’s high-velocity descent toward the Galactic plane and its interaction between H I clouds. Consequently, this highlights the significance of dynamics in influencing the chemical evolution within interstellar clouds.
We start with a description of the sources (Sect. 2) and the observations (Sect. 3). The observations are presented in Sect. 4 and analyzed in Sect. 5. Section 6 provides a discussion of the results, and Sect. 7 presents a summary of the paper.
2 The observational cloud sample
Draco and Spider are both part of the interstellar cirrus, associated with diffuse H I clouds (Heiles & Habing 1974). Draco constitutes a relatively isolated feature, containing gas concentrated within local, intermediate, and high-velocity clouds, referred to as LVC, IVC, and HVC, respectively. The distances to the IVC and LVC were established to be within the range of 463–618 pc by Gladders et al. (1998) through the utilization of sodium doublet absorption. In a recent study, Zucker et al. (2020) employed Gaia DR2 parallax measurements to deduce a distance of 481 ± 50 pc, a value we will adopt in this paper. Spider and Polaris are situated within the North Celestial H I Loop (Meyerdierks et al. 1991). Using Gaia data, Zucker et al. (2020) determined distances ranging from 341 to 472 pc (with uncertainties between 10 and 40 pc) for three locations close to the Polaris cloud. It is important to note that these locations are distant from the area of the [C II] observation, which primarily focuses on the brightest region evident in dust and CO emissions. An additional Gaia-based study by Yan et al. (2019) reports a distance of 489 pc. These distances surpass earlier estimates. Heithausen & Thaddeus (1990) discussed various potential distances to Polaris and proposed an upper limit of 240 pc, while Falgarone et al. (2009) employed a distance of 150 pc. In order to maintain consistency with our prior work on dust column density probability distribution functions (Schneider et al. 2022), the results of which will be employed herein, we opt for adopting a distance of 489 pc. For Spider, Zucker et al. (2020) determined a value of 369 ± 18 pc (we will use here) for the distance which places this region further away than earlier estimated of around 100 pc (de Vries et al. 1987). Musca is located in the southern Chamaleon-Musca cloud complex. Distances between 140 and 225 pc are reported (Franco 1991; Knude & Hog 1998; Bonne et al. 2020b). We here adopt a value of 150 pc to be consistent with Schneider et al. (2022). It is not straightforward to give an error range of this value, see Appendix A in Bonne et al. (2020b). The reddening of stars due to cloud material starts at 90 pc and reaches its peak at ≈180 pc. It is, however, difficult to assess at which distance the gas of the Musca filament is located.
Figure 1 provides an overview of the Herschel 250 µm map of Draco, outlined by a white dashed square, situated within a larger scale Planck map at the same wavelength (left panel). Additionally, the right panel depicts H I emission across the intermediate and low velocity range spanning from −60 to 30 km s−1. Notably, the velocity structure within the H I data becomes even more intricate when dissecting the velocity ranges. Refer to Fig. A.1 for a depiction of faint gas emission at local velocities ranging between −10 and 30 km s−1, a prominent component representing intermediate velocities spanning from −30 to −10 km s−1 , and focused emission at high velocities ranging from −200 to −100 km s−1. Figure 2 shows the combined Herschel and Planck 250 µm map for the Spider region where distinct LVC (−10 to 30 km s−1) and IVC (−80 to −10 km s−1) components are observable, although no HVC is apparent. It is important to highlight that Draco stands out as the only region dominated by H I emission of the IVC, whereas Spider solely exhibits a weak IVC component. Furthermore, Polaris and Musca exclusively feature gas at local velocities, derived from CO observations, which correspond to H I emission velocities of −3.7 km s−1 and 3 km s−1, respectively.
Draco (IVC G091.0+38.0, MBM41) is located at b = 38.4° at a height of around 298 pc above the Galactic plane, considering a distance of 481 pc. There are no OB stars in the immediate environment, but there is noteworthy 160 µm flux in the Herschel map. Emission at 70 µm is at the noise level. Assuming that the dust is only heated by external FUV radiation of stars, the 160 µm flux can be translated into a FUV field (see Sect. 5.1) and we derive a field of 3.6 Go averaged over the 4 positions (the average FUV field is 1.6 Go from a census of the stars).
It has been recognized for quite some time (Mebold et al. 1985) that the IVC descends toward the Galactic plane with a significant velocity and experiences deceleration due to its interaction with the surrounding warm neutral medium. Notably, observations have revealed high FIR emissivities and elevated CO abundances (Herbstmeier et al. 1993), which were interpreted as arising from a direct interaction with the HVC. This high-velocity gas could originate from the infall of extragalactic material. However, recent H I surveys (Westmeier 2018) have identified a velocity gap between the IVC and the HVC in Draco (Fig. B.1), rendering a collision scenario less plausible. Furthermore, the Draco region prominently exhibits emissions at intermediate velocities. A proposed explanation for Draco’s origin involves a Galactic fountain process, where material from the Galactic disk is lifted above the plane and subsequently returns at high velocities to the disk (as elaborated in Lenz et al. 2015 and references therein). For a more comprehensive discourse on the underlying physics and potential sources of IVCs, readers are encouraged to explore Putman et al. (2012), Röhser et al. (2014, 2016a,b), Kerp et al. (2016), and the accompanying references.
By investigating probability distribution functions of H I (NHI-PDF) and of Herschel derived total hydrogen column density (N-PDFs), Schneider et al. (2022) showed that the N-PDF of Draco has the form of a double-log-normal. The authors propose that one log-normal arises from atomic gas and the other one from molecular gas. The H I-to-H2 transition is defined where the two log-normal dust N-PDFs have equal contributions and takes place at AV = 0.33 (N(H) = 6.2 × 1020 cm−2). Importantly, the absence of a power-law tail in the distribution implies that self-gravity does not currently play a significant role in the region. Nevertheless, certain regions within Draco have exhibited detections of [C I], CO, and other molecules with critical densities exceeding 103 cm−3 (Mebold et al. 1985; Herbstmeier et al. 1993) and are thus mostly molecular. Furthermore, Miville-Deschênes et al. (2017), utilizing Herschel dust observations, inferred that the molecular gas primarily comprises small (~0.1 pc), dense (n ~1000 cm−3), and cold (T ~ 10–20 K) clumps. Despite the presence of such molecular structures, no indications of active star formation have been observed within the cloud, as evidenced by the lack of detected pre- or proto-stellar cores.
In contrast to Draco, the Spider region has received significantly less attention. Barriault et al. (2010a,b) presented maps of H I, OH, and CO emission and concluded that around 20% of the gas exists in the molecular phase. CO, serving as a tracer of CO-bright H2, is found where two H I velocity components merge into one component or where there is a velocity shear. Barriault et al. (2010b) derived an upper limit for the volume density of 2 × 103 cm−3. The Herschel dust and Effelsberg H I emission distributions, shown in in Fig. 2, support qualitatively this idea because the densest parts of the Spider cloud are located in the center of various flows. As already pointed out, in contrast to Draco, H I emission in Spider is dominated by the LVC and not the IVC (see Fig. A.2) and has no HVC component. Similarly to Draco, we derive the FUV field from the 160 µm flux, assuming radiative excitation, yielding a maximum value of 2.9 Go.
The Polaris flare exhibits abundant extended, diffuse emission previously observed through IRAS at 100 µm (Low et al. 1984), and now unveiled in large detail using Herschel (Miville-Deschênes et al. 2010). The most densely concentrated region, MCLD 123.5+24.9, referred to as the ‘saxophone’, has been scrutinized across various CO lines (Heithausen & Thaddeus 1990; Falgarone et al. 1998), as well as in [C I] (Bensch et al. 2003), housing a handful of prestellar cores. The peak column density at the core positions ranges from 6 to 13 × 1021 cm−2 (Ward-Thompson et al. 2010). The density at this position, which coincides with our [C II] position, is derived to be between 2 and 5 × 104 cm−3 from CO, HCN, and Herschel FIR data (Grossmann & Heithausen 1992; Heithausen et al. 1995; Ward-Thompson et al. 2010). The incident FUV field at the cloud’s location was estimated to be approximately one Go (Bensch et al. 2003). By leveraging the methodology that converts the 160 µm flux to a FUV field, we ascertain a field strength of around ~1.5 Go at the precise coordinates of the [C II] observation site. In an earlier investigation, Heithausen & Thaddeus (1990) approximated that roughly 40% of the hydrogen in the Polaris flare is molecular. Consequently, it follows that this cloud is more advanced in its evolutionary stage compared to Draco and Spider, supported by its N-PDF (Schneider et al. 2013, 2022).
Musca is located in the south, embedded in the extended Chameleon complex. It presents itself as a prominent filamentary structure extending over 6 pc, as illustrated in previous works (Kainulainen et al. 2009, 2016; Cox et al. 2016), yet exhibits minimal star-formation activity. Notably, a sole protostar has been identified in the northernmost part of the filament, while the cloud remains relatively unaffected by protostellar feedback. The external FUV field is approximated to be 3.4 Go as an upper limit (without considering extinction), as deduced from an analysis of neighboring stars (Bonne et al. 2020b,a). Alternative estimates place the FUV field at 5.8 Go based on the 160 µm flux and roughly 10 Go according to the Musca map featured in Xia et al. (2022). Within the dense crest region, peak column densities surpass those observed in Polaris, reaching N ~ 1022 cm−2 (Cox et al. 2016) at the position of the protostar. In all other locations, the column densities are smaller than 8 × 1021 cm−2 and the (column)-densities are also notably lower at the exact location of the [C II] observation. The volume density at this position is at least 7 × 103 cm−3, based on CO and [C I] observations presented in Bonne et al. (2020a). They performed a non-LTE analysis of the observed tracers and obtained this density for the warm gas layer slightly outside of the denser (up to 104 cm−3) Musca ridge.
 |
Fig. 1 FIR and H I maps of Draco. Left: combined Herschel and Planck 250 µm map of the Draco cloud and its environment. The offsets in degrees correspond to the center position of RA(2000) = 16h47m57s, Dec(2000) = 61°45′16″ (l = 91.829, b = 38.156). The angular resolution of the Herschel map (in the image center) is 36″ and the one of the Planck map is ~5′. The white dashed square indicates the area for which we show the dust column density map. Right: velocity integrated H I map from the Eſſelsberg H I survey (EBHIS) at 10′ resolution. The velocity range covers the IVC and LVC. Maps of the other velocity ranges are shown in Appendix A. |
 |
Fig. 2 Same as Fig. 1 but for Spider. The offsets correspond to the center position of RA(2000) = 10h37m58s, Dec(2000) = 72º59′42″ (l = 135.200, b = 40.800). |
3 Observations
3.1 SOFIA
Draco was observed during Cycle-5, both within guaranteed time and open time allocations, under the program number 05_0208, with N. Schneider as the principal investigator (PI). A total of five positions were targeted for observation, with their coordinates provided in Table 1, and their locations given in Fig. 3. These observations took place over the course of three flights utilizing the Stratospheric Observatory for infrared Astronomy (SOFiA), operating from Palmdale, California. Among the selected positions, two were situated at peaks in dust column density in the southern region, designated as Nose 1 and Nose 2. These locations had previously exhibited detections of CO (refer to Fig. 4 for our CO spectra) and other molecular lines. Additionally, two positions were chosen within the eastern region, labeled as Front 1 and Front 2. it is noteworthy that all these positions display prominent H I emission within the IVC and LVC velocity ranges. in contrast, the position denoted as IVC is positioned farther away from the regions of high column density.
This position is exclusively discernible within the IVC and HVC velocity range.
The Front 1 position was observed on November 8, 2016, using the GREAT instrument (Heyminck et al. 2012). The 7-pixel GREAT/LFA array was tuned to the [C II] 158 µm line, and the single-pixel L1 channel was tuned to the [N II] 1.461 THz line. This observation was repeated, and another position (Nose 1) was added on February 3, 2017, employing upGREAT (Risacher et al. 2018). The 2 × 7 pixels LFA array was again tuned to the [C II] 158 µm line, and the L1 channel on the [N II] 1.461 THz line. Three further positions (Nose 2, Front 2, and IVC) were observed on February 14, 15, 16, and 17, 2017, in the same upGREAT/LFA setup, but tuning the L1 channel to the CO 11 → 10 line at 1.1 THz. All observations were carried out in total power mode, and different emission-free positions with offsets of typically 10′–15′ to the center positions were used. The total observing time for each position (ON+OFF) was typically one hour. Beam efficiencies used in this paper were determined using Mars as a calibrator for each pixel; the average is 0.64 for the LFA and 0.65 for L1. Third-order spectral baselines were applied to the LFA/L1 spectra and then averaged with a fixed velocity axis and 1/rms2 weighting, smoothed to a channel width of 0.6 km s−1. The main beam sizes are 19″ at 1.1 THz, 17″ at 1.4 THz, and 14.1″ at 158 µm, respectively.
Spider was observed during Cycle-6 under the program number 06_0153 (PI N. Schneider). The observations were carried out on May 23, 2018, from Palmdale, California, using upGREAT on SOFIA. The upGREAT/LFA array (2 × 7 pixels) was tuned to the [C II] 158 µm line, and the HFA array (7 pixels) was tuned to the [O I] 63 µm line. Two pointings were performed in total power mode, centering on positions Spider 1 at RA(2000) = 10h40m59s, Dec(2000) = 73°22′21″, and Spider 2 at RA(2000) = 10h33m58s (Fig. 5), Dec(2000) = 73°56′12″. The reference positions were located at an offset of 15′ east of the center positions. Spider 1 is identical with ‘S3’ in Barriault et al. (2010a) and represents the peak of IR emission at 100 µm. Spider 2 coincides with position ‘S6’ in Barriault et al. (2010a) and has peak emission in the atomic phase. The total observing time for each position (ON+OFF) was typically one hour. The determination of beam efficiencies was accomplished by utilizing Mars as a calibrator for each pixel. The calculated averages are 0.64 for the Low-Frequency Array (LFA) and 0.66 for the High-Frequency Array (HFA). For the LFA/HFA spectra, baseline corrections of the first and third orders were applied. The corrected spectra were then subjected to averaging, employing a fixed velocity axis and a weighting scheme of 1/rms2. Further refinement was achieved by smoothing to a channel width of 0.6 km s−1. The physical dimensions of the main beams are 6.3″ at a wavelength of 63 µm and 14.1″ at 158 µm, respectively.
We also use archival [C II] data from a SOFIA PI-program on Polaris (Cycle-5, 75_0020 PI W. Reach) and Musca (Cycle-6, 06_0177, PI S. Bontemps).
In the Polaris flare a single position-switch pointing at RA(2000) = 01h59m32.0s, Dec(2000) = 87°39′41.0″ was performed 2017 June 14 from Palmdale, California, in the LFA/HFA configuration with the [C II] 158 µm line and the [O I] 63 µm line, respectively. The reduced data on a main beam brightness temperature scale were taken from the SOFIA archive4. The position corresponds to the ‘core 4’ position in Ward-Thompson et al. (2010) within the MCLD 123.5+24.9 region.
Musca was observed 2018 June from Christchurch, New Zealand. A single pointing in position-switch at RA(2000) = 12h24m41.6s, Dec(2000) = −71°46′41.0″ was carried out in the same [C II] and [O I] configuration as for Polaris. The total duration of the observations was 70 min. No line was detected in [C II] or [O I] in the individual array spectra (see Fig. A.1 in Bonne et al. 2020b).
Observational parameters for the [C II] data.
3.2 (Sub)Millimeter line data
For Draco and Spider, we utilized unpublished CO data acquired at the IRAM 30 m telescope in 2017 and 2018 for two projects (002-17, led by PI: Q. Salome; 003-18, led by PI: J. Kerp).
In August 2017, we conducted small-scale maps in the 12CO and 13CO 1→0 and 2→1 lines, centered on the five SOFIA positions in Draco, employing the EMIR E090 and E230 receivers in frequency-switching mode. In this study, we leveraged 13CO 2→1 observations from all positions and all CO data for the Front 2 and Nose 2 positions from this program, as they were excluded from the 2018 observing campaign. All data were smoothed to a velocity resolution of 0.5 km s−1 for the 1→0 line observations and 0.25 km s−1 for the 2→ 1 line to match the 2018 observations.
In July 2018, the observation focus shifted to other regions in Draco. Nevertheless, we conducted small-scale maps around the Front 1 position (110″×110″) and the Nose 1 position (400″ × 400″). For Spider, a map of dimensions 140″ × 140″ was obtained around the Spider 1 position, while Spider 2 involved a single extended integration. All observations were performed in total power mode with a reference position situated 33′ east of the map center. We used the EMIR E090 and E230 receivers in parallel, tuned to the 12CO 1→0 and 2→1 lines at 115.271 GHz and 230.538 GHz, respectively, ensuring that the 13CO 1→0 line fell within the bandpass. As the backend, we utilized the Fourier Transform Spectrometer (FTS) in a configuration that yielded velocity resolutions of 0.51 and 0.53 km s−1 for the 12CO and 13CO 1→0 data, and 0.25 km s−1 for the 12CO 2 → 1 data. The beamsize of the CO 2→1 data is 11″ and of the CO 1 →0 data 22″. In this study, we incorporated all CO data from the Front 1, Nose 1, and IVC positions, as well as the CO data from Spider, which was not covered in 2017. The Front 1 and Nose 1 positions were also observed in 2017, and the spectra exhibit consistent line positions and intensities. All data are presented on a main beam brightness temperature scale (using main beam efficiencies5 of 0.78 at 115 GHz and 0.59 at 230 GHz).
For Polaris, we use data from the IRAM key-project “Small-scale structure of pre-star forming regions” (PIs E. Falgarone, J. Stutzki). The data were made available via the Centre de données astronomique Strasbourg (CDS). We here only employ spatially smoothed isotopomeric CO 2→1 and 1 → 0 spectra extracted for the [C II] position (the maps are all large enough to allow for smoothing to 70″). For more details on the observations see Falgarone et al. (1998). For Musca, we use CO data presented in Bonne et al. (2020b,a) that stem from various CO observing runs at the APEX telescope. For technical details we refer to the relevant papers given above. In order to allow for a comparison to the array-averaged [C II] data, we smoothed all CO spectra for all sources to a beam of 70″.
For one position in Draco (Nose 1), we use integrated intensities of the 1 → 0 line of atomic carbon ([C I]) at 490 GHz, given in Table 1 in Heithausen et al. (2001) that stem from observations performed with the Heinrich-Hertɀ telescope (HHT) located on Mount Graham in Arizona. Four positions in Draco were covered, with one observations (0″, 0″) very close to our Nose 1 position and the others in steps of 30″ offset in x-direction. The beamsize of the HHT at 490 GHz is 16″ and thus smaller than what we use here to compare line intensities and ratios (70″). However, the [C I] line intensity does not change significantly over the range of 0 to 90″ so that we can assume to first order a beam filling of unity. This will be important for the PDR modeling.
 |
Fig. 3 Spectra and column density map of Draco. Right panel: Herschel hydrogen column density map derived from dust in color in which the observed [C II] positions are indicated with black crosses. In the panels around, spectra of the [C II] 158 µm line and the H I 21 cm line (DRAO), both at ~1′ resolution, are displayed. We note that the H I line was reduced for better visibility. The green curve indicates a single Gaussian fit to the [C II] line. |
 |
Fig. 4 Spectra of [C II] and CO emission at the 4 positions. For better visibility of the [C II] spectra, only the Gaussian fit is shown (in green) and the 12CO line intensities were reduced by a factor of 10. |
 |
Fig. 5 Spectra and column density map of Spider. Right panel: Herschel hydrogen column density map derived from dust in color in which the observed [C II] positions are indicated with black crosses. Left panels: Spectra of the [C II] 158 µm, CO, and H I (DRAO) lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
3.3 Complementary data sets
We use publicly available6 observations of the H I 21 cm line (1420 MHz) for the Draco and Spider regions from the DRAO Synthesis Telescope and the Green Bank Telescope (GBT; Blagrave et al. 2017). The data have an angular resolution of 1′ and a velocity resolution of 1.32 km s−1 for a channel spacing of 0.824 km s−1 and comprise a total velocity range of −103 to 33 km s−1 for Draco and −164 to 44 km s−1 for Spider.
Additionally, we make use of the all-sky H I data from the Effelsberg-Bonn HI survey (Winkel et al. 2016) at an angular resolution of ~10′. The EBHIS survey7 is a joined project of the AIf A and the MPIfR to image the neutral hydrogen content of the Milky Way galaxy and trace extragalactic sources. The spectra have a channel width of 1.3 km s−1, the rms noise is less than 90 mK, and the data is corrected for stray radiation (Röhser et al. 2014). We obtained fits data cubes from the CDS.
4 Results
4.1 Draco
Figure 3 displays the total hydrogen column density map at 36″ of Draco, derived from Herschel dust flux maps (Schneider et al. 2022). The positions observed in [C II] with SOFIA and CO with the IRAM 30 m telescope are indicated. The [C II] spectra, averaged over the entire array for each position, resulting in an effective angular resolution of 70″, are shown in the surrounding panels, along with H I spectra from the DRAO survey. Figure 4 presents the [C II] spectra alongside various CO isotopologues and transitions (12CO and 13CO 1→0 and 2→1), all at an angular resolution of 70″. The IVC position is not displayed due to the absence of a [C II] detection. Table 2 provides the observed [C II] main beam brightness temperature, line position and width, and line-integrated intensity resulting from a single Gaussian line fit. Additionally, it includes the total hydrogen column density and dust temperature from Herschel, both measured within a 70″ beam. Table 3 lists the main beam brightness temperatures, line positions and widths, and line-integrated temperatures for the 12CO and 13CO 2→1 and 1 → 0 lines, derived from Gaussian fits with two components. The [C II] line was detected at a level of 0.1–0.2 K, corresponding to a S/N of 3–5 (Table 1), within velocities ranging from −22 to −26 km s−1 at four out of the five positions. Only the IVC position did not exhibit a [C II] line above the noise threshold. Neither the [N II] nor the [O I] line or the CO 11 → 10 line were detected at any position.
While the CO and H I spectra exhibit a complex line shape characterized by at least two distinct components, the [C II] line corresponds to one of these velocity components (Front 1a at −25.6 km s−1, Front 2a at −22.4 km s−1), Nose 1 at −23.9 km s−1, and Nose 2 at −24.9 km s−1). The −22 km s−1 component is evident in both CO and H I spectra for both Front 1 and Front 2 positions. However, the Front 2 position displays an additional component ranging from −18 to −20 km s−1 in both H I and CO spectra. In contrast, no significant velocity difference is discernible between the two nose positions. Overall, the H I line exhibits larger width compared to the [C II] and CO lines. The distinct components of the CO lines are unmistakably distinct velocity features and are not attributed to self-absorption effects. This assertion is supported by the observation that the optically thin 13CO lines present the same two-component line profile.
Physical parameters of Draco for the five observed positions.
Draco’s CO line parameters determined from a Gaussian line fit with two velocity components.
4.2 Spider
Figure 5 presents a map of the total hydrogen column density in Spider at a resolution of 36″, utilizing Herschel dust observations. This methodology is the same as the one employed for Draco, as described in Schneider et al. (2022). The plot identifies the positions observed for [C II] using SOFIA and for CO using the iRAM 30 m telescope. The left panels display the CO and H I DRAO spectra, while Table 4 provides a summary of observations from SOFiA, Herschel, and iRAM 30 m. No emission in CO or [C II] within the IVC or LVC velocity ranges is detected at the Spider 2 position. The column density is notably low, measuring 2.4 × 1020 cm−2 (within a ~1′ beam). In Spider 1, narrow 12CO 1→0 and 2→1 lines in the LVC were observed. A prominent velocity component at 4.2 km s−1 is evident, with a corresponding main beam brightness of Tmb = 1.6 K for 12CO 1→0, along with a weaker component at 1.6 km s−1 with Tmb = 0.3 K for 12CO 1→0. It is worth noting that the emission between ~ 1 and 4 km s−1 corresponds to just one component of the broader LVC H I line, which spans significantly wider velocities (refer to Fig. A.2). The Herschel data yields a column density value of N(H) = 6.3 × 1020 cm−2 at the Spider 1 position. This aligns with a peak in IR excess emission, where Barriault et al. (2010a) derived a column density of N(H) = 4.05 × 1020 cm−2. The authors highlight that this excess suggests a potential decrease in the quantity of small grains and/or a possible reduction in the temperature of larger grains (Abergel et al. 1996). Such conditions may provide a favorable environment for H2 formation, as a lower temperature is conducive to this process.
Spider observational [C II] and CO data.
 |
Fig. 6 Spectra and column density map of Polaris. Right panel: cutout of the Herschel hydrogen column density map derived from dust of Polaris in color in which the observed [C II] position indicated with black crosses. Left panel: spectra of the [C II] 158 µm and CO lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
4.3 Polaris and Musca
Figures 6 and 7 display the Herschel total hydrogen column density maps from dust for Polaris and Musca (Schneider et al. 2022), respectively, with the observed [C II] position indicated. The left panels show various CO lines, all at a resolution of 70″, to indicate the velocity of the molecular gas. For Polaris, the bulk emission of the cloud is traced by the 13CO 2→1 line at υ ≈ −4.5 km s−1. The 12CO 2→1 and 1→0 lines have an additional component at lower velocities around −3 km s−1. These velocity features are present throughout the Polaris region and were studied in detail by Hily-Blant & Falgarone (2009). They concluded that the occurrence of these two velocity components is a signature of intermittency in turbulent molecular gas.
In the case of Musca, the main velocity component occurs at υ ≈ 3 km s−1, while the 12CO line shows an additional component around 2.5 km s−1. This emission feature was interpreted by Bonne et al. (2020b) as being caused by the dissipation of turbulence in a low-velocity shock. The [C II] line was not detected above the noise limit. The physical properties of both regions are summarized in Table 5.
5 Analysis
In the following, we will determine the FUV field in the sources using different methods (Sect. 5.1), and then derive the physical properties of the gas in the PDR with the help of a PDR model (Sect. 5.2), a non-LTE radiative transfer code (Sect. 5.3), and a shock model (Sect. 5.4). The objective of this exercise is to distinguish which heating mechanism is responsible for the emission of the [C II] and CO lines.
5.1 Determination of the FUV field
For the determination of the FUV field, we employed several approaches we summarize in the following.
Firstly, we translated the observed 160 µm flux into an FUV field, assuming that only radiation from stars is responsible for heating the dust, which is then fully re-radiated at FIR wavelengths. The FUV field was estimated using the correlation (Kramer et al. 2008; Roccatagliata et al. 2013; Schneider et al. 2016): FFUV[Go] = (4π/1.6) IFIR × 1000 where the 160 µm intensity IFIR is given in units of 10−17 erg cm−2 s−1 sr−1.
Secondly, we used the continuous model proposed by Parravano et al. (2003) to estimate the FUV field impinging on our sources. They assumed a statistically homogeneous distribution of OB stars in the Galactic plane with a scale height of 85 pc for the OB stars and typical dust properties for the FUV absorption and scattering (see below). Despite the local and temporal variations of these properties, they showed that the model reproduces the typical radiation field in the solar neighbourhood with a median value of about 1.6 Go. We treated the distribution of the OB stars as a continuous UV source and used the same properties for the dust (κabsorption, FUV = 8.0 × 10−22 cm2/H-atom, κscatterin, FUV = 7.5 × 10−22 cm2/H-atom, mean scattering angle 𝑔 ≳ 0.75 (Appendix B from Parravano et al. 2003) and the vertical gas density distribution (see their Eq. (22) and also our Eq. (4)) of the ISM8 to compute the flux above the Galactic plane. In this one-dimensional configuration no geometrical dilution occurs but only dust extinction and scattering. The effective optical depth for the FUV radiation is then τFUV = N(H) × [κabsorption,FUV + (1 − R)κscattering,FUV], where 0.9 < R < 1 depending on the number of scattering events. That means that practically only absorption acts as an effective extinction. For Musca falling within the disk of OB stars, the intensity is then only slightly smaller than in the Galactic midplane, but even for the highest latitude cloud, Draco, the radiation field is only reduced by a factor of 0.8 due to the extinction by the dust column above the Galactic plane of N(H) = 2.6 × 1020 cm−2. In such a continuous model, all our clouds thus experience an external radiation field between 1.2 and 1.6 Go.
In a third approach we dropped the assumption of a homogeneous stellar distribution since a molecular cloud located in the vicinity to an OB-cluster can experience a higher FUV field than the one typical for the solar neighborhood. Thus, we compiled a stellar census from Gaia DR3 and compared to the information in SIMBAD, the astronomical database in Strasbourg9 and utilized the distances provided in the Introduction (also mostly Gaia based). Since the data base in Gaia DR3 is much larger than the one in SIMBAD, we finally only used the stellar census from Gaia. We note, however, a discrepancy we found for one star in Draco that was declared as a B-star in SIMBAD via the original HD star catalog (see compilation in Cannon & Pickering 1993). In the more recent Apogee survey, Jönsson et al. (2020) determined a reliable temperature fit of 6800 K, which puts it at a spectral type F2V. This is in agreement with the Gaia parallax, with sets its distance to 300 pc, which is actually not the one considered for Draco (480 pc following Zucker et al. 2020). We checked in addition the Apogee spectrum and it shows that the metallicity is subsolar. In summary, everything agrees with the star being an old F2V star at a distance of 300 pc. The FUV field was then calculated by taking all stars into account from the latest Gaia DR3 release (Creevey et al. 2023; Gaia Collaboration 2023), which provides the necessary information such as the stellar position, distance, temperature and luminosity. Since most stars are not hot enough to contribute significantly to the FUV field, we only considered stars with a effective temperature Teff above 10 000 K, thus all spectral types O and B, resulting in 1 192 351 stars10. This number is a lower limit since highly embedded stars were not detected. However, such embedded stars do not contribute significantly to the FUV field at our sources since their radiation is extinct in all directions. On the other hand, there can be a substantial column between the star and the observed cloud and therefore a direction dependent extinction. However, the sources of this study all lie within a radius of 0.5 kpc, see Table 6, and it is therefore unlikely that the source is exposed to a radiation field of an undetected stellar cluster. The temperature information of each star is provided by the GSP-Phot (General Stellar Parametrizer from photometry) module11 and the corresponding luminosity information was taken from the FLAME (Final Luminosity Age Mass Estimator) module. If the stellar luminosity was not provided by FLAME we used the stellar radius and temperature, provided by GSP-Phot to derive the (bolometric) luminosity L:
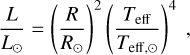 (1)
(1)
with the effective temperature of the Sun Teff,⊙ = 5772 K, the solar radius R⊙ and solar luminosity L⊙. The distance to each star was derived from the parallax information. However, if the parallax error is large, more than half of the parallax, we used instead the distance provided by the GSP-Phot module.
We determined the FUV luminosity by assuming that the spectral radiance of each star can be approximated by a black-body curve. The Planck function was integrated over the FUV range spanning from 910 to 2066 Å, corresponding to a photon energy range of 6–13.6 eV. The FUV luminosity is then defined through the ratio of the spectral radiance in the FUV range and the entirety of the black-body spectrum:
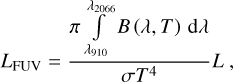 (2)
(2)
with the Stefan-Boltzmann constant σ. The superposition of the stellar FUV flux of all stars considered gives the FUV field at every point in the map:
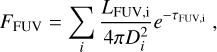 (3)
(3)
where Di represents the distance from the source to each star. The FUV optical depth is defined as described above and the attenuating column NH is calculated for each star individually, based on its position with respect to the source. This differs from the continuous model, where the column is simply determined by galactic height of the source. Thus, the hydrogen density nH(ɀ) (Eq. (22) in Parravano et al. 2003) integrated along the path connecting each star at the galactic height ɀi with the source at the galactic height ɀs results in the hydrogen column density:
![$\matrix{ {{N_{{\rm{H}},{\rm{i}}}}\left( {{z_s},{z_i},{D_i}} \right) = {{{D_i}} \over {{z_s} - {z_i}}}\mathop \smallint \nolimits^ _{{z_i}}^{{z_s}}{n_{\rm{H}}}(z){\rm{d}}z} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {{{D_i}} \over {{z_s} - {z_i}}}\mathop \smallint \nolimits^ _{{z_i}}^{{z_s}}0.566\left[ {0.69\exp {{\left( { - {z \over {127{\rm{pc}}}}} \right)}^2}} \right.} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.189\exp {{\left( { - {z \over {318{\rm{pc}}}}} \right)}^2}} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.113\exp \left( { - {{|z|} \over {403{\rm{pc}}}}} \right){\rm{d}}z} \right]{\rm{c}}{{\rm{m}}^{ - 2}}.} \hfill \cr } $](/articles/aa/full_html/2024/06/aa48349-23/aa48349-23-eq35.png) (4)
(4)
Equation (4) is valid for ɀi ≠ ɀs, for ɀi = ɀs the equation simplifies to NH,i = DinH(ɀi) (with the distance in cm). While Gaia DR3 data allow for a more sophisticated 3D treatment of the extinction (Zucker et al. 2022), this goes beyond the scope of this paper. Thus, for the sake of comparison with the previous approach given by Parravano et al. (2003) we use the above Eq. (4). The method is schematically illustrated in Fig. 8. The resulting values for the FUV field are around 1.3–1.6 Go and given in Table 6. They are similar to the ones estimated with the second method and again close to the typical value in the solar neighborhood. When sticking to this approximation of the interstellar extinction, we can only quantify the change of values considering the error of the distance (Table 2 for Draco, the variation is very small for the other sources and thus not given) but note that a larger error is introduced by the uncertain detailed n(H) distribution in the galaxy.
As a fourth method, we compared our numbers to a study conducted by Xia et al. (2022). This study derived the FUV field through the fitting of a spectral energy distribution (SED) to the Herschel fluxes. Furthermore, a dust radiative transfer analysis was performed using the DUSTY code (Nenkova et al. 2000). The results are presented for a selection of sources, which includes Polaris and Musca. Moreover, the empirical correlation log(Go) = (0.62 ± 0.12) log(N(H2)[cm−2]) − (11.56 ± 2.87) was given in Xia et al. (2022) to derive the FUV field. In order to estimate a value for the molecular hydrogen column density in Draco, we used the N-PDF presented in Schneider et al. (2022). This N-PDF consists of two lognormals with one peak at AV = 0.4 that we attribute to molecular hydrogen (Schneider et al. 2022). With that value of the column density, we obtained a field of 15.7 Go from the correlation given in Xia et al. (2022). For Spider, we adopted a value of 7.3 × 1019 cm−2 for the molecular hydrogen column density N(H2), cited in Barriault et al. (2010a), and derived a field of 6 Go.
Table 6 summarizes the values for the 160 µm flux and the FUV field for all sources at the observed positions. There is obviously a discrepancy between the values derived from the Herschel fluxes and the census of the stars. We will come back to this point in the discussion.
 |
Fig. 7 Spectra and column density map of Musca. Right panel: cutout of the Herschel hydrogen column density map derived from dust of Musca in color in which the observed [C II] position indicated with black crosses. Left panel: spectra of the [C II] 158 µm and CO lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
Polaris and Musca observational [C II] and CO data.
Distance and FUV field.
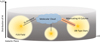 |
Fig. 8 Schematic illustration of the method to derive the FUV field at each source. The gray cylinder indicates the hydrogen distribution with respect to the galactic height ɀ. The yellow stars indicate the 3D stellar distribution in the Milky Way. The solid black lines originating from the stars indicate the distance from the star to the source. The yellow halo around the star illustrates the FUV field generated by each star. The orange cylinder placed along the path between the star and the source shows schematically the hydrogen column which attenuates the FUV field. |
5.2 PDR modeling of line emission
For modeling the observed [C II], CO and [C I] intensities and ratios, we used the KOSMA-τ 1D spherical model (Röllig & Ossenkopf-Okada 2022) with an isotropic radiation field. The model results are included in the PDR toolbox12 (Pound & Wolfire 2023) that also delivers results from a plane-parallel PDR model, the Wolfire-Kaufman models from 2006 and 2020 (see references in Pound & Wolfire 2023). The toolbox presents the models as grids of model predictions for the intensity or intensity ratio as a function of the hydrogen nucleus density n and the radiation field strength FUV. Here, we stick to the KOSMA-τ model because this represents a finite configuration that we can adjust to the geometry of the sources while the plane-parallel models adopted a fixed PDR depth of AV = 7, too high for the sources in our study.
The KOSMA-τ model solves the radiative transfer equation with chemical balance and thermal equilibrium for a clumpy PDR exposed to a variable FUV radiation field and cosmic rays according to the typical primary ionization rate of 2 × 10−16 s−1. The model that we used assumes a dust composition that produces a reddening parameter RV = 3.1, where RV is the ratio of visual extinction AV to reddening E(B − V), typical for diffuse clouds (model 7 from Weingartner & Draine 2001). It assumes a spherical cloud configuration with a radial density profile approximating a critical Bonnor-Ebert sphere with a constant central density and a power law density decay in the outer 80% of the radius. Models are characterized by clump mass, density at the surface, and impinging FUV field. From the simple geometry the average density is 1.92 times the density at the surface and we get a fixed relation between clump mass, Mclump, density at the surface, n, and average column density
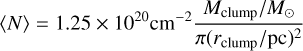 (5)
(5)
combining to a fixed relation between column density and density at the surface
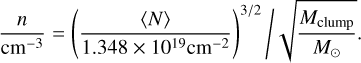 (7)
(7)
From Eq. (7) we obtained for a column density of 1021 cm−2 (average value for the 4 positions in Draco) a density at the surface of 2020 cm−3 when using a clump mass of 0.1 M⊙ or 640 cm−3 for a clump mass of 1 M⊙. This is the density range we expect to be seen in the PDR modeling of the observed lines.
We show here the line intensities and ratios of [C II], CO and [C I] emission and fit the line ratios to obtain the most likely value for density and FUV field. We only use the velocity components that correspond to the velocity of the [C II] line (for example −25 km s−1 for Draco Front 1a and −22 km s−1 for Draco Front 2a, respectively). However, each source has a different set of lines available so that a comparison is difficult. We emphasize that the CO lines are very sensitive to the assumed total depth of the cloud. The [C II] intensity and the surface temperature trace surface properties while the CO emission only arises from the layers deeper in the cloud where CO can form. It is a simplified approach to consider a single density only and not a density distribution. A surface tracer like [C II] traces somewhat thinner material than the molecular lines. However, Fig. 9 shows that this has no significant impact on our results. The curves for the [C II] intensity have a very shallow density dependence. Because of the low critical density of the [C II] transition, a shift in density has little effect on the [C II] lumninosity and consequently our fit results do not depend on the density of the [C II] emitting material.
KOSMA-τ provides models for different clump masses integrating over that mass. Using the Herschel total hydrogen column densities with a beamsize of 70″ they are all well below 1 M⊙, except for Polaris with a value of ~1 M⊙. Specifically, we determine a mass of 0.21 M⊙, 0.14 M⊙, 0.31 M⊙, and 0.32 M⊙ for the Draco F1, F2, N1, and N2 positions, 0.09 M⊙ for Spider, 0.08 M⊙ for Musca, and 0.8 M⊙ for Polaris. For simplicity, and because these models are directly available in the open access PDR toolbox and all results can thus easily be verified, we used pre-calculated models with M = 0.1 M⊙ for Draco, Spider, and Musca and with M =1 M⊙ for Polaris. Note that using models with M = 0.3 M⊙ (Röllig, Ossenkopf, priv. comm.) do not significantly change the results. With the higher mass the solution for the absolute intensities of the CO and [C I] lines shift by about a factor of two to lower densities while the [C II] intensity and the ratios remain almost unchanged.
Figures 9 and 10 display the results of the PDR model in a parameter space of FUV field and hydrogen density for all sources. The observed lines and line ratios are presented as isocontours, along with their associated errors. It should be noted that for [C II] in Spider, Polaris, and Musca, only the noise level is available, effectively serving as an upper limit. We show in Fig. C.1 the full model results for [C II] emission for masses M = 0.1 M⊙ and M = 1 M⊙ and in Fig. C.2 the model result (as an example) for CO 2→ 1. In terms of representing the FUV field, a dashed red horizontal line corresponds to the field determined through the translation of the 160 µm fluxes, while a blue line signifies the field established via the stellar census. Notably, data from Xia et al. (2022), which tend to be higher than other values, are omitted. This omission does not alter the interpretation of the PDR modeling.
A solution for the density and FUV field from the PDR plots is defined by a common crossing point of all lines. Because the absolute line intensities depend on geometrical details like beam dilution effects, line ratios are more reliable. We thus used the line ratios in the LineRatioFit method in the PDR toolbox to determine the most likely values of total hydrogen density density and FUV field including errors and χ2. These values are listed in Table 7.
For the Front1 position, the observations align with a very low FUV field of around 0.4 Go and densities of approximately 500 cm−3 by eye-inspection of Fig. 9. The FUV field and the density from the fit are lower, that is, 0.23 Go and 311 cm−3.
For the Front 2 position, the [C II] line crosses the CO intensities for a density of ~2 × 103 cm−3 at an UV field of 1 Go. The CO 2 → 1/1 → 0 ratio points toward a lower UV field of around 0.4 Go. The fitted values are much lower with a FUV field of 0.17 Go and a density of 370 cm−3.
For the Nose 1 position, we also consider the CO 3→2 line intensity (Heithausen, priv. comm.) and the [C II]/CO 3→2 and CO 3→2/2→1 line ratios and the [C I] line intensity. We derived the latter by averaging over the 4 positions observed in Draco close to the Nose 1 position (Heithausen et al. 2001) and arrive to a value of 4.3 × 10−7 erg s−1 sr−1 cm−2. The CO 3→2/2→1 ratio falls essentially outside the parameter space (very low FUV field and densities) and is not visible in the plot. On the other hand, the [C II]/CO 3→2 ratio, the [C I] line, and the CO 2→1 and 1 →0 intensities could align for densities of approximately 3 × 103 cm−3 for a low FUV field of around 1—2 Go. Fitting only the line ratios, however, leads to a lower FUV field of 0.23 Go and a density of 636 cm−3.
For the Nose 2 position, the individual CO line intensities intersect with the [C II] line at densities around 103 cm−3 at an UV field of around 0.6 Go. In contrast, the line ratio fitting leads to a much smaller density of 272 cm−3 and a FUV field of 0.17 Go. It is mostly the CO(2→ 1)/(1 →0) ratio that leads to these low values.
Figure 10 displays the PDR modeling results for Spider, Polaris, and Musca. Note that the [C II] value is only the noise level and that there are fewer complementary lines. The FUV field needs to be around 0.1 Go for Polaris to explain the observed lines and ratios and then yields a density of 2 × 103 cm−3. The line ratio fitting gives a higher value of 3838 cm−3 for the density but a lower value of 0.35 Go for the FUV field. The same mismatch was already noticed by Bensch et al. (2003) when analysing [CI] observations of Polaris. They proposed some kind of preshielding of the gas to explain the low FUV field. For Musca, it is very difficult to make any definitive statements since we only have two line intensities and no ratios. However, the tendency is that the FUV field is very low (<0.1 Go) and the density is around 103 cm−3.
Summarizing, it becomes obvious that the line ratio fitting in the PDR model always arrives to a very low FUV field (<0.35 Go) for all sources, which is neither supported by the FUV field determined from the 160 µm flux by us and by Xia et al. (2022) nor by the theoretical prediction of 1.2–1.6 Go we obtained using the procedure outlined in Parravano et al. (2003) or the census of the stars. The densities are also lower than in the case where we also consider line intensities.
Density and FUV field from the PDR model.
 |
Fig. 9 PDR modeling results for Draco. Parameter space of hydrogen surface density n and FUV field calculated from the KOSMA-τ model for 0.1 M⊙ clumps taken from the PDR toolbox for the Draco Front 1 and Front 2 (left) positions and the Nose 1 and Nose 2 (right) positions. The isocontours at different colors show the observed line integrated intensities or ratios, including the rms noise. The estimated FUV field for each source from the 160 µm flux is indicated by a red dashed line. The FUV field from the census of the stars is given as a dashed blue line. |
 |
Fig. 10 PDR modeling results for Spider, Polaris, and Musca. Parameter space of hydrogen density n and FUV field calculated from the KOSMA-τ model taken from the PDR toolbox for the Spider 1 position (left, 0.1 M⊙ clumps), the Polaris single pointing (middle, 1 M⊙ clumps ), and the Musca single pointing (right, 0.1 M⊙ clumps). The isocontours at different colors show the observed line integrated intensities or ratios, including the rms noise. The estimated FUV field for each source from the 160 µm flux is indicated by a red dashed line. The FUV field from the census of the stars is given as a dashed blue line. |
5.3 Non-LTE line analysis with RADEX
The PDR modeling provided results for observations of warm surface gas tracers such as [C II] and [C I] as well as CO lines for the cooler interior of the gas clump. We used RADEX (van der Tak et al. 2007) to determine the physical properties of the cooler, molecular gas. We investigated whether the observed 13CO 1→0, 2→1 and 12CO 1→0 and 2→1 lines and their ratios can be reproduced with this non-LTE molecular radiative transfer code. We excluded the [C II] line since it is not possible to determine independently the density, temperature and column density only from one line intensity. In other words, the determination of the [C II] column density is possible, but not independent of the line brightness and vice versa.
RADEX computes the line intensities as a function of temperature, H2 density (assuming that H2 is the main collision partner) and the column density of the species for the configuration of an isothermal homogeneous medium with a given velocity dispersion in the simplified shape of a uniform sphere. Using an 12CO/13CO abundance ratio of 70 (Langer & Penzias 1990) and a total carbon abundance of X(C)/X(H) = 2.34 × 10−4 (Simón-Díaz & Stasińska 2011) we translated the column densities of 13CO and CO into minimum hydrogen column densities by assuming all carbon is in CO.
To estimate the velocity dispersion of the molecular gas we used the mean of the line width of the two 13CO lines observed. For all calculations, we only used the CO velocity component (Table 3) that corresponds to the [C II] velocity component. For example, the Front 1 position only has a velocity component for [C II] at −25.6 km s−1 (Table 2), while the CO lines have two components (Table 3). We thus used only the Front 1a velocity component at −25.1 km with a mean velocity dispersion of 0.96 km s−1 in the RADEX fit.
We display the results for RADEX in two different ways, either using the line intensities or the ratios. The line fit for the intensities computed a three dimensional χ2 distribution in the space of the parameters. The minimum gives the numerically best solution. This is visualized in Figs. 11 and 12 for the data from the F1 position in Draco. The figures show perpendicular cuts through the 3D cube of column density, density and temperature at the location of the χ2 minimum. Each plot shows the integrated intensity of one of the four CO and 13CO lines in colors and the global χ2 distribution. The observed values are marked by a red line. From the crossing of the intensity isocontours it is obvious that the density is best constrained by the combination of the CO 2→ 1 and the 13CO 1→0 lines but that the fit overpredicts the intensity of the CO 1→0 line. The kinetic gas temperature is well constrained by the combination of the CO lines and the 13CO 1→0 line. The column density is also well constrained by the total intensities.
The best fit parameters for all four positions in Draco are given in Table 8. The corresponding plots for the other three positions are very similar to Figs. 11 and 12, this is why we omit showing all positions. The intensities just have to be shifted according to the values given in Table 3. The minimum χ2 values fall between 4 and 13, which indicates a reasonable but imperfect fit by this model with one degree of freedom, based on four observed line intensities and three model parameters. The assumption of a homogeneous medium is obviously an oversimplification but the parameters are quite well constrained. It is interesting that the column density of gas traced by the CO isotopologues falls significantly below the column density measured through the dust emission (Table 2). This is partially due to the fact that the RADEX fit considers only one velocity component but in particular for the F1 and the N2 positions the difference is so large that it indicates a large fraction of atomic or CO-dark molecular material that is not traceable through CO. This is in agreement with the estimate from Schneider et al. (2022) that identified only 11% of the gas mass is molecular.
Unfortunately, we cannot perform the same RADEX fit for the other clouds where no 13CO data are available as a three-dimensional problem cannot be constrained from two measured values only.
For a more intuitive visualization we also plot the RADEX output brightness ratios of 13CO 1→0/2→1 and 12CO 1→0/2→1 as a function of temperature and H2 density in Fig. 13 for the Draco positions. Here, the column densities were determined in the classical way from the 13CO 1→0 line integrated intensity using an excitation temperature Tex that was determined from the 12CO 1→0 line peak brightness, assuming optically thick emission (Mangum & Shirley 2015). The upper panels show the results for the Front 1 and Front 2 positions, the lower ones for the two nose positions. The model ratios for Draco are compared to the observed ones (indicated as a solid black and dashed line) and have the advantage that the ratios are independent of beam filling to first order. We can start from the PDR modeling densities to compare our ratios with the RADEX results. For that, we use the upper limits from the PDR modeling obtained by eye inspection of the observed line intensities and ratios. With the PDR model density of 500 cm−3 for Front 1 we obtain no solution at all. The density must be at least 3 × 103 cm−3 at a temperature of around 10 K. Note that from Table 8, we derive a density of 4.9 × 103 cm−3 at a temperature of 9 K. The Front 2 position can be reproduced by the upper limit PDR model with a density of 2 × 103 cm−3 (note that the density from the line ratio fitting is only 370 cm−3) and leads to a consistent temperature of 15 K for both, 13CO and 12CO line ratios. This also fits with our values from Table 8 with the most likely density of 1.65 × 103 cm−3 at a temperature of 14 K. The Nose 1 position has the highest PDR model density of 3 × 103 cm−3 (but only 636 cm−3 from the line ratio fitting) that would give a low temperature of 10 K, again for both, 13CO and 12CO line ratios. From RADEX, we obtain slightly smaller densities of around 2 × 103 cm−3 at a temperature of 16 K. For the Nose 2 position, it is more difficult to obtain a fully coherent output from the analysis: a PDR model density of 103 cm−3 requires a temperature of 25 K for 13CO. But the RADEX 12CO line ratio is much higher (around 3) at this temperature (and also for lower temperatures) than the observed one of 1.57. Only high densities of around at least 3 × 103 cm−3 make the observed 12CO line ratio fitting with low temperatures of around 10 K.
Note that PDR model densities are by no means the ‘exact’ values. They only give an estimate of the density in case of a very low FUV field and we observe a discrepancy between the densities and FUV field determined from line intensities and ratios and from line ratios alone. For the optical depths, we derived values below 1 for temperatures above 5 K for the 13CO lines. For the 12CO lines the values range between the optical thin case with τ ≲ 0.3 for Front 1 and the optical thick case with mostly τ > 1 for the Front 2 position over all temperatures. In both nose positions the opacity lies above 1 throughout the whole parameter range of temperatures.
Summarising, we have a parameter space of possible solutions for all positions from the RADEX model alone. The densities are between 1650 and 4900 cm−3 at a temperature of 9–16 K (Table 8). Overall, these values align mostly with the ones of Miville-Deschênes et al. (2017) who found molecular clumps in Draco at a temperature of 10 K and an average density of ~103 cm−3 (note that the density of individual molecular clumps is sometimes higher). The dust temperatures in Draco are low (around 13 K, see Table 2), so that in case the dust and gas is well mixed, the low gas temperatures are consistent.
Figure 14 displays the RADEX results for the 12CO 1→0/2→1 ratio in Spider and Polaris since only these lines are available. We omit Musca because we only have the 12CO 2→1 line brightness. It is noteworthy that for Spider, the 12CO 1→0 line is optically thin with values between ~0.2 and ~0.5 for a temperature range of 10–20 K and the 12CO 2→1 line is optically thick with values above 1 for the whole parameter space, whereas for Polaris, the optical depth is mostly above 1 for both 12CO lines. This discrepancy renders the interpretation of the results somewhat less reliable. The PDR modeling for Spider did not yield reasonable density estimates, even for very low FUV fields (outside the model’s range). We anticipate that the densities and temperatures are low in this relatively diffuse region with a substantial atomic contribution. Assuming the curve with the lowest density for the CO clump in Spider that would fit with our observations (n = 1.5 × 103 cm−3) yields a temperature of 20 K. Interestingly, the dust temperature in Spider is also approximately this value (~18 K), slightly higher than in all other sources. For Polaris, the PDR modeling provides a density of ~2 × 103 cm−3 and even 3838 cm−3 from the line ratio fit for a very low FUV field. The observed 12CO ratio then fits well with a temperature of around 25 K. However, it is important to note that the 12CO lines in Polaris are optically thick. Hence, we propose that the resulting possible temperature and density range is approximately 10–25 K at densities of around 2–3 × 103 cm−3.
 |
Fig. 11 Visualization of the RADEX fit to the four CO and 13CO lines at the F1 position in Draco. Each plot shows a constant temperature cut through the three dimensional distribution of line intensities and χ2 values. The kinetic temperature of the χ2 minimum, that is, 9 K (see Table 8) was used. The colors in the plot show the integrated line intensities for the four lines, the observed value is marked by a red line. The gray contours give χ2 values of 8, 16, 32, 64, and 128. As the χ2 distribution is a global property, those contours are the same in all four subplots. |
 |
Fig. 12 Same as Fig. 11 but for a cut at the constant density of the χ2 minimum of 4.9 × 103 cm−3 (see Table 8). |
 |
Fig. 13 RADEX results for the 13CO 1→0/2→1 and 12CO 1→0/2 → 1 brightness ratios as a function of density and temperature for the Draco front and nose positions. The observed ratios are shown as a solid and dashed black line. The density obtained with PDR modeling is marked in bold. |
 |
Fig. 14 RADEX results for the 12CO 1→0/2→1 brightness ratios as a function of density and temperature for the Spider 1a position (left panel) and the Polaris positions (right panel). The observed ratios are shown as a solid and dashed black line. The density obtained with PDR modeling is marked in bold. |
Parameters of the minima of the RADEX fits to all four measured intensities in Draco.
5.4 Shock modeling of line emission in Draco
For modeling a potential shock-origin of the [C II] emission, we utilized the Paris-Durham shock code13. Our objective was not to conduct an exhaustive modeling but rather to assess whether the observed quantities can be preliminary explained by shocks. The pre-calculated model grids14 were employed for this purpose. The shock models are executed using shock code version 1.1.0, revision 115, and encompass C-type shocks at moderate velocities (<100 km s−1), or J-type shocks at low velocities (<30 km s−1), both propagating in weakly magnetized environments. The shocks are implemented as propagating through a layer of gas and dust, manifested as stationary, plane-parallel, multifluid shock waves, in environments with or without external UV radiation. The parameters that are parameterized include the shock velocity (2–90 km s−1), initial density of the preshock medium (100–108 cm−3), intensity of the UV radiation field (0–1700 Go), cosmic ray ionization rate (10−17−10−15 s−1 /H2), and the magnetic field strength, expressed in terms of β and ranging from 0.1 to 10. β defines the initial transverse magnetic field strength in µG and is equal to ![$\beta \times \sqrt {n(H)\left[ {{\rm{c}}{{\rm{m}}^{ - 3}}} \right]} $](/articles/aa/full_html/2024/06/aa48349-23/aa48349-23-eq41.png) . The fractional abundance of PAHs is fixed at 10−8, and the chemistry incorporates 140 species through a chemical network involving about 3000 reactions. Surface reactions, adsorption, and desorption processes are not considered except for H2 formation. For further elaboration, refer to Gusdorf et al. (2008), Lesaffre et al. (2013), Goddard et al. (2019), Lehmann et al. (2020, 2022) and the references therein.
. The fractional abundance of PAHs is fixed at 10−8, and the chemistry incorporates 140 species through a chemical network involving about 3000 reactions. Surface reactions, adsorption, and desorption processes are not considered except for H2 formation. For further elaboration, refer to Gusdorf et al. (2008), Lesaffre et al. (2013), Goddard et al. (2019), Lehmann et al. (2020, 2022) and the references therein.
The code generates output containing the thermodynamic and chemical structure of the shock, including temperature, fluid velocities, abundances, column density profiles, and line intensities of H2 as well as several ionized or neutral atoms. We utilized this output to analyze [C II] line intensities and the total hydrogen column density, N(H), in comparison with Draco observations. Specifically, we applied the observed [C II] line intensities and Herschel hydrogen column density values from Table 2 to positions Draco Front 1 and 2, and Nose 1 and 2. The [C II] intensities at the Front 1, Front 2, Nose 1, and Nose 2 positions are 1.55, 2.60, 2.67, and 2.53, respectively, measured in units of 10−6 erg s−1 sr−1 cm2. For our model, we fixed the radiation field at 1.7 Go (note that available values are 0.17, 1.7, 17, … Go) and the preshock density at n = 100 cm−3 which is the lowest possible density to select. We tried also higher densities but could not find a match between the shock model results and the observations. We thus used a preshock gas of 100 cm−3, though the preshock density can indeed be lower. However, densities lower than 1000 cm−3 are a reasonable assumption since the density of the densest molecular clumps currently found in Draco is between 1000 and 4900 cm−3 (Sects. 5.2 and 5.3 and Miville-Deschênes et al. 2017). We then explored variations in other parameters, such as the cosmic ray rate, β, and shock speed, within reasonable ranges. Different cosmic ray rates (10−15, 10−16, and 10−17 s−1/H2) have limited impact on the [C II] intensity and H column density. We choosed 10−16 s−1/H2 as it is suggested as the average value for the diffuse ISM in the Milky Way (Dalgarno 2006; Indriolo & McCall 2012). The magnetic field strength, characterized by low values of β (0.1, 0.3), results in diminished [C II] intensities and H column densities. Higher values of β (3, 10) produce larger hydrogen column densities, but these values do not align well with the [C II] emission. in summary, our analysis provides insights into the impact of various parameters on the [C II] emission and hydrogen column density, revealing the influence of factors such as the radiation field, density, cosmic ray rate, and magnetic field strength in the Draco region.
The best match between model values and observations is found for the Front 1 position, with a shock velocity of 20 km s−1, preshock density n = 100 cm−3, and β = 1. The model predicts a [C II] intensity of 1.63 × 10−6 erg s−1 sr−1 cm2 at a total hydrogen column density of 3.73 × 1020 cm−2. it is important to note that the column density is calculated for a single layer, representing a lower limit. When comparing all Draco positions, the [C II] intensity is roughly consistent across all of them. Running models with different preshock densities would probably better match the observed intensities, but this is for the moment out of the scope of this paper. The hydrogen column density is approximately four times higher than the model’s predicted values for the nose positions. However, this discrepancy could be attributed to the limitations of the single layer model. it is evident that higher shock speeds are not feasible. Beyond a threshold of υ = 25 km s−1, the [C II] intensity experiences a significant drop. J-type shocks prove ineffective, while only C-type shocks with velocities ≤ 20 km s−1 yield reasonable results. Nonetheless, reducing the velocities further leads to a decline in the [C II] intensity.
Summary of physical parameters.
6 Discussion
The main result of this study is that the [C II] 158 µm line was detected at several positions in the Draco cloud, but not in any of the other quiescent clouds (Spider, Polaris, Musca), even though these regions have similar column and volume densities, 160 µm fluxes, and FUV fields (see Table 9). We note that the volume densities are similar for all sources (a few times 103 cm−3), only Polaris has a higher density of 2–5×104 cm−3 and should thus emit even stronger in [C II] than Draco because subthermal, optically thin [C II] intensities scale with n2 (Goldsmith et al. 2012). As we explained in Sect. 5.2, though the density of the gas is higher in the interior of a molecular clump than at the surface, we can consider similar densities for the CO and [C II] emitting gas because the [C II] line shows a very weak dependency on the density.
It is important to emphasize that the accurate derivation of the FUV field is a critical point. As discussed in Sect. 5.1, different methods yield variations in the estimated FUV field. A census of Galactic OB-stars and a continuous approximation (Parravano et al. 2003) using the distribution and birthrates of OB stars in the Milky Way from McKee & Williams (1997) and considering the extinction toward our sources, yields values between 1.2 and 1.6 Go. On the other hand, the calculation based on the 160 µm flux and a dust model (Xia et al. 2022) results in larger values (at least a few Go) when assuming that the dust is only heated through the FUV radiation.
We checked if the FUV field determined from the 160 µm emission may be underestimated because the wavelength range below 160 µm is not taken into account. This is not the case. There is nearly no or only weak 70 µm emission visible in the Herschel maps of all sources and only very weak 12 µm emission (Meisner & Finkbeiner 2014). There is also no overestimation of the 160 µm flux due to the contribution of cold thermal dust emission from the molecular cloud. It is thus difficult to understand why the 160 µm fluxes are so high in all sources if it is not an external FUV field that heats the dust.
When looking for alternative mechanisms for the heating of the dust we can quickly exclude cosmic rays. At a typical cosmic ray ionization rate of 2 × 10−16 s−1 and heating efficiencies below 10 eV per ionization event (Glassgold et al. 2012) the cosmic ray heating rate falls more than three orders of magnitude below the UV heating rate at one Habing field so that even an enhanced cosmic ray rate is probably insufficient to explain the observed dust heating. Instead shock heating from cloud collisions can in principle inject enough energies. For example, with a rather low hydrogen gas density of 500 cm−3 (Front 1 position in Draco), a kinetic temperature of 100 K, and relative velocities of 20 km s−1, like the difference between the IVC and LVC in Draco, the thermalization time, τtherm is at maximum 30 years when assuming perfectly elastic collisions (Sauder 1967). Inelastic contributions may shorten this. The compressive heating from the shock, 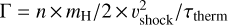 is then more than four orders of magnitude above the UV heating rate at one Habing field. Higher densities would even increase Γ. Although the details of the shock physics may modify this rate relative to the idealized value, the order of magnitude estimate shows that shock heating at our conditions could easily feed enough energy into the dust to explain the enhanced 160 µm emission. Note that referring to Lehmann et al. (2020, 2022) up to 10–30% of shock energy can be irradiated away in LyAlpha (which then can be absorbed and reemitted by the dust, potentially resulting in an increase of the 160 µm emission; see also Bonne et al. 2022). This, however, requires shock velocities around 30 km s−1. Nevertheless, lower velocity shocks may still have a measurable impact.
is then more than four orders of magnitude above the UV heating rate at one Habing field. Higher densities would even increase Γ. Although the details of the shock physics may modify this rate relative to the idealized value, the order of magnitude estimate shows that shock heating at our conditions could easily feed enough energy into the dust to explain the enhanced 160 µm emission. Note that referring to Lehmann et al. (2020, 2022) up to 10–30% of shock energy can be irradiated away in LyAlpha (which then can be absorbed and reemitted by the dust, potentially resulting in an increase of the 160 µm emission; see also Bonne et al. 2022). This, however, requires shock velocities around 30 km s−1. Nevertheless, lower velocity shocks may still have a measurable impact.
The ‘cloud collision’ in Draco that can give an explanation to the increased 160 µm emission and the [C II] emission can be seen as an interaction of the atomic/molecular IVC with mostly atomic gas (the LVC) while the Draco cloud moves through the ISM. Notably, local gas within the velocity range of −10 to 30 km s−1 contributes to these interactions, while the high-velocity gas (−200 to −100 km s−1) remains excluded from this process (refer to Figs. A.1 and B.1). Figure 3 presents a clear representation of the complex velocity structure of H I in Draco, with a minimum of two components observed between approximately −16 and −30 km s−1. At the forefront, the two positions in Draco distinctly exhibit two H I components, out of which only one corresponds to the [C II] line, situated around −26 and −24 km s−1 for the Front 1 and Front 2 positions, respectively. The Nose 1 and Nose 2 H I spectra are more complex and do not show clearly two components. This is not surprising because the gas is here mostly molecular and denser. Conversely to Draco, the other sources primarily exhibit inconspicuous dynamics. Musca stands out as having more pronounced dynamics due to filament formation (Bonne et al. 2020b,a). The dissipation of turbulence through the emergence of dense structures results in low-velocity shocks that elevate both gas and dust temperatures and may thus also explain the rather high 160 µm flux. However, it is noteworthy that no detection of [C II] occurred in Musca. Spider and Polaris have lower 160 µm fluxes compared to Draco and Musca, but the emission is mostly at local velocities and does not seem to involve cloud collisions.
The PDR modeling indicates that the [C II] and CO lines can only be accounted for by a significantly small UV field, much smaller than 1 Go. Among the positions studied, only Draco Nose 1, Nose 2, and Front 2 positions exhibit some compatibility with a model where CO emission originates from the inside of high-density (1–3 × 103 cm−3), cold (T ~ 10–20 K) molecular clumps. The CO emission is then a result of thermal excitation within the dense gas clumps, which likely possess a limited filling factor. [C II] may then arise from the PDR surfaces at those densities but it can also stem from a mostly atomic interclump component. As for the Draco Front 1 position, as well as Polaris and Musca, their [C II] and CO line emissions (and the corresponding upper limits) are reconcilable with a PDR model featuring very low FUV fields, less than 0.2 Go, coupled with densities around 103 cm−3. Only the Front 1 positions falls out of this with its density of only 500 cm−3. The Spider position cannot be modeled with very low FUV intensities. RADEX modeling of the observed CO line ratios in all sources determines mostly higher densities than estimated from the PDR modeling (except of the low densities for the Draco Front 1 position), but we cannot make a statement about [C II]. The puzzling result is still why the [C II] line was observed in Draco and not in all other quiescent sources. The only differences between Draco on one hand, and Spider, Polaris, and Musca on the other hand, is the higher dynamics of Draco because of a possible cloud interaction. An approach of shock modeling applied to the [C II] emission in Draco reveals that the observed intensities are compatible with conditions akin to a preshock density of 100 cm3 and a shock velocity of 20 km s−1 . The shock velocity is not very high which may explain why the [C II] line widths (between 1.3 km s−1 for Front 1 and 4 km s−1 for Front 2) are not very broad and not significantly larger than the ones of CO.
In consideration of these findings, it is plausible that Draco contains dense, cold, molecular clumps that are enveloped by a diffuse atomic phase (≃10–100 cm−3, T > 50 K), serving as the source of the [C II] emission. This emission, in turn, acts as a cooling line to dissipate kinetic energy stemming from interactions between H I clouds or as the IVC descends onto the galactic disk. in such a scenario, the primary factor driving this process is the ram pressure exerted on the cloud by the escalating halo density, as stated by Desert et al. (1990).
7 Summary
The [C II] 158 µm line was observed with SOFIA at selected positions in the quiescent clouds Draco, Spider, Polaris, and Musca. Emission on a level of ~0.2 to 0.4 K km s−1 (S/N ~ 4) of the [C II] line was only detected in four positions in the Draco cloud, and CO lines (12CO and 13CO 1→0, 2→1) were observed with the IRAM 30 m and APEX and mostly detected in all sources. The flux at 160 µm is rather high in all sources (18 MJy sr−1 for Polaris; 44 MJy sr−1 for Draco; up to 61 MJy sr−1 for Musca), while the FUV field is very low. Converting the 160 µm flux gave values of 1.5–6 Go, while the FUV field from a stellar census is around 1.3–1.6 Go. A theoretical determination considering the distribution of OB stars in the galaxy and extinction yielded a value of 1.2–1.6 Go. The PDR modeling ([C II], [C I], and CO) and RADEX modeling (CO) can partly explain the observed emission arising from clumps with a density of a few 103 cm−3 at a temperature of 10–20 K in Draco. The PDR model, however, requires a very low UV field, much lower than 1 Go, which is not provided by the different methods of our FUV field determinations. For Draco, heating by collisions of H I clouds could explain the high level of the 160 µm flux and the [C II] emission, which is reproduced by a shock model with a preshock density of 100 cm−3 and a C-shock with a velocity of 20 km s−1 . We propose that the shock arises from the interaction of the H I clouds associated with Draco.
Acknowledgements
This study was based on observations made with the NASA/DLR Stratospheric Observatory for Infrared Astronomy (SOFIA). SOFIA is jointly operated by the Universities Space Research Association Inc. (USRA), under NASA contract NNA17BF53C, and the Deutsches SOFIA Institut (DSI), under DLR contract 50 OK 0901 to the University of Stuttgart. upGREAT is a development by the MPIfR and the KOSMA/University Cologne, in cooperation with the DLR institut für Optische Sensorsysteme. N.S. acknowledges support from the FEEDBACK-plus project that is supported by the BMWI via DLR, Projekt Number 50OR2217. S.K. acknowledges support by the BMWI via DLR, project number 50OR2311. This work is supported by the Collaborative Research Center 1601 (SFB 1601 sub-project A6 and B2) funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 500700252.
Appendix A Velocity integrated HI maps of Draco and Spider
Figures A.1 and A.2 show the column density contributions of the different velocity components to the total column density in Draco and Spider derived from the H I observations. They should be compared to the dust column densities in Figs. 4 and 5. Comparing the morphology we can assign the individual velocity components to the analyzed dust maps. For Draco we find a clear correspondence of the dust column with the IVC (−30 to −10 km s−1, for Spider to the local velocity component (− 10 to 30 km s−1).
 |
Fig. A.1 Velocity integrated H I maps of the Draco region from the EBHIS survey. The panels show the H I line integrated emission over all velocity ranges, covering the HVC (left, v=−200 to −100 km s−1), the IVC (middle, v=−30 to −10 km s−1), and the LVC (right, −10 to 30 km s−1. For better comparison, the scale in K kms−1 was kept constant. |
 |
Fig. A.2 Velocity integrated H I maps of the Spider region from the EBHIS survey. The panels show the H I line integrated emission over all velocity ranges, covering the IVC (left, v=−80 to −10 km s−1), and the LVC (right, −10 to 30 km s−1). |
Appendix B Position-velocity cut for Draco
Figure B.1 displays a position-velocity cut in Draco at constant declination of 62 deg in the H I line emission on a logarithmic scale. The LVC, IVC, and HVC, respectively, are indicated in the plot. While LVC and IVC are closely connected in velocity space, there is no velocity bridge between the HVC and LVC/IVC.
 |
Fig. B.1 Postion-velocity cut in Draco at a constant declination of 62 deg in the H I line emission. The full velocity range comprising the LVC, IVC, and HVC is shown and indicated in the plot. There is no clear velocity bridge between the HVC and LVC. |
Appendix C PDR toolbox results for [C II] emission
Figure C.1 displays the calculated parameter range of density and UV field from the KOSMA-τ model for [C II] 158 µm emission for masses of M = 0.1 M⊙ and M = 1 M⊙ in units of erg cm−2 s−1 sr−1. Figure C.2 displays as one example (M = 0.1 M⊙) such a plot for 12CO 2→1. Since the [C II] observations in Polaris, Musca, and Spider only represent the noise level, these figures illustrate in which direction the density and UV field goes in case of higher/lower [C II] limits.
 |
Fig. C.1 PDR toolbox predictions for the density and FUV field from [C II] 158 µm emission in erg cm−2 s−1 sr−1 using the KOSMA-τ model. The model using a mass of M = 0.1 M⊙ (Draco, Spider, Musca) is shown in the top panel, the one with M = 1 M⊙ (Polaris) in the lower panel. |
 |
Fig. C.2 PDR toolbox predictions for density and FUV field from CO(2→1) emission in erg cm−2 s−1 sr−1 using the KOSMA-τ model with the model using a mass of M = 0.1 M⊙. |
References
- Abergel, A., Boulanger, F., Delouis, J. M., Dudziak, G., & Steindling, S. 1996, A&A, 309, 245 [NASA ADS] [Google Scholar]
- Barriault, L., Joncas, G., Falgarone, E., et al. 2010a, MNRAS, 406, 2713 [NASA ADS] [CrossRef] [Google Scholar]
- Barriault, L., Joncas, G., Lockman, F. J., & Martin, P. G. 2010b, MNRAS, 407, 2645 [NASA ADS] [CrossRef] [Google Scholar]
- Bensch, F., Leuenhagen, U., Stutzki, J., & Schieder, R. 2003, ApJ, 591, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Ragan, S. E., Ossenkopf, V., et al. 2014, A&A, 571, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bialy, S., Burkhart, B., & Sternberg, A. 2017, ApJ, 843, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bisbas, T. G., Schruba, A., & van Dishoeck, E. F. 2019, MNRAS, 485, 3097 [NASA ADS] [Google Scholar]
- Blagrave, K., Martin, P. G., Joncas, G., et al. 2017, ApJ, 834, 126 [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Bonne, L., Bontemps, S., Schneider, N., et al. 2020a, A&A, 644, A27 [EDP Sciences] [Google Scholar]
- Bonne, L., Schneider, N., Bontemps, S., et al. 2020b, A&A, 641, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonne, L., Peretto, N., Duarte-Cabral, A., et al. 2022, A&A, 665, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cannon, A. J., & Pickering, E. C. 1993, VizieR Online Data Catalog: III/135A [Google Scholar]
- Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bonnell, I. A. 2012, MNRAS, 424, 2599 [CrossRef] [Google Scholar]
- Cox, N. L. J., Arzoumanian, D., André, P., et al. 2016, A&A, 590, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Creevey, O. L., Sordo, R., Pailler, F., et al. 2023, A&A, 674, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalgarno, A. 2006, Proc. Natl. Acad. Sci., 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F. X., Bazell, D., & Blitz, L. 1990, ApJ, 355, L51 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, H. W., Heithausen, A., & Thaddeus, P. 1987, ApJ, 319, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L. 2008, MNRAS, 391, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [Google Scholar]
- Falgarone, E., Panis, J. F., Heithausen, A., et al. 1998, A&A, 331, 669 [NASA ADS] [Google Scholar]
- Falgarone, E., Pety, J., & Hily-Blant, P. 2009, A&A, 507, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Franco, G. A. P. 1991, A&A, 251, 581 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Drimmel, R. et al.) 2023, A&A, 674, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Gladders, M. D., Clarke, T. E., Burns, C. R., et al. 1998, ApJ, 507, L161 [CrossRef] [Google Scholar]
- Glassgold, A. E., Galli, D., & Padovani, M. 2012, ApJ, 756, 157 [Google Scholar]
- Glover, S. C. O., & Mac Low, M.-M. 2007, ApJ, 659, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., Federrath, C., Mac Low, M. M., & Klessen, R. S. 2010, MNRAS, 404, 2 [Google Scholar]
- Glover, S. C. O., Clark, P. C., Micic, M., & Molina, F. 2015, MNRAS, 448, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, C. R., Nakariakov, V. M., & Pascoe, D. J. 2019, A&A, 624, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Langer, W. D., Pineda, J. L., & Velusamy, T. 2012, ApJS, 203, 13 [Google Scholar]
- Goldsmith, P. F., Pineda, J. L., Neufeld, D. A., et al. 2018, ApJ, 856, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Grossmann, V., & Heithausen, A. 1992, A&A, 264, 195 [NASA ADS] [Google Scholar]
- Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau Des Forêts, G. 2008, A&A, 482, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Heiles, C., & Habing, H. J. 1974, A&AS, 14, 1 [NASA ADS] [Google Scholar]
- Heithausen, A., & Thaddeus, P. 1990, ApJ, 353, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Heithausen, A., Corneliussen, U., & Grossmann, V. 1995, A&A, 301, 941 [NASA ADS] [Google Scholar]
- Heithausen, A., Weiß, A., Kerp, J., & Fritz, T. 2001, ApJ, 561, 238 [CrossRef] [Google Scholar]
- Heitsch, F., Slyz, A. D., Devriendt, J. E. G., Hartmann, L. W., & Burkert, A. 2006, ApJ, 648, 1052 [CrossRef] [MathSciNet] [Google Scholar]
- Herbstmeier, U., Heithausen, A., & Mebold, U. 1993, A&A, 272, 514 [NASA ADS] [Google Scholar]
- Heyminck, S., Graf, U. U., Güsten, R., et al. 2012, A&A, 542, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., & Falgarone, E. 2009, A&A, 500, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Imara, N., & Burkhart, B. 2016, ApJ, 829, 102 [CrossRef] [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, H., Holtzman, J. A., Allende Prieto, C., et al. 2020, AJ, 160, 120 [Google Scholar]
- Kabanovic, S., Schneider, N., Ossenkopf-Okada, V., et al. 2022, A&A, 659, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Hacar, A., Alves, J., et al. 2016, A&A, 586, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerp, J., Lenz, D., & Röhser, T. 2016, A&A, 589, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J., & Hog, E. 1998, A&A, 338, 897 [NASA ADS] [Google Scholar]
- Kramer, C., Cubick, M., Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2008, ApJ, 689, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [Google Scholar]
- Lee, H. H., Herbst, E., Pineau des Forets, G., Roueff, E., & Le Bourlot, J. 1996, A&A, 311, 690 [Google Scholar]
- Lehmann, A., Godard, B., Pineau des Forêts, G., & Falgarone, E. 2020, A&A, 643, A101 [EDP Sciences] [Google Scholar]
- Lehmann, A., Godard, B., Pineau des Forêts, G., Vidal-García, A., & Falgarone, E. 2022, A&A, 658, A165 [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, D., Kerp, J., Flöer, L., et al. 2015, A&A, 573, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesaffre, P., Pineau des Forêts, G., Godard, B., et al. 2013, A&A, 550, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Low, F. J., Beintema, D. A., Gautier, T. N., et al. 1984, ApJ, 278, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
- Marasco, A., Fraternali, F., van der Hulst, J. M., & Oosterloo, T. 2017, A&A, 607, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [CrossRef] [Google Scholar]
- Mebold, U., Cernicharo, J., Velden, L., et al. 1985, A&A, 151, 427 [Google Scholar]
- Meisner, A. M., & Finkbeiner, D. P. 2014, ApJ, 781, 5 [Google Scholar]
- Meyerdierks, H., Heithausen, A., & Reif, K. 1991, A&A, 245, 247 [NASA ADS] [Google Scholar]
- Miville-Deschênes, M. A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M. A., Salomé, Q., Martin, P. G., et al. 2017, A&A, 599, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nenkova, M., Ivezic, Ž., & Elitzur, M. 2000, ASP Conf. Ser., 196, 77 [NASA ADS] [Google Scholar]
- Ossenkopf, V., Röllig, M., Neufeld, D. A., et al. 2013, A&A, 550, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parravano, A., Hollenbach, D. J., & McKee, C. F. 2003, ApJ, 584, 797 [Google Scholar]
- Pineda, J. L., Langer, W. D., Velusamy, T., & Goldsmith, P. F. 2013, A&A, 554, A103 [CrossRef] [EDP Sciences] [Google Scholar]
- Pound, M. W., & Wolfire, M. G. 2023, AJ, 165, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Putman, M. E., Peek, J. E. G., & Joung, M. R. 2012, ARA&A, 50, 491 [Google Scholar]
- Risacher, C., Güsten, R., Stutzki, J., et al. 2018, J. Astron. Instrum., 7, 1840014 [NASA ADS] [CrossRef] [Google Scholar]
- Roccatagliata, V., Preibisch, T., Ratzka, T., & Gaczkowski, B. 2013, A&A, 554, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röhser, T., Kerp, J., Winkel, B., Boulanger, F., & Lagache, G. 2014, A&A, 564, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röhser, T., Kerp, J., Ben Bekhti, N., & Winkel, B. 2016a, A&A, 592, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röhser, T., Kerp, J., Lenz, D., & Winkel, B. 2016b, A&A, 596, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., & Ossenkopf-Okada, V. 2022, A&A, 664, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T., et al. 2007, A&A, 467, 187 [Google Scholar]
- Sauder, W. C. 1967, J. Res. Natl. Bureau Standards A. Phys. Chem., 72A, 91 [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Bontemps, S., Motte, F., et al. 2016, A&A, 591, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Ossenkopf-Okada, V., Clarke, S., et al. 2022, A&A, 666, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bonne, L., Bontemps, S., et al. 2023, Nat. Astron., 7, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Haid, S., Walch, S., Borchert, E. M. A., & Bisbas, T. G. 2020, MNRAS, 492, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Beuther, H., Walch, S., et al. 2022, MNRAS, 512, 4765 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S. & Stasinska, G. 2011, A&A, 526, A48 [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [Google Scholar]
- Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [Google Scholar]
- Valdivia, V., Hennebelle, P., Gérin, M., & Lesaffre, P. 2016, A&A, 587, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F. & Black, J. H. 1988, ApJ, 334, 771 [Google Scholar]
- Vázquez-Semadeni, E., Ryu, D., Passot, T., González, R. F., & Gazol, A. 2006, ApJ, 643, 245 [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walder, R., & Folini, D. 1998, A&A, 330, L21 [NASA ADS] [Google Scholar]
- Ward-Thompson, D., Kirk, J. M., André, P., et al. 2010, A&A, 518, L92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Westmeier, T. 2018, MNRAS, 474, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Winkel, B., Kerp, J., Flöer, L., et al. 2016, A&A, 585, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [Google Scholar]
- Xia, J., Tang, N., Zhi, Q., et al. 2022, Res. Astron. Astrophys., 22, 085017 [CrossRef] [Google Scholar]
- Yan, Q.-Z., Zhang, B., Xu, Y., et al. 2019, A&A, 624, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2020, A&A, 633, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucker, C., Goodman, A. A., Alves, J., et al. 2022, Nature, 601, 334 [NASA ADS] [CrossRef] [Google Scholar]
We express the far ultraviolet (FUV) field in units of Habing Go (Habing 1968) or Draine χ (Draine 1978), with χ = 1.71 Go.
We used the conversion N(H) = 1.87 AV 1021 cm−2 mag−1 and N(H2) = 0.94 AV 1021 cm−2 mag−1 (Bohlin et al. 1978) with the total hydrogen column density N(H) and the molecular hydrogen column density N(H2) and the visual extinction AV.
Clouds with AV < 1, AV = 1–5, and AV > 5 are typically called diffuse, translucent, and low-column density or dark clouds (Barriault et al. 2010a) respectively.
Newer numbers for the vertically integrated column from Marasco et al. (2017) are only higher by 6%.
See https://gea.esac.esa.int/archive/documentation/GDR3 for the Gaia DR3 manual.
All Tables
Draco’s CO line parameters determined from a Gaussian line fit with two velocity components.
Parameters of the minima of the RADEX fits to all four measured intensities in Draco.
All Figures
 |
Fig. 1 FIR and H I maps of Draco. Left: combined Herschel and Planck 250 µm map of the Draco cloud and its environment. The offsets in degrees correspond to the center position of RA(2000) = 16h47m57s, Dec(2000) = 61°45′16″ (l = 91.829, b = 38.156). The angular resolution of the Herschel map (in the image center) is 36″ and the one of the Planck map is ~5′. The white dashed square indicates the area for which we show the dust column density map. Right: velocity integrated H I map from the Eſſelsberg H I survey (EBHIS) at 10′ resolution. The velocity range covers the IVC and LVC. Maps of the other velocity ranges are shown in Appendix A. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for Spider. The offsets correspond to the center position of RA(2000) = 10h37m58s, Dec(2000) = 72º59′42″ (l = 135.200, b = 40.800). |
| In the text | |
 |
Fig. 3 Spectra and column density map of Draco. Right panel: Herschel hydrogen column density map derived from dust in color in which the observed [C II] positions are indicated with black crosses. In the panels around, spectra of the [C II] 158 µm line and the H I 21 cm line (DRAO), both at ~1′ resolution, are displayed. We note that the H I line was reduced for better visibility. The green curve indicates a single Gaussian fit to the [C II] line. |
| In the text | |
 |
Fig. 4 Spectra of [C II] and CO emission at the 4 positions. For better visibility of the [C II] spectra, only the Gaussian fit is shown (in green) and the 12CO line intensities were reduced by a factor of 10. |
| In the text | |
 |
Fig. 5 Spectra and column density map of Spider. Right panel: Herschel hydrogen column density map derived from dust in color in which the observed [C II] positions are indicated with black crosses. Left panels: Spectra of the [C II] 158 µm, CO, and H I (DRAO) lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
| In the text | |
 |
Fig. 6 Spectra and column density map of Polaris. Right panel: cutout of the Herschel hydrogen column density map derived from dust of Polaris in color in which the observed [C II] position indicated with black crosses. Left panel: spectra of the [C II] 158 µm and CO lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
| In the text | |
 |
Fig. 7 Spectra and column density map of Musca. Right panel: cutout of the Herschel hydrogen column density map derived from dust of Musca in color in which the observed [C II] position indicated with black crosses. Left panel: spectra of the [C II] 158 µm and CO lines, all at ~1′ resolution. We note that some line intensities were reduced for better visibility. |
| In the text | |
 |
Fig. 8 Schematic illustration of the method to derive the FUV field at each source. The gray cylinder indicates the hydrogen distribution with respect to the galactic height ɀ. The yellow stars indicate the 3D stellar distribution in the Milky Way. The solid black lines originating from the stars indicate the distance from the star to the source. The yellow halo around the star illustrates the FUV field generated by each star. The orange cylinder placed along the path between the star and the source shows schematically the hydrogen column which attenuates the FUV field. |
| In the text | |
 |
Fig. 9 PDR modeling results for Draco. Parameter space of hydrogen surface density n and FUV field calculated from the KOSMA-τ model for 0.1 M⊙ clumps taken from the PDR toolbox for the Draco Front 1 and Front 2 (left) positions and the Nose 1 and Nose 2 (right) positions. The isocontours at different colors show the observed line integrated intensities or ratios, including the rms noise. The estimated FUV field for each source from the 160 µm flux is indicated by a red dashed line. The FUV field from the census of the stars is given as a dashed blue line. |
| In the text | |
 |
Fig. 10 PDR modeling results for Spider, Polaris, and Musca. Parameter space of hydrogen density n and FUV field calculated from the KOSMA-τ model taken from the PDR toolbox for the Spider 1 position (left, 0.1 M⊙ clumps), the Polaris single pointing (middle, 1 M⊙ clumps ), and the Musca single pointing (right, 0.1 M⊙ clumps). The isocontours at different colors show the observed line integrated intensities or ratios, including the rms noise. The estimated FUV field for each source from the 160 µm flux is indicated by a red dashed line. The FUV field from the census of the stars is given as a dashed blue line. |
| In the text | |
 |
Fig. 11 Visualization of the RADEX fit to the four CO and 13CO lines at the F1 position in Draco. Each plot shows a constant temperature cut through the three dimensional distribution of line intensities and χ2 values. The kinetic temperature of the χ2 minimum, that is, 9 K (see Table 8) was used. The colors in the plot show the integrated line intensities for the four lines, the observed value is marked by a red line. The gray contours give χ2 values of 8, 16, 32, 64, and 128. As the χ2 distribution is a global property, those contours are the same in all four subplots. |
| In the text | |
 |
Fig. 12 Same as Fig. 11 but for a cut at the constant density of the χ2 minimum of 4.9 × 103 cm−3 (see Table 8). |
| In the text | |
 |
Fig. 13 RADEX results for the 13CO 1→0/2→1 and 12CO 1→0/2 → 1 brightness ratios as a function of density and temperature for the Draco front and nose positions. The observed ratios are shown as a solid and dashed black line. The density obtained with PDR modeling is marked in bold. |
| In the text | |
 |
Fig. 14 RADEX results for the 12CO 1→0/2→1 brightness ratios as a function of density and temperature for the Spider 1a position (left panel) and the Polaris positions (right panel). The observed ratios are shown as a solid and dashed black line. The density obtained with PDR modeling is marked in bold. |
| In the text | |
 |
Fig. A.1 Velocity integrated H I maps of the Draco region from the EBHIS survey. The panels show the H I line integrated emission over all velocity ranges, covering the HVC (left, v=−200 to −100 km s−1), the IVC (middle, v=−30 to −10 km s−1), and the LVC (right, −10 to 30 km s−1. For better comparison, the scale in K kms−1 was kept constant. |
| In the text | |
 |
Fig. A.2 Velocity integrated H I maps of the Spider region from the EBHIS survey. The panels show the H I line integrated emission over all velocity ranges, covering the IVC (left, v=−80 to −10 km s−1), and the LVC (right, −10 to 30 km s−1). |
| In the text | |
 |
Fig. B.1 Postion-velocity cut in Draco at a constant declination of 62 deg in the H I line emission. The full velocity range comprising the LVC, IVC, and HVC is shown and indicated in the plot. There is no clear velocity bridge between the HVC and LVC. |
| In the text | |
 |
Fig. C.1 PDR toolbox predictions for the density and FUV field from [C II] 158 µm emission in erg cm−2 s−1 sr−1 using the KOSMA-τ model. The model using a mass of M = 0.1 M⊙ (Draco, Spider, Musca) is shown in the top panel, the one with M = 1 M⊙ (Polaris) in the lower panel. |
| In the text | |
 |
Fig. C.2 PDR toolbox predictions for density and FUV field from CO(2→1) emission in erg cm−2 s−1 sr−1 using the KOSMA-τ model with the model using a mass of M = 0.1 M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.