EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 685 (May 2024) A&A, 685 (2024) A149 Full HTML
Open Access
Issue
A&A
Volume 685, May 2024
Article Number A149
Number of page(s) 15
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202449344
Published online 17 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open Access funding provided by Max Planck Society.

1 Introduction

Isotopic fractionation is an important tool to study interstellar chemistry and trace the evolution of material from molecular clouds to planetary systems (e.g., Caselli & Ceccarelli 2012; Cleeves et al. 2014; Colzi et al. 2018a; Jensen et al. 2021). In particular, the nitrogen isotopic ratio 14N/15N can trace the evolution of primordial Solar System material up to the present day (e.g., Wampfler et al. 2014; Wirström & Charnley 2018).

The 14N/15N ratio in the primitive solar nebula has been derived from measurements of the solar wind, with a result of 440 (Marty et al. 2011). While a consistent ratio was found in the atmosphere of Jupiter (14N/15N=450, Fouchet et al. 2004), an enrichment of 15N is observed towards the terrestrial atmosphere (14N/15N=272, Nier 1950) and comets (14N/15N=139, Shinnaka et al. 2014). The Solar and Jovian nitrogen isotope ratios are believed to represent the composition of the protosolar nebula, whereas the origin of the 15N-enrichment in terrestrial planets atmospheres, comets, and some meteorites is not yet fully understood. In the interstellar medium (ISM), the 14N/15N ratio varies among different sources as well as with different molecular tracers. The 14N/15N ratio in N2H+ towards starless cores has been observed to be as high as 1000 (Bizzocchi et al. 2013; Redaelli et al. 2018), while lower values of ~420 are observed toward protostars (Redaelli et al. 2020). The 14N/15N ratio in ammonia ranges between 210 and 800 in starless and protostel-lar cores (Gerin et al. 2009; Redaelli et al. 2023). The 14N/15N ratio in nitriles (CN, HCN, and HNC) observed towards low-mass starless cores ranges between 140 and 360 (Hily-Blant et al. 2020, and references therein).

An overview of the nitrogen fractionation in HCN is presented in Fig. 1. Observations cover all evolutionary stages from the starless core stages through the protoplanetary disk stage and, finally, the cometary values from the Solar System. Nonetheless, the current observational sample has proven insufficient in determining what physical and chemical processes regulate the degree of fractionation in nitrogen-bearing species and how the fractionation evolves throughout star and planet formation. Both environmental effects (e.g., differences in irradiation and temperature) and nucleosynthetic effects are possible drivers of the fractionation (see, e.g., Hily-Blant et al. 2013b; Furuya & Aikawa 2018; Colzi et al. 2018b, and references therein). Spezzano et al. (2022) mapped the column densities of nitriles in the pre-stellar core L1544 and displayed local variations in the 14N/15N ratio of HCN. These variations are consistent with a local gradient in the irradiation of the core, which could indicate that isotope-selective photodissociation plays a key role in the fractionation of nitrogen. Deciphering the underlying processes will provide a significant input to the study of chemical evolution during star- and planet formation as well as volatile delivery in the Solar System.

Previous measurements of the 14N/15N ratio in starless and pre-stellar cores have primarily used the indirect double isotope method. This method combines observations of H13CN and HC15N and assumes a fixed 12C/13C ratio to derive the abundance of the main isotopolog H12C14N and the 14N/15N ratio. The advantage of this method is that observations of the optically thick HCN are avoided. However, the assumption of a fixed12 C/13 C ratio is uncertain. Recent chemical models studying the evolution of the 12C/13C ratio in young cores have suggested that the ratio may vary significantly over time and may also depend on the local cosmic-ray ionization rate (Colzi et al. 2020; Loison et al. 2020).

As an alternative to the indirect method, the HCN abundance can be directly determined through non-Local Ther-modynamic Equilibrium (NLTE) radiative transfer modeling. Daniel et al. (2013) determined the 12C/13C and 14N/15N ratios in Barnard B1b region by combining observations of multiple HCN, H13CN, and HC15N transitions with one-dimensional (1D) NLTE radiative transfer modeling. They found a 12C/13C ratio of ~30 and a 14N/15N ratio of ~165 in HCN. Similarly, Magalhães et al. (2018) performed a direct determination of the 14N/15N ratio toward the starless core L1498, by combining observations of the 1-0 and 3-2 transition of HCN with observations of the 1-0 transitions of H13CN and HC15N and performing NLTE radiative transfer modeling. That study found that the 14N/15N ratio is consistent with the elemental value in L1495, suggesting that no fractionation of nitrogen had occurred, while a 12C/13C ratio of 45±3 was derived, suggesting instead that carbon is fractionated in the core and not consistent with the elemental ISM value of 68 (Milam et al. 2005). A third method to derive the 14N/15N and/or 12C/13C ratio of HCN is to observe the double substituted H13C15N, along with HC15N and/or H13CN. Since these isotopologs are generally optically thin, circumventing issues related to optical depth of the main HCN isotopolog. H13C15N was recently observed in the dense core surrounding the class 0 source L483. In Agúndez et al. (2019), 14N/15N = 321±96 and 12C/13C = 34±10 was found in HCN. This method has the advantage that it does not require radiative transfer modeling of the core as the direct method, but instead requires enough sensitivity and spectral resolution to observe the weaker H13C15N isotopolog at sufficiently high signal-to-noise ratio (S/N).

In this work, we present both indirect and direct determinations of the 14N/15N and 12C/13C ratios for five starless cores and one pre-stellar core. The classification of the evolutionary stage of the cores is taken from Crapsi et al. (2005), where the more evolved cores with higher central densities, higher N2D+/N2H+ ratio, and higher CO depletion are characterized as pre-stellar. The primary aim is to increase the sample of reported 14N/15N and 12C/13C ratios in starless and pre-stellar cores to determine how much variation is present at this evolutionary stage. Furthermore, we also compare the direct and indirect methods and discuss the reliability of the indirect method when determining the 14N/15N ratio of HCN.

thumbnail Fig. 1

Overview of reported 14N/15N ratios in HCN at various evolutionary stages from cores to disks. The majority of the measurements for HCN are derived using the indirect double isotope method; hence, a fixed 12C/13C ratio of 68 is assumed. Protoplanetary disks are abbreviated to PPDs in the figure. References are provided in Appendix A.

2 Observations

Six cores were observed with the IRAM 30m single-dish (Pico Veleta, Spain) in 2022. The ground-state 1-0 transition of HCN, H13CN, and HC15N were observed with the EMIR E090 receiver, using the Fourier Transform Spectrometer (FTS) with a resolution of 50 kHz. Observations of the 3–2 transition of HCN were performed with the E230 receiver using both the FTS (50 kHz resolution) and the VESPA (20 kHz resolution) back-ends simultaneously. However, issues with the VESPA backend resulted in low S/N and, consequently, this work relies on the FTS data. For each source, a single pointing toward the dust continuum peak was observed. The source sample was selected based on bright HCN 1–0 detections in a previous dataset (Colzi et al. 2018a) and Herschel/SPIKE coverage to determine the density profiles as described in the next section. An overview of the observations is provided in the log presented in Table 1. Frequency switching was performed with a frequency throw of ±3.9 MHz. Telescope pointing was checked every 1.5–2 h and focus every 3–4 h depending on the weather conditions. The data were calibrated and continuum-subtracted using the GILDAS software1.

Table 1

Observation summary.

3 Results

The observed spectra are shown in Figs. 2-5. For the 1–0 transitions of HCN, H13CN, and HC15N, a signal-to-noise ratio S/N > 10 was achieved toward all sources. For the 3-2 transition of HCN, the S/N varied significantly from source to source. This is due to the higher atmospheric absorption τ at 1 mm which makes observations of the 3–2 line more sensitive to local weather variations at Pico Veleta.

3.1 Spectral line fitting and the indirect method

The nitrogen fractionation in HCN was first determined using the indirect method assuming a fixed 12C/13C ratio of 68. The approach involves fitting the hyperfine components of the 1–0 transition of H13CN using the HFS fitting function in GILDAS CLASS software. The optical depth, column density, and excitation temperature of H13CN are determined from the HFS fit. The best fit for each core is shown in Fig. 2, along with the residuals. A summary of the physical parameters of the HFS fits is presented in Table 2. For H13CN, the 1–0 transition is optically thin (τ < 0.4 for the weakest HFS component) and the model fits the observed lines well as shown by the uniform residuals. The 1–0 transition of HC15N is fitted using a single Gaussian line profile and the column density of HC15N is determined by assuming the same excitation temperature as H13CN. Then, the HCN column density is estimated by multiplying the H13CN column density by a factor of 68 from the canonical 12C/13C ratio. The results using this method are listed in Table 3.

thumbnail Fig. 2

Observed spectra for the 1–0 transition of H13CN for the six cores. The best fit to the hyperfine structure is shown in red and residuals between the fit and the observed spectra are shown in the shaded region (shifted for clarity).
thumbnail Fig. 3

Observed spectra for the 1–0 transition of HC15N for the six cores. The best Gaussian fit to the emission line is shown in red and residuals between the fit and the observed spectra are shown in the shaded region (shifted for clarity).
thumbnail Fig. 4

Observed spectra for the 1–0 transition of HCN for the six cores.
thumbnail Fig. 5

Observed spectra for the 3-2 transition of HCN for the six cores.

3.2 Spectral modeling with LOC and the direct method

To model the observed spectra, we used the NLTE line radiative transfer code LOC (Juvela 2020). Collisional rates for HCN were sourced from the LAMDA database (Schöier et al. 2005), relying on data from the CDMS database (Müller et al. 2001; Endres et al. 2016) compiled from the studies of Ahrens et al. (2002); Fuchs et al. (2004); Cazzoli & Puzzarini (2005); Cazzoli et al. (2005); Dumouchel et al. (2010); Denis-Alpizar et al. (2013); Guzmán et al. (2017).

For a direct determination of the HCN, H13CN, and HC15N column densities, we performed ID radiative transfer modeling of each isotopolog. For the radiative transfer modeling of the emission lines a source model is needed. To derive this model, we used Herschel/SPIKE continuum maps of the cores at 250 µm, 350 µm, and 500 µm (Griffin et al. 2010). The maps were obtained from the pipeline images available in the Herschel Science Archive 2. From the three maps, the column density of molecular hydrogen N(H2) was derived following the method of Spezzano et al. (2016). Briefly, each map was smoothed to the resolution of the 500 µm image (~40”) and resampled to the same grid. Next, a modified blackbody function with the dust emissivity spectral index β = 2 was fitted to each pixel (Schnee et al. 2010). For the dust emissivity, we adopted the value κ250µm = 0.1 cm2g−1 from Hildebrand (1983). The column density maps derived for the six cores are shown in Fig. 6.

The density structure is fitted using a Plummer profile following Arzoumanian et al. (2011): ρ(r)=ρc[ 1+(r/Rflat )2 ]p/2,$\rho (r) = {{{\rho _{\rm{c}}}} \over {{{\left[ {1 + {{\left( {r/{R_{{\rm{?itat }}}}} \right)}^2}} \right]}^{p/2}}}},$(1)

where ρc is the central density, Rflat is the characteristic radius of the inner flat region, and p characterizes the slope of the density profile. The derived central densities n(H2) lie in the range (5– 20) × 104 cm−3 and are comparable to the values presented in Crapsi et al. (2005) for a subset of the cores.

For the radial temperature profile, the non-thermal line broadening, and the (infall) velocity, we adopted the parametric functions presented in Magalhães et al. (2018). The non-thermal velocity dispersion σ is defined as: σnth =σc+σext−σcπ[ π2+tanh(r−rjΔrj) ], ${\sigma _{{\rm{nth }}}} = {\sigma _{\rm{c}}} + {{{\sigma _{{\rm{ext}}}} - {\sigma _{\rm{c}}}} \over \pi }\left[ {{\pi \over 2} + \tanh \left( {{{r - {r_{\rm{j}}}} \over {\Delta {r_{\rm{j}}}}}} \right)} \right]{\rm{, }}$(2)

where σc and σext are the non-thermal broadening at the core center and core edge, respectively, and rj and Δrj define the position and the width of the transition between the two boundary values. The collapse velocity profile is presented by a Gaussian profile: v=vcexp[ −(r−rv)2/2Δrv2 ],$v = {v_{\rm{c}}}\exp \left[ { - {{\left( {r - {r_{\rm{v}}}} \right)}^2}/2\Delta r_{\rm{v}}^2} \right],$(3)

where vc denotes the peak collapse velocity, rv denotes the position of the peak collapse velocity, and Δrv defines the width of the collapsing region. The temperature structure is defined as: T=Tin +Tout −Tin 2[ 1+tanh(r−rTΔrT) ], $T = {T_{{\rm{in }}}} + {{{T_{{\rm{out }}}} - {T_{{\rm{in }}}}} \over 2}\left[ {1 + \tanh \left( {{{r - {r_{\rm{T}}}} \over {\Delta {r_{\rm{T}}}}}} \right)} \right]{\rm{, }}$(4)

where Tin and Tout denote the central and edge temperature, respectively, and rT and ΔrT define the position and the width of the transition between the two boundary values. Figure 7 shows an example of the physical core structure derived for TMC2 based on these profiles. We note that the dust temperature can also be derived from the Herschel/SPIRE fitting performed to determine the densities, displaying a good agreement with the gas temperatures derived in the outer part of the core. We chose not to use these for the temperature profiles when fitting because of the low spatial resolution, which does not resolve the lower temperatures in the center of the cores.

Because the cores have relatively low central densities (≲105 cm−3) and are not as evolved as, for instance, L1544, we also ran models with a constant velocity throughout the core. For L1495, this approach was found to give a better result than the collapsing velocity profile and is therefore used instead. In addition to the Gaussian velocity profile in Eq. (3), a number of different profiles (e.g., log-normal and Weibul) were also tested, however these did not increase the quality of the fit.

The abundance of HCN is assumed to follow a step-function with an inner and outer abundance of HCN and a variable step radius. Each parameter in the above parameterizations is free in the subsequent modeling of the HCN lines. The spectral line modeling is optimized using the Markov chain Monte Carlo (MCMC) code EMCEE (Foreman-Mackey et al. 2013). The complete process for the determination of the 14N/15N ratio with the direct method is described below.

First, the density structure of the core is derived from the Herschel/SPIRE maps. Then the 1–0 and 3–2 transitions of HCN are fitted simultaneously using the MCMC module combined with LOC. The intensities of the modeled spectra are compared bin-by-bin to the observed spectra and the χ2 is minimized.

A total of 300 walkers and 500 steps are used for the MCMC chain. The first 200 steps are discarded as burn-in. Following this, a visual inspection of the median parameters from the MCMC chain is done to determine whether a satisfactory solution was found. Once the HCN transitions have been fitted, the 1–0 transitions of H13 CN and HC15 N are fitted independently using the same physical source model derived from the HCN optimization. Hence, the only free parameters are the abundances of the 13C and 15N isotopologs. This approach assumes that the three isotopologs are co-spatial, which is a common assumption in fractionation studies, but it should be noted that some local effects may arise from isotope-selective photodissociation. However, from the single-pointing data presented here, toward the dust continuum peak of each source, we do not expect a substantial impact on the results in this work.

Figures 8–12 show the median solution from the MCMC analysis for all sources except L1495AN, which was excluded as no satisfying solution was found. TMC2, L1512, and CB23 show the smallest residuals between the spectra and the spectral model across the four transitions, while the spectral models for L1495 and L1517B show larger residuals.

Corner plots showing the distribution of the parameter space explored by the workers are shown in Fig. 13 for TMC2. Figures B.1–B.4 show the corner plots for the remaining sources. In the case of TMC2, the plot indicates that most parameters are well-constrained, with approximately Gaussian distributions around the median. The results of the direct method are listed in Table 4 and a comparison between the HCN column densities derived using the direct and indirect methods are presented in Fig. 14. The direct method generally predicts higher HCN column densities than the indirect, corresponding to a lower 12C/13C ratio.

Table 2

Parameters for the HFS fit for H13CN.

Table 3

Estimated column densities derived using the indirect (double isotope) method assuming a fixed 12C/13C ratio of 68.

thumbnail Fig. 6

Column density maps of H2 derived from Herschel/SPIRE maps. The black cross marks the center of the core. The beam size is shown for the largest beam at 500 µm and identical for all the maps. A distance of 140 pc is assumed for all sources.
thumbnail Fig. 7

Physical structure of TMC2 according to the best-fit model. The velocities are scaled for clarity.
thumbnail Fig. 8

Comparison between the modeled and observed spectra for the three isotopologs toward TMC2. Each panel shows the 1D spectral model in red and the observed spectrum in blue. Residuals between the model and the data are shown in black, offset for clarity.
thumbnail Fig. 9

Same as Fig. 8, for CB23.
thumbnail Fig. 10

Same as Fig. 8, for L1495.
thumbnail Fig. 11

Same as Fig. 8, for L1512.
thumbnail Fig. 12

Same as Fig. 8, for L1517B.
thumbnail Fig. 13

Corner plot for the fitting of HCN and the physical structure of the core for TMC2.
Table 4

Estimated column densities derived using the direct method.

thumbnail Fig. 14

Comparison between estimated HCN column densities using the direct and indirect methods. In general, the column densities are underestimated using the indirect method, except for CB23 and L1517B where the results of the two methods are within the uncertainties.

4 Discussion

4.1 Comparison of the direct and indirect method

Determining the abundance of HCN is often challenging due to its high optical thickness. This issue can be circumvented by using the indirect double isotope method, where a fixed 12C/13C ratio is assumed. However, the extent to which the assumption of a fixed 12C/13C ratio is reliable is unclear and may depend on both the type of source studied and the molecule in question.

In Fig. 15, we present the 14N/15N ratio of HCN for various evolutionary stages when using both the indirect double isotope method (blue) and the direct method (brown) for starless and pre-stellar cores in the literature as well as those presented in this work. A clear shift in the mean 14N/15N ratio (dash-dotted lines) between the two methods is present. This shift is large enough to alter the interpretation of the current data, as discussed in the next section. The observed shift in the nitrogen fractionation is directly related to the 12C/13C ratios in HCN, which are generally between 20 and 40, instead of the local ISM values of 68. Here, one exception is TMC2, which is consistent with the ISM value. The derived 12C/13C ratios are generally consistent with those derived in other cold sources such as L1498 (45±3, Magalhães et al. 2018), B1-b (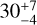30−4+7$30_{ - 4}^{ + 7}$, Daniel et al. 2013), and the cold envelope of L483 (34±10, Agúndez et al. 2019). If we assume a lower ratio of, for instance, 12C/13C = 30 for all starless and pre-stellar cores, the shift between the two methods falls within the uncertainty of these measurements. This underlines the significance of the assumed 12C/13C ratio and the weakness of the indirect method. With the data presented here and the results from other cold sources listed above, the assumption of a fixed 12C/13C ratio in the starless and pre-stellar core stage appear not to be valid. This is also supported by the recent astrochemical modeling of the 12C/13C ratio in HCN, which does not find that a fixed value of the 12C/13C ratio is a good assumption (Colzi et al. 2020; Loison et al. 2020). These modeling efforts suggest that the ratio varies significantly over time and with physical conditions. Sipilä et al. (2023) modeled the fractionation ratios of HCN including both 13C and 15N in their network. By comparing the modeled abundances of HCN, HC15N, and H13CN, they demonstrated that the indirect method using 12C/13C = 68 can lead to errors of an order of magnitude in the inferred 14N/15N ratio. Their chemical model predicts 12C/13C ratios below 50 in cold and dense environments (T = 7 K, 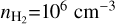nH2=106 cm−3${n_{{{\rm{H}}_2}}} = {10^6}{\rm{c}}{{\rm{m}}^{ - 3}}$, t > 105 yr, priv. comm.), in agreement with the observational results for cold sources.

The indirect method is widely used at the protostellar and protoplanetary disk stages (e.g., Wampfler et al. 2014; Guzmán et al. 2017), where the effects of the double isotope method is less studied. Currently, the 14N/15N ratio of HCN have been estimated directly in one disk, TW Hydra (Hily-Blant et al. 2019), in which a disk-averaged 12C/13C ratio of 84±4 and 14N/15N ratio of 223±21 was found. Again, the carbon fractionation ratio differs from 68 and may induce systematic errors if the indirect double isotope method is used in protoplanetary disks. More direct determinations of the HCN abundance and the 12C/13C and 14N/15N ratios toward protostars and protoplanetary disks are needed to determine the robustness of the indirect method in these sources.

4.2 Inheritance or processing of HCN during star formation

Nitrogen fractionation can serve as a powerful tracer of the chemical evolution during star- and planet formation. This requires robust determinations of the different isotopic abundances at different stages of the star and planet formation process to trace how the fractionation evolves with time. Due to the possible systematic errors when using the indirect method as highlighted in the previous section, care should be taken when comparing nitrogen fractionation ratios across evolutionary stages using different methods.

The majority of the measurements presented in Fig. 15 are derived using the indirect method. If we only consider isotopic ratios derived using the direct method, then the nitrogen fraction-ation ratio in HCN remains almost constant within the reported errors. This is suggesting that no significant processing of HCN occurs between the different evolutionary stages, which influences the nitrogen fractionation. However, the picture is different if we include all measurements from indirect measurements. Here, a lower 14N/15N ratio is seen at the protoplanetary disk stage compared to the starless and pre-stellar core stage. Based on the current data, we cannot determine whether HCN is processed during the collapse of the core to form the protostar and protoplanetary disk.

thumbnail Fig. 15

Overview of reported 14N/15N ratios in HCN at various evolutionary stages from cores to disks. For cores, the indirect measurements are indicated in blue and the direct in brown. The majority of the measurements for both protostars and protoplanetary disks (PPDs) are derived using the indirect double isotope method and hence assume a fixed 12C/13C ratio of 68. The dashed-dotted lines show the weighted average of each population.

4.3 Challenges of the direct method

The results presented here, along with the recent astrochemical modeling of carbon and nitrogen fractionation (e.g., Sipilä et al. 2023) suggest that the indirect method is unreliable and should be used cautiously. However, using radiative transfer modeling to provide direct estimates of the HCN abundances is also challenging, as this work shows. The uncertainty on the source structure results in a large number of free parameters. The models presented here include up to 14 parameters when fitting the HCN 1–0 and 3–2 hyperfine lines. This number can be reduced if better constraints on the physical structure of the cores can be obtained, for example, through additional continuum observations with a broader wavelength coverage and higher spatial resolution. Furthermore, the assumption of a 1D core structure is also in itself a limitation, as shown by chemical segregation in L1544 (e.g., Spezzano et al. 2016) and recent astrochemical modeling (e.g., Priestley et al. 2023; Jensen et al. 2023). Another challenge when modeling HCN arises from the hyperfine anomalies reported for a wide number of different sources (Mullins et al. 2016). The cause of these anomalies is not yet understood and they make the spectral fitting challenging. Because of the challenges listed above, the approach of observing H13C15N, H13CN, and HC15N should also be considered in future works when sufficient S/N can be achieved, as this method does not rely on a well-constrained source structure. However, robust detections of the weaker H13C15N transition in the sources presented here would require decreasing the root mean square (RMS) noise level by a factor of ~ 10, meaning a increased integration time by a factor of ~100. Measurements of H13C15N are therefore likely to be reserved for sources with higher column densities or deep studies of individual sources.

5 Conclusions

This paper presents IRAM 30m observations of HCN, H13CN, and HC15N toward six starless and pre-stellar cores. The nitrogen fractionation ratio 14N/15N is determined using first the indirect double isotope method and later directly by fitting the spectra with NLTE radiative transfer models of the cores to determine the molecular abundances. The latter method is challenging and only successful for five of the six cores.

With the results of the indirect method, an apparent trend in the 14N/15N ratio of HCN from starless cores to protostars and protoplantery disks is present, with higher values around 14N/15N ~ 300-550 in the earlier core phases and 14N/15N < 250 in the later protoplanetary disk phase. However, this trend is not present when we instead use the direct method to determine both 14N/15N and 12C/13C ratios directly. The difference between the two methods can be attributed to a lower 12C/13C ratio in HCN within the range 20–40 for most cores instead of the ISM values of 68. When the results of the direct method are used, the apparent evolutionary trend in the 14N/15N ratio is eliminated, which could suggest that HCN is inherited from the earliest stages of star formation and does not experience significant processing. However, as many of the previous measurements are done using the indirect method, more direct measurements needs to be done in the protostellar and protoplanetary disk phases to test this statement. Since this work shows a substantial difference in the interpretation of the data when the direct and indirect methods are used, caution should be exercised while comparing direct and indirect data points in the search for evolutionary trends. Ultimately, the indirect method appears unreliable and future work should aim to obtain direct estimates of the 14N/15N ratio at all evolutionary stages to determine whether HCN is inherited or processed during the formation of stars and planets. This can be achieved either through radiative transfer modeling (as in this work) or by observing the double-substituted H13C15N (when feasible). While these direct methods are more challenging, they provide additional data on the carbon fractionation during star and planet formation, further improving our understanding of chemical evolution in the interstellar medium.

Acknowledgements

The authors wish to thank the referee for useful comments which helped improve the manuscript. S.S.J., S.S., and K.G. wish to thank the Max Planck Society for the Max Planck Research Group funding. All other authors affiliated to the MPE wish to thank the Max Planck Society for financial support. The Tycho supercomputer hosted at the SCIENCE HPC center at the University of Copenhagen was used for supporting this work. We acknowledge project support by the Max Planck Computing and Data Facility. This paper makes use of MATPLOTLIB (Hunter 2007), EMCEE (Foreman-Mackey et al. 2013), and SCIPY (Virtanen et al. 2020).

Appendix A Table of 14N/15N ratios in HCN

Values reported in Figs. 1 and 15 are presented in Table A.1, along with the method used and references.

Table A.1

Measured HC14N/HC15N ratios for various sources.

Appendix B Corner plots

thumbnail Fig. B.1

Corner plot for the fitting of HCN and the physical structure of the core for CB23.
thumbnail Fig. B.2

Corner plot for the fitting of HCN and the physical structure of the core for L1495.
thumbnail Fig. B.3

Corner plot for the fitting of HCN and the physical structure of the core for L1512.
thumbnail Fig. B.4

Corner plot for the fitting of HCN and the physical structure of the core for L1517B.

References

  1. Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
  2. Ahrens, V., Lewen, F., Takano, S., et al. 2002, Zeitsch. Naturforsch. Teil A, 57, 669 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, A6 [Google Scholar]
  4. Bizzocchi, L., Caselli, P., Leonardo, E., & Dore, L. 2013, A&A, 555, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bockelée-Morvan, D., Biver, N., Jehin, E., et al. 2008, ApJ, 679, L49 [CrossRef] [Google Scholar]
  6. Caselli, P., & Ceccarelli, C. 2012, A&A Rev., 20, 56 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cazzoli, G., & Puzzarini, C. 2005, J. Mol. Spectrosc., 233, 280 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cazzoli, G., Puzzarini, C., & Gauss, J. 2005, ApJS, 159, 181 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cleeves, L. I., Bergin, E. A., Alexander, C. M. O. D., et al. 2014, Science, 345, 1590 [NASA ADS] [CrossRef] [Google Scholar]
  10. Colzi, L., Fontani, F., Caselli, P., et al. 2018a, A&A, 609, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Colzi, L., Fontani, F., Rivilla, V. M., et al. 2018b, MNRAS, 478, 3693 [Google Scholar]
  12. Colzi, L., Sipilä, O., Roueff, E., Caselli, P., & Fontani, F. 2020, A&A, 640, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
  14. Daniel, F., Gérin, M., Roueff, E., et al. 2013, A&A, 560, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Denis-Alpizar, O., Kalugina, Y., Stoecklin, T., Vera, M. H., & Lique, F. 2013, J. Chem. Phys., 139, 224301 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dumouchel, F., Faure, A., & Lique, F. 2010, MNRAS, 406, 2488 [NASA ADS] [CrossRef] [Google Scholar]
  17. Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
  18. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  19. Fouchet, T., Irwin, P. G. J., Parrish, P., et al. 2004, Icarus, 172, 50 [CrossRef] [Google Scholar]
  20. Fuchs, U., Bruenken, S., Fuchs, G. W., et al. 2004, Zeitsch. Naturforsch. Teil A, 59, 861 [NASA ADS] [CrossRef] [Google Scholar]
  21. Furuya, K., & Aikawa, Y. 2018, ApJ, 857, 105 [Google Scholar]
  22. Galli, P. A. B., Loinard, L., Ortiz-Léon, G. N., et al. 2018, ApJ, 859, 33 [Google Scholar]
  23. Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [EDP Sciences] [Google Scholar]
  25. Guzmán, V. V., Öberg, K. I., Huang, J., Loomis, R., & Qi, C. 2017, ApJ, 836, 30 [Google Scholar]
  26. Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
  27. Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013a, Icarus, 223, 582 [Google Scholar]
  28. Hily-Blant, P., Pineau des Forêts, G., Faure, A., Le Gal, R., & Padovani, M. 2013b, A&A, 557, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hily-Blant, P., Magalhaes de Souza, V., Kastner, J., & Forveille, T. 2019, A&A, 632, A12 [Google Scholar]
  30. Hily-Blant, P., Pineau des Forêts, G., Faure, A., & Flower, D. R. 2020, A&A, 643, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  32. Ikeda, M., Hirota, T., & Yamamoto, S. 2002, ApJ, 575, 250 [NASA ADS] [CrossRef] [Google Scholar]
  33. Jensen, S. S., Jørgensen, J. K., Kristensen, L. E., et al. 2021, A&A, 650, A172 [EDP Sciences] [Google Scholar]
  34. Jensen, S. S., Spezzano, S., Caselli, P., Grassi, T., & Haugbølle, T. 2023, A&A, 675, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Juvela, M. 2020, A&A, 644, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Loison, J.-C., Wakelam, V., Gratier, P., & Hickson, K. M. 2020, MNRAS, 498, 4663 [Google Scholar]
  37. Magalhães, V. S., Hily-Blant, P., Faure, A., Hernandez-Vera, M., & Lique, F. 2018, A&A, 615, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
  39. Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [Google Scholar]
  40. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
  41. Mullins, A. M., Loughnane, R. M., Redman, M. P., et al. 2016, MNRAS, 459, 2882 [Google Scholar]
  42. Nier, A. O. 1950, Phys. Rev., 77, 789 [NASA ADS] [CrossRef] [Google Scholar]
  43. Priestley, F. D., Whitworth, A. P., & Fogerty, E. 2023, MNRAS, 518, 4839 [Google Scholar]
  44. Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2018, A&A, 617, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Redaelli, E., Bizzocchi, L., & Caselli, P. 2020, A&A, 644, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Redaelli, E., Bizzocchi, L., Caselli, P., & Pineda, J. E. 2023, A&A, 674, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Schnee, S., Enoch, M., Noriega-Crespo, A., et al. 2010, ApJ, 708, 127 [NASA ADS] [CrossRef] [Google Scholar]
  48. Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [Google Scholar]
  49. Shinnaka, Y., Kawakita, H., Kobayashi, H., Nagashima, M., & Boice, D. C. 2014, ApJ, 782, L16 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sipilä, O., Colzi, L., Roueff, E., et al. 2023, A&A, 678, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Spezzano, S., Bizzocchi, L., Caselli, P., Harju, J., & Brünken, S. 2016, A&A, 592, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Spezzano, S., Caselli, P., Sipilä, O., & Bizzocchi, L. 2022, A&A, 664, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261 [CrossRef] [Google Scholar]
  54. Wampfler, S. F., Jørgensen, J. K., Bizzarro, M., & Bisschop, S. E. 2014, A&A, 572, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Wirström, E. S., & Charnley, S. B. 2018, MNRAS, 474, 3720 [CrossRef] [Google Scholar]
  56. Yoshida, K., Sakai, N., Nishimura, Y., et al. 2019, PASJ, 71, S18 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observation summary.

In the text
Table 2

Parameters for the HFS fit for H13CN.

In the text
Table 3

Estimated column densities derived using the indirect (double isotope) method assuming a fixed 12C/13C ratio of 68.

In the text
Table 4

Estimated column densities derived using the direct method.

In the text
Table A.1

Measured HC14N/HC15N ratios for various sources.

In the text

All Figures

thumbnail Fig. 1

Overview of reported 14N/15N ratios in HCN at various evolutionary stages from cores to disks. The majority of the measurements for HCN are derived using the indirect double isotope method; hence, a fixed 12C/13C ratio of 68 is assumed. Protoplanetary disks are abbreviated to PPDs in the figure. References are provided in Appendix A.
In the text
thumbnail Fig. 2

Observed spectra for the 1–0 transition of H13CN for the six cores. The best fit to the hyperfine structure is shown in red and residuals between the fit and the observed spectra are shown in the shaded region (shifted for clarity).
In the text
thumbnail Fig. 3

Observed spectra for the 1–0 transition of HC15N for the six cores. The best Gaussian fit to the emission line is shown in red and residuals between the fit and the observed spectra are shown in the shaded region (shifted for clarity).
In the text
thumbnail Fig. 4

Observed spectra for the 1–0 transition of HCN for the six cores.
In the text
thumbnail Fig. 5

Observed spectra for the 3-2 transition of HCN for the six cores.
In the text
thumbnail Fig. 6

Column density maps of H2 derived from Herschel/SPIRE maps. The black cross marks the center of the core. The beam size is shown for the largest beam at 500 µm and identical for all the maps. A distance of 140 pc is assumed for all sources.
In the text
thumbnail Fig. 7

Physical structure of TMC2 according to the best-fit model. The velocities are scaled for clarity.
In the text
thumbnail Fig. 8

Comparison between the modeled and observed spectra for the three isotopologs toward TMC2. Each panel shows the 1D spectral model in red and the observed spectrum in blue. Residuals between the model and the data are shown in black, offset for clarity.
In the text
thumbnail Fig. 9

Same as Fig. 8, for CB23.
In the text
thumbnail Fig. 10

Same as Fig. 8, for L1495.
In the text
thumbnail Fig. 11

Same as Fig. 8, for L1512.
In the text
thumbnail Fig. 12

Same as Fig. 8, for L1517B.
In the text
thumbnail Fig. 13

Corner plot for the fitting of HCN and the physical structure of the core for TMC2.
In the text
thumbnail Fig. 14

Comparison between estimated HCN column densities using the direct and indirect methods. In general, the column densities are underestimated using the indirect method, except for CB23 and L1517B where the results of the two methods are within the uncertainties.
In the text
thumbnail Fig. 15

Overview of reported 14N/15N ratios in HCN at various evolutionary stages from cores to disks. For cores, the indirect measurements are indicated in blue and the direct in brown. The majority of the measurements for both protostars and protoplanetary disks (PPDs) are derived using the indirect double isotope method and hence assume a fixed 12C/13C ratio of 68. The dashed-dotted lines show the weighted average of each population.
In the text
thumbnail Fig. B.1

Corner plot for the fitting of HCN and the physical structure of the core for CB23.
In the text
thumbnail Fig. B.2

Corner plot for the fitting of HCN and the physical structure of the core for L1495.
In the text
thumbnail Fig. B.3

Corner plot for the fitting of HCN and the physical structure of the core for L1512.
In the text
thumbnail Fig. B.4

Corner plot for the fitting of HCN and the physical structure of the core for L1517B.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.