| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202347628 | |
| Published online | 15 May 2024 | |
A parsec-scale Galactic 3D dust map out to 1.25 kpc from the Sun★
1
Max Planck Institute for Astrophysics,
Karl-Schwarzschild-Straße 1,
85748
Garching bei München,
Germany
e-mail: edh@mpa-garching.mpg.de
2
Ludwig Maximilian University of Munich,
Geschwister-Scholl-Platz 1,
80539
München,
Germany
3
Center for Astrophysics | Harvard & Smithsonian,
60 Garden St.,
Cambridge,
MA 02138,
USA
4
Space Telescope Science Institute,
3700 San Martin Dr,
Baltimore,
MD 21218,
USA
5
Department of Statistical Sciences, University of Toronto,
Toronto
ON M5G 1Z5,
Canada
6
David A. Dunlap Department of Astronomy & Astrophysics, University of Toronto,
Toronto,
ON M5S 3H4
Canada
7
Dunlap Institute for Astronomy & Astrophysics, University of Toronto,
Toronto,
ON M5S 3H4,
Canada
8
Data Sciences Institute, University of Toronto,
Toronto,
ON M5G 1Z5,
Canada
Received:
2
August
2023
Accepted:
19
January
2024
Context. High-resolution 3D maps of interstellar dust are critical for probing the underlying physics shaping the structure of the interstellar medium, and for foreground correction of astrophysical observations affected by dust.
Aims. We aim to construct a new 3D map of the spatial distribution of interstellar dust extinction out to a distance of 1.25 kpc from the Sun.
Methods. We leveraged distance and extinction estimates to 54 million nearby stars derived from the Gaia BP/RP spectra. Using the stellar distance and extinction information, we inferred the spatial distribution of dust extinction. We modeled the logarithmic dust extinction with a Gaussian process in a spherical coordinate system via iterative charted refinement and a correlation kernel inferred in previous work. In total, our posterior has over 661 million degrees of freedom. We probed the posterior distribution using the variational inference method MGVI.
Results. Our 3D dust map has an angular resolution of up to 14′ (Nside = 256), and we achieve parsec-scale distance resolution, sampling the dust in 516 logarithmically spaced distance bins spanning 69 pc to 1250 pc. We generated 12 samples from the variational posterior of the 3D dust distribution and release the samples alongside the mean 3D dust map and its corresponding uncertainty.
Conclusions. Our map resolves the internal structure of hundreds of molecular clouds in the solar neighborhood and will be broadly useful for studies of star formation, Galactic structure, and young stellar populations. It is available for download in a variety of coordinate systems online and can also be queried via the publicly available dustmaps Python package.
Key words: ISM: clouds / ISM: structure / dust, extinction / Galaxy: structure / methods: statistical
A movie and a 3D interactive figure associated with Fig. 5 are available at https://aanda.org
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Interstellar dust comprises only 1% of the interstellar medium by mass but absorbs and re-radiates >30% of starlight at infrared wavelengths (Popescu & Tuffs 2002). As such, dust plays an out-sized role in the evolution of galaxies, catalyzing the formation of molecular hydrogen, shielding complex molecules from the UV radiation field, coupling the magnetic field to interstellar gas, and regulating the overall heating and cooling of the interstellar medium (Draine 2011).
Dust's ability to scatter and absorb starlight is precisely the reason why we can probe it in three spatial dimensions. It preferentially absorbs shorter wavelengths of a stellar spectrum, thus leading to stars behind dense dust clouds appearing reddened relative to their intrinsic colors. The amount by which stars behind dust clouds appear reddened allows us to infer the amount of dust extinction between us and the reddened star. In combination with distance measurements to reddened stars, we can de-project the integrated extinction measurements into a 3D map of differential dust extinction.
Gaia has been transformative for the field by providing accurate distance information to more than 1 billion stars, primarily within a few kiloparsecs of the Sun. Precise distances not only improve our knowledge about a star's position, they also break degeneracies inherent in the modeling of extinction and significantly reduce the extinction uncertainties (Zucker et al. 2019). Thanks to the large quantity of extinction and distance measurements available in the era of large photometric, astrometric, and spectroscopic surveys, we can now probe the 3D distribution of dust in the Milky Way on parsec scales.
A number of 3D dust maps that combine Gaia and vast photometric and spectroscopic surveys already exist. These maps primarily differ in the way they account for the so-called fingers-of-god effect, or the tendency of dust structures to be smeared out along the line of sight (LOS). The effect stems from superior constraints on stars' plane-of-sky (POS) positions relative to their LOS distance uncertainties.
Three-dimensional dust maps predominantly fall into two categories, each representing a trade-off between angular resolution and distance resolution: reconstructions on a Cartesian grid and reconstructions on a spherical grid. Cartesian reconstructions commonly feature less pronounced fingers-of-god but scale poorly with the size of the reconstructed volume. They either encompass a limited volume of the Galaxy (Leike et al. 2020; Leike & Enßlin 2019) at a high resolution or cover a larger volume of the Galaxy at a low resolution (Vergely et al. 2022; Lallement et al. 2022, 2019, 2018; Capitanio et al. 2017). Spherical reconstructions often have a much higher resolution and probe larger volumes of the Galaxy but come with more strongly pronounced fingers-of-god artifacts (Green et al. 2019, 2018; Chen et al. 2019). Alternative approaches using many small reconstructions (Leike et al. 2022), an analytical approach (Rezaei Kh. & Kainulainen 2022; Rezaei Kh. et al. 2020, 2018, 2017), or inducing point methods (Dharmawardena et al. 2022) have so far been unsuccessful in reconstructing dust at high resolution over large volumes without artifacts.
Physical smoothness priors counterbalance the fingers-of-god effect as finger-like structures are a priori unlikely. In a Cartesian coordinate system it is comparatively easy to incorporate physical priors into the model, such as the distribution of dust being spatially smooth. Smoothness priors are often incorporated using Gaussian process (GP) priors. Sparsities and symmetries in the prior can be exploited to efficiently apply a GP to a regular Cartesian coordinate system.
Spherical coordinate systems break these sparsities and symmetries in the prior but are much better aligned with the desired spacing of voxels along the LOS. Nearby, voxels can be spaced densely, while at greater distances voxels can be spaced further apart. Naively using a GP prior is infeasible, and approximations either trade fingers-of-god artifacts for other artifacts (Leike et al. 2022) or are too weak to regularize the reconstructions (Green et al. 2019).
In this work, we present a 3D dust map that achieves high distance and angular resolution and probes a large volume of the Galaxy, all at a feasible computational cost. The map uses a new GP prior methodology to incorporate smoothness in a spherical coordinate system, mitigating fingers-of-god artifacts. With a spherical coordinate system we were able to probe dust beyond 1 kpc while still resolving nearby dust clouds at parsec-scale resolution. In Sec. 2, we present the stellar distance and extinction estimates upon which our map is based. In Sect. 3, we present our GP prior methodology for incorporating smoothness in a spherical coordinate system. Section 4 describes how we combine the data with our prior model and how we incorporate the distance uncertainties of stars. In Sect. 5, we describe our inference before recapitulating all approximations of the model and their implications in Sec. 6. Finally, in Sec. 7 we present the final map and compare it to existing 3D dust maps and 2D observations.
2 Stellar distance and extinction data
To construct a 3D dust map, we used the stellar distance and extinction estimates from Zhang et al. (2023), which are primarily based on the Gaia BP/RP spectra (spectral resolution R ~ 30-100). Zhang et al. (2023) adopted a data-driven approach to forward-model the extinction, distance, and intrinsic parameters of each star given the combination of the Gaia BP/RP spectra and infrared photometry from the two micron all sky survey (2MASS) and unWISE, a processed catalog based on the wide-field infrared survey explorer (WISE) (Carrasco et al. 2021; De Angeli et al. 2023; Gaia Collaboration 2023; Montegriffo et al. 2023; Schlafly et al. 2019; Wright et al. 2010; Skrutskie et al. 2006). The model is trained using a subset of stars with higher resolution spectra (R ~ 1800) available from the large sky area multi-object fibre spectroscopic telescope (LAMOST) (Wang et al. 2022; Xiang et al. 2022). The resulting catalog contains distance, extinction, and stellar type (Teff, [Fe/H], log g) information for 220 million stars. Throughout this work, we denote the Zhang et al. (2023) catalog by ZGR23.
Compared to other stellar distance and extinction catalogs, the ZGR23 catalog features smaller uncertainties on the extinction estimates while still targeting a significant number of stars. Approximately 87 million ZGR23 stars have an AV uncertainty below 60 mmag. Thus, ZGR23 achieves similar extinction uncertainties compared to the subset of 39,538 stars in the StarHorse catalog (Queiroz et al. 2023) that have both higher resolution spectra from the Apache point observatory galactic evolution experiment (APOGEE) and grizy photometry from the panoramic survey telescope and rapid response system (Pan-STARRS), specifically Pan-STARRS1 (PS1; Chambers et al. 2016) (typical AV extinction uncertainty of 60 mmag). While the ZGR23 catalog is limited to stars with Gaia BP/RP measurements, the quality of the data makes the inference from the ZGR23 catalog competitive with models based on catalogs with larger numbers of stars - 799 million stars in Bayestar19 (Green et al. 2019), 265 million in StarHorse DR2 (Anders et al. 2019), and 362 million in StarHorse EDR3 (Anders et al. 2022). We further find the ZGR23 catalog to have fewer systematic shifts in the extinction and reliable extinction uncertainties based on an analysis in dust-free regions; further details are given in Appendix A.
For our reconstruction, we restricted our analysis to ZGR23 stars that have quality_flags<8, as recommended by the authors. We further sub-selected the stars based on their distance. We required ![$\[1 /_\left(\omega-\sigma_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq1.png) < 1.8 kpc and
< 1.8 kpc and ![$\[1 /_\left(\omega-\sigma_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq2.png) > 40 pc with ω the parallax of a star and σω the parallax uncertainty to enforce that all stars are likely within our reconstructed volume. In total, we selected 53 880 655 stars.
> 40 pc with ω the parallax of a star and σω the parallax uncertainty to enforce that all stars are likely within our reconstructed volume. In total, we selected 53 880 655 stars.
The reliability of our reconstruction is predominantly limited by the quality and quantity of the data. Both strongly depend on the POS position and distance. Figure 1 shows 2D histograms of stellar density in heliocentric Galactic Cartesian (X, Y, Z) projections, as well as the number of stars as a function of distance. The densities of stars per distance bin first increases approximately quadratically with distance before falling off to a linear increase. At approximately 1.5 kpc the number of stars per distance bin levels off due to our requirement that stars have a >1 sigma chance of being within 1.8 kpc in distance. Figure 2 shows a POS histogram of the stars. A clear imprint of the Gaia BP/RP selection function is visible (cf. Cantat-Gaudin et al. 2023). A systematic under-sampling of stars behind dense dust clouds is also apparent. We expect our reconstruction to be more trustworthy in regions of higher stellar density. Due to the obscuring effect of dust, regions within and behind dense dust clouds should be treated with more caution.
3 Priors
Our quantity of interest is the 3D distribution of differential ZGR23 extinction ρ.1 By definition, the differential extinction is positive. Furthermore, we assumed it to be spatially smooth. A priori we assumed the level of smoothness to be spatially stationary and isotropic.
To reconstruct the 3D volume efficiently, we discretized it in spherical coordinates. Specifically, we discretized our reconstructed volume into HEALPix spheres at logarithmically spaced distances. We adopted an Nside of 256, which corresponds to 786 432 POS bins. This Nside corresponds to an angular size of our voxels of 14′. For the LOS direction, we adopted 772 logarithmically spaced distance bins, of which 256 are used for padding. Our highest distance discretization is 0.4 pc and our lowest distance discretization is 7 pc. In contrast to reconstructions with linearly spaced voxels in distance, we were able to probe much larger volumes while maintaining a high sampling at nearby distances. The discretization provides a lower bound on the minimum separation between dust structures that we are able to resolve. In practice the resolvable separation depends on the quantity and quality of the data and varies with the POS and LOS position.
We encoded both positivity and smoothness in our model by assuming the differential extinction to be log-normally distributed:
![$\[\rho=\exp s,\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq3.png) (1)
(1)
with normally distributed s, where s is drawn from a GP with a homogeneous and isotropic correlation kernel, k. From previous reconstructions of the differential extinction for the Gaia DR2 G-band AG (Leike et al. 2020), we have constraints on the correlation kernel of the logarithm of the differential extinction in a volume around the Sun (|X| < 370 pc, |Y| < 370 pc, |Z| < 270 pc). As part of our prior model, we used the inferred AG extinction kernel from Leike et al. (2020). To account for the conversion between the ZGR23 extinction and AG extinction, we added a global multiplicative factor to s in our model.2 Furthermore, we inferred an additive offset in the differential extinction. We placed a log-normal prior on the multiplicative parameter and a normal prior on the additive one.
We enforced the correlation kernel k using iterative charted refinement (ICR; Edenhofer et al. 2022). ICR enables us to enforce a kernel on arbitrarily spaced voxels by representing the modeled volume at multiple discretizations. It starts from a very coarse view of our modeled volume. On this coarsest scale, ICR models the GP with learned voxel excitations ![$\[\xi_e^{(0)}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq4.png) and an explicit full kernel covariance matrix. A priori the parameters
and an explicit full kernel covariance matrix. A priori the parameters ![$\[\xi_e^{(0)}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq5.png) are standard normally distributed and coupled according to k via ICR. It then iteratively refines nlvl times its coarse view of the space with local, fine, a priori standard normally distributed corrections
are standard normally distributed and coupled according to k via ICR. It then iteratively refines nlvl times its coarse view of the space with local, fine, a priori standard normally distributed corrections ![$\[\xi_e^{(1)}, \ldots, \xi_e^{\left(n_{\mathrm{lvl}}\right)}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq6.png) until reaching the desired discretization. In each refinement, it uses ncsz neighbors from the previous refinement to refine one coarse pixel into nfsz fine pixels (see Algorithm 1).
until reaching the desired discretization. In each refinement, it uses ncsz neighbors from the previous refinement to refine one coarse pixel into nfsz fine pixels (see Algorithm 1).
Iterative charted refinement uses local corrections at varying discretizations and within a refinement assumes the previous iteration to have modeled the GP without error. Both lead to slight errors in representing the kernel. For our use case, we encountered errors in representing the kernel of a few percent. We accepted these errors as a trade-off that enables the reconstruction to probe larger volumes. We refer to Edenhofer et al. (2022) for a detailed discussion of the kernel approximation errors.
![$\[ \left\{\xi_e^{(0)}, \ldots, \xi_e^{\left(n_\mathrm{lvl}\right)}\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq7.png) Each coarse pixel at location j is iteratively refined to nfsz fine pixels using ncsz coarse pixel neighbors. The correlation kernel is denoted by k. Square brackets after variables and the two functions ndindex and shape denote NumPy-like (Harris et al. 2020) indexing routines. The call explicit_gp refers to an unspecified Gaussian Process model explicitly representing the covariance of k for the pixel positions modeled by ξe(e)
Each coarse pixel at location j is iteratively refined to nfsz fine pixels using ncsz coarse pixel neighbors. The correlation kernel is denoted by k. Square brackets after variables and the two functions ndindex and shape denote NumPy-like (Harris et al. 2020) indexing routines. The call explicit_gp refers to an unspecified Gaussian Process model explicitly representing the covariance of k for the pixel positions modeled by ξe(e)
Overall, our model for the prior reads
![$\[\rho=\exp \left[\operatorname{scl}\left(\xi_{\text {scl }}\right) \cdot s\left(\xi_e^{(0)}, \ldots, \xi_e^{\left(n_{\mathrm{lvl}}\right)}\right)+\operatorname{off}\left(\xi_{\text {off }}\right)\right],\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq8.png) (2)
(2)
where we denote the learned multiplicative scaling of s by scl, the learned additive offset by off, and re-expressed both in terms of a priori standard normally distributed parameters ξscl and ξoff, respectively. The act of expressing scl, off and s via parameters with an a priori simpler distribution, here a standard normal distribution, is called re-parameterization. A detailed discussion on this subject is given in Rezende & Mohamed (2015).
 |
Fig. 1 2D histograms of the density of stars in heliocentric Galactic Cartesian (X, Y, Z) projections, as well as the density of stars as a function of distance, for the subset of the ZGR23 catalog used in the reconstruction of our 3D dust map. Panel a: heliocentric Galactic Cartesian-projected histograms. Panel b: number of stars as a function of distance. This panel also shows a linear growth and a quadratic growth with distance for comparison. |
 |
Fig. 2 POS distribution of the subset of ZGR23 stars used in the reconstruction of our 3D dust map. |
4 Likelihood
To construct the likelihood we first needed to define how the differential extinction ρ – our quantity of interest – connects to the measured data 𝒟. Our data comprise POS position, extinction 𝒟A, and parallax 𝒟ω data. The POS position is in essence without error. The extinction data 𝒟A = {A, σA} are in the form of integrated LOS extinctions to stars A and associated uncertainties σA The parallax data 𝒟ω = {ω, σω} similarly are in the form of parallax estimates ω and uncertainties σω.
Our model focuses on the measured extinction, A, and does not predict parallaxes to stars. Instead, we conditioned our model on the parallax data, 𝒟ω, and split the likelihood into the probability of the measured extinction given the true extinction, a, and the probability of the true extinction given uncertain parallax information:
![$\[P\left(A \mid \rho, \mathcal{D}_\omega\right)=\int \mathrm{d} a \,P\left(A, a \mid \rho, \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq15.png) (3)
(3)
![$\[=\int \mathrm{d} a \,P(A \mid a) \cdot P\left(a \mid \rho, \mathcal{D}_\omega\right) \text {. }\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq16.png) (4)
(4)
The first term of the integrand is constrained by the quality of the extinction measurements and the second by the quality of the parallax measurements.
4.1 Response
The second term in Eq. (4), P(a |ρ, 𝒟ω), can be expressed as the joint probability of extinction and true distance, d, marginalized over the true distance:
![$\[P\left(a \mid \rho, \mathcal{D}_\omega\right)=\int \mathrm{d} d \,P\left(a, d \mid \rho, \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq18.png) (5)
(5)
![$\[=\int \mathrm{d} d\, P\left(a \mid \rho, \mathcal{D}_\omega, d\right) \cdot P\left(d \mid \rho, \mathcal{D}_\omega\right).\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq19.png) (6)
(6)
We neglected data selection effects (i.e., a's dependence on 𝒟ω given d and d's dependence on ρ given 𝒟ω) and used the fact that the true extinction, a, at known distance d is simply the LOS integral of ρ along the LOS to the star from zero to d:
![$\[P\left(a \mid \rho, \mathcal{D}_\omega\right)=\int \mathrm{d} d \,P(a \mid \rho, d) \cdot P\left(d \mid \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq22.png) (7)
(7)
}_{:=R^d(\rho)}\right) \cdot P\left(d \mid \mathcal{D}_\omega\right),\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq23.png) (8)
(8)
with ρ[POS] the slice of ρ at the POS positions of the stars, δ the Dirac delta distribution defined by ![$\[\int_{-\infty}^{\infty} \mathrm{d} x\, f(x) \delta(x)=f(0)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq24.png) for any continuous f with compact support, and R the response that maps from ρ to the domain of the measured extinction.
for any continuous f with compact support, and R the response that maps from ρ to the domain of the measured extinction.
We approximated P(a|ρ, 𝒟ω) with a normal distribution,
![$\[P\left(a \mid \rho, \mathcal{D}_\omega\right) \approx \mathcal{G}\left(a \mid \bar{a}, \sigma_a^2\right),\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq26.png) (9)
(9)
with mean ![$\[\bar{a}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq27.png) and standard deviation σa to obtain a tractable expression for Eq. (4). The mean extinction,
and standard deviation σa to obtain a tractable expression for Eq. (4). The mean extinction, ![$\[\bar{a}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq28.png) , is
, is
![$\[\bar{a}:=\langle a\rangle_{P\left(a \mid \rho, \mathcal{D}_\omega\right)}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq29.png) (10)
(10)
![$\[=\int \mathrm{d} a\, a \int \mathrm{d} d\, \delta\left(a-R^d(\rho)\right) \cdot P\left(d \mid \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq30.png) (11)
(11)
![$\[=\int\,\int \mathrm{d} a \mathrm{~d} d \,a \cdot \delta\left(a-R^d(\rho)\right) \cdot P\left(d \mid \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq31.png) (12)
(12)
![$\[=\int \mathrm{d} d\, R^d(\rho) \cdot P\left(d \mid \mathcal{D}_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq32.png) (13)
(13)
![$\[=\left\langle R^d(\rho)\right\rangle_{P\left(d \mid \mathcal{D}_\omega\right)}.\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq33.png) (14)
(14)
Assuming the parallax 1/d is normally distributed (i.e., ![$\[P\left(d \mid \mathcal{D}_\omega\right)=\mathcal{G}\left(1 / d \mid \omega, \sigma_\omega^2\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq34.png) with mean ω and standard deviation σω), then
with mean ω and standard deviation σω), then
 \cdot \mathrm{sf}_{\mathcal{G}}\left(1 / \tilde{d} \mid \omega, \sigma_\omega^2\right),\end{aligned}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq35.png) (15)
(15)
with ![$\[\operatorname{sf}_{\mathcal{G}}\left(1 / d \mid \omega, \sigma_\omega^2\right):=1-\int_{-\infty}^{1 / d} \mathrm{~d} \omega^{\prime}\, \mathcal{G}\left(\omega^{\prime} \mid \omega, \sigma_\omega^2\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq36.png) the survival function of the normal distributed parallax.
the survival function of the normal distributed parallax.
The standard deviation ωa can be understood as an additional error contribution for marginalizing over the distance. The error depends on the distance uncertainty and the dust along the full LOS:
![$\[\sigma_a^2:=\left\langle\left(R^d(\rho)\right)^2\right\rangle_{\mathcal{G}\left(1 / d \mid \omega, \sigma_\omega^2\right)}-\left\langle R^d(\rho)\right\rangle_{\mathcal{G}\left(1 / d \mid \omega, \sigma_\omega^2\right)}^2.\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq37.png) (16)
(16)
Evaluating both ![$\[\bar{a}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq38.png) and
and ![$\[\sigma_a^2\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq39.png) is comparatively cheap in a spherical coordinate system since for a discretized sphere Rd(ρ) is simply the cumulative sum of ρ along the distance axis weighted by the radial extent of each voxel.
is comparatively cheap in a spherical coordinate system since for a discretized sphere Rd(ρ) is simply the cumulative sum of ρ along the distance axis weighted by the radial extent of each voxel.
Parameters of the prior distributions.
4.2 Likelihood and joint probability density
We assumed the measured extinction to be normally distributed around the true extinction a. We took the inferred extinction, A, from the catalog to be the mean of the normal distribution. The accompanying uncertainty σA in the catalog was assumed to be the standard deviation of P(A | a).
Some stars will have underestimated uncertainties due to either mismodeled intrinsic stellar properties in the inference or bad photometric measurements that were not flagged. We wanted our model to be able to detect and deselect stars that are in strong disagreement with the rest of the reconstruction. We achieved this by inferring an additional multiplicative factor per star, nσ, which scales σA. A priori, we assumed nσ to be drawn from a heavy-tailed distribution. Specially, we assumed nσ to follow an inverse gamma distributed. We again express nσ in terms of standard normally distributed parameters nσ(ξσ) in the inference.
To summarize, our approximate likelihood first introduced in Eq. (4), reads
![$\[\begin{aligned}& P\left(A \mid \rho, n_\sigma, \mathcal{D}_\omega\right) \\& \approx \int \mathrm{d} a\, \mathcal{G}\left(A \mid a,\left(n_\sigma \cdot \sigma_A\right)^2\right) \cdot \mathcal{G}\left(a \mid \bar{a}(\rho), \sigma_a^2(\rho)\right)\end{aligned}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq40.png) (17)
(17)
![$\[=\mathcal{G}\left(A \mid \bar{a}(\rho),\left[n_\sigma \cdot \sigma_A\right]^2+\sigma_a^2(\rho)\right) .\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq41.png) (18)
(18)
The uncertainty in the extinction σA is scaled by nσ to deselect outliers and increased by ![$\[\sigma_a^2\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq42.png) due to marginalizing over the distance uncertainty.
due to marginalizing over the distance uncertainty.
The joint probability density function of data and parameters reads
![$\[\begin{aligned}& P\left(A, \rho(\xi), n_\sigma(\xi) \mid \mathcal{D}_\omega\right) \\& \quad=\mathcal{G}\left(A \mid \bar{a}(\rho(\xi)),\left[n_\sigma(\xi) \cdot \sigma_A\right]^2+\sigma_a^2(\rho(\xi))\right) \cdot \mathcal{G}(\xi \mid 0,1),\end{aligned}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq43.png) (19)
(19)
with ξ the vector of all parameters of the model ![$\[\left\{\xi_e^{(0)}, \ldots, \xi_e^{\left(n_{\mathrm{lvl}}\right)}, \xi_{\mathrm{scl}}, \xi_{\mathrm{off}}, \xi_\sigma\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq44.png) . The complexity of the prior distributions has been fully absorbed into the transformations s(ξ), scl(ξ), off(ξ), and nσ(ξ) from the a priori standard normally distributed parameters ξ.
. The complexity of the prior distributions has been fully absorbed into the transformations s(ξ), scl(ξ), off(ξ), and nσ(ξ) from the a priori standard normally distributed parameters ξ.
Our priors in terms of nonstandard-normal parameters are summarized in Table 1. The priors for s, scl, and off are chosen to a priori yield the kernel reconstructed in Leike et al. (2020). In contrast to Leike et al. (2020), we do not learn a full non-parametric kernel. However, we do infer scl and off, the scale, and zero-mode of the kernel. The prior for nσ was chosen such that the inverse gamma distribution has mode 1 and standard deviation 2.
5 Posterior inference
In the previous section we took special care to express our model not only in terms of physical parameters, like the differential extinction density ρ, but also in terms of simpler parameters ξ. The act of expressing the parameters of the model scl, off, s, and nσ in terms of a priori standard normal distributed variables ξ is called standardization, a special from of re-parameterization (see Rezende & Mohamed 2015). Effectively, we are shifting complexity from the prior to the likelihood. However, both the nonstandardized and the standardized formulation of the joint model are equivalent. Standardizing models can lead to better conditioned inference problems as the parameters all vary on the same scales – if the prior is not in conflict with the likelihood. We used an inference scheme that relies on the standardized formulation.
We wanted to infer the posterior for our standardized model from Eq. (19). Directly probing the posterior via sampling methods such as Hamiltonian Monte Carlo Hoffman & Gelman (2014) is computationally infeasible. Instead, we used variational inference to approximate the true posterior. Specifically, we used metric Gaussian variational inference (MGVI; Knollmüller & Enßlin 2019). We summarize the main idea behind MGVI in Appendix B. We did not approximate the posterior of the noise inference parameter nσ(ξσ) via variational inference and instead used only the maximum of the posterior for ξσ.
To speed up the inference, we started the reconstruction at a lower resolution (196, 608 POS bins at Nside = 128 and 388 LOS distance bins) and restricted the inference to a subset of stars with a ≥2 sigma chance of being within 600 pc and a ≥2 sigma chance of being farther than 40 pc. We successively increased the distance range of the map up to which stars are incorporated in steps of 300 pc from 600 pc to 1.8 kpc. Every time we increased the distance range, we reset the parameters for nσ. Then, after all data were incorporated, we increased the angular and distance resolution of the reconstruction to the final resolution.
Our data selection deselects stars close to the maximum distance probed (cf. Fig. 1). This effect leads to the outer regions of the map being informed by relatively few stars compared to the inner regions. We observe that these regions are prone to producing spurious features. For our final data products, we removed the outermost 550 pc from the data-constrained volume as we observed artifacts aligned with our data incrementation strategy within these regions. We believe 550 pc to be a conservative cut but we advise caution when finding structures perfectly aligned with a sphere around the Sun at 600 pc, 900 pc, or 1200 pc.
ZGR23 assumes all extinctions to be strictly positive. We neglected this constraint by assuming Gaussian errors, which led to an artificial spike in extinction in the first few voxels in each direction. As we know those regions to be effectively free of dust from previous reconstructions cf. Leike et al. (2020), we removed the innermost 69 pc (see Appendix C). We release an additional HEALPix map of integrated extinction out to 69 pc from the Sun and suggest using it to correct integrated LOS predictions for the removed extinction.
Our inference heavily utilizes derivatives of various components of our model. Derivatives are used for the minimization as well as for the variational approximation of the posterior. Previous models such as those described in Leike & Enßlin (2019) and Leike et al. (2020) relied on the Numerical Information Field Theory (NIFTy) package (Selig et al. 2013; Steininger et al. 2019; Arras et al. 2019) and were limited to running on CPUs.
We employed a new framework called NIFTy.re (Edenhofer et al., in prep.) for deploying NIFTy models to GPUs. NIFTy.re is part of the NIFTy Python package and internally uses JAX (Bradbury et al. 2018) to run models on the GPU. We were able to speed up the evaluation of the value and gradient of Eq. (19) by two orders of magnitude by transitioning from CPUs to GPUs. Our reconstruction ran on a single NVIDIA A100 GPU with 80 GB of memory for about four weeks.
6 Caveats
We believe statistical uncertainties are the dominant source of uncertainty for our reconstruction. However, it is important to also consider sources of systematic uncertainties. Depending on the application, the systematic uncertainties may be more important than the statistical uncertainties. The data that informed the reconstruction, the model with which we inferred it, and the inference procedure all contribute to the model systematic uncertainties.
Naturally, the data themselves are a source of systematic uncertainties (spatially stationary reddening law, mismodeling of binaries, etc.; see Zhang et al. 2023) and additionally is known to be incomplete, cf. Fig. 2. A lower stellar density, for example in heavily obscured regions, limits the map's resolution and results in volumes of the map behind dense dust clouds being poorly constrained. Thus, we believe our dust reconstruction to be an underestimation of the true extinction toward dense dust clouds. Zucker et al. (2021) also note this effect when comparing the Leike et al. (2020) map with 2D integrated extinction maps based on infrared photometry, finding that the Leike et al. (2020) is not sensitive to regions with AV ≳ 2 mag.
We advise visualizing the stellar density in the region of interest to assess the magnitude of the systematic uncertainties due to data incompleteness. We release all stars used in the reconstruction as an additional data product. This data product can be used to visualize the stellar density. In regions with a significant underdensity of stars, we expect the systematic lack of stars to dominate the statistical uncertainties in the reconstruction. The reconstruction produced plausible infills in those regions based on adjacent stars. However, the resulting uncertainties do not capture the cause for the systematic lack of stars as the model implicitly assumes that underdensities of stars are not systematic but purely random.
Our model includes a number of approximations. First, we assumed a GP prior on the logarithmic dust extinction using the kernel from Leike et al. (2020) and additionally only applied it approximately via ICR. Second, we assumed 𝒟ω to be independent of 𝒟A. Third, we assumed the parallax error to be Gaussian, and fourth, we assumed the extinction error to be Gaussian.
For extremely low extinctions, the assumption of A being Gaussian is poor due to the positivity prior in the ZGR23 catalog. We corrected for this bias toward higher estimated extinction in regions with assumed extremely low true extinctions post-hoc by cutting away the innermost 69 pc as described in Sect. 5. We publish an auxiliary map of integrated extinction out to 69 pc from the Sun to correct integrated LOS predictions for the removed extinction. We suggest adding the removed local extinction back to the map when comparing integrated extinctions. By default, the removed local extinction is added back to the map when querying integrated extinctions via dustmaps.
We further release a catalog of the predicted extinctions of our model to all stars that we used for the reconstruction. In Appendix D, we perform a non-exhaustive consistency test comparing our predictions to the ZGR23 ones. We find that both predictions for the extinction to stars disagree below 50 mmag and above 4 mag; 34% more stars than expected have larger (respectively smaller) extinction predictions compared to ZGR23. We expect the range from 50 mmag to 4 mag to correspond to the range within which our map is reliable. More details are provided in Appendix D.
Furthermore, our posterior inference is an approximation. We assume our approximation of the true posterior accurately captures the intrinsic model uncertainties (cf. Arras et al. 2022; Leike & Enßlin 2019; Leike et al. 2020; Mertsch & Phan 2023; Roth et al. 2023a,b; Hutschenreuter et al. 2023, 2022; Tsouros et al. 2024). However, we worried about structures getting burned in when we increase the maximum distance probed during the inference from 600 pc to 1800 pc in steps of 300 pc as described in Sec. 5. We checked the final reconstruction for this effect by comparing it against a larger reconstruction that does not sub-select the stars based on their distance during the inference but uses only a small subsample of ZGR23 stars with more stringent quality flags. The larger reconstruction, which extends out to 2 kpc in distance, is released as an additional data product. We find no significant differences between both runs. Details on the larger reconstruction are provided in Appendix E.
 |
Fig. 3 Mollweide projection of the POS integrated AV extinction out to 250 pc, 500 pc, 750 pc, and up to the maximum distance of our map. The colorbar saturates at the 99.9% quantile. |
 |
Fig. 4 Same as Fig. 3 but showing the difference between the integrated extinctions in between distance slices projected on the POS. The colorbar saturates at the 99.9% quantile. |
7 Results
We reconstructed 12 samples (6 antithetically drawn samples) of the 3D dust extinction distribution, each of which encompasses 607 125 504 differential extinction voxels. The voxels are arranged on 772 HEALPix spheres with Nside = 256 spaced at logarithmically increasing distances. After removing the innermost <69 pc and outermost >1250 pc HEALPix spheres, we are left with 516 HEALPix spheres. The samples, the posterior mean, and the posterior standard deviation for the reconstruction are publicly available online.3 We strongly advise using the samples for any quantitative analysis. For convenience, we also provide the posterior mean and standard deviation of the reconstruction interpolated to heliocentric Galactic Cartesian Coordinates (X, Y, Z) and Galactic spherical Coordinates (l, b, d) as well as the scripts for the interpolation. Furthermore, the map can be queried via the dustmaps Python package (Green 2018). Further details on using the reconstruction are given in Appendix F.
The distance discretization in our reconstruction is highest for close-by voxels and decreases further out. Our highest distance discretization is 0.4 pc and our lowest distance discretization is 7 pc while our angular discretization is 14′ and is independent of the distance. The stated discretizations specify the lower bound on our resolution. The minimum separation that we are able to resolve depends on the position and is encoded in the posterior samples. For small regions, we suggest additionally analyzing the stellar density (see Sec. 6) to assess the strength of the systematic uncertainties due to the density of stars.
The reconstruction is in terms of the unitless ZGR23 extinction as defined in Zhang et al. (2023). For visualization purposes, we translated the ZGR23 extinction to Johnson's V-band λ = 540.0 nm, that is to say, Av : = A(V = 540.0 nm). To perform the conversion, we adopted the extinction curve published in ZGR23 and multiplied the unitless ZGR23 extinction by a factor of 2.8. We refer readers to the full extinction curve4 from Zhang et al. (2023) for the coefficients needed to translate the extinction to other bands.
Figure 3 depicts the POS projection of the posterior mean reconstruction integrated out to 250 pc, 500 pc, 750 pc, and up to the end of our sphere. The AV values are in units of magnitudes. We see that higher-latitude features like the Aquila Rift are comparatively close-by while structures in the Galactic plane appear only gradually. Figure 4 shows the difference between the integrated POS projections. We recover well-known features of integrated dust but are now able to de-project them.
Figure 5 shows a bird's eye (X, Y), side-on (X, Z), and (Y, Z) projection of the posterior mean of our reconstruction in heliocentric Galactic Cartesian coordinates. The image depicts the innermost 2.5 kpc × 2.5 kpc × 0.8 kpc around the Sun in AV extinction integrated over z from −400 pc to 400 pc, y in −1.25 kpc to 1.25 kpc, and x in −1.25 kpc to 1.25 kpc, respectively. In Fig. 6, we overlay a catalog of clusters of young stellar objects (YSOs; Kuhn 2023, priv. comm.) based on Kuhn et al. (2021), Winston et al. (2020), and Marton et al. (2023), which are shown as blue dots. The positions of the YSO clusters visually agree with the positions of dust clouds within the YSO clusters' reported distance uncertainties.
The posterior standard deviation divided by the posterior mean of the reconstruction is shown in Fig. 7. The map features a faint speckle pattern. This is likely due to the low number of samples relative to the number of degrees of freedom. The standard deviation is on the order of 10% of the posterior mean and slightly increases with distance. Toward the galactic center behind the dust in the immediate vicinity of roughly 300 pc, the relative uncertainty is noticeably higher.
The reconstruction has a high dynamic range and reveals faint dust lanes in the reconstructed volume. Small approximately spherical cavities are evident throughout the map. The dust clouds in the reconstruction are compact and only weakly elongated radially. Prominent large-scale features, such as the Radcliffe Wave (Alves et al. 2020) and the Split (Lallement et al. 2019), have been resolved at an unprecedented level of detail, previously only accessible for the most nearby dust clouds.
Comparison to existing 3D dust maps. In this section, we compare our map to other 3D dust maps in the literature. We denote the dust map described in Leike et al. (2020) by LGE20, Vergely et al. (2022) by VLC22, Green et al. (2019) by Bayestar19, and Leike et al. (2022) by L+22 in this section. For the purposes of comparison, we show the posterior mean. We release the statistical uncertainties as additional data products, and we strongly advise taking into account the released statistical uncertainties for any quantitative analysis. However, the differences between the various 3D dust reconstructions discussed here are systematic differences and are not captured by the reconstructed statistical uncertainties.
In Fig. 8, we show 3D (X, Y, Z) projections of the maps, comparing Bayestar19, VLC22, L+22, and this work side by side. All four maps agree on the general structure of the distribution of dust.
This work, L+22, and VLC22 have comparable distance resolutions, while Bayestar19 features comparatively few distance bins and more strongly pronounced fingers-of-god. Compared to L+22, we feature more homogeneously extended dust clouds and significantly fewer wiggles in the distances to dust clouds. Compared to VLC22, we feature more compact dust clouds, less grainy structures, and a higher dynamic range. Both this work and VLC22 feature dust clouds in a comparable volume around the Sun despite the VLC22 map technically extending out farther in Galactic heliocentric X and Y.
Figure 9 shows the same projections for the volume reconstructed in the LGE20 map and includes the LGE20 map for comparison. The zoom-in highlights the close similarity between this work and the LGE20 map. All larger structures have direct correspondences in the other map, yet the distances to the structures are slightly different. Furthermore, the LGE20 map appears slightly sharper. The model in LGE20 is very similar to ours but uses fewer approximations. LGE20 also uses compiled data (StarHorse DR2; see Anders et al. 2019). More work is needed to assess the validity of the sharper features in LGE20 not present in this work. The VLC22 map is in good agreement as well but lower resolution. Bayestar19 poorly resolves distances at the scale of the LGE20 map.
Figure 10 quantitatively compares our map with LGE20, VLC22, and Bayestar19. We compared the integrated extinction for each pixel center of a HEALPix sphere with Nside = 64 at 1182 test points that are placed at 1 pc intervals in distance starting at 69 pc. We compared integrated extinctions because slight shifts in the distances to extincted regions can be better distinguished from discrepant predictions with integrated extinctions than by directly comparing differential extinctions. Above 15 mmag, VLC22 and LGE20 are in good agreement with our map. Below an AV of 40 mmag and above an AV of approximately 3.5 mag, Bayestar19 significantly deviates from our predictions.
In Fig. 11, we compare the POS view of Bayestar19, L+22, VLC22, LGE20, and this work. The respective POS views are integrated out to the maximum distance probed by each map – <63 kpc in distance for Bayestar19 (maximum reliable distance 10 kpc), <4 kpc in distance for L+22 (authors trust structures up to 4 kpc though the map extends to 16 kpc), a heliocentric box of size 3 kpc × 3 kpc × 800 pc with 103 pc3 voxels for VLC22 with at most 2.16 kpc in distance, and a heliocentric box of size |X|, |Y| < 370 pc, |Z| < 270 pc and up to 590 pc in distance for LGE20. In addition, we show the Planck 2013 extragalactic dust map (Planck Collaboration XI 2014) and the Gaia total galactic extinction (TGE) 2022 map (Delchambre et al. 2023).
All maps agree on fine structures at high galactic latitudes but differ in the Galactic plane due to the difference in distance up to which the respective reconstruction extends. 3D dust reconstructions do not probe deep enough into the Galactic plane to fully recover the Planck 2013 extragalactic dust map. Bayestar19 and L+22 probe much deeper than VLC22, LGE20, and this work, yet they do not probe the full column of dust seen in Planck 2013 and Gaia TGE 2022. Both VLC22 and our map probe up to a similar depth while LGE20 only probes dust at much closer distances.
Figure 12 shows a zoomed-in comparison of the Perseus, Orion A, Taurus, Corona Australis (CrA), and Chamaeleon molecular clouds, integrated out to the maximum distance of each map (4 kpc for L+22). Among the 3D dust reconstructions, Bayestar19 and L+22 have arguably the highest angular resolution (angular discretization of Nside = 1024 or 3.4′ and 1.9′, respectively). They resolve the high latitude dust clouds with great detail although L+22 suffers from localized artifacts in patches of the sky. Both LGE20 (1 pc3 boxes) and this work (Nside = 256) achieve a comparable angular resolution. The VLC22 reconstruction (103 pc3 voxels) is noticeably lower in resolution and does not resolve the cloud substructure on the POS. A comparison between the same molecular clouds in different distance slices in VLC22, LGE20, and our map is provided in Appendix G.
 |
Fig. 5 Heliocentric Galactic Cartesian (X, Y, Z) projections of the posterior mean of our 3D dust map in a box with dimensions 2.5 kpc × 2.5 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. A GIF of the posterior samples and a low-resolution 3D interactive version of this figure are available online. |
 |
Fig. 6 Same as Fig. 5 but with a catalog of clusters of YSOs (Kuhn 2023, priv. comm.) based on Kuhn et al. (2021), Winston et al. (2020), and Marton et al. (2023) shown as blue dots on top of the reconstruction; their distance uncertainties are shown as extended lines. |
 |
Fig. 7 Heliocentric Galactic Cartesian (X, Y, Z) projections of the relative uncertainty of the reconstructed dust extinction integrated within a box of 2.5 kpc × 2.5 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. |
 |
Fig. 8 Side by side views of the 3D dust maps from Bayestar19, VLC22, L+22, and this work, shown in heliocentric Galactic Cartesian (X,Y,Z) projections. The colorbars are saturated at the 99.9% quantile of the respective reconstruction. |
 |
Fig. 9 Zoomed-in version of Fig. 8 for the volume reconstructed in Leike et al. (2020), now also showing the LGE20 reconstruction for comparison. We omit L+22 from the comparison because the authors explicitly focus on larger volumes and trade strongly pronounced artifacts in the inner couple hundred parsecs for a larger probed volume. The colorbars are again saturated at the 99.9% quantile of the respective reconstruction. |
 |
Fig. 10 Histogram of the mean posterior extinction of our map versus LGE20, VLC22, and Bayestar19 for 58 million test points. For each pixel center of a HEALPix sphere with Nside = 64, 1182 test points are placed at 1 pc intervals in distance starting at 69 pc. The orange lines show the 16th, 50th, and 84th quantiles of the predicted extinction by LGE20, VLC22, and Bayestar19, respectively, for each bin of our mean extinction. The respective quantiles of our predictions in bins of the other reconstruction are shown as blue lines. The bisectors are shown in red. The colorbars are logarithmic and truncated at the lower end at 1 mmag. |
 |
Fig. 11 Mollweide projections of total integrated extinction and 3D extinction maps integrated out the maximum distance of the respective map. Bayestar19 reconstructs up to a maximum distance of 63 kpc (maximum reliable distance 10 kpc) and is integrated out to that volume. L+22 reconstructs up to a maximum distance of 16 kpc but the authors trust their map only out to 4 kpc and we integrate their map only to 4 kpc. VLC22 reconstructs a heliocentric box of size 3 kpc × 3 kpc × 800 pc with 103 pc3 voxels with at most <2.16 kpc in distance and is integrated out to the end of the box. Likewise, LGE20 reconstructs a heliocentric box of size |X| < 370 pc, |Y| < 370 pc, |Z| < 270 pc covering at most <590 pc in distance and is integrated out to the end of the box. The colorbars saturate at the respective 99% quantile of the map except for the colorbar of Planck 2013, which saturates at 5 mag for better comparability. |
 |
Fig. 12 Zoomed-in views toward the individual molecular clouds (Perseus, Orion, Taurus, Corona Australis, and Chamaeleon) seen in Fig. 11. The colorbars are logarithmic and span the full dynamic range of the selected POS slice in every image. Each row is a separate region and each column a separate reconstruction. |
8 Conclusions
We present a 3D dust map with a POS and LOS resolution comparable to Leike et al. (2020) that extends out to 1.25 kpc. We used the distance and extinction estimates of Zhang et al. (2023), which have much lower extinction uncertainties than competing catalogs while probing a similar number of stars. Our reconstruction has a resolution comparable to the 2 pc resolution of Leike et al. (2020). Specifically, it has an angular resolution of up to 14′ and parsec-scale distance resolution. Our map is in good agreement with existing 3D dust maps and improves upon them in terms of volume covered at a high spatial resolution. The map is publicly available online5 and can be queried via the dustmaps Python package. We anticipate that the map will be useful for a wide range of applications in studying the distribution of dust and the interstellar medium more broadly.
Movies
Movie 1 associated with Fig. 5 (21b9_final) Access here
Interactive 3D version associated with Fig. 5 (3D_Dust_Edenhofer2023) Access here
Acknowledgements
We thank Joao Alves for many fruitful discussions at the “Self-Organization Across Scales: from nm to parsec (SOcraSCALES)” workshop at the Munich Institute for Astro-, Particle and BioPhysics, an institute of the Excellence Cluster ORIGINS in 2022 and afterwards. Furthermore, we thank Jakob Roth for many invaluable discussions about the model and for providing feedback on the early versions of the reconstruction. We thank Alyssa Goodman for providing invaluable feedback on the late versions of the reconstructions. We also thank Michael A. Kuhn for providing us with a unified catalog of YSOs. Gordian Edenhofer acknowledges the support of the German Academic Scholarship Foundation in the form of a PhD scholarship (“Promotionsstipendium der Studienstiftung des Deutschen Volkes”). Catherine Zucker acknowledges that support for this work was provided by NASA through the NASA Hubble Fellowship grant #HST-HF2-51498.001 awarded by the Space Telescope Science Institute (STScI), which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. Philipp Frank acknowledges funding through the German Federal Ministry of Education and Research for the project ErUM-IFT: Informationsfeldtheorie für Experimente an Großforschungsanlagen (Förderkennzeichen: 05D23EO1). Andrew K. Saydjari acknowledges support by a National Science Foundation Graduate Research Fellowship (DGE-1745303). Andrew K. Saydjari and Douglas Finkbeiner acknowledge support by NASA ADAP grant 80NSSC21K0634 “Knitting Together the Milky Way: An Integrated Model of the Galaxy's Stars, Gas, and Dust”. This work was supported by the National Science Foundation under Cooperative Agreement PHY-2019786 (The NSF AI Institute for Artificial Intelligence and Fundamental Interactions). A portion of this work was enabled by the FASRC Cannon cluster supported by the FAS Division of Science Research Computing Group at Harvard University. We acknowledge support by the Max-Planck Computing and Data Facility (MPCDF). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Appendix A ZGR23 in dust-free regions
To gauge the reliability of the ZGR23 catalog, we analyzed the extinction to stars in dust-free regions (cf. Leike & Enßlin 2019; Leike et al. 2020). In dust-free regions, we would expect the extinction to be zero within the uncertainties of the catalog. To classify a region as dust-free, we used the Planck dust emission map (Planck Collaboration XI 2014). A region is said to be dust-free if the Planck E(B – V) map is below or equal to 9.5 mmag or approximately 29 mmag in terms of AV.
 |
Fig. A.1 Absolute and relative ZGR23 extinction in dust-free regions. Panel (a): Histogram of the ZGR23 extinctions in dust-free regions translated to AV. The mean extinction in dust-free regions based on Planck is shown as a vertical green line, and the cutoff value translated to AV for our definition of dust-free is shown in red. Panel (b): Same as panel (a) but the extinctions are scaled by their accompanying uncertainties. A truncated standard normal distribution and a standard normal distribution are plotted on top. Both ordinates are logarithmic. |
The first panel of Figure A.1 shows the histogram of ZGR23 extinction to stars with quality_flags<8 in dust-free regions translated to AV. We see that the histogram of the extinction peaks at the cutoff value and coincides with the mean total extinction as measured by Planck in those regions translated to AV. The density of extinction values falls of exponentially after the cutoff value. Overall, the ZGR23 extinction seems to be in good agreement with Planck Collaboration XI (2014) for dust-free regions.
The second panel of Figure A.1 shows the extinction divided by their uncertainties for the stars from Figure A.1. The standardized extinctions are centered around unity, indicating that the ZGR23 extinction indeed are offset from zero by about one standard deviation in dust-free regions. This is in agreement with the previous finding that the extinctions are centered around the cutoff value instead of clustering around zero. The width around the center is comparable to a truncated standard normal distribution or a normal distribution. In total, about 1% of the probability mass lies outside the possible range of all ZGR23 extinction with quality_flags <8 if we assume a normal distribution for the extinctions.
Except for outliers far from the center, which can be captured by an outlier model, the ZGR23 catalog seems to be in agreement with POS measurements in dust-free regions and the spread around the cutoff value approximately follows a (truncated) normal distribution. We deem the ZGR23 catalog to be reliable for our purposes and approximate the uncertainties using a normal distribution. We accepted the mismodeling of a small fraction of probability mass for a simpler model (see Sections 5 and 6).
Appendix B Metric Gaussian variational inference
The variational inference method MGVI approximates the true posterior P(ξ|d) with a standard normal distribution in a linearly transformed space in which the posterior more closely resembles a standard normal. Let ![$\[Q_{\bar{\xi}}(y \mid d)=\mathcal{G}(y(\xi) \mid y(\bar{\xi}), \nVdash)\left|\frac{\mathrm{d} y}{\mathrm{~d} \xi}\right|\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq46.png) be the approximate posterior and y(ξ): ξ ↦ y(ξ) the coordinate transformation. In this space the transformed posterior reads
be the approximate posterior and y(ξ): ξ ↦ y(ξ) the coordinate transformation. In this space the transformed posterior reads ![$\[P(\xi(y) \mid d)\left|\frac{\mathrm{d} \xi}{\mathrm{d} y}\right|\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq47.png) . We denote the metric of the space in which
. We denote the metric of the space in which ![$\[P(\xi(y) \mid d)\left|\frac{\mathrm{d} \xi}{\mathrm{d} y}\right|\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq48.png) is “more” standard normal by
is “more” standard normal by ![$\[M:=\frac{\mathrm{d} y}{\mathrm{~d} \xi}\left(\frac{\mathrm{d} y}{\mathrm{~d} \xi}\right)^{\dagger}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq49.png) . Assuming y(ξ): ξ ↦ y(ξ) is known, the difficulty lies solely in finding the optimal
. Assuming y(ξ): ξ ↦ y(ξ) is known, the difficulty lies solely in finding the optimal ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq50.png) for
for ![$\[Q_{\bar{\xi}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq51.png) .
.
Based on the Fisher information metric and Frequentist statistics, Knollmüller & Enßlin derive a coordinate transformation ![$\[y_{\bar{\xi}}(\xi)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq52.png) centered on
centered on ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq53.png) that is linear in ξ. In Frank (2021), the authors find that a set of Riemannian normal coordinates
that is linear in ξ. In Frank (2021), the authors find that a set of Riemannian normal coordinates ![$\[y_{\bar{\xi}}(\xi)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq54.png) centered on
centered on ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq55.png) are an improved, nonlinear estimate of the coordinate transform
are an improved, nonlinear estimate of the coordinate transform ![$\[y(\xi) \approx y_{\bar{\xi}}(\xi)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq56.png) . The improvements though come at slightly higher computational costs. We refer the reader to Frank (2021) and Frank (2022) for further details on geoVI and its relation to MGVI, the choice of metric, and an analysis of its failure modes. For computational reasons, we used MGVI for our inference.
. The improvements though come at slightly higher computational costs. We refer the reader to Frank (2021) and Frank (2022) for further details on geoVI and its relation to MGVI, the choice of metric, and an analysis of its failure modes. For computational reasons, we used MGVI for our inference.
MGVI and geoVI start at a random initial position for ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq57.png) and draw nsamples standard normal samples in the space of y. Next, they transform the samples to the space of ξ via
and draw nsamples standard normal samples in the space of y. Next, they transform the samples to the space of ξ via ![$\[y \bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq58.png) , the local, linear (respectively, nonlinear for geoVI) approximation to y(ξ) at
, the local, linear (respectively, nonlinear for geoVI) approximation to y(ξ) at ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq59.png) . We denote the samples in parameter space by
. We denote the samples in parameter space by ![$\[\left\{\xi_1, \ldots, \xi_{n_{\text {sampels}}}\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq60.png) . Relative to the expansion point
. Relative to the expansion point ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq61.png) the samples read
the samples read ![$\[\{\Delta \xi_1:=\xi_1-\left.\bar{\xi}, \ldots, \Delta \xi_{n_{\text {samples }}}:=\xi_{n_{\text {sampels }}}-\bar{\xi}\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq62.png) . The samples
. The samples ![$\[\left\{\Delta \xi_1, \ldots, \Delta \xi_{n_{\text {samples }}}\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq63.png) around
around ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq64.png) provide an empirical, sampled approximation to
provide an empirical, sampled approximation to ![$\[Q_{\bar{\xi}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq65.png) which we denote by
which we denote by ![$\[Q_{\bar{\xi}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq66.png) . MGVI and geoVI then optimize
. MGVI and geoVI then optimize ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq67.png) of the sampled distribution,
of the sampled distribution, ![$\[Q_{\bar{\xi}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq68.png) , by minimizing the variational Kullback-Leibler (KL) divergence between
, by minimizing the variational Kullback-Leibler (KL) divergence between ![$\[Q_{\bar{\xi}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq69.png) and the true distribution P
and the true distribution P
![$\[\bar{\xi}^{\prime}=\underset{\bar{\xi}}{\arg \min } \mathrm{KL}\left(\tilde{Q}_{\bar{\xi}}, P(\xi \mid d)\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq70.png) (B.1)
(B.1)
![$\[=\underset{\bar{\xi}}{\arg \min }\left\langle\ln \frac{\tilde{Q}_{\bar{\xi}}}{P(\xi \mid d)}\right\rangle_{\bar{Q}_{\bar{\xi}}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq71.png) (B.2)
(B.2)
![$\[=\underset{\bar{\xi}}{\arg \min }\langle-\ln P(\xi \mid d)\rangle_{\tilde{Q}_{\bar{\xi}}}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq72.png) (B.3)
(B.3)
![$\[=\underset{\bar{\xi}}{\arg \min } \frac{-1}{n_{\text {samples }}} \sum_{i=1}^{n_{\text {samples }}} \ln P\left(\Delta \xi_i-\bar{\xi} \mid d\right) .\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq73.png) (B.4)
(B.4)
They keep the relative samples ![$\[\left\{\Delta \xi_1:=\xi_1-\bar{\xi}, \ldots, \Delta \xi_{n_{\text {samples }}}:=\right.\left.\xi_{n_{\text {sampels }}}-\bar{\xi}\right\}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq74.png) fixed during the optimization and only vary
fixed during the optimization and only vary ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq75.png) . Finally, they update the expansion point
. Finally, they update the expansion point ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq76.png) to the new found optimum
to the new found optimum ![$\[\bar{\xi}^{\prime}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq77.png) .
.
After the minimization, MGVI and geoVI draw a new set of samples, transform them via a local (linear) expansion of y, and then minimize again. The drawing of samples and minimization is repeated until a fixed point for ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq78.png) is reached. Algorithm 2 summarizes the algorithmic steps of the variational approximation to the true posterior.
is reached. Algorithm 2 summarizes the algorithmic steps of the variational approximation to the true posterior.
Appendix C Extinction within the innermost 69 pc
By construction of our likelihood, we know that our model is biased high for low extinction values because we neglected the positivity prior of the ZGR23 catalog. This imprints on to the map in the form of a thin layer of dust extinction right at the beginning of the modeled volume. As voxels in our reconstruction are correlated, the extincted first layer of voxels pulls the next layer of voxels to slightly higher extinctions too. At 69 pc the differential extinction as a function of distance reaches a local minimum, and we expect little to now influence of the innermost layers of voxels. Thus, we determined 69 pc to be our cutoff.
Figure C.1 shows the integrated extinction that is cut out from the final reconstruction. Most of the extinction is likely spurious. Overall, no structure contributes a significant amount of extinction. However, to be consistent with ZGR23, we suggest adding the removed extinction back to the map when comparing integrated extinction.
 |
Fig. C.1 Mollweide projection of the integrated AV extinction in the innermost 69 pc, which is likely dominated by spurious effects and is therefore excluded from the reconstruction. The colorbar is linear and covers the full range of the extinction that is cut out of the reconstruction. |
Appendix D Extinction catalog
We release a catalog of expected extinction for all stars within the subset of the ZGR23 catalog that we used for our reconstruction (see Section 2). We predict the expected extinction conditional on the known parallax including parallax uncertainties. Our prediction is the best guess of our model for the extinction toward a star but is not necessarily the best guess for the extinction at the mean parallax of the star.
Our extinction predictions (see Sections 3 and 4) differ from the extinctions in the ZGR23 catalog by coupling the individual stars via the 3D dust extinction density. By virtue of every star depending on all nearby stars via the prior, our extinction predictions come in the form of joint predictions for all stars. In regions where the 3D dust extinction density is well constrained, the joint predictions to first order factorize into predictions for individual stars, and we can compute expected extinctions for individual stars and their uncertainties.
Our catalog of extinction includes the innermost 69 pc from the beginning of our grid and the outer 550 pc beyond 1.25 kpc that we cut away in the 3D map. We advise caution when analyzing the stars of our catalog within those regions as they might carry additional biases. Details on why these regions were removed from the final map are given in Sections 5 and 6.
The top panel of Figure D.1 compares the ZGR23 extinctions to our mean extinction predictions for Gaia BP/RP stars. Overall, our mean extinctions are in very good agreement with the extinctions in the ZGR23 catalog for the vast majority of stars. However, below 50 mmag and above 4 mag, our extinction predictions deviate from the predictions in ZGR23. In any given extinction bin from ZGR23 respectively our work, we would expect half of the respective other extinctions to be below the bisector and the other half to be above. At 50 mmag, 34% more stars than expected have higher extinctions than the corresponding extinctions in ZGR23. The difference further widens for lower ZGR23 extinctions. At 4 mag, 34% more stars than expected have lower extinctions than the corresponding extinctions in ZGR23.
The bottom panel of Figure D.1 shows our and the ZGR23 extinction uncertainties. We note that our extinction uncertainties are predictions for the measured uncertainties of the ZGR23 catalog ![$\[\bar{\xi}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq79.png) and not the uncertainties of our extinction predictions std(ā) (see Section 4). Overall, both uncertainties agree well for the vast majority of stars. At low extinctions uncertainties our uncertainties only marginally inflate the ZGR23 uncertainties. However, at high extinction uncertainties, our predictions cover a larger range, and we find that the ZGR23 significantly underpredicts our extinction uncertainties of stars.
and not the uncertainties of our extinction predictions std(ā) (see Section 4). Overall, both uncertainties agree well for the vast majority of stars. At low extinctions uncertainties our uncertainties only marginally inflate the ZGR23 uncertainties. However, at high extinction uncertainties, our predictions cover a larger range, and we find that the ZGR23 significantly underpredicts our extinction uncertainties of stars.
 |
Fig. D.1 ZGR23's extinction versus our predicted extinction for Gaia BP/RP stars. Panel (a): Our mean posterior extinctions versus the ZGR23 extinctions to stars as 2D histogram. The 16th, 50th, and 84th quantiles of the ZGR23 extinctions for each bin of our mean extinction are shown as blue lines. The respective quantiles of our predictions in bins of the ZGR23 extinctions are shown as orange lines. Panel (b): Same comparison but for our posterior mean predictions for the ZGR23 measurement uncertainties, |
Figure D.2 summarizes the extinctions and the extinction uncertainties of both ZGR23 and our predictions into a single histogram of the mean standardized extinction. A standard Gaussian is shown as reference. The mean standardized residuals have two slight overdensities at each tail compared to the Gaussian.
Figure D.3 shows the posterior standard deviation of our extinction predictions versus the ZGR23 uncertainties. Our model yields approximately one order in magnitude lower extinction uncertainties than the ZGR23 uncertainties for the vast majority of stars. The effect is less pronounced for low ZGR23 extinction uncertainties.
Our predictions for the extinction to stars theoretically contain more information since we allow for the cross-talk of nearby stars via the 3D distribution of dust and thus might be more accurate. However, the ZGR23 catalog might yield better results in practice because it does not discretize the 3D volume within which the stars reside. By discretizing the modeled volume we can produce contradicting data that in a continuous space is non-contradicting, for example by putting highly extincted stars that lie in a dust cloud into the same voxel as less extincted stars that are adjacent to the dust cloud. Overall, both predictions agree very well for stars below between 50 mmag and 4 mag. More work is needed to validate the discrepant predictions at very low and very high extinctions.
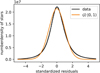 |
Fig. D.2 Mean standardized extinctions: |
 |
Fig. D.3 Similar to Figure D.1 but for the posterior standard deviation of our extinctions versus the ZGR23 uncertainties. The 16th, 50th, and 84th quantiles of the ZGR23 uncertainties for each bin of our standard deviation are shown as blue lines. The respective quantiles of our standard deviation in bins of the ZGR23 uncertainties are shown as orange lines. The bisectors are shown in red. The colorbars is logarithmic. |
Appendix E 2 kpc reconstruction
In Section 5 we describe how we iteratively increase the distance out to our maximum reconstructed distance. We did so to improve the convergence of the reconstruction. We also tried naively reconstructing the full volume at once. Using all the available data is computationally prohibitive, so we limited the reconstruction to high quality data using quality_flags ==0, σA ≤ 0.04, and σω/ω < 0.33.
 |
Fig. E.1 Axis parallel projections of the reconstructed dust extinction in a box of dimensions 4 kpc × 4 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. |
We used ![$\[1 /_\left(\omega-\sigma_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq82.png) < 3 kpc and
< 3 kpc and ![$\[1 /_\left(\omega-\sigma_\omega\right)\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq83.png) 40 pc to select the stars within a 3 kpc sphere. To further speed up the inference, we started the inference using at first only a sample of 10%, then 20%, 45%, 67%, and finally 100% of the stars. In total, we selected 59,334,214 stars. After the inference, we cut away the outermost 1 kpc of the sphere of the data-constrained region to avoid degradation effects due to the thinning out of stars at the edge. The overall reconstructed volume after removing the outermost HEALPix spheres extends out to 2 kpc in distance.
40 pc to select the stars within a 3 kpc sphere. To further speed up the inference, we started the inference using at first only a sample of 10%, then 20%, 45%, 67%, and finally 100% of the stars. In total, we selected 59,334,214 stars. After the inference, we cut away the outermost 1 kpc of the sphere of the data-constrained region to avoid degradation effects due to the thinning out of stars at the edge. The overall reconstructed volume after removing the outermost HEALPix spheres extends out to 2 kpc in distance.
The reconstruction is shown in Figure E.1 and again in Figure E.2 with a catalog of YSO clusters (Kuhn 2023, priv. comm.) overlaid on top. It shows the same large-scale features as the smaller reconstruction discussed in the main text. The distribution of dense dust clouds is in agreement with the positions of YSO clusters within the distance uncertainties of the YSO clusters. Compared to Figure 5 the reconstruction is less detailed and features more pronounced artifacts.
 |
Fig. E.2 Same as Figure E.1 but with a catalog of clusters of YSOs (Kuhn 2023, priv. comm.) based on Kuhn et al. (2021), Winston et al. (2020), and Marton et al. (2023) shown a blue dots on top of the reconstruction; their distance uncertainties are shown as extended lines. |
We used the larger reconstruction to validate the inference of the smaller one. Specifically, we used the larger reconstruction to ensure that structures aligned with or close to the radial boundaries at which we increased the distance of the main reconstruction are independent of the locations at which we increased the distance covered.
We release the larger reconstruction as an additional data product together with the main reconstruction. We advise using the main reconstruction for all regions that fall within its volume. Care should be taken when interpreting small-scale features or structures at high distances in the larger reconstruction.
Appendix F Using the reconstruction
All data products are made publicly available online6. The data products are stored in the FITS file format. The main data products are the posterior samples of the spatial 3D distribution of dust extinction discretized to HEALPix spheres at logarithmically spaced distances. For convenience, we also provide the posterior mean and standard deviation of the samples of the HEALPix spheres at logarithmically spaced distances.
We additionally interpolated the posterior mean and standard deviation to a Cartesian grid. The interpolation was carried out at a lower discretization using 23 pc3 voxels to keep the file size reasonably small. We recommend re-interpolating the map at a higher discretization for the study of individual regions within the map.
We release the interpolation script as part of the data release. Its signature reads interp2box.py [-h] [-o OUTPUT_DIRECTORY] [-b BOX] healpix_path. A box is a string of two tuples separated by two colons. The first tuple specifies the number of voxels along each axis of the box and the second tuple specifies the corners of the box in parsecs in heliocentric coordinates. To interpolate the map to a box with 1051 × 1051 × 351 voxels of size |X|, |Y| ≤ 2100 pc and |Z| ≤ 700 pc, use interp2box.py -b '(1051,1051,351) ::((−2100,2100),(−2100,2100),(−700,700))' --mean_and_std_healpix.fits.
In addition, we interpolated the posterior mean and standard deviation to galactic longitude, latitude, and distance. The signature of the interpolation script reads interp2lbd.py [-h] [-o OUTPUT_DIRECTORY] [-b BOX] healpix_path. Its behavior is similar to interp2box.py but the box is specified in terms of galactic longitude, latitude, and distance in units of degrees, degrees, and parsecs, respectively.
Both scripts require the Python packages numpy (Harris et al. 2020), astropy (Astropy Collaboration et al. 2013, 2018, 2022), and healpy (Górski et al. 2005; Zonca et al. 2019). Depending on the number of output voxels, the interpolation can be very memory intensive and computationally expensive.
Appendix G Molecular clouds by distance
Figures G.1 to G.5 depict zoomed-in views of Figure 11 at different distant slices, alongside histograms comparing the extinction of VLC22, LGE20, and our mean map toward Perseus, Orion A, Taurus, Corona Australis, and Chamaeleon. The top panels depict the same POS views for the clouds as in Figure 12, but now showing the dust extinction in finite distance bins, rather than integrated over the full distance range. A low-resolution 3D interactive figure of the reconstruction including all the above molecular clouds is available online7.
 |
Fig. G.1 Comparison of different dust maps for Perseus. Panel (a): Zoomed-in view of Figure 11 toward Perseus akin to Figure 12, in different distant slices. Columns depict dust reconstructions, while rows depict distance slices. The logarithmic colorbars are separate for the reconstructions but shared for different distance slices. Panel (b): Comparison of the mean posterior extinction integrated from the lowest distance of Panel (a) to regularly spaced points in the distance range of Panel (a). The extinction predictions for our map versus LGE20 and VLC22 are shown as histograms. The binning is linear and the colorbar logarithmic. The bisectors are shown in red. |
 |
Fig. G.2 Same as Figure G.1 but for Orion A. |
The bottom panels of the figures are akin to Figure 10 but compare the extinction within the selected distance and POS area of the respective molecular cloud only. The probing points to which we integrated are spaced in the distance range of the top panel. We started the integration at the lowermost distance of the top panel and successively integrated out in steps of 0.5 pc. The probing points are spaced 15′ apart along the POS.
 |
Fig. G.3 Same as Figure G.1 but for Taurus. |
LGE20 and our map agree well for Perseus, Orion A, Taurus, and Chamaeleon. Some structures appear at slightly larger distances in our map as indicated by the arches above the diagonal in the second panels. LGE20 saturates sooner than our map as it flattens off at high extinctions below the diagonal. The flattening off is less pronounced for Chamaeleon.
 |
Fig. G.4 Same as Figure G.1 but for Corona Australis (CrA). |
Corona Australis is an outlier among the generally good level of agreement. In the lower panel, there is noticeably more density off the diagonal. We see arches both above and below the diagonal indicating that some structures are closer while others are farther in our map compared with LGE20. While LGE20 puts the head of Corona Australis in the distance slice ranging from 140 pc to 160 pc, our map puts the head of Corona Australis dozens of parsecs farther in distance. Possible reasons for this shift include an insufficient number of stars to constrain the distance to the head of Corona Australis or a failure mode in our posterior approximation.
 |
Fig. G.5 Same as Figure G.1 but for Chamaeleon. |
VLC22 is much lower in resolution and does not resolve degree-scale high extinction regions. The extinction in VLC22 within the selected distance slice is much lower than in our map and by extension in LGE20. The missing extinction partially lies outside the selected box as it is strongly smeared out radially.
References
- Alves, J., Zucker, C., Goodman, A. A., et al. 2020, Nature, 578, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, F., Khalatyan, A., Chiappini, C., et al. 2019, A&A, 628, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, F., Khalatyan, A., Queiroz, A. B. A., et al. 2022, A&A, 658, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arras, P., Baltac, M., Ensslin, T. A., et al. 2019, Astrophysics Source Code Library [record ascl:1903.008] [Google Scholar]
- Arras, P., Frank, P., Haim, P., et al. 2022, Nat. Astron., 6, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bradbury, J., Frostig, R., Hawkins, P., et al. 2018, JAX: composable transformations of Python+NumPy programs, https://github.com/google/jax [Google Scholar]
- Cantat-Gaudin, T., Fouesneau, M., Rix, H.-W., et al. 2023, A&A, 669, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco, J. M., Weiler, M., Jordi, C., et al. 2021, A&A, 652, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, arXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Chen, B. Q., Huang, Y., Yuan, H. B., et al. 2019, MNRAS, 483, 4277 [Google Scholar]
- De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delchambre, L., Bailer-Jones, C. A. L., Bellas-Velidis, I., et al. 2023, A&A, 674, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dharmawardena, T. E., Bailer-Jones, C. A. L., Fouesneau, M., & Foreman-Mackey, D. 2022, A&A, 658, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Edenhofer, G., Leike, R. H., Frank, P., & Enßlin, T. A. 2022, arXiv e-prints [arXiv:2206.10634] [Google Scholar]
- Frank, P. 2022, Phys. Sci. Forum, 5, 6 [Google Scholar]
- Frank, P., Leike, R. H., & Enßlin, T. A. 2021, Entropy, 23, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Green, G. 2018, J. Open Source Softw., 3, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2014, J. Mach. Learn. Res., 15, 1593 [Google Scholar]
- Hutschenreuter, S., Anderson, C. S., Betti, S., et al. 2022, A&A, 657, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hutschenreuter, S., Haverkorn, M., Frank, P., Raycheva, N. C., & Enßlin, T. A. 2023, A&A, submitted [arXiv:2304.12350] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knollmüller, J., & Enßlin, T. A. 2019, arXiv e-prints [arXiv:1901.11033] [Google Scholar]
- Kuhn, M. A., de Souza, R. S., Krone-Martins, A., et al. 2021, ApJS, 254, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J. L., Babusiaux, C., & Cox, N. L. J. 2022, A&A, 661, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leike, R., & Enßlin, T. 2019, A&A, 631, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leike, R. L., Glatzle, M., & Enßlin, T. A. 2020, A&A, 639, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leike, R. H., Edenhofer, G., Knollmüller, J., et al. 2022, A&A, submitted [arXiv:2204.11715] [Google Scholar]
- Marton, G., Ábrahám, P., Rimoldini, L., et al. 2023, A&A, 674, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mertsch, P., & Phan, V. H. M. 2023, A&A, 671, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montegriffo, P., De Angeli, F., Andrae, R., et al. 2023, A&A, 674, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., & Tuffs, R. J. 2002, MNRAS, 335, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2023, A&A, 673, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei Kh., S., & Kainulainen, J. 2022, ApJ, 930, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Rezaei Kh., S., Bailer-Jones, C. A. L., Hanson, R. J., & Fouesneau, M. 2017, A&A, 598, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei Kh., S., Bailer-Jones, C. A. L., Hogg, D. W., & Schultheis, M. 2018, A&A, 618, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei Kh., S., Bailer-Jones, C. A. L., Soler, J. D., & Zari, E. 2020, A&A, 643, A151 [EDP Sciences] [Google Scholar]
- Rezende, D. J., & Mohamed, S. 2015, in Proceedings of the 32nd International Conference on International Conference on Machine Learning, 37, 1530 [Google Scholar]
- Roth, J., Arras, P., Reinecke, M., et al. 2023a, A&A, 678, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roth, J., Li Causi, G., Testa, V., Arras, P., & Ensslin, T. A. 2023b, AJ, 165, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Meisner, A. M., & Green, G. M. 2019, ApJS, 240, 30 [Google Scholar]
- Selig, M., Bell, M. R., Junklewitz, H., et al. 2013, Astrophysics Source Code Library [record ascl:1302.013] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Steininger, T., Dixit, J., Frank, P., et al. 2019, Ann. Phys., 531, 1800290 [NASA ADS] [CrossRef] [Google Scholar]
- Tsouros, A., Edenhofer, G., Enßlin, T., Mastorakis, M., & Pavlidou, V. 2024, A&A, 681, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J. L., Lallement, R., & Cox, N. L. J. 2022, A&A, 664, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, C., Huang, Y., Yuan, H., et al. 2022, ApJS, 259, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Winston, E., Hora, J. L., & Tolls, V. 2020, AJ, 160, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Xiang, M., Rix, H.-W., Ting, Y.-S., et al. 2022, A&A, 662, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, X., Green, G. M., & Rix, H.-W. 2023, MNRAS, 524, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Zonca, A., Singer, L., Lenz, D., et al. 2019, J. Open Source Softw., 4, 1298 [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Goodman, A., Alves, J., et al. 2021, ApJ, 919, 35 [NASA ADS] [CrossRef] [Google Scholar]
The ZGR23 extinction is in arbitrary units but can be translated to an extinction at any given wavelength by using the extinction curve published at https://doi.org/10.5281/zenodo.7692680. Furthermore, dust extinction can be translated to a rough hydrogen volume density by assuming a constant extinction to hydrogen column density ratio (see, e.g., Zucker et al. 2021).
All Tables
All Figures
 |
Fig. 1 2D histograms of the density of stars in heliocentric Galactic Cartesian (X, Y, Z) projections, as well as the density of stars as a function of distance, for the subset of the ZGR23 catalog used in the reconstruction of our 3D dust map. Panel a: heliocentric Galactic Cartesian-projected histograms. Panel b: number of stars as a function of distance. This panel also shows a linear growth and a quadratic growth with distance for comparison. |
| In the text | |
 |
Fig. 2 POS distribution of the subset of ZGR23 stars used in the reconstruction of our 3D dust map. |
| In the text | |
 |
Fig. 3 Mollweide projection of the POS integrated AV extinction out to 250 pc, 500 pc, 750 pc, and up to the maximum distance of our map. The colorbar saturates at the 99.9% quantile. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but showing the difference between the integrated extinctions in between distance slices projected on the POS. The colorbar saturates at the 99.9% quantile. |
| In the text | |
 |
Fig. 5 Heliocentric Galactic Cartesian (X, Y, Z) projections of the posterior mean of our 3D dust map in a box with dimensions 2.5 kpc × 2.5 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. A GIF of the posterior samples and a low-resolution 3D interactive version of this figure are available online. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but with a catalog of clusters of YSOs (Kuhn 2023, priv. comm.) based on Kuhn et al. (2021), Winston et al. (2020), and Marton et al. (2023) shown as blue dots on top of the reconstruction; their distance uncertainties are shown as extended lines. |
| In the text | |
 |
Fig. 7 Heliocentric Galactic Cartesian (X, Y, Z) projections of the relative uncertainty of the reconstructed dust extinction integrated within a box of 2.5 kpc × 2.5 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. |
| In the text | |
 |
Fig. 8 Side by side views of the 3D dust maps from Bayestar19, VLC22, L+22, and this work, shown in heliocentric Galactic Cartesian (X,Y,Z) projections. The colorbars are saturated at the 99.9% quantile of the respective reconstruction. |
| In the text | |
 |
Fig. 9 Zoomed-in version of Fig. 8 for the volume reconstructed in Leike et al. (2020), now also showing the LGE20 reconstruction for comparison. We omit L+22 from the comparison because the authors explicitly focus on larger volumes and trade strongly pronounced artifacts in the inner couple hundred parsecs for a larger probed volume. The colorbars are again saturated at the 99.9% quantile of the respective reconstruction. |
| In the text | |
 |
Fig. 10 Histogram of the mean posterior extinction of our map versus LGE20, VLC22, and Bayestar19 for 58 million test points. For each pixel center of a HEALPix sphere with Nside = 64, 1182 test points are placed at 1 pc intervals in distance starting at 69 pc. The orange lines show the 16th, 50th, and 84th quantiles of the predicted extinction by LGE20, VLC22, and Bayestar19, respectively, for each bin of our mean extinction. The respective quantiles of our predictions in bins of the other reconstruction are shown as blue lines. The bisectors are shown in red. The colorbars are logarithmic and truncated at the lower end at 1 mmag. |
| In the text | |
 |
Fig. 11 Mollweide projections of total integrated extinction and 3D extinction maps integrated out the maximum distance of the respective map. Bayestar19 reconstructs up to a maximum distance of 63 kpc (maximum reliable distance 10 kpc) and is integrated out to that volume. L+22 reconstructs up to a maximum distance of 16 kpc but the authors trust their map only out to 4 kpc and we integrate their map only to 4 kpc. VLC22 reconstructs a heliocentric box of size 3 kpc × 3 kpc × 800 pc with 103 pc3 voxels with at most <2.16 kpc in distance and is integrated out to the end of the box. Likewise, LGE20 reconstructs a heliocentric box of size |X| < 370 pc, |Y| < 370 pc, |Z| < 270 pc covering at most <590 pc in distance and is integrated out to the end of the box. The colorbars saturate at the respective 99% quantile of the map except for the colorbar of Planck 2013, which saturates at 5 mag for better comparability. |
| In the text | |
 |
Fig. 12 Zoomed-in views toward the individual molecular clouds (Perseus, Orion, Taurus, Corona Australis, and Chamaeleon) seen in Fig. 11. The colorbars are logarithmic and span the full dynamic range of the selected POS slice in every image. Each row is a separate region and each column a separate reconstruction. |
| In the text | |
 |
Fig. A.1 Absolute and relative ZGR23 extinction in dust-free regions. Panel (a): Histogram of the ZGR23 extinctions in dust-free regions translated to AV. The mean extinction in dust-free regions based on Planck is shown as a vertical green line, and the cutoff value translated to AV for our definition of dust-free is shown in red. Panel (b): Same as panel (a) but the extinctions are scaled by their accompanying uncertainties. A truncated standard normal distribution and a standard normal distribution are plotted on top. Both ordinates are logarithmic. |
| In the text | |
 |
Fig. C.1 Mollweide projection of the integrated AV extinction in the innermost 69 pc, which is likely dominated by spurious effects and is therefore excluded from the reconstruction. The colorbar is linear and covers the full range of the extinction that is cut out of the reconstruction. |
| In the text | |
 |
Fig. D.1 ZGR23's extinction versus our predicted extinction for Gaia BP/RP stars. Panel (a): Our mean posterior extinctions versus the ZGR23 extinctions to stars as 2D histogram. The 16th, 50th, and 84th quantiles of the ZGR23 extinctions for each bin of our mean extinction are shown as blue lines. The respective quantiles of our predictions in bins of the ZGR23 extinctions are shown as orange lines. Panel (b): Same comparison but for our posterior mean predictions for the ZGR23 measurement uncertainties, |
| In the text | |
 |
Fig. D.2 Mean standardized extinctions: |
| In the text | |
 |
Fig. D.3 Similar to Figure D.1 but for the posterior standard deviation of our extinctions versus the ZGR23 uncertainties. The 16th, 50th, and 84th quantiles of the ZGR23 uncertainties for each bin of our standard deviation are shown as blue lines. The respective quantiles of our standard deviation in bins of the ZGR23 uncertainties are shown as orange lines. The bisectors are shown in red. The colorbars is logarithmic. |
| In the text | |
 |
Fig. E.1 Axis parallel projections of the reconstructed dust extinction in a box of dimensions 4 kpc × 4 kpc × 0.8 kpc centered on the Sun. The colorbar is linear and saturates at the 99.9% quantile. |
| In the text | |
 |
Fig. E.2 Same as Figure E.1 but with a catalog of clusters of YSOs (Kuhn 2023, priv. comm.) based on Kuhn et al. (2021), Winston et al. (2020), and Marton et al. (2023) shown a blue dots on top of the reconstruction; their distance uncertainties are shown as extended lines. |
| In the text | |
 |
Fig. G.1 Comparison of different dust maps for Perseus. Panel (a): Zoomed-in view of Figure 11 toward Perseus akin to Figure 12, in different distant slices. Columns depict dust reconstructions, while rows depict distance slices. The logarithmic colorbars are separate for the reconstructions but shared for different distance slices. Panel (b): Comparison of the mean posterior extinction integrated from the lowest distance of Panel (a) to regularly spaced points in the distance range of Panel (a). The extinction predictions for our map versus LGE20 and VLC22 are shown as histograms. The binning is linear and the colorbar logarithmic. The bisectors are shown in red. |
| In the text | |
 |
Fig. G.2 Same as Figure G.1 but for Orion A. |
| In the text | |
 |
Fig. G.3 Same as Figure G.1 but for Taurus. |
| In the text | |
 |
Fig. G.4 Same as Figure G.1 but for Corona Australis (CrA). |
| In the text | |
 |
Fig. G.5 Same as Figure G.1 but for Chamaeleon. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![$\[\sqrt{\left[n_\sigma(\xi) \cdot \sigma_A\right]^2+\sigma_a^2}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq80.png)
![$\[(A-\bar{a}) / \sqrt{\left(n_\sigma \cdot \sigma_A\right)^2+\sigma_a^2}\]$](/articles/aa/full_html/2024/05/aa47628-23/aa47628-23-eq81.png)