| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A186 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202348745 | |
| Published online | 18 March 2024 | |
Eccentric black hole mergers via three-body interactions in young, globular, and nuclear star clusters
1
Physics and Astronomy Department Galileo Galilei, University of Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: marco.dallamico@phd.unipd.it
2
INFN-Padova, Via Marzolo 8, 35131 Padova, Italy
3
Institut für Theoretische Astrophysik, ZAH, Universität Heidelberg, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
e-mail: mapelli@uni-heidelberg.de
4
INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
5
Gran Sasso Science Institute (GSSI), 67100 L’Aquila, Italy
Received:
27
November
2023
Accepted:
22
January
2024
Eccentric mergers are a signature of the dynamical formation channel of binary black holes (BBHs) in dense stellar environments and hierarchical triple systems. Here, we investigate the formation of eccentric mergers via binary-single interactions by means of 2.5 × 105 direct N-body simulations. Our simulations include post-Newtonian terms up to the 2.5th order and model the typical environment of young (YSCs), globular (GCs), and nuclear star clusters (NSCs). Around 0.6% (1%) of our mergers in NSCs (GCs) have an eccentricity > 0.1 when the emitted gravitational wave frequency is 10 Hz in the source frame, while in YSCs this fraction rises to 1.6%. Approximately ∼63% of these mergers are produced by chaotic, resonant interactions where temporary binaries are continuously formed and destroyed, while ∼31% arise from an almost direct collision of two black holes (BHs). Lastly, ∼6% of these eccentric mergers occur in temporary hierarchical triples. We find that binaries undergoing a flyby generally develop smaller tilt angles with respect to exchanges. This result challenges the idea that perfectly isotropic spin orientations are produced by dynamics. The environment dramatically affects BH retention: 0%, 3.1%, and 19.9% of all the remnant BHs remain in YSCs, GCs, and NSCs, respectively. The fraction of massive BHs also depends on the host cluster properties, with pair-instability (60 ≤ MBH/M⊙ ≤ 100) and intermediate-mass (MBH ≥ 100 M⊙) BHs accounting for approximately ∼44% and 1.6% of the mergers in YSCs, ∼33% and 0.7% in GCs, and ∼28% and 0.4% in NSCs, respectively.
Key words: black hole physics / gravitational waves / methods: numerical / stars: black holes / stars: kinematics and dynamics / galaxies: star clusters: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Binary-single encounters dominate the interactions between black holes (BHs) in the core of star clusters (Heggie 1975; Hut & Bahcall 1983; Hut 1983, 1993; Banerjee et al. 2010). In this region, BHs form a dynamically decoupled sub-core where they can mostly interact via binary-single scatter due to the large cross-section of this process (e.g. Breen & Heggie 2013a,b; Samsing et al. 2014). This springs from star clusters’ tendency to evolve towards energy equipartition (Spitzer 1969; Trenti & van der Marel 2013; Spera et al. 2016; Bianchini et al. 2016), combined with dynamical friction acting on the most massive bodies of the cluster (Meylan & Heggie 1997; Fregeau et al. 2002; Gürkan et al. 2004).
Most binary black holes (BBHs) in star clusters belong to the family of hard binaries; that is, binary systems with a binding energy larger than the average star kinetic energy of the cluster. Since hard binaries statistically tend to get harder during binary-single encounters (Heggie 1975), BBHs tend to progressively decrease their semi-major axis, or even increase their total mass if a dynamical exchange with a single BH takes place (Hills & Fullerton 1980). Three-body interactions1 between BHs are therefore a key mechanism to speed up the merger before gravitational wave (GW) emission becomes efficient. These dynamical encounters not only efficiently produce BBH mergers (e.g. Sigurdsson & Phinney 1995; Portegies Zwart & McMillan 2000; Banerjee et al. 2010; Tanikawa 2013; Ziosi et al. 2014; Morscher et al. 2015; Rodriguez et al. 2015, 2016a,b; Mapelli 2016; Samsing et al. 2017, 2018a; Samsing & Ilan 2018; Trani et al. 2019, 2021; Dall’Amico et al. 2021) and BH-neutron star mergers (e.g. Clausen et al. 2013; Arca Sedda 2020, 2021), but they may also cause eccentric mergers (Gültekin et al. 2006; Samsing et al. 2014, 2018b; Samsing & Ramirez-Ruiz 2017; Samsing 2018; Rodriguez et al. 2018; Zevin et al. 2019; Arca Sedda et al. 2021; Trani et al. 2022; Codazzo et al. 2023). These are mergers in which the coalescence time of the binary is shorter than the timescale it takes for GW emission to circularise the orbit, such that the binary can merge with a non-zero eccentricity in the LIGO–Virgo sensitivity band (Abbott et al. 2019). In dynamical interactions, the energy exchange between the bodies can excite the eccentricity of a BBH and even induce it to merge. This is particularly true for three-body interactions, in which the system can evolve into a chaotic regime with temporary binaries that are continuously created and destroyed. In this unstable triple configuration, the single BH can perturb the temporary binary and induce it to merge rapidly enough that GWs are not sufficient to completely circularise the orbit (Samsing et al. 2014).
Isolated binaries, on the other hand, struggle to produce BBHs with a non-negligible eccentricity at merger. Tidal effects, mass transfer episodes, and common envelope events usually circularise the orbit of a binary star even before it evolves into a BBH (Hurley et al. 2002). Even if supernova kicks can increase the eccentricity of the system, GWs efficiently circularise the orbits by the merger time (Peters 1964). Eccentric mergers are therefore commonly associated with BBHs formed in a dynamically active environment. Eccentricity, if detected in the waveform of a merger, might be used as a tool to infer the dynamical origin of a BBH (Amaro-Seoane & Chen 2016; Chen & Amaro-Seoane 2017; Gayathri et al. 2022; Romero-Shaw et al. 2020, 2021; Zevin et al. 2021).
How often are these eccentric mergers produced by dynamical interactions? And in which environment should we expect them to be more frequent? Here, we aim to address these questions via direct N-body simulations of three-body encounters between BBHs and BHs. We performed three different sets of binary-single scattering experiments, each with different initial conditions appositely set to reproduce the properties of a class of star clusters: young star clusters (YSCs), globular clusters (GCs), and nuclear star clusters (NSCs). Our goal is to investigate the effect of the cluster properties on the interactions and to derive the influence that the hosting environment has on the outcomes and production of eccentric BBH mergers2.
Three-body interactions are the fundamental mechanism at the base of hierarchical mergers; in other words, the process in which two BHs merge and their merger remnant collides with other BHs of the cluster, giving rise to multiple generations of BBHs (Miller & Hamilton 2002; Gerosa & Berti 2017; Fishbach et al. 2017; Rodriguez et al. 2019; Antonini et al. 2019; Doctor et al. 2020; Arca Sedda et al. 2023; Mapelli et al. 2021; Gerosa & Fishbach 2021; Atallah et al. 2023). Here, we discuss the impact of three-body recoil velocities on hierarchical mergers, and how this effect, combined with relativistic kicks and star cluster evaporation, could dynamically eject the BHs from the cluster.
2. Methods
2.1. Direct N-body simulations
Three-body encounters are chaotic processes (Poincaré 1892; Valtonen & Karttunen 2006). Due to this nature, the orbits of the interacting bodies are highly unpredictable, and no general analytical solutions are known to exist. Potentially, even a perturbation of the Planck-scale order applied to the initial conditions can exponentially grow and lead to different final configurations of the system (Samsing & Ilan 2018; Manwadkar et al. 2020; Boekholt et al. 2020, 2021; Portegies Zwart et al. 2022; Parischewsky et al. 2023). Therefore, the most convenient approach to studying the three-body problem from the perspective of BBH mergers is to use a numerical integrator over a large set of interactions and derive the statistical properties of the encounters.
Here, we used the direct N-body code ARWV to simulate three different sets of three-body interactions, for a total of 2.5 × 105 simulations between a BBH and a single BH. Each of our three sets of simulations was initialised with different initial conditions, designed to reproduce the properties of three-body encounters that take place inside YSCs, GCs, and NSCs. ARWV is an algorithmic regularisation direct N-body code (Mikkola & Aarseth 1989, 1993; Arca-Sedda & Capuzzo-Dolcetta 2019; Chassonnery et al. 2019; Chassonnery & Capuzzo-Dolcetta 2021) that solves the equations of motion of the interacting bodies with post-Newtonian corrections up to the 2.5 order (Mikkola & Merritt 2008; Memmesheimer et al. 2004).
We integrated each system with ARWV for a minimum time of 105 yr. We stopped the integration at this time only if at least one merger took place, or if the three-body encounter was over. If none of these two conditions was satisfied (e.g. the three bodies were still interacting), we carried on the integration with ARWV for a longer time. We stopped the simulation if at least one of the two aforementioned conditions was fulfilled, or if the time reached a maximum of 1 Myr. Figure 1 shows three examples of our three-body simulations computed with ARWV.
 |
Fig. 1. Trajectories of three eccentric mergers triggered by a three-body interaction in NSCs (left- and right-hand panels) and GCs (central panel). In the three panels, the systems are centred in the centre of mass of the initial BBH, while the position at which the merger takes place is marked with a white star. The trajectories of the primary and secondary BH of the initial BBH (with mass m1 and m2), and the intruder (m3) are reported in red, blue, and grey, respectively. The incoming direction of the intruder is shown with an arrow. The insets in the left-hand and central panels display a close-up view of the merger region. In the left-hand and central panels, the initial binary is shown edge-on, while in the right-hand panel the view is face-on. The initial coalescence time of these BBHs, i.e. the coalescence time of the initial binary at the beginning of the interaction, is longer than the Hubble time. |
Most BBH mergers did not take place during the simulation with ARWV. Therefore, we evolved the remaining binary population according to Peters (1964):
where
Here, G is the gravity constant, c the speed of light, mi the primary mass, mj the secondary mass, a the semi-major axis, and e the orbital eccentricity. We assumed that two BHs merge when their mutual distance is less than the sum of their innermost stable circular orbits for non-spinning BHs; that is, when r ≤ 6 G(mi + mj)/c2. All the binaries that survive after the end of the three-body integration with ARW are long-lived and circularise their orbit through GW emission, unaffected by external perturbations. Hence, we can treat them with the simplified formalism described in Eq. (1), without the need for a more computationally expensive post-Newtonian formalism.
When two BHs merged, we implemented the relativistic fitting equations reported in Lousto et al. (2012) to compute the relativistic kick exerted on the BH remnant by the anisotropic GW emission at merger. These are:
where
Here, q = m2/m1 with m2 < m1, η = q (1 + q)−2, A = 1.2 × 104 km s−1, B = −0.93, H = 6.9 × 103 km s−1, V1, 1 = 3678 km s−1, VA = 2481 km s−1, VB = 1792 km s−1, and VC = 1506 km s−1. The equations incorporate the components of the dimensionless spin parameter vectors, χ1 and χ2, relative to the primary and secondary BHs. Specifically, χ1∥ and χ2∥ are the primary and secondary dimensionless spin components parallel to the orbital angular momentum of the binary, while χ1⊥ and χ2⊥ are the perpendicular spin components lying in the orbital plane. Furthermore, S∥ is the component parallel to the orbital angular momentum of the vector S = 2(χ1 + q2 χ2)/(1 + q)2. Moreover, ϕΔ is the angle between the direction of the infall at merger and the in-plane component of the vector Δ = (m1 + m2)2 (χ1 + q χ2)/(1+ q), while ϕ is the phase of the binary. For further details, we refer to Lousto et al. (2012). Finally, we computed the mass of the BH remnant and the magnitude of its spin with the fitting equations presented by Jiménez-Forteza et al. (2017).
2.2. Initial conditions
Simulating a three-body interaction with spinning BHs requires 21 initial parameters for each simulation. Since covering a 21-dimension parameter space with direct N-body simulations is computationally prohibitive, we initialised three different sets of 5 × 104, 105, and 105 simulations for YSCs, GCs, and NSCs, respectively. Table 1 reports all the initial conditions, the distribution used to generate each of them, and the interval in which the parameters are sampled. We initialised the properties of each encounter with the same procedure as in Dall’Amico et al. (2021), except for the masses, semi-major axis, and initial intruder velocity. Here, we summarise the main features of our initial conditions.
Initial conditions.
We assumed that the initial BH mass distribution does not change if the cluster is young, globular, or nuclear (Mapelli et al. 2021), and sampled the mass of all our single and binary BHs from a catalogue of synthetic BHs generated with the population synthesis code MOBSE (Mapelli et al. 2017; Giacobbo et al. 2018; Giacobbo & Mapelli 2018). With this method, our population is composed of first-generation BHs produced by the evolution of binary stars at metallicity Z = 0.1 Z⊙, with Z⊙ = 0.02. MOBSE implements up-to-date wind models for massive stars (Vink et al. 2001; Chen et al. 2015), the core-collapse supernova models by Fryer et al. (2012) and the (pulsational) pair-instability supernova treatment presented in Mapelli et al. (2020). We adopted the rapid core-collapse supernova model by Fryer et al. (2012). With this choice, our BH mass spectrum ranges between 5 and 60 M⊙ BHs.
The semi-major axis, a, of the initial binaries was sampled from a log-normal distribution as
with limits [max(aej, agw),ahard], where
Here, ahard is the limit for a binary to be considered hard (Heggie 1975), aej is the maximum semi-major axis for ejection by three-body encounters, and agw is the limit below which the semi-major axis shrinking by the emission of GWs becomes dominant with respect to dynamical hardening. In the above equations, m* is the average mass of a star in the cluster, σ the typical 3D velocity dispersion of the cluster, vesc ∼ 2σ the escape velocity, ρc the star cluster core density, and ξ ∼ 3 a numerically calibrated constant (Hills 1983; Quinlan 1996). The mean of the log-normal distribution of the semi-major axes was computed as the average of the logarithmic limits, such that it resulted in μlog(a/AU) = 2.42, 1.22, 0.42 in the cases of YSCs, GCs, and NSCs, respectively. The dispersion was derived from the simulations of Di Carlo et al. (2019, 2020), and set as σlog(a/AU) = 0.92 in all three samples of simulations, as was already done in Dall’Amico et al. (2021). With this prescription, all our BBHs are hard binaries for which GW emission is negligible if compared to hardening, but at the same time their semi-major axis is large enough such that previous interactions did not lead to a dynamical ejection of the binary from the cluster.
We assumed that the BHs were in thermal equilibrium with the rest of the cluster core so that the initial velocity at infinity, v∞, of the single BH with respect to the centre of mass of the binary could be sampled from a Maxwell-Boltzmann distribution (Heggie 1975). For the three sets of simulations, we assumed a 3D velocity dispersion of 5, 20, and 50 km s−1 in the cases of YSCs (Portegies Zwart et al. 2010), GCs (Pryor & Meylan 1993), and NSCs (Neumayer et al. 2020), respectively.
We set the initial distance of the single BH from the centre of mass of the binary as D = 103 a. This guaranteed that the BBH had not been perturbed by the intruder before the beginning of the integration.
The impact parameter, b, of the interaction was sampled from a uniform probability distribution proportional to b2 (Hut & Bahcall 1983) in the range [0, bmax], with bmax defined as
This is the maximum impact parameter for a strong three-body interaction with a hard binary derived by Sigurdsson & Phinney (1993). As v∞ and a change between YSCs, GCs, and NSCs, the impact parameter in these three environments will also be different. Equation (12) assumes strong gravitational focusing, that is, 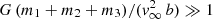 , and a minimum intruder-binary star distance, rp = a. In Appendix A, we discuss the impact of this assumption on our results.
, and a minimum intruder-binary star distance, rp = a. In Appendix A, we discuss the impact of this assumption on our results.
LIGO–Virgo observations favour a population of low-spin BHs (Abbott et al. 2023). Therefore, we extracted the magnitude of the dimensionless spin, χ, of each BH from a Maxwell-Boltzmann distribution with root mean square σχ = 0.1 and truncated to χ = 1. Furthermore, we isotropically sampled the spin directions, accounting for the fact that dynamical encounters randomise them (Rodriguez et al. 2016c).
3. Results
3.1. Outcomes
We divided the outcomes of the interactions into five classes, as a function of the system configuration at 1 Myr since the beginning of the simulation. We classified each simulation as follows:
-
Flyby: the final binary has the same components as the initial binary. If the encounter hardens it enough, this binary may merge during or after the simulation.
-
Exch13: the three-body interaction ends with a binary composed of the primary BH of the initial binary and the intruder (m1 − m3). If this exchanged binary merges during the simulation, we still classify the interaction as an exch13 event.
-
Exch23: the three-body interaction ends with a binary composed of the secondary BH of the initial binary and the intruder (m2 − m3). If this exchanged binary merges during the simulation, we still classify the interaction as an exch23 event.
-
Ionisation: the encounter splits the initial binary, resulting in three single BHs.
-
Triple: the system is still in an unstable triple configuration at the end of the simulation.
The upper panel of Fig. 2 classifies the end states of our binary-single scattering experiments. Flybys are the most frequent end state in all three cluster types, followed by exchanges. This result is expected, since these encounters generally have a larger impact parameter, b, than the semi-major axis of the initial binary, a: if b ≫ a the intruder sees the binary as a point-like object, and the interaction evolves into a flyby.
 |
Fig. 2. Upper panel: percentage of different interaction outcomes for each cluster type. From left to right: (i) flyby events, (ii) exchanges in which the intruder replaces the secondary BH, (iii) exchanges in which the intruder replaces the primary BH, (iv) ionisations, and (v) unstable triples. Lower panel: percentage of BBH mergers. From left to right: (i) BBH mergers occurring after a flyby, (ii) an exchange interaction with the secondary BH replaced by the intruder, (iii) an exchange with the primary BH replaced by the intruder, and (iv) second-generation BBH mergers. In both the upper and lower panels, the colours mark the cluster type in which the interaction takes place. |
In YSCs, the number of ionisations is lower with respect to both GCs and NSCs. Vice versa, exchanges are more common in YSCs than in both GCs and NSCs. This happens because the typical dispersion velocities of YSCs are around 5 km s−1, much smaller than GCs and NSCs, where the intruder can likely have a velocity higher than the critical velocity required to break up the binary system (Hut & Bahcall 1983). At 1 Myr, unstable triples are much more numerous in YSCs than in GCs, while we find no triple systems in NSCs at the end of our simulations. In YSCs, the encounter takes place later than in more dense clusters, since the interparticle distance is much larger while the dispersion velocity is lower. The intruder takes more time to reach the binary and the interaction begins at later times in the simulation, resulting in several systems that at 1 Myr are still in an unstable triple configuration.
3.2. BBH mergers
We find that 0.2%, 2.4%, and 11.8% of the simulations produce BBHs that merge within a Hubble time (13.8 Gyr) in YSCs, GCs, and NSCs, respectively. Of these mergers, 14.8%, 4.6%, and 4% take place in the first Myr of integration with ARWV. These results, which are also reported in Table 2, imply that the denser and more massive the cluster is, the larger the fraction of mergers produced via three-body interactions. This happens because the minimum binding energy of a hard binary is higher in more massive clusters. As a result, BBHs in NSCs are consistently closer to the GW regime than in YSCs, making it more likely for a single interaction to push them into the GW emission regime. The lower panel of Fig. 2 classifies these mergers by their formation channel: flyby, exch13, or exch23, and second-generation mergers (i.e., mergers that occur between the remnant of a previous merger and the third BH). The bar plot shows that flybys account for ∼53% of all our encounters, but ∼61 − 64% of the BBH mergers. Hence, flybys are more efficient in inducing mergers than, for example, exch23 events, which in turn are ∼11% of the outcomes but account only for ∼7% of the mergers. This happens because exchanges usually produce new BBHs with a larger total mass but also with a larger semi-major axis than BBHs involved in flyby events.
Percentage of peculiar events in YSCs, GCs, and NSCs.
For some systems that produce a BBH merger, we find that the initial binary would have merged within a Hubble time even without the interaction. These are binaries that, if evolved as an unperturbed binary, would have produced a BBH merger without undergoing any three-body encounter. These systems are 1.6%, 11.4%, and 45.0% of the BBH mergers in YSCs, GCs, and NSCs respectively. Even for these systems, the interaction has efficiently sped up the merger. This can be seen in Fig. 3, which shows the coalescence time of the unperturbed binaries (if the three-body interaction would not have taken place), and the coalescence time resulting from the three-body simulation. For instance, all the BBH mergers that take place during the simulation with ARWV within the first 1 Myr rapidly merge solely as a consequence of the three-body interaction.
 |
Fig. 3. Distribution of coalescence times for unperturbed initial binaries (filled histograms), and for the same initial binaries perturbed by the three-body interaction (unfilled histograms). The upper, central, and lower panels show the cases of YSCs, GCs, and NSCs, respectively. |
Finally, in a few cases, we find the formation of second-generation BBH mergers. In these simulations, two BHs merge during the three-body interaction, and their remnant forms a new BBH with the remaining BH, which in turn is able to reach coalescence in less than a Hubble time. We find the same percentage of second-generation mergers in GCs and NSCs, while no second-generation systems form in YSCs via three-body interactions (Fig. 2).
Despite the three simulation sets being initialised with the same BH mass spectrum, the total mass of the BBH mergers produced in YSCs, GCs, and NSCs differ, as is shown by Fig. 4. This difference in the mass of BBH mergers is clearly an effect of the environment.
 |
Fig. 4. Total mass of the BBH mergers in YSCs (blue), GCs (orange), and NSCs (purple). |
Mergers by dynamical exchange are slightly favoured in GCs and NSCs with respect to YSCs (Fig. 2). Since exchanges typically take place when the intruder is more massive than at least one of the two binary components, we should expect more massive BBH mergers in GCs and NSCs. Nevertheless, Fig. 4 shows that YSCs are more likely to produce massive mergers via three-body encounters than the other two sets of simulations. This happens because in YSCs only the most massive systems are able to merge within a Hubble time. In GCs and NSCs, given the larger velocity dispersions, the hard-soft boundary is shifted towards the lower semi-major axis (see Eq. (9)). Therefore, GW emission can also be efficient for relatively low-mass BBHs (Eq. (1)). In YSCs, instead, given the larger semi-major axis at formation, mergers are more biased towards the most massive BBHs. In this way, NSCs and GCs are more efficient in the production of BBH mergers with low-mass components than YSCs. This is further confirmed if we look at the percentage of massive BH remnants produced by these mergers in Table 2: pair-instability BHs, defined as BHs with mass in the range 60 − 100 M⊙, are 44.3%, 33.3%, and 27.7% over all the mergers produced in YSCs, GCs, and NSCs, respectively. Intermediate-mass BHs (IMBHs, i.e. BHs with a mass ≥102 M⊙) are 1.6%, 0.7%, and 0.4% over all the mergers in YSCs, GCs, and NSCs, respectively. The most massive remnant produced by a merger is ∼110 M⊙ in all three sets. In YSCs and GCs, the most massive remnants are produced by a flyby event, while in the NSC case the most massive remnant is produced by the merger of a second-generation BBH.
Pair-instability BHs and IMBHs form mainly via flybys, because these are the most frequent type of interaction among our simulations. Exch13 are the events most likely to create a BBH more massive than the initial binary. On the other hand, exch23 tend to produce less massive binaries than the initial ones. Nevertheless, the latter have a minor impact on the total mass distribution in Fig. 4 because they are rare events, representing only ≈7% of all mergers (Fig. 2). Finally, mergers of second-generation binaries are rare even among pair-instability BHs and IMBHs: they represent 0.25% and 0% of pair-instability BHs and IMBHs in GCs, and 0.12% and 4% in NSCs, respectively.
3.3. Eccentric mergers
Figure 5 shows the eccentricity of the BBH when the emitted GW frequency is 10 Hz in the source frame (hereafter, e10 Hz) as a function of the coalescence time from the beginning of the simulation. All three sets present two distinct families of mergers regarding their eccentricity. In the first one, and also the most common one, the mergers follow the relation, tcoal(e), of Eq. (1), such that e10 Hz decreases as the coalescence time of the binary increases. In these systems, the dynamical encounter ends before the merger takes place. This allows the BBH resulting from the interaction to evolve unperturbed up to the merger, such that the eccentricity evolution is ruled only by the angular momentum loss by GW emission3.
 |
Fig. 5. Orbital eccentricity at 10 Hz (e10 Hz) as a function of the coalescence time (tcoal) of BBH mergers in YSCs (left), GCs (centre), and NSCs (right). Different colours indicate mergers through flybys and the two families of exchanges. The yellow stars show second-generation BBH mergers. The empty black dots highlight the BBH progenitors of second-generation mergers. The dashed vertical line divides the plot into two regions: up to 1 Myr we evolve the systems with ARWV, above 1 Myr all the dynamical interactions are concluded, and with Eq. (1) we stop the ARWV integration and evolve the remaining BBHs. The three insets show a zoom for mergers with e10 Hz > 0.1. We note that some of the points at e10 Hz ∼ 1 overlap. |
The second family of mergers is composed by systems that do not follow the relation of Eq. (1), but rather reach the merger with e10 Hz > 10−3 in a relatively short time during the simulation with ARWV, while the dynamical interaction is still ongoing. Some of these systems even have e10 Hz > 0.1 (insets of Fig. 5). In the following, we refer to the mergers with e10 Hz > 0.1 simply as eccentric mergers. These are 1.6%, 1%, and 0.6% of all the mergers in YSCs, GCs, and NSCs, respectively (Table 2). Although YSCs exhibit a larger fraction of eccentric mergers, the only two eccentric events occurring in YSCs both have e10 Hz ∼ 0.1. Conversely, eccentric events in GCs and NSCs span eccentricities up to and beyond e10 Hz = 0.9. We can divide these eccentric mergers as a function of the type of interaction that triggered the coalescence:
-
Chaotic mergers are the product of three-body interactions in which temporary binaries with brand-new orbital parameters are continuously formed and destroyed. If the eccentricity of these temporary binaries is sufficiently high, and their lifetime is longer than the perturbation timescale of the outer body, a nearly radial merger can be triggered. These are the most common interactions to produce eccentric mergers, accounting for ∼63% of all the eccentric events with e10 Hz > 0.1 in GCs and NSCs. The left-hand panel of Fig. 1 shows one of these interactions and the subsequent eccentric merger.
-
Prompt mergers are the second most common event to cause eccentric mergers, representing ∼31% of all these events in GCs and NSCs. The right-hand panel of Fig. 1 shows an example of an eccentric merger that follows a prompt interaction. These mergers typically follow flyby events in which the intruder significantly extracts angular momentum from the binary, driving the two components into a nearly radial orbit and inducing a prompt merger. This is for example the case of the two eccentric mergers in the YSC set. We also call prompt mergers simulations in which the intruder tangentially intersects the orbital plane of the binary and approaches one of the two components with an almost anti-parallel velocity, such that they rapidly merge in a nearly head-on collision (as the simulation in the right-hand panel of Fig. 1 demonstrates). This is the case of the most eccentric mergers in our simulations. In NSCs, five head-on collisions trigger a merger, with e10 Hz ∼ 1 (right-hand panel of Fig. 5), while in GCs the maximum value of e10 Hz is 0.87 (central panel Fig. 5).
-
Temporary triple mergers take place when the system evolves as a hierarchical triple. Stable triple systems cannot form from three isolated unbound bodies (Naoz 2016); however, temporary stable hierarchical triples can be created via three-body interactions. In this configuration, the intruder sets in an outer orbit, perturbing the initial binary and causing it to merge rapidly enough that GW emission does not efficiently circularise the binary’s orbit. This is the case for the system shown in the central panel of Fig. 1. The merger occurs only if the system remains stable for a sufficient period of time for the perturbations to be effective. Binary systems involved in chaotic mergers exhibit considerably shorter lifespans than those within temporary triple systems. In contrast, temporary triple systems can survive for several orbital periods of the third body, which has enough time to orbit around the inner binary perturbing it. We define an eccentric merger as a temporary triple merger if the merger event involves the inner binary and if the outer orbiting third body is able to carry out at least two complete stable orbits with approximately the same period around the inner binary. If these conditions are not met, we define the merger as a chaotic merger. Due to the low stability of these systems, temporary triple mergers are responsible only for ∼6% of the eccentric mergers in GCs and NSCs.
Even if flybys are the most common formation path of BBH mergers in our simulations (lower panel of Fig. 2), eccentric mergers come in almost the same proportion from flybys and exchanges in both GCs and NSCs. Hence, eccentric mergers are more likely to form from exchanges. No second-generation BBH mergers belong to eccentric mergers. With our assumption of no further dynamical interactions beyond 1 Myr, second-generation binaries, after their formation, circularise their orbits before reaching coalescence. On the other hand, all the mergers that give birth to one of the two BHs that compose second-generation binaries are eccentric mergers. We refer to these systems as BBH progenitors of second-generation mergers. In the GC scenario, the progenitor systems of the two second-generation BBHs are both eccentric mergers with an eccentricity of 0.82 and 0.67, respectively, with the first being an almost head-on collision in a prompt event, and the latter coming from a chaotic merger. This is also true for the NSC case, in which all the nine progenitors have e10 Hz > 0.1, four of which merge in a head-on collision with e10 Hz ∼ 1.
Finally, Fig. 6 shows the same systems as Fig. 5 but with the eccentricity computed at the GW frequency of 1 Hz in the source frame. This frequency is the predicted lower limit in the sensitivity band of the Einstein Telescope (Punturo et al. 2010; Maggiore et al. 2020). In this regime, eccentric mergers constitute 0.9%, 1.8%, and 9% of all mergers in NSCs, GCs, and YSCs, respectively (Table 2). This is because, at lower frequencies, the two BHs are at a larger orbital separation and GWs still have to efficiently circularise the orbit, such that more systems have higher eccentricities.
3.4. Dynamical ejections
Our BBHs can escape from the cluster as a consequence of dynamical recoil. Three-body interactions with hard binaries tend to reduce the binary internal energy and convert it into kinetic energy of the system. This induces a recoil velocity, vrec, both on the binary and the single object. If this velocity is larger than the escape velocity, vesc, of the cluster, both the binary and the single object are dynamically ejected from the cluster (Heggie 1975; Hills 1975; Sigurdsson & Phinney 1993).
This has major implications for BBH mergers: on the one hand, the energy exchange speeds the merger up, reducing the semi-major axis and thus the coalescence time, tcoal; on the other hand, it might also kick out the binary from the cluster, preventing further encounters. If the ejection happens before the binary merges, the BH remnant produced by the coalescence will not be able to dynamically interact with other bodies of the cluster and produce new binaries. This may strongly affect the efficiency of the hierarchical merger mechanism by which repeated BH mergers produce massive BHs (e.g. Miller & Hamilton 2002; Mapelli et al. 2021). Figure 7 shows the impact of these dynamical ejections on BBH mergers. Here, we assume that all the mergers that take place during the three-body encounter merge inside the cluster. Therefore, the plots report only the BBH mergers that take place after 105 yr and for which the three-body interaction is concluded. These recoil velocities span from less than 1 km s−1 up to ∼40 km s−1 in YSCs, ∼200 km s−1 in GCs, and ∼400 km s−1 in NSCs. These differences are, once again, explained by the large binding energy of the binaries in GCs and NSCs, which translates into larger recoil kicks. In YSCs, for example, the BBHs have a larger semi-major axis than binaries in more dense clusters and the recoil velocities are lower.
 |
Fig. 7. BBH mergers that take place after the three-body interactions in YSCs, GCs, and NSCs (from top to bottom). All the mergers that take place during the three-body interaction, i.e. < 106 yr, are assumed to merge inside the cluster. The x axis reports the recoil velocity caused by the energy exchange in the three-body encounter. The y axis shows the coalescence time of the binary from the beginning of the simulation. Different outcomes are shown with different markers and colours. In the YSCs case, the horizontal dashed line reports the typical evaporation time of a YSC. The vertical dashed line in all the plots shows the escape velocity of the cluster. Distributions of the recoil velocities are displayed as marginal histograms. The colour legend is the same as the scatter plot. |
In the three simulation sets, the most likely population of ejected mergers is the one produced by exch23 events. The marginal plots of Fig. 7 and Table 3 show that these BBHs generally have larger recoil velocities with respect to the other two families of mergers. The fraction of BBH mergers ejected after the three-body interaction is 6% in NSCs, 18% in GCs, and 18% in YSCs. In YSCs, we must also keep into account the evaporation of the cluster; that is, when the cluster dissolves because of stellar mass loss and tidal stripping (Spitzer 1987; Heggie & Hut 2003; Binney & Tremaine 2008). Due to evaporation, most of the BBH mergers in YSCs happen in the field even without being dynamically ejected (e.g. Rastello et al. 2021; Torniamenti et al. 2022). If we assume a typical evaporation time, tevap ∼ 1 Gyr for a YSC4 (Torniamenti et al. 2022), 48% of the BBH mergers happen inside the cluster and 5% take place in the field because of dynamical recoil, while the remaining 47% occur in the field because of cluster evaporation. Finally, all the eccentric mergers in GCs and NSCs merge inside the cluster. They are mostly the product of chaotic interactions that take place over a short timescale and rapidly lead to the merger of two of the three BHs.
Three-body recoil velocities.
GWs emitted from a spiraling BBH are generally irradiated anisotropically due to the asymmetry of the system. This induces linear momentum transfer on the remnant BH produced by the merger, which translates into a relativistic kick that might accelerate the remnant even up to a few thousand of km s−1 (Fitchett 1983; Maggiore 2018). Figure 8 shows this relativistic kick produced by all the BBH mergers in our three sets of simulations. All three distributions peak at ∼200 km s−1, with velocities that are approximately one order of magnitude higher than the ones reported in Fig. 7. Hence, GW recoils are more efficient in ejecting BHs from their parent cluster than three-body recoils. Due to GW kicks, only 3.6% and 21.2% of the BH remnants are retained in GCs and NSCs, respectively. This fraction drops to 0 in YSCs.
 |
Fig. 8. Distribution of the relativistic recoil kick of the remnants produced by the BBH mergers in YSCs, GCs, and NSCs. The dashed vertical lines represent the escape velocities of the three types of star clusters. |
We can now count the overall fraction of BH remnants retained by the cluster for which (1) the relativistic recoil is below the escape velocity of the cluster, (2) the BBH progenitor is not ejected after a three-body interaction, and (3) the binary is able to merge inside the cluster before its evaporation. This fraction is 0% for YSCs, 3.1% for GCs, and 19.9% for NSCs (Table 2). Finally, all the second-generation BH remnants in GCs and NSCs are kicked out of the cluster due to GW recoils.
3.5. Orbital plane tilt
Figure 9 shows the tilt angle, i, defined as the angle between the orbital plane of the initial binary and the orbital plane of the final binary left after the three-body interaction. These distributions show that three-body interactions are capable of inducing large tilt angles in the BBH population, in good agreement with what was found by Trani et al. (2021, see also Banerjee et al. 2023). The magnitude of the tilt depends on the outcome of the interaction. Binaries that underwent a flyby generally experience smaller tilt angles with respect to exchanges, with the distribution peaking at ∼15° for the former and ∼90° for the latter. Since there is no strong correlation between the initial angle, θ (Sect. 2.2), of the interaction and the outcome, the distributions of Fig. 9 are a direct product of the interactions. This means that flybys statistically induce small perturbations in the orbital plane of the initial binary if compared to exchanges. Exchanges, on the other hand, favour the production of more massive newborn binaries with an orbital plane likely tilted with respect to the original one. This implies that the orientation of spins in dynamically assembled BBHs might not be perfectly isotropic. Our finding is consistent with Bouffanais et al. (2019), who assumes an isotropic spin orientation for exchanges, but nearly aligned spins for flybys, which are less perturbed by the encounter.
 |
Fig. 9. Tilt angle distributions of the BBH orbital plane in NSCs at the end of the simulation with respect to the initial binary orbital plane. Unfilled histograms are flybys (red), exch13 (blue), and exch23 (grey). The filled histogram (yellow) shows the total distribution. We do not show GCs and YSCs because they have exactly the same behaviour. |
4. Discussion and caveats
4.1. Merger rate density of eccentric mergers
In Sect. 3.3, we derived the fraction of eccentric mergers in YSCs, GCs, and NSCs; that is, those that have e10 Hz > 0.1. Through semi-analytical simulations, Mapelli et al. (2022) were able to derive the merger rate density of BBH mergers in YSCs, GCs, and NSCs. They find ℛYSC = 3.0 Gpc−3 yr−1, ℛGC = 4.4 Gpc−3 yr−1, and ℛNSC = 1.3 Gpc−3 yr−1 in their fiducial model. These rates refer to first-generation BBH mergers. Since our first-generation BHs are drawn from the same population as Mapelli et al. (2022), we combined these rates with the fraction of eccentric mergers produced by three-body interactions in our three simulation sets. In this way, we find the following rates of eccentric mergers as a function of the type of cluster: ∼2 × 10−3 Gpc−3 yr−1 in YSCs, ∼4 × 10−2 Gpc−3 yr−1 in GCs, and ∼8 × 10−3 Gpc−3 yr−1 in NSCs. These rates represent a rough estimate, since a more realistic evaluation requires taking into account the possible differences between the coalescence times of our eccentric mergers and the BBH merger population of Mapelli et al. (2022).
4.2. Single versus multiple three-body interactions
Our eccentric mergers (Fig. 5) qualitatively match the properties of eccentric mergers simulated by Samsing & Ramirez-Ruiz (2017) and Zevin et al. (2019). For example, Samsing & Ramirez-Ruiz (2017) and Samsing et al. (2018a) find that ∼1% of all the mergers by binary-single encounters in GCs are eccentric mergers, which is in excellent agreement with the fraction of eccentric events that we find in this work. On the other hand, Samsing (2018) and Rodriguez et al. (2018) find a fraction of eccentric mergers ∼5 times higher than the one we find in our simulations. This difference is a consequence of our choice to simulate one single interaction for each binary.
Assuming a single dynamical encounter per binary is particularly well founded in YSCs, since three-body interactions between BHs are expected to happen with a frequency of ∼1 per cluster (Di Carlo et al. 2019). In more dense clusters, it is more likely for a BBH to experience multiple interactions during its lifetime. However, as we presented in Sect. 3.3 and in Fig. 5, all the eccentric mergers take place while the dynamical interaction is still ongoing, meaning that in our simulations the typical timescale for an eccentric three-body merger is smaller compared to the timescale of a three-body interaction. Our results imply that even one single three-body encounter in a BBH lifetime is sufficient to speed up the merger and to produce an eccentric event in the LIGO–Virgo band. Nevertheless, the masses, eccentricities, and fraction of ejected BHs reported in this work must be interpreted as lower limits, since further interactions might produce more massive and eccentric mergers and more dynamical ejections. This is especially true for all the mergers that take place after 1 Myr in our simulations. The effects of multiple three-body interactions on the BBH population are going to be presented in a future paper.
Finally, our work does not consider the special case of an active galactic nucleus (AGN) disc. In AGN discs, eccentric mergers can be significantly boosted if binary-single scatters occur with small mutual inclinations (of less than a few degrees). This ultimately leads to a relatively flat distribution of the spin-tilt angle in eccentric mergers (Samsing et al. 2022), which is very different from the one we find here for NSCs. The reason for this difference is that three-body interactions in star clusters require completely distinct initial conditions with respect to the AGN case. We will include AGN discs in forthcoming studies.
5. Summary
In this work, we have presented the results of 2.5 × 105 three-body simulations performed via direct N-body integration with the ARWV code (Mikkola & Aarseth 1989; Chassonnery et al. 2019). Our simulations incorporate post-Newtonian corrections up to the 2.5th order and adopt initial conditions that mimic the properties of YSCs, GCs, and NSCs. With this approach, we aim to investigate the influence of the host environment on: (1) the outcomes of three-body encounters, (2) the populations of BBH mergers produced through interactions, and (3) the production of BBH mergers with non-negligible eccentricities in the LIGO–Virgo frequency range. Our results can be summarised as follows:
-
We divide the outcomes into flybys, exchanges in which the primary or the secondary BH component is replaced by the intruder, ionisations, and triples. Flybys dominate the interactions in all the simulation sets, accounting for approximately ∼53% of all the outcomes. YSCs differ from GCs and NSCs, with fewer ionisations (around ∼5% compared to ∼14% for GCs and NSCs) but more exchanges (about ∼41% compared to ∼33% for GCs and NSCs), and also a non-zero number of systems that are in an unstable triple configuration at the end of the simulation.
-
Three-body interactions in GCs and NSCs produce a higher number of mergers compared to YSCs. Approximately 2.4% and 11.8% of the simulations in GCs and NSCs, respectively, lead to a BBH merger within a Hubble time, compared to the 0.2% of the simulations in YSCs. Flybys are the most effective pathway to produce mergers as they significantly decrease the coalescence time. Of the three types of clusters we considered, YSCs are less efficient at producing low-mass BBH mergers than both GCs and NSCs.
-
Pair-instability BH remnants (60 − 100 M⊙) are ∼44%, ∼33%, and ∼28% of all the mergers produced in YSCs, GCs, and NSCs, while IMBHs (> 100 M⊙) are 1.6%, 0.7%, and 0.4%, respectively. Finally, we find second-generation BBH mergers only in GCs and NSCs, accounting for 0.08% of all mergers in both sets.
-
The percentage of BBH mergers with an orbital eccentricity higher than 0.1 at a GW frequency of 10 Hz in the source frame (e10 Hz > 0.1) is 1.6%, 1%, and 0.6% in YSCs, GCs, and NSCs, respectively. We additionally investigated the percentage of BBH mergers with an eccentricity exceeding 0.1 at a GW frequency of 1 Hz in the source frame. This frequency corresponds to the lower boundary of the sensitivity band of the Einstein Telescope. We find that 9% of all the BBH mergers in YSCs are eccentric in this frequency range, while this fraction drops to 1.8% for mergers in GCs and 0.9% for mergers in NSCs.
-
In both GCs and NSCs, the most frequent interactions leading to eccentric mergers are chaotic exchange events, accounting for approximately 63% of all eccentric mergers. These involve the creation and destruction of several temporary binaries before the merger takes place. Prompt interactions, including flybys in which the intruder extracts enough angular momentum from the binary to cause a radial merger, and head-on collisions between the intruder and one of the binary components, account for approximately 31% of eccentric events. Finally, BBH mergers in temporary stable hierarchical triples contribute to approximately 6% of all eccentric mergers in GCs and NSCs. In our simulations, all the progenitors of second-generation BBHs are eccentric mergers in both GCs and NSCs.
-
The percentage of remnant BHs that are not expelled from the cluster is 0% for YSCs, 3.1% for GCs, and 19.9% for NSCs. These are BHs that are not dynamically ejected from the cluster by the three-body and GW relativistic recoil kicks, and for which the progenitor BBHs merge before the evaporation of the star cluster. In YSCs, ∼50% of the BBH mergers take place in the field after the cluster has evaporated. Relativistic recoil kicks due to anisotropic GW emission are the primary cause of dynamical ejections, with typical velocities that exceed 100 km s−1. This strongly affects hierarchical mergers.
-
Three-body interactions alter the inclination of the original orbital plane, causing tilt angles that are not isotropically distributed, but that rather depend on the interaction outcome. Exchanges tend to produce new binary systems that have an isotropically oriented orbital plane with respect to the original one, while flybys usually result in relatively minor perturbations of ∼15° on the orbital plane. This result challenges the idea that dynamics produces perfectly isotropic spin orientations.
-
We estimate the merger rate density of eccentric BBH mergers to be ∼2 × 10−3 Gpc−3 yr−1 for YSCs, ∼4 × 10−2 Gpc−3 yr−1 for GCs, and ∼8 × 10−3 Gpc−3 yr−1 for NSCs. These rates must be regarded as lower limits, as we only considered a single three-body interaction per binary in our simulations. Additional dynamical interactions during the lifetime of these binaries may lead to an increase in the number of eccentric mergers.
The data underlying this article are available at the following Zenodo link: https://zenodo.org/records/7684085
This evaporation timescale refers to YSCs with mass ∼104 M⊙ and must be considered as an upper limit. Processes like galactic perturbations and encounters with giant molecular clouds might, in principle, accelerate the disruption of the cluster (e.g. Gieles et al. 2006).
Acknowledgments
We are grateful to Roberto Capuzzo Dolcetta, Pauline Chassonnery, and Seppo Mikkola for making the ARWV code available to us. We thank Alessandro Trani for the useful comments. We also thank the members of the DEMOBLACK team for the helpful discussions. M.D. acknowledges financial support from Cariparo Foundation under grant 55440. M.M. and S.T. acknowledge financial support from the European Research Council for the ERC Consolidator grant DEMOBLACK under contract no. 770017. M.A.S. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101025436 (project GRACE-BH, PI: Manuel Arca Sedda).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, ApJ, 883, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 041039 [Google Scholar]
- Amaro-Seoane, P., & Chen, X. 2016, MNRAS, 458, 3075 [NASA ADS] [CrossRef] [Google Scholar]
- Antonini, F., Gieles, M., & Gualandris, A. 2019, MNRAS, 486, 5008 [NASA ADS] [CrossRef] [Google Scholar]
- Arca Sedda, M. 2020, Commun. Phys., 3, 43 [CrossRef] [Google Scholar]
- Arca Sedda, M. 2021, ApJ, 908, L38 [Google Scholar]
- Arca-Sedda, M., & Capuzzo-Dolcetta, R. 2019, MNRAS, 483, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Arca Sedda, M., Li, G., & Kocsis, B. 2021, A&A, 650, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arca Sedda, M., Mapelli, M., Benacquista, M., & Spera, M. 2023, MNRAS, 520, 5259 [NASA ADS] [CrossRef] [Google Scholar]
- Atallah, D., Trani, A. A., Kremer, K., et al. 2023, MNRAS, 523, 4227 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., Baumgardt, H., & Kroupa, P. 2010, MNRAS, 402, 371 [Google Scholar]
- Banerjee, S., Olejak, A., & Belczynski, K. 2023, ApJ, 953, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchini, P., van de Ven, G., Norris, M. A., Schinnerer, E., & Varri, A. L. 2016, MNRAS, 458, 3644 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Boekholt, T. C. N., Portegies Zwart, S. F., & Valtonen, M. 2020, MNRAS, 493, 3932 [NASA ADS] [CrossRef] [Google Scholar]
- Boekholt, T. C. N., Moerman, A., & Portegies Zwart, S. F. 2021, Phys. Rev. D, 104, 083020 [CrossRef] [Google Scholar]
- Bouffanais, Y., Mapelli, M., Gerosa, D., et al. 2019, ApJ, 886, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Breen, P. G., & Heggie, D. C. 2013a, MNRAS, 432, 2779 [NASA ADS] [CrossRef] [Google Scholar]
- Breen, P. G., & Heggie, D. C. 2013b, MNRAS, 436, 584 [CrossRef] [Google Scholar]
- Chassonnery, P., & Capuzzo-Dolcetta, R. 2021, MNRAS, 504, 3909 [NASA ADS] [CrossRef] [Google Scholar]
- Chassonnery, P., Capuzzo-Dolcetta, R., & Mikkola, S. 2019, arXiv e-prints [arXiv:1910.05202] [Google Scholar]
- Chen, X., & Amaro-Seoane, P. 2017, ApJ, 842, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]
- Clausen, D., Sigurdsson, S., & Chernoff, D. F. 2013, MNRAS, 428, 3618 [CrossRef] [Google Scholar]
- Codazzo, E., Di Giovanni, M., Harms, J., Dall’Amico, M., & Mapelli, M. 2023, Phys. Rev. D, 107, 023023 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Amico, M., Mapelli, M., Di Carlo, U. N., et al. 2021, MNRAS, 508, 3045 [CrossRef] [Google Scholar]
- Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Di Carlo, U. N., Mapelli, M., Bouffanais, Y., et al. 2020, MNRAS, 497, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Doctor, Z., Wysocki, D., O’Shaughnessy, R., Holz, D. E., & Farr, B. 2020, ApJ, 893, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbach, M., Holz, D. E., & Farr, B. 2017, ApJ, 840, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Fitchett, M. J. 1983, MNRAS, 203, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Fregeau, J. M., Joshi, K. J., Portegies Zwart, S. F., & Rasio, F. A. 2002, ApJ, 570, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
- Gayathri, V., Healy, J., Lange, J., et al. 2022, Nat. Astron., 6, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Gerosa, D., & Berti, E. 2017, Phys. Rev. D, 95, 124046 [NASA ADS] [CrossRef] [Google Scholar]
- Gerosa, D., & Fishbach, M. 2021, Nat. Astron., 5, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Giacobbo, N., & Mapelli, M. 2018, MNRAS, 480, 2011 [Google Scholar]
- Giacobbo, N., Mapelli, M., & Spera, M. 2018, MNRAS, 474, 2959 [Google Scholar]
- Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006, MNRAS, 371, 793 [Google Scholar]
- Gültekin, K., Miller, M. C., & Hamilton, D. P. 2006, ApJ, 640, 156 [CrossRef] [Google Scholar]
- Gürkan, M. A., Freitag, M., & Rasio, F. A. 2004, ApJ, 604, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D., & Hut, P. 2003, The Gravitational Million-Body Problem: A Multidisciplinary Approach to Star Cluster Dynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Hills, J. G. 1975, AJ, 80, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1983, AJ, 88, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G., & Fullerton, L. W. 1980, AJ, 85, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
- Hut, P. 1983, ApJ, 268, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1993, ApJ, 403, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., & Bahcall, J. N. 1983, ApJ, 268, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Forteza, X., Keitel, D., Husa, S., et al. 2017, Phys. Rev. D, 95, 064024 [CrossRef] [Google Scholar]
- Lousto, C. O., Zlochower, Y., Dotti, M., & Volonteri, M. 2012, Phys. Rev. D, 85, 084015 [NASA ADS] [CrossRef] [Google Scholar]
- Maggiore, M. 2018, Gravitational Waves: Volume 2: Astrophysics and Cosmology (Oxford: Oxford University Press) [CrossRef] [Google Scholar]
- Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, JCAP, 2020, 050 [CrossRef] [Google Scholar]
- Manwadkar, V., Trani, A. A., & Leigh, N. W. C. 2020, MNRAS, 497, 3694 [CrossRef] [Google Scholar]
- Mapelli, M. 2016, MNRAS, 459, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Giacobbo, N., Ripamonti, E., & Spera, M. 2017, MNRAS, 472, 2422 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Spera, M., Montanari, E., et al. 2020, ApJ, 888, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Dall’Amico, M., Bouffanais, Y., et al. 2021, MNRAS, 505, 339 [CrossRef] [Google Scholar]
- Mapelli, M., Bouffanais, Y., Santoliquido, F., Arca Sedda, M., & Artale, M. C. 2022, MNRAS, 511, 5797 [NASA ADS] [CrossRef] [Google Scholar]
- Memmesheimer, R.-M., Gopakumar, A., & Schäfer, G. 2004, Phys. Rev. D, 70, 104011 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G., & Heggie, D. C. 1997, A&ARv, 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., & Aarseth, S. J. 1989, Celest. Mech. Dyn. Astron., 47, 375 [Google Scholar]
- Mikkola, S., & Aarseth, S. J. 1993, Celest. Mech. Dyn. Astron., 57, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., & Merritt, D. 2008, AJ, 135, 2398 [Google Scholar]
- Miller, M. C., & Hamilton, D. P. 2002, MNRAS, 330, 232 [Google Scholar]
- Morscher, M., Pattabiraman, B., Rodriguez, C., Rasio, F. A., & Umbreit, S. 2015, ApJ, 800, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
- Neumayer, N., Seth, A., & Böker, T. 2020, A&ARv, 28, 4 [Google Scholar]
- Parischewsky, H. D., Trani, A. A., & Leigh, N. W. C. 2023, SciPost Phys. Core, 6, 016 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Poincaré, H. 1892, Les méthodes nouvelles de la mécanique céleste (Paris: Gauthier-Villars et fils) [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2000, ApJ, 528, L17 [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Boekholt, T. C. N., Por, E. H., Hamers, A. S., & McMillan, S. L. W. 2022, A&A, 659, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357 [Google Scholar]
- Punturo, M., Abernathy, M., Acernese, F., et al. 2010, Class. Quant. Grav., 27, 194002 [Google Scholar]
- Quinlan, G. D. 1996, New Astron., 1, 35 [Google Scholar]
- Rastello, S., Mapelli, M., Di Carlo, U. N., et al. 2021, MNRAS, 507, 3612 [CrossRef] [Google Scholar]
- Rodriguez, C. L., Morscher, M., Pattabiraman, B., et al. 2015, Phys. Rev. Lett., 115, 051101 [Google Scholar]
- Rodriguez, C. L., Chatterjee, S., & Rasio, F. A. 2016a, Phys. Rev. D, 93, 084029 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Haster, C.-J., Chatterjee, S., Kalogera, V., & Rasio, F. A. 2016b, ApJ, 824, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Zevin, M., Pankow, C., Kalogera, V., & Rasio, F. A. 2016c, ApJ, 832, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Amaro-Seoane, P., Chatterjee, S., et al. 2018, Phys. Rev. D, 98, 123005 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [Google Scholar]
- Romero-Shaw, I., Lasky, P. D., Thrane, E., & Calderón Bustillo, J. 2020, ApJ, 903, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Romero-Shaw, I., Lasky, P. D., & Thrane, E. 2021, ApJ, 921, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J. 2018, Phys. Rev. D, 97, 103014 [CrossRef] [Google Scholar]
- Samsing, J., & Ilan, T. 2018, MNRAS, 476, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., & Ramirez-Ruiz, E. 2017, ApJ, 840, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., MacLeod, M., & Ramirez-Ruiz, E. 2014, ApJ, 784, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., MacLeod, M., & Ramirez-Ruiz, E. 2017, ApJ, 846, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., MacLeod, M., & Ramirez-Ruiz, E. 2018a, ApJ, 853, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., Askar, A., & Giersz, M. 2018b, ApJ, 855, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J., Bartos, I., D’Orazio, D. J., et al. 2022, Nature, 603, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Phinney, E. S. 1993, ApJ, 415, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Phinney, E. S. 1995, ApJS, 99, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Spera, M., Mapelli, M., & Jeffries, R. D. 2016, MNRAS, 460, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1969, ApJ, 158, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton: Princeton University Press) [Google Scholar]
- Tanikawa, A. 2013, MNRAS, 435, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Torniamenti, S., Rastello, S., Mapelli, M., et al. 2022, MNRAS, 517, 2953 [NASA ADS] [CrossRef] [Google Scholar]
- Trani, A. A., Spera, M., Leigh, N. W. C., & Fujii, M. S. 2019, ApJ, 885, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Trani, A. A., Tanikawa, A., Fujii, M. S., Leigh, N. W. C., & Kumamoto, J. 2021, MNRAS, 504, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Trani, A. A., Rastello, S., Di Carlo, U. N., et al. 2022, MNRAS, 511, 1362 [NASA ADS] [Google Scholar]
- Trenti, M., & van der Marel, R. 2013, MNRAS, 435, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M., & Karttunen, H. 2006, The Three-Body Problem (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zevin, M., Samsing, J., Rodriguez, C., Haster, C.-J., & Ramirez-Ruiz, E. 2019, ApJ, 871, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Zevin, M., Romero-Shaw, I. M., Kremer, K., Thrane, E., & Lasky, P. D. 2021, ApJ, 921, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Ziosi, B. M., Mapelli, M., Branchesi, M., & Tormen, G. 2014, MNRAS, 441, 3703 [Google Scholar]
Appendix A: Impact of the maximum impact parameter
Three-body scatterings are computationally advantageous with respect to full star cluster simulations. The price to pay is that the results depend on the choice of initial parameters, which must convey information about the properties of the host star clusters and their binary systems. For example, to compute the upper limit of the impact parameter, bmax (eq. 12), we assumed that the distance of closest approach, rp, is equal to the semi-major axis, a, of the binary system and that the strong gravitational focusing limit is valid, or in other words that 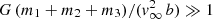 . These assumptions ensure that the majority of our three-body interactions are classified as hard encounters, where significant energy exchange occurs between the single and binary BHs. How critical is this assumption, and what are the effects on our results if we change this prescription? If we relax this hypothesis, the upper limit of the distribution takes the more general form
. These assumptions ensure that the majority of our three-body interactions are classified as hard encounters, where significant energy exchange occurs between the single and binary BHs. How critical is this assumption, and what are the effects on our results if we change this prescription? If we relax this hypothesis, the upper limit of the distribution takes the more general form
The distance of closest approach is typically defined as rp = k a, with k assumed as an arbitrary constant. To study how the strong gravitational focus approximation impacts our results, we ran 5 × 104 additional three-body interactions initialised as the main NSC set, but with impact parameters generated according to eq. A.1, with k = 1, 2, 3, 4, 5.
Figure A.1 shows the cumulative distribution function of the impact parameter if we consider bmax computed as in eq. 12 or eq. A.1, with various choices for k in the NSC case. By calculating bmax from eq. 12, it is more likely to generate interactions where the impact parameter favours closer encounters compared to the sample generated with eq. A.1. The difference between the distributions is marginal with k = 1, but it gradually grows with increasing k. For example, there is a probability of approximately 34% for a simulation that has an impact parameter ≤10 AU in our fiducial model, while this probability decreases to 23% for k = 1 and drops to 5% for k = 5.
 |
Fig. A.1. Cumulative distribution function of the impact parameter computed assuming bmax from eq. 12, and from eq. A.1 with k = 1, 2, 3, 4, 5. |
The probability of drawing an impact parameter, b > 103 AU is < 0.1% in our fiducial model, while this fraction rises to 3% and 4%, respectively, in the cases of k = 4 and k = 5 with eq. A.1. Assuming large values of k produces a non-negligible fraction of simulations where the impact parameter is of the same order of magnitude as the interparticle distance in the core of a NSC. In these simulations, the single BH is likely to interact with other members of the star cluster before reaching the target binary, and the simulated interaction may not occur.
Figure A.2 shows the outcomes of three-body interactions and BBH mergers as a function of the assumed bmax. The simulation sets with larger values of bmax result in fewer exchanges and ionisations while favouring more flybys, with this effect becoming more pronounced with larger values of k. For instance, in the cases of k = 4 and k = 5, almost eight to nine simulations out of ten evolve as a flyby. In contrast, our fiducial model produces flybys in almost 50% of cases. This happens because, when the strong gravitational focus approximation is not assumed, interactions with larger impact parameters become more common. In such encounters, the single BH is more likely to perceive the binary system as a point-like object, leading more frequently to weaker energy exchanges between the binary and the single object. It also disfavours exchanges, which require closer passages between the single BH and one of the two binary components.
 |
Fig. A.2. Same as Fig. 2 but assuming eq. A.1 for the choice of bmax. The plot shows the outcome of the three-body simulations (upper panel) and the formation channel of the BBH mergers (lower panel) for the main NSC set initialised with eq. 12 (dark red, fiducial model) and the smaller NSC sets initialised with eq. A.1 assuming k = 1 (orange), 2 (yellow), 3 (light green), 4 (dark green), and 5 (blue). |
The lower panel of Fig. A.2 shows that the choice of bmax also affects the percentage of mergers, even if less dramatically than the percentage of flybys, exchanges, and ionisations. The dependence of the percentage of BBH mergers on the choice of bmax is further shown in Fig. A.3. The fraction of BBH mergers decreases only by 1.7% from our fiducial model to the simulation set with k = 5. This plot also shows that the merger fraction linearly decreases with k as Pmerg = α k + β, with α = −0.38 ± 0.09 and β = 11.83 ± 0.31.
 |
Fig. A.3. Percentage of BBH mergers over all the simulated encounters in NSCs, where bmax was computed with eq. 12 and eq. A.1, assuming k = 1, 2, 3, 4, 5. The bar colours are the same as in Figs. A.1 and A.2. The dashed grey line is the linear fit to the percentage of mergers as a function of the k parameter. |
BBH mergers are less affected by the choice of bmax because both Eqs. 12 and A.1 encode the distribution of our semi-major axis, which shapes the overall impact parameter distribution through the bmax dependence on a. In our approach, we sample a in a way that ensures that all our binaries are hard, while also being sufficiently large to prevent efficient GW emission.
Different approaches are assumed in the literature to sample the parameter space of close encounters. For example, Hut & Bahcall (1983) and Zevin et al. (2019) computed bmax as eq. A.1 and set k = 1 with arbitrary fixed values for a. Samsing et al. (2014) chose k = 5 to ensure the sampling of distant interactions, but at the same time they kept the semi-major axis fixed at 10−5 AU, which corresponds to very hard binaries, close to the merger. Quinlan (1996), on the other hand, fixed a but varied the k parameter.
Here, we adopted a physically motivated semi-major axis distribution, ranging from the limit between hard and soft binaries down to the threshold for efficient GW decay. Moreover, in our models we aim to fully explore the parameter space for hard encounters. The price that we pay is that we do not consider encounters with large k. Their effect is shown in figs. A.2 and A.3, for completeness.
Finally, fig. A.4 shows the relative total energy variation of the binaries, dE/E = |Efin−Ein|/|Efin|, where Efin and Ein are the total binary energy at the beginning and end of the simulation, respectively. The peak of the distribution shifts from larger to lower values of the relative total binary energy variation, when k increases. For instance, the distributions for our fiducial model and for eq. A.1 with k = 1 peak more than one order of magnitude above the distributions obtained for k = 4 and k = 5. In the former, only 2.6% and 2.7% of the binary systems yield dE/E < 10−2, while this number increases to 20% and 31% for the latter.
 |
Fig. A.4. Histograms of the normalised variation in the binary total energy with respect to the final binary total energy as a function of bmax. The colours are the same as in Figs. A.1, A.2, and A.3. |
All Tables
All Figures
 |
Fig. 1. Trajectories of three eccentric mergers triggered by a three-body interaction in NSCs (left- and right-hand panels) and GCs (central panel). In the three panels, the systems are centred in the centre of mass of the initial BBH, while the position at which the merger takes place is marked with a white star. The trajectories of the primary and secondary BH of the initial BBH (with mass m1 and m2), and the intruder (m3) are reported in red, blue, and grey, respectively. The incoming direction of the intruder is shown with an arrow. The insets in the left-hand and central panels display a close-up view of the merger region. In the left-hand and central panels, the initial binary is shown edge-on, while in the right-hand panel the view is face-on. The initial coalescence time of these BBHs, i.e. the coalescence time of the initial binary at the beginning of the interaction, is longer than the Hubble time. |
| In the text | |
 |
Fig. 2. Upper panel: percentage of different interaction outcomes for each cluster type. From left to right: (i) flyby events, (ii) exchanges in which the intruder replaces the secondary BH, (iii) exchanges in which the intruder replaces the primary BH, (iv) ionisations, and (v) unstable triples. Lower panel: percentage of BBH mergers. From left to right: (i) BBH mergers occurring after a flyby, (ii) an exchange interaction with the secondary BH replaced by the intruder, (iii) an exchange with the primary BH replaced by the intruder, and (iv) second-generation BBH mergers. In both the upper and lower panels, the colours mark the cluster type in which the interaction takes place. |
| In the text | |
 |
Fig. 3. Distribution of coalescence times for unperturbed initial binaries (filled histograms), and for the same initial binaries perturbed by the three-body interaction (unfilled histograms). The upper, central, and lower panels show the cases of YSCs, GCs, and NSCs, respectively. |
| In the text | |
 |
Fig. 4. Total mass of the BBH mergers in YSCs (blue), GCs (orange), and NSCs (purple). |
| In the text | |
 |
Fig. 5. Orbital eccentricity at 10 Hz (e10 Hz) as a function of the coalescence time (tcoal) of BBH mergers in YSCs (left), GCs (centre), and NSCs (right). Different colours indicate mergers through flybys and the two families of exchanges. The yellow stars show second-generation BBH mergers. The empty black dots highlight the BBH progenitors of second-generation mergers. The dashed vertical line divides the plot into two regions: up to 1 Myr we evolve the systems with ARWV, above 1 Myr all the dynamical interactions are concluded, and with Eq. (1) we stop the ARWV integration and evolve the remaining BBHs. The three insets show a zoom for mergers with e10 Hz > 0.1. We note that some of the points at e10 Hz ∼ 1 overlap. |
| In the text | |
 |
Fig. 6. Same as Fig. 5 but with the orbital eccentricity computed at 1 Hz (e1 Hz). |
| In the text | |
 |
Fig. 7. BBH mergers that take place after the three-body interactions in YSCs, GCs, and NSCs (from top to bottom). All the mergers that take place during the three-body interaction, i.e. < 106 yr, are assumed to merge inside the cluster. The x axis reports the recoil velocity caused by the energy exchange in the three-body encounter. The y axis shows the coalescence time of the binary from the beginning of the simulation. Different outcomes are shown with different markers and colours. In the YSCs case, the horizontal dashed line reports the typical evaporation time of a YSC. The vertical dashed line in all the plots shows the escape velocity of the cluster. Distributions of the recoil velocities are displayed as marginal histograms. The colour legend is the same as the scatter plot. |
| In the text | |
 |
Fig. 8. Distribution of the relativistic recoil kick of the remnants produced by the BBH mergers in YSCs, GCs, and NSCs. The dashed vertical lines represent the escape velocities of the three types of star clusters. |
| In the text | |
 |
Fig. 9. Tilt angle distributions of the BBH orbital plane in NSCs at the end of the simulation with respect to the initial binary orbital plane. Unfilled histograms are flybys (red), exch13 (blue), and exch23 (grey). The filled histogram (yellow) shows the total distribution. We do not show GCs and YSCs because they have exactly the same behaviour. |
| In the text | |
 |
Fig. A.1. Cumulative distribution function of the impact parameter computed assuming bmax from eq. 12, and from eq. A.1 with k = 1, 2, 3, 4, 5. |
| In the text | |
 |
Fig. A.2. Same as Fig. 2 but assuming eq. A.1 for the choice of bmax. The plot shows the outcome of the three-body simulations (upper panel) and the formation channel of the BBH mergers (lower panel) for the main NSC set initialised with eq. 12 (dark red, fiducial model) and the smaller NSC sets initialised with eq. A.1 assuming k = 1 (orange), 2 (yellow), 3 (light green), 4 (dark green), and 5 (blue). |
| In the text | |
 |
Fig. A.3. Percentage of BBH mergers over all the simulated encounters in NSCs, where bmax was computed with eq. 12 and eq. A.1, assuming k = 1, 2, 3, 4, 5. The bar colours are the same as in Figs. A.1 and A.2. The dashed grey line is the linear fit to the percentage of mergers as a function of the k parameter. |
| In the text | |
 |
Fig. A.4. Histograms of the normalised variation in the binary total energy with respect to the final binary total energy as a function of bmax. The colours are the same as in Figs. A.1, A.2, and A.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



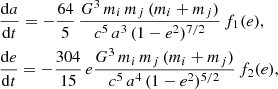
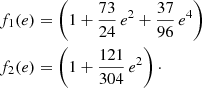
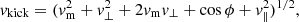
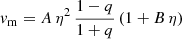
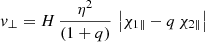
![$$ \begin{aligned} v_{\parallel }&= \frac{16\eta ^{2}}{(1+q)}\,\left[V_{1,1}+V_{\rm A}\,S_{\parallel } + V_{\rm B}\,S^{2}_{\parallel } + V_{\rm C}\,S^{3}_{\parallel }\right]\end{aligned} $$](/articles/aa/full_html/2024/03/aa48745-23/aa48745-23-eq6.gif)
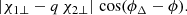
![$$ \begin{aligned} p(a)=\frac{1}{\sigma _{\rm log} \sqrt{2\pi }}\,\exp {\left[{-\frac{(\log {a}-\mu _{\rm log})^{2}}{2\sigma _{\rm log}^{2}}}\right]} \end{aligned} $$](/articles/aa/full_html/2024/03/aa48745-23/aa48745-23-eq8.gif)
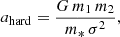
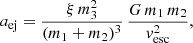
![$$ \begin{aligned} a_{\rm gw}&=\left[\frac{32\,G^2}{5\,\pi \,\xi \,c^5}\,\frac{\sigma \,m_1\,m_2\,(m_1+m_2)}{\rho _{\rm c}\,(1-e^2)^{7/2}}\,f_1(e)\right]^{1/5}. \end{aligned} $$](/articles/aa/full_html/2024/03/aa48745-23/aa48745-23-eq11.gif)
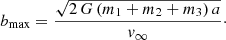
![$$ \begin{aligned} {b_{\rm max}^2 = r_{\rm p}^2\,\left[1 + 2\,\frac{G\,(m_1+m_2+m_3)}{r_{\rm p}\,{ v}_\infty ^2}\right]}\cdot \end{aligned} $$](/articles/aa/full_html/2024/03/aa48745-23/aa48745-23-eq21.gif)