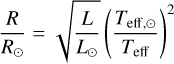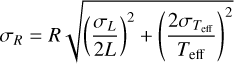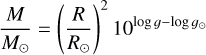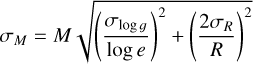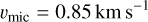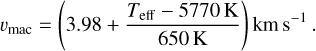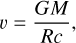EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A106 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A106
Number of page(s) 15
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202348150
Published online 13 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Currently, stellar activity is one of the primary obstacles to detecting the radial velocity (RV) signal of Earth-like exoplanets around solar-type stars. Solar variability has been thoroughly monitored (e.g. Phillips et al. 2016; Collier Cameron et al. 2019; Lin et al. 2022), characterized (e.g., Kjeldsen & Bedding 1995; Lefebvre et al. 2008; Al Moulla et al. 2023), and simulated (e.g., Boisse et al. 2012; Dumusque et al. 2014; Meunier et al. 2015; Ervin et al. 2022; Zhao & Dumusque 2023) in Sun-as-a-star RV observations. Extrapolating our knowledge of the Sun to other stars, we have come to understand that activity phenomena, such as acoustic oscillations (e.g., Kjeldsen et al. 2005; Arentoft et al. 2008; Chaplin et al. 2019), granulation (Dumusque et al. 2011b; Meunier & Lagrange 2019), and active regions (e.g. Meunier et al. 2010; Dumusque et al. 2011a; Lovis et al. 2011), that is, spots, faculae, and plages, all produce surface velocity variations on the order of tens of meters per second, which drown out the eventual ~0.1 ms¯1 semi-amplitude signal of an Earth analogue.

Previous efforts using stellar activity indicators, such as the full-width at half-maximum (FWHM) and the bisector inverse slope (BIS) of the cross-correlation function (CCF) (CCF; Queloz et al. 2001; Pepe et al. 2002) or the Mount Wilson S index extracted from the Ca II H and K lines (Baliunas et al. 1983), have not been able to sufficiently mitigate the activity signal since these indicators are seldom fully correlated with the RVs (Haywood et al. 2016). Recent studies (e.g., Cretignier et al. 2021, 2022) have instead attempted to implement mitigating techniques at the spectral level, before the CCF is applied to extract the RVs, since it is now well established that stellar activity (primarily the inhibition of convective blueshift (CB) by magnetically active regions), affects spectral lines to different extents (e.g., Reiners et al. 2016; Dumusque 2018).

In this study, we investigate how stellar activity affects individual spectral lines parts formed at various temperature regimes in the stellar photosphere. We apply the methodology of Al Moulla et al. (2022), which studied this dependence for the Sun and α Cen B (HD 128621, which is also included in our sample to be analyzed on the long-term), and found that RVs of line parts formed in hotter parts of the photosphere, close to the spectral continuum, are more strongly correlated with the RV contribution of the inhibition of CB compared to line parts formed at cooler temperatures. Here, we extend the work to a sample of 12 late-type (G to early M) dwarfs, in order to investigate whether similar effects can be seen in other spectral types.

In Sect. 2, we describe the stellar sample and the available spectral data. In Sect. 3, we describe the method used to compute the RV of selected line parts. In Sect. 4, we analyze the correlations between stellar activity and formation temperature-binned RV signals. In Sect. 5, we discuss our results and conclude.

Table 1

Observational specifications relevant to our analysis.

2 Data

2.1 Spectral pretreatment

The stellar sample consists of 12 G- to early M-type stars observed with the HARPS1 spectrograph, mounted on the ESO 3.6m Telescope at the La Silla Observatory, Chile, which covers a spectral range from 378 to 691 nm and provides an instrumental resolution of R = 115000. The targets have been frequently observed at relatively high signal-to-noise ratio (S/N) and exhibit clear S index variations indicative of magnetic activity cycles over the observed time span (except for HD 211038, which appears to have been quiet in recent years). They are listed in Table 1, with their observational data, detailing the number of spectra per target, the median S/N, the span in S index after smoothing with a 200-day rolling average (to be less affected by outliers and rotational modulation of the S index), and the span in log R′HK converted from the smoothed S index (Noyes et al. 1984). log R′HK is only a re-scaling of the S index; however, it also corrects for the photospheric contribution to the emission in the Ca II H and K lines using the B–V color of each star (see Table 2), permitting a better comparison between spectral types. We list the span in log R′HK in Table 1 to compare the relative variations within our stellar sample; however, we use the S index for the remainder of our analysis since we only consider correlations with the activity proxies and not their absolute values. The listed numbers of spectra represent the number of retained and nightly stacked spectra after processing with YARARA (Cretignier et al. 2021, 2023), during which a quality-based rejection could be made, and hence the numbers could differ compared to archival data. YARARA performs corrections of stellar activity, telluric absorption, and instrumental system-atics using mainly principal component analysis (PCA) applied on the residual of the spectral data matrix (residual flux versus time).

YARARA also provides a master spectrum computed as the inverse-variance weighted average of all individual spectra at each sampled wavelength point. The absolute RV shift of the master spectrum might lead to an arbitrary offset when template matching with the individual spectra (for example, if the RV of the master spectrum is high, low-activity spectra will appear to be slightly more blueshifted relative to the master compared to a master constructed using only the quietest observations). However, since we are only interested in RV variations, this offset should not be of much importance. More importantly, the YARARA corrections work better at higher S/N, which is why we opted to create master spectra using all available observations. These masters serve as the references both to compare the syntheses (Sect. 3.1) with true observations, and to perform template-matching when extracting the temperature-binned RV time series (Sect. 3.4). After the corrections, we only re-injected the corrected stellar activity of the individual spectra in order to isolate its effect at the spectral level.

2.2 Stellar parameters

The adopted stellar parameters are listed in Table 2. The spectral types and B–V colors were retrieved from SIMBAD2 (Wenger et al. 2000). The effective temperatures, Teff, surface gravities, log g, metallicities, [Fe/H], projected rotational velocities, υ sin i, masses, M, and radii, R, were retrieved from the references in the table foot. For HD 21693, the mass and the radius could not be found in the literature and were instead computed from the luminosity, L, using the following formulas from Valenti & Fischer (2005):

RR⊙=LL⊙(Teff,⊙Teff)2${R \over {{R_ \odot }}} = \sqrt {{L \over {{L_ \odot }}}} {\left( {{{{T_{{\rm{eff}}, \odot }}} \over {{T_{{\rm{eff}}}}}}} \right)^2}$(1a) σR=R(σL2L)2+(2σTeffTeff)2${\sigma _R} = R\sqrt {{{\left( {{{{\sigma _L}} \over {2L}}} \right)}^2} + {{\left( {{{2{\sigma _{{T_{{\rm{eff}}}}}}} \over {{T_{{\rm{eff}}}}}}} \right)}^2}} $(1b)

and

MM⊙=(RR⊙)210logg−logg⊙${M \over {{M_ \odot }}} = {\left( {{R \over {{R_ \odot }}}} \right)^2}{10^{\log g - \log {g_ \odot }}}$(2a) σM=M(σloggloge)2+(2σRR)2${\sigma _M} = M\sqrt {{{\left( {{{{\sigma _{\log g}}} \over {\log e}}} \right)}^2} + {{\left( {{{2{\sigma _R}} \over R}} \right)}^2}} $(2b)

where quantities with the subscript ⊙ denote solar values, and σM, σR, and σL are the uncertainties of the mass, radius, and luminosity, respectively. It should be noted that the masses and radii were solely used for the computation of the gravitational redshift (see Sect. 3.3) and not needed for the subsequent computations of the temperature-dependent RVs.

3 Methods

One of the primary ways of investigating the effects of stellar activity at the spectral level is to extract its differential effect on spectral l nes as s seen n l ne-by-l ne (LBL) RVs (Dumusque 2018; Cretignier et al. 2020; Artigau et al. 2022; Lafarga et al. 2023). In order to further trace the or g n of act v ty, one can, nstead of cons der ng ent re spectral l nes (or spectral reg ons bounded by two local max ma as n the case of M dwarfs where spectral l nes are everywhere), cons der var ous l ne or CCF parts (Al Moulla et al. 2022; Siegel et al. 2022) formed at certain temperature ranges n the stellar photosphere. Contrary to the LBL method, whose feasblty only reles on observational data, this part-by-part (PBP) method also requ res a prior knowledge about where certain spectral features are formed in the photosphere, which can be retrieved from synthetic spectra and thereafter mapped onto cross-matched lines n the observed spectra.

Table 2

Parameters of the stellar sample.

3.1 Spectral synthesis

For the spectral synthesis, we made use of PySME (Wehrhahn et al. 2023), a Python version of Spectroscopy Made Easy (SME; Valenti & Piskunov 1996; Piskunov & Valenti 2017). For each target we used a unique line list from the VALD33,4 database (Piskunov et al. 1995; Kupka et al. 2000; Ryabchikova et al. 2015), which were queried for a wavelength interval of 3500–7000 Å, slightly larger than the range of the HARPS spec-trograph. In the queries we used the stellar parameters in Table 1 and a normalized line depth threshold of 0 01 for all targets except the M dwarf (Gl 229), for which we used a threshold of 0 15 in order to produce line lists with less than a hundred thousand lines (the maximal output of VALD). We used a grid of MARCS (Gustafsson et al. 2008) model atmospheres interpolated for the same stellar parameters as for the queries. The syntheses were broadened with their adopted υ sin i (see Table 2), and micro- and macroturbulences adopted from Valenti & Fischer (2005). The microturbulence was fixed to

υmic=0.85 km s−1${\upsilon _{{\rm{mic}}}} = 0.85\,{\rm{km}}\,{{\rm{s}}^{ - 1}}$(3)

for all stars, and the macroturbulence was set to

υmac=(3.98+Teff−5770 K650 K)km s−1.${\upsilon _{{\rm{mac}}}} = \left( {3.98 + {{{T_{{\rm{eff}}}} - 5770\,{\rm{K}}} \over {650\,{\rm{K}}}}} \right){\rm{km}}\,{{\rm{s}}^{ - 1}}$(4)

In Eq. (4), we have changed the sign of the Teff-dependent term compared to Valenti & Fischer (2005), since their equation has an apparent typo. This is evident from the plotted relation in their Fig. 3 and was also pointed out by Takeda & UeNo (2017). Although the relations in Valenti & Fischer (2005) were derived for FGK stars, we assume they approximately extend to early M dwarfs as well. Furthermore, minor discrepancies in turbulence broadening are not a limiting factor for our analysis since the subsequent rejection of poorly synthesized lines is relative for each star, and hence if all lines are equally over-or under-broadened the final selection remains almost identical. The spectra were finally convolved with a Gaussian instrumental profile to resemble the HARPS resolution of R = 115 000. For each target, a second synthesis excluding rotational, turbulent, and instrumental broadening was computed for the identification of line blends not otherwise seen.

3.2 Average formation temperature

The average formation temperature, denoted as T1/2, was then calculated at each sampled wavelength point of these synthetic spectra by integrating the flux contribution function and inferring the value in the temperature grid at which it reached 50% of its maximum value (see Al Moulla et al. (2022) for further details). Although this value follows the flux variations on a line-by-line basis, it does not hold globally, and thus lines of equal flux depth do not necessarily form at the same average temperature subject to their atomic properties as well as the possibly different level of continuous absorption locally around them.

thumbnail Fig. 1

CB as a function of formation temperature at the line cores, T1/2,c, for the stellar sample. The stars and their spectral types are labeled in the upper left corner of each subplot, and ordered by effective temperature, from left to right and top to bottom. For most stars, the CB shows a linear trend with T1/2,c, indicating that lines formed at higher temperatures, i.e., deeper layers of the photosphere where convective motion is stronger, are subject to larger velocity shifts. The individual spectral lines are shown as points and the fitted linear trends are shown as dashed lines.

3.3 Convective blueshift

For each observed line in the master spectra (see Sect. 2.1), defined as a local minimum bounded by two local maxima, we recalibrated the central wavelength by fitting a second-order polynomial to the central-most seven points. Once the formation temperature spectra were computed, we interpolated their value at the line center, denoted as T1/2,c, of each observed line. We then identified the species of the observed lines using VALD line lists. The cross-match with VALD was done by querying a VALD line list according to the stellar parameters of each star, and then finding all VALD lines that fall within the left and right borders of the observed lines. For observed lines that only have one possible match in the VALD list, the VALD line was taken as the correct identification. Using these uniquely identified lines, an average wavelength dispersion (caused by uncorrected shifts and/or discrepancy in the wavelength solution) was measured. For observed lines that have multiple possible matches, the VALD line with the smallest Euclidean norm of the wavelength and depth differences was adopted if the wavelength was within the dispersion measured on uniquely identified lines. Some observed lines were expected to remain unidentified due to having poorly characterized atomic properties, being tellurics or noisy patterns falsely flagged as stellar lines. We thereafter computed the Doppler shift between the observed central wavelengths of identified lines and the restframe wavelengths from VALD, known as the convective blueshift (CB). This shift originates due to the motion of the convective surface layer in late-type stars, where ascending granules emit more light and cover a larger area than the descending intergranular lanes, causing a net blueshift (Dravins et al. 1981). In order to calibrate the CB to an absolute value, we also subtracted a constant gravitational redshift for each star,

υ=GMRc,$\upsilon = {{GM} \over {Rc}},$(5)

where G is the gravitational constant and c is the speed of light in vacuum. We note that the uncertainty on the gravitational redshift is not propagated into the individual line CBs, as the gravitational redshift is simply a constant offset for each star that we consider in order to have most of our values be negative, and hence truly blueshifts. For the remainder of our analysis we only focus on the CB slopes and not the zero points.

After rejecting blended lines (as determined both from the master spectra themselves and from the syntheses void of any broadening other than thermal) and poorly synthesized lines (see Al Moulla et al. 2022 for the detailed applied criteria), we were left with our final selection of lines, presented in Fig. 1. We remark that, for most stars, the CB decreases (to larger absolute values) with the average formation temperature in the line core as a result of probing hotter photospheric regions where the con-vective motions are more turbulent, and hence producing larger blueshifts. For each star, we regressed a linear model and present the best-fitting slopes in Fig. 2, where the distribution of slopes appears to also follow a linear relation with the effective temperature. The negative slope can be explained by the larger extent of the convective zone of later-type stars, where turnover timescales are longer, and thus the turbulent motions expected to be slower. The direction of this trend is also in agreement with the findings of Liebing et al. (2021), who fitted a scaling factor to the solar relation between the CB and the line depth for 810 F-M stars and found the scaling factor to increase with effective temperature, indicating a steeper slope for hotter stars.

From our limited sample, it remains unclear whether the CB slope plateaus to zero for the coolest stars, or becomes positive. Given the distribution of points in Fig. 1, the linear fits for Gl 229 (the M dwarf) and HD 85512 appear to be poorly constrained. For these stars, the spectral syntheses had larger discrepancies with observations compared to the earlier-type stars, and thus less reliable derived formation temperatures. Another outlier to be remarked upon is HD 211038, which has a steeper slope compared to the stars in the vicinity of its effective temperature. HD 211038 is the only subgiant in our sample of otherwise main-sequence (MS) stars, and it has a significantly lower surface gravity, log ɡ = 3.87±0.06, compared to all the other stars. The steeper slope, indicating a stronger convection strength compared to MS stars of a similar effective temperature, is in agreement with the empirical relations found by Liebing et al. (2023) for evolved stars.

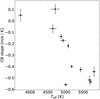thumbnail Fig. 2

Slope of the CB with respect to the average formation temperature of the line cores, as measured from the linear fits seen in Fig. 1. The slope shows a decrease with the stellar effective temperature.

3.4 Temperature-binned RVs

For this study we decided to divide the entire range of formation temperatures per star into intervals of equal size, denoted as ΔT1/2(N, n), where N is the number of intervals and n = [1, N] the interval index going from cooler to hotter temperatures. We considered the N= 1 (equivalent to no temperature binning, i.e., conventional LBL) and N = 4 cases, in order to have comparable results with Al Moulla et al. (2022). It should be noted that the bounds of the temperature intervals for different stars do not necessarily agree with each other, since the intervals were assessed relative to the line-forming temperature regime of each star, that is, the available range of temperatures as given by the spectral syntheses.

The PBP RV of a formation temperature interval was computed by template-matching segments of the individual observed lines, which happen to fall within the considered temperature interval with the same entire line in the master spectrum (Dumusque 2018). This was then repeated for each temperature interval, spectral line, and spectrum in the time series. After an iterative 4σ outlier rejection on the RMS of each interval and line, we computed a weighted average across all remaining lines, resulting in a single RV time series per temperature interval. We require a minimum of three points for the template-matching; however, three points alone will produce a large uncertainty for a given line and temperature interval, such that it will likely be sigma-clipped when computing the line-averaged RV per temperature interval. Furthermore, the temperature intervals will not necessarily be similar across the wavelength range. The primary reason for this is the influence of continuous absorption on the derived formation temperature (see Fig. 2 in Al Moulla et al. 2022). In the optical range of Sun-like stars, the continuous absorption is dominated by the negative hydrogen ion, which increases its opacity up to about 1 m (Gray 2008). Therefore, for the HARPS wavelength range, bluer wavelengths are biased to hotter temperatures and redder wavelengths to cooler ones (because the increased opacity allows us to probe less of the photosphere). But it is exactly these kinds of nuanced differences that we aim to achieve with our analysis.

The N = 1 and N = 4 RV time series are presented in Figs. A.1–A.12, together with the nightly averaged S indices and their respective generalized Lomb-Scargle (GLS; Lomb 1976; Scargle 1982; Zechmeister & Kürster 2009) periodograms. The S indices were retrieved from DACE5,6, which in turn archives them from the HARPS Data Reduction Software (DRS). The HARPS DRS computes the S index in an equivalent way to the original Mount Wilson survey (see Lovis et al. 2011).

4 Activity correlations of temperature-binned RVs

We computed the Pearson correlation coefficient between the S index and each temperature-binned RV time series, which are shown in Fig. 3. We find that for most stars, the RVs of line parts formed in hotter temperatures tend to be more positively correlated, and the RVs of line parts formed in cooler temperatures tend to be more negatively correlated. Furthermore, this relation appears to be amplified with the significance of the signal, as is shown both by the median S/N of the stellar spectra for each star and by the power of the largest periodogram peak for the S index relative to its 0.01% false alarm probability (FAP) level. The color-coded variable in Fig. 3 was selected as a quantification of how statistically significant the S index variations are. We believe that this is better than stating a potentially inaccurate estimate of the S index semi-amplitude since the cycles are not fully sampled. We find no clear dependence on the effective temperature.

These correlations are in agreement with the findings of Al Moulla et al. (2022; see their Figs. A.1 and B.3). However, while they attributed the measured signal at hotter temperature ranges to the suppression of CB by faculae, using simulations of the Sun with SOAP-GPU (Zhao & Dumusque 2023), no clear explanation has been established for the seemingly anti-correlated activity pattern observed at cooler temperatures. The S index, derived from the deep Ca II H and K lines, is known to exhibit chromospheric activity; however, the reason why activity signals at hotter to cooler formation temperatures transition from positively correlated, to weakly correlated, to negatively correlated with the S index requires a more fundamental understanding of the types of active regions and the velocity-altering processes to which chromospheric activity is connected. Forthcoming results by Siegel et al. (in prep.) show that RVs measured on the top versus the bottom parts of the CCF (approximately translating to spectral parts formed at hotter versus cooler temperature ranges) correlate with the photometric and convective influences of active regions, respectively. These results strongly indicate that spectral parts formed at different temperatures are primarily influenced by separate physical processes. Their connection to the S index remains the topic of future investigations. In this study, we showcase the consistency of the observed differential correlation for magnetically active stars.

For a few stars in our sample (HD 215152, HD 192310, and HD 128621), we find a striking, near-perfect (≤−0.8) anti-correlation for the ΔT1/2(4,1) time series. Due to the largely deviating covariances of these RVs, we decided to detrend the ΔT1/2(1, 1) time series (which contains all the RV information) with proxies composed of the differences of various combinations of the 4-bin RVs. The reason for taking the residual of two RV time series as an activity index and not the RV time series themselves was to cancel out the potential presence of a planetary signal in the proxy, since we expect pure Keplerian signals to be of equal amplitude regardless of the bin configuration. We compared the ratio of the RV root mean square (RMS) before and after detrending to assess the improvement factor of the RV precision. We tried detrending with the S index alone as a reference case, before we detrended with one RV residual at a time, followed by a multi-linear regression (MLR) with all combinations of 4-bin residuals, and then a MLR with all 4-bin residuals and the S index combined. The RMS improvement factors for each star and detrending method are shown in Fig. 4. We find that for a majority of stars in our sample the MLR regression with all bin residuals and the S index is able to decrease the RMS to a greater extent than the S index alone, indicating that the 4-bin RV time series are likely tracing different activity contributions than those of the S index.

thumbnail Fig. 3

Pearson correlation, ℛ, between the temperature-binned RVs and the S index. The stars are ordered by effective temperature. The marker size indicates the median S/N of the studied spectra of each star, and the marker color indicates the power, P, of the largest periodogram peak of the S index relative to its 0.01% FAP level. The color map inverts at 1, such that green points represent periodograms peaks above the 0.01% FAP, and red points represent peaks below it.

5 Discussion and conclusions

In Al Moulla et al. (2022), the authors demonstrated that for two MS stars for which we can reach extremely high S/N (>500 for the G2V Sun and the K1V α Cen B), it was possible to precisely measure the RV of different layers in the stellar atmosphere and to confidently measure the differential effect of stellar variability as a function of the line formation temperature, which is expected from our understanding of the RV activity signal (e.g., Meunier et al. 2017). In this paper, we further extend the analysis to 12 stars, with spectral types from G2V to M1V and observations that have a more reasonable S/N (~ 100–300). We show again the differential effect of stellar variability as a function of depth inside the stellar photosphere, which demonstrates that this technique can be used to probe and correct for stellar activity on a wide variety of MS stars that are observed at a high, but not extreme, S/N.

To confidently measure the differential effect of stellar variability as a function of line formation temperature, there are many aspects to consider and justify. Carrying out the analysis for solar observations has the advantage of theoretical models, such as the spectral synthesis used to derive the formation temperature itself, usually being optimized for the Sun as a reference target. In addition, solar observations enjoy the benefit of rarely being noise limited due to their wealth of photons. Hence, to extend the analysis to solar-like stars requires the assumption of precise enough spectral modeling for other stellar parameters, as well as efficient high-resolution spectrographs that can reach high S/N for stellar observations.

In our work, we justify the use and accuracy of synthetic spectra mapped to high-resolution observations by verifying the consistency of derived relations, such as the net blueshift of line cores (see Sect. 3.3). Selecting unblended lines with relatively small observation-synthesis flux residuals, we find a linear relation between the CB and core formation temperature analogous to the third signature of granulation observed when substituting temperature for line depth (Gray 2009; Reiners et al. 2016; Liebing et al. 2023). This also allows us to determine how our synthesis becomes successively less reliable for cooler stars as the relation becomes less constrained (cf. Fig. 1).

By nightly stacking and correcting our spectra for instrumental systematics using YARARA, we were able to extract temperature-binned RVs to an extent where the intrinsic variations still significantly exceed the white noise. Some of the selected stars do have confirmed planetary companions; however, planets with RV semi-amplitudes larger than a few meters per second were removed by YARARA. Any potentially remaining lower-mass planets would not affect our results significantly since they would contribute negligibly to the RV RMS and not be detectable with our limited methodology even after the improvement of the MLR.

We emphasize again the opposing effect of stellar activity on line parts formed at hotter versus cooler photospheric temperatures, as is seen in the correlation coefficients with the S index. The RVs originating from the coolest 25% appear to be the most sensitive to S index variations, and the negativity of the correlation alludes to this temperature regime being more sensitive to chromospheric activity differing from the dominating inhibition of CB at hotter temperatures. After detrending the RV time series computed on the entire range of formation temperatures with proxies composed of residuals of the time series computed on four temperature bins, we found that a MLR of all bin residuals together with the S index yielded an RMS improvement greater than detrending with the S index alone for a majority of the studied stars. On average, the improvement in RV RMS is on the order of 20% when using the MLR and S index. However, when analyzing the results of Fig. 4, it is still challenging to understand why in some cases the RV RMS is strongly reduced while in some other cases the improvement is minimal. For Gl 229, the RMS values after detrending are noticeably unchanged; the ratios are not exactly 1, but close enough to not be discernible. This is not too surprising, however, given the very low activity correlations of all its RV time series (see Fig. A.1).

From the results of this study, the residuals of the temperature-binned RVs are demonstrated as being excellent proxies with which to probe the stellar activity effect, mainly magnetic cycles, and to differentiate planetary long-period signals from stellar ones. However, since the efficiency of those proxies at correcting for the stellar signal changes from star to star, without a clear correlation with spectral type, it remains to be explored how the formalism of using line formation temperatures to extract PBP RVs can be further leveraged to attain RVs that target certain flavors of stellar activity or that are optimally mitigated for planet searches.

thumbnail Fig. 4

RMS improvement of the ∆T1/2(1,1) RV time series after linear detrending with different proxies. The markers represent detrending with either the S index alone (circles with orange edges), different 4-bin residuals (convex polygons with black edges), a multi-linear combination of all 4-bin residuals (crosses), or a multi-linear combination of all 4-bin residuals and the S index (stars). The marker sizes and colors indicate the same properties as described in Fig. 3.

Acknowledgements

We thank the anonymous referee for their valuable comments which improved the quality of our manuscript. This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. The authors acknowledge the financial support of the SNSF. M.C. acknowledges the SNSF support under the Post-Doc Mobility grant P500PT_211024. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement SCORE No. 851555). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.

Appendix A Temperature-dependent RV time series

thumbnail Fig. A.1

Time series and GLS periodograms of Gl 229. Left: Time series of the S index (first row), the RV computed for 1 formation temperature bin (second row), and the RV computed for four formation temperature bins (third to sixth row, in order of the coolest to hottest bin). For the S index, black points show nightly binned values and green points show nightly binned values smoothed with a 200-day rolling average. Middle: Correlations between the unsmoothed S index and corresponding RVs from the left panels. The Pearson correlation coefficients, which are summarized in Fig. 3, are shown in the upper left corners. Right: GLS periodograms of the S index and RVs from the left panels. The dashed lines show the corresponding 0.01% FAP levels.
thumbnail Fig. A.2

Same as Fig. A.1, but for HD 36003.
thumbnail Fig. A.3

Same as Fig. A.1, but for HD 85512.
thumbnail Fig. A.4

Same as Fig. A.1, but for HD 154577.
thumbnail Fig. A.5

Same as Fig. A.1, but for HD 215152.
thumbnail Fig. A.6

Same as Fig. A.1, but for HD 211038.
thumbnail Fig. A.7

Same as Fig. A.1, but for HD 192310.
thumbnail Fig. A.8

Same as Fig. A.1, but for HD 128621.
thumbnail Fig. A.9

Same as Fig. A.1, but for HD 21693.
thumbnail Fig. A.10

Same as Fig. A.1, but for HD 56274.
thumbnail Fig. A.11

Same as Fig. A.1, but for HD 189567.
thumbnail Fig. A.12

Same as Fig. A.1, but for HD 45184.

References

  1. Al Moulla, K., Dumusque, X., Cretignier, M., Zhao, Y., & Valenti, J. A. 2022, A&A, 664, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Al Moulla, K., Dumusque, X., Figueira, P., et al. 2023, A&A, 669, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Arentoft, T., Kjeldsen, H., Bedding, T. R., et al. 2008, ApJ, 687, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  4. Artigau, É., Cadieux, C., Cook, N. J., et al. 2022, AJ, 164, 84 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baliunas, S. L., Hartmann, L., Noyes, R. W., et al. 1983, ApJ, 275, 752 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boisse, I., Bonfils, X., & Santos, N. C. 2012, A&A, 545, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Chaplin, W. J., Cegla, H. M., Watson, C. A., Davies, G. R., & Ball, W. H. 2019, AJ, 157, 163 [Google Scholar]
  8. Collier Cameron, A., Mortier, A., Phillips, D., et al. 2019, MNRAS, 487, 1082 [Google Scholar]
  9. Cretignier, M., Dumusque, X., Allart, R., Pepe, F., & Lovis, C. 2020, A&A, 633, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cretignier, M., Dumusque, X., Hara, N. C., & Pepe, F. 2021, A&A, 653, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cretignier, M., Dumusque, X., & Pepe, F. 2022, A&A, 659, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cretignier, M., Dumusque, X., Aigrain, S., & Pepe, F. 2023, A&A, 678, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Delisle, J. B., Ségransan, D., Dumusque, X., et al. 2018, A&A, 614, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dravins, D., Lindegren, L., & Nordlund, A. 1981, A&A, 96, 345 [NASA ADS] [Google Scholar]
  15. Dumusque, X. 2018, A&A, 620, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Dumusque, X., Santos, N. C., Udry, S., Lovis, C., & Bonfils, X. 2011a, A&A, 527, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011b, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dumusque, X., Boisse, I., & Santos, N. C. 2014, ApJ, 796, 132 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ervin, T., Halverson, S., Burrows, A., et al. 2022, AJ, 163, 272 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
  21. Gray, D. F. 2009, ApJ, 697, 1032 [Google Scholar]
  22. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Haywood, R. D., Collier Cameron, A., Unruh, Y. C., et al. 2016, MNRAS, 457, 3637 [Google Scholar]
  24. Hojjatpanah, S., Oshagh, M., Figueira, P., et al. 2020, A&A, 639, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  26. Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [Google Scholar]
  28. Kuznetsov, M. K., del Burgo, C., Pavlenko, Y. V., & Frith, J. 2019, ApJ, 878, 134 [Google Scholar]
  29. Lafarga, M., Ribas, I., Zechmeister, M., et al. 2023, A&A, 674, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Lefebvre, S., García, R. A., Jiménez-Reyes, S. J., Turck-Chièze, S., & Mathur, S. 2008, A&A, 490, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Liebing, F., Jeffers, S. V., Reiners, A., & Zechmeister, M. 2021, A&A, 654, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Liebing, F., Jeffers, S. V., Zechmeister, M., & Reiners, A. 2023, A&A, 673, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Lin, A. S. J., Monson, A., Mahadevan, S., et al. 2022, AJ, 163, 184 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  35. Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, arXiv e-prints [arXiv:1107.5325] [Google Scholar]
  36. Meunier, N., & Lagrange, A. M. 2019, A&A, 625, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Meunier, N., Desort, M., & Lagrange, A.-M. 2010, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Meunier, N., Lagrange, A. M., Borgniet, S., & Rieutord, M. 2015, A&A, 583, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Meunier, N., Lagrange, A.-M., & Borgniet, S. 2017, A&A, 607, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  41. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Phillips, D. F., Glenday, A. G., Dumusque, X., et al. 2016, SPIE Conf. Ser., 9912, 99126Z [Google Scholar]
  43. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
  45. Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [Google Scholar]
  48. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  49. Siegel, J. C., Rubenzahl, R. A., Halverson, S., & Howard, A. W. 2022, AJ, 163, 260 [NASA ADS] [CrossRef] [Google Scholar]
  50. Soto, M. G., & Jenkins, J. S. 2018, A&A, 615, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Takeda, Y., & UeNo, S. 2017, PASJ, 69, 46 [NASA ADS] [Google Scholar]
  53. Takeda, G., Ford, E. B., Sills, A., et al. 2007, ApJS, 168, 297 [Google Scholar]
  54. Tuomi, M., Jones, H. R. A., Barnes, J. R., Anglada-Escudé, G., & Jenkins, J. S. 2014, MNRAS, 441, 1545 [Google Scholar]
  55. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
  56. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Wehrhahn, A., Piskunov, N., & Ryabchikova, T. 2023, A&A, 671, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
  60. Zhao, Y., & Dumusque, X. 2023, A&A, 671, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
*

Based on observations made with the HARPS instrument on the ESO 3.6m Telescope at the La Silla Observatory, Chile.

1

HARPS stands for High Accuracy Radial velocity Planet Searcher (HARPS).

3

VALD stands for Vienna Atomic Line Database.

5

DACE stands for Data & Analysis Center for Exoplanets.

All Tables

Table 1

Observational specifications relevant to our analysis.

In the text
Table 2

Parameters of the stellar sample.

In the text

All Figures

thumbnail Fig. 1

CB as a function of formation temperature at the line cores, T1/2,c, for the stellar sample. The stars and their spectral types are labeled in the upper left corner of each subplot, and ordered by effective temperature, from left to right and top to bottom. For most stars, the CB shows a linear trend with T1/2,c, indicating that lines formed at higher temperatures, i.e., deeper layers of the photosphere where convective motion is stronger, are subject to larger velocity shifts. The individual spectral lines are shown as points and the fitted linear trends are shown as dashed lines.
In the text
thumbnail Fig. 2

Slope of the CB with respect to the average formation temperature of the line cores, as measured from the linear fits seen in Fig. 1. The slope shows a decrease with the stellar effective temperature.
In the text
thumbnail Fig. 3

Pearson correlation, ℛ, between the temperature-binned RVs and the S index. The stars are ordered by effective temperature. The marker size indicates the median S/N of the studied spectra of each star, and the marker color indicates the power, P, of the largest periodogram peak of the S index relative to its 0.01% FAP level. The color map inverts at 1, such that green points represent periodograms peaks above the 0.01% FAP, and red points represent peaks below it.
In the text
thumbnail Fig. 4

RMS improvement of the ∆T1/2(1,1) RV time series after linear detrending with different proxies. The markers represent detrending with either the S index alone (circles with orange edges), different 4-bin residuals (convex polygons with black edges), a multi-linear combination of all 4-bin residuals (crosses), or a multi-linear combination of all 4-bin residuals and the S index (stars). The marker sizes and colors indicate the same properties as described in Fig. 3.
In the text
thumbnail Fig. A.1

Time series and GLS periodograms of Gl 229. Left: Time series of the S index (first row), the RV computed for 1 formation temperature bin (second row), and the RV computed for four formation temperature bins (third to sixth row, in order of the coolest to hottest bin). For the S index, black points show nightly binned values and green points show nightly binned values smoothed with a 200-day rolling average. Middle: Correlations between the unsmoothed S index and corresponding RVs from the left panels. The Pearson correlation coefficients, which are summarized in Fig. 3, are shown in the upper left corners. Right: GLS periodograms of the S index and RVs from the left panels. The dashed lines show the corresponding 0.01% FAP levels.
In the text
thumbnail Fig. A.2

Same as Fig. A.1, but for HD 36003.
In the text
thumbnail Fig. A.3

Same as Fig. A.1, but for HD 85512.
In the text
thumbnail Fig. A.4

Same as Fig. A.1, but for HD 154577.
In the text
thumbnail Fig. A.5

Same as Fig. A.1, but for HD 215152.
In the text
thumbnail Fig. A.6

Same as Fig. A.1, but for HD 211038.
In the text
thumbnail Fig. A.7

Same as Fig. A.1, but for HD 192310.
In the text
thumbnail Fig. A.8

Same as Fig. A.1, but for HD 128621.
In the text
thumbnail Fig. A.9

Same as Fig. A.1, but for HD 21693.
In the text
thumbnail Fig. A.10

Same as Fig. A.1, but for HD 56274.
In the text
thumbnail Fig. A.11

Same as Fig. A.1, but for HD 189567.
In the text
thumbnail Fig. A.12

Same as Fig. A.1, but for HD 45184.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.