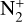| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348027 | |
| Published online | 05 March 2024 | |
12CO+ and 13CO+ fluorescence models for measuring the 12C/13C isotopic ratio in comets
1
Institut UTINAM – UMR 6213, CNRS / Univ. de Franche-Comté, OSU THETA, 41 bis Av. de l’Observatoire, BP 1615, 25010 Besançon Cedex, France
e-mail: philippe.rousselot@obs-besancon.fr
2
STAR Institute, Univ. of Liège, Allée du 6 Août 19c, 4000 Liège, Belgium
3
Institute for Astronomy, Univ. of Edinburgh, Royal Observatory, Edinburgh EH9 3HJ, UK
4
Laboratoire Interdisciplinaire Carnot de Bourgogne – UMR 6303, CNRS / Univ. de Bourgogne, 9 Av. A. Savary, BP 47870, 21078 Dijon Cedex, France
Received:
20
September
2023
Accepted:
1
December
2023
Context. CO is an abundant species in comets, creating CO+ ion with emission lines that can be observed in the optical spectral range. A good modeling of its fluorescence spectrum is important for a better measurement of the CO+ abundance. Such a species, if abundant enough, can also be used to measure the 12C/13C isotopic ratio.
Aims. This study uses the opportunity of a high CO content observed in the comet C/2016 R2 (PanSTARRS), which created bright CO+ emission lines in the optical range, to build and test a new fluorescence model of this species and to measure the 12C/13C isotopic ratio in this chemical species for the first time with ground-based observations.
Methods. Thanks to laboratory data and theoretical works available in the scientific literature, we developed a new fluorescence model both for 12CO+ and 13CO+ ions. The 13CO+ model can be used for coadding faint emission lines and to obtain a sufficient signal-to-noise ratio to detect this isotopologue.
Results. Our fluorescence model provides a good modeling of the 12CO+ emission lines, allowing us to publish revised fluorescence efficiencies. Based on similar transition probabilities for 12CO+ and 13CO+, we derive a 12C/13C isotopic ratio of 73±20 for CO+ in comet C/2016 R2. This value is in agreement with the Solar System ratio of 89±2 within the error bars, but is also consistent with the 12C/13C ratio in local interstellar medium (68±15).
Key words: line: identification / molecular data / comets: general / comets: individual: C/2016 R2
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Comets are small icy bodies that remain relatively unaltered by physico-chemical processes since their formation in the outer part of the Solar System. Studying their physical and chemical properties provides useful constraints on the physical and chemical properties of their formation place and, consequently, on the protosolar nebula. These small bodies present some significant differences in their chemical composition, but their main species have been known for a long time thanks to numerous spectroscopic observations. The main species detected in cometary coma is water molecules, with CO and CO2 being the second most abundant species (typically about 10–20% relative to water).
Carbon monoxide being much more volatile than water this species can drive cometary activity at a large distance from the Sun (heliocentric distance larger than 5 au), while water is responsible for the cometary activity usually observed, that is, for comets closer than about 3 au to the Sun. In the near-UV and optical ranges, where most spectroscopic observations are conducted, it is possible to observe CO+ emission lines, this ion being created by CO, or indirectly by CO2. This species was first reproduced in the laboratory by Fowler (1909a,b) for spectra obtained in the tails of comets C/1907 L2 (Daniel) and C/1908 R1 (Morehouse) and later assigned to CO+. The same author later noticed the presence of similar emission bands in Brorsen’s comet observed in 1868 by William Huggins (Fowler 1910). Swings (1965) mentions observations of CO+ bands (now called “comet tail system of CO+”) in the tail of several comets observed after C/1908 R1 (Morehouse).
Emission bands of CO+ are, nevertheless, not so often observed in comets. As mentioned above, such bands were first observed in the tails of comets at an epoch where spectrographs observed comets on a large scale, covering both the coma and the tail. The instruments later focused on the inner coma, where the signal-to-noise ratio is better and makes it possible to obtain high-resolution spectra. In this region, the detection of CO+ species is more difficult. A noticeable exception was the comet C/2016 R2 (PanSTARRS), whose coma presented an unusual composition dominated by the 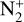 and CO+ ions (Cochran & McKay 2018; Opitom et al. 2019).
and CO+ ions (Cochran & McKay 2018; Opitom et al. 2019).
This comet was discovered on September 7, 2016 by the PanSTARRS survey (Weryk & Wainscoat 2016). It is a long period comet that developed a coma as far as 6 au to the Sun and started to display unusual coma morphology with a rapidly changing structure1, attributed to ions dominating the emission in the coma. Radio observations revealed a coma dominated by CO with a low abundance of HCN (Wierzchos & Womack 2018), and optical observations later revealed a spectrum dominated by CO+ and 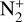 emission bands (Biver et al. 2018; Cochran & McKay 2018; Opitom et al. 2019). The unusually high abundance of CO+ ions in the inner coma of this relatively bright comet (and unusually low abundance of common species such as CN and C2) permitted us to obtain CO+ spectra with unprecedented quality (both with high resolution and high signal-to-noise ratio) for this species with the UVES spectrograph mounted on the 8.2-m ESO VLT telescope, which was already presented in Opitom et al. (2019).
emission bands (Biver et al. 2018; Cochran & McKay 2018; Opitom et al. 2019). The unusually high abundance of CO+ ions in the inner coma of this relatively bright comet (and unusually low abundance of common species such as CN and C2) permitted us to obtain CO+ spectra with unprecedented quality (both with high resolution and high signal-to-noise ratio) for this species with the UVES spectrograph mounted on the 8.2-m ESO VLT telescope, which was already presented in Opitom et al. (2019).
A correct analysis of such spectra implies a good modeling of the fluorescence spectrum of Co+ in comets. Such a modeling was already done by Magnani & A’Hearn (1986). Nevertheless, this work does not present any spectrum that could be confronted to our observational data and some new laboratory and theoretical works have been published after this pioneering work. For these reasons, we decided to build a new fluorescence model, based on more recent laboratory data and theoretical works.
In this paper, we first present our observational data before explaining our model in detail and comparing it to the observed spectra. This work also provides new information related to the fluorescence efficiencies. Because such data also open the possibility, for the first time, to measure the 12C/13C isotopic ratio in CO+, we also computed a fluorescence model of the 13CO+ isotopologue and searched for its emission lines. The result of the search of these faint lines is also presented, leading to a first estimate of the 12CO+/13CO+ ratio in a comet.
2 Observational data
The spectra used for this work were obtained with the Ultraviolet-Visual Echelle Spectrograph (UVES) mounted on the ESO 8.2 m UT2 telescope of the Very Large Telescope (VLT) located in Chile. They correspond to the dichroic #1 (390+580 settings) covering the 326–454 nm range in the blue and 476–684 nm in the red and the dichroic #2 (437+860 settings) covering the 373–499 nm range in the blue and 660–1060 nm in the red (the data obtained in this last spectral range were not used for this work). Three different observing nights have been used for observations with the dichroic #1, corresponding to February 11, 13, and 14, 2018. During each night one single exposure of 4800 s of integration time was obtained. We used a 0.44″ wide slit, providing a resolving power of R ~ 80 000. The slit length was 8″ for the 390 setting, corresponding to about 14 500 km at the distance of the comet (geocentric distance of 2.4 au), and 12″ for the 580 setting. The average heliocentric distance was 2.76 au, and the heliocentric velocity 5.99 km s−1. The observations performed with dichroic #2 (437+860) correspond to two observing nights on February 15 and 16. In that case a single exposure of 3000 s of integration time was obtained for both nights and the slit width was also 0.44″ with a slit length of 10″ (for the setting 437). Opitom et al. (2019) provided more details about these observations.
As explained by these authors the data were reduced using the ESO UVES pipeline combined with custom routines to perform the extraction and cosmic ray removal, and they were then corrected for the Doppler shift due to the relative velocity of the comet with respect to the Earth. The spectra are calibrated in absolute flux using either the archived master response curve or the response curve determined from a standard star observed at a similar airmass to the science spectrum (with no significant differences between these two methods). This data processing produced 2D spectra calibrated in wavelength and absolute flux units. Because a close examination of the ESO UVES sky emission spectrum2 allows us to check that telluric lines are below the noise level in this part of the spectrum, no specific data processing was done to remove these lines.
From these three different settings (390, 580, and 437), we computed average 1D spectra. These 1D spectra were further split in different parts corresponding to the different CO+ emission bands. The solar continuum was subtracted for each of these different spectra individually in order to adjust it as well as possible in a limited spectral range. Many CO+ bands can be identified in our observational data (see Sect. 5 for more details).
3 12CO+ fluorescence model
The CO+ emission lines observed in the optical range belong to the comet tail system, that is, to the A2Πi−X2Σ+ electronic transition. The A2Πi state is divided into two branches (2Π1/2 and 2Π3/2 labeled F2 and F1) with a large energy separation because the 2Π electronic state is intermediate between Hund’s cases (a) and (b) (the F2 states corresponding to higher energies). The rotational levels are split as a result of Λ doubling. Such a rotational structure gives rise to 12 branches, and each band is divided into two sub-bands corresponding to the 2Π1/2 − X2Σ+ and 2Π3/2 − X2Σ+ transitions. Figure 1 presents the energy levels diagram with the different types of lines involved in this transition.
A pioneering work was published by Magnani & A’Hearn (1986) presenting a fluorescence model for CO+ in cometary coma. This paper does not show any comparison between synthetic spectra and observational data. To model the 12CO+ and 13CO+ in comet C/2016 R2, it appears necessary to develop a new fluorescence model that can benefit from different experimental and theoretical articles published after Magnani & A’Hearn’s paper. Such works can significantly help to improve this modeling. Magnani & A’Hearn (1986) nevertheless contains interesting data to build such a new fluorescence model.
We developed our own fluorescence model of CO+ that takes into account the A2Πi and X2Σ+ electronic levels with the first six vibronic levels (υ = 0–5). The energy levels for the X2Σ+ state and the first three vibrational quantum numbers υ equal to 0, 1, and 2 were taken from Hakalla et al. (2019), as well as the υ = 0, 1 vibronic energy levels of the A2Πi· state. From the X2Σ+ υ = 0 levels, accurate energy levels of the A2Πi υ = 2,3,4 states were computed with the transition frequencies published by Kępa et al. (2004) for the (2,0), (3,0), and (4,0) bands. The remaining energy levels (υ = 3, 4, 5 of the X2Σ+ state and υ = 5 of the A2Πi state) were computed from the molecular parameters published by Kępa et al. (2004; rotational constants) and Coxon et al. (2010) (band origin). All the levels with a rotational quantum number J ≤ 10.5 are taken into account in our model.
The Einstein coefficients for the spontaneous transition probabilities were computed with the transition probabilities computed by Billoux et al. (2014) expressed in atomic units. These values need to be converted to spontaneous emission Einstein coefficients Aul from the upper level u to the lower level l of a given line by using the following formula (case of a Π–Σ transition):
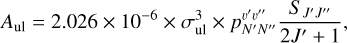
with 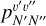 being the transition probability provided by Billoux et al. (2014) expressed in atomic units, σul the wavenumber expressed in cm−1, J′ the rotational quantum number of the upper state and S J′J″ the Hönl-London factor.
being the transition probability provided by Billoux et al. (2014) expressed in atomic units, σul the wavenumber expressed in cm−1, J′ the rotational quantum number of the upper state and S J′J″ the Hönl-London factor.
The Hönl-London factors were taken from Arpigny (1964b) and renormalized to follow the summation rule used by Billoux et al. (2014), that is:
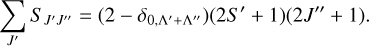
The Einstein absorption coefficients Blu were computed from the Aul coefficients and the wave numbers of the corresponding transitions. The probability of absorption is given by Blu × ρν, with ρν being the radiation density at the corresponding wavelength, expressed in erg cm−3 Hz−1. We used the high-resolution solar spectrum published by Kurucz et al. (1984) to compute the solar radiation density.
The pure vibrational transition probabilities of the ground X2Σ+ state were taken from Rosmus & Werner (1982) (Aν′ν″ Einstein coefficients), with Hönl-London factors from Magnani & A’Hearn (1986). The pure rotational transition probabilities were computed from the formulae published by Arpigny (1964a) for a 2Σ state in using an electric dipole moment µ = 2.771 Debye (Bell et al. 2007).
Apart the ground electronic state X2Σ+ and the first electronic excited state A2Πi, there is another excited electronic state B2Σ+ with a B2Σ+ – X2Σ+ transition called first negative system and a B2Σ+ − A2Πi transition called Baldet-Johnson system (see Fig. 1 in Magnani & A’Hearn 1986). Because the first negative system B2Σ+ – X2Σ+ transition can also slightly influence the relative populations of the ground electronic state some levels in the B2Σ+ (v = 0,1, 2) were also taken into account in our modeling with the first negative system (the Baldet-Johnson system implying two excited electronic states its influence can be neglected). The energy levels of the B2Σ+ have been computed with the molecular parameters published by Szajna et al. (2004) and the transition probabilities are taken from Magnani & A’Hearn (1986).
The relative population was computed at the equilibrium with the method described by Zucconi & Festou (1985). Such a method is justified by the heteronuclear nature of the CO+ ion that involves pure vibrational and rotational transitions that make it possible to reach the fluorescence equilibrium with a timescale well below the time spent by these ions in the observed cometary coma (this is not the case for homonuclear species such as C2 or  ). We assume that the coma is an optically thin medium for this spectrum, that is, that the radiation received by the telescope is proportional to the number of CO+ ions along the line of sight with the radiation emitted in units of energy in 4π steradian equal to xi × hv, with xi being the relative population, h the Planck constant, and v the frequency.
). We assume that the coma is an optically thin medium for this spectrum, that is, that the radiation received by the telescope is proportional to the number of CO+ ions along the line of sight with the radiation emitted in units of energy in 4π steradian equal to xi × hv, with xi being the relative population, h the Planck constant, and v the frequency.
 |
Fig. 1 Energy level diagram showing A2Πi–X2Σ+ transition with different lines involved in this transition. The number in parentheses refers to the J″ value of the line. |
4 13CO+ fluorescence model
For this isotopologue the energy levels come from the laboratory data published by Kępa et al. (2002); we used the (1,0), (3,0), (4,0), and (5,0) bands’ wave numbers of the lines observed to reconstruct all the energy levels of the X2Σ+ state v = 0. From this state it was then possible to compute the energy levels of the A2Πi υ = 1,2,3,4,5 states using the (l,0)(2,0)(3,0)(4,0)(5,0) transitions. After this computation the X2Σ+ state v = 1 was computed using the (2,1) band wave numbers. Such a method provides a high level of accuracy for the final wavelength (accuracy of about 0.01 Å, well below the full width at half maximum (FWHM) of our high-resolution spectra). The missing energy levels were computed from the molecular parameters published by Kępa et al. (2002) for the A2Πi υ = 0 state and X2Σ+ state υ = 2,3,4,5.
For the B2Σ+ level, we also used the molecular constants published by Szajna et al. (2004) but adapted for the 13CO+ iso-topologue. It was done using the reduced atomic mass µ′ of this isotopologue and the one of 12CO+ (µ) providing the parameter 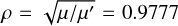 . This parameter was used to compute the molecular parameters of 13CO+ from the ones of 12CO+ thanks to the formulae given by Herzberg (1950).
. This parameter was used to compute the molecular parameters of 13CO+ from the ones of 12CO+ thanks to the formulae given by Herzberg (1950).
The transition probabilities have been assumed to be equal to the ones of 12CO+, such an approximation is justified by some calculations done for other diatomic species that show only small relative differences for the transition probabilities for different isotopologues (see, e.g., Ferchichi et al. (2022) for the different isotopologues of 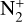 ).
).
5 Comparison with observational data and fluorescence efficiencies
With the 12CO+ emission lines being clearly visible in our C/2016 R2 spectra, it is possible to check, for the first time and with a high level of accuracy, the quality of our fluorescence model developed for this isotopologue. Our observational data permit us to observe different bands with the three different UVES settings mentioned in Sect. 2. These settings corresponding to different slit sizes, observation epochs, or exposure times show different relative intensities of the spectra.
We computed the 12CO+ fluorescence spectrum for the condition of observations of C/2016 R2 and adjusted its intensity for each setting. We kept the same relative intensity for all the different bands observed with a same setting in order to check the accuracy of the relative intensities provided by our model for different bands. Figure 2 provides an overview of all the CO+ emission bands identified in our observations, for the three different settings used for this work.
For a better comparison between observational data and the synthetic spectrum Figs. A.1–A.3 provide zoomed-in views of different bright bands to show the details of the rotational structure. The relative intensities for the different bands agree well with the observational data.
We can compute fluorescence efficiencies, also called 𝑔-factors or band luminosities, with our fluorescence model. Table 1 provides an overview of these important parameters for a heliocentric distance of 1 au and a heliocentric velocity of 0 km s−1. A comparison of this parameter with the results published by Magnani & A’Hearn (1986) in their Table 3 makes it possible to see a similar value for the (4,0) band (1.07 × 10−14 vs. 1.04 × 10−14 erg s−1 ion−1), which is one of the brightest bands. The relative differences in intensities between our model and the results published by Magnani & A’Hearn (1986) can reach a factor of about two for some bands. For the brightest ones (i.e., (3,0), (2,0), and (4,0) by decreasing intensity), which are displayed Fig. A.1 (and Fig. A.2 for (2,0) and (3,0)), our modeling shows a good fit with the observational data. Our computed intensity ratio 𝑔(3,0)/𝑔(4,0) = 1.63 appears in good agreement with the observational data, but disagrees with the ratio computed by Magnani & A’Hearn (1986), which is 2.03 and would not be able to fit such observational data as well as our model. We have no possibility to test the absolute values of the band luminosities, but our fit of the different bands confirms that their relative values are robust, at least to about 10%. Figure 3 shows the variation of fluorescence efficiencies as a function of the heliocentric velocity for the four brightest bands (i.e. (3,0), (2,0), (4,0), and (1,1) by decreasing intensity). Some variations can be observed but remain limited to less than about 15% between the smaller and the larger values. We also computed the product of the fluorescence efficiency by the square of heliocentric distance rh (expressed in au) for different heliocentric distances in order to check if there is any significant deviation from the usual scaling law with this parameter. Only some small variations can be observed (see Table 2).
We also computed fluorescence efficiencies for 13CO+ (see Table 3). As we assumed that 13CO+ and 12CO+ have similar transition probabilities these band luminosities are very close to the ones of 12CO+, but some differences appear due to the wavelength shifts, which implies some variations in the solar flux for absorption transitions. Such fluorescence efficiencies can be useful for future 12C/13C isotopic ratio measurements in CO+ (see below).
6 Measurement of 12CO+/13CO+ isotopic ratio in comet C/2016 R2
The high signal-to-noise and spectral resolution of our observational data opens the possibility, for the first time, to measure the 12C/13C isotopic ratio in the CO+ species with ground-based observations. It is possible thanks to the wavelength shift between the spectrum of the two isotopologues. Figure 4 presents the synthetic spectra of these two isotopologues superimposed on the observational data of the brightest band (i.e., the (3,0)). It can be seen that the 13CO+ emission lines are clearly separated from the 12CO+ ones. At this intensity scale no 13CO+ emission lines are visible.
To increase the signal-to-noise ratio of the possible 13CO+ emission lines, we decided to co-add the brightest 13CO+ emission lines for the two brightest bands, that is, the (3,0) and (2,0) ones. The wavelengths were carefully chosen to avoid any other possible emission lines due to other species. At the end we restricted our choice to 15 lines belonging to the (3,0) band and nine lines for the (2,0) band. Their counterpart for the 12CO+ were also co-added. Table 4 provides the details of the lines' wavelengths used and their 12CO+ counterparts. The work here was facilitated because C/2016 R2 is very poor in the usual bright and abundant lines of CN and C2 in the CO+ regions of interest.
Thanks to the co-adding of these lines we managed to detect a 13CO+ co-added emission line well above the background noise. The co-adding of the 12CO+ emission lines' counterpart and their fit with our fluorescence model allowed us to derive the 12C/13C isotopic ratio in the CO+ by adjusting our 13CO+ fluorescence model (co-adding of the same lines) to the observational data (see Fig. 5). This method provided 12C/13C = 73 ± 20. The main source of uncertainty comes from the exact background level that needs to be adjusted with a high level of accuracy.
A good test for the adjustment of this level, apart from the fact that the intensities should be positive and there should be a background close to zero in between the emission lines, is the quality of the fit with our modeling. The quality of this fit is very good for the FWHM if the model is adjusted to observational data with a background close to zero. If it is not the case, some discrepancies appear in the line width.
This estimate of the 12C/13C isotopic ratio in CO+ is similar to the other measurements done in the optical in C2 and CN (Manfroid et al. 2009), and in the submillimeter region for HCN. This ratio has so far been measured from ground-based facilities in dozens of comets (Bockelée-Morvan et al. 2015). Some other in situ measurements were more recently performed in the coma of comet 67P/Churyumov-Gerasimenko by the ROSINA mass spectrometer onboard the Rosetta spacecraft for C2H4, C2H5, CO (Rubin et al. 2017), and CO2 (Hässig et al. 2017) molecules. These measurements vary from about 60 (measured in C2 for comet West 1976 IV; Lambert & Danks 1983) to 165 (measured in CN with comet C/1995 O1 (Hale-Bopp) by Arpigny et al. 2003) with large error bars. Most of them are compatible with the terrestrial value of 89, within their (often large) error bars. For CO in comet 67P, the 12C/13C ratio measured is 86±9 (Rubin et al. 2017), that is, it is compatible with our result within the error bars. This one is the first ever published for the CO+ species.
 |
Fig. 2 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for the three different settings. The observational spectra appear in blue, while the model is in red (for clarity it appears with a negative scale). The different CO+ bands bright enough to be detected in the observational spectrum are identified in red for the model. The (6,0), (7,1), and (6,1) CO+ bands appear (weakly) on the observational spectrum and are identified in blue, but not on the model because this one is restricted to v″ and v′ ≤ 5. The intensity scale is arbitrary but proportional to units of ergs s-1. Some other species appear in the observational spectrum (e.g., |
Fluorescence efficiencies computed for 12CO+, for heliocentric distance rh = 1 au and heliocentric velocity vh = 0 km s−1, in units of erg s−1 ion−1.
 |
Fig. 3 Fluorescence efficiencies of the four brightest CO+ bands as a function of the heliocentric velocity for the heliocentric distance rh = 1 au. |
Fluorescence efficiencies multiplied by 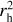 computed for 12CO+.
computed for 12CO+.
Fluorescence efficiencies computed for 13CO+, for heliocentric distance rh = 1 au and heliocentric velocity vh = 0 km s−1, in units of erg s−1 ion−1.
 |
Fig. 4 12CO+ and 13CO+ theoretical spectra superimposed on the observational data obtained on comet C/2016 R2. The relative intensity of 13CO+ emission lines are based on the 12CO+ fit of the emission lines (i.e., a theoretical ratio 12CO+/13CO+ = 1). They do not respect the intensities observed in this comet, the purpose of this plot being only to show the wavelength shift between the emission lines of these two isotopologues. |
 |
Fig. 5 Co-adding of the brightest (3,0) and (2,0) emission lines of 13CO+ (left) and 12CO+ (right) with the corresponding modeling (see Table 4 for the detailed list of co-added lines). Both figures display the co-added CO+ lines with their surroundings at a high signal-to-noise ratio. The features seen – especially for 13CO+, which has a lower intensity scale – are then most probably real features above the one-sigma noise level appearing on the left part of this plot. |
Wavelengths (Å) of 13CO+ lines co-added to measure the 12C/13C isotopic ratio with their 12CO+ counterpart.
7 Conclusion
Thanks to high-quality observational data obtained on comet C/2016 R2, a comet exceptionally rich in both CO+ and 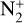 in the inner coma, it was possible to test, in detail, a new fluorescence model of 12CO+ that takes into account new laboratory data and theoretical works obtained since the pioneering work of Magnani & A'Hearn (1986). The confrontation of this model with our spectra provides good results, confirming the efficiency of this model. Some new fluorescence efficiencies (g factors) are also published, which are in relatively good agreement with observational data for the relative intensities. Such revised g factors can be used in the future for more accurate measurement of CO+ abundance in comets. Previous estimates of such abundances can now also be slightly revised. For example the N2/CO ratio computed by Opitom et al. (2019) and based on the g-factor of the (2,0) band published by Magnani & A'Hearn (1986) can be revised (in addition to the revised g-factors published for
in the inner coma, it was possible to test, in detail, a new fluorescence model of 12CO+ that takes into account new laboratory data and theoretical works obtained since the pioneering work of Magnani & A'Hearn (1986). The confrontation of this model with our spectra provides good results, confirming the efficiency of this model. Some new fluorescence efficiencies (g factors) are also published, which are in relatively good agreement with observational data for the relative intensities. Such revised g factors can be used in the future for more accurate measurement of CO+ abundance in comets. Previous estimates of such abundances can now also be slightly revised. For example the N2/CO ratio computed by Opitom et al. (2019) and based on the g-factor of the (2,0) band published by Magnani & A'Hearn (1986) can be revised (in addition to the revised g-factors published for 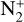 by Rousselot et al. 2022 and used by Anderson et al. 2022). The new ratio
by Rousselot et al. 2022 and used by Anderson et al. 2022). The new ratio 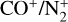 should be reduced by about 20% according to our revised values.
should be reduced by about 20% according to our revised values.
Our 13CO+ fluorescence model also opens the possibility of new measurements of the 12C/13C isotopic ratio in the CO+ species. This work shows that such a measurement becomes possible and provided a value of 73 ±20 for comet C/2016 R2, in agreement with similar measurements for other species and with the in situ measurement obtained in the coma of comet 67P by the ROSINA mass spectrometer. Due to the rather large error bar, it is not possible to exclude that C/2016 R2 is of interstellar origin, because 12C/13C in the local interstellar medium is around 68±15 (Milam et al. 2005), this lower value being due to galactic 13C enrichment by low-mass stars over the last 4.5 Gyr. The dynamical study of C/2016 R2 excludes, nevertheless, an interstellar origin (Opitom et al. 2019).
Acknowledgements
Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under program 2100.C-5035(A). E.J. is a Belgian FNRS Senior Research Associate, D. Hutsemékers is a Research Director, and J.M. is a Honorary Research Director of the FNRS. This work has been supported by the EIPHI Graduate School (contract ANR-17-EURE-0002) and Bourgogne-Franche-Comté Region.
Appendix A Comparison of 12CO+ modeling with observational data
 |
Fig. A.1 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2, for different bands observed with the setting 390. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue, while the modeling is in red. The emission lines of the (2,0) band are blended with some emission lines of the (5,2) band but this band represents only a few percent in intensity with respect to the (2,0) band. |
 |
Fig. A.2 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for different bands observed with the setting 437. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue, while the modeling is in red. The emission lines of the (1,0) Π1/2 band are mixed with the emission lines of the (4,2) Π3/2 band, these last ones being fainter (intensities roughly equal to the ones of the (3,2) Π3/2 band). |
 |
Fig. A.3 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for different bands observed with the setting 580l. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue while the modeling is in red. |
References
- Anderson, S. E., Rousselot, P., Noyelles, B., et al. 2022, MNRAS, 515, 5869 [NASA ADS] [CrossRef] [Google Scholar]
- Arpigny, C. 1964a, Annales d'Astrophysique, 27, 393 [NASA ADS] [Google Scholar]
- Arpigny, C. 1964b, Annales d'Astrophysique, 27, 406 [NASA ADS] [Google Scholar]
- Arpigny, C., Jehin, E., Manfroid, J., et al. 2003, Science, 301, 1522 [CrossRef] [PubMed] [Google Scholar]
- Bell, T. A., Whyatt, W., Viti, S., & Redman, M. P. 2007, MNRAS, 382, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Billoux, T., Cressault, Y., & Gleizes, A. 2014, J. Quant. Spec. Radiat. Transf., 133, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Paubert, G., et al. 2018, A&A, 619, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Calmonte, U., Charnley, S., et al. 2015, Space Sci. Rev., 197, 47 [Google Scholar]
- Cochran, A. L., & McKay, A. J. 2018, ApJ, 854, L10 [Google Scholar]
- Coxon, J. A., Kepa, R., & Piotrowska, I. 2010, J. Mol. Spectr., 262, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Ferchichi, O., Derbel, N., Alijah, A., & Rousselot, P. 2022, A&A, 661, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fowler, A. 1909a, MNRAS, 70, 176 [CrossRef] [Google Scholar]
- Fowler, A. 1909b, MNRAS, 70, 179 [Google Scholar]
- Fowler, A. 1910, MNRAS, 70, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Hakalla, R., Szajna, W., Piotrowska, I., et al. 2019, J. Quant. Spectrosc. Radiat. Transf., 234, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Hässig, M., Altwegg, K., Balsiger, H., et al. 2017, A&A, 605, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herzberg, G. 1950, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules (New York: V. N. R. company) [Google Scholar]
- Kepa, R., Kocan, A., Ostrowska, M., et al. 2002, J. Mol. Spectr., 214, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kępa, R., Kocan, A., Ostrowska-Kopec, M., Piotrowska-Domagala, I., & Zachwieja, M. 2004, J. Mol. Spectr., 228, 66 [CrossRef] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm (Cambridge: Cambridge University Press) [Google Scholar]
- Lambert, D. L., & Danks, A. C. 1983, ApJ, 268, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., & A'Hearn, M. F. 1986, ApJ, 302, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Manfroid, J., Jehin, E., Hutsemékers, D., et al. 2009, A&A, 503, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [Google Scholar]
- Opitom, C., Hutsemékers, D., Jehin, E., et al. 2019, A&A, 624, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosmus, P., & Werner, H.-J. 1982, Mol. Phys., 47, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Anderson, S. E., Alijah, A., et al. 2022, A&A, 661, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubin, M., Altwegg, K., Balsiger, H., et al. 2017, A&A, 601, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swings, P. 1965, QJRAS, 6, 28 [NASA ADS] [Google Scholar]
- Szajna, W., Kepa, R., & Zachwieja, M. 2004, Euro. Phys. J. D, 30, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Weryk, R., & Wainscoat, R. 2016, Central Bureau Electronic Telegrams, 4318 [Google Scholar]
- Wierzchos, K., & Womack, M. 2018, AJ, 156, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Zucconi, J. M., & Festou, M. C. 1985, A&A, 150, 180 [NASA ADS] [Google Scholar]
All Tables
Fluorescence efficiencies computed for 12CO+, for heliocentric distance rh = 1 au and heliocentric velocity vh = 0 km s−1, in units of erg s−1 ion−1.
Fluorescence efficiencies computed for 13CO+, for heliocentric distance rh = 1 au and heliocentric velocity vh = 0 km s−1, in units of erg s−1 ion−1.
Wavelengths (Å) of 13CO+ lines co-added to measure the 12C/13C isotopic ratio with their 12CO+ counterpart.
All Figures
 |
Fig. 1 Energy level diagram showing A2Πi–X2Σ+ transition with different lines involved in this transition. The number in parentheses refers to the J″ value of the line. |
| In the text | |
 |
Fig. 2 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for the three different settings. The observational spectra appear in blue, while the model is in red (for clarity it appears with a negative scale). The different CO+ bands bright enough to be detected in the observational spectrum are identified in red for the model. The (6,0), (7,1), and (6,1) CO+ bands appear (weakly) on the observational spectrum and are identified in blue, but not on the model because this one is restricted to v″ and v′ ≤ 5. The intensity scale is arbitrary but proportional to units of ergs s-1. Some other species appear in the observational spectrum (e.g., |
| In the text | |
 |
Fig. 3 Fluorescence efficiencies of the four brightest CO+ bands as a function of the heliocentric velocity for the heliocentric distance rh = 1 au. |
| In the text | |
 |
Fig. 4 12CO+ and 13CO+ theoretical spectra superimposed on the observational data obtained on comet C/2016 R2. The relative intensity of 13CO+ emission lines are based on the 12CO+ fit of the emission lines (i.e., a theoretical ratio 12CO+/13CO+ = 1). They do not respect the intensities observed in this comet, the purpose of this plot being only to show the wavelength shift between the emission lines of these two isotopologues. |
| In the text | |
 |
Fig. 5 Co-adding of the brightest (3,0) and (2,0) emission lines of 13CO+ (left) and 12CO+ (right) with the corresponding modeling (see Table 4 for the detailed list of co-added lines). Both figures display the co-added CO+ lines with their surroundings at a high signal-to-noise ratio. The features seen – especially for 13CO+, which has a lower intensity scale – are then most probably real features above the one-sigma noise level appearing on the left part of this plot. |
| In the text | |
 |
Fig. A.1 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2, for different bands observed with the setting 390. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue, while the modeling is in red. The emission lines of the (2,0) band are blended with some emission lines of the (5,2) band but this band represents only a few percent in intensity with respect to the (2,0) band. |
| In the text | |
 |
Fig. A.2 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for different bands observed with the setting 437. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue, while the modeling is in red. The emission lines of the (1,0) Π1/2 band are mixed with the emission lines of the (4,2) Π3/2 band, these last ones being fainter (intensities roughly equal to the ones of the (3,2) Π3/2 band). |
| In the text | |
 |
Fig. A.3 Comparison of our modeling of 12CO+ spectrum with our observational data obtained on comet C/2016 R2 for different bands observed with the setting 580l. The intensity scale is arbitrary but proportional to units of ergs s−1 and is the same for the different bands. The observational spectrum appears in blue while the modeling is in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.