| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202347748 | |
| Published online | 28 February 2024 | |
The orbit of HD 142527 B is too compact to explain many of the disc features
1
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
e-mail: mcn35@cam.ac.uk
2
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
3
Centre for Exoplanets and Habitability, University of Warwick, Coventry CV4 7AL, UK
4
Department of Physics, University of Warwick, Coventry CV4 7AL, UK
5
School of Physics and Astronomy, University of Leicester, Leicester LE1 7RH, UK
6
LESIA, Observatoire de Paris, PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Janssen, 92195 Meudon, France
7
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
8
School of Physics and Astronomy, Monash University, Clayton Vic 3800, Australia
Received:
17
August
2023
Accepted:
9
December
2023
Context. HD 142527 A is a young and massive Herbig Ae/Be star surrounded by a highly structured disc. The disc shows numerous morphological structures, such as spiral arms, a horseshoe region of dust emission, a set of shadows cast by an inner disc on the outer disc, and a large cavity extending from ≃30 au to ≃130 au. HD 142527 A also has a lower mass companion, HD 142527 B (M = 0.13 ± 0.03 M⊙), which is thought to be responsible for most of the structures observed in the surrounding disc.
Aims. We aim to fully constrain the orbit of HD 142527 B and determine whether the binary alone is truly responsible for the observed morphology of the HD 142527 disc.
Methods. We gathered VLTI/GRAVITY observations of HD 142527, either from our own programmes or from the ESO archive. We used this inhomogeneous set of data to extract a total of seven high-precision measurements of the relative astrometry between HD 142527 A and B, spread from mid-2017 to early 2021. Combined with what is available in the literature, these new measurements offer a total of 9 yr of astrometric monitoring on HD 142527. We used orbit fitting tools to determine the orbital parameters of HD 142527 B, and used them as inputs for a 3D hydrodynamical model of the disc to determine whether or not the binary is able to create the structures observed in the disc.
Results. Our VLTI/GRAVITY astrometry gives excellent constraints on the orbit of HD 142527 B. We show that the secondary is following an orbit of semi-major axis a = 10.80 ± 0.22 au, with moderate eccentricity (e = 0.47 ± 0.01), and has recently passed its periapsis (τ = 2020.42). With such a compact orbit, we show that HD 142527 B can only generate a gap and spiral arms of ~30 au in the disc, which is much smaller than what is revealed by observations.
Conclusions. Even from a theoretical standpoint, the observed cavity size of ~ 100 au far exceeds even the most generous predictions for a companion like HD 142527 B on such a compact orbit. Thus, we conclude that the low-mass companion cannot be solely responsible for the observed morphology of the disc surrounding the system.
Key words: techniques: high angular resolution / techniques: interferometric / protoplanetary disks / binaries: visual / circumstellar matter
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
HD 142527 A is a 5.0 ± 1.5 Myr old Herbig Ae/Be star of type F6-IIIV, with a mass of 2.0 ± 0.3 M⊙ (Mendigutía et al. 2014), located at a distance of 159.3 ± 0.7 pc (Gaia Collaboration 2021). The system has been extensively studied for its spectacular circumstellar disc, which harbours several enigmatic morphological features. Observations in the near-infrared with Subaru/CIAO have revealed the presence of a large spiral arm at >100 au (Fukagawa et al. 2006), with a counterpart in CO later detected with the Atacama Large Millimetre/submillimetre Array (ALMA, Christiaens et al. 2014). Smaller spiral arms were also detected in the near-IR (Casassus et al. 2012; Canovas et al. 2013; Avenhaus et al. 2014, 2017), as well as other larger ones, extending up to ≃500 au (Christiaens et al. 2014).
The main feature of the HD 142527 disc is arguably its large central cavity, which extends from ≃30 to ≃130au. Its presence was first suggested by Fukagawa et al. (2006), before being confirmed with ALMA by Casassus et al. (2013), who also detected a horseshoe structure of continuum emission surrounding this central cavity.
Early observations with the MIDI instrument at the Very Large Telescope Interferometer (VLTI) revealed the presence of an inner disc, which has since been detected in visible light with SPHERE/Zimpol (Avenhaus et al. 2017). This inner disc is thought to be inclined at ≃70 deg relative to the outer disc, thus casting a narrow shadow on it, and explaining some of the azimuthal asymmetries observed in the near-IR (Casassus et al. 2012; Marino et al. 2015).
Its highly structured morphology, eccentric outer disc, and high fraction of crystalline silicates (van Boekel et al. 2004; Avenhaus et al. 2017), have made HD 142527 a prime taget for planet searches. The low-mass companion HD 142527 B was discovered by Biller et al. (2012) using the Sparse Aperture Masking (SAM) mode of SPHERE/NACO, and this new object quickly became the prime suspect to explain the complex disc structures. Lacour et al. (2016) used the SAM mode of SPHERE/NACO and Gemini/GPI to further characterise the companion and its orbit. They showed that HD 142527 B was likely an M dwarf with a mass of 0.13 ± 0.03 M⊙ and a temperature of T = 3000 ± 100 K (i.e. with a contrast ratio of ≃1/75 and a mass ratio of ≃1/10 with respect to the primary). Their astrometric measurements covered epochs ranging from early 2012 to mid-2014, and suggested two possible families of orbits: one that had passed periapsis, and another approaching periapsis. Both families had moderate eccentricities (e ≃ 0.5), and semi-major axes ranging from 70 to 260 au.
The first comprehensive study linking the low-mass companion HD 142527 B to the morphological structure of the disc was conducted by Price et al. (2018a). With the use of a series of 3D hydrodynamical models of HD 142527, they showed that a low-mass companion, with characteristics compatible with that reported by Lacour et al. (2016), could explain most of the observed structures of the disc. Their study also strongly favoured the family of orbit approaching periapsis, as only this one was compatible with the disc features. Claudi et al. (2019) further refined the orbital parameters of the binary with a set of new astrometric measurements with SPHERE, and reinforced the suggestion of Price et al. (2018a) that HD 142527 B was approaching its periapsis.
More recently, Balmer et al. (2022) has presented the most extensive set of astrometric measurements to date on HD 142527 B, with epochs ranging from early 2012 to mid-2018. They were able to give good constraints on most of the orbital parameters, and concluded that the low-mass companion was indeed approaching its periapsis over this period. They reported a semi-major axis of ≃15 au, an eccentricity of ≃0.3, and an orbit close to perpendicular to the outer disc (mutual inclination of ≃80 deg). They concluded that this high mutual inclination supported the idea that the binary was sculpting the disc, as the nearly perpendicular orbit was one of their main assumptions needed by Price et al. (2018a) to explain the disc features.
We note, however, that both the semi-major axis and the eccentricity derived by Bohn et al. (2022) (a ≃ 15 au and e ≃ 0.3) are significantly smaller than the values used by Price et al. (2018a) (a ≃ 30 au and e ≃ 0.6–0.7). As the lower semi-major axis and eccentricity are expected to result in different disc structures, this raises the question of whether the companion can really explain the complex morphological structures observed in the disc.
In this work we attempt to answer this question with a set of VLTI/GRAVITY observations gathered both from the ESO archive and from our own observing programmes. These long-baseline interferometric obervations offer a significant gain in terms of astrometric precision compared to single-dish observations, resulting in better constraints on the orbital parameters of the binary.
The paper is structured as follows. In Sect. 2 we introduce our observations, and in Sect. 3 we give some details on how we extracted astrometric measurements from these data, which were obtained in a variety of modes and configurations. In Sect. 4 we focus on the orbit fit, and present our new constraints on the orbital parameters of the binary, and on its mutual inclination with the inner and outer discs. We use these orbital parameters as an input in a set of 3D hydrodynamical simulations of the disc, and discuss the results in Sect. 5. Finally, we give our conclusions in Sect. 6.
2 Observations
We gathered a number of observations of HD 142527, obtained with VLTI/GRAVITY between 2017 and 2021. The observations are spread over ten different nights. Some of them are part of regular programmes targeting HD 142527, whereas others were acquired using HD 142527 either as a backup target in case of bad weather, or as a target for technical tests with the instrument. As a consequence, the set of observations presented in this paper is inhomogeneous, with a mixture of VLTI configurations (auxiliary telescopes, ATs, or unit telescopes, UTs), spectral resolutions (medium or high), polarisation settings (combined or split), and observing modes (dual-field or single-field). The full observing log is presented in Table 1.
In principle, single-field observations with GRAVITY are used when the field of view of the fibre (~300 mas in diameter at half-maximum with the ATs, ~60 mas with the UTs) is larger than the separation of the observed binary. In this case the light from both components is injected into the fibre, and the data are analysed using the squared visibilities and closure phases formalism (see Sect. 3). However, when the separation is larger than the field of view of the fibre, the instrument is set to dual-field mode, where the two components can be observed sequentially by moving the fibre back and forth between the two. This strategy, used in particular for exoplanet observations, is described in GRAVITY Collaboration (2019, 2020).
In the case of HD 142527, the separation is typically ~50mas, and the observations were carried out in single-field when observing with the ATs, and in dual-field when observing with the UTs (see Table 1). However, we found that in all the dual-field observations, when the fibre is centred on HD 142527 B, it also collects a significant amount of flux from HD 142527 A, due to the small separation and high contrast ratio (~1/75 in K-band) between the two components. As a consequence, we decided to treat these observations as single-field rather than dual-field, and to discard the dual-field data in which the fibre is centred on the star, as they are too largely dominated by HD 142527 A. We report only the observations obtained at the location of HD 142527 B in Table 1. Finally, when the data obtained are in split polarisation, we treat the polarisations separately, as if they were independent exposures.
3 Data reduction
All the observations were initially reduced using the GRAVITY pipeline (Lapeyrere et al. 2014). We generated scivis files, which were averaged over all DITs of each exposure, and which contained the squared modulus of the interferometric visibilities, |V2|, and the closure phases, Cϕ, with the associated error bars. The squared visibilities and the closure phases both encode information about the separation of the two components of the binary, and we treated them as independent quantities.
The coherent flux received at time t, along the baseline b, and at wavelength λ can be written
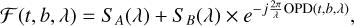 (1)
(1)
where SA and SB are the spectra of the two components of the binary, and OPD is the optical path difference between the two components of the binary along baseline b.
Using the coordinates of the baseline in the uv-plane b = (u, v), and the separation vector (∆α, ∆δ) of the binary in RA/Dec, the OPD can be written as
 (2)
(2)
Equation (1) thus becomes
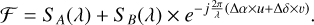 (3)
(3)
Equation (3) presents an idealised case, as it does not take into account the phase distortions introduced by the atmosphere. The fringe-tracker of GRAVITY (Lacour et al. 2019) corrects this atmospheric phase distortion up to a near-constant term, which affects the telescopes individually and can thus be represented by a set of four terms: 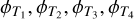 . For a baseline b linking telescope k to telescope l, the post fringe-tracker atmospheric phase distortion is
. For a baseline b linking telescope k to telescope l, the post fringe-tracker atmospheric phase distortion is 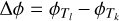 . This term affects both components of the binary in the same way, and Eq. (3) thus becomes
. This term affects both components of the binary in the same way, and Eq. (3) thus becomes
![${{\cal F}_{{T_k}{T_l}}} = \left[ {{S_A} + {S_B} \times {e^{ - j{{2\pi } \over \lambda }(\Delta \alpha \times u + \Delta \delta \times \upsilon )}}} \right]{e^{j\left( {{\phi _{{T_l}}} - {\phi _{{T_k}}}} \right)}},$](/articles/aa/full_html/2024/03/aa47748-23/aa47748-23-eq6.png) (4)
(4)
which shows that Eq. (4) encodes information about the separation of the binary in two forms: in the amplitude of the observed visibility and in the phase.
The flux received at each telescope T of the array is simply FT = SA + SB, and the interferometric visibility is therefore given by
![$\matrix{ {{V_{{T_k}{T_l}}} = {{{{\cal F}_{{T_k}{T_l}}}} \over {\sqrt {{F_{{T_k}}}{F_{{T_l}}}} }}} \hfill \cr {\,\,\,\,\,\,\,\,\,\, = {{\left[ {1 + C{e^{ - j{{2\pi } \over \lambda }(\Delta \alpha \times u + \Delta \delta \times \upsilon )}}} \right]{e^{j\left( {{\phi _{{T_l}}} - {\phi _{{T_k}}}} \right)}}} \over {1 + C}},} \hfill \cr } $](/articles/aa/full_html/2024/03/aa47748-23/aa47748-23-eq7.png)
where C = SB/SA is the contrast of the binary.
The squared modulus of the visibility for a baseline, TkTl, and the closure phase for a triangle, TkTlTm, are defined by
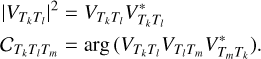
Using Eq. (4) in combination with these definitions, we see that the two quantities are independent of the residual atmospheric distortion term, and are given by
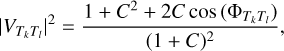 (5)
(5)
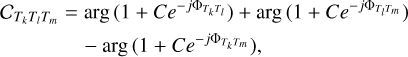 (6)
(6)
where 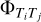 is the phase corresponding the baseline (uij,υij) linking telescope Ti to Tj:
is the phase corresponding the baseline (uij,υij) linking telescope Ti to Tj:
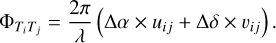
In principle, since the (u , υ) coordinates of the different baselines are known, Eqs. (5) and (6) can be used to model the GRAVITY data with only three parameters: the binary separation vector (∆α, ∆δ), and the contrast ratio C (under assumption of a constant contrast along the GRAVITY wavelength range, from ~1.9 to 2.4 µm).
In the absence of proper calibration, however, both the squared visibilities and the closure phases are affected by additional low-order terms, which we modelled with the use of an additional polynomial in wavelength of order 2. In Eq. (5) the constant terms can be absorbed in this low-order polynomial. Denoting a0, a1, a2 the coefficients of the additional polynomial term, and using β = 2C/(1 + C)2 as a parameter instead of C, our model for the squared visibility becomes linear in all parameters but (∆α, ∆δ). Our model for the closure phase remains non-linear in three parameters ((∆α, ∆δ), and C) and is written as
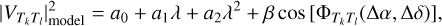 (7)
(7)
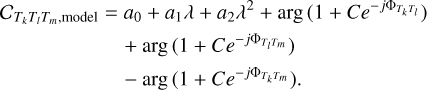 (8)
(8)
The GRAVITY pipeline reports the squared visibilities and the closure phases separately for each baseline and wavelength, with the associated error bars. Therefore, we were able to define two χ2 quantities for each file of each epoch of our single-field observations (see Table 1) by summing the χ2 obtained using the models defined in Eqs. (7) and (8) over the six baselines (for |V|2) and four triangles (for C):
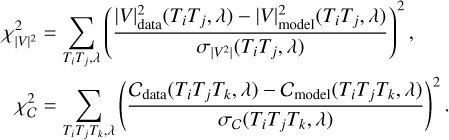
From this we calculated, for each file, a set of two χ2 maps as a function of ∆α, ∆δ, by minimising the two χ2 over all the nuisance parameters. This represents a minimisation over 19 linear parameters for the squared visibilities (a set of a0, a1, a2 for each of the six baselines, plus a value for β), and 12 linear parameters (a0, a1, a2 for each of the four triangles) plus one non-linear parameter (the contrast value C) for the closure phases:
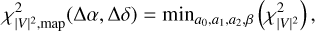 (9)
(9)
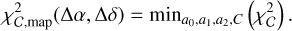 (10)
(10)
In Eq. (9) we used the closed-form solution of the minimisation problem since all parameters are linear. For Eq. (10) we used the closed-form solution to minimise over the linear parameters, and the Powel algorithm to perform the minimisation over the non-linear parameter C.
An example of a typical χ2 map is given in Fig. 1. It shows a structure with multiple adjacent minimums, which is characteristic of interferometric observations with a limited number of baselines. To identify the correct minimum, we make use of prior information on the orbit of the binary. We analysed our data sequentially, one epoch at a time, starting from the first one. For each epoch t, we took all the astrometric data available in the literature (see Table 2), to which we added our astrometric measurements obtained on the previous GRAVITY epochs (with t′ < t). We then used orbitize! (Blunt et al. 2020) to perform an orbit fit for the binary. We gathered a total of 100 000 posterior values for the orbital parameters of the binary, which we used to calculate the expected astrometry at epoch t (see Fig. 1). For all of our epochs, this a priori estimate was good enough to unambiguously determine the correct minimum in our χ2 maps.
Once we had identified the rough location of the correct minimum in each map, we took the location of the closest minimum to be our best estimate of the astrometry, making sure that the χ2 is calculated with a resolution that is much smaller than our final error bars.
For each epoch, we therefore obtained a set a 2 × Nexp estimates for the astrometry of the binary. Our final best estimate for this epoch was taken as the mean of all these measurements, and the error ellipse was calculated using an empirical estimate of the covariance matrix.
We were not able to obtain a proper astrometric measurement for three of our ten epochs. All these difficult datasets were obtained in single-field with the ATs.
The data obtained on March 19, 2017, appeared corrupted even on simple visual inspection, and were very badly fitted by our models, which makes us suspect a fringe-tracker problem during the observations. On April 27, 2019, the baselines were aligned in a very unfortunate way, such that only one of them produces a signal significantly different from the second-order polynomial used to detrend the data. With only a single useful baseline, a measurement of the astrometry is not possible, and thus the data were discarded. Finally, on May 10, 2019, the observations were performed using the small set-up with the ATs, which was unable to produce a signal significantly different from our second-order detrending polynomial due to the small separation of the target. The results obtained for the three epochs of dual-field UT observations, and the four epochs of single-field AT observations for which we were able to obtain an astrometric measurement are given in Table 2.
Observing log presenting all data acquired with VLTI/GRAVITY on HD 142527 and analysed in this paper.
 |
Fig. 1 Typical example of a χ2 map obtained when reducing our data (in this case, for the observation on 2019 April 28). The left panel shows the structure of the χ2 map on a large scale, where the multiple minimums (in purple) are clearly visible. The right panel is a zoomed-in version. In each panel the red dots are generated by performing an orbit fit with all the astrometric measurement data available (including all GRAVITY epochs up to 2019 April 28), and using the posterior distributions of orbital parameters to calculate the estimated position at epoch 2019 April 28. The purple ellipse corresponds to the 3σ contour for the astrometric solution. The blue dots are obtained in a similar way, but using a new orbit fit that includes the astrometry extracted from this epoch. In other words, the red dots represents the prediction using the a priori orbital solution, the purple ellipse represents the measurement obtained at this epoch, and the blue dots represent the prediction using the a posteriori updated orbital solution. |
Astrometry on HD 142527 B.
4 The orbit of HD 142527
4.1 Orbital parameters
Including both AT and UT observations, we report in this work a set of seven new astrometric measurements of HD 142527 B, with typical precisions ranging from a few 100 µas down to ≃10 µas, obtained between 2017 and early 2021. To this we added a total of 19 epochs compiled from the literature to create a dataset that covers almost one half of the orbit of the binary, from 2012 to 2021.
We used orbitize! (Blunt et al. 2020) to fit the relative motion of HD 142527 B around HD 142527 A, and to derive estimates of its orbital parameters. We used the parallel-tempering affine-invariant (Foreman-Mackey et al. 2013; Vousden et al. 2016) Markov chain Monte Carlo (MCMC) sampler available in orbitize! to determine the posterior distributions of the eight orbital parameters reported in Table 3. Except for the total mass of the system, Mtot, and the parallax, π, we used the default priors in orbitize!. Our priors on the total mass and parallax of the system are set to Gaussian priors, with Mtot = 2.49 ± 0.27 (Balmer et al. 2022) and π = 6.356 ± 0.047 (Gaia Collaboration 2021). The MCMC run is set up with 100 walkers and 20 temperatures for a burn-in phase of 50 000 steps, followed by an additional 100 000 steps to approximate the posterior distributions, keeping only one-tenth of the samples. The use of multiple temperatures allows the walkers to explore different minimums (at high temperatures), and to properly sample each available minimum (at lower temperatures).
Our best estimates for each orbital parameter are reported in Table 3, and a corner plot is given in Fig. 2. In Fig. 3 we show a sample of 100 orbits randomly chosen in our posterior distributions, overplotted on the astrometric measurements presented in Table 2.
Table 3 and Fig. 3 show that the orbit of HD 142527 B is now very well constrained, with a gain of one order of magnitude on the error bars of most orbital parameters compared to previous studies (Lacour et al. 2016; Claudi et al. 2019; Balmer et al. 2022). The companion is on an eccentric orbit (e = 0.47 ± 0.01), with a semi-major axis of a = 10.86 ± 0.26 au, about 2σ from the results of Balmer et al. (2022). The total mass of the system is Mtot = 2.24 ± 0.06 M⊙, resulting in an orbital period of P = 23.95 ± 0.99 yr. We also find that the perihelion passage occurred on June 02, 2020 (between May 15 and June 21, 2020, at Therefore, our last data point, from January 2021, was obtained after the perihelion passage. This, in combination with the excellent precision of our VLTI/GRAVITY measurements, explains the significant gain in precision on the orbit estimate.
We note that among all the measurements gathered from the literature, the two epochs of SPHERE/SAM data are the only ones that seem to have a systematic and significant disagreement with our orbit fit results. Each of these astrometric measurements is more than 3σ away from the best fit in terms of separation. However, running a second orbit fit with these two data points excluded produced similar results, with all estimates of the orbital parameters within the 1σ range of what is obtained with the SPHERE/SAM points. For completeness, we therefore decided to keep these points in our final fit.
 |
Fig. 2 Corner plot for the posterior distributions of the orbital elements of HD 142527 B. The distribution of ωB and ΩB is actually a bimodal distribution, with two peaks spaced 180 deg apart. This is a known degeneracy when radial velocity data are missing. For readability, only one peak, chosen arbitrarily, is shown here. |
 |
Fig. 3 Illustration of the orbit fit. The left panel shows 100 samples drawn randomly from our posterior distribution, overplotted on the astrometric measurements of Table 2. The two panels on the right present the same orbits in separation (upper panel) and position angle (lower panel). For each panel, we show the 100 orbits and the astrometric measurements in the upper graph, and the difference (in units of σ, the error bars on the measurements) in the lower plot. The two dotted lines show the 3σ interval. |
4.2 Mutual inclination relative to the discs
Contradictory values have been reported for the mutual inclination between the orbital plane of the binary and the disc, which is a quantity of particular interest to understand disc-binary interactions. This apparent contradiction seems to stem from a misunderstanding of the multiple conventions used to report disc parameters.
Czekala et al. (2019) reported an inclination relative to the outer disc of θout = 35 ± 5 deg (or 80 ± l0 deg1), which they obtained using an inclination iout = 153 deg and a longitude of the ascending node (LAN) of Ωout = 160.9 deg for the disc. Balmer et al. (2022) used the values iout = 38.21 deg and Ωout = 162.72 deg from Bohn et al. (2022) to calculate the mutual inclination, and found 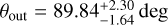 (or
(or 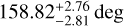 ).
).
The mutual inclination θout between the binary orbit and the outer disc can be calculated using the equation (Czekala et al. 2019)
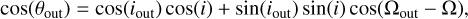 (11)
(11)
where iout and Ωout are the inclination and the LAN of the outer disc.
It is important to note, though, that in order to be used in Eq. (11), the parameters of the binary and of the disc must both follow the conventions used in Czekala et al. (2019). In this convention the inclination is the angle between the axis perpendicular to the plane of sky going towards the observer and the momentum vector of the disc or binary (see their Fig. 1). The LAN is defined as the angle (positive towards the east) between the north and the ascending node, which itself is defined as the point where the disc crosses the plane of sky receding away from us (i.e. redshifted).
This convention is widely accepted in the visual binary and exoplanet direct imaging fields, and is the one used in orbitize!. However, it seems that the disc parameters reported by Bohn et al. (2022) follow a different convention, in which the inclination is defined as the angle between the plane of sky and the orbital plane.
Two conventions seem to be in use to define disc parameters as utterly different values have been reported for the outer disc of HD 142527. For example, Casassus et al. (2015) use an inclination of 160 deg in their modelling, similar to the value of 153 deg reported in Czekala et al. (2019). These values correspond respectively to an angle between the plane of sky and the orbital plane of 30 deg and 27 deg, more similar to the values reported by Fukagawa et al. (2013; 26.9 deg) and Bohn et al. (2022; 38.21 deg).
Therefore, in order to be used in Eq. (11), the disc parameters need to be converted to the proper convention. For the outer disc, the parameters inferred by Bohn et al. (2022) from ALMA data correspond to
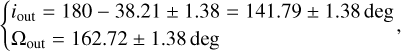 (12)
(12)
which corresponds to a disc inclined 38 deg relative to the plane of the sky where the east side is the far side of the disc (see Sect. 4.2 in Casassus et al. 2015 for a discussion), rotating clockwise on the sky, where the redshifted node is slightly east of south, in agreement with the velocity maps presented in Bohn et al. (2022).
To determine the values of the mutual inclination of the orbit of HD 142527 B with respect to the two different discs, we use the values of the disc parameters from Eq. (12) together with our posterior distribution of orbits. For each of our 106 sets of posterior orbit (100 000 samples for 100 walkers with a 1/10 thinning), we randomly draw a value for iout, Ωout using Gaussian distributions corresponding to Eq. (12), and we use Eq. (11) to calculate θout. The resulting posterior distributions are bimodal, due to the 180 deg degeneracy in Ω, and the values are reported in Table 3.
We note that the inclination reported by Bohn et al. (2022) for the outer disc is significantly different from previously reported values, which range from 20 to 28 deg (Verhoeff et al. 2011; Perez et al. 2014; Boehler et al. 2017; Garg et al. 2021). This raises the question of whether this is related to the modelling, or if this is a sign of a true physical effect, such as a potentially warped disc. In any case, assuming an inclination of 20 deg (i.e. 160 deg in the reference system of Eq. (11)) and a longitude of the ascending node of 160 deg (as in Pinte et al. 2018) results in a mutual inclination of 10.5 deg (or 50.5 deg, due to the degeneracy in Ω) relative to the outer disc.
Contrary to what was presented in Price et al. (2018a), and more recently in Balmer et al. (2022), who both suggested that the presence HD 142527 B is enough to explain the numerous features observed in the disc (central cavity, spiral arms, asymmetries), our new VLTI/GRAVITY data paint a very different picture. With an eccentric (e = 0.47 ± 0.01) but smaller (a = 10.86 ± 0.26 au) orbit, a maximum separation at aphelion of 15.85 ± 0.43 au, our new orbit once more raises the question of whether HD 142527 B can really be responsible for the morphology of the disc, and in particular for the large ≃100 au observed cavity.
 |
Fig. 4 Surface density rendered plots of the HD 142527 protoplanetary disc. Each panel shows a different simulation at the same moment in time, but with different disc and binary parameters. The left panel reproduces the results of the R2 orbit in Price et al. (2018a) where the companion was shown to be responsible for the observed disc features: a large cavity, prominent spiral arms, and a misaligned inner disc. The middle panel uses the same disc parameters as the left panel, but uses the updated binary parameters in Table 3. The right panel is set up with the second solution of the updated binary parameters, and a smaller inner disc boundary to match the ratio of Rin/Rapoapsis of the simulation in the left panel. In the middle and right panels we find that, due to the close configuration of the updated binary orbit, the companion cannot be solely responsible for the observed disc features. |
5 Disc-binary interaction
5.1 Hydrodynamical simulation
To explore whether the new orbit of the companion HD 142527 B is still able to explain the numerous features observed in the disc, we run three 3D gas only hydrodynamical simulations using PHANTOM, a 3D Smoothed Particle Hydrodynamics (SPH) code (Price et al. 2018b).
The first simulation recreates one of the simulations in Price et al. (2018a; the R2 orbit). This serves as our control simulation to study the effect the new companion orbit has on the disc. The second simulation uses the same disc parameters as that of Price et al. (2018a), but the updated orbital measurements of the companion as given in Table 3. This allows us to easily demonstrate the difference in disc evolution between our new orbit and that used in Price et al. (2018a). In this set-up, the mutual inclination is θout = 50.5 deg, obtained by adding 180 to ω and Ω in Table 3. The true anomaly is set as 74.31 deg. The third simulation is identical to the second simulation, except for a reduced inner boundary of the disc Rin, such that it matches the ratio of Rin /Rapoapsis in the first simulation.
All three simulations model a 0.01 M⊙ disc with Rout = 350 au. The surface density profile is given by Σ ∝ R−1. The temperature profile is given by T ∝ R−0.3, with H/R = 0.11 at R = Rout. The inner boundary of the first and second simulations is Rin = 50 au, whereas for the third simulation it is Rin = 12.67 au. We set a mean Shakura-Sunyaev disc viscosity αSS ≈ 0.005. This corresponds to an artificial viscosity αAV = 0.22 for the first and second simulation, and αAV = 0.18 for the third simulation. The artificial viscosity coefficient βAV is set to 2 (see Price et al. 2018b; Nealon et al. 2015).
Sink particles are used to model the binary (Bate et al. 1995). The mass and orbital parameters of the binary for the first simulation are identical to the R2 orbit in Price et al. (2018a), whereas for the second and third simulations the mass of the primary and secondary is 2.03 M⊙ and 0.26 M⊙, respectively, consistent with Claudi et al. (2019) and the total mass in Table 3. The accretion radius for both sinks is set to 1 au, as in Price et al. (2018a). The simulation recreating Price et al. (2018a) is shown at 20 orbital periods (3272 yr) corresponding to their Fig. 2. We present all of our results at the same time. For the updated companion orbit, this corresponds to 141 orbital periods.
Figure 4 shows all three of the simulations at the same moment in time. The left panel shows the simulation using the R2 orbit set-up from Price et al. (2018a), which was able to explain the observed features of the disc. In this orbit set-up, the companion is responsible for the large cavity (~ 100 au), the large spiral arms, and the misaligned inner disc casting a shadow. The middle panel shows the simulation where the only change is the companion’s orbit. As we have reproduced the results of Price et al. (2018a), we can attribute all differences in the disc structure to the change in the orbital measurements. The new orbit is unable to match any of the disc features mentioned above. The large separation between the inner edge of the disc and the companion results in little impact on the disc structure, resulting in a much smaller cavity (Bohn et al. 2022). Finally, the right panel shows the simulation where the inner boundary of the disc is closer in, such that the ratio Rin/Rapoapsis is equivalent to the original simulation from Price et al. (2018a; left panel). While there are improvements, the companion is still unable to carve open a large enough cavity. Furthermore, the lack of a pressure maximum to trap dust at ~100 au makes it difficult to explain the observed dust structures (Casassus et al. 2015).
The inability of the companion to clear a large enough cavity is unsurprising. From theoretical predictions (Artymowicz & Lubow 1994), a circular binary with µ = 0.1 as in this system, is expected to result in a disc inner edge of r = 1.74a, where µ = Mcompanion/Mtot is the mass fraction of the per-turber. Although eccentric companions result in larger cavities, there is no prediction where the companion is able to carve open a big enough cavity to match observations. Figure 4 in Artymowicz & Lubow (1994) shows that for a binary with µ = 0.1, an eccentricity of 0.47, and an assumed disc viscosity of 5 × 10−3, the disc inner edge is expected to be between r = 2.7a and 3a. For a semi-major axis of a = 10.8 au, this corresponds to a disc inner edge at r ≈ 30 au, which agrees well with the simulations in the middle and right panels of Fig. 4. Additionally, the disc is inclined relative to the orbital plane of the binary, which decreases the truncation radius (Lubow et al. 2015; Facchini et al. 2018). The observed cavity size of ~100 au far exceeds even the most generous predictions. Hence, the simulations here show that with the new orbital parameters, the companion cannot be solely responsible for the observed disc features.
For completeness, we also simulated the solution of the binary orbit using the values of Ω and ω listed in Table 3 resulting in θout = 10.5 deg. Figure 5 shows that neither solution is able to reproduce the disc features. Since both solutions produce similar results, we only use the simulation with the second solution (left panel) for the comparisons with the observations below.
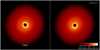 |
Fig. 5 Surface density rendered plots of the HD 142527 protoplanetary disc. Each panel shows a simulation at the same moment in time, but with different disc and binary parameters. The right panel is set up with the updated binary parameters as listed in Table 3. The left panel uses the second solution of the values in Table 3 obtained by adding 180 deg to both Ω and ω. We find that neither solution reproduces the observed disc features. |
5.2 Radiative transfer
For comparison with observations of the 12CO and 13CO J = 2 − 1 line emission, we use the radiative transfer code MCFOST (Pinte et al. 2006, 2009). As it uses a Voronoi tesselation where each cell in MCFOST corresponds to an individual SPH particle, MCFOST is well suited for post-processing SPH simulations.
A subset of the simulations above are post-processed, in particular the simulations using the binary orbit from Price et al. (2018a) and the updated binary orbit from this work. The sink particles are used to irradiate the disc using stellar spectral models based on their mass, and assuming a 3 Myr isochrone. For the former simulation, this corresponds to the luminosity and effective temperature of L = 2.69 L⊙ and Teff = 4813 K, respectively, for the primary, and L = 0.23 L⊙ and Teff = 3607 K, respectively, for the secondary. For the latter simulation, the luminosity and effective temperature is L = 3.89 L⊙ and Teff = 4991 K, respectively, for the primary, and L = 0.14 L⊙ and Teff = 3315 K, respectively, for the secondary.
We use 108 photon packets to calculate the temperatures in the disc. As these are gas-only simulations, the dust is assumed to be 1% of the gas mass, and perfectly coupled to the gas. The dust sizes vary between 0.3 and 1000 µm, and are distributed across 100 grain sizes with a power-law exponent of −3.5. We further assume that the dust particles are all spherical and homogeneous, and made up of astronomical silicates. The dust properties are computed using Mie theory. To predict the line emission of 12CO and 13CO, we assume constant abundances of 5 × 10−5 and 7 × 10−7, respectively.
Figure 6 compares the observations (left panels) with the predictions from simulations (middle and right panels). The top and bottom panels show the 12CO and 13CO J = 2 − 1 line emission, respectively. In general, the new binary orbit results in a lack of substructure with either molecule as seen by the right panels. In 13CO, the new orbit is unable to deplete the gas in the inner regions, highlighted by the lack of any cavity compared to either the observation (bottom left panel) or the simulation from Price et al. (2018a; bottom middle panel). Although the 12CO emission is lacking any substructure with the new binary orbit, it is more similar to the observation (top left panel) and the simulation Price et al. (2018a; top middle panel); all have an optically thick inner region. While there is a lot of gas in the cavity, this could clear out if the simulation evolved for longer. Additionally, the beam size washed out the cavity seen in the surface density.
 |
Fig. 6 Comparison between observed and simulated 12CO and 13CO maps for the HD142527 disc. The top and bottom panels show the 12CO and 13CO J = 2 − 1 emission, respectively. The left panels are the observations (Garg et al. 2021). The middle and right panels are synthetic emissions predicted from the simulations. The middle panels are from the simulation shown in the left panel of Fig. 4 which uses the disc and binary set-up as the R2 orbit in Price et al. (2018a). The right panels are from the simulations shown in the right panel of Fig. 4, which uses the updated binary parameters in Table 3. In general, the new binary orbit results in a lack of substructure in either molecule. Additionally, the lack of a cavity in 13CO further highlights that the companion alone cannot reproduce the disc features. |
6 Conclusion
Based on a VLTI/GRAVITY observations, we presented a set of new astrometric measurements of HD 142527 B relative to HD 142527 B obtained at seven epochs ranging from 2017 to early 2021. Combined with all the measurements available in the literature, this constitutes an astrometric monitoring of ~9 yr, which covers almost half of the orbital period of the binary.
From these measurements, we derived excellent estimates of the orbital parameters for the binary. We find that HD 142527 B is on a moderately eccentric orbit (e = 0.47 ± 0.01), with a semi-major axis of 10.80 ± 0.22 au. The orbital period is therefore P = 23.50 ± 0.85 yr, and we estimate that the low-mass companion passed its perihelion on June 02, 2020. We also report a total mass for the system of Mtot = 2.29 ± 0.06 M⊙.
Considering our constraints on the orbital parameters of HD 142527 B, we calculate that its maximum separation with respect to the central star HD 142527 A is Rapoapsis = 15.85 ± 0.43 au. Contrary to what has been previously suggested (Price et al. 2018a) based on different orbital estimates, this makes it highly unlikely that this low-mass companion can be solely responsible for the large ~100 au cavity observed in the near- to mid-infrared (Fukagawa et al. 2006; Verhoeff et al. 2011) and more recently with ALMA (Casassus et al. 2013).
To confirm this, we ran a set of three gas-only 3D hydrodynamical simulations of the disc around HD 142527 AB. We used the first simulation set-up as a control to demonstrate that we were able to reproduce the results obtained by Price et al. (2018a) under the same set of assumption regarding the orbital parameters of the binary. In the second simulation, we switched the orbit of the binary for our new estimate, based on the newly available VLTI/GRAVITY observations. We were unable to reproduce most of the features observed in the disc with this set-up: the low-mass companion HD 142527 B could only carve a ~30 au cavity, and did not interact with the disc. In the third set-up, we reduced the inner radius of the disc, allowing the companion to have a greater impact on the disc structure. However, the companion alone was still unable to explain the disc features.
A larger theoretical follow-up will be necessary to determine what else is required to match this new orbit of HD 142527 B with the observed disc structures. Additional observations could also prove useful as they could potentially reveal the presence of an additional companion in the system, which would help explain the disc structures and/or the presence of additional material extending further in the disc around HD 142527.
Acknowledgements
The authors thank Grant Kennedy for a helpful discussion on the calculation of mutual inclinations and the conventions used for expressing disc parameters. This work is based on observations collected at the European Southern Observatory under ESO programmes 098.D-0488, 60.A-9800, 60.A-9132 and 1104.C-0651. Most simulations in this work were performed using the DiRAC Data Intensive service at Leicester, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility. The equipment was funded by BEIS capital funding via STFC capital grants ST/K000373/1 and ST/R002363/1 and STFC DiRAC Operations grant ST/R001014/1. DiRAC is part of the National e-Infrastructure. S.R. acknowledges support from the Science & Technology Facilities Council (STFC) through Consolidated Grant ST/W000857/1. R.N. acknowledges support from UKRI/EPSRC through a Stephen Hawking Fellowship (EP/T017287/1). S.L. acknowledges the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-21-CE31-0017 (project ExoVLTI). D.P. acknowledges Australian Research Council funding via DP180104235.
References
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
- Avenhaus, H., Quanz, S. P., Schmid, H. M., et al. 2014, ApJ, 781, 87 [Google Scholar]
- Avenhaus, H., Quanz, S. P., Schmid, H. M., et al. 2017, AJ, 154, 33 [Google Scholar]
- Balmer, W. O., Follette, K. B., Close, L. M., et al. 2022, AJ, 164, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [Google Scholar]
- Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38 [Google Scholar]
- Blunt, S., Wang, J. J., Angelo, I., et al. 2020, AJ, 159, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Boehler, Y., Weaver, E., Isella, A., et al. 2017, ApJ, 840, 60 [Google Scholar]
- Bohn, A. J., Benisty, M., Perraut, K., et al. 2022, A&A, 658, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canovas, H., Ménard, F., Hales, A., et al. 2013, A&A, 556, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., M, S. P., Jordân, A., et al. 2012, ApJ, 754, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Hales, A., de Gregorio, I., et al. 2013, A&A, 553, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., Marino, S., Pérez, S., et al. 2015, ApJ, 811, 92 [Google Scholar]
- Christiaens, V., Casassus, S., Perez, S., van der Plas, G., & Ménard, F. 2014, ApJ, 785, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Christiaens, V., Casassus, S., Absil, O., et al. 2018, A&A, 617, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claudi, R., Maire, A.-L., Mesa, D., et al. 2019, A&A, 622, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cugno, G., Quanz, S. P., Hunziker, S., et al. 2019, A&A, 622, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czekala, I., Chiang, E., Andrews, S. M., et al. 2019, ApJ, 883, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Facchini, S., Juhász, A., & Lodato, G. 2018, MNRAS, 473, 4459 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fukagawa, M., Tamura, M., Itoh, Y., et al. 2006, ApJ, 636, L153 [Google Scholar]
- Fukagawa, M., Tsukagoshi, T., Momose, M., et al. 2013, PASJ, 65, L14 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garg, H., Pinte, C., Christiaens, V., et al. 2021, MNRAS, 504, 782 [Google Scholar]
- GRAVITY Collaboration (Lacour, S., et al.) 2019, A&A, 623, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Nowak, M., et al.) 2020, A&A, 633, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Biller, B., Cheetham, A., et al. 2016, A&A, 590, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Dembet, R., Abuter, R., et al. 2019, A&A, 624, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, SPIE, 9146, 735 [Google Scholar]
- Lubow, S. H., Martin, R. G., & Nixon, C. 2015, ApJ, 800, 96 [Google Scholar]
- Marino, S., Perez, S., & Casassus, S. 2015, ApJ, 798, L44 [Google Scholar]
- Mendigutía, I., Fairlamb, J., Montesinos, B., et al. 2014, ApJ, 790, 21 [CrossRef] [Google Scholar]
- Nealon, R., Price, D. J., & Nixon, C. J. 2015, MNRAS, 448, 1526 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, S., Casassus, S., Ménard, F., et al. 2014, ApJ, 798, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Harries, T. J., Min, M., et al. 2009, A&A, 498, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Price, D. J., Menard, F., et al. 2018, ApJ, 860, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Cuello, N., Pinte, C., et al. 2018a, MNRAS, 477, 1270 [Google Scholar]
- Price, D. J., Wurster, J., Tricco, T. S., et al. 2018b, PASA, 35, e031 [Google Scholar]
- Rodigas, T. J., Follette, K. B., Weinberger, A., Close, L., & Hines, D. C. 2014, ApJ, 791, L37 [Google Scholar]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vousden, W. D., Farr, W. M., & Mandel, I. 2016, MNRAS, 455, 1919 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observing log presenting all data acquired with VLTI/GRAVITY on HD 142527 and analysed in this paper.
All Figures
 |
Fig. 1 Typical example of a χ2 map obtained when reducing our data (in this case, for the observation on 2019 April 28). The left panel shows the structure of the χ2 map on a large scale, where the multiple minimums (in purple) are clearly visible. The right panel is a zoomed-in version. In each panel the red dots are generated by performing an orbit fit with all the astrometric measurement data available (including all GRAVITY epochs up to 2019 April 28), and using the posterior distributions of orbital parameters to calculate the estimated position at epoch 2019 April 28. The purple ellipse corresponds to the 3σ contour for the astrometric solution. The blue dots are obtained in a similar way, but using a new orbit fit that includes the astrometry extracted from this epoch. In other words, the red dots represents the prediction using the a priori orbital solution, the purple ellipse represents the measurement obtained at this epoch, and the blue dots represent the prediction using the a posteriori updated orbital solution. |
| In the text | |
 |
Fig. 2 Corner plot for the posterior distributions of the orbital elements of HD 142527 B. The distribution of ωB and ΩB is actually a bimodal distribution, with two peaks spaced 180 deg apart. This is a known degeneracy when radial velocity data are missing. For readability, only one peak, chosen arbitrarily, is shown here. |
| In the text | |
 |
Fig. 3 Illustration of the orbit fit. The left panel shows 100 samples drawn randomly from our posterior distribution, overplotted on the astrometric measurements of Table 2. The two panels on the right present the same orbits in separation (upper panel) and position angle (lower panel). For each panel, we show the 100 orbits and the astrometric measurements in the upper graph, and the difference (in units of σ, the error bars on the measurements) in the lower plot. The two dotted lines show the 3σ interval. |
| In the text | |
 |
Fig. 4 Surface density rendered plots of the HD 142527 protoplanetary disc. Each panel shows a different simulation at the same moment in time, but with different disc and binary parameters. The left panel reproduces the results of the R2 orbit in Price et al. (2018a) where the companion was shown to be responsible for the observed disc features: a large cavity, prominent spiral arms, and a misaligned inner disc. The middle panel uses the same disc parameters as the left panel, but uses the updated binary parameters in Table 3. The right panel is set up with the second solution of the updated binary parameters, and a smaller inner disc boundary to match the ratio of Rin/Rapoapsis of the simulation in the left panel. In the middle and right panels we find that, due to the close configuration of the updated binary orbit, the companion cannot be solely responsible for the observed disc features. |
| In the text | |
 |
Fig. 5 Surface density rendered plots of the HD 142527 protoplanetary disc. Each panel shows a simulation at the same moment in time, but with different disc and binary parameters. The right panel is set up with the updated binary parameters as listed in Table 3. The left panel uses the second solution of the values in Table 3 obtained by adding 180 deg to both Ω and ω. We find that neither solution reproduces the observed disc features. |
| In the text | |
 |
Fig. 6 Comparison between observed and simulated 12CO and 13CO maps for the HD142527 disc. The top and bottom panels show the 12CO and 13CO J = 2 − 1 emission, respectively. The left panels are the observations (Garg et al. 2021). The middle and right panels are synthetic emissions predicted from the simulations. The middle panels are from the simulation shown in the left panel of Fig. 4 which uses the disc and binary set-up as the R2 orbit in Price et al. (2018a). The right panels are from the simulations shown in the right panel of Fig. 4, which uses the updated binary parameters in Table 3. In general, the new binary orbit results in a lack of substructure in either molecule. Additionally, the lack of a cavity in 13CO further highlights that the companion alone cannot reproduce the disc features. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


