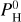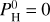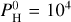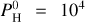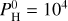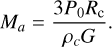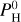© The Authors 2024

1 Introduction

Current developments in observational capabilities, including the launch of new telescopes such as the James Webb Space Telescope (JWST), have led to the study of relatively new categories of exoplanets that have not been so readily observable in the past. Going beyond solely the detection of species in the atmosphere of exoplanets, such observations may now enable a better characterization of the atmospheric structure and composition of these objects. These include ultra-hot rocky exoplanets (with equilibrium temperatures of >1500 K). This category of exoplanets have radii of <5 R_⊕ (Earth radii) and short periods (<10 days; Essack et al. 2020). Their surfaces are strongly irradiated by their host star and they can therefore be partially or fully melted. They can be subdivided into sub-categories such as “lava worlds”, “magma ocean worlds”, or “highly volcanic planets”, depending on the percentage of surface covered by lava or magma oceans (Henning et al. 2018). In this study, we primarily focus on super-Earths/sub-Neptunes that fit into the category of “lava worlds”, that is, we assume a fully melted surface, although we do intend to investigate partially melted surfaces in a future study.

According to Fig. 11 from Lebrun et al. (2013), the magma ocean phase would last longer than 100 Myr for planets that have orbital radii of less than 0.66 au. The possibility of a (partially or totally) melted surface offers an interesting setting whereby the atmosphere is strongly influenced by the chemical composition of the magma ocean (Dorn & Lichtenberg 2021). This allows for an inference of the interior composition through the study of the atmosphere composition obtained via observations. This could potentially also offer insights into early Earth characteristics, as magma oceans are speculated to be common in the past of large rocky planets (Schaefer & Elkins-Tanton 2018; Greenwood et al. 2005).

Although recent studies appear to report that temperate and rocky planets are not expected to have an observable atmosphere using current instrumentation (Kreidberg et al. 2019; Zieba et al. 2022; Crossfield et al. 2022; Keles et al. 2022), the high temperatures at the surface of these planets, due to their proximity with the star, should be enough to melt the surface into a magma ocean and create a thin silicate atmosphere (Schaefer & Fegley 2009; Miguel et al. 2011; Ito et al. 2015; Kite et al. 2016; Zilinskas et al. 2022). Schaefer & Fegley (2009) found silicate atmospheres would be composed primarily of Na, O₂, O, and SiO. They also suggest that large Na and K clouds could surround these hot super-Earths. Furthermore, 55 Cnc e and HD 149026 b are also expected to allow for the formation of mineral clouds in their atmosphere, according to Mahapatra et al. (2017). At the same time, they also found that the high temperatures on some hot, rocky super-Earths (e.g., the dayside of Corot-7 b) result in an ionized atmospheric gas and prevent gas condensation, thus it is unlikely that clouds form on their daysides. Studying pure Na, SiO, and SiO₂ atmospheres coupled with a magma ocean, Nguyen et al. (2020) found that a steady-state pure Na atmosphere would not be sustainable and the surface would change over time. Zieba et al. (2022) suggested that only K2-141 b and 55 Cnc e are hot enough to have a molten dayside, among the four small ultra-short-period planets observed by the JWST during its Cycle 1 General Observers program (also including LHS 3844 b and GJ 367 b). According to Zilinskas et al. (2022), the spectral energy distribution coming from hotter stars is much more weighted toward shorter wavelengths and the shape of the T-P profile of lava worlds (with a silicate atmosphere) is determined by the shortwave/IR absorption of stellar irradiation.

Otegi et al. (2020) suggested that volatile-rich and rocky atmospheres can be separated using their density. For example, they characterized 55 Cnc e as a rocky planet (density of 5.9 g cm⁻³, Crida et al. 2018). According to Rogers & Owen (2021), planets under 2 R_⊕ would be likely be stripped of H₂. However, some rocky planets have an unusually low density, such as TOI-561 b (density of ~4.4 g cm⁻³), which might be explained by an important volatile reservoir in their mantle (Piette et al. 2023). Since the volatiles should escape to space quite rapidly, the presence of such volatiles should be linked to an important volatile inventory in the interior, which may have been captured during their formation.

Terrestrial planets may have migrated inward during their formation due to efficient disk-planet interaction, so highly irradiated magma ocean exoplanets could have formed further away at much lower temperatures and with much higher hydrogen budgets than they have today (Charnoz et al. 2023). Newly formed planets may gravitationally capture a primordial atmosphere, rich in H₂, H₂O, and heavier elements, but largely dominated by mass by hydrogen (Fegley et al. 2020; Kite & Schaefer 2021); although hydrogen should amount to no more than 6% of the planet’s mass through degassing (Elkins-Tanton & Seager 2008). For planets on temperate orbits, H₂ is expected to be a strong contributor to the duration of the magma ocean phase (Lichtenberg et al. 2021), while H₂O, CO₂, and CH₄ are expected to have less of an effect; in addition, O₂, N₂, and CO are even less effective at keeping a magma ocean from solidifying. Hamano et al. (2013) also showed that increasing the H₂O content by tenfold would approximately increase the time before solidification by the same order of magnitude, due to the fact that the planet must lose water to cool down. Dorn & Lichtenberg (2021) suggested that even small amounts of greenhouse gases (e.g., a few tens of bars of H₂O or H₂) would melt the surface rocks of super-Earths and thus allow for a magma ocean to subsist underneath the surface. They hypothesized that water could still be present in the interior of 55 Cnc e, in which case, they predicted a non-zero partial pressure of water in a metal-rich atmosphere. More precisely, they forecast a 5% mass fraction of H₂O, partitioned between a wet magma ocean and a steam atmosphere, which could explain the relatively low bulk density of the planet. Finally, Kite et al. (2020) used a Fe-Mg-Si-O-H model to study sub-Neptunes and the absorption of volatiles in the magma. They found that on this type of planets, insulation due to the atmosphere would allow for magma oceans to last indefinitely and that the composition of the atmosphere is greatly influenced by the atmosphere-magma interaction. According to Kite & Schaefer (2021), the H₂ atmosphere lost is then replaced by a H₂O atmosphere, meaning the planet would not end up a bare rock and would maintain a 150–200 km-thick atmosphere.

Two effects could thus allow for a magma ocean to last longer than the initial stage of planetary evolution: (1) the stellar irradiation for ultra-short-period planets and (2) the presence of H₂ or H₂O in the atmosphere. In the current study, we are interested in the influence of hydrogen on the thermal structure of the atmosphere and the surface temperature of the planet, as well as its impact on spectral observations.

Larger bodies with a H₂ atmosphere could be easily probed via transmission spectroscopy (Hu et al. 2021), but smaller bodies (or silicate atmospheres) would require studies to be done using emission spectroscopy, characterizing the dayside of the planet (on which the atmosphere could be contained), when the planet is close to the secondary eclipse. Observations with the JWST in this context will still remain a challenge (Zilinskas et al. 2023). Therefore, we focus on the emission spectroscopy of hot rocky worlds with or without an hydrogenated atmosphere on top of a magma ocean, and characterize their atmospheric structure and emission.

The present study, which focuses on the atmospheric structure and observational implications of hot rocky super-Earths, follows the method described in Charnoz et al. (2023) for the computation of the gas-liquid equilibrium between a magma ocean and an atmosphere that contains a varying quantity of hydrogen, from H-poor to H-rich. As we are focused on ideal gases, our study is only suited to planets with less than 10⁵ bars of H, so we restricted ourselves to rocky and sub-Neptune planets. We discuss in Sect. 2 how we computed the equilibrium and how we took into account the effect of hydrogen, which corresponds to the method we have described in Charnoz et al. (2023). In Sect. 5, we compare this method (taking into account the gas equilibrium between the vapor and volatiles) to the sum of the vapor with volatiles, a method commonly used by the literature (e.g., Zilinskas et al. 2023; Piette et al. 2023). The atmospheric structure model is presented in Sect. 3. In Appendix A, we compare our model to LavAtmos (van Buchem et al. 2023) for atmospheres that have been completely deprived of hydrogen (silicate case). Atmospheres and spectra for cases with hydrogen are discussed in Sect. 4. We propose a criterion for selection of potential candidates for observation in Sect. 6.2.

2 Gas-liquid equilibrium

In Charnoz et al. (2023), we discussed a method for calculating the elementary content of the vapor arising from the magma ocean in the presence of a pre-existing hydrogen content. This method is referred to as the MAGMAVOL (MAGMa+Atmospheric VOLatiles) method throughout this study. We focus on a Na-K-Mg-Al-Fe-Si-O+H system, where H is present only in the atmosphere and is in equilibrium with the vapor released by the magma ocean. We summarize the main aspects here: the atmosphere is assumed to be at chemical equilibrium, so for a given elemental composition (number of moles of each atom) the molecules present for a given (P,T) are computed with the chemical equilibrium code CEA (Gordon & McBride 1996). In order to appropriately consider the interaction with the liquid magma ocean, partial pressures of atmospheric evaporated species (such as SiO, SiO₂, Mg, Na, K, Fe, and O₂) must satisfy a number of vaporisation reactions (these reactions are listed in Table1) ensuring gas-liquid equilibrium. More specifically, each reaction j listed in Table 1 implies an equilibrium reaction that is expressed as: 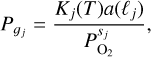$$P_{g_j}=\frac{K_j(T)a\left({\ell }_j\right)}{P_{{\text{O}}_2}^{s_j}},$$(1)

where g_j stands for the vapor species that bears the metal in the reaction j (for example Na_(g) in reaction #3), ℓ_j is the corresponding liquid oxide (NaO_0.5 for reaction #3), s_j is the stoichiometric coefficient (1/4 in reaction #3), K_j(T) is the reaction coefficient, a(ℓ_j) is the activity of the liquid j, with a(ℓ_j) = X_j × Γ_j, where X_j is the mole fraction of ℓ_j in the magma ocean (assumed to be fixed) and Γ_j is the activity coefficient of j in the liquid due to non ideal mixing effects. Activity coefficients, Γ_j, that are specific to the composition of the liquid, are interpolated using outputs of the VapoRock code (Wolf et al. 2023); our procedure is explained in detail in Charnoz et al. (2023). Initially, the atomic molar fractions and total pressure of the atmosphere are unknown variables. Their values were found by searching with an iterative procedure to satisfy all the above equations.

The oxygen fugacity (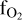${\text{f}}_{{\text{O}}_2}$) is computed by assuming congruent evaporation of melt oxides, so that 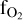${\text{f}}_{{\text{O}}_2}$ is found by solving for mass conservation of oxygen as in Charnoz et al. (2023) or in van Buchem et al. (2023). This is justified because our composition of planetary melted mantle is BSE, where all iron is under a single form, FeO, so there is no pressure buffer. The effective fO₂ can be found by checking the O₂ partial pressure displayed in Figs. B.1–B.4 in Charnoz et al. (2023). More details can be found in Charnoz et al. (2023). It’s important to highlight that our code does not consider the dissolution of volatiles in the liquid, such as H₂O. Instead, it computes the equilibrium between the magma ocean (with a fixed composition containing only silicate oxides) and an atmosphere, wherein we specify a particular hydrogen content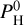$P_{\text{H}}^0.$

Figures B.1–B.4 of Charnoz et al. (2023) show the partial pressures of most abundant species in the vapor at the surface above the magma ocean, when the atmosphere is in equilibrium with the magma ocean. They are displayed for different values of the monoatomic pressure of H, 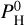$P_{\text{H}}^0$ (i.e., the pressure of hydrogen if all atoms of hydrogen were under the form of H). We consider P_mineral the sum of all partial pressures for an atmosphere devoid of H and containing only evaporated species. At a low H content, 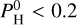$P_{\text{H}}^0<0.2$ bar, the atmosphere is not affected by the presence of H, and we have a close-to pure mineral atmosphere, with an almost constant total pressure P_vap ~ P_mineral. At 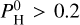$P_{\text{H}}^0>0.2$ bar, the atmosphere becomes strongly hydrogenated and the atmospheric composition drastically changes. P_mineral depends on the temperature and for a planet with Bulk-Silicate Earth (BSE) composition, we have found that P_mineral (expressed in bar) is aptly fitted by: 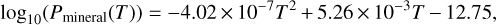$${\log }_{10}\left(P_{\text{mineral }}(T)\right)=-4.02\times {10}^{-7}{T}^2+5.26\times {10}^{-3}T-12.75,$$(2)

with T in Kelvins, using data from Charnoz et al. (2023).

At low hydrogen budgets, that is, 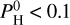$P_{\text{H}}^0<0.1$ bar, the dominant species are SiO and Na, closely followed by O₂. Fe is also quite abundant. For a higher hydrogen budget, that is, 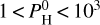$1<P_{\text{H}}^0<{10}^3$ bar, H₂ starts to dominate, followed by H₂O, SiO, and H, which become relatively less abundant as the partial pressure of H₂ increases. Notably, Na declines much faster than other species. For a very high hydrogen budget, that is, 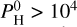$P_{\text{H}}^0>{10}^4$ bar, species such as SiH₄, SiH₃, and SiH₂ start to appear and even become quite abundant. In particular, SiH₄ is the third most abundant species after H₂ and H₂O for very high $P_{\text{H}}^0$.

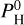The molar fractions of all considered atoms are shown in Fig. 1 for different values of 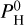$P_{\text{H}}^0$. As we consider the atmosphere to be well mixed vertically, the same atomic molar fractions will be used at every altitude in our vertical structure code. We note that hydrogen is not present when 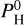$P_{\text{H}}^0$ is equal to 0. For 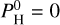$P_{\text{H}}^0=0$ (top plot), the most abundant element is Na for colder temperatures, but O becomes dominant for hotter temperatures (around 2500–3000 K), closely followed by Si. Then, K follows the same trend as Na but is less abundant, while Mg and Fe follow the trend of Si but also less abundant. For 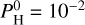$P_{\text{H}}^0={10}^{-2}$ bar, the dominant species at low temperatures is H, followed by O. The relative abundance of H is decreasing with increasing temperatures as heavy atoms (Si, Mg, Na, and K) are released by the magma ocean. The more volatile species such as Na, K, and Fe follow the same trend for temperatures of more than 2500 K. The dominant species for T > 2500 K becomes O, followed by Si. for 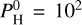$P_{\text{H}}^0={10}^2$ bar, the vapor is dominated by H, the second and third most abundant species are O and Si, respectively, which become more and more preponderant in the mix with increasing temperatures.

Fig. 1 Vapor element abundances, extracted from the output of MAGMAVOL (see Charnoz et al. 2023). The magma ocean releases more and more refractory species (Si, O, Mg, …) with increasing temperatures. The relative abundance of H thus decreases.

3 Radiative transfer and atmospheric structure

The atmospheric structure was computed via ATMO (Amundsen et al. 2014, 2017; Tremblin et al. 2015, 2016; Drummond et al. 2016) using the element abundances computed by the vaporization code (Sect. 2). ATMO solves for the pressure-temperature structure of an atmosphere by finding the energy flux balance in each model level, that is, 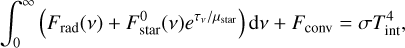$${\displaystyle {\int }_0^{\infty }\left(F_{\text{rad }}(v)+F_{\text{star }}^0(v)e^{{\tau }_v/{\mu }_{\text{star }}}\right)}\text{d}v+F_{\text{conv }}=\sigma T_{\text{int }}^4,$$(3)

where F_rad(ν) and F_conv are the spectral radiative flux and the convective flux, respectively, and τ_ν is the vertical monochromatic optical depth. T_int is the internal temperature of the object corresponding to the surface flux at which the object cools in the absence of irradiation; T_int is equivalent to the effective temperature, T_eff, in the absence of irradiation. 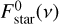$F_{\text{star }}^0(v)$ is the incoming irradiation flux from the star at the top of the atmosphere and µ_star = cos θ where θ is the angle of incoming radiation off the vertical.

As mentioned before, we focus on emission spectroscopy in this study. We rely on correlated-k opacities, which are more accurate than cross-sections (Amundsen et al. 2014). The list of opacities used is: Na, K, Fe, FeH, H₂-H₂, H₂O, MgO, SiO, SiO₂, SiH₄, and SiH₂. Optical absorbers include Na, K, Fe, SiO and MgO while H₂O will be the main source of infrared absorption. The spectral range goes from 0.2 to 2000 µm, with a resolution of 5000 for the synthetic spectra, while it is 32 for the computation of the PT profiles. For details on the opacities, see Appendix C.

The chemistry of the upper layers of the atmosphere is assumed to be in equilibrium and is computed via ATMO. The model does not include photochemical processes (however, this could be investigated in future studies). The code has been adapted to take into account the vapor elemental composition calculated by the gas-liquid equilibrium model (see Sect. 2). This includes inserting in the model the vapor pressure P_vap(T) computed by the model, namely, the total sum of the partial pressures of all outgassed species. The saturating-vapor pressure defines the limit between the ocean and the atmosphere, that is, when P is equal to the saturating vapor pressure of the magma ocean, we assume the atmosphere is in contact with the liquid and that this point defines the atmospheric base. It is a result of the MAGMAVOL code and is shown for different values of $P_{\text{H}}^0$ in Fig. 2. The more hydrogen we add, the higher the saturating vapor pressure. We took the LavAtmos code (van Buchem et al. 2023) as a reference for the hydrogen-free case. LavAtmos is an open-source code that computes the chemical gas-liquid equilibrium and thereby able to compute the vapor content above a magma ocean. A more extensive comparison of the MAGMAVOL and LavAtmos codes is discussed in Appendix A (along with a comparison of with MAGMA, Schaefer & Fegley 2009). Both the LavAtmos and the MAGMAVOL codes show very similar trends. We restrict this comparison to the hydrogen-free case as LavAtmos does not yet compute the equilibrium between the atmospheric volatiles, such as H, and the silicated vapor.

The atmospheric molecular composition is computed as follows: for each iteration of the solver, we use the pressure-temperature profile to identify the point (P,T) where the profile intersects with the vapor pressure curve, that is, we have P = P_vap(T). We extract the element abundances at this temperature from the MAGMAVOL code (Fig. 1). The element abundances are injected into ATMO, which recomputes the chemistry of the upper layers. For pressures higher than P_vap(T), the medium is considered to be liquid in ATMO. The ocean is assumed to be optically thick with a grey opacity of 1000 cm² g^–1 and zero albedo. We explored the sensitivity of the model to this opacity value and it makes no noticeable difference on the PT structure once the opacity is high enough to absorb the radiation reaching the surface in the first layer of the ocean. We assumed a zero convective flux in the ocean in this study: we tested this assumption by using a convective transport with an adiabatic index close to 1, finding it also makes no difference to the resulting PT structure.

Fig. 2 Vapor pressure Pvap(T) computed by MAGMAVOL for different temperatures, T, and for different content values of hydrogen, $P_{\text{H}}^0$, with LavAtmos taken as a reference.

4 Impact of hydrogen on the atmospheric structure

Here, we study how the presence of hydrogen impacts the atmospheric structure, surface temperature, and associated spectral observations.

4.1 Study parameters

We focused on a planet with a radius equal to 2 R_⊕ (Earth radii). The stellar spectrum used corresponds to 55 Cnc. The semi major-axis (or distance between the planet and the star) D is defined using the equilibrium temperature T_eq of the planet, using: 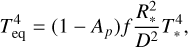$$T_{\text{eq}}^4=\left(1-A_p\right)f\frac{R_{*}^2}{D^2}{T}_{*}^4,$$(4)

where T_* and R_* are the temperature and radius of the star, respectively, f is the heat redistribution factor. For this definition, we have used a uniform heat redistribution, f = 1/4 (e.g. Essack et al. 2020) and the albedo A_p is considered to be zero. Table 2 can be used to quickly translate an equilibrium temperature from our results to an orbital distance. Since we have set the stellar parameters (to that of 55 Cnc), the higher T_eq corresponds to a smaller semi-major axis, D.

Fig. 3 Abundances in the atmosphere for cases with $P_{\text{H}}^0=0$, 10–2 and 102 bar (rows) and equilibrium temperatures of 2000, 2400 and 2800 K (columns). The y-axis scale is different from one plot to the other; the minimum pressure is constant (10–7 bar) while the surface pressure changes for each case.

4.2 Atmospheric structure

The molecular composition calculated by MAGMAVOL corresponds to the gas-liquid interface. However, it is not representative of the upper atmosphere as P and T change with altitude. The atmospheric structure is given in Fig. 3 (chemical composition) and Fig. 4 (PT profile). The correlated-k opacities used in the atmospheric code are detailed in Appendix C and have a spectral resolution of 32 points.

Examples are given here for cases with different hydrogen contents (Fig. 3). Appendix A also shows a comparison to LavAtmos in the hydrogen-free case. For cases with a very high hydrogen budget (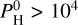$P_{\text{H}}^0>{10}^4$ bar), we will also discuss the abundance and the spectral features of SiH₄ in Sect. 4.6.

For lower equilibrium temperatures (see Eq. (4)), that is, T_eq = 2000 K in Fig. 3, the majority of the atmosphere is dominated by H₂ when 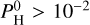$P_{\text{H}}^0>{10}^{-2}$ bar. The second more abundant molecule is then H₂O at 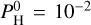$P_{\text{H}}^0>{10}^{-2}$ bar. SiO is slightly more abundant when 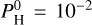$P_{\text{H}}^0>{10}^{-2}$ bar than in the pure silicate case, while Na and K are much less abundant (while Na is by far the most dominant species in the silicate case). The chemistry at such equilibrium temperatures (<2200 K) is mainly driven by the evaporation of the magma ocean. As can be seen in Fig. 8 of Charnoz et al. (2023), Na and K are less and less abundant when H increases. The abundance of SiO peaks at 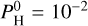$P_{\text{H}}^0>{10}^{-2}$ bar and then decreases though at a lesser rate than Na and K.

The intermediate case (T_eq = 2400 K) is very interesting, as it shows how the chemistry can drastically change when the hydrogen budget varies. MgO, H₂O and SiO₂ all start to thermally dissociate around 10^–5 bar for 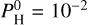$P_{\text{H}}^0>{10}^{-2}$ bar, while SiO dissociates only around 10^–6 bar. We note that here we refer to “dissociation” as the process of thermal dissociation of the molecular species in the high atmosphere as a result of chemical equilibrium in high-temperature and low-pressure environments. We emphasize that there are no photochemical processes here and the chemistry is considered to be at equilibrium. The chemistry of this range of equilibrium temperatures (>2200 K) is now partially driven by the evaporation of the magma ocean, but also by thermal dissociation.

For very hot planets (T_eq = 2800 K), hydrogen-bearing species are more abundant in the deep atmosphere and dissociate into H in the upper atmosphere, with the transition occurring between 10^–3 and 10^–5 bar. Furthermore, SiO is abundant for pressures >10^–5 bar and decreases in the upper layers. In the case of 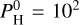$P_{\text{H}}^0={10}^2$ bar, H₂O is quite abundant (near 10% of the mix), but dissociates also below 10^–4 bar.

Chemistry and pressure-temperature profiles are interdependent. In Fig. 4, we show the pressure-temperature profiles of the atmosphere, for cases with different H content 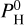$P_{\text{H}}^0$, and different equilibrium temperatures T_eq. The dashed line shows the vapor pressure line P_vap (T), the limit between the atmosphere and the magma ocean (extracted from Fig. 2). As indicated in Sect. 3, the region below the dashed line is treated as an ocean in the atmospheric model (ATMO), and the element abundances are derived from Fig. 1 at the temperature T corresponding to the intersection of the PT profile with P_vap (T).

For hydrogen-free cases (top plot), the atmospheric structure exhibits a pronounced thermal inversion, that is, the temperature increases with altitude. This is because the atmosphere is dominated by species that absorb in the visible (SiO, Na, K, Fe, …). This has been shown previously by Ito et al. (2015), Zilinskas et al. (2022). We refer the interested reader to Appendix A and the above papers for more information. Inverted PT profiles (which follow a thermal inversion) are linked to spectral emission features, while non-inverted PT profiles (for which the temperature decreases with altitude) are linked to absorption features. This is of interest for future observations, as the difference between an inverted and a non-inverted profile is more easily detectable than to observe molecular spectral features.

Since it acts as an infrared absorber, H₂O induces a greenhouse effect (reverse to the thermal inversion) when it is sufficiently abundant. Therefore, cases with a higher hydrogen content 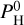$P_{\text{H}}^0$ are less prone to exhibit a thermal inversion. For example at T_eq = 2000 K and 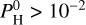$P_{\text{H}}^0>{10}^{-2}$ bar, the thermal inversion is completely removed, due to the fact that the atmosphere is dominated by H₂O (see Fig. 3).

In instances where T_eq = 2800 K, the thermal inversion persists for any hydrogen content. Indeed, for 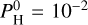$P_{\text{H}}^0={10}^{-2}$ bar, H₂O dissociates at around 10^–3 bar, and is therefore abundant enough only to reverse the thermal inversion in a very narrow pressure band between 10⁻¹ and 10⁻³ bar. At 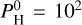$P_{\text{H}}^0={10}^2$ bar, H₂O dissociates at around 10⁻⁴ bar and is sufficiently abundant to eliminate the thermal inversion for pressures beyond 10⁻⁴ bar. The thermal inversion materializes at lower pressures, when H₂O is dissociated.

The case at T_eq = 2400 K is very interesting as it seems to be at a critical point between the non-inverted and the thermal inversion regimes. Figure 5 shows the pressure-temperature profiles at this equilibrium temperature, for the different values of hydrogen content 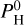$P_{\text{H}}^0$. The color indicates the hydrogen content 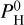$P_{\text{H}}^0$ of the atmosphere. The surface is indicated by a star. As the hydrogen content increases, we can see that the thermal inversion occurs at higher and higher altitudes until it disappears, replaced by an non-inverted profile. This is closely tied to the presence of H₂O. In pressure ranges where H₂O dissociates, the thermal inversion regime sets in. For the intermediate case with 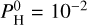$P_{\text{H}}^0={10}^{-2}$ bar, we can see on Fig. 3 that H₂O starts to dissociate around 10⁻⁵ bar, while SiO dissociates only around 10⁻⁶ bar. The non-inverted profile occurs when H₂O is abundant enough to be opaque, between 10⁻³ and 10⁻⁵ bar, and the upper layers maintain a thermal inversion (when H₂O is dissociated).

Fig. 4 Thermal structure of the atmosphere calculated by ATMO (colored lines) for different monoatomic pressure of hydrogen $P_{\text{H}}^0$. The colors indicate the equilibrium temperature, Teq, chosen for the simulation. The dotted lines show the vapor pressure corresponding to the limit between the magma ocean and the gaseous atmosphere, for each case. The silicate case (top plot) is more extensively discussed in Appendix A.

4.3 Thermal inversion

We here simplify the definition of the thermal inversion and assume it is given by the difference between the surface temperature and the temperature at high altitude, where the atmosphere is not sufficiently opaque for radiative effects to be detectable: 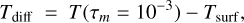$$T_{\text{diff }}=T\left({\tau }_m={10}^{-3}\right)-T_{\text{surf }},$$(5)

where τ_m is the mean optical depth for wavelengths between 0.5 and 20 µm. Here we have chosen to set τ_m at 10⁻³. The atmosphere becomes partially opaque in the lower layers and starts to absorb incoming stellar flux. As shown in Appendix D, τ_m = 10⁻³ corresponds to pressures around 10⁻⁶ or 10⁻⁵ bar. The surface pressure varies from case to case.

We analyzed the presence of a thermal inversion in the various cases proposed here, that is, when varying the equilibrium temperature of the planet T_eq and its hydrogen content 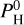$P_{\text{H}}^0$. Hotter planets can sustain a thermal inversion better than colder planets in the presence of hydrogen, as shown in Fig. 6.

The cases for which there is a thermal inversion either require a low content of hydrogen or for the planet to be strongly irradiated (i.e., a large T_eq). The thermal inversion is strongest (T_diff > 1000 K) in the cases with no hydrogen and a high equilibrium temperature. The profile is non-inverted in the case with a lot of hydrogen and less irradiated (T_diff ∼ −700 K). This effect is not linear. The transition between a thermal inversion and a non-inverted profile is very sharp. We fitted the transition by the red line in Fig. 6. Its formula is given by: 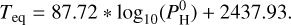$$T_{\text{eq }}=87.72*{\log }_{10}\left(P_{\text{H}}^0\right)+\mathrm{2437.93.}$$(6)

This very sharp transition is linked to the strong thermal difference between the bottom of the atmosphere and the upper atmosphere. As more hydrogen is introduced, the thermal inversion occurs at progressively higher altitudes. When the thermal inversion occurs in non-opaque pressure ranges (defined here as τ < 10⁻³), the profile is classified as non-inverted. Since the radiative effects are less strong for lower pressures (see Fig. D.1), the main contribution to the emission will come from the zone between the surface and the pressure level where τ > 10⁻³ (P > ~10⁻⁶ bar); this means that if there is a thermal inversion occurring at lower pressures, it will not be linked to emission features (see Sect. 4.5).

As shown by Fig. 6 and Eq. (6), the hydrogen threshold between the two regimes (thermal inversion and non-inverted profile) depends on the equilibrium temperature. For hotter planets, the hydrogen threshold is larger. In our simulations, it occurs at a very low 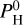$P_{\text{H}}^0$ for T_eq = 2000 K, around 10⁻³ bar for T_eq = 2200 K, 1 bar for T_eq = 2400 K and 10 bar for T_eq = 2600 K. The fit of Eq. (6) and the above values are to be taken with caution, as they will change for different mantle and volatile compositions (see also Sect. 6.3).

Fig. 5 Thermal structure of the atmosphere of a rocky planet at Teq = 2400 K calculated by ATMO (plain lines), for different hydrogen content $P_{\text{H}}^0$ (in bar), indicated by the colors. The stars indicate the surface of each case, that is, the point where the atmosphere reaches the vapor pressure (see Fig. 2), and therefore, the ocean below. The surface temperature and pressure increase for larger $P_{\text{H}}^0$.

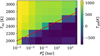Fig. 6 Difference in temperatures, Tdiff, shown in color, as defined in Eq. (5), at a pressure where τm = 10−3 (around 10−6 bar) and the surface, for different hydrogen content $P_{\text{H}}^0$ and equilibrium temperature, Teq. Positive values indicate inverted PT profiles (presence of thermal inversion). Negative values indicate non-inverted PT profiles (absence of thermal inversion). The shift between the two regimes does not occur at the same hydrogen content for different equilibrium temperatures (hotter planets require more hydrogen to fall into the non-inverted category). This is indicated by the (fitted) red line, for which the formula is given in Eq. (6).

Fig. 7 Surface temperature, Tsurf, for different equilibrium temperatures, Teq, depending on the hydrogen content of the atmosphere ($P_{\text{H}}^0$, in colors). The surface temperature may be underestimated for high values of $P_{\text{H}}^0$, as explained in Sect. 6.3 (see Tremblin et al. 2017). The green dashed line shows the case when Tsurf = Teq for reference.

4.4 Temperature at the surface of the magma ocean

The surface temperature is affected by the greenhouse effect of H₂O and, therefore, it increases with the amount of hydrogen in the system, as shown by Fig. 7. The difference between the surface temperature in the simulation with no hydrogen and the surface temperature in the simulation with a substantial amount of hydrogen for T_eq = 2400 K is approximately 500 K for example.

This figure also shows a non-linearity in the increase of the surface temperature: there is a jump between 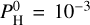$P_{\text{H}}^0={10}^{-3}$ and 10⁻² bar. The measurement of hydrogen is therefore quite critical to properly evaluate the surface temperature.

For lower T_eq (<2300 K), we can also see that there seems to be a limit to the increase of the surface temperature, which even decreases for very large hydrogen contents. This is due to the outgassing of the magma ocean. At T_eq = 2000 K for example, H₂O is much less abundant when adding 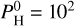$P_{\text{H}}^0={10}^2$ bar than at 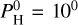$P_{\text{H}}^0={10}^0$ bar (see Fig. 3). This is better seen in Fig. 8 from Charnoz et al. (2023). Using Fig. 1, we can also see that at 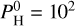$P_{\text{H}}^0={10}^2$ bar and 2000 K, O is much less abundant, which is the reason why H is primarily under the form of H₂ rather than H₂O. Due to its lower abundance, the presence of H₂O results in a milder greenhouse effect, leading to a less elevated surface temperature. At 2400 K, H₂O is also less abundant, but the difference is much less (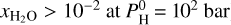$x_{{\text{H}}_2\text{O}}>{10}^{-2}\text{ at }{P}_{\text{H}}^0={10}^2\text{ bar }$), which makes the greenhouse effect more effective and thus does increase the surface temperature.

In these simulations, an isothermal layer is present in the deep atmosphere for cases with a high content of hydrogen. This could be an artefact from the 1D formulation, as discussed in Sect. 6.3 (see Tremblin et al. 2017). The surface temperatures shown here may therefore be underestimated.

Fig. 8 Emission spectra (planetary to stellar flux) for different equilibrium temperatures and compositions. Emission features are highlighted by top-down color gradients, while absorption features are highlighted by bottom-up gradients. SiO is shown in yellow-ish color, MgO in brown-ish, and H2O in blue.

Fig. 9 Emission spectra (planetary to stellar flux) and spectral contributions of molecules for an equilibrium temperature Teq of 2400 K and for a hydrogen-free and a hydrogen-rich case (i.e., $P_{\text{H}}^0=0$ and 102 bar).

4.5 Spectral features

We have calculated the synthetic emission spectra corresponding to the above temperature and chemistry profiles. The opacities that have been used are detailed in Appendix C. The spectral resolution is equal to 5000. The resulting spectra are shown in Fig. 8. The detailed spectral features for each species are also shown in Appendix E. The pressure-temperature profile and the chemistry have strong effects on the spectral features. Thermal inversion is linked to emission features for the species that are present in the corresponding pressure range. This is most notably visible for SiO, around 9 µm (a feature already identified by Ito et al. 2015; Zilinskas et al. 2022), but also for other species such as Na, K, Fe, and in some cases, MgO. Indeed, the feature of MgO is most prominent around 11 µm, in the silicate case at T_eq = 2800 K. Our model finds more MgO features than Ito et al. (2015), Zilinskas et al. (2022) due to the outgassing of the magma ocean, as discussed in Appendix A. MgO features are also present between 1 and 3 µm. These emission features tend to disappear for lower T_eq (i.e., longer orbital period) and when adding hydrogen. The spectral contributions of each molecule for a hydrogen-free case and a hydrogen-rich case are shown in Fig. 9. We can see how most spectral emitting features are reduced or even absorbing in the hydrogen-rich case. Interestingly, Fe is one of the only species that retains its spectral features when the hydrogen content is increased. This is more readily visible in Fig. 9 and Figs. E.1-E.3. We note that some species (in addition to H) are expected to escape to space over time, most readily Na and K (Charnoz et al. 2023), a small study has therefore been led in Appendix B to investigate atmospheres without these two species.

Some features, such as SiO at 4 µm, are linked to an emission peak or an absorption pit, following the PT profile. The feature is an emission peak for thermal inversions (i.e., for either low 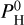$P_{\text{H}}^0$ or high T_eq), and an absorption pit in the presence of hydrogen due to the non-inverted PT profile. PT profiles that are non-inverted (i.e., that do not exhibit a thermal inversion) are linked to absorption features mainly from H₂O, along with absorption features from other species, such as the SiO feature aforementioned. Even though Zilinskas et al. (2023) have not considered the chemical equilibrium between the volatiles and the vapor from the magma ocean (see also Sect. 5), they obtain similar trends.

Fig. 10 Pressure-temperature profiles for a large hydrogen content $P_{\text{H}}^0={10}^4$ bar, and equilibrium temperature Teq ranging from 2000 to 3000 K.

4.6 A case with a very high hydrogen budget

We consider one final case with a very large amount of hydrogen in the atmosphere and, more precisely, with 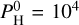$P_{\text{H}}^0={10}^4$ bar of monoatomic hydrogen. The pressure-temperature profiles are shown in Fig. 10. This amount of hydrogen should account for no more than 1% of the total mass of an Earth-like planet (Charnoz et al. 2023), which is in line with the limits or predictions made by Elkins-Tanton & Seager (2008), Dorn & Lichtenberg (2021). The case at T_eq = 3000 K shows a thermal inversion although there is a small non-inverted region around 10⁻³ bar. The remaining cases present a non-inverted profile that extends to the top of the atmosphere. As shown by Figs. 7–10 from Charnoz et al. (2023), the chemical composition of the vapor changes quite a lot from 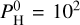$P_{\text{H}}^0={10}^2$ bar to 10⁴ bar. Notably, new hydrogenated species appear at 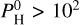$P_{\text{H}}^0>{10}^2$ bar, such as SiH₄, SiH₃ and SiH₂. They become dominant at 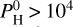$P_{\text{H}}^0>{10}^4$ bar. However, as one can see in Fig. 11, these species are only present in the lower part of the atmosphere, and disappear at high altitudes. Consequently, they do not have any spectral contribution, as shown by Fig. 12 (see Fig. F.1 for more details). The atmosphere is completely dominated by H₂, H being the second most dominant species (around 1% at T_eq = 2000 K). Then H₂O and SiO are both present in almost equal quantities (10⁻³ at 2000 K and 10⁻² at 3000 K). At T_eq = 3000 K, they both dissociate around 10⁻³ –10⁻⁴ bar. SiO dissociates at higher altitudes and is therefore linked to stronger emission features due to the thermal inversion for pressures <10⁻³ bar. H₂O is mostly present in isothermal layers and its spectral (absorption) signature is therefore diminished, although it is linked to emission features for wavelengths of >10 µm.

In this extreme case, only very hot planets will sustain a thermal inversion. If we compare this case (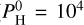$P_{\text{H}}^0={10}^4$ bar of hydrogen) to the hydrogen-free case for T_eq = 3000 K, we see that in both cases the temperatures reach 3700 K at high altitude.

However the surface temperatures of these two cases are quite different, as it is 2500 K in the hydrogen-free case and 3000 K for 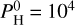$P_{\text{H}}^0={10}^4$ bar of hydrogen.

Fig. 11 Abundances for very large hydrogen content $P_{\text{H}}^0={10}^4$ bar, and Teq = 2000 K and Teq = 3000 K. Species also include SiH4 and SiH2 here, present at the surface but which dissociate at higher altitudes.

Fig. 12 Spectral contributions of different species for $P_{\text{H}}^0={10}^4$ bar of monoatomic hydrogen and for different equilibrium temperatures Teq. SiH4 and SiH2 are negligible. SiO is linked to very strong emission features at 2, 4, and 9 µm at Teq = 3000 K. H2O is also seen in emission at wavelengths >10 µm.

4.7 Summary

To summarize this section, (1) the presence of hydrogen tends to reduce the thermal inversion of short period super-Earths due to the formation of H₂O, watering down the silicate spectral features of such planets; (2) the transition between a thermal inversion and a non-inverted profile is very sharp and sensible to the quantity of hydrogen; (3) the surface temperature and pressure will be increased in the presence of hydrogen due to the greenhouse effect of H₂O; (4) planets that are strongly irradiated will retain some emission features, due to the dissociation of water at higher and higher pressures; (5) SiH₄ and SiH₂ (which form in very hydrogenated cases) are only present at the surface and have therefore no spectral contribution.

5 Volatiles and vapor: Sum versus equilibrium

To compute the atmospheric composition, as we proposed in Charnoz et al. (2023) and in the present study, we rely on the computation of a gas-liquid equilibrium, in which hydrogen is in equilibrium with the gases evaporated from the magma ocean. As described in Charnoz et al. (2023), the set of gas-liquid equilibrium reactions and gas-gas reactions are solved simultaneously (including species released by the magma ocean + atmospheric volatiles), ensuring a full equilibrium but at the cost of a relatively long computation time. However, some studies (Zilinskas et al. 2023; Piette et al. 2023) follow a different approach (as an approximation of the full equilibrium): they sum the atomic abundances resulting from the evaporation of the magma ocean (in the absence of atmospheric volatile species) with the atmospheric volatile species (H,O, etc.). Then the gas-gas equilibrium of the mixture is computed with a gas-equilibrium code (like FastChem). The latter approach allows a faster computation, but cannot be considered as an exact gas-liquid thermodynamical equilibrium. We study here the differences between the two methods and evaluate the impact of the latter method onto the chemistry of the atmosphere, the associated pressure-temperature profile and emission spectrum. The method in which the abundances of the vapor is summed to the volatiles (Zilinskas et al. 2023; Piette et al. 2023) will be referred to as the sum method, while the gas-liquid equilibrium discussed in this study and proposed by Charnoz et al. (2023) will be referred to as the equilibrium method. The sum method includes hydrogen compounds but does not include other volatiles such as carbon (while it is the case in Zilinskas et al. 2023; Piette et al. 2023), in order to be able to compare it to the equilibrium method proposed here, which only includes hydrogen as a volatile in the present study. Both methods are computed via the MAGMAVOL code.

Figure 13 shows the composition of the atmosphere at the surface using the equilibrium method (same as Fig. B.3 from Charnoz et al. 2023), and the sum method, when the atomic abundances of volatiles (H) are summed to the atomic abundances of the vapor. Without computing the gas-liquid equilibrium in a self-consistent approach, the chemical composition of the atmosphere is quite different. Overall, for a high hydrogen content (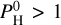$P_{\text{H}}^0>1$ bar), the sum method will underestimate the partial pressures of the gases outgassed by the magma ocean in the final mix, compared to the equilibrium method. This holds as well for H₂O.

The atmospheric chemistry (shown in Fig. 14) is therefore also quite different between the two methods. The main aspects of these differences are twofold: (1) the abundances of H₂O and silicates (SiO, Na, K, Fe, MgO) are lower in the sum method compared to the equilibrium method by at least one order of magnitude; (2) H₂ is more abundant in the sum method. Some species (such as FeH, H, etc.) have not been included in the graph as they have no spectral significance, although they are present in the model (see Fig. 3 for example).

This leads to a difference of a few hundred degrees Kelvin for pressures below 10^–3 bar, the equilibrium case being the hottest, as shown in Fig. 15. The surface temperature does not seem to be impacted. The thermal inversion is pushed to higher altitudes in the equilibrium case.

Due to its lower temperature, the emission spectrum of the sum case is also lower than that of the equilibrium case (as shown in Fig. 16). The spectra also exhibit different spectral features. We can see Na as an emission feature for example in the sum method, while it is invisible in the equilibrium method. The 9 µm SiO feature is visible in emission in the sum method while it is absent (and slightly absorbing) in the equilibrium method. The same can be said for the Na and K features between 0.6 and 0.8 µm. One can refer to Appendix G for more information on the exact spectral features contributing to these two spectra.

To conclude this section, we would like to stress that taking into account volatiles in the gas-liquid equilibrium changes fundamentally the whole atmospheric structure.

Fig. 13 Partial pressures of most abundant species in the vapor calculated using the equilibrium method (left plot, same as Fig. B.3 from Charnoz et al. 2023) and the sum method (right plot, methodology of Zilinskas et al. 2023; Piette et al. 2023), for different monoatomic hydrogen pressure $P_{\text{H}}^0$ when the atmosphere is at equilibrium with the magma ocean at T = 3000 K and hydrogen is not in equilibrium with the magma ocean.

Fig. 14 Abundances for a case with some hydrogen ($P_{\text{H}}^0=1$ bar), at Teq = 2400 K. Sum is the case where volatiles are summed to the vapor content. Equilibrium is the case where the gas-liquid equilibrium is computed.

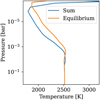Fig. 15 Thermal structure of the atmosphere calculated by ATMO for Teq = 2400 K and $P_{\text{H}}^0=1$ bar. Sum is the case where volatiles are summed to the vapor content. Equilibrium is the case where the gas-liquid equilibrium is computed.

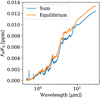Fig. 16 Emission spectra (planetary to stellar flux) for Teq = 2400 K and $P_{\text{H}}^0=1$ bar. sum is the case where volatiles are summed to the vapor content. equilibrium is the case where the gas-liquid equilibrium is computed.

6 Discussion

6.1 Observational target candidates

In this study, we aim to focus on targets that match the criteria necessary for maintaining a magma ocean on the dayside of the planet and of which the radius is sufficiently large for us to consider a potential (thin) hydrogen envelope, without falling into the category of gas giants. To that end, we have developed a hydrogenation potential index that will be discussed in Sect. 6.2. In Fig. 17, we show a list of potential targets of interest. The planets with the highest Emission Spectroscopy Metric (ESM; Kempton et al. 2018) are the best candidates for observation.

Only a limited number of targets match the criteria for being characterized as hot rocky super-Earths, with an equilibrium temperature sufficiently high to be capable of sustaining a magma ocean and simultaneously of a necessary size and low density to also consider a potential hydrogen envelope.

6.2 Maximum hydrogenation index: χ

In addition to the equilibrium temperature, we needed another selection criterion. Our objective is to provide a qualitative assessment of whether a given planet (among the high temperature rocky exoplanets displayed in Fig. 17) could potentially harbor a hydrogen layer above a magma ocean considering its measured mass and radius. This is not a simple question as the more hydrogen, the lower the average density of the planet, and the thicker the atmosphere. Indeed, as we add hydrogen, we increase the temperature at the bottom of the atmosphere due to the greenhouse effect of H₂O, and decrease the mean molar mass, m, thus increasing the scale-height of the atmosphere (H = RT/mg, with R standing for the ideal gas constant, g the surface gravity, and T for the atmosphere temperature). We tried to estimate the maximum hydrogen content of the planet.

For that, we considered a simple two-layer planet model and tested many atmospheric compositions to determine the maximum amount of hydrogen that can be put in the atmosphere while matching its measured planet mass and radius.

Thus, we considered a planet with measured mass, M_p, and measured radius, R_p, with an average density, ρ_p, and equilibrium temperature, T_p (here we simply use the published T_p value in the discovery paper). The planet is considered to consist of two layers: a “solid” planet with mass, M_c, and radius, R_c, surrounded by an atmosphere with a thickness, Z (Z << R_c). Here, Z is the distance between the solid surface and where the atmosphere becomes optically thin (low opacity), so that the equivalent transit radius of the planet is R_p = R_c + Z. If the planet has no atmosphere (which we do not know), then we have R_p = R_c, M_p = M_c and Z = 0. R_c and M_c are assumed to be constants (i.e., independent of atmospheric composition), as we do not account for the dissolution of H in the magma ocean. Dorn & Lichtenberg (2021) indeed reported that the density variation of the mantle is by about −1% for a 1% mass fraction of H₂O dissolved in the magma ocean (Bajgain et al. 2015). This variation is very small compared to all other approximated quantities in this simple model, so we have not taken that into account.

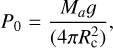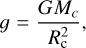If we assume some atmospheric composition with mean molar mass, m, and surface pressure, P₀, (where m and P₀ are taken from our MAGMAVOL model; see Sect. 2) we want the total mass of the planet to be equal to M_p. For a thin atmosphere, the atmosphere mass, M_a, is related to P₀ through: $$P_0=\frac{M_{a}g}{\left(4\pi R_{\text{c}}^2\right)},$$(7) $$g=\frac{G{M}_c}{R_{\text{c}}^2},$$(8)

G is the gravity constant. The solid planet average density, ρ_c, is: 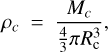$${\rho }_c=\frac{M_c}{\frac{4}{3}\pi R_{\text{c}}^3},$$(9)

so we get: $$M_a=\frac{3P_0{R}_{\text{c}}}{{\rho }_{c}G}.$$(10)

Since M_c + M_a = M_p, we have: 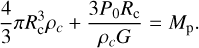$$\frac{4}{3}\pi R_{\text{c}}^3{\rho }_c+\frac{3P_0{R}_{\text{c}}}{{\rho }_{c}G}=M_{\text{p}}.$$(11)

For a simple hydrostatic and isothermal atmosphere, we have P(z) = P₀e^−zmg/RT. We set the pressure at which the atmosphere becomes transparent to be about 0.01 bar (= P_t), following Fig. D.1. This approximation should be taken with caution and needs to be refined in the future. We have Z = −(RT/mg)ln(P_t/P₀). Since Z + R_c = R_p, the following equation must be verified: 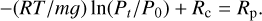$$-(RT/mg)\ln \left(P_t/P_0\right)+R_{\text{c}}=R_{\text{p}}.$$(12)

In Eqs. (11) and (12), M_p and R_p and T are observational data, m and P₀ are the mean molar mass and pressure of the atmosphere (considered to be free parameters), and R_c and M_c are the unknowns (that will depend on the choice of m and P₀). P₀ and m are chosen among the compositions given by our MAGMAVOL code at temperature T_p and for various amount of hydrogen 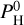$P_{\text{H}}^0$ For a given temperature T_p we determine R_c and M_c for all atmospheric composition (m) with 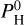$P_{\text{H}}^0$ ranging from 0 to 10⁵ bar. To stay in the regime of rocky-exoplanet or mini-neptune, we will consider as “valid” those solutions for which Z << R_c and those for which the ρ_c < 1.2 ρ_p (so that the solid planet average density is at a maximum of 20% higher than the planet’s average density). These choices are arbitrary but they ensure that our two-layer planet stays in the range of “rocky” world or “mini-neptune”. So for each planet we determine the maximum quantity of hydrogen, 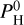$P_{\text{H}}^0$ we can put in the atmosphere, while matching the observations and the constrains above. It has been shown in Charnoz et al. (2023) that for a magma-ocean planet to be considered as “hydrogenated” (so that it contains lots of H₂O, H₂ in addition to Na, SiO, MgO, etc.) the hydrogen pressure (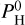$P_{\text{H}}^0$) must be larger than P_mineral (the pure-mineral atmosphere pressure) fitted by Eq. (2). Considering this finding, we define our maximum hydrogenation index as 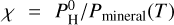$\chi =P_{\text{H}}^0/P_{\text{mineral}}(T)$; in other words, this is the maximum hydrogen pressure we can put in the planet’s atmosphere divided by the pressure of a pure mineral atmosphere at the same temperature. If χ<1 then the planet can only have a pure mineral atmosphere, dominated by Na, SiO, MgO, etc. If ;χ> 1 the atmosphere can potentially bear significant H and molecules like H₂, H₂O (in addition to Na, SiO, MgO, etc.). Of course, the larger χ the larger the H₂ and H₂O abundances (and all other hydrogenated species).

The maximum hydrogenation index (χ) is color plotted in Fig. 17 (bottom plot) for planets with T_p>1500 K. We see that lower temperature planets have a higher χ: this is because low temperature planets have a low P_mineral, and thus are more easily hydrogenated. Planets with larger g (in general larger planets) have also a high χ because their g can accept more massive atmosphere with small change in their transit radius. Interestingly all planets present in Fig. 17 (bottom plot) could have a hydrogenated atmosphere (χ> 1) while being molten. This figure may be useful to select planets that may be potentially molten while accepting a significant fraction of H.

Fig. 17 Subset of super-Earths of interest (with a better chance at being hydrogenated), displayed by their density and equilibrium temperature Teq. The size indicates the planet radius. Top plot: color indicates the planet Emission Spectroscopy Metric (ESM; Kempton et al. 2018); planets with the highest Teq are the best candidates for magma oceans planets. Bottom plot: color indicates the hydrogenation index χ (see Sect. 6.2); all colored planets are good candidates for hydrogenated planets (χ > 1), the others are not colored. Source: NASA Exoplanet Archive1.

6.3 Caveats

Some effects have not been taken into account which could be of some importance for future studies. Indeed, this study does not include the dissolution or the exsolution of H₂O in or from the magma ocean. We have assumed that H is already present in the atmosphere and does not exsolve from the magma ocean. The exsolution of H₂O will lead to a more oxidized atmosphere according to our preliminary investigations (not included in the current study), in which the atmosphere is dominated by H₂O rather than H₂. Moreover, according to Kite et al. (2020), atmospheric H₂O/H₂ ratio is proportional to magma FeO content. Concurrently, Bower et al. (2022), Maurice et al. (2023) have also shown that the H₂O/H₂ ratio increases when the magma ocean solidifies. The change is quite drastic, as the atmosphere can be dominated by H₂ in the early stages of the planet formation and rather dominated by water in later stages. This also depends on the proximity of the planet with the star, since the magma ocean is also expected to survive longer under intense stellar irradiation. Taking into account the dissolution of H₂O will change the activity coefficients of the melt and therefore also change the atmospheric composition. Overall, the main effect of the dissolution of H₂O to be expected is an increase in the abundance of H₂O in the atmosphere, and thus in the spectral signature of H₂O.

The inclusion of carbon as well as other volatiles in the system should also be considered for future studies, as this should have a considerable impact on the atmospheric structure and chemistry. Indeed, as shown by Sect. 5, taking into account hydrogen in the gas-liquid equilibrium changes drastically the chemistry of the atmosphere, in part due to its interactions with oxygen. Other species that also interact with oxygen may have a similar effect on the overall chemistry.

This study does not focus on atmospheric escape (although we have partially discussed this in Charnoz et al. 2023). H is expected to escape quite fast in smaller bodies. Its effect on the chemistry of the evaporated species is also promoting the escape to space of heavy elements such as Na and K. As discussed in Appendix B, the escape of Na and K is not fundamentally changing the characteristics of the atmospheric structure. The impact of the escape of H is the major aspect that should be taken into account in future studies. Young planets are expected to have retained more H than older planets. This study does not focus on either, although the content of H that we have used as input (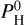$P_{\text{H}}^0$) could be constrained using parameters such as the age of the planet and its proximity to its host star.

The present study follows a 1D approach to studying the day-side thermal emission. However, as shown by Zieba et al. (2022) for K2-141 b, for example, 2D models better explain the data of hot rocky exoplanets. Kite et al. (2016) showed that for planets with a substellar temperature above 2400 K, the magma overturning circulation is slow compared to atmospheric transport. Castan & Menou (2011) also pointed out that rotation could break the substellar-point symmetry in a 2D equatorial simulation and, under conditions of permanent hemispheric forcing, could lead to the formation of superrotating equatorial winds (Showman & Polvani 2011). This is all a strong incentive to use a 2D atmospheric structure in order to model the winds and heat transport to the nightside.

In the context of gas giants, Tremblin et al. (2017) also discussed the effect of the two-dimensionality of the atmospheric model on the pressure-temperature profile of strongly irradiated planets. They showed how the 1D model follows an isothermal profile around 1 bar, while the 2D model becomes adiabatic, which could explain their inflated radius. This adiabatic profile is forced by the deep circulation forced by the asymmetric irradiation that transports energy downwards in the atmosphere. This becomes the main energy transport as soon as the atmosphere is sufficiently optically thick so that radiation is inefficient to transport energy. In a relatively thick H₂/He atmosphere of a rocky planet reaching up to hundreds of bars at the surface, this process should also take place and also lead to a much higher surface temperature, as compared to a 1D model ignoring circulation processes. This may also be applicable to the present study and our 1D model is thus likely to be underestimating the actual scale-height of the atmosphere.

7 Conclusion

We combined a vaporization model with an atmospheric model (MAGMAVOL and ATMO) to compute the thermal and chemical structure of the atmosphere of a molten rocky planet in the presence of a hydrogen layer. Our study focuses on the effect of H on the atmospheric structure and emission spectrum.

In a pure silicate atmosphere, an atmospheric thermal inversion occurs, due to absorption in the visible range, from Na, K, Fe, SiO, etc. We find the same emission peaks of SiO at 9 µm as Ito et al. (2015), Zilinskas et al. (2022). Our Na-K-Mg-Al-Fe-Si-O+H model (MAGMAVOL) also accounts for the presence of hydrogen in the atmosphere in the calculation of the gas-liquid equilibrium. We find that hydrogen drastically changes the atmospheric composition and, thus, changes the atmospheric structure. For atmospheres that are relatively “cool” (<2500 K), a low hydrogen budget is enough to remove the thermal inversion as water becomes dominant and molecules will dissociate only in the higher levels of the atmosphere, at low pressure. For hotter atmospheres (>2500 K), molecules start to dissociate at higher pressures (10^–3–10^–5 bar), and a higher hydrogen budget is not enough to remove the thermal inversion (as water is dissociated). This confirms previous trends observed by Zilinskas et al. (2023) as to the removal of thermal inversion due to water in the atmosphere.

Two distinct regimes appear, the transition from one state to the other being very sharp. At high hydrogen content, H forms water, and the resulting greenhouse effect increases the temperature at the surface of the magma ocean well above the equilibrium temperature by several hundred Kelvin degrees (Fig. 7). The effect is less strong for higher equilibrium temperatures. At a low hydrogen content, metallic species absorbing in the visible create a thermal inversion in the upper atmosphere. In that case the surface temperature is in general lower than the equilibrium temperature (for T > 2200 K). This effect is less strong for lower equilibrium temperatures.

Finally, we consider what spectral features we could expect from a hydrogenated magma ocean planet. In the absence (or very low abundance) of hydrogen, thermal inversion induces emission features from SiO, notably at 9 µm, but also MgO, Na, K and Fe. When the hydrogen content increases, the stronger greenhouse effect caused by the increase in water vapour induces a non-inverted pressure-temperature profile, and spectral absorption features, mainly from H₂O, but also SiO. The emission peak of SiO around 4 µm switches to absorption for a higher hydrogen budget. The emission features of other species is also reduced. Then, Fe is the only species that retains a quite strong emission feature, with or without the addition of hydrogen. At a high hydrogen content, SiH₄ is produced at the base of the atmosphere, near the surface, but disappears from the upper layers and is therefore not linked to any spectral features. This holds as well for SiH₂.

Future studies should focus on the inclusion of other volatiles in the calculation of the gas-liquid equilibrium, as it might prove to have a major influence over the whole atmospheric structure and chemistry, while also exhibiting quite different spectral features. Finally, in this work, we introduce and discuss a criterion, namely, the maximum hydrogenation index, which offers an insight as to the potential of a planet to host a hydrogenated atmosphere.

Acknowledgements

S.C., A.F., P.T. acknowledge financial support by LabEx UnivEarthS (ANR-10-LABX-0023 and ANR-18-IDEX-0001) and by the CNES (Centre National d'Études Spatiales). P.T. would also like to acknowledge and thank the ERC for funding this work under the Horizon 2020 program project ATMO (ID: 757858).

Appendix A Pure silicate case

Silicate atmospheres (i.e., hydrogen-free in our context) have been shown to exhibit a strong thermal inversion (Ito et al. 2015; Zilinskas et al. 2022), linked to an emission feature of SiO around 9 µm. We here confirm these results, and compare the vapor content calculated via MAGMAVOL to the LavAtmos code (van Buchem et al. 2023), discussing the differences produced on the resulting atmospheric structure and emission spectrum.

Fig. A.1 shows a comparison between the composition of the vapor calculated by our model (MAGMAVOL, Charnoz et al. (2023)), MAGMA (Schaefer & Fegley 2009) and LavAtmos (van Buchem et al. 2023; Zilinskas et al. 2022, 2023) for the silicate-only case ($P_{\text{H}}^0=0$). Our model predicts similar abundances as LavAtmos for Na, O₂, O, and Fe, but predicts less SiO (by a factor of ~2) and more K (by a factor of 3). MAGMA predicts less Na at low temperatures, and less SiO and Fe (by about one order of magnitude) and much less K (by two orders of magnitude) than the two other models. van Buchem et al. (2023) explain the significant difference between the K abundances by the difference in calibration of the thermodynamic models. Our model yields results that align more closely with LavAtmos than with MAGMA.

Fig. A.1 Comparison between the composition of the vapor calculated by our vaporization code, in solid lines, and MAGMA, in dashed lines (Schaefer & Fegley 2009), and LavAtmos, in dash-dotted lines (van Buchem et al. 2023). There is no Hydrogen in this case. LavAtmos includes Al, Ca, and Ti, which are not present in our code.

The atmospheric chemistry for MAGMAVOL and LavAt-mos is shown in Fig. A.2 for two equilibrium temperatures, T_eq = 2000 K and T_eq = 2800 K. The two models still agree very well, although, as could be expected from Fig. A.1, SiO is slightly more abundant in the vapor computed by LavAtmos.

Fig. A.2 Abundances in a silicate atmosphere, computed via ATMO, using the vapor computed by MAGMAVOL and LavAtmos. There is no fundamental difference in the chemistry computed using the vapor from both codes.

In Fig. A.3, we show the pressure-temperature profiles of atmospheres for which the equilibrium temperature T_eq is between 2000 and 3000 K in the case of a pure silicate atmosphere. We cannot see major differences between the atmospheres calculated from the two vaporization models.

Fig. A.3 Thermal structure of the silicate atmosphere calculated by ATMO for different equilibrium temperatures Teq (indicated by the colors), which translates as different orbital radii. The dash-dotted PT profiles use the vapor computed via LavAtmos, while the plain lines use MAGMAVOL. The dashed line show the vapor pressure Pvap(T) corresponding to the limit between the magma ocean and the gaseous atmosphere.

The slightly higher abundance of SiO of LavAtmos is visible in the simulated emission spectra, shown in Fig. A.4. On this figure, we can see that the baseline for the spectrum computed via MAGMAVOL is lower than that of LavAtmos, due to the fact that the corresponding temperature profiles are generally colder (Fig. A.3). But we can see the increased emission in the SiO band around 9 µm due to SiO being slightly more abundant in the LavAtmos model. On the contrary, the features of MgO are reduced using LavAtmos.

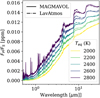Fig. A.4 Emission spectra (planetary to stellar flux) for vaporizations calculated by LavAtmos and MAGMAVOL. The vapor from LavAtmos contains slightly more Si, which is noticeable in the SiO band around 9 µm.

Appendix B Escape of Na and K

As shown by Charnoz et al. (2023), Na and K would be among the first species (apart from H) to escape from the atmosphere. Fig. B.1 shows the difference between the atmospheric structure for a case with Na and K compared to a case where Na and K have disappeared, for which we recompute the gas-liquid equilibrium. The upper atmosphere is not affected by this change. However, the surface temperature is increased by more than 100 K in the absence of Na and K (and up to 200 K for lower T_eq). This is not sufficient to have any spectral impact (except for Na and K features).

Fig. B.1 Thermal structure of the atmosphere calculated by ATMO for different equilibrium temperatures Teq (indicated by the colors) and thus different orbital radii. The partial pressure of monoatomic hydrogen $P_{\text{H}}^0$ is set to 1 bar. The dash-dotted lines indicate the case without Na nor K. The dashed line show the vapor pressure Pvap(T) corresponding to the limit between the magma ocean and the gaseous atmosphere.

Appendix C Opacity sources

Correlated-k opacities have mostly been computed through EXOCROSS (Yurchenko, Sergei N. et al. 2018) and SOCRATES (Edwards & Slingo 1996), though the SiOUVenIR opacity for SiO, and the opacities of SiH₄ and SiH₂ have been extracted from the DACE database² and converted to correlated-k opacities via Exo_k (Leconte 2021). It should be noted that they have been generated in the context of gas giants, with an assumed H₂ and He dominated atmosphere. This should have an effect on line broadening (see Fig. 1 from Amundsen et al. (2014) for an example). The opacities are shown at 2400 K at 10^–5 bar and 1 bar in Fig. C.1 for a resolution of 5000 spectral points between wavelengths λ = 0.2 and 2000 µm. All sources are listed in Table C.1. The resolution of the correlated-k opacities used is equally spaced in wavenumber and equal to 32 for the PT calculations (see Fig. 4 for example), while it is 5000 for the calculations of the spectra (see, e.g., Fig. 8).

Fig. C.1 Opacity sources used in this study, at 0.1 bar (top), and 10−5 bar (bottom), both at 2400 K.

Appendix D Optical depth

The optical depth can be written as: 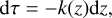$$\text{d}\tau =-k(z)\text{d}z,$$(D.1)

where k(z) is the sum of the opacities of all species weighted by their abundances. The optical depth of the atmosphere can be shown per pressure level, as in Fig. D.1. The figure shows two cases: one for a hydrogen-free case (top plot) and one for a hydrogen-rich case (with 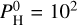$P_{\text{H}}^0={10}^2$ bar). The two cases, with an equilibrium temperature T_eq of 2400 K, are quite distinct. We can clearly see the interior boundary at a fixed pressure in the hydrogen-free case and the relatively thin layer of the atmosphere that is partially opaque. We can see Na, K (in the optical) and SiO (in the infrared) spectral features, which we discuss more extensively in Sect. 4.5. The hydrogen-rich case has a blurrier boundary since the bottom of the atmosphere becomes opaque before the interior is reached. The Na and K spectral features are still present, we can see the SiO spectral features at the top of the atmosphere, and H₂O bands between 1 and 5 µm.

Fig. D.1 Optical depth for Teq = 2400 K, for a hydrogen-free case (top plot), and a hydrogen-rich case, that is, $P_{\text{H}}^0={10}^2$ bar (bottom plot). The color indicates the value of the optical depth, namely the cumulative opacity of the atmosphere. Black is completely opaque while white is transparent.

Appendix E Spectral contribution of molecules

In Fig. E.1 to Fig. E.3, we show the contributions of each molecule to the spectrum for cases without hydrogen, with 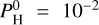$P_{\text{H}}^0={10}^{-2}$ bar and 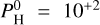$P_{\text{H}}^0={10}^{+2}$ bar, respectively, for the cases displayed in Appendix A and Sect. 4.

Fig. E.1 Spectral contributions of different molecules without hydrogen and for different equilibrium temperatures Teq. Positive contributions indicate emission features, while negative contributions indicate absorption features. The contribution of H2O and FeH is null here.

Fig. E.2 Spectral contributions of different molecules at $P_{\text{H}}^0={10}^{-2}$ bar and for different equilibrium temperatures Teq.

Fig. E.3 Spectral contributions of different molecules at $P_{\text{H}}^0={10}^2$ bar and for different equilibrium temperatures Teq.

Appendix F Spectral contribution of SiH₂, SiH₄ and SiO at high hydrogen concentration

The spectral contributions of SiH₂, SiH₄ and SiO are shown in Fig. 12 for 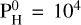$P_{\text{H}}^0={10}^4$ bar. We can see that SiH₄ and SiH₂ have no significant spectral contribution, especially put in perspective with SiO, which is coherent with their presence in the atmosphere being limited to the lower layers, near the surface.

Fig. F.1 Spectral contributions of SiO, SiH4 and SiH2 for $P_{\text{H}}^0={10}^4$ bar of monoatomic hydrogen and for different equilibrium temperatures Teq. SiH4 and SiH2 are negligible. SiO is linked to very strong emission features at 2, 4, and 9 µm at Teq = 3000 K.

The figure also shows how the spectral features of SiO are mixed between absorption features (mostly around 4 µm) for colder cases (low T_eq), and emission features (most prominent at 9µm) for hotter cases. The case at T_eq = 3000 K is the only case corresponding to a thermal inversion, in which we can better see the emission peaks of SiO (at 1.5, 2, 4, and 9 µm).

Appendix G Spectral contribution when summing volatiles and vapor vs gas-liquid equilibrium

We have compared in Sect. 5 the sum and equilibrium methods, the first one computing the element abundances by simply summing the volatile abundances with the vapor abundances, and the second one computing a gas-liquid equilibrium. Fig. G.1 shows the spectral contributions of relevant species for the two methods. We can see that H₂O is mainly the dominant absorbing species, but in the case of the sum method, a strong SiO feature is visible in emission, and also one Na and one K feature. In the equilibrium case, these features disappear, due to the thermal inversion occurring at pressures that are too low (see Fig. 15).

Fig. G.1 Spectral contributions for the sum and equilibrium methods, with $P_{\text{H}}^0=1$ bar and Teq = 2400 K.

References

All Tables

All Figures

	Fig. 1 Vapor element abundances, extracted from the output of MAGMAVOL (see Charnoz et al. 2023). The magma ocean releases more and more refractory species (Si, O, Mg, …) with increasing temperatures. The relative abundance of H thus decreases.
In the text

	Fig. 2 Vapor pressure Pvap(T) computed by MAGMAVOL for different temperatures, T, and for different content values of hydrogen, $P_{\text{H}}^0$, with LavAtmos taken as a reference.
In the text

	Fig. 3 Abundances in the atmosphere for cases with $P_{\text{H}}^0=0$, 10–2 and 102 bar (rows) and equilibrium temperatures of 2000, 2400 and 2800 K (columns). The y-axis scale is different from one plot to the other; the minimum pressure is constant (10–7 bar) while the surface pressure changes for each case.
In the text

Fig. 4 Thermal structure of the atmosphere calculated by ATMO (colored lines) for different monoatomic pressure of hydrogen $P_{\text{H}}^0$. The colors indicate the equilibrium temperature, Teq, chosen for the simulation. The dotted lines show the vapor pressure corresponding to the limit between the magma ocean and the gaseous atmosphere, for each case. The silicate case (top plot) is more extensively discussed in Appendix A.

In the text

Fig. 5 Thermal structure of the atmosphere of a rocky planet at Teq = 2400 K calculated by ATMO (plain lines), for different hydrogen content $P_{\text{H}}^0$ (in bar), indicated by the colors. The stars indicate the surface of each case, that is, the point where the atmosphere reaches the vapor pressure (see Fig. 2), and therefore, the ocean below. The surface temperature and pressure increase for larger $P_{\text{H}}^0$.

In the text

Fig. 6 Difference in temperatures, Tdiff, shown in color, as defined in Eq. (5), at a pressure where τm = 10−3 (around 10−6 bar) and the surface, for different hydrogen content $P_{\text{H}}^0$ and equilibrium temperature, Teq. Positive values indicate inverted PT profiles (presence of thermal inversion). Negative values indicate non-inverted PT profiles (absence of thermal inversion). The shift between the two regimes does not occur at the same hydrogen content for different equilibrium temperatures (hotter planets require more hydrogen to fall into the non-inverted category). This is indicated by the (fitted) red line, for which the formula is given in Eq. (6).

In the text

	Fig. 7 Surface temperature, Tsurf, for different equilibrium temperatures, Teq, depending on the hydrogen content of the atmosphere ($P_{\text{H}}^0$, in colors). The surface temperature may be underestimated for high values of $P_{\text{H}}^0$, as explained in Sect. 6.3 (see Tremblin et al. 2017). The green dashed line shows the case when Tsurf = Teq for reference.
In the text

	Fig. 8 Emission spectra (planetary to stellar flux) for different equilibrium temperatures and compositions. Emission features are highlighted by top-down color gradients, while absorption features are highlighted by bottom-up gradients. SiO is shown in yellow-ish color, MgO in brown-ish, and H2O in blue.
In the text

	Fig. 9 Emission spectra (planetary to stellar flux) and spectral contributions of molecules for an equilibrium temperature Teq of 2400 K and for a hydrogen-free and a hydrogen-rich case (i.e., $P_{\text{H}}^0=0$ and 102 bar).
In the text

	Fig. 10 Pressure-temperature profiles for a large hydrogen content $P_{\text{H}}^0={10}^4$ bar, and equilibrium temperature Teq ranging from 2000 to 3000 K.
In the text

	Fig. 11 Abundances for very large hydrogen content $P_{\text{H}}^0={10}^4$ bar, and Teq = 2000 K and Teq = 3000 K. Species also include SiH4 and SiH2 here, present at the surface but which dissociate at higher altitudes.
In the text

	Fig. 12 Spectral contributions of different species for $P_{\text{H}}^0={10}^4$ bar of monoatomic hydrogen and for different equilibrium temperatures Teq. SiH4 and SiH2 are negligible. SiO is linked to very strong emission features at 2, 4, and 9 µm at Teq = 3000 K. H2O is also seen in emission at wavelengths >10 µm.
In the text

Fig. 13 Partial pressures of most abundant species in the vapor calculated using the equilibrium method (left plot, same as Fig. B.3 from Charnoz et al. 2023) and the sum method (right plot, methodology of Zilinskas et al. 2023; Piette et al. 2023), for different monoatomic hydrogen pressure $P_{\text{H}}^0$ when the atmosphere is at equilibrium with the magma ocean at T = 3000 K and hydrogen is not in equilibrium with the magma ocean.

In the text

	Fig. 14 Abundances for a case with some hydrogen ($P_{\text{H}}^0=1$ bar), at Teq = 2400 K. Sum is the case where volatiles are summed to the vapor content. Equilibrium is the case where the gas-liquid equilibrium is computed.
In the text

	Fig. 15 Thermal structure of the atmosphere calculated by ATMO for Teq = 2400 K and $P_{\text{H}}^0=1$ bar. Sum is the case where volatiles are summed to the vapor content. Equilibrium is the case where the gas-liquid equilibrium is computed.
In the text

	Fig. 16 Emission spectra (planetary to stellar flux) for Teq = 2400 K and $P_{\text{H}}^0=1$ bar. sum is the case where volatiles are summed to the vapor content. equilibrium is the case where the gas-liquid equilibrium is computed.
In the text

Fig. 17 Subset of super-Earths of interest (with a better chance at being hydrogenated), displayed by their density and equilibrium temperature Teq. The size indicates the planet radius. Top plot: color indicates the planet Emission Spectroscopy Metric (ESM; Kempton et al. 2018); planets with the highest Teq are the best candidates for magma oceans planets. Bottom plot: color indicates the hydrogenation index χ (see Sect. 6.2); all colored planets are good candidates for hydrogenated planets (χ > 1), the others are not colored. Source: NASA Exoplanet Archive1.

In the text

	Fig. A.1 Comparison between the composition of the vapor calculated by our vaporization code, in solid lines, and MAGMA, in dashed lines (Schaefer & Fegley 2009), and LavAtmos, in dash-dotted lines (van Buchem et al. 2023). There is no Hydrogen in this case. LavAtmos includes Al, Ca, and Ti, which are not present in our code.
In the text

	Fig. A.2 Abundances in a silicate atmosphere, computed via ATMO, using the vapor computed by MAGMAVOL and LavAtmos. There is no fundamental difference in the chemistry computed using the vapor from both codes.
In the text

Fig. A.3 Thermal structure of the silicate atmosphere calculated by ATMO for different equilibrium temperatures Teq (indicated by the colors), which translates as different orbital radii. The dash-dotted PT profiles use the vapor computed via LavAtmos, while the plain lines use MAGMAVOL. The dashed line show the vapor pressure Pvap(T) corresponding to the limit between the magma ocean and the gaseous atmosphere.

In the text

	Fig. A.4 Emission spectra (planetary to stellar flux) for vaporizations calculated by LavAtmos and MAGMAVOL. The vapor from LavAtmos contains slightly more Si, which is noticeable in the SiO band around 9 µm.
In the text

Fig. B.1 Thermal structure of the atmosphere calculated by ATMO for different equilibrium temperatures Teq (indicated by the colors) and thus different orbital radii. The partial pressure of monoatomic hydrogen $P_{\text{H}}^0$ is set to 1 bar. The dash-dotted lines indicate the case without Na nor K. The dashed line show the vapor pressure Pvap(T) corresponding to the limit between the magma ocean and the gaseous atmosphere.

In the text

	Fig. C.1 Opacity sources used in this study, at 0.1 bar (top), and 10−5 bar (bottom), both at 2400 K.
In the text

	Fig. D.1 Optical depth for Teq = 2400 K, for a hydrogen-free case (top plot), and a hydrogen-rich case, that is, $P_{\text{H}}^0={10}^2$ bar (bottom plot). The color indicates the value of the optical depth, namely the cumulative opacity of the atmosphere. Black is completely opaque while white is transparent.
In the text

	Fig. E.1 Spectral contributions of different molecules without hydrogen and for different equilibrium temperatures Teq. Positive contributions indicate emission features, while negative contributions indicate absorption features. The contribution of H2O and FeH is null here.
In the text

	Fig. E.2 Spectral contributions of different molecules at $P_{\text{H}}^0={10}^{-2}$ bar and for different equilibrium temperatures Teq.
In the text

	Fig. E.3 Spectral contributions of different molecules at $P_{\text{H}}^0={10}^2$ bar and for different equilibrium temperatures Teq.
In the text

	Fig. F.1 Spectral contributions of SiO, SiH4 and SiH2 for $P_{\text{H}}^0={10}^4$ bar of monoatomic hydrogen and for different equilibrium temperatures Teq. SiH4 and SiH2 are negligible. SiO is linked to very strong emission features at 2, 4, and 9 µm at Teq = 3000 K.
In the text

	Fig. G.1 Spectral contributions for the sum and equilibrium methods, with $P_{\text{H}}^0=1$ bar and Teq = 2400 K.
In the text