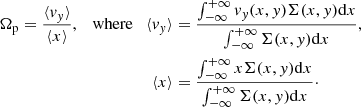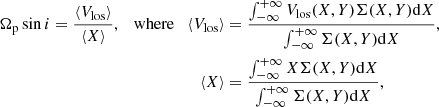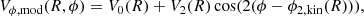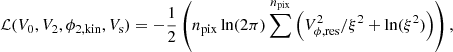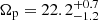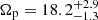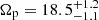| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347266 | |
| Published online | 12 March 2024 | |
The bar pattern speed of the Large Magellanic Cloud⋆
1
Departament de Física Quàntica i Astrofísica (FQA), Universitat de Barcelona (UB), C Martí i Franquès, 1, 08028 Barcelona, Spain
2
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: ojimenez@icc.ub.edu
3
Institut d’Estudis Espacials de Catalunya (IEEC), C Gran Capità, 2-4, 08034 Barcelona, Spain
4
Instituto de Astrofísica, Universidad Andres Bello, Fernandez Concha 700, Las Condes, Santiago RM, Chile
5
Centro de Astronomía – CITEVA, Universidad de Antofagasta, Avenida Angamos 601, Antofagasta 1270300, Chile
6
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
7
Lund Observatory, Division of Astrophysics, Department of Physics, Lund University, Box 43 221 00 Lund, Sweden
8
Departamento de Física de la Tierra y Astrofísica, UCM, and IPARCOS, Facultad de Ciencias Físicas, Plaza Ciencias, 1, Madrid 28040, Spain
9
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received:
23
June
2023
Accepted:
22
December
2023
Context. The internal kinematics of the Large Magellanic Cloud (LMC) have been studied in unprecedented depth thanks to the excellent quality of the Gaia mission data, thus revealing the disc’s non-axisymmetric structure.
Aims. We seek to constrain the LMC bar pattern speed using the astrometric and spectroscopic data from the Gaia mission.
Methods. We applied three methods to evaluate the bar pattern speed by measuring it via: the Tremaine-Weinberg (TW) method, the Dehnen method, and a bisymmetric velocity (BV) model. These methods provide additional information on the bar properties, such as the corotation radius as well as the bar length and strength. We tested the validity of the methods with numerical simulations.
Results. A wide range of pattern speeds are inferred by the TW method, owing to a strong dependency on the orientation of the galaxy frame and the viewing angle of the bar perturbation. The simulated bar pattern speeds (corotation radii, respectively) are well recovered by the Dehnen method (BV model). Applied to the LMC data, the Dehnen method finds a pattern speed of Ωp = −1.0 ± 0.5 km s−1 kpc−1, thus corresponding to a bar that barely rotates and is only slightly counter-rotating with respect to the LMC disc. The BV method gives a LMC bar corotation radius of Rc = 4.20 ± 0.25 kpc, corresponding to a pattern speed of Ωp = 18.5−1.1+1.2 km s−1 kpc−1.
Conclusions. It is not possible to determine which global value best represents an LMC bar pattern speed with the TW method, due to the strong variation with the orientation of the reference frame. The non-rotating bar from the Dehnen method would be at odds with the structure and kinematics of the LMC disc. The BV method result is consistent with previous estimates and gives a bar corotation-to-length ratio of 1.8 ± 0.1, suggesting that the LMC is hosting a slow bar.
Key words: astrometry / galaxies: kinematics and dynamics / Magellanic Clouds
Movies are available at https://www.aanda.org.
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The angular speed of stellar bars is a fundamental parameter in dynamics of galaxies from which the principal bar-disc resonances can be identified and the structure of stellar orbits can be studied in a given gravitational potential (e.g. Contopoulos & Grosbol 1989; Binney & Tremaine 2008). Furthermore, the bar pattern speed is thought to reflect certain properties of the halo density at low radius because bars and haloes of stars and/or dark matter are believed to continuously interact during galaxy evolution through dynamical friction. Numerical models and observations suggest that the bar speed is slower when the inner halo is denser (Debattista & Sellwood 2000; Buttitta et al. 2023). The pattern speed of simulated bars is also seen to slow down with the secular evolution, in contrast to its growing length and strength (Sellwood 2014).
The importance of measuring bar pattern speeds in the dynamics and evolution of galaxies has thus grown significantly with the emergence of large-scale long-slit and 3D spectroscopic surveys, which have enabled the estimations of a few hundreds of pattern speeds (Cuomo et al. 2019; Guo et al. 2019; Géron et al. 2023, and references therein). These works found that most stellar bars are fast, namely, bars show a ratio of corotation-to-bar radius smaller than 1.4 (following Athanassoula 1992), and that high angular speeds are for small and weak bars, and within faint galaxies (Cuomo et al. 2020). However, the large occurrence of fast bars is a critical issue for the simulations made in a cosmological context, as the inner density of simulated dark matter halos is so cuspy that the parent discs are expected to host mostly slow bars. This discrepancy suggests a failure in cosmological simulations (Roshan et al. 2021) or, perhaps, a bias in estimating pattern speeds of bars from observations (Fragkoudi et al. 2021). This highlights the difficult part of measuring pattern speeds from observation since it represents a single time instant in the entire evolution of galaxies.
Bar pattern speeds from these studies have been inferred exclusively by means of the Tremaine-Weinberg method (Tremaine & Weinberg 1984, hereafter TW). Its direct application makes use of integrals of kinematics and positions of a tracer that should obey the continuity equation, such as stars. Alternatively, Dehnen et al. (2023) proposed a new method for determining bar pattern speeds in numerical simulations using a single time snapshot. This involves measuring the Fourier amplitudes of particle positions and velocities within the bar region. In another work, Gaia Collaboration (2023a) proposed an indirect measurement of the bar angular speed by fitting a bisymmetric model to the tangential velocities to get the bar phase angle and corotation radius. Unfortunately, these last two methods have limited applicability due to their reliance on the availability of objects with individually measured planar (tangential and radial) velocities, which are rare. Only the Milky Way (MW) and the Large Magellanic Cloud (LMC) offer this possibility. To our knowledge, the Dehnen et al. (2023) formalism has never been applied to observations, while the method in Gaia Collaboration (2023a) estimated the bar corotation, orientation and pattern speed for the MW, using data from the Gaia mission (Gaia Collaboration 2016, 2021a). Interestingly, they found a Galactic bar speed consistent with the value inferred with the TW method (Bovy et al. 2019).
Our objective in this study is to determine the pattern speed and corotation region of the stellar bar in the LMC. The LMC is a dwarf spiral (or irregular) galaxy and one of the closest and brightest satellites of the MW, in interaction with the Small Magellanic Cloud (SMC) and the MW. It could thus be a challenge to study the properties of a system like the LMC, because of its structure and velocity field impacted by the interaction, at least in the outermost regions (e.g. Belokurov & Erkal 2019; Gaia Collaboration 2021b). It is, however, a unique object of its kind for testing the three aforementioned methods due to the availability of different kinds of kinematic data for the entire disc. To achieve this objective, we make use of the opportunity to use both astrometric and spectroscopic data from the Gaia mission. First, the TW method can be applied to line-of-sight (LoS) velocities of thousands of LMC stars, as measured by the Gaia Radial Velocity Spectrometer (Katz et al. 2023; Jiménez-Arranz et al. 2023), yielding a single value of the LMC bar pattern speed, similarly to other galaxies. Second, the Gaia astrometric data allow us to estimate the two components of the velocity tensor for millions of stars in the LMC plane (Gaia Collaboration 2021b). Unlike the LoS velocities given in the sky frame, these two components make it possible to apply the Dehnen method, the bisymmetric model, as well as a modified version of the TW method, adapted to the disc plane. In this latter case, multiple values of the LMC bar pattern speeds can be inferred, corresponding to multiple orientations of the Cartesian frame of the LMC plane, thus multiple viewing angles of the bar in the disc reference frame. This allows us to compare various estimates of the bar pattern speed, and assess the validity of the methods.
The paper is organised as follows. In Sect. 2, we describe the methods used to measure the bar pattern speed. In Sect. 3, we validate the methods using two N-body simulations: one representing an isolated disc and the other an interacting disc. In Sect. 4, we apply the three methods to the LMC sample (Jiménez-Arranz et al. 2023), to try to determine the pattern speed of the LMC bar. In Sect. 5, we discuss the implications of our findings for our understanding of the LMC and barred spiral galaxies in general. Finally, in Sect. 6, we summarise the main conclusions of this work.
2. Methods
In this section, we describe the three methods applied to the Gaia data to infer the bar pattern speed of the LMC. The first is the Dehnen method (Sect. 2.1), which can be applied to astrometric data. Secondly, we describe the Tremaine-Weinberg method (TW, Sect. 2.2), which can be applied to astrometric or spectroscopic data. Finally, we describe the bisymmetric velocity method (BV, Sect. 2.3), which can only be applied to astrometric data.
In the Cartesian frame of the galaxy, the methods assume that the disc is in equilibrium (which may not be fully the case for the LMC), rotation is done around the z-axis, the kinematic center is located at the origin of the Cartesian coordinate frame, and the density is stationary in the frame rotating at Ωp. Furthermore, it is also assumed that the region where Ωp is constrained should only contain the bar, that is well distinguishable from other structures in the galaxy, such as spiral arms. It is worth mentioning that other density perturbations may exist in the region where the bar influences the stellar dynamics, and thus could impact the estimation of the bar Ωp.
2.1. The Dehnen method
The first method we use in this work is that of Dehnen et al. (2023). We use the version of the code made publicly available with the paper. Here we summarise some of the main aspects of the method.
Dehnen et al. (2023) developed an unbiased, precise, and consistent method that simultaneously measures Ωp and the orientation angle ϕb of the bar from single snapshots of simulated barred galaxies. These parameters are found assuming that the continuity equation applies:
where vx and vy are the disc’s velocity components in Cartesian coordinates (x, y), where Σ = Σ(x, y, t) = Σ(R, ϕ − Ωpt) is the disc surface density, (R, ϕ) the corresponding cylindrical coordinates, and Ωp is the angular speed of the rotating frame of the bar perturbation, considered invariant with time. The method assumes that the centre of rotation is known, that the rotation is around the z-axis and that the density is stationary in the rotating frame. With these assumptions, ∂Σ/∂t = −Ωp∂Σ/∂ϕ and Eq. (1) becomes:
This expression is the traditionally used in the TW method (see Sect. 2.2 below). Here we use the Fourier method, as implemented in the public code, which consists of multiplying Eq. (2) by the weight function w(x) = W(R)e−imϕ, where m is the azimuthal wave number and W(R) a smooth window function (see their Eq. (25)), and integrating over all space. The smooth window function is necessary to avoid issues at the edges of radial bins. The resulting expression for the pattern speed of an N-body model is the real value form (see details in their Appendix A) of the following equation:
where μi are the individual particle masses.
In fact, the method is divided in two steps. First, it defines which particles belong to the bar region, [R0, R1], defined as a continuous range of radial bins with large amplitude of the bisymmetric density perturbation of second order, and having a roughly constant phase angle (see their Appendix B for details). Hereafter we will refer to R1 as the bar radius or length, as it agrees well with the definition of best estimates for bar lengths in numerical simulations (Ghosh & Di Matteo 2023). Second, once the bar region is determined, it computes the bar pattern speed and the bar phase angle together with their uncertainties using the covariance matrix of the real part of Eq. (3) with m = 2 (their Eq. (A.4)).
Dehnen et al. (2023) applied their method to a suite of N-body models of isolated barred spiral galaxies. By comparing the results to Ωp calculated using time-centred finite-differences from three consecutive snapshots, they found that their method is reliable and accurate, provided that the bar region is well-determined and a smooth window function is utilised.
2.2. The Tremaine-Weinberg method
The second method we use is the Tremaine-Weinberg (TW) method (Tremaine & Weinberg 1984). As mentioned above, the main assumption of the method developed is that the density and kinematics of the tracer obey the continuity equation (Eq. (1)). The method is designed for galactic systems in equilibrium and with a single pattern (see its application to a simulated disc with a bar perturbation in Appendix A). The best kinematic tracer satisfying this condition is the old stellar population of galaxies. Estimates of Ωp of galaxies using the TW method were thus mostly obtained from absorption lines of stellar populations, as observed by means of optical long-slit or integral field spectroscopy (e.g. Merrifield & Kuijken 1995; Gerssen et al. 1999; Aguerri et al. 2003, 2015; Debattista & Williams 2004; Cuomo et al. 2019), although emission lines of interstellar gas for a few galaxies were used as well (e.g. Bureau et al. 1999; Hernandez et al. 2005; Rand & Wallin 2004; Meidt et al. 2008; Chemin & Hernandez 2009; Williams et al. 2021).
As shown in Gaia Collaboration (2021b) and Jiménez-Arranz et al. (2023), we can select millions of stars in the LMC disc with proper motions, from which the in-plane components vx and vy can be measured. Therefore, Eq. (2) can be solved directly for the LMC, unlike any other galaxies. Integrating it with respect to x yields:
These integrals can be numerically solved by discretising the space, namely, by summing the surface density and kinematics along x-wedges at different y positions (hereafter, pseudo-slit). Then, the pattern speed Ωp can be determined by doing a linear fit of ⟨vy⟩ vs. ⟨x⟩. Interestingly, a permutation of x and y can be done in Eq. (4), so that Ωp can also be estimated from ⟨vx⟩ vs. ⟨y⟩. To keep the analysis simple, we defer to another study the test of this alternative derivation.
The continuity assumption is independent on the choice of the Cartesian frame. This implies that we can choose arbitrarily the orientation of the reference x − y plane by rotating it around the z-axis, and measure the TW integrals of Eq. (4) at various orientations. Only astrometric data can make such analysis possible, unlike spectroscopic data. This is thus a good opportunity for us to assess for the first time the effect of the viewing angle of the bar in the disc plane on the TW integrals of Eq. (4) (Sect. 3), and on the LMC bar pattern speed (Sect. 4).
To get an unbiased value of the bar angular speed, we must restrict the linear regression by selecting exclusively the integrals from the bar region. This is defined as the points located out to the radius R1 obtained with the Dehnen method (Sect. 2.1), and the best fit of the pattern speed Ωp arises from selecting the integrals with (⟨x⟩2 + y2)1/2 < R1, thus avoiding the outer disc that mostly traces the spiral structure, which is expected to show a lower angular speed from the bar (see e.g. Merrifield et al. 2006, with the example of the grand design spiral NGC 1068).
Additionally, the LMC is the only galaxy for which both transverse and LoS kinematics are available. Because of such a lack of galaxies having observed planar kinematics, Tremaine & Weinberg (1984) have historically adapted Eq. (4) to work with sky plane coordinates (X, Y) = (x, y cos i) and the LoS velocity Vlos = vy sin i + vz cos i, where i is the galaxy inclination, leading to:
with ⟨Vlos⟩ and ⟨X⟩ being the intensity-weighted means of the LoS velocity and position of the tracer, respectively. These integrals can numerically be solved by discretising the space, selecting the disc areas parallel to the disc major axis, yielding a value of ⟨X⟩ and ⟨Vlos⟩ for each Y. Unlike the previous case, we cannot vary the orientation of the reference frame here because the LoS kinematics is firmly attached to the unique position angle of line of nodes (disc major axis). Then, Ωp sin i is the result of the linear fit of ⟨Vlos⟩ vs. ⟨X⟩. Similarly to the planar velocities, only ⟨X⟩ and ⟨Vlos⟩ from the bar region must be considered, thus by selecting the TW points inside the sky region where R1 is projected. For clarity, we hereafter refer to the version of the TW method involving the planar velocities as the In-Plane TW method (IPTW, Eq. (4)), and the one using Vlos data as the LoS TW method (LTW, Eq. (5)).
2.3. Bisymmetric model of the tangential velocity
In Gaia Collaboration (2023a), indirect measurements of the pattern speed Ωp were performed by searching for the corotation radius Rc within a simulated barred galaxy. Here, a second order asymmetry of the tangential velocity field Vϕ was fitted. Variations at low radius of the phase angle ϕ2,kin of the bisymmetry were then studied to locate Rc. Ignoring the first-order perturbation (lopsidedness), the Fourier decomposition Vϕ, mod is given by:
where V0 and V2, which only depend on the galactocentric radius R, are the rotation curve of the disc and the amplitude of the bisymmetric perturbation, respectively. Despite its empirical nature, this method is based on the principle that the bar pattern heavily influences, if not entirely governs, the structure of stellar orbits and the velocity field within Rc. In the ideal case of only a barred perturbation, with no spiral arms, the periodic orbits inside corotation, called the x1 family, are elongated with the bisymmetric perturbation (they are the back-bone of bars), while beyond corotation, the orbits are elongated perpendicularly to the bar major axis (Contopoulos & Papayannopoulos 1980; Contopoulos & Grosbol 1989). Inside corotation, the tangential velocity is maximum (minimum) perpendicularly to (along) the direction of elongation of the orbits, and the opposite outside corotation. We thus expect ϕ2,kin roughly constant within the bar, then changing significantly its orientation near corotation, by an angle of ∼90°. This variation can be even larger in presence of a winding spiral structure beyond corotation which perturbs the orbits and kinematics as well. Furthermore, the possible existence of other resonances before corotation, like the ultra-harmonic one (Buta & Combes 1996), and the development of spiral arms before or near the bar ends complicate the shapes, orientations and kinematics of periodic orbits inside corotation. In these cases, we can also expect a variation of ϕ2,kin between the bar ends and the corotation radius. Once Rc is determined near the location where ϕ2,kin changes significantly, we can infer Ωp with the angular velocity curve, Ω(R) = V0/R, since stars move at the same speed as the bar at Rc, thus Ωp = Ω(Rc). One should note that the harmonic decomposition is reminiscent of the bisymmetric flow model applied to LoS kinematics of barred spirals (Spekkens & Sellwood 2007).
Gaia Collaboration (2023a) applied their recipe to data from the Third Data Release of Gaia (DR3, Gaia Collaboration 2021a, 2023b). They evidenced a region of steep change of phase angle of the kinematic bisymmetry of ∼70° over a range of 2 kpc. A comparison with a test-particle simulation in which the Gaia errors model was propagated made them find the MW corotation at the radius where ϕ2, kin is at the minimum, just after the location of the sharp transition of phase angle mentioned above. Gaia Collaboration (2023a) estimated a Galactic bar orientation with respect to the Galactic Center-Sun direction of ∼20°, the Galactic bar corotation at R ∼ 5.4 kpc, and a pattern speed of ∼38 km s−1 kpc−1, in good agreement with previous measurements involving a modified version of the TW method (Bovy et al. 2019).
3. Testing the methods with simulations
In this section we use a snapshot of a simulation of a MW-mass galaxy, with no external perturbations, and a snapshot of a simulation of a LMC-like system interacting with a SMC-mass and MW-like systems to apply and validate the Dehnen method, the two variations of the TW method, and the BV model.
First, we use the B5 N-body simulation of an isolated barred galaxy from Roca-Fàbrega et al. (2013), which consists of a live disc of 5 million particles and a Toomre parameter of Q = 1.2, and a live NFW halo. The disc to halo mass ratio is the appropriate so that the simulation develops a strong bar and two spiral arms which are transient in time. The snapshot we use has a counter-clockwise rotating bar with a pattern speed of Ωp = 21.5 ± 0.1 km s−1 kpc−1 determined as the average of finite-differences on the rate of change of the phase angle of the bar major axis in three consecutive snapshots over the radial range of the bar. The quoted uncertainty on the bar pattern speed refers to the standard deviation of the pattern speeds derived from the three successive snapshots. The simulation time step is 16 Myr, representing 6% of the bar period, which is appropriate to infer a robust bar pattern speed. The pattern speed places the bar corotation resonance at Rc = 8.3 ± 0.05 kpc, computed as the radius at which the angular frequency curve, Ω(R) = V0/R, of the particles is equal to the bar pattern speed, with V0 given by the bisymmetric model (see Eq. (6)). It corresponds to a fast bar with a rotation rate of 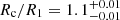 .
.
Second, we use the K6 simulation of the KRATOS (Kinematic Reconstruction of the mAgellanic sysTem within the OCRE Scenario) suite, a comprehensive suite of 11 sets of pure N-body simulations of isolated or single-interacting galaxies, for a total of 28 models (Jiménez-Arranz et al., in prep.). Hereafter, we refer to the K6 simulation of the KRATOS suite as the KRATOS simulation. The simulation we use in this paper models both an LMC-like and an SMC-mass system in the presence of a MW-mass system. We model the LMC-like system as a stellar exponential disc of 1.2 M stars embedded in a live dark matter NFW halo. We consider a disc and DM halo with a mass of 5 × 109 M⊙ and 1.8 × 1011 M⊙, respectively, in agreement with observations as discussed in Lucchini et al. (2022, and references therein). The disc’s Toomre Q parameter is 1.0, namely slightly gravitationally unstable. The SMC-mass system is modelled as a simple NFW halo. Both dark matter and stellar particles in the SMC-mass system are generated at once following the NFW profile with a total mass of 1.9 × 1010 M⊙ (Lucchini et al. 2022, and references therein). For the MW-mass system, we only model its DM content since we are not interested in its stellar component but only in its gravitational effects on the LMC-SMC-like system. The DM mass of the MW-mass system is considered to be 1012 M⊙ (Bobylev & Bajkova 2023, and references therein). In this work, we analyse a snapshot of the simulation taken just after the LMC-like system suffered a second close encounter with the SMC-mass system that generated an off-centred and out-of-equilibrium bar in the LMC-like system. The bar has a counter-clockwise rotation with a pattern speed of Ωp = 17.2 ± 1.6 km s−1 kpc−1 measured as the difference of the rate of change of the phase angle of the bar perturbation, using three consecutive snapshots with a time interval of 2 Myr. The pattern speed places the bar corotation resonance at 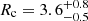 kpc. It corresponds to a bar rotation rate of
kpc. It corresponds to a bar rotation rate of 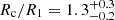 .
.
Figure 1 shows the surface density (left column), the radial velocity (middle column) and the residual tangential velocity maps for the B5 and KRATOS simulations (top and bottom rows, respectively). The map of the residuals has been obtained by subtracting the rotation curve to the Vϕ map. In the surface density plot, the B5 simulation shows a strong bar accompanied by two strong spiral arms. In the KRATOS simulation, we observe a strong bar accompanied by a broken interacting arm. The radial and residual tangential velocity maps show the characteristic kinematic imprint of the bar, namely a quadrupole pattern. Larger velocities are observed in the B5 simulation than in the KRATOS simulation (see also Sect. 3.3).
 |
Fig. 1. Application of the Dehnen method to B5 (top) and KRATOS (bottom) simulations. Surface density (left), median radial velocity map (centre) and median residual tangential velocity map (right). The bar region identified by Dehnen method (see values in Table 1) is indicated by green dashed circles. The grey dashed lines trace the bar minor and the major axes. |
We show first the results when applying the Dehnen method (Sect. 3.1) because it defines the bar region in the simulations, which are used by the TW method (Sect. 3.2). Finally, the results corresponding to the BV method are presented in Sect. 3.3.
3.1. Results of the Dehnen method
Dehnen et al. (2023) made their numerical tool to infer some bar properties from a single simulation snapshot available to the community. We thus used the Python code they provide, and, for both simulations we have set various parameters. We fixed a minimum and maximum number of particles in the radial bins to 104 and 5 × 104 (respectively) for the B5 and KRATOS simulations. We adopted a maximum size of the sampling of the radial bins of 1.25 kpc, a minimum ratio of the strength of the surface density in the bar region of Σ2/Σ0 = 0.1 (Σ0 and Σ2 being the amplitudes of the axisymmetric and bisymmetric surface density components), a maximum angular width of the bar of 10°, a minimum size of the bar of 1.25 kpc, respectively, with a minimum required number of particles in bar region of 1000. Following Dehnen et al. (2023) recommendations, we assumed a top-hat weighting function to constrain Σ2/Σ0 and ϕb in each bin from the surface density, and a smooth window to estimate Ωp and the bar orientation in the entire bar region. We refer the reader to Dehnen et al. (2023) for more complete information of the code. The application of the Dehnen method to a simulated disc with a barred perturbation and no spiral structure is given in Appendix A.
Figure 1 shows the performance of the Dehnen method with both simulations. Left, centre and right panels show the surface density, the median radial velocity map and median residual tangential velocity map, respectively. In every panel, we highlight the bar region identified by the method by green dashed circles, with inner and outer circles corresponding to R0 and R1, respectively. The grey dashed lines trace the bar minor and the major axes found by the method. For both simulations ϕb is in agreement with the orientation observed in the surface density, and separates remarkably the quadrupole patterns in two parts. For the B5 simulation (top panels), the method infers a value of Ωp = 21.2 ± 0.1 km s−1 kpc−1, in good agreement with the value found using finite-differences. For the KRATOS simulation (bottom panels), the method infers a value of Ωp = 16.5 ± 0.1 km s−1 kpc−1, also in agreement with the value obtained using finite-differences. Values are summarised in Table 1. These tests are thus another way to validate the method, in agreement to those performed in Dehnen et al. (2023). It can be concluded that, under ideal conditions in which data are devoid of observational and numerical noise, the Dehnen method successfully recovers the imposed values of Ωp.
Results of the Dehnen and the BV methods applied to B5 and KRATOS simulations, compared to the reference value (obtained using finite-differences).
This method yields a corotation radius of 8.3 kpc for the B5 simulation, corresponding to the ground-truth value. It gives a corotation radius of 4.0 kpc for KRATOS, which is very close to the ground-truth value.
3.2. Results of the TW method
As mentioned above, the applicability of the TW method in either of the two versions is designed for galaxies in equilibrium and, moreover, with a single pattern speed. We can nevertheless evaluate their performance by applying them to the simulations of isolated and interacting spiral discs. Application of the methods to a simulated disc with a barred perturbation and no spiral structure is given in Appendix A.
Hereafter, the domain [−∞/ + ∞] of the numerical integration of Eqs. (4) and (5) is the maximum extent of the disc allowed inside each pseudo-slit parallel to the x-axis at a given y coordinate, or the line-of-nodes for the LTW method. Within this maximum range, the integrals have converged to stable values. Furthermore, we investigated the impact of the width of the pseudo-slits. Within a range of 50−500 pc, we found that the width has no effect on the results described below. Only the uncertainties on Ωp are seen to increase for wider pseudo-slits, by a factor of 3.5 from 50 pc to 500 pc width. In this Section, we show the results obtained for a width of 200 pc.
3.2.1. Results of the LTW method
We simulated a galaxy observation by projecting the particles from each simulation onto a galactic plane with arbitrary inclination (i) and position angle (PA) of the semi-major axis of the receding half. For the result described here, we adopted a disc projected with PA = 60°, and inclinations of i = 25°, 45° and 75°. Assuming a mock disc distance of 10 Mpc, which is well suited to mock galaxies on which the LTW method can been applied, the maps of the projected density and LoS velocity have 512 × 512 pixels sampled at 1″ (∼50 pc pix−1). We do not investigate the impact of varying the distance of the mock disc on the results. We chose the x-axis aligned with the line of nodes, so that the reference of the azimuthal angle ϕ = 0° is along the semi-major axis of receding disc half. The small angle approximation can be applied, and the LoS kinematics of each particle simply resumes to Vlos = Vz cos i + Vy sin i = Vz cos i + (VR sin ϕ + Vϕ cos ϕ) sin i. The adopted velocity in each pixel of the map is the mean of the Vlos of the particles. The LTW integrals of Eq. (5) are performed at each Y-coordinate, selecting all pixels from the maps within pseudo-slits parallel to the disc major axis. The derivation of the slope Ωp sin i is performed using the ⟨X⟩−⟨Vlos⟩ points located inside the region encompassing the projected value of the bar radius R1 from in Table 1.
We investigated the impact of the variation of the orientation of the Cartesian frame on the results, by rotating the reference x and y axes around the z-axis in the simulation. The rotation of the Cartesian frame before projection on the sky plane allows the TW integrals to view the bar and spiral perturbations through various angles. In practice, this is achieved by adding a Δϕ to the angular position ϕ of each particle in the disc plane, from which new x and y positions are derived. Then, new density maps and LoS kinematics and Ωp can be inferred. A range of Δϕ spanning 180° has been probed, with a step of 3°. Figure 2 (upper panel) shows the resulting bar pattern speed as a function of the frame orientation Δϕ for the case i = 45° only (red open symbols) and the B5 simulation. The quoted uncertainties correspond to the 1σ error of the covariance matrix of the fitting. We highlight the frame orientations parallel and perpendicular to the bar major axis as orange and navy vertical lines, respectively. Results for the KRATOS simulation are shown in the lower panel of Fig. 2 for the three assumed inclinations.
 |
Fig. 2. Variation of Ωp as as function of the reference frame orientation Δϕ. Results for the B5 and KRATOS simulations are shown in the upper and lower panels, respectively. Results of the IPTW method are shown as open symbols, while those of the LTW method are drawn as a solid line (for the i = 45° case, upper panel), and as dotted, solid and dashed lines (for the i = 25, 45 and 75° cases, lower panel). Horizontal dashed green lines are the ground-truth bar pattern speeds. The vertical orange (navy) vertical line corresponds to the frame orientation where the x-axis of the disc lies along the major axis of the bar (y-axis, respectively). |
The variation of the pattern speed with Δϕ is very important in both simulations, and makes it rarely consistent with the ground-truth values (shown as horizontal green dashed lines), whatever the adopted disc inclination. The strongest disagreement occurs at frame orientations very close to the major axis of the bar, and ∼15° before its minor axis. For the B5 simulation, the LTW results are consistent with the real value only at frame orientations Δϕ ∼ 70 − 75°, thus when the x-axis in the galaxy plane makes an angle of ∼55 − 60° with respect to the bar major axis. The LTW pattern speeds agree with the ground-truth value only occasionally for the KRATOS simulation, within the quoted uncertainties (shown as shaded areas). A strong dependency with the inclination of the disc is observed. The best agreement with ground-truth is for a mock disc at i = 45°, for 7 ° < Δϕ < 38°, thus when the x-axis in the galaxy plane makes an angle of ∼30 − 60° with respect to the bar major axis. Another interesting result is that no symmetry around the bar minor axis is observed, indicating that having a wide range of agreement with ground-truth is unlikely (see Sect. 3.2.2 for more details).
3.2.2. Results of the IPTW method
As in the LTW method, we varied Δϕ between 0° and 180° to study the dependency of the in-plane TW integrals of Eq. (4) with the frame orientation. Figure 3 shows results for the B5 simulation for two examples of frame orientations1. The upper row corresponds to the original frame orientation, with Δϕ = 0°, while in the bottom row, the x-axis is chosen aligned with the bar major axis, corresponding to a frame orientation of 16.5°, which corresponds to Δϕ = 16°. The left panels show the surface density maps, with the bar region outer radius R1 identified with the Dehnen method highlighted by a green dashed circle. The coloured dots represent the ⟨x⟩ integrals for each slice in y, with greener (redder) colours for larger (smaller) values of |y|. In the case where the bar major axis is parallel to the x-axis, ⟨x⟩ is observed close to the x = 0 axis in the bar region, thus rather aligned with the bar minor axis. In the case where the bar major axis is 30° rotated counter-clockwise with respect to the x-axis, ⟨x⟩ varies significantly in the bar region, almost tracing the bar major axis.
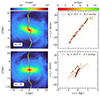 |
Fig. 3. Application of the IPTW method to B5 simulation. Top: bar major axis at ϕb = 163.5°, as in the original snapshot and shown in Fig. 1. Bottom: after applying a rotation of Δϕ = 16.5° to put the bar major axis along the x-axis. Left: surface density where the bar region (obtained using Dehnen method) is indicated by the green dashed circle. A scatter plot representing the value of ⟨x⟩ for each slice in y is overlapped. The scatter plot varies its colour as function of the distance to the centre in the y-axis, being the red points close to the centre and the green close to the external parts of the galaxy. Right: scatter plot of the Tremaine-Weinberg integrals ⟨x⟩ and ⟨vy⟩ for the different slices in the y-axis. The colour of the scatter plot is the same in both left and right panels. In the right panel, the points with a black circle are inside of the bar region and, therefore, the only considered for fitting Ωp. |
The right panels show the TW integrals, ⟨x⟩ vs. ⟨vy⟩, with the same colour code for the various y as those in the left panels. The points with a black circle are those located inside R1, while the rest of the points are the ones outside the bar region, therefore, not considered for fitting Ωp. In the case with Δϕ = 0°, thus the original frame orientation, there is a clear linear trend with small dispersion for points inside the bar region, as shown by the dashed straight line fit. In the case where the bar major axis is parallel to the x-axis, several linear trends are observed, hence a significantly larger dispersion. The fitted slope of the TW integrals is 10.3 ± 2.1 km s−1 kpc−1, as shown by a dashed straight line. However, none of these values are consistent with the real pattern speed of 21.5 ± 0.1 km s−1 kpc−1, or the value of 21.2 ± 0.1 km s−1 kpc−1 from the Dehnen method.
Figure 4 presents results of the IPTW method for the KRATOS simulation. Again, we show here two different reference frame orientations: the original one, with Δϕ = 0° (top row) and the one with the bar major axis parallel to the x-axis, Δϕ = 156° (bottom row). In the first case, there is a linear trend and the IPTW recovers a bar pattern speed Ωp = 15.5 ± 1.7 km s−1 kpc−1, compatible with the real pattern speed. In the second case, the TW x-integrals are perfectly aligned with the bar major axis, as expected in the presence of only a bar potential. The ⟨x⟩ values are then very close to zero, so there is not a clear trend in this case (it would give similar results when the TW integrals are evaluated at another viewing angle along the bar minor axis). We recovered a clockwise pattern speed of Ωp = −4.2 ± 4.0 km s−1 kpc−1 which differs from the real value. We note also that in this configuration, the linear trend is more scattered, not as clear as the configuration from the upper panel, in agreement with what was seen with for the B5 simulation.
We then assess whether there is (or not) a favoured frame orientation where the IPTW method works better, by plotting the fitted Ωp as a function of Δϕ (filled blue symbols in Fig. 2). Qualitatively, the IPTW and LTW methods show similar trends: the agreement with the ground-truth bar pattern speed is rarely observed, no symmetry with respect to the bar major axis is found, and stronger discrepancies are near the positions of the major and minor axes of the bar. The B5 simulation (upper panel) shows that Δϕ ∼ 135° is also a location of stronger disagreement, which was not observed for the LTW method. Since the IPTW method works directly with coordinates and velocities in the Cartesian frame of the disc, no variation with inclination needs to be evaluated here. It is interesting to note that the LTW pattern speeds with better agreement with the IPTW method are for the intermediate inclination of 45° (lower panel for the KRATOS simulation). It is important to remind that the Dehnen method does not show such systematic variation with Δϕ, as its results are invariant with respect to the frame orientation.
The median and mean absolute deviation of all the IPTW values are 17.9 ± 1.9 km s−1 kpc−1 and 11.0 ± 3.7 km s−1 kpc−1 for the B5 and KRATOS simulations, respectively. We note that the difference is larger in the KRATOS simulation. While the B5 simulation presents a strong spiral pattern in the outer disc, the KRATOS simulation additionally is not in equilibrium.
Finally, we can estimate the incidence of finding a bar pattern speed consistent with the ground-truth value for both the LTW and IPTW methods, with the two simulations. We define this likelihood as the number of frame orientations where the measured and real Ωp agree within the quoted (1σ) uncertainties on measured and ground truth values. For the B5 simulation, the IPTW and LTW methods give a correct Ωp in 5% and 8% of the cases only. For the KRATOS simulation, the incidence is 37% (IPTW case), 57% (LTW case at i = 25°), 48% (LTW case at i = 45°) and 42% (LTW case at i = 75°). Larger inclinations are thus less prone to the LTW method. More generally, our two sets of simulations show it is highly unlikely to find a consistent Ωp by means of the TW method. It is also hard to reconcile the strong variations with Δϕ seen here, i.e the bar orientation with respect to the disc x-axis, with the wide range of “allowed” orientations quoted in other studies (e.g. Zou et al. 2019, see also Sect. 5 for the LMC).
3.3. Results of the bisymmetric velocity model
Bayesian inferences of Fourier coefficients to the tangential velocities were performed in radial bins through Markov chain Monte Carlo fits, using the Python library Emcee (Foreman-Mackey et al. 2013). The model is fitted to a map of Vϕ (pixel size of 50 pc), where the velocity at each pixel of the map is the median of the velocity distribution from all particles/stars inside the given pixel. Defining the residual velocity as Vϕ, res = Vϕ − Vϕ, mod, the conditional likelihood function at each radial bin is expressed by:
where V0, V2 and ϕ2 are as in Eq. (6), 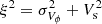 , σVϕ are the Vϕ uncertainties, Vs is the scatter of the modelling, and npix the number of pixels of the map inside the corresponding radial bin at which parameters are fitted. No uncertainties are measured while making the velocity map, thus σVϕ = 0. Therefore, measuring Vs is an indirect way to take into account the lack of uncertainties (Hogg et al. 2010).
, σVϕ are the Vϕ uncertainties, Vs is the scatter of the modelling, and npix the number of pixels of the map inside the corresponding radial bin at which parameters are fitted. No uncertainties are measured while making the velocity map, thus σVϕ = 0. Therefore, measuring Vs is an indirect way to take into account the lack of uncertainties (Hogg et al. 2010).
The left column of Fig. 5 shows the results of the model to the B5 simulation. In the top panel, we show the rotation curve of the simulated disc (gray solid line, measured as the median velocity in the map a each R), the fitted axisymmetric velocity component (black solid line, V0), the amplitude of the bisymmetry V2 (blue dashed line), and the scatter in Vϕ, res (orange dotted line, Vs). The bar strength is maximum at R ∼ 2 kpc, reaching more than 50% of V0. Within R = 5 kpc, V0 and the median rotation curve can differ by up to ∼20 km s−1, which indicates the significant impact of the bisymmetry on the rotation curve. In the middle panel, we show the phase angle ϕ2, kin of the bar recovered from the modelling of the tangential velocity map. The phase angle of the bar is well recovered by the bisymmetric model at low radius, then smoothly varies. At R ∼ 7.5 kpc, an abrupt change in ϕ2, kin is observed. Following prescriptions given in Sect. 2, we can identify the corotation radius just after the steep change of phase angle, Rc = 8.0 ± 0.5 kpc, which corresponds to a bar pattern speed is 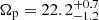 km s−1 kpc−1 (bottom panel, the Ω curve being derived from the solid curve of the upper panel, namely the 0th order Fourier coefficient). This agrees with the value computed using finite-differences. By construction, the bisymmetric velocity model is invariant with the frame orientation, as ϕ2, kin are shifted by Δϕ when a rotation of Δϕ is applied to the x − y plane.
km s−1 kpc−1 (bottom panel, the Ω curve being derived from the solid curve of the upper panel, namely the 0th order Fourier coefficient). This agrees with the value computed using finite-differences. By construction, the bisymmetric velocity model is invariant with the frame orientation, as ϕ2, kin are shifted by Δϕ when a rotation of Δϕ is applied to the x − y plane.
 |
Fig. 5. Results of the BV model of the stellar tangential velocity map of the B5 (left panels) and KRATOS (right panels) simulations: amplitude (upper panels), phase angle, ϕ2,kin of the Fourier modes (middle panels), and angular frequency Ω (bottom panels). In the top panels, the black solid line is the fitted axisymmetric velocity component V0 (the rotation curve), the grey line is the median velocity (initial value for the model), the blue dashed curve is the amplitude of the tangential bisymmetry V2, and the orange dotted line is the scatter of the model Vs. In the middle and bottom panels, the vertical light coral area and dashed line shows the adopted bar corotation radius, Rc = 8.0 ± 0.5 kpc for B5 and Rc = 3.3 ± 0.5 kpc for KRATOS simulations. In the bottom panel, the black solid line is the angular velocity derived from V0, while the horizontal green area and dotted line shows the corresponding bar pattern speed |
Similarly, in the right panels of Fig. 5, we show the results of applying this method to the KRATOS simulation, the value for corotation we derive is Rc = 3.3 ± 0.5 kpc, and the bar pattern speed is 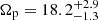 km s−1 kpc−1, which is consistent with the true value of 17.2 ± 1.6 km s−1 kpc−1, within the quoted uncertainties. The values are summarised in Table 1. This method yields a bar rotation rate of Rc/R1 = 1.1 and 1.2 for the B5 and KRATOS simulations, respectively, in agreement with the ground-truth values.
km s−1 kpc−1, which is consistent with the true value of 17.2 ± 1.6 km s−1 kpc−1, within the quoted uncertainties. The values are summarised in Table 1. This method yields a bar rotation rate of Rc/R1 = 1.1 and 1.2 for the B5 and KRATOS simulations, respectively, in agreement with the ground-truth values.
4. Measuring the LMC bar pattern speed
In the previous section, we assess the performance, robustness and limitations of the methods when applied to simulated data. The TW method, in both versions using either LoS or in-plane velocities, shows a clear dependence of the measured pattern speed on the frame orientation, and significant differences with the ground-truth values. The recovered value can be lower or higher than the simulated speed when both bar and spiral arms intervene in the simulation. These results already warn us to take the value of the LMC pattern speed inferred from the TW method with caution.
The LMC stars we use in this study are those in the NN complete sample of Jiménez-Arranz et al. (2023). The selection of LMC stars was based on a supervised neural network classifier, using full astrometric and photometric data from Gaia DR3. Based on this classifier, the authors select three samples of candidate LMC stars with different degrees of completeness and purity. The NN complete sample corresponds to the sample that prioritises not missing LMC stars at the price of a possible increased MW contamination. It contains 12 116 762 stars. The sample is dominated by older stellar populations (see, e.g. Fig. 3 from Gaia Collaboration 2021b), thus fulfilling the continuity equation necessary to the TW and Dehnen methods. Combining the selection function of the Gaia parent catalogue (Cantat-Gaudin et al. 2023) and the selection effects from the generation of the LMC NN complete sample (estimated as in Castro-Ginard et al. 2023), the completeness estimates of our sample are above 50% in the bar region for G = 19 − 19.5 mag. As seen in Fig. 6 of Jiménez-Arranz et al. (2023), 60% of stars in the LMC NN complete sample have magnitude below G < 19.5. To better estimate the completeness and purity of the LMC NN complete sample, and their effect on the inner kinematics, a more detailed study of the selection function is required, which is beyond the scope of this paper.
For each star, we applied the coordinate transformation detailed in Jiménez-Arranz et al. (2023) to express the deprojected positions and velocities in the in-plane coordinate system of the LMC, using the inclination, position angle, systemic velocity, and position of the LMC centre given in Jiménez-Arranz et al. (2023), assuming all stars lying in the z = 0 plane. The LMC centre used is the same as in Gaia Collaboration (2018); Gaia Collaboration (2021b), which corresponds to the LMC photometric center (van der Marel 2001). The infinitely thin disc approximation is inherent to any studies of the kinematics of disc galaxies because the 3D position space of stars in galaxies is never available, unlike stars in the MW (e.g. Gaia Collaboration 2023a) or a few variable young stars in the LMC (Ripepi et al. 2022).
Figure 6 shows the results of the application of the Dehnen method to the LMC. The left, middle, and right panels show the surface density, the median Galactocentric radial velocity, and residual of the median tangential velocity, respectively. Both the radial and residual tangential velocity maps show the imprint of a rigidly rotating bar in the galactic centre, as clear hints of x1 stellar orbits (see also Gaia Collaboration 2021b; Niederhofer et al. 2022; Jiménez-Arranz et al. 2023). The quadrupole pattern is the natural reflex of the motion of stars in elliptical orbits present in the bar potential. In contrast to the simulations, the method was not able to find the bar region [R0, R1] on its own, probably due to the fact that the quadrupole is not perfectly symmetric, or that the contrast of the bar region with respect to the disc is not as clear as in simulations because of the presence of dust lanes and spiral arms at low radius. We solved this issue by analyzing the outputs of the numerical code of Dehnen et al. (2023) which, in addition to the bar parameters and pattern speed, provide results of a second order Fourier model of the stellar density. Figure 7 shows the amplitude Σ2 of the m = 2 Fourier coefficient, relatively to the axisymmetric density Σ0, and the phase angle ϕ2 of the bisymmetric density perturbation. In the upper panel, a peak of the relative strength ∼0.2 is observed at R ∼ 2 kpc. This amplitude is comparable to that at larger radius, meaning a small contrast between the LMC bar and the spiral arm(s) within the selected sample of stars. This probably explains why the Dehnen method cannot establish properly the bar region in its automated way. The phase angle (bottom panel of Fig. 7) has a constant value of ϕ2 ≃ 15 − 20° from R = 0.75 kpc to R ∼ 2.3 kpc. We can establish that the bar region is therefore [R0, R1]=[0.75, 2.3] kpc. Within this region, the Dehnen method gives a value of Ωp = −1.0 ± 0.5 km s−1 kpc−1, thus corresponding to an almost non-rotating stellar bar, seemingly in counter-rotation.
 |
Fig. 6. Application of the Dehnen method to the LMC NN complete sample. Surface density (left), median radial velocity map (center) and median residual tangential velocity map (right). The bar region identified by Dehnen method is indicated by green dashed circles, [R0, R1]=[0.75, 2.3] kpc. The grey dashed lines trace the bar minor and the major axes. |
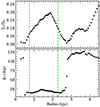 |
Fig. 7. Application of the Dehnen method to the LMC NN complete sample. The relative m = 2 Fourier amplitude (top) and orientation (bottom). The bar region identified by the method is indicated by green dashed vertical lines, [R0, R1]=[0.75, 2.3] kpc. |
Now for the TW method, we adopted an pseudo-slit length and width of [ − ∞, +∞] and 50 pc, respectively. For both versions of the method, the slopes of the integrals are fitted using only points located inside the bar radius (for the IPTW case) and projected radius (for the LTW case), as defined by R1 = 2.3 kpc.
In Fig. 8, we show the stellar LoS velocity field corrected for the systemic motion of the LMC NN complete Vlos sub-sample, which contains 30 749 stars. These are predominantly the AGB stars from Gaia Collaboration (2021b). This is in good agreement with the LoS velocity field traced by carbon stars (van der Marel et al. 2002). We apply the LTW method to this LoS velocity map, as described in Sect. 2.2, with pseudo-slits parallel to the line-of-nodes. Figure 9 shows the linear fit to the LTW integrals, yielding a bar pattern speed of Ωp = 30.4 ± 1.3 km s−1 kpc−1, using an inclination of i = 34°.
 |
Fig. 8. Stellar line-of-sight velocity field of the LMC NN complete Vlos sub-sample, corrected from the systemic motions. Data are from Gaia RVS (Katz et al. 2023; Jiménez-Arranz et al. 2023). |
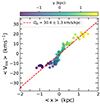 |
Fig. 9. Result of the TW method applied to the LoS velocity field of the LMC from Fig. 8. Only points within the radius R1 defined by the Dehnen method are shown. The red dashed line shows the result of the linear fit to the points, Ωp sin i, with Ωp = 30.4 ± 1.3 km s−1 kpc−1. |
Figure 10 shows the results of the IPTW method applied to the LMC Cartesian velocity fields (not shown here, but obtained from the cylindrical velocities shown in Fig. 6). We recover as many values as adopted orientations Δϕ of the Cartesian frame in the LMC plane. Interestingly, a good agreement is seen between the LTW Ωp (open red dot at Δϕ = 0°) and the IPTW Ωp inferred at this orientation. However, and unsurprisingly, the estimated values of the IPTW method display a strong variation with the frame orientation. A wide range of possibilities is found for the LMC Ωp, from 0 to 55 km s−1 kpc−1. Note also the clear correlation between the bar major and minor axis with the orientations where the shape of the Ωp curve vary significantly. The median of all IPTW values seen in this graph is 23 ± 12 km s−1 kpc−1, adopting here the mean absolute deviation as the uncertainty.
 |
Fig. 10. Results of applying the LTW and IPTW to the LMC NN complete sample. The open red dot shows the bar pattern speed recovered with the LTW method. The blue dotted curve shows the bar pattern speed obtained using the IPTW with different frame orientations Δϕ. The dashed purple (brown) line shows the bar pattern speed obtained using the Dehnen (BV) method. |
Finally, in Fig. 11 we show the results of the BV method applied to the LMC tangential velocity map of Fig. 6. The LMC rotation curve from the NN complete sample (upper panel, light grey) is very similar to the 0th order Fourier component of the BV model (black solid line). The amplitude of the LMC bar perturbation is stronger at R = 0.75 kpc (blue line). The orange dotted line showing the scatter in the residual tangential velocity is often larger than the bisymmetric mode. It thus shows that the bar is not the only perturber in the LMC disc, but this does not prevent the bisymmetry from being detected efficiently by the method. Note that seeing the scatter in the model stronger with radius is reminiscent to the finding of the KRATOS simulation (top right panel of Fig. 5). This is consistent with the observed complex stellar morphology in this region. A roughly constant value of ϕ2,kin ≃ 15 − 20° is seen out to R = 2 kpc, in good agreement with the phase angle of the bisymmetry of the density (Fig. 7, bottom panel), followed with a smooth decrease out to R = 3.95 kpc, as evidence of the impact of arms in the kinematics even in the bar region. This radius is the location from where the amplitude V2 starts to increase. At this radius, ϕ2, kin changes by ∼100° to recover a constant value comparable to the bar phase angle at low radius. Following prescriptions from the numerical modelling, we adopt the radius just after the sharp transition of phase angle as the bar corotation radius, placing the LMC bar corotation at Rc = 4.20 ± 0.25 kpc. Relative to the angular velocity curve Ω (solid line in the bottom panel of Fig. 11), it corresponds to a LMC bar pattern speed of 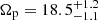 km s−1 kpc−1.
km s−1 kpc−1.
 |
Fig. 11. Results of the BV model of the stellar tangential velocity map of the LMC NN complete sample: strength (upper row) and phase angle (lower row, ϕ2, kin) of the bisymmetric Fourier mode. The black solid line is the fitted axisymmetric velocity component (the rotation curve), the grey line is the median velocity (initial value for the model), the blue dashed curve is the strength of the tangential bisymmetry, and the orange dotted line is the scatter of the model. The vertical light coral area and dashed line shows the adopted bar corotation radius of the LMC, Rc = 4.20 ± 0.25 kpc. In the bottom panel, we show the angular velocity of the LMC as a function of radius. The vertical light coral area and dashed line show the corotation radius of the bar. The horizontal green area and dotted line shows the corresponding bar pattern speed |
5. Discussion
Table 2 provides a summary of the LMC bar properties obtained with the different methods in the previous section. At first glance, it is difficult to conclude the pattern speed of the stellar bar of the LMC given the large range of values. Only a few studies have provided estimates of the LMC bar pattern speed. Shimizu & Yoshii (2012) derived a value for the bar pattern speed based on the idea that the Shapley Constellation III star forming region (Shapley 1951) is located at the L4 Lagrangian point of the non-axisymmetric bar potential rotating frame. The authors found Ωp = 21 ± 3 km s−1 kpc−1. Unfortunately, they did not report on the distance to the LMC they have assumed, which makes the comparison with our results not trivial. Nevertheless, the value they quote is in good agreement with the one inferred from the BV method. In another work, Wan et al. (2020) used SkyMapper (Wolf et al. 2018) data to study the internal kinematics of the LMC populations, following coordinate transformations described in van der Marel (2001) and van der Marel et al. (2002), thus, the same transformations we applied here. For their Carbon Stars, Wan et al. (2020) fit a rotation curve built on a constant angular speed of stars as a function of radius. This may seem a simplistic assumption because Ω must vary with radius (see e.g. Fig. 11). Therefore, they did not constrain the pattern speed of the bar, but their result gives an estimate of what the rough angular frequency of stars should be within R ∼ 8 kpc, thus on Ωp since at corotation Ω equals the desired pattern speed. They found Ω = 24.6 ± 0.6 km s−1 kpc−1, which is not far from the BV value derived in our work.
Results of applying the method used in this work to the LMC complete sample.
An additional important result is that the TW method is extremely sensitive to the orientation of the x − y frame, and therefore to the way the integrals view the bar perturbation in the disc. Finding a dependency of the TW integrals with viewing angles in galaxies is not a new result. Using a numerical simulation, Zou et al. (2019) found that the accuracy on bar pattern speeds could be kept under ∼10% for a bar orientated by 10 ° −75° and 105 ° −170° with respect to the reference axis of the disc, while configurations where the integrals are measured perpendicularly to the bar major axis were shown to imply values systematically different from reality. This led for instance Cuomo et al. (2019) to define their sample of barred galaxies with bar position angles by 10° or more apart from the disc major and minor axes. With our simulations, although frame orientations near the principal axes of the bar should be avoided, which agrees with the findings of Zou et al. (2019), the results of Sects. 3 and 4 did not allow us to identify any particular wide range of orientations where the bar pattern speed estimates are reliable, and that the probability of agreement is low. It is worth mentioning here that bar pattern speeds of galaxies, as measured with the LTW method, are also known to be sensitive to the orientation of the pseudo-slits with respect to the disc line-of-nodes (Debattista 2003). Still with the help of numerical simulations, these authors showed that assuming an incorrect position angle for the disc major axis can lead to large errors on Ωp when performing the numerical LTW integrals. Of course, this is not directly linked to the viewing angle of the bar itself in the considered disc plane, as shown above in the IPTW case, but it illustrates nicely how sensitive to orientations the TW method can be.
The origin of the strong variations with the bar angle, and of the large discrepancy with true values, may be the impact of patterns other than the bar in the TW integrals, like spiral arms in the N-body simulation and the LMC. A possible solution to overcome this issue could be to measure Ωp as a function of radius, as done in Merrifield et al. (2006) or Meidt et al. (2008) for other galaxies. However, such analysis is beyond the scope of this article.
Nevertheless, the impact of other patterns than the bar on Ωp can be tested by studying the convergence of the TW integrals as a function of the aperture |Δx| in which the integrals are measured. This is achieved by progressively increasing |Δx| (see e.g. Chemin & Hernandez 2009; Zou et al. 2019). In particular, if the outer LMC spiral arms contaminate the TW integrals when the maximum range of |Δx| allowed by the extent of the observation is adopted (as we did in previous sections), then the derived pattern speed is mixing both the bar and spiral patterns, and the bar speed may be underestimated. Indeed, pattern speeds of spiral arms are expected to be lower than those of bars (Merrifield et al. 2006; Zou et al. 2019). But with a smaller domain of integration, chosen wisely, the pattern speed could converge to another Ωp, that of the bar only. We thus varied |Δx| within 1 to 9 kpc in the LMC, for two examples of frame orientations, Δϕ = 30° and Δϕ = 105° (directions outside the LMC principal bar axes, see Fig. 10). Figure 12 presents results of this test for the IPTW method. We find that the integrals have converged at |Δx| = 6 kpc at the constant values reported in Fig. 10 at the selected Δϕ (∼25 and ∼10 km s−1 kpc−1, respectively). But, for |Δx|< 6 kpc, Ωp varies significantly, either increasing and/or decreasing. In other words, we do not find hints of secondary convergence regions of the integrals that would correspond to the LMC bar Ωp only. To the benefits of the TW method, we can nonetheless see that a rough LMC pattern speed Ωp found by averaging the TW values over all Δϕ orientations is 23.1 km s−1 kpc−1, but with a large scatter of 12 km s−1 kpc−1. This compares with the value found with the BV model, but not with the one from the Dehnen method.
 |
Fig. 12. Convergence tests of the LMC pattern speed from the IPTW method. |Δx| is the domain of the numerical integrations of the TW equations (Eq. (4)). The convergence has been measured at two orientations of the frame Δϕ = 30° and 105°. |
As consequence, without agreement among the trends found with the various simulations used in the previous works and our present study, and without an identifiable region of bar orientation where ground-truth and measured pattern speeds agree within simulations, the individual pattern speeds found by the TW method in Fig. 10 cannot be representative of the real LMC bar Ωp. The agreement of Ωp found by the LTW method with the value found by the IPTW method for the LMC also indicates that the pattern speed of bars measured by means of the LTW method may likely be only representative of any value stemming from random frame orientations fixed by the position angle of the major axis of discs on the sky plane, but not of a global bar angular frequency. The reason of the failure of the TW method in giving a coherent LMC bar pattern speed is unclear. It could be that the tidal interaction with the SMC has broken the conditions of applicability of the method, the disc being no more in full equilibrium. However, both isolated and interacting discs in the simulations show similarities with the observations. It could also indicate that the impact of the spiral arms on the TW integrals is not as negligible as initially thought. More work will be necessary to investigate the origin of this issue with the TW method applied to the simulations and the LMC data.
The pattern speed obtained with the Dehnen method is significantly different from the one of the BV model. Unlike the TW method, we have shown that the Dehnen method performs nicely with an idealised simulation with a well defined rotationally supported stellar disc and no external perturbations and a simulation of an interacting and out-of-equilibrium disc, as it is insensitive to the bar orientation and the outer spiral perturbation, by construction. Applied to the LMC NN complete sample, it surprisingly results in a bar with null rotation, perhaps slightly counter-rotating with respect to the LMC disc. Is this finding realistic? Peculiar bars with such property exist in numerical simulations. In a recent work, it was shown how a bar embedded in a counter-rotating dark matter halo can decelerate, then flip its pattern speed, and finally decoupling its rotation from the disc (Collier & Madigan 2023). After the sign flip, the bar suffers from a large inclination and develops a warped disc. This scenario is difficult to test in real data because we need an observable to check the dark matter halo rotation. Evidence exists that LMC disc is warped (e.g. Choi et al. 2018; Ripepi et al. 2022), however we do not observe in the kinematic maps a decoupling of the bar motion from that of the disc. Another possible origin of the bar deceleration and counter-rotation could be external and due to the interaction with the SMC and/or the MW. This scenario could be tested with appropriate numerical simulations such as the KRATOS suite of simulations of LMC-SMC-MW-like tidal encounters (Jiménez-Arranz et al., in prep.).
This result does not come without issues, however. An almost non-rotating LMC bar would indeed not show any corotation within the disc since such Ωp should never cross the Ω curve. It is not an easy task to imagine how the orbits and the disc structure would respond to this peculiar circumstance. An absence of corotation could allow the bar to increase its length and strength out to the disc outskirts, that is, make the orbits of stars and the LMC stellar gravitational potential very elongated throughout the whole LMC disc. Indeed, nothing could prevent it here from growing significantly owing to the absence of corotation and the expected destructive orbits perpendicular to the bar beyond corotation. The LMC stellar density map shows that the outer LMC disc is elliptical (see Fig. 6, and also e.g. Gaia Collaboration 2021b), but the elongation occurs along a direction that is not aligned with the LMC bar. The elongated potential of the LMC likely comes from the tidal interaction with the MW and the SMC. Furthermore, the absence of bar resonances in the inner disc in this framework would make it difficult to interpret the strong variation of the orientation of the velocity bisymmetry evidenced in Fig. 11, which is expected to occur naturally around corotation. We think that the method may be sensitive to dust extinction and completeness effects in the inner LMC region, perhaps more strongly than the other methods. Also, the inner disc is not fully traced by a bar pattern, and the density map clearly shows pieces of spiral arms inside the circle encompassing the bar region. The inner kinematics is not fully dominated by the bar either, due to the smoothly varying phase angle of the velocity bisymmetry within R = 2 − 4 kpc (see Fig. 11), likely caused by a winding spiral structure near the tips of the bar. All of these effects may hamper the method from yielding a Ωp representative of the bar.
Assuming that the corotation radius Rc = 4.20 ± 0.25 kpc measured by the BV model is more representative of the bar properties, it corresponds to a pattern speed of 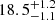 km s−1 kpc−1. The LTW pattern speed of 30.4 ± 1.3 km s−1 kpc−1 would thus be discrepant by 64% from the one inferred here. When compared to its radius of 2.3 kpc, the LMC stellar bar has Rc/R1 = 1.8 ± 0.1, thus corresponding to a slow bar, according to numerical methods (Athanassoula 1992). Finally, if we assume that the pattern speed has to be estimated using a velocity curve tracing more closely the circular velocity (the rotation curve of the younger stellar populations in Jiménez-Arranz et al. 2023) than the tangential velocity of the whole sample dominated by older stars (upper panel of Fig. 11), then Rc = 4.2 kpc would translate into Ωp = 20.9 ± 1.1 km s−1 kpc−1, which still compares well with the value found for the whole sample.
km s−1 kpc−1. The LTW pattern speed of 30.4 ± 1.3 km s−1 kpc−1 would thus be discrepant by 64% from the one inferred here. When compared to its radius of 2.3 kpc, the LMC stellar bar has Rc/R1 = 1.8 ± 0.1, thus corresponding to a slow bar, according to numerical methods (Athanassoula 1992). Finally, if we assume that the pattern speed has to be estimated using a velocity curve tracing more closely the circular velocity (the rotation curve of the younger stellar populations in Jiménez-Arranz et al. 2023) than the tangential velocity of the whole sample dominated by older stars (upper panel of Fig. 11), then Rc = 4.2 kpc would translate into Ωp = 20.9 ± 1.1 km s−1 kpc−1, which still compares well with the value found for the whole sample.
6. Conclusions
In this work, we use three different methods to determine the LMC bar pattern speed, namely: the TW method in its original form, when only LoS velocities are available (LTW), as well as a variation on that method that also makes use of astrometric data and in-plane velocity fields (IPTW); the Dehnen method, which was recently published and tested using single snapshots of N-body simulations; and the bisymmetric velocity (BV) method, which is based on the Fourier decomposition of the tangential velocity of a bisymmetric model to constrain the corotation radius of the bar. In order to characterise the strengths and limitations of each of the methods, we applied them to two different simulated barred galaxies. One snapshot of an N-body simulation of an isolated disc galaxy (B5, Roca-Fàbrega et al. 2013) and one snapshot of a N-body simulation of an interacting disc galaxy (KRATOS, Jiménez-Arranz et al., in prep.). The results show that:
-
The TW method shows a large dependency on the frame orientation when applied to both B5 and KRATOS simulations.
-
The Dehnen method recovers with good accuracy and precision the true pattern speed when applied to both: an idealised simulation with a well defined rotationally supported stellar disc and no external perturbations and a simulation of an interacting and out-of-equilibrium disc.
-
The BV method determines the corotation radius and pattern speed of both simulations. The accurate constraint of the strong variation of the kinematic phase angle is crucial for the determination of the corotation radius and thus the bar pattern speed.
From these points, and when applying the methods to the LMC sample, we are inclined to:
-
Discard the pattern speeds found with the TW method, because no obvious privileged value is found with the IPTW method, owing to the strong variation of the integrals with the orientation of the x − y plane, thus with the bar viewing angle inside the LMC disc. Also, the unique pattern speed found by the LTW method cannot be representative of a global bar frequency either.
-
Evaluate the validity of the bar pattern speed obtained with the Dehnen method. It corresponds to a non-rotating bar, with implications hard to reconcile with the structure and kinematics of the LMC disc.
-
Provide a first tentative value of the LMC bar corotation radius at R = 4.20 ± 0.25 kpc with the BV method, as the sharp change of the kinematic phase angle measured through a Fourier modelling is very reminiscent to the signature of corotation seen in numerical simulations. It gives a bar corotation-to-size ratio of Rc/R1 = 1.8 ± 0.1, which places the LMC bar in the slow rotation regime. The corresponding LMC bar pattern speed is
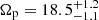 km s−1 kpc−1, reasonably consistent with other estimates found in the literature.
km s−1 kpc−1, reasonably consistent with other estimates found in the literature.
This research sets novel constraints on the corotation and pattern speed of the stellar bar of the LMC. Our intention is to continue this investigation, taking advantage of forthcoming releases from the Gaia mission that will offer improved data quality. With enhanced angular resolution, more precise proper motion measurements, and increased access to LoS velocities, we anticipate it will become easier to establish an LMC sample with reduced limitations, such as the crowding of stars at low radius, or contamination from foreground MW stars. Moreover, working with the 3D velocities of LMC stars will offer new opportunities. These approaches have already been initiated by Jiménez-Arranz et al. (2023). By doing so, we will obtain more reliable estimates of the LMC pattern speed and potentially alleviate tensions that exist among the Dehnen and bisymmetric velocity methodologies tested in this study, which may arise because of the perturbed equilibrium of the LMC. This could be tested with various numerical simulations of the LMC, SMC, and MW encounters. We will also study possible variations of the bar pattern speed among various stellar evolutionary phases of the LMC.
Movies
Movie 1 associated with Fig. 4 (00_IPTW_B5) Access here
Movie 2 associated with Fig. 4 (01_IPTW_KRATOS) Access here
Movie 3 associated with Fig. 4 (02_IPTW_LMC_data) Access here
Animations of the variation of the pattern speed Ωp inferred by the IPTW with different frame orientations Δϕ are available online, for both simulations and data.
Acknowledgments
We are grateful to W. Dehnen, M. Semczuk and V.P. Debattista for fruitful discussions. We thank Dr A.G.A. Brown for his comments on the completeness estimation. We thank an anonymous referee for a critical review and constructive suggestions that helped improving the manuscript. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. O.J.A. acknowledges funding by l’Agència de Gestió d’Ajuts Universitaris i de Recerca (AGAUR) official doctoral program for the development of a R+D+i project under the FI-SDUR grant (2020 FISDU 00011). O.J.A., M.R.G. and X.L. acknowledge funding by the Spanish MICIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe” by the “European Union” through grant PID2021-122842OB-C21, and the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia “María de Maeztu”) through grant CEX2019-000918-M. L.C. acknowledges financial support from the Chilean Agencia Nacional de Investigación y Desarrollo (ANID) through the Fondo Nacional de Desarrollo Científico y Tecnológico (FONDECYT) Regular Project 1210992 and the Institute of Cosmos Sciences University of Barcelona (ICCUB, Unidad de Excelencia “María de Maeztu”) through grant CEX2019-000918-M which founded a two-weeks visit in Barcelona. P.A. and L.C. warmly acknowledge the financial support of the Comité Mixto European Southern Observatory-Gobierno de Chile. S.R.F. acknowledges support from the Knut and Alice Wallenberg Foundation and the Swedish Research Council (grant 2019-04659). P.M. gratefully acknowledges support from project grants from the Swedish Research Council (Vetenskaprådet, Reg: 2017-03721; 2021-04153).
References
- Aguerri, J. A. L., Debattista, V. P., & Corsini, E. M. 2003, MNRAS, 338, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Méndez-Abreu, J., Falcón-Barroso, J., et al. 2015, A&A, 576, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, C., & Santillan, A. 1991, Rev. Mex. Astron. Astrofis., 22, 255 [NASA ADS] [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [Google Scholar]
- Belokurov, V. A., & Erkal, D. 2019, MNRAS, 482, L9 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton: Princeton University Press) [Google Scholar]
- Bobylev, V. V., & Bajkova, A. T. 2023, ArXiv e-prints [arXiv:2305.18408] [Google Scholar]
- Bovy, J., Leung, H. W., Hunt, J. A. S., et al. 2019, MNRAS, 490, 4740 [Google Scholar]
- Bureau, M., Freeman, K. C., Pfitzner, D. W., & Meurer, G. R. 1999, AJ, 118, 2158 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., & Combes, F. 1996, Fund. Cosmic Phys., 17, 95 [Google Scholar]
- Buttitta, C., Corsini, E. M., Aguerri, J. A. L., et al. 2023, MNRAS, 521, 2227 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Fouesneau, M., Rix, H.-W., et al. 2023, A&A, 669, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Ginard, A., Brown, A. G. A., Kostrzewa-Rutkowska, Z., et al. 2023, A&A, 677, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chemin, L., & Hernandez, O. 2009, A&A, 499, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, Y., Nidever, D. L., Olsen, K., et al. 2018, ApJ, 866, 90 [Google Scholar]
- Collier, A., & Madigan, A. M. 2023, MNRAS, submitted [arXiv:2305.06383] [Google Scholar]
- Contopoulos, G., & Grosbol, P. 1989, A&ARv, 1, 261 [Google Scholar]
- Contopoulos, G., & Papayannopoulos, T. 1980, A&A, 92, 33 [NASA ADS] [Google Scholar]
- Cuomo, V., Lopez Aguerri, J. A., Corsini, E. M., et al. 2019, A&A, 632, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuomo, V., Aguerri, J. A. L., Corsini, E. M., & Debattista, V. P. 2020, A&A, 641, A111 [EDP Sciences] [Google Scholar]
- Debattista, V. P. 2003, MNRAS, 342, 1194 [Google Scholar]
- Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [Google Scholar]
- Debattista, V. P., & Williams, T. B. 2004, ApJ, 605, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., Semczuk, M., & Schönrich, R. 2023, MNRAS, 518, 2712 [Google Scholar]
- Ferrers, N. 1877, Q. J. Pure Appl. Math., 14, 1 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fragkoudi, F., Grand, R. J. J., Pakmor, R., et al. 2021, A&A, 650, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Luri, X., et al.) 2021b, A&A, 649, A7 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Drimmel, R., et al.) 2023a, A&A, 674, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Géron, T., Smethurst, R. J., Lintott, C., et al. 2023, MNRAS, 521, 1775 [CrossRef] [Google Scholar]
- Gerssen, J., Kuijken, K., & Merrifield, M. R. 1999, MNRAS, 306, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, S., & Di Matteo, P. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202347763 [Google Scholar]
- Guo, R., Mao, S., Athanassoula, E., et al. 2019, MNRAS, 482, 1733 [Google Scholar]
- Hernandez, O., Wozniak, H., Carignan, C., et al. 2005, ApJ, 632, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, ArXiv e-prints [arXiv:1008.4686] [Google Scholar]
- Jiménez-Arranz, Ó., Romero-Gómez, M., Luri, X., et al. 2023, A&A, 669, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucchini, S., D’Onghia, E., & Fox, A. 2022, AAS/Division of Dynamical Astronomy Meeting, 54, 201.01 [NASA ADS] [Google Scholar]
- Meidt, S. E., Rand, R. J., Merrifield, M. R., Shetty, R., & Vogel, S. N. 2008, ApJ, 688, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Merrifield, M. R., & Kuijken, K. 1995, MNRAS, 274, 933 [Google Scholar]
- Merrifield, M. R., Rand, R. J., & Meidt, S. E. 2006, MNRAS, 366, L17 [NASA ADS] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Niederhofer, F., Cioni, M.-R. L., Schmidt, T., et al. 2022, MNRAS, 512, 5423 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J., & Wallin, J. F. 2004, ApJ, 614, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Chemin, L., Molinaro, R., et al. 2022, MNRAS, 512, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Roca-Fàbrega, S., Valenzuela, O., Figueras, F., et al. 2013, MNRAS, 432, 2878 [Google Scholar]
- Romero-Gómez, M., Figueras, F., Antoja, T., Abedi, H., & Aguilar, L. 2015, MNRAS, 447, 218 [CrossRef] [Google Scholar]
- Roshan, M., Ghafourian, N., Kashfi, T., et al. 2021, MNRAS, 508, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A. 2014, Rev. Mod. Phys., 86, 1 [Google Scholar]
- Shapley, H. 1951, Publ. Mich. Obs., 10, 79 [Google Scholar]
- Shimizu, T., & Yoshii, Y. 2012, in Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, eds. W. Aoki, M. Ishigaki, T. Suda, T. Tsujimoto, & N. Arimoto, ASP Conf. Ser., 458, 341 [NASA ADS] [Google Scholar]
- Spekkens, K., & Sellwood, J. A. 2007, ApJ, 664, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, ApJ, 282, L5 [Google Scholar]
- van der Marel, R. P. 2001, AJ, 122, 1827 [Google Scholar]
- van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, Z., Guglielmo, M., Lewis, G. F., Mackey, D., & Ibata, R. A. 2020, MNRAS, 492, 782 [Google Scholar]
- Williams, T. G., Schinnerer, E., Emsellem, E., et al. 2021, AJ, 161, 185 [Google Scholar]
- Wolf, C., Onken, C. A., Luvaul, L. C., et al. 2018, PASA, 35, e010 [Google Scholar]
- Zou, Y., Shen, J., Bureau, M., & Li, Z.-Y. 2019, ApJ, 884, 23 [Google Scholar]
Appendix A: Test-particle simulation
In this section, we apply the methods described in Section 2 to an idealised simulation of a barred disc galaxy in statistical equilibrium with the imposed potential. We briefly describe the characteristics of the simulation and the results of the methods applied to it.
We use a 5 million test particle simulation with initial conditions, galactic potential, and steps performed in the integration process as described in Romero-Gómez et al. (2015). We refer to this simulation as the TP simulation. The initial conditions for positions and velocities were drawn for a disc density distribution following a Miyamoto-Nagai disc potential (Miyamoto & Nagai 1975) with a typical scale-height (hz = 300 pc) and radial velocity dispersion (σU = 30.3 km s−1) of a red clump star. Then we integrate the initial conditions in the axisymmetric potential of Allen & Santillan (1991) for 10 Gyr, after that we introduce the Galactic bar potential adiabatically during four bar rotations, and we integrated another 16 bar rotations so that the particles achieve a statistical equilibrium with the final bar potential. The galactic bar consists of the superposition of two aligned Ferrers ellipsoids (Ferrers 1877), one modelling a triaxial bulge with a semi-major axis of 3.13 kpc, and the second modelling a long thin bar with a semi-major axis of 4.5 kpc, with an angular orientation of 20°. In the TP simulation, we impose that the bar rotates counter-clockwise as a rigid body with a constant pattern speed of 42 km s−1 kpc−1, placing the corotation resonance at Rc = 4.9 kpc, measured as in the B5 simulation. The TP simulation represents the ideal configuration to estimate a bar pattern speed with the different methods due to the only barred perturbation and being in statistical equilibrium with the imposed potential.
Figure A.1 shows the surface density (left panel), the radial velocity (middle panel) and the residual tangential velocity (right panel) maps for the TP simulation. The map of the residuals has been obtained by subtracting the rotation curve to the Vϕ map. We observe the bar and no obvious spiral arms, which is expected because only a bar potential is modelled. In both radial and residual tangential velocity maps, we also observe a kinematic quadrupole caused by the stellar orbits shaping the bar. In every panel, we highlight the bar region identified by the Dehnen method by green dashed circles, with inner and outer circles corresponding to R0 and R1, respectively. The grey dashed lines trace the bar minor and the major axes found by the method. The bar orientation ϕb is in agreement with the orientation observed in the surface density, and separates remarkably the quadrupole patterns in two parts. The Dehnen method infers a value of Ωp = 42.0 ± 0.2 km s−1 kpc−1, in agreement with the imposed value. Values are summarised in Table A.1.
 |
Fig. A.1. Application of the Dehnen method to the TP simulation. Surface density (left), median radial velocity map (center) and median residual tangential velocity map (right). The bar region identified by Dehnen method (see values in Table A.1) is indicated by green dashed circles. The grey dashed lines trace the bar minor and the major axes. |
Results of the Dehnen and the BV methods applied to TP simulation, compared to the reference value (obtained using finite-differences).
Figure A.2 shows the impact of the variation of the orientation of the Cartesian frame on the derived pattern speed using the LTW and IPTW methods, by rotating the reference x and y axes around the z−axis in the simulation. The rotation of the Cartesian frame before sky projection allows the TW integrals (measured parallel to the major axis) to view the bar and spiral perturbations through various angles. Note that in this case, where no other non-axisymmetric component but the bar, and being in statistical equilibrium, the recovered pattern speed using both versions of the TW method show comparable trends. As a known issue of the TW, the integrals do not converge when the slit is aligned with the bar axes (Tremaine & Weinberg 1984). The IPTW shows a pattern speed systematically lower by ∼10% from the true value, about twice as large as the systematic shown by the LTW method.
Figure A.3 presents results of the IPTW method for the TP simulation. Again, we show here two different reference frame orientations: the original one, with Δϕ = 0° (top row) and the one with the bar major axis parallel to the x-axis, Δϕ = 159° (bottom row), for illustrative purposes. In the first case, there is a clear linear trend and the IPTW recovers a bar pattern speed of Ωp = 39.9 ± 0.4 km s−1 kpc−1, with a relative difference smaller than 5% from the imposed value. In the second case, the TW x−integrals are perfectly aligned with the bar major axis, as expected in the presence of only a bar potential. The ⟨x⟩ values are then very close to zero, so there is no clear trend in this case (it would give similar results when the TW integrals are evaluated at another viewing angle along the bar minor axis). We recover here a counter-clockwise pattern speed of Ωp = 23.4 ± 2.8 km s−1 kpc−1 which differs by almost 50% from the imposed value. The TW method thus performs better when no prominent sub-structures exist in the disc, as a well-known issue, integrals should not be made along the major or minor axes of the bar.
Finally, in Fig. A.4, we show the results of applying the BV method to the TP simulation, the value for corotation we derive is Rc = 4.8 ± 0.5 kpc, and the bar pattern speed is 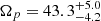 km s−1 kpc−1, which exceeds the true value of 42 km s−1 kpc−1, although remaining comparable with it given the lower quoted uncertainties. The values are summarised in Table A.1.
km s−1 kpc−1, which exceeds the true value of 42 km s−1 kpc−1, although remaining comparable with it given the lower quoted uncertainties. The values are summarised in Table A.1.
All Tables
Results of the Dehnen and the BV methods applied to B5 and KRATOS simulations, compared to the reference value (obtained using finite-differences).
Results of the Dehnen and the BV methods applied to TP simulation, compared to the reference value (obtained using finite-differences).
All Figures
 |
Fig. 1. Application of the Dehnen method to B5 (top) and KRATOS (bottom) simulations. Surface density (left), median radial velocity map (centre) and median residual tangential velocity map (right). The bar region identified by Dehnen method (see values in Table 1) is indicated by green dashed circles. The grey dashed lines trace the bar minor and the major axes. |
| In the text | |
 |
Fig. 2. Variation of Ωp as as function of the reference frame orientation Δϕ. Results for the B5 and KRATOS simulations are shown in the upper and lower panels, respectively. Results of the IPTW method are shown as open symbols, while those of the LTW method are drawn as a solid line (for the i = 45° case, upper panel), and as dotted, solid and dashed lines (for the i = 25, 45 and 75° cases, lower panel). Horizontal dashed green lines are the ground-truth bar pattern speeds. The vertical orange (navy) vertical line corresponds to the frame orientation where the x-axis of the disc lies along the major axis of the bar (y-axis, respectively). |
| In the text | |
 |
Fig. 3. Application of the IPTW method to B5 simulation. Top: bar major axis at ϕb = 163.5°, as in the original snapshot and shown in Fig. 1. Bottom: after applying a rotation of Δϕ = 16.5° to put the bar major axis along the x-axis. Left: surface density where the bar region (obtained using Dehnen method) is indicated by the green dashed circle. A scatter plot representing the value of ⟨x⟩ for each slice in y is overlapped. The scatter plot varies its colour as function of the distance to the centre in the y-axis, being the red points close to the centre and the green close to the external parts of the galaxy. Right: scatter plot of the Tremaine-Weinberg integrals ⟨x⟩ and ⟨vy⟩ for the different slices in the y-axis. The colour of the scatter plot is the same in both left and right panels. In the right panel, the points with a black circle are inside of the bar region and, therefore, the only considered for fitting Ωp. |
| In the text | |
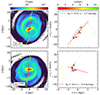 |
Fig. 4. Same as Fig. 3, but for the KRATOS simulation. |
| In the text | |
 |
Fig. 5. Results of the BV model of the stellar tangential velocity map of the B5 (left panels) and KRATOS (right panels) simulations: amplitude (upper panels), phase angle, ϕ2,kin of the Fourier modes (middle panels), and angular frequency Ω (bottom panels). In the top panels, the black solid line is the fitted axisymmetric velocity component V0 (the rotation curve), the grey line is the median velocity (initial value for the model), the blue dashed curve is the amplitude of the tangential bisymmetry V2, and the orange dotted line is the scatter of the model Vs. In the middle and bottom panels, the vertical light coral area and dashed line shows the adopted bar corotation radius, Rc = 8.0 ± 0.5 kpc for B5 and Rc = 3.3 ± 0.5 kpc for KRATOS simulations. In the bottom panel, the black solid line is the angular velocity derived from V0, while the horizontal green area and dotted line shows the corresponding bar pattern speed |
| In the text | |
 |
Fig. 6. Application of the Dehnen method to the LMC NN complete sample. Surface density (left), median radial velocity map (center) and median residual tangential velocity map (right). The bar region identified by Dehnen method is indicated by green dashed circles, [R0, R1]=[0.75, 2.3] kpc. The grey dashed lines trace the bar minor and the major axes. |
| In the text | |
 |
Fig. 7. Application of the Dehnen method to the LMC NN complete sample. The relative m = 2 Fourier amplitude (top) and orientation (bottom). The bar region identified by the method is indicated by green dashed vertical lines, [R0, R1]=[0.75, 2.3] kpc. |
| In the text | |
 |
Fig. 8. Stellar line-of-sight velocity field of the LMC NN complete Vlos sub-sample, corrected from the systemic motions. Data are from Gaia RVS (Katz et al. 2023; Jiménez-Arranz et al. 2023). |
| In the text | |
 |
Fig. 9. Result of the TW method applied to the LoS velocity field of the LMC from Fig. 8. Only points within the radius R1 defined by the Dehnen method are shown. The red dashed line shows the result of the linear fit to the points, Ωp sin i, with Ωp = 30.4 ± 1.3 km s−1 kpc−1. |
| In the text | |
 |
Fig. 10. Results of applying the LTW and IPTW to the LMC NN complete sample. The open red dot shows the bar pattern speed recovered with the LTW method. The blue dotted curve shows the bar pattern speed obtained using the IPTW with different frame orientations Δϕ. The dashed purple (brown) line shows the bar pattern speed obtained using the Dehnen (BV) method. |
| In the text | |
 |
Fig. 11. Results of the BV model of the stellar tangential velocity map of the LMC NN complete sample: strength (upper row) and phase angle (lower row, ϕ2, kin) of the bisymmetric Fourier mode. The black solid line is the fitted axisymmetric velocity component (the rotation curve), the grey line is the median velocity (initial value for the model), the blue dashed curve is the strength of the tangential bisymmetry, and the orange dotted line is the scatter of the model. The vertical light coral area and dashed line shows the adopted bar corotation radius of the LMC, Rc = 4.20 ± 0.25 kpc. In the bottom panel, we show the angular velocity of the LMC as a function of radius. The vertical light coral area and dashed line show the corotation radius of the bar. The horizontal green area and dotted line shows the corresponding bar pattern speed |
| In the text | |
 |
Fig. 12. Convergence tests of the LMC pattern speed from the IPTW method. |Δx| is the domain of the numerical integrations of the TW equations (Eq. (4)). The convergence has been measured at two orientations of the frame Δϕ = 30° and 105°. |
| In the text | |
 |
Fig. A.1. Application of the Dehnen method to the TP simulation. Surface density (left), median radial velocity map (center) and median residual tangential velocity map (right). The bar region identified by Dehnen method (see values in Table A.1) is indicated by green dashed circles. The grey dashed lines trace the bar minor and the major axes. |
| In the text | |
 |
Fig. A.2. Same as Fig. 2, but for the TP simulation. |
| In the text | |
 |
Fig. A.3. Same as in Fig. 3, for the TP simulation. |
| In the text | |
 |
Fig. A.4. Same as in Fig. 5, but for the TP simulation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



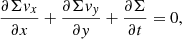
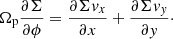
![$$ \begin{aligned} \Omega _{\rm p}+\frac{i}{m}\frac{\dot{\Sigma }_m}{\Sigma _m} = \frac{\Sigma _i\mu _i\left[\dot{\phi }_iW_i+\frac{i}{m}\dot{R}_i (\partial W/\partial R)_i\right]e^{-im\phi _i}}{\Sigma _i\mu _iW_ie^{-im\phi _i}}, \end{aligned} $$](/articles/aa/full_html/2024/03/aa47266-23/aa47266-23-eq4.gif)