EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) A38 Full HTML
Open Access
Issue
A&A
Volume 681, January 2024
Article Number A38
Number of page(s) 11
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202347547
Published online 05 January 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Globular clusters (GCs) are the oldest and largest stellar aggregates in the Galaxy, with ages t > 10 Gyr and stellar populations made of up to 106 stars. They orbit the Galactic halo and bulge, and the study of their structural, kinematic, and dynamical properties allows us to trace the formation history of the Galaxy back up to its very early stages. In this context, we performed a detailed kinematic exploration using the ESO Multi-Instrument Kinematic Survey (MIKiS; Ferraro et al. 2018a; Lanzoni et al. 2018a,b; Leanza et al. 2022, 2023; Pallanca et al. 2023) and photometric investigation of GCs in different Galactic environments (e.g. Origlia et al. 2002, 2003; Valenti et al. 2010; Dalessandro et al. 2014; Pallanca et al. 2019, 2021a; Cadelano et al. 2020a; Raso et al. 2020; Deras et al. 2023) with the aim to perform a complete characterisation of these stellar systems in terms of structure, age, stellar content (see examples in Ferraro et al. 1997, 2009; Lanzoni et al. 2010; Miocchi et al. 2013; Dalessandro et al. 2013; Pallanca et al. 2021b; Cadelano et al. 2022), and dynamical evolutionary stage (Ferraro et al. 2012, 2018b, 2019, 2023; Lanzoni et al. 2016). This approach led to the discovery of a few anomalous stellar systems in the Galactic bulge harbouring multi-age and multi-iron sub-populations (see Ferraro et al. 2009, 2016, 2021; Origlia et al. 2011; Massari et al. 2014; Dalessandro et al. 2022; Crociati et al. 2023; Romano et al. 2023), which might be remnants of giant clumps of gas and stars that, 12 Gyr ago, contributed to generate the Galactic bulge.

The target of the present paper is the poorly studied Galactic GC NGC 6284. This is a cluster possibly associated with the thick disk (see Casetti-Dinescu et al. 2010) and located in the background of the Galactic bulge: in projection in the sky, it appears north of the bulge, at Galactocentric coordinates l = 358.35 deg and b = 9.94 deg. According to the Harris (1996, 2010 edition) catalogue, it is located at a distance of 15.2 kpc from the Sun, while Baumgardt & Vasiliev (2021) report 14.2 kpc. It follows a highly eccentric orbit (Bajkova & Bobylev 2021, e = 0.83) that extends up to ∼5.5 kpc along the meridional direction of the Galactic plane, with a perigalactic distance of 6.32 kpc (Baumgardt & Hilker 2018). From the analysis of the cluster integrals of motion, Massari et al. (2019) suggest that NGC 6284 may not have been generated in situ, but it has been rather accreted by the Milky Way from the Gaia-Enceladus Sausage. On the other hand, Bellazzini et al. (2020) ruled out NGC 6284 to be associated with the Sagittarius dwarf spheroidal galaxy. In addition, based on the destruction rates estimated by Gnedin & Ostriker (1997), Kundu et al. (2022) suggest that the system is substantially affected by bulge and disk shocks during its orbit crossing the plane. From the shape of its surface brightness profile, NGC 6284 has been catalogued as a post-core collapse (PCC) cluster since the very first surveys of Galactic PCC systems (see Djorgovski & King 1986; see also Trager et al. 1993, 1995; Lugger et al. 1995). The PCC state is the most advanced phase of internal dynamical evolution of collisional systems. Recurrent stellar encounters cause kinetic-energy exchanges among stars, with the most massive stars therefore transferring kinetic energy to lower mass objects and progressively sinking towards the system’s centre. The energy transfer from the centre to the cluster outer regions yields a progressive contraction of the core leading to core collapse. The event is accompanied by a substantial increase in the central density, and its observational manifestation is the setup of a steep power-law cusp in the innermost region of the projected density profile (Meylan & Heggie 1997, see also Bhat et al. 2022). Approximately 20% of the GCs in the Galaxy are currently in this dynamical evolutionary stage (Trager et al. 1993; Bianchini et al. 2018). In terms of its chemical properties, there is a general consensus on the fact that NGC 6284 is a mid-metallicity cluster, but no results from high-resolution spectroscopy are available at the moment, and the values reported in the literature show a considerable spread: [Fe/H] = −0.91 (Smith & Perkins 1982, from RR Lyrae), [Fe/H] = −0.99 (Usher et al. 2019, from the measure of Calcium abundance), [Fe/H] = −1.07 (Dias et al. 2016, from low-resolution spectra of just seven stars), and [Fe/H] = −1.26 (Harris 1996), which is the value obtained from low-resolution spectra by Zinn & West (1984, [Fe/H] = −1.40) after conversion to the Carretta-Gratton scale. The system is affected by a moderate reddening, E(B − V) = 0.27 − 0.29, in most of the available studies (e.g. Smith & Perkins 1982; Webbink 1985; Zinn 1985; Recio-Blanco et al. 2005), although Minniti et al. (1995) quote E(B − V) = 0.40. Given its location towards the bulge direction, the extinction is likely to show differential variations within the cluster field of view. Currently, there is no consensus about the absolute age of NGC 6284. The available estimates in the literature are the following: t = 11.0 ± 0.1 Gyr (De Angeli et al. 2005), t = 11.00 ± 0.25 Gyr (Meissner & Weiss 2006), t = 11.8 ± 0.3 Gyr (Cabrera-Ziri & Conroy 2022), t = 12.3 Gyr (Carretta et al. 2010), and t = 13.0 Gyr (Dias et al. 2016).

The goal of this work is to carry out the first in-depth photometric analysis of NGC 6284 to characterise its structure and stellar population through a set of high-resolution images sampling its innermost regions. The paper is structured as follows: In Sect. 2 we describe the photometric analysis performed on the acquired dataset. In Sect. 3, we explain how we determined the centre of gravity of the cluster, its projected density profile, and its structural parameters. In Sect. 4 we describe the differential reddening correction performed on the colour-magnitude diagram (CMD). In Sect. 5, we explain how we performed isochrone fitting to the differential reddening corrected CMD to estimate the age, distance, metallicity, and absolute colour excess of the system. Section 6 is devoted to the determination of the red giant branch (RGB) bump luminosity from both the differential and the integrated luminosity functions. Finally, in Sect. 7 we summarise our results.

2. Observations and data reduction

The present study is based on a dataset obtained with the Wide Field Camera 3 (WFC3) on board the HST (GO: 15232, PI: Ferraro). The dataset comprises seven images (6 × 27 s and 1 × 666 s exposures) in the F555W filter, and seven images (6 × 15 s and 1 × 617 s exposures) in the F814W filter.

The photometric analysis has been carried out on the -flc images, which are already corrected for dark-subtraction, flat-field, bias, and charge transfer efficiency. We have used the standard package DAOPHOT IV (Stetson 1987) following the prescriptions by Cadelano et al. (2019, 2020a). We start by modelling the shape of the point spread function (PSF) by selecting 200 isolated stars present in each image. For the WFC3 camera, the full width at half maximum (FWHM) is set at 1.5 pixels ( ∼ 0 . ″ 06 $ {\sim}0{{\overset{\prime\prime}{.}}}06 $), and we sampled each of the selected stars within a 20-pixel radius ( ∼ 0 . 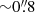″ 8 $ {\sim}0{{\overset{\prime\prime}{.}}}8 $). For each image, the best PSF model was provided by a Moffat function (Moffat 1969) and a Penny function (Penny 1976) for the F555W and the F814W filters, respectively, based on a χ2 statistic. These models were applied to all the sources detected in our images above a 5σ threshold from the local background level. We then built a master catalogue containing the instrumental magnitudes and positions of each stellar source detected in at least 3 images. At the corresponding positions of all these sources, a fit was forced in each image using DAOPHOT/ALLFRAME (Stetson 1994). The results have been combined together using DAOPHOT/DAOMASTER to finally obtain homogenised instrumental magnitudes and their related photometric errors. The instrumental magnitudes have been calibrated to the VEGAMAG system using the latest zero points derived by Calamida et al. (2022) and reported at the HST WFC3 website1, namely, ZPF555W1 = 25.838 and ZPF555W2 = 25.825 in the F555W filter for the stars detected in chips 1 and 2, respectively, and ZPF814W1 = 24.699 and ZPF814W2 = 24.684 for those detected in chips 1 and 2 in the F814W filter. Finally, we applied independent aperture and encircled energy corrections for each chip and filter. The instrumental positions of the stars present in our images were corrected for geometric distortions in both chips, following the procedure described in Bellini et al. (2011). We then converted these updated instrumental positions into the absolute system celestial coordinates (RA and Dec) through cross-correlation with the stars in common with the Gaia-DR3 catalogue (Gaia Collaboration 2023).

The star catalogue thus obtained allowed us to generate the first deep CMD of NGC 6284 extending more than 6 mag below the main-sequence turnoff (MS-TO; see Fig. 1). For comparison, the previously available CMDs reached just ∼2 mag below the horizontal branch in the J and K filters (Minniti et al. 1995), and ∼2 mag below the MS-TO in the F439W and F555W filters (Piotto et al. 2002). As mentioned in Sect. 1, the sky position of the cluster towards the outskirts of the bulge causes a mild level of contamination of the CMD from field interlopers. Unfortunately, at the moment, a cluster membership selection cannot be applied with the available datasets, neither through proper motions, nor through a statistical decontamination (see e.g. Dalessandro et al. 2019; Cadelano et al. 2017a). Nevertheless, the main features of the CMD are easily distinguishable. The MS spans a range of magnitudes between 21.0 < mF555W < 26.5 and shows the MS-TO point at around mF555W = 20.8. The CMD also shows a horizontal branch at about mF555W = 17.3 that is mainly populated in the blue side, well-defined sub-giant and red giant branches (SGB and RGB, respectively) with the characteristic RGB bump (Fusi Pecci et al. 1990; Ferraro et al. 1999a) at mF555W = 17.5, and a rather tenuous asymptotic giant branch above the horizontal branch.

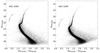thumbnail Fig. 1.

CMD of NGC 6284 obtained from the HST WFC3 dataset used in this work. F555W and F814W magnitudes have been plotted along the y-axis on the left and right panels, respectively.

3. The gravitational centre and star density profile of NGC 6284

3.1. Centre of gravity

To build the projected density profile and to estimate the structural parameters of NGC 6284, we first need an accurate determination of its gravitational centre (Cgrav). The presence of a few luminous stars in the surveyed field can generate an offset between the surface brightness peak and the true gravitational centre of the cluster (“shot-noise bias”). Hence, we estimated Cgrav from the position of resolved stars, following the procedure already employed in many previous works (e.g. Montegriffo et al. 1995; Lanzoni et al. 2007a, 2019; Raso et al. 2020). Briefly, starting from a first-guess centre (the one reported in the catalogue of Orbital Parameters of Galactic Globular Cluster; Baumgardt & Hilker 2018), we iteratively calculated the average of the projected x- and y-coordinates of a sample of stars selected above a given limiting magnitude (bright enough to avoid incompleteness issues) and within a cluster-centric distance larger than the literature core value (to sample the radial region where the density profile starts to decrease). The procedure stops when 10 consecutive iterations yield values that differ by less than 0.01″.

We repeated the computation for three different magnitude limits (mF555W = 20.4, 20.7 and 21.2) and for cluster-centric distances ranging from 25″ to 36″ in steps of 2″, 3″, and 5″. The final coordinates of Cgrav correspond to the average of the centres determined for each combination of selection magnitudes and radii, and they turn out to be RA = 256.1192583° (17h 04m 28.622s) and Dec = −24.7648085° (−24° 45′ 53.31″), with an uncertainty of ∼0.1″. Our estimate is located ∼2.9″ west from the first-guess centre (Baumgardt & Hilker 2018), and ∼1.5″ east from that quoted in the Harris (1996) catalogue.

3.2. Stellar density profile

The shot-noise bias mentioned above may also have a significant impact on the shape of the surface brightness profile and, as a consequence, on the cluster structural parameters estimated from it (see, e.g. Noyola & Gebhardt 2006). To circumvent this issue, we have promoted (Montegriffo et al. 1995; Ferraro et al. 1999b, 2003) and then systematically adopted the use of resolved star counts to construct projected star density profiles and to determine the cluster structural parameters (e.g. Lanzoni et al. 2007a,b,c; Ibata et al. 2009; Miocchi et al. 2013).

To construct the stellar density profile of NGC 6284, we combined our WFC3 photometric catalogue (which extends out to ∼115″ from the newly determined centre) with a Gaia-DR3 (Gaia Collaboration 2023) catalogue covering a circular area with a radius of 1°. This allowed us to accurately sample both the innermost and the outermost regions of the cluster. We followed the procedure described in Miocchi et al. (2013, see also, e.g. Cadelano et al. 2017b; Lanzoni et al. 2019; Raso et al. 2020), selecting stars brighter than the MS-TO in both catalogues: to this end, a magnitude cut at mF555W < 21.0 has been applied to the WFC3 catalogue, while Gmag < 20.0 has been adopted for the Gaia one. Such a selection is made to include only stars with approximately the same mass and to avoid spurious effects from photometric incompleteness. For the WFC3 catalogue we then considered 17 concentric rings around Cgrav with radii up to 115″. This allowed us to sample the inner portion of the density profile. In the case of the Gaia-DR3 data, we used 8 concentric rings (always centred around Cgrav) with radii between 38″ and 3600″ to sample the outer cluster regions, as well as the Galactic background density. We then divided each ring into three subsectors and determined the surface density in each of them as the ratio between the number of stars and the subsector area. Finally, we adopted the average and standard deviation of the density measurements in each subsector as the resulting density value of the ring and its related uncertainty, respectively. The Gaia profile was then vertically rescaled to match that of the WFC3 using 5 points in the common radial range (between 38″ and 115″). This provided us with the full stellar density profile of the cluster that is plotted with empty circles in Fig. 2.

thumbnail Fig. 2.

Star density profile of NGC 6284. The left panel shows the observed profile (empty circles) and the background-subtracted profile (filled circles). The dashed horizontal line is the background density value used to decontaminate the cluster profile from the Galactic field contribution. The solid red curve is the King model that best fits the innermost portion of the profile, obtained for illustrative purposes by artificially increasing the errors of the outer points. The corresponding values of some structural parameters are labelled. The bottom panel shows the residuals between the best-fit King model and the cluster density profile. In the right panel, the circles are the same as in the left panel, but the four innermost points are coloured in red to highlight the presence of a central density cusp. These have been fitted with the power-law function shown as a red dashed line, with slope αcusp = −0.53. The best-fit King model to the profile beyond the four inner points (black solid circles) is shown with the red solid curve, and is characterised by the labelled structural parameters.

Clearly, the stellar density is not constant in the innermost region, at odds with the expectation from the King (1966) model behaviour observed in most GCs. Indeed, the stellar density progressively increases towards the centre of NGC 6284, drawing a steep cusp. As discussed in the Introduction, this is the typical signature of a GC that has undergone core collapse. The projected density keeps decreasing for increasing distance from the centre out to r ∼ 200″, where the Galactic field becomes dominant over the cluster population. On the surveyed spatial scale the distribution of background stars is expected to be approximately uniform, thus explaining the well-defined density plateau visible in the outermost portion of the profile (six outer empty circles in Fig. 2). To obtain the intrinsic density profile of the system, the contribution from field stars must be quantified and removed. To this end, the level of Galactic field contamination has been estimated by averaging the six values on the plateau (see the horizontal dashed line in Fig. 2), and then subtracted from the observed distribution (empty circles). The field-subtracted star density profile of NGC 6284 thus obtained is marked by the filled circles in the figure. It remains virtually unchanged at small radii because at these distances from the centre the cluster population is by far dominant. Conversely, the subtracted profile progressively diverges from the observed one as the radius increases because the cluster population decreases in number, while the field contribution remains constant and starts to dominate. This highlights the importance of accurately quantifying the background level for a reliable determination of the true density profile of stellar systems.

Given that the profile has been determined by using stars of approximately the same mass, we can now fit it with single-mass King (1966) models to derive the structural parameters of the cluster under the assumption of spherical symmetry and orbital isotropy, as it is commonly done for GCs. Of course, in the presence of a central density cusp, a proper fit to the entire profile with core-like models cannot be obtained (e.g. Ferraro et al. 2003; Zocchi et al. 2016). Nevertheless, it is customary (e.g. Harris 1996; Meylan & Heggie 1997) to fit the density (or surface brightness) distribution of PCC clusters with King models of high concentration parameter (c ≥ 2 − 2.5) and small core radius (rc). For illustrative purposes, we therefore forced the King model fitting by artificially increasing the errors of the most external points, thus giving larger weight to the innermost values. As expected, the best-fit is provided by a model with c = 2.55 and rc = 2.8″ (see the left-hand panel of Fig. 2). While it reasonably reproduces (by construction) the innermost portion of the profile, it clearly fails in properly fitting also the external part.

The only way to obtain an acceptable match of the entire star density profile is by combining a King model in the outer regions, with a power-law function in the centre. Indeed the innermost region (r < 4.5″, corresponding to the first 4 points of the profile) can be nicely modelled by a straight line with slope αcusp = −0.53 ± 0.2. Then after excluding this portion, the profile is well reproduced by a King model with c = 1.54 and rc = 10.3″. The best-fit solution has been searched by using a MCMC approach implemented by the emcee package (Foreman-Mackey et al. 2013, 2019), following Cadelano et al. (2022). We assumed uniform priors on the parameters of the fit (i.e. the King concentration parameter c, the core radius rc, and the value of the central density). Therefore, the posterior probability distribution functions are proportional to the likelihood L = exp(−χ2/2), where the χ2 statistic is calculated between the measured density values and those predicted by the whole family of adopted models.

As a final note, Fig. 3 shows the comparison between the observed density profile obtained in this work (grey circles), and those derived with respect to the centres quoted in the Harris (1996) catalogue and in Baumgardt & Hilker (2018), which are offset, respectively, by ∼1.5 − 3″ from our estimate of Cgrav. This nicely illustrates the importance of correctly determining the cluster centre, especially in the case of very concentrated GCs: indeed, a mismatch of just a few arcseconds makes the central density cusp disappear.

thumbnail Fig. 3.

Density profile obtained in this work, calculated with respect to the value of Cgrav quoted in Sect. 3.1, is shown with grey circles (same as the empty circles in Fig. 2). Left and right panels show the projected density profile calculated with respect to the cluster centres quoted in the Harris (1996) catalogue and in Baumgardt & Hilker (2018), respectively (black circles). Only the inner portion of the profile, out to r ∼ 100″, is shown in the figure.

4. Differential reddening correction

Although the Harris (1996) catalogue quotes a moderate colour excess for NGC 6284, E(B − V) = 0.28, and the evolutionary sequences in the CMDs of Fig. 1 appear only mildly distorted or broadened, the fact that the cluster lies in the direction of the bulge outskirts naturally recommends to quantify the possible effects of differential reddening. We therefore determined a detailed reddening map towards the system, making use of the iterative method fully described in Pallanca et al. (2019, 2021a) and Cadelano et al. (2020b).

Briefly, we start by generating the CMD of a reference sample including likely member stars, that is, stars located at r < 30″ from the centre of the cluster (to minimise the possible contamination from field interlopers) and in a fixed magnitude range (15.0 < mF555W < 23.0) to include well-measured stars along the MS, SGB, and RGB. We then divided this CMD into magnitude bins of 0.3 mag each, except at the level of the MS-TO and SGB (20.0 < mF555W < 21.25) where we used 0.05 mag bins to obtain a finer sampling. For each bin, we estimated the 3σ-clipped median values of the (mF555W − mF814W) colour and of the mF555W magnitude. These medians were then interpolated to determine the mean ridge line, which was used to estimate the geometric distance ΔX of all the stellar sources in the reference sample, along the direction of the reddening vector. By assuming the standard extinction coefficient RV = 3.1, this vector is defined by the extinction coefficients RF555W = 3.227 and RF814W = 1.856, obtained from Cardelli et al. (1989) and Girardi et al. (2002). For every source in our catalogue, we then identified the n closest reference stars and computed the σ-clipped median of their geometric distances: the result is the ΔX value finally assigned to the source, which is transformed into the relative differential reddening δE(B − V) by using Eq. (1) in Deras et al. (2023). To increase the spatial resolution we iteratively performed this computation three times using the n = 100, 50, and 25 closest stars.

This allowed us to generate the reddening map shown in Fig. 4, which clearly shows the inhomogeneity of the medium causing differential reddening across the cluster. The differential variations of the colour excess are admittedly modest, ranging between −0.04 < δE(B − V) < 0.03 within the sampled field of view. Nevertheless, the broadening of the main evolutionary sequences is significantly reduced and the main features in the CMD look sharper after correction for differential reddening (see Fig. 5). We use this corrected CMD in the subsequent analyses of this work.

thumbnail Fig. 4.

Differential reddening map of NGC 6284 within the field of view sampled by the WFC3 images. Lighter colours correspond to less extincted areas (see the colour bar). The blue cross marks the cluster Cgrav and the coordinates along the x- and y-axes are referred to it.

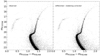thumbnail Fig. 5.

Comparison between the original CMD obtained from the HST WFC3 observations used in this work (left panel), and the CMD after it has been corrected for differential reddening (right panel).

5. Isochrone fitting

To simultaneously obtain a photometric estimate of the absolute age, metallicity, distance modulus, and absolute average reddening of NGC 6284, we have applied a Bayesian procedure similar to that used by Cadelano et al. (2020b, see also Saracino et al. 2019; Cadelano et al. 2019, 2020a; Deras et al. 2023), which consists in performing an isochrone fitting of the CMD corrected for differential reddening. The isochrones were extracted from three different databases, namely, DSED (Dotter et al. 2008), BaSTI (Pietrinferni et al. 2021), and PARSEC (Marigo et al. 2017). For each isochrone, we assumed a standard He mass fraction (Y = 0.25), and [α/Fe] = +0.4, which is a typical value for Galactic GCs. To minimise the contamination from field interlopers and further improve the accuracy of our results, we only considered stars within 50″ of Cgrav (see Sect. 3), with high-quality photometry (i.e. sharpness parameter |sh|≤0.025) and observed in the MS-TO, SGB, and RGB up to the RGB bump, that is, in the magnitude range 17.5 < mF555W < 21.0. In fact, this is the region most sensitive to stellar age and metallicity variations. A grid of isochrones was computed in a wide range of ages (from 10.0 to 15.0 Gyr), metallicities (from [Fe/H] = −2.10 to [Fe/H] = −0.90), distance moduli (between 15.00 and 17.00), and colour excess E(B − V) (between 0.10 and 0.50). The comparison between the CMD and the adopted grid of isochrones has been performed by using the MCMC sampling technique, following the same computational approach described in Cadelano et al. (2020b, see their Sect. 4.2). To sample the posterior probability distribution in the n-dimensional parameter space, we used the emcee code (Foreman-Mackey et al. 2013, 2019). For reddening and distance modulus we adopted Gaussian prior distributions peaked at E(B − V) = 0.28 ± 0.03 (Harris 1996) and (m − M)0 = 15.76 ± 0.06 (Baumgardt & Vasiliev 2021), respectively. For the age and metallicity, we assumed flat priors in the adopted range of values. When converting absolute magnitudes to the observed frame, we adopted the temperature-dependent extinction coefficients from Casagrande & VandenBerg (2014).

The left panels of Fig. 6 show the CMD and the best-fit isochrones with their 1σ uncertainty for the three adopted sets of theoretical models (see labels). The one- and two-dimensional posterior probabilities for all of the parameter combinations are presented on the right panels as corner plots. Table 1 summarises the best-fit values of the four parameters and their uncertainties (based on the 16th, 50th, 84th percentiles). The results obtained from the different sets of models are consistent within the uncertainties, and we therefore adopted their average as final best-fit estimate of the four parameters: namely, t = 13.3 ± 0.4 Gyr, [Fe/H] = −1.36 ± 0.01, E(B − V) = 0.32 ± 0.01, and (m − M)0 = 15.61 ± 0.04 (corresponding to a distance of 13.2 kpc).

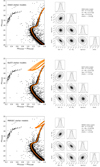thumbnail Fig. 6.

Isochrone fitting of the CMD of NGC 6284 corrected for differential reddening. Left panels show the best-fit corresponding to the DSED, BaSTI and PARSEC isochrones (top, middle and bottom panel, respectively) plotted as a red solid line, and the 1σ envelope shaded in orange. Right panels show the corner plots with the one- and two-dimensional projections of the posterior probability distributions for all the parameters as obtained from DSED, BaSTI and PARSEC isochrones (top, middle and bottom panel, respectively). The contours correspond to the 1σ, 2σ, and 3σ levels.

Table 1.

Best-fit values of age, metallicity, colour excess, and absolute distance modulus obtained from isochrone fitting.

6. The RGB bump

One of the most notable features along the RGB is the so-called RGB bump. This evolutionary feature flags the moment when the hydrogen-burning shell reaches the hydrogen discontinuity left by the innermost penetration of the convective envelope (see the seminal works by Fusi Pecci et al. 1990; Ferraro et al. 1991, 1992, 1999a, 2000; see also the compilations by Zoccali et al. 1999; Valenti et al. 2004, and more recently by Nataf et al. 2013).

During the RGB evolution, the luminosity of low-mass stars is provided by hydrogen burning reactions in a shell that progressively moves outwards. At the same time, the convective envelope recedes towards the stellar surface, leaving behind chemically mixed material. This translates in a constant hydrogen abundance down to the innermost radial distance reached by convection, which is flagged by a sharp chemical discontinuity (see, e.g. Fig. 5.15 of Salaris & Cassisi 2006). The RGB bump corresponds to the moment when the hydrogen-burning shell passes through this discontinuity. Hence, the predicted luminosity of the RGB bump depends on the parameters and physical processes regulating the ability of convection to penetrate deep into the stellar interior (for instance, the parameters affecting the stellar opacity, as the heavy element and the helium abundances): in the case of a deeper penetration, the hydrogen burning shell crosses at earlier times the chemical discontinuity left by the convective envelope, and the bump occurs at fainter magnitudes along the RGB. The observational determination of the RGB-bump luminosity therefore provides crucial constraints to stellar evolutionary models, especially if measured in large samples of stellar systems with different properties (e.g. with different metallicities).

From the observational point of view, this event produces two main signatures that are intimately linked to the physical processes occurring in the stellar interior: (1) a bump in the RGB differential luminosity function (i.e. an increase in star counts at the RGB-bump luminosity) due to a temporary hesitation in the star evolutionary path while climbing the RGB, and (2) a change in the slope of the RGB-integrated luminosity function due to a change in the evolutionary speed when the burning shell passes from a region of variable hydrogen abundance (moderate climbing speed), to a region of constant hydrogen abundance (fast climbing speed). As discussed in many papers (e.g. Fusi Pecci et al. 1990; Ferraro et al. 1999a, 2000), the latter observable is a powerful diagnostic especially in situations of poor statistics, since it is obtained from incremental star counts over a range of several magnitudes: this makes it much less prone to statistical fluctuations with respect to the case of a differential luminosity function, where stars are counted in discrete bins of magnitude.

To add further contribution to the observational estimate of the RGB-bump luminosity in clusters with different properties, here we determined these two diagnostics in the case of NGC 6284. From a visual inspection of Fig. 5, the location of the RGB bump is easily recognisable in the CMD as a grouping of stars about halfway along the RGB. However, to properly determine its magnitude level, we selected the RGB population from the differential reddening-corrected CMD and we determined its integrated and differential luminosity functions (top and bottom panels of Fig. 7, respectively). A clear change in the slope in the integrated luminosity function (due to a variation in the climbing speed of stars along the RGB), and a star count excess in the differential luminosity function (testifying their temporary evolutionary hesitation) are well apparent in the figure, and they allow the precise determination of the RGB-bump magnitude (see the arrows): mF555W = 17.46 ± 0.05 and mF814W = 16.00 ± 0.05.

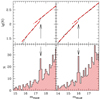thumbnail Fig. 7.

Integrated (top panels) and differential (bottom panels) luminosity functions of RGB stars in the F555W and F814W filters (left and right panels, respectively). The two vertical arrows mark the change in the slope (top) and the local peak (bottom) unequivocally indicating the occurrence of the RGB bump.

One of the parameters affecting the RGB-bump luminosity is the cluster overall metallicity: for increasing metallicity, the stellar opacity increases, the convective envelope penetrates deeper in the interior of the star, and the RGB-bump therefore occurs at fainter magnitudes along the RGB. Indeed, a strong relation is observed between the metallicity and the RGB-bump magnitude of Galactic GCs, a recent compilation (also including NGC 6284) being presented in Nataf et al. (2013). To compare our determination with the values in this compilation, we first need to convert our WFC3 F555W and F814W magnitudes into the standard (Johnson) V and I magnitudes. According to Harris (2018), the following simple transformations can be adopted: (V − mF555W)0 = −0.093 × (V − I)0 and (I − mF814W)0 = 0, where the subscript refers to reddening-corrected magnitudes. We therefore used the average colour excess estimated in the previous section, E(B − V) = 0.32, to determine the reddening-corrected WFC3 magnitudes of the RGB-bump. Then, by applying the transformations above, we found 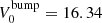V 0 bump =16.34 $ V_0^{\rm bump} = 16.34 $. By adopting the true distance modulus previously estimated, (m − M)0 = 15.61, this corresponds to a Johnson V-band absolute magnitude 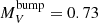M V bump =0.73 $ M_V^{\rm bump} = 0.73 $, with an uncertainty of about 0.05 mag. To determine the cluster global metallicity we used the relation reported in Salaris et al. (1993), adopting [α/Fe] = +0.4 and the photometric estimate of the iron abundance derived in the previous section ([Fe/H] = −1.36), thus finding [M/H] = −1.07. Figure 8 shows our estimate (large blue circle) compared to the values listed in the Nataf et al. (2013) compilation. While fitting into the overall trend, the value found in the present study is ∼0.2 mag fainter than that quoted by Nataf et al. (2013, which is highlighted by a red empty circle in the figure).

thumbnail Fig. 8.

Absolute magnitude of the RGB bump in the Johnson V band as a function of the global metallicity [M/H] for a large sample of Galactic GCs (grey symbols, from Nataf et al. 2013). The large blue circle marks the value determined in this work for NGC 6284, while the red empty circle marks the measure quoted in Nataf et al. (2013).

7. Summary and conclusions

By using high-resolution HST observations, we obtained the first high-quality CMD of NGC 6284, extending down to ∼6 mag below its MS-TO. This allowed us to properly characterise the innermost regions of this high-density and poorly studied GC, which is located in the direction of the Galactic bulge outskirts.

For the first time, we determined the centre of gravity and the density profile of the cluster from resolved star counts. We found that Cgrav is displaced by 1.5 − 3″ from the values reported in the literature (Harris 1996; Baumgardt & Hilker 2018). The correct determination of the cluster centre allowed us to clearly detect the presence of a steep power-law cusp in the innermost portion (r < 4.5″) of the projected density profile, in agreement with previous findings from surface brightness investigations that classified NGC 6284 as a PCC cluster (see Lugger et al. 1995, and references therein). By complementing our HST photometry with a wide-field catalogue from Gaia-DR3, we determined the cluster density profile over its entire radial extension and properly characterised (and then subtracted) the contribution from the Galactic field, which starts to become dominating at r ∼ 200″ from the centre. As expected, the overall profile cannot be properly described by a King model, due to the presence of the central cusp (see Fig. 2). By forcing the fit in the innermost portion of the profile, the best solution is a King model with a very high concentration parameter (c = 2.55) and very small core radius (rc = 2.8″, corresponding to 0.18 pc at the distance determined in this work). However, this model clearly overestimates the stellar density in the cluster outskirts, leading to unreliably large values of the half-mass and tidal radii. A proper fit to the entire profile requires a two component model, consisting in a power law with slope αcusp = −0.53 in the innermost region (r < 5″), and a single-mass King model with concentration c = 1.54, core radius rc = 10.3″ (0.66 pc), and half-mass radius rh = 43″ (2.75 pc) at larger distances. These are the typical features observed in the case of highly evolved GCs that already experienced core collapse.

The acquired observations also allowed us to determine a high-resolution reddening map in the cluster direction, which shows moderate inhomogeneities (Fig. 4). In particular, it is worth noticing the patchy semi-horizontal strip in the northern hemisphere, near Cgrav. We extracted isochrones from three different sets of models (DSED, BaSTI, and PARSEC) and used them to perform a fit to the MS-TO and RGB regions of the differential reddening corrected CMD. With the caveat that a fit with four free parameters may be prone to degeneracies, this allowed us to obtain updated estimates of the absolute age, metallicity, distance modulus, and reddening of this poorly studied cluster (see Table 1). Our estimate of the age yields 13.3 ± 0.4 Gyr, which is about 2 Gyr older than some values reported in the literature (see Sect. 1), but consistent with the age of most GCs in our Galaxy. The derived a metallicity ([Fe/H] = −1.36 ± 0.01) is consistent with the value measured back in 1984 from low-resolution spectroscopy (Zinn & West 1984, see also Harris 1996). The distance modulus (m − M)0 = 15.61 ± 0.04 translates into a distance of 13.2 ± 0.2 kpc. This is ∼1 kpc smaller than the one reported by Baumgardt & Vasiliev (2021, 14.2 kpc), and ∼2 kpc smaller than the one quoted by Harris (1996, 15.2 kpc), but consistent with that obtained from RR Lyrae by Clement et al. (1980, 12.9 kpc). We estimate an absolute reddening E(B − V) = 0.32 ± 0.01, which is slightly larger than the average value found in the literature (0.28), but still consistent with it within the typically adopted 10% uncertainty.

The high quality of the CMD derived in this work also allowed for the clear identification of the RGB bump. Based on the integrated and differential RGB luminosity functions (Fig. 7), we find that this feature is ∼0.2 mag fainter than in previous identifications, but still fits the relation between the RGB-bump absolute magnitude and the global metallicity of the system drawn by Galactic GCs (see Fig. 8).

The King structural parameters are commonly used to estimate the central and half-mass relaxation times of star clusters, by using Eqs. (10) and (11) in Djorgovski (1993). In practice, however, this is not obvious in the case of core collapsed systems, where the King model family is unable to properly reproduce the observed density distribution. Keeping these limitations in mind, a possible way to circumvent this problem is to estimate the central relaxation time trc from the King model that best fits the innermost portion of the density profile (left panel in Fig. 2), and the half-mass relaxation time trh from the King model reproducing the outer part of it (right panel in the same figure). This is because trc primarily depends on the values of rc, while trh is mainly driven by the half-mass radius rh (see Djorgovski 1993), and the two mentioned profiles provide the most appropriate estimates of these two radial scales, respectively. Hence, by adopting rc = 2.8″, together with c = 2.55, the distance modulus and reddening estimated in this work, and the integrated V-band magnitude and central surface brightness quoted in the Harris (1996) catalogue, we find log(trc)≃6.72 (in units of years). Adopting rh = 43″ (from the fit to the outer portion of the profile), we find log(trh) = 9.06. The latter value is in good agreement with the estimates reported in Harris (1996) and in Baumgardt & Hilker (2018), and we verified that it remains almost unchanged even by adopting alternative King models aimed at simultaneously reproducing as much as possible both the inner and the outer portions of the density profile (see an example in Fig. 9). This is because the value of rh varies only slightly. Conversely, the central relaxation time quoted in the Harris (1996) catalogue is much larger, log(trc) = 7.24, mainly because of a larger value adopted for the core radius (rc = 0.3 pc), resulting from a fit to the surface brightness profile obtained by fixing c = 2.5 (Trager et al. 1993). This highlights the importance of forcing the fit to the innermost portion of the density profile (as in the left panel of Fig. 2) if one aims to estimate their central relaxation time of PCC clusters.

thumbnail Fig. 9.

As in Fig. 2, but with a King model (red line) that aimed to approximately reproduce both the inner and the outer regions of the profile simultaneously.

Table 2 summarises the value of the main parameters obtained in this work for NGC 6284. A solid determination of the cluster distance from independent methods and the measure of iron and α-element abundances from high-resolution spectroscopy are now urged to improve these values. In fact, once the distance and the metallicity are properly fixed, the number of free parameters in the isochrone fitting procedure would decrease and a more accurate estimate of all the other quantities characterising this poorly investigated cluster would finally be obtained.

Table 2.

General parameters of NGC 6284.

Acknowledgments

This research is part of the project Cosmic-Lab (“Star Clusters as cosmic laboratories”) at the Physics and Astronomy Department of the University of Bologna (http://www.cosmic-lab.eu/Cosmic-Lab/Home.html). The research has been funded by project Light-on-Dark, granted by the Italian MIUR through contract PRIN-2017K7REXT (PI: Ferraro). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Bajkova, A. T., & Bobylev, V. V. 2021, Res. Astron. Astrophys., 21, 173 [CrossRef] [Google Scholar]
  2. Bhat, B., Lanzoni, B., Ferraro, F. R., et al. 2022, ApJ, 926, 118 [NASA ADS] [CrossRef] [Google Scholar]
  3. Baumgardt, H., & Hilker, M. 2018, MNRAS, 478, 1520 [Google Scholar]
  4. Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bellazzini, M., Ibata, R., Malhan, K., et al. 2020, A&A, 636, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bellini, A., Anderson, J., & Bedin, L. R. 2011, PASP, 123, 622 [CrossRef] [Google Scholar]
  7. Bianchini, P., Webb, J. J., Sills, A., & Vesperini, E. 2018, MNRAS, 475, L96 [CrossRef] [Google Scholar]
  8. Cabrera-Ziri, I., & Conroy, C. 2022, MNRAS, 511, 341 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cadelano, M., Pallanca, C., Ferraro, F. R., et al. 2017a, ApJ, 844, 53 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cadelano, M., Dalessandro, E., Ferraro, F. R., et al. 2017b, ApJ, 836, 170 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cadelano, M., Ferraro, F. R., Istrate, A. G., et al. 2019, ApJ, 875, 25 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cadelano, M., Saracino, S., Dalessandro, E., et al. 2020a, ApJ, 895, 54 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cadelano, M., Chen, J., Pallanca, C., et al. 2020b, ApJ, 905, 63 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cadelano, M., Ferraro, F. R., Dalessandro, E., et al. 2022, ApJ, 941, 69 [CrossRef] [Google Scholar]
  15. Calamida, A., Bajaj, V., Mack, J., et al. 2022, AJ, 164, 32 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  17. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
  19. Casetti-Dinescu, D. I., Girard, T. M., Korchagin, V. I., et al. 2010, AJ, 140, 1282 [NASA ADS] [CrossRef] [Google Scholar]
  20. Clement, C. M., Sawyer Hogg, H., & Wells, T. R. 1980, AJ, 85, 1604 [NASA ADS] [CrossRef] [Google Scholar]
  21. Crociati, C., Valenti, E., Ferraro, F. R., et al. 2023, ApJ, 951, 17 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dalessandro, E., Salaris, M., Ferraro, F. R., et al. 2013, MNRAS, 430, 459 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dalessandro, E., Massari, D., Bellazzini, M., et al. 2014, ApJ, 791, L4 [NASA ADS] [CrossRef] [Google Scholar]
  24. Dalessandro, E., Ferraro, F. R., Bastian, N., et al. 2019, A&A, 621, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dalessandro, E., Crociati, C., Cignoni, M., et al. 2022, ApJ, 940, 170 [NASA ADS] [CrossRef] [Google Scholar]
  26. De Angeli, F., Piotto, G., Cassisi, S., et al. 2005, AJ, 130, 116 [NASA ADS] [CrossRef] [Google Scholar]
  27. Deras, D., Cadelano, M., Ferraro, F. R., Lanzoni, B., & Pallanca, C. 2023, ApJ, 942, 104 [CrossRef] [Google Scholar]
  28. Dias, B., Barbuy, B., Saviane, I., et al. 2016, A&A, 590, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Djorgovski, S. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 373 [NASA ADS] [Google Scholar]
  30. Djorgovski, S., & King, I. R. 1986, ApJ, 305, L61 [Google Scholar]
  31. Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [Google Scholar]
  32. Ferraro, F. R., Clementini, G., Fusi Pecci, F., et al. 1991, MNRAS, 252, 357 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ferraro, F. R., Clementini, G., Fusi Pecci, F., et al. 1992, MNRAS, 256, 391 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ferraro, F. R., Paltrinieri, B., Fusi Pecci, F., et al. 1997, ApJ, 484, L145 [Google Scholar]
  35. Ferraro, F. R., Messineo, M., Fusi Pecci, F., et al. 1999a, AJ, 118, 1738 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ferraro, F. R., Paltrinieri, B., Rood, R. T., et al. 1999b, ApJ, 522, 983 [CrossRef] [Google Scholar]
  37. Ferraro, F. R., Montegriffo, P., Origlia, L., et al. 2000, AJ, 119, 1282 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ferraro, F. R., Possenti, A., Sabbi, E., et al. 2003, ApJ, 595, 179 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ferraro, F. R., Dalessandro, E., Mucciarelli, A., et al. 2009, Nature, 462, 483 [Google Scholar]
  40. Ferraro, F. R., Lanzoni, B., Dalessandro, E., et al. 2012, Nature, 492, 393 [Google Scholar]
  41. Ferraro, F. R., Massari, D., Dalessandro, E., et al. 2016, ApJ, 828, 75 [NASA ADS] [CrossRef] [Google Scholar]
  42. Ferraro, F. R., Mucciarelli, A., Lanzoni, B., et al. 2018a, ApJ, 860, 50 [NASA ADS] [CrossRef] [Google Scholar]
  43. Ferraro, F. R., Lanzoni, B., Raso, S., et al. 2018b, ApJ, 860, 36 [NASA ADS] [CrossRef] [Google Scholar]
  44. Ferraro, F. R., Lanzoni, B., Dalessandro, E., et al. 2019, Nat. Astron., 3, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ferraro, F. R., Pallanca, C., Lanzoni, B., et al. 2021, Nat. Astron., 5, 311 [Google Scholar]
  46. Ferraro, F. R., Lanzoni, B., Vesperini, E., et al. 2023, ApJ, 950, 145 [NASA ADS] [CrossRef] [Google Scholar]
  47. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  48. Foreman-Mackey, D., Farr, W., Sinha, M., et al. 2019, J. Open Source Softw., 4, 1864 [NASA ADS] [CrossRef] [Google Scholar]
  49. Fusi Pecci, F., Ferraro, F. R., Crocker, D. A., et al. 1990, A&A, 238, 95 [NASA ADS] [Google Scholar]
  50. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Gnedin, O. Y., & Ostriker, J. P. 1997, ApJ, 474, 223 [Google Scholar]
  53. Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
  54. Harris, W. E. 2018, AJ, 156, 296 [NASA ADS] [CrossRef] [Google Scholar]
  55. Ibata, R., Bellazzini, M., Chapman, S. C., et al. 2009, ApJ, 699, L169 [NASA ADS] [CrossRef] [Google Scholar]
  56. King, I. R. 1966, AJ, 71, 64 [Google Scholar]
  57. Kundu, R., Navarrete, C., Sbordone, L., et al. 2022, A&A, 665, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Lanzoni, B., Dalessandro, E., Ferraro, F. R., et al. 2007a, ApJ, 668, L139 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lanzoni, B., Dalessandro, E., Ferraro, F. R., et al. 2007b, ApJ, 663, 267 [NASA ADS] [CrossRef] [Google Scholar]
  60. Lanzoni, B., Sanna, N., Ferraro, F. R., et al. 2007c, ApJ, 663, 1040 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lanzoni, B., Ferraro, F. R., Dalessandro, E., et al. 2010, ApJ, 717, 653 [Google Scholar]
  62. Lanzoni, B., Ferraro, F. R., Alessandrini, E., et al. 2016, ApJ, 833, L29 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lanzoni, B., Ferraro, F. R., Mucciarelli, A., et al. 2018a, ApJ, 861, 16 [NASA ADS] [CrossRef] [Google Scholar]
  64. Lanzoni, B., Ferraro, F. R., Mucciarelli, A., et al. 2018b, ApJ, 865, 11 [NASA ADS] [CrossRef] [Google Scholar]
  65. Lanzoni, B., Ferraro, F. R., & Dalessandro, E. 2019, ApJ, 887, 176 [NASA ADS] [CrossRef] [Google Scholar]
  66. Leanza, S., Pallanca, C., Ferraro, F. R., et al. 2022, ApJ, 929, 186 [NASA ADS] [CrossRef] [Google Scholar]
  67. Leanza, S., Pallanca, C., Ferraro, F. R., et al. 2023, ApJ, 944, 162 [NASA ADS] [CrossRef] [Google Scholar]
  68. Lugger, P. M., Cohn, H. N., & Grindlay, J. E. 1995, ApJ, 439, 191 [Google Scholar]
  69. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
  70. Massari, D., Mucciarelli, A., Ferraro, F. R., et al. 2014, ApJ, 795, 22 [NASA ADS] [CrossRef] [Google Scholar]
  71. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Meissner, F., & Weiss, A. 2006, A&A, 456, 1085 [CrossRef] [EDP Sciences] [Google Scholar]
  73. Meylan, G., & Heggie, D. C. 1997, A&ARv, 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
  74. Minniti, D., Olszewski, E. W., & Rieke, M. 1995, AJ, 110, 1686 [NASA ADS] [CrossRef] [Google Scholar]
  75. Miocchi, P., Lanzoni, B., Ferraro, F. R., et al. 2013, ApJ, 774, 151 [Google Scholar]
  76. Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
  77. Montegriffo, P., Ferraro, F. R., Fusi Pecci, F., & Origlia, L. 1995, MNRAS, 276, 739 [NASA ADS] [Google Scholar]
  78. Nataf, D. M., Gould, A. P., Pinsonneault, M. H., et al. 2013, ApJ, 766, 77 [NASA ADS] [CrossRef] [Google Scholar]
  79. Noyola, E., & Gebhardt, K. 2006, AJ, 132, 447 [Google Scholar]
  80. Origlia, L., Ferraro, F. R., Fusi Pecci, F., et al. 2002, ApJ, 571, 458 [NASA ADS] [CrossRef] [Google Scholar]
  81. Origlia, L., Ferraro, F. R., Bellazzini, M., et al. 2003, ApJ, 591, 916 [CrossRef] [Google Scholar]
  82. Origlia, L., Rich, R. M., Ferraro, F. R., et al. 2011, ApJ, 726, L20 [CrossRef] [Google Scholar]
  83. Pallanca, C., Ferraro, F. R., Lanzoni, B., et al. 2019, ApJ, 882, 159 [NASA ADS] [CrossRef] [Google Scholar]
  84. Pallanca, C., Ferraro, F. R., Lanzoni, B., et al. 2021a, ApJ, 917, 92 [NASA ADS] [CrossRef] [Google Scholar]
  85. Pallanca, C., Lanzoni, B., Ferraro, F. R., et al. 2021b, ApJ, 913, 137 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pallanca, C., Leanza, S., Ferraro, F. R., et al. 2023, ApJ, 950, 138 [NASA ADS] [CrossRef] [Google Scholar]
  87. Penny, A. J. 1976, PhD Thesis, University of Sussex, UK [Google Scholar]
  88. Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
  89. Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Raso, S., Libralato, M., Bellini, A., et al. 2020, ApJ, 895, 15 [NASA ADS] [CrossRef] [Google Scholar]
  91. Recio-Blanco, A., Piotto, G., de Angeli, F., et al. 2005, A&A, 432, 851 [CrossRef] [EDP Sciences] [Google Scholar]
  92. Romano, D., Ferraro, F. R., Origlia, L., et al. 2023, ApJ, 951, 85 [NASA ADS] [CrossRef] [Google Scholar]
  93. Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
  94. Salaris, M., & Cassisi, S. 2006, Evolution of Stars and Stellar Populations by Maurizio Salaris and Santi Cassisi (Wiley) [Google Scholar]
  95. Saracino, S., Dalessandro, E., Ferraro, F. R., et al. 2019, ApJ, 874, 86 [Google Scholar]
  96. Smith, H. A., & Perkins, G. J. 1982, ApJ, 261, 576 [CrossRef] [Google Scholar]
  97. Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
  98. Stetson, P. B. 1994, PASP, 106, 250 [Google Scholar]
  99. Trager, S. C., Djorgovski, S., & King, I. R. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 347 [Google Scholar]
  100. Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef] [Google Scholar]
  101. Usher, C., Beckwith, T., Bellstedt, S., et al. 2019, MNRAS, 482, 1275 [Google Scholar]
  102. Valenti, E., Ferraro, F. R., & Origlia, L. 2004, MNRAS, 354, 815 [NASA ADS] [CrossRef] [Google Scholar]
  103. Valenti, E., Ferraro, F. R., & Origlia, L. 2010, MNRAS, 402, 1729 [NASA ADS] [CrossRef] [Google Scholar]
  104. Webbink, R. F. 1985, in Dynamics of Star Clusters, eds. J. Goodman, & P. Hut, 113, 541 [Google Scholar]
  105. Zinn, R. 1985, ApJ, 293, 424 [Google Scholar]
  106. Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [Google Scholar]
  107. Zoccali, M., Cassisi, S., Piotto, G., et al. 1999, ApJ, 518, L49 [CrossRef] [Google Scholar]
  108. Zocchi, A., Gieles, M., Hénault-Brunet, V., & Varri, A. L. 2016, MNRAS, 462, 696 [Google Scholar]

All Tables

Table 1.

Best-fit values of age, metallicity, colour excess, and absolute distance modulus obtained from isochrone fitting.

In the text
Table 2.

General parameters of NGC 6284.

In the text

All Figures

thumbnail Fig. 1.

CMD of NGC 6284 obtained from the HST WFC3 dataset used in this work. F555W and F814W magnitudes have been plotted along the y-axis on the left and right panels, respectively.
In the text
thumbnail Fig. 2.

Star density profile of NGC 6284. The left panel shows the observed profile (empty circles) and the background-subtracted profile (filled circles). The dashed horizontal line is the background density value used to decontaminate the cluster profile from the Galactic field contribution. The solid red curve is the King model that best fits the innermost portion of the profile, obtained for illustrative purposes by artificially increasing the errors of the outer points. The corresponding values of some structural parameters are labelled. The bottom panel shows the residuals between the best-fit King model and the cluster density profile. In the right panel, the circles are the same as in the left panel, but the four innermost points are coloured in red to highlight the presence of a central density cusp. These have been fitted with the power-law function shown as a red dashed line, with slope αcusp = −0.53. The best-fit King model to the profile beyond the four inner points (black solid circles) is shown with the red solid curve, and is characterised by the labelled structural parameters.
In the text
thumbnail Fig. 3.

Density profile obtained in this work, calculated with respect to the value of Cgrav quoted in Sect. 3.1, is shown with grey circles (same as the empty circles in Fig. 2). Left and right panels show the projected density profile calculated with respect to the cluster centres quoted in the Harris (1996) catalogue and in Baumgardt & Hilker (2018), respectively (black circles). Only the inner portion of the profile, out to r ∼ 100″, is shown in the figure.
In the text
thumbnail Fig. 4.

Differential reddening map of NGC 6284 within the field of view sampled by the WFC3 images. Lighter colours correspond to less extincted areas (see the colour bar). The blue cross marks the cluster Cgrav and the coordinates along the x- and y-axes are referred to it.
In the text
thumbnail Fig. 5.

Comparison between the original CMD obtained from the HST WFC3 observations used in this work (left panel), and the CMD after it has been corrected for differential reddening (right panel).
In the text
thumbnail Fig. 6.

Isochrone fitting of the CMD of NGC 6284 corrected for differential reddening. Left panels show the best-fit corresponding to the DSED, BaSTI and PARSEC isochrones (top, middle and bottom panel, respectively) plotted as a red solid line, and the 1σ envelope shaded in orange. Right panels show the corner plots with the one- and two-dimensional projections of the posterior probability distributions for all the parameters as obtained from DSED, BaSTI and PARSEC isochrones (top, middle and bottom panel, respectively). The contours correspond to the 1σ, 2σ, and 3σ levels.
In the text
thumbnail Fig. 7.

Integrated (top panels) and differential (bottom panels) luminosity functions of RGB stars in the F555W and F814W filters (left and right panels, respectively). The two vertical arrows mark the change in the slope (top) and the local peak (bottom) unequivocally indicating the occurrence of the RGB bump.
In the text
thumbnail Fig. 8.

Absolute magnitude of the RGB bump in the Johnson V band as a function of the global metallicity [M/H] for a large sample of Galactic GCs (grey symbols, from Nataf et al. 2013). The large blue circle marks the value determined in this work for NGC 6284, while the red empty circle marks the measure quoted in Nataf et al. (2013).
In the text
thumbnail Fig. 9.

As in Fig. 2, but with a King model (red line) that aimed to approximately reproduce both the inner and the outer regions of the profile simultaneously.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.