| Issue |
A&A
Volume 681, January 2024
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202346099 | |
| Published online | 18 January 2024 | |
Testing MURaM and MPS-ATLAS against the quiet solar spectrum
1
Max Planck Institute for Solar System Research,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
e-mail: witzke@mps.mpg.de
2
Institut Supérieur de l’Aéronautique et de l’Espace (ISAE-SUPAERO),
31400
Toulouse,
France
3
Institut für Astrophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
4
Center for Space Science, NYUAD Institute, New York University Abu Dhabi,
PO Box 129188,
Abu Dhabi,
UAE
5
Department of Physics, Imperial College London,
London
SW7 2AZ,
UK
6
Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences,
PR China
Received:
7
February
2023
Accepted:
6
October
2023
Context. Three-dimensional (3D) radiative magnetohydrodynamic (MHD) simulations are the only way to model stellar atmospheres without any ad hoc parameterisations. Several 3D radiative MHD codes have achieved good quantitative agreement with observables for our Sun.
Aims. We aim to validate the most recent version of the MURaM code by comparing MURaM results to well-established quiet-Sun measurements, in particular spatially averaged measurements that are relevant for stellar studies. This extends the number of solar observables that MURaM can reproduce with high precision. Our validation is an essential condition to ensure that MURaM can be used to accurately calculate the spectra of other cool stars.
Methods. We simulated the solar photosphere and upper convection zone, which harbours a small-scale-dynamo. Using time series of 3D snapshots, we calculated the spectral irradiance, limb darkening, and selected spectral lines, which we compared to observations.
Results. The computed observables agree well with the observations; in particular, the limb darkening of the quiet Sun is reproduced remarkably well.
Key words: methods: numerical / magnetohydrodynamics (MHD) / radiative transfer / Sun: photosphere
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
The conditions and physical processes in the solar photosphere are complex; not only does the radiative transfer (RT) in the photosphere play a role, but so does the convective motion in the layer beneath it, the convection zone, and the magnetic field. Accordingly, the solar photosphere needs to be described by means of radiative magnetohydrodynamics (MHD). A milestone was reached when realistic 3D hydrodynamic (HD) simulations (i.e. without magnetic fields) of the lower solar atmosphere became numerically feasible (Nordlund 1982) and allowed the transfer of energy in stellar atmospheres to be reproduced without any additional ad hoc parameterisations (e.g. mixing length approximation; see Böhm-Vitense 1958).
Following the success of solar 3D HD simulations, they were extended to other cool stars, resulting in grids of stellar models that cover the spectral classes F–M (Magic et al. 2013). Such HD simulations were used for numerous applications, for example modelling stellar limb darkening (Magic et al. 2015) and stellar spectra (Chiavassa et al. 2018). At the same time, MHD simulations were introduced to take various magnetic phenomena in the solar near-surface layers into account, for example network and facular regions (Nordlund & Stein 1990; Vögler et al. 2005), pores (Cameron et al. 2007), and sunspots (Rempel et al. 2009).
In the last decade, 3D MHD simulations of the solar atmosphere were further developed and have achieved extraordinary agreement with detailed solar observations. Therefore, once more, the concept was expanded to stars other than the Sun. For example, Beeck et al. (2015) and Salhab et al. (2018) calculated faculae on stars of various effective temperatures.
Until recently, quiet solar regions, despite being covered by small-scale magnetic fields of mixed polarity (which are sometimes called turbulent magnetic fields) even in their quietest state (Khomenko et al. 2003; Berdyugina & Fluri 2004; Trujillo Bueno et al. 2004; Lites & Socas-Navarro 2004; Stenflo 2013), were modelled based on non-magnetic HD simulations. This changed with the effort to model the solar quiet regions using the state-of-the-art code MURaM and including a small-scale dynamo (SSD) driven by near-surface convection (Vögler & Schüssler 2007; Schüssler & Vögler 2008; Rempel 2014). With the new version of the MURaM code, which includes an updated equation of state (EOS) and opacity table, we have started to calculate an extensive grid of stellar 3D model atmospheres that also accounts for the action of the SSD.
Previous studies focused on spatially resolved solar observations, showing good agreement with MURaM simulations (e.g. Schüssler et al. 2003; Shelyag et al. 2004; Keller et al. 2004; Hirzberger et al. 2010; Riethmüller et al. 2014). Moreover, using averaged quantities, it has been shown that facular contrasts are sufficiently well modelled to accurately reproduce total solar irradiance (TSI) variations (Yeo et al. 2017). However, careful comparisons with the quiet-Sun centre-to-limb variations (CLVs), the solar spectral irradiance (SSI) spectrum, and line bisectors have not yet been carried out. Since they are necessary to validate the accuracy of the 3D model atmospheres for high precision stellar studies, we have taken on the perhaps overdue task of confronting MURaM with observations of the quiet Sun, concentrating on spatially averaged data.
The paper is structured as follow: in Sect. 2, we give a brief description of the codes used and review the most recent improvements of the MURaM code. We then compare the calculated low-resolution spectra and a few high-resolution spectral lines to observations in Sect. 3 and present our conclusions in Sect. 4.
2 MURaM 3D cubes and MPS-ATLAS radiative transfer
To model the dynamics and energy transfer in the upper con-vective zone and photosphere, the MURaM code takes the box-in-a-star approach. For that, the conservative MHD equations for a compressible, partially ionised plasma are solved numerically in a Cartesian box that spans the upper convection zone, the solar surface, and the photosphere. Partial ionisation is crucial for the convective energy transfer in the upper convective zone and for the transfer of radiative energy, which takes over from convection as the dominant energy transport mechanism in the solar photosphere. The RT in the MURaM code is taken care of by a multi-group scheme (Nordlund 1982) with short characteristics (for a detailed description, see Vögler et al. 2004, and references therein). More detailed descriptions of the governing equations and numerical implementation are given in Vögler et al. (2004), Rempel (2014), Przybylski et al. (2022), and Bhatia et al. (2022).
Since the development of the MURaM code (Vögler et al. 2004, 2005) for simulations of the solar convection zone and photosphere, much effort has been put into further advancing the code to achieve more accurate calculations and a wider range of applications. For example, boundary conditions that take the effect of the deeper convection layers into account were implemented. This results in a good agreement between the observed and modelled turbulent magnetic flux in the photosphere (Rempel 2014). The EOS look-up table, which in the new MURaM setup is generated by the FreeEOS code (Irwin 2012), and the opacity table were updated to the most accurate element composition (Asplund et al. 2009), hereafter referred to as the Asplund composition. Furthermore, the radiative treatment was upgraded to consider 12 multi-group bins with similar thresholds as in Magic et al. (2013) Finally, the implementation was modified to reduce the diffusive terms as much as possible (Rempel 2014).
We used the same box size, grid resolution, and boundary conditions as in Witzke et al. (2022). In particular, the entropy inflow and pressure at the bottom were chosen such that an effective temperature of 5787 K is sustained. The simulation domain reaches 4 Mm below the optical surface into the convection zone and 1 Mm above it (which covers the photosphere up to the temperature minimum) with a grid resolution of (512 × 512 × 500) grid points. We ran four independent sets, each of at least 1 h solar time and saved cubes every 90s, resulting in 160 cubes. We verified that this is sufficient to average out temporal fluctuations of all the observables we synthesised.
To synthesise emergent spectra from the 3D simulations, we applied the so-called 1.5D approach, that is, we calculated the RT along many mutually parallel rays passing through a 3D cube. Due to the large number of RT calculations necessary for this approach, it is computationally expensive but feasible using the recently developed MPS-ATLAS code (Witzke et al. 2021). MPS-ATLAS pre-tabulates opacity tables (using Kurucz’s original line lists1) either with a high resolving power that allows for separate spectral line calculations or using the opacity distribution functions (ODF) approach on a low-resolution wavelength grid. We note that the opacity tables used in the MURaM code were also calculated using the MPS-ATLAS code. For the high-resolution spectral line synthesis, we accounted for the Doppler effect using the line-of-sight component of the velocity from the 3D cubes (for a more detailed description of the Doppler shift implementation, see Mauviard, in prep.). This allowed us to compute both emergent low-spectral-resolution spectra and profiles of individual spectral lines.
We considered different viewing angles, µ = cos(θ), where θ is the angle between the observer’s direction and the position vector defined with respect to the centre of the star. For that, we rotated the 3D cube around a pivot axis at the optical surface using the corresponding θ and computed the temperature, pressure, density, and velocity along the line of sight from the cube. For the so-obtained 3D cube, we interpolated to keep a vertical resolution of 10 km between the grid points, as in the original cube. The RT calculations for each viewing angle were then performed using the corresponding rotated cube. The resulting intensity along any particular direction is obtained by combining the intensities along parallel rays, which sample the whole simulation cube. Subsequently, we averaged the intensities over all 160 cubes. For the solar irradiance and CLVs, we computed ten viewing angles from disk centre (µ = 1.0) in steps of 0.1 towards the limb. The high-resolution spectral line calculations were only performed for the disk centre.
3 Comparison to observations
We chose three different observed quantities, the spectral irradiance (Sect. 3.1), limb darkening (Sect. 3.2), and profiles and bisectors of spectral lines (Sect. 3.3), to test how accurately the MURaM code models the spatially averaged solar photosphere. The vertical temperature structure of the MURaM 3D cubes can be assessed when comparing the modelled irradiance and its limb darkening to observations. In particular, the limb darkening behaviour is very sensitive to temperature in all photospheric layers. At the same time, line bisectors provide a standard test of the convective velocities (Asplund et al. 2000) and temperature inhomogeneities produced by MURaM.
3.1 Solar spectral irradiance
For the spectral irradiance, we computed emergent spectra at 1 AU from the Sun with a low spectral resolution using the ODF approach and the ‘little’ wavelength grid from Castelli (2005) in the interval 250nm to 2000nm. In order to calculate the disk-integrated flux and the limb darkening, we considered ten viewing angles starting at the disk centre (µ = 1.0) and proceeding in steps of 0.1 towards the limb until µ = 0.1. After obtaining all viewing angles for one cube, we calculated for each viewing angle the average over the cube and subsequently the disk-integrated flux of the cube. This procedure was then repeated for every cube and the average over all cubes was obtained along with the standard deviation (shown in Fig. 1 as the red shaded band).
We compared our calculations to solar irradiance reference spectra (SIRS) for the 2008 Whole Heliosphere Interval (WHI; Woods et al. 2009). We also considered irradiance measurements obtained by the Solar Spectral Irradiance Monitor (SSIM) on board the Fengyun-3E Satellite (FY-3E) launched in July 2021. SSIM measures irradiance from 165 nm to 2400 nm with a spectral resolution from 1 nm in the ultraviolet (UV) and visible to 8 nm in the infrared (IR). The measurements had been performed daily, and we averaged all the data from 2022. For a better comparison, the SSIM data and the calculated fluxes were smoothed out using a trapezoidal kernel (Harder, priv. comm.) to match the WHI resolution in wavelength regions where the ODF resolution is higher than that of the WHI. We kept the original resolution otherwise.
Figure 1 shows the solar irradiance calculated from the MURaM cubes together with the WHI and SSIM measurement. One can see that shortwards of 350 nm, our calculations overestimate the observed flux. This is a well-known problem common to all codes used for irradiance modelling (see e.g. Shapiro et al. 2010; Criscuoli 2019; Witzke et al. 2021, and references therein). It is thought to be caused by the lack of weak atomic and molecular lines in available line lists. In other spectral regions, our irradiance calculations are very close to the observed values and remain within the measurement uncertainties. In particular, they remain within the WHI uncertainties between 350 nm and 1400 nm. This demonstrates that MURaM properly reproduces the vertical temperature structure at the very lowest photosphere and, especially, the transfer of energy by convective overshoot and radiation in the lower solar photosphere. Interestingly, SSIM data deviate from SIRS by up to 10% longwards of 1600 nm, with our calculations lying in between the two measured spectra. We note that the absolute measurements of the IR irradiance are particularly challenging and that there are significant deviations between different datasets (Thuillier et al. 2014, 2015; Meftah et al. 2021).
To further understand which modifications in the MURaM simulations lead to a better match with the observations, we compared spectral irradiance calculated from 3D cubes using different MURaM versions and, in Figs. A.1–A.3, illustrate the effect of inconsistent abundances. In this comparison we include spectral irradiance calculations obtained using the following different MURaM cubes: (i) 3D cubes calculated for this study using the most up-to-date MURaM version with 12 multi-group bins in the RT calculations (hereafter MULTI12), (ii) pure HD MURaM cubes with the most up-to-date MURaM version, but with the same setup as our SSD calculation presented here (hereafter Hydro12), (iii) 3D cubes obtained using the newest MURaM setup but with only four multi-group bins in the RT (hereafter MULTI4), and (iv) 3D cubes generated using the older MURaM version by Beeck et al. (2013, hereafter Beeck2013). The spectral irradiance calculations for the fourth set of cubes were performed by Norris et al. (2017).
The comparison of spectral irradiance shows that the differences when using MULTI4 cubes and MULTI12 cubes are significantly smaller than the difference between spectral irradiance calculations using Beeck2013 and MULTI12. Thus, the largest improvement in the spectral irradiance comes from the new EOS and opacity tables, as well as potentially from the new diffusive terms in MURaM. While there are noticeable differences between Hydro12 cubes and the SSD cubes from MULTI12, SSD mainly affects velocities, whose effect will become visible in individual spectral line calculations (see Appendix A for a more detailed discussion).
 |
Fig. 1 Comparison of the calculated and measured solar irradiance spectrum. The grey shaded area indicates the measurement error of the SIRS for the 2008 WHI (see Woods et al. 2009 for a detailed description). The light blue shaded area indicates one standard deviation of the 145 measurements taken in 2022 by SSIM on board the FY-3E. The averaged solar irradiance spectrum computed from MURaM cubes is represented by the red line; the light red shaded area indicates one standard deviation in the temporal fluctuations. |
3.2 Centre-to-limb variations of solar intensity
In the next step, we compared the limb darkening computed with MURaM and post-processed with MPS-ATLAS to the measurements performed by Pierce et al. (1977) and Neckel & Labs (1994) at the National Solar Observatory/Kitt Peak with the large vertical spectrograph at the McMath Solar Telescope. Pierce et al. (1977) performed measurements at 50 continuum wavelengths in the range 740 nm to 2402 nm, while Neckel & Labs (1994) observed at 30 continuum wavelengths in the range 303 nm to 1099 nm.
Both studies fitted the derived limb darkening curves by fifth-order polynomials and presented the obtained coefficients. We note that for the fitting procedure, the intensity at the limb – µ < 0.12 for Neckel & Labs (1994) and µ < 0.2 for Pierce et al. (1977) – were excluded, which implies a somewhat lower accuracy of the measurements at µ = 0.1, particularly for the values found by Pierce et al. (1977). Figure 2 shows the comparison of limb darkening curves, I(µ)/I(1.0), calculated from these polynomial coefficients to our computations with MURaM and MPS-ATLAS. The comparison was performed in a broad spectral range from the UV (303.3 nm) to the wavelength corresponding roughly to the H-opacity minimum (1622.2 nm), where the disk centre intensity originates in the deepest layers of the solar photosphere. The MURaM and MPS-ATLAS calculations are in remarkable agreement with the measured values. Deviations are mainly noticeable very close to the limb at the µ value of 0.1, at which the plotted symbols (red) do not represent direct measurements but rather correspond to extrapolations from measurements at larger µ values. Further, minor deviations are also visible at µ = 0.8 and µ = 0.9 for the wavelengths 1158.3 nm and 1622.2 nm. The deviations vary with wavelength and thus might be explained by noisy observational data at these wavelengths.
To pinpoint which improvement in the MURaM simulation results in this remarkable match, we compared the present results with the CLVs calculated by Norris et al. (2017). Figure B.1 shows that the accurate match of the CLVs comes from the increase in the number of spectral bins used for multi-grouping (for a detailed discussion, see Appendix B).
 |
Fig. 2 Limb darkening obtained from 3D MURaM cubes (black lines) and from solar measurements (green dots) at different wavelengths: (a) measurements from NL94 (Neckel & Labs 1994) and (b) measurements from PSW77 (Pierce et al. 1977). The three sigma error of the mean for the calculated CLV from MURaM is shown as the grey shaded area. Panel c shows a zoomed-in view of the CLV for λ = 1046.6 nm from panel a. |
Selected spectral lines and their atomic parameters.
3.3 Spectral lines and their bisectors
Having tested low-resolution spectra emerging from MURaM cubes against observations, we next focused on profiles of individual spectral lines as well as their bisectors. While low-spectral-resolution spectra are mainly defined by the vertical temperature structure of the cubes, the detailed shapes of spectral lines and especially their bisectors are determined by the convective velocities and temperature contrasts and, thus, allow us to test if MURaM can accurately reproduce them. For that we considered four iron spectral lines, which were also used by Asplund et al. (2000) and which are only slightly blended by neighbouring lines (listed in Table 1): the line Fe I (624.2 nm), the line Fe I (627.3 nm), the line Fe I (680.6 nm), and the line Fe II (771.3 nm). We chose two weak and two rather strong lines with significantly different excitation energies of the lower level, χ1. Since χ1 defines the temperature sensitivity of the line, bisectors of the lines are expected to show different shapes (e.g. Dravins et al. 1981, 1986).
Generally, the wavelengths of spectral line centre positions, λ0, have large uncertainties (Nave et al. 1994). Therefore, we focused only on the spectral line shape and the resulting bisectors, not on the position (we introduced shifts for a better comparison). For the calculations, we used the atomic data from Kurucz’s line list2. The spectral line intensities, I, were synthesised along all rays at disk centre and averaged over all cubes. Subsequently, we calculated the ratio of the averaged intensity over the averaged continuum intensity, I/Ic, shown in Fig. 3. The bisectors were calculated from the averaged line profiles.
We compared the calculated disk centre spectral lines and their bisectors to those from the Hamburg atlases of the observed solar spectrum recorded with the Fourier-Transform Spectrometer (FTS) at the McMath telescope3. The calculated I/Ic for the spectral lines shows good agreement with the observations. The observed departures might be due to different accuracies of the atomic data or our assumption of local thermodynamic equilibrium (LTE). Non-LTE effects are considerably larger in Fe I lines due to overionisation and usually lead to somewhat weaker and narrower lines compared to LTE. Moreover, our calculated bisectors agree very well with observations for all four lines; the best agreement is achieved for the Fe I 627 line. Since the bisector shape is very sensitive to the velocity field and horizontal temperature inhomogeneities introduced by convection, we conclude that MURaM SSD simulations accurately reproduce convection and overshoot.
 |
Fig. 3 Calculated and observed line profiles, I/Ic (left-top panels), their residuals (as a percentage; left-bottom panels), and the corresponding bisectors (right panels) for four lines. The bisector curves were fitted using a sixth-degree polynomial (black and yellow curves) and the actual data (in gray) are shown. In the individual panels we show the Fe I 624 line (a), the Fe 1627 line (b), the Fe 1680 line (c), and Fe II 771 line (d). |
4 Conclusions
We have demonstrated that the most up-to-date 3D MURaM simulations that include an SSD reproduce the quiet-Sun observables remarkably well at low spatial resolution, such as the SSI and the limb darkening in the continuum and in selected spectral lines. We show that various improvements in the simulation setup are responsible for the agreement of the model with observations. These include a consistent EOS table, a consistent opacity table, and updated diffusive terms, which lead to an improvement in the agreement of the computed spectral irradiance with state-of-the-art observations. Another improvement consists in the more accurate radiative energy transfer in the MURaM code produced by the increase in the number of spectral bins used for multi-grouping. This improvement leads to an extraordinarily good agreement of the computed CLV with standard measurements. This version of MURaM also reproduces line bisectors with high accuracy (which had until now not been tested using this code).
We conclude that the newest MURaM setup reproduces both the temperature structure and the convective velocities of the quiet Sun. Having established a very good agreement between simulations and selected observables for the quiet Sun, we now have a solid justification for extending the MURaM atmospheric simulations to other stars.
Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 715947). N.M.K. and L.G. acknowledge support from the German Aerospace Center (DLR FKZ 50OP1902). L.G. acknowledges funding from ERC Synergy Grant WHOLE SUN 810218. We kindly thank Qi Jin for providing us the observational data from the Solar Spectral Irradiance Monitor onboard the Fengyun-3E Satellite. We would like to thank the anonymous referee for helpful comments.
Appendix A Spectral irradiance using different 3D simulations and setups
In the following we showcase the differences in the spectral irradiance resulting from different MURaM versions and setups.
Appendix A.1 Effect of small-scale dynamo on the low-resolution spectrum
MURaM is capable of simulating the action of a small-scale turbulent dynamo, that is, the interaction between solar convection and magnetic flux (see e.g. Rempel 2014, and references therein). Since it is not computationally feasible to simulate the whole convection zone, we used the boundary conditions that successfully mimic a deeper convection zone found by Rempel (2018). To demonstrate the effect of an SSD on the spectral irradiance, we determined the deviations between the calculated and the observed spectral irradiance. Figure A.1 shows these deviations; the spectral irradiance for the SSD was computed using more than 300 SSD cubes, and for the HD simulation more than 130 HD cubes. For these 3D simulations, the radiative cooling and heating rates were computed using 12 multi-group bins.
The action of the SSD leads to an increase in spectral irradiance by about 1% in the visible spectral domain, but the effect of the SSD on the IR irradiance is much smaller. We note that the action of the SSD strongly affects the velocity field (see the bottom panel of Fig. 5 in Witzke et al. 2023). Thus, while the effect on the low-resolution spectrum is relatively small, we expect a bigger effect on the profiles of spectral lines (Mauviard et al., in prep.).
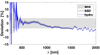 |
Fig. A.1 Deviations, calculated as (theory – measurements)/measurements, of the spectral irradiance between the WHI spectrum and the spectral solar irradiance calculated using SSD and HD cubes. The light grey shaded area around the x-axis indicates the uncertainty of the WHI spectrum. The light blue and dark grey shaded areas around the curves representing HD and SSD simulations indicate the error of the mean due to the temporal fluctuations of the simulations. |
Appendix A.2 The importance of using consistent abundances throughout the calculations
Another essential feature of our calculations is a fully consistent treatment of the element composition that is used in all calculations: the same element composition was used in the EOS, in the opacity tables used for the 3D MURaM simulations, and in calculating spectra emerging from the 3D cubes. To illustrate the importance of the consistent treatment of abundances, we performed the following exercise: we re-calculated the spectral irradiance from one particular cube, but instead of using the consistent Asplund composition, we used the element composition from Anders & Grevesse (1989) for calculating spectra emerging from the 3D cubes with MPS-ATLAS. Figure A.2 shows the deviation in the intensities when an inconsistent element composition is used for two viewing angles. In the visible, the deviations can be as much as 10%, decreasing towards the IR. In the UV, deviations of more than 35% are reached at disc centre.
 |
Fig. A.2 Deviations in emergent intensities of one particular cube between RT calculations performed using two different sets of element compositions: the first is the same as that used in the 3D calculations of the underlying model (Asplund composition) and the second the element composition from Anders & Grevesse (1989). The comparison is shown for two viewing angles. |
Appendix A.3 Comparison to the Beeck2013 cubes
Finally, we compared the spectral irradiance computed from Beeck2013 cubes and cubes using the newest MURaM setup, as in Bhatia et al. (2022), performed with four multi-group bins (MULTI4; Witzke et al. 2023) and with 12 multi-group bins (MULTI12) to obtain the radiative cooling and heating rates. We note that the Beeck2013 cubes were computed with the main aim of understanding the physical mechanism of near-surface convection in main sequence stars. While the Sun was modelled using realistic 3D MHD simulations, there was no goal to accurately match available observations. In particular, radiative cooling and heating rates in Beeck et al. (2013) were computed using only four multi-group bins, which is not sufficient for obtaining precise values (Perdomo García et al. 2023). Furthermore, the EOS look-up tables were taken from the OPAL project (Rogers et al. 1996) and had a different element composition than the generated opacity tables. In contrast, the simulations by Bhatia et al. (2022) and Witzke et al. (2023) were performed to model the Sun as accurately as possible. The EOS was changed to the FreeEOS code (Irwin 2012), and the element composition from Asplund et al. (2009) was used for both opacity and EOS calculations. We also computed the cooling and heating rates with 4 multi-group bins (MULTI4; see Witzke et al. 2023) and using 12 multi-group bins (MULTI12), as done throughout this paper.
To investigate the improvements in these more recent simulations, we show in Fig. A.3 spectral irradiance calculated with Beeck2013 cubes (calculations are taken from Norris et al. 2017) and spectral irradiance obtained from the MULTI4 and MULTI12 3D cubes. The Beeck2013 calculations show a slightly higher effective temperature and greater spectral irradiance in the visible spectral domain, with a steeper drop towards IR than the MULTI4 and MULTI12 calculations. Focusing on the visible domain, we see that the shapes for most of the spectral line features show good agreement with the observations, but the overall flux is higher. All in all, both the MULTI4 and MULTI12 calculations have a much better agreement with the WHI reference spectrum. In particular, the gradient of the irradiance from the visible to the IR matches the observation much better. This indicates that the continuum opacities and the atmospheric structure in the MULTI4 and MULTI12 simulations are more accurate.
 |
Fig. A.3 Calculated irradiance spectrum using different versions and setups of the MURaM code together with the measured SIRS WHI solar irradiance spectrum. The grey shaded area indicates the measurement error of the SIRS WHI, as in Fig. 1. The averaged solar irradiance spectrum computed from Beeck2013 cubes is shown in blue; the light blue shaded area indicates one standard deviation in the temporal fluctuations. The red and black lines show the averaged spectrum from cubes simulated with the updated MURaM code version but using different multi-group binning (MULTI4 and MULTI12). The light red and dark grey shaded areas indicate one standard deviation in the temporal fluctuations of these two sets of 3D cubes. |
However, the calculated spectral irradiance from MULTI12 simulations matches the WHI slightly better in the visible and near IR compared to the calculations from MULTI4. Moreover, it shows a stronger drop towards the IR. This can be explained as follows: in the MULTI12 cubes, the photospheric layers are heated as the RT becomes more efficient and the temperature gradient becomes less steep compared to the MULTI4 cubes. This clearly manifests itself in the CLVs presented in Appendix B.
Appendix B Improvement of the CLVs
The CLVs are more sensitive to the temperature gradient in the photosphere than the spectral irradiance. Figure B.1 displays the CLVs from the Beeck2013 simulations (calculations are taken from Norris et al. 2017) and the CLVs from the MULTI4 and MULTI12 simulations.
The limb darkening computed from the Beeck2013 simulations and from MULTI4 cubes is much steeper than the observed CLVs. The MULTI12 simulations lead to a smaller drop in intensity towards the limb and, thus, a much better agreement with observations. This is because in the MULTI12 simulations the photosphere is heated more due to the more efficient RT. Such a heating leads to a shallower temperature gradient and a more accurate CLV. Since the CLV from the MULTI12 cubes leads to an excellent agreement with observations, we conclude that 12 multi-group bins are sufficient to accurately model the RT in 3D simulations, at least for continuum wavelengths.
The difference between MULTI4 and MULTI12 is smallest at 1622.2 nm, which is close to the H- opacity minimum, where the CLVs from MULTI4 and MULTI12 cube computations almost coincide. This is because the intensity at this wavelength is formed at the deepest photospheric layers, where the energy is transported mainly by convective motions, and thus, a more efficient RT does not have a big impact on the temperature structure.
 |
Fig. B.1 Limb darkening obtained from different MURaM cubes (MULTI4, MULTI12, and Beeck2013) and from solar measurements NL94 (Neckel & Labs 1994) and PSW77 (Pierce et al. 1977) at different wavelengths. A three sigma error of the mean is plotted for all MURaM results: light blue shaded for MULTI4, grey shaded for MULTI12, and light red shaded for the calculations from Beeck2013 cubes. |
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C., & Stein, R. F. 2000, A&A, 359, 729 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013, A&A, 558, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Schüssler, M., Cameron, R. H., & Reiners, A. 2015, A&A, 581, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatia, T. S., Cameron, R. H., Solanki, S. K., et al. 2022, A&A, 663, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F. 2005, Mem. Soc. Astron. Ital. Suppl., 8, 34 [NASA ADS] [Google Scholar]
- Chiavassa, A., Casagrande, L., Collet, R., et al. 2018, A&A, 611, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Criscuoli, S. 2019, ApJ, 872, 52 [Google Scholar]
- Dravins, D., Lindegren, L., & Nordlund, A. 1981, A&A, 96, 345 [NASA ADS] [Google Scholar]
- Dravins, D., Larsson, B., & Nordlund, A. 1986, A&A, 158, 83 [NASA ADS] [Google Scholar]
- Hirzberger, J., Feller, A., Riethmüller, T. L., et al. 2010, ApJ, 723, L154 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, A. W. 2012, FreeEOS: equation of State for stellar interiors calculations, Astrophysics Source Code Library [record ascl:1211.002] [Google Scholar]
- Keller, C. U., Schüssler, M., Vögler, A., & Zakharov, V. 2004, ApJ, 607, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Collados, M., Solanki, S. K., Lagg, A., & Trujillo Bueno, J. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., & Socas-Navarro, H. 2004, ApJ, 613, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meftah, M., Snow, M., Damé, L., et al. 2021, A&A, 645, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [CrossRef] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [Google Scholar]
- Nordlund, Å., & Stein, R. F. 1990, Comput. Phys. Commun., 59, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, C. M., Beeck, B., Unruh, Y. C., et al. 2017, A&A, 605, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perdomo García, A., Vitas, N., Khomenko, E., et al. 2023, A&A, 675, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierce, A. K., Slaughter, C. D., & Weinberger, D. 1977, Sol. Phys., 52, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Przybylski, D., Cameron, R., Solanki, S. K., et al. 2022, A&A, 664, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rempel, M. 2014, ApJ, 789, 132 [Google Scholar]
- Rempel, M. 2018, ApJ, 859, 161 [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009, ApJ, 691, 640 [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., Berdyugina, S. V., et al. 2014, A&A, 568, A13 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [Google Scholar]
- Salhab, R. G., Steiner, O., Berdyugina, S. V., et al. 2018, A&A, 614, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A., & Solanki, S. K. 2003, ApJ, 597, L173 [CrossRef] [Google Scholar]
- Shapiro, A. I., Schmutz, W., Schoell, M., Haberreiter, M., & Rozanov, E. 2010, A&A, 517, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shelyag, S., Schüssler, M., Solanki, S. K., Berdyugina, S. V., & Vögler, A. 2004, A&A, 427, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 2013, A&ARv. 21, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Bolsée, D., Schmidtke, G., et al. 2014, Sol. Phys., 289, 1931 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Harder, J. W., Shapiro, A., et al. 2015, Sol. Phys., 290, 1581 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Witzke, V., Shapiro, A. I., Cernetic, M., et al. 2021, A&A, 653, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witzke, V., Shapiro, A. I., Kostogryz, N. M., et al. 2022, ApJ, 941, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Witzke, V., Duehnen, H. B., Shapiro, A. I., et al. 2023, A&A, 669, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, T. N., Chamberlin, P. C., Harder, J. W., et al. 2009, Geophys. Res. Lett., 36, L01101 [NASA ADS] [CrossRef] [Google Scholar]
- Yeo, K. L., Solanki, S. K., Norris, C. M., et al. 2017, Phys. Rev. Lett., 119, 091102 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison of the calculated and measured solar irradiance spectrum. The grey shaded area indicates the measurement error of the SIRS for the 2008 WHI (see Woods et al. 2009 for a detailed description). The light blue shaded area indicates one standard deviation of the 145 measurements taken in 2022 by SSIM on board the FY-3E. The averaged solar irradiance spectrum computed from MURaM cubes is represented by the red line; the light red shaded area indicates one standard deviation in the temporal fluctuations. |
| In the text | |
 |
Fig. 2 Limb darkening obtained from 3D MURaM cubes (black lines) and from solar measurements (green dots) at different wavelengths: (a) measurements from NL94 (Neckel & Labs 1994) and (b) measurements from PSW77 (Pierce et al. 1977). The three sigma error of the mean for the calculated CLV from MURaM is shown as the grey shaded area. Panel c shows a zoomed-in view of the CLV for λ = 1046.6 nm from panel a. |
| In the text | |
 |
Fig. 3 Calculated and observed line profiles, I/Ic (left-top panels), their residuals (as a percentage; left-bottom panels), and the corresponding bisectors (right panels) for four lines. The bisector curves were fitted using a sixth-degree polynomial (black and yellow curves) and the actual data (in gray) are shown. In the individual panels we show the Fe I 624 line (a), the Fe 1627 line (b), the Fe 1680 line (c), and Fe II 771 line (d). |
| In the text | |
 |
Fig. A.1 Deviations, calculated as (theory – measurements)/measurements, of the spectral irradiance between the WHI spectrum and the spectral solar irradiance calculated using SSD and HD cubes. The light grey shaded area around the x-axis indicates the uncertainty of the WHI spectrum. The light blue and dark grey shaded areas around the curves representing HD and SSD simulations indicate the error of the mean due to the temporal fluctuations of the simulations. |
| In the text | |
 |
Fig. A.2 Deviations in emergent intensities of one particular cube between RT calculations performed using two different sets of element compositions: the first is the same as that used in the 3D calculations of the underlying model (Asplund composition) and the second the element composition from Anders & Grevesse (1989). The comparison is shown for two viewing angles. |
| In the text | |
 |
Fig. A.3 Calculated irradiance spectrum using different versions and setups of the MURaM code together with the measured SIRS WHI solar irradiance spectrum. The grey shaded area indicates the measurement error of the SIRS WHI, as in Fig. 1. The averaged solar irradiance spectrum computed from Beeck2013 cubes is shown in blue; the light blue shaded area indicates one standard deviation in the temporal fluctuations. The red and black lines show the averaged spectrum from cubes simulated with the updated MURaM code version but using different multi-group binning (MULTI4 and MULTI12). The light red and dark grey shaded areas indicate one standard deviation in the temporal fluctuations of these two sets of 3D cubes. |
| In the text | |
 |
Fig. B.1 Limb darkening obtained from different MURaM cubes (MULTI4, MULTI12, and Beeck2013) and from solar measurements NL94 (Neckel & Labs 1994) and PSW77 (Pierce et al. 1977) at different wavelengths. A three sigma error of the mean is plotted for all MURaM results: light blue shaded for MULTI4, grey shaded for MULTI12, and light red shaded for the calculations from Beeck2013 cubes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


