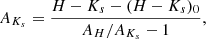EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 680 (December 2023) A&A, 680 (2023) A75 Full HTML
Open Access
Issue
A&A
Volume 680, December 2023
Article Number A75
Number of page(s) 13
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202347421
Published online 12 December 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The innermost regions of most galaxies host a nuclear star cluster (NSC). NSCs are extremely dense and massive stellar clusters that are normally identified as luminous compact sources different from their surrounding area (Neumayer et al. 2020). These clusters are not the only stellar structure that can be present in galactic nuclei. In particular, the TIMER survey analysed the inner few kpc of 21 nearby massive and barred galaxies and found the presence of nuclear stellar discs (NSDs) in 19 of them (Gadotti et al. 2020). These stellar structures are significantly larger than NSCs and their formation is attributed to gas that was funnelled by the galactic bar towards the innermost regions of the galaxies (Bittner et al. 2020). NSCs and NSDs can co-exist in galactic nuclei (e.g. Lyubenova et al. 2013), although their relationship is not yet well studied.

The Milky Way’s centre is the closest galaxy nucleus, located at only ∼8 kpc from Earth (e.g. GRAVITY Collaboration 2018; Do et al. 2019), and the only one where it is possible to resolve individual stars down to milli-parsec scales (e.g. Schödel et al. 2010; Nogueras-Lara et al. 2018a). It hosts the Milky Way’s nuclear star cluster (MWNSC), which has a total stellar mass of ∼2.5 × 107 M⊙ (e.g. Launhardt et al. 2002; Schödel et al. 2014a; Feldmeier et al. 2014; Chatzopoulos et al. 2015a; Fritz et al. 2016; Feldmeier-Krause et al. 2017a) and an effective radius of ∼4 − 5 pc (e.g. Schödel et al. 2014b; Gallego-Cano et al. 2020). It is embedded in the Milky Way’s nuclear stellar disc (MWNSD), a much larger and flatter stellar structure with a total mass of ∼109 M⊙ (e.g. Launhardt et al. 2002; Nogueras-Lara et al. 2020a; Sormani et al. 2020, 2022), a scale length of ∼100 pc, and a scale height of ∼40 pc (e.g. Launhardt et al. 2002; Gallego-Cano et al. 2020; Sormani et al. 2022). Hence, an NSC and an NSD coexist in the Milky Way, which can thus serve as a laboratory to understand the relation between these Galactic centre components.

In spite of their proximity, the study of the MWNSC and the MWNSD is hampered by the extreme source crowding and the high extinction that characterise the Galactic centre (e.g. Scoville et al. 2003; Nishiyama et al. 2008; Fritz et al. 2011; Chatzopoulos et al. 2015b). Understanding the relation between the MWNSC and the MWNSD is challenging due to the 2D projection effects, and requires an analysis of their stellar populations along the line of sight towards the MWNSC. Hence, it is necessary to obtain clean samples of stars from each component to be able to determine their properties.

Recent photometric studies have shown that the MWNSC and the MWNSD appear to contain different stellar populations and may have experienced independent formation histories (Nogueras-Lara et al. 2020a, 2021a; Schödel et al. 2020). Although both structures seem to be dominated by an old stellar population, around 15% of the total MWNSC stellar mass formed ∼3 Gyr ago, while the central regions of the MWNSD underwent a quiescence phase with little star formation in between ∼2 − 7 Gyr ago (Nogueras-Lara et al. 2023). Moreover, around 5% of the total stellar mass of the MWNSD formed in a very energetic and short (∼100 Myr) star formation episode ∼1 Gyr ago (Nogueras-Lara et al. 2020a), which did not happen in the MWNSC. On the other hand, a recent spectrophotometric analysis of the star formation history of the NSC suggests that the dominant stellar population could be younger that previously found (5 ± 3 Gyr old, Chen et al. 2023), implying an even starker difference in comparison to the MWNSD.

Nogueras-Lara (2022a) found an extinction gradient along the line of sight towards the Galactic centre and used it to identify differences between mean kinematics and metallicity of the MWNSC and the MWNSD. The MWNSD was found to rotate faster than the MWNSC, and to have a lower metallicity than the MWNSC, which is arguably the most metal rich region of the Galaxy.

Nevertheless, previous studies analysed the average properties of the MWNSC and MWNSD, mixing stars located at very different Galactic centre radii along the line of sight due to the 2D projection effect (e.g. Schultheis et al. 2021). Therefore, considering the transition region between the MWNSC and the MWNSD along the line of sight towards the MWNSC is fundamental to understand their nature and to properly constrain their relation and apparently different properties. In this paper, we study the line of sight towards the MWNSC and find a correlation between extinction and distance of the stars from the Galactic centre. In this way, we are able to characterise the kinematics and metallicity of stars at different Galactic centre radii. We find that the transition between the MWNSD and the MWNSC is smooth and we detect the presence of kinematic and metallicity gradients towards the supermassive black hole at the heart of the MWNSC.

2. Data

2.1. Photometry

We used near infrared JHKs high-resolution (∼0.2″) photometric observations of a region of ∼2.8′×4.9′ (∼6.5 pc × 11.4 pc at the Galactic centre distance) centred on the MWNSC, obtained with the HAWK-I camera at the VLT (Kissler-Patig et al. 2008). Figure 1 shows the analysed region and its position with respect to the MWNSD. The observations consisted in a series of short-exposure frames (DIT = 1.26 s for J, and DIT = 0.85 s for H and Ks) that were combined through applying the speckle holography algorithm (Schödel et al. 2013). This reconstruction technique uses an averaged division of quantities in Fourier space (Eq. (1) in Schödel et al. 2013) to combine several hundreds of frames by convolving them with a Gaussian point spread function which defines the angular resolution of the final image (FWHM of 0.2″).

thumbnail Fig. 1.

Target region centred on the MWNSC. The lower panel shows a Spitzer false colour image (3.6 μm (blue), 4.5 μm (green), 5.8 μm (red), Stolovy et al. 2006). The upper panel corresponds to a false colour JHKs GALACTICNUCLEUS image adapted from Nogueras-Lara (2022a). The circular dashed region outlines the effective radius of the MWNSC, the white dotted contour shows the region with KMOS data, and the white filled boxes indicate regions without proper motion data. The position of the supermassive black hole Sagittarius A* (Sgr A*) and the approximate size of the fields at the Galactic centre distance are also indicated in the figure.

The J-band data correspond to the GALACTICNUCLEUS survey (Field 1 observed on 6 June 2015, see Table A.1 in Nogueras-Lara et al. 2019 for further details), and the H- and Ks-band data correspond to a pilot study for the same survey (Nogueras-Lara et al. 2018a) obtained under significantly better conditions than the actual survey (seeing in Ks ∼ 0.4″, data observed on 7 June 2013), which allowed us to achieve photometric measurements ∼1 mag deeper than the GALACTICNUCLEUS catalogue. The Ks-band data presented significant saturation problems for Ks < 11.5 mag, which were corrected using the SIRIUS IRSF survey (Nagayama et al. 2003; Nishiyama et al. 2006), as explained in Nogueras-Lara et al. (2020a).

2.2. Proper motions

We used the proper motion catalogue from Shahzamanian et al. (2022) which covers the majority (∼80%) of the target region (Fig. 1). The proper motions were obtained combining the H-band data from the GALACTICNUCLEUS survey (Nogueras-Lara et al. 2018a, 2019), and the HST Paschen-α survey (Wang et al. 2010; Dong et al. 2011), with a timeline of 7−8 years between them.

The computed proper motions are relative, meaning that they were calculated assuming an average zero motion of the stellar population. Hence, an offset exists between the proper motions with respect to a reference frame that is at rest at Sgr A*, and the ones in the catalogue, which depends on the real average motion of the stellar population (mainly dominated by stars moving eastwards, e.g. Trippe et al. 2008; Chatzopoulos et al. 2015a; Shahzamanian et al. 2022; Martínez-Arranz et al. 2022; Nogueras-Lara 2022a). To correct this offset affecting the proper motion component parallel to the Galactic plane (μl), we applied a correction of +0.36 mas yr−1 for the μl calculation when using the CMD Ks versus J − Ks to select stars belonging to the MWNSC and the MWNSD. This correction was computed by Nogueras-Lara (2022a) by applying a Gaussian Mixture model (GMM; Pedregosa et al. 2011) to fit the μl distribution of the MWNSC stars. This distribution is best represented by a three-Gaussians model corresponding to stars moving eastwards and westwards, and also to a central, more slowly rotating component. They estimated the correction for the relative proper motion calculation as the offset of the central Gaussian component with respect to zero. Applying this correction to the mean values of the Gaussian corresponding to the stars moving eastwards and westwards, they obtained a similar absolute μl value for each component, as expected (see Table 1 and Sect. 3.3 in Nogueras-Lara 2022a).

We applied an analogous process to estimate the offset for the proper motion calculation when using the CMD Ks versus H − Ks to choose stars from the MWNSC and the MWNSD. We obtained an offset of μl = 0.5 mas yr−1. This value is slightly larger than the one obtained by Nogueras-Lara (2022a) when using the CMD Ks versus J − Ks as a reference, probably due to the higher completeness in the HKs bands. In any case, the presence of a μl offset does not pose any problems for the subsequent analysis because we compare the MWNSC and the MWNSD using data along the same line of sight, and thus this potential offset will affect all stars in the field in a similar way.

2.3. Metallicity and line-of-sight velocities

We used the KMOS spectroscopic data obtained by Feldmeier-Krause et al. (2017b, 2020). They analysed K-band medium-resolution spectra using a full spectral fitting method with PHOENIX models (Husser et al. 2013).

They also obtained line-of-sight velocities using the STARKIT code developed by Kerzendorf & Do (2015). We cross-correlated our photometry with the spectroscopic data and ended up with ∼1000 stars with measured [M/H] and line-of-sight velocities in the target field.

3. Kinematics along the line of sight

Previous work analysing the line of sight towards the MWNSC determined that the MWNSD and the MWNSC can be distinguished via their different extinction (Nogueras-Lara et al. 2021a; Nogueras-Lara 2022a). Figure 2 shows the colour magnitude diagrams (CMDs) Ks versus J − Ks and Ks versus H − Ks, where the separation between the MWNSD and the MWNSC is indicated in agreement with previous studies. This allows us to distinguish between these two Galactic centre components in the CMDs. Moreover, the extreme extinction towards the Galactic centre also helps us exclude foreground stars which mainly belong to the disc of the Milky Way, and to some extent to the Galactic bar (e.g. Nishiyama et al. 2008; Gonzalez et al. 2012; Surot et al. 2020; Nogueras-Lara et al. 2021b).

thumbnail Fig. 2.

CMDs Ks versus J − Ks (left panel) and Ks versus H − Ks (right panel) for the target region. The red dashed lines indicate the separation between the foreground population, the MWNSD, and the MWNSC. The blue box in the CMD Ks versus H − Ks shows the reference stars to build the extinction map in Sect. 5.1. The scale bars indicate stellar densities using a power stretch scale.

Identifying the MWNSD and the MWNSC along the line of sight towards the MWNSC implies a statistical correlation between extinction and distance. The stars from the near side of the MWNSD are on average less extinguished than stars from the MWNSC along the same line of sight, and can be identified by their different colour. In this work, we aim to go further and analyse the kinematic behaviour of the stellar population from the MWNSD and the MWNSC by applying colour cuts to evenly sample the colour space. In this way, we consider MWNSD and MWNSC stars located at different Galactic centre radii instead of averaging over all the stars from each of the components, as done in previous work (e.g. Schultheis et al. 2021; Nogueras-Lara et al. 2021a; Nogueras-Lara 2022a).

3.1. CMDs and proper motion distribution

We cross-correlated the photometric and proper motion catalogues for the target region, and restricted our analysis to stars with proper motion uncertainties < 0.5 mas yr−1 to avoid potential bias due to stars with large kinematic uncertainties. We ended up with ∼2100, and ∼2500 stars with well defined proper motions and a photometric counterpart in JKs and HKs, respectively. The lower number of stars with photometric counterpart in JKs is because shorter wavelengths are more affected by extinction and thus the J catalogue is less complete.

Figure 3 shows the CMDs Ks versus J − Ks and Ks versus H − Ks for the common stars between the used catalogues. To analyse the proper motion distribution, we defined colour bins for each CMD with a width equivalent to AKs ∼ 0.25 mag. This corresponds to a variation in colour of J − Ks = 0.5 mag and H − Ks = 0.2 mag assuming the extinction curve AJ/AKs = 1.84 and AJ/AKs = 3.44 (Nogueras-Lara et al. 2020b). The inclination of the colour bins was chosen to be parallel to a stellar isochrone of ∼10 Gyr which corresponds to the dominant old stellar population in both the MWNSD and the MWNSC (e.g. Nogueras-Lara et al. 2020a; Schödel et al. 2020), in agreement with previous work (see Fig. 3 in Nogueras-Lara 2022a).

thumbnail Fig. 3.

CMDs Ks versus J − Ks and Ks versus H − Ks obtained for stars with well defined proper motions (i.e. proper motion uncertainties < 0.5 mas yr−1). The red dashed boxes indicate the assumed colour cuts to analyse the variation of the proper motion distribution with respect to the extinction.

We considered the data completeness for the bright and the faint end of the colour cuts, and limited our analysis to stars with Ks ∈ [10, 14.2] mag (Nogueras-Lara 2022a). Given the higher completeness for the CMD Ks versus H − Ks, we selected 8 colour bins instead of the 7 chosen for the CMD Ks versus J − Ks.

3.1.1. MWNSD and MWNSC in the CMDs

We checked the consistency of our statistical distinction between MWNSD and MWNSC stars when applying the colour cuts J − Ks and H − Ks, as specified in Fig. 2. For this, we used all the stars fulfilling the previously specified criteria and with available JHKs photometry. We obtained that the agreement between stars identified as belonging to the MWNSD in the CMDs Ks versus J − Ks and Ks versus H − Ks is ≳85%, whereas this number rises up to ≳95% in the case of MWNSC stars. Therefore, we conclude that our selection criterion is consistent regardless of the colour used.

3.1.2. Results

We computed the median value of the proper motion components parallel and perpendicular to the Galactic plane for each of the colour bins previously defined. Tables A.1 and A.2 show the results. The uncertainties, dμi, were estimated assuming the standard error of the median values, where the subindex i indicates proper motion component parallel (l), or perpendicular (b) to the Galactic plane. Figure 4 shows the behaviour of the median μl value for the selected colour cuts. We found a clear dependence of μl with respect to the applied colour cuts, which agrees for both CMDs.

thumbnail Fig. 4.

Variation of the proper motion component parallel to the Galactic plane versus colour. The proper motion values were calculated assuming the median value of the stars in each colour bin. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.

Our results are compatible with the eastwards rotation of the Galactic centre stellar components (e.g. Trippe et al. 2008; Chatzopoulos et al. 2015a; Shahzamanian et al. 2022; Sormani et al. 2022). Following previous work (Nogueras-Lara et al. 2021a; Nogueras-Lara 2022a), we distinguished between the stars likely belonging to the MWNSD and the MWNSC by applying an extinction criterion, as indicated in Fig. 2. In this way, the red and grey squares in Fig. 4 show the μl distribution for MWNSD and MWNSC stars, respectively. We observed that the μl velocity of the MWNSD is maximum for stars from its outer edge (Nogueras-Lara 2022b; Nogueras-Lara et al. 2023), whereas stars from its innermost regions present lower μl values. This tendency continues for MWNSC stars, and reaches a zero value at J − Ks ∼ 6.5 mag, and H − Ks ∼ 2.5 mag, probably dominated by stars close to Sgr A*, which are mainly pressure-supported (see Trippe et al. 2008; Schödel et al. 2009). This μl behaviour is also in agreement with the minimum value obtained for the line-of-sight velocity of MWNSC stars close to Sgr A* (see Fig. 6 in Nogueras-Lara 2022a).

The detected variation of μl with colour (i.e. extinction) also validates our initial assumption of the statistical identification of stars from different Galactic centre radii along the line of sight towards the MWNSC by applying colour cuts in the CMDs. Our analysis does not imply that each assumed colour cut is a clean sample of stars at different Galactic centre radii. It is a statistical approach meaning that the majority of stars in the sample are at larger distances along the line of sight for higher extinctions.

Previous work analysed the bulk μl distribution of the MWNSD and the MWNSC and found that, in both cases, they are best represented by the combination of three Gaussians (Shahzamanian et al. 2022; Martínez-Arranz et al. 2022; Nogueras-Lara 2022a). They obtained a rotation velocity of ∼2.3 mas yr−1 and ∼2.1 mas yr−1 (after correcting for the relative proper motion calculation, Nogueras-Lara 2022a), for the MWNSD and the MWNSC, respectively. An average of our results for the corresponding stellar populations is somewhat smaller than previous results. This is explained by the different methodology (we computed median values) and the potential contamination from stars deeper inside the line of sight, that is accounted by a GMM approach in previous work. Our analysis is also able to detect the differential rotation of the MWNSC (e.g. Trippe et al. 2008; Schödel et al. 2009), which is shown by the different μl values obtained at different colour bins in Fig. 4.

We also analysed the median values of the proper motion component perpendicular to the Galactic plane (μb). We found that they do not depend on colour and are close to zero (Tables A.1 and A.2). Our results are compatible with previous work (e.g. Shahzamanian et al. 2022; Nogueras-Lara 2022b).

3.1.3. Completeness analysis

To check the impact of the completeness on the detected μl gradient, we assumed that our Ks photometric catalogue is fully complete for stars with Ks ∈ [10, 14.2] mag in the analysed region (Nogueras-Lara et al. 2018a). We built a Ks-luminosity function with the previously used stars with well defined proper motions (uncertainty below 0.5 mas yr−1), and compared it with an analogous luminosity function created using all the stars in our photometric catalogue (see cut in Fig. 2). Given the different spatial coverage of the catalogues, we excluded regions which were not covered by our proper motion catalogue (white filled boxes in Fig. 1) to create the photometric-data luminosity function. We obtained that the proper motion completeness is ≳60% in the range Ks ∈ [10, 13] mag. Finally, we repeated our μl analysis considering only stars in that brightness range to guarantee a large completeness. We obtained similar results within the uncertainties and concluded that the completeness does not impact our results in any significant way.

3.2. Velocity dispersion

We complemented our previous analysis by computing the distribution of the velocity dispersion for the ∼1000 KMOS stars with available photometry and line-of-sight velocities. We used this stellar sample because line-of-sight velocities were obtained with a considerably lower uncertainty (≲0.2 mas yr−1, Feldmeier-Krause et al. 2017b, 2020) in comparison to the proper motion uncertainties for each star (< 0.5 mas yr−1, see Sect. 3.1). We applied the same colour cuts indicated in Fig. 3 and analysed the velocity dispersion of the KMOS stars. We estimated the velocity dispersion of the stars within each colour bin and its corresponding uncertainty by applying a bootstrap resampling method with 1000 iterations. We created 1000 samples by randomly resampling the original data set with replacement. We estimated the velocity dispersion and its associated uncertainty as the mean and the standard deviation of the result computed for each sample. Table B.1 and Fig. 5 show the obtained results.

thumbnail Fig. 5.

Variation of the dispersion of line-of-sight velocities as a function of colour. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3. The x-coordinates of the data points were calculated assuming the median value of the stars in each colour bin.

We observe a smooth kinematic variation between the MWNSD and the MWNSC, which shows an increase of the velocity dispersion with respect to the colour (i.e. extinction), reaching a maximum for J − Ks ∼ 7 mag and H − Ks ∼ 2.3 mag and then decreasing. This is compatible with the correlation between the extinction and the position of the stars along the line of sight, and agrees with the larger velocity dispersion expected for stars close to Sgr A* (e.g. Trippe et al. 2008; Schödel et al. 2009; Feldmeier et al. 2014).

To assess our results and check the maximum velocity dispersion values that we obtained, we repeated our analysis considering only stars in a projected radius of ∼1.25′ (∼3 pc at the Galactic centre distance) from Sgr A*. In this way, we reduced the contamination from stars with similar extinction to the ones near Sgr A*, but located at a much larger distance due to the 2D projection. We did not observe any significant difference within the uncertainties.

Our results are compatible within the uncertainties with the mean velocity dispersion profile for the MWNSC and the inner regions of the MWNSD obtained by Feldmeier-Krause (2022, see their Fig. 12). Moreover, the maximum velocity dispersion value also agrees with previous values for the innermost MWNSC ∼10″ − 40″, equivalent to ∼0.4 − 1.5 pc at the Galactic centre distance (see Fig. 7 in Fritz et al. 2016).

The larger uncertainties obtained for the two first data points corresponding to MWNSD stars might be due to the lower number of stars in these colour bins and/or some residual contamination from the Galactic bulge/bar. This contamination could account for up to 20% of the MWNSD stars with H − Ks > 1.3 mag (see Table 2 in Sormani et al. 2022). Due to the expected extinction for Galactic bulge/bar stars (e.g. Gonzalez et al. 2012; Nogueras-Lara et al. 2018b; Surot et al. 2020), and the impossibility to observe stars from the Galactic bulge/bar beyond the MWNSC because of the extreme extinction (e.g. Schödel et al. 2010; Chatzopoulos et al. 2015b), this contamination mainly affects the low extinction regime of the analysed field (i.e. MWNSD stars).

To check our results, we repeated the same analysis computing the velocity dispersion distribution of the proper motion components μl and μb. We obtained consistent results although the uncertainties are larger than the ones obtained when considering line-of-sight velocities, as it was expected given the larger proper motion errors (< 0.5 mas yr−1).

4. Metallicity

We used the ∼1000 KMOS stars (Feldmeier-Krause et al. 2017b, 2020) with available metallicity and photometry. Given that the spectral fitting was calibrated using existing empirical spectra for [M/H] < 0.3 dex, the metallicities for stars with [M/H] > 0.3 dex could have been overestimated. To asses the results, Schultheis et al. (2021) applied the metallicity-spectral index relation derived by Fritz et al. (2021) on empirical spectra of stars with [M/H] < 0.6 dex. They found consistent result with the full spectral fitting method using synthetic spectra for [M/H] ≲ 0.5 dex. In addition, Feldmeier-Krause (2022) tested the full spectral fitting technique on empirical spectra over a wide range of metallicities, and found consistent results with the literature at [M/H] < 0.5 dex. Therefore, for this study we restricted our subsequent study to stars with [M/H] < 0.5 dex, as done in Sect. 5 of Nogueras-Lara (2022a). We applied the same colour cuts previously specified in Fig. 3 and carried out an analysis of the metallicity distribution for each colour bin.

4.1. Metallicity distribution

Previous work indicates the presence of a bi-modal metallicity distribution for both, the MWNSD and the MWNSC (Schultheis et al. 2021; Nogueras-Lara 2022a). Thus, we used a GMM (Pedregosa et al. 2011) to derive the number of Gaussian models which best reproduces the metallicity distribution in each colour bin J − Ks and H − Ks. We distinguished between one and two Gaussians by applying the Akaike information criterion (AIC; Akaike 1974), and obtained that for all the colour bins in J − Ks and H − Ks the probability density function of the data is always best represented by a two-Gaussians model. Figure 6 shows the results. To estimate the final GMM values and their associated uncertainties, we resorted to MonteCarlo (MC) simulations and repeated the GMM approach assuming a bi-modal distribution on 1000 MC samples generated randomly varying the metallicity of each star, assuming Gaussian uncertainties. Tables C.1 and C.2 show the results, where the mean values and their uncertainties were obtained averaging over the 1000 MC samples and applying a three sigma outlier-resistant criterion.

thumbnail Fig. 6.

Metallicity distribution for the stars belonging to each colour bin in J − Ks (upper row), and H − Ks (lower cut). As we move from left to right, we move deeper inside the MWNSD along the line of sight. The range of the colour bins is indicated in each panel. The orange line shows the obtained GMM model for each metallicity distribution, whereas the red and blue dashed lines correspond to each of the Gaussian models.

Figure 7 shows the variation of the metallicity for the metal poor and rich components with respect to the applied colour cuts. We obtained that both stellar populations follow an increasing trend towards high colour values whose maximum is approximately at J − Ks ∼ 6.5 − 7 and H − Ks ∼ 2.5 mag, which is in agreement within one sigma uncertainties with the position of Sgr A* that we derived in our kinematic analysis (i.e. μl ∼ 0 mas yr−1, see Sect. 3).

thumbnail Fig. 7.

Metallicity as a function of colour. Upper panels: metal rich stellar population. Lower panels: metal poor stellar population. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.

The most metal rich values obtained for MWNSC stars with high extinction, are somewhat larger than the metal rich peak obtained in previous work using the same data set (Nogueras-Lara 2022a) but analysing the mean properties of the MWNSC without considering colour cuts. This is consistent with the presence of a metallicity gradient, and can be justified by the averaged values obtained in previous work combining stars at different MWNSC radii.

4.2. Completeness analysis

We estimated the completeness of our KMOS sample following the technique described in Sect. 3.1.3. We created Ks luminosity functions for the KMOS stars and for all the stars with Ks photometry in the same region excluding foreground stars (see Fig. 1). Assuming that our Ks photometry is fully complete for the magnitude range covered by the KMOS data, we obtained that the completeness of the KMOS sample is ∼50% for Ks ∈ [10, 11.5] mag. The slightly lower completeness obtained in comparison with the one estimated by Feldmeier-Krause et al. (2020) is because we removed stars with [M/H] > 0.5 dex, as it was previously explained.

To check the effect of completeness on the obtained metallicity gradients, we repeated the analysis considering only stars with Ks ∈ [10, 11.5] mag. Given the lower number of stars in this magnitude bin, we doubled the size of the colour bins to have a sufficient number of stars per colour bin. We obtained similar results within the uncertainties and thus concluded that the completeness is not affecting our results.

4.3. Spatial distribution of stars with different metallicities

To check whether the detected metallicity gradient along the line of sight towards Sgr A* is real, we also studied the spatial distribution of the KMOS stars depending on the defined colour bins. We computed the median and the standard deviation of the position of the stars in each colour bin in the CMDs Ks versus J − Ks and Ks versus H − Ks, by applying a bootstrap resampling method as explained in Sect. 3.2. Figure 8 and Table C.3 show the results. We obtained that the standard deviation of the position distribution in x and y (Δx and Δy, respectively) tends to decrease for stars with higher extinction. Therefore these stars are more centrally concentrated than stars with lower extinction which potentially belong to the MWNSD and the external regions of the MWNSC. Our results are compatible with the presence of a correlation between extinction and different Galactic centre radii along the line of sight, and support that stars with J − Ks ∼ 6.5 mag and H − Ks ∼ 2.5 − 3 mag are probably associated to the innermost regions of the MWNSC.

thumbnail Fig. 8.

Standard deviation of the stellar positions of KMOS stars for each colour bin in J − Ks and H − Ks. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.

On the other hand, the average distribution of the stars is roughly centred on Sgr A*, although some scatter is detected which can be associated to data incompleteness (see Sect. 4.2), differential extinction, and/or asymmetries in the stellar distribution for different colour cuts. This might be related to the presence of stars from recent merger events, as the one proposed in Feldmeier-Krause et al. (2020) and Do et al. (2020).

5. Discussion

5.1. Effect of differential extinction on our results

The extinction towards the Galactic centre is extreme and significantly varies along the line of sight (e.g. Nishiyama et al. 2006, 2008; Schödel et al. 2010; Chatzopoulos et al. 2015b; Nogueras-Lara et al. 2018a). Hence, the differential extinction might affect the correlation that we found between distance and extinction, and also the detected kinematics and metallicity gradients. To assess our results, we built an extinction map to repeat our analysis excluding regions whose extinction is more than one standard deviation away from the median AKs value of the extinction map.

We applied the technique described in Nogueras-Lara et al. (2021c) and used red clump stars (helium core-burning stars with well characterised intrinsic properties, e.g. Girardi 2016) and other red giant stars with similar intrinsic colours, as reference stars. Figure 2 shows the box that we used to choose the reference stars in the CMD Ks versus H − Ks. We defined a pixel size of ∼10″ for the map and used the five closest reference stars to a given pixel within a radius of ∼15″ to compute its extinction using the equation:

(1)

where (H − Ks)0 = 0.10 ± 0.01 is the intrinsic colour of the reference stars (e.g. Nogueras-Lara et al. 2021c), and AH/AKs = 1.84 ± 0.03 (Nogueras-Lara et al. 2020b) is the extinction curve in the near infrared between the H and Ks bands. To account for the different distance of the reference stars from the centre of each pixel, we applied an inverse weight distance method (for further details see Nogueras-Lara et al. 2021c). To avoid mixing reference stars with too different extinctions, we constrained the maximum colour variation between the reference stars to be within 0.3 mag from the central-most reference star for each pixel. We only assigned an extinction value to a given pixel if at least 5 reference stars were found.

We obtained a median extinction value of AKs = 2.35 mag, with a standard deviation of 0.40 mag. Figure 9 shows the resulting extinction map (left panel), and the map after excluding the pixels more than one standard deviation away from the median extinction value (right panel). We repeated our μl analysis (see Sect. 3.1) excluding all the regions where the differential extinction varies more than one standard deviation, in agreement with the obtained map. We did not observe any variation within the uncertainties. Analogously, we also repeated the analysis of the metallicity gradient in Sect. 4.1 and obtained similar results within the uncertainties. Therefore, we conclude that our analysis is robust and is not affected by the differential extinction in the analysed region.

thumbnail Fig. 9.

Extinction map for the entire analysed (left panel) and the same map excluding pixels (in black) that deviate by more than one standard deviation from the median extinction (right panel). The x and y axes indicate the distance from Sgr A* (red star) in arc-seconds. The extinction value of each pixel, AKs, is indicated by the scale bar.

An alternative way of assessing the effect of the differential extinction on our results is to increase the size of the colour bins in our analysis (see cuts in Fig. 3). In this way, the colour bins contain stars with a wider range of extinction. We repeated our analysis of μl, the velocity dispersion, and the metallicity gradients, doubling the size of the colour bins (J − Ks = 1 mag and H − Ks = 0.4 mag), and did not observe any significant difference in the results. Moreover, this approach allowed us to increase the number of stars per colour bin minimising potential problems in colour bins that previously had a relatively low number of stars.

5.2. Stellar contamination between components

The detected gradients suggest a smooth transition between the kinematic and metallicity properties of the MWNSC and the MWNSD, in contrast to previous analysis on their bulk population (e.g. Schultheis et al. 2021; Nogueras-Lara 2022a). Nevertheless, this observation could be explained by a changing ratio of stars from these two Galactic centre components. To check this hypothesis, we focused on the metal rich stellar population and assumed that the MWNSD and the MWNSC are different components with different metallicities (e.g. Schultheis et al. 2021; Nogueras-Lara 2022a) equal to [M/H]MWNSD ∼ 0.2 dex and [M/H]MWNSC ∼ 0.4 dex (i.e. the extreme computed values in Tables C.1 and C.2).

We used all the stars detected in the photometric catalogue to avoid completeness issues and also considered the effect of the reddening vector to avoid including more stars in the bluer colour bins in comparison to the redder ones given the magnitude cut Ks ∈ [10, 14.2] mag. We assumed that the two first colour bins in the CMDs in Fig. 3 have negligible or very low contamination from the MWNSC (see Fig. 9 in Sormani et al. 2022), and a maximum contamination of ∼20% from Galactic bulge/bar stars (e.g. Sormani et al. 2022). For the remaining colour bins, we computed the number of stars from the MWNSD and the MWNSC that are necessary to obtain the metallicities in Tables C.1 and C.2. We obtained that for both CMDs (Ks versus J − Ks and Ks versus H − Ks), ∼1800 stars from the MWNSD are necessary to explain the detected gradient given the total number of ∼3300 stars in the samples. This means that 55% of the stars must belong to the MWNSD to justify the gradients.

To check whether this is possible, we estimated the 2D-projected mass density for the MWNSD and the MWNSC. For the MWNSC, we considered a distance of 3, 4, and 5 pc from its centre and assumed the mass distribution presented in Fig. 7 in Feldmeier-Krause et al. (2017a). We obtained an average 2D-projected mass density of ∼3 × 105 M⊙ pc−2. For the MWNSD, we considered the total stellar mass of ∼1.3 × 108 M⊙ obtained for a region of ∼800 pc2 near the MWNSC but excluding the region dominated by its effective radius (Nogueras-Lara et al. 2023), and estimated a total MWNSD 2D-projected mass of ∼1.6 × 105 M⊙ pc−2. To compute the final MWNSD 2D-projected mass density, we removed half of the mass because the extreme source crowding and extinction along the target line of sight impedes to observe the MWNSD beyond the MWNSC (e.g. Schödel et al. 2010; Chatzopoulos et al. 2015b; Nogueras-Lara et al. 2021a). We concluded that the stellar mass ratio between the MWNSD and the MWNSC is ∼25% for the observed region, which is also in agreement with previous estimates (e.g. Nogueras-Lara et al. 2021a). Therefore, although some mixing of stars from the MWNSD and MWNSC is expected, the contribution of the MWNSD stars in the region would need to be approximately double to fully account for the detected metallicity gradient. The same conclusion is also valid for the metal poor population, in which the variation between the extreme metallicity values is even larger (∼0.4 dex), and thus the mixture of different average populations from the MWNSD and the MWNSC is even more unlikely to explain the detected gradient.

To compare the estimated 2D-projected mass density and the number of stars from each component that are necessary to account for the detected gradients, we assumed that the MWNSD and MWNSC are both dominated by an old stellar population (Nogueras-Lara et al. 2020a; Schödel et al. 2020), and thus differences in their stellar population will not cause any effect on the estimated stellar mass ratio of ∼25% between the MWNSD and the MWNSC in the analysed magnitude range of Ks ∈ [10, 14.2] mag.

The same analysis also applies to the potential effect of radial migration to mix the stellar populations. Although some mixture is expected, the number of stars is not enough to produce the observed metallicity gradient.

5.3. Formation of the MWNSD and MWNSC

We obtained a bi-modal metallicity distribution for all the colour cuts and bands used in our analysis. This indicates that the previously found bi-modality on the bulk population of the MWNSD and MWNSC (Schultheis et al. 2021; Nogueras-Lara 2022a) is probably not a consequence of mixing of stellar populations located at different line-of-sight distance and/or from different Galactic centre components, but it is actually a real feature present in both the MWNSD and the MWNSC at different distances from Sgr A*. Moreover, the ratio between the metal poor and rich stars is approximately constant (∼0.6, see W1/W2 in Tables C.1 and C.2) for all the colour bins within the uncertainties (although they are relatively large for the colour bins dominated by the MWNSD, where the number of stars per colour bin is smaller). This means that metal rich stars dominate all the analysed colour bins and that the fraction between the metal poor and rich stars does not significantly vary with extinction and/or distance from Sgr A*.

We speculate that the detected metal poor and rich components might have different origins, which is in agreement with the slower rotation profile found for the metal poor stars in comparison to the metal rich ones in the MWNSD (Schultheis et al. 2021). Metal rich stars show a rotation which agrees with the gas motion in the central molecular zone suggesting in-situ formation, whereas metal poor stars might have been accreted from stellar clusters contributing to building the MWNSC and the MWNSD. This is in agreement with previous work proposing a hybrid formation scenario for the MWNSC (e.g. Guillard et al. 2016; van Donkelaar et al. 2023) combining in-situ star formation (e.g. Milosavljević & Loeb 2004; McLaughlin et al. 2006; Bekki 2007) and accretion of star clusters (e.g. Tremaine et al. 1975; Capuzzo-Dolcetta 1993; Antonini et al. 2012; Antonini 2013; Perets & Mastrobuono-Battisti 2014; Gnedin et al. 2014; Arca-Sedda et al. 2015, 2020; Tsatsi et al. 2017). In the framework of this model, we could interpret the metal poor stars in the MWNSC and MWNSD as stars accreted from clusters within a radius of 1.5 kpc at z > 4 (van Donkelaar et al. 2023).

If a significant part of the MWNSC mass originated from accretion of stellar clusters, we would expect that some of these clusters were destroyed before getting to the centre, whereas others could have lost a significant part of their mass in the MWNSD, potentially originating the detected smooth transition between both Galactic centre components. Alternatively, recent simulations have shown that in the case of a galaxy merger, part of the stellar population of the MWNSD might come from the NSCs of the progenitor galaxies and thus part of the MWNSD would share a common origin with the MWNSC (Mastrobuono-Battisti et al. 2023), which can also contribute to the detected smooth transition between the MWNSD and the MWNSC.

The current paradigm for the formation of NSDs in barred spiral galaxies assumes that gas from the galactic disc is funnelled towards the innermost regions of the galaxy by a bar, growing NSDs from inside out and generating a gradient in the properties of their stellar population (e.g. Shlosman 2001; Sormani et al. 2015; Seo et al. 2019; Bittner et al. 2020; de Sá-Freitas et al. 2023). This is compatible with the detected kinematic and metallicity gradients and also with previous results on the MWNSD stellar population which show that this mechanism is also at play in the Milky Way (e.g. Nogueras-Lara et al. 2023).

5.4. Metallicity gradients in other clusters

Metallicity gradients resembling the one that we detect in the MWNSC have also been found in other NSCs (e.g. M 54, NGC 5102, or NGC 5206, see Siegel et al. 2007; Hannah et al. 2021). They were explained as the combination of a young (several Gyr old) and metal rich stellar population concentrated towards the central regions of the clusters, and an older and metal poorer stellar population which extends to larger radii. Although a direct comparison with the detected gradient in the MWNSC is hard, this mechanism can also contribute to the detected metallicity gradient, given the presence of a young stellar population (several Myr old) in the central region of the MWNSC (Pfuhl et al. 2011; Nishiyama et al. 2016; Schödel et al. 2020). This scenario is in agreement with previous simulations showing that even evolved NSCs with in situ star formation can contain stellar populations segregated by age (Aharon & Perets 2015). Particularly, Mastrobuono-Battisti et al. (2019) found that MWNSC stellar populations born at different epochs present different morphologies and kinematics, being the oldest stars (presumably metal poor) more relaxed and extended (Mastrobuono-Battisti et al. 2019).

5.5. Different components of the same structure

Our results open the possibility that the MWNSC and the MWNSD could be part of the same structure with the MWNSD being an extended wing of the MWNSC. In this scenario, previous work showing different stellar properties between these components such as different kinematics and metallicity (e.g. Schultheis et al. 2021; Nogueras-Lara 2022a), would correspond to partial results that only refer to average quantities obtained in regions dominated by either the MWNSC or the MWNSD, without considering the transition between them. In this way, the detected metallicity gradient also agrees with the results obtained by Feldmeier-Krause (2022) for two regions located at ∼20 pc to the Galactic east and west of the MWNSC (corresponding to the transition region between the MWNSD and the MWNSC), where the metallicity was found to be lower than that of the MWNSC.

Regarding stellar populations, the bulk of stars in both Galactic centre components was found to be old (≳8 Gyr, e.g. Nogueras-Lara et al. 2020a, 2021a; Schödel et al. 2020), which is compatible with a potential common origin. Subsequent different star formation histories do not pose any problem for this scenario because different star forming processes can be operating on different scales and distance from the Galactic centre. In this way, the MWNSD might have grown from the MWNSC and then, the evolution of the Galactic bar and its efficiency at transporting gas towards the Galactic centre (e.g. Bittner et al. 2020; Nogueras-Lara et al. 2023), might have produced different stellar populations in the MWNSD and the MWNSC. Moreover, in-situ star formation and infall of stellar cluster in the MWNSC might explain the different evolution of their star formation histories (e.g. Pfuhl et al. 2011; Feldmeier-Krause et al. 2020), after a plausible common formation.

The possibility that the MWNSC and the MWNSD are part of the same structure might also explain the detection of very large NSCs (such as the one in FCC 47, with an effective radius of ∼70 pc, Fahrion et al. 2019), where maybe the two components are present and indistinguishable. Although NSCs are well studied structures (e.g. Neumayer et al. 2020), this is not the case for NSDs which have only been analysed for several tens of galaxies (e.g. Pizzella et al. 2002; Ledo et al. 2010; de Lorenzo-Cáceres et al. 2019; Gadotti et al. 2020). In this way, to shed light on the relation between NSCs and NSDs in general, it is imperative to conduct a statistical study of the coexistence of these two structures in external galaxies as well as a characterisation of their stellar properties.

To further investigate this question, it is necessary to analyse a larger field of view and also obtain more accurate proper motions and line-of-sight velocities to enable an orbit analysis that will allow us to better characterise the transition between the MWNSD and the MWNSC. Moreover, deeper data along the line of sight will also allow us to improve the study of the stellar population from the backside of the MWNSC and the MWNSD.

6. Conclusions

We studied the stellar population along the line of sight towards the MWNSC in a field of ∼2.8′×4.9′ centred on the MWNSC, to better characterise the relation between the MWNSD and the MWNSC. We used a photometric survey covering the region (Nogueras-Lara et al. 2018a, 2019), a proper motion catalogue (Shahzamanian et al. 2022), and an independent spectroscopic survey of ∼1000 stars with photometric counterparts in the analysed region, and measured [M/H] and line-of-sight velocities (Feldmeier-Krause et al. 2017b, 2020).

We applied colour-cuts to independently analyse stars with different extinctions, and distinguish between stars belonging to the MWNSD and the MWNSC (Nogueras-Lara et al. 2021a; Nogueras-Lara 2022a). We detected a gradient in the proper motion component parallel to the Galactic plane which indicates that there is a correlation between colour (i.e. extinction) and distance from the Galactic centre. We found a smooth kinematic transition between regions dominated by the MWNSD and the MWNSC. We confirmed the correlation between extinction and distance to the Galactic centre by analysing the line-of-sight velocity dispersion of spectroscopically characterised stars, and found that the velocity dispersion is largest for stars with J − Ks ∼ 7 mag and H − Ks ∼ 2.5 mag, supporting that they are on average closest to Sgr A* (e.g. Trippe et al. 2008; Schödel et al. 2009).

We studied the metallicity distribution of the stars in the field for the previously defined colour cuts. We concluded that there is a bimodal metallicity distribution for all the colour bins, in agreement with previous results on the bulk population of the MWNSD and the MWNSC (Nogueras-Lara 2022a; Schultheis et al. 2021). We found that the ratio between the metal poor and rich stars is approximately constant within the uncertainties for all the colour bins, indicating that the relative fraction between metal poor and rich stars is not affected by extinction and/or distance from Sgr A*. This suggests that the metallicity bi-modality found in previous work when analysing the bulk population of the MWNSC and the MWNSD (Nogueras-Lara 2022a; Schultheis et al. 2021) is a real feature of the MWNSD and the MWNSC. We speculate that metal rich stars might have formed in-situ from gas transported by the Galactic bar (Schultheis et al. 2021; Bittner et al. 2020), whereas metal poor stars might have been accreted from stellar clusters contributing to building the MWNSD and the MWNSC (Antonini et al. 2012; Tsatsi et al. 2017; van Donkelaar et al. 2023).

We also analysed the variation of metallicity with extinction for the MWNSD and MWNSC metal poor and rich stars and detected a metallicity gradient for both stellar populations towards the innermost regions of the MWNSC. This metallicity gradient agrees with the results obtained for two regions ∼20 pc to the Galactic east and west of the MWNSC, where the metallicity was found to decrease in comparison with the values found for the MWNSC (Feldmeier-Krause 2022). Moreover, similar metallicity gradients have been found in the central regions of nearby external barred spiral galaxies (Gadotti et al. 2020; Bittner et al. 2020; de Sá-Freitas et al. 2023), pointing towards an inside-out growth of these nuclear stellar structures and indicating that they are connecting to the galactic bar.

The detected kinematic and metallicity gradients cannot be explained by the mixture of stars from the MWNSD and the MWNSC, and thus an intrinsic variation of their properties seems to be the most plausible explanation. To further constrain our results a full kinematic characterisation of the stars in the transition region between the MWNSD and the MWNSC is necessary to assign membership probabilities, and determine the origin of stars with different metallicities. Our results suggest a smooth transition between the MWNSD and the MWNSC and open the possibility that they might be part of the same structure with the MWNSD being the grown edge of the MWNSC.

Acknowledgments

We thank the anonymous referee for helpful comments and suggestions that improved this manuscript. This work is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under program IDs 60.A-9450(A), 091.B-0418, 093.B-0368, and 195.B-0283. F.N.-L. gratefully acknowledges the sponsorship provided by the European Southern Observatory through a research fellowship. R.S. acknowledges financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709) and from grant EUR2022-134031 funded by MCIN/AEI/ 10.13039/501100011033 and by the European Union NextGenerationEU/PRTR. Ad.L.C. acknowledges support from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (MCIN/AEI) under grant CoBEARD and the European Regional Development Fund (ERDF) with reference PID2021-128131NB-I00. Ad.L.C. also acknowledges financial support from MCIN through the Spanish State Research Agency, under the Severo Ochoa Centres of Excellence Programme 2020-2023 (CEX2019-000920-S), as well as from grant AYA2016-77237-C3-1-P from the Spanish Ministry of Economy and Competitiveness (MINECO).

References

  1. Aharon, D., & Perets, H. B. 2015, ApJ, 799, 185 [NASA ADS] [CrossRef] [Google Scholar]
  2. Akaike, H. 1974, IEEE Trans. Autom. Control, 19, 716 [Google Scholar]
  3. Antonini, F. 2013, ApJ, 763, 62 [Google Scholar]
  4. Antonini, F., Capuzzo-Dolcetta, R., Mastrobuono-Battisti, A., & Merritt, D. 2012, ApJ, 750, 111 [NASA ADS] [CrossRef] [Google Scholar]
  5. Arca-Sedda, M., Capuzzo-Dolcetta, R., Antonini, F., & Seth, A. 2015, ApJ, 806, 220 [NASA ADS] [CrossRef] [Google Scholar]
  6. Arca-Sedda, M., Gualandris, A., Do, T., et al. 2020, ApJ, 901, L29 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bekki, K. 2007, PASA, 24, 77 [Google Scholar]
  8. Bittner, A., Sánchez-Blázquez, P., Gadotti, D. A., et al. 2020, A&A, 643, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Capuzzo-Dolcetta, R. 1993, ApJ, 415, 616 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chatzopoulos, S., Fritz, T. K., Gerhard, O., et al. 2015a, MNRAS, 447, 948 [Google Scholar]
  11. Chatzopoulos, S., Gerhard, O., Fritz, T. K., et al. 2015b, MNRAS, 453, 939 [Google Scholar]
  12. Chen, Z., Do, T., Ghez, A. M., et al. 2023, ApJ, 944, 79 [NASA ADS] [CrossRef] [Google Scholar]
  13. de Lorenzo-Cáceres, A., Sánchez-Blázquez, P., Méndez-Abreu, J., et al. 2019, MNRAS, 484, 5296 [Google Scholar]
  14. de Sá-Freitas, C., Fragkoudi, F., Gadotti, D. A., et al. 2023, A&A, 671, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [Google Scholar]
  16. Do, T., David Martinez, G., Kerzendorf, W., et al. 2020, ApJ, 901, L28 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dong, H., Wang, Q. D., Cotera, A., et al. 2011, MNRAS, 417, 114 [Google Scholar]
  18. Fahrion, K., Lyubenova, M., van de Ven, G., et al. 2019, A&A, 628, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Feldmeier, A., Neumayer, N., Seth, A., et al. 2014, A&A, 570, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Feldmeier-Krause, A. 2022, MNRAS, 513, 5920 [Google Scholar]
  21. Feldmeier-Krause, A., Zhu, L., Neumayer, N., et al. 2017a, MNRAS, 466, 4040 [NASA ADS] [Google Scholar]
  22. Feldmeier-Krause, A., Kerzendorf, W., Neumayer, N., et al. 2017b, MNRAS, 464, 194 [Google Scholar]
  23. Feldmeier-Krause, A., Kerzendorf, W., Do, T., et al. 2020, MNRAS, 494, 396 [Google Scholar]
  24. Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [Google Scholar]
  25. Fritz, T. K., Chatzopoulos, S., Gerhard, O., et al. 2016, ApJ, 821, 44 [Google Scholar]
  26. Fritz, T. K., Patrick, L. R., Feldmeier-Krause, A., et al. 2021, A&A, 649, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gadotti, D. A., Bittner, A., Falcón-Barroso, J., et al. 2020, A&A, 643, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Gallego-Cano, E., Schödel, R., Nogueras-Lara, F., et al. 2020, A&A, 634, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Girardi, L. 2016, ARA&A, 54, 95 [Google Scholar]
  30. Gnedin, O. Y., Ostriker, J. P., & Tremaine, S. 2014, ApJ, 785, 71 [Google Scholar]
  31. Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Guillard, N., Emsellem, E., & Renaud, F. 2016, MNRAS, 461, 3620 [Google Scholar]
  34. Hannah, C. H., Seth, A. C., Nguyen, D. D., et al. 2021, AJ, 162, 281 [NASA ADS] [CrossRef] [Google Scholar]
  35. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kerzendorf, W., & Do, T. 2015, https://doi.org/10.5281/zenodo.28016 [Google Scholar]
  37. Kissler-Patig, M., Pirard, J.-F., Casali, M., et al. 2008, A&A, 491, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Launhardt, R., Zylka, R., & Mezger, P. G. 2002, A&A, 384, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Ledo, H. R., Sarzi, M., Dotti, M., Khochfar, S., & Morelli, L. 2010, MNRAS, 407, 969 [CrossRef] [Google Scholar]
  40. Lyubenova, M., van den Bosch, R. C. E., Côté, P., et al. 2013, MNRAS, 431, 3364 [Google Scholar]
  41. Martínez-Arranz, Á., Schödel, R., Nogueras-Lara, F., & Shahzamanian, B. 2022, A&A, 660, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Mastrobuono-Battisti, A., Perets, H. B., Gualandris, A., Neumayer, N., & Sippel, A. C. 2019, MNRAS, 490, 5820 [Google Scholar]
  43. Mastrobuono-Battisti, A., Ogiya, G., Hahn, O., & Schultheis, M. 2023, MNRAS, 521, 6089 [NASA ADS] [CrossRef] [Google Scholar]
  44. McLaughlin, D. E., Anderson, J., Meylan, G., et al. 2006, ApJS, 166, 249 [NASA ADS] [CrossRef] [Google Scholar]
  45. Milosavljević, M., & Loeb, A. 2004, ApJ, 604, L45 [CrossRef] [Google Scholar]
  46. Nagayama, T., Nagashima, C., Nakajima, Y., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 459 [Google Scholar]
  47. Neumayer, N., Seth, A., & Böker, T. 2020, A&ARv, 28, 4 [Google Scholar]
  48. Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [Google Scholar]
  49. Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174 [Google Scholar]
  50. Nishiyama, S., Schödel, R., Yoshikawa, T., et al. 2016, A&A, 588, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Nogueras-Lara, F. 2022a, A&A, 666, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Nogueras-Lara, F. 2022b, A&A, 668, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Nogueras-Lara, F., Gallego-Calvente, A. T., Dong, H., et al. 2018a, A&A, 610, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Nogueras-Lara, F., Schödel, R., Dong, H., et al. 2018b, A&A, 620, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2019, A&A, 631, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2020a, Nat. Astron., 4, 377 [Google Scholar]
  57. Nogueras-Lara, F., Schödel, R., Neumayer, N., et al. 2020b, A&A, 641, A141 [EDP Sciences] [Google Scholar]
  58. Nogueras-Lara, F., Schödel, R., & Neumayer, N. 2021a, ApJ, 920, 97 [NASA ADS] [CrossRef] [Google Scholar]
  59. Nogueras-Lara, F., Schödel, R., & Neumayer, N. 2021b, A&A, 653, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Nogueras-Lara, F., Schödel, R., & Neumayer, N. 2021c, A&A, 653, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Nogueras-Lara, F., Schultheis, M., Najarro, F., et al. 2023, A&A, 671, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  63. Perets, H. B., & Mastrobuono-Battisti, A. 2014, ApJ, 784, L44 [NASA ADS] [CrossRef] [Google Scholar]
  64. Pfuhl, O., Fritz, T. K., Zilka, M., et al. 2011, ApJ, 741, 108 [Google Scholar]
  65. Pizzella, A., Corsini, E. M., Morelli, L., et al. 2002, ApJ, 573, 131 [NASA ADS] [CrossRef] [Google Scholar]
  66. Schödel, R., Merritt, D., & Eckart, A. 2009, A&A, 502, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [Google Scholar]
  68. Schödel, R., Yelda, S., Ghez, A., et al. 2013, MNRAS, 429, 1367 [Google Scholar]
  69. Schödel, R., Feldmeier, A., Neumayer, N., Meyer, L., & Yelda, S. 2014a, Class. Quant. Grav., 31, 244007 [CrossRef] [Google Scholar]
  70. Schödel, R., Feldmeier, A., Kunneriath, D., et al. 2014b, A&A, 566, A47 [Google Scholar]
  71. Schödel, R., Nogueras-Lara, F., Gallego-Cano, E., et al. 2020, A&A, 641, A102 [Google Scholar]
  72. Schultheis, M., Fritz, T. K., Nandakumar, G., et al. 2021, A&A, 650, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Scoville, N. Z., Stolovy, S. R., Rieke, M., Christopher, M., & Yusef-Zadeh, F. 2003, ApJ, 594, 294 [Google Scholar]
  74. Seo, W.-Y., Kim, W.-T., Kwak, S., et al. 2019, ApJ, 872, 5 [NASA ADS] [CrossRef] [Google Scholar]
  75. Shahzamanian, B., Schödel, R., Nogueras-Lara, F., et al. 2022, A&A, 662, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Shlosman, I. 2001, ASP Conf. Proc., 249, 55 [NASA ADS] [Google Scholar]
  77. Siegel, M. H., Dotter, A., Majewski, S. R., et al. 2007, ApJ, 667, L57 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sormani, M. C., Binney, J., & Magorrian, J. 2015, MNRAS, 449, 2421 [NASA ADS] [CrossRef] [Google Scholar]
  79. Sormani, M. C., Magorrian, J., Nogueras-Lara, F., et al. 2020, MNRAS, 499, 7 [Google Scholar]
  80. Sormani, M. C., Sanders, J. L., Fritz, T. K., et al. 2022, MNRAS, 512, 1857 [CrossRef] [Google Scholar]
  81. Stolovy, S., Ramirez, S., Arendt, R. G., et al. 2006, J. Phys. Conf. Ser., 54, 176 [CrossRef] [Google Scholar]
  82. Surot, F., Valenti, E., Gonzalez, O. A., et al. 2020, A&A, 644, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Tremaine, S. D., Ostriker, J. P., & Spitzer, L., Jr. 1975, ApJ, 196, 407 [NASA ADS] [CrossRef] [Google Scholar]
  84. Trippe, S., Gillessen, S., Gerhard, O. E., et al. 2008, A&A, 492, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Tsatsi, A., Mastrobuono-Battisti, A., van de Ven, G., et al. 2017, MNRAS, 464, 3720 [Google Scholar]
  86. van Donkelaar, F., Mayer, L., Capelo, P. R., et al. 2023, MNRAS, 522, 1726 [NASA ADS] [CrossRef] [Google Scholar]
  87. Wang, Q. D., Dong, H., Cotera, A., et al. 2010, MNRAS, 402, 895 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Proper motion analysis

Table A.1.

Median proper motions and their uncertainties for the colour bins in the CMD Ks versus J − Ks.

Table A.2.

Median proper motions and their uncertainties for the colour bins in the CMD Ks versus H − Ks.

Appendix B: Line-of-sight velocity dispersion

Table B.1.

Line-of-sight velocity dispersion for the colour cuts in the CMDs.

Appendix C: Metallicity analysis

Table C.1.

Results from the GMM analysis of the metallicity distribution using the CMD Ks versus J − Ks.

Table C.2.

Results from the GMM analysis of the metallicity distribution using the CMD Ks versus H − Ks.

Table C.3.

Spatial distribution of stars with different metallicities.

All Tables

Table A.1.

Median proper motions and their uncertainties for the colour bins in the CMD Ks versus J − Ks.

In the text
Table A.2.

Median proper motions and their uncertainties for the colour bins in the CMD Ks versus H − Ks.

In the text
Table B.1.

Line-of-sight velocity dispersion for the colour cuts in the CMDs.

In the text
Table C.1.

Results from the GMM analysis of the metallicity distribution using the CMD Ks versus J − Ks.

In the text
Table C.2.

Results from the GMM analysis of the metallicity distribution using the CMD Ks versus H − Ks.

In the text
Table C.3.

Spatial distribution of stars with different metallicities.

In the text

All Figures

thumbnail Fig. 1.

Target region centred on the MWNSC. The lower panel shows a Spitzer false colour image (3.6 μm (blue), 4.5 μm (green), 5.8 μm (red), Stolovy et al. 2006). The upper panel corresponds to a false colour JHKs GALACTICNUCLEUS image adapted from Nogueras-Lara (2022a). The circular dashed region outlines the effective radius of the MWNSC, the white dotted contour shows the region with KMOS data, and the white filled boxes indicate regions without proper motion data. The position of the supermassive black hole Sagittarius A* (Sgr A*) and the approximate size of the fields at the Galactic centre distance are also indicated in the figure.
In the text
thumbnail Fig. 2.

CMDs Ks versus J − Ks (left panel) and Ks versus H − Ks (right panel) for the target region. The red dashed lines indicate the separation between the foreground population, the MWNSD, and the MWNSC. The blue box in the CMD Ks versus H − Ks shows the reference stars to build the extinction map in Sect. 5.1. The scale bars indicate stellar densities using a power stretch scale.
In the text
thumbnail Fig. 3.

CMDs Ks versus J − Ks and Ks versus H − Ks obtained for stars with well defined proper motions (i.e. proper motion uncertainties < 0.5 mas yr−1). The red dashed boxes indicate the assumed colour cuts to analyse the variation of the proper motion distribution with respect to the extinction.
In the text
thumbnail Fig. 4.

Variation of the proper motion component parallel to the Galactic plane versus colour. The proper motion values were calculated assuming the median value of the stars in each colour bin. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.
In the text
thumbnail Fig. 5.

Variation of the dispersion of line-of-sight velocities as a function of colour. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3. The x-coordinates of the data points were calculated assuming the median value of the stars in each colour bin.
In the text
thumbnail Fig. 6.

Metallicity distribution for the stars belonging to each colour bin in J − Ks (upper row), and H − Ks (lower cut). As we move from left to right, we move deeper inside the MWNSD along the line of sight. The range of the colour bins is indicated in each panel. The orange line shows the obtained GMM model for each metallicity distribution, whereas the red and blue dashed lines correspond to each of the Gaussian models.
In the text
thumbnail Fig. 7.

Metallicity as a function of colour. Upper panels: metal rich stellar population. Lower panels: metal poor stellar population. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.
In the text
thumbnail Fig. 8.

Standard deviation of the stellar positions of KMOS stars for each colour bin in J − Ks and H − Ks. The red and grey squares correspond to stars from the MWNSD and MWNSC following the extinction criterion in Sect. 3.
In the text
thumbnail Fig. 9.

Extinction map for the entire analysed (left panel) and the same map excluding pixels (in black) that deviate by more than one standard deviation from the median extinction (right panel). The x and y axes indicate the distance from Sgr A* (red star) in arc-seconds. The extinction value of each pixel, AKs, is indicated by the scale bar.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.