| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 12 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202346636 | |
| Published online | 08 December 2023 | |
Asymmetric capture into Neptunian 1:2 resonance
1
School of Astronomy and Space Science, Nanjing University,
163 Xianlin Avenue,
Nanjing
210046,
PR China
2
Key Laboratory of Modern Astronomy and Astrophysics in Ministry of Education, Nanjing University,
PR China
e-mail: zhouly@nju.edu.cn
Received:
11
April
2023
Accepted:
12
September
2023
The asymmetric resonance configuration characterised by the critical angle librating around centres other than 0° or 180° is found in the 1:N mean motion resonance. The asymmetric 1:2 resonance with Neptune is of particular interest because the two asymmetric islands seem to host different populations, and this might be a direct clue to understanding the early evolution of the Solar System. The asymmetry has been investigated from both observational and theoretical perspectives, but conclusions among studies vary widely. In this paper, using toy models, we carefully designed a series of tests to systematically study the capture of planetesimals into the leading and trailing resonance islands. Although these tests may not exactly reproduce the real processes the Solar System experienced, they reveal some typical dynamics in the resonance capture. Since the real Twotinos have small to moderate inclinations, as a first attempt, we adopted planar models in this paper in order to investigate the mechanisms that may lead to asymmetric capture by the leading and trailing islands, including their size variation during the outward migration of Neptune, the stickiness of the leading island, and the migration slowdown effect. We find that the ratio between the populations of the leading and trailing islands can be easily tuned by introducing the slowdown effect into the migration model, and thus it may not be a good tracer of the migration history. However, the eccentricity of objects trapped in two asymmetric islands may conserve some valuable information of the early evolution of the Solar System.
Key words: celestial mechanics / Kuiper belt: general / methods: miscellaneous
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The distribution of trans-neptunian objects (TNOs) in space bears major clues to the early evolution of the Solar System. Among TNOs, the resonant population is believed to have been captured into mean motion resonances (MMRs) with Neptune (see e.g. Malhotra 1995; Zhou et al. 2002) during the late stage of the Solar System’s formation, when Neptune (as well as other planets) was migrating due to its scattering of a large number of planetesimals (Fernandez & Ip 1984). Thus, the existence of resonant populations, their physical and chemical characteristics, and their orbital distributions as the consequences of resonance capture processes are all of great interest and deserve thorough analysis.
For a 1:N MMR with Neptune, except for the symmetric resonance configuration characterised by the resonance angle librating around 0° or 180°, asymmetric resonance configurations in which the libration is around values other than 0° or 180° exist (e.g. Frangakis 1973; Malhotra 1996). The asymmetric configuration with the resonance angle librating between 0° and 180° is called the ‘leading resonance island’, while the configuration that librates between 180° and 360° is referred to as the ‘trailing resonance island’. Theoretically, these two asymmetric islands are absolutely the same from the point of view of dynamics under current planetary configuration. As a matter of fact, the resonance could have a complicated structure. For instance, a new resonance island may emerge at very high eccentricity in the planar circular restricted three-body model (e.g. Beauge 1994; Lan & Malhotra 2019), while in the non-planar case, very high inclination may introduce significant distortion to asymmetric islands (e.g. Gallardo 2006, 2020; Saillenfest et al. 2016; Efimov & Sidorenko 2020). In the study of the primordial planetesimal disc in the early stage of the Solar System, it is still appropriate to consider the two asymmetric islands as identical to each other, given that these planetesimals are anticipated to have relatively flat and circular orbits. Observations, however, have shown that the leading island is always superior in population. The most well-known example of such population asymmetry is the asymmetrical distribution of Trojan asteroids in the 1:1 MMR with Jupiter, where the Greek camp (around the Lagrange point L4) hosts about 90% more asteroids than the Trojan camp (L5), according to the database of IAU Minor Planet Center (MPC)1. Similar asymmetry can be clearly seen in the 1:N resonances with Neptune (see Table 1 in Sect. 2.2).
Many studies have been devoted to the apparently asymmetric distribution of resonant TNOs in the 1:2 MMR with Neptune, which are generally called ‘Twotinos’. In the latest observation, Chen et al. (2019) report 34 Twotinos, among which 17 are in the leading island, 8 in the trailing island, and the remaining 9 in the symmetric configuration. Thus, the ratio of numbers of objects detected in the leading and trailing islands (hereafter L/T ratio) is 17/8 ≈ 2.1. After taking the observation bias into account, Chen et al. (2019) estimated a population of 4400 Twotinos with Hr < 8.66 (diameter ≳ 100 km), among which 1600 are in the leading island and 1500 in the trailing island. They also deduced an overall L/T ratio within 0.25–1.86 with a confidence of 95%. We note that the observational bias favouring the detection of the leading librator is due to the location of the trailing island, which is in the direction of the Galaxy centre as seen from Earth. Since Neptune has not moved a considerable distance after the TNOs were observed in quantity in last three decades, this observational bias may continue to blur the true distribution of TNOs in the asymmetric resonant islands in all the 1:N resonances with Neptune.
Chen et al. (2019) claim that the ‘real’ Twotino populations in the two asymmetric islands are not so different from each other after accounting for the observational bias, which means the value of the L/T ratio is almost one. However, numerical simulations of the capturing of planetesimals into the resonance yield widely different L/T ratios. Chiang & Jordan (2002) modelled the capturing of planetesimals into MMRs during the migration of Neptune and found that the L/T ratio of Twotinos was 0.91 and 0.30, respectively, when the migration timescale is 10 Myr and 1 Myr. Later, Murray-Clay & Chiang (2005) suggested that the migration should not be too fast in order to avoid an overwhelming capture fraction in the trailing island. Li et al. (2014) investigated the resonant capture of objects at different inclinations and obtained an L/T ratio of ~1.1 in low inclination, where the migration timescale is 20 Myr. Pike & Lawler (2017), however, found a leading-island-dominant result with an L/T ratio of 2.24 in their numerical simulations of the evolution of the outer Solar System following a specific version of the Nice model (Brasser & Morbidelli 2013) where Neptune undergoes a high-eccentricity (0.3) phase. The authors suggest that the orbital circularisation of Neptune is not the reason for the leading island enhancement. Adopting four different Neptunian migration models (as proposed by Kaib & Sheppard 2016) characterised by ‘grainy slow’, ‘grainy fast’, ’smooth slow’, and ‘smooth fast’, Lawler et al. (2019) calculated the capture efficiency of Twotinos, from which Chen et al. (2019) derived the fraction of asymmetric Twotinos in the leading island in these migration models as 0.36, 0.54, 0.52, and 0.56. Translated into L/T ratios, these numbers are 0.56, 1.17, 1.08, and 1.27, respectively.
So far, both in observational data and in numerical simulations, the asymmetric distribution of TNOs in the two resonant islands of 1:N MMRs is often recognised, but the L/T ratio is reported in a wide range, and the possible mechanisms that may result in this asymmetry are still vague. We note that the non-gravitational effects, in particular the Yarkovsky effect, may contribute to the asymmetric distribution of asteroids in the 1:1 MMR with inner planets like the Earth and Venus (see e.g. Zhou et al. 2019; Xu et al. 2022), but they could hardly have any influence on TNOs due to the large distance to the Sun. Therefore, we have to search for the mechanisms leading to the asymmetric distribution of Twotinos mainly during the process of their being captured.
Murray-Clay & Chiang (2005) have proposed three mechanisms that may contribute to the asymmetric capture of planetesimals into the 1:2 resonance. First, the size of the leading asymmetric resonant island shrinks while the trailing one expands when Neptune migrates outwards. Consequently, an object will have a larger probability of being trapped and staying around the trailing island than the leading one. In particular, the leading island might even completely disappear if the migration is fast enough so that the capture is totally dominated by the trailing island. The second mechanism is that the difference between the leading and trailing islands become less significant as the planetesimal’s initial eccentricity increases. Thus, the trailing island’s advantage in population decreases. And thirdly, an object’s libration around the leading island is slower; thus, an object spends more time in the vicinity of the leading island than near the trailing one before it is finally trapped by either island.
This paper is devoted to studying the details of the resonant capturing process of TNOs into the 1:2 MMR with Neptune through carefully designed numerical simulations and quantitative analyses that are aimed at understanding the influences of migration models and initial conditions of planetesimals on the distribution of Twotinos in the leading and trailing islands. We note that the models adopted in this paper are often intentionally simplified in order to emphasise the dynamical effects of certain capturing processes, and we do not imply that Neptune migrated exactly in the way presented by the models.
The rest of this paper is arranged as follows. In Sect. 2, as background to our investigations, we introduce the dynamical structure of the 1:2 MMR. The numerical models adopted in this paper are also introduced in this section. The numerical simulations of the Neptunian migration and resonance captures are then presented in Sect. 3, and the mechanisms that can cause the asymmetry between two asymmetric resonance islands are analysed. The discussion and conclusion are given in Sect. 4.
2 Asymmetric resonance islands
For a 1:N MMR in a planar restricted three-body model, the asymmetric resonance islands appear only when the eccentricity is larger than a specific value. For the 1:2 MMR with Neptune, the critical eccentricity is ~0.04, and the asymmetric resonance islands disappear again after the eccentricity exceeds ~0.95 (see e.g. Lan & Malhotra 2019).
2.1 Dynamical structure of 1:2 resonance
To provide a general description of the structure of the 1:2 MMR with Neptune, we conducted some numerical simulations of the motion of test particles in the 1:2 MMR in the circular planar restricted three-body model where the primary bodies are the Sun and Neptune. The initial semimajor axis of test particles was set at the nominal location of the 1:2 MMR a0 = 22/3aN ≈ 47.622 AU, where the subscript ‘N’ stands for Neptune. The initial mean anomaly was chosen as M0 = 0°, and the initial eccentricity e0 and longitude of pericentre ϖ0 were evenly distributed in the range [0, 0.6) and [0°, 360°].
The equations of motion were then numerically integrated for 1 Myr, and we monitored the resonant angle ϕ = 2λ − λN − ϖ of these test particles in the evolution, where λ and λN are the mean longitudes of the test particle and Neptune, respectively. In Fig. 1, we summarise the libration amplitudes of ϕ, which are indicated by colour. The blank space represents the non-resonance objects, and the black curves roughly give the boundary between symmetric and asymmetric resonances.
The libration centre corresponds to the equilibrium solution for the equations of motion, which can be obtained by determining the minimum of the perturbation function, and the red lines in Fig. 1 represent these equilibrium points. We note that the red lines fit the location of minimal libration amplitude of ϕ very well (indicated by the bluest colour), which was obtained from numerical simulations of the motion.
We set M0 = 0° for the test particles, and without loss of generality, λN0 = 0° for Neptune. In Fig. 1, a pair of asymmetric resonant islands are shown to start from the bifurcation of symmetric resonance (ϕc = 180°) when e0 ≳ 0.04. The libration centre of asymmetric resonance deviates away from ϕc = 180° as e0 increases, and the deviation reaches the maximum when e0 ≈ 0.44, where ϕc ≈ 70° (leading island) and 290° (trailing island). We stopped our calculation at e0 = 0.6 because, in the Solar System, a Twotino will cross Neptune’s orbit if its eccentricity exceeds 0.37, and it will cross Uranus’s orbit if it is larger than 0.6. In the restricted three-body model, however, the two asymmetric resonant islands maintain until e ≈ 0.95, after which they meet each other and merge again at ϕc = 180° (Lan & Malhotra 2019).
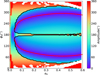 |
Fig. 1 Libration amplitude of resonance angle in numerical simulations of the circular planar restricted three-body model. The abscissa and ordinate are the initial eccentricity e0 and resonance angle ϕ0, respectively, and the libration amplitude is indicated by colour. The asymmetric islands are enclosed with black lines, and the red lines indicate the locations of asymmetric resonance centres (see text). |
2.2 Asymmetric population in 1:2 resonance
Figure 1 implies a symmetry between the leading and trailing asymmetric resonant islands, that is, the two resonant configurations are dynamically identical to each other, and the same amount of objects may be expected in the two islands, if these objects do exist. However, contrary to this expectation, many 1:N (not only the 1:2) MMRs in the Solar System have been found to have an apparent asymmetry in hosting objects between the leading and trailing island. For example, for the 1:1 resonance with Jupiter, Szabó et al. (2007) obtained an L/T ratio of 1.6 ± 0.1, while Grav et al. (2011) estimated a value of ~ 1.4 ± 0.2. In Table 1, we list the number of objects located in some major 1:N resonances in the Solar System. In Table 1, objects in the 1:1 resonance with Jupiter or Neptune are also known as Trojans, and their data is from the ‘Lists of Trojan minor planets’ of IAU MPC on date October 20232. For other 1:N resonances, the numbers in the table are from our numerical simulations as follows. We downloaded the orbital elements of objects located near the 1:N resonance from the Asteroids-Dynamic Site (AstDyS)3, and for each object we generated 20 clone orbits within the observational error bars. These orbits were then integrated for 1 Myr using Swifter_symba (Levison & Duncan 2000) in a gravitational model consisting of the Sun and four giant planets. The resonant angles of clone orbits were monitored during the simulations, and the proportion of them staying in the leading or trailing islands was calculated. Thus, the decimal numbers in Table 1 imply that either some objects are located in the boundary zone of the resonance islands or the observation errors are large.
It is clear that the leading island possesses a larger population than the trailing one for all the 1:N MMRs. For Neptune’s resonances, the L/T ratio is always larger than three. Chen et al. (2019) attribute the L/T ratio of observed Twotinos to observational bias, and for similar reasons, all other small objects in the Neptune 1:N resonance are strongly affected by observational bias. Although current observations are not adequate enough to confirm whether the leading and trailing islands of the 1:2 resonance are identical or not in population, there are mechanisms in the dynamics that could result in different capture preferences in these islands (see, e.g., Murray-Clay & Chiang 2005). Therefore, further theoretical investigation is necessary to explore the possibility of asymmetric capture of Twotinos and explain the discrepancies between the results obtained from different models (e.g. Chiang & Jordan 2002; Li et al. 2014; Pike & Lawler 2017; Lawler et al. 2019). This will provide an insight into the accuracy of our predictions regarding the actual distribution of Twotinos.
Number of asteroids in the leading and trailing resonance islands and their ratios (L/T) in some major 1:N resonances.
2.3 Numerical model
Since the leading and trailing islands are dynamically symmetric to each other under the current configuration of the Solar System, the asymmetric populations must be the result of the capturing of objects into the resonances and/or the subsequent evolution in the resonances before planets attained their current orbits. This paper is devoted to investigating the formation of populations of Twotinos in the asymmetric islands. For this purpose, we carried out numerical simulations of different scenarios of planetary migration and of the capture of fictitious objects that represent the planetesimals in the disc.
The capturing of planetesimals into an MMR is a short-term process compared to the secular perturbations from planets other than Neptune. Thus, the effects of secular perturbations can be neglected if focus is placed on the dynamics of capturing. Moreover, the outcome of resonant capture sensitively depends on the initial eccentricity of planetesimals and the migration rate but not as strongly on the inclination. In the simulation of Li et al. (2014), the L/T ratio does not vary much in the low-inclination (i < 20°) regime, while for high inclination (i > 20°), the capture efficiency is very low and thus not statistically significant. In addition, this paper focuses on the primordial capture process, that is, when the inclination of planetesimals in the disc have not yet been excited. Therefore, in this paper, in the numerical simulations of the capture of planetesimals into the 1:2 MMR with Neptune, a planar circular restricted three-body model was adopted, which consisted of the Sun, Neptune on a circular orbit, and a number of zero-mass planetesimals.
In our simulations, an artificial force was exerted on Neptune to make it migrate at a given rate ȧN. If ȧN is constant, migration is linear. We note that an exponential migration is often applied in the literature (e.g. Malhotra 1995). In such a case, the migration from an initial orbit ai to the final one af is characterised by a timescale τ: a(t) = af − (af − ai) exp(−t/τ). For cases in which ȧN is not constant, the average rate 〈ȧ〉 is often used to characterise the migration and compare with the linear migration speed. We note that the averaging should be calculated over the semimajor axis (not over time as usual) because the planetesimals are usually distributed according to their distances from the Sun. During the migration, any migration rate change, such as that in grainy migration (Nesvorný & Vokrouhlický 2016) and the major ‘jump’ of Neptune (Nesvorný & Morbidelli 2012), increases the value of 〈ȧ〉 because high-rate stages are weighted more.
3 Neptunian migration and resonance capture
3.1 An example case
We first ran some numerical simulations to get an overall view of the planet’s orbital migration and resonant capture. In these simulations, Neptune migrates from 26 AU to 30 AU at a constant migration rate, and several migration rates from ȧN = 0.1 AU Myr−1 to 16 AU Myr−1 were selected. We note that a wide range of migration rates were adopted in previous works. For instance, for a Neptune migration of 7 AU (from 23 to 30 AU), the e-folding timescales τ = 0.1 Myr, 1 Myr, and 10 Myr were tested in Chiang & Jordan (2002), and the longest τ was suggested. Nesvorný (2015b) tried several timescales from 1 Myr to 100 Myr and suggests τ ≳ 10 Myr is appropriate. The linear migration rates we adopted in this work are approximately equivalent to the e-folding timescales of 0.2 Myr (ȧN = 16 AU Myr−1) to 35 Myr (ȧN = 0.1 AU Myr−1).
For a certain ȧN, we selected 10 000 test particles representing the planetesimals originally evenly occupying the region from 44.45 AU to 46.03 AU and corresponding to the nominal positions of the 1:2 MMR with Neptune when its semimajor axis is 28 and 29 AU, respectively. At the moment when Neptune stops migrating at 30 AU, the simulation continued for another 0.2 Myr, and we checked the resonant state of each test particle. The initial eccentricities of the test particles were randomly distributed in [0, 0.3], and the initial longitudes of the pericentre and mean anomalies were randomly in [0°, 360°]. One may notice that the planetesimals are overexcited in eccentricity and might be quite different from the primordial planetesimal disc (Stern & Colwell 1997; Kenyon et al. 2008). This is because we were not trying to reproduce the distribution of real planetesimals through these simulations but probing the dynamical mechanisms in theory. The results of our simulations are summarised in Fig. 2.
As Fig. 2 shows, the capture efficiency decreases from ~ 15% (for ȧN ≤ 1 AU Myr−1) to ~2% (16 AU Myr−1) as the migration gets faster. Although it is always smaller than one, the L/T ratio shows a tendency of increasing to one when migration is either very fast or very slow, while significantly fewer test particles are captured by the leading island than the trailing one when the migration rate is around 1 AU Myr−1.
A slower migration favours capturing test particles with lower eccentricities. In addition, the leading island tends to trap more highly eccentric particles than the trailing island, and the difference in eccentricity between them becomes more significant when the migration is faster. Although the eccentricities of particles trapped by the trailing island are smaller than those of the particles trapped by the leading island, the eccentricity range available for being captured is wider for the trailing island, especially for fast migration (ȧN ≳ 4 AU Myr−1).
Except for the slow migration cases (ȧN ≲ 2 AU Myr−1), the eccentricity ranges for objects being captured by the two islands have only a little overlap. This implies that not only may one expect more eccentric orbits in the leading island, but also one can determine which island an object will join based on its eccentricity under a given migration rate.
 |
Fig. 2 Initial eccentricities of test particles captured by the leading island (red) and trailing island (blue) at different migration rates of Neptune. The box plots indicate the minimum, maximum, median, and upper and lower quartiles as usual. The solid diamonds are the mean value of eccentricities. The L/T ratios are plotted as solid circles and are connected by a dotted line (right ordinate). The total capture efficiencies (in percent) are labelled at the top of the panels. The upper and lower panels correspond to fast and slow migration rate ranges, respectively. |
3.2 Size variation of asymmetric islands
In Fig. 3, we have plotted some orbits of planetesimals with different initial eccentricities in the 1:2 MMR with Neptune migrating at different rates. In the simulations, Neptune was supposed to migrate outwards from 29 AU, and the initial semi-major axis of test particles was set at the nominal 1:2 MMR with Neptune (i.e. a0 = 46.03 AU). For these test particles, 36 different ϖ0 were selected at 10° intervals, while M0 = 0° remained fixed. The initial eccentricity of the test particles and the migration rates of Neptune are shown in each panel. As can be seen in the figure, the sizes of the asymmetric islands vary, and the difference in size between the two islands becomes more significant as Neptune migrates faster, but it becomes less significant as the initial eccentricity of planetesimals increases.
The size of the resonance islands can be measured by the extents of libration of a and ϕ in the resonance. Thus, a quantitative description of the size variation of resonance islands can be obtained through a series of numerical simulations. In these more detailed simulations, 180 different ϖ0 from 0° to 360° at a 2° interval and 20 different e0 from 0.02 to 0.40 were set for the test particles. Other initial conditions remained similar to those of the simulations presented in Fig. 3. Neptune was supposed to migrate outwards from 29 AU, and the initial semimajor axis of 3600 test particles was set at the nominal 1:2 MMR with Neptune (i.e. a0 = 46.03 AU). Several migration rates of Neptune from 0 AU Myr−1 (no migration) to 15 AU Myr−1 were tested.
From each simulation ran with a given initial eccentricity and Neptune migration rate, we picked out the test particle that has the largest libration amplitude of resonance angle ϕ. The libration amplitudes in ϕ and a were then used as the indicator of the size of resonance islands. We provide a summary of the results in Fig. 4.
As shown in Fig. 4, the asymmetric islands get bigger as the initial eccentricity increases. For ȧN = 0, the island extends to have a ϕ amplitude of ~140º and an a amplitude of ≳0.6 AU. The leading island shrinks as the migration rate increases. For example, for a given initial eccentricity e0 = 0.2, the ϕ libration decreases from ≳130° at ȧN = 0 to ≲90° at ȧN = 9 AU Myr−1, and the leading island even vanishes completely at a larger migration rate. Conversely, the trailing island expands as Neptune migrates faster. Also for e0 = 0.2, the libration amplitude of ϕ increases from ≲140º to ≳180º as ȧN increases from 0 to 9 AU Myr−1. The trailing island’s expansion can also be observed at the libration of the semimajor axis a in the lower panels in Fig. 4. We note that the blank region in the corner of the small eccentricity e0 and fast migration ȧN in Fig. 4 indicates that resonant motion is forbidden there. In other words, in fast migration, only those planetesimals with an eccentricity higher than a specific value can be captured into either the leading or trailing island.
Thus far, we have confirmed that the size variation of the asymmetric resonance islands is in favour of more planetesimals being trapped by the trailing island during the outward migration of Neptune. The two asymmetric islands host planetesimals with different eccentricities, and the overall difference in the islands’ sizes diminishes gradually as the eccentricity increases.
 |
Fig. 3 Evolution of objects close to the 1:2 resonance demonstrating the sizes of the resonance islands. The abscissa and ordinate represent the resonance angle ϕ and the semimajor axis (in Neptune’s semimajor axis aN), respectively. The planetesimal’s eccentricity and Neptune’s migration rate are indicated in each panel. For each particle, the time interval between two adjacent points is 1000 yr. |
 |
Fig. 4 Dependence of the resonance island size on the migration rate of Neptune (ȧN) and initial eccentricity of test particles (e0). The maximal libration amplitude of the resonance angle is shown in the upper panels, while the lower panels show the libration of the semimajor axis (see text). The left and right columns are respectively for the leading and trailing island. |
3.3 Stickiness of leading island
As Murray-Clay & Chiang (2005) suggested, the only mechanism that might favour the leading island’s capturing of objects is its shrinkage during the orbital migration, as this causes objects to slow down and thus aggregate around the leading island. This effect is called ‘stickiness’ here, and we checked this idea quantitatively as follows in this section. We note that the word ‘stickiness’ in this case is used to describe the fact that an orbit spends more time around one resonance island than around the other during the planetary migration, and the term has nothing to do with the usual ‘resonance stickiness’ that happens around resonances without planetary migration (see, e.g., Malyshkin & Tremaine 1999; Lykawka & Mukai 2007; Sun & Zhou 2009; Bannister et al. 2016; Gallardo 2018).
Again in our simulations, Neptune migrates outwards from 29.0 AU, and 10 000 test particles are supposed to locate in the nominal 1:2 resonance at 46.03 AU. The initial eccentricities of them are in [0, 0.3], and angular elements (ϖ and M) are uniformly distributed in [0°, 360º], respectively. Three migration rates of Neptune were tested: 0.2 AU Myr−1, 1 AU Myr−1, and 2 AU Myr−1.
A test particle of small eccentricity in the simulation may start from the symmetric resonance with a resonant angle ϕ librating around 180º, and its libration amplitude grows and is accompanied by an increasing eccentricity as Neptune migrates outwards. The test particle may then evolve into an asymmetric resonance island, but before that, it experiences some complete symmetric resonance cycles. We show in Fig. 5 an example of this typical evolution. The stickiness effect of the leading island can be recognised in the bottom-left panel of Fig. 5. Below 180º, the resonant angle ϕ oscillates at a relatively slower pace than above 180º so that it stays around the leading island (red area) for more time than around the trailing island (blue area), although the latter area is wider (which can be inferred from the larger amplitude of ϕ).
In order to quantify the stickiness effect of the leading island, for each test particle in our simulations that experienced the transferring from symmetric to asymmetric resonance, we examined the last symmetrical libration period before the particle was captured by either one of the asymmetric islands and recorded length of time that it stayed on each side of 180º (the red and blue shadowed areas in Fig. 5) as well as its mean eccentricity during this period. We summarise the results of the cases with migration rates 0.2 AU Myr−1 and 2 AU Myr−1 in Fig. 6.
According to Fig. 6, 80% of the test particles in the slow migration model (0.2 AU Myr−1) and 100% of the test particles in the fast migration model (2 AU Myr−1) stayed around the leading island (ϕ < 180°) for a longer period of time during their last symmetric period. Taking the slower migration model as an example, the test particles spent about 12% more time around the leading side than in the trailing side, even though the leading island is smaller (see Fig. 3). Assuming the probability of being captured by either one of the resonance islands is proportional to the time an object spends around the island before the capture, we may expect 12% more objects would be trapped in the leading island. We also found that the ratio between the two times decreases as the eccentricity of the test particles increases, implying that the stickiness effect of the leading island abates. In fact, when the eccentricity is large, both islands expand (see Fig. 3), and the difference in island size caused by Neptune migration becomes less significant. A faster migration amplifies the asymmetry between the two islands, just as it enhances their difference in size.
So far, we have found that the size variation of asymmetric islands favours the capture of planetesimals into the trailing island, while the stickiness effect favours the leading island. Moreover, these two opposite effects are both enhanced if the initial eccentricity of planetesimals is small or if the migration is fast.
 |
Fig. 5 Evolution of a test particle when transferring from symmetric to asymmetric resonance. The left column is for Neptune migrating at a rate of 1 AU Myr−1, while the right column is for the same test particle but the migration stops at 0.3 Myr. From top to bottom, the panels show the semimajor axis a, eccentricity e, and resonant angle ϕ of the test particle with solid lines. The dashed lines in the top panels represent the nominal semimajor axis of the 1:2 resonance. The magenta area in the middle-left panel indicates the duration of the last symmetric cycle, while the red and blue areas in the bottom-left panel indicate the time intervals around the leading and trailing island, respectively. |
 |
Fig. 6 Stickiness effect of the leading island. The times an object stayed on both sides of ϕ = 180° when it was transferring from symmetric to asymmetric resonances (see text and Fig. 5) are plotted in the two left panels, and the ratio of the two time durations are shown in the right panels. The abscissa is the mean eccentricity in the last cycle before being captured by the asymmetric resonance. The red and blue dots represent the time spent in the leading and trailing side, respectively. The upper and lower panels represent the results from the simulations of migration rate: ȧN = 0.2 AU Myr−1 and ȧN = 2 AU Myr−1, respectively. In the former simulation, 1833 out of 10 000 initial objects are shown, and 435 objects for the latter are shown. |
3.4 Migration slowdown effect
When Neptune migrates outwards, the leading island shrinks while the trailing island expands, and the faster the migration, the greater the size difference between the two islands. Certainly, if the migration decelerates, the difference between the asymmetric islands diminishes until the migration stops, and the two islands regain the same size. During this migration slowdown process, the leading island may capture extra objects that were wandering in its neighbouring region as it expands, while some objects may escape from the trailing island. In this paper, this phenomenon is referred to as the ‘slowdown effect’, by which we mean the deceleration of Neptune’s outward migration. We note that the migration may stop completely or even reverse (i.e. migrate inwards to the Sun) if the deceleration is large enough. Considering the stochasticity of scattering events between Neptune and planetesimals that drives the migration, such temporary reverse migration may not be uncommon, but of course the most common scenario must be that the migration slows down due to the gradual depletion of planetesimals. This migration slowdown will change the L/T ratio, and we investigated this effect through some numerical simulations.
3.4.1 Numerical simulations
Neptune was set to migrate from a semimajor axis of 29 AU at an initial rate of ȧN1 = 5 AU Myr−1. The migration was changed to a new speed ȧN2 after 0.2 Myr when Neptune reached 30 AU. All test particles were placed at 47.62 AU, exactly the nominal position of the 1:2 resonance with Neptune at 30 AU. In such an arrangement, when the migration slowdown occurs, the test particles are only ‘touched’ by the resonance, and thus they do not experience the eccentricity evolution ‘inside’ the resonance. The initial eccentricities were set from 0 to 0.3, with an interval of 0.015, thus making 20 groups in total. For each group of test particles with a given eccentricity, the longitude of the pericentre ϖ was uniformly chosen from 0° to 360° with a 2° interval, and the mean anomaly was M = 0° for all test particles. The total number of test particles was then 3600.
Selecting some migration rates ȧN2, we continued the simulations up to 0.4 Myr, and during the simulation, the libration of the resonant angle ϕ for every object was monitored to check whether it was captured by either of the asymmetric resonant islands. The results are summarised in Table 2. Again, we state that the migration rate of Neptune in reality does not change to another value instantaneously. We used these ‘unphysical’ tests to exaggerate and emphasise the effect of the migration rate changing.
Migrating at a constant rate ȧN1 = ȧN2 = 5 AU Myr−1, Neptune captures only a small fraction (2.33% = 84/3600) of test particles into the 1:2 resonance, and most of them are in the trailing resonant island rather than the leading island (82 versus 2). If the migration accelerates to ȧN2 = 6 AU Myr−1, the capture efficiency drops down to 1.06%, and all the 38 particles are trapped in the trailing island (see Table 2).
However, the capture efficiency, particularly for the leading island, increases if the migration decelerates (ȧN2 < ȧN1 = 5 AU Myr−1), as shown in Table 2. As a result, the L/T ratio increases significantly from 0.02 (for a constant migration rate 5 AU Myr−1) to 6.46 (for a complete stop of migration, ȧN2 = 0). We also tested a reverse migration by setting aN2 = −1 AU Myr−1, and all test particles were found trapped in the leading island.
Clearly, changing Neptune’s migration rate can substantially influence the outcome of resonant captures. In fact, due to Neptune’s outward migration, the leading resonant island could be much smaller than the trailing island (Fig. 3); thus, the majority of test particles are captured by the trailing island. However, at the moment when the migration is ‘interrupted’ by a slower migration rate (deceleration), the leading island expands, while the trailing island shrinks, relatively. Consequently, the leading island may capture the objects formerly wandering around or passing by the island. In contrast, some objects formerly trapped in the trailing island may fall out from the island as it shrinks. Both of the above processes may contribute to the increase of the L/T ratio of the captured test particles. In addition, the stickiness of the leading island contributes to the L/T ratio in this migration slowdown process because the stickiness effect accumulates more particles near the leading island, providing a greater probability for them to be captured by the expanding island at the moment of migration deceleration.
At this point, we find that it is worth revisiting the resonance capturing process described in Sect. 3.1, where the results of being captured into the two asymmetric islands (Fig. 2) were calculated in 0.2 Myr after Neptune’s migration stopped (i.e. the slowdown effect had in fact taken effect in those simulations). If the difference between the two migration rates applied in one simulation (ΔȧN = ȧN1 − ȧN2) is regarded as a rough estimate of the strength of the slowdown effect, the trends of the L/T ratio changing with ΔȧN in Fig. 2 and in Table 2 will be found to agree with each other. However, the values of the L/T ratios in these two numerical experiments, for example Case 8 in Table 2 and the case of ȧN = 5 Au Myr−1 in Fig. 2, should not be compared directly because different settings have been used in the simulations, particularly different initial populations of test particles.
Number of asymmetric resonance captures at different migration rate changings.
3.4.2 Resonance capturing process
By setting all test particles to have the same initial semimajor axis (47.62 AU) corresponding to the nominal 1:2 resonance exactly when Neptune changes its migration rate, we have shown how a prompt acceleration or deceleration of migration may influence the capture of objects to asymmetric resonant islands. However, the resonance capture must be a rather continuous process as opposed to a momentary event. To further clarify how the slowdown effect may influence the resonance capturing process, we repeated the simulation as Case 8 in Table 2, but this time 10 000 test particles were distributed evenly in a spatial range of 1 AU before 47.62 AU. Thus, the 1:2 resonance would sweep across these test particles as Neptune migrated at a constant rate of 5 AU Myr−1 until the migration was removed when the nominal resonance reached the outer edge of the test particle belt. After that, the evolution of the test particles was followed for another 0.2 Myr, and we checked their resonance configurations. The aim for these simulations was to find out how the ‘capture process’ by a sweeping resonance coordinates the destinations of test particles. We illustrate our results in Fig. 7, where we plot the initial semimajor axes and eccentricities of test particles that were captured by one of the asymmetric islands.
In Fig. 7, the test particles are shown to form two groups separated from each other by a semimajor axis, ~47.35 AU, around which almost no successful capture into the resonance occurs. Group 1 on the left side of the figure hosts 109 objects, less than half of which were captured into the leading resonance island, yielding an L/T ratio of 0.88 (=51/58). On the right-hand side, 132 test particles make up Group 2, in which more objects are obviously captured by the leading island, and the L/T ratio is 3.89 (= 105/27). Since the initial semimajor axes of test particles are evenly distributed in the 1 AU range from 46.62 to 47.62 AU, the original population (located from 46.62 to 47.35 AU) from which Group 1 arises is about four times the initial population of Group 2, and the second group’s capture efficiency is much higher than that of the first group.
In our model, the 1:2 resonance sweeps through the region from 46.62 to 47.62 AU at a constant rate, and the migration stops when the resonance just passes the right edge of the test particle belt. Thus, in Group 1, the latest-captured objects with an initial semimajor axis ~47.35 AU meet the resonance 0.034 Myr before the migration stops (it takes 0.034 Myr for the nominal resonance to travel 0.27 AU from 47.35 AU to 47.62 AU when Neptune migrates at 5 AU Myr−1). Meanwhile, we found in our simulations that the typical resonant libration period around the asymmetric island is ~0.07 Myr. Thus, the objects in Group 1 finished at least half a resonance libration period before the migration stops. Therefore, when the migration deceleration occurs (migration rate changes from 5 AU Myr−1 to 0 AU Myr−1 in this case), the objects in Group 1 have already been deeply in the resonance, and they are less affected by the deceleration. For objects in Group 2, the capture process is ongoing when the migration stops, and the deceleration significantly affects their final resonance configuration. Even for the objects on the right edge of the region (47.62 AU), where the nominal resonance just arrives as the migration is removed, the slowdown effect is obviously ‘felt’. As a result, the L/T ratio can be increased significantly by the slowdown effect of migration.
Another feature that can be seen in Fig. 7 is that the leading island captures objects from high-eccentricity orbits more easily, which is consistent with the results in Figs. 2 and 6. In addition, if the high L/T ratio was the result of a migration slowdown mechanism, apart from more eccentric orbits being found in the leading island, we would also expect that the leading island would capture objects later and from the region more distant from the Sun when the deceleration of migration begins to take effect. If the chemical composition and physical property of planetesimals change radially with their distances from the Sun (see e.g. Wong & Brown 2016; Morbidelli & Nesvorný 2020), we argue that the objects now in the two asymmetric resonance islands may be different in colour, albedo, size, and composition, although such a discrepancy has not yet been observed (Chen et al. 2019).
The resonance capture process requires a certain amount of time to be completed. The difference between the two groups in Fig. 7 implies that the outcome of the process can be altered if the migration changes during that period of time. In fact, the resonance begins its trapping of objects before the nominal position reaches the objects.
From Case 8 in Table 2, we arbitrarily chose again the group of test particles with eccentricity e0 = 0.09 and plotted their snapshots in Fig. 8 on the (ϕ, a) plane at t = −30, −20, −10 and 0 kyr, with t = 0 being the moment when the nominal resonance reaches the initial position of test particles at 47.62 AU.
As shown in Fig. 8, the distribution of the test particles in the (ϕ, a) plane has been disturbed by the resonance no later than t = −30 kyr (about half of the resonance libration period) before the nominal resonance arrives, when the nominal resonance is about 0.15 AU (=5 AU Myr−1 ×30 kyr) away. Test particles feel the strongest perturbation from Neptune as they pass through the conjunction position (resonant angle ϕ = 0°) where their semimajor axes are altered and thus clearly deviate from their original values. Although they have not yet been locked in the libration, many particles show signs of a collective motion, and they gather around the leading island. The leading island expands when the migration is removed (at t = 0 kyr in the simulation) and traps these objects with a high probability. Of course, if the migration continues at the same speed, many more objects will be captured by the trailing island instead because it is much bigger than the leading island (Fig. 3). We note that in the example shown in Fig. 8, the eccentricity (0.09) is relatively too large to be efficiently captured by the trailing island (see Fig. 7), and that is why only one object (blue point in Fig. 8) is ultimately in the trailing island.
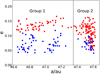 |
Fig. 7 Distribution of test particles captured by the sweeping 1:2 resonance. The resonance swept through these particles as Neptune migrated at a constant rate of 5 AU Myr−1, and the migration was stopped when the nominal resonance reached 47.62 AU. The abscissa and ordinate are for the initial semimajor axis and eccentricity of test particles. The red and blue colours indicate that an object was captured by the leading and trailing resonance island, respectively. The dashed line at 47.35 AU separates test particles into two groups (see text). |
 |
Fig. 8 Distribution of test particles on the (ϕ, a) plane as the 1:2 resonance approaches. Four snapshots at different moments with t = 0 kyr representing exactly when the nominal resonance reaches the initial position of test particles are given in each of the four panels. Objects later captured by the leading and trailing island are in red and blue, respectively, while those not captured by any asymmetric resonance are in purple. The horizontal line stands for the nominal position of 1:2 resonance. |
3.5 Exponential migration
As we have shown, the instantaneous change of migration rate may influence the outcome of resonance capture, especially altering the L/T ratio considerably. In the simulations discussed so far, the migration has been assumed to have constant rates (linear migration), and the rate change occurred abruptly. This is an oversimplified model, and in fact, an exponential model (Malhotra 1995) might be much closer to the real migration process. Meanwhile, we note that the instant migration speed in an exponential migration model decreases continuously. Thus, the slowdown effect might take place all the way. To examine this possibility, we performed some numerical simulations with an exponential migration of Neptune.
If Neptune migrates from ai to af in an exponential way characterised by a timescale τ, the mean migration rate will be (af − ai)/(2τ). In our simulations presented below, Neptune migrates outwards from ai = 26 AU to af = 30 AU following the exponential rules with timescales τ = 0.1, 0.2, and 0.5 Myr. As in Sect. 3.1, 10000 test particles with eccentricities randomly in [0,0.3] were located from a1 = 44.45 to a2 = 46.03 AU (corresponding to the nominal 1:2 resonance when Neptune is at 28 and 29 AU, respectively), and their angular orbital elements were set randomly in [0°, 360°]. The model is sketched in Fig. 9.
We integrated the system to 8τ and checked whether each particle was locked in any one of the resonance configurations in the end. The results are summarised in Table 3 and Fig. 10. The overall efficiency of the resonance capture in these simulations was low, and it was a little higher when the migration is slower. This is consistent with the results in Fig. 2, where linear migrations were adopted. Out of the 10 000 test particles, 445, 462, and 583 objects were captured in the asymmetric resonance islands for τ = 0.1, 0.2, and 0.5 Myr, respectively. The overall capture efficiency is roughly comparable to the results in Fig. 2.
As for the asymmetric preference, the L/T ratio in the linear migration model (in fact with somewhat of a slowdown effect, as we explained previously) increased from ~0.4 to ~0.8 as the migration rate increased from 1 AU Myr−1 to 16 AU Myr−1 (Fig. 2). Because of the continuous slowdown effect in the exponential migration, the L/T ratio is remarkably higher than in the linear migration model with a comparable migration speed. As shown in Table 3, the L/T ratio clearly increased as the migration timescale τ became shorter (faster migration). A simple algebraic calculation reveals that the migration speed (ȧN) and deceleration (äN) of Neptune are 2 AU/τ and −2 AU/τ2 when the nominal resonance reaches the inner edge (a1) of the planetesimal belt. For the outer edge (a2), these values are 1 AU/τ and −1 AU/τ2, respectively. Thus, for a migration in a short timescale, the slowdown effect must be much more significant than a migration with a longer timescale, and a much larger L/T ratio can be seen in the former case.
In the work by Chiang & Jordan (2002) and Li et al. (2014), the L/T ratio was 0.30, 0.91, and 1.1 when the migration timescale was 1, 10, and 20 Myr, respectively. Although the models adopted in their work were not identical, we see a consistent trend, that is, the L/T ratio increases as the migration rate becomes slower. This trend is opposite to our results in Table 3, where a faster migration rate leads to a larger L/T ratio. In fact, we have seen such opposite trends in Fig. 2, where the L/T ratio drops to a minimum at a migration rate of 1 AU Myr−1. Starting from this point, both faster and slower migration elevate the L/T ratio. Thus, opposite trends can be seen at the two ends of the slower and faster migration.
In an exponential migration model, the migration speed changes constantly. Thus, all planetesimals in the belt encounter the resonance at different speeds, and they all experience the deceleration of migration. Therefore, all phenomena observed in the migration slowdown scenario can be identified easily in the exponential migration model (Fig. 10). For example, a faster migration captures objects with higher eccentricities, and for the same migration rate, the leading island traps objects with higher eccentricities, while the trailing island traps those with lower eccentricities.
As the outward migration continues, the eccentricities of objects trapped in the resonance increase, which may drive some of them to travel from the symmetric resonance to the asymmetric island, particularly to the leading island. We note that in our simulations, the advantage of the leading island in population is enhanced further through this transferring among resonance configurations.
The timescales (τ) we adopted in Table 3 are all quite short compared to what we expect to see in the early evolution of the Solar System. We used these short timescales in our toy models to enhance the dynamical effects of the migration slowdown. If a longer, thus more comparable timescale to ‘reality’ is applied, we would expect the effects of migration slowdown to become weaker. To verify this, we carried out another simulation, where Neptune migrates outwards from ai = 23 AU to af = 30 AU with a timescale τ = 3 Myr, which is relatively closer to the real situation.
In this simulation, 10,000 test particles were located from a1 = 38.10 to a2 = 46.03 AU (corresponding to the nominal 1:2 resonance when Neptune is at 24 and 29 AU respectively), and their initial eccentricities were randomly distributed in [0,0.2], covering well the range suitable for being captured when migration is slower than 2 AU Myr−1 (see Fig. 2). We recorded the moment when the resonance angle crossed 180° for the last time before finally librating around either one of the asymmetric islands as the ‘capture time’ for each object. The capture times of 612 leading objects and 1132 trailing objects are plotted in Fig. 11.
In this model, the nominal 1:2 resonance with Neptune reaches the planetesimal disc at ~0.56 Myr, and leaves the disc at ~6.4 Myr. Most of the trailing objects are captured at the moment of their first contacts with the nominal resonance. On the other hand, the capture of the leading objects is delayed for a long time, with a significant fraction of captures occurring after 6 Myr as a result of Neptune’s migration slowdown. There is also a tendency that the higher the eccentricity, the later the capture time. The trailing objects also have a late-captured portion, mainly in the high-eccentricity region.
In the simulations by Chiang & Jordan (2002) and Li et al. (2014), Neptune migrates 7 AU. Thus the average migration rates (7AU/2τ) are 3.5, 0.35, and 0.175 AU Myr−1 when τ = 1, 10, and 20 Myr, respectively. In our experiment of τ = 3 Myr (Fig. 11), the average migration rate is ~ 1.2 AU Myr−1 (=7 AU/(2 × 3Myr)), and we obtained an L/T ratio of 0.54, which is slightly higher than the L/T ratio of 0.42 obtained in a linear migration of 1 AU Myr−1 in Fig. 2. However, the L/T ratio 0.30 obtained by Chiang & Jordan (2002) for τ = 1 Myr (average migration rate 3.5 AU Myr−1) is much lower than the L/T ratio in the linear model with a comparable migration rate of 4 AU Myr−1 (see Fig. 2). This is because the eccentricities in the former model (from 0 to 0.05) are much lower than in the latter one (from 0 to 0.3), and thus the leading island’s capture of high-eccentricity objects in fast migration during our experiments did not occur in their experiment.
Therefore, in a more realistic model with a longer migration timescale and a less eccentricity-excited planetesimal disc, the effects arising from the migration slowdown, such as a tuned L/T ratio (the stronger the slowdown effect, the larger the L/T ratio) and a selective capture according to eccentricity (the leading island captures objects with a higher eccentricity in a later stage), can be still observed. In addition, the real migration of planets caused by their encounters with planetesimals must be a significantly stochastic process (see e.g. Zhou et al. 2002; Nesvorný & Vokrouhlický 2016). Therefore, such acceleration and deceleration in the migration must be a common phenomenon, and the slowdown effects must leave their imprints in the distribution of objects trapped in the asymmetric resonance islands.
 |
Fig. 9 Belt of test particles (shaded range) and time evolution of the nominal 1:2 resonance with Neptune. |
Objects captured by the asymmetric resonance islands in the exponential migration model.
 |
Fig. 10 Initial semimajor axes and eccentricities of objects captured by leading (red) and trailing (blue) islands in the exponential migration model. The timescales of migration τ are marked in each panel. The vertical dashed lines are the inner and outer edge of the belt of test particles, and the numbers near them are the instant migration rates of Neptune when the nominal resonance arrives at both edges of the planetesimals’ belt. |
 |
Fig. 11 Initial semimajor axes and eccentricities of objects that are captured by the leading (upper panel) and trailing (bottom panel) islands in the exponential migration model with timescale τ = 3 Myr. The capture time of each object is indicated by colour. The numbers near the vertical dashed lines are the instant migration rates of Neptune when the nominal resonance arrives at corresponding locations. |
4 Conclusion and discussion
In the 1:2 mean motion resonance with Neptune, apart from the symmetric configuration in which the resonant angle librates around 0° or 180°, two asymmetric resonance islands exist beyond a certain eccentricity value (Fig. 1). One of the islands is the leading resonance island, which has a libration centre smaller than 180°, and the other one is the trailing island. Although the dynamics of these two resonance islands are identical to each other in the current planetary configuration, the populations detected in each island show an advantage in the leading island (Table 1). On the other hand, numerical simulations of the planetary migration and resonance capture tend to attain apparently unequal populations for these two islands, often with a preference for the trailing one (Fig. 2).
When Neptune migrates outwards, the trailing island expands, while the leading island shrinks. As a result, the capture into the trailing island can be more dominant, leading to a small L/T ratio between the populations in the leading and trailing islands. The sizes of both islands are determined by the migration speed of Neptune and the initial eccentricities of planetesimals. The advantage of the trailing island is most significant when the resonance slowly sweeps through a dynamically cold belt full of planetesimals with small eccentricities (Figs. 3 and 4).
The advantage of the trailing island may be reduced by the stickiness of the leading island, which refers to the fact that an object travels at a slower pace around the leading island (Figs. 5 and 6). Depending on the initial eccentricity, an object may spend nearly one and a half to twice as long wandering around the leading island as around the trailing one. This difference is more pronounced if the migration is faster, as it increases the possibility of an object being captured by the leading island.
If the migration of Neptune continues at a constant speed, the competition of the two mechanisms would still make the trailing island’s capture dominant (Case 2 of Table 2). But the migration has to slow down and stop at some stage. Moreover, the migration is likely to be a grainy process rather than a smooth one, and we found that the acceleration and deceleration of migration may significantly alter the populations captured into the two islands and thus the L/T ratio.
When the migration decelerates, the leading island expands (recovering from the depressed size in migration) and swallows planetesimals in the neighbouring region, and its stickiness helps by gathering more objects around it. In contrast, the trailing island shrinks and releases some objects that had been captured before. This slowdown effect of migration can dramatically increase the L/T ratio. In fact, by setting an appropriate deceleration (change of migration rate), any value of the L/T ratio can be obtained (Table 2). Surely, when doing this to adjust the L/T ratio, any type of change of migration rate should be possible in physical reality. Considering that the overall migration of Neptune is composed of a large number of semimajor axis shifts due to the scattering events of planetesimals of a variety of sizes and masses, we still expect a great possibility of migration rate changes.
The planetesimals most affected by this migration slowdown effect are those that experience the deceleration when the capturing is ongoing (Group 2 in Fig. 7). Those that have been deep in the resonance when the slowdown occurs are influenced much less (Group 1 in Fig. 7). However, if the migration is not smooth, such events of deceleration must be quite common. And in the widely adopted exponential migration model (Fig. 9), although it is smooth, the migration decelerates continuously. Thus, the slowdown effect evidently works (Table 3 and Figs. 10 and 11).
We note that the L/T ratio can be arbitrarily tuned by setting the appropriate slowdown effect. Therefore, it seems that nowadays the ratio of Twotinos populations trapped in the two asymmetric resonant islands cannot serve as a good indicator of Neptune’s migration history. However, if the migration always ends up with a slowdown, which is a reasonable assumption, we would expect that more objects will be captured into the leading islands from the outer edge of the planetesimal belt at the final age of Neptune’s migration. This may leave some traces in the populations trapped in the two islands concerning the source regions of these objects.
Some other clues about the history of migration can be found in the eccentricities of the two populations. In a slow migration, the resonance only captures objects in nearly circular orbits, and the capture is dominated by the trailing island. Therefore, the existence of objects observed in the leading island nowadays implies that the initial orbits of planetesimals had been excited to some extent before they were captured. At a relatively higher migration rate, only those planetesimals with eccentricities in a specific range can be captured, and the leading island tends to trap objects with higher eccentricities than the trailing island. This phenomenon of the leading island preferring high eccentricity becomes more evident when the migration is faster. Comparing the eccentricity distributions in both asymmetric islands may also reveal some important information about the origin of these objects. Solid conclusions may be made when the sample size of Twotinos is eventually large enough.
In the past, many attempts have been made to constrain the timescale of migration. Studies have explored a wide range of migration timescales, from 0.1 Myr to 100 Myr, yet no definitive timescale has been determined. Murray-Clay & Chiang (2005) argued against fast migration, as it may lead to an overwhelming capture by the trailing island. Nesvorný (2015b) also favours an e-folding timescale greater than 10 Myr to ensure efficient excitation of inclination. Conversely, Volk & Malhotra (2019) find that timescales from 5 to 50 Myr can produce inclination distributions that match observations. Lawler et al. (2019) suggest that the grainy slow migration model (Kaib & Sheppard 2016), with timescales of 30 Myr and 100 Myr before and after the Neptune jump, respectively, is the most consistent with observations, but confirmation of this conclusion requires additional observations.
The migration of planets in the Solar System could have been a complicated process. For example, Nesvorný & Morbidelli (2012) suggested that five or six giant planets ever existed in the system, and when a giant planet was ejected, Neptune’s semimajor underwent a jump. Such a major jump up to ~0.5 AU has been adopted in several subsequent models (see e.g. Nesvorný 2015a; Nesvorný & Vokrouhlický 2016; Kaib & Sheppard 2016). Close encounters with large planetesimals also influence Neptune, resulting in grainy migration. The variation of Neptune’s semimajor axis due to close encounters with Pluto-sized objects is estimated to be |ΔaN| ≲ 0.005 AU, and thousands of such encounters with massive objects may occur in a grainy migration model (e.g. Nesvorný & Vokrouhlický 2016; Kaib & Sheppard 2016).
Qualitatively, a complex migration process can be a combination of a series of events simulated by simple models presented in this paper. However, as our simulations show, the outcomes of the Neptune migration and resonance capture depend sensitively on the migration model and the planetesimals’ initial conditions, which makes it very difficult to reconstruct the history of planetary migration from current orbits and the distribution of TNOs.
Through a series of carefully designed numerical experiments, we found that a planetesimal around the 1:2 MMR of Neptune can ‘perceive’ only the average migration rate within a time window of about 0.05 to 0.1 Myr, which is roughly equivalent to the libration period of the 1:2 resonance angle. This time interval is much longer than the typical duration of the semimajor axis variation caused by a close encounter between Neptune and a planetesimal, which usually completes in only years. This, in fact, strongly restricts our ability to retrieve the history of Neptune’s migration through the current distribution of Twotinos. On the other hand, we note that a major jump of 0.5 AU in Neptune’s semimajor axis due to the ejection of a planet in such a time window would increase (or decrease) the local migration rate by approximately 5–10 AU Myr−1. However, the average migration rate can hardly be affected by a single event of a close encounter with a Pluto-sized planetesimal because this would bring Neptune only a semimajor axis shift of ~0.005 AU. In this sense, the migration rate variation that can significantly change the L/T ratio (as shown by the simulations in this paper) should be the result of planet-Neptune scattering or should arise from a particular distribution of planetesimals with which Neptune exchanges angular momentum (thus migrates) rather than be merely due to the randomness of scattering events between Neptune and numerous small planetesimals.
In this paper, we have shown a variety of mechanisms that can regulate the L/T ratio. The mechanisms that favour the leading island’s capture of planetesimals include higher eccentricity of planetesimals, migration slowdown (either abrupt or gradual), occasional inward migration, and a rate of migration that is much higher or lower than 1 AU Myr−1. Opposite mechanisms are in favour of capture by the trailing island. All of these mechanisms can cooperate to attain a more physically realistic migration model to regulate the L/T ratio.
Most of the time in this paper, we adopted the planar-restricted three-body problem in the numerical simulations. In fact, we have also tried a large number of simulations that include other planets and take into account the influences of orbital inclinations, both of planets and planetesimals. We found that the additional perturbations from other giant planets introduce a little more chaos into the evolution of planetesimals, but the capture efficiency of Neptune’s 1:2 MMR hardly changes, and thus the conclusions about the different L/T ratios in different models are nearly the same as in the simple model presented in this paper. In addition, higher inclinations can bring changes in the resonant structure (e.g. Gallardo 2006, 2020; Saillenfest et al. 2016; Efimov & Sidorenko 2020), which may break the symmetry between leading and trailing islands or result in a sharp decrease in the capture efficiency. Of course, if the inclination is not too high, the inclination itself brings no considerable changes to the results. Considering that the original planetesimal disc is dynamically cold, a planar model still works and produces valuable information.
Acknowledgements
Our sincere appreciations go to the anonymous referee, whose insightful comments and constructive suggestions have improved this paper greatly. This work has been supported by the science research grant from the China Manned Space Project with No. CMS-CSST-2021-B08. We also thank the supports from the National Key R&D Program of China (2019YFA0706601) and National Natural Science Foundation of China (NSFC, Grant Nos. 11933001, 12150009 and 12373081).
References
- Bannister, M. T., Alexandersen, M., Benecchi, S. D., et al. 2016, AJ, 152, 212 [CrossRef] [Google Scholar]
- Beauge, C. 1994, Celest. Mech. Dyn. Astron., 60, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [Google Scholar]
- Chen, Y.-T., Gladman, B., Volk, K., et al. 2019, AJ, 158, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Jordan, A. B. 2002, AJ, 124, 3430 [NASA ADS] [CrossRef] [Google Scholar]
- Efimov, S. S., & Sidorenko, V. V. 2020, Celest. Mech. Dyn. Astron., 132, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, J. A., & Ip, W. H. 1984, Icarus, 58, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Frangakis, C. N. 1973, Ap&SS, 22, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Gallardo, T. 2006, Icarus, 184, 29 [Google Scholar]
- Gallardo, T. 2018, Planet. Space Sci., 157, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Gallardo, T. 2020, Celest. Mech. Dyn. Astron., 132, 9 [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J., et al. 2011, ApJ, 742, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Sheppard, S. S. 2016, AJ, 152, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., Bromley, B. C., O’Brien, D. P., & Davis, D. R. 2008, in The Solar System Beyond Neptune, eds. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, A. Morbidelli, & R. Dotson, 293 [Google Scholar]
- Lan, L., & Malhotra, R. 2019, Celest. Mech. Dyn. Astron., 131, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, S. M., Pike, R. E., Kaib, N., et al. 2019, AJ, 157, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 2000, AJ, 120, 2117 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Zhou, L.-Y., & Sun, Y.-S. 2014, MNRAS, 443, 1346 [NASA ADS] [CrossRef] [Google Scholar]
- Lykawka, P. S., & Mukai, T. 2007, Icarus, 192, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1995, AJ, 110, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1996, AJ, 111, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Malyshkin, L., & Tremaine, S. 1999, Icarus, 141, 341 [CrossRef] [Google Scholar]
- Morbidelli, A., & Nesvorný, D. 2020, Kuiper belt: Formation and Evolution, eds. D. Prialnik, M. A. Barucci, & L. Young, 25 [Google Scholar]
- Murray-Clay, R. A., & Chiang, E. I. 2005, ApJ, 619, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D. 2015a, AJ, 150, 73 [CrossRef] [Google Scholar]
- Nesvorný, D. 2015b, AJ, 150, 68 [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2012, AJ, 144, 117 [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2016, ApJ, 825, 94 [CrossRef] [Google Scholar]
- Pike, R. E., & Lawler, S. M. 2017, AJ, 154, 171 [CrossRef] [Google Scholar]
- Saillenfest, M., Fouchard, M., Tommei, G., & Valsecchi, G. B. 2016, Celest. Mech. Dyn. Astron., 126, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., & Colwell, J. E. 1997, AJ, 114, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, Y.-S., & Zhou, L.-Y. 2009, Celest. Mech. Dyn. Astron., 103, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G. M., Ivezic, Ž., Juric, M., & Lupton, R. 2007, MNRAS, 377, 1393 [CrossRef] [Google Scholar]
- Volk, K., & Malhotra, R. 2019, AJ, 158, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., & Brown, M. E. 2016, AJ, 152, 90 [Google Scholar]
- Xu, Y.-B., Zhou, L., Lhotka, C., Zhou, L.-Y., & Ip, W.-H. 2022, A&A, 666, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, L.-Y., Sun, Y.-S., Zhou, J.-L., Zheng, J.-Q., & Valtonen, M. 2002, MNRAS, 336, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L., Xu, Y.-B., Zhou, L.-Y., Dvorak, R., & Li, J. 2019, A&A, 622, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Number of asteroids in the leading and trailing resonance islands and their ratios (L/T) in some major 1:N resonances.
Objects captured by the asymmetric resonance islands in the exponential migration model.
All Figures
 |
Fig. 1 Libration amplitude of resonance angle in numerical simulations of the circular planar restricted three-body model. The abscissa and ordinate are the initial eccentricity e0 and resonance angle ϕ0, respectively, and the libration amplitude is indicated by colour. The asymmetric islands are enclosed with black lines, and the red lines indicate the locations of asymmetric resonance centres (see text). |
| In the text | |
 |
Fig. 2 Initial eccentricities of test particles captured by the leading island (red) and trailing island (blue) at different migration rates of Neptune. The box plots indicate the minimum, maximum, median, and upper and lower quartiles as usual. The solid diamonds are the mean value of eccentricities. The L/T ratios are plotted as solid circles and are connected by a dotted line (right ordinate). The total capture efficiencies (in percent) are labelled at the top of the panels. The upper and lower panels correspond to fast and slow migration rate ranges, respectively. |
| In the text | |
 |
Fig. 3 Evolution of objects close to the 1:2 resonance demonstrating the sizes of the resonance islands. The abscissa and ordinate represent the resonance angle ϕ and the semimajor axis (in Neptune’s semimajor axis aN), respectively. The planetesimal’s eccentricity and Neptune’s migration rate are indicated in each panel. For each particle, the time interval between two adjacent points is 1000 yr. |
| In the text | |
 |
Fig. 4 Dependence of the resonance island size on the migration rate of Neptune (ȧN) and initial eccentricity of test particles (e0). The maximal libration amplitude of the resonance angle is shown in the upper panels, while the lower panels show the libration of the semimajor axis (see text). The left and right columns are respectively for the leading and trailing island. |
| In the text | |
 |
Fig. 5 Evolution of a test particle when transferring from symmetric to asymmetric resonance. The left column is for Neptune migrating at a rate of 1 AU Myr−1, while the right column is for the same test particle but the migration stops at 0.3 Myr. From top to bottom, the panels show the semimajor axis a, eccentricity e, and resonant angle ϕ of the test particle with solid lines. The dashed lines in the top panels represent the nominal semimajor axis of the 1:2 resonance. The magenta area in the middle-left panel indicates the duration of the last symmetric cycle, while the red and blue areas in the bottom-left panel indicate the time intervals around the leading and trailing island, respectively. |
| In the text | |
 |
Fig. 6 Stickiness effect of the leading island. The times an object stayed on both sides of ϕ = 180° when it was transferring from symmetric to asymmetric resonances (see text and Fig. 5) are plotted in the two left panels, and the ratio of the two time durations are shown in the right panels. The abscissa is the mean eccentricity in the last cycle before being captured by the asymmetric resonance. The red and blue dots represent the time spent in the leading and trailing side, respectively. The upper and lower panels represent the results from the simulations of migration rate: ȧN = 0.2 AU Myr−1 and ȧN = 2 AU Myr−1, respectively. In the former simulation, 1833 out of 10 000 initial objects are shown, and 435 objects for the latter are shown. |
| In the text | |
 |
Fig. 7 Distribution of test particles captured by the sweeping 1:2 resonance. The resonance swept through these particles as Neptune migrated at a constant rate of 5 AU Myr−1, and the migration was stopped when the nominal resonance reached 47.62 AU. The abscissa and ordinate are for the initial semimajor axis and eccentricity of test particles. The red and blue colours indicate that an object was captured by the leading and trailing resonance island, respectively. The dashed line at 47.35 AU separates test particles into two groups (see text). |
| In the text | |
 |
Fig. 8 Distribution of test particles on the (ϕ, a) plane as the 1:2 resonance approaches. Four snapshots at different moments with t = 0 kyr representing exactly when the nominal resonance reaches the initial position of test particles are given in each of the four panels. Objects later captured by the leading and trailing island are in red and blue, respectively, while those not captured by any asymmetric resonance are in purple. The horizontal line stands for the nominal position of 1:2 resonance. |
| In the text | |
 |
Fig. 9 Belt of test particles (shaded range) and time evolution of the nominal 1:2 resonance with Neptune. |
| In the text | |
 |
Fig. 10 Initial semimajor axes and eccentricities of objects captured by leading (red) and trailing (blue) islands in the exponential migration model. The timescales of migration τ are marked in each panel. The vertical dashed lines are the inner and outer edge of the belt of test particles, and the numbers near them are the instant migration rates of Neptune when the nominal resonance arrives at both edges of the planetesimals’ belt. |
| In the text | |
 |
Fig. 11 Initial semimajor axes and eccentricities of objects that are captured by the leading (upper panel) and trailing (bottom panel) islands in the exponential migration model with timescale τ = 3 Myr. The capture time of each object is indicated by colour. The numbers near the vertical dashed lines are the instant migration rates of Neptune when the nominal resonance arrives at corresponding locations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


