| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245218 | |
| Published online | 01 November 2023 | |
A model for the infrared-radio correlation of main sequence galaxies at gigahertz frequencies and its variation with redshift and stellar mass
1
Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), 1290 Sauverny, Switzerland
e-mail: jennifer.schober@epfl.ch
2
International Space Science Institute (ISSI), Hallerstrasse 6, 3012 Bern, Switzerland
3
Astronomy Centre, Department of Physics and Astronomy, University of Sussex, Brighton BN1 9QH, UK
4
Universität Heidelberg, Zentrum für Astronomie, Institut für theoretische Astrophysik, Albert-Ueberle-Straße 2, 69120 Heidelberg, Germany
5
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany
6
Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción, Av. Esteban Iturra s/n Barrio Universitario, Concepción, Chile
Received:
14
October
2022
Accepted:
25
August
2023
Context. The infrared-radio correlation (IRRC) of star-forming galaxies can be used to estimate their star formation rate (SFR) based on the radio continuum luminosity at MHz–GHz frequencies. For its practical application in future deep radio surveys, it is crucial to know whether the IRRC persists at high redshift z.
Aims. Previous works have reported that the 1.4 GHz IRRC correlation of star-forming galaxies is nearly z-invariant up to z ≈ 4, but depends strongly on the stellar mass M⋆. This should be taken into account for SFR calibrations based on radio luminosity.
Methods. To understand the physical cause behind the M⋆ dependence of the IRRC and its properties at higher z, we constructed a phenomenological model for galactic radio emission. Our model is based on a dynamo-generated magnetic field and a steady-state cosmic ray population. It includes a number of free parameters that determine the galaxy properties. To reduce the overall number of model parameters, we also employed observed scaling relations.
Results. We find that the resulting spread of the infrared-to-radio luminosity ratio, q(z, M⋆), with respect to M⋆ is mostly determined by the scaling of the galactic radius with M⋆, while the absolute value of the q(z, M⋆) curves decreases with more efficient conversion of supernova energy to magnetic fields and cosmic rays. Additionally, decreasing the slope of the cosmic ray injection spectrum, αCR, results in higher radio luminosity, decreasing the absolute values of the q(z, M⋆) curves. Within the uncertainty range of our model, the observed dependence of the IRRC on M⋆ and z can be reproduced when the efficiency of supernova-driven turbulence is 5%, 10% of the kinetic energy is converted into magnetic energy, and αCR ≈ 3.0.
Conclusions. For galaxies with intermediate to high (M⋆ ≈ 109.5 − 1011 M⊙) stellar masses, our model results in an IRRC that is nearly independent of z. For galaxies with lower masses (M⋆ ≈ 108.5 M⊙), we find that the IR-to-radio flux ratio increases with increasing redshift. This matches the observational data in that mass bin which, however, only extends to z ≈ 1.5. The increase in the IR-to-radio flux ratio for low-mass galaxies at z ≳ 1.5 that is predicted by our model could be tested with future deep radio observations.
Key words: galaxies: star formation / radio continuum: galaxies / infrared: galaxies / galaxies: high-redshift / galaxies: evolution
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Local star-forming galaxies lie on the “infrared-radio correlation” (IRRC), which spans at least three orders in magnitude of radio continuum luminosity. It was first observed at a rest frame frequency of 1.4 GHz (e.g., van der Kruit 1971, 1973; Helou et al. 1985; de Jong et al. 1985; Yun et al. 2001), and has increasingly also been studied all the way down to the MHz-regime with the advent of LOFAR (e.g., Smith et al. 2021; Bonato et al. 2021; McCheyne et al. 2022). At 1.4 GHz, the IRRC is commonly parametrized in terms of the IR-to-radio luminosity ratio, namely:
with L1.4 being the rest-frame 1.4 GHz radio continuum luminosity, and LIR the dust continuum luminosity integrated over the rest-frame wavelength region 8 − 1000 μm in the infrared. The parameter q is constant as long as the correlation is linear.
The origin of the IRRC lies within the physics of cosmic rays, magnetic fields, and interstellar dust, which are intertwined through star formation activity. Young stars heat their surrounding dust that re-emits thermal continuum in the IR (measured quantitatively via the luminosity LIR over the wavelength range 8–1000 μm) and the supernova explosions of short-lived massive stars produce CRs that emit non-thermal radio continuum (the intrinsic brightness of which is quantified, e.g., at 1.4 GHz, via the luminosity L1.4) in the form of synchrotron radiation (Draine 2011; Klessen & Glover 2016). One of the first quantitative models of the IRRC was proposed by Voelk (1989), who assumes that cosmic ray electrons lose all their energy via synchrotron radiation within the galaxy and that all UV photons emitted by young stars are absorbed by dust and then re-emitted in the infrared (Draine 2003). However, this calorimeter model lacks to explain certain observed properties of galaxies, for instance: it predicts overly steep radio spectra (see, e.g., Vollmer et al. 2022, and references within). Various refined models explaining the IRRC have been subsequently proposed (Murphy et al. 2006; Schleicher & Beck 2013; Schober et al. 2016), including extensions to dwarf galaxies (Schleicher & Beck 2016). A common key ingredient of models of the IRRC is star formation and, therefore, it opens up a pathway for calibrating the star formation rate (SFR) with radio observations (Condon 1992; Bell 2003; Murphy et al. 2011; Schober et al. 2017; Molnár et al. 2021), as long as an active galactic nuclei (AGN) contribution to the radio flux can be excluded.
The question of whether current calibrations of GHz radio continuum emission as an SFR tracer in low-redshift galaxies remain valid out to high redshifts is still open (Schober et al. 2017; Smith et al. 2021). The minimum requirements for the correlation to uphold in young galaxies are: (i) a sufficient cosmic ray (CR) population; (ii) strong magnetic fields; and (iii) the presence of interstellar dust. While the CR production rate increases with the increasing SFR and the accompanying increase in supernova shocks at high z, CR electrons suffer from increasing energy losses via inverse Compton scattering with the cosmic microwave background. Schleicher & Beck (2013) proposed that this leads to a breakdown of the correlation at high z. Requirement (ii) of a strong magnetization of the interstellar medium (ISM) should be satisfied by efficient turbulent dynamo amplification (Schober et al. 2013; Rieder & Teyssier 2016, 2017; Martin-Alvarez et al. 2021; Liu et al. 2022). Regarding requirement (iii), a breakdown of the IRRC due to a lack of interstellar dust can likely be excluded for the currently observationally accessible galaxies. Observations at (sub-)millimetre wavelengths have provided convincing evidence of rapid dust enrichment in high-z galaxies (Inami et al. 2022; Sommovigo et al. 2022). Efficient dust production explaining these observations has been suggested by various ISM models (Mancini et al. 2015; Michałowski 2015; Marassi et al. 2019; Graziani et al. 2020).
On observational grounds, the potential evolution of the IRRC over cosmic timescales is still much discussed. Several studies report a mild or moderate evolution of the correlation with redshift (Seymour et al. 2009; Ivison et al. 2010a,b; Michałowski et al. 2010a,b; Magnelli et al. 2015; Basu et al. 2015; Delhaize et al. 2017; Calistro Rivera et al. 2017). Other authors, however, have found no significant evidence for evolution (Garrett 2002; Appleton et al. 2004; Jarvis et al. 2010; Sargent et al. 2010; Bourne et al. 2011) and have instead considered other interpretations, such as observational biases or an evolution of the dust temperature (Smith et al. 2014). In a recent study, Delvecchio et al. (2021) report that the infrared-radio correlation of star-forming galaxies is strongly M⋆-dependent but nearly z-invariant up to z ≈ 4.
Here, we present a model of the FIR-radio correlation that uses M⋆ and z as the basis for setting the underlying free parameters of our model, using observationally established scaling relations and/or constraints from theory. We aim to find the conditions under which the observations by Delvecchio et al. (2021) can be reproduced and to make predictions for higher redshift. The paper is organized as follows: in Sect. 2, we present our semi-analytical model for galactic radio emission. The results for different parameters of the model are presented in Sect. 3 and compared to the data of Delvecchio et al. (2021). We draw our conclusions in Sect. 5.
2. Model for galactic emission
To calculate the radio luminosity, we used a semi-analytical galaxy model that is based on the following steps. 1) The input is the stellar mass, M⋆, and redshift, z. 2) The global galaxy properties are calculated from observational correlations, which include the gas mass, Mgas, the star formation rate, Ṁ⋆, and galactic radius and scale height, Rgal and Hgal, respectively. 3) On a 3D grid, the galaxy is modeled with an exponential gas density profile, using Rgal and Hgal from step 2. The total Mgas from step 2 is used for the normalization of the gas density. Likewise, the distribution of the star formation rate density is modeled and normalized by Ṁ⋆. A cosmic ray population is implemented based on a steady-state assumption and the magnetic energy distribution is implemented based on a saturated small-scale dynamo. The synchrotron and free-free emission are calculated in each grid cell. 4) Absorption processes are taken into account to construct 2D maps for observations with different lines of sight. 5) Integration over the 2D maps yields the total radio luminosity which is used to calculate q.
These steps are summarized in Fig. 1 and the default values of the free parameters of the model are presented in Table 1. The dependence on the free parameters is systematically explored and different series of models are introduced in Table 2.
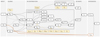 |
Fig. 1. Overview of the model for the radio and far-infrared emission with which the q parameter can be calculated. The input parameters, redshift z and total stellar mass M⋆, are shown on the left and the final output is the q parameter that combines 1.4 GHz luminosity L1.4 and the rest-frame 8 − 1000 μm luminosity LIR. For the galactic scale height, Hgal, different scenarios are considered which is indicated by the dashed lines; see Sect. 2.1.3. Free parameters of the model are highlighted by yellow boxes and their default values are listed in Table 1. See Sect. 2 for details of the model. |
Different series of models.
2.1. Global observational correlations
In this paper, we focus on mass-selected star-forming galaxies on the galaxy main sequence. We do not attempt to model starburst galaxies with high efficiencies and high specific SFRs, which would require different values for the gas or SFR density, for instance, compared to the ones adopted in the following.
To reduce the number of free parameters in our model, we set the global properties of our model galaxies in accordance with observational scaling relations from the literature for a given M⋆ and z (see Sects. 2.1.1–2.1.3 below). These scaling relations have been derived using galaxy samples with stellar masses typically in the range M⋆ > 109 M⊙ and drawn from studies probing a redshift range up to z ≈ 3 or 4. This approach is thus well constrained in the redshift and mass range of the Delvecchio et al. (2021) study of the joint mass- and redshift dependence of the IRRC, which we aim to match here. Extrapolations to higher redshift will, however, necessarily be more speculative.
2.1.1. Total SFR
For a given M⋆ and z, the total star formation rate of a galaxy, Ṁ⋆, is calculated from the observational calibration of Schreiber et al. (2015):
with r ≡ log10(1 + z) and m ≡ log10[M⋆/(109 M⊙)] and the constants m0 = 0.5 ± 0.07, m1 = 0.36 ± 0.3, a0 = 1.5 ± 0.15, a1 = 0.3 ± 0.08, and a2 = 2.5 ± 0.6. Equation (2) is based on a Salpeter initial mass function (IMF). By multiplying both M⋆ and Ṁ⋆ by a factor of 1.7, we can convert Eq. (2) to make it consistent with a Chabrier IMF, so that all parts of our model are based on the same IMF.
2.1.2. Total gas mass
Following Sargent et al. (2014), we estimated the total gas mass, Mgas, of a star-forming galaxy based on its SFR (which, in turn, follows from its stellar mass via Eq. (2)) as:
Here, α2, SFR = 9.22 ± 0.02 and β2 = 0.81 ± 0.031.
2.1.3. Galactic radius and scale height
For a given stellar mass and redshift, the characteristic half-light radius of the galaxy is (Jiménez-Andrade et al. 2019) as follows:
with Rgal, 0 = (2100 ± 200) pc, αz = 0.26 ± 0.08, and M⋆, 0 = (6.08 ± 1.14)×1010 M⊙ being used as the default values (Licquia & Newman 2015). We note that this size scale was derived for massive main-sequence galaxies over the range 0 < z < 2. Based on the observed mild dependence on stellar mass, as reported in Jiménez-Andrade et al. (2021), we also introduced a scaling with the power law index, αgal. As a default, we used αgal = 0.05. A weak dependence of Rgal on M⋆ is also found for the stellar component of star-forming galaxies (e.g., Mowla et al. 2019). Equation (4) was obtained in the radio continuum, namely, it is a directly relevant quantity here, since it is an estimate of the spatial extent of the star formation.
Following Thompson et al. (2005), we assume that the galactic scale height depends on the radius as:
where we use a Toomre parameter of Q = 1. Since Eq. (5) is obtained under the assumption of a Salpeter IMF, we correct M⋆ by a factor of 1.7 to adjust to a Chabrier IMF. Additionally, we present scenarios based on two other models: Hgal ∝ Rgal(M⋆, z) and Hgal ∝ (1 + z).
2.2. 3D galaxy model
Based on the global galaxy parameters estimated in the previous section, we set up a three-dimensional (3D) model of the gas density, the cosmic ray distribution, and other relevant parameters. This allows us to calculate the galactic synchrotron emission including absorption processes that occur along a given line of sight.
The model is constructed on a grid in a box with length L. The volume of a single grid cell Vcell = L3/ℛ3 depends on the resolution ℛ. We typically use ℛ = 100 and L is adjusted to the size of the galaxy (as default we use L = 10 Rgal). We refer to Appendix C for a discussion on convergence.
2.2.1. Gas distribution
The gas density distribution is set up as a double exponential profile:
where the normalization ρgas, c is chosen such that
and Rgal and Hgal are taken from the expressions presented in Sect. 2.1.3. The gas mass is related to the star formation rate and stellar mass (see Eq. (3)). The gas number density is calculated as
where we assume that the gas is composed of atoms with average mass 1.75mp (for a primordial mixture of gas with 75% hydrogen and 25% helium). In Fig. A.1, the radial dependence of ngas is presented for different values of M⋆ and z.
In Fig. 2, the typical volume average of the density is presented for the parameter range of interest. Since the volume average depends on the size of the box, L, we show the average value in the central region of the galaxy instead. We define this central average of the gas density as 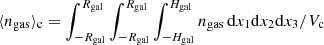 , with
, with 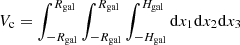 .
.
 |
Fig. 2. Input relations for the reference galaxy model (see Table 2). Upper panel: mean density in the central region of the galaxy obtained from integrating Eq. (8). Middle panel: total SFR from Eq. (2) shown by dotted lines and the SFR in the core region of the galaxy obtained from integrating Eq. (9) shown by solid lines. Lower panel: mean magnetic field strength in the core region of the galaxy obtained from integrating Eq. (14) with the default value fB = 0.1. |
2.2.2. Star formation and supernova rate
Supernova (SN) explosions are responsible for producing two key ingredients of galactic synchrotron emission: magnetic fields and CRs. Therefore, we need to model the spatial distribution of the SN rate which depends on the galactic star formation activity. To this end, we make use of the empirical Kennicutt-Schmitt law (Kennicutt 1998; Kennicutt & Evans 2012), which relates the SFR surface density to the gas surface density. Moving from surface densities to volume densities, we calculate the local SFR density:
in each grid cell. In Eq. (9), the same profile as the one of the gas density in Eq. (6) is used but with nSFR as the exponent. The observed Kennicutt-Schmidt relation for surface densities has nSFR = 1.4. However, we note that a relation between 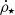 and ρgas can also be derived theoretically when assuming that the SFR is proportional to the gas density over the dynamical timescale. This yields
and ρgas can also be derived theoretically when assuming that the SFR is proportional to the gas density over the dynamical timescale. This yields 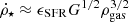 , where ϵSFR is the star formation efficiency and G is the gravitational constant. If ϵSFR is independent of ρgas then nSFR = 3/2 (Schaye & Dalla Vecchia 2008), which we use in our model 2. The normalization in Eq. (9),
, where ϵSFR is the star formation efficiency and G is the gravitational constant. If ϵSFR is independent of ρgas then nSFR = 3/2 (Schaye & Dalla Vecchia 2008), which we use in our model 2. The normalization in Eq. (9), 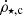 , is chosen such that
, is chosen such that
The global SFR, Ṁ⋆, and the SFR in the core region, 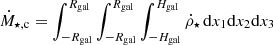 , are presented in Fig. 2.
, are presented in Fig. 2.
Assuming a Chabrier initial mass function and a minimum mass of stars that result in a SN of 8 M⊙, the supernova rate in each grid cell is:
where  is the average mass of a star that ends in a supernova. The corresponding SN rate density in a grid cell is given by
is the average mass of a star that ends in a supernova. The corresponding SN rate density in a grid cell is given by
2.2.3. Magnetic field strength
A key assumption in this work is that magnetic fields are produced on short timescales by a turbulent dynamo (Kazantsev 1968; Kulsrud & Anderson 1992; Brandenburg & Subramanian 2005). This mechanism converts turbulent kinetic energy to magnetic energy exponentially over time, until the magnetic energy becomes comparable to the kinetic energy and a back reaction on the velocity field sets in. The characteristic timescale of the small-scale turbulent dynamo is the eddy turnover time on the viscous spatial scale determined by the Reynolds number in the system (Rogachevskii & Kleeorin 1997; Schober et al. 2012a,b).
In the context of galaxy formation, a seed magnetic field is first amplified by compression during the gravitational collapse. The end of the collapse phase can be defined as the moment when the gas density has become approximately constant. Then the main mechanism of magnetic field amplification is the small-scale dynamo that is sourced by turbulence due to accretion and SN explosions. Since galaxies have very high Reynolds numbers (≈1010 − 1012), the small-scale dynamo timescale is very short (≈10−2 − 10−1 Myr) compared to other dynamical timescales. Therefore, once the small-scale dynamo is activated, the magnetic field quickly reaches the equipartition value already in young galaxies (Schober et al. 2013; Schleicher et al. 2013). This magnetic field evolution is being seen in cosmological simulations that solve the magnetohydrodynamical equations and have sufficient resolution (Rieder & Teyssier 2016, 2017; Martin-Alvarez et al. 2018). In the case described by Martin-Alvarez et al. (2018), the collapse phase of the galaxy ends at z ≈ 12 and the timescale of the subsequent small-scale dynamo is on the order of 2 Gyr. The timescale, however, is much longer than what is expected in real galaxies due to the limited resolution of cosmological simulations3.
The energy source of the small-scale dynamo is turbulence. Here, we assume that the main drivers of turbulence are supernova explosions in the ISM (Mac Low & Klessen 2004). Under steady state the turbulent velocity vturb can be estimated from a balance between the loss rate 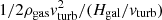 and the energy injection rate ṅSNfturbESN. Here, fturbESN is the fraction of supernova energy converted into turbulence with the default values of fturb = 0.05 and ESN = 1051 erg. Solving for vturb gives the following result:
and the energy injection rate ṅSNfturbESN. Here, fturbESN is the fraction of supernova energy converted into turbulence with the default values of fturb = 0.05 and ESN = 1051 erg. Solving for vturb gives the following result:
Assuming that at saturation, the magnetic energy reaches a fraction fB of the turbulent kinetic energy, the magnetic field strength is then:
Since 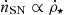 in our model, Eq. (14) leads to
in our model, Eq. (14) leads to 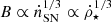 . This is close to the observed scaling of
. This is close to the observed scaling of 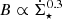 in various types of galaxies (Niklas & Beck 1997; Chyży et al. 2011; Basu et al. 2017), where
in various types of galaxies (Niklas & Beck 1997; Chyży et al. 2011; Basu et al. 2017), where 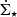 is the SFR surface density.
is the SFR surface density.
MHD dynamo theory makes predictions for the saturation level, fB. In the most ideal case, namely, of incompressible (or Kolmogorov) turbulence, fB reaches its maximum value of ≈0.4. However, in the SN-driven case, turbulence is typically compressive with Mach numbers reaching values on the order of 10. In that case, direct numerical simulations (DNS) with driven turbulence result in saturation levels of fB ≈ 0.01 (Federrath et al. 2011, 2014; Seta & Federrath 2021) and fB ≈ 0.05 in SN-driven simulations of the ISM (Gent et al. 2021). On the other hand, observations indicate that a large faction of the interstellar medium, in particular, the warm ionized medium, has relatively low Mach numbers, implying sub- to transonic turbulence (Burkhart et al. 2010; Gaensler et al. 2011; Koley & Roy 2019). Therefore, we use fB ≈ 0.1 as the default value in our model. However, we explore the dependence of the results on fB in Sect. 3.2.1. The mean magnetic field strength in the central region of the galaxy, defined as 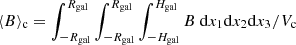 , is shown in the bottom panel of Fig. 2. The resulting field strength in the central part of the modeled galaxies is, at low redshifts, larger than the CMB equivalent field strength BCMB(z)≈3.25(1 + z)2 μG. At a higher z, the value of ⟨B⟩c eventually drops below BCMB.
, is shown in the bottom panel of Fig. 2. The resulting field strength in the central part of the modeled galaxies is, at low redshifts, larger than the CMB equivalent field strength BCMB(z)≈3.25(1 + z)2 μG. At a higher z, the value of ⟨B⟩c eventually drops below BCMB.
2.2.4. Cosmic ray electrons
In every grid cell, the cosmic ray (CR) energy spectrum is modeled. We assume that CR protons are produced in diffusive shock acceleration within supernova shock fronts and that CR electrons are composed of both primaries and secondaries from decays of CR protons. Following Lacki & Beck (2013), we further assume that CR electrons are in a steady state. The full CR implementation is sketched in the following.
The energy spectrum of injected protons is (Bell 1978a,b)
with the normalization Qp, 0 and the injection power law index αCR. Integration from lowest energy to infinity gives the total energy injected as protons, namely:
where γp, 0 = 1 GeV/(mpc2)≈1. The normalization of Eq. (16) is obtained by comparison with the energy injected by supernovae, fCRṄSNESN. Using fCR = 0.1 as the fraction of SN energy that is converted into CRs and a characteristic energy per SN of ESN = 1051 erg yields
The CR protons produce secondary CR electrons with a spectrum
which, in γ = E/(mc2) space, is:
The factor fπ is the fraction of CR protons that decay into pions and we assume fπ = 0.2 in the reference model. It follows (with Ep = 20 Esec, Lacki & Beck 2013):
where γe is the Lorentz factor of the electrons. The total injection rate of CR electrons (primaries and secondaries) is related to the secondary rate Qe, sec by the factor fsec:
We use fsec = 0.8 as a default value (Lacki & Beck 2013). For steady state, the total number of cosmic ray electrons can be estimated as:
The CR cooling time τe is determined by different loss channels, including ionization (τion), bremsstrahlung (τbrems), inverse Compton scattering (τIC), and synchrotron losses (τsynch),
with
In the expression for τbrems, αem and r0 are the fine-structure constant and the electron radius, respectively, 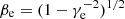 , and nion is the ion density, for which we assume nion = fionngas with fion being the ionization degree (Blumenthal & Gould 1970). Further, in the expressions for τIC and τsynch, σT is the Thomson cross-section for an electron and uISRF and uB = B2/(8π) are the energy density of the interstellar radiation field and the magnetic energy density, respectively. The model of uISRF includes both, contributions from the stellar population and the cosmic microwave background (see Appendix B for details).
, and nion is the ion density, for which we assume nion = fionngas with fion being the ionization degree (Blumenthal & Gould 1970). Further, in the expressions for τIC and τsynch, σT is the Thomson cross-section for an electron and uISRF and uB = B2/(8π) are the energy density of the interstellar radiation field and the magnetic energy density, respectively. The model of uISRF includes both, contributions from the stellar population and the cosmic microwave background (see Appendix B for details).
The number of CR electrons, modeled here via Eq. (22), determines the resulting radio emission of the galaxy. It includes several free parameters. In particular, Ne is proportional to the ratio fπfCR/fsec but it also depends on the slope of the injection spectrum αCR. Analytical models for diffusive shock acceleration (DSA) predict values of αCR = 2.0 for non-relativistic gas and αCR = 2.5 for relativistic gas (Bell 1978b; Blandford & Eichler 1987). Detailed models of supernova shock fronts result αCR = 2.1 − 3 (Bogdan & Völk 1983), whereas more recent studies of diffusive shock acceleration based on PIC/hybrid approach predict αCR ≈ 1.5 for Mach numbers ≳10 and non-relativistic ions (Caprioli & Spitkovsky 2014). In our reference model, a steeper value of αCR = 3 is used to reproduce the observed values of q(z). A more detailed cosmic ray model of cosmic ray propagation, including diffusion and losses via galactic winds, could allow for values of αCR that are closer to the DSA predictions.
2.3. Radio emission
2.3.1. Synchrotron emission and self-absorption
Synchrotron emission (in [erg s−1 Hz−1]) of a single particle is calculated via:
where K5/3(ξ) is the modified Bessel function of the second kind (Blumenthal & Gould 1970). This spectrum peaks roughly at the critical frequency,
For a distribution of electrons with different energies according to Eq. (22), the spectral emission per grid cell (in [erg s−1 Hz−1 cm−3]) is determined by (Blumenthal & Gould 1970)
The last integral in Eq. (30) over the pitch angle α is on the order of 10 for αCR = 3.0 and if isotropy is assumed, namely, the distribution of pitch angles is N(α)≈1.
The numerical integration of Eq. (30) is expensive and therefore we use the following two approximations. First, instead of performing the expensive numerical integration of the Bessel function in Eq. (28), we follow Aharonian et al. (2010) and use
Second, it is useful to note that the function 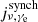 peaks at the characteristic frequency νc(γe). This implies that synchrotron radiation at a given frequency νobs is emitted by cosmic ray electrons with a specific Lorentz factor of
peaks at the characteristic frequency νc(γe). This implies that synchrotron radiation at a given frequency νobs is emitted by cosmic ray electrons with a specific Lorentz factor of
or, in terms of energy,
The resulting value of 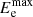 is shown for νobs = 1.4 GHz as a function of magnetic field strength in Fig. 3. To save computational time, the integration over γe in Eq. (30) is performed in the interval
is shown for νobs = 1.4 GHz as a function of magnetic field strength in Fig. 3. To save computational time, the integration over γe in Eq. (30) is performed in the interval ![$ [\mathrm{max}(1,0.01~\gamma_{\rm e}^\mathrm{max}), 100~\gamma_{\rm e}^\mathrm{max}] $](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq56.gif) .
.
 |
Fig. 3. Energy (left ordinate) and Lorentz factor (right ordinate) of CR electrons that contribute mostly to the synchrotron emission at different observing frequencies νobs and different magnetic field strengths B; see Eq. (33). |
Knowing the characteristic energy of the CRs that emit synchrotron radiation at νobs allows us to determine the most relevant cooling processes of the emission. The numerical value of the cosmic ray cooling timescale, τe, and its different contributions are shown in Fig. 4 for 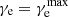 . For the default values of the free parameters, the dominant process determining the population CR electrons that emit synchrotron radiation at νobs = 1.4 GHz at z = 0 are synchrotron (for low and intermediate M⋆) and ionization (for the highest M⋆ considered in this study) in the center of the galaxy and inverse Compton (with the CMB) in the outer, very low gas density regions of the simulation box. With increasing z, inverse Compton becomes the dominant cooling process even in more central parts of the galaxy. The reason for this is the CMB radiation field which increases proportional to (1 + z)4.
. For the default values of the free parameters, the dominant process determining the population CR electrons that emit synchrotron radiation at νobs = 1.4 GHz at z = 0 are synchrotron (for low and intermediate M⋆) and ionization (for the highest M⋆ considered in this study) in the center of the galaxy and inverse Compton (with the CMB) in the outer, very low gas density regions of the simulation box. With increasing z, inverse Compton becomes the dominant cooling process even in more central parts of the galaxy. The reason for this is the CMB radiation field which increases proportional to (1 + z)4.
 |
Fig. 4. Cooling timescales of CR electrons in a slice through the center of galaxies with different stellar masses, M⋆, (top to bottom panels) and different redshifts, z (left to right panels). The value of γe used in this plot corresponds to the one at which CR electrons contribute mostly to the synchrotron emission at 1.4 GHz, i.e., at which νc = νobs = 1.4 GHz; see Eq. (32). The total timescale, τe, (solid lines) has contributions from bremsstrahlung (τbrems, dashed lines), synchrotron losses (τsynch, dotted lines), inverse Compton losses (τIC, dashed-dotted lines), and ionization losses (τion, dashed-dotted-dotted lines). Grey vertical lines indicate the characteristic radius Rgal, i.e., they enclose 2Rgal. |
If absorption is ignored, the total synchrotron emission is obtained by
However, at low frequencies and/or high gas density, absorption of synchrotron photons can become significant. The synchrotron self-absorption (SSA) coefficient is given by (Schlickeiser 2002),
and leads to a corresponding optical depth of
We note that the optical depth depends on the thickness of the layer of synchrotron emitting CRs considered. If the most distant emission occurs at position s0, then Eq. (36) gives the value of 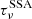 at position s1. Another absorption channel is free-free absorption which is discussed in the subsequent section.
at position s1. Another absorption channel is free-free absorption which is discussed in the subsequent section.
2.3.2. Free-free emission and absorption
The free-free emission adds a contribution to the total radio flux with the emissivity calculated as follows (Rybicki & Lightman 1986):
The velocity-averaged Gaunt factor is given by Novikov & Thorne (1973):
with ξ ≈ 1.781. We assume that the ion and electron densities are comparable, that is, nion ≈ ne = fionngas and Z = 1. As the default value for the ionization degree, we use fion = 0.1 and we assume an electron temperature of Te = 104 K.
With the free-free absorption coefficient,
the optical depth along a line of sight between s0 and s1 can be calculated as
The intensity at a slice of the box at the position s1 along a line of sight is then given as
and the luminosity can be obtained by integrating over the slice, namely, in the case of a face-on galaxy, via
where L is the size of the numerical domain and the integration variable in Eq. (40) is s = x3. For an edge-on galaxy, the line of sight is parallel to the x1 direction, namely, s = x1, and the total free-free luminosity is:
2.3.3. Total radio luminosity
The total radio emission is composed of both free-free and synchrotron radiation with relative contributions that depend on the frequency range. Furthermore, the geometry of the emitting galaxy plays a role in the sense that the line of sight of the observation becomes relevant when including absorption processes. In this work, we consider the two extreme cases, face-on and edge-on observations, to bracket reality.
Following Werhahn et al. (2021), we use 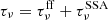 to calculate the absorption of synchrotron intensity at a position s1 as:
to calculate the absorption of synchrotron intensity at a position s1 as:
where 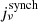 is given in Eq. (30).
is given in Eq. (30).
Again, the total synchrotron luminosity depends on whether the galaxy is observed face-on, for which
with s = x3 or edge-on, for which
with s = x1 in Eq. (44).
The total radio luminosity is
with 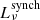 and
and 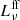 given by Eqs. (45) and (42) for face-on observation and Eqs. (46) and (43) for edge-on observation, respectively.
given by Eqs. (45) and (42) for face-on observation and Eqs. (46) and (43) for edge-on observation, respectively.
2.4. q parameter
To account for the stellar mass-dependent balance between obscured and unobscured SFR, when calculating the infrared luminosity, we adopt the calibration of Bernhard et al. (2014):
where 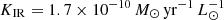 ,
, 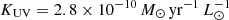 , and
, and
with α = 0.71 and IRX0 = 1.32. The calibration given in Eq. (48) is based on a self-consistent of model the redshift evolution of the UV and IR luminosity functions, which takes into account that the fraction of escaping UV photons increases with increasing redshift (e.g., Burgarella et al. 2013).
The comparison between IR and radio luminosity is typically expressed in terms of the logarithm of their ratio. This value is named q and has been defined in Eq. (1). The luminosities in this definition are in the rest frame.
3. Results and comparison with observations
3.1. Radio emission and IR-radio correlation in the reference model
In this section, we present results for the model that describes the observed dependence of the IR-radio correlation on stellar mass best. The parameters of this reference model are given in Table 1.
Radio spectra obtained for the reference model of galaxies with stellar masses of 109 M⊙, 1010 M⊙, and 1011 M⊙ that are observed face-on are shown in Fig. 5. The total radio emission Lν includes contributions from both free-free emission, 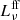 , the intrinsic synchrotron emission,
, the intrinsic synchrotron emission, 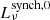 . The absorption processes included in our model affect the radio spectra mostly at low frequencies. Here, the free-free emission increases at very low frequencies of ∝ν3/2 (for most cases, this range is below the minimum frequency, as shown in Fig. 5) and at high frequencies it decreases at ∝ν−0.1. The spectrum of
. The absorption processes included in our model affect the radio spectra mostly at low frequencies. Here, the free-free emission increases at very low frequencies of ∝ν3/2 (for most cases, this range is below the minimum frequency, as shown in Fig. 5) and at high frequencies it decreases at ∝ν−0.1. The spectrum of 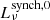 is close to a power law, but mildly curved due to cosmic ray cooling processes, over the frequency range presented in Fig. 5. Such mildly curved synchrotron spectra have also been seen in the observations of Klein et al. (2018).
is close to a power law, but mildly curved due to cosmic ray cooling processes, over the frequency range presented in Fig. 5. Such mildly curved synchrotron spectra have also been seen in the observations of Klein et al. (2018).
 |
Fig. 5. Rest-frame spectral luminosities at different redshifts for galaxies that are observed face-on. Different colors indicate results from models with different stellar masses: M⋆ = 109 M⊙ (blue), M⋆ = 1010 M⊙ (green), and M⋆ = 1011 M⊙ (red). Different linestyles refer to different emission types: the total radio emission Lν (solid lines) depends on the free-free luminosity |
For z = 0, synchrotron emission at ν = 1.4 GHz dominates over free-free emission for all stellar masses by at least two orders of magnitude. Absorption affects the spectrum only for ν ≲ 0.02 GHz for the case of M⋆ = 1010 M⊙, for instance, which is below the frequency range presented in Fig. 5. However, for z = 4, the slope of 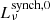 is affected by absorption at ν ≲ 0.3 GHz for M⋆ = 1010 M⊙. At high radio frequencies, the free-free emission dominates the spectra. For a galaxy with M⋆ = 1010 M⊙ this crossover from synchrotron to free-free dominance occurs at ≈30 GHz at z = 0 (see the upper panel of Fig. 5). With increasing M⋆ and increasing z, the crossover point moves to lower ν. In the KINGFISHER sample of nearby galaxies (Tabatabaei et al. 2017) the transition from synchrotron-dominated emission to free-free-dominated emission occurs, on average around ≈10 GHz, yet the sample includes several galaxies with crossover frequencies that are comparable to our model. The sample of local luminous infrared galaxies presented by Dey et al. (2022) includes several galaxies with crossover frequencies of ≳30 GHz. Overall, our model predicts that the free-free contribution increases strongly with z and starts affecting the slope of the total spectrum at ν = 1.4 GHz already at z ≈ 4. In the top panel of Fig. 6, the ratio of non-thermal (
is affected by absorption at ν ≲ 0.3 GHz for M⋆ = 1010 M⊙. At high radio frequencies, the free-free emission dominates the spectra. For a galaxy with M⋆ = 1010 M⊙ this crossover from synchrotron to free-free dominance occurs at ≈30 GHz at z = 0 (see the upper panel of Fig. 5). With increasing M⋆ and increasing z, the crossover point moves to lower ν. In the KINGFISHER sample of nearby galaxies (Tabatabaei et al. 2017) the transition from synchrotron-dominated emission to free-free-dominated emission occurs, on average around ≈10 GHz, yet the sample includes several galaxies with crossover frequencies that are comparable to our model. The sample of local luminous infrared galaxies presented by Dey et al. (2022) includes several galaxies with crossover frequencies of ≳30 GHz. Overall, our model predicts that the free-free contribution increases strongly with z and starts affecting the slope of the total spectrum at ν = 1.4 GHz already at z ≈ 4. In the top panel of Fig. 6, the ratio of non-thermal (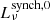 ) to thermal (
) to thermal (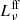 ) luminosity at ν = 1.4 GHz is presented, demonstrating the clear dominance of
) luminosity at ν = 1.4 GHz is presented, demonstrating the clear dominance of 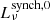 at low z for all M⋆ considered and the increase in the non-thermal contribution with increasing z. Therefore, especially at higher redshifts, one needs to be careful when shifting the observed spectrum to the rest frame for extracting the value of L1.4 due to the change in the spectral slope.
at low z for all M⋆ considered and the increase in the non-thermal contribution with increasing z. Therefore, especially at higher redshifts, one needs to be careful when shifting the observed spectrum to the rest frame for extracting the value of L1.4 due to the change in the spectral slope.
 |
Fig. 6. Analysis of radio spectra at ν = 1.4 GHz. The top panel shows the ratio of non-thermal ( |
The slope of 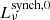 resulting from our model depends mostly on the slope of the proton injection spectrum αCR. It can be estimated4 as −(αCR − 1)/2 = −1.0 for αCR = 3.0, although there can be effects on the slope from the electron energy losses that contribute differently at different frequencies. However, the reference model results in a scaling of synchrotron emission close to ∝ν−1.0 as indicated in Fig. 5. Therefore, the resulting spectrum Lν at ν = 1.4 GHz is steeper than the assumption used in the analysis of Delvecchio et al. (2021), which is Lν ∝ ν−0.75. We show the results of power-law fits (with a fitting range of 0.43 − 4.5 GHz) of the model spectra to both
resulting from our model depends mostly on the slope of the proton injection spectrum αCR. It can be estimated4 as −(αCR − 1)/2 = −1.0 for αCR = 3.0, although there can be effects on the slope from the electron energy losses that contribute differently at different frequencies. However, the reference model results in a scaling of synchrotron emission close to ∝ν−1.0 as indicated in Fig. 5. Therefore, the resulting spectrum Lν at ν = 1.4 GHz is steeper than the assumption used in the analysis of Delvecchio et al. (2021), which is Lν ∝ ν−0.75. We show the results of power-law fits (with a fitting range of 0.43 − 4.5 GHz) of the model spectra to both 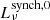 and Lν at ν = 1.4 GHz in the lower panel of Fig. 6. There, a clear dependence of the power law index α1.4 on M⋆ is demonstrated. We note that a dependence of the slope of radio spectra on the SFR, which in our model is coupled to M⋆, has also been seen in observations (Tabatabaei et al. 2017; Klein et al. 2018). Furthermore, Fig. 6 shows the significant flattening of the radio spectra at ν = 1.4 GHz in high-mass galaxies due to the increase in the thermal contribution. We note, however, that the opposite trend has been reported from observations (An et al. 2021; Heesen et al. 2022), where radio spectra become steeper with increasing SFR, namely, increasing M⋆. The discrepancy could be caused by the fact that we do not model the escape of CR electrons through galactic winds. Another caveat of our reference model is that it produces a thermal fraction at z = 0 at least an order of magnitude smaller than the observed fraction in local galaxies of ≈10% (Tabatabaei et al. 2017). More details on this are shown in the upper panel of Fig. 6. With increasing redshift, however, the reference model produces higher thermal fractions.
and Lν at ν = 1.4 GHz in the lower panel of Fig. 6. There, a clear dependence of the power law index α1.4 on M⋆ is demonstrated. We note that a dependence of the slope of radio spectra on the SFR, which in our model is coupled to M⋆, has also been seen in observations (Tabatabaei et al. 2017; Klein et al. 2018). Furthermore, Fig. 6 shows the significant flattening of the radio spectra at ν = 1.4 GHz in high-mass galaxies due to the increase in the thermal contribution. We note, however, that the opposite trend has been reported from observations (An et al. 2021; Heesen et al. 2022), where radio spectra become steeper with increasing SFR, namely, increasing M⋆. The discrepancy could be caused by the fact that we do not model the escape of CR electrons through galactic winds. Another caveat of our reference model is that it produces a thermal fraction at z = 0 at least an order of magnitude smaller than the observed fraction in local galaxies of ≈10% (Tabatabaei et al. 2017). More details on this are shown in the upper panel of Fig. 6. With increasing redshift, however, the reference model produces higher thermal fractions.
Next, we compare the radio emission at νobs = 1.4 GHz and to the IR emission obtained from Eq. (48). In the top panel of Fig. 7, we present the output of the reference model and compare it to the Molnár et al. (2021) data set of local sources. As indicated by the color of the large dots, the model predicts low mass galaxies to be located in the low luminosity end of the observed correlation and high mass galaxies in the intermediate/high luminosity end. The trend of the observed correlation as well as the absolute value are in good agreement with our model at z = 0. The extensive catalog of low-redshift star-forming galaxies presented by Molnár et al. (2021) indeed reveals a nonlinear IRRC with a slope of 1.11 ± 0.01. When fitting our model at z = 0 with the following function:
 |
Fig. 7. Radio luminosity L1.4 as a function of the IR luminosity LIR. Top: solid dots show the result using the default parameters of the model (with αCR = 3.0). The different colors are models with different stellar masses M⋆, according to the color bar. The data in the background are local observations of Molnár et al. (2021). The lines show the results of different fits to the reference model (see Eq. (50)). The model predictions for different cosmic ray spectral indexes, αCR = 2.8 and αCR = 3.2, are shown for comparison. Bottom: model predictions for L1.4 and LIR for αCR = 3.0 at different redshifts as indicated but the marker size (smallest to biggest: z = 0 − 5). Different symbols indicate different treatments of absorption (circles: face-on observation, diamonds: edge-on observation). |
we find a slope of m = 1.03 ± 0.01 and b = 2.92 ± 0.10. We note that for m = 1, b = q. The correlation resulting from our model is, therefore, similar to the observed correlation, namely: it is close to linear. The fit to the model is presented as a black line in the top panel of Fig. 7. In Appendix D, we present fits to the function (50) for the modelled IRRC at 0 ≤ z ≤ 5. To illustrate the dependence of the model on the free parameters, the results for changing αCR, while using the reference values for all other free parameters, are presented in Fig. 7. We find that varying αCR between 2.8 and 3.2 captures the entire observed scatter of the IRRC. However, changing other free parameters, like fB and αCR, has a similar effect on the resulting IRRC. The systematics of the free parameters will be analyzed in detail in Sect. 3.2.
In the bottom panel of Fig. 7, we show the evolution of the luminosities with redshift, as indicated by the increasing size of the markers. With increasing redshift, both L1.4 and LIR increase in our model, but the correlation remains conserved. Even at the highest redshift considered in this plot, z = 5, only small deviations from the correlation can be seen for high-mass galaxies (see the symbols of the largest size). Here, the correlation becomes more nonlinear; for details, we refer to the discussion on nonlinearity in Appendix D. Furthermore, there is no dependence on the line of sight for the redshift range presented in Fig. 7. This is not surprising because the only way differences between face-on and edge-on cases can arise in our current model is through free-free and synchrotron self-absorption processes, namely, opacity differences arising from different path lengths. Stronger variations with respect to the line of sight can be expected in models that account for cosmic ray transport and ordered large-scale magnetic fields, which is beyond the scope of the present study. Since there seems to be no dependence on galaxy orientation up to z = 5, we use the face-on assumption as the default unless indicated otherwise.
In Fig. 8, the redshift evolution of q for the reference model is directly compared to the AGN-corrected observations of Delvecchio et al. (2021). Generally, there is an agreement between model and observation: With the exception of galaxies with low M⋆, the value of q is nearly independent of redshift, but there is a spread of q for different masses. As for the observed data set, our reference model results in a spread of q from q ≈ 2.4 for M⋆ ≈ 1011 M⊙ up to, for z ≲ 2, q ≈ 3.2 for M⋆ ≈ 108.5 M⊙. We note that in the z = 0 − 1 range, the spread of q vanishes for masses of M⋆ ≳ 1010 M⊙ which is also seen in the observation. Towards the highest z shown in Fig. 8 the spread between different masses becomes larger. We note that the 1-σ uncertainty regions (as indicated by the shaded regions in the top panel of Fig. 8), caused by uncertainties in the input empirical relations, are barely overlapping. Even at low stellar masses, where the error bands are the largest, we find a systematic trend of q with M⋆. This strengthens our conclusion that the IRRC is indeed dependent on the stellar mass (see also the comparison to M⋆-agnostic observations of the IRRC in Appendix E. Finally, it is worth mentioning that our model predicts different redshift dependencies of q for different values of M⋆. This is in contrast to the fitting formula used in Delvecchio et al. (2021), who report the same redshift dependence of (1 + z)−0.023 for the mass bins 10.5 < log10(M⋆/M⊙) < 11 and 11 < log10(M⋆/M⊙) < 12. Deeper radio and IR observations, and complete input galaxy samples, capable of homogeneously probing all stellar masses M⋆ ≥ 109 M⊙ over a larger redshift range, are required to establish the true level of complexity present in the mass dependence of the IRRC out to higher redshift.
 |
Fig. 8. q parameter as defined in Eq. (1) versus redshift z. Top: lines show the results of our reference galaxy model and the stars with grey contours are observations (AGN-corrected values from Delvecchio et al. 2021). Colors refer to different stellar masses M⋆ as indicated by the color bar. For solid lines the galaxies are observed face-on and for dashed lines edge-on. Shaded regions indicate the standard deviation. Bottom: difference between the observed values of qobs and the corresponding model predictions qmod. The errors include only the uncertainties of the observational data. |
3.2. Dependence model parameters
So far, we have discussed the results of the reference model for which all free parameters have been fixed to values that are listed in Table 1 and that produce q(z, M⋆) curves that are in good agreement with the observed IRRC. However, some of the free parameters in our model are not well constrained and a systematic exploration of the parameter space is required. The goal of this section is to analyze the sensitivity of the model to the various free parameters and to identify the most crucial dependencies.
3.2.1. Ratio of synchrotron to free-free emission
In Fig. 8, we show that in the reference model, the spread of q with respect to M⋆ increases with increasing z. This might be caused by the transition from the dominance of nonthermal to thermal emission (see Figs. 5 and 6). With model series A (see Table 2), we tested the role of the ratio of free-free to synchrotron emission in the dependence of q on M⋆ This series includes the reference model plus eight models in which the magnetic field strength and the ionization degree are changed systematically. The magnetic field strength determines the synchrotron flux and is controlled by the parameters fB and fturb (see Eq. (14)) and the ionization degree fion determines the free-free emission (see Eq. (37)).
In the individual panels of Fig. 9, we present q(z, M⋆) for different values of fB, fturb, and fion. The reference model is presented in the center panel. From left to right the magnetic field strength increases as we increase the value of 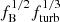 . As expected, with smaller B the q(z) curves move up, because L1.4 decreases. Additionally, we find that the dependence of q(z, M⋆) on M⋆ becomes stronger as
. As expected, with smaller B the q(z) curves move up, because L1.4 decreases. Additionally, we find that the dependence of q(z, M⋆) on M⋆ becomes stronger as 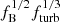 , namely, the magnetic field strength decreases.
, namely, the magnetic field strength decreases.
 |
Fig. 9. q parameter as a function of redshift, z, for galaxies with different stellar mass, M⋆, as given in the colorbar. The reference model compared to the observed data set of Delvecchio et al. (2021) is presented in the middle panel. In panels from left to right, the magnetic field strength in the model is increased; see the discussion around Eq. (14) for the parameters fB and fturb. From bottom to top, the ionization degree is increased via the parameter fion which affects the free-free emission; see Sect. 2.3.2. |
From bottom to top, we show models with different values of the ionization degree. Lowering fion affects the q(z, M⋆) mostly at higher redshifts as expected. Generally, we find that the q(z, M⋆) curves tend to become closer again at high z, if the value of fion is higher. In conclusion, the dependence of q(z, M⋆) on M⋆ seems to be stronger if the radio flux is dominated by synchrotron emission.
3.2.2. CR model
Our cosmic ray model includes several assumptions and parameters that are not very well constrained. Therefore, we explored the dependence of our model on these parameters in series B (see Table 2). In particular, we changed the value of fπfCR/fsec, which determines the number of CR protons Qp, 0 (see Eq. (17)). The number of CR electrons which ultimately produce the synchrotron emission depends on Qp, 0 but also on the cooling time scale, and the slope of the injection spectrum αCR (see Eq. (15)). As discussed before, the slope αCR is strongly connected to the slope of the radio spectrum. In series B, we changed both fπfCR/fsec and αCR systematically to explore the effect of the key parameters of the CR model.
The dependence of q(z, M⋆) on the number of CR protons and the slope of the injection spectrum is presented in Fig. 10. Again, the reference model is shown in the center panel of the figure. For both, decreasing the slope of the CR injection spectrum and the total number of CR protons leads to a shift of the q(z, M⋆) curves toward lower values. The origin of the decrease in q(z, M⋆) for an increase in the total number of CR protons is trivial since more CR protons imply more CR electrons and, therefore, more synchrotron emission. For a steeper Ne(γe) spectrum, 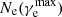 is smaller, which implies that there are fewer electrons to emit synchrotron at νobs = 1.4 GHz. Hence, the radio emission, L1.4, decreases for an increasing αCR and consequently q increases. We do not find significant changes in the overall shape of the q(z, M⋆) curves; namely, there is no change in the M⋆ and z trend and only the absolute values are shifted. We note that Fig. 10 indicates that in our model, increasing the total number of CR protons has a very similar effect to flattening the CR injection spectrum.
is smaller, which implies that there are fewer electrons to emit synchrotron at νobs = 1.4 GHz. Hence, the radio emission, L1.4, decreases for an increasing αCR and consequently q increases. We do not find significant changes in the overall shape of the q(z, M⋆) curves; namely, there is no change in the M⋆ and z trend and only the absolute values are shifted. We note that Fig. 10 indicates that in our model, increasing the total number of CR protons has a very similar effect to flattening the CR injection spectrum.
 |
Fig. 10. q parameter as a function of redshift, z, for galaxies with different stellar mass, M⋆, as given in the colorbar. The reference model compared to the observed data set of Delvecchio et al. (2021) is presented in the middle panel. From left to right, the slope of the CR injection spectrum gets steeper via the parameter αCR; see Eq. (15). From bottom to top, the number of CR protons in the model is increased via the parameters fπ, fCR, and fsec; see Eq. (22). |
3.2.3. Galactic radius and scale height models
In this section, we present the dependence of the resulting IRRC on our models of the galactic radius Rgal and scale height Hgal. The default evolution is given in Eqs. (4) and (5), however, in series C and D we test alternative scenarios.
The results for series C are presented in Fig. 11, where the strong effect of αgal on the spread of the q(z, M⋆) is evident. While our reference model (αgal = 0.05) reproduces the observed data best within the uncertainty regime, lower values of αgal result in a stronger M⋆ dependence of q. For stronger scaling of Rgal with M⋆, for instance, for αgal = 0.1 the q(z, M⋆) curves are closer together.
 |
Fig. 11. Different dependence of the galactic radius on stellar mass (by variation of αgal, see Eq. (4)) compared to the reference model (αgal = 0.05). |
The model for Hgal seems to affect the resulting q(z, M⋆) less, at least for the scenarios we present in Fig. 12. In the upper panel of Fig. 12, a scaling of Hgal with the galactic radius is assumed and appears to result is a similar scaling of q(z, M⋆) as the reference model, even though the M⋆ dependence at z ≈ 0 is slightly stronger for the models with Hgal ∝ Rgal. Therefore, at low z, the reference model is closer to the observed data. A scaling of Hgal ∝ (1 + z) is presented in the lower panel of Fig. 12, results in a good agreement with observations at intermediate redshifts. At high z, however, the q(z, M⋆) curves increase faster for galaxies with small M⋆ if Hgal ∝ (1 + z).
 |
Fig. 12. Different models of the galactic scale height Hgal compared to the reference model. Top:Hgal scales with the characteristic galactic radius Rgal as modeled in Eq. (4). Bottom: model in which Hgal increases with redshift. |
3.3. Extrapolation to high redshift
The reference model describes the observed IR-radio correlation well up to the maximum redshift of z = 4. In principle, the model can be extrapolated to redshifts beyond that. However, we note that some of the input scaling relations for the model as well as the assumption of well-settled, double-exponential disks might break down at extreme z and therefore the results of this section are rather speculative. We note, however, that early observations with the James Webb Space Telescope (JWST) reveal that disk galaxies dominate the population even at z > 1.5 (Ferreira et al. 2022).
Another assumption that will break down at high redshifts is the saturation of the small-scale dynamo. While the kinematic phase is very short (Kazantsev 1968; Kulsrud & Anderson 1992; Rogachevskii & Kleeorin 1997; Schober et al. 2012b), at z ≫ 4 the dynamo could still be in the nonlinear stage. In this phase (Beresnyak 2012), saturation is reached at the smallest length scales of the turbulent inertial range and there is an inverse cascade of magnetic energy to larger scales. Semi-analytical models by Schober et al. (2013) predict that the dynamo saturates on time scales of 4 − 270 Myr, depending on the driving mechanism of turbulence.
In Fig. 13, the q(z, M⋆) curves are shown up to z = 10. The redshift and mass dependence predicted by our model does not significantly change at higher z. However, with absorption processes becoming more relevant in high-z galaxies, the observed radio flux depends on whether the galaxy is face-on or edge-on. For galaxies with high M⋆, this orientation effect becomes important at z ≳ 6. We note, however, that our model only includes orientation effects for the radio emission. A more detailed model of the IR emission that takes into account the dust absorption/emission with respect to the orientation of the disk might affect the high-z evolution of q (see also Li et al. 2016, for an observational study of the difference between the IR-to-radio luminosity ratio in local face-on and edge-on galaxies).
 |
Fig. 13. Extension of the reference model to high z. |
The interesting trends predicted by the model at 6 ≳ z ≳ 8 will be testable in the near future. Based on the currently proposed SFR-L1.4 calibrations for galaxies at intermediate and high redshift, objects with SFR in the range ∼5 − 10 M⊙ yr−1 are expected to be detectable at z ∼ 6 in the deepest future Square Kilometre Array (SKA) continuum surveys (using the parameters of the Square Kilometre Array (SKA) continuum reference surveys as outlined in Prandoni & Seymour 2015). For z ∼ 6 main sequence galaxies (e.g., Duncan et al. 2014; Salmon et al. 2015), this would imply an accessible stellar mass range of ≳5 × 109 M⊙.
4. Discussion
4.1. Novel interpretations of the IRRC with our semi-analytical model
The strength of a simplified galaxy model as presented in this paper is that it allows for an exploration of a large parameter range and tests of different scenarios of galaxy evolution. This makes it possible to identify the underlying physical processes behind observed correlations, such as the IRRC.
The dependence of the IRRC on stellar mass, M⋆, for instance arises from the empirical input relations (see Sect. 2.1) that make up the foundation of our model. The SFR rate in Eq. (2) that is used as an input is not a simple power-law, but the M⋆ dependence can be roughly approximated as 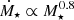 . Therefore the gas mass, as given in Eq. (3) scales as
. Therefore the gas mass, as given in Eq. (3) scales as 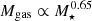 . Together with
. Together with 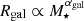 (Eq. (4)) and Hgal ∝ Rgal (Eq. (5)), the gas density (Eq. (8)) scales as
(Eq. (4)) and Hgal ∝ Rgal (Eq. (5)), the gas density (Eq. (8)) scales as 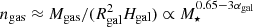 . This results in a scaling of the magnetic field strength of
. This results in a scaling of the magnetic field strength of 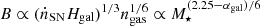 , where we use ṅSN ∝ Ṁ⋆/Vgal. The number of cosmic ray electrons as a function of the Lorentz factor is given in Eq. (22). For synchrotron emission, the number of cosmic rays with a Lorentz factor
, where we use ṅSN ∝ Ṁ⋆/Vgal. The number of cosmic ray electrons as a function of the Lorentz factor is given in Eq. (22). For synchrotron emission, the number of cosmic rays with a Lorentz factor 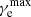 is relevant. This number is
is relevant. This number is 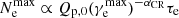 . For our model, we find that
. For our model, we find that 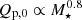 and
and 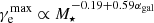 , while the CR cooling time, τe, is dominated by different processes for different stellar masses. In low-mass galaxies and low-to-moderate redshifts, typically
, while the CR cooling time, τe, is dominated by different processes for different stellar masses. In low-mass galaxies and low-to-moderate redshifts, typically 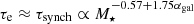 ; whereas for high-mass galaxies,
; whereas for high-mass galaxies, 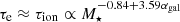 . Therefore, we find
. Therefore, we find
The 1.4 GHz emission can then be estimated as 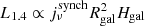 , assuming that it is dominated by synchrotron emission. According to Eq. (30), we have
, assuming that it is dominated by synchrotron emission. According to Eq. (30), we have 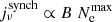 and we find the following for the regimes with different CR cooling channels:
and we find the following for the regimes with different CR cooling channels:
For our reference model with αgal = 0.05 and αCR = 3, we find 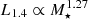 and
and 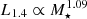 for low- and high-mass galaxies respectively. Therefore, in both cases, radio emission increases more strongly with M⋆ than the IR emission that scales as
for low- and high-mass galaxies respectively. Therefore, in both cases, radio emission increases more strongly with M⋆ than the IR emission that scales as 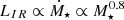 (see Eq. (48)). Hence, we expect q to decrease with increasing M⋆. This trend is consistent with the results of the full model presented in this work and is, for instance, presented in Fig. 8. Additionally, we expect the dependence of q on M⋆ to be less if αgal is larger, which can also be seen in Fig. 11.
(see Eq. (48)). Hence, we expect q to decrease with increasing M⋆. This trend is consistent with the results of the full model presented in this work and is, for instance, presented in Fig. 8. Additionally, we expect the dependence of q on M⋆ to be less if αgal is larger, which can also be seen in Fig. 11.
Calculations with the full model, which are presented in Sect. 3, are needed to understand the detailed dependence of q on M⋆ and z. In particular, the contributions of free-free emission and different cooling mechanisms of cosmic ray electrons cannot be included in a simple estimate as discussed in the previous paragraph.
4.2. Comparison to other models for the IRRC
The first attempts at understanding the observed IRRC were one-zone models. The so-called calorimeter theory by Voelk (1989) was based on the assumption that CR electrons lose their energy via synchrotron emission before escaping the galaxy and that the galaxy is optically thick in the UV, such that emission by young stars is absorbed by dust and re-radiated in the FIR. This calorimeter model results in a tight IRRC but the slope of the radio spectra is too steep in comparison to observations. Non-calorimeter one-zone models were subsequently proposed (Niklas & Beck 1997; Lacki et al. 2010; Schleicher & Beck 2013; Schober et al. 2016), but they have generally needed to be finetuned to maintain the tightness of the IRRC. For example, in the non-calorimeter model proposed by Lacki et al. (2010), the efficient cooling of CR electrons decreases radio emission. To maintain a tight IRRC, the decreasing radio emission is either balanced by the decreasing FIR emission in lower surface density galaxies or by secondary CRs and the dependence of synchrotron frequency on energy in starbursts. However, the predicted spectral slopes by Lacki et al. (2010) are still in conflict with observations, even if such one-zone models include a large number of free parameters.
To model more realistic galaxies and to better understand the underlying physics of the IRRC, Vollmer et al. (2022) developed a 1D model of turbulent clumpy star-forming galactic disks, including a recipe for the nonthermal radio continuum emission. They conclude that the observed SFR-radio correlation can be reproduced by their fiducial model in a reasonable way (within ≈4σ). However, the mass range of the model galaxies in Vollmer et al. (2022) is not broad enough to explore a mass dependence of the IRRC. This is a central advantage of the model we present in this study and ultimately allows us to interpret the observations by Delvecchio et al. (2021).
1D models are still significantly simplified in comparison to real galaxies and therefore other authors have chosen to simulate individual galaxies in detail, with the goal of identifying the origin of the IRRC. Werhahn et al. (2021) is one the first studies that used 3D magneto-hydrodynamical (MHD) simulations of isolated galaxies including a self-consistent evolution of the CR proton energy density. In post-processing, they calculate the steady-state spectra of CR electrons to estimate the radio luminosity. Werhahn et al. (2021) confirmed the findings of Lacki et al. (2010) and, in particular, revealed that the increasing bremsstrahlung and Coulomb losses at high gas surface densities is almost exactly counteracted by an increasing contribution of secondary radio emission with increasing Ṁ⋆. In a companion study, Pfrommer et al. (2022) showed that the global IRRC is indeed connected to the saturated stage of the small-scale dynamo. The approach via full 3D MHD-CR simulations exhibits fewer free parameters and thus can be considered to be more predictive than one-zone models. However, such simulations are computationally expensive and are not suitable for exploring a large parameter space, unlike models such as the one presented in this work.
4.3. Weaknesses of the semi-analytical approach
With the model proposed in this paper, we can explore the parameter space at low computational costs. However, the galaxies are modelled in a very idealized way. They are characterized by exponential density profiles, but lack spiral arms, bulges, and a multi-phase interstellar medium. In the evolution of the galaxies, neither accretion nor merging events are taken into account directly. Full 3D simulations of galaxies as presented by Werhahn et al. (2021) and Pfrommer et al. (2022) are much more suitable for exploring the role of detailed galaxy properties.
Instead, we used observed scaling relations to model the global properties of the galaxies. However, these might break down at extreme redshift. This might be also the case for the assumed scaling relation in Eq. (48), which we used to estimate the IR luminosity; in particular, if the dust properties in the early Universe differ from those of the local galaxies. We note that IR emission may be modified not only with a change in the dust density, but also through temperature variations, changes in metallicity, and a change in sources for the ISM heating as well as the details of radiative transfer physics. An expansion of our model by a description of the IR emission that goes beyond an observed scaling relation could therefore be very insightful. On the other hand, such an extension of the model would imply a larger number of free parameters.
Another central ingredient of synchrotron emission is the cosmic ray model, in which we assume steady-state and neglect diffusion and propagation effects. Since the distribution of CRs is homogenous and follows the distribution of the gas and the SFR, face-on and edge-on views result in similar radio luminosities. This effect is enhanced by our assumption of isotropic magnetic fields that are not composed of small-scale and large-scale components.
Our galaxy model is based on a simplified model of a star-forming galaxy that is described by a set of free parameters (see the yellow boxes in Fig. 1). A combination of free parameters that results in q parameters that are comparable to the observed values by Delvecchio et al. (2021) is listed in Table 1 and makes up our reference model. In Figs. 9, 10, and 12, we show how the model curves change when the respective free parameters are changed individually. We go on to consider a galaxy population in which the free parameters vary. In particular, we consider fturb, fCR, fB, fπ, fsec, fion, and fsISRF, which have average values that match the one of the reference model but are assumed to vary up to ±25% within a population of galaxies. The resulting error bands are presented in the top panel of Fig. 14. The one-sigma error bands are overlapping, nearly washing out the dependence of q on stellar mass M⋆. We note, however, that a covariance between some of the free parameters in our model can be expected and therefore, the error bands in Fig. 14 are likely to be overestimated. Nevertheless, this analysis, in addition to the results presented in Figs. 9, 10, and 12, demonstrates that a fine-tuning of our model is required to describe the observation by Delvecchio et al. (2021).
 |
Fig. 14. Model predictions for galaxy populations in which the free parameters have a range of values. Top: model predictions for a galaxy population, which on average has the parameters of our reference model, but in which fturb, fCR, fB, fπ, fsec, fion and fsISRF vary randomly with up to ±25% scatter around the default values. Bottom: model predictions for a galaxy population with parameters that match the ones of of the reference model, except for the value of αCR. Here, a galaxy population with 1.75 ≤ αCR ≤ 3.25 is considered which results in 0.4 ≲ α1.4 ≲ 1.3. |
A final obstacle when comparing with the observational data from Delvecchio et al. (2021), is the fact that they used a constant spectral slope of α1.4 = 0.75 in their analysis. In our model, however, α1.4 is not an input parameter, but an output that mostly depends on the slope of injection spectrum, αCR, but also on the thermal to non-thermal ratio. If we use our reference model, but lower the value of the αCR such that α1.4 ≈ 0.75, the q(z) curves decrease significantly (see the trend in Fig. 10). The decrease in q(z) with decreasing αCR is caused by an increase in the number of cosmic ray electrons with energies 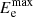 (see Eq. (33)) that lead to synchrotron emission at 1.4 GHz. If, in addition, a distribution of α1.4 is considered, an additional uncertainty arises. The strong dependence of the radio luminosity on αCR can be seen in the top panel of Fig. 7, where αCR is only varied between 2.8 and 3.2, implying 0.9 ≲ α1.4 ≲ 1.1, but the resulting L1.4 captures the entire observed scatter. Therefore, the input parameter αCR, alongside the efficiency of the dynamo, fB, and the efficiency of cosmic ray production fCR, are the key parameters that determine the value of q(z). To approximately reproduce an observed scatter of 0.4 ≲ α1.4 ≲ 1.3 (see e.g., Tabatabaei et al. 2017), we then used our reference model with a galaxy population that includes members with parameters 1.75 ≤ αCR ≤ 3.25. The resulting uncertainty in the q(z) curves is large, as can be seen in the lower panel of Fig. 14, and the q(z) curves are lower than the observed values.
(see Eq. (33)) that lead to synchrotron emission at 1.4 GHz. If, in addition, a distribution of α1.4 is considered, an additional uncertainty arises. The strong dependence of the radio luminosity on αCR can be seen in the top panel of Fig. 7, where αCR is only varied between 2.8 and 3.2, implying 0.9 ≲ α1.4 ≲ 1.1, but the resulting L1.4 captures the entire observed scatter. Therefore, the input parameter αCR, alongside the efficiency of the dynamo, fB, and the efficiency of cosmic ray production fCR, are the key parameters that determine the value of q(z). To approximately reproduce an observed scatter of 0.4 ≲ α1.4 ≲ 1.3 (see e.g., Tabatabaei et al. 2017), we then used our reference model with a galaxy population that includes members with parameters 1.75 ≤ αCR ≤ 3.25. The resulting uncertainty in the q(z) curves is large, as can be seen in the lower panel of Fig. 14, and the q(z) curves are lower than the observed values.
4.4. Potential extensions of the model
There are several potential extensions of the galaxy model. For instance, a model for clumping of the density field could be implemented or a redshift evolution of various galaxy properties, such as the small-scale dynamo efficiency, the ionization degree, or the dust temperature. Furthermore, it would be possible to consider distributions of galactic radii and scale height at a given z to obtain an estimate for errors of q(z, M⋆). However, since our current idealized galaxy model is successful in explaining the observed IRRC, adding further free parameters to the model is not necessary at present.
5. Conclusion
In this study, we modeled the radio and infrared emission of idealized galaxies with the aim of understanding the origin of the IRRC and, in particular, its evolution across cosmic history. While our semi-analytical galaxy model includes a list of free parameters, the focus lies on how these underlying model parameters vary with two physical galaxy properties (assuming that the model galaxies follow the scaling relations for main sequence galaxies): stellar mass, M⋆, and redshift, z. Our approach is summarized as follows. In the first step, global aspects of the galaxies, namely, the scale height, radius, gas mass, and star formation rate, are estimated from observational correlations. Then a 3D distribution of the interstellar gas, the SFR, as well as the magnetic field, the thermal and non-thermal electron population is constructed that allows us to calculate the galactic radio emission. Finally, absorption processes that depend on the line of sight of the observation are included.
The model reproduces the observed dependence of the IRRC on M⋆ and z by Delvecchio et al. (2021) well. The best working model requires a fraction of 5% of the SN energy to be converted into turbulence and 10% of that being converted to magnetic energy by a turbulent dynamo. This results in a magnetic field strength in the core of the galaxy of 100.5 − 101.5 μG at z = 0 up to 101.2 − 102.3 μG at z = 5 for galaxies with M⋆ = 108.5 − 1011 M⊙, respectively. Then the observed trend of q, with values of q ≈ 2.8 for M⋆ = 108.5 M⊙ and q ≈ 2.4 for M⋆ = 1011 M⊙ and vanishing dependence on z can be reproduced, if ≈4% of the SN energy is converted into CR protons; see Fig. 8.
We used our model to explore the effect of varying galaxy properties on the evolution of q with z systematically. In particular, we find that increasing the ionization degree, which implies an increase in the free-free emission, only affects galaxies with high stellar mass. Minor modifications of the q(z, M⋆) curves when changing the ionization degree between fion = 0.05 − 0.2 can only be seen for galaxies with M⋆ = 1011 M⊙. Increasing the magnetic field strength, by varying the efficiency of the dynamo with the parameters fB and fturb, shifts the q(z, M⋆) curves to lower values while weakening the M⋆ dependence (see Fig. 9). Naturally, the q(z, M⋆) curves also depend on the free parameters of the cosmic ray model. More cosmic rays, namely, larger values of fCR, shift the q(z, M⋆) curves to lower values since the synchrotron luminosity increases (see Fig. 10). The q(z, M⋆) curves also move down when the slope of the CR injection spectrum αCR is decreased. The latter effect is caused by the fact that the CR population consists of fewer electrons with the characteristic energy for synchrotron emission at ν = 1.4 GHz and the typical galactic magnetic field strengths when the injection spectrum is steeper.
The semi-analytical galaxy model presented in this paper is a powerful tool for testing different scenarios of galaxy evolution and, in particular, for efficient exploration of the free parameter space. This is the central benefit of such a phenomenological model compared to high-resolution (magneto)hydrodynamical simulations. Comparison between the model predictions with currently available data sets allows us to constrain parameters of galaxy evolution and the dynamics of the magnetized ISM. For instance, it can be used to test turbulent dynamo theory across galaxy evolution. Finally, our model allows for the construction of a robust and physically motivated radio-calibration of the SFR that can be employed for current and future ultra-deep radio surveys with the Square Kilometer Array and its pathfinders.
We note that the classic Kennicutt-Schmidt relation (Kennicutt 1998; Kennicutt & Evans 2012) relates surface densities from the regime of normal galaxies to starburst galaxies, with an empirical power law index of 1.4. In contrast, Eq. (3) represents the galaxy-integrated star-formation law for main-sequence galaxies only (e.g., Daddi et al. 2010; Sargent et al. 2012). For this population, the relation between gas mass and total SFR has an index of 1/β2 ≈ 1.23.
We note that the value of the index nSFR = 3/2 differs a corresponding value appearing in Eq. (3) that is 1/β2 ≈ 1.23. Since Eq. (3) is an empirical relation that relates masses and Eq. (9) is based on mass density, a difference between nSFR and 1/β2 should not be considered to be an inconsistency.
The growth rate of the small-scale dynamo depends on the Reynolds number Re which is on the order of Re ≈ 1010 − 1012 for young galaxies. In simulations such high values of Re can never be achieved due to limited resolution. For example, the runs presented in Martin-Alvarez et al. (2018) reach Re ≈ 15 − 160. Therefore, the dynamo timescale in simulations is always overestimated by orders of magnitudes.
The spectral synchrotron emission 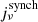 is given in Eq. (30) and is proportional to the emission
is given in Eq. (30) and is proportional to the emission 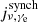 that corresponds to electrons with a fixed Lorentz factor γe and the number of CR electrons at a given energy, Ne(γe), times γe. From Eq. (28), which holds for a homogeneous magnetic field, we see that
that corresponds to electrons with a fixed Lorentz factor γe and the number of CR electrons at a given energy, Ne(γe), times γe. From Eq. (28), which holds for a homogeneous magnetic field, we see that 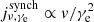 and from Eq. (22) that
and from Eq. (22) that 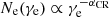 , if the total cooling timescale does not depend strongly on γe. Therefore,
, if the total cooling timescale does not depend strongly on γe. Therefore, 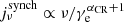 . Using Eq. (32) for the estimate of the energy that contributes mostly to the emission at a given frequency gives γe ∝ ν1/2 and therefore
. Using Eq. (32) for the estimate of the energy that contributes mostly to the emission at a given frequency gives γe ∝ ν1/2 and therefore 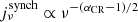 . For an inhomogeneous magnetic field deviations from this scaling can be expected.
. For an inhomogeneous magnetic field deviations from this scaling can be expected.
Acknowledgments
We thank Ivan Delvecchio for providing the observational data set and for useful discussions. The detailed comments by the referee Aritra Basu are highly appreciated and have improved the manuscript significantly. JS acknowledges the support by the Swiss National Science Foundation under Grant No. 185863. MTS acknowledges support from a Scientific Exchanges visitor fellowship (IZSEZO_202357) from the Swiss National Science Foundation. RSK acknowledges financial support from the European Research Council via the ERC Synergy Grant “ECOGAL” (project ID 855130), from the Deutsche Forschungsgemeinschaft (DFG) via the Collaborative Research Center “The Milky Way System” (SFB 881 – funding ID 138713538 – subprojects A1, B1, B2 and B8), from the Heidelberg Cluster of Excellence (EXC 2181 – 390900948) “STRUCTURES”, funded by the German Excellence Strategy, and from the German Ministry for Economic Affairs and Climate Action in project “MAINN” (funding ID 50OO2206). RSK also thanks for computing resources provided by the Ministry of Science, Research and the Arts (MWK) of the State of Baden-Württemberg through bwHPC and DFG through grant INST 35/1134-1 FUGG and for data storage at SDS@hd through grant INST 35/1314-1 FUGG. DRGS gratefully acknowledges support by the ANID BASAL projects ACE210002 and FB210003, as well as via the Millenium Nucleus NCN19-058 (TITANs). DRGS thanks for funding via Fondecyt Regular (project code 1201280).
References
- Aharonian, F. A., Kelner, S. R., & Prosekin, A. Y. 2010, Phys. Rev. D, 82, 043002 [Google Scholar]
- An, F., Vaccari, M., Smail, I., et al. 2021, MNRAS, 507, 2643 [NASA ADS] [CrossRef] [Google Scholar]
- Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS, 154, 147 [Google Scholar]
- Basu, A., Wadadekar, Y., Beelen, A., et al. 2015, ApJ, 803, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, A., Roychowdhury, S., Heesen, V., et al. 2017, MNRAS, 471, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Berkhuijsen, E. M., Gießübel, R., & Mulcahy, D. D. 2020, A&A, 633, A5 [EDP Sciences] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [Google Scholar]
- Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
- Beresnyak, A. 2012, Phys. Rev. Lett., 108, 035002 [NASA ADS] [CrossRef] [Google Scholar]
- Bernhard, E., Béthermin, M., Sargent, M., et al. 2014, MNRAS, 442, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [Google Scholar]
- Bogdan, T. J., & Völk, H. J. 1983, A&A, 122, 129 [NASA ADS] [Google Scholar]
- Bonato, M., Prandoni, I., De Zotti, G., et al. 2021, A&A, 656, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourne, N., Dunne, L., Ivison, R. J., et al. 2011, MNRAS, 410, 1155 [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burkhart, B., Stanimirović, S., Lazarian, A., & Kowal, G. 2010, ApJ, 708, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [CrossRef] [Google Scholar]
- Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. J. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, T., Klein, U., Wielebinski, R., & Wunderlich, E. 1985, A&A, 147, L6 [NASA ADS] [Google Scholar]
- Delhaize, J., Smolčić, V., Delvecchio, I., et al. 2017, A&A, 602, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Daddi, E., Sargent, M. T., et al. 2021, A&A, 647, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dey, S., Goyal, A., Małek, K., et al. 2022, ApJ, 938, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Duncan, K., Conselice, C. J., Mortlock, A., et al. 2014, MNRAS, 444, 2960 [Google Scholar]
- Federrath, C., Chabrier, G., Schober, J., et al. 2011, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Schober, J., Bovino, S., & Schleicher, D. R. G. 2014, ApJ, 797, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, L., Adams, N., Conselice, C. J., et al. 2022, ApJ, 938, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Burkhart, B., et al. 2011, Nature, 478, 214 [Google Scholar]
- Garrett, M. A. 2002, A&A, 384, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gent, F. A., Mac Low, M.-M., Käpylä, M. J., & Singh, N. K. 2021, ApJ, 910, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Graziani, L., Schneider, R., Ginolfi, M., et al. 2020, MNRAS, 494, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Staffehl, M., Basu, A., et al. 2022, A&A, 664, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Inami, H., Algera, H. S. B., Schouws, S., et al. 2022, MNRAS, 515, 3126 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Alexander, D. M., Biggs, A. D., et al. 2010a, MNRAS, 402, 245 [Google Scholar]
- Ivison, R. J., Magnelli, B., Ibar, E., et al. 2010b, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M. J., Smith, D. J. B., Bonfield, D. G., et al. 2010, MNRAS, 409, 92 [Google Scholar]
- Jiménez-Andrade, E. F., Magnelli, B., Karim, A., et al. 2019, A&A, 625, A114 [EDP Sciences] [Google Scholar]
- Jiménez-Andrade, E. F., Murphy, E. J., Heywood, I., et al. 2021, ApJ, 910, 106 [CrossRef] [Google Scholar]
- Kazantsev, A. P. 1968, Sov. J. Exp. Theor. Phys., 26, 1031 [NASA ADS] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., Lisenfeld, U., & Verley, S. 2018, A&A, 611, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, Saas-Fee Adv. Course, 43, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Koley, A., & Roy, N. 2019, MNRAS, 483, 593 [CrossRef] [Google Scholar]
- Kulsrud, R. M., & Anderson, S. W. 1992, ApJ, 396, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C., & Beck, R. 2013, MNRAS, 430, 3171 [CrossRef] [Google Scholar]
- Lacki, B. C., Thompson, T. A., & Quataert, E. 2010, ApJ, 717, 1 [Google Scholar]
- Li, J.-T., Beck, R., Dettmar, R.-J., et al. 2016, MNRAS, 456, 1723 [NASA ADS] [CrossRef] [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Kretschmer, M., & Teyssier, R. 2022, MNRAS, 513, 6028 [NASA ADS] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [Google Scholar]
- Magnelli, B., Ivison, R. J., Lutz, D., et al. 2015, A&A, 573, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancini, M., Schneider, R., Graziani, L., et al. 2015, MNRAS, 451, L70 [CrossRef] [Google Scholar]
- Marassi, S., Schneider, R., Limongi, M., et al. 2019, MNRAS, 484, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Martin-Alvarez, S., Devriendt, J., Slyz, A., & Teyssier, R. 2018, MNRAS, 479, 3343 [NASA ADS] [CrossRef] [Google Scholar]
- Martin-Alvarez, S., Katz, H., Sijacki, D., Devriendt, J., & Slyz, A. 2021, MNRAS, 504, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- McCheyne, I., Oliver, S., Sargent, M., et al. 2022, A&A, 662, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M. J. 2015, A&A, 577, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M., Hjorth, J., & Watson, D. 2010a, A&A, 514, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M. J., Watson, D., & Hjorth, J. 2010b, ApJ, 712, 942 [CrossRef] [Google Scholar]
- Molnár, D. C., Sargent, M. T., Leslie, S., et al. 2021, MNRAS, 504, 118 [CrossRef] [Google Scholar]
- Mowla, L. A., van Dokkum, P., Brammer, G. B., et al. 2019, ApJ, 880, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Braun, R., et al. 2006, ApJ, 651, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [Google Scholar]
- Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, Black Holes (Les Astres Occlus) (New York: Gordon and Breach), 343 [Google Scholar]
- Ocran, E. F., Taylor, A. R., Vaccari, M., et al. 2020, MNRAS, 491, 5911 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., Werhahn, M., Pakmor, R., Girichidis, P., & Simpson, C. M. 2022, MNRAS, 515, 4229 [NASA ADS] [CrossRef] [Google Scholar]
- Prandoni, I., & Seymour, N. 2015, in Advancing Astrophysics with the Square Kilometre Array (AASKA14), 67 [Google Scholar]
- Rieder, M., & Teyssier, R. 2016, MNRAS, 457, 1722 [NASA ADS] [CrossRef] [Google Scholar]
- Rieder, M., & Teyssier, R. 2017, MNRAS, 471, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 1997, Phys. Rev. E, 56, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Schinnerer, E., Murphy, E., et al. 2010, ApJ, 714, L190 [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., & Dalla Vecchia, C. 2008, MNRAS, 383, 1210 [Google Scholar]
- Schleicher, D. R. G., & Beck, R. 2013, A&A, 556, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., & Beck, R. 2016, A&A, 593, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Schober, J., Federrath, C., Bovino, S., & Schmidt, W. 2013, New J. Plasma Phys., 15, 023017 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D., Bovino, S., & Klessen, R. S. 2012a, Phys. Rev. E, 86, 066412 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., Klessen, R., & Banerjee, R. 2012b, Phys. Rev. E, 85, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2013, A&A, 560, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2016, ApJ, 827, 109 [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2017, MNRAS, 468, 946 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seta, A., & Federrath, C. 2021, Phys. Rev. Fluids, 6, 103701 [NASA ADS] [CrossRef] [Google Scholar]
- Seymour, N., Huynh, M., Dwelly, T., et al. 2009, MNRAS, 398, 1573 [CrossRef] [Google Scholar]
- Sinha, A., Basu, A., Datta, A., & Chakraborty, A. 2022, MNRAS, 514, 4343 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Jarvis, M. J., Hardcastle, M. J., et al. 2014, MNRAS, 445, 2232 [Google Scholar]
- Smith, D. J. B., Haskell, P., Gürkan, G., et al. 2021, A&A, 648, A6 [EDP Sciences] [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Schinnerer, E., Krause, M., et al. 2017, ApJ, 836, 185 [Google Scholar]
- Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [Google Scholar]
- van der Kruit, P. C. 1971, A&A, 15, 110 [NASA ADS] [Google Scholar]
- van der Kruit, P. C. 1973, A&A, 29, 263 [NASA ADS] [Google Scholar]
- Voelk, H. J. 1989, A&A, 218, 67 [NASA ADS] [Google Scholar]
- Vollmer, B., Soida, M., & Dallant, J. 2022, A&A, 667, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werhahn, M., Pfrommer, C., & Girichidis, P. 2021, MNRAS, 508, 4072 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [Google Scholar]
Appendix A: Radial profiles
In Fig. A.1, the radial profiles of the gas density ngas and the magnetic field strength B are presented. The figure shows the result for the reference galaxy model.
 |
Fig. A.1. Radial profiles of the gas density ngas and the magnetic field strength B. For comparison the CMB equivalent field strength BCMB is shown. Grey vertical lines indicate the characteristic radius Rgal, i.e., they enclose 2Rgal. |
We note that the radial profiles of the magnetic field strength in our model show certain dissimilarities compared to observations of non-thermal radio emission in star-forming galaxies. Observed profiles are naturally more complex than an exponential profile. For example, Beck et al. (2020) reported that the radial variations of radio intensities peaks of M51 between a radius of 8 and 12 kpc, but their scale lengths differ and are on the order of 3 − 4 kpc, depending on the fitting range.
For a better agreement with the observed profiles, our model would need to be extended. First of all, the transport of cosmic ray electrons needs to be implemented, which is challenging. Also, an extension of the magnetic field model would be needed, potentially in the form of a dynamo efficiency factor, fB, that depends on the distance from the center of the galaxy.
Appendix B: Model for the interstellar radiation field
For the thermal interstellar radiation field, we employed a model that includes both a stellar contribution as well as the cosmic microwave background (CMB). To this end, we follow Schleicher & Beck (2013) and scale the energy density of the ISRF with the SFR in a given galaxy:
We note that we have made the assumption that the SFR surface density is given by Ṁ⋆(M⋆,z)Rgal(Ṁ⋆,z)−2. The CMB temperature evolves with redshift as TCMB = 2.73(1 + z) K.
To mimic a stronger radiation field in regions where the SFR is higher, we multiply equation B.1 by a dimensionless weighting factor :
For the typical SFR surface density of a MW-like galaxy we use 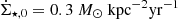 . The function ω(x1, x2, x3) has the same spatial dependence as the SFR density:
. The function ω(x1, x2, x3) has the same spatial dependence as the SFR density:
and the default value of fsISRF is chosen such that the ω(x1, x2, x3) has a value of 1 in the center of the galaxy, namely, fsISRF = 1.
Appendix C: Dependence on resolution and box size
In this section, we discuss the numerical convergence of our results and justify the default values of spatial resolution ℛ and box size L.
The 3D model of the galaxy is set up on a grid and we assume that the gas density has a double exponential profile (see Eq. 6). The quantities relevant to the radio emission, such as the magnetic field strength and the cosmic ray density, are coupled to the gas density and therefore also decrease exponentially with increasing distance from the center of the box. For results that are independent of the numerical model, the value of L needs to be at least larger than the effective radius and scale height, Rgal and Hgal, of the galaxy. There can be, however, significant contributions coming from radio emission at radii larger than Rgal. The default value in our study is L = 10Rgal.
The result of the convergence study is presented in Fig. C.1. There, we plot the value of L1.4 for face-on galaxies with different stellar masses and redshifts. The resolution is increased from ℛ = 15 to ℛ = 200. Different sizes of the numerical domain, namely, L = 5Rgal, L = 10Rgal, and L = 15Rgal, are presented by different colors. The small box sizes converge at the lowest resolution, but generally converges can be expected for ℛ ≳ 100.
 |
Fig. C.1. Rest-frame 1.4 GHz luminosity L1.4 for different box sizes L and resolution ℛ. Here, the default model (see Table 1) of face-on galaxies is used and a convergence analysis at different redshift z and stellar mass M⋆ is present as given in the labels. |
Appendix D: Nonlinearity of the IRRC
The result for fitting the modeled IRRC at different redshifts with the function given in Eq. 50 is presented in Fig. D.1 for the reference model. In agreement with the observational study of Molnár et al. (2021), we find that the IRRC is slightly nonlinear at z = 0. The nonlinearity, that is, the value of the slope m, increases slightly up to z ≈ 1 but decreases at z ≳ 1. Strictly speaking, a linear IRRC is never obtained from our reference model for 0 ≤ z ≤ 5.
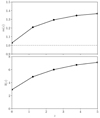 |
Fig. D.1. Results for the fits in the IRRC obtained from the reference model to the function (50). The fitting parameters, m and b, are presented as a function of redshift z. |
The fitting parameter b is found to increase up to z ≈ 2.5 and decreases for higher z. This parameter would correspond to q, in the case of a linear IRRC, i.e. for m = 1.
Appendix E: Comparison to M⋆-agnostic observations of the IRRC
The aim of this study is to understand the origin of the dependence of the IRRC on both redshift z and stellar mass M⋆. To our knowledge, the first observational study on these different dependencies was presented by Delvecchio et al. (2021) and we compare our phenomenological model to their data set. However, an extensive amount of literature on the evolution of the IRRC on z exists and we present the comparison between other, M⋆ agnostic, observational studies with our model in this appendix.
In Fig. E.1, our reference model is compared to results from different studies in which the stellar mass dependence is not explicitly considered (Bell 2003; Magnelli et al. 2015; Delhaize et al. 2017; Ocran et al. 2020; Sinha et al. 2022) as well as with the Delvecchio et al. (2021) data. At z = 0, observational results presented in Fig. E.1 agree well with both the Delvecchio et al. (2021) data and our reference model. For increasing z, the majority of observational studies predict a decrease in q. This can be interpreted as an observational bias caused by the fact that galaxies with smaller M⋆ fall below the sensitivity limit at lower z compared to more massive galaxies. This leads to an increase in the average M⋆ in a given galaxy sample with z and, according to our model, to a systematic decrease in the average q value.
 |
Fig. E.1. Comparison of the (face-on) reference model with other observational results that do not include the dependence of q on the stellar mass. The lines of the observational relations are shown over the redshift ranges of the individual data sets. The short vertical line at the q axis indicates the value of q = 2.64 ± 0.02 obtained by Bell (2003) from observations of local star-forming galaxies. |
All Tables
All Figures
 |
Fig. 1. Overview of the model for the radio and far-infrared emission with which the q parameter can be calculated. The input parameters, redshift z and total stellar mass M⋆, are shown on the left and the final output is the q parameter that combines 1.4 GHz luminosity L1.4 and the rest-frame 8 − 1000 μm luminosity LIR. For the galactic scale height, Hgal, different scenarios are considered which is indicated by the dashed lines; see Sect. 2.1.3. Free parameters of the model are highlighted by yellow boxes and their default values are listed in Table 1. See Sect. 2 for details of the model. |
| In the text | |
 |
Fig. 2. Input relations for the reference galaxy model (see Table 2). Upper panel: mean density in the central region of the galaxy obtained from integrating Eq. (8). Middle panel: total SFR from Eq. (2) shown by dotted lines and the SFR in the core region of the galaxy obtained from integrating Eq. (9) shown by solid lines. Lower panel: mean magnetic field strength in the core region of the galaxy obtained from integrating Eq. (14) with the default value fB = 0.1. |
| In the text | |
 |
Fig. 3. Energy (left ordinate) and Lorentz factor (right ordinate) of CR electrons that contribute mostly to the synchrotron emission at different observing frequencies νobs and different magnetic field strengths B; see Eq. (33). |
| In the text | |
 |
Fig. 4. Cooling timescales of CR electrons in a slice through the center of galaxies with different stellar masses, M⋆, (top to bottom panels) and different redshifts, z (left to right panels). The value of γe used in this plot corresponds to the one at which CR electrons contribute mostly to the synchrotron emission at 1.4 GHz, i.e., at which νc = νobs = 1.4 GHz; see Eq. (32). The total timescale, τe, (solid lines) has contributions from bremsstrahlung (τbrems, dashed lines), synchrotron losses (τsynch, dotted lines), inverse Compton losses (τIC, dashed-dotted lines), and ionization losses (τion, dashed-dotted-dotted lines). Grey vertical lines indicate the characteristic radius Rgal, i.e., they enclose 2Rgal. |
| In the text | |
 |
Fig. 5. Rest-frame spectral luminosities at different redshifts for galaxies that are observed face-on. Different colors indicate results from models with different stellar masses: M⋆ = 109 M⊙ (blue), M⋆ = 1010 M⊙ (green), and M⋆ = 1011 M⊙ (red). Different linestyles refer to different emission types: the total radio emission Lν (solid lines) depends on the free-free luminosity |
| In the text | |
 |
Fig. 6. Analysis of radio spectra at ν = 1.4 GHz. The top panel shows the ratio of non-thermal ( |
| In the text | |
 |
Fig. 7. Radio luminosity L1.4 as a function of the IR luminosity LIR. Top: solid dots show the result using the default parameters of the model (with αCR = 3.0). The different colors are models with different stellar masses M⋆, according to the color bar. The data in the background are local observations of Molnár et al. (2021). The lines show the results of different fits to the reference model (see Eq. (50)). The model predictions for different cosmic ray spectral indexes, αCR = 2.8 and αCR = 3.2, are shown for comparison. Bottom: model predictions for L1.4 and LIR for αCR = 3.0 at different redshifts as indicated but the marker size (smallest to biggest: z = 0 − 5). Different symbols indicate different treatments of absorption (circles: face-on observation, diamonds: edge-on observation). |
| In the text | |
 |
Fig. 8. q parameter as defined in Eq. (1) versus redshift z. Top: lines show the results of our reference galaxy model and the stars with grey contours are observations (AGN-corrected values from Delvecchio et al. 2021). Colors refer to different stellar masses M⋆ as indicated by the color bar. For solid lines the galaxies are observed face-on and for dashed lines edge-on. Shaded regions indicate the standard deviation. Bottom: difference between the observed values of qobs and the corresponding model predictions qmod. The errors include only the uncertainties of the observational data. |
| In the text | |
 |
Fig. 9. q parameter as a function of redshift, z, for galaxies with different stellar mass, M⋆, as given in the colorbar. The reference model compared to the observed data set of Delvecchio et al. (2021) is presented in the middle panel. In panels from left to right, the magnetic field strength in the model is increased; see the discussion around Eq. (14) for the parameters fB and fturb. From bottom to top, the ionization degree is increased via the parameter fion which affects the free-free emission; see Sect. 2.3.2. |
| In the text | |
 |
Fig. 10. q parameter as a function of redshift, z, for galaxies with different stellar mass, M⋆, as given in the colorbar. The reference model compared to the observed data set of Delvecchio et al. (2021) is presented in the middle panel. From left to right, the slope of the CR injection spectrum gets steeper via the parameter αCR; see Eq. (15). From bottom to top, the number of CR protons in the model is increased via the parameters fπ, fCR, and fsec; see Eq. (22). |
| In the text | |
 |
Fig. 11. Different dependence of the galactic radius on stellar mass (by variation of αgal, see Eq. (4)) compared to the reference model (αgal = 0.05). |
| In the text | |
 |
Fig. 12. Different models of the galactic scale height Hgal compared to the reference model. Top:Hgal scales with the characteristic galactic radius Rgal as modeled in Eq. (4). Bottom: model in which Hgal increases with redshift. |
| In the text | |
 |
Fig. 13. Extension of the reference model to high z. |
| In the text | |
 |
Fig. 14. Model predictions for galaxy populations in which the free parameters have a range of values. Top: model predictions for a galaxy population, which on average has the parameters of our reference model, but in which fturb, fCR, fB, fπ, fsec, fion and fsISRF vary randomly with up to ±25% scatter around the default values. Bottom: model predictions for a galaxy population with parameters that match the ones of of the reference model, except for the value of αCR. Here, a galaxy population with 1.75 ≤ αCR ≤ 3.25 is considered which results in 0.4 ≲ α1.4 ≲ 1.3. |
| In the text | |
 |
Fig. A.1. Radial profiles of the gas density ngas and the magnetic field strength B. For comparison the CMB equivalent field strength BCMB is shown. Grey vertical lines indicate the characteristic radius Rgal, i.e., they enclose 2Rgal. |
| In the text | |
 |
Fig. C.1. Rest-frame 1.4 GHz luminosity L1.4 for different box sizes L and resolution ℛ. Here, the default model (see Table 1) of face-on galaxies is used and a convergence analysis at different redshift z and stellar mass M⋆ is present as given in the labels. |
| In the text | |
 |
Fig. D.1. Results for the fits in the IRRC obtained from the reference model to the function (50). The fitting parameters, m and b, are presented as a function of redshift z. |
| In the text | |
 |
Fig. E.1. Comparison of the (face-on) reference model with other observational results that do not include the dependence of q on the stellar mass. The lines of the observational relations are shown over the redshift ranges of the individual data sets. The short vertical line at the q axis indicates the value of q = 2.64 ± 0.02 obtained by Bell (2003) from observations of local star-forming galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



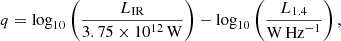
![$$ \begin{aligned}&\mathrm{log} _{10}\left[\frac{\dot{M}_\star (M_\star ,z)}{M_\odot \,\mathrm{yr} ^{-1}}\right] = m - m_0 + a_0 r \nonumber \\&\qquad \qquad \qquad \qquad - a_1 \left[\mathrm{max} (0, m - m_1 - a_2 r) \right]^2, \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq8.gif)
![$$ \begin{aligned} \mathrm{log} _{10}\left[\frac{M_\mathrm{gas} (M_\star ,z)}{M_\odot }\right] = \alpha _{2,\mathrm{SFR} } + \beta _2 \, \mathrm{log} _{10}\left[\frac{\dot{M}_\star (M_\star ,z)}{M_\odot \, \mathrm{yr} ^{-1}}\right]. \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq9.gif)
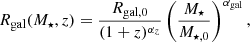
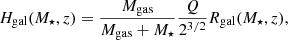
![$$ \begin{aligned} \rho _\mathrm{gas} (x_1,x_2,x_3)&= \rho _\mathrm{gas,c} \left[ \mathrm{exp} \left(-\frac{(x_1^2+x_2^2)^{1/2}}{R_\mathrm{gal} } \right) \mathrm{exp} \left(-\frac{x_3}{H_\mathrm{gal} } \right)\right],\nonumber \\ \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq12.gif)
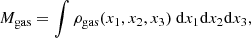
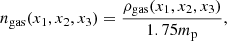
![$$ \begin{aligned} \dot{\rho }_\star (x_1,x_2,x_3)&= \dot{\rho }_{\star ,\mathrm{c} } \left[ \mathrm{exp} \left(-\frac{(x_1^2+x_2^2)^{1/2}}{R_\mathrm{gal} } \right) \mathrm{exp} \left(-\frac{x_3}{H_\mathrm{gal} } \right)\right]^{n_\mathrm{SFR} }, \nonumber \\ \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq17.gif)
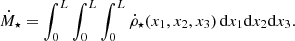
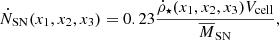
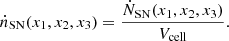
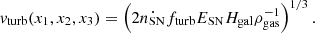
![$$ \begin{aligned}&B(x_1,x_2,x_3) = \left[f_{\rm B} ~ 8\pi ~\frac{1}{2} \rho _\mathrm{gas} \left(v_\mathrm{turb} \right)^2\right]^{1/2} \nonumber \\&\qquad \qquad \quad = \left( 4\pi f_{\rm B} \right)^{1/2} \left(2 \dot{n_\mathrm{SN} } f_\mathrm{turb} E_\mathrm{SN} H_\mathrm{gal} \right)^{1/3} \rho _\mathrm{gas} ^{1/6}. \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq28.gif)
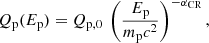
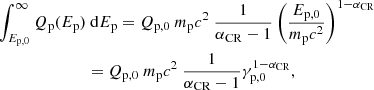
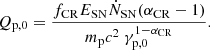
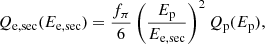
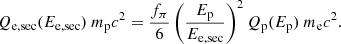
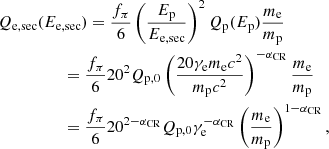
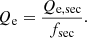
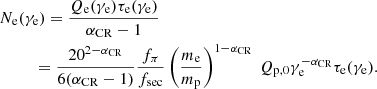
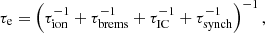
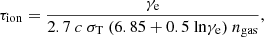
![$$ \begin{aligned}&\tau _\mathrm{brems} = \frac{1}{4 \alpha _\mathrm{em} r_0^2 c n_\mathrm{ion} \beta _{\rm e}} \left[\mathrm{ln} (2\gamma _{\rm e}) -\frac{1}{3}\right]^{-1} , \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq44.gif)
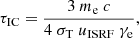
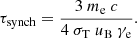
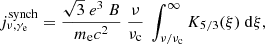
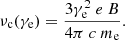
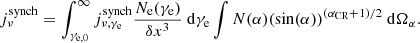
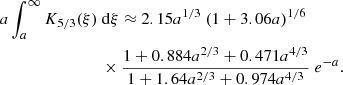
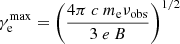
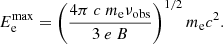
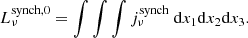
![$$ \begin{aligned} \kappa ^{\mathrm{SSA} }_\nu = - \frac{c^2}{8 \pi m_{\rm e} c^2 \nu ^2} \int _1^\infty j^\mathrm{synch} _\nu \gamma _{\rm e}^2 \frac{\mathrm{d} }{\mathrm{d} \gamma _{\rm e}} \left[\frac{N_{\rm e}(\gamma _{\rm e})}{\gamma _{\rm e}^2}\right] ~\mathrm{d} \gamma _{\rm e}, \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq59.gif)
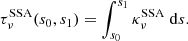
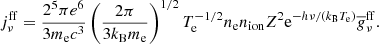
![$$ \begin{aligned} \overline{g}^\mathrm{ff} _\nu = \frac{\sqrt{3}}{\pi } \mathrm{ln} \left[ \frac{1}{4\xi ^{5/2}Z} \left(\frac{k_\mathrm{B} T_{\rm e}}{ h \nu }\right) \left(\frac{k_\mathrm{B} T_{\rm e}}{ 13.6\,\mathrm{eV} }\right)^{0.5} \right], \end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq63.gif)
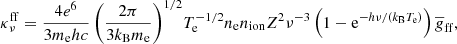
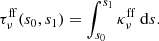
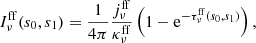
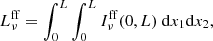
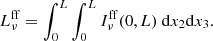
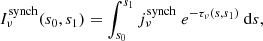
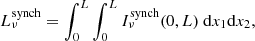
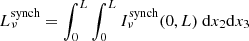
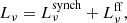
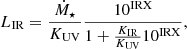
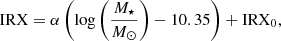
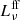
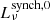
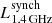
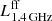
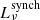
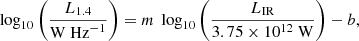
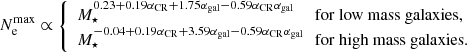
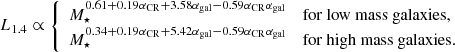
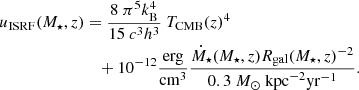
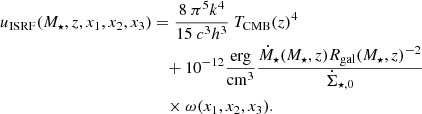
![$$ \begin{aligned} \omega (x_1,x_2,x_3) = f_\mathrm{sISRF} \left[ \mathrm{exp} \left(-\frac{(x_1^2+x_2^2)^{1/2}}{R_\mathrm{gal} } \right) \mathrm{exp} \left(-\frac{x_3}{H_\mathrm{gal} } \right)\right]^{n_\mathrm{SFR} } ,\end{aligned} $$](/articles/aa/full_html/2023/11/aa45218-22/aa45218-22-eq127.gif)