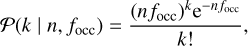| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 20 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346476 | |
| Published online | 13 September 2023 | |
The GAPS programme at TNG
XLVI. Deep search for low-mass planets in late-dwarf systems hosting cold Jupiters★,★★
1
INAF – Osservatorio Astrofisico di Torino,
via Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: matteo.pinamonti@inaf.it
2
Observatoire de Genève, Université de Genève,
51 Chemin des Maillettes,
1290
Sauverny, Switzerland
3
INAF – Osservatorio Astronomico di Palermo,
piazza del Parlamento 1,
I-90134
Palermo, Italy
4
INAF – Osservatorio Astrofisico di Catania,
via S. Sofia 78,
95123
Catania, Italy
5
INAF – Osservatorio Astronomico di Trieste,
via G. B. Tiepolo 11,
34143
Trieste, Italy
6
INAF – Osservatorio Astronomico di Brera,
via E. Bianchi 46,
23807
Merate, Italy
7
INAF – Osservatorio Astronomico di Padova,
vicolo dell’Osservatorio 5,
35122
Padova, Italy
8
Dipartimento di Fisica, Università di Roma “Tor Vergata”,
via della Ricerca Scientifica 1,
00133
Roma, Italy
9
Max Planck Institute for Astronomy,
Kõnigstuhl 17,
69117
Heidelberg, Germany
10
Dipartimento di Fisica e Astronomia, Università di Firenze,
Largo Enrico Fermi 5,
50125
Firenze, Italy
11
Fundación Galileo Galilei – INAF,
Ramble José Ana Fernandez Pérez 7,
38712
Breña Baja, TF, Spain
12
INAF – Osservatorio Astronomico di Roma,
via Frascati 33,
00078
Monte Porzio Catone, Italy
13
Instituto de Astrofísica de Canarias (IAC),
38205
La Laguna, Tenerife, Spain
14
INAF – Osservatorio Astronomico di Capodimonte,
Salita Moiariello 16,
I80131,
Napoli, Italy
15
INAF – Osservatorio di Cagliari,
via della Scienza 5,
I09047
Selargius, Italy
16
Dipartimento di Fisica e Astronomia, Università di Padova,
via Marzolo 8,
35131
Padova, Italy
Received:
21
March
2023
Accepted:
7
June
2023
Context. With the growth of comparative exoplanetology, it is increasingly clear that the relationship between inner and outer planets plays a key role in unveiling the mechanisms governing formation and evolution models. For this reason, it is important to probe the inner region of systems hosting long-period giants in search of undetected lower mass planetary companions.
Aims. We aim to present the results of a high-cadence and high-precision radial velocity (RV) monitoring of three late-type dwarf stars hosting long-period giants with well-measured orbits in order to search for short-period sub-Neptunes (SN, M sin i < 30 M⊕).
Methods. Building on the results and expertise of our previous studies, we carried out combined fits of our HARPS-N data with literature RVs. We used Markov chain Monte Carlo (MCMC) analyses to refine the literature orbital solutions and search for additional inner planets, applying Gaussian process regression techniques to deal with the stellar activity signals where required. We then used the results of our survey to estimate the frequency of sub-Neptunes in systems hosting cold Jupiters, f(SN|CJ), and compared it with the frequency around field M dwarfs, f(SN).
Results. We identify a new short-period, low-mass planet orbiting GJ 328, GJ 328 c, with Pc = 241.8-1.7+1.3 days and Mc sin i = 21.4-3.2+3.4M⊕. We moreover identify and model the chromospheric activity signals and rotation periods of GJ 649 and GJ 849, around which no additional planet is found. Then, taking into account also planetary system around the previously analysed low-mass star BD-11 4672, we derive an estimate of the frequencies of inner planets in such systems. In particular, f(SN|CJ) = 0.25-0.07+0.58 for mini-Neptunes (10 M⊕ < M sin i < 30 M⊕, P < 150 d), marginally larger than f(SN). For lower mass planets (M sin i < 10 M⊕) instead f(SN|CJ) < 0.69, which is compatible with f(SN).
Conclusions. In light of the newly detected mini-Neptune, we find tentative evidence of a positive correlation between the presence of long-period giant planets and that of inner low-mass planets, f(SN|CJ) > f(SN). This might indicate that cold Jupiters have an opposite influence in the formation of inner sub-Neptunes around late-type dwarfs as opposed to their solar-type counterparts, boosting the formation of mini-Neptunes instead of impeding it.
Key words: techniques: radial velocities / stars: individual: GJ 328 / stars: individual: GJ 649 / stars: individual: GJ 849 / stars: activity / planets and satellites: detection
The complete time series of all spectroscopic data used in this work is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A122
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The growing abundance of known exoplanetary systems has fostered an increasing number of comparative studies on their mass distribution and global architecture (Winn & Fabrycky 2015; Hobson & Gomez 2017), many of which focus on the role of multiplicity and architecture in supporting or disproving the current and competing formation models for both giant and terrestrial planets (e.g. Raymond et al. 2008; Cossou et al. 2014; Schlaufman 2014; Morbidelli & Raymond 2016). A key parameter in distinguishing between different formation models is the fraction of planetary systems featuring both gas giants and lower mass planets. A still-debated aspect of planetary formation models is that of the formation of sub-Neptunes in systems hosting long-period giant planets1. If low-mass planets’ embryos form in situ, that is, close to their host star, the presence of an outer giant planet could block the inward flux of pebbles, impeding significant growth of the embryo above ≃1 M⊕, (Lambrechts et al. 2019); this would cause an anti-correlation between the presence of outer giant planets and inner super-Earths, with the important difference that the presence of terrestrial or sub-terrestrial planets would not be significantly affected. On the other hand, other models of in-situ formation of super-Earths require massive protoplanetary discs (Chiang & Laughlin 2013), which would consequently produce a correlated population of giant planets. Instead, in the inward migration model, planetary embryos form in the outer protoplanetary disc and migrate inwards to become hot mini-Neptunes; however, if the innermost embryo grows into a gas-giant planet before starting to migrate, it will block the inward migration of more distant cores, creating a dynamical barrier (Izidoro et al. 2015) and causing an anti-correlation between the gas-giant planets and inner low-mass planets. However, if cold Jupiters originate instead from the more distant cores, the cores formed near the snowline can freely migrate inward (Bitsch et al. 2015). Even in the presence of a giant planet acting as migration barrier, simulations predict that a small fraction of planetary cores could be able to ‘jump’ the obstacle (Izidoro et al. 2015), producing a small population of close-in mini-Neptunes in systems with Jupiter-like planets.
To investigate the occurrence of solar-type stars hosting inner sub-Neptunes in the presence of outer giant planets, Barbato et al. (2018) previously RV monitored 20 bright stars orbited by at least one long-period giant planet with low-to-moderate eccentricity with HARPS at ESO-3.6m in order to search for inner additional lower mass planets and produce a first assessment of their frequency around solar-type stars. However, no convincing evidence of additional inner low-mass planets in the selected systems was found, most probably due to the low number of data collected, limiting the sample completeness for planets below Msini < 30 M⊕. This highlights the importance of collecting a high number of dense observations in order to detect any possible low-mass planet present in the sample. Moreover, the importance of continuing to observe planet-hosting stars that were already the subject of planet-searching radial velocity surveys at high precision and cadence levels has been clearly showcased by the TESS space telescope and its recent discovery of transiting hot super-Earths around stars hosting long-period giant planets (e.g. Gandolfi et al. 2018; Huang et al. 2018; Lillo-Box et al. 2023).
Different previous studies reported a high frequency of cold-Jupiter companions in transiting sub-Neptune systems (Zhu & Wu 2018; Bryan et al. 2019). However, since the observable directly related to the formation models is in fact the frequency of sub-Neptunes in cold-Jupiter systems, f(SN|CJ), these studies might be painting a blurry picture. It is not straightforward to deduce f(SN|CJ) from the opposite measurement f(CJ|SN), that is, the frequency of cold Jupiters in sub-Neptune systems, since its calculation depends on the respective absolute frequencies of both classes of planets, f(CJ) and f(SN). Both Zhu & Wu (2018) and Bryan et al. (2019), assuming f(CJ) and f(SN) from other surveys, obtained f(SN|CJ) ≃ 100%. However, adopting absolute frequencies from other surveys could introduce bias in the calculations, since different samples of stars might not be affected by the same formation and evolution, and thus host different planetary populations with different architectural properties. Even with high-precision RV time series, studies of the frequency of cold Jupiters in systems with known low-mass planets can be biased due to the short temporal baseline of the data. In short time series, long-period companions can only be identified from RV linear trends, which could affect the results due to the inherent degeneracies in such detections; for example, the derived orbital parameters for cold Jupiters identified from the RV trends by Bryan et al. (2019) have very large uncertainties, spanning on average two orders of magnitude in mass and one order of magnitude in semi-major axis.
On the other hand, an estimate of f(SN|CJ) could be computed from systems with known long-period giant planets with well-resolved orbits and would not suffer from the same biases discussed before. Moreover, the measured frequency would be directly comparable with theoretical predictions (e.g. Izidoro et al. 2015), without requiring the use of inferential statistics. However, systematic studies in this direction are scarce in the recent literature (Barbato et al. 2018; Rosenthal et al. 2022).
The observational programme Global Architecture of Planetary Systems (GAPS; Covino et al. 2013; Desidera et al. 2013) aims to investigate the variety and origins of the architecture of exoplanetary systems with the High Accuracy Radial velocity Planet Searcher in the Northern hemisphere (HARPS-N, Cosentino et al. 2012) at the Telescopio Nazionale Galileo (TNG) in La Palma. Within this context, a subset of planethosting late-K and M dwarfs has been selected and observed in order to search for inner super-Earth and mini-Neptune planetary companions to outer long-period giants and assessing the impact of inefficient migration of planets formed beyond the snowline of such dwarf stellar hosts. The size of the sample was limited by the low frequency of giant planets around late-type stars, with only four targets accessible in the northern hemisphere.
In this paper, we present the analyses of three M dwarfs hosting long-period giant planets in the search for inner low-mass planets. This work follows the analysis carried out by Barbato et al. (2020) for the low-mass star BD-11 4672, which is the fourth target observed within the survey. Moreover, we present a statistical analysis of the detection limits of the observed sample, in order to estimate the frequency f(SN|CJ) around late-type dwarfs, following the Bayesian approach adopted in Pinamonti et al. (2022).
The star GJ 328 is a nearby (d = 20 pc) early-M dwarf of type M0. Robertson et al. (2013) detected a long-period (P = 11 yr) 2 Jupiter-mass planet on an eccentric orbit, namely GJ 328 b. At the time of publication, it was the most massive, most distant planet found orbiting a red dwarf star. Robertson et al. (2013) studied the magnetic activity of the star and argued that it produced a significant RV signal with an amplitude of 6–10 m s−1, which was partly masking the eccentricity of GJ 328 b’s orbit. GJ 649 is a nearby (d = 10 pc) M1 dwarf, around which Johnson et al. (2010) detected a Saturn-mass planet (mbsin i = 0.328 MJup) on an eccentric (e = 0.30) 600 days orbit. Johnson et al. (2010) also found evidence of stellar rotation (Prot = 24.8 ± 1.0 d) and long-term magnetic evolution from spectroscopic and photometric monitoring of the star. Finally, GJ 849 is a nearby (d = 8.8 pc) M3.5 dwarf, around which one of the first M-dwarf planets was discovered (Butler et al. 2006): mb sin i = 0.82 MJup, Pb = 1890 ± 130 days. A linear trend was observed in the RV data by Butler et al. (2006), which was later confirmed to be due to an outer planetary companion by Feng et al. (2015), with a minimum mass of mc sin i = 0.944 ± 0.07 MJup and period of Pc = 15.1 ± 0.66 yr. The planets already known from the literature orbiting the targets are shown in Fig. 1.
In Sect. 2, we describe the Doppler measurements of our targets collected for this analysis. We then describe our analyses of the RV data and stellar activity indices of the targets in Sect. 3, following with the description of the adopted technique to derive the detection limits and planetary occurrence rates in Sect. 4, where we also discuss our estimates of the occurrence rates in comparison with the literature. Finally, we summarise our findings in Sect. 5.
 |
Fig. 1 Orbital architecture of known planets in the observed systems. The giant planets in the sample are shown as red circles, with the symbol size proportional to the minimum planetary mass. The yellow circle shows the Neptune-mass planet BD-114672 c (Barbato et al. 2020). The conservative and optimistic limits of the habitable zone of each system (Kopparapu et al. 2013) are shown as thick dark green and light green bands, respectively. |
2 Spectroscopic observations
As part of the GAPS RV programme, the target stars were observed from April 2018 to May 2021 with the HARPS-N spectrograph, connected by fibres to the Nasmyth B focus through a front end unit of the 3.58 m TNG in La Palma, Spain. HARPS-N is a fibre-fed, cross-dispersed echelle spectrograph with a spectral resolution of 115 000, covering a wavelength range from 3830 to 6900 Å (Cosentino et al. 2012). Observations were performed using a fixed integration time of 900 s to obtain data of sufficient per-pixel signal-to-noise ratio (average S/N > 50 at 550 nm) and to average out potential short-term periodic oscillations of the star (Dumusque et al. 2011). As discussed in previous studies of M dwarfs with HARPS-N within the HADES programme (e.g. Affer et al. 2016), the spectra were collected without simultaneous Th–Ar calibration, that could contaminate the Ca II H and K lines, which are an important activity indicator in M dwarfs (Forveille et al. 2009; Lovis et al. 2011). Furthermore, previous analyses proved that no significant instrumental drift is observed, even without simultaneous calibration (Perger et al. 2017; Affer et al. 2019; Pinamonti et al. 2019). The RVs collected within our survey are combined in our analysis with archival public data from different instruments, including those used in the original discovery of the cold Jupiters present in the observed systems. In the following, we discuss in some detail the spectroscopic time series collected for each analysed system.
Whenever available, we used data from the following instruments: the High Resolution Spectrograph (HRS, Tull 1998) on the 9.2 m HET (Ramsey et al. 1998) at McDonald Observatory; the Robert J. Tull Coudé spectrograph (Tull et al. 1995) on McDonald’s 2.7 m Harlan J. Smith Telescope (HJST); the High Resolution Echelle Spectrometer (HIRES, Vogt et al. 1994) spectrograph on the 10 m Keck I telescope at Mauna Kea; the Spectrographe pour l'Observation des Phénomènes des Intérieurs stellaires et des Exoplanètes (SOPHIE, Bouchy et al. 2013) at the 1.93 m OHP telescope; the Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Échelle Spectrographs (CARMENES, Quirrenbach et al. 2014) at the 3.5 m telescope at the Calar Alto Observatory; and the High Accuracy Radial velocity Planet Searcher (HARPS, Mayor et al. 2003) at the ESO La Silla 3.6m telescope. Details on the data used for each system are discussed in the respective subsections. The complete time series of all spectroscopic data used in this work is available at the CDS.
We derived HARPS-N and HARPS RVs adopting the template-matching approach of the Template-Enhanced Radial velocity Re-analysis Application (TERRA, Anglada-Escudé & Butler 2012), which has proven to be more effective than the standard CCF techniques in the analysis of M-dwarf spectra (Affer et al. 2016; Perger et al. 2017). Moreover, in order to avoid the low-signal-to-noise-ratio (S/N) blue part of the M dwarf’s spectra, we computed the TERRA RVs considering only spectral orders redder than λ > 440 nm (Anglada-Escudé & Butler 2012), corresponding to the 22nd and 18th order for HARPS and HARPS-N, respectively.
We derived the stellar parameters of the three targets following the procedure by Maldonado et al. (2017). We also derived the log 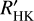 following the procedures to extend its definition to M dwarfs (Suárez Mascareño et al. 2016 and references therein). All the derived stellar parameters, along with the relevant astrometric and photometric information of the targets, are listed in Table 1.
following the procedures to extend its definition to M dwarfs (Suárez Mascareño et al. 2016 and references therein). All the derived stellar parameters, along with the relevant astrometric and photometric information of the targets, are listed in Table 1.
2.1 GJ 328
As part of the GAPS survey, GJ 328 was observed from BJD = 2458213.4 (4 April 2018) to BJD = 2459345.4 (10 May 2021) with the HARPS-N spectrograph. The total number of data points acquired was 131 over a time span of 1132 days. The mean internal error of the TERRA HARPS-N data is 0.97 m s−1, and the rms is 11.57 m s−1. We additionally retrieved public RV measurements of GJ 328 from HET/HRS, Keck/HIRES, HJST/Tull, the same used for the detection of GJ 328 b (Robertson et al. 2013). In addition to these data, we collected public RV measurements collected from OHP/SOPHIE (Moultaka et al. 2004). The details of the adopted literature time series are listed in Table 2. Combining all the data, we obtain a time series of 206 RVs, spanning 6700 days, from BJD = 2452645.8 (6 January 2003) to BJD = 2459345.4 (10 May 2021), with a mean internal error of σ = 3.0 m s−1 and an rms of 17.4 m s−1, as reported in the final line of Table 2.
Moreover, in order to measure the stellar activity of GJ328, we computed the stellar activity indexes based on the Ca II H and K, Hα, Na I D1 D2, and He I D3 spectral lines, applying the procedure described in Gomes da Silva et al. (2011) to all the available HARPS-N spectra. Robertson et al. (2013) found clues of a long-period activity cycle in the time series of the Na I D1 D2 activity index and used it to correct the stellar noise in the RV data. For this reason, we collected the activity index data from the HRS spectra used in their analysis, paying particular attention to the time series of Na I D1 D2 derived from our HARPS-N spectra. We derived the Na I D1 D2 activity index using both a 0.5 Å window and a 1 Å window, as Robertson et al. (2013) stated that the stellar magnetic behaviour of GJ328 was best measured by adopting a 1 Å window, as opposed to the standard recipe (Gomes da Silva et al. 2011). We avoided using CCF-based activity indicators, such as the BIS or FWHM, since the CCF of M dwarfs is usually heavily distorted and difficult to reliably measure (Rainer et al. 2020).
2.2 GJ 649
The star GJ 649 was observed with HARPS-N from BJD = 2458213.6 (5 April 2018) to BJD = 2459130.3 (8 October 2020), for a total of 147 spectra over a time span of 917 days. The mean internal error of the TERRA HARPS-N data is 0.76 m s−1, and the rms is 7.88 m s−1. We collected public Keck/HIRES RV measurements of GJ 649 from the California Legacy Survey catalogue (Rosenthal et al. 2021), as well as public CARMENES RV measurements from CARMENES GTO DR1 (Ribas et al. 2023). The details of all the adopted RV time series are listed in Table 3. Combining the data together, we obtain a time series of 269 RVs, spanning 7720 days, from BJD = 2451409.8 (19 August 1999) to BJD = 2459130.3 (8 October 2020), with mean internal error of σ = 1.11 m s−1, and an rms of 7.75 m s−1, as reported in the final line of Table 3. We also computed the stellar Ca II H and K, Hα, Na I D1 D2, and He I D3 activity indexes from the HARPS-N spectra, as detailed in the previous section.
Stellar parameters of the observed targets.
RV time series of GJ328.
2.3 GJ 849
The star GJ 849 was observed with HARPS-N from BJD = 2458269.7 (31 May 2018) to BJD = 2459213.3 (29 December 2020) for a total of 94 spectra over a time span of 944 days. The mean internal error of the TERRA HARPS-N data is 0.81 m s−1, and the rms is 13.50 m s−1. We collected public Keck/HIRES RV measurements of GJ 849 from the California Legacy Survey catalogue (Rosenthal et al. 2021) and public HARPS spectra from the ESO archive (ESO programs 072.C-0488(E) and 183.C-0437(A)), from which we computed the RVs using TERRA. Moreover, we collected public CARMENES RV measurements from CARMENES GTO DR1 (Ribas et al. 2023). The details of all the adopted RV time series are listed in Table 4. Combining the data together, we obtain a time series of 323 RVs, spanning 8607 days, from BJD = 2450606.1 (6 June 1997) to BJD = 2459213.3 (29 December 2020), with a mean internal error of 1.39 m s−1 and an rms of 17.87 m s−1, as reported in the final line of Table 4. We also computed the stellar Ca II H and K, Hα, Na I D1 D2, and He I D3 activity indexes from the HARPS-N and HARPS spectra, as detailed in Sect. 2.1.
RV time series of GJ 649.
3 Spectroscopic time-series analyses
In this section, we discuss the analyses of the RV and activity time series of the three targets of the sample in detail. In all analyses, the identification of periodic signals in a time series is performed via generalised Lomb-Scargle periodograms (GLS, Zechmeister & Kürster 2009). The complete fits of stellar and planetary signals are instead performed via a Markov chain Monte Carlo (MCMC) method; this technique was applied via the emcee Affine Invariant MCMC Ensemble sampler by Foreman-Mackey et al. (2013). We modelled the RV time series with multi-Keplerian models, depending on the number of planets present in each system, taking into account linear RV trends when necessary and separate offset and jitter terms for each of the data-collecting instruments. This general model can be expressed by the following equation:
where γinstr represents each instrument’s RV offset, 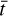 is the mean epoch of the time series, Np is the number of planets in the system, and ΔRVKep,j(t) is the Keplerian RV term of the jth planet as a function of the orbital parameters as follows:
is the mean epoch of the time series, Np is the number of planets in the system, and ΔRVKep,j(t) is the Keplerian RV term of the jth planet as a function of the orbital parameters as follows:
In addition to the general model in Eq. (1), we tested an additional long-term RV acceleration component, d(t – 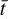 ), to determine the presence of possible long-term trends due to stellar cycles and very-long-period additional companions. This term would be added to the model whenever statistically favoured. To compare different models and select the statistically favoured one, we adopted the Bayesian information criterion (BIC, Schwarz 1978).
), to determine the presence of possible long-term trends due to stellar cycles and very-long-period additional companions. This term would be added to the model whenever statistically favoured. To compare different models and select the statistically favoured one, we adopted the Bayesian information criterion (BIC, Schwarz 1978).
Moreover, in order to model and subtract stellar activity signals in the RV data, when present, we employed the Gaussian process (GP) regression technique. We adopted the most common kernel to model stellar activity signals (e.g. Haywood et al. 2014; Affer et al. 2016; Pinamonti et al. 2019), that is, the Quasi-Periodic (QP) kernel:
where Ki,j is the ij element of the covariance matrix, and the covariance is described by four hyper-parameters. h is the amplitude of the correlation, λ is the timescale of decay of the exponential correlation, θ is the period of the periodic component, and w is the weight of the periodic component. The last term of Eq. (3) describes the white noise component of the covariance matrix, where δi,j is the Kronecker delta and σ is the RV total uncertainty defined as 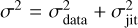 , with σdata being the internal error of the data and σjit the uncorrelated jitter fitted by the MCMC model.
, with σdata being the internal error of the data and σjit the uncorrelated jitter fitted by the MCMC model.
Due to the HIRES CCD upgrade that occurred in August 2004, whenever HIRES data were used in the RV analyses, we considered the data before and after the upgrade as two independent datasets. For each HIRES dataset, we computed independent offset and jitter terms, to avoid zero-point errors (Pinamonti et al. 2018 and references therein).
RV time series of GJ 849.
 |
Fig. 2 GJ 328: best-fit RV one-planet model, corrected for the instrumental offsets and RV residuals (top panel), GLS periodogram of the RV residuals (bottom panel). |
3.1 GJ 328
As a first test in the study of the GJ 328 system, we used our combined RV time series to fit the known planet’s signal in order to see how the newly taken HARPS-N observations affect its orbital parameters. We modelled the combined datasets with a single-Keplerian model, as specified by Eq. (1) with Np = 1.
From this 1-Keplerian model, we obtained an amplitude of 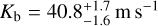 and a period of
and a period of 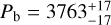 days, in agreement (~1σ) with the values reported by Robertson et al. (2013). The complete resulting best-fit parameters of this model are listed in Table A.1, and the best-fit model is shown Fig. 2a, after correcting for the instrumental offsets. We tested the addition of a linear trend to the model, but the resulting acceleration was not strongly significant (
days, in agreement (~1σ) with the values reported by Robertson et al. (2013). The complete resulting best-fit parameters of this model are listed in Table A.1, and the best-fit model is shown Fig. 2a, after correcting for the instrumental offsets. We tested the addition of a linear trend to the model, but the resulting acceleration was not strongly significant (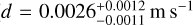 d−1, i.e. 2.4σ), it was strongly correlated with the HARPS-N offset, γHARPS-N, and did not increase the BIC, ΔBIC ≃ 0. In Fig. 2b, we can see the GLS periodogram of the RV residuals after subtracting the one-planet model, which is dominated by a significant peak false alarm probability (FAP) ≪ 0.1% at around 227 d, with a strong alias at 242 d. Figure 3 shows the window function structure of the P = 242 days peak, which shows a strong alias at Δf = 0.00025 day−1 corresponding to P = 227 days: this is caused by the large gap between the SOPHIE and HARPS-N observations. We can also see the one-year alias at Δf = 0.0027 d−1 corresponding to P = 145 days. This signal was not previously reported in the original analysis by Robertson et al. (2013), and thus we check the HARPS-N activity indicators time series of GJ 328 to ascertain its nature: Fig. 4 shows the GLS periodogram of the activity indexes. The Ca II and Hα periodograms show prominent peaks at around 35–40 days, which are probably related to the rotation period of the star. Applying the activity–rotation relationships for early-M dwarfs by Suárez Mascareño et al. (2018), we obtain an estimate of
d−1, i.e. 2.4σ), it was strongly correlated with the HARPS-N offset, γHARPS-N, and did not increase the BIC, ΔBIC ≃ 0. In Fig. 2b, we can see the GLS periodogram of the RV residuals after subtracting the one-planet model, which is dominated by a significant peak false alarm probability (FAP) ≪ 0.1% at around 227 d, with a strong alias at 242 d. Figure 3 shows the window function structure of the P = 242 days peak, which shows a strong alias at Δf = 0.00025 day−1 corresponding to P = 227 days: this is caused by the large gap between the SOPHIE and HARPS-N observations. We can also see the one-year alias at Δf = 0.0027 d−1 corresponding to P = 145 days. This signal was not previously reported in the original analysis by Robertson et al. (2013), and thus we check the HARPS-N activity indicators time series of GJ 328 to ascertain its nature: Fig. 4 shows the GLS periodogram of the activity indexes. The Ca II and Hα periodograms show prominent peaks at around 35–40 days, which are probably related to the rotation period of the star. Applying the activity–rotation relationships for early-M dwarfs by Suárez Mascareño et al. (2018), we obtain an estimate of 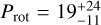 days, which is compatible with the observed peaks in the Ca II and Hα periodograms. Moreover, the Ca II time series is dominated by strong long-term periodicities at ≃300 days and ≃1300 days; these additional periodic signals may be related to a long-term magnetic cycle of the star; however, it is difficult to confirm as the current HARPS-N data cover less than one full 1300 days cycle. We tested for correlation between the HARPS-N activity time-series and the RVs, and found no significant correlation (|ρ| < 0.3). Finally, we can see, no significant peak is found near the 227–242 days periods identified in the RVs.
days, which is compatible with the observed peaks in the Ca II and Hα periodograms. Moreover, the Ca II time series is dominated by strong long-term periodicities at ≃300 days and ≃1300 days; these additional periodic signals may be related to a long-term magnetic cycle of the star; however, it is difficult to confirm as the current HARPS-N data cover less than one full 1300 days cycle. We tested for correlation between the HARPS-N activity time-series and the RVs, and found no significant correlation (|ρ| < 0.3). Finally, we can see, no significant peak is found near the 227–242 days periods identified in the RVs.
We then tested the coherency of the 227–242 days periodicity over time by means of a stacked Bayesian GLS (BGLS, Mortier & Collier Cameron 2017), as Keplerian signals should always increase in strength, while stellar signals grow stronger and weaker over time due to their evolving nature. Figure 5 shows the stacked BGLS of GJ 328 RVs after subtracting the long-period planet model, starting from the beginning of HARPS-N observations; we can see how the strength of the peaks at 227–242 days increases steadily throughout the observations.
We then proceeded to model the RV time series with a two-Keplerian model, taking into account both the known 3700 days planet and the new 227–242 days signal. This was done by adding another Keplerian signal ΔRVKep,2(t) to Eq. (2). The model favoured the 242 days period as the best fit of the data, with 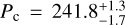 days and
days and 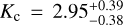 m s−1. Figure 6 shows how the MCMC fit strongly favoured the Pc = 242 days solution in the posterior distribution due to its higher likelihood. We thus adopted that as the true signal’s period, considering 227 days to be its alias. To test the significance of the eccentricity of this new signal, we performed two separate analyses: one fixing the eccentricity to ec = 0 and one leaving it free. All the best-fit parameters of these models are listed in Table A.1. The addition of a second signal to the model produces a significant decrease of the BIC, ΔBIC ≃ −40, confirming the presence of the additional signal in the RV data. Moreover, there is a significant improvement in the BIC of the tested two-Keplerian ec = 0 model (ΔBIC ≃ −8), and we thus adopted it as the best model to describe GJ 328’s time series. The computed eccentricity in the eccentric model,
m s−1. Figure 6 shows how the MCMC fit strongly favoured the Pc = 242 days solution in the posterior distribution due to its higher likelihood. We thus adopted that as the true signal’s period, considering 227 days to be its alias. To test the significance of the eccentricity of this new signal, we performed two separate analyses: one fixing the eccentricity to ec = 0 and one leaving it free. All the best-fit parameters of these models are listed in Table A.1. The addition of a second signal to the model produces a significant decrease of the BIC, ΔBIC ≃ −40, confirming the presence of the additional signal in the RV data. Moreover, there is a significant improvement in the BIC of the tested two-Keplerian ec = 0 model (ΔBIC ≃ −8), and we thus adopted it as the best model to describe GJ 328’s time series. The computed eccentricity in the eccentric model, 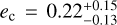 , is not significant (1.7σ), and it corresponds to an upper limit of ec < 0.28 from the 68th percentile of the posterior distribution.
, is not significant (1.7σ), and it corresponds to an upper limit of ec < 0.28 from the 68th percentile of the posterior distribution.
Robertson et al. (2013) suggested the presence of a long-period magnetic cycle in GJ 328 activity data. The authors found a 2000 days periodicity in the Na I D1 D2 HRS time series, measuring a ρ = 0.41 correlation with the HRS RVs, and they then proceeded to correct the influence of the magnetic cycles via a linear fit of the RV-activity dependence. We tested the presence of this magnetic cycle, both in our newly acquired HARPS-N data and in the archival spectroscopic data. The Na I activity index was not available for HIRES and Tull data, so we only studied the HRS and HARPS-N data. Figure 7 shows the Na I time series and correlation with the respective RVs for the two instruments. As shown in the bottom part of the figure, we measure a Pearson correlation coefficient of ρ = 0.39 and ρ = 0.08 for HRS and HARPS-N data, respectively. We find no evidence of a strong correlation, in particular in the HARPS-N data. We also tested the Na I activity index computed from HARPS-N spectra following the Robertson et al. (2013) recipe, again finding no significant correlation: ρ = −0.03. Moreover, as shown in Fig. 4, the HARPS-N Na I time series does not show any long-term periodic signal. We thus find no evidence of the 2000 days magnetic cycle reported by Robertson et al. (2013), and we decided not to take it into account in our modelling of GJ 328’s planetary signals. As an additional precaution, we reproduced our one-Keplerian model of the RV data after correcting the HRS RVs following the linear fit with Na I proposed in Robertson et al. (2013), and we found no significant difference (<1σ) in the resulting planetary parameters.
As an additional test on the presence of stellar noise in the RV time series, we performed an additional MCMC fit including a GP component, to model possible stellar signals in the data. The resulting amplitude of the stellar GP component was consistent with 0, and the model was statistically disfavoured (ΔBIC ≃ −10). We thus see no evidence of stellar signals in the RV data.
We thus confirm that the 242 days RV signal is best explained by the presence of an additional planetary companion, hereafter GJ 328 c, a sub-Neptune of minimum-mass 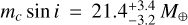 . The best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. The phase-folded RV curves of the two planetary signals are shown in Fig. 8. It is worth noting in Fig. 8b that the model of GJ 328 c closely follows the HARPS-N RV data, while the other time series are widely spread due to the large uncertainties and jitters (see Table A.1). No significant signal was identified in the GLS periodogram of the RV residuals of the two-Keplerian model.
. The best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. The phase-folded RV curves of the two planetary signals are shown in Fig. 8. It is worth noting in Fig. 8b that the model of GJ 328 c closely follows the HARPS-N RV data, while the other time series are widely spread due to the large uncertainties and jitters (see Table A.1). No significant signal was identified in the GLS periodogram of the RV residuals of the two-Keplerian model.
 |
Fig. 3 GJ 328: window function GLS periodogram structure of the P = 242 days signal. |
3.2 GJ 649
At first, we used our combined RV time series to test and update the one-Keplerian model corresponding to the known planet GJ 649 b signal, following Eqs. (1) and (2) as previously discussed. The best-fit model and GLS periodogram of the RV residuals are shown in Figs. 9a and b, respectively, while the complete set of adopted priors and best-fit parameters is listed in Table A.2. We did not include an acceleration term, d, in Eq. (1) as its inclusion in the model decreased the statistical significance of the model (higher BIC) and resulted in a best-fit acceleration compatible with zero (<2σ). From this fit, we obtain an amplitude of 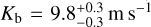 , a period of
, a period of 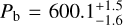 days, and an eccentricity of
days, and an eccentricity of 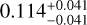 ; it is worth noting that, while the measured period is compatible within 1σ with the value reported by Johnson et al. (2010), the amplitude and the eccentricity are smaller (≃2σ) than their values. Moreover, as we can see in Fig. 9b, the periodogram of the residuals shows a significant peak at around 12 d. This period is close to half the stellar rotation period measured by Johnson et al. (2010), Prot = 24.8 ± 1.0 days, and later confirmed by Díez Alonso et al. (2019), Prot = 23.8 ± 0.1 days. This leads us to suspect it is in fact a harmonic of the stellar rotation period caused by chromo-spheric activity. This stellar rotation period is confirmed by the GLS analyses of the HARPS-N activity indicators (not shown), which identify strong ~24 days periodicities in the Ca II and Hα time series.
; it is worth noting that, while the measured period is compatible within 1σ with the value reported by Johnson et al. (2010), the amplitude and the eccentricity are smaller (≃2σ) than their values. Moreover, as we can see in Fig. 9b, the periodogram of the residuals shows a significant peak at around 12 d. This period is close to half the stellar rotation period measured by Johnson et al. (2010), Prot = 24.8 ± 1.0 days, and later confirmed by Díez Alonso et al. (2019), Prot = 23.8 ± 0.1 days. This leads us to suspect it is in fact a harmonic of the stellar rotation period caused by chromo-spheric activity. This stellar rotation period is confirmed by the GLS analyses of the HARPS-N activity indicators (not shown), which identify strong ~24 days periodicities in the Ca II and Hα time series.
To confirm the stellar origin of the 12 days RV signal, we applied the GP regression as described in Eq. (3). As listed in Table A.2, we adopted a broad uniform prior for the hyperparameter 9, which corresponds to the stellar rotation period, 𝒰(10,50) days, in order to include both the identified periodicity of 12 days and the expected stellar rotation period of 24 days. The GP model converged to 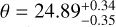 days, and the 12 days signal disappeared from the RV residuals, proving it was in fact produced by the chromospheric activity of the target. Our measured value of 9 confirms the 24 days rotation period measured in the literature. It is also worth highlighting that, contrary to the claim by Johnson et al. (2010), we do not find a significant orbital eccentricity in our final model (
days, and the 12 days signal disappeared from the RV residuals, proving it was in fact produced by the chromospheric activity of the target. Our measured value of 9 confirms the 24 days rotation period measured in the literature. It is also worth highlighting that, contrary to the claim by Johnson et al. (2010), we do not find a significant orbital eccentricity in our final model (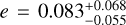 ), which could mean that the apparent eccentricity measured in their fit was due to the sub-optimal sampling of the original RV time series, as well as to the lack of stellar activity correction. The other orbital parameters do not vary significantly between the two fits with and without GP modelling of the stellar activity (see Table A.2). All the best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. The full details of the model are shown in Appendix A. The phase-folded RV signal of GJ 649 b and quasi-periodic stellar model obtained from the simultaneous GP + 1 planet fit are shown in Figs. 10a and b, respectively. No additional signal is found in GLS periodograms of the residuals, and thus we adopted the Keplerian + GP model as the best fit to GJ 649’s RV time series.
), which could mean that the apparent eccentricity measured in their fit was due to the sub-optimal sampling of the original RV time series, as well as to the lack of stellar activity correction. The other orbital parameters do not vary significantly between the two fits with and without GP modelling of the stellar activity (see Table A.2). All the best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. The full details of the model are shown in Appendix A. The phase-folded RV signal of GJ 649 b and quasi-periodic stellar model obtained from the simultaneous GP + 1 planet fit are shown in Figs. 10a and b, respectively. No additional signal is found in GLS periodograms of the residuals, and thus we adopted the Keplerian + GP model as the best fit to GJ 649’s RV time series.
 |
Fig. 4 GJ 328: GLS periodograms of HARPS-N activity indexes computed following the procedure by Gomes da Silva et al. (2011). The red dotted vertical lines indicate the 227–242 days period of the signals identified in the RV residuals. The horizontal lines indicate the FAP levels as in Fig. 2b. |
 |
Fig. 5 GJ 328: stacked BGLS of RV residuals after subtracting GJ 328 b model. The blue dashed line marks the 242 days periodicity identified in the data. |
3.3 GJ 849
To recover and update the orbital RV signals of GJ 849 b and c, we fitted a two-Keplerian model via our emcee setup on the combined RV time series of GJ 849, expressed by Eq. (1) with Np = 2. As in the previous section, we did not include an acceleration term, d, in the RV model, as it resulted in a higher BIC and a best-fit acceleration ≃0.
The best-fit model and GLS periodogram of the RV residuals are shown in Figs. 11a and b, respectively, while the complete set of adopted priors and best-fit parameters is listed in Table A.3. Our results confirm, within the error bars, the minimum masses computed by Feng et al. (2015) for the two planets, as well as the orbital period of GJ 849 b, while we find a marginally longer orbital period for GJ849 c with respect to Feng et al. (2015; <2σ). Moreover, we confirm the low values of the orbital eccentricities of the two planets, and thus also the dynamical stability of the system (Feng et al. 2015).
The residuals show a significant periodic signal at P = 20 days (see Fig. 11b). This short-period signal could be related to the stellar rotation period of GJ 849; Suárez Mascareño et al. (2015) measured a rotation period of Prot = 39.2 ± 6.3 days from the activity indicators derived from 42 HARPS spectra, and the periodic signal we observe in the RV residuals is close to Prot/2. We tested this by analysing the activity indices derived from all the available HARPS and HARPS-N spectra. The GLS periodogram of both Ca II H and K and Hα time series (not shown) are dominated by periodic signals at both ≃22 days and ≃40 days, which support the measured Prot by Suárez Mascareño et al. (2015) and confirm the presence of a strong harmonic signal at Prot/2.
To confirm the stellar nature of the RV short-period signal, we applied the GP regression on the complete RV time series of GJ 849, adopting the quasi-periodic kernel described in Eq. (3). We adopted a large uninformative prior for the rotation period, 9, 𝒰(10,50) in order to include both the ≃20 days and ≃40 days periodicities identified in the RV residuals and activity indices. This fit results in a clear rotation period of 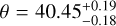 days, confirming the measurement by Suárez Mascareño et al. (2015), and the quasi-periodic model completely absorbs the 20 days signal seen in the previous residuals, confirming that it was related to stellar activity. The phase-folded signals of the two planets are shown in Figs. 12a and b, the quasi-periodic stellar model is shown in Fig. 13, and the full details of the model and results are discussed in Appendix A. After correcting the stellar activity via GP regression, we found no significant difference in the orbital parameters of the two planets with respect to the previous fit. The best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. No additional signal is identified in the RV residuals after the subtraction of the planetary and stellar signals.
days, confirming the measurement by Suárez Mascareño et al. (2015), and the quasi-periodic model completely absorbs the 20 days signal seen in the previous residuals, confirming that it was related to stellar activity. The phase-folded signals of the two planets are shown in Figs. 12a and b, the quasi-periodic stellar model is shown in Fig. 13, and the full details of the model and results are discussed in Appendix A. After correcting the stellar activity via GP regression, we found no significant difference in the orbital parameters of the two planets with respect to the previous fit. The best-fit orbital parameters of the planetary signals in the final MCMC model are listed in Table 5. No additional signal is identified in the RV residuals after the subtraction of the planetary and stellar signals.
 |
Fig. 6 GJ 328: comparison of Pc = 227 days and Pc = 242 days signals in the two-Keplerian model, shown as the histogram of the posterior distribution of Pc (top panel), and the log-likelihood as a function of Pc (bottom panel). |
4 Detection limits and planetary occurrence rates
Although our sample of late-type stars hosting cold Jupiters is limited to four targets, we use it to estimate the planetary occurrence rate in such systems, with a particular focus on the frequency of short-period sub-Neptunes. We do this following the Bayesian approach adopted by Pinamonti et al. (2022), which takes advantage of the emcee framework described above to compute the detection limits of the RV time series. For a complete description of the statistical approach, we invite the reader to consult Sect. 3 of Pinamonti et al. (2022) and references therein.
We computed the detection limits for the three targets analysed in this work, as well as for BD-114672 (Barbato et al. 2020). The resulting average detection map is shown in Fig. 14.
Given the detectability function, p, the planetary occurrence rate, ƒocc, expressed as the number of planets per star, can be computed from the Poisson distribution:
where k is the number of detected planets, and the expected value is computed as the product between n, the number of targets sensitive to planets, and ƒocc.
To compute meaningful occurrence rates to test the influence of cold Jupiters on inner low-mass planet formation, we have to exactly define the intervals in the parameter space corresponding to the definition of inner low-mass planet. Unfortunately, the literature on the subject is quite inconsistent, with different definitions being used by different authors, such as M < 10 M⊕, a < 1 AU (Zhu & Wu 2018), 10 M⊕ < M sin i < 30 M⊕, P < 150 days (Barbato et al. 2018), M < 10 M⊕, a < 0.5 AU (Bryan et al. 2019), 2 M⊕ < M sin i < 30 M⊕, 0.023 < a < 1 AU (Rosenthal et al. 2022). We take the definitions from Barbato et al. (2018) and Bryan et al. (2019) as references as they cover two adjacent ranges of mass and similar period intervals, and we define them hereafter as mini-Neptunes and super-Earths, respectively. These two intervals are depicted in Fig. 142. For the mini-Neptune interval, in which one planet was detected around our sample, we obtain an occurrence rate of 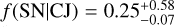 , while for the super-Earth bin in which no planet was detected we obtain a 68% upper limit of ƒ(SN|CJ) < 0.64.
, while for the super-Earth bin in which no planet was detected we obtain a 68% upper limit of ƒ(SN|CJ) < 0.64.
To test whether and how the presence of cold Jupiters has a significant effect on the frequency of inner sub-Neptunes, we have to compare the computed occurrence rates with the respective values computed for a sample of field-M dwarfs of similar spectral type, ƒ(SN). We adopted the HADES sample of early-M dwarfs as a reference sample (Pinamonti et al. 2022), as it is composed of field M dwarfs of similar masses to our sample of Jupiter-hosting stars. We can thus compute the frequencies of mini-Neptunes and super-Earths around field M dwarfs, which are 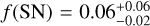 and
and 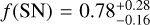 respectively.
respectively.
The derived estimates of the occurrence rate of inner sub-Neptunes in late-type systems hosting cold Jupiters show some interesting features; most notably, we can see that for mini-Neptunes (10 M⊕ < M sin i < 30 M⊕) ƒ(SN|CJ) > ƒ(SN) at a 2σ level. Although not strongly significant, this could be an indication that mini-Neptunes are more frequent around late-type stars hosting long-period giant planets, and that a positive correlation exists between the two populations. This is all the more interesting considering that previous studies on solar-type stars observed an opposite behaviour. Barbato et al. (2018), studying a sample of 20 solar cold-Jupiter hosts, found an upper limit to the frequency of mini-Neptunes of ƒ(SN|CJ) < 9.84%, which is significantly lower than the occurrence rates for field solar-type stars: ƒ(SN) = 38.8 ± 7.1% (Mayor et al. 2011).
Considering instead super-Earths (M sin i < 10 M⊕), we notice that while we detected no planet with such characteristics orbiting our targets, the corrected occurrence rate ƒ(SN|CJ) could still be compatible with the field frequency ƒ(SN), being different by only ≃1.2σ due to the large uncertainties on the derived upper limit of ƒ(SN|CJ). Although not significant, this is again a very different behaviour than what has been observed in the literature for solar-type stars, since Bryan et al. (2019) derived a much higher frequency of sub-Neptunes in systems hosting long-period giant planets, ƒ(SN|CJ) ≫ ƒ(SN)3.
Considering the other definition intervals from the literature (Zhu & Wu 2018; Rosenthal et al. 2022), the observed behaviours do not change significantly. Computing the occurrence rates for inner super-Earths as defined by Zhu & Wu (2018), we obtain ƒ(SN|CJ) < 0.76, compatible with the respective 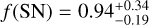 (1.2σ). On the other hand, following the definition adopted by Rosenthal et al. (2022) that includes both high- and low-mass inner companions, we derive
(1.2σ). On the other hand, following the definition adopted by Rosenthal et al. (2022) that includes both high- and low-mass inner companions, we derive 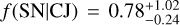 , which is higher than but compatible with the corresponding field occurrence rate of
, which is higher than but compatible with the corresponding field occurrence rate of 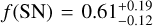 . It is worth pointing out that our results suggest a strong difference in the behaviour of late-type and solar-type systems hosting long-period giant planets. This highlights once again the importance of considering the host mass in planetary population studies (e.g. Gaidos et al. 2016; Sabotta et al. 2021; Pinamonti et al. 2022), and underlines the risks of drawing conclusions on planetary populations from heterogeneous samples of stars of different masses and spectral types (e.g. Bryan et al. 2019; Rosenthal et al. 2022).
. It is worth pointing out that our results suggest a strong difference in the behaviour of late-type and solar-type systems hosting long-period giant planets. This highlights once again the importance of considering the host mass in planetary population studies (e.g. Gaidos et al. 2016; Sabotta et al. 2021; Pinamonti et al. 2022), and underlines the risks of drawing conclusions on planetary populations from heterogeneous samples of stars of different masses and spectral types (e.g. Bryan et al. 2019; Rosenthal et al. 2022).
 |
Fig. 7 GJ 328: time series of the Na I D1 D2 activity index computed from HRS (upper left) and HARPS-N (upper right). Correlation between the RV and Na I activity index computed for HRS (lower left) and HARPS-N (lower right) data. |
Best-fit orbital parameters for the planets in the studied systems.
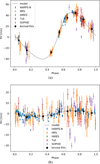 |
Fig. 8 GJ 328: phase-folded RV signal of GJ 328 b (upper panel) and GJ 328 c (lower panel). The black points and error bars represent the binned weighted averages and standard deviations of the data. |
 |
Fig. 9 GJ 649: best-fit RV one-planet model, corrected for the instrumental offsets and RV residuals (top panel), and GLS periodogram of the RV residuals (bottom panel). |
5 Discussion and conclusions
We present the RV monitoring of three early-M dwarfs hosting long-period giant planets, carried out within the GAPS programme. We detect one new low-mass planet around GJ 328, GJ328c, with a period of 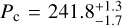 days and a minimum mass of
days and a minimum mass of 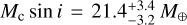 . This is a mini-Neptune in the mass range we were looking for, although on a slightly longer orbital period. The other two observed systems, GJ 649 and GJ 849, also show short-period RV variability, but we confirm it to be caused by the stellar chromospheric activity, measuring a rotation period of
. This is a mini-Neptune in the mass range we were looking for, although on a slightly longer orbital period. The other two observed systems, GJ 649 and GJ 849, also show short-period RV variability, but we confirm it to be caused by the stellar chromospheric activity, measuring a rotation period of 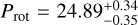 days and
days and 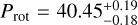 days for GJ 649 and GJ 849, respectively. We correctly model the activity signals via GP regression and found no evidence of additional planetary companions in those systems.
days for GJ 649 and GJ 849, respectively. We correctly model the activity signals via GP regression and found no evidence of additional planetary companions in those systems.
Moreover, we updat the orbital parameters of the known cold Jupiters orbiting in these systems. For GJ328 b, we obtain a lower eccentricity than the original values (Robertson et al. 2013), although this difference is not strongly significant (≃2.7σ).
On the other hand, the period and minimum mass are consistent with the literature. For GJ 649 b we find no evidence of the eccentric orbit, e = 0.3, reported by Johnson et al. (2010) and, after the activity correction, find that the orbital eccentricity is consistent with 0. Finally, for the GJ 849 system, the GP activity correction confirms the updated orbital parameters of GJ 849 b derived by Feng et al. (2015), and improves the precision on the orbit of GJ 849 c.
We then perform a Bayesian analysis of the three systems presented in this work and BD-11 4672 (Barbato et al. 2020) in order to estimate the unbiased occurrence rate of low-mass inner planets around late-type stars hosting cold Jupiters. We derive a frequency of 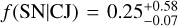 for mini-Neptunes (10 M⊕ < M sin i < 30 M⊕, P < 150 d), which is marginally higher than the frequency for field stars f(SN) (2σ) and might thus be an indication of a positive correlation between the population of cold Jupiters and mini-Neptunes around late-type stars, contrary to what is observed for solar-type stars. With no planet detected with M sin i < 10 M⊕, we measure an upper limit to the frequency of super-Earths f(SN|CJ) < 0.64, which is compatible with the corresponding occurrence rate around field M dwarfs. This is again different than what observed for solar-type stars, where the occurrence rate of super-Earths appears to be boosted by the presence of outer cold Jupiters, although the exact magnitude of this effect is still debated in the literature (e.g. Bryan et al. 2019; Rosenthal et al. 2022). These results, although limited by the size of our sample, suggest that the formation of hierarchical systems around late-type stars follow a different path than around solar-type stars, as the influence of long-period giant planets appears to be the opposite for the two classes of stars. This adds another piece to the puzzle of the dependence of planetary formation on the characteristics of the host stars, in particular on the mass, which is known to greatly influence the resulting frequency of planets both in size and orbital separation.
for mini-Neptunes (10 M⊕ < M sin i < 30 M⊕, P < 150 d), which is marginally higher than the frequency for field stars f(SN) (2σ) and might thus be an indication of a positive correlation between the population of cold Jupiters and mini-Neptunes around late-type stars, contrary to what is observed for solar-type stars. With no planet detected with M sin i < 10 M⊕, we measure an upper limit to the frequency of super-Earths f(SN|CJ) < 0.64, which is compatible with the corresponding occurrence rate around field M dwarfs. This is again different than what observed for solar-type stars, where the occurrence rate of super-Earths appears to be boosted by the presence of outer cold Jupiters, although the exact magnitude of this effect is still debated in the literature (e.g. Bryan et al. 2019; Rosenthal et al. 2022). These results, although limited by the size of our sample, suggest that the formation of hierarchical systems around late-type stars follow a different path than around solar-type stars, as the influence of long-period giant planets appears to be the opposite for the two classes of stars. This adds another piece to the puzzle of the dependence of planetary formation on the characteristics of the host stars, in particular on the mass, which is known to greatly influence the resulting frequency of planets both in size and orbital separation.
We stress that our results, although interesting, are limited by the small number of observed objects (4). Although there is an intrinsic physical limitation in analyses such as ours, due to the low frequency of cold Jupiters around M dwarfs (Clanton & Gaudi 2014)4, a few additional similar systems are present in the literature and could be added to the sample to improve the statis-tics5. However, including these systems in the statistics would require additional observations to enhance the sensitivity of the RV time series of such additional targets down to super-Earth masses, and thus is beyond the scope of this current work, the aim of which is to present the data and results of our survey.
The objective of the presented survey was the intensive monitoring of the four observed late-K to M dwarfs hosting known long-period giant planets, in order to allow the detection of low-mass planets in inner orbits. We detect new sub-Neptunes around two of the targets, BD-11 4672 c (Barbato et al. 2020) and GJ 328 c, and exclud the presence of additional short-period companions around the other two targets down to super-Earth masses. Comparing our sensitivity to the previous HARPS solar survey, Barbato et al. (2020) achieved detection completeness over their 20-star sample for masses of M sin i > 30 M⊕ for periods below 50 days and for masses of M sin i > 50 M⊕ for periods below 150 days; considering the same period thresholds, over our sample we are sensitive to masses of M sin i > 15 M⊕ for periods below 50 days and masses of M sin i > 20 M⊕ for periods below 150 days. This highlights the importance of high-cadence, high-precision RV observations in the study of low-mass short-period planets.
We plan additional observations of other late-type stars, from K to M, some of which are already ongoing with HARPS-N at TNG and FIES at NOT. Moreover, within the GAPS programme a survey of 19 solar-type host of cold Jupiters was conducted over the recent years, producing the detection of a close-in super-Earth around HD 164922 (Benatti et al. 2020), and additional detections yet to be published. The thorough discussion of the frequencies of small mass planets around cold-Jupiter hosts of different spectral types, from these surveys and future observations, will be the content of future works.
 |
Fig. 10 GJ 649. Upper panel: phase-folded RV signal of GJ 649 b (as in Fig. 8), after subtracting the stellar correlated signal. Lower panel: best-fit stellar quasi-periodic signal obtained from the GP + 1 planet model (black line) compared to the RV residuals. |
 |
Fig. 11 GJ 849. Upper panel: best-fit two-Keplerian model of GJ 849 b and c corrected for the instrumental offsets, and RV residuals. Lower panel: GLS periodogram of RV residuals. |
 |
Fig. 12 GJ 849. Upper panel: phase-folded RV signal of GJ 849 b, after subtracting the stellar correlated signal. Lower panel: phase-folded RV signal of GJ 849 c, after subtracting the stellar correlated signal. |
 |
Fig. 13 GJ 849. Upper panel: best-fit stellar quasi-periodic signal obtained from the GP + one-Keplerian model (black line) compared to RV residuals. Lower panel: close-up view of CARMENES and HARPS-N time series. |
 |
Fig. 14 Survey detection map. The grey scale expresses the global detection function, p. The red circles mark the position in the parameter space of the known cold Jupiters (see Fig. 1), while the yellow circles indicate the short-period planet detected in this study and that discovered by Barbato et al. (2020). The orange and red dashed contours show the definitions of inner mini-Neptunes by Barbato et al. (2018) and super-Earths by Bryan et al. (2019). |
Acknowledgements
G.A.P.S. acknowledges support from INAF through the ‘Progetti Premiali’ funding scheme of the Italian Ministry of Education, University, and Research. The HARPS-N Project is a collaboration between the Astronomical Observatory of the Geneva University (lead), the CfA in Cambridge, the Universities of St. Andrews and Edinburgh, the Queen’s University of Belfast, and the TNG-INAF Observatory. We acknowledge support from the PRIN-INAF 2019 “Planetary systems at young ages (PLATEA)”, ASI-INAF agreement no. 2018-16-HH.0, and ASI-INAF no. 2021-5-HH.0 “Partecipazione italiana alla fase B2/C della missione Ariel”. M.Pi. acknowledges the financial support from the ASI-INAF Addendum no. 2018-24-HH.1-2022 “Partecipazione italiana al Gaia DPAC – Operazioni e attività di analisi dati”. D.B. acknowledges the financial support of the National Centre for Competence in Research PlanetS of the Swiss National Science Foundation (SNSF). L.M. acknowledges support from the “Fondi di Ricerca Scientifica d’Ateneo 2021” of the University of Rome “Tor Vergata”. D.N. acknowledges the support from the French Centre National d’Etudes Spatiales (CNES). The HARPS-N Project is a collaboration between the Astronomical Observatory of the Geneva University (lead), the CfA in Cambridge, the Universities of St. Andrews and Edinburgh, the Queen’s University of Belfast, and the TNG-INAF Observatory. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This research has made use of data retrieved from the SOPHIE archive at Observatoire de Haute-Provence (OHP), available at http://atlas.obs-hp.fr/sophie. This research has made use of observations made with ESO Telescopes at the La Silla Paranal Observatory under programmes IDs 072.C-0488(E) and 183.C-0437(A). M.Pi. and D.B. also wish to thank A. Baglio, G. Storti, G. Poretti, and M. Massironi for their inspirational work in precision mechanics and advanced technology.
Appendix A emcee priors, posteriors, and best-fit parameters
In this section, we report the priors and best-fit parameters for all the tested models on the analysed systems and all the posterior distributions. Tab. A.1 lists the information for the three models tested on the GJ 328 RV time series, and Fig. A.1 shows the posterior distributions of the fitted parameters in the final two-Keplerians (ec = 0) model. Tab. A.2 lists the details of the models tested on the GJ 649 RV time series, and Fig. A.2 shows the posterior distributions of the final Keplerian + GP model. Tab. A.3 lists the priors and best-fit parameters of the models applied to GJ 849 RV data, and the posterior distributions of the final two-Keplerian + GP model are shown in Fig. A.3.
GJ 328: Priors and best-fit parameters for the tested MCMC models.
 |
Fig. A.1 GJ 328: Posterior distributions of fitted parameters of the two-Keplerian (ec = 0) model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The parameters shown are, in order, kb, Pb, T0b, eb, ωb, γHARPS-N, σjit,HARPS-N, γHRS, σjit,HRS, γHIRES, σjit,HIRES, γTull, σjit, Tull, γSOPHIE, σjit,SOPHIE, kc, Pc, and T0c. |
GJ 649: Priors and best-fit parameters for the tested MCMC models.
 |
Fig. A.2 GJ 649: Posterior distributions of fitted parameters of the Keplerian + GP model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The shown parameters are, in order, Kb, Pb, T0b, eb, ωb, γHARPS-N, σjit,HARPS-N, γHIRES-pre, σjit,HIRES-pre, γHIRES-post, σjit,HIRES-post, γCARMENES, σjit,CARMENES, h, λ, w, and θ. |
GJ 849: Priors and best-fit parameters for the tested MCMC models.
 |
Fig. A.3 GJ 849: Posterior distributions of fitted parameters of the two-Keplerian + GP model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The shown parameters are, in order, h, λ, w, θ, γHIRES-pre, σjit,HIRES-pre, γHIRES-post σjit,HIRES-post γHARPS-N, σjit,HARPS-N, γHARPS, σjit,HARPS, γCARMENES, σjit,CARMENES, Kb, Pb, T0b, eb, ωb, Kc, Pc, T0c, ec, and ωc. |
References
- Affer, L., Micela, G., Damasso, M., et al. 2016, A&A, 593, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Affer, L., Damasso, M., Micela, G., et al. 2019, A&A, 622, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [Google Scholar]
- Barbato, D., Sozzetti, A., Desidera, S., et al. 2018, A&A, 615, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbato, D., Pinamonti, M., Sozzetti, A., et al. 2020, A&A, 641, A68 [EDP Sciences] [Google Scholar]
- Benatti, S., Damasso, M., Desidera, S., et al. 2020, A&A, 639, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Dumusque, X., Massa, A., et al. 2023, A&A, 677, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Díaz, R. F., Hébrard, G., et al. 2013, A&A, 549, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryan, M. L., Knutson, H. A., Lee, E. J., et al. 2019, AJ, 157, 52 [Google Scholar]
- Butler, R. P., Johnson, J. A., Marcy, G. W., et al. 2006, PASP, 118, 1685 [Google Scholar]
- Chiang, E., & Laughlin, G. 2013, MNRAS, 431, 3444 [Google Scholar]
- Clanton, C., & Gaudi, B. S. 2014, ApJ, 791, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Proc. SPIE, 8446, Ground-based and Airborne Instrumentation for Astronomy IV, 84461V [Google Scholar]
- Cossou, C., Raymond, S. N., Hersant, F., & Pierens, A. 2014, A&A, 569, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Desidera, S., Sozzetti, A., Bonomo, A. S., et al. 2013, A&A, 554, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díez Alonso, E., Caballero, J. A., Montes, D., et al. 2019, A&A, 621, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Lovis, C., Udry, S., & Santos, N. C. 2011, in IAU Symp., 276, The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 530 [Google Scholar]
- Feng, Y. K., Wright, J. T., Nelson, B., et al. 2015, ApJ, 800, 22 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaidos, E., Mann, A. W., Kraus, A. L., & Ireland, M. 2016, MNRAS, 457, 2877 [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A&A, 619, A10 [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [Google Scholar]
- Hobson, M. J., & Gomez, M. 2017, New A, 55, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018, ApJ, 868, L39 [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., Hersant, F., & Pierens, A. 2015, ApJ, 800, L22 [Google Scholar]
- Johnson, J. A., Howard, A. W., Marcy, G. W., et al. 2010, PASP, 122, 149 [NASA ADS] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Gandolfi, D., Armstrong, D. J., et al. 2023, A&A, 669, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Maldonado, J., Scandariato, G., Stelzer, B., et al. 2017, A&A, 598, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv: 1109.2497] [Google Scholar]
- Morbidelli, A., & Raymond, S. N. 2016, J. Geophys. Res. (Planets), 121, 1r962 [Google Scholar]
- Mortier, A., & Collier Cameron, A. 2017, A&A, 601, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Perger, M., García-Piquer, A., Ribas, I., et al. 2017, A&A, 598, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinamonti, M., Damasso, M., Marzari, F., et al. 2018, A&A, 617, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinamonti, M., Sozzetti, A., Giacobbe, P., et al. 2019, A&A, 625, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinamonti, M., Sozzetti, A., Maldonado, J., et al. 2022, A&A, 664, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Proc. SPIE, 9147, Ground-based and Airborne Instrumentation for Astronomy V, 91471F [Google Scholar]
- Rainer, M., Borsa, F., & Affer, L. 2020, Exp. Astron., 49, 73 [Google Scholar]
- Ramsey, L. W., Adams, M. T., Barnes, T. G., et al. 1998, SPIE Conf. Ser., 3352, 34 [Google Scholar]
- Raymond, S. N., Barnes, R., & Mandell, A. M. 2008, MNRAS, 384, 663 [Google Scholar]
- Ribas, I., Reiners, A., Zechmeister, M., et al. 2023, A&A, 670, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, P., Endl, M., Cochran, W. D., MacQueen, P. J., & Boss, A. P. 2013, ApJ, 774, 147 [Google Scholar]
- Rosenthal, L. J., Fulton, B. J., Hirsch, L. A., et al. 2021, ApJS, 255, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, L. J., Knutson, H. A., Chachan, Y., et al. 2022, ApJS, 262, 1 [Google Scholar]
- Sabotta, S., Schlecker, M., Chaturvedi, P., et al. 2021, A&A, 653, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlaufman, K. C. 2014, ApJ, 790, 91 [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., & González Hernández, J. I. 2016, A&A, 595, A12 [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., et al. 2018, A&A, 612, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tull, R. G. 1998, SPIE Conf. Ser., 3355, 387 [Google Scholar]
- Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, SPIE Conf. Ser., 2198, 362 [NASA ADS] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, W., & Wu, Y. 2018, AJ, 156, 92 [Google Scholar]
Hereafter, we adopt a broad definition of ‘sub-Neptune’ commonly used in the literature, i.e. M sin i < 30 M⊕, that encompasses planets commonly referred to as mini-Neptunes (10 M⊕ < M sin i < 30 M⊕) and super-Earths (M sin i < 10 M⊕). Moreover, we define long-period giant planets, or cold Jupiters, as planets with semi-major axes of a > 1 AU and M sin i > 0 .1 MJ.
We emphasise, however, that more recent studies are not confirming the high, ∼100% frequencies derived by Bryan et al. (2019; e.g. Rosenthal et al. 2022; Bonomo et al. 2023).
Although some preliminary analyses on RV long-term trends suggest that the frequency could be higher (Pinamonti et al. (2022) and references therein).
All Tables
All Figures
 |
Fig. 1 Orbital architecture of known planets in the observed systems. The giant planets in the sample are shown as red circles, with the symbol size proportional to the minimum planetary mass. The yellow circle shows the Neptune-mass planet BD-114672 c (Barbato et al. 2020). The conservative and optimistic limits of the habitable zone of each system (Kopparapu et al. 2013) are shown as thick dark green and light green bands, respectively. |
| In the text | |
 |
Fig. 2 GJ 328: best-fit RV one-planet model, corrected for the instrumental offsets and RV residuals (top panel), GLS periodogram of the RV residuals (bottom panel). |
| In the text | |
 |
Fig. 3 GJ 328: window function GLS periodogram structure of the P = 242 days signal. |
| In the text | |
 |
Fig. 4 GJ 328: GLS periodograms of HARPS-N activity indexes computed following the procedure by Gomes da Silva et al. (2011). The red dotted vertical lines indicate the 227–242 days period of the signals identified in the RV residuals. The horizontal lines indicate the FAP levels as in Fig. 2b. |
| In the text | |
 |
Fig. 5 GJ 328: stacked BGLS of RV residuals after subtracting GJ 328 b model. The blue dashed line marks the 242 days periodicity identified in the data. |
| In the text | |
 |
Fig. 6 GJ 328: comparison of Pc = 227 days and Pc = 242 days signals in the two-Keplerian model, shown as the histogram of the posterior distribution of Pc (top panel), and the log-likelihood as a function of Pc (bottom panel). |
| In the text | |
 |
Fig. 7 GJ 328: time series of the Na I D1 D2 activity index computed from HRS (upper left) and HARPS-N (upper right). Correlation between the RV and Na I activity index computed for HRS (lower left) and HARPS-N (lower right) data. |
| In the text | |
 |
Fig. 8 GJ 328: phase-folded RV signal of GJ 328 b (upper panel) and GJ 328 c (lower panel). The black points and error bars represent the binned weighted averages and standard deviations of the data. |
| In the text | |
 |
Fig. 9 GJ 649: best-fit RV one-planet model, corrected for the instrumental offsets and RV residuals (top panel), and GLS periodogram of the RV residuals (bottom panel). |
| In the text | |
 |
Fig. 10 GJ 649. Upper panel: phase-folded RV signal of GJ 649 b (as in Fig. 8), after subtracting the stellar correlated signal. Lower panel: best-fit stellar quasi-periodic signal obtained from the GP + 1 planet model (black line) compared to the RV residuals. |
| In the text | |
 |
Fig. 11 GJ 849. Upper panel: best-fit two-Keplerian model of GJ 849 b and c corrected for the instrumental offsets, and RV residuals. Lower panel: GLS periodogram of RV residuals. |
| In the text | |
 |
Fig. 12 GJ 849. Upper panel: phase-folded RV signal of GJ 849 b, after subtracting the stellar correlated signal. Lower panel: phase-folded RV signal of GJ 849 c, after subtracting the stellar correlated signal. |
| In the text | |
 |
Fig. 13 GJ 849. Upper panel: best-fit stellar quasi-periodic signal obtained from the GP + one-Keplerian model (black line) compared to RV residuals. Lower panel: close-up view of CARMENES and HARPS-N time series. |
| In the text | |
 |
Fig. 14 Survey detection map. The grey scale expresses the global detection function, p. The red circles mark the position in the parameter space of the known cold Jupiters (see Fig. 1), while the yellow circles indicate the short-period planet detected in this study and that discovered by Barbato et al. (2020). The orange and red dashed contours show the definitions of inner mini-Neptunes by Barbato et al. (2018) and super-Earths by Bryan et al. (2019). |
| In the text | |
 |
Fig. A.1 GJ 328: Posterior distributions of fitted parameters of the two-Keplerian (ec = 0) model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The parameters shown are, in order, kb, Pb, T0b, eb, ωb, γHARPS-N, σjit,HARPS-N, γHRS, σjit,HRS, γHIRES, σjit,HIRES, γTull, σjit, Tull, γSOPHIE, σjit,SOPHIE, kc, Pc, and T0c. |
| In the text | |
 |
Fig. A.2 GJ 649: Posterior distributions of fitted parameters of the Keplerian + GP model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The shown parameters are, in order, Kb, Pb, T0b, eb, ωb, γHARPS-N, σjit,HARPS-N, γHIRES-pre, σjit,HIRES-pre, γHIRES-post, σjit,HIRES-post, γCARMENES, σjit,CARMENES, h, λ, w, and θ. |
| In the text | |
 |
Fig. A.3 GJ 849: Posterior distributions of fitted parameters of the two-Keplerian + GP model applied to the RV time series. The vertical dashed lines denote the median and the 16th and 84th percentiles. The shown parameters are, in order, h, λ, w, θ, γHIRES-pre, σjit,HIRES-pre, γHIRES-post σjit,HIRES-post γHARPS-N, σjit,HARPS-N, γHARPS, σjit,HARPS, γCARMENES, σjit,CARMENES, Kb, Pb, T0b, eb, ωb, Kc, Pc, T0c, ec, and ωc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



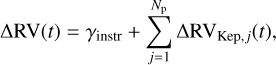
![${\rm{\Delta }}R{V_{{\rm{Kep}}}}\left( t \right) = K\left[ {\cos \left( {v\left( {t,e,{T_0},P} \right) + \omega } \right) + e\,{\rm{cos}}\left( \omega \right)} \right].$](/articles/aa/full_html/2023/09/aa46476-23/aa46476-23-eq8.png)
![${K_{i,j}} = {h^2} \cdot \exp \,\left[ { - {{{{\left( {{t_i} - {t_j}} \right)}^2}} \over {2{\lambda ^2}}} - {{{{\sin }^2}\left( {{{\pi \left( {{t_i} - {t_j}} \right)} \mathord{\left/ {\vphantom {{\pi \left( {{t_i} - {t_j}} \right)} \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)} \over {2{w^2}}}} \right] + {\sigma ^2} \cdot {\delta _{i,j}},$](/articles/aa/full_html/2023/09/aa46476-23/aa46476-23-eq10.png)