EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A168 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A168
Number of page(s) 11
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/202346359
Published online 22 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Adaptive optics (AO) for astronomy is a well-developed technique that is meant to compensate for the effects of atmospheric distortion. Currently, several instruments in the 8 m-class telescope are assisted by this technique: i.e., SPHERE (Beuzit et al. 2019), MUSE+GALACSI (Hartke et al. 2020), ERIS (Davies et al. 2023), OSIRIS (Larkin et al. 2006), KAPA (Wizinowich et al. 2022), SCEXAO (Currie et al. 2020), LUCI (Heidt et al. 2018), however, this is not an exhaustive list. The next generation of optical and infrared instruments for ground-based telescopes will also be equipped with AO modules to improve the image quality of the scientific instruments (i.e., Davies et al. 2021; Ciliegi et al. 2021; Thatte et al. 2021; Hammer et al. 2021; Brandl et al. 2021; Marconi et al. 2021; Crane et al. 2018; Bouchez et al. 2018, again, this is not exhaustive list). While the current generation of AO systems generally includes a Shack–Hartmann wavefront sensor (SHS, Hartmann 1900), most of the future single conjugate AO (SCAO) systems are designed with a pyramid wavefront sensor (PWFS, Ragazzoni 1996). This sensor exhibits a better sensitivity than the SHS as shown in Vérinaud (2004) and proved on sky to produce a high level of wavefront correction on a large range of natural guide star (NGS) magnitudes (see Esposito et al. 2010; Pinna et al. 2019).

One of the key characteristics of the PWFS is the ability to tune the sensitivity and the linearity range through tip-tilt modulation. In current SCAO systems, the PWFS is used with a tip-tilt modulation radius of a few λ/D (where λ is the sensing wavelength and D is the telescope diameter) to increase the linearity range of the sensor at the cost of a reduced sensitivity. In Esposito & Riccardi (2001), it was shown that the wavefront reconstruction error variance for a non-modulated PWFS is higher than the one of a modulated PWFS, except in cases of low flux and small input variance levels. These and similar results (see e.g., Bertrou-Cantou et al. 2022) have persuaded the designers of AO PWFS-based systems to discard the non-modulated configuration. However, the non-modulated PWFS, as demonstrated in Vérinaud (2004), is able (in principle) and excluding non-linearity, to correct almost perfectly the lower spatial frequencies and to offer an increased sensitivity that is particularly attractive for extreme AO (XAO) systems and for differential piston sensing. In fact, for example, Cerpa-Urra et al. (2022) proposed a second stage AO system with a non-modulated PWFS, Pinna et al. (2014) proposed a PWFS-based system with a small modulation radius to balance atmospheric and differential segment piston modes correction, while Engler et al. (2022) proposed a mixed approach where PWFS modulation alternates between modulated and non-modulated. In the latter case, the measurement done during non-modulated frames are used for the correction of differential segment piston modes.

The limitations of non-modulated PWFS shown in Esposito & Riccardi (2001) are real, but in this paper we show that a different calibration of such a sensor can help to overcome them. This is the main point of this work: to propose a new calibration approach allowing smooth operation of non-modulated PWFS.

We based our approach on two previous works: Costa (2005) and Pinna et al. (2012). In the former, it is shown that the residual turbulence on the PWFS has an effect similar to the one of the modulation: it affects the sensitivity of the wavefront sensor (WFS). This means, on the one hand, that the effective sensitivity is lowered when the residual level increases (this is in the right direction because the linearity of the PWFS increases when it is required to be larger) and on the other hand, a calibration taking into account this effect would help improve the performance of the system. In Pinna et al. (2012), the authors present an on-sky calibration, in partial correction regime, that is representative of the effective operation point of the sensor. The goal of this work is to reproduce synthetically the effect of this residual turbulence to include it in the interaction matrix model. The method to generate such matrices is called SIMPC for synthetic interaction matrix model in partial correction. In this paper, its characteristics are compared to a classical modulated PWFS for the calibration.

The work is organized as follows. The parameters used in the simulations are summarized in Table 1 and detailed in Appendix A. In Sect. 2, we present the approach proposed to calibrate the PWFS (this is a general approach valid for both modulated and non-modulated configurations), then we show the sensitivity, linear range, and flat wavefront signal of the modulated and non-modulated PWFS (in Sects. 3, 4, and 5 respectively - for the case of an 8 m-class telescope). Sections 6 and 7 present full end-to-end simulations to assess the performance of the method, respectively, with 8 m- and 39 m-class telescopes. Finally, conclusions are presented in Sect. 8.

Table 1

Simulation parameters.

2 How to use this approach

This section is focused on the SIMPC approach to calibrate a non-modulated PWFS. As noted in the introduction, the method is based on two key-points: (i) that AO residuals affect the sensitivity as a modulation would (Costa 2005) and (ii) that the system can be calibrated around this working point (Pinna et al. 2012).

The effects of partial correction on PWFS, the so-called optical gain, has been studied in a number of papers (Esposito et al. 2015, 2020; Deo et al. 2018, 2019; Chambouleyron et al. 2020, 2021b). It is a well-known feature of the PWFS and it decreases for smaller modulation radius (see Deo et al. 2018, Fig. 5). Optical gain is a loss of sensitivity due to partial correction and its effect on the closed loop gain is a model error between the interaction matrix, calibrated under controlled or diffraction-limited conditions and the actual interaction matrix in partial correction regime. Thus, while we cannot recover the sensitivity of the PWFS working in diffraction-limited conditions, we can eliminate this model error (or greatly reduce it) by calibrating the system in a condition as close as possible to the one obtained during operation. Although this is a general approach, this is particularly critical for non-modulated PWFS, as the model error is important between operation around a diffraction-limited PSF and on-sky operations impacted by AO residuals. We note that this approach is not equivalent to the modal optical gain compensation proposed in Deo et al. (2018), Chambouleyron et al. (2021b), and Agapito et al. (2021) because all these methods are based on the approximation that the modal optical gain matrix is diagonal, while the SIMPC also accounts for the extra-diagonal elements of this matrix (see Sect. 3). The SIMPC method consists then in calibrating the interaction matrix around typical AO residuals, similarly to what is presented in Pinna et al. (2012), with the difference that everything is done synthetically and does not requires on-sky access. Another difference, which is not explicitly discussed in Pinna et al. (2012), is that the partial correction used for the calibration must also include any possible static or quasi-static non-common path aberration between science and PWFS paths that the PWFS would see to ensure a good correction of the science field. Heritier et al. (2018) has shown a synthetic reconstruction matrix can be computed for the PWFS and used on sky for an 8 m telescope AO system and this strategy is the baseline on AOF and ERIS at VLT (see Oberti et al. 2018; Riccardi et al. 2022). We note that this does not resolve all effects related to optical gains because the SIMPC will be computed for a given partial correction (or a set of partial corrections) and cannot account for all the working conditions an AO system will face during on-sky operations. Nevertheless, the SIMPC provides an important advantage as the model errors between the calibration working point and on-sky working point will be much smaller than if the calibration is made under diffraction limit conditions.

In practice, the synthetic calibration is done mode-by-mode, with a push-pull signal repeated N times, each time with a different (ideally statistically independent) realization of the desired partial correction level (an example for one mode and a casual realization of partial correction is shown in Fig. 1). So, the ith column of the interaction matrix, D, will be: 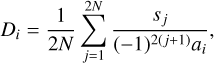Di=12N∑j=12Nsj(−1)2(j+1)ai,${D_i} = {1 \over {2N}}\sum\limits_{j = 1}^{2N} {{{{s_j}} \over {{{\left( { - 1} \right)}^{2\left( {j + 1} \right)}}{a_i}}}} ,$(1)

where s is the slope vector (whose description is given in Appendix A) and a is the absolute value of the amplitude of the mode applied. In principle, this can be done also considering M different levels of partial correction for a total of NM repetitions. In this case, Eq. (1) becomes: 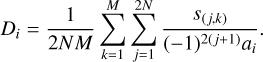Di=12NM∑k=1M∑j=12Ns(j,k)(−1)2(j+1)ai.${D_i} = {1 \over {2NM}}\sum\limits_{k = 1}^M {\sum\limits_{j = 1}^{2N} {{{{s_{\left( {j,k} \right)}}} \over {{{\left( { - 1} \right)}^{2\left( {j + 1} \right)}}{a_i}}}} } .$(2)

An example of the effect of the number of repetitions is shown in Fig. 2: a single realization gives noisy signals and only with several tens of realizations the convergence is reached for the worst seeing considered. In particular, for a case with sub-aperture sizes of 0.2, 0.4, 0.6, and 0.8 m, we will use N = 70, 100, 200, and 200, respectively, in the rest of the paper. The RMS of the difference between the IM computed with N and N − 1 realizations is <0.02 of the RMS of IM computed with N with the values of N mentioned above for a seeing of 1.4 arcsec. An example of this convergence is shown in Fig. 3 for the sub-aperture size of 0.2 m. Note: the realizations we used were generated from a single simulation, we selected turbulence residual samples separated by 100 simulation steps (0.059 s for the maximum framerate of 1700 Hz). Adjacent samples are not statistically independent, they have correlation levels of about 10%.

thumbnail Fig. 1

Example of the phase used to run a single step of the push-pull calibration with partial correction (for the 8 m-class telescope case and 0.2 m sup-aperture size): on the left part mode no. 50 of the modal base with positive (top, push) and negative (bottom, pull) sign, on the central part a random realization of the partial correction (i.e., turbulence residual), and on the right part the combination of mode and partial correction. The wavefront root mean square (RMS) of the mode is 40 nm and the wavefront RMS of the random realization of the partial correction is 46 nm (corresponding to the residual correction level expected for a seeing of 0.4arcsec). We note that these RMS values are selected for display purpose, in general, the amplitude of the push-pull (i.e., the wavefront RMS of the mode) is much smaller than the RMS of the partial correction.
thumbnail Fig. 2

Tip (left) and mode no. 100 (right) signals (x and y) from interaction matrices with different numbers of partial correction realizations (from left to right): 1, 8, and 70. Top: partial correction for a seeing of 0.4 arcsec, middle, partial correction for a seeing of 0.8 arcsec, bottom, partial correction for a seeing of 1.2 arcsec. Note: the signals amplitude is reduced when seeing increases. Refers to the sub-aperture size of 0.2 m. 8 m-class telescope case.

3 Sensitivity and optical gains

The main reason to use a non-modulated PWFS is for the gain in sensitivity. This is particularly true for low-order spatial frequencies as presented in Chambouleyron et al. (2021a). This higher sensitivity is relevant when dealing with differential piston sensing as shown, for example, in Engler et al. (2022) and Levraud et al. (2022).

The sensitivity in partial correction as a function of mode number and seeing value expressed as the RMS, xRMS, of the WFS signal (also known as slope) for an aberration with a wave-front RMS of 1nm is reported in Fig. 4. The ith element of the xRMS vector is: 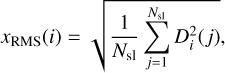xRMS(i)=1Nsl∑j=1NslDi2(j),${x_{RMS}}\left( i \right) = \sqrt {{1 \over {{N_{{\rm{sl}}}}}}\sum\limits_{j = 1}^{{N_{{\rm{sl}}}}} {D_i^2\left( j \right)} } ,$(3)

where D is the interaction matrix and Nsl is the number of elements of the wavefront sensor (WFS) signal vector. Here, we are considering a partial correction given by a PWFS working in high-flux conditions. As can be deduced from Fig. 4, there are 48 sets of turbulence residuals (i.e., with a partial correction) used to calculate the SIMPCs: their RMS and the RMS of the WFS signals calculated along with them are given in Tables 2 and 3.

The result shown in Fig. 4 confirms the qualitative analysis provided in the first part of this section, the non-modulated PWFS is generally more sensitive than a modulated PWFS (we chose a modulation radius of 3λ/D for the comparison because is the current value used for SOUL at LBT, see Pinna et al. 2019): the sensitivity gain is larger for smaller sub-aperture size, where the residual is lower because the fitting error is lower (a larger number of modes is corrected) and is larger for lower order modes, in particular, for the first two, tip and tilt. The gain is between a factor 4 (bad seeing) and 10 (good seeing) for tip and tilt and a factor 1.5 on mode 500 when the sub-aperture size is 0.2 m. The gain decreases when the sub-aperture size is reduced: it becomes 1 for bad seeing and a sub-aperture of 0.8 m.

Since this work is particularly relevant for pupil fragmentation sensing, Fig. 5 gives the sensitivity to a differential piston mode in partial correction as a function seeing value expressed as the RMS of the WFS signal for an aberration with a wavefront RMS of 1nm (an infinite signal-to-noise ratio, S/N). We note that the piston mode is the one produced by one petal of a six-petal configuration with no gap (see Fig. 6). This ability to better see phase jumps is of particular interest for the next generation of AO instruments, as well as for existing systems that may be impacted by thermal effects of the spiders (Sauvage et al. 2015; Wilby et al. 2018; Pourré et al. 2022).

We defined the optical gains as the scalar coefficients expressing the change in PWFS sensitivity due to partial correction. An example is shown in Fig. 7 for a PWFS calibrated in diffraction-limited conditions.

These gains must be compensated to provide the best performance but as well to get a proper non-common path correction, as shown in Esposito et al. (2015, 2020), Deo et al. (2018), Chambouleyron et al. (2020), and Chambouleyron et al. (2021b). When the PWFS calibration takes into account a partial correction equivalent to that found in operation, the optical gains are equal to 1; however, if there is a discrepancy between the residual level in calibration and in operation, the optical gains are different from 1 (may also be greater than 1). A summary of this effect is shown in Fig. 8. Interestingly, the gains are closer to 1 than the diffraction-limited case and the mode-by-mode difference is small. Here, we consider the diagonal approximation, but we note that (as mentioned earlier in this paper) the modal optical gains matrix is a full matrix (as can be seen in Fig. 9, where, an example of the product between reconstruction matrix in diffraction-limited condition and SIMPC is shown) and not a diagonal matrix.

thumbnail Fig. 3

RMS of the difference between the IM computed with x + 1 and x realizations of partial correction normalized by the RMS of the IM computed with N = 70 realizations. Seeing is 1.4 arcsec and sub-aperture size is 0.2 m for the 8 m-class telescope case.
Table 2

RMS of turbulence residuals (i.e. partial correction) in nm for a bright star condition.

Table 3

RMS of the slopes (WFS signals) computed on the sets of turbulence residual (i.e., partial correction) samples used to compute the SIMPCs (see Sect. 2).

thumbnail Fig. 4

PWFS sensitivity in partial correction as a function of mode number and seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Mode 1 is tip, 2 is tilt and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Top-left: sub-aperture size of 0.2 m, top-right, sub-aperture size of 0.4 m. Bottom-left: sub-aperture size of 0.6 m. Bottom-right: sub-aperture size of 0.8 m for the 8 m-class telescope case.
thumbnail Fig. 5

PWFS sensitivity to a differential piston mode in partial correction as a function of seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. The differential piston mode is the one produced by one petal of a six-petal configuration with no gap. Solid line correspond to a non-modulated PWFS and dashed line correspond to a PWFS with a modulation radius of 3λ/D. Sub-aperture size is 0.2 m. Refers to the 8 m-class telescope case.

4 Linearity

While the sensitivity of an non-modulated PWFS is greater than that of a modulated PWFS, the linearity of a non-modulated PWFS is reduced1 and this is still valid even when using the SIMPC approach. The model error can be reduced but the linearity cannot be changed when operating in a non-null working point2. The linearity is improved by the partial correction as reported in Costa (2005), but there is no direct control on this. Typically, in closed loop, the aberration to be sensed are proportional to the residual aberration. Another point to consider is the fitting error: when the number of modes and actuators decreases, as it happens for SOUL with dimmer stars when the detector is binned (see Pinna et al. 2016, 2019), the fitting error increases, and higher level of residual reduces the PWFS sensitivity. This means that it is less important to modulate the PWFS when few modes or actuators are corrected. We must then consider that higher sensitivity gives greater benefits when the signal-to-noise ratio is lower, so, in general, a non-modulated PWFS is preferable on dimmer stars, where we would also expect worse correction and higher residual.

As for the previous section, a partial correction given by a PWFS working in high flux condition is considered (equivalent to the one presented in in Sect. 6 for an R magnitude of 8). We report in Fig. 10 the response of the PWFS to a set of modes with increasing wavefront RMS. The correction condition range from diffraction limit to a seeing of 1.2 arcsec and the sub-aperture size is 0.2 m. The modulated PWFS has a clear advantage on the first three modes considered, 0, 5, and 10. Specifically, the modulated PWFS under diffraction limited conditions is linear up to about 600 nm on mode 0 (tip), 400 nm on mode 5, and 200 nm on mode 10. The linearity increases with partial correction well beyond these value (see Fig. 10). The non-modulated PWFS has a significant smaller linearity range, but it increases with partial correction, and the PWFS response on the lower order modes (a few tens) is monotonous except for the diffraction limited condition. Interestingly, by increasing the sub-aperture size (thus the fitting error) the linear range greatly improves, as can be seen in Fig. 11.

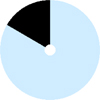thumbnail Fig. 6

Differential piston mode in black (also known as petal mode) produced by one segment (petal) of a six-segment (petals) configuration with no gap. The pupil is shown in light blue. Refers to the 8 m-class telescope case.
thumbnail Fig. 7

Modal optical gain for the PWFS calibrated in diffraction limited conditions. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen-Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
thumbnail Fig. 8

Modal optical gains for the PWFS calibrated in partial correction with a seeing value of 0.8arcsec. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen-Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
thumbnail Fig. 9

Results of the product between reconstruction matrix in diffraction limited condition and SIMPC for seeing of 1.4 arcsec, without modulation and with sub-aperture size of 0.2 m. This is the so called modal optical gain matrix. An absolute value is used and only the first 100 × 100 elements of the matrix is shown for clarity reasons. It can be easily seen that that the matrix is not diagonal. The diagonal of this matrix is shown in Fig. 7 (orange solid line). Refers to the 8 m-class telescope case.

5 Flat wavefront WFS response

This section focuses on the slope vector associated with a flat wavefront. For the PWFS, this signal is not a vector of zeros. It is interesting to note that in case of a non-modulated PWFS the amplitude of the signal corresponding to a flat wavefront is greater than the one of a modulated PWFS, so it is more important to take it into account in this configuration. For a sub-aperture size of 0.20 m, it is a signal corresponding to an aberration of about 20 nm, about a factor 2 above the value found for a modulated PWFS with modulation radius of 3λ/D. Following a similar approach as the SIMPC (and as the one presented in Engler et al. 2022), we computed the flat wavefront slope vector as the average of a set of 500 slopes measured with a random residual that is given by the fitting error only: the wave-front spectrum has a zero amplitude up to the maximum spatial frequency that can be corrected by the AO system. Examples of these signals are shown in Fig. 12. We note that the slope intensity decreases with increasing partial correction (i.e., the seeing value); this means that when the seeing is changing, the flat wavefront slope reference should be changed as well (Engler et al. 2022).

6 Simulation results

6.1 Simulation with no calibration error of the optical gain

In this section, we present simulations where the value of seeing found during operation is the same value used for the calibration. In this case, the optical gain should be automatically compensated by the SIMPC.

We ran a set of simulations with PASSATA (see Agapito et al. 2016) to evaluate the closed loop performance of the non-modulated PWFS for the 8 m-class telescope case. We used a control based on leaky integrators (see Agapito et al. 2019) and we optimized the modal gain online, as described in Agapito et al. (2021). Additional information on the parameters used and on the details of the simulation can be found in Table 1 and in Appendix A. We explored several magnitudes from R = 8 to 16.5 and we used a system configuration analogous to the one of SOUL (see Pinna et al. 2019) where we binned the detector to deal with lower fluxes. The summary of the results is presented in Table 4. Non-modulated PWFS shows better performance when observing faint objects under very good seeings. Under these conditions, the limited linear range is not a problem and the lower propagation noise of the non-modulated PWFS can be fully exploited. In contrast, the modulated PWFS is preferable for bright objects observed under poor seeing conditions, that is, when the extended linear range of this configuration is most critical. Under all other conditions, performance is similar. Interestingly, non-modulated PWFS have a better correction on low-order modes and the difference from modulated PWFS is greater for good seeing values (see Fig. 13).

thumbnail Fig. 10

Response of the PWFS to modes with different value of wavefront RMS and for different partial correction levels (s = 0.00 arcsec correspond to diffraction limited conditions). Top-left: mode 0 (tip). Top-right: mode 10. Bottom-left: mode 100. Bottom-right: mode 499. Mode 0 is tip, 1 is tilt, and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Sub-aperture size is 0.2 m. Optical gain is corrected considering an aberration RMS of 20 nm. Refers to the 8 m-class telescope case.
thumbnail Fig. 11

Response of the PWFS to a tip with different value of wave-front RMS and for different sub-aperture size and for a seeing value of 0.8 arcsec. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
thumbnail Fig. 12

Signals corresponding to a flat wavefront for a non-modulated PWFS with a 0.2 m sub-aperture and different level of partial correction corresponding to seeing values of 0.4, 0.6, 0.8, 1.0, 1.2, and 1.4 arcsec, respectively. Refers to the 8 m-class telescope case.

6.2 Simulations with a compensation of the optical gain

In this section, we considered the calibration error, namely: the level of partial correction used for calibration is different with respect to the one found during operation. So, the optical gain is not correctly compensated by the SIMPC: the calibration method we present in the previous sections gives an accurate model of the PSWF response when the value of seeing found during operation is the same value that was used for the calibration.

In principle, we could update the reconstruction matrix regularly, following the level of seeing, but here we want to explore the effect of an optical gain not equal to 1 and how it can be compensated for. We considered a well established approach, tested on-sky on a 8 m-class telescope: the one presented in Esposito et al. (2015, 2020) for the optical gain compensation, along with the one presented in Agapito et al. (2021) for online gain optimization. We note that other methods to deal with optical gain do exist, which may be considered (see Korkiakoski et al. 2008; Deo et al. 2018, Deo et al. 2019, 2021; Chambouleyron et al. 2020, Chambouleyron et al. 2021b), but in this case, we are not interested in finding a general solution for this issue. Our objective is to understand whether a non-modulated PWFS calibrated for a certain seeing value can operate with a different seeing value and if one method developed for a diffraction-limited IM can work also for the SIMPC presented in this paper. We considered a sub-aperture size of 0.2 m, a bright NGS (R magnitude 8), seeing cases ranging from 0.4 to 1.4 arcsec, and interaction matrices with different levels of partial correction (computed for diffraction limited coniditions and seeing values between 0.4 and 1.4 arcsec).

A summary of the results is presented in Fig. 14. Here, we can see that the interaction matrices computed for the worst seeing (performance given by SIMPC with seeing 1.2 arcsec is equivalent to the one with seeing 1.4 arcsec) are able to work with any seeing level with a performance comparable to the one given by the correct calibration, while the ones computed in diffraction-limited conditions or for good seeing become unstable for the case with the worst seeing. A couple of examples of the results are shown in Figs. 15 and 16. In the first case, the H band (1650 nm) SR reached is 0.966, equal to the one given by an IM without calibration error, while in the second case, trie closed loop is not stable and the H band (1650 nm) SR goes to 0. It is interesting to note that the estimated value of optical gain for the first case is above 1 because in this case the SIMPC has a lower sensitivity than the actual interaction matrix.

As mentioned above, we note that the result found here is not general, but it is valid for the optical gain compensation and modal gain optimization methods considered. In particular, a dif-ferent approach could allow for stable performance even in the case of a calibration performed with significantly lower levels of partial correction. Nevertheless, this is an interesting result that proves that this issue can be solved and it could be a topic for further study in future work.

Table 4

H band (1650 nm) SR as a function of natural guide star R magnitude and seeing for a non-modulated and a modulated PWFS.

thumbnail Fig. 13

Turbulence (black lines) and residuals (colored lines) modal RMS amplitudes for a NGS of magnitude R = 12, different seeing values and for a non-modulated and modulated (modulation radius of 3λ/D, dashed lines) PWFS. Sub-aperture size is 0.2 m and 500 modes are corrected. Refers to the 8 m-class telescope case.
thumbnail Fig. 14

H band (1650 nm) SR as a function of seeing for simulations with a non-modulated PWFS with bright NGS (R magnitude 8). Different colors correspond to different PWFS calibration: black refer s to a classic calibration in diffraction limited conditions, while the other colors are the SIMPC for different seeing levels. Please note that low values of SR correspond to unstable closed loops. Blue and green asterisks correspond to the cases illustrated in Figs. 15 and 16. Refer to the 8 m-class telescope case.
thumbnail Fig. 15

Results for a simulation with a non-modulated PWFS with bright NGS (R magnitude 8) and with seeing of 0.4 arcsec with a calibration error: PWFS was calibrated for aseeing of 1.2 arcsec. The black line is the ostimation of the opticel goin (done on mode 30), red line is tho H band (168C nm) SR (orange line is the avorage on 1 s), and green line is the average value of the modal gain. Refers to too 8 m-class telescope case.
thumbnail Fig. 16

Results for a simulation with a non-modulated PWFS with bright NGS (R magnitude 8) and with seeing of 1.4 arcsec with a calibration error: PWFS was caibrated for a seeing of 0.8 arcsec. The black line is the estimation of the optical gain (done on mode 30), red line is the H band (1650 nm) SR (orange line is tha averageon 1 s), and green line is the average value of the modal gain. Refers to the 8 m-class telescope case.

7 ELT case

In this section, we present an analysis carried out for the Extremely Large Telescope (ELT, Tamai & al. 2020) PWFS system. We considered the configuration reported in Xompero et al. (2018): a system wish 99×90 sub-apertures (sub-aperture size 0.433 m) and a sensing waveleneth of 798 nm in a telescope of 39 m diameter without any spider shadow (more details can be found in Table 1 and in Appendix A).

We siudied the sensitivity for this configurationas we describe in Sect. 3, with the results shown in Fig. 17 These results are similar to those of the 8 m-class telescope case for a sub-aperture size of 0.4 m; between unmodulated and modulated PWFS, there is a factor oh 9 for good seeing (1.5 for dad seeing) on the sensitivity of tip and tilt and a factor of 1.3 for good seeing (1 for bad seeing) on the sensitvity of the last mode.

We also replicated the sensitivity analysis for differential piston modes considering both a gap-less configuration a configuration with 0.5 m thick spider arms. We can see in Fig. 18 that the non-modulated PWFS has an advantage over modulated PWFS and that this advantage is greater in the presence of spaders: a factor of 10 for good seeing values and a factor of 2 dor bad seeing values when 0.5 m thick spider arms are present.

Finally, we studied the performance of such system with a bright star (magnitude R = 8) and we see that the results exhibit consistent behaviors between the cases of the 8 m- (reported in Sect. 6) and the 39 m-class telescope: K band (2200 nm) SR for a seeing value of 0.4 arcsec is the same for non-modulated and modulated PWFS, 0.963, and there is an advantage of 0.03 K band (2200 nm) SR for modulated PWFS for a seeing value of 1.2 arcsec (0.750 w.r.t. 0703). We note that; these are preliminary results and this topic should be further studded to have a full assessment of the performance in the presence of the segmented pupil and the spider shadow of the ELT.

thumbnail Fig. 17

ELT PWFS sensitivity in partial correction as a function of mode number and seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWTS and dashed lines correspond to a PWFS with a modulation radius of 4λ/D. Sub-aperture size of 0.433 m. Refers to the ELT case.
thumbnail Fig. 18

ELT PWFS sensitivity to a differential piston mode in partial correction as a function of seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Differential pieton mode is the one produced by one petal of a 6 pntals configuration with no gap and with a 0.5 m gyp. Solid line correspond to a non-modulated PWFS and dashed fine correspond to a PWFS with a modulation radius of 4λ/D. Sub-aperture size is 0.433 m and seeing range is [0.4,1.4] arcsec. Refers to the ELT case.

8 Conclusions

In this work, we focus on the non-modulated PWFS and demonstrate the way it can be used to effectively sense and correct atmospheric turbulence. Our goal is to show why, how, and when the PWFS ought to be used with non-modulation.

The “why” is related to the higher sensitivity of the non-modulated compared to the modulated PWFS, particularly for differential segment piston sensing. We show that the gain in sensitivity is greater for the best partial correction conditions (up to a factor of 10 for low order modes) – thus, it is generally appropriate for good seeing and for AO systems with high sensing and correction sampling (i.e., for extreme AO systems).

The “how” is based on a new approach to calibration of this sensor to model the PWFS response in the presence of a partial correction. We call the interaction matrix computed with this approach the synthetic interaction matrix model with partial correction (SIMPC). It is synthetic because the calibration is done in the simulations and the partial correction allows to reduce the model error between the PWFS response in calibration and in operation. We show that this can also be used for the modulated case (demonstrated with simulations) that it is effective under a wide range of conditions for SCAO systems working with 8m-and 39 m-class telescopes. We also present a possible approach to deal with a partial correction that is different than the one used in the calibration.

Finally, with respect to the “when,” we have shown that the performance of a non-modulated PWFS is very close to the one of a modulated PWFS. The non-modulated PWFS has a small advantage under conditions of good partial correction (high sensing and correction sampling and/or good seeing) and when the flux is low, while it has a small disadvantage under conditions of bad partial correction (low sensing and correction sampling and/or bad seeing) and when the flux is high. Thus, in principle, the answer is that it can be always used, but the regime in which non-modulated PWFS performs better than modulated PWFS is when the contributions of fitting and temporal errors are low relative to noise. Another interesting case is the system with mirror segmentation: we did not study these systems in detail because this is not the focus of this work, but we showed that the gain in sensitivity in differential piston sensing can be important and is not associated with a loss of linearity. We would like to point out an interesting fact (at the heart of Engler et al. 2022), namely, that a modulated PWFS system can easily switch to a non-modulated case by simply turning off the tip-tilt modulator, so this configuration can be used only when required.

A new calibration option for PWFS base AO system is available, which removes the constraints on the minimum value of modulation amplitude, potentially boosting the sensitivity and allowing for a better optimization of such a sensor.

Acknowledgements

The authors thank Cédric Plantet, Thierry Fusco, Benoît Neichel, Jean-François Sauvage, Nicolas Levraud, Miska Le Louarn, Christophe Vérinaud, and Jean-Pierre Véran for fruitful discussions.

Appendix A Details on the simulations

In this section, we report several key details of the simulations presented in this work. We note that the 8 m-class telescope case is equivalent to that of single conjugate adaptive optics upgrade for LBT (SOUL, Pinna et al. 2019) and the ELT case is equivalent to the configuration reported in Xompero et al. (2018). A few notes to the parameters summarized in Table 1 are:

  • Zenith angle is used to scale the distance of the layers from the entrance pupil. Seeing values reported in the text are always line-of-sight ones.

  • Simulations are monochromatic.

  • In the 8 m-class telescope case different sub-aperture numbers are obtained by binning the detector pixels. The maximum value is 40×40 (sub-ap. size of 0.2 m), while 20×20 (sub-ap. size of 0.4 m), 13×13 (sub-ap. size of 0.6 m), and 10×10 (sub-ap. size of 0.8 m) cases are obtained by binning the detector pixels by 2×2, 3×3, and 4×4, respectively.

  • The selected sub-pupil separation values derive from the glass pyramid geometry of SOUL. In SOUL there is a ratio between pixel on the diameter of the sub-pupil and separation that is 48/40.

  • The influence functions for the 8 m-class telescope case are measurements from the LBT adaptive secondary mirror (Riccardi et al. 2008). Instead, an ideal modal basis (pure Zernike and Karhunen-Loéve modes Wang & Markey 1978) was used for the ELT case.

  • Leaky integrators: we consider the discrete time case, H(z) = g/(1 − fz−1) (see Agapito et al. 2019), their gains, ɡ, are optimized (modal gain optimization as described in Agapito et al. 2021), and the forgetting factors, f, ranging from 1 to 0.9 (as reported in Sect. 7.2 of Agapito et al. 2019, noting that for the ELT case, x is scaled by 0.15).

  • The delay in the case of the 8 m-class telescope is between 2 (1700 Hz framerate) and 5 ms (250 Hz framerate), as shown in Fig. 3 of Agapito et al. (2021).

Additional information on the simulations is provided below.

  • Turbulence is generated by moving phase screens. They have the same sampling as the pupil (8/220 m/pixel for the 8 m-class telescope case and 39/512 m/pixel for the ELT case) and they are made of 32768×32768 pixels. The phase screens are generated by computing the inverse fast Fourier transform of a complex array having amplitude equal to the square root of the von Karman power spectrum and having a spatially uncorrelated and uniformly distributed phase. Their amplitude is scaled considering line-of-sight seeing value and 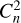Cn2$C_n^2$ fraction.

  • A geometrical propagation of the electric field is used from the turbulence layer to the telescope pupil. This propagation consider the geometrical information as the guide star altitude and position, the phase screens altitude, the deformable mirror (DM) conjugation altitude, the entrance pupil position (its conjugation altitude is 0 m), and the zenith angle, etc.

  • The PWFS is implemented as described in Pinna (2004) with a sampling of the electric field in the focal plane of 1/3 λ/D (where λ is the sensing wavelength and D is the telescope diameter). In the simulation presented in this work, we considered a monochromatic sensor.

  • The electro-multipling process of the detector is simulated following Carbillet & Riccardi (2010).

  • X- and y-sensor signals from the PWFS, also referred to in the text as slopes or vector of slopes, are calculated using a quad-cell-like calculation and normalized with the average intensity over all valid sub-apertures. So, for the j-th subaperture, the X-sensor signal is computed as: 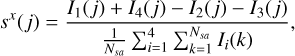sx(j)=I1(j)+I4(j)−I2(j)−I3(j)1NsaΣi=14Σk=1NsaIi(k),${s^x}\left( j \right) = {{{I_1}\left( j \right) + {I_4}\left( j \right) - {I_2}\left( j \right) - {I_3}\left( j \right)} \over {{1 \over {{N_{sa}}}}{\rm{\Sigma }}_{i = 1}^4{\rm{\Sigma }}_{k = 1}^{{N_{sa}}}{I_i}\left( k \right)}},$(A.1)

    where Ii is the intensity on the i-th sub-pupil, k is the valid sub-aperture index, and Nsa is the number of valid sub-aperture.

  • The DM surface is computed as a linear combination of the influence functions (the conversion between surface and wavefront is given by a factor 2) projected on the pupil.

  • In the cases reported in this work, the simulation time step is equal to the detector integration time. Non-integer delays are approximated with linear interpolation of the DM commands.

  • Calibration amplitude is 20nm RMS for tip and tilt and then it is scaled by 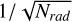1/Nrad${1 \mathord{\left/ {\vphantom {1 {\sqrt {{N_{rad}}} }}} \right. \kern-\nulldelimiterspace} {\sqrt {{N_{rad}}} }}$, where Nrad is the radial order of the considered mode.

References

  1. Agapito, G., Arcidiacono, C., Quirós-Pacheco, F., & Esposito, S. 2014, Exp. Astron., 37, 503 [NASA ADS] [CrossRef] [Google Scholar]
  2. Agapito, G., Puglisi, A., & Esposito, S. 2016, SPIE Conf. Ser., 9909, 99097E [NASA ADS] [Google Scholar]
  3. Agapito, G., Pinna, E., Puglisi, A., & Rossi, F. 2019, ArXiv e-prints [arXiv:1911.05989] [Google Scholar]
  4. Agapito, G., Rossi, F., Plantet, C., Puglisi, A., & Pinna, E. 2021, MNRAS, 508, 1745 [CrossRef] [Google Scholar]
  5. Archinuk, F., Hafeez, R., Fabbro, S., Teimoorinia, H., & Véran, J.-P. 2023, ArXiv e-prints [arXiv:2305.09805] [Google Scholar]
  6. Bertrou-Cantou, A., Gendron, E., Rousset, G., et al. 2022, A&A, 658, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bouchez, A. H., Angeli, G. Z., Ashby, D. S., et al. 2018, SPIE Conf. Ser., 10703, 107030W [NASA ADS] [Google Scholar]
  9. Brandl, B., Bettonvil, F., van Boekel, R., et al. 2021, The Messenger, 182, 22 [NASA ADS] [Google Scholar]
  10. Carbillet, M., & Riccardi, A. 2010, Appl. Opt., 49, G167 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cerpa-Urra, N., Kasper, M., Kulcsár, C., Raynaud, H.-F., & Taïssir Heritier, C. 2022, J. Astron. Telescopes Instrum. Syst., 8, 019001 [NASA ADS] [Google Scholar]
  12. Chambouleyron, V., Fauvarque, O., Janin-Potiron, P., et al. 2020, A&A, 644, A6 [EDP Sciences] [Google Scholar]
  13. Chambouleyron, V., Fauvarque, O., Sauvage, J. F., et al. 2021a, A&A, 650, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Chambouleyron, V., Fauvarque, O., Sauvage, J. F., Neichel, B., & Fusco, T. 2021b, A&A, 649, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Ciliegi, P., Agapito, G., Aliverti, M., et al. 2021, The Messenger, 182, 13 [NASA ADS] [Google Scholar]
  16. Costa, J. B. 2005, Appl. Opt., 44, 60 [Google Scholar]
  17. Crane, J., Herriot, G., Andersen, D., et al. 2018, SPIE Conf. Ser., 10703, 107033V [NASA ADS] [Google Scholar]
  18. Currie, T., Guyon, O., Lozi, J., et al. 2020, SPIE Conf. Ser., 11448, 114487H [Google Scholar]
  19. Davies, R., Hörmann, V., Rabien, S., et al. 2021, The Messenger, 182, 17 [NASA ADS] [Google Scholar]
  20. Davies, R., Absil, O., Agapito, G., et al. 2023, A&A, 674, A207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Deo, V., Gendron, É., Rousset, G., Vidal, F., & Buey, T. 2018, SPIE Conf. Ser. 10703, 1070320 [NASA ADS] [Google Scholar]
  22. Deo, V., Gendron, É., Rousset, G., et al. 2019, A&A, 629, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Deo, V., Gendron, É., Vidal, F., et al. 2021, A&A, 650, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Engler, B., Le Louarn, M., Vérinaud, C., Weddell, S., & Clare, R. 2022, J. Astron. Telescopes Instrum. Syst., 8, 021502 [NASA ADS] [Google Scholar]
  25. Esposito, S., & Devaney, N. 2002, in European Southern Observatory Conference and Workshop Proceedings, 58, 161 [NASA ADS] [Google Scholar]
  26. Esposito, S., & Riccardi, A. 2001, A&A, 369, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Esposito, S., Riccardi, A., Fini, L., et al. 2010, SPIE Conf. Ser., 7736, 107 [Google Scholar]
  28. Esposito, S., Pinna, E., Puglisi, A., et al. 2015, in Adaptive Optics for Extremely Large Telescopes IV (AO4ELT4), E36 [Google Scholar]
  29. Esposito, S., Puglisi, A., Pinna, E., et al. 2020, A&A, 636, A88 [EDP Sciences] [Google Scholar]
  30. Frazin, R. A. 2018, J. Opt. Soc. Am. A, 35, 594 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hammer, F., Morris, S., Cuby, J. G., et al. 2021, The Messenger, 182, 33 [NASA ADS] [Google Scholar]
  32. Hartke, J., Kakkad, D., Reyes, C., et al. 2020, SPIE Conf. Ser., 11448, 114480V [NASA ADS] [Google Scholar]
  33. Hartmann, J. 1900, Naturwissenschaften, 20, 17 [Google Scholar]
  34. Heidt, J., Pramskiy, A., Thompson, D., et al. 2018, Proc. SPIE, 10702, 107020B [Google Scholar]
  35. Heritier, C. T., Esposito, S., Fusco, T., et al. 2018, MNRAS, 481, 2829 [Google Scholar]
  36. Hutterer, V., & Ramlau, R. 2018, Appl. Opt., 57, 8790 [NASA ADS] [CrossRef] [Google Scholar]
  37. Korkiakoski, V., Vérinaud, C., & Louarn, M. L. 2008, Appl. Opt., 47, 79 [NASA ADS] [CrossRef] [Google Scholar]
  38. Larkin, J., Barczys, M., Krabbe, A., et al. 2006, SPIE Conf. Ser., 6269, 62691A [NASA ADS] [Google Scholar]
  39. Levraud, N., Chambouleyron, V., Fauvarque, O., et al. 2022, SPIE Conf. Ser., 12185, 1218559 [NASA ADS] [Google Scholar]
  40. Marconi, A., Abreu, M., Adibekyan, V., et al. 2021, The Messenger, 182, 27 [NASA ADS] [Google Scholar]
  41. Oberti, S., Kolb, J., Madec, P.-Y., et al. 2018, SPIE Conf. Ser., 10703, 107031G [NASA ADS] [Google Scholar]
  42. Pinna, E. 2004, Master’s thesis, Università degli Studi di Firenze, Facoltà di Scienze Matematiche, Fisiche e Naturali, Italy [Google Scholar]
  43. Pinna, E., Quirós-Pacheco, F., Riccardi, A., et al. 2012, SPIE Conf. Ser., 8447, 84472B [NASA ADS] [Google Scholar]
  44. Pinna, E., Agapito, G., Quirós-Pacheco, F., et al. 2014, SPIE Conf. Ser., 9148, 91482M [NASA ADS] [Google Scholar]
  45. Pinna, E., Esposito, S., Hinz, P., et al. 2016, in Adaptive Optics Systems V, 9909, eds. E. Marchetti, L.M. Close, & J.-P. Veran, International Society for Optics and Photonics (SPIE), 1183 [Google Scholar]
  46. Pinna, E., Rossi, F., Puglisi, A., et al. 2019, ArXiv e-prints [arXiv:2101.07091] [Google Scholar]
  47. Pourré, N., Le Bouquin, J. B., Milli, J., et al. 2022, A&A, 665, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Ragazzoni, R. 1996, J. Mod. Opt., 43, 289 [Google Scholar]
  49. Riccardi, A., Xompero, M., Zanotti, D., et al. 2008, SPIE Conf. Ser., 7015, 701512 [NASA ADS] [Google Scholar]
  50. Riccardi, A., Puglisi, A., Grani, P., et al. 2022, SPIE Conf. Ser., 12185, 1218508 [NASA ADS] [Google Scholar]
  51. Sarazin, M., Le Louarn, M., Ascenso, J., Lombardi, G., & Navarrete, J. 2013, in Proceedings of the Third AO4ELT Conference, eds. S. Esposito, & L. Fini, 89 [Google Scholar]
  52. Sauvage, J.-F., Fusco, T., Guesalaga, A., et al. 2015, in Adaptive Optics for Extremely Large Telescopes IV (AO4ELT4), E9 [Google Scholar]
  53. Tamai, R., Koehler, B., Cirasuolo, M., et al. 2020, SPIE Conf. Ser., 11445, 114451E [NASA ADS] [Google Scholar]
  54. Thatte, N., Tecza, M., Schnetler, H., et al. 2021, The Messenger, 182, 7 [NASA ADS] [Google Scholar]
  55. Vérinaud, C. 2004, Opt. Commun., 233, 27 [Google Scholar]
  56. Wang, J. Y., & Markey, J. K. 1978, J. Opt. Soc. Am., 68, 78 [NASA ADS] [CrossRef] [Google Scholar]
  57. Wilby, M. J., Keller, C. U., Sauvage, J. F., et al. 2018, A&A, 615, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Wizinowich, P., Lu, J. R., Cetre, S., et al. 2022, SPIE Conf. Ser., 12185, 121850Q [NASA ADS] [Google Scholar]
  59. Xompero, M., Giordano, C., Bonaglia, M., et al. 2018, SPIE Conf. Ser., 10703, 1070341 [NASA ADS] [Google Scholar]
1

Except for differential piston, because the response for both nonmodulated and modulated PWFS to such aberrations is sinusoidal as it is shown in Esposito & Devaney (2002).

2

An exception is exotic approaches such as the ones presented in Frazin (2018), Hutterer & Ramlau (2018) and Archinuk et al. (2023).

All Tables

Table 1

Simulation parameters.

In the text
Table 2

RMS of turbulence residuals (i.e. partial correction) in nm for a bright star condition.

In the text
Table 3

RMS of the slopes (WFS signals) computed on the sets of turbulence residual (i.e., partial correction) samples used to compute the SIMPCs (see Sect. 2).

In the text
Table 4

H band (1650 nm) SR as a function of natural guide star R magnitude and seeing for a non-modulated and a modulated PWFS.

In the text

All Figures

thumbnail Fig. 1

Example of the phase used to run a single step of the push-pull calibration with partial correction (for the 8 m-class telescope case and 0.2 m sup-aperture size): on the left part mode no. 50 of the modal base with positive (top, push) and negative (bottom, pull) sign, on the central part a random realization of the partial correction (i.e., turbulence residual), and on the right part the combination of mode and partial correction. The wavefront root mean square (RMS) of the mode is 40 nm and the wavefront RMS of the random realization of the partial correction is 46 nm (corresponding to the residual correction level expected for a seeing of 0.4arcsec). We note that these RMS values are selected for display purpose, in general, the amplitude of the push-pull (i.e., the wavefront RMS of the mode) is much smaller than the RMS of the partial correction.
In the text
thumbnail Fig. 2

Tip (left) and mode no. 100 (right) signals (x and y) from interaction matrices with different numbers of partial correction realizations (from left to right): 1, 8, and 70. Top: partial correction for a seeing of 0.4 arcsec, middle, partial correction for a seeing of 0.8 arcsec, bottom, partial correction for a seeing of 1.2 arcsec. Note: the signals amplitude is reduced when seeing increases. Refers to the sub-aperture size of 0.2 m. 8 m-class telescope case.
In the text
thumbnail Fig. 3

RMS of the difference between the IM computed with x + 1 and x realizations of partial correction normalized by the RMS of the IM computed with N = 70 realizations. Seeing is 1.4 arcsec and sub-aperture size is 0.2 m for the 8 m-class telescope case.
In the text
thumbnail Fig. 4

PWFS sensitivity in partial correction as a function of mode number and seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Mode 1 is tip, 2 is tilt and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Top-left: sub-aperture size of 0.2 m, top-right, sub-aperture size of 0.4 m. Bottom-left: sub-aperture size of 0.6 m. Bottom-right: sub-aperture size of 0.8 m for the 8 m-class telescope case.
In the text
thumbnail Fig. 5

PWFS sensitivity to a differential piston mode in partial correction as a function of seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. The differential piston mode is the one produced by one petal of a six-petal configuration with no gap. Solid line correspond to a non-modulated PWFS and dashed line correspond to a PWFS with a modulation radius of 3λ/D. Sub-aperture size is 0.2 m. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 6

Differential piston mode in black (also known as petal mode) produced by one segment (petal) of a six-segment (petals) configuration with no gap. The pupil is shown in light blue. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 7

Modal optical gain for the PWFS calibrated in diffraction limited conditions. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen-Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 8

Modal optical gains for the PWFS calibrated in partial correction with a seeing value of 0.8arcsec. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen-Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 9

Results of the product between reconstruction matrix in diffraction limited condition and SIMPC for seeing of 1.4 arcsec, without modulation and with sub-aperture size of 0.2 m. This is the so called modal optical gain matrix. An absolute value is used and only the first 100 × 100 elements of the matrix is shown for clarity reasons. It can be easily seen that that the matrix is not diagonal. The diagonal of this matrix is shown in Fig. 7 (orange solid line). Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 10

Response of the PWFS to modes with different value of wavefront RMS and for different partial correction levels (s = 0.00 arcsec correspond to diffraction limited conditions). Top-left: mode 0 (tip). Top-right: mode 10. Bottom-left: mode 100. Bottom-right: mode 499. Mode 0 is tip, 1 is tilt, and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Sub-aperture size is 0.2 m. Optical gain is corrected considering an aberration RMS of 20 nm. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 11

Response of the PWFS to a tip with different value of wave-front RMS and for different sub-aperture size and for a seeing value of 0.8 arcsec. Solid lines correspond to a non-modulated PWFS and dashed lines correspond to a PWFS with a modulation radius of 3λ/D. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 12

Signals corresponding to a flat wavefront for a non-modulated PWFS with a 0.2 m sub-aperture and different level of partial correction corresponding to seeing values of 0.4, 0.6, 0.8, 1.0, 1.2, and 1.4 arcsec, respectively. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 13

Turbulence (black lines) and residuals (colored lines) modal RMS amplitudes for a NGS of magnitude R = 12, different seeing values and for a non-modulated and modulated (modulation radius of 3λ/D, dashed lines) PWFS. Sub-aperture size is 0.2 m and 500 modes are corrected. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 14

H band (1650 nm) SR as a function of seeing for simulations with a non-modulated PWFS with bright NGS (R magnitude 8). Different colors correspond to different PWFS calibration: black refer s to a classic calibration in diffraction limited conditions, while the other colors are the SIMPC for different seeing levels. Please note that low values of SR correspond to unstable closed loops. Blue and green asterisks correspond to the cases illustrated in Figs. 15 and 16. Refer to the 8 m-class telescope case.
In the text
thumbnail Fig. 15

Results for a simulation with a non-modulated PWFS with bright NGS (R magnitude 8) and with seeing of 0.4 arcsec with a calibration error: PWFS was calibrated for aseeing of 1.2 arcsec. The black line is the ostimation of the opticel goin (done on mode 30), red line is tho H band (168C nm) SR (orange line is the avorage on 1 s), and green line is the average value of the modal gain. Refers to too 8 m-class telescope case.
In the text
thumbnail Fig. 16

Results for a simulation with a non-modulated PWFS with bright NGS (R magnitude 8) and with seeing of 1.4 arcsec with a calibration error: PWFS was caibrated for a seeing of 0.8 arcsec. The black line is the estimation of the optical gain (done on mode 30), red line is the H band (1650 nm) SR (orange line is tha averageon 1 s), and green line is the average value of the modal gain. Refers to the 8 m-class telescope case.
In the text
thumbnail Fig. 17

ELT PWFS sensitivity in partial correction as a function of mode number and seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Mode 1 is tip, 2 is tilt, and the other modes are Karhunen–Loève modes. Solid lines correspond to a non-modulated PWTS and dashed lines correspond to a PWFS with a modulation radius of 4λ/D. Sub-aperture size of 0.433 m. Refers to the ELT case.
In the text
thumbnail Fig. 18

ELT PWFS sensitivity to a differential piston mode in partial correction as a function of seeing value expressed as the RMS of the slope for an aberration with a wavefront RMS of 1nm. Differential pieton mode is the one produced by one petal of a 6 pntals configuration with no gap and with a 0.5 m gyp. Solid line correspond to a non-modulated PWFS and dashed fine correspond to a PWFS with a modulation radius of 4λ/D. Sub-aperture size is 0.433 m and seeing range is [0.4,1.4] arcsec. Refers to the ELT case.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.