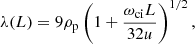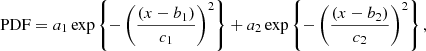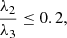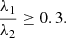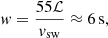| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 12 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202345879 | |
| Published online | 24 August 2023 | |
Magnetic holes between Earth and Mercury: BepiColombo cruise phase
1
Space Research Institute, Austrian Academy of Sciences, Schmiedlstraße 6, 8042 Graz, Austria
e-mail: martin.volwerk@oeaw.ac.at
2
Department of Space and Plasma Physics, School of Electrical Engineering and Computer Science, Royal Institute of Technology, Teknikringen 31, 100-44 Stockholm, Sweden
3
Institute for Geophysics and Extraterrestrial Physics, Technische Universität Braunschweig, Mendelssohnstraße 3, 38106 Braunschweig, Germany
4
Dept. of Mathematics, Physics and Electrical Engineering, Ellison Building, Northumbria University, Newcastle upon Tyne, NE1 8ST Newcastle, UK
5
Data Analysis Center for Geomagnetism and Space Magnetism, Graduate School of Science, Kyoto University, 606-8501 Yoshida-honmachi, Sakyo-ku, Kyoto-sh, Japan
Received:
10
January
2023
Accepted:
30
June
2023
Context. Magnetic holes are ubiquitous structures in the solar wind and in planetary magnetosheaths. They consist of a strong depression of the magnetic field strength, most likely in pressure balance through increased plasma pressure, which is convected with the plasma flow. These structures are created through a plasma temperature anisotropy, where the perpendicular temperature (with respect to the magnetic field) is greater than the parallel temperature. The occurrence rate of these magnetic holes between Earth and Mercury can give us information about how the solar wind conditions develop on their way from the Sun to the outer Solar System. They also give information about basic plasma processes such as diffusion of magnetic structures.
Aims. In this study we investigate the occurrence, size, and depth of magnetic holes during the cruise phase of BepiColombo and compare them with earlier studies.
Methods. The BepiColombo magnetometer data were used to find the magnetic holes. We determined the size in seconds, the depth with respect to the background field, and the rotation angle of the background field across the structure. Minimum variance analysis delivers the polarization state of the magnetic holes. A direct comparison is made to the results obtained from the MESSENGER cruise phase.
Results. We find an almost constant occurrence rate for magnetic holes between Mercury and Earth. The size of the holes is determined by the plasma conditions at the location where they are created and they grow in size, due to diffusion, as they move outwards in the Solar System. The greater the rotation of the background magnetic field across the structure, the larger the minimum size of the magnetic hole is.
Key words: instabilities / magnetic fields / plasmas / waves / solar wind
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The first discussion on magnetic holes (MHs) in the solar wind was raised in the late 1970s by Turner et al. (1977), where they found decreases in the magnetic field strength of up to 90% of the background magnetic field, using magnetometer data from Explorer 43 (also known as IMP 1). A special case of these depressions was when the magnetic field rotation across the structure was less than θ ≤ 10°; these, basically non-rotating, structures were called linear magnetic holes (LMHs). These are ubiquitous structures in the solar wind (Sperveslage et al. 2000; Winterhalter et al. 2000; Burlaga et al. 2007; Stevens & Kasper 2007; Zhang et al. 2008; Volwerk et al. 2020) as well as around and inside planetary magnetosheaths (Xiao et al. 2014; Plaschke et al. 2018; Madanian et al. 2020; Karlsson et al. 2021; Volwerk et al. 2021).
Initially it was thought that LMHs were diamagnetic structures (Turner et al. 1977) and Burlaga & Lemaire (1978) discussed this possibility theoretically, positing that increased plasma pressure inside the LMHs would allow for pressure balance of the structure with the ambient solar wind. Burlaga et al. (1990) and Winterhalter et al. (1995) showed that there is indeed an increase in plasma pressure in these structures. Volwerk et al. (2021) used the Magnetospheric MultiScale (MMS) magnetometer and plasma data and show that in the solar wind there was an almost perfect pressure balance of the LMHs with the ambient solar wind, taking magnetic and ion pressure into account.
Magnetic holes are usually believed to be the result of the mirror instability (Gary 1992) in a high-β plasma with a temperature anisotropy. For a multi-component plasma, the instability criterion is given by the following:
where
is the perpendicular plasma β of species l, the ratio of perpendicular (to the magnetic field) plasma pressure, and the magnetic pressure. Here, nl is the density of species l, kB is Bolzmann’s constant, and μ0 is the permeability of the vacuum. This temperature anisotropy can give rise to two different instabilities: the (Alfvén) ion cyclotron instability for low-β plasma and the mirror mode (MM) instability for high-β plasma (Gary 1992; Gary et al. 1993). Southwood & Kivelson (1993) re-organized the instability criterion, for protons p only, as RSK > 1, where
The increase in the perpendicular temperature or pressure can be created in various ways, which may be concurrent in the plasma: through pick-up, where the newly created ion starts gyrating around the magnetic field; through perpendicular energization whilst crossing the quasi-perpendicular bow shock; and through slow changes in magnetic field strength with conservation of the first adiabatic invariant. The first process mainly occurs in the solar wind interaction with the planetary exosphere (with the exception of Jupiter’s magnetosphere and the Galilean moons, where the Jovian co-rotating magnetic field and magnetospheric plasma takes the role of the solar wind) in the low-β plasma case and generation of ion cyclotron waves takes place (Delva et al. 2008, 2009, 2011, 2015; Schmid et al. 2021).
Magnetic holes and MMs1 are expected to be convected with the ambient plasma velocity; furthermore, using the Cluster spacecraft magnetometer data (Balogh et al. 2001; Horbury et al. 2004) found that in the Earth’s magnetosheath these structures move with a spread of ∼30 km s−1 around the plasma flow velocity. In the solar wind, Trollvik et al. (2023) found a similar spread of the velocity of MHs in the solar wind.
Another way of looking at MHs was presented by Baumgärtel (1999). As these structures, which are frequently assumed to result from the mirror instability in the solar wind (Gary 1992), are often observed in mirror-stable plasmas (Winterhalter et al. 1995), Baumgärtel (1999) proposed that MHs can be seen as ‘magnetically rarefactive (‘dark’) magneto-hydrodynamic (MHD) solitons’. In this model it is assumed that these structures have an anti-phase between the magnetic field strength and plasma density and that they move with a small velocity at large angles to the ambient magnetic field. Starting from an MHD description of the plasma, including Hall effects, a derivative non-linear Schrödinger (DNLS) equation is used as an approximation for the Hall-MHD description of the plasma, and it describes solitons in plasmas well (for details see e.g., Mjølhus & Hada 1997). Baumgärtel (1999) states that the transverse scale, which is referred to as width w in this paper, of the MHs is given by the ion inertial length,
rather than the ion gyro radius, with c being the speed of light and ωpi the ion plasma frequency. From Helios and Voyager data, it was determined that the width of the MHs was between 55 and 35 ℒ between Mercury and Earth (Sperveslage et al. 2000). The soliton solution for MHs leads, depending on input parameters, to a width 8ℒ ≤ w ≤ 60ℒ, agreeing well with observations.
Yet another approach to the final stage of fully saturated MMs is given by Treumann & Baumjohann (2018), who show that the MM can be seen as an analogue of a superconducting effect in a plasma with a temperature anisotropy. The authors replaced the ion gyro radius for a spatial scale of the structures by the following temperature-dependent scale:
where τ = T∥/T⊥ is the temperature ratio and 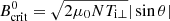 is the critical threshold magnetic field with θ being the propagation angle of the waves with respect to the magnetic field. Furthermore, m is the particle’s mass, and a and b are the Taylor expansion parameters of the Landau-free energy density (Kittel & Kroemer 1980) with respect to the normalized plasma density, respectively.
is the critical threshold magnetic field with θ being the propagation angle of the waves with respect to the magnetic field. Furthermore, m is the particle’s mass, and a and b are the Taylor expansion parameters of the Landau-free energy density (Kittel & Kroemer 1980) with respect to the normalized plasma density, respectively.
Hasegawa & Tsurutani (2011) discussed the generation mechanism and expansion of MMs in planetary magnetosheaths. Using a diffusion model, they deduced that the maximum growth rate for MMs is taking place at wavenumber k = k0 = 0.7/ρp, corresponding to a wavelength λ0 = 2πρp/0.7 = 9ρp, with ρp being the proton gyro radius. When the MMs are then convected with the plasma flow, they subsequently diffuse and their size, as a function of distance L from the source location, is given by the following:
with ωci being the ion cyclotron frequency and u the convection speed of the MMs. It is assumed that Bohm-like diffusion (Bohm et al. 1949) is taking place in the MM structures, where the higher frequencies of the structure diffuse faster than the lower ones, and thereby the MMs grow in size. In this way, one can determine the source region of MMs observed somewhere in a planetary magnetosheath, under the assumption that there is only one such region. This phenomenon was shown to occur at Venus and at comet 1P/Halley (Schmid et al. 2014). This could be a process by which MHs can be generated out of MMs, when a structure of two or more depressions undergoes diffusion and the dips merge to one larger structure (see e.g., event 1, discussed below). However, it is still rather unclear what the exact relationship between MMs and MHs is, apart from both being driven by a temperature anisotropy in the plasma.
The occurrence rate of MHs in the solar wind, as a function of radial distance R from the Sun in astronomical units (au), is an important quantity. It provides information about the development of the structures as they are transported by the solar wind. If, for example, the occurrence rate remains constant in a diverging solar wind, where one could expect an R−1 dilution of the occurrence rate of MHs because of the same number of structures passing through a circle with an increasing radius, there must be a source of these objects along the way.
An overview of all published occurrence rates for linear MHs in the Solar System is listed in Table 1 (adapted from Volwerk et al. 2021). Direct comparison of occurrence rates is often difficult, as each paper has its own definition of LMHs, for example, with respect to the magnetic field rotation angle across the structure, called θ, and its own search algorithm. However, the papers listed in Table 1 all use approximately the same definitions and therefore can be compared to each other.
Occurrence rates of linear MHs in the solar wind throughout the Solar System.
As can be seen in Table 1, there have been many studies of MHs in the solar wind since their discovery by Turner et al. (1977). One of the largest studies was performed by Sperveslage et al. (2000), using the Helios and Voyager spacecraft to study solar wind between Mercury and 17 au away from the Sun. They showed that the occurrence rate is very different in the inner Solar System (∼2 per day) and the outer Solar System (∼0.1 per day). In the same year, another important study was published by Winterhalter et al. (2000), using the Ulysses data. They showed the differences between MMs and MHs, where the MHs were mainly found in MM-stable plasma regions.
Recently, Volwerk et al. (2020) used the MESSENGER cruise-phase magnetometer data, between Earth and Mercury, in order to obtain the occurrence rate between 0.3 ≤ R ≤ 1 au. Unfortunately, the magnetometer data outside Venus’s orbit are irrecoverably disturbed, and thus only the region between 0.3 ≤ R ≤ 0.7 au was studied. In a subsequent paper, Volwerk et al. (2021) used the MMS data to obtain the occurrence rate near Earth, so at R = 1 au. For the present paper, the cruise phase data from BepiColombo were used to fill in the gap between Earth and Venus, and obtain the joint occurrence rate over the region 0.3 ≤ R ≤ 1.2 au during periods around solar minimum.
Karlsson et al. (2021) studied MHs around Mercury using MESSENGER data, and split the events up into two categories: solar wind and magnetosheath. They found that the distribution of the rotation of the magnetic field across the structures was very similar for both categories with a mean(median) value of 30° (13° ) for solar wind events and 24° (14° ) for magnetosheath events. They found, however, a strong difference in the slope of the probability density function (PDF) as a function of the rotational angle. There are two different intervals: MHs with angles of Δϕ < 30° show a slope of λ = 0.099 in a fit with f(Δϕ) = λexp{−λΔϕ}, whereas MHs with angles of Δϕ ≥ 30° show a slope of λ = 0.013. Taking the crossover point of these two fits, at ϕ = 25°, this would be a logical value for the boundary put on the field rotation across LMHs. The mean size of the MHs is estimated to be ∼29ρcp.
Yu et al. (2021) studied MHs with Parker Solar Probe (PSP, Fox et al. 2016) over a solar radial distance of 0.166–0.82 au, where they define LMHs as structures with a depth Bmin/Bavg < 0.75 and a maximum rotation of the field across the structure of ω < 15°. Over two periods in 2018 and 2019, totalling 158 days, they observed 1381 LMHs, leading to an average occurrence rate of ∼8.7 per day, which is much higher than in other studies (see Table 1). Split into different radial bins, there is a variation between ∼0.16(3.8) and ∼0.60(14.4) per hour(day). For the duration of the events, they split the observations into three bins, 0.16–0.38/0.38–0.60/0.5–0.82 au, and found slightly increasing sizes of 11.8/16.1/17.7 s.
The source of the MHs in the solar wind is still under debate. Stevens & Kasper (2007) suggested that the MHs are remnants of magnetic pressure depletions that are generated in a source region close to the Sun. Russell et al. (2008) discussed MMs and deduced from the decrease in the occurrence rate with a radial distance from the Sun that the source region should be well inside the orbit of Mercury.
Lately, so-called switchbacks (see e.g., Tenerani et al. 2021, and references therein) have come into view as a possible source for MHs. Switchbacks are characterized by abrupt Alfvénic rotations of the magnetic field, where the radial component of the magnetic field can even reverse, and they are accompanied with an increase in the radial proton velocity (e.g., Bale et al. 2019; Kasper et al. 2019). Using PSP data, it was found that fast transitioning structures have a decrease in the magnetic field strength at their boundaries of ∼7% (Farrell et al. 2020), indicating the presence of a diamagnetic current. Agapitov et al. (2020) found whistler waves in the PSP observations, which often coincide with magnetic depressions such as MHs (Baumjohann et al. 1999; Ahmadi et al. 2018) or with switchbacks (Krasnoselskikh et al. 2020). The events shown by Agapitov et al. (2020) show that on the boundaries of switchbacks there are magnetic depressions combined with increases in proton density. Because of the nature of switchbacks, these magnetic signatures are inherently rotational.
In this paper we present the analysis of the BepiColombo cruise-phase magnetometer data. In Sect. 2 we introduce the magnetometer data from MPO-MAG and the search method by which the MHs were found in the data. Also, a statistical study of the MHs was performed. In Sect. 3, we explain how we combined the results from this study with those from Volwerk et al. (2020) based on MESSENGER data. In Sect. 4 we introduce the data from the second magnetometer on board BepiColombo, MIO-MGF. And finally in Sect. 5 we discuss the results presented in this paper.
2. Data analysis
The BepiColombo mission (Anselmi & Scoon 2001; Benkhoff et al. 2010, 2021) magnetometer MPO-MAG on board the Mercury Planetary Orbiter (MPO) spacecraft (Glassmeier et al. 2010; Heyner et al. 2021), at a cadence of one vector per second, were used to search for MHs in the solar wind, similar to earlier studies (Plaschke et al. 2018; Volwerk et al. 2020, 2021). The background magnetic field (B300) was determined by a 300 s sliding window average and the data were smoothed by a 2 s sliding window (B2) to reduce some of the noise. These values have been shown to work well in the previous studies mentioned above. The ratio of the variations were calculated through ΔB/B300 = (B300 − B2)/B300, in which the deepest holes were searched with a minimum distance of 300 s. We note that the depth of the MH is defined here as a positive number, even though there is a decrease in the magnetic field strength. Further conditions are that B300 > 2 nT and that ΔB/B300 > 0.5. The search programme delivered the location (t0) of the MH as well as the full width at half minimum (w, which also reduces to the well-known acronym FWHM). To determine the field rotation over the structure, the average magnetic fields, Bbef and Baft, were calculated over the intervals t0 − 2w ≤ tint ≤ t0 − w and t0 + w ≤ tint ≤ t0 + 2w, respectively. The rotation angle of the magnetic field across the structure is then given by θ = cos−1{(Bbef · Baft)/(|Bbef||Baft|)}.
Using observations between 15 December 2018 and 07 July 2022, a total number of 5078 MHs were found. In Fig. 1 the MHs along the orbit of BepiColombo are shown as black dots, as compared to the orbits of Mercury, Venus, and Earth in e2k coordinates2. The figure shows that there are some data gaps, which are caused by the electric propulsion of BepiColombo switching on (see e.g., Benkhoff et al. 2010) and the scientific instruments switching off. The figure also shows that we are covering interplanetary space from slightly beyond Earth’s orbit to the perihelion of Mercury’s orbit.
 |
Fig. 1. Location of MHs (black dots) observed along the orbit of BepiColombo. The locations of LMHs is overplotted as red dots. The dashed circles show the orbits of Mars (perihelion distance), Earth, Venus, and Mercury (perihelion distance), and the dotted circle shows Mercury (aphelion distance). |
To categorize the MHs, we use the rotation angle of the magnetic field across the structure, θ, where we define the structures as follows: LMH, θ ≤ 10°; Rotational magnetic hole (ROT), 10° < θ < 135°; and CURrent sheet (CUR), θ ≥ 135° (super-rotational hole in Karlsson et al. 2021). A total of 5078 MHs were identified of which 2554 are LMHs, 2377 are ROTs, and 127 are CURs. The number of events observed along the cruise phase is shown in Fig. 2 (panel C), in weekly blue bins and a four-bin smoothing in red overplotted. Panels A and B show the solar F10.7 flux as an indicator for solar activity and the radial distance of BepiColombo to the Sun, respectively. There is a slight anti-phase between the distance to the Sun and the smoothed curve, but there seems to be no relationship with the F10.7 flux.
 |
Fig. 2. Number of weekly observed MHs as a function of the cruising time of BepiColombo. Panel A: solar F10.7 flux for each identified MH. Panel B: radial distance of BepiColombo to the Sun for each MH. Panel C: histogram of the number of events observed per week, with the overplotted red line showing a smoothing of the numbers over 4 weeks. |
The total number of MHs observed as a function of the radial distance from the Sun and colour-coded with respect to the rotation angle θ is shown in the top panel of Fig. 3, where the rotational MHs have been split up into smaller angular groups. The radial heliocentric distance, R, of the spacecraft was binned in 0.05 au bins. In the middle panel, the dwelling time in hours is shown for each radial bin. The occurrence rate for MHs was then calculated in #/day, with panel A divided by panel B, shown in the bottom panel. The average occurrence rate for all structures is 6.3 day−1, though with a standard deviation of 2.6 day−1 showing strong variations per bin.
 |
Fig. 3. Number of events, dwelling time of the spacecraft (s/c), and occurrence rate as a function of the radial distance from the Sun with a binning size of 0.05 au. The colour-coding shows the rotation θ over the structures as given in the legend. |
Three examples of MHs are shown in Fig. 4: the first one being a LMH for which the rotation of the magnetic field over the structure is less than 10°; the second one being a ROT; and the third one being a CUR crossing. The top panels show the magnetic field components in e2k coordinates. The middle panels show the magnitude of the magnetic field, Bm, and the background field B300. The bottom panels show ΔB/B300 = (B300 − B2)/B300. The grey-shaded boxes show the width w (FWHM) of the structures.
 |
Fig. 4. Three examples of MHs found with the automated search programme. The left column shows event 1, which is a linear MH with a field rotation θ < 1°. Panel A: magnetic field components in e2k coordinates. Panel B: magnetic field magnitude Bm and the background magnetic field strength B300. Panel C: ΔB/B300 = (B300 − B2)/B300. The middle column shows event 2, which is a rotational MH with θ > 30°, and the right column shows event 3, which is a current sheet crossing with θ > 175°. The grey-shaded boxes show the width w (FWHM) of the structures. |
These three examples show that, although the sizes of the holes are different, the ΔB/B300 maximum amplitude looks rather similar, with decreases of more than 60% of the background field. We note that in the LMH, B300 is possibly underestimating the background field. It is indeed necessary to look at the components of the magnetic field. For the CUR, one can see that all three components change signs.
A set of LMHs with very small rotation over the structure, θ < 1°, is shown in Fig. 5, which shows how LMHs can appear in various settings: for example the left column shows LMHs embedded in a larger rotational structure in Bx. A more detailed description of the structures is given below in Sect. 2.2.
2.1. MH width
The distribution of the width, w, of the LMHs (i.e., the MHs with θ < 10°) is shown in Fig. 6 as a 2D histogram. The peak of the width distribution is between 5 and 20 s. The magenta line shows the peak in the width distribution for each bin and the cyan line shows the width determined by Sperveslage et al. (2000). The two lines line up well and show a similar development in regards to the width of the LMHs with radial distance from the Sun.
 |
Fig. 6. 2D histogram of the LMH width (in seconds) with the magenta line connecting the bins with the maximum number, and the cyan line is the width determined by Sperveslage et al. (2000). |
As the solar wind conditions slowly change with radial distance (see e.g., Stansby et al. 2018), we converted the widths of the MHs and LMHs from seconds to a spatial size, the local solar wind proton gyro radius, ρc, p. We used the following parameters to scale the width to ρc, p: the solar wind velocity is taken as, vsw = 400 km s−1, which gives a spatial scale L = wvsw, and it should be noted that this is an average number and does not account for strong variations; the perpendicular proton temperature is given by Stansby et al. (2018) to be T⊥ = 42.3 × 103(R/1au)−1.07 K; and the gyro radius was calculated as ρc, p = mpv⊥/eB, with 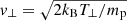 . Thereby we transformed w in seconds into Λ = L/ρc, p in units of ρc, p, which transformed the LMHs of Fig. 6 into Fig. 7, which does not show a significant structure for the size as a function of the radial distance.
. Thereby we transformed w in seconds into Λ = L/ρc, p in units of ρc, p, which transformed the LMHs of Fig. 6 into Fig. 7, which does not show a significant structure for the size as a function of the radial distance.
 |
Fig. 7. 2D histogram of the LMH width (in solar wind proton gyro radii, ρc, p). |
In order to study the size distribution of the MHs and LMHs, a PDF was calculated for both w and Λ (Figs. 8 and 9). The red lines in the figures show a smoothed curve over two data points. The distributions are reminiscent of log-normal distributions (see e.g., Siano 1972; Mitzenmacher 2004); however, fitting the data to such a function did not result in a meaningful result. Therefore, we fitted the data with the following bi-Gaussian fit (yellow line):
 |
Fig. 8. Distribution of widths of MHs (top) and LMHs (bottom). The red line shows the smoothed distribution over two bins. A log-normal (yellow) and a double Gaussian fit (purple) were carried out for the distribution. The bi-Gaussian fitting parameters are listed in Table 2. |
 |
Fig. 9. Distribution of widths of MHs (top) and LMHs (bottom) in local proton gyro radii. The bi-Gaussian fitting parameters are listed in Table 2. |
where x stands for either the FWHM or Λ. From the parameter b1, we get the value of x where the PDF peaks and c1 gives the range in x around b1 within which ∼68% of the PDF lies. The parameters with the subscript ‘2’ describe the variation in the higher values of x. The fitting parameters are listed in Table 2. Using a bi-Gaussian fit indicates that there might be two separate distributions of MHs in the solar wind: a dominant small-sized one and a larger-sized one (a bi-Gaussian is e.g., also used to describe the fast and slow solar wind, Larrodera & Cid 2020).
Results of the bi-Gaussian fittings: f(x) = a1exp{−((x−b1)/c1)2} + a2exp{−((x−b2)/c2)2}.
A study of the width, w, of the holes as a function of the rotation angle, θ, shows that there may be a lower boundary (Fig. 10), which increases with increasing angle θ. It can clearly be seen that most of the events are within a region of 0° ≤θ ≤ 40° and 0 ≤ w ≤ 60 s. However, the events with large rotation angles θ ≥ 80° have a minimum width, w ≥ 30 s, indicating that these rotational structures and current sheets start at larger sizes.
 |
Fig. 10. Width of MHs as a function of the rotation of the magnetic field over the structure. |
2.2. MH characteristics
In order to study further characteristics of the MHs, we performed a minimum variance analysis (MVA, Sonnerup & Scheible 1998) on the structures in the grey boxes in Figs. 4 and 5. From the MVA the wave-vector k can be determined from the minimum variance directions. However, for MMs and MHs, this is non-trivial because of the ellipticity of the structures, where the minimum and intermediate variance directions are difficult to separate, and they often become degenerate (e.g., Génot et al. 2001).
In Table 3 we show the results of the MVA, where the three eigenvalues are listed in increasing order λ1, 2, 3, the error estimate on the MVA directions Δϕ31 and Δϕ31 describe the error in the angles between the maximum and the intermediate variance directions with the minimum variance direction (in radians), and ΔB3 is the error in the magnetic component in the minimum variance direction (in nT). Also shown are the ratios of the eigenvalues, λ3/λ2 and λ2/λ1, to get an estimate of the goodness of the MVA and to get information about the polarization of the structures. Furthermore, the angle between the maximum variance direction and the background magnetic field, α, was calculated to show the compressiveness of the structures.
Génot et al. (2001) discussed the polarization of MMs and provide the following criteria for linearly polarized structures, as these are characterized by a well-defined maximum variance direction,
and the not clearly separated intermediate and minimum variance directions:
These eigenvalue ratios are listed in Table 3. A more detailed look at the six events to see the shape of the structure is provided below, where it should be noted that Eq. (8) is fulfilled for all events. First, we provide a short characterization of the three different structures:
-
Structure one is a linear MH, where the maximum variance direction is well aligned with the background magnetic field, α = 5.7°, indicating a compressional structure. The eigenvalue ratios show that inequality Eq. (9) is not fulfilled, making the LMH more elliptically polarized, that is to say a fat elliptical pancake shape. The ‘double-peaked’ structure of the hole is interesting in this case, and it might indicate that two holes are merging into one, either by slightly different velocities in the plasma frame (Trollvik et al. 2023) or through diffusion of a short MM train (Hasegawa & Tsurutani 2011).
-
Structure two is a rotational hole, where the maximum variance direction is more tilted with respect to the background magnetic field, α = 35°. The eigenvalue ratios show that Eq. (9) is fulfilled, describing a linearly polarized shape.
-
The third structure is a current sheet, where the maximum variance direction is almost perpendicular to the background magnetic field, α = 114°. Equation (9) is not fulfilled, which is to be expected for a current sheet, where the minimum variance direction is normal for the current sheet.
Then we took a look at the three LMHs, which seem to occur under different conditions:
-
4.
The LMH is located in a rotational structure of the solar wind. We note that Bx changes from −5 nT to 3 nT and then turns back again after about 1.5 min. The total magnetic field reduces over the structure, ΔB/B ≈ 0.2, and the MHs (the one marked and the one just before that, which is not marked by the searching program) are visible in all components. Equation (9) is fulfilled, indicating a linearly polarized structure.
-
5.
The LMH is located in relatively constant Bx and By and changing Bz, with the marked hole visible in all components. In this case Eq. (9) is not fulfilled, which indicates an elliptically polarized structure.
-
6.
The LMH is located in a relatively strong southward inter-planetary magnetic field (IMF) with Bz ≈ Bx and little By. The structure is linearly polarized.
2.3. MH occurrence rate
As mentioned above, the average occurrence rate for all structures is 6.3 day−1, with a standard deviation of 2.6 day−1, indicating strong variations per bin, clearly visible in the bottom panel of Fig. 3. It can be clearly seen that the structures with a small rotation of the magnetic field, θ ≤ 45° have the highest occurrence rate throughout the investigated region. The average occurrence rate for LMHs is 3.0 day−1, with a standard deviation of 1.2 day−1. The occurrence rates of MHs and LMHs as a function of the radial distance from the Sun, as determined in the current paper, are shown in Fig. 11.
 |
Fig. 11. Occurrence rate as a function of the radial distance from the Sun from this study (with the MHs in red and the LMHs in blue) compared with the rate of PSP-observed holes (black) by Yu et al. (2021) and SSMHs (green) as determined by Yu et al. (2022). |
Yu et al. (2021) used PSP data to determine the occurrence rate of MHs, as discussed in the introduction above, with slightly different selection criteria: a depth Bmin/Bavg < 0.75 and a maximum rotation ω = 15°. We have transformed their occurrence rate shown in their Fig. 8 from per hour to per day. There are strong variations in the occurrence rate, as also mentioned in Yu et al. (2021). Partially, between 0.4 ≤ R ≤ 0.675 au, their results agree well with the red MH line.
Lately, Yu et al. (2022) studied so-called small-scale magnetic holes (SSMHs), which are LMHs characterized by having a size of the order of the proton gyro radius, first discussed in the Earth’s magnetotail by Ge et al. (2011) using THEMIS data. These SSMHs have also been observed in other environments, such as in the solar wind (Wang et al. 2020). These SSMHs would fall into the first size bin used in this current paper. These small structures, however, show a clear (exponential) fall in radial distance, and thus seem to dissipate faster than regular MHs.
2.4. Linear MH depth
The variation of the depth, ΔB/B300 = (B300 − B2)/B300, of the LMHs with radial distance from the Sun did not show any evidence of a pattern; however, as a function of the background magnetic field strength, Volwerk et al. (2020) show the possible presence of an upper boundary for the depth in the MESSENGER data. A 2D histogram of the depths of LMHs measured by BepiColombo was obtained (Fig. 12). There does not seem to be a field-strength-dependent upper boundary to the depth of the LMHs.
 |
Fig. 12. Depth of LMHs as a function of the background magnetic field strength. The dashed white line shows the purported upper boundary for the depth from Volwerk et al. (2020). |
3. Combining our results with MESSENGER and other missions
This study was started because the MESSENGER magnetometer cruise data between Earth and Venus were strongly disturbed and not recoverable for data analysis (Brian Anderson, priv. comm.; Volwerk et al. 2020). With the BepiColombo MPO-MAG data, this hole in the data can be filled. In addition, one can also use Solar Orbiter data, as currently analysed by Tomas Karlsson (priv. comm.) or PSP data (Yu et al. 2022). Here the results from the MESSENGER and BepiColombo cruise phases are combined. Both datasets are around the minimum phase of the solar cycle as can be seen in Fig. 13, which shows the sunspot number and the F10.7 flux between 2000 and 2023; although, for BepiColombo the activity starts to rise, F10.7 > 100, in 2022.
 |
Fig. 13. Monthly average sunspot number and F10.7 flux since January 2000. The red line shows the MESSENGER cruise phase and the green line shows the BepiColombo cruise phase used in this paper. |
Combining the number of LMHs for MESSENGER and BepiColombo, a distribution over a radial distance 0.3 ≤ R ≤ 1.2 au is obtained, and shown in Fig. 14 in the same format as for Fig. 3. When normalizing the number of events (Fig. 14A) by the spacecraft residence time (Fig. 14B), it appears that the daily occurrence rate of LMHs (Fig. 14C) hardly varies between BepiColombo (red) and MESSENGER (blue). Combining the results of these two missions, we obtain an LMH occurrence rate of 3.0 day−1 with a standard deviation of 1.0 day−1. Moreover, we do not observe the purported radial decrease in the occurrence rate reported in Volwerk et al. (2020) based on the MESSENGER data only. In order to compare the derived occurrence rates for LMHs in this study with other studies, the values given in Table 1 for the radial distance of 0.3 ≤ R ≤ 1.2 au have been provided in Fig. 14C. For the MMS study by Volwerk et al. (2021), an occurrence rate of 2.3/0.9 per day was found, where the lower number was obtained by excluding possible foreshock structures.
 |
Fig. 14. Combination of LMHs observed by MESSENGER (blue) and BepiColombo (red). The same format is used as in Fig. 3. The horizontal blue dashed line in panel C shows the average rate for MESSENGER and BepiColombo at 2.98 day−1, and the magenta dashed lines show the range of rates from Sperveslage et al. (2000). The magenta asterisks give other local occurrence rates listed in Table 1. |
In order to compare the MESSENGER LMHs with those from BepiColombo, we performed the same analysis of the widths of the holes, both in seconds and in proton gyro radii (Fig. 15). The distribution peaks at Λ ≈ 47ρc, p with a width of σ ≈ 29ρc, p. These values are slightly larger than those for BepiColombo. A better comparison can be made when only the BepiColombo data between Mercury and Venus are analysed (Fig. 16); however, the statistics are hampered by the lower number of observations: 703 events for BepiColombo vs. 3381 events for MESSENGER. This is clearly visible in the bottom panel of Fig. 14.
 |
Fig. 15. Distribution of the FWHM and size in local solar wind proton gyro radii of the LMHS detected by MESSENGER. The results are taken from the analysis by Volwerk et al. (2020). |
 |
Fig. 16. Distribution of the FWHM and size in local solar wind proton gyro radii of the LMHs detected by BepiColombo LMHs located between Mercury and Venus, similar to the detection region of MESSENGER in Fig. 15. |
The depth of the LMHs in the combined dataset of BepiColombo and MESSENGER is also investigated in a 2D histogram (Fig. 17). Similar as in Fig. 12, there does not seem to be a dependence of the maximum depth with the magnetic field strength as previously reported by Volwerk et al. (2020) and indicated by the dashed white line.
 |
Fig. 17. Depth of LMHs as a function of the background magnetic field strength of the combined data from BepiColombo and MESSENGER. The dashed white line shows the purported upper boundary for the depth from Volwerk et al. (2020). |
4. Mio-MGF
During the cruise phase of BepiColombo, only MPO-MAG is continuously operational. However, there is a second magnetometer on board Mio, Mio-MGF (Baumjohann et al. 2020), from which the boom has not yet been deployed. This will first happen when the spacecraft reaches its final orbit around Mercury and gets split up into the separate probes MPO and Mio. However, during the cruise phase, there are specific time intervals at which Mio-BFG is switched on to check the health of the instrument. One of the longer intervals was from 17 to 26 March 2022.
We used this interval to check whether Mio-MGF detects the same MHs as found by MPO-MAG. We have taken the MHs from the MPO-MAG determination, which are in the mentioned time interval. Two examples of LMHs are shown in Fig. 18, where both the MPO-MAG (panels A) and the Mio-MGF (panels B) are shown, where the coordinate systems and resolutions are different; MPO-MAG is in e2k coordinates and 1 s resolution, and Mio-MGF is in spacecraft coordinates and 4 s resolution.
 |
Fig. 18. Two examples of LMHs measured by MPO-MAG and Mio-MGF. A: MPO-MAG magnetic field components in e2k coordinates at 1 s resolution. B: Mio-MGF magnetic field components in spacecraft coordinates at 4 s resolution. C: magnitude of the magnetic field for MPO-MAG (blue) and Mio-MGF (red). We note that both instruments measured the same structure; however, the calibration is not yet finished, hence the difference in magnitude between the two. |
Nevertheless, the same LMHs are found with both instruments. We provide a brief summary of the two events:
-
7.
Structure seven is an LMH with θ = 2.4° and w = 13 s observed during strong IMF By and little Bx and Bz. Interestingly, there is an increase in Bx at the centre of the LMH for MPO-MAG (panel A), indicating a small rotation of the field from Bz into Bx inside the LMH. Such a behaviour is not found in the Mio-MGF data (panel B). The MVA characteristics listed in Table 3 show that the structure is elliptically polarized, and the maximum variance direction is less aligned with the background magnetic field.
-
8.
Structure eight is an LMH with θ = 6.3° and w = 54 s, where the deepest magnetic field minimum is within a much longer drop in Bt, asymmetric placed (that is, near the boundary of the long decrease in Bt). Overall, the whole large structure just fulfills Eq. (9), indicating a linear polarization. None of the components in the e2k coordinate system change sign, in contrast to event 4. The rotation oif the magnetic field across the structure is slightly larger than in the other LMH examples (θ ≈ 6.3°) and the maximum variance direction is slightly less aligned with the background magnetic field (∼160°). With multiple small dips at the ‘bottom’ of the structure, this could well be created by the merging of multiple MHs.
5. Discussion
We have studied the occurrence rate of MHs and LMHs between Earth and Venus, using the BepiColombo cruise-phase data for the period 15 December 2018–7 July 2022. A total of 5078 MHs were found, with an average occurrence rate of 6.3 day−1 with a standard deviation of 2.6 day−1. Of these structures, 2554 were labelled as LMHs, with an average occurrence rate of 3.0 day−1 and a standard deviation of 1.2 day−1. There does not seem to be a radial dependence on the occurrence rates of MHs and LMHs. Combining the BepiColombo data with the MESSENGER cruise-phase data gives an average occurrence rate for LMHs of 3.0 day−1 with a standard deviation of 1.0 day−1. The near-Earth MMS rate was 2.3 day−1, which fits well with these results, as can be seen in Fig. 14; however, when taking out possible foreshock structures, the rate reduces to 0.9 days−1 (Volwerk et al. 2021). Other near-Earth studies also showed lower rates (see also Table 1) and near Venus Zhang et al. (2008) found a higher rate than the average but in agreement with the red bar in the 0.65–0.70 au bin in Fig. 14, similarly near Mercury Karlsson et al. (2021) found a higher rate than the average but in agreement with red bar in the 0.40–0.45 au bin.
Interestingly, the lack of a radial dependence on the occurrence rate is in contrast to the conclusions that are drawn in Volwerk et al. (2020), where it was posited, albeit with meager evidence, that the occurrence rate drops with increasing distance from the Sun between Mercury and Venus. The results now obtained lead us to believe that there is a constant occurrence rate in this region of 0.3 ≤ R ≤ 1.2 au, in agreement with the results of Yu et al. (2021). However, this is in sharp contrast with the SSMHs reported by Yu et al. (2022), which show an exponential decay with an ordinate of −6.8R/au. This has consequences as to the hypothesis for the creation and development of MHs in the solar wind moving through interplanetary space. An approximately constant occurrence rate means that through ever larger spherical surfaces around the Sun (going radially outwards), we still observe the same number. This can be due to various reasons. First, the holes can increase in physical size so they cover an equal percentage of the circumference of the growing circle; however, this would not be in agreement with the sizes determined for the events as shown in Fig. 6, where there is an average increase from an ∼7 to ∼15 s duration not quite doubling in physical size taking into account a decreasing solar wind velocity, whereas the circle would increase fourfold in circumference. Second, here is a continuous creation and annihilation of MHs in the heliosphere at all radial distances from the Sun. However, the behaviour of MHs as they are transported along with the solar wind and diffuse (Hasegawa & Tsurutani 2011) is still not very clear and should be investigated by simulations.
The sizes of the MHs varies with radial distance from the Sun: from ∼7 s near Mercury to ∼15 s near Earth, which agrees with the findings of Sperveslage et al. (2000) well. Transforming the size from a timescale to a spatial scale, using the solar wind velocity and the local proton gyro radius, shows that this slow increase in a timescale is not reflected in an ordered increase in a spatial scale. If MHs behave similarly to MMs, then there are diffusion mechanisms, such as the Bohm-like diffusion (Bohm et al. 1949) proposed by Hasegawa & Tsurutani (2011), making the size of MMs bigger, as shown by Schmid et al. (2014), for example. The higher-frequency components of the MH structure diffuse faster than the lower frequencies. As this growth is seen in the temporal scale w of the events but not in their size as a function of the local Larmor radius, Λ, the local Larmor radius does not play a role in the size of the MHs. The width, w, is probably determined by the value at the location where the MH is created. As discussed above in the introduction, Baumgärtel (1999) provided the width, w, as the ion inertial length scale (see Eq. (4)) with a range of 55 ≥ ℒ ≥ 35, from Mercury to Earth. Converting this at Mercury to a temporal size, we obtain the following:
where we had np = 30 cm−3, vsw = 400 km s−1 and a scale of 55ℒ. This is quite close to the observed peak in the width, w, in Fig. 6 for both this study and for Sperveslage et al. (2000). Near Earth, with np = 3 cm−3 and a scale of 35ℒ (Baumgärtel 1999), we find w ≈ 9 s, which is well below what has been observed in this study and that by Sperveslage et al. (2000). So we are observing MHs that are created near Mercury and along the way to Earth, which then develop as they move along with the solar wind.
In the data there is a gap produced by the instruments being turned off when the electric propulsion was switched on the first time; however, at later stages in the cruise phase, the magnetometer remained switched on during the operation of the electric propulsion. This could have an influence on the detection of MHs. In order to see whether there is an influence, we took the intervals when the propulsion was switched on and compared the occurrence rate of MHs with the same intervals shifted forwards and backwards in time over a few days. There was no statistically significant difference in the occurrence rates of MHs. At higher frequencies, though, the electric propulsion does have an influence on the observed wave power (Heyner, priv. comm.).
e2k: Mean ecliptic and equinox of the J2000 coordinate system. The origin is the Sun’s centre, the plane of reference is the ecliptic plane, and the primary direction (the x-axis) is the vernal equinox. A right-handed rule specifies a y-axis 90° to the west on the fundamental plane. The z-axis points towards the north ecliptic pole.
Acknowledgments
The work by CSW is supported by the Austrian Science Fund (FWF) under project N32035-N36. Daniel Heyner is supported by the German Ministerium für Wirtschaft und Energie and the German Zentrum für Luft- und Raumfahrt under contract 50 QW 1501 and 50 QW 2202. The authors thank ISSI for facilitating research between the members of ISSI international team 517 ‘Towards a Unifying Model for Magnetic Depressions in Space Plasmas’. The BepiColombo data are available through ESA’s PSA (https://archives.esac.esa.int/psa). The sunspot number was obtained from silso (http://sidc.be/silso/monthlyssnplot) and the F10.7 data were obtained from lisird (https://lasp.colorado.edu/lisird/data/penticton_radio_flux/).
References
- Agapitov, O. V., Dudok de Wit, T., Mozer, F. S., et al. 2020, ApJ, 891, L20 [Google Scholar]
- Ahmadi, N., Wilder, F. D., Ergun, R. E., et al. 2018, J. Geophys. Res., 123, 6383 [NASA ADS] [CrossRef] [Google Scholar]
- Anselmi, A., & Scoon, G. E. N. 2001, Planet. Space Sci., 49, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, A., Carr, C. M., Acuña, M. H., et al. 2001, Ann. Geophys., 19, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgärtel, K. 1999, J. Geophys. Res., 104, 28295 [CrossRef] [Google Scholar]
- Baumjohann, W., Treumann, R. A., Georgescu, E., et al. 1999, Ann. Geophys., 17, 1528 [CrossRef] [Google Scholar]
- Baumjohann, W., Matsuoka, A., Narita, Y., et al. 2020, Space Sci. Rev., 216, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., Casteren, J., Hayakawa, H., et al. 2010, Planet. Space Sci., 58, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhoff, J., Murakami, G., Baumjohann, W., et al. 2021, Space Sci. Rev., 217, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Bohm, D., Burhop, E. H. S., & Massey, H. S. W. 1949, in The characteristics of electrical discharges in magnetic fields, eds. A. Guthrie, & R. K. Wakerling (New York: McGraw-Hill), 13 [Google Scholar]
- Burlaga, L. F., & Lemaire, J. F. 1978, J. Geophys. Res., 83, 5157 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L., Scudder, J., Klein, L., & Isenberg, P. 1990, J. Geophys. Res., 95, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., & Acuna, M. H. 2007, J. Geophys. Res., 112, A07106 [NASA ADS] [Google Scholar]
- Delva, M., Zhang, T. L., Volwerk, M., Vörös, Z., & Pope, S. A. 2008, Geophys. Res., 113, E00B06 [CrossRef] [Google Scholar]
- Delva, M., Volwerk, M., Mazelle, C., et al. 2009, Geophys. Res. Lett., 36, L01203 [NASA ADS] [CrossRef] [Google Scholar]
- Delva, M., Mazelle, C., Bertucci, C., et al. 2011, J. Geophys. Res., 116, A02318 [NASA ADS] [Google Scholar]
- Delva, M., Bertucci, C., Volwerk, M., et al. 2015, J. Geophys. Res., 120, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, W. M., MacDowall, R. J., Gruesbeck, J. R., Bale, S. D., & Kasper, J. C. 2020, ApJS, 249, 28 [Google Scholar]
- Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Gary, S. P. 1992, J. Geophys. Res., 97, 8519 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Fuselier, S. A., & Anderson, B. J. 1993, J. Geophys. Res., 98, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, Y. S., McFadden, J. P., Raeder, J., et al. 2011, J. Geophys. Res., 116, A01209 [NASA ADS] [Google Scholar]
- Génot, V., Schwartz, S. J., Mazelle, C., et al. 2001, J. Geophys. Res., 106, 21611 [CrossRef] [Google Scholar]
- Glassmeier, K. H., Auster, H. U., Heyner, D., et al. 2010, Planet. Space Sci., 58, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, A., & Tsurutani, B. T. 2011, Phys. Rev. Lett., 107, 245005 [NASA ADS] [CrossRef] [Google Scholar]
- Heyner, D., Auster, H.-U., Fornacon, K.-H., et al. 2021, Space Sci. Rev., 217, 52 [CrossRef] [Google Scholar]
- Horbury, T. S., Lucek, E. A., Balogh, A., Dandouras, I., & Rème, H. 2004, J. Geophys. Res., 109, A09209 [NASA ADS] [Google Scholar]
- Karlsson, T., Heyner, D., Volwerk, M., et al. 2021, J. Geophys. Res., 126, e2020JA028961 [CrossRef] [Google Scholar]
- Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228 [Google Scholar]
- Kittel, C., & Kroemer, H. 1980, Thermal Physics (New York: W. H. Freeman and Company) [Google Scholar]
- Krasnoselskikh, V., Larosa, A., Agapitov, O., et al. 2020, ApJ, 893, 93 [Google Scholar]
- Larrodera, C., & Cid, C. 2020, A&A, 635, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madanian, H., Halekas, J. S., Mazelle, C. X., et al. 2020, J. Geophys. Res., 125, e27198 [NASA ADS] [CrossRef] [Google Scholar]
- Mitzenmacher, M. 2004, Internet Math., 1, 226 [CrossRef] [Google Scholar]
- Mjølhus, E., & Hada, T. 1997, in Nonlinear Waves and Chaos in Space Plasmas, eds. T. Hada, & H. Matsumoto (Japan: Terra Scientific Publishing Company), 121 [Google Scholar]
- Plaschke, F., Karlsson, T., Götz, C., et al. 2018, A&A, 618, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, C. T., Jian, L. K., Luhmann, J. G., et al. 2008, Geophys. Res. Lett., 35, L15101 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, D., Volwerk, M., Plaschke, F., et al. 2014, Ann. Geophys., 32, 651 [CrossRef] [Google Scholar]
- Schmid, D., Narita, Y., Plaschke, F., et al. 2021, Geophys. Res. Lett., 48, e2021GL092606 [CrossRef] [Google Scholar]
- Siano, D. B. 1972, J. Chem. Educ., 11, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U. Ö., & Scheible, M. 1998, in Analysis Methods for Multi-Spacecraft Data, eds. G. Paschmann, & P. Daly (Noordwijk: ESA), 185 [Google Scholar]
- Southwood, D. J., & Kivelson, M. G. 1993, J. Geophys. Res., 98, 9181 [NASA ADS] [CrossRef] [Google Scholar]
- Sperveslage, K., Neubauer, F. M., Baumgärtel, K., & Ness, N. F. 2000, Nonlin. Proc. Geophys., 7, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stansby, D., Salem, C., Matteini, L., & Horbury, T. 2018, Sol. Phys., 293, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, M. L., & Kasper, J. C. 2007, J. Geophys. Res., 112, A05109 [NASA ADS] [Google Scholar]
- Tenerani, A., Sioulas, N., Matteini, L., et al. 2021, ApJ, 919 [Google Scholar]
- Treumann, R. A., & Baumjohann, W. 2018, Ann. Geophys., 36, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Trollvik, H., Karlsson, T., & Raptis, S. 2023, Ann. Geophys. Discuss., in press, https://doi.org/10.5194/angeo-2023-5 [Google Scholar]
- Turner, J. M., Burlaga, L. F., Ness, N. F., & Lemaire, J. F. 1977, J. Geophys. Res., 82, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Volwerk, M., Goetz, C., Plaschke, F., et al. 2020, Ann. Geophys., 38, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Volwerk, M., Mautner, D., Simon Wedlund, C., et al. 2021, Ann. Geophys., 39, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, G. Q., Zhang, T. L., Xiao, S. D., et al. 2020, J. Geophys. Res., 125, e28320 [NASA ADS] [Google Scholar]
- Winterhalter, D., Neugebauer, M., Goldstein, B. E., et al. 1995, Space Sci. Rev., 72, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Winterhalter, D., Smith, E. J., Neugebauer, M., Goldstein, B. E., & Tsurutani, B. T. 2000, Geophys. Res. Lett., 27, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, T., Shi, Q. Q., Tian, A. M., et al. 2014, Sol. Phys., 289, 3175 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, L., Huang, S. Y., Yuan, Z. G., et al. 2021, ApJ, 908, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, L., Huang, S. Y., Yuan, Z. G., et al. 2022, J. Geophys. Res., 127, e30505 [NASA ADS] [Google Scholar]
- Zhang, T. L., Russell, C. T., Baumjohann, W., et al. 2008, Geophys. Res. Lett., 35, L10106 [NASA ADS] [Google Scholar]
All Tables
Results of the bi-Gaussian fittings: f(x) = a1exp{−((x−b1)/c1)2} + a2exp{−((x−b2)/c2)2}.
All Figures
 |
Fig. 1. Location of MHs (black dots) observed along the orbit of BepiColombo. The locations of LMHs is overplotted as red dots. The dashed circles show the orbits of Mars (perihelion distance), Earth, Venus, and Mercury (perihelion distance), and the dotted circle shows Mercury (aphelion distance). |
| In the text | |
 |
Fig. 2. Number of weekly observed MHs as a function of the cruising time of BepiColombo. Panel A: solar F10.7 flux for each identified MH. Panel B: radial distance of BepiColombo to the Sun for each MH. Panel C: histogram of the number of events observed per week, with the overplotted red line showing a smoothing of the numbers over 4 weeks. |
| In the text | |
 |
Fig. 3. Number of events, dwelling time of the spacecraft (s/c), and occurrence rate as a function of the radial distance from the Sun with a binning size of 0.05 au. The colour-coding shows the rotation θ over the structures as given in the legend. |
| In the text | |
 |
Fig. 4. Three examples of MHs found with the automated search programme. The left column shows event 1, which is a linear MH with a field rotation θ < 1°. Panel A: magnetic field components in e2k coordinates. Panel B: magnetic field magnitude Bm and the background magnetic field strength B300. Panel C: ΔB/B300 = (B300 − B2)/B300. The middle column shows event 2, which is a rotational MH with θ > 30°, and the right column shows event 3, which is a current sheet crossing with θ > 175°. The grey-shaded boxes show the width w (FWHM) of the structures. |
| In the text | |
 |
Fig. 5. Three examples of linear MHs in the same format as Fig. 4. |
| In the text | |
 |
Fig. 6. 2D histogram of the LMH width (in seconds) with the magenta line connecting the bins with the maximum number, and the cyan line is the width determined by Sperveslage et al. (2000). |
| In the text | |
 |
Fig. 7. 2D histogram of the LMH width (in solar wind proton gyro radii, ρc, p). |
| In the text | |
 |
Fig. 8. Distribution of widths of MHs (top) and LMHs (bottom). The red line shows the smoothed distribution over two bins. A log-normal (yellow) and a double Gaussian fit (purple) were carried out for the distribution. The bi-Gaussian fitting parameters are listed in Table 2. |
| In the text | |
 |
Fig. 9. Distribution of widths of MHs (top) and LMHs (bottom) in local proton gyro radii. The bi-Gaussian fitting parameters are listed in Table 2. |
| In the text | |
 |
Fig. 10. Width of MHs as a function of the rotation of the magnetic field over the structure. |
| In the text | |
 |
Fig. 11. Occurrence rate as a function of the radial distance from the Sun from this study (with the MHs in red and the LMHs in blue) compared with the rate of PSP-observed holes (black) by Yu et al. (2021) and SSMHs (green) as determined by Yu et al. (2022). |
| In the text | |
 |
Fig. 12. Depth of LMHs as a function of the background magnetic field strength. The dashed white line shows the purported upper boundary for the depth from Volwerk et al. (2020). |
| In the text | |
 |
Fig. 13. Monthly average sunspot number and F10.7 flux since January 2000. The red line shows the MESSENGER cruise phase and the green line shows the BepiColombo cruise phase used in this paper. |
| In the text | |
 |
Fig. 14. Combination of LMHs observed by MESSENGER (blue) and BepiColombo (red). The same format is used as in Fig. 3. The horizontal blue dashed line in panel C shows the average rate for MESSENGER and BepiColombo at 2.98 day−1, and the magenta dashed lines show the range of rates from Sperveslage et al. (2000). The magenta asterisks give other local occurrence rates listed in Table 1. |
| In the text | |
 |
Fig. 15. Distribution of the FWHM and size in local solar wind proton gyro radii of the LMHS detected by MESSENGER. The results are taken from the analysis by Volwerk et al. (2020). |
| In the text | |
 |
Fig. 16. Distribution of the FWHM and size in local solar wind proton gyro radii of the LMHs detected by BepiColombo LMHs located between Mercury and Venus, similar to the detection region of MESSENGER in Fig. 15. |
| In the text | |
 |
Fig. 17. Depth of LMHs as a function of the background magnetic field strength of the combined data from BepiColombo and MESSENGER. The dashed white line shows the purported upper boundary for the depth from Volwerk et al. (2020). |
| In the text | |
 |
Fig. 18. Two examples of LMHs measured by MPO-MAG and Mio-MGF. A: MPO-MAG magnetic field components in e2k coordinates at 1 s resolution. B: Mio-MGF magnetic field components in spacecraft coordinates at 4 s resolution. C: magnitude of the magnetic field for MPO-MAG (blue) and Mio-MGF (red). We note that both instruments measured the same structure; however, the calibration is not yet finished, hence the difference in magnitude between the two. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



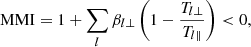
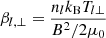
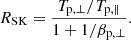
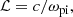
![$$ \begin{aligned} \lambda _{\rm im} = \left[ \frac{m^2 b}{\mu _0 q^4(N_0 B_{\rm crit}^0)^2} \frac{\tau }{1-\tau } \right]^{1/4}\,\mathrm{m } ,\end{aligned} $$](/articles/aa/full_html/2023/09/aa45879-23/aa45879-23-eq5.gif)