| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A194 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202345921 | |
| Published online | 21 June 2023 | |
Photometric metallicity for 694 233 Galactic giant stars from Gaia DR3 synthetic Strömgren photometry
Metallicity distribution functions of halo substructures⋆
1
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
e-mail: michele.bellazzini@inaf.it
2
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge, CB3 0HA
UK
3
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
Received:
17
January
2023
Accepted:
17
April
2023
We used two previous calibrations and the standardised synthetic photometry in the v, b, and y Strömgren passbands from Gaia DR3 BP/RP spectra to obtain photometric metallicities for a selected sample of 694 233 old Galactic giant stars having |b|> 20.0° and parallax uncertainties lower than 10%. The zero point of both sets of photometric metallicities has been shifted to ensure an optimal match with the spectroscopic [Fe/H] values for 44 785 stars in common with APOGEE DR17, focusing on the metallicity range where they provide the highest accuracy. The metallicities derived in this way from one calibration display a typical accuracy of ≲0.1 dex and 1σ precision ≲0.2 dex in the range −2.2 ≲ [Fe/H] ≲ −0.4, while they show a systematic trend with [Fe/H] at higher metallicity, beyond the applicability range of the relation. Those derived from the other calibration display, in general, reduced precision, and lower accuracy in the metal-poor regime, but have a median accuracy < 0.05 dex for [Fe/H] ≥ − 0.8. These results are confirmed and, consequently, the metallicities are validated, by comparison with large sets of spectroscopic metallicities from various surveys. The newly obtained metallicities are used to derive metallicity distributions for several previously identified substructures in the Galactic halo with an unprecedented number of stars. The catalogue including the two sets of metallicities and the associated uncertainties is made publicly available.
Key words: catalogs / techniques: photometric / stars: abundances / Galaxy: structure / Galaxy: evolution / Galaxy: halo
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/674/A194
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Photometric metallicities have a long and distinguished history. For example, they were key observational ingredients for the two seminal papers on the formation of the Milky Way of the past century: Eggen et al. (1962) and Searle & Zinn (1978). After a long period in which the technique was relegated to a minor role, it is gaining considerable credit and growing momentum (among the most recent examples, see Starkenburg et al. 2017; Longeard et al. 2018; Arentsen et al. 2020; Chiti et al. 2021; Yang et al. 2022; Xu et al. 2022; Lucey et al. 2023; Fallows & Sanders 2022; An et al. 2022; Rix et al. 2022; Chandra et al. 2022; Li et al. 2023).
In our view, there are two main factors driving this revival. First, the advent of modern digital surveys providing high-precision photometry over wide areas of the sky (e.g. 2MASS, SDSS, PS1; see Skrutskie et al. 2006; Magnier et al. 2020; Thanjavur et al. 2021, respectively, and references therein), some of which especially focused on photometric metallicities (e.g. Pristine, Starkenburg et al. 2017, and SkyMapper, Chiti et al. 2021). Second, the availability of large samples of stellar abundances from modern spectroscopic surveys (e.g. APOGEE, Gaia-ESO, GALAH, LAMOST; see Cui et al. 2012; Majewski et al. 2017; Buder et al. 2021; Gilmore et al. 2022, respectively), allowing robust empirical calibration and validation of photometric metallicities.
An additional factor facilitating the production and the successful scientific use of large samples of photometric metallicities is the advent of the various data releases of the ESA/Gaia astrometric mission (see Gaia Collaboration 2016, 2021, 2023a; Lindegren et al. 2021, and references therein). These greatly boosted our capability of revealing the key connections between chemical and kinematical properties of stars and, for instance, pushed our ability to reliably distinguish giants from dwarfs to an unprecedented level, at least for stars with high-precision parallaxes. It may be worth noting here that Gaia is also beginning to provide a significant contribution in terms of chemical abundances from medium-resolution spectra in the Ca triplet region (Recio-Blanco et al. 2023; Gaia Collaboration 2023b), providing an additional all-sky spectroscopic survey.
With Gaia DR3 (Gaia Collaboration 2023a), the first release of spectrophotometry from the BP/RP (XP) low-resolution spectrometers1 (Carrasco et al. 2021; De Angeli et al. 2023; Montegriffo et al. 2023) opened a completely new window to our capability of deriving metallicities for a huge number of stars. Andrae et al. (2023) demonstrated the enormous potential of the full-forward modelling of the entire XP spectra to derive stellar astrophysical parameters; however, this will be fully exploited only in future Gaia data releases when several issues related to systematics in XP spectra and the tuning of their complex modelling have been fixed.
On the other hand, Gaia Collaboration (2023c) showed that very precise all-sky space-based synthetic photometry (SP) can be obtained from XP spectra for any medium to wide passband whose transmission curve (TC) is completely enclosed in the XP spectral range (330 nm−1100 nm). The residual systematic errors in externally calibrated XP spectra (Montegriffo et al. 2023) still prevent accurate reproduction of existing photometry in some regions of the spectra, notably below ≃550 nm and especially at λ < 400 nm. However, using reliable sets of external photometric standards for a second-level calibration, with a process they denote as ‘standardisation’, Gaia Collaboration (2023c) were able to reproduce the existing photometry in several widely used systems to millimag accuracy over large colour ranges. In Gaia Collaboration (2023c) it was also demonstrated that narrow to medium band synthetic photometry is able to efficiently extract the information on metallicity and, to a lesser extent, on α-element abundance, encoded in XP spectra (see also Rix et al. 2022; Chandra et al. 2022). Synthetic photometry with well suited passbands, on the one hand focuses on the region of the spectrum that is most sensitive to the information of interest, and on the other maximises the signal-to-noise ratio (S/N) by making use of all the photons in the considered wavelength range.
The Strömgren index m1 = (v − b)−(b − y) is widely used to estimate metallicity of giant stars (see e.g. Richter et al. 1999; Hilker 2000; Anthony-Twarog & Twarog 2000; Dirsch et al. 2000; Faria et al. 2007; Calamida et al. 2009; Árnadóttir et al. 2010; Piatti 2020; Narloch et al. 2021, 2022). Strömgren vby is the only widely used medium-width band system for which XP SP has been standardised by Gaia Collaboration (2023c). Moreover, m1 is the only photometric tracer of metallicity that does not imply the use of a passband sampling the critical region of XP spectra below 400 nm, among those explored by Gaia Collaboration (2023c).
In this paper we follow up the successful experiments illustrated in Gaia Collaboration (2023c); we used standardised synthetic Strömgren vby photometry from Gaia DR3 XP spectra to obtain metallicity estimates for ≃700 000 Galactic red giant branch (RGB), red horizontal branch (RHB), and asymptotic giant branch (AGB) stars fainter than the RGB tip, and have made the catalogue publicly available. As a first step, we limited ourselves to stars at relatively high Galactic latitude (|b|> 20.0°) and having parallax uncertainties lower than 10%, thus ensuring a proper separation between giants and dwarfs. The analysis and validation presented here provide the basis for future more extensive applications.
It is very likely that the optimal way to obtain metallicity estimates from photometry and/or very low-resolution spectrophotometry is by making use of as many indices as possible through extensively trained machine learning algorithms, as has been done in several works (e.g. Fallows & Sanders 2022; Lucey et al. 2023; Yang et al. 2022; Chandra et al. 2022). Rix et al. (2022), in particular, combined Gaia XP spectra, photometric indices from XP SP, and infrared AllWISE photometry (Cutri et al. 2021) to obtain metallicities with a typical precision of about 0.1 dex with an efficient machine learning algorithm trained with APOGEE metallicities. Here we show, under certain conditions, that we can achieve similar performance using a completely transparent analytic relation between Strömgren colour indices and [Fe/H], taking advantage of the excellent precision of standardised Strömgren XP SP from Gaia DR3 and of the possibility to refine and validate the results using large samples of well-measured spectroscopic metallicities.
We decided to rely on two existing and widely used calibrations, those by Calamida et al. (2007, hereafter C07) and by Hilker (2000, hereafter H00). Then we used a large sample of well-measured spectroscopic metallicities from APOGEE DR17 (Abdurro’uf et al. 2022) to adjust the zero point of the resulting metallicity scales to the APOGEE DR17 scale. This a posteriori recalibration simultaneously accounts for differences in the adopted metallicity scale between the calibrating relations and APOGEE DR17 and for inhomogeneities in the calibration of Strömgren indices between the various authors and Gaia XP synthetic photometry. The metallicities we derived from the C07 calibration are found to be more accurate and precise than those obtained from the H00 calibration in the range [Fe/H] ≲ −0.5. Since we are more interested in the metal-poor regime, we tailored our sample selection to the properties of the C07 relation (see Sect. 3).
The results shown here provide a simple recipe for deriving reliable photometric metallicity for old giant stars from well-measured Strömgren XP SP that can be of general use.
The plan of the paper is the following. In Sect. 2 we present the adopted calibrating relations and we briefly discuss the dependence of the photometric metallicity on age. In Sect. 3 we present the adopted sample, with all the selections we applied. In Sect. 4 we show the comparison with APOGEE spectroscopic metallicity and the recalibration of our photometric metallicities to the APOGEE DR17 scale. In Sect. 5 we use our dataset to study the metallicity distribution function of several known substructures in the local Galactic halo, based on much larger samples than those previously considered in the literature. Finally, in Sect. 6 we briefly summarise and discuss the main results of our analysis. In Appendix A we validate our photometric metallicities against their spectroscopic counterparts from various surveys. In Appendix C we use known member stars of star clusters included in our dataset to explore the performance of our photometric metallicities in different regimes. In Appendices D and E we discuss the impact of reddening and of α-element abundance on our metallicity estimates, respectively.
2. The calibrating relations
In the following, we correct Strömgren indices from reddening as recommended by C07. We adopted the extinction laws m1, 0 = m1 + 0.24E(B − V), (v − y)0 = (v − y)−1.24E(B − V), and (b − y)0 = (b − y)−0.74E(B − V) from Crawford & Mandwewala (1976).
As our preferred choice, we convert reddening-corrected Strömgren indices m1, 0 and (v − y)0 into metallicity estimates using the empirical relation
calibrated by C07 on selected Galactic globular clusters in the range −2.2 ≤ [Fe/H] ≤ −0.7, adopting the Zinn & West (1984) metallicity scale2. According to C07 the uncertainty associated with the calibration itself is ≃0.10 dex. C07 note that the relation is linear over the range 0.85 ≲ (v − y)0 ≲ 3.0. However, we preferred to limit the application of the calibration, conservatively, to the narrower range 1.0 < (v − y)0 < 2.4, also using their Fig. 11 as a guideline. Our choice was aimed (a) on the blue side, at excluding the colour range most prone to contamination from non-RGB stars and where the sensitivity of m1, 0 to metallicity is at its minimum, and (b) on the red side, at avoiding the colour range that can be reached only by relatively metal-rich stars, and thus minimising selection biases in metallicity distribution functions.
All the relations provided by C07 are calibrated on old stellar populations or old age stellar models and on a metallicity range never exceeding −2.6 ≤ [Fe/H] ≤ −0.6 (see Appendix B). In principle they should not be used beyond their applicability range. Hence, their performance may not be optimal for young and/or very metal-rich or very metal-poor stars (see Sect. 4 for further discussion).
Alternatively, we used the relation provided by H00, calibrated using globular clusters and field stars in the range −2.2 ≤ [Fe/H] ≤ 0.0,
with metallicity in the Zinn & West (1984) scale. The colour range of validity is 0.5 ≤ (b − y)0 ≤ 1.1. The uncertainty associated with the calibration, as measured by H00, is in the range 0.11 − 0.16 dex, after the rejection of stars whose absolute difference between [Fe/H]phot and [Fe/H]spec was larger than 0.25 dex.
The subscripts v and b assigned to the two different estimates of the photometric metallicity refer to the dependence on the (v − y)0 and (b − y)0 colours of the C07 and H00 calibrations, respectively. One-sigma errors on [Fe/H]phot from both relations were computed following Piatti (2020), who provides error propagation formulae for the C07 and H00 calibrations, including the contribution of uncertainties on the coefficients of the calibrating relations. Uncertainties on observed magnitudes, computed as 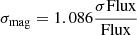 , were combined with uncertainties on extinction to compute uncertainties in the extinction-corrected indices and colours actually used in Eqs. (1) and (2). In practice, uncertainties on all the input quantities of these equations, including coefficients, are propagated into the uncertainty of the derived photometric metallicities.
, were combined with uncertainties on extinction to compute uncertainties in the extinction-corrected indices and colours actually used in Eqs. (1) and (2). In practice, uncertainties on all the input quantities of these equations, including coefficients, are propagated into the uncertainty of the derived photometric metallicities.
The comparison with reliable spectroscopic samples, shown below, demonstrates that the typical standard deviation of the differences between photometric and spectroscopic metallicities is of similar order to the computed uncertainties. Even so, they cannot properly account for all the sources of uncertainty, and hence they must be interpreted with caution. Individual uncertainties should be considered as educated guesses, mainly driven by the signal-to-noise ratio of the magnitudes used to derive the Strömgren indices and by the reddening (see also Appendix C).
Metallicity derived from the m1, 0 index for RGB stars are generally believed to be nearly independent of age (see e.g. Hilker 2000; Dirsch et al. 2000; Faria et al. 2007; Narloch et al. 2022), but arguments against this view have recently been presented by Piatti (2020) and Gaia Collaboration (2023c). In Fig. 1 we show the results of a small experiment we made using PARSEC solar-scaled isochrones (Bressan et al. 2012; Chen et al. 2019) produced with the dedicated web tool3. Five bundles of RGB isochrones spanning the global metallicity ([M/H] = log(Z/X)−log(Z/X)⊙) range from solar to ≃0.006 times solar are plotted in the (v − y)0, m1, 0 plane (left panel) and in the (b − y)0, m1, 0 plane (right panel). Each bundle is composed of three isochrones of the same metallicity, but different ages: 2, 7, and 14 Gyr. The figure strongly supports the hypothesis of age independence of m1, 0, at least in the metal-poor regime. For [M/H] ≤ −1.0 the isochrones of each bundle are virtually indistinguishable over the entire colour range of interest. At [M/H] = −0.5 the differences between the 14 Gyr and the 7 Gyr isochrones are negligible; those with the 2 Gyr isochrone become relatively large only in certain ranges of colour. It is only with the isochrone bundle at solar metallicity that age-metallicity degeneracies may be relevant, especially for (v − y)0 ≳ 2.0 ((b − y)0 ≳ 0.7). In this metallicity regime, the dependence on age is significantly weaker in the (b − y)0, m1, 0 plane than in the (v − y)0, m1, 0 plane.
 |
Fig. 1. RGB isochrones from the PARSEC set (Bressan et al. 2012; Chen et al. 2019) in the (v − y)0 − m1, 0 plane (left panel) and in the (b − y)0 − m1, 0 plane (right panel). The five bundles of three isochrones of different ages (2, 7, and 14 Gyr) are labelled with their global metallicity [M/H] = 0.0, −0.5, −1.0, −1.5, −2.2 (from top to bottom). The plot in the left panel is limited to the (v − y)0 colour range in which the photometric metallicities are actually computed. In the right panel are plotted only the part of the isochrones whose (v − y)0 colour is in the permitted range, while the range of validity of the H00 calibration in (b − y)0 is enclosed between the two grey vertical lines. |
The possible effect, as also illustrated by Piatti (2020) and Gaia Collaboration (2023c), is to underestimate the metallicity of stars significantly younger than the typical globular cluster. This behaviour should be kept in mind when interpreting results based on this kind of photometric metallicities, especially when the application of the C07 relation is extrapolated beyond the metal-rich limit of the calibration.
Another well-known problem that may affect metallicities derived from m1, 0 is due to the strong CN molecular features in the v band that can mimic the effect of higher metallicity (see e.g. Richter et al. 1999; Hilker 2000; Narloch et al. 2022). However, there is no way to prevent or mitigate this issue that is not expected to affect a large number of field stars. The highest frequency of CN strong stars is observed to occur in old clusters (see Narloch et al. 2022, for a brief discussion and references). In the massive old globular cluster ω Cen Calamida et al. (2009) estimates that 19% ± 1% of RGB stars are CN strong. The comparison between photometric and spectroscopic metallicities in Sect. 4 and in Appendix A suggests that the fraction of CN strong stars is significantly lower in our sample of field stars (see Sect. 4 for discussion). According to these comparisons, the impact on our metallicity estimates is smaller than the typical uncertainty for the vast majority of the considered stars.
3. The sample
We used the GaiaXPy tool4 to get standardised vby photometry from the Gaia archive5. We retrieved from the archive all the stars that (a) are included in the Gaia Synthetic Photometry Catalogue (GSPC; Gaia Collaboration 2023c), (b) have Galactic latitude |b|> 20.0°, (c) have parallax_over_error > 10, (d) have RUWE < 1.3 (Lindegren et al. 2021), and (e) have |C⋆|< σC⋆(G), according to Eq. (18) of Riello et al. (2021).
Condition (a) merely ensures that the stars have XP spectra from which at least one of the wide band magnitudes included in the GSPC can be obtained with S/N > 30, while condition (b) is intended to avoid the most crowded and extinct regions of the Galaxy. Condition (c) guarantees that reliable geometric distances of all the stars can be obtained simply as the inverse of the parallax (Bailer-Jones 2015), and thus allowing a simple and robust selection of giant stars from the distance and reddening corrected colour magnitude diagram (CMD), while conditions (d) and (e) are intended to remove the sample stars with less reliable astrometry (Lindegren et al. 2021) and stars whose fluxes are contaminated by crowding and/or poor background subtraction (Riello et al. 2021). Finally, to include only stars with precisely measured Strömgren magnitudes we imposed that they must have S/N > 20 in all the three vby bands, that is StromgrenStd_flux_i/StromgrenStd_flux_error_i > 20 for i = v,b,y.
Applying all these conditions leads to a sample of 16 435 526 stars, for which we obtained the reddening E(B − V) by interpolating into the Schlegel et al. (1998) maps, recalibrated according to Schlafly & Finkbeiner (2011, some discussion on this choice is provided in Appendix D). A reddening uncertainty of 0.1E(B − V) was assumed in computing the uncertainty on photometric metallicity (Schlegel et al. 1998). Then, we applied a first coarse selection of candidate RGB stars, keeping only those having 0.8 < (GBP − GRP)0 < 2.2 and −4.0 < MG < 2.0, hence reducing the sample to less than 900 000 stars. The MG < 2.0 cut is mainly aimed at limiting the contamination by non-RGB stars on the blue side of the selected sample, as moving towards fainter MG the RGB and the blue plume of young main sequence, subgiant, and blue loop stars converge to similar colours, leading to some overlap between the two populations in the CMD (see Fig. 2). We also removed from the sample 11 896 sources classified as non-single and 5615 sources classified as variables in the Gaiadr3.Gaia_source table6, plus 23 265 sources having E(B − V)≥0.3 to exclude stars whose Strömgren indices are significantly impacted by interstellar extinction.
 |
Fig. 2. Colour and magnitude distribution of selected stars. Panel a: CMD in the Gaia DR3 photometric system for the entire sample of 16 435 526 stars extracted from the Gaia archive. Stars are colour-coded according to the logarithm of the local density. Panel b: on the same CMD our final selected sample of old giants superposed with stars colour-coded according to the mean local value of [Fe/H]phot, v. |
Limiting the (v − y)0 range to the adopted validity range of Eq. (1) removed 36 477 additional stars. At this stage we found that 925 out of the 760 535 stars in our sample had photometric metallicities outside the broad range −5.0 ≤ [Fe/H]phot, v ≤ +0.5, and we excluded this handful of unrealistic estimates.
Finally, the inspection of the CMD with stars coloured according to their [Fe/H]phot, v values, revealed the residual presence of stars whose location in the RGB was not consistent with their metallicity. Anomalously metal-rich stars on the blue side of the RGB were likely largely contributed by non-genuine RGB stars (i.e. mainly young He-burning stars) or, possibly, by some CN-strong RGBs. Anomalously metal-poor stars on the red side of the RGB are more difficult to interpret; even so, they turn out to constitute only about 0.1% of the sample. Both classes of stars were removed using metallicity-dependent conditions, similar to those adopted by Hasselquist et al. (2021) to avoid contamination from young stars in their sample of RGB stars in the Large Magellanic Clouds. In practice, on the blue side we removed the stars having [Fe/H]phot, v ≥ −1.0 whose colour was (GBP − GRP)0 < t(MG) as well as those having (GBP − GRP)0 < 0.98 and [Fe/H]phot, v ≥ −1.5 (61 180 stars and 3160 stars, respectively); on the red side those having (GBP − GRP)0 > t(MG)+0.1 and [Fe/H]phot, v ≤ −1.5 (772 stars), where
is a convenient threshold in colour approximately following the curvature of the RGB in the CMD. Finally we removed 265 stars with ϵ[Fe/H]phot, v ≥ 0.4 dex.
The main characteristics of the final sample, which contains 694 233 stars, are illustrated in Fig. 2. In particular, Fig. 2a shows the distance and reddening corrected CMD of the entire sample of 16 435 526 stars that we extracted from the Gaia archive, with stars colour-coded according to the local density on the CMD, to highlight all the relevant evolutionary features of the diagram. In Fig. 2b, the stars belonging to the final sample are superposed to the same overall CMD, but are colour-coded according to the mean local value of [Fe/H]phot, v, illustrating both the colour-magnitude limits of the sample and the expected correlation between [Fe/H]phot, v and the colour along the RGB. Figure 3 shows how clean and clear this correlation is if the (v − y)0 colour is used, instead of (GBP − GRP)0, and illustrates very clearly the adopted thresholds in (v − y)0.
The comparison between the two panels of Fig. 2 also shows that, while the sample is dominated by RGB stars, a significant population of He-burning red clump (RC) stars, around MG ≃ +0.5, is also included, as well as a minor contribution from AGB stars fainter than the RGB tip, the AGB clump of the metal-rich population being barely visible at MG ∼ −0.4 and (GBP − GRP)0 ∼ 1.3. Since m1.0 is supposed to trace blanketing from metal lines in the range ≃400 − 425 nm in a gravity-independent way (for giants; Árnadóttir et al. 2010), it should also trace stars of similar spectral type independently of their evolutionary stage, as in any case we are dealing with old stars (age ≳ 2 Gyr). A close inspection of Figs. 2b and 3 reveals that, on average, RC stars are recognised to be more metal rich than RGBs of the same colour, and supports this view. The comparisons with spectroscopic metallicities (Sect. 4 and Appendix A) demonstrate that reliable photometric metallicities can be obtained for all kinds of stars included in our sample. We carefully verified that our photometric metallicities of RC and AGB stars are indistinguishable from those of RGB stars when compared to their spectroscopic counterparts (see also Appendix C).
It is clear that the assembled sample cannot be considered in any way complete, nor does it sample the underlying metallicity distribution function (MDF) in a fully uniform and/or fair way, as it is subject to biases induced by the adopted colour-dependent (and to a lesser extent metallicity-dependent) selection criteria, in addition to those associated with the selections in latitude and extinction. Our main goal was the reliability of the metallicity estimates, which comes at the cost of excluding all the stars that we can identify as possibly having a badly measured metallicity. However, any bias is expected to have only mild effects on MDFs, especially in the metallicity range far from the extremes reached by our sample, where colour cuts and contamination by non-RGB stars may play a role (e.g. for [Fe/H] ≲ −2.2 and [Fe/H] ≳ 0.0).
Figure 4 displays the distribution of ϵ[Fe/H]phot, v and ϵ[Fe/H]phot, b as a function of G magnitude and [Fe/H]phot, v. All stars in our sample have G < 16.0, 50% of them have G ≤ 12.76, and 95% have G ≤ 14.48. The sample is dominated by metal-rich stars, 50% having [Fe/H]phot, v ≥ −0.41 and 95% having [Fe/H]phot, v ≥ −0.96. The distribution of ϵ[Fe/H]phot, v seems well behaved, with very mild dependence on [Fe/H]phot, v and increasing median error at fainter magnitudes, as expected. The median (P50) uncertainties are ≲0.15 dex for nearly the entire ranges of G and [Fe/H]phot, v. The 99th percentile (P99) is < 0.2 dex for G ≲ 12.5. A total of 638 551 of the 694 233 stars included in our final sample have individual metallicity uncertainties ϵ[Fe/H]phot, v ≤ 0.2 dex.
 |
Fig. 4. Distributions of individual uncertainties on [Fe/H]phot, v (upper panels) and on [Fe/H]phot, b (lower panels) as a function of [Fe/H]phot, v (left panels) and of G magnitude (right panels). In all cases the colour scale is coded according to the logarithm of local density. In all panels the continuous red curve traces the median of the ϵ[Fe/H]phot, v distribution, while the red dashed curves trace the 16th and 84th percentiles of the same distribution. The scales of the y-axis between the upper and lower panels are different. |
On the other hand, ϵ[Fe/H]phot, b are significantly larger than ϵ[Fe/H]phot, v, with a median as a function of magnitude of about 0.25 dex and strong trends with [Fe/H]phot, v. We attribute this behaviour to the stronger dependence on colour of Eq. (2) with respect to Eq. (1) and to the significantly larger uncertainties associated with the coefficients of Eq. (2) than to those of Eq. (1).
4. Refining the calibration with APOGEE data
Among the spectroscopic datasets we considered to validate our photometric metallicities (see Appendix A), APOGEE DR17 (Abdurro’uf et al. 2022) has both a large number of well-measured stars in common with our sample and a good sampling of stars in the metal-poor regime. Moreover, it is widely used to calibrate machine learning algorithms aimed at deriving photometric metallicities (see e.g. Rix et al. 2022; Yang et al. 2022) and for validation. For these reasons we adopt a selected set of APOGEE DR17 stars for a first validation of our dataset and to refine the calibration of [Fe/H]phot by minimisation of the median difference between spectroscopic and photometric metallicities, always expressed as Δ[Fe/H] = [Fe/H]spec − [Fe/H]phot in the following.
To select a set of well-measured APOGEE DR17 metallicities to compare with, we retain only stars having SNR ≥ 70, ASPCAPFLAG = 0, FE_H_ERR < 0.1, and ALPHA_M_ERR < 0.27. We found 44782 of these stars in common with our sample, which hereafter we denote as the APOGEE Validating Sample (VS). Figure 5 illustrates very clearly how well the m1, 0 index we derived from Gaia XP synthetic photometry correlates with spectroscopic metallicities from the APOGEE VS, for a given (v − y)0 or (b − y)0 colour.
 |
Fig. 5. Stars of the APOGEE VS plotted in (v − y)0, m1, 0 (left panel) and (b − y)0, m1, 0 diagrams. The points are coloured according to their [Fe/H]spec values from APOGEE DR17. |
The distributions of Δ[Fe/H] as a function of [Fe/H]spec for [Fe/H]phot, v and [Fe/H]phot, b are shown in Fig. 6. In this figure, and in all the other figures of this kind in the following, the distributions are represented as 2D histograms, with hexagonal bins colour-coded according to the logarithm of the number of stars in the bin. The continuous red line traces the median (P50) of the Δ[Fe/H] distribution computed in bins of 0.2 dex width, while the dashed red lines enclose the 15.87th (P16) and the 84.13th (P84) percentiles, as a proxy for the ±1σ interval around the median.
 |
Fig. 6. Differences between the spectroscopic and photometric metallicities as a function of spectroscopic metallicity for APOGEE VS, for [Fe/H]phot, v (upper panel) and [Fe/H]phot, b (lower panel). The horizontal grey lines are located at Δ[Fe/H] = ±0.5 dex. The continuous red lines trace P50 and the dashed red lines P16 and P84 of the Δ[Fe/H] distribution. A shift of +0.14 dex has been applied to [Fe/H]phot, v to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≤ −0.8, while a shift of −0.36 dex was applied to [Fe/H]phot, b to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≥ −0.8. |
A +0.14 dex shift was applied to [Fe/H]phot, v to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≤ −0.7, corresponding to the validity range of the C07 calibration where there is no perceivable trend between Δ[Fe/H] and [Fe/H]spec. Once this shift is applied, the spectroscopic metallicities are reproduced with a median accuracy of ≤0.10 dex over the range −2.0 ≤ [Fe/H]spec ≤ −0.4, while a trend of Δ[Fe/H] with [Fe/H]spec arises at higher metallicities, reaching a median offset of +0.50 dex at [Fe/H]spec = +0.4 (see Table 1). The sense of the trend is that spectroscopic metallicities are underestimated by their photometric counterparts for [Fe/H]spec ≳ −0.4. It is important to note here that this trend with metallicity arises in a metallicity regime that is well beyond the strict applicability range of the C07 calibration (−2.2 ≤ [Fe/H] ≤ −0.7), and hence it does not come as a surprise. For the entire sample, one-half of the difference between P84 and P16, which we take here as a proxy for the standard deviation, is < 0.20 dex for [Fe/H]spec ≥ −1.6 and < 0.15 dex for [Fe/H]spec ≥ −0.8, ranging between 0.21 dex and 0.26 dex in the most metal-poor, sparsely populated bins, at [Fe/H]spec ≤ −1.8. If not otherwise stated, we denote this quantity, which traces the precision of our measurements, as σ.
Comparison with the APOGEE VS. Percentiles of the Δ[Fe/H]C and Δ[Fe/H]H distributions.
A −0.36 dex shift was applied to [Fe/H]phot, b, to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≥ −0.8, where there is virtually no trend between Δ[Fe/H] and [Fe/H]spec. Once this shift is applied, the spectroscopic metallicities are reproduced with a median accuracy of ≤0.04 dex over the range −0.8 ≤ [Fe/H]spec ≤ +0.4, while at lower metallicity, the deviations of Δ[Fe/H] reach amplitudes ≳0.2 dex. The value of σ ranges between 0.17 dex and 0.32 dex, and it is ≥0.2 dex in all bins except two (Table 1).
The features emerging from the comparison of our photometric metallicities with the APOGEE DR17 VS and described above are also found when the comparison is performed with validating samples from other spectroscopic surveys, as shown in Appendix A. The overall performance of our corrected [Fe/H]phot, v is satisfactory, comparable to many of the most recent examples found in the literature (see e.g. Yang et al. 2022; Chandra et al. 2022, and references therein).
In the range [Fe/H]spec ≤ −0.8 there is a small asymmetry in the distribution of Δ[Fe/H], with a sparse set of stars on the negative side, beyond the bulk of well-behaved stars. The amplitude of the discrepancy is large only for a handful of them: 37 of the 1804 stars with [Fe/H]spec ≤ −0.8 have Δ[Fe/H] < −0.5 dex, while only 6 have Δ[Fe/H] > +0.5 dex in the same metallicity range. For these stars the corrected [Fe/H]phot, v overestimates [Fe/H]spec by a significant amount. For the stars around [Fe/H] ≃ −1.0 this is possibly due to anomalously strong CN features in their spectra. On the other hand, the asymmetry towards negative residuals for [Fe/H] ≲ −1.5 is mainly due to stars close to the blue edge of the assumed validity range of the C07 calibration, (v − y)0 ≲ 1.2, where the response of m1, 0 to metallicity variations is minimal. However this comparison, as well as those presented in Appendix A, suggest that this kind of problem affects only a small percentage of metal-poor stars.
The typical precision of [Fe/H]phot, b is significantly worse than [Fe/H]phot, v, at any metallicity. However, it may be a useful tool in the metal-rich range beyond the applicability range of the C07 calibration, where it provides a higher median accuracy than [Fe/H]phot, v as well as a weaker dependence on age.
Given the results and discussion above, we define our final photometric metallicities as follows:
and
for the C07 calibration;
and
for the H00 calibration. In this way our photometric metallicities are calibrated on the APOGEE DR17 scale. These are the metallicity values, together with their uncertainties, that we provide in the publicly released dataset. The (v − y)0 cuts adopted in Sect. 3 include in the final sample 37 020 stars (5% of the entire dataset) having (b − y)0 colours slightly bluer that the validity limit of the H00 calibration, down to (b − y)0 = 0.43, where the blue limit is (b − y)0 = 0.50. To facilitate the identification of stars whose [Fe/H]H values are actually extrapolated, we also provide a flag (flagH) that is valued 1 for stars bluer than (b − y)0 = 0.50 and 0 otherwise.
The first rows of the dataset are reported in Table 2, as a sample of its content. In the following analysis, focused on metal-poor populations, we always use metallicity from the C07 calibration ([Fe/H]C).
First five rows of our dataset of photometric metallicities.
5. Chemo-kinematics of the sample
The main goal of large samples of stellar metallicities is to probe the chemo-dynamical properties of the stars in the various Galactic components. In this sense, an indirect test of the reliability and power of our dataset is to verify whether, and to what degree, the main correlations that are known to exist between position, kinematics, and chemical composition are recovered. Figure 7 shows that this is clearly the case8. The metallicity stratification with distance from the Galactic Plane (Z), with more metal-rich disk stars lying near the plane and progressively more metal-poor stars at larger Z, is apparent in the left panel of the figure. The Toomre diagram in the right panel of the figure shows the corresponding kinematic properties, with the most metal-rich stars showing high rotation, with a mode close to the assumed rotation velocity of the Sun (Vϕ, ⊙ = 231 km s−1; McMillan 2017), and the metal-poor stars at higher 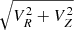 velocities, also reaching highly retrograde orbits.
velocities, also reaching highly retrograde orbits.
 |
Fig. 7. Location in the Galaxy and kinematics of the stars in our sample. Left panel: bi-dimensional histogram in the Z vs |
The two plots are very similar to analogous diagrams obtained with spectroscopic samples (see e.g. Helmi 2020; Gaia Collaboration 2023b, and references therein), demonstrating that our sample can indeed be fruitfully used to explore the properties of Galactic components and substructures. As an example, in Sects. 5.1 and 5.2 we show how the metallicity distribution functions of known relics of past merging events can be investigated with unprecedentedly large samples.
5.1. Metallicity of known substructures
A natural application for our sample of stellar metallicities is related to Galactic archaeology, and in particular to the chemical characterisation of the dynamical substructures that have recently been discovered to populate the Milky Way Halo (see e.g. Helmi 2020 for a detailed review). Some of these substructures are the phase-mixed debris of past merger events that the Milky Way experienced several billion years ago with now-disrupted dwarf galaxies. These debris still preserve coherency in the dynamical space described by the integrals of motion (Helmi & de Zeeuw 2000). To reconstruct the properties of the parent dwarf galaxies, a key ingredient comes from the MDF of the substructures. To date, this information has been gathered by pairing the dynamical information from Gaia with the spectroscopic measurements provided by large surveys such as APOGEE (Ahumada et al. 2020), GALAH (Buder et al. 2021), LAMOST (Wang et al. 2020), RAVE (Steinmetz et al. 2020), and Gaia DR3 (Gaia Collaboration 2023b). In this way, though, the availability of spectroscopic information has always played the limiting role, and the MDFs of the different substructures have typically been constructed using a few hundred stars at best (Helmi et al. 2018; Koppelman et al. 2019a; Naidu et al. 2020; Myeong et al. 2022), while the dynamical information is available for many thousands of stars.
The method proposed in this paper allows us to overcome this limitation, obtaining metallicity information for the entirety of our Gaia-based sample of stars. Therefore, with the aim of characterising the MDFs of the most prominent substructures populating the Milky Way Halo, we first computed the orbital parameters for each of the 694 233 stars of our catalogue. To do so, we used the script described in detail and made publicly available by Vasiliev & Baumgardt (2021), which in turn is based on the AGAMA library for Galactic dynamics (Vasiliev 2019). Orbits were computed by assuming the static Milky Way potential by McMillan (2017). The result of the orbital integration is summarised in Fig. 8, where the stars in our sample are plotted as grey dots in the Lz − Lperp, Lz − E, and Lperp − E planes (Lz and Lperp being the vertical and the perpendicular components of the angular momentum, respectively, and E being the orbital energy).
 |
Fig. 8. Example of substructure selection. The upper panels and the lower left panel show the location of the whole sample (grey dots) in the dynamical spaces described by Lz, Lperp, and E. The red thick dots indicate stars in common with the list of GES stars from Lövdal et al. (2022) and Ruiz-Lara et al. (2022). The blue symbols indicate our selection of likely GES members. The lower right panel shows the MDF for this selection of GES stars (black histogram) and that for the entire sample, normalised to the peak of the former (grey histogram). The red dashed line is the mean [Fe/H] quoted by Ruiz-Lara et al. (2022) for their own GES selection. |
In order to select stellar members of the most significant merger events experienced by the Milky Way, we relied on the dynamical classification of a sample of halo stars within 2.5 kpc proposed by Lövdal et al. (2022) and further discussed in Ruiz-Lara et al. (2022, hereafter RL22). Since these authors used a different assumption on the shape of the Galactic potential compared to ours, to identify each RL22 substructure we first looked for stars in common between our catalogue and theirs, and then we identified the location of each RL22 substructure in the dynamical spaces (as computed by us), and finally we performed an elliptical selection designed to include all of the members of the RL22 substructures. An example of such a procedure is summarised in Fig. 8 for the Gaia-Enceladus-Sausage (GES; Helmi et al. 2018; Belokurov et al. 2018) merger event. Stars shown as red symbols are those labelled as GES stars by RL22 and in common with our catalogue. Blue symbols indicate our final selection of GES members among the 694 233 giants subject of this study. The bottom right panel of Fig. 8 shows the MDF for the selected GES members (black histogram), which is significantly more metal poor on average than the distribution for the entire sample, normalised to the peak of the former (grey histogram).
We followed the same procedure to select five other substructures. These are Sequoia (Myeong et al. 2019), the Helmi streams (Helmi et al. 1999, hereafter H99), Thamnos (Koppelman et al. 2019b), and RL22 substructure-A and substructure-3 (hereafter sub-A and sub-3, respectively). The other substructures (or clusters) listed in RL22 have no stars in common with our sample, possibly because they limit their analysis to a sample of stars within a distance of 2.5 kpc. Figure 9 shows the comparison between the MDF (normalised to the total number of involved stars) for each of the substructures obtained when using the stars in common with RL22 (red histograms), and when using our sample of metallicities (blue histograms), after the application of a quality cut on ϵ[Fe/H] (see the labels). The similarity between the results obtained with the two different approaches is remarkable, with the MDFs of the extended samples based on selections analogous to that illustrated in Fig. 8 nicely reproducing those obtained from the original labelling by RL22, both in terms of peak location and metallicity range.
 |
Fig. 9. Normalised MDFs for the six substructure under study, labelled at the top of each panel. The red histograms show the results obtained when only using stars in common with RL22, whereas the blue histograms show the distributions obtained with our own selection. The total number of stars used to build them is quoted in each panel, and is listed in Table 3. |
Table 3 summarises the main properties of these MDFs in terms of 50th, 16th, and 84th percentiles. In good agreement with what has already been shown in the literature, sub-A and sub-3 are on average the most metal rich. This is not surprising given that sub-A effectively corresponds to the hot thick disk (RL22), and that sub-3 (also named L-RL3 in the most recent analysis by Dodd et al. 2023) is dominated by a similar disky population and additionally shows an extended metal-poor tail of likely accreted stars that is also evident from our findings. On the other hand, Sequoia and H99 are the most metal-poor substructures.
Characteristics of the high-quality MDFs of the six substructures, expressed in terms of 50th, 16th, and 84th percentile.
Sub-A shows the tightest MDF, with ![$ \sigma_{\mathrm{[Fe/H]}}^{\mathrm{sub-A}}=0.31 $](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq20.gif) dex; GES, Sequoia, and Thamnos have the broadest MDFs, all with σ[Fe/H] ≃ 0.8. While the still low number of members might explain this large value for Sequoia and Thamnos, this feature fits the fact that the GES progenitor was the most massive among these.
dex; GES, Sequoia, and Thamnos have the broadest MDFs, all with σ[Fe/H] ≃ 0.8. While the still low number of members might explain this large value for Sequoia and Thamnos, this feature fits the fact that the GES progenitor was the most massive among these.
5.2. Discussion
Once we have demonstrated with a high-quality subsample that our selection produces MDFs that closely match those obtained from selections found in the literature, we can investigate the MDFs of the six substructures when built with no quality selection whatsoever. The results are shown in Fig. 10. The overall shape of the MDF of each substructure is preserved, but the number of members in this case increases to reach several thousand stars in the two most populous cases, GES and sub-3.
 |
Fig. 10. MDFs for the six substructures. The red dashed line is the metallicity of the best-fit theoretical model used by RL22 to fit the CMD of each substructure, and is shown as reference. |
In Fig. 10 we find it very interesting that (a) all the MDFs except that of Sequoia display very clear modes, as well as shapes resembling those of existing Milky Way satellites (see e.g. Kirby et al. 2011; Hasselquist et al. 2021), (b) the mean and mode of the derived MDFs are in good agreement with analogous estimates obtained from (much smaller) spectroscopic samples (e.g. Koppelman et al. 2019b; Naidu et al. 2020; Horta et al. 2023; Ruiz-Lara et al. 2022), and (c) the multi-modal MDF of Sequoia matches previous findings (e.g. Naidu et al. 2020; Monty et al. 2020; Horta et al. 2023) that lead to the suggestion that the stars included in the Sequoia bin come from two or three independent structures that happen to lie close by in the space of integral of motion (see RL22).
We note that all the considered substructures have relatively metal-rich mode (and median, see Table 3), for example with respect to the MDF of dwarf spheroidals like Draco, Ursa Minor, and Sextans (Kirby et al. 2011). GES and Thamnos have median metallicity between Leo I ([Fe/H]med = −1.42) and Fornax ([Fe/H]med = −1.01), two dwarf spheroidals with total mass ranging from 1.2 × 107 M⊙ and 5.6 × 107 M⊙ (McConnachie 2012).
The remarkably wide MDF of sub-3 displays a strong peak at [Fe/H] ≃ −0.7, significantly more metal rich than the mode of the GES MDF, with an extended metal-poor tail that reaches [Fe/H] < −2.5. As shown in RL22 and Dodd et al. (2023), stars in this metal-poor component display chemical abundances of elements like Al, Mg, and Mn that are typical of accreted stars, while the dominant metal-rich component shows chemistry consistent with that of an in situ population. Our selection includes 516 sub-3 stars having [Fe/H] < −1.5, which could be ideal targets for a high-resolution spectroscopic follow-up to better understand this possibly accreted component. This shows how powerful the metallicities derived with the method discussed in this paper are, and opens new opportunities in the investigation and characterisation of these merger events.
One simple example in this sense is provided when combining the metallicity information with a dynamical quantity like the orbital eccentricity, expressed as ecc = (apo − peri)/(apo + peri), where apo and peri are the orbital apocentre and pericentre, respectively. Figure 11 shows how well this pair of parameters (plotted for stars with ϵ[Fe/H] < 0.15) is able to distinguish the six substructures. Another interesting feature stemming from this plane is that Thamnos stars (red triangles) are evidently split into two populations having significantly different eccentricity, one located at ecc ≃ 0.4 and the other at ecc ≃ 0.85. Very likely these two populations correspond to the two components that are already known to build Thamnos up, called Thamnos-1 and Thamnos-2 (Koppelman et al. 2019b). This interpretation is supported by the fact that the population with lower eccentricity, which should correspond to Thamnos-1, is in fact more metal-poor on average ([Fe/H] ≃ −1.4) than that at higher eccentricity ([Fe/H] ≃ −1.15), as already found in the discovery paper by Koppelman et al. (2019b). However, in this context, comparing MDFs should provide more insight than comparing just means. This is done in Fig. 12, which shows that Thamnos-2 MDF is indeed more metal rich than Thamnos-1. A Kolmogorov-Smirnov test states that the probability for the two distributions to have been drawn from the same population is only 6%.
 |
Fig. 11. Distribution of the six substructures in the chemo-dynamical plane described by [Fe/H] vs orbital eccentricity. |
 |
Fig. 12. Comparison between the cumulative metallicity distributions of the low-eccentricity (solid line) and the high-eccentricity (dashed line) populations of Thamnos. |
6. Summary and conclusions
We used Strömgren vby synthetic photometry from Gaia DR3 XP spectra (Gaia Collaboration 2023c) and the calibrations by C07 and H00, based on the m1, 0 index, to derive photometric metallicities for 694 233 selected Galactic old giant stars. These calibrations are generally believed to provide age-independent metallicities (see e.g. Dirsch et al. 2000; Narloch et al. 2022). A simple analysis performed with theoretical isochrones confirms that the age dependence of m1, 0 is indeed negligible, at least for [Fe/H] ≲ −0.5.
A subset of 44 782 stars in common with the APOGEE DR17 sample (Abdurro’uf et al. 2022) were used to re-calibrate the photometric metallicities on this spectroscopic scale, by means of shifts that minimise the median difference Δ[Fe/H] in the metallicity regime where no significant trend between Δ[Fe/H] and [Fe/H]spec is present. This occurs in the range −2.0 ≲ [Fe/H] ≲ −0.4 for the metallicities derived from the C07 calibration ([Fe/H]C), broadly corresponding with its validity range, and [Fe/H] ≳ −0.8 for those from the H00 calibration ([Fe/H]H).
The [Fe/H]C metallicity reproduces the spectroscopic APOGEE DR17 metallicity with a median accuracy ≤0.10 dex in the range −2.0 ≤ [Fe/H]spec ≤ −0.4. At higher metallicity, beyond the applicability limit of the relation, a monotonic trend with [Fe/H]spec arises, reaching a median amplitude of 0.50 dex at [Fe/H]spec = +0.4, with [Fe/H]C systematically underestimating [Fe/H]spec. This trend may be related to the onset of a significant age dependence arising in the high-metallicity regime (see Sect. 1 and Appendix E). The precision, as measured by σ = 0.5(P84 − P16), is < 0.25 dex over the entire metallicity range considered, < 0.20 dex for [Fe/H]spec ≥ −1.60, and ≤0.16 dex for [Fe/H]spec ≥ −1.20.
The [Fe/H]H metallicity reproduces the spectroscopic APOGEE DR17 metallicity with a median accuracy ≤0.05 dex in the range −0.8 ≤ [Fe/H]spec ≤ +0.4, while, at lower metallicities, it displays trends with [Fe/H]spec reaching amplitudes > 0.20 dex. The precision is nearly everywhere ≳0.2 dex, reaching values ≥0.3 dex towards the metal-poor limit. Theoretical and empirical arguments suggest that the age-dependence of [Fe/H]H is weaker than that affecting [Fe/H]C, in the [Fe/H] > −0.5 regime. However, since we are mainly interested in the metal-poor regime and given the higher precision, we take [Fe/H]C as our preferred metallicity indicator, tailoring the sample selection on the properties of the C07 calibration.
We provide a publicly available catalogue with the re-calibrated photometric metallicities for all the stars in our sample together with the associated uncertainties. Our final metallicity values were validated by comparison with large samples of spectroscopic metallicities from various surveys, with chemical abundances derived from spectra of different resolution (GALAH, Gaia DR3 GSP-spec, LAMOST, and Gaia-ESO; see Appendix A). The overall performance is remarkably similar to that described above for the comparison with APOGEE DR17, implying that our photometric metallicity scales are robust and have general validity. We have demonstrated that while individual values may be significantly inaccurate, the overall dataset traces the spectroscopic metallicities with sufficient accuracy and precision to allow useful scientific applications.
Once the intrinsic uncertainties and applicability range of the adopted calibrating relation are taken into account, as well as those associated with the spectroscopic metallicity scale taken as reference, there are three main factors that hamper the accuracy and the precision of the metallicities derived here: uncertainties on interstellar extinction, either statistic or systematic, photometric precision, and spectral features mimicking the effect of metallicity (e.g. the well-known effect of CN bands; H00). Improvements in the first two factors can be foreseen for the next Gaia data releases.
In Sect. 5 we show how well our photometric metallicity is able to trace the chemo-kinematic trends of the stars included in our dataset. This is conducive to derive the most richly populated MDFs ever presented in the literature of several known substructures in the surroundings of the Sun (GES, Thamnos, Sequoia, sub-3, sub-A; H99), in some cases providing precious insights into the actual nature of the considered substructures and/or their progenitors.
This work provides a simple and tested way to get photometric metallicity of old giants from standardised Strömgren XP synthetic photometry. The method adopted here can be extended to larger samples of Galactic stars or applied to stellar systems with known distance and extinction. Finally, it provides additional proof that very useful astrophysical information is encoded in Gaia XP spectra (De Angeli et al. 2023; Montegriffo et al. 2023) and that it can be efficiently extracted using synthetic photometry (Gaia Collaboration 2023c).
The Blue Photometer (BP) and the Red Photometer (RP) are the instruments on board the Gaia spacecraft providing low-resolution (R ≃ 20 − 80) spectrophotometry of astronomical sources, in the ranges 330 nm ≤ λ ≤ 680 nm and 640 nm ≤ λ ≤ 1050 nm, respectively (Gaia Collaboration 2016). The external calibration process joins the two output spectra together into a single continuous flux table from 330 nm to 1050 nm (Montegriffo et al. 2023). For brevity, we refer to the spectra from the BP and RP instruments as well as the merged externally calibrated spectra as XP spectra, where X stands for ‘B and R’ (Gaia Collaboration 2023c).
In Appendix B we briefly explore the performance of two additional calibrating relations provided by C07.
Out of 694 233 stars in our sample, 685 087 (98.7%) have valid line-of-sight velocity estimates from Gaia DR3 (Katz et al. 2023).
See Recio-Blanco et al. (2023) for a selection criterion that retains a significantly more conspicuous sample of metal-poor stars.
This, in turn, can be the secondary effect of a trend primarily driven by age, as suggested in Appendix E.
Acknowledgments
M.B., P.M., A.B. and D.M. acknowledge the support to activities related to the ESA/Gaia mission by the Italian Space Agency (ASI) through contract 2018-24-HH.0 and its addendum 2018-24-HH.1-2022 to the National Institute for Astrophysics (INAF). M.B., A.B. and D.M. acknowledge the support to this study by the PRIN INAF 2019 grant ObFu 1.05.01.85.14 (Building up the halo: chemo-dynamical tagging in the age of large surveys, PI. S. Lucatello). M.B. is grateful to R. Pascale for his help in the production of figures with Python. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/Gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/Gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. In this analysis we made use of TOPCAT (http://www.starlink.ac.uk/topcat/, Taylor 2005). This work made use of SDSS-IV data. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High Performance Computing at the University of Utah. The SDSS website is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, Center for Astrophysics | Harvard & Smithsonian, the Chilean Participation Group, the French Participation Group, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This work made use of the Third Data Release of the GALAH Survey (Buder et al. 2021). The GALAH Survey is based on data acquired through the Australian Astronomical Observatory, under programs: A/2013B/13 (The GALAH pilot survey); A/2014A/25, A/2015A/19, A2017A/18 (The GALAH survey phase 1); A2018A/18 (Open clusters with HERMES); A2019A/1 (Hierarchical star formation in Ori OB1); A2019A/15 (The GALAH survey phase 2); A/2015B/19, A/2016A/22, A/2016B/10, A/2017B/16, A/2018B/15 (The HERMES-TESS program); and A/2015A/3, A/2015B/1, A/2015B/19, A/2016A/22, A/2016B/12, A/2017A/14 (The HERMES K2-follow-up program). We acknowledge the traditional owners of the land on which the AAT stands, the Gamilaraay people, and pay our respects to elders past and present. This paper includes data that has been provided by AAO Data Central (datacentral.org.au). This work made use of LAMOST data. Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences. This work made use of Gaia-ESO Public Spectroscopic Survey data products from observations made with the ESO Very Large Telescope at the La Silla Paranal Observatory under programme ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. The Gaia-ESO Survey Data Archive is prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council.
References
- Abdurro’uf, Accetta, K., Aerts, C., et al. 2022, ApJS, 259, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Ahumada, R., Allende Prieto, C., Almeida, A., et al. 2020, ApJS, 249, 3 [NASA ADS] [CrossRef] [Google Scholar]
- An, D., Beers, T. C., Lee, Y. S., & Masseron, T. 2022, AAS J., submitted [arXiv:2210.07542] [Google Scholar]
- Andrae, R., Fouesneau, M., Sordo, R., et al. 2023, A&A, 674, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anthony-Twarog, B. J., & Twarog, B. A. 2000, AJ, 120, 3111 [Google Scholar]
- Arentsen, A., Starkenburg, E., Martin, N. F., et al. 2020, MNRAS, 491, L11 [Google Scholar]
- Árnadóttir, A. S., Feltzing, S., & Lundström, I. 2010, A&A, 521, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Bono, G., Stetson, P. B., et al. 2007, ApJ, 670, 400 [Google Scholar]
- Calamida, A., Bono, G., Stetson, P. B., et al. 2009, ApJ, 706, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco, J. M., Weiler, M., Jordi, C., et al. 2021, A&A, 652, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandra, V., Naidu, R. P., Conroy, C., et al. 2022, ApJ, submitted [arXiv:2212.00806] [Google Scholar]
- Chen, Y., Girardi, L., Fu, X., et al. 2019, A&A, 632, A105 [EDP Sciences] [Google Scholar]
- Chiti, A., Frebel, A., Mardini, M. K., et al. 2021, ApJS, 254, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Mandwewala, N. 1976, PASP, 88, 917 [CrossRef] [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, RAA, 12, 1197 [NASA ADS] [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR Online Data Catalog: II/328 [Google Scholar]
- De Angeli, F., Weiler, M., Montegriffo, P., et al. 2023, A&A, 674, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Dirsch, B., Richtler, T., Gieren, W. P., & Hilker, M. 2000, A&A, 360, 133 [NASA ADS] [Google Scholar]
- Dodd, E., Callingham, T. M., Helmi, A., et al. 2023, A&A, 670, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Fallows, C. P., & Sanders, J. L. 2022, MNRAS, 516, 5521 [NASA ADS] [CrossRef] [Google Scholar]
- Faria, D., Feltzing, S., Lundström, I., et al. 2007, A&A, 465, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023a, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Recio-Blanco, A., et al.) 2023b, A&A, 674, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Montegriffo, P., et al.) 2023c, A&A, 674, A33 [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Worley, C. C., et al. 2022, A&A, 666, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Hasselquist, S., Hayes, C. R., Lian, J., et al. 2021, ApJ, 923, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Hayden, M. R., Recio-Blanco, A., de Laverny, P., Mikolaitis, S., & Worley, C. C. 2017, A&A, 608, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayden, M. R., Sharma, S., Bland-Hawthorn, J., et al. 2022, MNRAS, 517, 5325 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Hilker, M. 2000, A&A, 355, 994 [NASA ADS] [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2023, MNRAS, 520, 5671 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirby, E. N., Lanfranchi, G. A., Simon, J. D., Cohen, J. G., & Guhathakurta, P. 2011, ApJ, 727, 78 [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Roelenga, S., & Bastian, U. 2019a, A&A, 625, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019b, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J. L., Babusiaux, C., & Cox, N. L. J. 2022, A&A, 661, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, X.-Y., Huang, Y., Liu, G.-C., Beers, T. C., & Zhang, H.-W. 2023, ApJ, 944, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Longeard, N., Martin, N., Starkenburg, E., et al. 2018, MNRAS, 480, 2609 [NASA ADS] [CrossRef] [Google Scholar]
- Lövdal, S. S., Ruiz-Lara, T., Koppelman, H. H., et al. 2022, A&A, 665, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucey, M., Al Kharusi, N., Hawkins, K., et al. 2023, MNRAS, in press, https://doi.org/10.1093/mnras/stad1675 [Google Scholar]
- Magnier, E. A., Schlafly, E. F., Finkbeiner, D. P., et al. 2020, ApJS, 251, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Montegriffo, P., De Angeli, F., Andrae, R., et al. 2023, A&A, 674, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monty, S., Venn, K. A., Lane, J. M. M., Lokhorst, D., & Yong, D. 2020, MNRAS, 497, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2012, MNRAS, 426, 2889 [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
- Myeong, G. C., Belokurov, V., Aguado, D. S., et al. 2022, ApJ, 938, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, N., Donor, J., Spoo, T., et al. 2022, AJ, 164, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Narloch, W., Pietrzyński, G., Gieren, W., et al. 2021, A&A, 647, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narloch, W., Pietrzyński, G., Gieren, W., et al. 2022, A&A, 666, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piatti, A. E. 2020, A&A, 642, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, ASP Conf. Ser., 50, 357 [NASA ADS] [Google Scholar]
- Randich, S., Gilmore, G., Magrini, L., et al. 2022, A&A, 666, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Palicio, P. A., et al. 2023, A&A, 674, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richter, P., Hilker, M., & Richtler, T. 1999, A&A, 350, 476 [NASA ADS] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rix, H.-W., Chandra, W., Andrae, R., et al. 2022, ApJ, 941, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lara, T., Matsuno, T., Lövdal, S. S., et al. 2022, A&A, 665, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Martin, N., Youakim, K., et al. 2017, MNRAS, 471, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Thanjavur, K., Ivezić, Ž., Allam, S. S., et al. 2021, MNRAS, 505, 5941 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E. 2019, MNRAS, 482, 1525 [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fu, J.-N., Zong, W., et al. 2020, ApJS, 251, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., Huang, Y., Yuan, H., et al. 2022, ApJS, 259, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., Yuan, H., Niu, Z., et al. 2022, ApJS, 258, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, L., Yuan, H., Xiang, M., et al. 2022, A&A, 659, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [Google Scholar]
Appendix A: Validation with GALAH, GSP-Spec, LAMOST and Gaia-ESO spectroscopic metallicities
Here we show the same kind of analysis performed in Sect. 4 for four additional VSs, composed of stars with well-measured [Fe/H]spec from the GALAH (Buder et al. 2021), LAMOST (Wang et al. 2020), and Gaia-ESO (Gilmore et al. 2022; Randich et al. 2022) surveys, and from the GSP-Spec set of chemical abundances derived from RVS spectra for Gaia DR3 (Recio-Blanco et al. 2023).
In Sect. 4 we used the APOGEE VS to calibrate our photometric metallicities, adjusting the zero points of our [Fe/H] scales to the APOGEE scale in the most appropriate metallicity ranges. Here, on the other hand, we compare our final calibrated metallicities, as defined in Eq. 4 and Eq. 6, with large and reliable external spectroscopic samples, for validation purposes. It is important to recall that part of the trends or zero point differences in the median Δ[Fe/H] as a function of [Fe/H]spec that arise in the comparisons presented below may be due to non-homogeneity between the abundance scale of APOGEE and that of the other surveys. The main result of the following analysis is that our photometric metallicities, calibrated on APOGEE data, nicely reproduce spectroscopic metallicity for the considered VS, with typical accuracy and precision similar to those described in Sect. 4.
A.1. Validation with GALAH data
The GALactic Archaeology with HERMES (GALAH) survey (De Silva et al. 2015; Buder et al. 2021) collects high-resolution (R ≃ 28000) optical spectra of Milky Way stars, deriving chemical abundances of many elements. From the third data release of the survey (Buder et al. 2021), we selected for our VS-only stars with good quality flags and small uncertainty in [Fe/H] and [α/Fe]. The requirement on [α/Fe] was motivated to allow the possibility of looking for trends of photometric metallicity with this abundance parameter. The issue is briefly discussed in Appendix E. We extracted from GALAH_DR3_main_allstar_v2.fits stars having flag_sp=0, flag_fe_h=0, e_fe_h< 0.1, and e_alpha_fe< 0.29, finding 26286 of them in common with our sample.
The distributions of Δ[Fe/H]C and Δ[Fe/H]H as a function of [Fe/H]spec are shown in Fig. A.1. Median accuracy, precision, and the overall behaviour of the distributions are very similar to those observed for the APOGEE VS.
 |
Fig. A.1. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the GALAH VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
A.2. Validation with Gaia DR3 GSP-Spec data
With the third Gaia data release, for the first time, chemical abundances were derived from the medium-resolution spectra (R ≃ 11500) in a narrow range around the Calcium triplet (845 − 872 nm) from the RVS spectrograph, with the GSP-Spec module (Recio-Blanco et al. 2023, and references therein). For our VS we selected the best-measured stars by keeping only those with the 13 first bits of astrophysical_parameters.flags_gspspec equal to zero10. This selection leaves less than a hundred of stars with [Fe/H]spec ≲ −1.011, but provides 224404 optimally measured stars in common with our sample. GSP-spec abundances were corrected for the gravity-dependent bias using Eq. 2 and Eq. 3 of Recio-Blanco et al. (2023).
Figure A.2 shows that our [Fe/H]C values reproduce those by GSP-Spec with an accuracy and precision similar to those observed for the APOGEE and GALAH VSs, in the range well sampled by the GSP-Spec VS. The behaviour of [Fe/H]H is also broadly similar to that seen in previously considered VSs; however, the precision is slightly worse everywhere and a trend with [Fe/H]spec emerges for [Fe/H]spec ≳ 0.0.
 |
Fig. A.2. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the GSP-Spec VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
A.3. Validation with LAMOST data
To have a comparison with a VS with metallicities from low-resolution spectra we selected stars from the eighth data release (DR8; Wang et al. 2022) of the Large Sky Area Multi-object Fiber Spectroscopic Telescope (LAMOST) survey (Cui et al. 2012). The LAMOST catalogue collects abundances derived from spectra at R ≃ 1800 over the wavelength range 369-910 nm.
We extracted the best-measured sources for the LAMOST VS data from the DR8 table dr8_v2.0_LRS_stellar.fits, requiring that snrg> 100, feh_err≤0.1, alpha_m_err≤0.1, and -1.0< alpha_m< 2.012. We found 10581 stars with these properties in common with our sample. For this VS the distributions of Δ[Fe/H] as a function of [Fe/H]spec are displayed in Fig. A.3. For the comparison with [Fe/H]C, as expected, σ[Fe/H] is slightly larger than that measured in the comparison with metallicity from high-resolution high-S/N spectra, owing to the larger uncertainties associated with LAMOST [Fe/H]spec. On the other hand, the median accuracy is better than 0.15 dex over most of the considered metallicity range. Also in this case the precision of [Fe/H]H is worse than [Fe/H]C, but the median precision is ≤0.12 over the entire metallicity range sampled by the VS.
 |
Fig. A.3. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the LAMOST VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
 |
Fig. A.4. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the Gaia-ESO VS. The arrangement and the meaning of the symbols is the same as in Fig. 6, but the median and percentile lines are computed in 0.3 dex bin, due to the small dimension of the sample. |
A.4. Validation with Gaia-ESO data
Gaia-ESO (Gilmore et al. 2022; Randich et al. 2022) collected high-resolution spectra of about 115000 stars in the MW field and in stellar clusters, using FLAMES at the ESO VLT. The subset of stars observed with UVES at resolution R ≃ 45000 using the U580 set-up (480-680 nm) provides the highest precision stellar parameters and abundances, so we concentrated on it. We used the final data release (available from the ESO catalogue archive13, cross-matched it with Gaia DR3, and kept only stars with U580 spectra. Then, using TOPCAT (Taylor 2005), we selected red giant stars based on the Kiel diagram (Teff, log g) and applied a final cut on errors, keeping only stars with errors in Teff, log g, and [Fe/H] less than 100 K, 0.25 dex, and 0.1 dex, respectively. This led to a sample of 1759 stars, 368 of which are in common with our sample. The small numbers of stars involved makes the distribution quite noisy, especially for [Fe/H] ≤ − 1.0. Still, in all the bins with more than ten stars the median Δ[Fe/H]C as well as σ are ≲0.25 dex. As usual Δ[Fe/H]H displays lower precision at any metallicity and larger median deviations from zero in the metal-poor regime, while the trend with [Fe/H]spec is virtually null for [Fe/H]spec ≳ −0.5.
Appendix B: Performance of C07 semi-empirical calibrations
In addition to the empirical calibration we used here (Eq. 1), C07 also provide theoretical and semi-empirical calibrations to obtain metallicity from Strömgren indices. Here we briefly explore the performance of C07 semi-empirical calibrations against the APOGEE VS since they have a wider range of applicability than those adopted here, extending to −2.6 ≤ [Fe/H] ≤ −0.6, instead of −2.2 ≤ [Fe/H] ≤ −0.7. Among the C07 semi-empirical calibrations, there is also one where the reddening-independent [m]=m + 0.3(b − y) index is used as metallicity indicator instead of m1, 0. We note, however, that metallicities derived in this way are not fully reddening-independent, as the calibrating relation depends on [m] and on (v − y)0.
The semi-empirical calibration as a function of m1, 0 and (v − y)0 is
while that as a function of [m] and (v − y)0 is
In Fig. B.1 we show the comparison of these photometric metallicities with [Fe/H]APO after the following zero-point adjustments are performed, analogously to Eq. 4 and Eq. 6,
 |
Fig. B.1. Δ[Fe/H] for [Fe/H]C, s[m] (upper panel) and [Fe/H]C, sm0 (lower panel) as a function of [Fe/H]spec for the APOGEE VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
and
to minimise the median Δ[Fe/H] in the metal-poor regime. It is interesting to note that C07 finds similar shifts when comparing photometric metallicities from the same calibrating relations to spectroscopic metallicities for the sample of 85 field giants they use for validation.
The behaviour of both photometric metallicities is qualitatively similar to [Fe/H]C. The precision is very similar at all metallicities, but the median accuracy is slightly worse in the metal-poor and in the metal-rich regimes. For example, at [Fe/H] = −2.0, |Δ[Fe/H]| is 0.08 dex for [Fe/H]C and 0.15 dex for [Fe/H]C, s[m]; at [Fe/H] = −0.4, |Δ[Fe/H]| is 0.07 dex for [Fe/H]C and 0.15 dex for [Fe/H]C, s[m].14
Hence, [Fe/H]C is the C07-based metallicity that reproduces most accurately [Fe/H]APO for stars of the APOGEE VS among those considered here. For this reason we decided to include only [Fe/H]C in our final catalogue (Table 2), together with [Fe/H]H. However, Eq. B.3 and Eq. B.4 make it possible to derive both [Fe/H]C, s[m] and [Fe/H]C, sm0 in a scale fully homogeneous to [Fe/H]C, based on APOGEE DR17, with Fig. B.1 providing the validation and illustrating the performance as a function of metallicity.
Appendix C: Experiments with star clusters
Star clusters are essentially composed of stars with the same age and metallicity. For this reason they may provide a useful testbed to check the performance of our photometric metallicities in real and somehow challenging cases. The latter is especially true for globular clusters (GCs) as they are relatively distant and crowding may affect XP synthetic photometry of their stars in spite of the strict selection criteria adopted in our catalogue, especially at faint magnitudes (see Gaia Collaboration 2023c).
Globular cluster stars are rare in our sample, due to the adopted selections. Among the clusters with |b|> 20.0° and D < 10.0 kpc, we found only six having more than five member stars included in our catalogue (see Table C.1). We considered as members only stars having probability membership P ≥ 0.99, as assigned in Vasiliev & Baumgardt (2021). We adopted GC spectroscopic metallicities from the 2010 edition of the (Harris 1996) catalogue, that are in the Carretta et al. (2009) metallicity scale. Since all the considered GCs have [Fe/H]spec < −0.70, we use only photometric metallicities from the C07 calibration.
Mean [Fe/H]C for selected globular clusters with more than five stars in our sample. Comparison with [Fe/H]spec.
In Fig. C.1 we show [Fe/H]C as a function of apparent G magnitude for stars in the two clusters with the largest number of members included in our catalogue, NGC 104 (47 Tuc) and NGC 6752. The distributions seems reasonably well behaved: both the scatter about the mean and the uncertainties on individual [Fe/H]C increase with increasing G (fainter magnitudes). A systematic shift occurs for G > 13.0 in the NGC 6752 sample. This can be attributed to the fact that this cluster is very concentrated (concentration parameter C = 2.5, Harris 1996), and hence crowding may have a significant impact at faint magnitudes. On the other hand, it is interesting to note that many stars belonging to the red HB are present in the NGC 104 sample and they behave indistinguishably from RGB stars in Fig. C.1. We verified that the same also holds for AGB stars, within the uncertainties. The diagram suggests that both G magnitude and ϵ[Fe/H]C can be used to select high-quality subsamples from our catalogue.
 |
Fig. C.1. [Fe/H]C as a function of apparent G magnitude for member stars of NGC 104 and NGC 6752 included in our catalogue. Points are colour-coded according to their uncertainty in the photometric metallicity ϵ[Fe/H]C. The thick horizontal lines are the value of the mean spectroscopic metallicity as tabulated in the 2010 edition of the Harris (1996) catalogue. The red horizontal branch stars of NGC 104 lie around G ≃ 14.2. |
In Table C.1 we compare the mean metallicity obtained from GC stars in our catalogue with [Fe/H]spec from Harris (1996). Mean metallicities and standard deviations are derived taking into account the individual uncertainties, by means of the maximum likelihood (ML) algorithm used in Mucciarelli et al. (2012), and originally developed for other purposes by Pryor & Meylan (1993). Different cuts on ϵ[Fe/H]C were adopted, when possible, to explore the effect on the accuracy of the mean [Fe/H]C obtained. The main results of this analysis can be summarised as follows: (1) Independently of the adopted ϵ[Fe/H]C cut, the derived mean photometric metallicities are within ≲0.15 of the spectroscopic metallicity; (2) Cuts in ϵ[Fe/H]phot result in more accurate mean metallicities; (3) Errors on the mean metallicity are, in some cases, significantly smaller than the difference between [Fe/H]spec and [Fe/H]C, suggesting that individual uncertainties are somehow underestimated, as expected; (4) Probably for the same reason, in some case σ[Fe/H]C values not consistent with zero are found.
Well-populated open clusters (OCs) are even rarer than GCs in our sample, mainly due to the selection imposed on Galactic latitude, reddening, and implicitly on age, since only clusters older than ≃1 − 2 Gyr have RGB stars. In Table C.2 we show a comparison analogous to that performed for GCs for three OCs having more than five members included in our sample, NGC 752, NGC 188, and NGC 2682 (M 67), aged 1.2 Gyr, 7.1 Gyr, and 4.3 Gyr, respectively (Myers et al. 2022). We compare the mean spectroscopic metallicities recently provided by Myers et al. (2022, based on APOGEE DR17) with the means obtained from both our photometric metallicities. The absolute differences with the spectroscopic values are in the range 0.06-0.27 dex for [Fe/H]C, and 0.01-0.11 for [Fe/H]phot, H, confirming that the latter indicator is indeed more accurate in the metallicity and age ranges covered by these clusters.
Mean [Fe/H]phot for selected open clusters with more than five stars in our sample. Comparison with [Fe/H]spec.
Appendix D: Impact of interstellar extinction on photometric metallicity
Uncertainty and unaccounted for systematic errors in the extinction and, possibly, in the adopted extinction laws can be a major limitation for the accuracy and the precision of photometric metallicities, especially when derived from medium-width passbands, as in our case. Here, for simplicity, we adopted the values from the Schlegel et al. (1998) maps, recalibrated following Schlafly & Finkbeiner (2011, S11) as they are the most widely used. However, these are asymptotic values for large distances and may not be appropriate for the nearest stars. According to Lallement et al. (2019), in most intermediate latitude directions the extinction profile stabilises near the asymptotic value for D ≳ 1 − 2 kpc. Mainly due to the selection in Galactic latitude, only ≤14% of the stars in our sample lie at D ≤ 1.0 kpc, and we consider only stars with E(B − V) < 0.3, and hence we do not expect our choice to have a major impact on our overall metallicity scale, while it can make a significant difference on individual stars.
In Fig. D.1 we plot the difference between the S11 reddening values we adopted and those derived from the distance-dependent maps by Lallement et al. (2022, L22), as a function of distance for the APOGEE DR17 VS. While the boundaries of the ΔE(B − V) distribution shrinks with increasing distance, as expected, the (asymmetric) ±1σ interval remains remarkably constant, and the median difference very close to zero, over the entire range of distances. Hence, the two reddening scales are in good agreement for the bulk of stars in our sample. Moreover, asymptotic E(B − V)S11 are expected to systematically overestimate reddening for nearby stars. While there is some asymmetry towards positive values in the ΔE(B − V) distribution at low distances, with stars deviating by more than +0.05 mag from zero being two times more abundant than those with ΔE(B − V) < − 0.05, negative deviations are not so rare and display amplitudes comparable with those observed on the positive side. This strongly suggest that both the considered sources of reddening estimates bring in their own systematic errors. At low E(B − V)L22 values S11 seems to overestimate the extinction for a fraction of stars, while at high E(B − V)L22 the opposite occurs, with the distance-dependent estimates significantly exceeding the asymptotic values from S11. Hence, each choice of the reddening scale comes at a comparable cost in terms of errors in the photometric metallicity.
 |
Fig. D.1. Difference between the reddening estimates adopted here, from Schlafly & Finkbeiner (2011, S11), and those obtained from the distance-dependent maps by Lallement et al. (2022, L22) as a function of distance from the Sun. Points are colour-coded according to Δ[Fe/H]APO − C = [Fe/H]APO − [Fe/H]C. The thick red line is P50 and the thin red lines are P16 and P84 of the distribution of the E(B-V) difference computed over 0.5 kpc wide bins. |
The colour-coding according to Δ[Fe/H]APO − C shows that some broad correlation between ΔE(B − V) and Δ[Fe/H]APO − C is there, but it is very weak (Pearson’s correlation coefficient = +0.102), showing that reddening errors are not the main driver of correlated metallicity errors (see below). Analogous conclusions can be drawn if the analysis is repeated for [Fe/H]H.
In Fig. D.2 we explore possible dependences of [Fe/H]C from the adopted reddening values. The upper panel of Fig. D.2 shows that Δ[Fe/H] indeed strongly correlates with E(B − V), with an amplitude reaching ≃0.2 dex for E(B − V) ≥ 0.2. This does not affect the bulk of the stars in our sample, as only 4%(21%) of them have E(B − V) > 0.2(0.1). The sense of the trend is that photometric metallicities underestimate their spectroscopic counterparts.
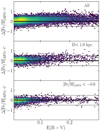 |
Fig. D.2. Δ[Fe/H]APO − C as a function of E(B − V) for the APOGEE VS. Upper panel: Entire sample; middle panel: Stars with distance lower than 1 kpc; lower panel: Stars with [Fe/H]APO < −0.6. The horizontal lines indicate the Δ[Fe/H] = 0.0 ± 0.5 dex levels. |
However the middle and lower panels of the same figure provide robust evidence that this is a secondary correlation, i.e. a manifestation of the trend of Δ[Fe/H]APO − C with [Fe/H]spec arising at [Fe/H]spec ≳ −0.5 discussed in Sect. 4 and Appendix A. This occurs because sources that are more reddened are more likely to lie at low Z and, consequently, to have higher metallicity in the regime where the quoted trend has a sizeable amplitude.
In the middle panel of Fig. D.2 we show that the subset of the nearest stars (D < 1.0 kpc) displays the same trend as the entire sample. Hence, the observed trend is not driven by nearby stars overcorrected by our assumption of asymptotic reddening values. This result also supports the validity of our choice of the source of reddening values.
The lower panel of the figure shows that stars with [Fe/H]spec ≤ −0.6 do not display any appreciable trend of Δ[Fe/H] with E(B − V), thus confirming that the effect seen in the uppermost panel is indeed driven by the most metal-rich stars, also providing further support to the reliability of our [Fe/H]C estimates in the metallicity regime we are most interested in. We also verified that the trend becomes increasingly evident as we include more metal-rich stars. All of these results support the idea that the trend in the upper panel of Fig. D.2 is indeed a secondary effect of the trend of Δ[Fe/H]APO − C with [Fe/H]spec in the metal-rich regime15. Consistent with this conclusion, the trend of Δ[Fe/H]APO − H with [Fe/H]spec was verified to be significantly weaker than that of Δ[Fe/H]APO − C.
Appendix E: Trends with [α/Fe]
The α elements (e.g. O, Mg, Si, Ca, Ti) are among the most abundant metals in the atmosphere of stars and their strong lines may have a non-negligible impact on photometric metallicities, especially as the [α/Fe] distribution at a given metallicity is known to be be strongly bimodal in the Galaxy, at least for [Fe/H] ≳ −1.5 (see e.g. Hasselquist et al. 2021; Hayden et al. 2022, and references therein).
For this reason it may be worth checking whether our photometric metallicities display some dependence on abundances of α elements. In Fig. E.1 we show the distribution of Δ[Fe/H]APO − C and Δ[Fe/H]APO − H as a function of the mean α element abundance provided by APOGEE [α/M], for the APOGEE DR17 VS. Indeed, Δ[Fe/H]APO − C shows a strong anti-correlation with [α/M]: [Fe/H]C tends to underestimate the spectroscopic metallicity with decreasing [α/M]. Similar results are obtained for all the considered VSs.
 |
Fig. E.1. Δ[Fe/H]APO − C (upper panel) and Δ[Fe/H]APO − H (lower panel) as a function of mean spectroscopic α elements abundance for the APOGEE VS. The red lines are linear fits to the data. |
This is the same kind of trend observed for increasing [Fe/H]spec for [Fe/H]spec ≳ −0.5. Since in that metallicity range the sample is dominated by low [α/Fe] stars, it seems plausible that the correlation is mainly a by-product of the Δ[Fe/H]APO − C trend with metallicity, as in the case of the correlation with reddening discussed in Appendix D. The fact that Δ[Fe/H]APO − H displays a much weaker correlation with [α/M], and in the opposite sense, confirms this hypothesis. However, given the strong correlation between age and [α/Fe] in the solar neighbourhood (see e.g. Haywood et al. 2013; Bensby et al. 2014; Hayden et al. 2017, 2022), it cannot be excluded that differences in age are also playing a role in the high-metallicity regime (see Sect. 1). In fact, it is possible that the onset of the dependence on age at high metallicity (Sect. 1) is the original driver of the trend with metallicity of [Fe/H]C, in that metallicity range.
All Tables
Comparison with the APOGEE VS. Percentiles of the Δ[Fe/H]C and Δ[Fe/H]H distributions.
Characteristics of the high-quality MDFs of the six substructures, expressed in terms of 50th, 16th, and 84th percentile.
Mean [Fe/H]C for selected globular clusters with more than five stars in our sample. Comparison with [Fe/H]spec.
Mean [Fe/H]phot for selected open clusters with more than five stars in our sample. Comparison with [Fe/H]spec.
All Figures
 |
Fig. 1. RGB isochrones from the PARSEC set (Bressan et al. 2012; Chen et al. 2019) in the (v − y)0 − m1, 0 plane (left panel) and in the (b − y)0 − m1, 0 plane (right panel). The five bundles of three isochrones of different ages (2, 7, and 14 Gyr) are labelled with their global metallicity [M/H] = 0.0, −0.5, −1.0, −1.5, −2.2 (from top to bottom). The plot in the left panel is limited to the (v − y)0 colour range in which the photometric metallicities are actually computed. In the right panel are plotted only the part of the isochrones whose (v − y)0 colour is in the permitted range, while the range of validity of the H00 calibration in (b − y)0 is enclosed between the two grey vertical lines. |
| In the text | |
 |
Fig. 2. Colour and magnitude distribution of selected stars. Panel a: CMD in the Gaia DR3 photometric system for the entire sample of 16 435 526 stars extracted from the Gaia archive. Stars are colour-coded according to the logarithm of the local density. Panel b: on the same CMD our final selected sample of old giants superposed with stars colour-coded according to the mean local value of [Fe/H]phot, v. |
| In the text | |
 |
Fig. 3. Same as Fig. 2b, but using (v − y)0 colour, instead of (GBP − GRP)0. |
| In the text | |
 |
Fig. 4. Distributions of individual uncertainties on [Fe/H]phot, v (upper panels) and on [Fe/H]phot, b (lower panels) as a function of [Fe/H]phot, v (left panels) and of G magnitude (right panels). In all cases the colour scale is coded according to the logarithm of local density. In all panels the continuous red curve traces the median of the ϵ[Fe/H]phot, v distribution, while the red dashed curves trace the 16th and 84th percentiles of the same distribution. The scales of the y-axis between the upper and lower panels are different. |
| In the text | |
 |
Fig. 5. Stars of the APOGEE VS plotted in (v − y)0, m1, 0 (left panel) and (b − y)0, m1, 0 diagrams. The points are coloured according to their [Fe/H]spec values from APOGEE DR17. |
| In the text | |
 |
Fig. 6. Differences between the spectroscopic and photometric metallicities as a function of spectroscopic metallicity for APOGEE VS, for [Fe/H]phot, v (upper panel) and [Fe/H]phot, b (lower panel). The horizontal grey lines are located at Δ[Fe/H] = ±0.5 dex. The continuous red lines trace P50 and the dashed red lines P16 and P84 of the Δ[Fe/H] distribution. A shift of +0.14 dex has been applied to [Fe/H]phot, v to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≤ −0.8, while a shift of −0.36 dex was applied to [Fe/H]phot, b to minimise the median Δ[Fe/H] in the region [Fe/H]spec ≥ −0.8. |
| In the text | |
 |
Fig. 7. Location in the Galaxy and kinematics of the stars in our sample. Left panel: bi-dimensional histogram in the Z vs |
| In the text | |
 |
Fig. 8. Example of substructure selection. The upper panels and the lower left panel show the location of the whole sample (grey dots) in the dynamical spaces described by Lz, Lperp, and E. The red thick dots indicate stars in common with the list of GES stars from Lövdal et al. (2022) and Ruiz-Lara et al. (2022). The blue symbols indicate our selection of likely GES members. The lower right panel shows the MDF for this selection of GES stars (black histogram) and that for the entire sample, normalised to the peak of the former (grey histogram). The red dashed line is the mean [Fe/H] quoted by Ruiz-Lara et al. (2022) for their own GES selection. |
| In the text | |
 |
Fig. 9. Normalised MDFs for the six substructure under study, labelled at the top of each panel. The red histograms show the results obtained when only using stars in common with RL22, whereas the blue histograms show the distributions obtained with our own selection. The total number of stars used to build them is quoted in each panel, and is listed in Table 3. |
| In the text | |
 |
Fig. 10. MDFs for the six substructures. The red dashed line is the metallicity of the best-fit theoretical model used by RL22 to fit the CMD of each substructure, and is shown as reference. |
| In the text | |
 |
Fig. 11. Distribution of the six substructures in the chemo-dynamical plane described by [Fe/H] vs orbital eccentricity. |
| In the text | |
 |
Fig. 12. Comparison between the cumulative metallicity distributions of the low-eccentricity (solid line) and the high-eccentricity (dashed line) populations of Thamnos. |
| In the text | |
 |
Fig. A.1. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the GALAH VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
| In the text | |
 |
Fig. A.2. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the GSP-Spec VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
| In the text | |
 |
Fig. A.3. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the LAMOST VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
| In the text | |
 |
Fig. A.4. Δ[Fe/H] for [Fe/H]C (upper panel) and [Fe/H]H (lower panel) as a function of [Fe/H]spec for the Gaia-ESO VS. The arrangement and the meaning of the symbols is the same as in Fig. 6, but the median and percentile lines are computed in 0.3 dex bin, due to the small dimension of the sample. |
| In the text | |
 |
Fig. B.1. Δ[Fe/H] for [Fe/H]C, s[m] (upper panel) and [Fe/H]C, sm0 (lower panel) as a function of [Fe/H]spec for the APOGEE VS. The arrangement and the meaning of the symbols is the same as in Fig. 6. |
| In the text | |
 |
Fig. C.1. [Fe/H]C as a function of apparent G magnitude for member stars of NGC 104 and NGC 6752 included in our catalogue. Points are colour-coded according to their uncertainty in the photometric metallicity ϵ[Fe/H]C. The thick horizontal lines are the value of the mean spectroscopic metallicity as tabulated in the 2010 edition of the Harris (1996) catalogue. The red horizontal branch stars of NGC 104 lie around G ≃ 14.2. |
| In the text | |
 |
Fig. D.1. Difference between the reddening estimates adopted here, from Schlafly & Finkbeiner (2011, S11), and those obtained from the distance-dependent maps by Lallement et al. (2022, L22) as a function of distance from the Sun. Points are colour-coded according to Δ[Fe/H]APO − C = [Fe/H]APO − [Fe/H]C. The thick red line is P50 and the thin red lines are P16 and P84 of the distribution of the E(B-V) difference computed over 0.5 kpc wide bins. |
| In the text | |
 |
Fig. D.2. Δ[Fe/H]APO − C as a function of E(B − V) for the APOGEE VS. Upper panel: Entire sample; middle panel: Stars with distance lower than 1 kpc; lower panel: Stars with [Fe/H]APO < −0.6. The horizontal lines indicate the Δ[Fe/H] = 0.0 ± 0.5 dex levels. |
| In the text | |
 |
Fig. E.1. Δ[Fe/H]APO − C (upper panel) and Δ[Fe/H]APO − H (lower panel) as a function of mean spectroscopic α elements abundance for the APOGEE VS. The red lines are linear fits to the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \mathrm{[Fe/H]_{phot,v}} = \frac{m_{1,0}-0.513(v-{ y})_0+0.312}{0.154(v-{ y})_0-0.096} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq1.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]_{phot,b}} = \frac{m_{1,0}-1.277(b-{ y})_0+0.331}{0.324(b-{ y})_0-0.032}, \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq2.gif)
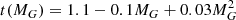
![$$ \begin{aligned} \mathrm{[Fe/H]_{C} = [Fe/H]_{phot,v} +0.14} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq11.gif)
![$$ \begin{aligned} \mathrm{\epsilon [Fe/H]_{C} = \epsilon [Fe/H]_{phot,v}} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq12.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]_{H} = [Fe/H]_{phot,b} -0.36} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq13.gif)
![$$ \begin{aligned} \mathrm{\epsilon [Fe/H]_{H} = \epsilon [Fe/H]_{phot,b}} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq14.gif)
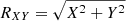
![$$ \begin{aligned} \mathrm{[Fe/H]_{phot,s}} = \frac{m_{1,0}-0.521(v-{ y})_0+0.309}{0.159(v-{ y})_0-0.090}, \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq21.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]_{phot,[m]}} = \frac{[m]-0.585(v-{ y})_0+0.251}{0.131(v-{ y})_0-0.070}\cdot \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq22.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]_{C,sm_0} = [Fe/H]_{phot,s} + 0.10} \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq23.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]_{C,s[m]} = [Fe/H]_{phot,[m]} +0.10}, \end{aligned} $$](/articles/aa/full_html/2023/06/aa45921-23/aa45921-23-eq24.gif)