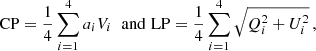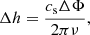| Issue |
A&A
Volume 674, June 2023
Solar Orbiter First Results (Nominal Mission Phase)
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245826 | |
| Published online | 09 June 2023 | |
Spectropolarimetric investigation of magnetohydrodynamic wave modes in the photosphere: First results from PHI on board Solar Orbiter
1
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: calchetti@mps.mpg.de
2
ASI, Italian Space Agency, Via del Politecnico snc, 00133 Rome, Italy
3
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
4
Instituto Nacional de Técnica Aeroespacial, Carretera de Ajalvir, km 4, 28850 Torrejón de Ardoz, Spain
5
Univ. Paris-Sud, Institut d’Astrophysique Spatiale, UMR 8617, CNRS, Bâtiment 121, 91405 Orsay Cedex, France
6
Instituto de Astrofísica de Andalucía (IAA-CSIC), Apartado de Correos 3004, 18080 Granada, Spain
7
Universitat de València, Catedrático José Beltrán 2, 46980 Paterna-Valencia, Spain
8
Instituto Universitario “Ignacio da Riva”, Universidad Politécnica de Madrid, IDR/UPM, Plaza Cardenal Cisneros 3, 28040 Madrid, Spain
9
Leibniz-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
10
Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received:
30
December
2022
Accepted:
21
April
2023
Context. In November 2021, Solar Orbiter started its nominal mission phase. The remote-sensing instruments on board the spacecraft acquired scientific data during three observing windows surrounding the perihelion of the first orbit of this phase.
Aims. The aim of the analysis is the detection of magnetohydrodynamic (MHD) wave modes in an active region by exploiting the capabilities of spectropolarimetric measurements.
Mthods. The High Resolution Telescope (HRT) of the Polarimetric and Helioseismic Imager (SO/PHI) on board the Solar Orbiter acquired a high-cadence data set of an active region. This is studied in the paper. B-ω and phase-difference analyses are applied on line-of-sight velocity and circular polarization maps and other averaged quantities.
Results. We find that several MHD modes at different frequencies are excited in all analysed structures. The leading sunspot shows a linear dependence of the phase lag on the angle between the magnetic field and the line of sight of the observer in its penumbra. The magnetic pore exhibits global resonances at several frequencies, which are also excited by different wave modes.
Conclusions. The SO/PHI measurements clearly confirm the presence of magnetic and velocity oscillations that are compatible with one or more MHD wave modes in pores and a sunspot. Improvements in modelling are still necessary to interpret the relation between the fluctuations of different diagnostics.
Key words: Sun: magnetic fields / Sun: photosphere / Sun: oscillations
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
Wave phenomena in the solar atmosphere can traditionally be divided into regions dominated by five-minute oscillations (3 mHz, in the photosphere) and three-minute oscillations (5 mHz, in the chromosphere). This division is the result of the density stratification and therefore of a cut-off frequency, thus making the solar atmosphere a filter for low-frequency waves below approximately 5 mHz (e.g. Felipe et al. 2010; Khomenko & Collados 2015).
Howard et al. (1968) measured for the first time that the five-minute oscillations in umbrae and penumbrae of sunspots have a smaller amplitude than five-minute oscillations in the quiet Sun (QS). Many mechanisms have been suggested to explain this particular behaviour, such as the reduction in the efficiency of the excitation (Goldreich & Keeley 1977; Goldreich & Kumar 1988) or the absorption of p-mode oscillations (Cally 1995; Rijs et al. 2016) and the subsequent conversion into magnetohydrodynamic (MHD) modes. In addition to p-mode conversion, recent studies have also revealed resonant oscillations in sunspots and pores. The resonant frequencies are dependent on the structure itself and on its shape (Jess et al. 2017, 2020; Keys et al. 2018; Stangalini et al. 2021a, 2022; Grant et al. 2022). These results have been obtained not only by analysing the intensity or velocity fluctuations, but in some cases, also by exploiting the potential of spectropolarimetric measurements. Spectropolarimetric data allow the inference of magnetic field properties (del Toro Iniesta & Ruiz Cobo 2016), opening up new possibilities for the study of MHD waves in the solar atmosphere. A peculiar case regarding this phenomenon was first reported by Stangalini et al. (2011). They presented a magnetic pore that against expectations showed almost no fluctuations in the 3 mHz band in the photospheric layer, but showed clear oscillations at other frequencies. More recently, it was shown that these unexpected frequencies in the photosphere were resonant oscillations of the magnetic structure (Stangalini et al. 2021a).
Spurious signals in polarimetric measurements usually originate from opacity effects or cross-talk between different Stokes parameters. Highly stable instruments are needed in order to disentangle these effects from real oscillations (Bellot Rubio et al. 2000). One way to do this is by computing the phase-difference between different quantities, such as the line-of-sight (LoS) velocity field or the continuum intensity (Rüedi et al. 1998; Fujimura & Tsuneta 2009; Joshi & de la Cruz Rodríguez 2018), and between different layers of the solar atmosphere (e.g. Fujimura & Tsuneta 2009; Martínez González et al. 2011; Stangalini et al. 2021b). Only points with very high coherence should be considered in the analysis in order to guarantee a reliable relation between the signals. These phase values can also be compared to models of wave modes in magnetic flux tubes, such as those described in Fujimura & Tsuneta (2009), Moreels & Van Doorsselaere (2013), and Moreels et al. (2013, 2015). Spectropolarimetric data are also necessary to constrain the excitation mechanisms of these wave modes (Vigeesh et al. 2011).
The solar magnetic field that is concentrated in flux tubes connects different layers of the solar atmosphere. Waves propagating in magnetic structures, or global resonant modes of the whole flux tube, can transport energy from the base of the solar atmosphere and dissipate it in the chromosphere or corona (Khomenko & Collados 2015; Gafeira et al. 2017; Jafarzadeh et al. 2017a,b; Grant et al. 2018; Jess et al. 2020; Van Doorsselaere et al. 2020). MHD waves can also cause changes in the plasma composition, such as the plasma fractionation (e.g. Laming 2015; Baker et al. 2021; Murabito et al. 2021), thus enabling new ways to investigate the sources of the slow solar wind (e.g. Brooks et al. 2022).
In March 2022, Solar Orbiter (SO Müller 2020) started its first remote-sensing window of the nominal mission phase (Zouganelis et al. 2020). The Polarimetric and Helioseismic Imager (PHI, Solanki et al. 2020) on board the Solar Orbiter mission observed many different targets during the three remote-sensing windows of this orbit and provided photospheric spectropolarimetric data. SO/PHI returned full-Stokes vectors and/or inverted parameters at high resolution and high sensitivity. The stability of the instrument and the absence of the Earth’s atmosphere play a key role in providing these high-quality data, which are also necessary for the detection of high-order and high-frequency MHD wave modes (Stangalini et al. 2022).
This paper further investigates the ability of detecting real magnetic field oscillations (e.g. Stangalini et al. 2021b; Keys et al. 2021) associated with particular MHD wave modes (e.g. Roberts 2019; see Jess et al. 2023 for a recent review). We describe the first high-cadence observations taken by SO/PHI. A Fourier analysis is performed on a magnetic field diagnostic and the LoS velocity to detect MHD wave modes in the sunspots and pores of the observed active region. This investigation has been conducted by studying the B-ω diagrams of and the phase lags between these quantities. The results show magnetic and velocity oscillations that are compatible with one or more MHD wave modes.
2. Observations
2.1. Observational data
The data set analysed in this work was acquired by the SO/PHI High Resolution Telescope (HRT, Gandorfer et al. 2018) for the Nanoflares Solar Orbiter Observing Plan1 during the inferior conjunction on 7 March 2022 from 00:00:09 to 00:45:09 UT. The spacecraft position was exactly in between the Earth and the Sun at that time.
This time series consists of a 45-min observation with a cadence of 60 s, sampling the active region (AR) with NOAA number 12960. The distance from the Sun at the time of observation was 0.501 au, resulting in a pixel scale of 181 km at disc centre on the SO/PHI-HRT detector. The AR was observed at a cosine of heliocentric angle (μ) of 0.87, located at −31.2° in longitude and −17.5° in latitude in heliographic Stonyhurst coordinates (see Thompson 2006 for more details about solar coordinates). SO/PHI-HRT acquired 45 spectral-line scans at six wavelength positions (five points within the Fe I line centred at 617.3 nm, and one point in the near continuum), all with four different polarimetric modulation states. The exposure time of each individual frame is 6 ms, and individual images result from the accumulation over 16 exposures to reach the required S/N. The total cadence for obtaining a single data set of 24 images is 60 s.
2.2. Data reduction
The data were down-linked as raw and were then processed and calibrated using the SO/PHI-HRT on-ground pipeline (Sinjan et al. 2022). The full-Stokes vector at each wavelength and the results of the inversion of the radiative transfer equations (RTE) in Milne-Eddington approximation were obtained with C-MILOS (Orozco Suárez & Del Toro Iniesta 2007).
A new processing step was added to the data calibration pipeline prior to the RTE inversion for this work compared to Sinjan et al. (2022). The step is currently being included into the standard version of the pipeline. We retrieved the point spread function (PSF) of the instrument with a phase diversity (PD) analysis (Kahil et al. 2022; based on Paxman et al. 1992; Löfdahl & Scharmer 1994).
The images were corrected for optical aberrations introduced mostly by the entrance window of the instrument. For this restoration, called aberration correction, the images are deconvolved by a reduced PSF. The latter is obtained by dividing the full PSF obtained from the PD calibration by the pure diffraction-limited PSF of a circular aperture (Airy function) corresponding to the ideal (aberration-free) entrance pupil of the instrument. This convolution is done mainly to reduce the additional noise introduced by the deconvolution algorithm. More information about the PD analysis and retrieval of the wavefront error of the SO/PHI-HRT can be found in Kahil et al. (2022, 2023).
The noise level obtained at the end of the processing is 1.8 × 10−3 in Stokes V and Q and 2.2 × 10−3 in Stokes U in units of the continuum intensity (Icavg). For operational reasons, the image stabilisation system (ISS, Volkmer et al. 2012) of the instrument was off during the acquisition. One of the main functions of the ISS is to prevent motion-induced polarimetric cross-talk and improve polarimetric precision that can be affected by the spacecraft jitter. However, they can only be partially compensated for by the data reduction pipeline. Therefore, the absence of the ISS and the deconvolution algorithm cause the higher noise with respect to the nominal level of 10−3 (see Sinjan et al. 2022, 2023).
The spacecraft jitter induces movements of the image on the detector plane. The solar scene is therefore sampled at different spectral points due to the cavity errors of the etalon, which are anchored to the detector plane. The effect of this shift in the sampling wavelength during the accumulations of each frame was tested using synthetic Stokes profiles of the Fe I line with non-local thermodynamic equilibrium (NLTE) effects (described in Smitha et al. 2023). The effects are negligible and do not produce any artefacts in the data.
In addition to the processing and calibration procedures described above, we decided to post-process the full Stokes vectors in order to obtain a time series ready for scientific analysis. First, we selected a sub-region of 1024 × 1024 px, which includes the whole AR. We then co-aligned the image time-series using a cross-correlation algorithm with sub-pixel accuracy (based on Guizar-Sicairos et al. 2008) that is applied to the continuum intensity maps. Once we modulated the Stokes vectors using the inverted demodulation matrix, we performed a pixel-by-pixel linear interpolation between consecutive data sets to produce pseudo co-temporal modulated data in which all the polarimetric and wavelength scans, that contribute to a given set of Stokes profiles, have the same observation time (following the technique by Oba et al. 2017). Lastly, we demodulated and corrected for cross-talk to remove any possible spurious effects from the interpolation of modulated polarimetric frames and then we ran the RTE inversion of the pseudo co-temporal full-Stokes vectors with C-MILOS. The fully reduced full-Stokes vectors were also used to compute circular polarization (CP) and linear polarization (LP) maps following the definitions by Martínez Pillet et al. (2011),
where Qi, Ui, and Vi are the polarized components of the Stokes vectors in the blue (i = [1, 2]) and red (i = [3, 4]) line wings, and a = [1, 1, −1, −1]. One example of the data products for the first time step of the time series is shown in Fig. 1. The full field of view (FoV) shown in all the panels is 1024 × 1024 px, and the maps in panels (b–d) are results of the RTE inversion. The continuum intensity and the CP and LP maps in panels (a), (e) and (f) are shown in units of the continuum intensity. Negative velocities in panel (b) are flows towards the observer, and angles smaller than 90° in panel (d) point towards the observer.
 |
Fig. 1. First image of the post-processed time series acquired on 7 March 2022 at 00:00:09UT. From panel (a) to (f): intensity in the continuum wavelength, LoS velocity, LoS magnetic field, inclination of the magnetic field vector, circular polarization, and linear polarization. Panels (b) to (d) are results of the RTE inversion with C-MILOS (Orozco Suárez & Del Toro Iniesta 2007). Panels (e) and (f) show maps obtained with Eq. (1). The blue arrow in panel (a) points towards the disc centre. |
3. Methods and desults
We investigated the velocity and magnetic oscillations in AR12960. We decided to focus on the LoS velocity and on a magnetic diagnostic, such as CP instead of the LoS magnetic field. We made this decision to avoid the higher spatial noise from the RTE inversion and to have a decreased noise through the spectral average that was performed to obtain the CP maps. A similar choice was also made by Martínez González et al. (2011), Jafarzadeh et al. (2013), Stangalini et al. (2021a,c), for instance. A Fourier analysis, pixel by pixel, was carried out to study the oscillations in the whole FoV. Furthermore, we obtained the power spectral density (PSD) in each pixel of the time series with a highest detectable frequency of 8.33 mHz.
In order to investigate the dependence of the velocity and magnetic dynamics on the photospheric magnetic field, we constructed B-ω diagrams (Stangalini et al. 2021a) of different magnetic structures in the FoV. This technique is particularly suited to find coherent oscillations in magnetic structures with irregular shapes because it is not directly dependent on the spatial extension of the magnetic field, unlike the k-ω analysis (e.g. Duvall 1983) or the power-distance diagram (Sobotka et al. 2013). The B-ω diagram was obtained by dividing each region of interest (RoI) into magnetic bins (100 G each in this case) and by averaging the PSDs of the chosen quantity (LoS velocity and CP in this work) in each magnetic bin. To do this, we used the absolute values of the LoS magnetic fields for the binning. In this case, the LoS magnetic field was preferred to CP as a more straightforward quantity when binning the chosen RoI.
The B-ω diagrams of the LoS velocity field and of the CP time series are illustrated in Figs. 2 and 3, respectively. We present four of the magnetic structures in the FoV in this paper. They show the most interesting wave modes. RoI (1) represents the leading spot of AR12960. Its velocity field clearly shows 3 mHz oscillations in the QS region, and two small high-power regions are evident for magnetic field values above 1000 G. Nevertheless, smaller peaks are present in the umbra of the sunspot at 3 mHz and 4 mHz for magnetic field values higher than 1500 G. On the other hand, the B-ω diagram of CP of the same region in Fig. 3 shows similar peaks, but the overall distribution of the power is different, for example the small increase in power at 4 mHz in the umbra. The other three regions represent small pores next to the leading and trailing sunspots. In all of these cases, different oscillation modes in the QS and the magnetic regions are clearly visible, which shows very peculiar modes in different magnetic field ranges. Differences are also visible between the LoS velocity and CP diagrams. In particular, the ratio of the amplitudes of the power peaks are different for each wave mode that is detected in the magnetic structures.
 |
Fig. 2. Results of the B-ω analysis of the LoS velocity field. Central panel: continuum intensity map showing the four RoIs. Panels (1–4): B-ω diagrams of the PSD of the LoS velocity field in the corresponding RoIs. The absolute value of the LoS magnetic field is plotted on the x-axes, and the frequency is plotted on the y axes. The same colour scale has been used for all these panels and is shown below the central panel. We have chosen the saturation levels in order to emphasise the power increases in the magnetic regions. |
 |
Fig. 3. Results of the B-ω analysis on the CP time series. Central panel: same as for Fig. 2. Panels (1–4): B-ω diagrams of the PSD of the CP time series in the corresponding RoIs. The absolute value of the LoS magnetic field is plotted on the x-axes, and the frequency is plotted on the y-axes. The same colour scale has been used for all these panels and is shown below the central panel. We have chosen the saturation levels in order to emphasise the power increases in the magnetic regions. a.u. indicates arbitrary units. |
In order to further investigate the oscillation modes shown in the B-ω diagrams, we performed two different analyses depending on the type of structure. In RoI (1), we carried out a pixel by pixel phase-difference analysis between the LoS velocity and the CP series within the leading sunspot. In RoIs (2), (3), and (4), we computed the average signals of the LoS velocity, CP, continuum intensity, and cross section of the magnetic structures and we used those to detect MHD modes. This choice was motivated mostly by the size of the analysed structures. First, a pixel-by-pixel analysis is better suited for larger regions, such as the leading sunspot. Second, the averaged analysis is less well suited for the sunspot due to the definition of the cross section, which includes the umbra and not the penumbra.
Figure 4 shows results obtained for the sunspot in RoI (1). The upper plot illustrates some of the phase differences between the LoS velocity and the CP signal obtained from a Fourier analysis, over-plotted on a continuum intensity map. A frequency range centred on 3.3 mHz (with 1 mHz width) was considered in order to include most of the oscillating power detected with the B-ω diagram. This analysis was performed pixel by pixel in locations in which the continuum intensity was lower than 0.9 in order to exclude QS and plage regions. The points represented here are only those with an average coherence over the frequency bin higher than 90%. The coherence between the signals represents a linear relation between them and it is not directly related to the amplitudes or the phases of the signals. The high coherence ensures high reliability in the phase measurements between the two series (Vigeesh et al. 2017; Stangalini et al. 2018).
 |
Fig. 4. Results of the Fourier analysis for RoI (1). Top panel: continuum intensity of RoI (1). The phase-differences for the pixels show a high coherence between the LoS velocity and CP time series at 3.3 mHz that is over-plotted. The colour scale represents the values of the phase difference in each considered point. Bottom panel: 2D histogram as a function of the angle between the magnetic field vector and the LoS (x-axis) and the phase difference between the LoS velocity and CP time series at 3.3 mHz. The same points as in the upper panel have been used to build this diagram. The withe dots represent the central position obtained with a Gaussian fit of the phase-difference value at different angle bins. |
The lower panel of Fig. 4 shows a 2D histogram of the phase-difference obtained from the analysis. The background colour displays the histogram density (i.e. counts), plotting the phase difference between the LoS velocity and the CP signal as a function of the angle between the vector magnetic field and the LoS. This analysis was made by retrieving the vector magnetic field from the C-MILOS inversion and by disambiguation of the azimuth of the magnetic field with the minimal energy method (Metcalf 1994) adapted from the SDO/HMI pipeline (Hoeksema et al. 2014). The angle between the LoS and the magnetic field was obtained using Eq. (1) in Gary & Hagyard (1990). We also performed a Gaussian fit of the phase-lag distribution at each angle bin to obtain the central phase difference at that specific interval. The mean values of the fit are plotted as white dots in the same diagram. The diagram clearly shows a change in the phase difference from 140° to 180° in the angle range between 40° and 90°.
A different approach was pursued on smaller magnetic structures in RoIs (2), (3), and (4). We tracked each magnetic structure as in Morton et al. (2011). We took the median value of the continuum intensity in a QS region next to the RoI and considered only pixels with values at least 3σ below the median. This technique provides a 99% confidence level that the dark magnetic pores or umbrae are contoured. The most interesting result is obtained from RoI (4), which is represented in Fig. 5. The same plots for RoIs (2) and (3) are shown in Figs. A.1 and A.2. The bottom panel of Fig. 5 shows the PSDs of four different quantities from averaged signals in the contoured magnetic pore at each time step (i.e. CP, LoS velocity, continuum intensity, and the cross section of the pore). The cross section is defined as the surface inside the bounds of the contour. The PSDs were normalized by dividing them by their total power. This was done mostly for representation purposes. This plot clearly shows three main peaks that are common to all the PSDs at 1.9, 2.9, and 4.1 mHz. In Table 1 we show the phase differences between these quantities, computed for the frequencies corresponding to the maxima of the PSDs. The phase differences at 1.9 mHz and 2.9 mHz show similar values, but this is different for the other peak at 4.1 mHz. This last peak is dominated by oscillations in CP and LoS velocities, whereas the continuum intensity and cross section have almost negligible amplitude.
 |
Fig. 5. Results of the Fourier analysis of RoI (4). Top panel: continuum intensity of RoI (4). The green contour shows the tracked region at this specific time step. Bottom panel: PSDs obtained by averaging the signal in the pore in RoI (4). Black line: CP. Red line: LoS velocity field. Yellow line: Continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power (i.e. frequency integrated). |
Phase differences between averaged CP, LoS velocity (vLoS), cross section (CS), and continuum intensity (Icnt) at 1.9, 2.9, and 4.1 mHz in the magnetic pore in RoI (4).
4. Discussion
The analysis performed on this first high-cadence time series acquired by SO/PHI-HRT has shown various MHD modes in different magnetic structures in AR12960. The B-ω diagrams in Figs. 2 and 3 reveal a separation between the QS and the magnetic structures. While the power of the LoS velocity in the QS always peaks around 3.3 mHz, the oscillations in regions with LoS magnetic fields higher than 500 G show several different patterns. The diagrams in Fig. 3 also show different frequencies of oscillations in each structure, with only low frequency power in the QS regime, as in Fig. 2: this is likely generated by the noise in the data. However, we cannot exclude a physical source such as plasma motions, granulation, or even internal gravity waves, which can be distinguished by their different properties in a phase-difference diagram (e.g. Vigeesh et al. 2017; Calchetti et al. 2021). The B-ω analysis remains a powerful tool for investigating the presence of wave modes in these structures, allowing the detection of a clear separation between QS oscillation patterns and the global eigenmodes of the magnetic flux tubes in each RoI.
The phase relation between the LoS velocity and CP was taken into consideration in the case of the leading sunspot in RoI (1). The relation of the phase difference to the angle between the magnetic field vector and the LoS of the observer is particularly interesting, as shown in Fig. 4. This analysis is motivated by an increase in power and coherence in regions of the penumbra that point towards the disc centre. This difference in the inclination angle of the magnetic field vector is also visible in the increased amplitude of the CP and is reduced in LP in Fig. 1. The behaviour of magneto-acoustic waves in an environment with an inclined magnetic field has broadly been investigated by many authors (e.g. Schunker & Cally 2006). The mode transmission and conversion strongly depend on the attack angle of the wave, which is the angle between the wave vector and the magnetic field vector. As an effect of the polarization of the slow wave modes (which are expected to have a small attack angle; see e.g. Jess et al. 2015), we would expect to observe this type of waves along inclined magnetic field lines all around the penumbra of the sunspot. However, Fig. 4 shows a linear relation between the phase difference between the LoS velocity and CP and the angle between the LoS of the observer and the magnetic field vector. This relation is evident in the phase-lag window between 140° and 180° and in the separation angle between 40° and 90°. The top panel in Fig. 4 clearly shows that most of the points with high coherence lie in the region of the penumbra towards the disc centre, and most of the points with smaller phase lag are close to the umbra-penumbra boundary. We would also expect high coherence between the CP and LoS velocity in a slow magneto-acoustic mode, but there is no information regarding their phase relation in the literature.
One possible explanation for this variation in the phase difference might be the variation in the height difference between the CP and the LoS velocity maps. When we consider the same height in the QS with a phase difference of 180°, we would expect a height difference at the umbra-penumbra boundary of
where cs is the sound speed, ν is the frequency, and ΔΦ is the phase difference. Considering cs = 7 km s−1, ν = 3 mHz, and ΔΦ = 40° (which is the change in the phase difference as reported in the lower panel of Fig. 4), we obtain Δh ≈ 250 km. According to Fleck et al. (2011), the formation height of the line core of the Fe I line is ∼250 km, so that we would not expect a height difference comparable to this value. This is also due to the response functions to the LoS velocity in C-MILOS presented by Orozco Suárez & Del Toro Iniesta (2007), which are more peaked in the wings of the line. One more possible interpretation of this result is that the propagation speed of the waves changes because of the different physical properties of the photospheric plasma in the sunspot penumbra. This might explain a variation in the phase difference, but further investigations are needed to understand this behaviour better.
For the small pores and spots in RoIs (2), (3), and (4), we performed an analysis similar to Morton et al. (2011) to detect MHD modes in these magnetic flux tubes. The bottom panel of Fig. 5 shows the PSDs obtained on averaged quantities in a small magnetic pore. The results obtained from the phase analysis (Table 1) can be used to infer which type of wave mode dominates at each frequency (see Moreels & Van Doorsselaere 2013; Moreels et al. 2013). The two peaks at 1.9 mHz and 2.9 mHz show very similar phase differences, particularly between the CP and LoS velocity and between the cross section and continuum intensity. According to the findings of Moreels & Van Doorsselaere (2013), these values can represent a slow standing surface mode, and the peaks might be harmonics of the same mode, even though the averaged PSDs show different power ratios at different peaks. It is also important to consider that the observed phase lags are not exactly identical to those predicted by Moreels & Van Doorsselaere (2013). This is expected, because their values were found for a straight cylinder with constant plasma parameters inside and outside the flux tube. Moreover, only one wave mode was excited in the flux tube simulated by Moreels & Van Doorsselaere (2013), whereas at least two different modes occur here at the same time in the same magnetic pore. The wave mode detected at 4.1 mHz shows different phase lags and a very low oscillatory power in the cross section and continuum intensity. This indicates a different wave mode in the same magnetic structure that then resonates at different frequencies and with different MHD modes at the same time. According to the simplified model described in Fujimura & Tsuneta (2009), the phase lag between CP and LoS velocity and the small oscillating power in intensity and cross section might have been generated by a non-compressible kink mode. In particular, this might be caused by a mix of ascending and descending propagating modes or by a standing kink mode.
Furthermore, it is worth noting that the frequency peaks found in the spatially averaged LoS velocity and CP time series are the same as we found in the B-ω diagrams in Figs. 2 and 3. The same result is obtained by averaging the signals and the PSDs in the same magnetic structures. This shows that a coherent and global oscillation of the flux tube generated by a given wave mode has been detected with two different techniques.
5. Summary and conclusion
We reported the detection of MHD modes in AR12960 using spectropolarimetric data acquired by SO/PHI-HRT during the first remote-sensing window of Solar Orbiter on 7 March 2022 during the inferior conjunction. The 45-min time series was calibrated with the SO/PHI-HRT on-ground pipeline and was then post-processed with the procedures described in Sect. 2.2. Magnetohydrodynamic modes were detected in the leading sunspot of the AR and in several small magnetic structures. The B-ω diagrams of the RoIs, shown in Figs. 2 and 3, were used to detect the wave modes at different frequencies and magnetic field ranges. The leading sunspot in RoI (1) and the pore in RoI (4) show a clear relation in the oscillations between different quantities and diagnostics.
We detected a high coherence between oscillations in the CP and LoS velocity in the sunspot in RoI (1), with a phase lag ranging from 140° to 180°. These lags depend approximately linearly on the angle of separation between the magnetic field vector and the LoS of the observer. The reason for this dependence is not fully understood yet, but we can exclude the height difference between the two time series as the source of the effect.
The small pore in RoI (4) was tracked with the technique presented in Morton et al. (2011) to measure the oscillation of the whole structure in the LoS velocity, CP, intensity, and cross section. The identified modes in which the oscillation power peaked at 1.9 mHz and 2.9 mHz are compatible with slow standing sausage modes according to Moreels & Van Doorsselaere (2013), whereas the peak at 4.1 mHz might be generated by a non-compressible kink mode. These modes are compatible with the frequencies observed in the B-ω diagrams and demonstrate the possible presence of multiple MHD modes in magnetic structures in the solar photosphere.
In the future, a longer time series with higher spatial resolution and signal-to-noise ratio would facilitate the detection of wave modes at higher frequencies and higher-order modes. Co-observations from different vantage points with ground-based and Earth-orbiting instruments can also be extremely important to measure the ratio of the horizontal to vertical displacement in p- and f- modes (e.g. Schou et al. 2023) or to distinguish longitudinal and transverse oscillations.
More information can be found here: https://issues.cosmos.esa.int/solarorbiterwiki/display/SOSP/SOOP+pages.
Acknowledgments
D. C. would like to thank H. N. Smitha for her valuable inputs. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. We are grateful to the ESA SOC and MOC teams for their support. The German contribution to SO/PHI is funded by the BMWi through DLR and by MPG central funds. The Spanish contribution is funded by AEI/MCIN/10.13039/501100011033/ (RTI2018-096886-C5, PID2021-125325OB-C5, PCI2022-135009-2) and ERDF “A way of making Europe”; “Center of Excellence Severo Ochoa” awards to IAA-CSIC (SEV-2017-0709, CEX2021-001131-S); and a Ramón y Cajal fellowship awarded to DOS. The French contribution is funded by CNES. The authors wish to acknowledge scientific discussions with the Waves in the Lower Solar Atmosphere (WaLSA; https://WaLSA.team) team, which has been supported by the Research Council of Norway (project no. 262622), The Royal Society (award no. Hooke18b/SCTM), and the International Space Science Institute (ISSI Team 502).
References
- Baker, D., Stangalini, M., Valori, G., et al. 2021, ApJ, 907, 16 [Google Scholar]
- Bellot Rubio, L. R., Collados, M., Ruiz Cobo, B., & Rodríguez Hidalgo, I. 2000, ApJ, 534, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, D. H., Janvier, M., Baker, D., et al. 2022, ApJ, 940, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Calchetti, D., Jefferies, S. M., Fleck, B., Berrilli, F., & Shcherbik, D. V. 2021, Philos. Trans. R. Soc. London Ser. A, 379, 20200178 [NASA ADS] [Google Scholar]
- Cally, P. S. 1995, ApJ, 451, 372 [NASA ADS] [CrossRef] [Google Scholar]
- del Toro Iniesta, J. C., & Ruiz Cobo, B. 2016, Liv. Rev. Sol. Phys., 13, 4 [Google Scholar]
- Duvall, T. L. J., &Harvey, J. W., 1983, Nature, 302, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Khomenko, E., & Collados, M. 2010, ApJ, 719, 357 [Google Scholar]
- Fleck, B., Couvidat, S., & Straus, T. 2011, Sol. Phys., 271, 27 [Google Scholar]
- Fujimura, D., & Tsuneta, S. 2009, ApJ, 702, 1443 [Google Scholar]
- Gafeira, R., Jafarzadeh, S., Solanki, S. K., et al. 2017, ApJS, 229, 7 [Google Scholar]
- Gandorfer, A., Grauf, B., Staub, J., et al. 2018, SPIE, 10698, 1403 [Google Scholar]
- Gary, G. A., & Hagyard, M. J. 1990, Sol. Phys., 126, 21 [Google Scholar]
- Goldreich, P., & Keeley, D. A. 1977, ApJ, 212, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Kumar, P. 1988, ApJ, 326, 462 [CrossRef] [Google Scholar]
- Grant, S. D. T., Jess, D. B., Zaqarashvili, T. V., et al. 2018, Nat. Phys., 14, 480 [Google Scholar]
- Grant, S. D. T., Jess, D. B., Stangalini, M., et al. 2022, ApJ, 938, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Guizar-Sicairos, M., Thurman, S. T., & Fienup, J. R. 2008, Opt. Lett., 33, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeksema, J. T., Liu, Y., Hayashi, K., et al. 2014, Sol. Phys., 289, 3483 [Google Scholar]
- Howard, R., Tanenbaum, A. S., & Wilcox, J. M. 1968, Sol. Phys., 4, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Feller, A., et al. 2013, A&A, 549, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Gafeira, R., et al. 2017a, ApJS, 229, 9 [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Stangalini, M., et al. 2017b, ApJS, 229, 10 [Google Scholar]
- Jess, D. B., Morton, R. J., Verth, G., et al. 2015, Space Sci. Rev., 190, 103 [Google Scholar]
- Jess, D. B., Van Doorsselaere, T., Verth, G., et al. 2017, ApJ, 842, 59 [Google Scholar]
- Jess, D. B., Snow, B., Houston, S. J., et al. 2020, Nat. Astron., 4, 220 [Google Scholar]
- Jess, D. B., Jafarzadeh, S., Keys, P. K., et al. 2023, Liv. Rev. Sol. Phys., 20, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, J., & de la Cruz Rodríguez, J. 2018, A&A, 619, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahil, F., Gandorfer, A., & Hirzberger, J. 2022, in Space Telescopes and Instrumentation 2022: Optical, Infrared, and Millimeter Wave, eds. L. E. Coyle, S. Matsuura, & M. D. Perrin, SPIE Conf. Ser., 12180, 121803F [Google Scholar]
- Kahil, F., Gandorfer, A., Hirzberger, J., et al. 2023, ArXiv e-prints [arXiv:2306.00163] [Google Scholar]
- Keys, P. H., Morton, R. J., Jess, D. B., et al. 2018, ApJ, 857, 28 [Google Scholar]
- Keys, P. H., Steiner, O., & Vigeesh, G. 2021, Philos. Trans. R. Soc. London Ser. A, 379, 20200182 [NASA ADS] [Google Scholar]
- Khomenko, E., & Collados, M. 2015, Liv. Rev. Sol. Phys., 12, 6 [Google Scholar]
- Laming, J. M. 2015, Liv. Rev. Sol. Phys., 12, 2 [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 1994, A&AS, 107, 243 [NASA ADS] [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., Manso Sainz, R., et al. 2011, ApJ, 730, L37 [Google Scholar]
- Martínez Pillet, V., del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [CrossRef] [Google Scholar]
- Metcalf, T. R. 1994, Sol. Phys., 155, 235 [Google Scholar]
- Moreels, M. G., & Van Doorsselaere, T. 2013, A&A, 551, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreels, M. G., Goossens, M., & Van Doorsselaere, T. 2013, A&A, 555, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreels, M. G., Freij, N., Erdélyi, R., Van Doorsselaere, T., & Verth, G. 2015, A&A, 579, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Erdélyi, R., Jess, D. B., & Mathioudakis, M. 2011, ApJ, 729, L18 [Google Scholar]
- Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Murabito, M., Stangalini, M., Baker, D., et al. 2021, A&A, 656, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oba, T., Riethmüller, T. L., Solanki, S. K., et al. 2017, ApJ, 849, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., & Del Toro Iniesta, J. C. 2007, A&A, 462, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992, J. Opt. Soc. Am. A, 9, 1072 [CrossRef] [Google Scholar]
- Rijs, C., Rajaguru, S. P., Przybylski, D., et al. 2016, ApJ, 817, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 2019, MHD Waves in the Solar Atmosphere (Cambridge, United Kingdom: Cambridge University Press) [Google Scholar]
- Rüedi, I., Solanki, S. K., Stenflo, J. O., Tarbell, T., & Scherrer, P. H. 1998, A&A, 335, L97 [NASA ADS] [Google Scholar]
- Schou, J., Hirzberger, J., Orozco Suárez, D., et al. 2023, A&A, 673, A84 (SO Nominal Mission Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schunker, H., & Cally, P. S. 2006, MNRAS, 372, 551 [Google Scholar]
- Sinjan, J., Calchetti, D., Hirzberger, J., et al. 2022, SPIE, 12189, 121891J [Google Scholar]
- Sinjan, J., Calchetti, D., Hirzberger, J., et al. 2023, A&A, 673, A31 (SO Nominal Mission Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smitha, H. N., van Noort, M., Solanki, S. K., & Castellanos Durán, J. S. 2023, A&A, 669, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobotka, M., Švanda, M., Jurčák, J., et al. 2013, A&A, 560, A84 [EDP Sciences] [Google Scholar]
- Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stangalini, M., Del Moro, D., Berrilli, F., & Jefferies, S. M. 2011, A&A, 534, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stangalini, M., Jafarzadeh, S., Ermolli, I., et al. 2018, ApJ, 869, 110 [Google Scholar]
- Stangalini, M., Jess, D. B., Verth, G., et al. 2021a, A&A, 649, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stangalini, M., Baker, D., Valori, G., et al. 2021b, Philos. Trans. R. Soc. London Ser. A, 379, 20200216 [NASA ADS] [Google Scholar]
- Stangalini, M., Erdélyi, R., Boocock, C., et al. 2021c, Nat. Astron., 5, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Stangalini, M., Verth, G., Fedun, V., et al. 2022, Nat. Commun., 13, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, W. T. 2006, A&A, 449, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Srivastava, A. K., Antolin, P., et al. 2020, Space Sci. Rev., 216, 140 [Google Scholar]
- Vigeesh, G., Steiner, O., & Hasan, S. S. 2011, Sol. Phys., 273, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Vigeesh, G., Jackiewicz, J., & Steiner, O. 2017, ApJ, 835, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Volkmer, R., Bosch, J., & Feger, B. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, eds. M. C. Clampin, G. G. Fazio, H. A. MacEwen, & J. Oschmann, SPIE Conf. Ser., 8442, 84424P [NASA ADS] [CrossRef] [Google Scholar]
- Zouganelis, I., De Groof, A., Walsh, A. P., et al. 2020, A&A, 642, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Results from RoIs (2) and (3)
The analysis performed on RoI (4) (shown in Fig. 5) was also carried out on RoIs (2) and (3) (see Fig. 2 and 3 for the context and B-ω diagrams). The PSDs of the averaged quantities obtained after the tracking of the magnetic structures is shown in Fig. A.1 and A.2 for RoIs (2) and (3), respectively.
 |
Fig. A.1. PSDs obtained by averaging the signal in the pore in RoI (2). Black line: CP. Red line: LoS velocity field. Yellow line: continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power. |
 |
Fig. A.2. PSDs obtained by averaging the signal in the pore in RoI (3). Black line: CP. Red line: LoS velocity field. Yellow line: continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power. |
The PSDs show several peaks, particularly in the CP and LoS velocity, whereas the continuum intensity and the cross section are dominated by low-frequency oscillations. In the same way as for RoI (4), but much more pronounced, the power peaks between different quantities shift weakly. For this reason, we did not perform a phase analysis for any of the time series for RoIs (2) and (3). This type of behaviour was also reported in Stangalini et al. (2021a). The authors suggested a mix of slow and fast wave modes or different formation heights of the signals as a possible explanation, but a clear answer is still lacking.
All Tables
Phase differences between averaged CP, LoS velocity (vLoS), cross section (CS), and continuum intensity (Icnt) at 1.9, 2.9, and 4.1 mHz in the magnetic pore in RoI (4).
All Figures
 |
Fig. 1. First image of the post-processed time series acquired on 7 March 2022 at 00:00:09UT. From panel (a) to (f): intensity in the continuum wavelength, LoS velocity, LoS magnetic field, inclination of the magnetic field vector, circular polarization, and linear polarization. Panels (b) to (d) are results of the RTE inversion with C-MILOS (Orozco Suárez & Del Toro Iniesta 2007). Panels (e) and (f) show maps obtained with Eq. (1). The blue arrow in panel (a) points towards the disc centre. |
| In the text | |
 |
Fig. 2. Results of the B-ω analysis of the LoS velocity field. Central panel: continuum intensity map showing the four RoIs. Panels (1–4): B-ω diagrams of the PSD of the LoS velocity field in the corresponding RoIs. The absolute value of the LoS magnetic field is plotted on the x-axes, and the frequency is plotted on the y axes. The same colour scale has been used for all these panels and is shown below the central panel. We have chosen the saturation levels in order to emphasise the power increases in the magnetic regions. |
| In the text | |
 |
Fig. 3. Results of the B-ω analysis on the CP time series. Central panel: same as for Fig. 2. Panels (1–4): B-ω diagrams of the PSD of the CP time series in the corresponding RoIs. The absolute value of the LoS magnetic field is plotted on the x-axes, and the frequency is plotted on the y-axes. The same colour scale has been used for all these panels and is shown below the central panel. We have chosen the saturation levels in order to emphasise the power increases in the magnetic regions. a.u. indicates arbitrary units. |
| In the text | |
 |
Fig. 4. Results of the Fourier analysis for RoI (1). Top panel: continuum intensity of RoI (1). The phase-differences for the pixels show a high coherence between the LoS velocity and CP time series at 3.3 mHz that is over-plotted. The colour scale represents the values of the phase difference in each considered point. Bottom panel: 2D histogram as a function of the angle between the magnetic field vector and the LoS (x-axis) and the phase difference between the LoS velocity and CP time series at 3.3 mHz. The same points as in the upper panel have been used to build this diagram. The withe dots represent the central position obtained with a Gaussian fit of the phase-difference value at different angle bins. |
| In the text | |
 |
Fig. 5. Results of the Fourier analysis of RoI (4). Top panel: continuum intensity of RoI (4). The green contour shows the tracked region at this specific time step. Bottom panel: PSDs obtained by averaging the signal in the pore in RoI (4). Black line: CP. Red line: LoS velocity field. Yellow line: Continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power (i.e. frequency integrated). |
| In the text | |
 |
Fig. A.1. PSDs obtained by averaging the signal in the pore in RoI (2). Black line: CP. Red line: LoS velocity field. Yellow line: continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power. |
| In the text | |
 |
Fig. A.2. PSDs obtained by averaging the signal in the pore in RoI (3). Black line: CP. Red line: LoS velocity field. Yellow line: continuum intensity. Blue line: Cross section. The PSDs have been normalized to their total power. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.