EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 674 (June 2023) A&A, 674 (2023) A49 Full HTML
Open Access
Issue
A&A
Volume 674, June 2023
Article Number A49
Number of page(s) 10
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202245450
Published online 29 May 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Heat transport in the solar corona and wind plays a key role in coronal heating and wind acceleration; however, it is not yet fully understood. Due to the large mass difference between ions and electrons, we know that electrons mainly transport energy, whereas ions mainly transport momentum. Therefore, electrons are expected to play a key role in the thermally driven solar wind expansion. Furthermore, the accurately measured electron temperature radial profile is not only of prime interest for understanding the energy transport in the solar wind, but also an important ingredient for constraining thermally driven solar wind models (e.g., Meyer-Vernet & Issautier 1998; Issautier et al. 1999a, 2001b; Maksimovic et al. 1997; Zouganelis et al. 2004). For simplicity, the electron temperature is generally assumed to be fitted with a power law of the distance to the Sun, assuming no large-scale temporal variations: Te = T0 × (R/R⊙)β. β is observed to range between 0 (isothermal) and −4/3 (adiabatic), which indicates that electrons cool off with radial profiles spanning from nearly isothermal to almost adiabatic (e.g., Marsch et al. 1989; Pilipp et al. 1990; Issautier et al. 1998; Le Chat et al. 2011; Maksimovic et al. 2000; Štverák et al. 2015; Moncuquet et al. 2020). The large scatter in the measurements of β is not surprising and may be due to several reasons: (i) it is difficult to separate genuine variations along stream flux tubes from those across them; (ii) transient structures such as coronal mass ejections, co-rotating interaction regions, and interplanetary shocks can cause nongeneric effects; (iii) the observations from different spacecraft have been carried out in different latitudinal and radial ranges and/or in different phases of the solar activity; and (iv) the classification of data based on the solar wind speed, Coulomb collisions, and plasma beta has not always been carried out. In contrast, the exospheric solar wind models give another theoretical radial profile of the total electron temperature with the expression Te = T0 + T1 × (R/R⊙)−4/3 for (R/R⊙)2 ≫ 1 (e.g., Meyer-Vernet & Issautier 1998; Meyer-Vernet et al. 2003; Issautier et al. 2001b), which yields a profile that flattens at large distances, in agreement with Helios measurements (between 0.3 and 1 AU) (Marsch et al. 1989; Pilipp et al. 1990). Since this model has the same number of free parameters as the power-law model, it is difficult to distinguish both models from observations in a small radial range. Le Chat et al. (2011) verified this fact with Ulysses observations of high-speed solar wind during its first pole-to-pole latitude scan (from 1.5 to 2.3 AU).

Observations from Parker Solar Probe (PSP; Fox et al. 2016) indicate that there is an anticorrelation between the proton bulk speed, Vp, and the electron temperature, Te, close to the Sun (e.g., Maksimovic et al. 2020; Halekas et al. 2020, 2022), whereas the correlation between Vp and the proton temperature, Tp, persists throughout the heliosphere (see Lopez & Freeman 1986; Totten et al. 1995; Matthaeus et al. 2006; Démoulin 2009, and references therein). Specifically, Maksimovic et al. (2020) found that the anticorrelation between Vp and Te observed below 0.3 AU disappears as the wind expands, evolves, and mixes with different electron temperature gradients for different wind speeds. The exospheric solar wind model (e.g., Maksimovic et al. 1997, 2001) showed that the fast wind from the polar coronal hole regions (low-temperature regions) might be produced by the non-thermal electron distributions in the corona, which then might explain the anticorrelated (Vp, Te) close to the Sun. Furthermore, the exospheric model predicted that the temperature profile is flatter in the fast wind as previously observed (Meyer-Vernet & Issautier 1998). However, exospheric models use simplified hypotheses and challenging questions remain about the heating and cooling mechanisms for electrons. The PSP observations close to the Sun therefore give us an opportunity to investigate the solar wind electron thermal dynamics in the inner heliosphere.

The quasi-thermal noise (QTN) technique yields accurate electron density and temperature measurements in the solar wind. It has been used in a number of space missions (e.g., Meyer-Vernet 1979; Meyer-Vernet et al. 1986, 1993, 2017; Issautier et al. 1999b, 2001a,c; Issautier et al. 2005, 2008; Maksimovic et al. 1995, 2005a; Moncuquet et al. 1995, 1997, 2005; Moncuquet et al. 2006; Martinović et al. 2020; Le Chat et al. 2011; Salem et al. 2001; Lund et al. 1994; Schippers et al. 2013). Recent investigations (see Moncuquet et al. 2020; Maksimovic et al. 2020; Martinović et al. 2022) have already applied this technique on PSP based on electric voltage spectra acquired by the Radio Frequency Spectrometer (RFS/FIELDS) (Pulupa et al. 2017). Besides, SWEAP/PSP consists of the Solar Probe Cup (SPC) and the Solar Probe Analyzers (SPAN) (Kasper et al. 2016; Case et al. 2020; Whittlesey et al. 2020; Livi et al. 2022). In particular, SPC is a fast Faraday cup designed to measure the one dimensional velocity distribution function (VDF) of ions, while SPAN is a combination of three electrostatic analyzers operated to measure the three-dimensional ion and electron VDFs. Usually, traditional particle analyzers are affected by spacecraft photoelectrons and charging effects. Since the QTN electron density is deduced from a spectral peak, this measurement is independent of gain calibrations. Due to its reliability and accuracy, the electron number density derived from the QTN spectroscopy is called the gold standard density and serves routinely to calibrate other instruments (e.g., Maksimovic et al. 1995; Issautier et al. 2001c; Salem et al. 2001). Until now, on PSP, electron number density provided by the QTN technique has been playing an important role as a calibration standard for the scientific analysis (e.g., Kasper et al. 2021; Zhao et al. 2021; Liu et al. 2021a,b).

We derived the total electron temperature from the QTN spectroscopy in the so-called pristine or nascent solar wind observed by PSP. Specifically, a combination of a 12-day period of observations around each perihelion from encounter one (E01) to ten (E10) of PSP are presented with the heliocentric distance varying from about 13 to 60 R⊙. Currently, observations from E08 are not considered due to the unusual biasing setting for the electric antenna at that time. In Sect. 2, we describe a simple but practical and effective way to deduce the total electron temperature with the high-frequency part of the quasi-thermal noise spectra provided by the dipole electric antenna on board PSP. The corresponding results are compared to those from Maksimovic et al. (2020) (Te from a different QTN technique) and Moncuquet et al. (2020) (Tc from a simplified QTN technique) for a preliminary cross-checking. In Sect. 3, we first provide the mean radial electron temperature profile and then investigate the electron temperature gradients for different solar wind populations classified by the proton bulk speed and the solar wind mass flux, respectively. Also, we examine how the anticorrelation between Vp and Te are affected by radial evolution. In Sect. 4, the results and their implications for the electron thermal dynamics are summarized and discussed.

2. Data analysis

The QTN spectroscopy technique provides in situ macroscopic plasma properties by analyzing the power spectrum of the electric field voltage induced on an electric antenna by the plasma particle quasi-thermal motions. The QTN spectra are determined by both the ambient plasma properties and the antenna configuration because of the strong coupling between the plasma particles and the electric field. For an ideal electric antenna configuration, the longer and thinner the electric antenna, the better the QTN technique performs. Specifically, the length of the electric antenna (L) should exceed the local Debye length LD to ensure accurate temperature measurements. Fat antennas (with thick radius a) collect or emit more electrons so that the corresponding shot noise may exceed the quasi-thermal noise. Therefore, the electric antenna should be both long enough and thin enough (a < LD < L), so that the QTN technique can work well. When the antenna is configured in a proper way (see Meyer-Vernet et al. 2017; Meyer-Vernet & Moncuquet 2020), the QTN spectra are completely determined by the particle velocity distributions of the ambient plasma.

The QTN spectrum around the electron plasma frequency (fp) contains a wealth of infomation about the solar wind, whose basic shape can be explained based on simple plasma physics (Meyer-Vernet & Perche 1989). The quasi-thermal motion of the ambient plasma electrons passing by the antenna induces electric voltage pulses. At timescales exceeding 1/(2πfp), corresponding to frequencies of f < fp, the electrons are Debye shielded so that each ambient thermal electron passing closer than LD produces on the antenna an electric voltage pulse with a duration (roughly equal to 1/(2πfp)) shorter than the inverse frequency of observation. Thus, the Fourier transform of such a pulse is a constant for f <  fp, producing a plateau whose amplitude is determined by the bulk of the thermal electrons. In contrast, at higher frequencies (f > fp), the electron quasi-thermal motion excites Langmuir waves, thereby producing a spectral peak near fp as well as a power spectrum proportional to the total electron pressure at high frequencies (Meyer-Vernet & Perche 1989; Meyer-Vernet et al. 2017). Furthermore, the height of the peak near fp depends on the mean energy of suprathermal electrons, whereas the peak width depends on suprathermal electron concentration (Chateau & Meyer-Vernet 1991; Meyer-Vernet et al. 2017).

For the first several encounters, PSP is still not close enough to the Sun and therefore LD generally exceeds the antenna length (L ≃ 2 m). Nevertheless, the plasma peak emerges because of the suprathermal electrons (Meyer-Vernet et al. 2022). Therefore, Moncuquet et al. (2020) gave the first results of QTN measurements on PSP based on a simplified QTN technique. The preliminary results include the electron number density, ne, the core electron temperature, Tc, and an estimation of the suprathermal electron temperature Th (contribution of both the halo and Strahl electron thermal pressure). Based on the derived ne from Moncuquet et al. (2020), Maksimovic et al. (2020) yields the total electron temperature Te during the first encounter of PSP by fitting the high-frequency part of the QTN spectra recorded by RFS/FIELDS. In this paper, we apply another simple and fast but effective method on PSP observations to derive Te. In the next subsection, we provide details of the method that enables us to derive the total electron temperature from the high-frequency part of the electric field voltage spectra measured by RFS/FIELDS. Finally, we present the preliminary cross-checking between the total electron temperature derived in this work and those obtained via different QTN techniques.

2.1. Determination of Te from QTN Spectroscopy

In practice, the measured electric field voltage power spectrum at the receiver ports is expressed as:

(1)

where 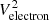, , 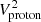, , 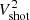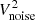and 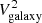represent the electron QTN, the Doppler-shifted proton thermal noise, the shot noise, the instrument noise, and the galactic radio background noise, respectively. In Eq. (1), 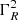is the gain factor of the receiver, expressed as:

(2)

where CA and CB are the dipole antenna capacitance and the (dipole) stray capacitance, respectively. Since 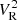is the power spectrum at the receiver ports, 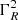is in factor of the first three terms. We note that 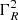has already been included in the expression of 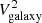(see below). For the frequencies satisfying fL/(fpLD)≫1, the electron QTN can be approximated as 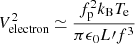(Meyer-Vernet & Perche 1989), where fp is the local electron plasma frequency, L′ is equal to the physical length (L) of one boom (or arm) of the dipole antenna when it is long enough (i.e., L ≫ LD), kB is the Boltzmann constant, and ϵ0 is the permittivity of free space. PSP/FIELDS antennas are separated by the heat shield and the physical separation is ∼3 meters for both |V1 − V2| and |V3 − V4| dipole antennas. Since the antenna physical length (L ≃ 2 m) is not long enough, the gap should be considered for L′ with L′=3.5 m. The high-frequency electron QTN (above fp) is proportional to the electron kinetic temperature whatever the shape of the velocity distribution is like. For the frequency ranges considered, CA ≃ πϵ0L/[ln(L/a)−1] (Meyer-Vernet et al. 2017) and CB ≃ 18 pF (Moncuquet et al. 2020), where L ≃ 2 m is the electric antenna physical length and a ≃ 1.5 mm is the wire radius. We note that when performing the fitting using the whole QTN spectra, the derived electron temperatures depend on the choice of the velocity distribution function for the electrons (Meyer-Vernet & Perche 1989). This is similar to the analysis to fit the velocity distribution functions observed by the particle analyzer. However, in the present work, the derived total electron temperature is not model-dependent. This is because when deriving the expression of 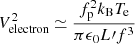, Te is defined directly from the second moment of the electron velocity distribution functions and no models are assumed (Meyer-Vernet & Perche 1989; Chateau & Meyer-Vernet 1991; Meyer-Vernet et al. 2017).

When fL/(fpLD)≫1, the Doppler-shifted proton thermal noise and the shot noise are negligible compared to the electron QTN (Meyer-Vernet et al. 2017). We note that the periodic antenna biasing performed for measuring the DC electric fields, which affect the shot noise, do not perturb our results, contrary to the perturbations these biasing bring to the QTN at smaller frequencies. In contrast, the contributions of the galactic radio background noise (Novaco & Brown 1978; Cane 1979; Zaslavsky et al. 2011) and the instrument noise become important and need to be substracted to obtain the effective electron QTN spectrum at high frequencies. The galaxy noise is almost constant in time and nearly isotropic in angular distribution with the modulation as a function of the observed solid angle being less than 20% in the considered frequency range (Manning & Dulk 2001). Therefore, it has frequently been used to calibrate the antenna on board previous spacecraft missions (e.g., Zaslavsky et al. 2011; Maksimovic et al. 2020). Specifically, the calibration is performed by relating the measured radio background radiation of the galaxy to the modelled flux of the source. The use of the empirical isotropic galaxy noise model from Novaco & Brown (1978) is justified by the good agreement between the data and the model. Due to the high sensitivity of RFS/FIELDS/PSP (Pulupa et al. 2017), the galaxy noise lies within the RFS bandwidth and can be accurately measured. As a result, following the method outlined in Zaslavsky et al. (2011), Maksimovic et al. (2020) used an RFS spectrum measured when PSP was close to 1 AU to derive an accurate absolute value of the reduced effective length of |V1 − V2| dipole antenna. Below, the galaxy noise measured by RFS/FIELDS/PSP is modelled based on the newly derived reduced effective length of |V1 − V2| dipole antenna. The pre-deployment internal noise of RFS/FIELDS (after launch) in the considered frequency range was estimated to be 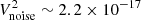V2 Hz−1 (Pulupa et al. 2020; Maksimovic et al. 2020). The background radio galactic noise is modelled following the procedures of Zaslavsky et al. (2011) and Maksimovic et al. (2020). The specific steps are summarized below.

The background radio galactic noise is modelled according to Equation 11 from Zaslavsky et al. (2011), 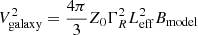, where 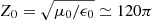is the impedance of vacuum, ΓRLeff = 1.17 is the reduced effective length (see Maksimovic et al. 2020), and Bmodel is the empirical model for the isotropic sky background brightness (Novaco & Brown 1978), expressed as:

(3)

where B0 = 1.38 × 10−19 W/m2/Hz/sr, fMHz is the frequency expressed in MHz, and .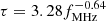

thumbnail Fig. 1.

Example of a voltage power spectrum (between 100 kHz and 10 MHz) recorded by the RFS receiver using the |V1 − V2| dipole electric antennas from FIELDS instrumentation (full black curve connected by crosses). Dot-dashed line gives the position of the local plasma peak (Moncuquet et al. 2020). Dotted horizontal line represents the pre-deployment RFS instrument noise (after launch) of ∼2.2 × 10−17 V2 Hz−1. Black dashed line shows the modelled radio galaxy noise. Blue and green lines represent the effective QTN signal and linear fit (f−3 variation that the QTN spectrum should follow when f ≫ fpLD/L), respectively. Black dots on the blue line are used to derive the linear fit. Red line is the sum of the fitted QTN signal, the modelled radio galaxy noise, and the instrument noise. More details are given in the text.

Figure 1 presents a typical example of electric field voltage power spectrum plot ranging between 100 kHz and 10 MHz measured by the FIELDS |V1 − V2| dipole antenna connected to the RFS receiver. We obtain the observations (crosses connected by the black curve) by merging the spectra measured by LFR/RFS and that by HFR/RFS. The dotted horizontal line represents the pre-deployment internal noise of RFS/FIELDS as mentioned above. The black dashed line is the radio galaxy background noise calculated as described above. Both the intrument noise and radio galaxy noise are deducted from the observed electric field voltage spectrum so that the so-called pure QTN spectrum 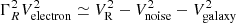(blue curved line) is derived following the similar requirement set by Maksimovic et al. (2020). Specifically, the data points are selected as: (1) the lower frequency limit is set as fL/(fpLD)≥2, so that both the proton thermal noise and the shot noise can be neglected; (2) the derived so-called pure QTN spectrum should be larger than both the instrument noise and radio galaxy noise, which is used to set the higher-frequency limit. Then, we further selected the dataset for the linear fitting to derive Te following fL/(fpLD)≥8, which is a much stricter requirement. The green line represents the linear fitted results and there is only one free parameter which is the total electron temperature. The electron plasma frequency used for each fitted spectrum is derived from the plasma peak tracking technique (see Moncuquet et al. 2020). In Fig. 1, the vertical black dashed-dotted line, which represents the location of the local electron plasma frequency, is plotted for reference. Specifically, we perform the numerical process by fitting the theoretical voltage spectral density 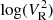to each measured spectrum via minimizing the χ2 merit function with the implementation of a nonlinear least-squares Levenberg-Marquardt technique (Markwardt 2009). Here, χ2 is defined as 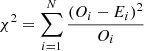, where Oi is the value of the measured spectrum and Ei is the corresponding expected value (theoretical one). All the electric field voltage spectra measured by the RFS/FIELDS are fitted following the same procedure mentioned above. The spectra fitted in this work usually comprise a number of frequency points ranging between ∼5 and ∼15. We further quantify the quality of the fit with the overall standard deviation (σfit) of the numerical fitted values to the corresponding measurements. In general, σfit < 2.5% indicates the goodness of the fittings. The physical uncertainty of Te is estimated from the uncertainty of the plasma frequency, the uncertainty of the so-called pure QTN spectrum and the uncertainty of the numerical process. The uncertainty of the plasma frequency is about 4% (∼8% for 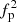) (Moncuquet et al. 2020), which is the standard frequency resolution of the RFS/FIELDS. The uncertainty of the so-called pure QTN spectrum comes from the variations of the instrument noise and the empirical isotropic galaxy noise model, which is in total less than 20% (see Manning & Dulk 2001; Zaslavsky et al. 2011; Pulupa et al. 2017; Maksimovic et al. 2020). The uncertainty for the sum of the instrument noise and the empirical isotropic galaxy noise model mainly affect the pure QTN spectrum at the highest selected frequency, whereas it is negligible at the lowest selected frequency. For simplicity, the mean uncertainty of the so-called pure QTN spectrum is estimated to be about 10%. Therefore, the physical uncertainty of the derived Te is at most 20%, which is almost the same as that of Tc (see Moncuquet et al. 2020; Liu et al. 2020, 2021a). This estimated physical uncertainty for Te is consistent with the statistical uncertainty for Te shown in Fig. 4.

We note that the high-frequency part of the QTN spectrum can be strongly perturbed by the electromagnetic emissions (e.g., Type II and/or III radio emissions) and it cannot always be used for deriving Te. In particular, such electromagnetic emissions were frequently detected during E02 (Pulupa et al. 2020) and these need to be carefully removed. In this work, for cases where the QTN technique cannot be implemented in the presence of electromagnetic emissions, no Te value is derived. The electric field voltage power spectrum below fp in general remains unperturbed and both ne and Tc can still be obtained (Moncuquet et al. 2020). As a byproduct, we managed to derive a database of spectra affected by bursty Langmuir waves and/or electromagnetic emissions.

2.2. Preliminary cross-checking

Figure 2 shows an overview of the solar wind electron temperatures and the proton bulk speed measured by PSP during E01 (from October 31, 2018 to November 12, 2018 UTC). The electron temperatures derived from different techniques including Te from QTN (this study) and Tc from QTN are compared for cross-checking. In the top panel, we present Te in black, labeled as Te, QTN(linear), derived from our linear fit QTN technique explained above. We compare it to Te shown in blue and Te, QTN(kappa) derived from the generalized Lorentzian QTN model (Maksimovic et al. 2020). In general, these values are in broad agreement with each other. Therefore, both the absolute values and variations of Te, QTN(linear) should be reliable. Similarly, Tc from QTN (Moncuquet et al. 2020) is displayed in blue in the bottom panel and are compared to Te, QTN(linear), shown in black. The ratio Te/Tc reflects the contribution of suprathermal electrons and should not be a constant. The median value of the Te, QTN(linear)/Tc, QTN is about 1.41, which is close to the median value of Te, QTN(kappa)/Tc, SPAN − E that is ∼1.47 (Maksimovic et al. 2020). Tc, SPAN − E is the core electron temperature derived from SPAN-E (Halekas et al. 2021, 2020). Finally, the proton bulk speed from SPC/SWEAP is presented in the top panel for reference. The example time interval considered also shows an anticorrelation between Vp and Te, previously reported in Maksimovic et al. (2020). We further discuss this result in Sect. 3.3.

thumbnail Fig. 2.

Comparison of observations of solar wind electron temperatures derived from different methods from PSP. An example of 12-day period of measurements from PSP during encounter one (from October 31, 2018 00:00:00 to November 12, 2018 00:00:00 UTC) is shown for reference. The heliocentric distance (in units of the solar radius R⊙) is indicated at the top of the top panel and the black vertical line denotes the first perihelion of the PSP orbit. From the top to bottom panels, the total electron temperature derived from the linear fit QTN technique is displayed in black. In the top panel, the total electron temperature obtained by fitting the high-frequency part of the spectrum with the generalized Lorentzian QTN model (Maksimovic et al. 2020) is shown in blue for comparison. The bottom panel follows the same format as the first panel but for the core electron temperature derived from the simplified QTN technique (Moncuquet et al. 2020). The proton bulk speed from SPC/SWEAP is presented in the top panel for reference. An anticorrelation between Vp and Te, which was also previously reported in Maksimovic et al. (2020), is visible during the time interval considered. We note that we have already smoothed Te, QTN(linear), Tc, QTN, and Te, QTN(kappa), so that the comparison between them is clear.

We note that the ratio of Te/Tc mentioned in this paper seems to disagree with that discussed by Halekas et al. (2020), especially near the perihelion (i.e., ≤0.2 AU). This may be due to a systematic discrepancy in measuring the suprathermal electrons between the QTN technique and the SPAN-E instrument. For the SPAN-E instrument, measurements of both halo and Strahl electrons may have some caveats (see Whittlesey et al. 2020; Halekas et al. 2020; Maksimovic et al. 2021; Berčič et al. 2020). These caveats combined make it more complicated to accuratly measure the total electron temperature by SPAN-E than the core electron temperature. For the QTN spectroscopy, uncertainties on the measurements are discussed in Sect. 2.1. All these factors may at least partly contribute to the systematic difference, but they cannot explain the magnitude of the difference. Therefore, an accurate and detailed comparison of the QTN total electron temperature with the one measured by SPAN-E should be made with more care and needs further investigations. Similarly, an in-depth comparison between the core temperatures measured by the QTN (e.g., Moncuquet et al. 2020) and SPAN-E (e.g., Halekas et al. 2020, 2022) would also be useful, but this is beyond the scope of the present paper which is focused on the total electron temperature measurements from the high frequency part of the QTN spectra.

3. Observations and results

PSP was designed to gradually shrink its orbit around the Sun and get closer step by step via seven Venus gravity assist flybys within about seven years. In this work, we focus on the 12-day period of observations around each perihelion from E01 to E10 (E08 not included), with the heliocentric distance varying from about 13.0 to 60.0 R⊙. During its first three encounters, PSP followed similar trajectories and reached the perihelion of 35.66 R⊙ (∼0.17 AU). In the following two orbits (from E04 to E05), PSP travelled closer to the Sun and reached perihelion of 27.8 R⊙ (∼0.13 AU). The perihelia of PSP orbits became about 20.8 R⊙ for both E06 and E07 and about 16 R⊙ for both E08 and E09. During E10, PSP reached as close to the Sun as 13 R⊙. In Sect. 3.1, we provide an overview of the radial evolution of the total electron temperature derived from the QTN technique, combining the datasets from E01 to E10 (E08 not included). In Sect. 3.2, we analyze and discuss the electron temperature gradients for different solar wind populations classified by the proton bulk speed and the solar wind mass flux, respectively. In Sect. 3.3, we investigate the radial evolution of anticorrelation between Vp and Te.

3.1. Mean radial profiles of Te

Figure 3 presents the total electron temperature derived from the QTN technique as a function of the heliocentric distance in units of solar radius R⊙, combining a 12-day period of observations near the perihelion of each encounter from E01 to E10 (E08 not included). Since PSP nearly corotates with the Sun near the perihelion of each encounter, its observations only cover a very small heliographic latitude and longitude span (Kasper et al. 2019; Halekas et al. 2021). This means that in each encounter, PSP detects the solar wind from only a limited number of sources. Therefore, a large data set from different encounters is necessary to remove or reduce the effects of transient structures such as CMEs or small-scale flux ropes (e.g., Hess et al. 2020; Zhao et al. 2020; Korreck et al. 2020; Chen et al. 2021), switchbacks (e.g., Bale et al. 2019; Dudok de Wit et al. 2020; Martinović et al. 2021; Fargette et al. 2021), magnetic holes associated with slow shock pairs (e.g., Chen et al. 2021; Zhou et al. 2022), and so on. As explained below, we fit the total electron temperature with respect to the heliocentric distance with both the power law model and the exospheric model to get their mean radial profiles.

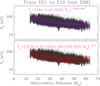thumbnail Fig. 3.

Radial variation of the total electron temperature (Te) combining observations from encounters one (E01) to ten (E10), with E08 excluded. From top to bottom, Te is fitted with the power law expression Te = T0 × (R/R⊙)β (purple) and the expression given by the large distance exospheric solar wind model Te = T0 + T1 × (R/R⊙)−4/3 (red), respectively. The fitted profile and expression with corresponding color are superimposed for comparison. The variations of the free parameters in the fitted expressions are the corresponding 1-sigma (1-σ) fit uncertainties. The vertical error bars indicate the 2-σ fit uncertainties, which covers about 95% data points in total.

Specifically, we performed the fittings for each model by minimizing the χ2 value with the implementation of a nonlinear least-squares Levenberg-Marquardt technique (Markwardt 2009). This technique takes into account the heliocentric distance and all the data points, as is generally the case for previous studies (e.g., Issautier et al. 1998; Štverák et al. 2015; Hellinger et al. 2013; Moncuquet et al. 2020). In total, there are N ∼ 882 361 data points and there are two adjustable free parameters for each model fit. Therefore, the degree of freedom is d.o.f. = N − 2 = 882 359. χ2 is defined as 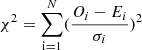, where Oi is the value of the observations (Te), Ei is the corresponding expected value (fit), and σi is the uncertainty of the measured Te. As shown in Sect. 2.1, we estimate a value of σ ∼ 0.2 × Te. The power-law model is derived with χ2 ≃ 1 178 937 and the so-called reduced (normalized) 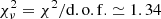. The exospheric model is derived with χ2 ≃ 1 235 002 and the so-called reduced (normalized) 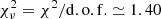. Since the 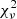values for both model fits are close to unity and are comparable in the two cases, we can conclude that the exospheric temperature model of the form Te = T0 + T1 × r(− 4/3) is as good as the power-law approximation in fitting the observed total electron temperature gradient in the small radial range considered. The fitted profiles and expressions for both models are shown on Fig. 3. Furthermore, both the mean and median values of 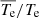are very close to unity for both model fits, where 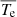is the fitted value and Te is the measured value. This again indicates the goodness of both model fittings. The 1-σ value of 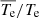for both model fits is around 0.2, based on which the uncertainties of the two free parameters for each model fit are derived. The 2-σ fit uncertainties are plotted in Fig. 3 for reference, which in total covers about 95% data points.

The total electron temperature fitted by the power law model (Te ∝ r−0.66, where r is the heliocentric distance in unit of solar radius) is displayed in purple. The derived total electron temperature profile is flatter than that of the core electron temperature (Tc ∝ r−0.74, see Moncuquet et al. 2020), which is consistent with the results in the outer heliosphere (e.g., Issautier et al. 1998; Le Chat et al. 2011). The total electron temperature consists of the contribution of the core, halo, and Strahl electron thermal pressure. Therefore, the flatter radial profile of Te may be explained by the nearly isothermal behavior of suprathermal electrons (see Moncuquet et al. 2020). We note that in that study, the suprathermal temperature is the total contribution of both the halo and Strahl electron thermal pressures. Based on the SPAN-E observations (Berčič et al. 2020), there is no strong trend in variation of the Strahl electron temperature with radial distance. Also, the Strahl electrons are more pronounced closer to the Sun while the density ratio between the halo and Strahl electrons increases with the radial distance (Maksimovic et al. 2005b; Štverák et al. 2009), which suggests a conversion of some Strahl electrons into halo ones. As a result, the fact that the Te profile is flatter than the Tc one may mainly be due to the flatness of the Strahl electron temperature profile. The recent results from PSP (see Abraham et al. 2022) suggest that the physical picture is somewhat different from a simple conversion of Strahl to halo, as discussed above. PSP results instead show that the overall suprathermal electron fraction (halo + Strahl) increases with respect to the heliocentric distance below 0.25 AU, and that the halo and Strahl relative density are quite small near perihelion. However, as is discussed in Sect. 2.2, close to the Sun, there are some caveats to measure both halo and Strahl electrons by SPAN-E. The overall suprathermal fraction (halo + Strahl) close to the Sun (e.g., Abraham et al. 2022; Maksimovic et al. 2021) may be underestimated, both of which should be treated with more care.

Then, based on the power-law fitted Te profile (Te ∝ r−0.66), we extrapolate Te to 10 R⊙, 0.3 AU, and 1 AU, respectively. Figures 4a–c show the corresponding distributions of the scaled Te combining the observations from E01 to E10 (E08 not included). A Gaussian function (blue line) was fitted on each histogram distribution and the corresponding center value (the most probable value) and 1-σ standard deviation of Gaussian fit are shown in comparison with the mean and median values. The histogram distributions of Te are very symmetrical and almost Gaussian. Again, the difference between the mean, median, and the center value of Gaussian fit is quite small (less than 6%). This may be explained by the fact that we combine observations from several different encounters (different types of wind from different sources). The exospheric solar wind model indicates that for r < 10 R⊙, the Te radial profile becomes less steep (Zouganelis et al. 2004). So, when extrapolating Te back to the Sun with a constant slope, we stop the extrapolation at about 10 R⊙. The value of Te scaled to 10 R⊙ is around 100.6 ± 19.9 eV. The predicted absolute values here are somewhat larger than the predictions shown in Bale et al. (2016); however, they are similar to the Strahl electron temperature measured by SPAN-E/SWEAP (Berčič et al. 2020; Maksimovic et al. 2021). The Strahl electron temperature is considered to be closely related to or almost equal to the coronal electron temperature. At 10 R⊙, this extrapolated temperature is also consistent with the exospheric solar wind model prediction derived from an electron velocity distribution with a kappa index ranging between 4 and 6 (Zouganelis et al. 2004), which indicates that the electron distribution has a suprathermal tail as measured by the QTN measurements (e.g., Maksimovic et al. 2020). That same model yields a solar wind bulk speed between 250 and 350 km s−1. We note that the kappa index mentioned here is based on one unique generalized Lorentzian or kappa function that is an alternative to the Maxwellian core plus kappa (or Maxwellian) halo model. However, the suprathermal tail itself may have a large kappa index, as found by SPAN-E near perihelion (e.g., Maksimovic et al. 2021; Abraham et al. 2022). Indeed, Zouganelis et al. (2004) showed that the acceleration provided by the exospheric model does not specifically require a kappa function, but is a more general outcome due to the existence of nonthermal distributions. Our results show that the agreement between the extrapolated Te based on PSP observations and the exospheric solar wind model prediction is quite good, given the simplifications made in both the Te measurements and the solar wind model. We note that Te scaled to 0.3 AU is ∼29.3±5.8 eV, which is consistent with the Helios observations at the same heliocentric distance (Maksimovic et al. 2005b). For Te scaled to 1 AU, the value is ∼13.1±2.6 eV, which is almost the same as the long-term (∼10 years) Wind observations (Wilson 2018). Then, Te scaled to 1 AU is also approximately the same as the mean and median values of the one-year statistical analysis based on STEREO observations (Martinović et al. 2016). We also note that the extrapolated electron temperatures from the exospheric model fit (not shown here) are always higher than but still comparable to those from the power law model fit.

thumbnail Fig. 4.

(a–c): Histograms of the total electron temperature (Te) scaled to 10 solar radii, 0.3 AU and 1 AU, based on observations displayed in Fig. 3 and their corresponding power law modelling fit results. Gaussian fit is superimposed in blue on each histogram. The corresponding average and median values are also indicated together with the center value and 1-σ standard deviation of the Gaussian fit.

3.2. Temperature gradients for different solar wind populations

As discussed in previous investigations (e.g., Meyer-Vernet & Issautier 1998; Le Chat et al. 2011; Maksimovic et al. 2005b, 2020; Štverák et al. 2009, 2015), solar wind classified based on the proton bulk speed may have different electron heating and cooling behaviors. Therefore, in order to do direct comparisons with the previous studies, we also separate solar wind populations based on the proton bulk speed. The dataset was split into four proton bulk speed bins as illustrated by Fig. 5a. In this way, each proton bulk speed bin contains the same number of data points, which is 882 361/4 ∼ 220 590. We used the total proton bulk speed (Vp) provided by SPC/SWEAP for E01 and E02 and from SPAN-I/SWEAP after E02 (Kasper et al. 2016; Case et al. 2020). For each proton bulk speed bin, we fit the Te radial profile with a power-law model using the method described in Sect. 3.1. The derived power law indices are plotted against the corresponding proton bulk speed in Fig. 5b. We use the proton bulk velocity measured in the RTN coordinate system. The radial component of the velocity (VR) measured by SPC and SPAN-I are in good agreement, but there is a systematic disprepancy for the tangential component (VT) (Woodham et al. 2021). However, VR is the main component of Vp (total proton bulk speed), and their absolute values are very close to each other. Furthermore, we used both VR and Vp to cross-check the results below in this section and in Sect. 3.3. We verify that the measurement uncertainty of Vp does not affect our conclusions.

thumbnail Fig. 5.

Power indices as a function of the proton bulk speed. (a) We define the four wind families based on the proton bulk speed histogram. Each colored histogram has the same number of observations. (b) Outcome of the power law modelling in the form Te = T0 × (R/R⊙)β for total electron temperature: β versus Vp. More details are described in the main text.

The Te radial gradients have a tendency (albeit weak) for the slower wind electrons to cool down with a steeper profile than the faster wind ones. It is noteworthy that with only a 12-day period of observations for each encounter (from E01 to E10, with E08 excluded) and a limited latitude exploration, we were able to find similar behavior for electrons in the inner heliosphere as seen in previous long-term investigations (e.g., Maksimovic et al. 2005b, 2020; Štverák et al. 2015) at various latitudes and longitudes and at a much larger span of heliocentric distances in the outer heliosphere. This is also consistent with the exospheric model predictions shown in Meyer-Vernet & Issautier (1998). Also, we note that the Te radial gradient within each proton bulk speed bin is steeper than that in the outer heliosphere based on Ulysses observations (Te ∝ r−0.53, see Le Chat et al. 2011). This may verify the exospheric model prediction that the electron temperature profile becomes steeper when getting closer to the Sun (Meyer-Vernet & Issautier 1998).

Moreover, since PSP is very close to the Sun during the encounter phase when the solar wind is still under acceleration, the proton bulk speed detected by PSP may not, in fact, be the final speed. Therefore, because of the different types of winds coming from different source regions, we then used another basic physical quantity to partition the dataset based on an almost constant streamline, namely: the solar wind mass flux, Fw = nempVpr2 (e.g., Wang & Sheeley 1990; Bemporad 2017). The resulting histogram distribution of Fw is shown in Fig. 6a. The derived values (Fw ∼ 2 × 1010 − 3 × 1011g s−1) are in agreement with the remote-sensing observations from SOHO at altitudes higher than 3.5 R⊙ (Bemporad 2017), in situ measurements from ACE at 1 AU (Wang 2010), and in situ data by Ulysses from ∼1.4 to ∼1.8 AU (Issautier et al. 2008; Wang 2010). As expected, this indicates the conservation of the solar wind mass flux. Wang (2010) showed that the solar wind mass flux at the corona base increases roughly with the footpoint field strength. This indicates, to some degree, both the corona base conditions and the propagation effects are considered for Fw, in contrast to the proton bulk speed. Thus, as displayed in Fig. 6a, we split the dataset into four solar wind mass flux tubes and check the corresponding electron temperature gradients. Figure 6b shows that solar wind electrons within the flux tube with a larger mass flux cool down faster.

thumbnail Fig. 6.

Power indices as a function of the solar wind mass flux. Follows the same format as Fig. 5 but for the solar wind mass flux.

3.3. Anticorrelated parameters: Vp and Te

As shown in Sect. 2.2, PSP observations display a clear anticorrelation between Vp and Te during E01. A similar anticorrelaton was observed during E04, E05, E07 and E09. During E02 and E10, frequent Type III radio emissions were detected by PSP and fewer effective data points of Te derived from the QTN technique were obtained than during other encounters. This may affect the analysis of the relation between Vp and Te. In contrast, slightly correlated (Vp, Te) values were observed during E03 and E06 based on the QTN observations. The Vp–Te relation measured in the solar wind may indeed depend on both the source region (Griton et al. 2021) and the radial evolution (Maksimovic et al. 2020; Pierrard et al. 2020; Halekas et al. 2022). The complexity of the electron temperature behaviors, especially the anticorrelation between Vp and Te, contrasts with the correlation between the proton temperature and the wind speed that persists throughout the heliosphere (see Maksimovic et al. 2020, and references therein). We selected the data points from E01, E04, E05, E07, and E09, and further analyzed the effect of the radial evolution on the anticorrelation between Vp and Te.

Figure 7a compares Te and Vp combining observations from E01, E04, E05, E07, and E09. A clear (Vp, Te) anticorrelation is displayed. We also equally split the dataset into four radial distance bins, as illustrated by Fig. 7b. For each radial distance bin, the datasets were equally split into four proton bulk speed bins, following the method mentioned in Sect. 3.2. We then compute the median values of Vp and Te for each proton bulk speed bin. The calculated median values of Vp and Te belonging to each radial distance bin are presented in the same color in Fig. 7c. For comparison, median values of Vp and Te of the whole dataset equally divided into eight proton bulk speed bins are plotted in black.

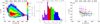thumbnail Fig. 7.

Illustration of Te against Vp combining observations from E01, E04, E05, E07, and E09. (a) 2D histogram ditribution of Te versus Vp with the color bar on the right side indicating the number of data points. Both the mean (red curve) and median values (black curve) are superimposed for reference. A clear anticorrelated (Vp, Te) is displayed. (b) We define the four wind families based on the heliocentric distance histogram. Each colored histogram has the same number of observations. (c) Relation between Vp and Te for each wind family, as defined in panel b. The results are displayed in the same color as the corresponding heliocentric distance histogram in panel b. More details are given in the main text.

We find that the (Vp, Te) anticorrelation is stronger when the solar wind is slower, as shown by the black curve in Fig. 7c. For the solar wind considered, most of them are slow wind and they are generally being accelerated during the expansion. Therefore, the slower solar wind is detected closer to the Sun. This is consistent with the fact that the most pronounced anticorrelated Vp–Te is observed close to the Sun (see purple curve in Fig. 7c). The results may also indicate that the (Vp, Te) anticorrelation is reduced or removed during the acceleration process of the slow solar wind. Based on both the Helios and PSP measurements, Berčič et al. (2020) found a clear anticorrelation between the parallel Strahl electron temperature Ts∥ (proxy coronal electron temperature) and the local solar wind speed. Halekas et al. (2022) grouped the PSP observations by the asymptotic wind speed, and found that both the in situ electron temperature (parallel core electron temperature, Tc∥) and the proxy coronal electron temperature (Ts∥) are anticorrelated with the asymptotic wind speed. As a result, the (Vp, Te) anticorrelation herein may be the remnants of the coronal conditions.

4. Summary and discussion

In this work, we implemented a simple, fast, and effective method based on QTN spectroscopy of PSP observations to derive the total electron temperature. To do so, we used the linear fit of the high frequency part of the QTN spectra observed by RFS/FIELDS. The derived total electron temperature is in broad agreement with Te obtained from the QTN model with Lorentzian velocity distribution functions (Maksimovic et al. 2020). We present the radial evolution of the total electron temperature by combining a 12-day period of observations around each perihelion from E01 to E10 (E08 not included) with the heliocentric distance ranging from about 13 to 60 R⊙.

The radial profile of the total electron temperature (Te ∝ r−0.66) in the inner heliosphere falls within the range between adiabatic and isothermal and is flatter than that of the electron core temperature (Tc ∝ r−0.74, see Moncuquet et al. 2020). This is consistent with previous Helios and Ulysses observations farther out (e.g., Pilipp et al. 1990; Issautier et al. 1998; Le Chat et al. 2011). The flatness of the radial profile of Te may mainly be due to the contribution of the Strahl electrons. The Te values extrapolated to 0.3 AU and 1 AU using the fitted power law are almost the same as the Helios and Wind observations at the same heliocentric distance (see Maksimovic et al. 2005b; Wilson 2018), respectively. The total electron temperature extrapolated back to 10 R⊙ is almost the same as the solar corona Strahl electron temperature (Berčič et al. 2020). This may confirm that the Strahl electron temperature is closely related to or even almost equals to the coronal electron temperature. The temperature extrapolated back to 10 R⊙ is also consistent with the exospheric solar wind model prediction, assuming an electron velocity distribution with the kappa index ranging between 4 and 6 (Zouganelis et al. 2004). The extrapolated Te based on the exospheric solar wind model is systematically higher (but still comparable to) than that derived from the power-law model fit.

The radial Te profiles in the slower solar wind are relatively steeper than those in the faster solar wind. Stated in another way, electrons in the slower solar wind cool down more quickly than those in the faster wind. It is remarkable that with only a 12-day period of observations for each encounter (from E01 to E10, with E08 excluded) and a limited latitude exploration, we find the similar results on electron cooling and heating behaviors in the inner heliosphere as previous long-term investigations (e.g., Maksimovic et al. 2005b, 2020; Štverák et al. 2015) with a much larger span of the latitude, longitude, and heliocentric distance explorations in the outer heliosphere. In general, the radial Te profile observed in the pristine solar wind is steeper than that in the outer heliosphere, which to some extent, verifies the exospheric model prediction in the inner heliosphere (Meyer-Vernet & Issautier 1998). This indicates that the exospheric solar wind model explains (in part) the electron behaviors in the inner heliosphere. Furthermore, the solar wind mass flux derived from the in situ dataset in the inner heliosphere from PSP are in agreement with those even closer to the corona base (Bemporad 2017) and further out in interplanetary space (Issautier et al. 2008; Wang 2010). Interestingly, the electron temperature cools down faster within the flux tube with larger mass flux. Given the solar wind mass flux conservation and the fact that the mass flux at the corona base increases with the footpoint field strength (Wang 2010), it can be used as an effective physical quantity to distinguish the solar wind into different populations. This considers both the corona base conditions and the propagation effects in contrast to the proton bulk speed. In particular, as the solar wind at distances of PSP orbit perihelia may be still accelerating, the speed should not be considered as the final speed.

With PSP observations from E01, E04, E05, E07, and E09, we find that the (Vp, Te) anticorrelation is more pronounced when the solar wind is slower in the inner heliosphere. During the time period considered, most of the detected solar wind is slow wind, which on average is still being accelerated during the spherical expansion. Furthermore, the results may indicate that the slow solar wind acceleration during the expansion reduces or fully removes the strong (Vp, Te) anticorrelation detected near the Sun. This is verified by the fact that the most pronounced anticorrelated Vp–Te is observed close to the Sun, in agreement with Maksimovic et al. (2020). The solar wind Vp–Te relation is still an interesting issue, which may depend on both the source region in the Sun (Griton et al. 2021) and the radial evolution during the expansion (Maksimovic et al. 2020; Pierrard et al. 2020). To comprehensively understand the Vp–Te relation, more work is needed to distinguish and/or connect the effects from the source region, spherical expansion, and the transient structures detected locally.

Based on the Helios and preliminary PSP observations (e.g., Maksimovic et al. 2005b; Štverák et al. 2009; Halekas et al. 2021, 2020; Berčič et al. 2020), the Strahl electrons become more pronounced when PSP gets closer to the Sun. However, the QTN technique currently cannot resolve the Strahl electrons well, so this issue requires further theoretical and modeling extensions. When PSP gets closer to the Sun, L/LD is expected to become greater. This assumption will enable us to derive the electron properties (e.g., ne, Te, and kappa index) with smaller uncertainties by fitting the whole QTN spectrum with the generalized Lorentzian (or so-called kappa) QTN model. Also, we await well-calibrated fixed Te values from SPAN-E for all encounters to make systematic cross-checking with Te provided by the QTN technique, which should prove advantageous for both methods.

Acknowledgments

The research was supported by the CNES and DIM ACAV+ PhD funding. Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission. We acknowledge the use of data from FIELDS/PSP (http://research.ssl.berkeley.edu/data/psp/data/sci/fields/l2/) and SWEAP/PSP (http://sweap.cfa.harvard.edu/pub/data/sci/sweap/). We thank the CDPP (Centre de Données de la Physique des plasmas) and CNES (Centre National d’Etudes Spatiales) for their archiving and provision of SQTN data (https://cdpp-archive.cnes.fr/).

References

  1. Abraham, J. B., Owen, C. J., Verscharen, D., et al. 2022, ApJ, 931, 118 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  3. Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bemporad, A. 2017, ApJ, 846, 86 [Google Scholar]
  5. Berčič, L., Larson, D., Whittlesey, P., et al. 2020, ApJ, 892, 88 [Google Scholar]
  6. Cane, H. V. 1979, MNRAS, 189, 465 [NASA ADS] [Google Scholar]
  7. Case, A. W., Kasper, J. C., Stevens, M. L., et al. 2020, ApJS, 246, 43 [Google Scholar]
  8. Chateau, Y. F., & Meyer-Vernet, N. 1991, J. Geophys. Res., 96, 5825 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chen, Y., Hu, Q., Zhao, L., Kasper, J. C., & Huang, J. 2021, ApJ, 914, 108 [NASA ADS] [CrossRef] [Google Scholar]
  10. Démoulin, P. 2009, Sol. Phys., 257, 169 [Google Scholar]
  11. Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., et al. 2020, ApJS, 246, 39 [Google Scholar]
  12. Fargette, N., Lavraud, B., Rouillard, A. P., et al. 2021, ApJ, 919, 96 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
  14. Griton, L., Rouillard, A. P., Poirier, N., et al. 2021, ApJ, 910, 63 [CrossRef] [Google Scholar]
  15. Halekas, J. S., Whittlesey, P., Larson, D. E., et al. 2020, ApJS, 246, 22 [Google Scholar]
  16. Halekas, J. S., Whittlesey, P. L., Larson, D. E., et al. 2021, A&A, 650, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Halekas, J. S., Whittlesey, P., Larson, D. E., et al. 2022, ApJ, 936, 53 [CrossRef] [Google Scholar]
  18. Hellinger, P., Trávníček, P. M., Štverák, Š., Matteini, L., & Velli, M. 2013, J. Geophys. Res. (Space Phys.), 118, 1351 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hess, P., Rouillard, A. P., Kouloumvakos, A., et al. 2020, ApJS, 246, 25 [Google Scholar]
  20. Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1998, J. Geophys. Res., 103, 1969 [NASA ADS] [CrossRef] [Google Scholar]
  21. Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1999a, in Solar Wind Nine, eds. S. R. Habbal, R. Esser, J. V. Hollweg, & P. A. Isenberg, Am. Inst. Phys. Conf. Ser., 471, 581 [NASA ADS] [CrossRef] [Google Scholar]
  22. Issautier, K., Meyer-Vernet, N., Moncuquet, M., Hoang, S., & McComas, D. J. 1999b, J. Geophys. Res., 104, 6691 [Google Scholar]
  23. Issautier, K., Hoang, S., Moncuquet, M., & Meyer-Vernet, N. 2001a, Space Sci. Rev., 97, 105 [Google Scholar]
  24. Issautier, K., Meyer-Vernet, N., Pierrard, V., & Lemaire, J. 2001b, Ap&SS, 277, 189 [Google Scholar]
  25. Issautier, K., Skoug, R. M., Gosling, J. T., Gary, S. P., & McComas, D. J. 2001c, J. Geophys. Res., 106, 15665 [NASA ADS] [CrossRef] [Google Scholar]
  26. Issautier, K., Perche, C., Hoang, S., et al. 2005, Adv. Space Res., 35, 2141 [NASA ADS] [CrossRef] [Google Scholar]
  27. Issautier, K., Le Chat, G., Meyer-Vernet, N., et al. 2008, Geophys. Rev. Lett., 35, L19101 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [Google Scholar]
  29. Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228 [Google Scholar]
  30. Kasper, J. C., Klein, K. G., Lichko, E., et al. 2021, Phys. Rev. Lett., 127, 255101 [NASA ADS] [CrossRef] [Google Scholar]
  31. Korreck, K. E., Szabo, A., Nieves Chinchilla, T., et al. 2020, ApJS, 246, 69 [Google Scholar]
  32. Le Chat, G., Issautier, K., Meyer-Vernet, N., & Hoang, S. 2011, Sol. Phys., 271, 141 [NASA ADS] [CrossRef] [Google Scholar]
  33. Liu, M., Issautier, K., Meyer-Vernet, N., et al. 2020, AGU Fall Meeting Abstracts, 2020, SH052-04 [Google Scholar]
  34. Liu, M., Issautier, K., Meyer-Vernet, N., et al. 2021a, A&A, 650, A14 [Google Scholar]
  35. Liu, Y. D., Chen, C., Stevens, M. L., & Liu, M. 2021b, ApJ, 908, L41 [CrossRef] [Google Scholar]
  36. Livi, R., Larson, D. E., Kasper, J. C., et al. 2022, ApJ, 938, 138 [NASA ADS] [CrossRef] [Google Scholar]
  37. Lopez, R. E., & Freeman, J. W. 1986, J. Geophys. Res., 91, 1701 [Google Scholar]
  38. Lund, E. J., Labelle, J., & Treumann, R. A. 1994, J. Geophys. Res., 99, 23651 [NASA ADS] [CrossRef] [Google Scholar]
  39. Maksimovic, M., Hoang, S., Meyer-Vernet, N., et al. 1995, J. Geophys. Res., 100, 19881 [Google Scholar]
  40. Maksimovic, M., Pierrard, V., & Lemaire, J. F. 1997, A&A, 324, 725 [NASA ADS] [Google Scholar]
  41. Maksimovic, M., Gary, S. P., & Skoug, R. M. 2000, J. Geophys. Res., 105, 18337 [NASA ADS] [CrossRef] [Google Scholar]
  42. Maksimovic, M., Pierrard, V., & Lemaire, J. 2001, Ap&SS, 277, 181 [Google Scholar]
  43. Maksimovic, M., Issautier, K., Meyer-Vernet, N., et al. 2005a, Adv. Space Res., 36, 1471 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maksimovic, M., Zouganelis, I., Chaufray, J. Y., et al. 2005b, J. Geophys. Res. (Space Phys.), 110, A09104 [NASA ADS] [CrossRef] [Google Scholar]
  45. Maksimovic, M., Bale, S. D., Berčič, L., et al. 2020, ApJS, 246, 62 [Google Scholar]
  46. Maksimovic, M., Walsh, A. P., Pierrard, V., Štverák, Š., & Zouganelis, I. 2021, in Kappa Distributions; From Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas, eds. M. Lazar, & H. Fichtner (Cham: Springer International Publishing), 464, 39 [NASA ADS] [CrossRef] [Google Scholar]
  47. Manning, R., & Dulk, G. A. 2001, A&A, 372, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  49. Marsch, E., Pilipp, W. G., Thieme, K. M., & Rosenbauer, H. 1989, J. Geophys. Res., 94, 6893 [NASA ADS] [CrossRef] [Google Scholar]
  50. Martinović, M. M., Zaslavsky, A., Maksimović, M., et al. 2016, J. Geophys. Res. (Space Phys.), 121, 129 [CrossRef] [Google Scholar]
  51. Martinović, M. M., Klein, K. G., Gramze, S. R., et al. 2020, J. Geophys. Res. (Space Phys.), 125, e28113 [Google Scholar]
  52. Martinović, M. M., Klein, K. G., Huang, J., et al. 2021, ApJ, 912, 28 [CrossRef] [Google Scholar]
  53. Martinović, M. M., Dordević, A. R., Klein, K. G., et al. 2022, J. Geophys. Res. (Space Phys.), 127, e30182 [Google Scholar]
  54. Matthaeus, W. H., Elliott, H. A., & McComas, D. J. 2006, J. Geophys. Res. (Space Phys.), 111, A10103 [NASA ADS] [CrossRef] [Google Scholar]
  55. Meyer-Vernet, N. 1979, J. Geophys. Res., 84, 5373 [Google Scholar]
  56. Meyer-Vernet, N., & Issautier, K. 1998, J. Geophys. Res., 103, 29705 [NASA ADS] [CrossRef] [Google Scholar]
  57. Meyer-Vernet, N., & Moncuquet, M. 2020, J. Geophys. Res. (Space Phys.), 125, e27723 [NASA ADS] [Google Scholar]
  58. Meyer-Vernet, N., & Perche, C. 1989, J. Geophys. Res., 94, 2405 [NASA ADS] [CrossRef] [Google Scholar]
  59. Meyer-Vernet, N., Couturier, P., Hoang, S., et al. 1986, Science, 232, 370 [Google Scholar]
  60. Meyer-Vernet, N., Hoang, S., & Moncuquet, M. 1993, J. Geophys. Res., 98, 21163 [NASA ADS] [CrossRef] [Google Scholar]
  61. Meyer-Vernet, N., Issautier, K., & Moncuquet, M. 2017, J. Geophys. Res., 122, 7925 [Google Scholar]
  62. Meyer-Vernet, N., Lecacheux, A., Issautier, K., & Moncuquet, M. 2022, A&A, 658, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Meyer-Vernet, N., Mangeney, A., Maksimovic, M., Pantellini, F., & Issautier, K. 2003, in Solar Wind Ten, eds. M. Velli, R. Bruno, F. Malara, & B. Bucci, Am. Inst. Phys. Conf. Ser., 679, 263 [NASA ADS] [CrossRef] [Google Scholar]
  64. Moncuquet, M., Meyer-Vernet, N., & Hoang, S. 1995, J. Geophys. Res., 100, 21697 [NASA ADS] [CrossRef] [Google Scholar]
  65. Moncuquet, M., Meyer-Vernet, N., Hoang, S., Forsyth, R. J., & Canu, P. 1997, J. Geophys. Res., 102, 2373 [NASA ADS] [CrossRef] [Google Scholar]
  66. Moncuquet, M., Lecacheux, A., Meyer-Vernet, N., Cecconi, B., & Kurth, W. S. 2005, Geophys. Rev. Lett., 32, L20S02 [NASA ADS] [CrossRef] [Google Scholar]
  67. Moncuquet, M., Matsumoto, H., Bougeret, J. L., et al. 2006, Adv. Space Res., 38, 680 [Google Scholar]
  68. Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, ApJS, 246, 44 [Google Scholar]
  69. Novaco, J. C., & Brown, L. W. 1978, ApJ, 221, 114 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pierrard, V., Lazar, M., & Štverák, S. 2020, Sol. Phys., 295, 151 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pilipp, W. G., Muehlhaeuser, K. H., Miggenrieder, H., Rosenbauer, H., & Schwenn, R. 1990, J. Geophys. Res., 95, 6305 [Google Scholar]
  72. Pulupa, M., Bale, S. D., Bonnell, J. W., et al. 2017, J. Geophys. Res., 122, 2836 [Google Scholar]
  73. Pulupa, M., Bale, S. D., Badman, S. T., et al. 2020, ApJS, 246, 49 [Google Scholar]
  74. Salem, C., Bosqued, J. M., Larson, D. E., et al. 2001, J. Geophys. Res., 106, 21701 [NASA ADS] [CrossRef] [Google Scholar]
  75. Schippers, P., Moncuquet, M., Meyer-Vernet, N., & Lecacheux, A. 2013, J. Geophys. Res. (Space Phys.), 118, 7170 [NASA ADS] [CrossRef] [Google Scholar]
  76. Totten, T. L., Freeman, J. W., & Arya, S. 1995, J. Geophys. Res., 100, 13 [Google Scholar]
  77. Štverák, Š., Maksimovic, M., Trávníček, P. M., et al. 2009, J. Geophys. Res., 114, A05104 [Google Scholar]
  78. Štverák, Š., Trávníček, P. M., & Hellinger, P. 2015, J. Geophys. Res. (Space Phys.), 120, 8177 [CrossRef] [Google Scholar]
  79. Wang, Y. M. 2010, ApJ, 715, L121 [CrossRef] [Google Scholar]
  80. Wang, Y. M., & Sheeley, N. R. Jr. 1990, ApJ, 355, 726 [NASA ADS] [CrossRef] [Google Scholar]
  81. Whittlesey, P. L., Larson, D. E., Kasper, J. C., et al. 2020, ApJS, 246, 74 [Google Scholar]
  82. Wilson, Lynn B. I., Stevens, M. L., Kasper, J. C., et al. 2018, ApJS, 236, 41 [NASA ADS] [CrossRef] [Google Scholar]
  83. Woodham, L. D., Horbury, T. S., Matteini, L., et al. 2021, A&A, 650, L1 [EDP Sciences] [Google Scholar]
  84. Zaslavsky, A., Meyer-Vernet, N., Hoang, S., Maksimovic, M., & Bale, S. D. 2011, Radio Sci., 46, RS2008 [Google Scholar]
  85. Zhao, L. L., Zank, G. P., Adhikari, L., et al. 2020, ApJS, 246, 26 [Google Scholar]
  86. Zhao, S. Q., Yan, H., Liu, T. Z., Liu, M., & Shi, M. 2021, ApJ, 923, 253 [NASA ADS] [CrossRef] [Google Scholar]
  87. Zhou, Z., Xu, X., Zuo, P., et al. 2022, Geophys. Rev. Lett., 49 [Google Scholar]
  88. Zouganelis, I., Maksimovic, M., Meyer-Vernet, N., Lamy, H., & Issautier, K. 2004, ApJ, 606, 542 [Google Scholar]

All Figures

thumbnail Fig. 1.

Example of a voltage power spectrum (between 100 kHz and 10 MHz) recorded by the RFS receiver using the |V1 − V2| dipole electric antennas from FIELDS instrumentation (full black curve connected by crosses). Dot-dashed line gives the position of the local plasma peak (Moncuquet et al. 2020). Dotted horizontal line represents the pre-deployment RFS instrument noise (after launch) of ∼2.2 × 10−17 V2 Hz−1. Black dashed line shows the modelled radio galaxy noise. Blue and green lines represent the effective QTN signal and linear fit (f−3 variation that the QTN spectrum should follow when f ≫ fpLD/L), respectively. Black dots on the blue line are used to derive the linear fit. Red line is the sum of the fitted QTN signal, the modelled radio galaxy noise, and the instrument noise. More details are given in the text.
In the text
thumbnail Fig. 2.

Comparison of observations of solar wind electron temperatures derived from different methods from PSP. An example of 12-day period of measurements from PSP during encounter one (from October 31, 2018 00:00:00 to November 12, 2018 00:00:00 UTC) is shown for reference. The heliocentric distance (in units of the solar radius R⊙) is indicated at the top of the top panel and the black vertical line denotes the first perihelion of the PSP orbit. From the top to bottom panels, the total electron temperature derived from the linear fit QTN technique is displayed in black. In the top panel, the total electron temperature obtained by fitting the high-frequency part of the spectrum with the generalized Lorentzian QTN model (Maksimovic et al. 2020) is shown in blue for comparison. The bottom panel follows the same format as the first panel but for the core electron temperature derived from the simplified QTN technique (Moncuquet et al. 2020). The proton bulk speed from SPC/SWEAP is presented in the top panel for reference. An anticorrelation between Vp and Te, which was also previously reported in Maksimovic et al. (2020), is visible during the time interval considered. We note that we have already smoothed Te, QTN(linear), Tc, QTN, and Te, QTN(kappa), so that the comparison between them is clear.
In the text
thumbnail Fig. 3.

Radial variation of the total electron temperature (Te) combining observations from encounters one (E01) to ten (E10), with E08 excluded. From top to bottom, Te is fitted with the power law expression Te = T0 × (R/R⊙)β (purple) and the expression given by the large distance exospheric solar wind model Te = T0 + T1 × (R/R⊙)−4/3 (red), respectively. The fitted profile and expression with corresponding color are superimposed for comparison. The variations of the free parameters in the fitted expressions are the corresponding 1-sigma (1-σ) fit uncertainties. The vertical error bars indicate the 2-σ fit uncertainties, which covers about 95% data points in total.
In the text
thumbnail Fig. 4.

(a–c): Histograms of the total electron temperature (Te) scaled to 10 solar radii, 0.3 AU and 1 AU, based on observations displayed in Fig. 3 and their corresponding power law modelling fit results. Gaussian fit is superimposed in blue on each histogram. The corresponding average and median values are also indicated together with the center value and 1-σ standard deviation of the Gaussian fit.
In the text
thumbnail Fig. 5.

Power indices as a function of the proton bulk speed. (a) We define the four wind families based on the proton bulk speed histogram. Each colored histogram has the same number of observations. (b) Outcome of the power law modelling in the form Te = T0 × (R/R⊙)β for total electron temperature: β versus Vp. More details are described in the main text.
In the text
thumbnail Fig. 6.

Power indices as a function of the solar wind mass flux. Follows the same format as Fig. 5 but for the solar wind mass flux.
In the text
thumbnail Fig. 7.

Illustration of Te against Vp combining observations from E01, E04, E05, E07, and E09. (a) 2D histogram ditribution of Te versus Vp with the color bar on the right side indicating the number of data points. Both the mean (red curve) and median values (black curve) are superimposed for reference. A clear anticorrelated (Vp, Te) is displayed. (b) We define the four wind families based on the heliocentric distance histogram. Each colored histogram has the same number of observations. (c) Relation between Vp and Te for each wind family, as defined in panel b. The results are displayed in the same color as the corresponding heliocentric distance histogram in panel b. More details are given in the main text.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.