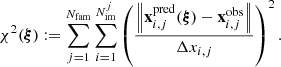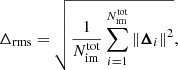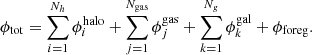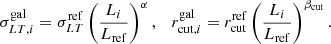| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202244834 | |
| Published online | 06 June 2023 | |
A state-of-the-art strong-lensing model of MACS J0416.1−2403 with the largest sample of spectroscopic multiple images⋆
1
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
e-mail: pietro.bergamini@unimi.it
2
INAF – OAS, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
3
INAF – IASF Milano, Via A. Corti 12, 20133 Milano, Italy
4
Dipartimento di Fisica e Scienze della Terra, Università degli Studi di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
5
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
6
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
7
INAF – Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
Received:
29
August
2022
Accepted:
3
February
2023
The combination of multi-band imaging from the Hubble Space Telescope with Multi-Unit Spectroscopic Explorer integral field spectroscopy, obtained at the Very Large Telescope, has recently driven remarkable progress in strong-lensing (SL) modeling of galaxy clusters. From a few tens of multiple images with photometric redshifts per cluster, a new generation of high-precision SL models have recently been developed by exploiting in some cases over a hundred spectroscopically confirmed multiple images and cluster member galaxies. A further step forward is expected with James Webb Space Telescope observations of SL clusters (from hundreds of multiple images to possibly a thousand). In this context, we present a new state-of-the-art SL model of the galaxy cluster MACS J0416.1−2403, utilizing 237 spectroscopically confirmed multiple images, which is the largest sample of secure multiply-lensed sources utilized to date. In addition, this model incorporates stellar kinematics information of 64 cluster galaxies and the hot-gas mass distribution of the cluster, determined from Chandra X-ray observations. The observed positions of the many multiple images are reproduced with a remarkable average accuracy of 0.43″. To further assess the reliability of this lens model and to highlight the improvement over previously published models, we show the extended surface brightness reconstruction of several lensed galaxies through a newly developed forward modeling software. The comparison with other SL models of the same cluster demonstrates that this new model is better able to accurately reproduce the positions, shapes, and fluxes of the observed multiple images. In addition to a robust characterization of the total mass distribution of the cluster, our model can provide accurate and precise magnification maps that are key to studying the intrinsic physical properties of faint high-redshift lensed sources. The model is made publicly available through our newly developed Strong Lensing Online Tool (SLOT); thanks to a simple graphical interface SLOT allows astronomers (including lensing non-experts) to take full advantage of the predictive power of the model, including statistical uncertainties on the relevant quantities associated with the multiply-lensed sources.
Key words: gravitational lensing: strong / galaxies: clusters: general / dark matter / cosmology: observations / galaxies: clusters: individual: MACS J0416.1−2403
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/674/A79
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Strong gravitational lensing has become a powerful technique to characterize the total mass distribution in the core of galaxy clusters (see, e.g., Caminha et al. 2017b; Diego et al. 2020; Sharon et al. 2020; Pignataro et al. 2021; Jauzac et al. 2021); to discover and study the physical properties of high-redshift galaxies (Coe et al. 2013; Bouwens et al. 2014; Zitrin et al. 2015; Hashimoto et al. 2018), even resolving their structures at sub-kiloparsec scales (Johnson et al. 2017; Dessauges-Zavadsky et al. 2017; Meštrić et al. 2022); and to investigate the expansion and the geometry of the Universe (Jullo et al. 2010; Caminha et al. 2016, 2022; Grillo et al. 2018, 2020). All of these studies rely on accurate strong-lensing models, where the accuracy critically depends on the number of spectroscopically confirmed multiple images (Grillo et al. 2015; Johnson & Sharon 2016; Caminha et al. 2019).
The recent surge of high-quality photometric and spectroscopic data on galaxy clusters has made for some important progress in cluster lens models and their subsequent applications. In particular, the combination of high-resolution, panchromatic, and deep imaging data from the Hubble Space Telescope (Hubble) with follow-up spectroscopy with the Multi-Unit Spectroscopic Explorer (MUSE, Bacon et al. 2012) on the Very Large Telescope (VLT) has lead to a significant increase in the number of multiple images securely identified in the core of galaxy clusters (see, e.g., Grillo et al. 2016; Karman et al. 2017; Lagattuta et al. 2017; Bergamini et al. 2023; Richard et al. 2021, hereafter R21).
The cluster MACS J0416.1−2403 (hereafter M0416, see Fig. 1), discovered within the Massive Cluster Survey (Ebeling et al. 2001), has been the target of several imaging programs with Hubble, such as the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al. 2012), the Hubble Frontier Fields (HFF, Lotz et al. 2017), the Beyond Ultra-deep Frontier Fields And Legacy Observations (BUFFALO, Steinhardt et al. 2020). M0416 is a massive (as found from weak-lensing studies; Umetsu et al. 2014)1 and X-ray luminous (Mann & Ebeling 2012) galaxy cluster at redshift z = 0.396. The system presents a complex and mostly bi-modal mass distribution, which is likely the result of a pre-collisional phase (Balestra et al. 2016). In addition, its highly elongated geometry, typical of merging clusters, makes M0416 a remarkably efficient gravitational lens compared to other cluster lenses, as illustrated by the first strong-lensing analysis (Zitrin et al. 2013). Taking advantage of the CLASH imaging data and the CLASH-VLT spectroscopic follow-up program (Balestra et al. 2016), Grillo et al. (2015) presented a strong-lensing model of M0416 including 30 spectroscopic multiple images from ten different sources. Subsequent parametric and free-form studies were carried out, combining weak- and strong-lensing analyses and testing the impact of line-of-sight mass structures (Jauzac et al. 2014, 2015; Richard et al. 2014; Hoag et al. 2016; Chirivì et al. 2018). In particular, Hoag et al. (2016) included spectroscopic data from the Grism Lens-Amplified Survey from Space (GLASS, Treu et al. 2015), resulting in 30 secure multiple images belonging to 15 distinct sources. A high-precision strong-lens model exploiting the first MUSE observations of M0416, which lead to the identification of a large sample of 102 spectroscopic multiple images from 37 background sources, was then presented in Caminha et al. (2017a). This model was improved upon with the inclusion of the mass component associated with the hot gas (Bonamigo et al. 2017, 2018), and the kinematic measurements of a large sample of cluster galaxies, which independently constrained the sub-halo mass component (Bergamini et al. 2019). In Bergamini et al. (2021, hereafter B21) we combined the analysis of the MUSE Deep Lens Field (MDLF; see Vanzella et al. 2021) carried out in the northeast region of the cluster, with a careful re-inspection of the Hubble images, and identified 182 secure images from 66 different background sources or source substructures, ∼80% more multiple images compared to previous works (Caminha et al. 2017a; Bergamini et al. 2019). Thanks to the large number of observational constraints and the detailed modeling of the cluster total mass distribution, the B21 lens model achieved a high level of precision and accuracy. This was shown by the reproduction of the relative distances and orientations of pairs of multiply-imaged clumps, inside well-resolved sources in the vicinity of the critical lines, with typical values of less than 0.33″ and 5.9°, respectively, for 90% of the image pairs.
 |
Fig. 1. Color-composite image (credits https://esahubble.org/images/heic1416a/) of the galaxy cluster M0416. White circles show the sample of 182 multiple images in common with the lens model by Bergamini et al. (2021). The 55 new images added to the previous ones and used to optimize the lens model described in this work are plotted in red. A blue circle indicates the galaxy optimized separately from the cluster member scaling relations (see Sect. 3). Colored squares highlight the systems of multiple images analyzed using a new forward modeling approach (described in Sect. 4) that provides a further validation of our lens model. The two BCGs (BCG-N and BCG-S) and a foreground galaxy at z = 0.112 are encircled in gray. |
In this work we further exploit the Hubble multi-color imaging and MUSE spectroscopy to develop a refined high-precision strong-lensing model of M0416. We identified 55 additional spectroscopically confirmed multiple images, an increase of ∼30% compared to the previous catalog published in B21. The new set of multiple images mainly consists of multiply-lensed clumps within resolved extended sources, which are particularly useful to constrain locally the position of the critical lines (as shown in Grillo et al. 2016; Bergamini et al. 2021, 2023). The final multiple-image sample consists of 237 multiple images from 88 different background sources, spanning a wide redshift range z= 0.94–6.63 (see Fig. 2). Thus, this work presents the largest set of secure multiple images ever constructed (see Fig. 3), paving the way for a new generation of cluster strong-lensing models, with an unprecedented level of accuracy and precision.
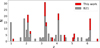 |
Fig. 2. Redshift distribution of the observed 237 multiple images exploited to constrain the reference lens model described in this work. The multiple images used by B21 are plotted in gray, while the new images are shown in red. |
 |
Fig. 3. Cumulative distributions of the number of multiple images as a function of their projected distance from the northern BCG (BCG-N) of M0416. The distribution of the images used as constraints in the new model described in this work are plotted in red (237 multiple images in total). As a comparison, the multiple images from the B21, R21, and CATS models are shown in black, blue, and green, respectively. |
The paper is organized as follows. In Sect. 2 we present the imaging and spectroscopic data used to develop the lens model. In Sect. 3 we describe the sample of multiple images used as model constraints and the adopted mass parameterization. In Sect. 4 we discuss the results of the mass model, and compare it to that presented in B21. The new lens model of M0416, including the largest set of secure multiple image to date, is then used to reconstruct the shape and luminosity of several multiply-imaged sources, highlighting the high precision and accuracy achieved. The main conclusions of this work are summarized in Sect. 5.
Throughout this work we adopt a flat ΛCDM cosmology with Ωm = 0.3 and H0 = 70 km s−1 Mpc−1. Using this cosmology, a projected distance of 1″ corresponds to a physical scale of 5.34 kpc at the M0416 redshift of z = 0.396. All magnitudes are given in the AB system.
2. Data
The updated high-precision strong-lensing model for the galaxy cluster M0416 presented in this work is based on the same observational dataset described in B21. For the photometric data, Hubble multi-band observations were collected within the CLASH survey (16 filters) and the HFF program (7 filters). For the spectroscopic data, VLT/VIMOS observations provided redshift measurements over a ∼20′ field of view (see Balestra et al. 2016). Several MUSE observations were also performed on the cluster core. In particular, one MUSE pointing (GTO 094.A-0115B, P.I. J. Richard) was centered on the northeast (NE) region of M0416 (2h of exposure and 0.6″ seeing). A second MUSE observation (094.A0525(A), P.I. F. E. Bauer) was pointed to the southwest region of the cluster (11h of integration and 1.0″ seeing). We refer to the work by Caminha et al. (2017a) for a comprehensive description of these MUSE observations. Finally, an ultra-deep MUSE observation on the NE region of M0416 was performed through the observational program 0100.A-0763(A) with P.I. E. Vanzella (Vanzella et al. 2021). This is the deepest MUSE observation obtained on a galaxy cluster to date, reaching an integration time of 17.1h in most of the NE field of M0416 with a seeing of approximately 0.6″.
3. Model description
The M0416 lens model presented in this work was developed using the publicly available software LensTool2 (Kneib et al. 1996; Jullo et al. 2007; Jullo & Kneib 2009). To determine the total mass distribution of a galaxy cluster, LensTool exploits a Bayesian approach that minimizes the following χ2 function, which quantifies how good the lens model is at reproducing the point-like positions of the 237 observed multiple images included in the sample:
In this equation 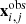 is the observed position of the ith multiple image of the j-th background source (images from the same source are called a family of multiple images);
is the observed position of the ith multiple image of the j-th background source (images from the same source are called a family of multiple images); 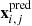 is its predicted position, given the set of model free parameters ξ; and Δxi, j represents the positional uncertainty of the image.
is its predicted position, given the set of model free parameters ξ; and Δxi, j represents the positional uncertainty of the image.
Throughout this work we quote the optimized parameter values, and their associated errors, from the 50th, 16th, and 84th percentiles of the marginalized posterior distribution of each parameter. We note that we re-scaled the Δxi, j values in such a way that the χ2 value is equal to the number of degrees of freedom (![$ \mathrm{d.o.f.}=2\times [N^{\mathrm{tot}}_{\mathrm{im}} - N_{\mathrm{fam}}] - N_{\mathrm{freepar}} $](/articles/aa/full_html/2023/06/aa44834-22/aa44834-22-eq4.gif) ) of the model, before sampling the posterior distributions.
) of the model, before sampling the posterior distributions.
Other than the χ2, the most common figure of merit to quantify the goodness of a lens model is the root mean square separation between the observed and model-predicted positions of the multiple images. This is defined as
where 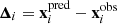 is the separation between the model-predicted and observed positions of the ith image.
is the separation between the model-predicted and observed positions of the ith image.
3.1. Multiple images
The strong-lensing model of the galaxy cluster M0416 developed in this work considers as constraints the point-like positions of the 182 multiple images used by B21. In addition to these images, 55 newly identified images are included in the catalog (see Fig. 2 and Table A.1) and are briefly discussed below.
Of the new images with respect to B21, 50 were identified after cross-matching and complementing the spectroscopic catalog by R21, considering only the images with the highest (> 1) confidence quality flags (QFs), with the samples from Vanzella et al. (2021) and Meštrić et al. (2022). Going beyond the analysis presented in R21, we identify multiply-lensed, nearly point-like substructures inside most of these images that are used as constraints in our model. The inclusion of these sub-knots in the lens model proved to be extremely useful to reconstruct the fine details of the cluster gravitational potential and the positions of the critical lines (see also Grillo et al. 2016; Bergamini et al. 2023). For all the new images, we then revisited the redshift value provided in R21 by cross-correlating and/or reanalyzing the MUSE spectra, extracted within customized apertures following the shape of the distorted images. In particular, we corrected the redshift value of system 202 (system 81 in the R21 catalog), that was incorrectly quoted as being equal to 1.827 by R21, instead of 2.091 (see Table A.1).
Two of the remaining five images, with ID 211b and 211c, were identified by Vanzella et al. (2020). In addition, we securely associate a third counter-image (205c) with the image family 205 (family 91 in R21), that was not considered by R21. The last two new images belong to Sys16, a galaxy-galaxy strong-lensing system around the cluster galaxy identified as Gal-8785 (see Fig. 1 and Sect. 4). A careful inspection of the multiple images around this galaxy and of the lens model predictions have allowed us to correct a few inaccurate associations (with no impact on the overall cluster lens model) assumed in B21. As a result, two additional images of Sys16 are included near the galaxy Gal-8785 (see Table A.1 and the bottom left panel of Fig. 11).
Compared to the R21 multiple image lensing catalog, this work includes 75 new images. On the other hand, 36 images from R21 are not considered here based on low-confidence redshift measurements (QF < 1) and/or unclear identifications based on the HST imaging.
3.2. Mass parameterization
Bergamini et al. (2021) explored several total mass parameterizations by varying the number of large-scale DM halos and testing the impact of additional external shear and convergence terms. In this work we adopt for M0416 the total mass parameterization of the reference model in B21, which was significantly favored by all the considered statistical estimators. We refer to that reference for a detailed overview, and provide here a brief summary. LensTool implements a parametric approach to model the total mass distribution of galaxy clusters. This means that the total gravitational potential of M0416 is divided into the following sum of different components:
The first sum runs over the mass density profiles used to parameterize the cluster-scale halos of the cluster (mainly made of dark matter); the second sum describes the contribution of the hot gas to the total cluster mass; the third sum takes into account the total mass distribution of the cluster member galaxies (the sub-halo component); and finally, the last term is used to represent a foreground galaxy, at z = 0.112, residing in the southern region of M0416 (see Fig. 1). In the model we present here, each mass component (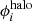 ,
, 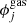 ,
, 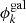 , and ϕforeg) is described by a dual pseudo-isothermal elliptical mass profile (dPIE, Limousin et al. 2005; Elíasdóttir et al. 2007; Bergamini et al. 2019) that is characterized by seven free parameters: two parameters define the position on the sky (x, y), two correspond to the ellipticity (
, and ϕforeg) is described by a dual pseudo-isothermal elliptical mass profile (dPIE, Limousin et al. 2005; Elíasdóttir et al. 2007; Bergamini et al. 2019) that is characterized by seven free parameters: two parameters define the position on the sky (x, y), two correspond to the ellipticity (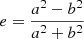 , where a and b are the values of the semi-major and semi-minor axes of the ellipsoid, respectively) and the position angle (θ, computed counterclockwise from the west direction), while the last three parameters, σ0, rcore, and rcut, are the central velocity dispersion, the core radius, and the truncation radius, respectively. In passing, we note that instead of using σ0, LensTool implements a scaled version of this quantity, identified as σLT, such that
, where a and b are the values of the semi-major and semi-minor axes of the ellipsoid, respectively) and the position angle (θ, computed counterclockwise from the west direction), while the last three parameters, σ0, rcore, and rcut, are the central velocity dispersion, the core radius, and the truncation radius, respectively. In passing, we note that instead of using σ0, LensTool implements a scaled version of this quantity, identified as σLT, such that 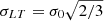 .
.
The cluster-scale component (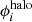 ) of our new lens model is parameterized by three non-truncated elliptical dPIE profiles. Two are centered on the brightest cluster galaxies, BCG-N and BCG-S in Fig. 1, while the position of the third profile is free to vary in the southern part of the cluster, and it is necessary to provide second-order corrections to the total cluster mass distribution around the southern BCG. An additional circular and non-truncated dPIE profile is included in the lens model to account for a small overdensity of galaxies in the northeast region of the cluster (around Sys4a,b in Fig. 1).
) of our new lens model is parameterized by three non-truncated elliptical dPIE profiles. Two are centered on the brightest cluster galaxies, BCG-N and BCG-S in Fig. 1, while the position of the third profile is free to vary in the southern part of the cluster, and it is necessary to provide second-order corrections to the total cluster mass distribution around the southern BCG. An additional circular and non-truncated dPIE profile is included in the lens model to account for a small overdensity of galaxies in the northeast region of the cluster (around Sys4a,b in Fig. 1).
For the values of the dPIE parameters describing the hot-gas component of M0416 (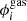 ), we make use of the results of Bonamigo et al. (2017, 2018). In particular, Bonamigo et al. (2018) found that the total hot-gas content of M0416, inferred from the Chandra X-ray observations, can be well characterized using four elliptical dPIE profiles. Since the values of the parameters of these profiles are kept fixed, the hot-gas component does not introduce any extra free parameter in the lens model.
), we make use of the results of Bonamigo et al. (2017, 2018). In particular, Bonamigo et al. (2018) found that the total hot-gas content of M0416, inferred from the Chandra X-ray observations, can be well characterized using four elliptical dPIE profiles. Since the values of the parameters of these profiles are kept fixed, the hot-gas component does not introduce any extra free parameter in the lens model.
The cluster member galaxies (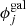 ) are modeled with singular, circular dPIE profiles, for which the velocity dispersion,
) are modeled with singular, circular dPIE profiles, for which the velocity dispersion, 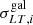 , and truncation radius,
, and truncation radius, 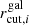 , values scale with that of the galaxy luminosity, Li, according to the following relations (which are used to sensibly reduce the number of free parameters of the lens model):
, values scale with that of the galaxy luminosity, Li, according to the following relations (which are used to sensibly reduce the number of free parameters of the lens model):
In these equations the reference luminosity, Lref, corresponds to the BCG-N magnitude in the HubbleF160W band (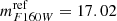 ). Following B21, we fix α = 0.3 and βcut = 0.6, while a Gaussian prior with a mean value of 248 km s−1 and a standard deviation value of 28 km s−1 is assumed on the reference velocity dispersion value,
). Following B21, we fix α = 0.3 and βcut = 0.6, while a Gaussian prior with a mean value of 248 km s−1 and a standard deviation value of 28 km s−1 is assumed on the reference velocity dispersion value, 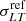 . All these values are inferred from the measured inner stellar kinematics of 64 cluster member galaxies, obtained by exploiting the high-quality MUSE data (see B21). A uniform prior between 1″ and 50″ is assumed on the
. All these values are inferred from the measured inner stellar kinematics of 64 cluster member galaxies, obtained by exploiting the high-quality MUSE data (see B21). A uniform prior between 1″ and 50″ is assumed on the 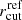 value. As in B21, we model the galaxy identified as Gal-8971 with a singular dPIE profile, outside of the cluster member scaling relations (thus resulting in four additional free parameters). The total mass distribution of this galaxy is mostly responsible for the formation of a galaxy-scale strong-lensing event composed of four multiple images (separated by ∼1″) of the same background source at z = 3.221 (Vanzella et al. 2017).
value. As in B21, we model the galaxy identified as Gal-8971 with a singular dPIE profile, outside of the cluster member scaling relations (thus resulting in four additional free parameters). The total mass distribution of this galaxy is mostly responsible for the formation of a galaxy-scale strong-lensing event composed of four multiple images (separated by ∼1″) of the same background source at z = 3.221 (Vanzella et al. 2017).
Finally, the total mass contribution of the bright foreground galaxy at z = 0.112, ϕforeg is modeled as a first approximation at the cluster redshift (as done in previous works; see, e.g., Richard et al. 2014; Grillo et al. 2015; Kawamata et al. 2016; Caminha et al. 2017a). Located in the southern region of the cluster (see Fig. 1), the galaxy lies angularly very close to families 36 and 37, impacting the observed positions of the multiple images belonging to these families. This foreground perturber is parameterized using a singular circular dPIE profile with its position fixed on the centroid of the galaxy light emission. This extra profile adds two more free parameters to the lens model.
The lens model includes a total of 30 free parameters and 298 constraints, which corresponds to 268 dof. At the top of Table 1 we summarize the fixed values and the priors assumed for the parameter values of the mass profiles included in the lens model. At the bottom of the same table, we show instead the median values and confidence intervals obtained from the sampling.
Input and output optimized parameters of the M0416 lens model presented in this work.
4. Results
In Fig. 4 we show the displacements, Δi, along the x and y directions, between the observed and model-predicted positions of the multiple images used to constrain the lens model. Of the 237 images, only four have a ∥Δi∥ value larger than 1″. One of them, identified as 101c in the image catalog (with z = 4.2994 and ∥Δ101c∥ = 1.75″), resides between two background galaxies. The first, at a projected distance of ∼2.5″, has z = 0.5377 and a total magnitude of mF160W = 20.76, while the second, at a projected distance of ∼0.8″, has z = 0.5660 and mF160W = 24.46. Neither of these two galaxies is included in the lens model, and this can marginally affect the Δrms value of the images in their vicinity. A second image, labeled with 102c, with ∥Δ102c∥ = 1.05″ and z = 6.0644, lies in the same region of the cluster just 3.8″ away from 101c. Another image, identified as 1a, with z = 3.238 and ∥Δ1a∥ = 1.04″, is located at a projected distance of 6.2″ from a background spiral galaxy at z = 0.5277 not included in the lens model. We note that considering background galaxies in the modeling is not straightforward since their position and magnitude values are affected by the lensing effect of the cluster. The inclusion of these galaxies, effectively at the redshift of the cluster, could introduce potential biases. For instance, the real (i.e., delensed) positions of the background galaxies, at their correct redshifts, depend on the optimized total mass distribution of the cluster. We also note that the work of Chirivì et al. (2018) showed that the perturbing lensing effect of foreground galaxies is more important than that of background galaxies. For all these reasons, the background galaxies mentioned above have been for now excluded from the modeling. Finally, the fourth multiple image, denominated 210.4b (∥Δ210.4b∥ = 1.15″), consists in a Lyα emitter at z = 6.149. This image forms close (just 1.3″ away) to a bright cluster galaxy, identified as Gal-7955, with mF160W = 21.29. Since the total mass of this cluster member is approximated through the lens model scaling relations (see Eq. (4)), a deviation of its real mass distribution from the predictions of the best-fit relations could justify the displacement of this image.
 |
Fig. 4. Displacements Δi (see Eq. (2)) along the x and y directions of the 237 observed multiple images used to optimize the reference lens model described in this work. Histograms show the displacement distribution along each direction. Gray circles correspond to the images in common with B21, while the new images are plotted in red. |
The global Δrms value of the lens model stands at 0.43″; about 80% of the multiple images have ∥Δi∥ < 0.5″, while more than 68% of them have ∥Δi∥ < Δrms = 0.43″. The model we are presenting is characterized by a sample of secure multiple images that is ∼30% larger than the already large sample in B21 (see Fig. 3). The additional multiple images allow us to better constrain the fine details of the M0416 total mass distribution. In the right panel of Fig. 5 we compare the total projected mass distribution obtained using the current model with that presented by B21. To account for the statistical errors, we consider 500 realizations of both models randomly extracting samples of free parameter values from the LensTool Markov chain Monte Carlo (MCMC) chains. The total mass map associated with each random realization of the B21 model is then subtracted from one of those obtained using our new model, in order to get distributions with 500 values of total mass difference in every pixel. In the right panel of Fig. 5 we plot a map showing for each pixel the median values of these distributions. A similar procedure is also applied to obtain the two panels in Fig. 6, where we compare the convergence and shear maps, computed fixing the ratio of the lens-source to observer-source distances equal to 1. We note that differently from Fig. 5, we consider here distributions of normalized values. These are obtained by dividing each of the 500 convergence and/or shear differences by the median map of the 500 realizations of our new model.
 |
Fig. 5. Projected total mass density distribution of M0416 from the best-fit lens model presented in this work. Left: Projected total mass density distribution of M0416. Contour levels correspond to values of [0.70,1.85,3.00] × 109 M⊙ kpc−2. Right: Difference between the cluster total mass density distributions inferred from the present reference lens model and that by B21. This map is obtained by considering 500 realizations of the lens models randomly extracting samples of free parameter values from the MCMC chains. The procedure adopted to generate this map is detailed in Sect. 4. Contour levels correspond to values of [−5,5] × 107 M⊙ kpc−2 (i.e., the limits of the color bar). The observed positions of the 237 multiple images used as model constraints are shown as black crosses. |
 |
Fig. 6. Percentage difference for the convergence (on the left) and the shear (on the right) distributions derived from our new reference lens model and that by B21. To generate these maps 500 random realizations of the lens models were used by extracting samples of free parameter values from the MCMC chains (for a detailed description of how the maps are created, see Sect. 4). Contour levels correspond to values of −5%, 5% and −10%, 10%, respectively. These are the limits of the plot color bars. The observed positions of the 237 multiple images used to constrain the lens model are shown as red or white crosses. |
The right panel of Fig. 5 and the left panel of Fig. 6 both illustrate that in the core of M0416, where we observe the multiple images that constrain the lens models, the B21 and the new models are characterized by very similar total mass distributions. In that region the mass difference between the two models is mostly smaller than 5%, corresponding to just a few tens of millions of solar masses per square kiloparsec for the projected total mass density. As a reference, we show in the left panel of Fig. 5 the total projected mass distribution of M0416 obtained from our new best-fit lens model. This small difference is also reflected in the small offsets visible in Fig. 7, which shows the cumulative total mass distributions of the cluster, from the model by B21 and that we are presenting here, as a function of the distance from the two BCGs. This plot highlights differences of about 5% close to BCG centers (there are no multiple images constraining the lens mass in these regions), decreasing to less than 1% at distances larger than 20 kpc, where the first multiple images are observed. As shown in the right panel of Fig. 6, slightly larger differences, but mostly below 10%, are found between the shear maps of the new and B21 lens models. When comparing with the R21 and Clusters As TelescopeS (CATS, Jauzac et al. 2014, 2015; Richard et al. 2014) models (more details about these models are provided below), we find that the resulting cumulative total profiles are consistent in the regions where multiple images are identified (between ∼20 and ∼200 kpc from the BCG-N and the BCG-S). The differences outside of these regions are about 10%.
 |
Fig. 7. Comparison of the cumulative projected total mass profiles of M0416 from this work and that by B21. Top: Cumulative projected total mass profiles of M0416 as a function of the projected distance R from the northern and southern BCG, obtained from our new reference lens model (MThis work(BCG-N), MThis work(BCG-S)) and from the model by B21 (MB21(BCG-N), MB21(BCG-S)). The distances of the observed multiple images from the BCGs used in this work are plotted using small vertical bars. Bottom: Ratio of the same mass profiles as derived from our new reference model and that by B21. |
In Fig. 8 we show the absolute relative difference between the absolute magnification values obtained by using our current model and that by B21. This analysis demonstrates that the two models predict very similar magnification values for most of the multiple images. Of the 182 multiple images shared with the model by B21, 95 (141) have absolute relative differences smaller than 0.05 (0.1) in the magnification values. As expected, larger differences are observed for the most magnified images. In fact, ∼60% of the images with a magnification value lower than 10 have an absolute relative difference lower than 0.05, while less than 20% of the images with a magnification larger than 10 have an absolute relative difference lower than 0.05. These most magnified images lie closer to the cluster critical lines, and are thus more affected by the small differences between the two lens models.
 |
Fig. 8. Absolute relative difference between the absolute magnification factors obtained from the current model and the B21 lens model as a function of the magnification values from this work. The data points represent the different observed multiple images included in both models. The data points are color-coded according to the redshift of the background sources. The absolute magnification value, μ, corresponds to the median absolute magnification computed considering 100 different realizations randomly extracted from the final MCMC chains. The errors in the magnification values are computed from the 16th and 84th percentiles. The distributions of the absolute image magnifications obtained from the current model and their absolute relative differences with the values obtained by B21 are shown in the top and right histograms, respectively. The red histogram in the top panel shows the absolute magnification distribution of the newly identified images (i.e., not used by B21). |
Even though the Δrms value, defined in Eq. (2), is a valid figure of merit to quantify the overall goodness of a lens model, this estimator is computed considering only the point-like positions of the observed and model-predicted multiple images. As a result, lens models with comparable Δrms values might not necessarily be equally good at reproducing the distorted surface brightness distribution of multiply-lensed sources. To make some progress on this, we present a comparison between our new model and two previously published lens models for M0416, with the aim of testing their ability in predicting the details of the extended emission of five systems of multiple images. The first public model was presented by R21. It counts 198 spectroscopically confirmed multiple images from 71 sources, and it has Δrms = 0.58″. Based on the publicly available files of the R21 lens model, M0416 is parameterized with three cluster-scale dark matter halos; 98 cluster members, 97 of which are modeled within the scaling relations; and two additional galaxies (one in the foreground and one in the background) that are modeled separately. The second available model was developed by the CATS team, which is known as the v4 CATS lens model (labeled here as CATS model). This model is constrained by 116 multiple images from 41 sources, and it provides Δrms = 0.67″. The CATS lens model also includes three cluster-scale dark matter halos, 98 member galaxies (two of which are modeled outside of the scaling relations), and a foreground galaxy modeled separately. We note that neither of these lens models includes any information about the gas content of the cluster, based on X-ray observations and the stellar kinematics of the cluster galaxies to accurately constrain the sub-halo component. In Table 2 we summarize the main characteristics of the compared lens models, while in Fig. 3 we plot the cumulative distributions of the number of multiple images, used as constraints for the different models, as a function of their distance from the northern BCG.
Comparison between our new lens model for M0416 and other published models for the same cluster.
The five analyzed systems of extended multiple images are indicated by colored rectangles in Fig. 1 and are selected according to the following criteria: (i) they are included in the catalogs of multiple images used as constraints by all the lens models we are comparing; (ii) the morphology of the observed extended images is sufficiently simple to be well approximated by a single Sérsic light model on the source plane; (iii) they are located in different regions of the cluster, and they are distributed across the whole cluster field of view, one in the north, two at the center, and two in the south.
The reconstruction of the surface brightness distribution of the multiple images is entrusted to a novel forward modeling code we developed, named GRAVITYFM. GRAVITYFM is a Python-based software that, through a high-level interface, optimizes the parameter values of light models chosen to represent background sources from the observed, distorted, and magnified surface brightness distributions in a given filter of their multiple images. In particular, GRAVITYFM implements a Bayesian approach to minimize the residuals between the observed and model-predicted surface brightness of the multiple images. For a detailed description of this software, we refer to the reference paper by Bergamini et al. (in prep.). By adopting the deflection maps of the best-fit lens models we are comparing, we use GRAVITYFM to find the best-fit parameter values of the Sérsic profile, which we use to describe the background source, corresponding to one of the observed multiple images of a given system. In all the cases we assume that the background source can be well approximated by a single Sérsic model with an index value n = 1, while the following parameter values are left free to vary: the coordinates X and Y of the center on the source plane, the effective radius Re, the axis ratio q, the position angle θ, and the total emitted flux F. The image pixels considered in the optimization process are encircled in green in Figs. 9–12, and 13. For each system, these images are the least distorted ones and without significant contamination from other bright sources in their vicinity. First, the selected single image of a system is used to optimize the parameter values of the corresponding background source. Then we use that reconstructed source and GRAVITYFM, with the deflection maps obtained from each different lens model, to predict a posteriori the surface brightness distributions of the other counter-images. To create the color multiple images displayed in the figures, we performed for each system three forward modeling optimizations using the F814W, F606W, and F435WHubble filters. The model predictions in each band are then combined to obtain the RGB images.
 |
Fig. 9. Forward modeling reconstruction of multiple image system 4, highlighted in cyan in Fig. 1. The RGB images in the leftmost column are obtained by combining the HubbleF435W, F606W, and F814W filters. The next three columns, from left to right, show the model-predicted images obtained by using our forward modeling code GRAVITYFM (see Sect. 4) and adopting the deflection maps of our new reference model, the R21 model, and the CATS model, respectively. The green polygon in the top left image contains the pixels associated with the single image (4c) that is exploited by GRAVITYFM to determine the best-fit parameter values of the background source, while the other images (4a and 4b) are used as test images and predicted a posteriori. The cluster tangential critical lines, computed at the source redshift, are plotted in red. Magenta crosses give the positions of the cluster member galaxies included in each model. |
 |
Fig. 11. Same as Fig. 9, but for Sys16, highlighted in orange in Fig. 1. In the bottom left panel the blue crosses give the observed positions of the multiple images adopted by B21 and the red circles are the image configuration included in the current model (see Sect. 3.1). The inset in the bottom left panel shows a liner combination of two Hubble filters to subtract the cluster member light contribution. |
As expected, the R21 model, the CATS model, and our new lens model are equally good at reproducing the chosen first images of every system. This is not surprising since these images are located in regions of low magnification for all lens models and, by changing the values of the free parameters of the Sérsic profile of the background sources, satisfactory fits to the data are achieved. We note that the different lens models reconstruct sources with different best-fit values for the parameters (i.e., centroid, ellipticity, and intensity) of their surface brightness distribution. It is not straightforward instead if the optimized source can also reproduce well, a posteriori, the position, shape and flux of the other extended images of each system, because their observations are not considered during the reconstruction of the corresponding sources.
In Fig. 9 we show the results for Sys4. In this case, our lens model is the only one that is able to reproduce the correct observed configuration of the two multiple images identified as Sys4a,b. On the contrary, the R21 and CATS models predict the formation of several additional bright images, some of them in the form of an extended arc, that are not observed in the Hubble images.
Sys13, illustrated in Fig. 10, is composed of three multiple images, two of which (a and b) merge into an extended arc that crosses the main cluster critical line at the source redshift (z = 1.005). For this system, our model and the R21 model both successfully predict the observed arc configuration, while in the CATS model the arc is so faint that it is just barely visible.
In Sys16 (Fig. 11), the test extended images (i.e., b, c, d, and e) form around a cluster galaxy with mF160W = 21.48. We note that this galaxy is included in all the lens models and its total mass parameter values are optimized within the adopted cluster member scaling relations (see Eq. (4)). Remarkably, only our lens model can accurately reproduce the observed number of multiple images and their detailed surface brightness distributions. Finally, while all the lens models perform fairly well in reproducing the images b and c of Sys24, as shown in Fig. 12, our model provides the best predictions for the positions and shapes (i.e., ellipticity and orientation) of the two test images b and c of Sys29, as visible in Fig. 13.
These results further demonstrate the importance of including the stellar kinematic information of the cluster member galaxies to accurately constrain the sub-halo scaling relations, following Bergamini et al. (2019) and B21. Recent comparisons between lensing models of massive clusters, such as M0416, and state-of-the art hydrodynamical simulations have shown a significant discrepancy between the observed and simulated probability of clusters to produce galaxy-galaxy strong-lensing (GGSL) events (e.g., Meneghetti et al. 2020, 2022; Ragagnin et al. 2022). This result can be interpreted as observed cluster members being more compact than their simulated analogs. Given its accuracy in reproducing the observed features of the multiple images lensed by single cluster members, this model will be used as a basis for further deeper studies on GGSL systems (Granata et al. in prep.), which may provide us with an independent probe of the compactness of the member galaxies.
5. Conclusions
We presented our latest high-precision strong-lensing model for the galaxy cluster M0416 (z = 0.396), based on the largest spectroscopic sample of multiple images available to date. We took advantage of panchromatic Hubble observations in combination with deep high-quality MUSE spectroscopic data to identify 237 multiple images, 55 more than in B21 (and 75 new images with respect to R21), from 88 background sources, as well as a pure and complete sample of cluster member galaxies. The multiple images cover a redshift range between 0.94 and 6.63 and are uniformly distributed across the entire cluster field of view. The model incorporates the contribution to the cluster total mass of the baryonic hot-gas component (derived from the Chandra X-ray data in Bonamigo et al. 2018) and includes the measured stellar velocity dispersions of 64 cluster galaxies (corresponding to approximately 30% of the total number of selected cluster members) to accurately characterize the sub-halo total mass component of the cluster. This new dataset makes M0416 arguably the best known cluster lens to date.
By comparing our new results with those from previously published models for M0416, we find that our model outperforms the others in terms of ability to reconstruct the observed positions, shapes, and magnifications of the multiply imaged sources. Thus, other than to robustly characterize the total mass distribution of the cluster down to the galaxy scale, our model can provide accurate and precise magnification maps that are crucial for the study of the intrinsic physical properties of faint high-redshift sources magnified by the lensing cluster (Meštrić et al. 2022). These low-luminosity sources, the progenitors of the galaxies in the local Universe, may play an important role in the cosmic re-ionization, making them interesting targets for the James Webb Space Telescope (JWST) telescope. Our main results can be summarized as follows:
-
The total root mean square separation between the observed and model-predicted positions of the 237 multiple images is Δrms = 0.43″. This value is very similar to the previous value by B21, despite a ∼30% increase in the number of multiple images used to constrain the model. Moreover, the distance between the observed and predicted positions, ∥Δi∥, is lower than the Δrms value for ∼69% of the images.
-
The projected total mass density distribution, the cumulative total mass profile, and the convergence and the shear maps obtained from our new model are highly consistent with those obtained by B21. This result, in combination with a nearly unchanged Δrms value and a significantly larger sample of multiple images, demonstrates that our modeling parameterization is well suited to robustly characterize the total mass distribution of M0416.
-
Thanks to a novel forward modeling code developed in this work, we tested that our new lens model is able to faithfully reproduce the extended and distorted surface brightness distributions of several observed multiple images. In this context, our new high-precision model outperforms the results of previously published lens models (based on smaller samples of multiple images, in some cases not spectroscopically confirmed, and different modeling prescriptions for the total mass of cluster members) at reproducing the observed positions, shapes, and magnifications of the extended lensed systems.
The M0416 lens model presented here will be made publicly available with the publication of this paper through our newly developed Strong Lensing Online Tool, also known as SLOT (Bergamini et al. 2023). With a simple graphical interface, SLOT offers the opportunity for non-lensing experts to access all the results and to exploit the predictive power of our models for their studies, specifically those based on upcoming JWST observations of M0416, which will reveal even more multiple images. For example, SLOT can quickly predict all the multiple images of a given source, also computing associated quantities (such as positions, magnification factors, and time delays) with statistical errors obtained from the model MCMC chains. Moreover, it can be used to create maps of magnification, projected total mass, and deflection angle, for example. These high-level products can, for instance, be used in combination with the forward modeling software (Bergamini et al. in preparation) to test the accuracy of different strong-lensing models (see Fig. 9–12, and 13) and to study the intrinsic physical proprieties of the lensed background sources. We finally note that, as is happening for other clusters recently observed by the JWST (e.g., Treu et al. 2022; Bezanson et al. 2022; Windhorst et al. 2023), the presented lens model and its future refinements will have a fundamental role in the study of lensed high-redshift sources that will soon be observed or discovered by the JWST (e.g., Vanzella et al. 2022; Roberts-Borsani et al. 2022; Castellano et al. 2022).
Acknowledgments
We thank the anonymous referee for the useful comments that have helped improve the clarity of the manuscript. Based on observations collected at the European Southern Observatory for Astronomical research in the Southern Hemisphere under ESO programmes with IDs: NE-deep (15.1h): 0100.A-0763(A), (P.I. E. Vanzella), NE (2h): GTO 094.A-0115B (P.I. J. Richard), SW (11h): 094.A0525(A), (P.I. F.E. Bauer). The Hubble Frontier Field program (HFF) is based on the data made with the NASA/ESA Hubble Space Telescope. The Space Telescope Science Institute is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. ACS was developed under NASA Contract NAS 5-32864. We acknowledge financial support through grants PRIN-MIUR 2015W7KAWC, 2017WSCC32, and 2020SKSTHZ. AA has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 101024195 – ROSEAU. GBC thanks the Max Planck Society for support through the Max Planck Research Group for S. H. Suyu and the academic support from the German Centre for Cosmological Lensing. MM acknowledges support from the Italian Space Agency (ASI) through contract “Euclid – Phase D". We acknowledge funding from the INAF “main-stream” grants 1.05.01.86.20 and 1.05.01.86.31.
References
- Bacon, R., Accardo, M., Adjali, L., et al. 2012, The Messenger, 147, 4 [NASA ADS] [Google Scholar]
- Balestra, I., Mercurio, A., Sartoris, B., et al. 2016, ApJS, 224, 33 [Google Scholar]
- Bergamini, P., Rosati, P., Mercurio, A., et al. 2019, A&A, 631, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergamini, P., Rosati, P., Vanzella, E., et al. 2021, A&A, 645, A140 [EDP Sciences] [Google Scholar]
- Bergamini, P., Acebron, A., Grillo, C., et al. 2023, A&A, 670, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., Labbe, I., Whitaker, K. E., et al. 2022, ApJ, submitted [arXiv:2212.04026] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2017, ApJ, 842, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [Google Scholar]
- Bouwens, R. J., Bradley, L., Zitrin, A., et al. 2014, ApJ, 795, 126 [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2016, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017a, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017b, A&A, 607, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Rosati, P., Grillo, C., et al. 2019, A&A, 632, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Suyu, S. H., Grillo, C., & Rosati, P. 2022, A&A, 657, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Fontana, A., Treu, T., et al. 2022, ApJL, submitted [arXiv:2212.06666] [Google Scholar]
- Chirivì, G., Suyu, S. H., Grillo, C., et al. 2018, A&A, 614, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coe, D., Zitrin, A., Carrasco, M., et al. 2013, ApJ, 762, 32 [Google Scholar]
- Dessauges-Zavadsky, M., Schaerer, D., Cava, A., Mayer, L., & Tamburello, V. 2017, ApJ, 836, L22 [Google Scholar]
- Diego, J. M., Molnar, S. M., Cerny, C., et al. 2020, ApJ, 904, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007, ArXiv eprints [arXiv:0710.5636] [Google Scholar]
- Grillo, C., Suyu, S. H., Rosati, P., et al. 2015, ApJ, 800, 38 [Google Scholar]
- Grillo, C., Karman, W., Suyu, S. H., et al. 2016, ApJ, 822, 78 [Google Scholar]
- Grillo, C., Rosati, P., Suyu, S. H., et al. 2018, ApJ, 860, 94 [Google Scholar]
- Grillo, C., Rosati, P., Suyu, S. H., et al. 2020, ApJ, 898, 87 [Google Scholar]
- Hashimoto, T., Laporte, N., Mawatari, K., et al. 2018, Nature, 557, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Hoag, A., Huang, K. H., Treu, T., et al. 2016, ApJ, 831, 182 [Google Scholar]
- Jauzac, M., Clément, B., Limousin, M., et al. 2014, MNRAS, 443, 1549 [Google Scholar]
- Jauzac, M., Richard, J., Jullo, E., et al. 2015, MNRAS, 452, 1437 [Google Scholar]
- Jauzac, M., Klein, B., Kneib, J.-P., et al. 2021, MNRAS, 508, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, T. L., & Sharon, K. 2016, ApJ, 832, 82 [Google Scholar]
- Johnson, T. L., Rigby, J. R., Sharon, K., et al. 2017, ApJ, 843, L21 [Google Scholar]
- Jullo, E., & Kneib, J.-P. 2009, MNRAS, 395, 1319 [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Jullo, E., Natarajan, P., Kneib, J. P., et al. 2010, Science, 329, 924 [Google Scholar]
- Karman, W., Caputi, K. I., Caminha, G. B., et al. 2017, A&A, 599, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawamata, R., Oguri, M., Ishigaki, M., Shimasaku, K., & Ouchi, M. 2016, ApJ, 819, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [Google Scholar]
- Lagattuta, D. J., Richard, J., Clément, B., et al. 2017, MNRAS, 469, 3946 [Google Scholar]
- Limousin, M., Kneib, J.-P., & Natarajan, P. 2005, MNRAS, 356, 309 [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Mann, A. W., & Ebeling, H. 2012, MNRAS, 420, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Davoli, G., Bergamini, P., et al. 2020, Science, 369, 1347 [Google Scholar]
- Meneghetti, M., Ragagnin, A., Borgani, S., et al. 2022, A&A, 668, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meštrić, U., Vanzella, E., Zanella, A., et al. 2022, MNRAS, 516, 3532 [CrossRef] [Google Scholar]
- Pignataro, G. V., Bergamini, P., Meneghetti, M., et al. 2021, A&A, 655, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Ragagnin, A., Meneghetti, M., Bassini, L., et al. 2022, A&A, 665, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Jauzac, M., Limousin, M., et al. 2014, MNRAS, 444, 268 [Google Scholar]
- Richard, J., Claeyssens, A., Lagattuta, D., et al. 2021, A&A, 646, A83 [EDP Sciences] [Google Scholar]
- Roberts-Borsani, G., Treu, T., Chen, W., et al. 2022, Nature, submitted [Google Scholar]
- Sharon, K., Bayliss, M. B., Dahle, H., et al. 2020, ApJS, 247, 12 [CrossRef] [Google Scholar]
- Steinhardt, C. L., Jauzac, M., Acebron, A., et al. 2020, ApJS, 247, 64 [Google Scholar]
- Treu, T., Schmidt, K. B., Brammer, G. B., et al. 2015, ApJ, 812, 114 [Google Scholar]
- Treu, T., Roberts-Borsani, G., Bradac, M., et al. 2022, ApJ, 935, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Castellano, M., Meneghetti, M., et al. 2017, ApJ, 842, 47 [Google Scholar]
- Vanzella, E., Meneghetti, M., Caminha, G. B., et al. 2020, MNRAS, 494, L81 [Google Scholar]
- Vanzella, E., Caminha, G. B., Rosati, P., et al. 2021, A&A, 646, A57 [EDP Sciences] [Google Scholar]
- Vanzella, E., Castellano, M., Bergamini, P., et al. 2022, ApJ, 940, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Windhorst, R. A., Cohen, S. H., Jansen, R. A., et al. 2023, AJ, 165, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Meneghetti, M., Umetsu, K., et al. 2013, ApJ, 762, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Labbé, I., Belli, S., et al. 2015, ApJ, 810, L12 [Google Scholar]
Appendix A: Multiple images
In Table A.1 we show the catalog of the 237 secure multiple images used as constraints in our new high-precision strong-lensing model of the galaxy cluster M0416. This currently represents the largest dataset of secure multiple images used in a lens model. The full table is available at the CDS.
Extract of the catalog of the spectroscopic multiple images included in the strong-lensing modeling of M0416. In the Col. 2 we specify the images that are new with respect to B21 (a), the new images that were not included in the R21 lens catalog (b), the images in common with R21 for which we revisited the redshift measurement (c), and the images of Sys16 with corrected positions and associations with respect to B21 (c), as discussed in Sect. 3.1 and shown in Fig. 11.
All Tables
Input and output optimized parameters of the M0416 lens model presented in this work.
Comparison between our new lens model for M0416 and other published models for the same cluster.
Extract of the catalog of the spectroscopic multiple images included in the strong-lensing modeling of M0416. In the Col. 2 we specify the images that are new with respect to B21 (a), the new images that were not included in the R21 lens catalog (b), the images in common with R21 for which we revisited the redshift measurement (c), and the images of Sys16 with corrected positions and associations with respect to B21 (c), as discussed in Sect. 3.1 and shown in Fig. 11.
All Figures
 |
Fig. 1. Color-composite image (credits https://esahubble.org/images/heic1416a/) of the galaxy cluster M0416. White circles show the sample of 182 multiple images in common with the lens model by Bergamini et al. (2021). The 55 new images added to the previous ones and used to optimize the lens model described in this work are plotted in red. A blue circle indicates the galaxy optimized separately from the cluster member scaling relations (see Sect. 3). Colored squares highlight the systems of multiple images analyzed using a new forward modeling approach (described in Sect. 4) that provides a further validation of our lens model. The two BCGs (BCG-N and BCG-S) and a foreground galaxy at z = 0.112 are encircled in gray. |
| In the text | |
 |
Fig. 2. Redshift distribution of the observed 237 multiple images exploited to constrain the reference lens model described in this work. The multiple images used by B21 are plotted in gray, while the new images are shown in red. |
| In the text | |
 |
Fig. 3. Cumulative distributions of the number of multiple images as a function of their projected distance from the northern BCG (BCG-N) of M0416. The distribution of the images used as constraints in the new model described in this work are plotted in red (237 multiple images in total). As a comparison, the multiple images from the B21, R21, and CATS models are shown in black, blue, and green, respectively. |
| In the text | |
 |
Fig. 4. Displacements Δi (see Eq. (2)) along the x and y directions of the 237 observed multiple images used to optimize the reference lens model described in this work. Histograms show the displacement distribution along each direction. Gray circles correspond to the images in common with B21, while the new images are plotted in red. |
| In the text | |
 |
Fig. 5. Projected total mass density distribution of M0416 from the best-fit lens model presented in this work. Left: Projected total mass density distribution of M0416. Contour levels correspond to values of [0.70,1.85,3.00] × 109 M⊙ kpc−2. Right: Difference between the cluster total mass density distributions inferred from the present reference lens model and that by B21. This map is obtained by considering 500 realizations of the lens models randomly extracting samples of free parameter values from the MCMC chains. The procedure adopted to generate this map is detailed in Sect. 4. Contour levels correspond to values of [−5,5] × 107 M⊙ kpc−2 (i.e., the limits of the color bar). The observed positions of the 237 multiple images used as model constraints are shown as black crosses. |
| In the text | |
 |
Fig. 6. Percentage difference for the convergence (on the left) and the shear (on the right) distributions derived from our new reference lens model and that by B21. To generate these maps 500 random realizations of the lens models were used by extracting samples of free parameter values from the MCMC chains (for a detailed description of how the maps are created, see Sect. 4). Contour levels correspond to values of −5%, 5% and −10%, 10%, respectively. These are the limits of the plot color bars. The observed positions of the 237 multiple images used to constrain the lens model are shown as red or white crosses. |
| In the text | |
 |
Fig. 7. Comparison of the cumulative projected total mass profiles of M0416 from this work and that by B21. Top: Cumulative projected total mass profiles of M0416 as a function of the projected distance R from the northern and southern BCG, obtained from our new reference lens model (MThis work(BCG-N), MThis work(BCG-S)) and from the model by B21 (MB21(BCG-N), MB21(BCG-S)). The distances of the observed multiple images from the BCGs used in this work are plotted using small vertical bars. Bottom: Ratio of the same mass profiles as derived from our new reference model and that by B21. |
| In the text | |
 |
Fig. 8. Absolute relative difference between the absolute magnification factors obtained from the current model and the B21 lens model as a function of the magnification values from this work. The data points represent the different observed multiple images included in both models. The data points are color-coded according to the redshift of the background sources. The absolute magnification value, μ, corresponds to the median absolute magnification computed considering 100 different realizations randomly extracted from the final MCMC chains. The errors in the magnification values are computed from the 16th and 84th percentiles. The distributions of the absolute image magnifications obtained from the current model and their absolute relative differences with the values obtained by B21 are shown in the top and right histograms, respectively. The red histogram in the top panel shows the absolute magnification distribution of the newly identified images (i.e., not used by B21). |
| In the text | |
 |
Fig. 9. Forward modeling reconstruction of multiple image system 4, highlighted in cyan in Fig. 1. The RGB images in the leftmost column are obtained by combining the HubbleF435W, F606W, and F814W filters. The next three columns, from left to right, show the model-predicted images obtained by using our forward modeling code GRAVITYFM (see Sect. 4) and adopting the deflection maps of our new reference model, the R21 model, and the CATS model, respectively. The green polygon in the top left image contains the pixels associated with the single image (4c) that is exploited by GRAVITYFM to determine the best-fit parameter values of the background source, while the other images (4a and 4b) are used as test images and predicted a posteriori. The cluster tangential critical lines, computed at the source redshift, are plotted in red. Magenta crosses give the positions of the cluster member galaxies included in each model. |
| In the text | |
 |
Fig. 10. Same as Fig. 9, but for Sys13, highlighted in yellow in Fig. 1. |
| In the text | |
 |
Fig. 11. Same as Fig. 9, but for Sys16, highlighted in orange in Fig. 1. In the bottom left panel the blue crosses give the observed positions of the multiple images adopted by B21 and the red circles are the image configuration included in the current model (see Sect. 3.1). The inset in the bottom left panel shows a liner combination of two Hubble filters to subtract the cluster member light contribution. |
| In the text | |
 |
Fig. 12. Same as Fig. 9, but for Sys24, highlighted in pink in Fig. 1. |
| In the text | |
 |
Fig. 13. Same as Fig. 9, but for Sys29, highlighted in green in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.