EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 673 (May 2023) A&A, 673 (2023) A160 Full HTML
Open Access
Issue
A&A
Volume 673, May 2023
Article Number A160
Number of page(s) 8
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202345953
Published online 24 May 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

In a Lambda cold dark matter (ΛCDM) cosmology, matter clusters on all scales; from the biggest clusters of galaxies down to the smallest stars. Every dark matter halo possesses dark matter substructure. For galactic-scale dark matter halos, the well-known substructure is constituted by dwarf galaxies swarming their giant host galaxies. The connection between substructure galactic halos has been extensively used to test ΛCDM predictions (e.g., Moore et al. 1999; Kroupa et al. 2005; Libeskind et al. 2010; Boylan-Kolchin et al. 2011; Sawala et al. 2016; Pawlowski et al. 2017; Javanmardi et al. 2019; Müller & Jerjen 2020).

While the study of the substructure is highly dependent on the resolution of the dark matter and baryonic particles, modern simulations are capable of simulating the faintest known dwarf galaxies (e.g., Revaz & Jablonka 2018; Wheeler et al. 2019), but with some caveats, such as the size of the simulation box. This makes it possible to predict and study the substructures-of-substructure.

The closest satellite within the Milky Way halo for which we can study the satellite population is the Large Magellanic Cloud (LMC). The LMC has one bright satellite – the Small Magellanic Cloud (SMC) – as well as potentially several ultrafaint dwarf companions (Erkal & Belokurov 2020; Patel et al. 2020; Battaglia et al. 2022; Pace et al. 2022). Dooley et al. (2017) calculated the expected number of bright (M*> 104 M⊙) and faint (M*< 104 M⊙) satellites associated with the LMC using abundance matching and simulations. These authors noted that observations may be in tension with the LMC system, because between four and eight bright galaxies of this kind are predicted but only one is known. This indicates that there may be an anomaly in the abundance of satellite systems. However, it has also been argued that the classical dwarf Carina may be associated with the LMC based on its orbital angular momentum, which would lessen this tension (Jahn et al. 2019; Patel et al. 2020; Battaglia et al. 2022).

To extend the studies of LMC satellites, Dooley et al. (2017) made predictions of the number of satellites more massive than 105 M⊙ for several nearby LMC-like galaxies. Müller & Jerjen (2020) searched for dwarf galaxies around two of those galaxies, and added data for four additional galaxies from the literature (Martin et al. 2009; Carlin et al. 2016; Carlsten et al. 2020). Müller & Jerjen (2020) found that the observed satellite numbers tend to be on the lower side of the expected range. Either there are more luminous subhalos in ΛCDM than what is suggested by predictions or observational biases may lead to underestimation of the true number of satellites, or a combination of both. The former is reminiscent of the too-big-to-fail problem (Boylan-Kolchin et al. 2011); the latter could arise because of, for example, projections of bright foreground stars or background galaxies at the position of an – overlooked – dwarf galaxy.

To further study the abundance of substructure, it is therefore imperative to survey different environments and test whether there is a problem in ΛCDM or the tension described above is due to observational uncertainties. In this article, we present the discovery of a satellite of a dwarf galaxy in the nearby Leo-I group. We further discuss the luminosity ratios of other observed satellites and their satellites and what is expected in ΛCDM.

2. Data and methods

In this section, we first present the data and the search for dwarf galaxies upon which this paper is based, and then present surface and point source photometry and estimate the stellar over-density of the newly discovered dwarf galaxy.

2.1. Search for dwarf-galaxy satellites

To search for satellites of dwarf galaxies, we used the Extragalactic Distance Database1 (EDD, Tully et al. 2009) CMD/TRGB catalog (Anand et al. 2021). We downloaded Hubble Space Telescope (HST) images of 117 dwarf galaxies with a distance estimate of greater than 8 Mpc and carefully inspected them by eye. We chose 8 Mpc as a minimal distance so that a potential satellite will fall on the field of view of ACS. With 202 × 202 arcsec2, ACS covers at least a radial distance of 4 kpc. However, we note that the targeted dwarf galaxy was often centered on one of the two CCDs, and therefore the area around the dwarf was not covered uniformly to the same distance in all directions.

For PGC 4689210, a dwarf galaxy in the M96 group – also known as Leo I 09 (Trentham & Tully 2002), NGC 3384-DF6, or M96-DF6 (Cohen et al. 2018) –, we detected a faint stellar over-density, hereafter called dw1046+1244, close to the galaxy (see Fig. 1). It has a similar color and surface-brightness granulation, indicating that it may be at the same distance as M96-DF6. In the HST image, M96-DF6 is barely resolved into stars. M96-DF6 is an ultradiffuse galaxy in the Leo-I group with a tip of the red giant branch (TRGB) distance of 10.2 ± 0.3 Mpc (Cohen et al. 2018).

thumbnail Fig. 1.

Pseudo-color image created from HST/ACS F606W and F814W images showing the ultradiffuse galaxy M96-DF6 (below the bright foreground star to the left). The large square box shows the location of the new satellite dw1046+1244 and is 23 × 23 arcsec2. To visualize this faint dwarf, we blurred the box with a Gaussian filter and adjusted the brightness curve (small white box). North is up and east is to the left. Image from the HST Program 14644.

2.2. Point source photometry

We perform point-spread function (PSF) photometry with the DOLPHOT software package (Dolphin 2000, 2016). Using the parameters used in the EDD pipeline (Anand et al. 2021), which are based on the recommended parameters in the DOLPHOT manual2, we performed photometry on the *.flc images, which are corrected for losses due to imperfect charge-transfer efficiency. We used the F814W drizzled (*.drc) image as a reference frame for both alignment and source detection. Using the photometry measured from the individual frames, DOLPHOT provides combined photometry and uncertainties for each source overall. The output photometry is supplied in the Vega magnitude system.

We retained objects that matched in both F606W and F814W pass bands and showed a global quality flag = 1, crowding parameter < 0.5, chi-square parameter < 1.5, mag err < 0.4, and sharpness parameter of between −1.5 and 1.5. Restricting the sharpness and chi parameters excludes background galaxies as well as any remaining blemishes. The resulting color–magnitude diagrams are shown in Fig. 2.

thumbnail Fig. 2.

CMDs for M96-DF6 and the M96-DF6 satellite dw1046+1244. The gray dots are all point sources passing the photometric quality cuts detected over the entire FoV. The dashed line in the left graph indicates the magnitude of the TRGB derived by Cohen et al. (2018).

2.3. Surface photometry

The newly detected dwarf galaxy is faint and has an extremely diffuse stellar distribution in the HST images, which makes surface photometry measurements difficult. Modeling the galaxy light with GALFIT (Peng et al. 2002) out of the box did not produce meaningful results. Therefore, we first used a growth-curve analysis to measure the photometric parameters of the dwarf. This two-step approach has been successfully applied on dwarf galaxies in nearby groups (e.g., Müller et al. 2015, 2017b). To this end, we masked all sources using the Python implementation of Source Extractor (Bertin & Arnouts 1996), SEP (Barbary 2016), with a threshold of 5σ. This threshold was chosen via trial and error. Source Extractor generates a source map, which we can use as a mask. However, because Source Extractor struggles to detect the low-surface brightness edges of objects, we dilate this mask with a circular kernel of 10 pixels in radius. We then calculated the radial cumulative curve. Masked patches of the sky were replaced with the median estimate of the global background on the masked image. To estimate the local background of the growth curve, the curve was varied until the outer part – which corresponds to the background – became flat. We find the best value for the local background by stepping through different values and fitting a line for pixel values that are well outside of the visible galaxy profile (12.5–22.5 arcsec). The local background value that results in a slope of zero gives the best estimate. Because the growth curve is a cumulative sum, the total collected light from the galaxy corresponds to where the curve becomes flat. We find this sum by estimating the median value of the background region (i.e., within 12.5 to 22.5 arcsec). The error is given by two times the standard deviation within this region (0.11 mag). We then estimated the radius at which the galaxy reaches half of its cumulative sum. This corresponds to the effective radius. Its uncertainty is derived from the uncertainty of the cumulative sum (0.5 arcsec); see Fig. 3 for a plot of the growth curve. We note that this method of structural-parameter estimation is independent of models such as a Sérsic profile. The effective surface brightness is calculated from the apparent magnitude and effective radius.

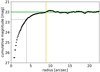thumbnail Fig. 3.

Magnitude growth curve in the F606W band of the newly discovered dwarf galaxy dw1046+1244. The thick green horizontal line indicates the estimated total magnitude, and the two thin green lines correspond to ±2 standard deviations around it. The vertical yellow line indicates the radius where the magnitude reaches the background. The two black lines correspond to the distance where the curve reaches half the flux, which is the estimation of the effective radius.

To test our implementation of the growth-curve fitting and estimate the overall uncertainty, we injected 200 artificial dwarf galaxies into the HST data. The injected dwarfs were made to resemble the detected object, with their apparent magnitudes and effective radius uniformly distributed within the 2σ measurement uncertainty and between 3 and 5 arcsec for the effective radius, respectively. For each of these dwarfs, we repeated the growth-curve fitting and estimated the difference between the injected and the extracted structural parameters, namely the apparent magnitude and the effective radius. For the apparent magnitude, we find an offset of −0.09 mag and a standard deviation of 0.11 mag. For the effective radius, we find an offset of 0.3 arcsec and a standard deviation of 0.4 arcsec. This is likely coming from underestimating the flux due to the masking and can be corrected by making the dwarf galaxy brighter and larger by these estimated values. We correct the apparent magnitude and effective radius by these values, and derive the final photometric errors as a root sum square of the uncertainty of the growth curve and the offset from the artificial galaxy experiment. The uncertainty in the effective surface brightness is calculated from a Gaussian error propagation of the apparent magnitude and effective radius. The structural parameters and the final errors are listed in Table 1.

Table 1.

Structural properties of the newly discovered dwarf galaxy dw1046+1244.

As a last step, we used GALFIT to model the galaxy. We fixed the effective radius and the ellipticity (0.9 < e < 1.0), and used an exponential profile (Sérsic n = 1). The results of the GALFIT modeling are presented in Fig. 4. The dwarf galaxy light is well subtracted.

thumbnail Fig. 4.

GALFIT modeling of the newly discovered dwarf galaxy dw1046+1244 in the F606W band. The images were smoothed with a Gaussian kernel and binned. From left to right: snapshot of the dwarf, mask of all sources with a threshold of 5σ identified by Source Extractor, best GALFIT model, and residual image.

2.4. Stellar overdensity

To quantify the stellar overdensity associated with the newly discovered ultrafaint dwarf galaxy, we compare the local stellar density at its location with the mean stellar density in its environment. To do this, we split the field and only consider point sources that pass the photometry quality cuts and reside on the chip of the dwarf. Starting at the center of the dwarf, we draw a small circle around it and compute the stellar density in this region. We then normalize this with the mean stellar density on this side of the field (i.e., on the chip where the dwarf galaxy resides). We increase the radius in steps of 20 pix and repeat the calculation for the annuli with radii rinner = ri and router = ri + 1. We note a stellar overdensity of 3 at the location of the dwarf when compared to its environment, which corresponds to a 3.4 σ signal. The density drops down to the background level at a radius of r = 220 pix, which corresponds to 10.8 arcsec. This is similar to the break we find in our growth curve analysis (see Fig. 3). We repeat this test for the dwarf M96-DF6 in its environment and obtain a stellar overdensity radius of 33.1 arcsec. Figure 5 shows a 2D histogram of the field with 50  ×  50 pix2 bins and indicates the radii of the stellar overdensities of the two dwarf galaxies.

thumbnail Fig. 5.

Density map of presumed RGB stars (yellow dots) using a binning of 50  ×  50 pix2. The yellow circles indicate where the stellar density of the dwarf galaxies drops to the background. The colors of the bins indicate the stellar density: dark blue meaning no stars and yellow meaning ten stars.

3. Discussion

3.1. Scaling relation

Dwarf galaxies follow specific scaling relations, such as the luminosity–effective radius relation (Martin et al. 2008; Poulain et al. 2021) and these can therefore be used to assess the nature of the detected object (see e.g., Fig. 11 in Müller et al. 2017a). Figure 6 presents the luminosity–effective radius relation defined by the Local Group dwarf galaxies as compiled by McConnachie (2012). As expected, both the dwarf galaxy M96-DF6 and its newly discovered satellite follow this relation. The dwarf galaxy dw1046+1244 is similar to AndXXX (Martin et al. 2016), also known as CassII, with MV = −8.0 mag and rh = 260 pc. This latter dwarf has a velocity dispersion of 11.8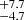 − 4.7 + 7.7 $ ^{+7.7}_{-4.7} $ and is dark matter dominated (Collins et al. 2013). If dw1046+1244 has a similar dark matter halo, such a velocity dispersion can be measured with modern facilities such as Keck (see e.g., Danieli et al. 2019) or the VLT (e.g., Emsellem et al. 2019).

thumbnail Fig. 6.

Luminosity–effective radius relation defined by the Local Group dwarf galaxies (gray dots). The blue square is the ultradiffuse galaxy M 96-DF6, and the red star corresponds to the newly discovered ultrafaint dwarf dw1046+1244.

With a solar mass of 2 × 105 M⊙, dw1046+1244 is at the threshold of the ultrafaint dwarf galaxy regime (< 105 M⊙ according to Bullock & Boylan-Kolchin 2017). While this is not a physical distinction to dwarf spheroidals, it denotes the class of objects in the Local Group discovered in the CCD era (e.g., Willman et al. 2005; Belokurov et al. 2007, 2010; Martin et al. 2009; Kim et al. 2015; Kim & Jerjen 2015), and separates them from the classical dwarfs, such as Fornax or Sculptor (Shapley 1938), which were discovered on photographic plates. Because dw1046+1244 is extremely faint and shallow in surface brightness, we find it appropriate to classify it as an ultrafaint dwarf galaxy.

3.2. Satellite of a satellite

The Leo-I galaxy group has been surveyed by many research teams. Müller et al. (2018) presented the results from a wide search for dwarf galaxies using SDSS. Extrapolating the luminosity function of Leo-I from their Fig. 6, we expect roughly 160 dwarf galaxies in the environment of the Leo-I group with a luminosity of −8 mag or more. So what is the likelihood of finding two dwarf galaxies within the ACS field of view simply by chance? Care must be taken here because ACS was pointing towards one dwarf. The probability we are therefore interested in is that of finding one additional dwarf galaxy in an ACS image by chance. Assuming the dwarf galaxies are uniformly distributed within a circular area of 4 degree radius centered on M 96, they are distributed within 50.6 deg2. The ACS instrument has a field of view of 202 × 202 arcsec2. The M 96 footprint is therefore 16 000 times larger than the ACS field of view. With 160 potential dwarf galaxies, the probability that one dwarf galaxy falls into the area of the ACS footprint is one percent. It is therefore unlikely, but not impossible, that we see the two of them in the same image simply by chance. For now, we consider dw1046+1244 to be a satellite of M 96-DF6. One caveat is that the previous estimate is simplified. Rather than using a uniform distribution, we would need to assume a three-dimensional radial profile and calculate the cone defined by the ACS field of view. However, ultimately, the nature of the satellite needs to be confirmed with velocity measurements, and so any contamination estimation can only be used a rough guideline.

The ultradiffuse galaxy M96-DF6 has a stellar luminosity of 2 × 107 L⊙. This is about 100 times more luminous than its presumed satellite galaxy. It is separated from dw1046+1244 by only 1.75 arcmin, which corresponds to 5.4 kpc at their measured distance. Crnojević et al. (2014) reported the first discovery of a satellite-of-satellite system in a group of galaxies outside of the Local Group. The two galaxies, Cen A-MM-dw1 and Cen A-MM-dw2, reside in the nearby Centaurus Group and have stellar luminosities of 2.0 × 106 L⊙ and 2.0 × 105 L⊙, respectively, which is a luminosity ratio of 10. The host, Cen A-MM-dw1, has an effective radius of 1.4 kpc and therefore on the border of the ultradiffuse galaxy regime. The satellite, Cen A-MM-dw2, is an ultrafaint dwarf galaxy similar to the dwarf galaxy reported here, but is slightly larger (360 ± 80 pc). Cen A-MM-dw1 and Cen A-MM-dw2 are separated by 3 kpc. This system is therefore highly similar to the one found here. It is especially intriguing that both M96-DF6 and Cen A-MM-dw1 can be considered ultradiffuse galaxies, which have received attention due to measurements showing that some of them either host a very massive dark matter halo (van Dokkum et al. 2016; Müller et al. 2021a) or a small – if any – dark matter halo (van Dokkum et al. 2018; Emsellem et al. 2019; Danieli et al. 2019).

Another satellite-of-satellite system was reported by Makarova et al. (2018). This system, namely LV J1157+5638 and LV J1157+5638 sat, was also discovered to be on one ACS field. The two galaxies have luminosities of 1.7 × 107 L⊙ and 4.8 × 105 L⊙, respectively, which is a factor of 36, and are separated from each other by 3.9 kpc. Again, this is similar to the properties found for the dwarf galaxy we study here.

In the Centaurus group, two other potential galaxy pairs were reported by Müller et al. (2017a), namely dw1243-42/dw1243-42b and dw1251-40/dw1252-40, with projected separations of 1.6 kpc and 2.9 kpc, respectively. While the first pair share similar luminosities (a magnitude difference of only 0.5 mag), the second pair of galaxies have a luminosity ratio of 16 with 4.5 × 105 L⊙ and 7.3 × 106 L⊙. However, the two pairs both lack accurate distance estimates, and so it is not clear whether or not they reside in the same group. We compile all these systems in Table 2.

Table 2.

Satellite-of-satellite systems observed in the nearby Universe.

Figure 7 shows the luminosity ratio of the satellite-of-satellite systems as a function of the stellar mass of the brighter dwarf of the pair. Furthermore, we add six satellite-of-satellite systems from the Feedback in Realistic Environment (FIRE)/GIZMO hydrodynamic zoom-in simulations of isolated dark matter halos (Wheeler et al. 2015), which span host stellar masses of between 104 and 106 M⊙. Half of these systems have a similar stellar mass to CenA-MM-dw1 – the faintest main dwarf in our sample – and half are fainter. Wheeler et al. (2015) give the stellar masses of the brightest satellites of the simulated dwarfs. Generally, these authors find higher luminosity ratios (≈1000) than what is observed in the local Universe (< 100). However, one system at a lower stellar mass than observed has a luminosity ratio of three. Also using FIRE, Jahn et al. (2019) studied the luminosity function of isolated LMC-like galaxies. Based on their Fig. 4, we estimate that the luminosity ratio between their LMC-like galaxies and the most massive satellite ranges between 1 and 160, which is of the same order of magnitude as for the observed LMC and the other observed dwarfs here (which are nevertheless at lower stellar masses).

thumbnail Fig. 7.

Simulated and observed luminosity ratios of satellite-of-satellite systems as a function of the luminosity of the main dwarf. The gray dots correspond to the six satellite-of-satellite systems analyzed in the FIRE simulation (Wheeler et al. 2015), and the black dots show the 14 satellite-of-satellite systems identified in the zoom-in simulations of Revaz & Jablonka (2018). The colored square and triangles are measurements from observed satellite-of-satellite systems. The line indicates the resolution limit of the Illustris-TNG50 simulation.

Another 14 satellite-of-satellite systems are drawn from the cosmological zoom-in simulations of Revaz & Jablonka (2018). We found these satellite-of-satellites whilst looking for subhalos hosting stars in the virial halo of the four dwarf models with a luminosity (at z = 0) of between 105 and 108 L⊙. For all of these dwarf halos, we find ultrafaint galaxy satellites associated with them (see Table 3). For the three hosts resembling the M96-DF6 system in luminosity, namely h076, h048, and h050 (see Table 1 of Revaz & Jablonka 2018), we find satellites with luminosities of 2  ×  103, 2  ×  103 L⊙, and 1.8  ×  103 and distances to the host dwarf of 27, 20, and 17 kpc, respectively. For these models, the luminosity ratio is even larger with values of above 1000. There are some dwarf models with higher masses (≈108 M⊙) that have a luminosity ratio of the order of 10 000. For the fainter models, which have masses of around 105 M⊙, we find the luminosity ratios to range from 1 to 300, and therefore to be a better match to observations, but they are of lower stellar mass than the observations would suggest. It is worth mentioning that, owing to the resolution, finding satellite-of-satellite systems at shorter distances is difficult (r12 = 0.6 kpc). With only a few systems, especially at the observed stellar mass of the main dwarf, whether there is a trend or not remains to be determined; however, it is conceivable that ΛCDM does not produce satellite-of-satellite systems that are as bright as what is observed for dwarf galaxies of between 105 M⊙ and 108 M⊙.

Table 3.

Satellite-of-satellite systems from the cosmological zoom-in simulations of Revaz & Jablonka (2018).

We furthermore show the resolution limit of IllustrisTNG50 (Pillepich et al. 2019; Nelson et al. 2019), which has a particle gas mass of 8.5 × 104 M⊙. Assuming we need 10 particles to identify an object as a satellite, we can calculate the minimal luminosity ratio as a function of host mass. In Fig. 7, systems below this calculated line are in principle resolved in IllustrisTNG50. However, we note that the observed dwarf galaxies are sitting at the edge of or above this resolution limit, meaning that they are not resolved in IllustrisTNG50. For our observed galaxies, the simulations would need a stellar mass resolution of two orders of magnitude larger than what is currently available with IllustrisTNG50.

4. Summary and conclusions

By searching through the EDD, we established a sample of 117 dwarf galaxies with available HST observations and with distances of 8 Mpc or greater. We searched for dwarf-galaxy satellites of dwarf galaxies and in these HST images found one known satellite-of-satellite for LV J1157+5638 and one previously unknown dwarf galaxy in the immediate vicinity of M96-DF6, namely an ultradiffuse galaxy in the nearby Leo-I group that appears as an extremely faint overdensity of stars. Using a growth curve to measure structural parameters, we find this new dwarf, named here as dw1046+1244, to be an ultrafaint dwarf with a stellar luminosity of 1.5 × 105 L⊙ and an effective radius of 205 pc. These parameter values are similar to those of other ultrafaint dwarfs in the Local Group, such as AndXXX. This newly discovered dwarf follows the size–luminosity relation as defined by the Local Group dwarf and is 100 times fainter than its host. Other known satellite-of-satellite systems in the nearby Universe share similar properties in terms of their separation (2–20 kpc) and luminosity ratio (2–135). Noteworthy is that for two out of the four known satellite-of-satellite systems, the central dwarf galaxy is ultradiffuse. It has been suggested that some ultradiffuse galaxies are failed galaxies (van Dokkum et al. 2016) and therefore host a vast dark matter halo. If this were found to be the case, it could explain why they have a – still relatively massive – satellite associated with them.

There currently exist only a few cosmological simulations that can resolve dwarf galaxies and their dwarf galaxy satellites. One of them is FIRE, a hydrodynamic zoom-in simulation of isolated dark matter halos. Wheeler et al. (2015) simulated six such satellite-of-satellite systems, of which five have luminosity ratios of the order of 1000, a factor 10 higher than what is observed in the nearby Universe. Again using FIRE, Jahn et al. (2019) looked at five isolated LMC-like systems and their satellites. Extracting the luminosity of their brightest satellites, we find that these systems have luminosity ratios of between 1 and 160, which is in the range of the observed dwarf systems here. However, apart from the LMC, these simulated systems are all much more massive than the observed dwarfs.

Another set are the cosmological zoom-in simulations of Revaz & Jablonka (2018). Within 14 of their dwarf-galaxy models, we searched for their most luminous satellite. For the more massive dwarfs (> 106 M⊙), we find luminosity ratios of much larger than 1000. For the less massive dwarf models, the ratios range between 1 and 300, which is closer to our observations. However, these latter dwarf models are all less luminous than the observed dwarfs we consider here. Only three of the dwarf models have a similar stellar mass and these all have much higher luminosity ratios than observed, which is consistent with the simulated dwarfs from Wheeler et al. (2015) for this mass range. It is interesting to note that the three brightest hosts from Revaz & Jablonka (2018) have similar stellar masses to the faintest hosts from the FIRE simulation in Jahn et al. (2019), but rather different luminosity ratios. This could indicate that different simulations produce different satellite systems. However, this would then put the ΛCDM into question, and whether or not it has solved the abundance problem, when the predicted luminosity functions depend on the simulations.

For three out of four observed dwarf-galaxy satellite systems, cosmological simulations do not reproduce the observed luminosity ratio between the dwarfs and their brightest satellites. If the two candidate satellite systems around Cen A are confirmed as true satellites, they will have similar luminosity ratios. It is therefore conceivable that, in ΛCDM, the brightest satellites of dwarf galaxies are missing, at least in the regime of the classical dwarfs, which is reminiscent of the too-big-to-fail problem (in reverse). The problem here is not that we are missing observations of dwarf satellite systems with a large luminosity ratio, but that we observe satellite-of-satellite systems with a low luminosity ratio, which we do not find in cosmological simulations (at given stellar mass). Further observations and more detailed cosmological simulations of dwarfs at the observed stellar mass are needed to assess whether or not there is a satellite-of-satellite (SoS) problem; in any case, the data and two independent sets of simulations indicate that this may be the case.

1

https://edd.ifa.hawaii.edu/, last accessed: 10.11.2022.

Acknowledgments

We thank the referee Guillaume Thomas for the constructive report, which helped to clarify and improve the manuscript. O.M. and N.H. are grateful to the Swiss National Science Foundation for financial support under the grant number PZ00P2_202104. O.M. likes to thank Mridul K Thomas (@mridulkthomas) for pointing out on Twitter the online tool automeris (https://apps.automeris.io/wpd/) to extract data points from figures, which we used to reproduce the values of Jahn et al. (2019) in Fig. 7.

References

  1. Anand, G. S., Rizzi, L., Tully, R. B., et al. 2021, AJ, 162, 80 [CrossRef] [Google Scholar]
  2. Barbary, K. 2016, J. Open Source Software, 1, 58 [NASA ADS] [CrossRef] [Google Scholar]
  3. Battaglia, G., Taibi, S., Thomas, G. F., & Fritz, T. K. 2022, A&A, 657, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2007, ApJ, 654, 897 [Google Scholar]
  5. Belokurov, V., Walker, M. G., Evans, N. W., et al. 2010, ApJ, 712, L103 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [Google Scholar]
  9. Carlin, J. L., Sand, D. J., Price, P., et al. 2016, ApJ, 828, L5 [NASA ADS] [CrossRef] [Google Scholar]
  10. Carlsten, S. G., Greco, J. P., Beaton, R. L., & Greene, J. E. 2020, ApJ, 891, 144 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cohen, Y., van Dokkum, P., Danieli, S., et al. 2018, ApJ, 868, 96 [Google Scholar]
  12. Collins, M. L. M., Chapman, S. C., Rich, R. M., et al. 2013, ApJ, 768, 172 [NASA ADS] [CrossRef] [Google Scholar]
  13. Crnojević, D., Sand, D. J., Caldwell, N., et al. 2014, ApJ, 795, L35 [CrossRef] [Google Scholar]
  14. Danieli, S., van Dokkum, P., Conroy, C., Abraham, R., & Romanowsky, A. J. 2019, ApJ, 874, L12 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dolphin, A. E. 2000, PASP, 112, 1383 [Google Scholar]
  16. Dolphin, A. 2016, Astrophysics Source Code Library [record ascl:1608.013] [Google Scholar]
  17. Dooley, G. A., Peter, A. H. G., Carlin, J. L., et al. 2017, MNRAS, 472, 1060 [NASA ADS] [CrossRef] [Google Scholar]
  18. Emsellem, E., van der Burg, R. F. J., Fensch, J., et al. 2019, A&A, 625, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Erkal, D., & Belokurov, V. A. 2020, MNRAS, 495, 2554 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jahn, E. D., Sales, L. V., Wetzel, A., et al. 2019, MNRAS, 489, 5348 [NASA ADS] [CrossRef] [Google Scholar]
  21. Javanmardi, B., Raouf, M., Khosroshahi, H. G., et al. 2019, ApJ, 870, 50 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kim, D., & Jerjen, H. 2015, ApJ, 808, L39 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kim, D., Jerjen, H., Mackey, D., Da Costa, G. S., & Milone, A. P. 2015, ApJ, 804, L44 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kroupa, P., Theis, C., & Boily, C. M. 2005, A&A, 431, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Libeskind, N. I., Yepes, G., Knebe, A., et al. 2010, MNRAS, 401, 1889 [CrossRef] [Google Scholar]
  26. Makarova, L. N., Makarov, D. I., Antipova, A. V., Karachentsev, I. D., & Tully, R. B. 2018, MNRAS, 474, 3221 [NASA ADS] [CrossRef] [Google Scholar]
  27. Martin, N. F., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  28. Martin, N. F., McConnachie, A. W., Irwin, M., et al. 2009, ApJ, 705, 758 [NASA ADS] [CrossRef] [Google Scholar]
  29. Martin, N. F., Ibata, R. A., Lewis, G. F., et al. 2016, ApJ, 833, 167 [NASA ADS] [CrossRef] [Google Scholar]
  30. McConnachie, A. W. 2012, AJ, 144, 4 [Google Scholar]
  31. Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
  32. Müller, O., & Jerjen, H. 2020, A&A, 644, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Müller, O., Jerjen, H., & Binggeli, B. 2015, A&A, 583, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Müller, O., Scalera, R., Binggeli, B., & Jerjen, H. 2017a, A&A, 602, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Müller, O., Jerjen, H., & Binggeli, B. 2017b, A&A, 597, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Müller, O., Jerjen, H., & Binggeli, B. 2018, A&A, 615, A105 [Google Scholar]
  37. Müller, O., Fahrion, K., Rejkuba, M., et al. 2021a, A&A, 645, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Müller, O., Durrell, P. R., Marleau, F. R., et al. 2021b, ApJ, 923, 9 [CrossRef] [Google Scholar]
  39. Nelson, D., Pillepich, A., Springel, V., et al. 2019, MNRAS, 490, 3234 [Google Scholar]
  40. Pace, A. B., Erkal, D., & Li, T. S. 2022, ApJ, 940, 136 [NASA ADS] [CrossRef] [Google Scholar]
  41. Patel, E., Kallivayalil, N., Garavito-Camargo, N., et al. 2020, ApJ, 893, 121 [Google Scholar]
  42. Pawlowski, M. S., Ibata, R. A., & Bullock, J. S. 2017, ApJ, 850, 132 [NASA ADS] [CrossRef] [Google Scholar]
  43. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
  44. Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [Google Scholar]
  45. Poulain, M., Marleau, F. R., Habas, R., et al. 2021, MNRAS, 506, 5494 [NASA ADS] [CrossRef] [Google Scholar]
  46. Revaz, Y., & Jablonka, P. 2018, A&A, 616, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 457, 1931 [Google Scholar]
  48. Shapley, H. 1938, Nature, 142, 715 [NASA ADS] [CrossRef] [Google Scholar]
  49. Trentham, N., & Tully, R. B. 2002, MNRAS, 335, 712 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tully, R. B., Rizzi, L., Shaya, E. J., et al. 2009, AJ, 138, 323 [NASA ADS] [CrossRef] [Google Scholar]
  51. van Dokkum, P., Abraham, R., Brodie, J., et al. 2016, ApJ, 828, L6 [Google Scholar]
  52. van Dokkum, P., Danieli, S., Cohen, Y., et al. 2018, Nature, 555, 629 [Google Scholar]
  53. Wheeler, C., Oñorbe, J., Bullock, J. S., et al. 2015, MNRAS, 453, 1305 [NASA ADS] [CrossRef] [Google Scholar]
  54. Wheeler, C., Hopkins, P. F., Pace, A. B., et al. 2019, MNRAS, 490, 4447 [CrossRef] [Google Scholar]
  55. Willman, B., Dalcanton, J. J., Martinez-Delgado, D., et al. 2005, ApJ, 626, L85 [Google Scholar]

All Tables

Table 1.

Structural properties of the newly discovered dwarf galaxy dw1046+1244.

In the text
Table 2.

Satellite-of-satellite systems observed in the nearby Universe.

In the text
Table 3.

Satellite-of-satellite systems from the cosmological zoom-in simulations of Revaz & Jablonka (2018).

In the text

All Figures

thumbnail Fig. 1.

Pseudo-color image created from HST/ACS F606W and F814W images showing the ultradiffuse galaxy M96-DF6 (below the bright foreground star to the left). The large square box shows the location of the new satellite dw1046+1244 and is 23 × 23 arcsec2. To visualize this faint dwarf, we blurred the box with a Gaussian filter and adjusted the brightness curve (small white box). North is up and east is to the left. Image from the HST Program 14644.
In the text
thumbnail Fig. 2.

CMDs for M96-DF6 and the M96-DF6 satellite dw1046+1244. The gray dots are all point sources passing the photometric quality cuts detected over the entire FoV. The dashed line in the left graph indicates the magnitude of the TRGB derived by Cohen et al. (2018).
In the text
thumbnail Fig. 3.

Magnitude growth curve in the F606W band of the newly discovered dwarf galaxy dw1046+1244. The thick green horizontal line indicates the estimated total magnitude, and the two thin green lines correspond to ±2 standard deviations around it. The vertical yellow line indicates the radius where the magnitude reaches the background. The two black lines correspond to the distance where the curve reaches half the flux, which is the estimation of the effective radius.
In the text
thumbnail Fig. 4.

GALFIT modeling of the newly discovered dwarf galaxy dw1046+1244 in the F606W band. The images were smoothed with a Gaussian kernel and binned. From left to right: snapshot of the dwarf, mask of all sources with a threshold of 5σ identified by Source Extractor, best GALFIT model, and residual image.
In the text
thumbnail Fig. 5.

Density map of presumed RGB stars (yellow dots) using a binning of 50  ×  50 pix2. The yellow circles indicate where the stellar density of the dwarf galaxies drops to the background. The colors of the bins indicate the stellar density: dark blue meaning no stars and yellow meaning ten stars.
In the text
thumbnail Fig. 6.

Luminosity–effective radius relation defined by the Local Group dwarf galaxies (gray dots). The blue square is the ultradiffuse galaxy M 96-DF6, and the red star corresponds to the newly discovered ultrafaint dwarf dw1046+1244.
In the text
thumbnail Fig. 7.

Simulated and observed luminosity ratios of satellite-of-satellite systems as a function of the luminosity of the main dwarf. The gray dots correspond to the six satellite-of-satellite systems analyzed in the FIRE simulation (Wheeler et al. 2015), and the black dots show the 14 satellite-of-satellite systems identified in the zoom-in simulations of Revaz & Jablonka (2018). The colored square and triangles are measurements from observed satellite-of-satellite systems. The line indicates the resolution limit of the Illustris-TNG50 simulation.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.