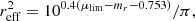| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038862 | |
| Published online | 03 December 2020 | |
Abundance of dwarf galaxies around low-mass spiral galaxies in the Local Volume
1
Observatoire Astronomique de Strasbourg (ObAS), Université de Strasbourg – CNRS, UMR 7550, Strasbourg, France
e-mail: oliver.muller@astro.unistra.fr
2
Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia
Received:
7
July
2020
Accepted:
15
September
2020
The abundance of satellite dwarf galaxies has long been considered a crucial test for the current model of cosmology leading to the well-known missing satellite problem. Recent advances in simulations and observations have allowed the study of dwarf galaxies around host galaxies in more detail. Using the Dark Energy Camera we surveyed a 72 deg2 area of the nearby Sculptor group, also encompassing the two low-mass Local Volume galaxies NGC 24 and NGC 45 residing behind the group, to search for as yet undetected dwarf galaxies. Apart from the previously known dwarf galaxies we found only two new candidates down to a 3σ surface brightness detection limit of 27.4 r mag arcsec−2. Both systems are in projection close to NGC 24. However, one of these candidates could be an ultra-diffuse galaxy associated with a background galaxy. We compared the number of known dwarf galaxy candidates around NGC 24, NGC 45, and five other well-studied low-mass spiral galaxies (NGC 1156, NGC 2403, NGC 5023, M 33, and the LMC) with predictions from cosmological simulations, and found that for the stellar-to-halo mass models considered, the observed satellite numbers tend to be on the lower end of the expected range. This could mean either that there is an overprediction of luminous subhalos in ΛCDM or that we are missing some of the satellite members due to observational biases.
Key words: galaxies: dwarf / galaxies: abundances / galaxies: groups: individual: Sculptor group / galaxies: groups: general
© O. Müller and H. Jerjen 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In the standard cosmological framework dwarf galaxies are thought to be the building blocks of the visible Universe. Larger galaxies form through a cascade of minor mergers of these dwarf galaxies (Frenk & White 2012) leading to a strong correlation between the number of dwarf galaxy satellites and the mass of the host galaxy (e.g., Javanmardi et al. 2019) as the more massive halos are able to accrete more matter. The “leftovers” from these accretion processes are still detectable today as satellite galaxies swarming the central galaxies. The specific frequency of satellites and their luminosities can be described by the galaxy luminosity function (LF; Binggeli et al. 1988) and can be compared to cosmological predictions. This led to the well-known missing satellite (Moore et al. 1999) and the too-big-to-fail (Boylan-Kolchin et al. 2011) problems. These challenges for the ΛCDM model of cosmology, however, have mainly been studied in the Local Group of galaxies. Only recently has new technology allowed dwarf galaxies to be surveyed in other nearby groups to a sufficient surface brightness depth such that cosmological tests can be conducted more systematically.
The Local Volume (D < 11-pagination Mpc, Kraan-Korteweg & Tammann 1979; Karachentsev et al. 2004, 2013) hosts over 30 large galaxies with total luminosities in excess of Mtot ≈ −20 K mag. Several surveys have targeted the more prominent of these giant galaxies like M 83 (Müller et al. 2015), Centaurus A (Crnojević et al. 2014, 2016; Müller et al. 2017; Taylor et al. 2018), and others (Merritt et al. 2014; Karachentsev et al. 2015; Javanmardi et al. 2016; Park et al. 2017; Smercina et al. 2018; Bennet et al. 2019; Carlsten et al. 2020; Davis et al. 2020). Furthermore, dwarf galaxy surveys reach even more distant galaxy clusters (Venhola et al. 2017; Wittmann et al. 2019), groups (Geha et al. 2017; Cohen et al. 2018; Habas et al. 2020), and the field (Greco et al. 2018; Prole et al. 2019).
These surveys have revealed first interesting results. For instance, the recent deep search for dwarf galaxies around the giant spiral galaxy M 94 (NGC 4736; M* ≈ 4 × 1010 M⊙, Karachentsev et al. 2013; D = 4.2 Mpc, Radburn-Smith et al. 2011) has detected only two satellites (Smercina et al. 2018). Its LF seems to be inconsistent with predictions from high-resolution dark matter simulations, having far too few satellites for such a massive galaxy. In addition, Bennet et al. (2019) argued for a strong variation in the LF derived from the environments of the giant galaxies in the Local Volume. This scatter seems to be larger than what is expected from the concordance model (but see also Carlsten et al. 2020 for a different view). On the other hand, there seems to be a correlation between the number of satellites and the bulge-to-disk ratio of the host galaxies, which is again unexpected in ΛCDM (Javanmardi et al. 2019; Javanmardi & Kroupa 2020). All these findings require more observations of different environments. While there appears to be a consensus that the missing satellite problem for the Milky Way and the Andromeda galaxy have already been resolved (Simon & Geha 2007; Sawala et al. 2016; Simpson et al. 2018), there are still discrepancies between observations and the ΛCDM model when it comes to the abundance of dwarf galaxies around the giants in the Local Volume.
One of the closest galaxy aggregates from our point of view is the Sculptor group in the southern hemisphere. It is known to be a loose association of galaxies (Jerjen et al. 1998, 2000) stretching approximately from NGC 55 (D = 2.13 Mpc, Tikhonov et al. 2005) to NGC 59 (4.89 Mpc, Tully et al. 2013), with the starburst spiral galaxy NGC 253 at a distance of 3.7 Mpc (Karachentsev et al. 2013; Lucero et al. 2015) being the dominant member. An imaging survey of its immediate surroundings has revealed only two faint companions (Sand et al. 2014; Toloba et al. 2016), which already suggests that the Sculptor group is indeed a low-density environment. This is surprising because NGC 253 is as massive as the Milky Way or the Andromeda galaxy (Lucero et al. 2015), which both host a plethora of dwarf galaxies (e.g., Belokurov et al. 2010; Richardson et al. 2011; Kim et al. 2015a). Due to its proximity to us, the Sculptor group covers several hundred square degrees in the sky, making a full coverage of the group observationally very demanding. Here we present the results from a first 72 deg2 survey based on dedicated CCD observations of the eastern part of the Sculptor group, which encompasses two additional giant galaxies, NGC 24 (D = 7.67 Mpc; Tully et al. 2013) and NGC 45 (D = 6.67 Mpc; Tully et al. 2013), which are behind the group but still in the Local Volume.
This paper is structured as follows. In Sect. 2 we present the observations and data reduction, in Sect. 3 we discuss the visual and automated search for dwarf galaxies and perform photometry, in Sect. 4 we argue the membership of the newly found dwarf galaxy candidates, in Sect. 5 we compare the luminosity function of seven low-mass host galaxies to predictions from dark matter simulations, and finally in Sect. 6 we draw our conclusions.
2. Observation and data reduction
The gr CCD images for our search of Sculptor group dwarf candidates were obtained as part of the Stromlo Milky Way Satellite Survey (e.g., Kim et al. 2015b, 2016). Imaging data were collected for a total of ∼500 deg2 with the DECam at the 4 m Blanco telescope at the Cerro Tololo Inter-American Observatory (CTIO) over three photometric nights from 17 to 19 July 2014. DECam is an array of 62 2k × 4k CCD detectors with a 2.2 deg2 field of view and a pixel scale of 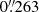 (unbinned). We obtained a series of 4 × 60 s dithered exposures in the g and r band for each pointing under photometric conditions. To cover the 72 deg2 of the Sculptor region we acquired a total of 24 pointings (see Fig. 1 for the survey footprint). The seeing in the Sculptor fields were in the ranges
(unbinned). We obtained a series of 4 × 60 s dithered exposures in the g and r band for each pointing under photometric conditions. To cover the 72 deg2 of the Sculptor region we acquired a total of 24 pointings (see Fig. 1 for the survey footprint). The seeing in the Sculptor fields were in the ranges 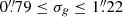 and
and 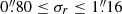 , with median values
, with median values 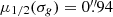 and
and 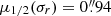 , respectively.
, respectively.
 |
Fig. 1. Field of the Sculptor group. The small black dots correspond to dwarf galaxies in the Sculptor group with its main galaxy NGC 253 (large black dot). The small gray dots are background dwarf galaxies, which are still within the Local Volume (D < 11 Mpc. The two large gray dots are the two LSB giants NGC 24 and NGC 45. The red dots are our dwarf galaxy candidates dw0009-25 and dw0010-25. The gray area corresponds to our survey footprint. |
The images were reduced via the DECam community pipeline (Valdes et al. 2014), which included overscan subtraction, bias calibration, flat field gain calibration, single exposure cosmic ray masking, illumination correction, astrometric calibration to refine the world coordinate system of each frame, and photometric calibration. For the sky subtraction we employed SEP, which is the python version (Barbary 2016) of Source Extractor (Bertin & Arnouts 1996). A 400 × 400 px2 box was used as reference for the local background measurement. This is large enough (≈2 kpc × 2 kpc) to avoid oversubtraction of the sky on the scales we are interested in (i.e., the typical angular size of a dwarf galaxy at the distance of the Sculptor group). After the individual pointings were background subtracted, the two bands were combined using the SWarp program (Bertin et al. 2002) to make a final, deep image.
The photometric zero points of the g and r images were derived using the PanSTARRS DR2 catalog (Magnier et al. 2016). We performed aperture photometry with the python package photutils (Bradley et al. 2019) and compared them to standard stars in the magnitude range 15.0–19.5 mag. A linear regression with a 0.3 mag clipping was applied to derive the slope and intercept in each band and for each field. The slope was consistent with 1.0 so that the intercept corresponds to the zero point. The errors are 0.04 mag in the g band and 0.08 mag in the r band.
3. Search for new dwarf galaxies in the Scl Group region
In our survey area only four Local Volume dwarf galaxies were known: ESO 409-15 (D = 8.7 Mpc; Tully et al. 2013), NGC 59 (D = 4.9; Tully et al. 2013), Sculptor-dE1 (Jerjen et al. 2000, D = 4.2 Mpc Karachentsev et al. 2003), and ESO 473-24 (D = 9.9 Mpc; Karachentsev et al. 2013). Additionally, two Local Volume spiral galaxies reside in the field: NGC 24 (D = 7.7 Mpc; Tully et al. 2013), an edge-on Sc galaxy, and NGC 45 (D = 6.7 Mpc; Tully et al. 2013), a low surface brightness Sdm galaxy. These two galaxies are of low mass, with total baryonic plus dark matter mass estimates of 2.8 × 1010M⊙ and 3.7 × 1010M⊙, respectively (Chemin et al. 2006).
To find new dwarf galaxies we rely on visual inspection of the images and on an automatic detection pipeline. The search is done on the stacked gr images.
3.1. Visual inspection
The classical approach to search for faint low surface brightness galaxies is via careful visual inspection of the digital images. This approach has been proven successful in the detection of dozens of new dwarf galaxies in surveys around other nearby galaxies (e.g., Jerjen et al. 2000; Karachentsev et al. 2000; Trentham & Tully 2002; Chiboucas et al. 2009; Merritt et al. 2014; Park et al. 2017; Müller et al. 2018; Habas et al. 2020; Byun et al. 2020). To enhance any low surface brightness features, a standard image processing algorithm is applied to the images: convolution with a Gaussian kernel (with σ of 1.5 px). Afterwards, all images are scanned by eye for diffuse and extended patches that resemble the morphology of dwarf galaxies. This approach leads to a good understanding of the quality and limitations of the data at hand, which will also benefit the more automated detection techniques. Assuming that a faint dwarf galaxy detectable in our images has a typical effective radius of reff = 140 pc (Müller et al. 2019b) this would give an angular size of 30 px at the mean distance of the Sculptor Group (3.45 Mpc) and 14 px at the distance of NGC 24. Such an object is clearly distinguishable from larger background dwarf galaxies, the latter being more compact compared to their surface brightness. Our visual search revealed one good dwarf galaxy candidate that we dubbed dw0010-25, and another potential candidate named dw009-25 (see Fig. 2).
 |
Fig. 2. Stacked gr-band images of the newly discovered dwarf galaxy candidates dw0009-25 (left) and dw0010-25 (right). North is to the top, east to the left, and the vertical length of the images corresponds to one arcmin. dw0009-25 was detected close to the CCD edge. |
3.2. Automated detection with MTObjects
Novel development of automated detection algorithms show promising results. One of the best software packages available today is MTObjects (Teeninga et al. 2013, 2015), a max-tree based algorithm developed for medical image analysis and re-written for astronomical purposes (see, e.g., Prole et al. 2019). It is non-parametric; that is, it automatically searches for the best parameters for a given image, which makes MTObjects straightforward to use. MTObjects provides a segmentation map and a catalog of basic photometric parameters for each detection. On these preliminary catalogs we apply further quality cuts for size, total magnitude, and surface brightness. The limits for the effective radius reff was set to be 0.1–3.0 kpc at the adopted distance of the Sculptor group (3.7 Mpc), This reduced the number of objects to a total of 3372 for the whole survey area. We inspected each of the detections by eye and only kept the good dwarf galaxy candidates leaving us with only one object, the already known Sculptor-dE1 dwarf. This means the visually detected dwarf galaxy candidate dw0010-25 was not picked up by MTObjects. We attribute this to the presence of a background spiral galaxy in close proximity (see Fig. 2). The other dwarf galaxy candidate dw0009-25 was too faint to get detected by MTObjects (see next paragraph). The large number of false positives were mainly from artifacts at the edges of the CCD images.
To assess the completeness of the dwarf galaxy detection, we injected artificial dwarf galaxies into the images and re-ran MTObjects with the same quality cuts. The dwarfs were modeled with a Sérsic profile (Sersic 1968), employing different apparent magnitudes (i.e., between 14 mag and 19 mag) and effective radii (i.e., between 5 arcsec and 160 arcsec). Sérsic indices between n = 0.5 and n = 1.5 were chosen to model the dwarfs, with randomly drawn ellipticities between e = 0.0 and e = 0.6. Each dwarf was separated by 1000 pixels and was arranged in an equidistant grid. The separation of 1000 pixels corresponds to roughly two times the maximum allowed effective radius in our quality cuts. This ensures that there is no issue of overcrowding the field. By design, some of the artificial dwarf galaxies will be at the edge of the image, such that we also probe any bias coming from dwarf galaxies being at the edge of the camera. Ultimately, the detection rate was derived from a comparison between the input and detection list, with an error tolerance of one effective radius for the position of the dwarf. This process was repeated across different fields with a total of 8000 artificial dwarf galaxies per field, where the position of the grid was randomized during each iteration. From the detection rate we derived the mean surface brightness limit by binning the magnitudes and effective radii, as in Fig. 3, with bin sizes of 0.2 mag and 10 arcsec, respectively. Then we extracted the bins as data points where we achieved a detection rate between 70% and 80% for the 75% completeness limit, data points between 45% and 55% for the 50% completeness limit, and data points between 20% and 30% for the 25% completeness limit. Through these data points we fitted the formula
 |
Fig. 3. Result from the artificial dwarf galaxy test with MTObjects showing the recovery rate (color scheme) as a function of total apparent magnitude mr and half-light radius reff. The red line indicates the lower surface brightness cut (22 mag arcesc−2), the white line the estimated completeness at 50% (27.3 mag arcesc−2), and the dashed white lines the 75% (26.7 mag arcsec−2) and 25% (27.7 mag arcsec−2) limit. The black dot indicates the known dwarf galaxy Sculptor-dE1. |
where μlim is the quantity we are solving for. We performed this limit estimation on six different fields and find 50% completeness limits: 27.19 ± 0.10 mag arcsec−2, 27.55 ± 0.09 mag arcsec−2, 27.17 ± 0.09 mag arcsec−2, 27.09 ± 0.12 mag arcsec−2, 27.38 ± 0.12 mag arcsec−2, and 27.07 ± 0.09 mag arcsec−2. To estimate the overall completeness limit of the survey, we combined these individual runs into one final diagram with bin sizes of 0.1 mag and 5 arcsec. A mean surface brightness limit μlim of 27.34 ± 0.08 mag arcsec−2 in the r band best describes our 50% detection rate limit (26.68 ± 0.10 mag arcsec−2 at 75% and 27.65 ± 0.08 mag arcsec−2 at 25%). The results are illustrated in Fig. 3. This is consistent with the numbers estimated in Müller et al. (2015), which was part of the same imaging campaign with the same observation strategy. For the apparent magnitude mr (x-axis in Fig. 3), the recovery rate drops below 50% at 18.2 mag in the r band, which translates into a completeness limit for the automated detection of dwarf galaxies of Mr = −9.6 mag at the distance of NGC 253, −11.1 mag at the distance of NGC 24, and −10.9 mag at the distance of NGC 45. The faintest detectable objects have a total apparent r magnitude of ∼18.5. This limit is two magnitudes brighter than one of the dwarf candidate we detected by eye (mr = 20.6 mag), meaning that at the faint end of the luminosity function the visual inspection performs better than the automated detection pipeline with MTObjects.
We also looked into the question of how much of the survey area is covered by extended objects such as the main galaxies, background galaxies, and bright or saturated stars which could potentially hide dwarf galaxies. To estimate a number we used the parameters given by MTObjects. Specifically, we integrated the area of all objects with effective radii larger than 7.5 px. To do this, we approximated the area of each object fulfilling the criteria as a circle with two times the effective radius. This gives a coverage of 0.2%, which can potentially hide the dwarf galaxies. This is indeed negligible, and will not significantly alter the abundance of dwarf galaxies.
3.3. Photometry
The photometry for the two dwarf galaxy candidates was done using GALFIT (Peng et al. 2002). To achieve the best Sérsic fit we provided GALFIT with a mask created from the segmentation map of MTObjects, which we further adjusted by hand. Due to their low surface brightness levels we had to impose tighter constraints on the center of the object (i.e., ±5 px from our initial guess based on the overall surface brightness distribution of the object). We performed photometry in both the g and r bands. The errors for the magnitudes are a combination of the uncertainty from the photometric zero point and the error from GALFIT, the rest is taken from the uncertainties provided by GALFIT. The measured photometric parameters are given in Table 1. We measured the surface brightness limit around our dwarf galaxy candidates in randomly distributed 10 × 10 arcsec boxes (Müller et al. 2019c) and derived a 3σ limit of 27.4 mag arcsec−2 in the r band. This limit is consistent with the 50% detection limit we derived from our artificial galaxy tests.
Photometric properties of the dwarf galaxy candidates.
4. Membership of the dwarf galaxy candidate
Both dwarf galaxy candidates dw0009-25 and dw0010-25 are in projection close to the edge-on spiral galaxy NGC 24 and also close to each other (see Fig. 1). Their on-sky separation is only 0.11 deg and 0.40 deg from NGC 24, which at its distance (D = 7.3 Mpc) corresponds to 14.5 kpc and 52.5 kpc, respectively. Assuming that the two dwarfs are satellites of NGC 24, the effective radius and absolute magnitude would be reff = 283 pc and Mr = − 8.7 mag for dw0009-25 and reff = 1069 pc and Mr = − 11.9 mag for dw0010-25. The next nearest luminous galaxy is NGC 45, which has an on-sky separation to the dwarfs of more than 2.3 deg, corresponding to a distance larger than 240 kpc at the distance of D = 6.6 Mpc for both, which is comparable to the virial radius, and thus a rather large distance for any satellite galaxy. There is a remote possibility that the dwarf candidates are associated with NGC 253 (D = 3.7 Mpc). They have an on-sky separation of ~8.3 deg, which translates into linear distances of ~550 kpc. The physical properties of the dwarf galaxy candidate then would boil down to Mr = −7.2 mag and reff = 144 pc for dw0009-25 and Mr = −10.4 mag and reff = 542 pc for dw0010-25.
How do these quantities compare to the structural parameters of other known dwarf galaxies? Habas et al. (2020) studied a population of over 2000 dwarf galaxies in the nearby universe and presented the structural parameters in their Fig. 11. Our dwarf galaxy candidates are compatible with these dwarf galaxies at either distance, so no potential membership can be confirmed or excluded. The integrated (g − r)0 color of 0.87 mag and 0.55 mag are also consistent with the mean color of 0.46 ± 0.26 mag of dwarfs in the Cen A group (Müller et al. 2018), being part of the same survey. Due to their proximity we assign dw0009-25 and dw0010-25 to NGC 24 until follow-up distance measurements can confirm their true association.
There is one caveat: dw0010-25 is very close to the interacting background spiral LEDA 133604 (see Fig. 2), which is at a redshift of z = 0.065 (Loveday et al. 1996), i.e., ≈290 Mpc from us. At that distance dw0010-25 would have an absolute magnitude of Mr = −19.8 mag and an effective radius of reff = 42 kpc, which seems highly unrealistic. The same is true for dw0009-25. It has the background galaxy LEDA 783199 in its vicinity, but no distance information is available in that case. Assuming a conservative distance of 100 Mpc, this would translate into Mr = −14.4 mag and an effective radius of reff = 4 kpc, which are plausible properties for an ultra-diffuse galaxy in the background (e.g., Barbosa et al. 2020).
5. Luminosity function of low-mass spiral galaxies
All dwarf galaxy satellites of the two host galaxies NGC 24 and NGC 45 should have been identified within the MV < −10 mag luminosity range by now. For NGC 24, we find two possible satellites while there are none for NGC 45. Is this expected? Indeed, with total masses of 2.8 × 1010M⊙ and 3.7 × 1010M⊙ (Chemin et al. 2006), respectively, the two host galaxies are at the low-mass end of the spiral galaxy population. Let us compare these results to other such galaxies. The LMC is probably the most iconic low-mass spiral galaxy with an enclosed mass of 2.5 × 1011M⊙ (Peñarrubia et al. 2016; Erkal & Belokurov 2020). It has one satellite, the SMC, more massive than 105M⊙, but also has many low-mass satellites (Erkal & Belokurov 2020) which would be impossible to detect outside of the Local Group. Carlsten et al. (2020) conducted a deep survey of dwarf galaxies around ten giants within the Local Volume and studied their luminosity functions. Two of these, NGC 1156 and NGC 5023 are of similar low mass to the two giants studied here. NGC 1156 has one confirmed (Minchin et al. 2010) and two possible dwarf galaxy satellites, and one is known for NGC 5023. Another well-studied low-mass spiral galaxy is M 33 with an observed dark matter mass of 5 × 1010M⊙ or higher (Corbelli 2003). Only one possible satellite has been reported for M 33 to date (Martin et al. 2009). The MADCASH survey (Carlin et al. 2016) aimed at finding satellite companions of LMC analogs. In a first search around NGC 2403 one dwarf galaxy was discovered, increasing the number of known NGC 2403 satellites to two. The flat part of the rotation curves of all these low-mass spiral galaxies reaches between vrot, flat = 75 and 131 km s−1, which sets them apart from galaxies like the Milky Way (Fich et al. 1989) or NGC 253 (Lucero et al. 2015), with significantly higher rotation velocities in the range between 200 < vrot, flat < 220 km s−1. We have compiled the values for these low-mass spiral galaxies in Table 2.
Low-mass spiral galaxies and their number of satellite galaxies within the virial radius.
How do the observed number of possible dwarf satellites compare with predictions from the current ΛCDM model of cosmology? Dooley et al. (2017) has calculated the expected number of satellites with masses higher than 105M⊙. This mass limit coincides with the depths reached in the various surveys allowing an approximately direct comparison (because the completeness to this limit has still not been fully reached), underestimating the total abundance of observed satellite galaxies. In Table 2 and Fig. 4 we present the number of expected and observed satellites for the stellar-to-halo mass models by Brook et al. (2014) and Garrison-Kimmel et al. (2017). They correspond to the low and high end of the estimates. For the Brook model, the number of possible dwarf galaxies coincides, for all seven of the systems studied here, with the 80% confidence interval of Dooley et al. (2017). However, there is a systematic trend. The observed satellite number for most of the low-mass host galaxies is at the lower end of the ΛCDM predictions. The difference is even more evident compared to the predictions from the GK17 model. Half of the systems seem to differ from the observations. This can be interpreted in two ways: either ΛCDM is over-producing massive subhalos or, more likely, some dwarf satellites have been overlooked in all these surveys. The former is a known problem in simulations (Garrison-Kimmel et al. 2014), while the latter is observationally unavoidable because some dwarf galaxy satellites are potentially obscured by the host galaxy or other sources (i.e., cirrus, bright stars, large background galaxies, or noise), or are simply too faint to be detectable. This incompleteness becomes an even larger problem towards the faint end of the luminosity function where larger numbers of smaller dwarf galaxies are expected. For NGC 24, the automated detection limit is at −10.9 mag, which translates into a stellar luminosity of 17 × 105L⊙ (with an absolute r-band luminosity of the Sun of 4.61, Willmer 2018). This is still a factor of ten higher than what was used in the predictions by Dooley et al. (2017), although we note that the dwarf galaxy candidate dw0009-25 has a luminosity of −8.7 mag at the distance of NGC 24, corresponding to 2 × 105L⊙, so “in the ballpark” of the luminosity limit. For a statistically robust comparison the luminosity function should be complete down to ≈ − 8 mag or below (complete in the sense that both the depth and the recovery rate are of high enough quality to be certain that all satellites were observed). So the most natural explanation for any deviation from the predictions is that the currently missing satellites are in this incomplete luminosity range. However, for NGC 2403 a sufficient depth was reached, but the field of view was too small to cover its virial radius, and thus the survey lacks the full coverage of the satellite system. There could be a handful of dwarf galaxies still residing outside the survey footprint (Carlin et al. 2016). The same is true for M 33, where only up to one-half of the virial radius was covered by deep imaging from the PAndAS survey (Martin et al. 2013; see, e.g., Fig. 1 in Patel et al. 2018).
 |
Fig. 4. Predicted (gray boxes) and observed (red lines) number of satellites as a function of the rotation curve of the host galaxy. For the predictions, the assumed stellar-to-halo mass model by Brook et al. (2014) and Garrison-Kimmel et al. (2017) in Dooley et al. (2017) are employed. |
6. Summary and conclusion
The Sculptor group is the closest galaxy aggregate to the Milky Way, and thus extends over a large area of the sky. With the Dark Energy Camera and in the g and r bands, we observed a 72 deg2 area in the eastern part of the Sculptor group. This region also encloses the two low-mass spiral galaxies NGC 24 and NGC 45 of the Local Volume, which are further in the background and therefore unrelated to the Sculptor group. We searched for low surface brightness dwarf galaxies employing two different strategies. We visually inspected all CCD images by eye and we applied automatic detection methods to find the dwarf galaxies. To test the level of completeness for the search we injected artificial dwarf galaxies and found them to be 50% complete down to 18.2 mag or Mr ≈ −11 to −10 mag. In our visual search we found only two dwarf galaxy candidates; they are in projection closest to NGC 24. These candidate were not picked up by the automated detection algorithm due to the proximity to a background galaxy in one case, and to its faint luminosity in the other. The latter case is noteworthy, as it shows that a visual search for dwarf galaxies can reach a deeper limit than the automated one. The physical properties of the candidates are compatible with the scaling relations defined by known dwarf galaxies (Habas et al. 2020), independent of the association with the two background Local Volume galaxies or the Sculptor group. Follow-up observations are needed to pin down their true host galaxy memberships via distance measurements (Carlsten et al. 2019; Müller et al. 2019a; Monelli & Trujillo 2019).
We compared the observed number of dwarf galaxy candidates around NGC 24 and NGC 45, and around five other well-studied low-mass spiral galaxies (NGC 1156, NGC 2403, NGC 5023, M 33, and the LMC) to predictions from high-resolution dark matter simulations employing different stellar-to-halo mass models. We find that for the mass model by Brook et al. (2014) the observed abundance of dwarf galaxies generally follows the predictions, but it is still systematically on the lower end. As we are dealing with low number statistics the difference could either arise from observational biases or be the first evidence of a true tension between the observed and predicted satellite population for low-mass spiral galaxies. For the Garrison-Kimmel et al. (2017) model there seems to be an overprediction of satellites and the tension becomes more evident. The strongest disagreement is found for the most luminous sample galaxy NGC 2403. It will be interesting to see whether this trend persists once the environments of more low-mass spirals have been carefully investigated, for example by the MADCASH survey (Carlin et al. 2016), or whether it is an observational bias due to the incompleteness kicking in at the low end of the luminosity function. Regarding this aspect, it is interesting that a recent Hubble Space Telescope study of low-mass spiral galaxies at redshifts 0.1 to 0.8 finds good agreement between the observed luminosity function down to MV = − 15 mag and the predicted abundance of satellites (Roberts et al. 2020). Furthermore, Carlsten et al. (2020) finds that the abundance of satellites of more massive Local Volume galaxies is in good agreement between the observed and expected number of satellites. This is compatible with our earlier assessment of the Cen A group, where we found that the luminosity function matches the prediction within the 90% confidence interval (Müller et al. 2019b). This indicates that in general, the luminosity function is well described by our current model of cosmology.
Acknowledgments
We thank the referee for the constructive report, which helped to clarify and improve the manuscript. We also thank Igor Karachentsev for his comments on the number of satellites. O.M. wants to thank the Swiss National Science Foundation for financial support. H.J. acknowledges support from the Australian Research Council through the Discovery Project DP150100862.
References
- Barbary, K. 2016, J. Open Source Softw., 1, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Barbosa, C. E., Zaritsky, D., Donnerstein, R., et al. 2020, ApJS, 247, 46 [CrossRef] [Google Scholar]
- Belokurov, V., Walker, M. G., Evans, N. W., et al. 2010, ApJ, 712, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Bennet, P., Sand, D. J., Crnojević, D., et al. 2019, ApJ, 885, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, eds. D. A. Bohlender, D. Durand, T. H. Handley, et al., ASP Conf. Ser., 281, 228 [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1988, ARA&A, 26, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Merrifield, M. 1998, Galactic Astron. (Princeton, NJ: Princeton University Press) [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [CrossRef] [Google Scholar]
- Bradley, L., Sipőcz, B., Robitaille, T., et al. 2019, https://doi.org/10.5281/zenodo.4044744 [Google Scholar]
- Brook, C. B., Di Cintio, A., Knebe, A., et al. 2014, ApJ, 784, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, W., Sheen, Y.-K., Park, H. S., et al. 2020, ApJ, 891, 18 [CrossRef] [Google Scholar]
- Carlin, J. L., Sand, D. J., Price, P., et al. 2016, ApJ, 828, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsten, S. G., Beaton, R. L., Greco, J. P., & Greene, J. E. 2019, ApJ, 879, 13 [CrossRef] [Google Scholar]
- Carlsten, S. G., Greco, J. P., Beaton, R. L., & Greene, J. E. 2020, ApJ, 891, 144 [CrossRef] [Google Scholar]
- Chemin, L., Carignan, C., Drouin, N., & Freeman, K. C. 2006, AJ, 132, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Chiboucas, K., Karachentsev, I. D., & Tully, R. B. 2009, AJ, 137, 3009 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, Y., van Dokkum, P., Danieli, S., et al. 2018, ApJ, 868, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E. 2003, MNRAS, 342, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., Thilker, D., Zibetti, S., Giovanardi, C., & Salucci, P. 2014, A&A, 572, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crnojević, D., Sand, D. J., Caldwell, N., et al. 2014, ApJ, 795, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Daigle, O., Carignan, C., Amram, P., et al. 2006, MNRAS, 367, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, A. B., Nierenberg, A. M., Peter, A. H. G., et al. 2020, ArXiv e-prints [arXiv:2003.08352] [Google Scholar]
- Dicaire, I., Carignan, C., Amram, P., et al. 2008, MNRAS, 385, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Dooley, G. A., Peter, A. H. G., Carlin, J. L., et al. 2017, MNRAS, 472, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., & Belokurov, V. A. 2020, MNRAS, 495, 2554 [CrossRef] [Google Scholar]
- Fich, M., Blitz, L., & Stark, A. A. 1989, ApJ, 342, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Frenk, C. S., & White, S. D. M. 2012, Ann. Phys., 524, 507 [CrossRef] [Google Scholar]
- Garrison-Kimmel, S., Boylan-Kolchin, M., Bullock, J. S., & Lee, K. 2014, MNRAS, 438, 2578 [NASA ADS] [CrossRef] [Google Scholar]
- Garrison-Kimmel, S., Wetzel, A., Bullock, J. S., et al. 2017, MNRAS, 471, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Geha, M., Wechsler, R. H., Mao, Y.-Y., et al. 2017, ApJ, 847, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Greco, J. P., Greene, J. E., Strauss, M. A., et al. 2018, ApJ, 857, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Habas, R., Marleau, F. R., Duc, P.-A., et al. 2020, MNRAS, 491, 1901 [Google Scholar]
- Javanmardi, B., & Kroupa, P. 2020, MNRAS, 493, L44 [CrossRef] [Google Scholar]
- Javanmardi, B., Martinez-Delgado, D., Kroupa, P., et al. 2016, A&A, 588, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Javanmardi, B., Raouf, M., Khosroshahi, H. G., et al. 2019, ApJ, 870, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Jerjen, H., Freeman, K. C., & Binggeli, B. 1998, AJ, 116, 2873 [NASA ADS] [CrossRef] [Google Scholar]
- Jerjen, H., Binggeli, B., & Freeman, K. C. 2000, AJ, 119, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Kamphuis, P., Rand, R. J., Józsa, G. I. G., et al. 2013, MNRAS, 434, 2069 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I., & Petit, M. 1990, A&AS, 86, 1 [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Suchkov, A. A., & Grebel, E. K. 2000, A&AS, 145, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Grebel, E. K., Sharina, M. E., et al. 2003, A&A, 404, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Riepe, P., Zilch, T., et al. 2015, Astrophys. Bull., 70, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Jerjen, H., Mackey, D., Da Costa, G. S., & Milone, A. P. 2015a, ApJ, 804, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Jerjen, H., Milone, A. P., Mackey, D., & Da Costa, G. S. 2015b, ApJ, 803, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Jerjen, H., Mackey, D., Da Costa, G. S., & Milone, A. P. 2016, ApJ, 820, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Kraan-Korteweg, R. C., & Tammann, G. A. 1979, Astron. Nachr., 300, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
- Loveday, J., Peterson, B. A., Maddox, S. J., & Efstathiou, G. 1996, ApJS, 107, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Lucero, D. M., Carignan, C., Elson, E. C., et al. 2015, MNRAS, 450, 3935 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., Schlafly, E. F., Finkbeiner, D. P., et al. 2016, ArXiv e-prints [arXiv:1612.05242] [Google Scholar]
- Martin, N. F., McConnachie, A. W., Irwin, M., et al. 2009, ApJ, 705, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Ibata, R. A., McConnachie, A. W., et al. 2013, ApJ, 776, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, A., van Dokkum, P., & Abraham, R. 2014, ApJ, 787, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Minchin, R. F., Momjian, E., Auld, R., et al. 2010, AJ, 140, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., & Trujillo, I. 2019, ApJ, 880, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Müller, O., Jerjen, H., & Binggeli, B. 2015, A&A, 583, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Jerjen, H., & Binggeli, B. 2017, A&A, 597, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Jerjen, H., & Binggeli, B. 2018, A&A, 615, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Rich, R. M., Román, J., et al. 2019a, A&A, 624, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Ibata, R., Rejkuba, M., & Posti, L. 2019b, A&A, 629, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Rejkuba, M., Pawlowski, M. S., et al. 2019c, A&A, 629, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, H. S., Moon, D.-S., Zaritsky, D., et al. 2017, ApJ, 848, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, E., Carlin, J. L., Tollerud, E. J., Collins, M. L. M., & Dooley, G. A. 2018, MNRAS, 480, 1883 [CrossRef] [Google Scholar]
- Peñarrubia, J., Gómez, F. A., Besla, G., Erkal, D., & Ma, Y.-Z. 2016, MNRAS, 456, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
- Prole, D. J., van der Burg, R. F. J., Hilker, M., & Davies, J. I. 2019, MNRAS, 488, 2143 [NASA ADS] [Google Scholar]
- Radburn-Smith, D. J., de Jong, R. S., Seth, A. C., et al. 2011, ApJS, 195, 18 [Google Scholar]
- Richardson, J. C., Irwin, M. J., McConnachie, A. W., et al. 2011, ApJ, 732, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, D. M., Nierenberg, A. M., & Peter, A. H. G. 2020, ArXiv e-prints [arXiv:2008.05479] [Google Scholar]
- Sand, D. J., Crnojević, D., Strader, J., et al. 2014, ApJ, 793, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 457, 1931 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes (Observatorio Astronomico, Universidad Nacional de Cordoba) [Google Scholar]
- Simon, J. D., & Geha, M. 2007, ApJ, 670, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C. M., Grand, R. J. J., Gómez, F. A., et al. 2018, MNRAS, 478, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Smercina, A., Bell, E. F., Price, P. A., et al. 2018, ApJ, 863, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. A., Eigenthaler, P., Puzia, T. H., et al. 2018, ApJ, 867, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Teeninga, P., Moschini, U., & Trager, S. 2013, Power, 2, 1 [Google Scholar]
- Teeninga, P., Moschini, U., Trager, S. C., & Wilkinson, M. H. 2015, International Symposium on Mathematical Morphology and Its Applications to Signal and Image Processing (Springer), 157 [Google Scholar]
- Tikhonov, N. A., Galazutdinova, O. A., & Drozdovsky, I. O. 2005, A&A, 431, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toloba, E., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 816, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Trentham, N., & Tully, R. B. 2002, MNRAS, 335, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., & Gruendl, R.DES Project 2014, in Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, ASP Conf. Ser., 485, 379 [Google Scholar]
- van der Marel, R. P., & Kallivayalil, N. 2014, ApJ, 781, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2017, A&A, 608, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willmer, C. N. A. 2018, ApJS, 236, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, C., Kotulla, R., Lisker, T., et al. 2019, ApJS, 245, 10 [Google Scholar]
All Tables
Low-mass spiral galaxies and their number of satellite galaxies within the virial radius.
All Figures
 |
Fig. 1. Field of the Sculptor group. The small black dots correspond to dwarf galaxies in the Sculptor group with its main galaxy NGC 253 (large black dot). The small gray dots are background dwarf galaxies, which are still within the Local Volume (D < 11 Mpc. The two large gray dots are the two LSB giants NGC 24 and NGC 45. The red dots are our dwarf galaxy candidates dw0009-25 and dw0010-25. The gray area corresponds to our survey footprint. |
| In the text | |
 |
Fig. 2. Stacked gr-band images of the newly discovered dwarf galaxy candidates dw0009-25 (left) and dw0010-25 (right). North is to the top, east to the left, and the vertical length of the images corresponds to one arcmin. dw0009-25 was detected close to the CCD edge. |
| In the text | |
 |
Fig. 3. Result from the artificial dwarf galaxy test with MTObjects showing the recovery rate (color scheme) as a function of total apparent magnitude mr and half-light radius reff. The red line indicates the lower surface brightness cut (22 mag arcesc−2), the white line the estimated completeness at 50% (27.3 mag arcesc−2), and the dashed white lines the 75% (26.7 mag arcsec−2) and 25% (27.7 mag arcsec−2) limit. The black dot indicates the known dwarf galaxy Sculptor-dE1. |
| In the text | |
 |
Fig. 4. Predicted (gray boxes) and observed (red lines) number of satellites as a function of the rotation curve of the host galaxy. For the predictions, the assumed stellar-to-halo mass model by Brook et al. (2014) and Garrison-Kimmel et al. (2017) in Dooley et al. (2017) are employed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.