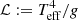| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202345847 | |
| Published online | 16 May 2023 | |
Evolution of rotating massive stars with new hydrodynamic wind models
1
Departamento de Ciencias, Facultad de Artes Liberales, Universidad Adolfo Ibáñez, Av. Padre Hurtado 750, Viña del Mar, Chile
e-mail: alex.gormaz@uv.cl
2
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, 782-0436 Santiago, Chile
3
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warsaw, Poland
4
Geneva Observatory, University of Geneva, Maillettes 51, 1290 Sauverny, Switzerland
5
Instituto de Física y Astronomía, Universidad de Valparaíso, Av. Gran Bretaña 1111, Casilla, 5030 Valparaíso, Chile
6
Centro de Astrofísica, Universidad de Valparaíso, Av. Gran Bretaña 1111, Casilla, 5030 Valparaíso, Chile
Received:
5
January
2023
Accepted:
21
March
2023
Context. Mass loss due to radiatively line-driven winds is central to our understanding of the evolution of massive stars in both single and multiple systems. This mass loss plays a key role in modulating the stellar evolution at different metallicities, particularly in the case of massive stars with M* ≥ 25 M⊙.
Aims. We extend the evolution models introduced in Paper I, where the mass-loss recipe is based on the simultaneous calculation of the wind hydrodynamics and the line acceleration, by incorporating the effects of stellar rotation.
Methods. As in Paper I, we introduce a grid of self-consistent line-force parameters (k, α, δ) for a set of standard evolutionary tracks using GENEC. Based on this grid, we analysed the effects of stellar rotation, CNO abundances, and He/H ratio on the wind solutions to derive additional terms for the recipe with which we predict the self-consistent mass-loss rate, Ṁsc. With this, we generated a new set of evolutionary tracks with rotation for MZAMS = 25, 40, 70, and 120 M⊙, and for metallicities Z = 0.014 (Galactic) and 0.006 (Large Magellanic Cloud).
Results. In addition to the expected correction factor due to rotation, the mass-loss rate decreases when the surface becomes more helium rich, especially in the later moments of the main-sequence phase. The self-consistent approach gives lower mass-loss rates than the standard values adopted in previous GENEC evolution models. This decrease strongly affects the tracks of the most massive models. Weaker winds allow the star to retain more mass, but also more angular momentum. As a consequence, weaker wind models rotate faster and show a less efficient mixing in their inner stellar structure at a given age.
Conclusions. The self-consistent tracks predict an evolution of the rotational velocities through the main sequence that closely agrees with the range of v sin i values found by recent surveys of Galactic O-type stars. As subsequent implications, the weaker winds from self-consistent models also suggest a reduction of the contribution of the isotope 26Al to the interstellar medium due to stellar winds of massive stars during the MS phase. Moreover, the higher luminosities found for the self-consistent evolutionary models suggest that some populations of massive stars might be less massive than previously thought, as in the case of Ofpe stars at the Galactic centre. Therefore, this study opens a wide range of consequences for further research based on the evolution of massive stars.
Key words: stars: evolution / stars: massive / stars: mass-loss / stars: rotation / stars: winds / outflows
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The evolution of massive stars is an important topic in stellar astrophysics. Some of them are the progenitors of core-collapse supernova events and give birth to neutron stars and black holes (Heger et al. 2003). Massive stars are also important for the study of nucleosynthesis, for the production of ionising flux, for feedback due to wind momentum, for studies of star formation history, and for galaxy evolution.
Massive stars with M* ≳ 25 M⊙ are characterised by strong stellar winds and high mass-loss rates (Ṁ), which determine the evolution of the star, such as the phases involving luminous blue Variables (LBV) and Wolf-Rayet (WR) stars (Groh et al. 2014). The wind properties through all these stages constrain the type of core-collapse process the star will experience at the end of its life, and the final mass of the remnant (Belczynski et al. 2010). This last item is relevant because theoretical masses of stellar black holes need to agree with those measured by gravitational waves, in merger events detected by the Advanced-LIGO interferometers (Abbott et al. 2016). The study of stellar winds has further implications that reach far beyond stellar astrophysics. For instance, stellar winds from numerous evolved massive stars collide to produce the plasma that fills up the interstellar medium in the Galactic centre (e.g. Cuadra et al. 2008, 2015; Ressler et al. 2018, 2020; Calderón et al. 2020a). The properties of the stellar winds determine whether the plasma is able to cool and form clumps, which affects the accretion process onto the Galactic supermassive black hole, Sgr A* (Cuadra et al. 2005; Calderón et al. 2016, 2020b). Therefore, a proper determination of the stellar winds is needed to correctly interpret the images of the black hole silhouette obtained by the Event Horizon Telescope Collaboration (2022). These examples highlight that theoretical calculations for the stellar winds can even influence the field of relativistic astrophysics.
In the past decade, computational codes such as MESA (Paxton et al. 2019) and the Geneva evolution code (hereafter GENEC, Eggenberger et al. 2008) have been used to study stellar evolution. The recipe for theoretical mass-loss rate varies, depending on the stellar evolution stage and the region of the Hertzsprung-Russel diagram (HRD). For O-type main-sequence (MS) stars, the most commonly adopted recipe has been the so-called Vink formula (Vink et al. 2001). However, diagnostics of mass-loss rates performed in recent years considered that values from Vink’s formula are overestimated by a factor of ∼3 (Bouret et al. 2012; Šurlan et al. 2013; Vink 2022), and therefore, the quest has been the development of evolution models that adopt more updated and accurate recipes for the mass-loss rate. In this context, we mention the studies by Björklund et al. (2023) using MESA, and by Gormaz-Matamala et al. (2022a, hereafter Paper I) using GENEC.
In Paper I, we developed new evolution models for stars born with masses Mzams ≥ 25 M⊙, introducing a new recipe for the theoretical mass-loss rate based on the self-consistent m-CAK wind solutions from Gormaz-Matamala et al. (2019, 2022b). These new self-consistent tracks show that stars retain more mass through their evolution, therefore remaining larger and more luminous compared with models for massive stars using Vink’s formula for Ṁ (Ekström et al. 2012; Georgy et al. 2013; Eggenberger et al. 2021). A similar result is obtained by Björklund et al. (2023), where evolution models adopting new mass-loss rates are shifted to higher luminosities in the HRD. It is important to remark that to our knowledge, Björklund et al. (2023) and Gormaz-Matamala et al. (2022a) are the first studies on developing tracks for stellar evolution of massive stars adopting a self-consistent treatment for the stellar wind.
In this work, we extend the self-consistent evolutionary tracks introduced in Paper I by including rotation in our models. Rotation is important because it modifies the mass-loss rate and the surface abundances due to the rotational mixing (Maeder & Meynet 2010), and because it causes the star not only to lose mass, but also angular momentum through the stellar wind (Georgy et al. 2011; Keszthelyi et al. 2017). Because of the additional details that are to be considered in the analysis of our results, this work includes only Galactic (Z = 0.014) and LMC (Z = 0.006) metallicities. We leave the supra-solar (Z > 0.014) and SMC and lower-metallicity (Z ≤ 0.002) cases to forthcoming studies.
This paper is organised as follows. Section 2 summarises the most relevant results and conclusions obtained from our self-consistent evolutionary tracks in Paper I. Section 3 introduces the updates on Ṁsc to account for the effects of rotation. Section 4 presents the new evolution models that adopt self-consistent winds, whereas their comparison with observational diagnostics is analysed in Sect. 5. In Sect. 6 we discuss the implications of these new evolution models on the Galactic scale. Finally, the conclusions of this work are summarised in Sect. 7.
2. Self-consistent evolution models
We call the evolution models that adopt a self-consistent recipe for the mass-loss rate self-consistent evolutionary tracks. Self-consistency implies that the wind hydrodynamics (i.e. the velocity and density profiles for the wind) are calculated in agreement with the radiative acceleration (i.e. the acceleration over the wind particles due to the stellar radiation). As a consequence, the mass-loss rate is a direct solution for the wind under a specific set of stellar parameters (temperature, radius, mass, and abundances) without assuming any additional condition a priori for the wind (e.g. a velocity law or a v∞/vesc ratio). For this purpose, we simultaneously calculated the line-acceleration gline by means of the so-called line-force parameters (k, α, δ) from m-CAK theory (Castor et al. 1975; Abbott 1982; Pauldrach et al. 1986), whereas we calculated the hydrodynamics by solving the stationary equation of motion for the wind using the code HYDWIND (Curé 2004) for different sets of stellar parameters for massive stars. This iterative procedure is hereafter named m-CAK prescription. It was introduced in Gormaz-Matamala et al. (2019) and has been demonstrated to provide values for Ṁ that are of the same order of magnitude as those obtained with self-consistent NLTE studies in the co-moving frame, such as Krtička & Kubát (2017, 2018) or Gormaz-Matamala et al. (2021). Moreover, the wind hydrodynamics used as input in the NLTE radiative transport code is able to reproduce reliable synthetic spectra that agree with the observations (Gormaz-Matamala et al. 2022b).
However, although the calculation of the line-force parameters has been extended for even cooler temperatures (Lattimer & Cranmer 2021; Poniatowski et al. 2022), in Gormaz-Matamala et al. (2019), our m-CAK prescription was restricted into the range of stellar parameters in which (k, α, δ) can be assumed to be constants. This is an important consideration because even though line-force parameters have commonly been treated as constants (Shimada et al. 1994; Noebauer & Sim 2015), some studies have suggested that the values for k, α, and δ may radially change with the wind (Schaerer & Schmutz 1994; Puls et al. 2000). About this, Gormaz-Matamala et al. (2022b, Sect. 2) performed an quantitative analysis of the standard deviation and numerical errors in the calculation of our line-force parameters, and by extension, of the error margins for the self-consistent wind parameters Ṁ and v∞. They reported that uncertainties for (k, α, δ) can be neglected for stars with Teff ≥ 30 kK and log g ≥ 3.2. Therefore, we set these thresholds as the range of validity for our m-CAK prescription.
Thus, the self-consistent mass-loss rate (Ṁsc) derived from the m-CAK prescription is parametrised as a function of stellar parameters as shown in Eq. (7) from Paper I,
where w, x, y, and z are defined as
In addition to minimising the separation with respect to the real calculated wind solution by line-force parameters, this intervariable fitting allows a deeper examination of the dependence of the mass-loss rate on stellar parameters. As an example, we found from Eq. (1) that the dependence on metallicity does not follow the classical exponential law Ṁ ∝ Za with a constant exponent, but with a ranging from ∼0.53 for M* ∼ 120 M⊙ to ∼1.02 for M* ∼ 25 M⊙. In other words, we can approximate this Z-dependence for the mass-loss rate as an intrinsic relation of stellar mass, as
An analogous result, but for an intrinsic luminosity dependence, was found by Krtička & Kubát (2018) for their global wind models, where the exponent for the metallicity was less steep for higher stellar luminosity (and subsequently, stellar mass). Explanations of this intrinsic mass dependence may rely on the fact that the more massive the star, the nearer it is to the Eddington limit. In this case, the contribution of the continuum to the radiative acceleration grad is expected to increase in the decline of the line driving (see Eq. (6) from Gormaz-Matamala et al. 2021). The effect of the continuum is less dependent on metallicity because it does not involve interaction between the radiative field and absorption lines. This condition for the mass-loss rate was previously pointed out by Gräfener & Hamann (2008) for WNL stars, where the Z-dependence was weaker closer to the Eddington limit (i.e. more mass). All in all, we can state that Eq. (2) is an important step for understanding the dependence on metallicity for the mass-loss rates in the earlier evolutionary stages of massive stars.
Our new recipe for the mass-loss rate is implemented in the GENEC code, which runs stellar evolutionary models to explain and predict the physical properties of massive stars (Eggenberger et al. 2008). We used the same prescriptions as described in Ekström et al. (2012), that is, solar abundances from Asplund et al. (2005, 2009), opacities from Iglesias & Rogers (1996), and an overshoot parameter αov ≃ 0.10, except for the mass-loss rates. The self-consistent m-CAK prescription has already been incorporated in GENEC for stars satisfying Teff ≥ 30 kK and log g ≥ 3.2. Below these thresholds, the recipe for the mass-loss rate reverts to Vink’s formula.
Because self-consistent mass-loss rates are a factor of ∼3 lower than Vink’s formula at the beginning of the MS (i.e. for Teff ≳ 40 kK and log g ∼ 4.0; see Gormaz-Matamala et al. 2022b), self-consistent evolution models predict that stars will retain more mass during their H-core burning stage and therefore are larger and more luminous. These changes are proportional to the initial mass of the star; from important differences in the final stellar properties at the end of the MS for Mzams = 120 M⊙, to almost negligible differences for Mzams = 25 M⊙. Moreover, evolution models adopting Ṁsc predict less production of the isotope aluminium-26, which means that massive stars contribute less to feeding the interstellar medium with this isotope than other sources (Palacios et al. 2005; Wang et al. 2009).
These results are important, but still represent only a first glance of the implications of the self-consistent wind models for stellar evolution. The next step is the incorporation of rotation. Stellar rotation is important for stellar evolution because of two reasons. First, because the angular momentum in the core at the time of core collapse may strongly impact the final stages of a massive star (Yoon et al. 2006). Powerful stellar winds not only cause stars to lose mass, but also angular momentum, subsequently affecting the rotation and the evolution of the star (Georgy et al. 2011; Keszthelyi et al. 2017). Second, because rotational mixing (Maeder & Meynet 2010) changes the distribution of the abundances of the elements inside the star and in particular at the surface (see e.g. Brott et al. 2011; Ekström et al. 2012). The changes in the abundances at the surface is particularly interesting because modification in the chemical composition of the atmosphere induces variations in the line acceleration and therefore in the self-consistent mass-loss rate. This has either not been considered or neglected by previous authors (Björklund et al. 2023). For this reason, it is necessary to study the influence of rotation on the m-CAK prescription before running new evolution models with rotation adopting Ṁsc.
3. Rotation at the m-CAK prescription
3.1. Enhancing mass loss due to rotational effects
Models by GENEC are computed based on the formula by Vink (Vink et al. 2001) with the correcting factor induced by rotation as given by Maeder & Meynet (2000, hereafter MM00), that is,
where Ṁ(0) is the mass-loss rate without rotation, α is the line-force parameter from CAK theory, ω is the angular velocity at the stellar surface, and ΓEdd is the Eddington factor,
with κ being the total opacity. Equation (3) introduces a correction factor that is independent of the adopted recipe for the mass-loss rate without rotation; in other words, Ṁ(0) can be computed either from Vink’s formula or from Eq. (1). Ṁ(ω) results from an integration over the surface, and the integration accounts for the change in local mass-loss rate with the latitude.
Equation (3) incorporates the impacts on mass-loss rate produced not only by rotation, but also by the radiative acceleration due to the continuum (hence the Eddington factor) through the so-called ΩΓ limit. This formulation implies that the stellar break-up or Ω limit (i.e. when the centrifugal forces compensate for gravity in a rotating star) is reached for reduced rotation velocities if Γ is large enough. The velocity associated with this break-up is the so called critical rotational speed,
and hence, the rotation of the star is commonly expressed as a dimensionless ratio of the rotational velocity and this critical value as
On the other hand, the m-CAK prescription incorporates rotational effects in the hydrodynamic solution calculated by HYDWIND (Curé 2004), also using Ω as an input. HYDWIND solves the equation of motion for the stationary standard line-driven theory,
by finding the eigenfunction that satisfies the velocity profile, v = v (r), and the eigenvalue, which is proportional to the mass-loss rate, Ṁ (Curé & Rial 2007). The rotation factor Ω is implicitly included in Eq. (7) by means of vϕ = vrotR*/r, whereas the additional terms are the same as described by Araya et al. (2017, 2021) or Gormaz-Matamala et al. (2022b). In this work, we use moderate to intermediate values of Ω (=0.4), therefore all our wind solutions are in the fast-wind regime and not in the Ω slow-wind regime, which starts approximately from Ω ≳ 0.75 (Araya & Curé 2018).
In order to evaluate the effect of the rotation on the self-consistent wind solutions, we repeated the method of Paper I and ran evolutionary rotating models in GENEC for initial masses of 120, 70, 40, and 25 M⊙ adopting Vink’s formula for these tracks, hereafter original tracks, as shown in Fig. 1. Then we selected a set of representative points on these original tracks, and based on their stellar parameters (Teff, log g, R*/R⊙, and Ω), we calculated the line-force parameters (k, α, and δ) and their respective self-consistent wind parameters Ṁsc and v∞, sc. The initial rotational velocity for all evolution models was Ω = 0.4, as in Ekström et al. (2012). The results are tabulated in Table 1, where in addition to the former columns already included in Tables 2–4 from Paper I, we add the rotation factor Ω as an additional stellar parameter for the input. For each one of the points, we calculated an independent solution for (k, α, and δ) for the tabulated Ω, but also for Ω = 0.0 (i.e. without rotation), with their respective self-consistent solutions for terminal velocity and mass-loss rate. The difference in the self-consistent mass loss due to the incorporation of rotation is expressed as the ratio Ṁ(Ω)/Ṁ(0), which is compared with the correction factor predicted by MM00 (i.e. Eq. (3)). Here, we found that both approaches for the rotational effects over Ṁ produce similar results, which is remarkable considering the error bars associated with the self-consistent mass-loss rate. Based on this outcome, we decided to perform our new evolutionary tracks keeping Eq. (3) as correction factor for Ṁsc.
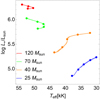 |
Fig. 1. Evolutionary tracks across the HRD for models with rotation using ṀVink and Z/Z⊙ = 1.0, covering the main-sequence stage, hereafter original tracks. Circles represent the location of the selected stellar models that are to be tabulated in Table 1. |
The other physical ingredients related to rotation were the same as in Ekström et al. (2012), Georgy et al. (2013), and Eggenberger et al. (2021). Angular momentum was transported by an advective equation as described in Zahn (1992). The horizontal and vertical shear diffusion coefficients were from Zahn (1992) and Maeder (1997), respectively.
3.2. Variation in abundances
In addition to the stellar parameters such as temperature, surface gravity, radius, and rotation, we include in Table 1 the values for the abundances of helium (expressed as a fraction of the hydrogen abundance by number) and the individual abundances of carbon, nitrogen, and oxygen (expressed as a fraction of the solar abundances). Because of the nature of the CNO-cycle, the abundances of helium and nitrogen increase over time, whereas carbon and oxygen decrease (Przybilla et al. 2010). The chemical composition of the surface is enriched in material that is processed in the core by rotational mixing in the outer radiative envelope. Because we assumed that chemical composition in the stellar wind is exactly the same as in the photosphere, the chemical composition of the stellar wind is altered. The question that arises here is whether these alterations in the wind chemical abundances affect the line-acceleration and afterwards the self-consistent mass-loss rate.
To solve this question, we artificially altered the individual abundances for the He and CNO elements from our stellar models of Table 1, and then calculated the respective line-force parameters and self-consistent mass-loss rate for each one of the modifications. For example, we compared the Ṁsc for the stellar model P070z10-04 (with N/N⊙ = 10.86) with the expected Ṁsc if N/N⊙ = 1, whereas the other individual abundances and the remaining stellar parameters (Teff, log g, etc.) were kept fixed. The same was performed for the helium: We compared the self-consistent mass-loss rate for He/H = 0.20, for instance, with the expected value for Ṁsc if He/H = 0.085. These differences are expressed as
with Ṁsc the mass losses tabulated in Table 1, and Ṁsc,⊙ the self-consistent mass-loss rate calculated if the abundance of the evaluated element were solar.
The results of these modifications of Ṁsc are displayed in Fig. 2a for changes in the He/H ratio, and in Fig. 2b for modifications of the CNO elements. The variation of each one of the CNO elements even by a factor of ∼10 barely affects the Ṁsc, keeping the difference Δ log Ṁsc close to zero. The differences in the mass-loss rate are indeed just of the order of ±0.05 in log scale (∼12% of Ṁsc), which is smaller than the error bars shown in Table 1. Conversely, the increase in the He/H ratio causes Ṁsc to decrease in larger magnitudes.
 |
Fig. 2. Differences in the resulting self-consistent mass-loss rate Δlog Ṁsc for the abundances tabulated in Table 1, (a) due to the modification of the He/H ratio with respect to the default He/H = 0.085, and (b) due to the modification of any of the CNO elements with respect to ξ/ξ⊙ = 1.0 (with ξ being carbon, nitrogen, or oxygen, depending on the respective symbol). |
The results from Fig. 2 are quickly explained by their absolute numbers of the evaluated abundances. Even though the CNO abundances change by a factor of ∼10 (compared with the initial values at ZAMS), they still represent a low percentage of the total composition of the star. Conversely, the abundance of helium plays a main role because it grows (in mass fraction) from ∼26% to ∼70%, which significantly changes the mean molecular weight of the wind. Moreover, the helium abundance is involved in the computation of the ratio Ne/ρ and in the radiative acceleration due to Thomson scattering1,
where XHe is the helium abundance by number, Ne is the density of free electrons, and mp is the proton mass (the meaning of the other symbols is detailed in Curé 2004, Sect. 2). Hence, when the helium abundance increases, the number of free electrons is reduced, and then Γ decreases. As a consequence, the effective mass Meff = M*(1 − Γ) becomes higher in Eq. (7), and accordingly, so does the effective gravity, meaning that the line acceleration now is able to remove less material than the stellar wind (i.e. the mass-loss rate decreases). However, it is important to mention that this theoretical analysis is based upon the isolated alteration of the He/H ratio, and therefore, this decrease in the resulting Ṁ does not imply any modifications in temperature or in any other stellar parameter. For this reason, it differs from the Ṁ ∝ XHe relation found by Hamann et al. (1995), which was the result of a global analysis over the wind regime of WR stars.
Thus we decided to introduce an additional variable to the recipe of Eq. (1), based on a simple fit of Fig. 2a,
where (He/H)0 is the He/H ratio at the ZAMS (0.085 from Asplund et al. 2009). Table 1 shows that (He/H)* may grow to ∼0.3 − 0.45 at the end of the self-consistent regime, thus leading to a reduction of the mass-loss rate of ∼30 − 40%. However, as in Paper I, this modification applies only when the self-consistent mass-loss rate is adopted in the evolutionary tracks for Teff ≥ 30 kK and log g ≥ 3.2, and hence the magnitude of the decreasing factor in Ṁ prior to the end of the MS is still unknown, when the hydrogen abundance is X = 0.3 at the surface. Finally, details of the formulae used for both old and new evolution models are summarised in Table 2.
Summary of the formulae implemented for old and new evolutionary tracks.
4. Results
Evolutionary models with rotation, both original and self-consistent, are shown in Fig. 3 in the HR diagram, whereas the rotation and equatorial velocities for tracks adopting both mass-loss recipes are shown in Fig. 4. Additional plots such as the comparison with self-consistent non-rotating models from Paper I, the evolutionary tracks in the log g versus Teff plane, the evolution of the mass-loss rate, the stellar mass and radii, the He/H ratio, the Eddington factor, and the convective core mass are shown in Appendix A. Furthermore, hereafter, all plots comparing new and old recipes of the mass-loss rate use solid lines for models with Ṁsc and dashed lines for models with ṀVink. The main features of the stellar models at the end of the MS, comparing self-consistent tracks with the tracks adopting Vink’s formula (Ekström et al. 2012; Eggenberger et al. 2021), are listed in Table 3.
 |
Fig. 3. HR diagram for the self-consistent evolution models (solid lines), compared with classical evolutionary tracks (darker dashed lines) from Ekström et al. (2012, Z = 0.014) and Eggenberger et al. (2021, Z = 0.006). All plots cover the main sequence and part of the Hertzsprung gap. Self-consistent tracks are marked with two black dots that represent the zero-age main sequence and the switch of the mass-loss recipe from self-consistent to Vink’s formula (when either Teff = 30 kK or log g = 3.2), whereas the TAMS is represented with a black cross. |
Properties of the stellar models at the end of the main sequence.
Overall, compared with Paper I (see Table 8 from Gormaz-Matamala et al. 2022a), we find that the lifetime during the main sequence is ∼18 − 22% longer than for the non-rotating models, regardless of the adopted mass-loss recipe. The difference with non-rotating models is also clear in Fig. A.1, where the evolutionary tracks with and without rotation are compared. The rotating tracks remain in the bluer regions of the HR diagram than the non-rotating tracks. Similar to Paper I, self-consistent mass-loss rates are lower by a factor of about three than the mass-loss rates from Vink’s formula (Fig. A.3), which causes the stars to retain more mass (Fig. A.4) and have larger radii (Fig. A.5) when Ṁsc is adopted. Moreover, in addition to the straightforward differences in the final masses and the final radii, we also observe that the weaker winds from the self-consistent prescription predict weaker surface enrichments of helium and nitrogen at the surface in general, as seen in the last columns of Table 3 and in the evolution of the He/H ratio (Fig. A.6). The only noticeable exception is the model with Mzams = 25 M⊙ and Z = 0.006, which is described in detail in the subsection below.
The self-consistent evolutionary tracks have higher velocities with rotation for all models, as clearly shown in Fig. 4, where we compute equatorial velocities and Ω = veq/vcrit as a function of the core hydrogen abundance from the ZAMS (starting with Xcore ∼ 0.72) until the end of the main sequence. As in Paper I, the largest impact of the new self-consistent mass-loss rates is obtained for the higher initial mass stars: the weaker Ṁsc produces stars that rotate faster. Even though the rotational velocity drops at the TAMS for all models, this braking is slower than the breaking expected for models with the old mass-loss recipe. This weaker braking is more prominent for the low metallicity, where stars with Ṁsc maintain almost constant rotational velocity for a longer time before the final deceleration. This implies that in our regime of metallicities (between Z = 0.006 and Z = 0.014), mass loss is still a prominent process that impacts the evolution of the rotational velocity. The evolution of rotational velocities is explained by the balance between the transport of angular momentum from the convective core (which contracts during the main-sequence stage) to the stellar surface, and the removal of outer layers due to mass loss (Ekström et al. 2008; de Mink et al. 2013). At extremely low metallicities (Z = 0.0002 = 1/35 Z⊙), massive stars increase their vrot because their mass losses are not strong enough to counteract the transport of angular momentum from the contracting core (Szécsi et al. 2015). For Z = 0.006, Ω, which is set initially as = 0.4, also increases up to a constant peak of ∼0.55 before the final decrease as a direct consequence of the initial constancy in the equatorial velocity and of the decrease in the evolution of the critical velocity (Eq. (5)). Weaker winds predict a nearly exponential increase in the stellar radii for all initial masses and both metallicities (Fig. A.5), whereas both the stellar mass and Eddington factor show a line- and metallicity-dependent difference with respect to the models computed with the Vink formula (Figs. A.4 and A.7). Because they are weaker, self-consistent winds therefore cause our evolution models to approach the break-up limit for rotational velocity more closely, in agreement with Ekström et al. (2008), prior to the final drop in vrot at the end of main sequence, in agreement with Szécsi et al. (2015). We discuss some more detailed effects of the use of the new mass-loss rate for the different initial mass models considered in the present work.
 |
Fig. 4. Evolution of surface equatorial velocities and rotation parameter Ω as a function of the mass fraction of hydrogen at the core, which decreases from Xcore ∼ 0.72 at ZAMS to Xcore ∼ 0.05 at the end of the H-core burning stage. The symbols (dots and crosses) have the same meanings as indicated in the caption of Fig. 3. |
4.1. Case Mzams = 120 M⊙
In this range lie the very massive stars (VMS; Yusof et al. 2013), whose properties and evolution have aroused great interest in recent years (Higgins et al. 2022; Sabhahit et al. 2022). Here, the tracks with Z = 0.006 are particularly relevant because the most frequently studied cluster containing VMSs is 30 Dor, which is located in the LMC (Crowther et al. 2010; Bestenlehner et al. 2014).
As in Yusof et al. (2013), we considered that the star becomes a Wolf-Rayet star (i.e. it changes from optically thin to optically thick wind) when its surface hydrogen abundance decreases below 0.3 and Teff > 10 kK. After this point, the mass-loss rate is assumed to follow the recipe from Gräfener & Hamann (2008) for WR winds, generating the discontinuity in Ṁ after the black cross, as observed at Fig. A.3. Before the change in the recipe, the evolution of the self-consistent mass-loss rate proceeded as expected due to the large increment in the He/H ratio (Fig. A.6) as a consequence of Eq. (11). Because of the extreme strength of the winds, the VMS is depleted from 70% of its surface hydrogen even before H is completely exhausted in its core, generating the stars with spectral type WNh (Hamann et al. 2006; Martins & Palacios 2022). This switch not only in the Ṁ prescription, but also in the wind regime (from optically thin to optically thick wind) is also shown in Fig. A.5, where the radius needs to be recalculated after the black crosses based on the wind opacity (see e.g. Meynet & Maeder 2005) due to the absence of a well-defined photosphere (Schaller et al. 1992).
The most remarkable difference between classical and self-consistent tracks in Fig. 3 is the drift redwards (i.e. towards the cool range of temperatures in the HRD) of the self-consistent models since the beginning of the main sequence. For both metallicities, stars with Ṁsc end their MS lifetime as O-type stars at Teff ∼ 40 kK before their temperature suddenly increases and they become WNh stars. We note that the model using the weaker self-consistent Ṁ shows a slightly stronger surface enrichment than the original model in general. This explains why these models evolve to redder regions of the HRD during the MS phase. It is a well-known effect that a star showing a nearly homogeneous internal chemical composition keeps blue colours in the HRD diagram (Maeder 1987). A homogeneous chemical composition can result from very strong internal mixing, from very strong mass losses, or from both processes. In contrast, an internal inhomogeneous composition will produce a redwards evolution on the HRD. The extension to the red is favoured when a larger convective core is present and the radiative envelope is not too efficiently mixed, otherwise, the situation would approach a homogeneous internal composition and the track would remain in the blue region of the HRD (Martinet et al. 2021). A reduction in the mass loss favours redwards tracks. In Fig. 5 we show the diffusion coefficients in the new and old mass-loss rate models in the middle of the MS phase. For the case of 120 M⊙ and Z = 0.014, the model with a lower mass-loss rate has a more massive convective core at this stage, even though it represents a slightly small fraction of the total mass: ∼84% for the self-consistent model, against ∼87% for the old one. This is a result of the higher difference in the mass retained and also of the possibly higher value of the effective diffusion coefficient, Deff, just above the convective core. In the remaining radiative envelope, the values of Deff do not differ much. Because the diffusion timescale varies as R2/Deff, and because the radius of the self-consistent model is larger, the self-consistent model will take a longer time to reach a given level of surface enrichment than the original one. This imposes redder evolutionary tracks for the model with Ṁsc.
 |
Fig. 5. Diffusion factors for convective turbulence (Dconv), shear turbulence (Dsh), and effective turbulence (Deff) as a function of the Lagrangian mass coordinate for our evolution models with Mzams = 120 M⊙ and Z = 0.014, adopting old and new winds at an intermediate point in the main-sequence stage (Xcore = 0.3). Vertical grey lines represent the total mass of both models. The symbols for the solid and dashed lines are the same as in Fig. 3. |
Figure 6a compares the chemical composition of the self-consistent and original models at the end of the MS phase. As expected, the model with the lower mass-loss rate shows the greatest contrasts between the surface and the core composition. Figure 7a shows the variation in the specific angular momentum jr = r2ω in the 120 M⊙ at the beginning and end of the MS phase for the two different mass-loss prescriptions. We recall that in the absence of any angular momentum transport, jr remains constant. The evolution between the beginning and end of the core H-burning phase (a global decrease in jr in the whole star) arises because the transport processes will in general transport angular momentum from the inner to the outer layers of the star. At the surface, the angular momentum is removed by stellar winds, and when the mass-loss rates are lower, jr is therefore larger. By decreasing the mass-loss rate by about a factor of three during the main sequence (compared to Vink’s formula), we obtain that the specific angular momentum is shifted by 0.3 dex upwards when Ṁsc is used, whereas the angular velocity of the core increases by a factor of about two (see Fig. 7b).
 |
Fig. 6. Variation on the logarithmic scale of the mass fraction of hydrogen, helium, and CNO elements as a function of the Lagrangian mass coordinate in solar units in the (a) 120 M⊙ model and (b) the 70 M⊙ model for the two prescriptions of the mass losses studied in the present work at the end of the main-sequence stage. The meaning of the different line styles is the same as in Fig. 3. Vertical grey lines represent the total mass of both models, which correspond to the final masses at the end of MS tabulated in Table 3. |
 |
Fig. 7. Angular properties for the inner structure of our 120 M⊙ model on the ZAMS and at the end of the MS phase for the two prescriptions of the mass losses. (a) Variation in logarithmic scale of the specific angular momentum as a function of the Lagrangian mass coordinate in solar units. (b) Angular velocity in radians per second, also as a function of the Lagrangian mass coordinate. |
Finally, our rotating models reach the WNh stage at Teff ≳ 40 kK for both metallicities. Because we know that stars will increase their temperature through the WR stage, this means that rotating models with Mzams = 120 M⊙ do not cross the temperature regime at ∼25 kK during their MS phase, where the so-called bi-stability jump (Vink et al. 1999) takes place. Because of this, and in contrast to the non-rotating models from Paper I, we do not observe LBV behaviour such as eruptive mass losses in this mass range. The fact that only initially slow rotating models can go through an eruptive mass-loss regime at the end of the main sequence supports the idea that the LBV phenomenon is very rare for very massive stars (Gräfener 2021).
4.2. Case Mzams = 70 M⊙
As before, in addition to the differences in the stellar mass (Fig. A.4), we also observe a divergence bluewards-redwards for the evolution across the HR diagram (Fig. 3). However, unlike the previous case, this time, the beginning of the WR wind stage coincides with the end of the H-core burning, which is shown in Fig. 6b, where hydrogen is depleted in the core at the end of both tracks (standard and self-consistent). Again, the slope of the evolution in mass-loss rate changes (Fig. A.3), this time, with a flattening in Ṁ prior to reaching the second black dot, which is associated with the increase in the He/H ratio (Fig. A.6).
Concerning rotation, the braking in the equatorial velocity only becomes significant after the star has burnt almost half of the hydrogen in its core: Xc ∼ 0.38 for Z = 0.014 and Xc ∼ 0.36 for Z = 0.006, which also represents the peak of Ω ∼ 0.42 for Galactic metallicities and Ω ∼ 0.54 for SMC metallicities (Fig. 4). This is interconnected one more time with the retaining of more specific angular momentum for the models adopting Ṁsc, and with the larger stellar radii (Fig. A.5). The switch in the wind regime from Ṁsc to ṀVink (marked with an abrupt increase in the mass-loss rate after the second black dot of Fig. A.3) causes an important drop in the rotational velocity, which creates some numerical instability, but does not affect the general trend in the evolution we observed for all the rotation models.
Figure 6b shows that the variation in the element abundances across the stellar structure from core to surface is more prominent for the model with Ṁsc, which is evidence that rotational mixing for the weaker wind is less efficient. However, in contrast to the case with Mzams = 120 M⊙, where the inner structure was almost fully homogeneous, now there are remarkable distinctions between core and surface abundances because the mass loss has been less efficient in reducing the mass of the envelope and revealing the inner layers.
The redward drift of the evolutionary tracks for the reduced mass-loss rate models is in line with the results found by Björklund et al. (2023), who implemented a mass-loss recipe derived from the theoretical prescription for wind from Björklund et al. (2021), where Ṁ is also about three times lower than the values obtained from Vink’s formula. In their study, they used MESA to trace the evolutionary track of a star with Mzams = 60 M⊙, vrot, ini = 350 km s−1, and solar metallicity; where they found the drift bluewards at Teff ∼ 26 kK (see their Fig. 6). By an eye inspection of Figs. 3 and A.1, we conjecture that the point of turning bluewards for one of our self-consistent models with 60 M⊙ and Z = 0.014 must be between ∼29 − 31 kK, that is, ∼5 kK hotter than was found by Björklund et al. (2023). This discrepancy is relatively minor considering the differences between GENEC and MESA (see the comparison for the models of these two codes, as done by Agrawal et al. 2022). Therefore, we can conclude that the self-consistent m-CAK prescription for stellar winds predicts evolutionary tracks that agree fairly well with the recent study of Björklund et al. (2023), as expected because both studies are based on mass-loss rates of the same order of magnitude.
4.3. Cases Mzams = 25 and 40 M⊙
The effects of self-consistent mass-loss rates over the evolution of stars within these mass ranges are less pronounced, as shown in Fig. 3 and in the resulting final masses and radii from Table 3. We also observe a redder evolution for the models adopting Ṁsc, but it is still bluer than non-rotating cases (Fig. A.1). The differences in the rotational velocities are also less remarkable, but still follow the same trend as the more massive models. For the case of Z = 0.006 (LMC), we observe that the end of H-burning is reached inside the region in which the self-consistent tracks are valid (Fig. A.2), and therefore, the second dot again overlaps with the cross. Because we observe this situation only with Z = 0.002 (SMC) in the non-rotating cases from the Paper I, it implies that the evolution models adopting m-CAK wind prescription cover a broader range of the main sequence when rotation is incorporated.
The impact of the different mass losses on the chemical structures of the 25 and 40 M⊙ stellar models is shown in Fig. 8. The convective cores are 8.5 and 18.5 M⊙ for the 25 and 40 M⊙ stars, respectively, when the high mass-loss rates are used (Fig. A.8). The composition in the radiative envelope shows some significant differences between the two models. This is particularly visible for the 40 M⊙ star, where in the low mass-loss rate model a convective region is associated with the H-burning shell (between about 17 and 25 M⊙ coordinates), while no convective zone is associated with this shell in the high mass-loss rate model. We see therefore, that reducing the mass of the envelope disfavours the formation of an intermediate convective shell associated to the H-burning shell.
The specific angular momentum in our model of 25 M⊙ is shown in Fig. 9a. The curves vary weakly and abruptly (e.g. around 9 M⊙ at the end of the MS phase). These variations come from transition regions between a convective and a radiative zone, where the chemical composition changes. This is also observed as an abrupt jump in the inner angular velocity (Fig. 9b). Like for the 120 M⊙ star, the model computed with the self-consistent mass-loss rates ends the MS phase with slightly higher values of the specific angular momentum. The increase is weaker because the mass-loss rates are weaker when the initial mass decreases. The changes in the interior angular velocity distribution are also much weaker than for the 120 M⊙ model. We note a slightly faster rotating core in the self-consistent stellar model compared to the original, as expected.
5. Comparison with rotational surveys
Because the self-consistent m-CAK prescription predicts weaker winds than previous studies, stellar models computed with this prescription evolve at higher luminosities and reach larger radii during the MS phase than the models of Ekström et al. (2012) or Eggenberger et al. (2021), as already detailed in Sect. 4. In addition, evolutionary tracks adopting Ṁsc also predict that the rotational velocity during the main sequence will be higher, as shown in Fig. 4, implying a weaker braking in the equatorial velocity of massive stars. This weaker braking is also represented in Fig. 10, where we plot rotational velocities as a function of the effective temperatures for evolutionary tracks adopting old and new winds, and where the time steps of 0.5 Myr are illustrated with the respective coloured circles. Velocities from evolution models with ṀVink quickly decreases after the first ∼1 − 2 Myr, passing from little variations in temperature for Mzams = 120 M⊙ to moderate variations for Mzams = 25 M⊙. Conversely, the vrot from self-consistent evolutionary tracks remains relatively constant at the beginning of the main sequence for all tracks at timescales that are inversely proportional to their initial masses (from ∼1.0 Myr for Mzams = 120 M⊙ to ∼6.0 Myr for Mzams = 25 M⊙), whereas Teff decreases by ∼8 kK in each model prior to the final braking.
 |
Fig. 10. Rotational velocities as a function of the effective temperature for evolutionary tracks adopting old (dashed) and new (solid) winds. The coloured dots represent the intervals of age with a step of 0.5 Myr. Grey dots represent the sample of O-type stars taken from the survey of Holgado et al. (2022). |
In parallel, we plot in Fig. 10 the sample of 285 O-type stars taken from the recent survey of Holgado et al. (2022), whose catalogue is available online2. In their study, they revisited the rotational properties of 285 Galactic massive O-type as part of the IACOB Project (Simón-Díaz et al. 2015; Holgado et al. 2018, 2020). This survey covers a range of stellar masses from 15 to 80 solar masses, and a mixture of ages within the main-sequence stage. They also compared the rotation of these stars with the custom evolution models (Brott et al. 2011 and Ekström et al. 2012), finding that neither of the two sets of rotating evolutionary tracks was able to reproduce the features of the survey. On the one hand, the models from Brott et al. (2011) cannot reproduce stars with vrot ≲ 150 km s−1 across the entire domain of O-type stars (see Fig. 9 of Holgado et al. 2022). On the other hand, the models from Ekström et al. (2012) cannot adequately reproduce the scarcity of stars with vrot ≳ 75 km s−1 for the left side of Fig. 10, which is also shown by the lack of stars matching the old tracks with 70 and 120 M⊙.
In contrast, in Fig. 10 we observe that the new self-consistent evolutionary tracks can adequately explain both issues. The tracks from 25 to 70 M⊙ match the set of stars with rotational velocities lower than 150 km s−1 for the range of temperatures from 27 to 40 kK. Moreover, the empty region of stars with Teff ≥ 42.5 kK and vrot ≥ 75 km s−1 would only be populated by our 120 M⊙ model, which is beyond the mass range of the sample. Therefore, evolution models adopting weaker winds interpret the rotational properties of the survey of Holgado et al. (2022) better, keeping the initial Ω = 0.4 and without the need of decreasing the initial equatorial velocity for our models.
Nonetheless, despite this encouraging result, there are still important aspects of the rotational properties of Galactic O-type stars that need to be taken into account. For instance, although our track of Minit = 25 M⊙ can encircle a larger fraction of stars in the top-right side of Fig. 10, there are still fast rotators (vrot > 300 km s−1) outside the scope of any track, which only could be explained by binary interaction effects (de Mink et al. 2013; Wang et al. 2020). Moreover, the slow braking observed for self-consistent evolutionary tracks indicates that stars born with masses between 25 and 70 M⊙ should spend the ∼75% of the lifetime in the main sequence stage with vrot between ∼250 km s−1 and ∼330 km s−1. As a consequence, we should expect to find a larger fraction of O-type stars in this range of rotational velocities. However, because of its proximity to the ZAMS, this range also covers an important portion of the region in which empirically detected O-type stars are rare, as shown in Fig. 11 and described by Holgado et al. (2020). For this reason, it is not surprising to find a moderate number of stars in the range from 250 to 330 km s−1 and temperatures between 30 and 42.5 kK. Even though our evolution models adopting self-consistent winds represent a relevant upgrade, important challenges in the study of O-type stars therefore still remain, such as the expansion of current samples to more hidden places by the use of infrared observations.
 |
Fig. 11. Spectroscopic Hertzsprung-Russell diagram (Langer & Kudritzki 2014, sHRD, with |
6. Implications of evolution models with self-consistent winds
The evolutionary tracks across the HRD from our rotating models adopting self-consistent winds exhibit considerable contrasts with the old models adopting Vink’s formula. They describe the rotational properties of the most recent observational diagnostics better. In this section we move one step beyond and explore some of the implications that the incorporation of these self-consistent models has at the Galactic scale. We remark, however, that these implications are discussed at an introductory level here, and their respective conclusions are part of forthcoming studies.
6.1. Enrichment of the 26Al isotope
Figure 12 shows how the new mass-loss rates impact the quantity of 26Al ejected by the stellar winds of our 120 M⊙ models computed with the two mass-loss rate prescriptions. Compared to the models discussed in Paper I for the non-rotating case, the current rotating models allow 26Al to appear at the surface well before layers enriched by nuclear burning in 26Al are uncovered by the stellar winds. This is the effect of the rotational mixing, which allows diffusion of the 26Al produced in the core to reach the surface. As in Paper I, reducing the mass-loss rate reduces the maximum value of the abundance of 26Al reached at the surface. This maximum also occurs at a more advanced age for the model with self-consistent wind, even though the peak of production of 26Al in the core is found at almost the same age for both (old and new) wind prescriptions. This time difference between the peak abundance at the centre and the surface is easily explained by the reduced mass-loss rate, which causes the star to take more time to remove their outer layers and then expose its inner composition, and for the less intense mixing as previously shown in Fig. 6a.
 |
Fig. 12. Variation as a function of time of the total mass (upper red curves), of the mass fraction of 26Al at the centre (bottom cyan curves), and at the surface (grey curves beginning at an ordinate equal to 60) in the 120 M⊙ rotating models with the old (upper panel) and new (lower panel) mass-loss rates. |
The total amount of 26Al released from the stellar surface to the interstellar medium during the MS for each one of our wind prescriptions, together with previous results from Paper I, is tabulated in Table 4. Although the total amount of aluminium-26 ejected by old winds is almost the same regardless of whether rotation is considered, for self-consistent winds, the rotating model predicts the ejection of a fraction about eight times smaller of the isotope during the MS, compared to the rotating evolution model adopting Vink’s formula. This difference is related not only to the mass loss due to the line-driven mechanism. Whereas non-rotating models predict eruptive processes associated with LBVs (Fig. 7 from Paper I), rotating models for Mzams = 120 M⊙ never reach these magnitudes for Ṁ (Fig. A.3). Therefore, the contribution of 26Al to the interstellar medium predicted by self-consistent winds is even weaker (compared with models adopting Vink’s formula) for rotating models than for non-rotating models.
However, it is important to remark that Fig. 12 only covers the lifetime of the star when the wind is optically thick, then excluding optically thick winds from WNh (H-core burning) and WR (He-core burning) phases. In contrast, Martinet et al. (2022) calculated the evolution of 26Al for evolution models with mass ranges from 12 to 300 M⊙ and metallicities from Z = 0.002 to Z = 0.020, but without distinguishing between thin- and thick-wind regimes. Instead, they distinguished between H-core and He-core burning stages, showing that the production of 26Al abruptly decreases when the star enters He-burning. As a consequence, even though here we selected only one mass and one metallicity for a quick comparison with the more complete analysis from Martinet et al. (2022), we infer that the larger contribution of 26Al from very massive stars to the ISM must stem from the later stages exhibiting optically thick winds, such as H-core WNh stars, to explain the current estimates of the 26Al total abundance in the Milky Way (Knödlseder 1999; Diehl et al. 2006; Wang et al. 2009; Pleintinger et al. 2019). Certainly, we need a extensive study implementing self-consistent evolution models for wider ranges of masses and metallicities, together with updates in the convection criteria (Georgy et al. 2014; Kaiser et al. 2020) and overshooting values (Martinet et al. 2021) for a more complete analysis.
6.2. Massive stars at the Galactic centre
The implications of the new evolution models for massive stars with a self-consistent mass-loss rate are large, not only across the main sequence, but also over the subsequent evolutionary stages. One consequences is that using models computed with the weaker self-consistent mass-loss rates may provide estimates of evolutionary masses that are lower than when models with Ṁ from Vink et al. (2001) are adopted.
An example of this situation is the study of the Ofpe3 stars located at the Galactic centre. Massive stars at the Galactic centre play an important role in feeding the supermassive black hole Sgr A* by means of their stellar winds (Cuadra et al. 2015; Ressler et al. 2018; Calderón et al. 2020a). This is a consequence of the remarkable situation of OB and WR stars, which represent a large fraction of the stars at the Galactic centre (e.g. Lu et al. 2013; von Fellenberg et al. 2022), even though this region is thought to be hostile to star formation (e.g. Genzel et al. 2010). The wind properties of these massive stars have been analysed and constrained by Martins et al. (2007) for the O-type stars and WRs, and by Habibi et al. (2017) for the B-type stars. Martins et al. (2007) calculated the stellar and wind parameters for a set of stars at evolved stages such as Ofpe and WN, which are particularly relevant for feeding Sgr A*. Their analysis was performed by spectral fitting using the CMFGEN code and the evolutionary tracks from Meynet & Maeder (2005). Therefore, it is important to confirm whether the current evolutionary tracks suggest a revision of the properties of the massive stars at the Galactic centre, and the consequences these modifications imply for the accretion on to Sgr A*.
To illustrate the issue, Fig. 13 shows the hydrogen abundance at the stellar surface as a function of luminosity for standard and self-consistent evolutionary tracks, plus five of the Ofpe stars analysed by Martins et al. (2007, compare with their Fig. 21). Figure 13 shows that for a given hydrogen surface abundance and for a given initial mass, the tracks computed with the weaker self-consistent mass-loss rates are overluminous. These tracks also end the MS phase with higher surface hydrogen abundances. The lowest-luminosity Ofpe star in the sample cannot be reproduced by any of the two track families. The other four stars can reasonably be fitted by either models on average, although the initial masses that will be deduced from a comparison with self-consistent mass-loss rate tracks are lower than the masses deduced from tracks computed with Vink’s mass-loss rates.
 |
Fig. 13. Surface hydrogen abundance (in mass fraction) as a function of the stellar luminosity for different evolutionary tracks. Continuous lines are models computed with the self-consistent mass-loss rate, and dashed lines are computed with Vink’s original recipe. Magenta symbols are the Ofpe stars from the Galactic centre as plotted by Martins et al. (2007, compare with their Fig. 21). |
Because the observed Ofpe stars in the Galactic centre would have lower initial masses, we can speculate that their wind parameters (terminal velocity and mass-loss rate) will be lower as well. The terminal velocity is an important parameter in this context because the Galactic centre is a region with a high stellar density, and the winds collide with each other, creating a high-temperature medium. However, slower winds (≲600 km s−1) produce a plasma of lower temperature (≲4 × 106 K) at the collision, which becomes susceptible to hydrodynamical instabilities and finally forms high-density clumps and streams. These clumps can then be captured by the central black hole, increasing its accretion rate (Cuadra et al. 2005, 2008; Calderón et al. 2016, 2020a,b).
In a forthcoming paper, we will perform a more complete analysis of the Galactic centre massive star population by extending the tracks to the WR stage and taking the non-standard chemical abundance deduced for this region into account. From the observational side, we will also include data collected after Martins et al. (2007), which is expected to afford a reduction in the typical error bars for the stellar luminosities from 0.2 down to 0.1 dex (S. von Fellenberg, priv. comm.). The comparison between models and observations will allow us to update the estimates for the initial masses and ages of this population, and also its wind parameters, which strongly affect the current accretion onto Sgr A*.
7. Conclusion
We have extended the stellar evolution models performed in Gormaz-Matamala et al. (2022a, Paper I) by adopting a self-consistent m-CAK prescription (Gormaz-Matamala et al. 2019, 2022b) for the mass-loss rate recipe (Eq. (1)) by including the rotational effects. Stellar rotation affects the mass loss of a massive star not only by changing the balance between gravitational, radiative, and centrifugal forces (Maeder & Meynet 2000), but also because rotational mixing considerably modifies the internal distribution of the chemical elements and thus impacts the evolutionary tracks in the HRD and hence the mass-loss rates. The progressive increase in the helium-to-hydrogen ratio in the wind impacts the line-force parameters (k, α, δ) and therefore the self-consistent solution of the equation of motion, leading to a decrease of 0.2 dex in the absolute value of the mass-loss rate (Eq. (11)).
The updated mass-loss rates were implemented for a set of evolutionary models at different initial stellar masses for metallicities Z = 0.014 (Galactic) and Z = 0.006 (LMC). The new tracks show important differences with respect to the studies of Ekström et al. (2012) and Eggenberger et al. (2021), who adopted the formula from Vink et al. (2001) for the winds of massive stars, but they are fairly similar to the studies of Sabhahit et al. (2022) for VMS and Björklund et al. (2023) and their own self-consistent wind prescription. In addition to the differences in the tracks across the HRD that we discussed in Paper I, we find for rotating evolutionary tracks that the surface rotation maintains a higher value when the weaker self-consistent mass-loss rates are adopted, as expected. We observe that for the initial rotation considered here, tracks computed with the self-consistent mass-loss rates extend more to the red part of the HR diagram during the MS phase. This effect is stronger for masses higher than about 40 M⊙.
The new tracks predict an evolution of the surface rotational velocities for O-type stars that, at first sight, appears to agree better with the most recent observational diagnostics. The slow braking in the evolution of vrot explains the rotational properties of the survey of Holgado et al. (2022) for O-type stars better, such as the lack of fast rotators for stars with Teff ≳ 42.5 kK and the abundance of stars with vrot ≤ 150 km s−1 and temperatures between 27 and 40 kK. The implications of these new evolution models are also wide. For example, lower mass-loss rate predict a weaker stellar wind contribution to the aluminium-26 enrichment of the ISM during the main-sequence phase, at least when the stellar wind is optically thin. Likewise, the fact that self-consistent models are more luminous in the HRD suggests that the initial mass deduced from evolutionary tracks might be lower when the self-consistent tracks are used. This may apply to the mass estimates of Ofpe and WN stars at the Galactic centre, which leads us to expect that their wind properties (mass-loss rate and terminal velocity) might also be overestimated. Nevertheless, a more accurate analysis of the stars surrounding Sgr A* and their stellar winds is deferred to a forthcoming paper.
Ofpe is a spectral classification for stars showing properties intermediate between O-type and WR stars (Walborn 1977, 1982). They are therefore assumed to be a transition between the two spectroscopic phases according to the Conti scenario (Conti 1975).
Acknowledgments
We are very grateful for the anonymous referee and their very constructive comments and feedback. We also acknowledge useful discussions with Sebastiano von Fellenberg and Stefan Gillessen. This project was partially funded by the Max Planck Society through a “Partner Group” grant. J.C. acknowledges financial support from FONDECYT Regular 1211429. G.M. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement N° 833925, project STAREX). M.C. thanks the support from FONDECYT projects 1190485 and 1230131.
References
- Abbott, D. C. 1982, ApJ, 259, 282 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, ApJ, 818, L22 [Google Scholar]
- Agrawal, P., Szécsi, D., Stevenson, S., Eldridge, J. J., & Hurley, J. 2022, MNRAS, 512, 5717 [NASA ADS] [CrossRef] [Google Scholar]
- Araya, I., Jones, C. E., Curé, M., et al. 2017, ApJ, 846, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Araya, I., Curé, M., Ud-Doula, A., Santillán, A., & Cidale, L., 2018, MNRAS, 477, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Araya, I., Christen, A., Curé, M., et al. 2021, MNRAS, 504, 2550 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Bulik, T., Fryer, C. L., et al. 2010, ApJ, 714, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Björklund, R., Sundqvist, J. O., Puls, J., & Najarro, F. 2021, A&A, 648, A36 [EDP Sciences] [Google Scholar]
- Björklund, R., Sundqvist, J. O., Singh, S. M., Puls, J., & Najarro, F. 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202141948 [Google Scholar]
- Bouret, J. C., Hillier, D. J., Lanz, T., & Fullerton, A. W. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calderón, D., Ballone, A., Cuadra, J., et al. 2016, MNRAS, 455, 4388 [Google Scholar]
- Calderón, D., Cuadra, J., Schartmann, M., Burkert, A., & Russell, C. M. P. 2020a, ApJ, 888, L2 [Google Scholar]
- Calderón, D., Cuadra, J., Schartmann, M., et al. 2020b, MNRAS, 493, 447 [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [Google Scholar]
- Conti, P. S. 1975, Mem. Soc. R. Sci. Liege, 9, 193 [NASA ADS] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [Google Scholar]
- Cuadra, J., Nayakshin, S., Springel, V., & Di Matteo, T. 2005, MNRAS, 360, L55 [CrossRef] [Google Scholar]
- Cuadra, J., Nayakshin, S., & Martins, F. 2008, MNRAS, 383, 458 [NASA ADS] [Google Scholar]
- Cuadra, J., Nayakshin, S., & Wang, Q. D. 2015, MNRAS, 450, 277 [CrossRef] [Google Scholar]
- Curé, M. 2004, ApJ, 614, 929 [CrossRef] [Google Scholar]
- Curé, M., & Rial, D. F. 2007, Astron. Nachr., 328, 513 [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
- Diehl, R., Halloin, H., Kretschmer, K., et al. 2006, Nature, 439, 45 [CrossRef] [PubMed] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
- Eggenberger, P., Ekström, S., Georgy, C., et al. 2021, A&A, 652, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- Georgy, C., Meynet, G., & Maeder, A. 2011, A&A, 527, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Saio, H., & Meynet, G. 2014, MNRAS, 439, L6 [Google Scholar]
- Gormaz-Matamala, A. C., Curé, M., Cidale, L. S., & Venero, R. O. J. 2019, ApJ, 873, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Gormaz-Matamala, A. C., Curé, M., Hillier, D. J., et al. 2021, ApJ, 920, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gormaz-Matamala, A. C., Curé, M., Meynet, G., et al. 2022a, A&A, 665, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gormaz-Matamala, A. C., Curé, M., Lobel, A., et al. 2022b, A&A, 661, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G. 2021, A&A, 647, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Hamann, W. R. 2008, A&A, 482, 945 [Google Scholar]
- Groh, J. H., Meynet, G., Ekström, S., & Georgy, C. 2014, A&A, 564, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habibi, M., Gillessen, S., Martins, F., et al. 2017, ApJ, 847, 120 [Google Scholar]
- Hamann, W. R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [Google Scholar]
- Hamann, W. R., Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [CrossRef] [Google Scholar]
- Higgins, E. R., Vink, J. S., Sabhahit, G. N., & Sander, A. A. C. 2022, MNRAS, 516, 4052 [NASA ADS] [CrossRef] [Google Scholar]
- Holgado, G., Simón-Díaz, S., Barbá, R. H., et al. 2018, A&A, 613, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holgado, G., Simón-Díaz, S., Haemmerlé, L., et al. 2020, A&A, 638, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holgado, G., Simón-Díaz, S., Herrero, A., & Barbá, R. H. 2022, A&A, 665, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, E. A., Hirschi, R., Arnett, W. D., et al. 2020, MNRAS, 496, 1967 [Google Scholar]
- Keszthelyi, Z., Puls, J., & Wade, G. A. 2017, A&A, 598, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knödlseder, J. 1999, ApJ, 510, 915 [CrossRef] [Google Scholar]
- Krtička, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2018, A&A, 612, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, N., & Kudritzki, R. P. 2014, A&A, 564, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattimer, A. S., & Cranmer, S. R. 2021, ApJ, 910, 48 [CrossRef] [Google Scholar]
- Lu, J. R., Do, T., Ghez, A. M., et al. 2013, ApJ, 764, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1987, A&A, 178, 159 [NASA ADS] [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2010, New Astron. Rev., 54, 32 [CrossRef] [Google Scholar]
- Martinet, S., Meynet, G., Ekström, S., et al. 2021, A&A, 648, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinet, S., Meynet, G., Nandal, D., et al. 2022, A&A, 664, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., & Palacios, A. 2022, A&A, 659, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Genzel, R., Hillier, D. J., et al. 2007, A&A, 468, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [CrossRef] [EDP Sciences] [Google Scholar]
- Noebauer, U. M., & Sim, S. A. 2015, MNRAS, 453, 3120 [Google Scholar]
- Palacios, A., Meynet, G., Vuissoz, C., et al. 2005, A&A, 429, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pleintinger, M. M. M., Siegert, T., Diehl, R., et al. 2019, A&A, 632, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poniatowski, L. G., Kee, N. D., Sundqvist, J. O., et al. 2022, A&A, 667, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2018, MNRAS, 478, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2020, MNRAS, 492, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Sabhahit, G. N., Vink, J. S., Higgins, E. R., & Sander, A. A. C. 2022, MNRAS, 514, 3736 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & Schmutz, W. 1994, A&A, 288, 231 [NASA ADS] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Shimada, M. R., Ito, M., Hirata, B., & Horaguchi, T. 1994, in Pulsation, Rotation, and Mass Loss in Early-Type Stars, eds. L. A. Balona, H. F. Henrichs, & J. M. Le Contel, 162, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Negueruela, I., Maíz Apellániz, J., et al. 2015, in Highlights of Spanish Astrophysics VIII, eds. A. J. Cenarro, F. Figueras, C. Hernández-Monteagudo, J. Trujillo Bueno & L. Valdivielso, 576 [Google Scholar]
- Šurlan, B., Hamann, W. R., Aret, A., et al. 2013, A&A, 559, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S. 2022, ARA&A, 60, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 1999, A&A, 350, 181 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Fellenberg, S. D., Gillessen, S., Stadler, J., et al. 2022, ApJ, 932, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1977, ApJ, 215, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1982, ApJ, 256, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., Lang, M. G., Diehl, R., et al. 2009, A&A, 496, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, C., Langer, N., Schootemeijer, A., et al. 2020, ApJ, 888, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S. C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yusof, N., Hirschi, R., Meynet, G., et al. 2013, MNRAS, 433, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Appendix A: Additional plots
 |
Fig. A.1. Self-consistent evolution tracks from Fig. 3, compared with the respective self-consistent non-rotating models from Paper I (Gormaz-Matamala et al. 2022a). |
 |
Fig. A.2. Self-consistent evolution tracks (solid lines), compared with classical evolutionary tracks (darker dashed lines) from Ekström et al. (2012, Z = 0.014) and Eggenberger et al. (2021, Z = 0.006), across the plane (Teff, log g). The shadowed region constrains the validity range for the m-CAK prescription, as defined in Section 2. |
 |
Fig. A.3. Evolution of the self-consistent mass-loss rate, Ṁsc (solid lines), compared with the models using Vink’s formula (darker dashed lines). |
 |
Fig. A.4. Evolution of stellar mass. |
 |
Fig. A.5. Evolution of stellar radii. |
 |
Fig. A.6. Evolution of He/H ratio. |
 |
Fig. A.7. Evolution of Eddington factor, ΓEdd. |
 |
Fig. A.8. Evolution of the mass of the stellar convective core. |
All Tables
All Figures
 |
Fig. 1. Evolutionary tracks across the HRD for models with rotation using ṀVink and Z/Z⊙ = 1.0, covering the main-sequence stage, hereafter original tracks. Circles represent the location of the selected stellar models that are to be tabulated in Table 1. |
| In the text | |
 |
Fig. 2. Differences in the resulting self-consistent mass-loss rate Δlog Ṁsc for the abundances tabulated in Table 1, (a) due to the modification of the He/H ratio with respect to the default He/H = 0.085, and (b) due to the modification of any of the CNO elements with respect to ξ/ξ⊙ = 1.0 (with ξ being carbon, nitrogen, or oxygen, depending on the respective symbol). |
| In the text | |
 |
Fig. 3. HR diagram for the self-consistent evolution models (solid lines), compared with classical evolutionary tracks (darker dashed lines) from Ekström et al. (2012, Z = 0.014) and Eggenberger et al. (2021, Z = 0.006). All plots cover the main sequence and part of the Hertzsprung gap. Self-consistent tracks are marked with two black dots that represent the zero-age main sequence and the switch of the mass-loss recipe from self-consistent to Vink’s formula (when either Teff = 30 kK or log g = 3.2), whereas the TAMS is represented with a black cross. |
| In the text | |
 |
Fig. 4. Evolution of surface equatorial velocities and rotation parameter Ω as a function of the mass fraction of hydrogen at the core, which decreases from Xcore ∼ 0.72 at ZAMS to Xcore ∼ 0.05 at the end of the H-core burning stage. The symbols (dots and crosses) have the same meanings as indicated in the caption of Fig. 3. |
| In the text | |
 |
Fig. 5. Diffusion factors for convective turbulence (Dconv), shear turbulence (Dsh), and effective turbulence (Deff) as a function of the Lagrangian mass coordinate for our evolution models with Mzams = 120 M⊙ and Z = 0.014, adopting old and new winds at an intermediate point in the main-sequence stage (Xcore = 0.3). Vertical grey lines represent the total mass of both models. The symbols for the solid and dashed lines are the same as in Fig. 3. |
| In the text | |
 |
Fig. 6. Variation on the logarithmic scale of the mass fraction of hydrogen, helium, and CNO elements as a function of the Lagrangian mass coordinate in solar units in the (a) 120 M⊙ model and (b) the 70 M⊙ model for the two prescriptions of the mass losses studied in the present work at the end of the main-sequence stage. The meaning of the different line styles is the same as in Fig. 3. Vertical grey lines represent the total mass of both models, which correspond to the final masses at the end of MS tabulated in Table 3. |
| In the text | |
 |
Fig. 7. Angular properties for the inner structure of our 120 M⊙ model on the ZAMS and at the end of the MS phase for the two prescriptions of the mass losses. (a) Variation in logarithmic scale of the specific angular momentum as a function of the Lagrangian mass coordinate in solar units. (b) Angular velocity in radians per second, also as a function of the Lagrangian mass coordinate. |
| In the text | |
 |
Fig. 8. Same as Fig. 6, but for models with 40 (a) and 25 M⊙ (b). |
| In the text | |
 |
Fig. 9. Same as Fig. 7, but for our model with Mzams = 25 M⊙ and Z = 0.014. |
| In the text | |
 |
Fig. 10. Rotational velocities as a function of the effective temperature for evolutionary tracks adopting old (dashed) and new (solid) winds. The coloured dots represent the intervals of age with a step of 0.5 Myr. Grey dots represent the sample of O-type stars taken from the survey of Holgado et al. (2022). |
| In the text | |
 |
Fig. 11. Spectroscopic Hertzsprung-Russell diagram (Langer & Kudritzki 2014, sHRD, with |
| In the text | |
 |
Fig. 12. Variation as a function of time of the total mass (upper red curves), of the mass fraction of 26Al at the centre (bottom cyan curves), and at the surface (grey curves beginning at an ordinate equal to 60) in the 120 M⊙ rotating models with the old (upper panel) and new (lower panel) mass-loss rates. |
| In the text | |
 |
Fig. 13. Surface hydrogen abundance (in mass fraction) as a function of the stellar luminosity for different evolutionary tracks. Continuous lines are models computed with the self-consistent mass-loss rate, and dashed lines are computed with Vink’s original recipe. Magenta symbols are the Ofpe stars from the Galactic centre as plotted by Martins et al. (2007, compare with their Fig. 21). |
| In the text | |
 |
Fig. A.1. Self-consistent evolution tracks from Fig. 3, compared with the respective self-consistent non-rotating models from Paper I (Gormaz-Matamala et al. 2022a). |
| In the text | |
 |
Fig. A.2. Self-consistent evolution tracks (solid lines), compared with classical evolutionary tracks (darker dashed lines) from Ekström et al. (2012, Z = 0.014) and Eggenberger et al. (2021, Z = 0.006), across the plane (Teff, log g). The shadowed region constrains the validity range for the m-CAK prescription, as defined in Section 2. |
| In the text | |
 |
Fig. A.3. Evolution of the self-consistent mass-loss rate, Ṁsc (solid lines), compared with the models using Vink’s formula (darker dashed lines). |
| In the text | |
 |
Fig. A.4. Evolution of stellar mass. |
| In the text | |
 |
Fig. A.5. Evolution of stellar radii. |
| In the text | |
 |
Fig. A.6. Evolution of He/H ratio. |
| In the text | |
 |
Fig. A.7. Evolution of Eddington factor, ΓEdd. |
| In the text | |
 |
Fig. A.8. Evolution of the mass of the stellar convective core. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



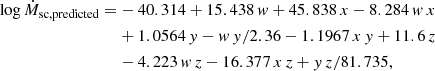
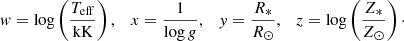
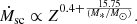
![$$ \begin{aligned} \dot{M}(\omega )&= F_\omega \dot{M}(0)\nonumber \\ \mathrm{with}\quad F_\omega&= \frac{(1-\Gamma _{\rm Edd})^{\frac{1}{\alpha }-1}}{\left[1-\frac{\omega ^2}{2\pi G\rho _{\rm m}}-\Gamma _{\rm Edd}\right]^{\frac{1}{\alpha }-1}}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45847-23/aa45847-23-eq4.gif)
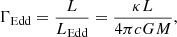
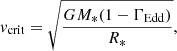
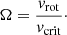
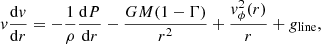
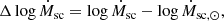
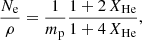
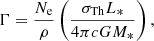
![$$ \begin{aligned} \log \dot{M}_{\rm sc} = \log \dot{M}_{\rm sc,0}-0.559 \times \left[\left(\mathrm{He}/\mathrm{H}\right)_*-\left(\mathrm{He}/\mathrm{H}\right)_0\right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45847-23/aa45847-23-eq14.gif)