| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243938 | |
| Published online | 23 December 2022 | |
KOBEsim: A Bayesian observing strategy algorithm for planet detection in radial velocity blind-search surveys★
1
Centro de Astrobiología (CAB), CSIC-INTA,
Camino Bajo del Castillo s/n,
28692,
Villanueva de la Cañada, Madrid, Spain
e-mail: obalsalobre@cab.inta-csic.es
2
Depto. Estadística e Investigación Operativa, Universidad de Cádiz,
Avda. República Saharaui s/n,
11510
Puerto Real, Cádiz, Spain
3
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP,
Rua das Estrelas,
4150-762
Porto, Portugal
4
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto,
Rua do Campo Alegre,
4169-007
Porto, Portugal
5
Centro Astronómico Hispano en Andalucía, Observatorio de Calar Alto,
Sierra de los Filabres,
04550
Gérgal, Almería, Spain
6
Instituto de Astrofísica de Andalucia,
Glorieta de la Astronomia s/n,
Granada, Spain
7
Aix-Marseille Univ, CNRS, CNES, LAM,
Marseille, France
Received:
3
May
2022
Accepted:
20
October
2022
Context. Ground-based observing time is precious in the era of exoplanet follow-up and characterization, especially in high-precision radial velocity instruments. Blind-search radial velocity surveys thus require a dedicated observational strategy in order to optimize the observing time, which is particularly crucial for the detection of small rocky worlds at large orbital periods.
Aims. We developed an algorithm with the purpose of improving the efficiency of radial velocity observations in the context of exoplanet searches, and we applied it to the K-dwarfs Orbited By habitable Exoplanets experiment. Our aim is to accelerate exoplanet confirmations or, alternatively, reject false signals as early as possible in order to save telescope time and increase the efficiency of both blind-search surveys and follow-up of transiting candidates.
Methods. Once a minimum initial number of radial velocity datapoints is reached in such a way that a periodicity starts to emerge according to generalized Lomb-Scargle periodograms, that period is targeted with the proposed algorithm, named KOBEsim. The algorithm selects the next observing date that maximizes the Bayesian evidence for this periodicity in comparison with a model with no Keplerian orbits.
Results. By means of simulated data, we proved that the algorithm accelerates the exoplanet detection, needing 29-33% fewer observations and a 41–47% smaller time span of the full dataset for low-mass planets (mp < 10 M⊕) in comparison with a conventional monotonic cadence strategy. For 20 M⊕ planets we found a 16% enhancement in the number of datapoints. We also tested KOBEsim with real data for a particular KOBE target and for the confirmed planet HD 102365 b. These two tests demonstrate that the strategy is capable of speeding up the detection by up to a factor of 2 (i.e., reducing both the time span and number of observations by half).
Key words: planets and satellites: detection / methods: statistical / techniques: radial velocities / stars: solar-type
© The Authors 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Over the last three decades numerous exoplanets have been detected (more than 5000 confirmed according to the NASA Exoplanet Archive1, Akeson et al. 2013). Ever since the first hot Jupiters were discovered (Mayor & Queloz 1995; Butler et al. 1997) the instrumentation has improved, thus making it possible to detect less massive worlds. Specifically in the radial velocity (RV) method, the development of highly stabilized spectrographs, from CORALIE (Queloz et al. 2000) to ESPRESSO (Pepe et al. 2021), have allowed the detection of lighter planets located farther away from the host star (e.g., Damasso et al. 2020; Demangeon et al. 2021; Lillo-Box et al. 2021; Faria et al. 2022).
However, detection and characterization are still challenging, especially in non-transiting planetary systems since they require many observations distributed over long periods of time. When searching for potentially habitable worlds, this becomes crucial as they orbit at larger periods than those typically detected. That is why the improvement in the efficiency of observations is decisive. It saves valuable telescope time and allows us to find a type of planet that would otherwise be undetectable throughout conventional observing programs.
To address the problem of observational efficiency, it is increasingly common that observatories and scientific programs develop their own tools to avoid wasting telescope time through a good scheduling strategy. Some of these approaches have been presented, such as for ALMA (Espada et al. 2014), JWST (Giuliano et al. 2007), and the CARMENES Guaranteed Time Observation (GTO) survey (Garcia-Piquer et al. 2017). In the context of RV searches, Cabona et al. (2021) proposed that uniformly distributed data along the phase-folded RV diagram favors efficiency. As a consequence, observing in an already explored orbital phase (ϕ) does not significantly increase the information in hand. In this paper we present KOBEsim2, a Bayesian algorithm to improve the efficiency of planet detections in RV-blind searches through optimizing the scheduling of observations. It is an open source code written in Python language available to the community. Bayesian adaptative scheduling algorithms have been already demonstrated to be powerful in previous works (e.g., Loredo 2004; Ford 2008; Loredo et al. 2011). They propose improving observational efficiency on-the-fly by developing algorithms composed of two steps: inference and decision. The former quantifies the knowledge acquired with the available data and the latter chooses the optimum date depending on the scientific goal (more information in Sect. 2.3) and based on the predictions. Particularly, Ford (2008) shows through simulations that their algorithm has the potential not only to increase planet detections, but also to increase the sensitivity compared to conventional strategies.
KOBEsim was developed to enhance the planet detection in the K-dwarfs Orbited By habitable Exoplanets (KOBE) experiment3, a blind-search RV survey devoted to the hunt for rocky and potentially habitable exoplanets around K-dwarf stars (Lillo-Box et al. 2022). KOBE is a legacy program of the Calar Alto Observatory (CAHA; Almería, Spain), making use of the Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Echelle Spectrographs (CARMENES), a fiber-fed échelle spectrograph (Quirrenbach et al. 2020) at the 3.5 m telescope. KOBE observations began in January 2021 and will be monitoring 50 late K-dwarf stars over five consecutive semesters. The main goal of this experiment is to bridge the gap between G and M dwarfs in the search for planets within the habitable zone (HZ), a parameter space that has been barely explored (see Fig. 1 in Lillo-Box et al. 2022).
This paper is organized as follows. In Sect. 2 we describe the methodology, and provide a description of the architecture of the KOBEsim code. In Sect. 3 we show the results of testing the strategy by applying the algorithm to simulated and real datasets. We also briefly illustrate how the data simulation is performed, we show the efficiency of KOBEsim in detecting planets of different masses by comparison with monotonic cadence strategies, and we study the case of targeting false positive periodicities. Finally, in Sect. 4 we summarize the results and present our conclusions.
 |
Fig. 1 KOBEsim workflow scheme. It starts by gathering RV data until it finds a dominant period (step 1), from which the KOBEsim algorithm provides the next optimum observing date (step 2). |
2 Methodology
The proposed observational strategy consists of two steps (see Fig. 1). First, the star is monitored with the usual survey strategy; for example, in the KOBE experiment the targets are observed with a cadence of ~10% with respect to the orbital period that a planet would have in the middle of the HZ. This step lasts until there are enough RV data gathered (n) to see an emerging peak in the periodogram. Second, that period (Ppeak) is pursued by the KOBEsim algorithm. By ranking all the possible observing dates, the algorithm proposes the optimum next observing night. In Sect. 3 we show that this turns out to be faster than a monotonic cadence strategy (i.e., continuing to use the strategy followed in the first step) to determine whether Ppeak is due to a strictly periodic signal (induced by the presence of a planet).
2.1 Statistical framework
In this work we assume the concept of planet detection based on a Bayes factor threshold for two competing models: the null hypothesis H0 where the parameters (θ) do not include any Keplerian orbit, against the alternative H1, where the parameters include a Keplerian orbit. In statistical notation we write
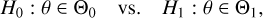 (1)
(1)
where Θi represents a restricted range of values where the model includes a planet or not. In the first step of KOBEsim, we infer the parameters that describe these competing models (detailed in Sect. 2.2). For this purpose we model the jth RV observation as
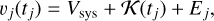 (2)
(2)
where Vsys is the systemic RV, 𝒦(tj) is the equation of RV corresponding to a Keplerian signal depending on the time of the measurement tj, and Ej is the noise contribution obtained from a Gaussian distribution with zero mean and variance 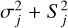 . The value
. The value 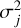 is the uncertainty associated with the j-th measurement due to the photon noise, and
is the uncertainty associated with the j-th measurement due to the photon noise, and 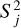 are variances of unmodeled sources of noise. In the particular case of a RV signal induced by one planet (H1), 𝒦(tj) can be written as
are variances of unmodeled sources of noise. In the particular case of a RV signal induced by one planet (H1), 𝒦(tj) can be written as
![$K\left( {{t_j}} \right) = L\left[ {\cos \left( {v\left( {{t_j},e,P,{t_0}} \right) + \omega } \right) + e\cos \omega } \right],$](/articles/aa/full_html/2023/01/aa43938-22/aa43938-22-eq6.png) (3)
(3)
where K is the RV semi-amplitude, v is the true anomaly of the planet (angle between the periastron and the position of the planet in the elliptical orbit measured from the central star), e is its eccentricity (degree of deviation of the elliptical orbit from a circle), P is the orbital period of the planet, t0 is the inferior conjunction time, and ω is the argument of the periastron (angular distance between the line of nodes and the periastron). Thus, vj depends on the following parameters:
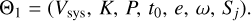 (4)
(4)
Meanwhile, 𝒦(tj) is zero for the null hypothesis H0, thus the parameters are
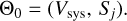 (5)
(5)
We estimate the posterior probability of each hypothesis using the Bayes relation
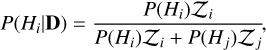 (6)
(6)
where 𝒵i is the evidence (i.e., marginal likelihood) under the hypothesis i, and D is an array of datapoints. Thus, the ratio for the competing models (the posterior odds) is
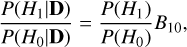 (7)
(7)
where B10 is the evidence (or marginal likelihood) ratio, called the Bayes factor. Assuming the same prior probability of a star hosting one or no planets (i.e., P(H1)/P(H0) = 1), we can use B10 as a metric to analyze how significant one model is compared to another for a given dataset. An intrinsic feature of this mathematical construction is Occam’s razor (e.g., Mackay 2003; Thrane & Talbot 2019), which penalizes the most complex models (i.e., those with more parameters). In this work we set the limit to consider a planet detection at ln (B10) > 6, which is a conservative criterion since it is four times greater than the evidence Jeffreys (1961) proposed as decisive.
2.2 Estimating the evidence of the models
Once we have a predominant signal (Ppeak) we are ready to run KOBEsim. First, it derives the set of parameters from the data for both the null (H0) and planet (H1) hypotheses (corresponding to Fig. 1 panel a). We explore the parameter space and sample the posterior distribution by using the Markov chain Monte Carlo (MCMC) affine invariant ensemble sampler emcee (Foreman-Mackey et al. 2013). To compute the Keplerian in the H1 model, Eq. (3), we use the python module RadVel (Fulton et al. 2018). Considering normally distributed data around the theoretical value of the model, our selection of likelihood function is a Gaussian-noise
![$ - 2\ln L\left( {{\bf{D}}|\theta } \right) = Q + \sum\limits_{j = 1}^n {\ln \left( {\sigma _j^2 + S_j^2} \right) + \sum\limits_{j = 1}^n {{{{{\left[ {{V_{{\rm{sys}}}} + K\left( {{t_j}} \right) - {v_j}} \right]}^2}} \over {\sigma _j^2 + S_j^2}}} } $](/articles/aa/full_html/2023/01/aa43938-22/aa43938-22-eq11.png) (8)
(8)
where D is our RV measurement and its associated uncertainties 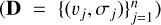 , and Q is a constant. We assume the prior distributions to be uniform, except for those parameters we are more informed about, for which we select a narrow normal distribution (e.g., Ppeak). The prior distributions used for each parameter are shown in Table 1, where t0,input is the value of t0 that can be optionally given as input, t1 is the first day that the target was observed, and 𝒢t corresponds to a truncated Gaussian between −1 and 1. To sample the parameter space, we employ four times the number of parameters of the model and 2 × 104 steps in each of them4. To speed up the convergence, we start new chains in a ball around the best solutions from the previous sampling with half the number of steps. Following the criterion suggested in the documentation of emcee5, we consider our sampling to be successful when the chains are longer than 50 times the autocorrelation time.
, and Q is a constant. We assume the prior distributions to be uniform, except for those parameters we are more informed about, for which we select a narrow normal distribution (e.g., Ppeak). The prior distributions used for each parameter are shown in Table 1, where t0,input is the value of t0 that can be optionally given as input, t1 is the first day that the target was observed, and 𝒢t corresponds to a truncated Gaussian between −1 and 1. To sample the parameter space, we employ four times the number of parameters of the model and 2 × 104 steps in each of them4. To speed up the convergence, we start new chains in a ball around the best solutions from the previous sampling with half the number of steps. Following the criterion suggested in the documentation of emcee5, we consider our sampling to be successful when the chains are longer than 50 times the autocorrelation time.
To calculate the Bayes factor metric we employ the bayev code (Díaz et al. 2016), which uses the estimator defined in Perrakis et al. (2014). Giving as input a representative fraction of the marginalized posterior distributions provided by emcee, the likelihood function, and the priors, we obtain the ln(𝒵) distribution. The authors of the bayev code estimate the uncertainty of this distribution repeatedly reshuffling the joint posterior sample to produce new samples. In our case we opt for just one fraction of the distributions for computational time reasons since we checked that the chosen fraction (15% of the iterations) is representative enough and the standard deviation of the resulting distributions does not change significantly (around 20%). Carrying out this procedure for the two competing models, and considering a priori the same probability for each hypothesis, P(H1) = P(H0), we obtain an estimation of ln(B10) with its associated uncertainty.
Prior distributions to perform the MCMC fit.
2.3 Forecasting the optimum observing date
In the second step of the code we use the existing data to select the future date that most (or more optimally) increases the evidence of the planet model at the targeted periodicity. For this purpose, we predict and compare the expected increase in the ln(B10) for each candidate date in our schedule. The Bayes factor is our metric for measuring the gain, which in decision theory is called the utility function. This quantity is commonly used in RV datasets to test different hypotheses, and thus can be used to claim a planet candidate (e.g., Lillo-Box et al. 2020; Mortier et al. 2020; Faria et al. 2022). Previous works on Bayesian adaptative schedulers adopt other utility functions based on their goals. For instance, Loredo et al. (2011) opt for the Shannon entropy as they aim to improve the efficiency in constraining the parameter inference, and this utility function is used to reduce the posterior uncertainties.
The prediction is the stage illustrated in Fig. 1 panel b. To find the candidate dates we divide the period into a total of Nphases orbital sub-phases (i.e., spliting the orbital phase Nphases times). We choose the next assigned date from the schedule at the telescope that matches each sub-phase. In this selection of the candidate dates, we take into account twilights, altitude of the target, and exposure time (see Sect. 3.1 for further details). Next, using the whole posterior probability distributions inferred for our model parameters through the MCMC algorithm (obtained in the stage shown in Fig. 1 panel a), we sample the posterior predictive distribution for the RVs at each potential observing date by using Eq. (2). We take the uncertainty of the predicted RV from the quadratic sum of the standard deviation of the predictive distribution (uncertainty due to the parameter inference) and a random value from a normal distribution of same mean and standard deviation as the uncertainities (σj) of the n RV datapoints already gathered (simulating the expected photon noise).
Running again emcee and bayev over each of the datasets (including one additional datapoint corresponding to each predicted RV at a proposed date), we end up with an estimation of ∆ ln(B10) for each of the proposed future dates. KOBEsim sorts the tested dates according to the utility function, giving the maximum priority to the highest ∆ ln(B10) (stage illustrated in Fig. 1 panel c).
For long targeted periodicities, the largest ln(B10) increase may occur at a very distant date, which is against the efficiency of the observations. Consequently, the detection using KOBEsim could require a long time span despite needing a lower number of measurements. To prevent this situation, we introduce a weight to the utility function with the shape of a density function of a beta distribution, such that
![${\rm{\Delta }}\,\ln \left( {{B_{10}}} \right) = \beta \left( {{\rm{\Delta }}t,a,b} \right)\left[ {\ln \left( {{B_{10,n + 1}}} \right) - \ln \left( {{B_{10,n}}} \right)} \right],$](/articles/aa/full_html/2023/01/aa43938-22/aa43938-22-eq15.png) (9)
(9)
where ∆t is the difference in days between the new proposed observation and the current date (normalized on all candidate dates), and n denotes the number of gathered datapoints at the moment of running KOBEsim. We choose the arguments of the beta distribution in such a way that in order to end up with a time gap (i.e., time between the last observation and the next one) greater than 40% of the targeted periodicity, the increase in the ln(B10) should be at least five times greater than for the next date in the priority list (a = 1 and b = 5). The beta distribution weight is an optional parameter of KOBEsim and it is activated by default.
3 Results
In this section, we show different analyses to test the algorithm against simulated (Sect. 3.1) and real (Sect. 3.2) datasets.
Values of the orbital parameters used for the RV simulation.
3.1 Testing KOBEsim on simulated datasets
3.1.1 Simulated data
To generate synthetic data we first had to simulate the observing dates. The observing time must be between the astronomical twilights from the observatory location (i.e., when the Sun is at 18 degrees below the horizon) and the elevation of the target over the horizon must be greater than a given minimum altitude during the exposure time to avoid large chromatic distortions and extinction due to the atmosphere (e.g., Dumusque et al. 2011). Through the following examples, we consider a probability of 55% for a night to be assigned to the project, and we assume that 70% of the nights meet the appropriate weather conditions to perform the observations.
Second, we simulated the RV measurements. The Vsys, P, and t0 were drawn from uniform distributions. For this example, we decided the boundary values for P to cover the properties of the KOBE sample (orbital periods inside the HZ of late-type K dwarfs calculated as defined by Kopparapu et al. 2014). We calculated the RV semi-amplitude as
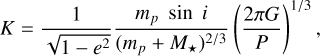 (10)
(10)
which requires four more parameters: the planetary mass (mp), the orbital inclination (i), the eccentricity (e), and the stellar mass (M★). We note that G represents the gravitational constant. We assume M★ to be equal to 0.5 M⊙ since it is the mean value of the KOBE sample (spectral types from K5 to M0). For mp we explore different scientific cases (5, 10, 20, and 60 M⊕). Finally, to simplify the problem, we assume an edge-on system (i = 90°) and a circular orbit (e = 0). In Table 2 we show the parameter selection used for this test. In this case Vsys, P, and t0 has a value within the indicated range, while the mp value is selected from the four given options. We add white noise to the mock RVs through a normal distribution with a mean of 0 m s−1 and a standard deviation of 3 m s−1 mimicking the instrumental noise (conservative values for the CARMENES instrument). We consider a Gaussian uncertainty associated with the simulated RV data, with a mean of 3 m s−1 and a standard deviation of 0.3 m s−1. Since the aim of KOBEsim is to improve the efficiency of Keplerian modulation detection, we work under the assumption of a well-characterized stellar activity (e.g., Dumusque et al. 2011; Oshagh et al. 2017). Therefore, we do not include red noise in our simulated data, and it is a caveat the user must bear in mind.
3.1.2 Running KOBEsim
KOBEsim should always be executed after obtaining a new dat-apoint for a given target. In this way the state of knowledge is updated and provides a list of the next possible observing dates ordered by priority as detailed in Sect. 2. We use the above-described simulation tool to generate simulated observations taking into account the visibility from CAHA for one of the KOBE targets. We generated the first ten observations assuming a model in which mp = 20 M⊕ and P = 59 d. In Fig. 2 we show the GLS periodogram (left panel) and the phase-folded RV curve after the parameter inference is performed for both competing models (right panel). Thus, Ppeak = 62.6 d is our target periodicity to test with KOBEsim (compatible with the true period P used in the model as the prior is Gaussian with a σ = 4 d; see Table 1). The goal now is to predict the best observing date for the next datapoint (the 11th in the time series) in order to speed up a possible planet detection at that periodicity.
The two models we employ to fit the data allow us to quantify how well supported the planet model is against the null hypothesis with the available data. In this case we obtain ln(B10,initial) = −3.74 ± 0.05. KOBEsim now generates a new synthetic datapoint based on the inferred planetary orbital and physical parameters and adds it to the previous datapoints, calculating the increase in ln(B10). This process is repeated independently for different orbital phases. Here we compare a total of 20 candidate orbital phases (Nphases = 20), which for this simulated planet is equivalent to comparing dates around three days apart from each other. In this particular simulation, we imposed the constraint that if the next matching date is more than three months away from the current date, that sub-phase is discarded6: since the KOBE program monitors 50 targets and it was awarded with ~55% of the nights, the chances of observing the target are high, and waiting that long would imply a waste of telescope time. Once all of the candidate dates are calculated, KOBEsim computes which is the best given the current data and assuming the input periodicity. The execution of the code takes ~32 s/phase and is repeated Nphases + 1 times, which leads to a total runtime of ~15 min.
In Fig. 3 we show the output plot returned by the algorithm. The difference in ln(B10) of the one-planet model against the null hypothesis is shown for each orbital phase. The figure shows that the algorithm generated fewer than 20 candidate points. This is caused by the impossibility of observing the target over the next three months, either because the corresponding dates are not assigned to the program or because the star has already set. As in this example, we use the beta distribution, meaning that the criterion for selecting the best observing date is not the one that maximizes the increase in ln(B10). Instead, KOBEsim maximizes the weighted ∆ln(B10) given by Eq. (9), thus finding a trade-off between efficiency and the time we have to wait until the next observation. In this example, we find out that this occurs for an orbital phase around ϕ = 0.17, reaching ∆ ln(B10) = +0.35 ± 0.06. In Appendix A we show the corresponding csv output (Table A.2). In view of Fig. 3, every candidate observation will lead to a positive increase in ln(B10) or it will be maintained at the initial value. This may not occur if we are targeting the wrong period, as we discuss in Sect. 3.1.4.
 |
Fig. 2 Simulation of ten RV datapoints to test KOBEsim. Left: GLS periodogram showing an emerging period at Ppeak = 62.6 d nearly reaching a false alarm probability (FAP) of 0.1 (y-axis equal to 1). The lighter green region corresponds to the optimistic HZ, the darker region to the conservative HZ as defined in Kopparapu et al. (2014). Right: Fit of the simulated RV data. The solid black line is the fit for one-planet hypothesis (H1); the dash-dotted line is fit for the null hypothesis (H0); and the dotted line is the true model used to simulate the datapoints (in red). The shaded region shows the confidence interval at 1σ (dark gray) and 2σ (light gray) for the hypothesis with a planet. The lower panel shows the residuals for the one-planet hypothesis fit. |
 |
Fig. 3 KOBEsim output figure. The y-axis shows the logarithm of the expected Bayes factor and the x-axis shows the orbital phase. The vertical dashed line gives the phase selected as the optimal option, and gives its corresponding date. The horizontal dashed lines indicate the initial ln(B10) (lower line) and the expected value at the selected phase (upper line). The increment is shown with a gray arrow. The color-coding shows the priority order for selecting the next observing date. |
3.1.3 Efficiency
To study the efficiency of KOBEsim, we estimate how long it would take to detect planets of different masses within the HZ for the particular case of the KOBE experiment. We compare this with the time and the number of observations that a monotonic cadence approach (i.e., obtaining observations every N days) would require. For this purpose, we simulate the future observations for a given target, cumulatively, until we obtain enough evidence from the one-planet model over the null hypothesis to claim the detection. We set this limit at ln(B10) > 6. We performed this procedure for both KOBEsim modes (with and without the beta distribution), and spacing the observations with the cadence assigned to our testing target (6 ± 2 d) as long as that day meets good weather conditions and if it is a date granted for the project (see Sect. 3.1.1), otherwise it is postponed to the next plausible day. Hereafter, we refer to the strategies as K (for KOBEsim), Kβ (KOBEsim beta), and MC (monotonic cadence). We note that the simulations of new observations (corresponding to the right circle in Fig. 1) are computed independently from KOBEsim and with the sole idea of testing the efficiency of our methodology. Thus, after deciding the optimum next date, we predicted again the RV value at the corresponding orbital phase. Contrary to the KOBEsim simulation stage (Fig. 1 panel b), in this case we included white noise, as explained in Sect. 3.1.1, but we did not include in the associated uncertainty the component due to the inference (the standard deviation from the RV predictive distribution) since the sources of uncertainty in real observations are only the jitter (Ej) and the photon noise (σj).
In Fig. 4 we show the results for planets of 5, 10, 20, and 60 M⊕ using P = 59 d and Ppeak = 62.6 d. In this section we do not update Ppeak; we keep it fixed to run KOBEsim at each iteration. For all of these planetary masses except for 5 M⊕, we considered the visibility of our testing target. As the precision of CARMENES in its optical arm is around 1 m s−1, a planet of 5 M⊕ corresponds to the detectability limit case for the KOBE experiment (RV semi-amplitude within the HZ of late K dwarfs between 0.72 and 1.15 m s−1). Since such a detection is very demanding, we simulated these measurements considering a circumpolar star, and thus every night of the year can be used to collect data if the weather conditions are favorable. In addition, to achieve a detection of this kind in the time that the KOBE program lasts, it would be necessary to increase the exposure time (thereby increasing the signal-to-noise ratio to reduce the uncertainty). In practice, this would only be feasible with the brightest targets as the maximum exposure time allowed by the CARMENES instrument is 1800 s. For this reason for 10, 20, and 60 M⊕ (see Fig. 4), we considered a conservative uncertainty following a normal distribution with a mean of 3 m s−1, whereas for 5 M⊕ we reduced the mean to 1.5 m s−1. We started with ten initial datapoints. In every planetary mass case, we see the gradual increase in ln(B10) that each strategy follows as new observations are added. We checked that different initial sets of simulated data (i.e., varying the white noise in the RV, the first observing date, and phase coverage, but keeping the same time span and number of measurements) did not significantly change the results. Particularly, in Fig. 4 the standard deviation in the y-axis (ln(B10)) is below 1 for every number of observations and the relative error in the corresponding slopes are 6%. At first glance, it is clear that the number of observations needed to confirm the planetary signal is greatly reduced when using the KOBEsim approach, especially for the less massive planets. Furthermore, the number of days invested in these observations is also greatly reduced even for the most massive planets when using Kβ.
The large time span required for detecting the two most massive simulated planets when applying the K strategy (147 d for the 60 M⊕ simulation) in comparison with both Kβ (48 d) and MC (124 d) strategies, can be explained by the altitude of the testing star. This target sets over three months after starting the simulations. Therefore, the detection in the former strategy, unlike the other two, is postponed until after the target rises again. This example highlights the importance of using the beta distribution since the efficiency of the observations requires finding a compromise between time span and number of measurements. These four simulations show that greatly reduces the time span, and the gain in terms of number of observations is nearly as good as in K.
The efficiency gain by means of Kβ in comparison with MC strategy is shown in Table 3. It collects the key information to support the strength of this algorithm in the context of blind-search surveys. In terms of the number of observations, the improvement varies from 16% for the heavy planets (20 M⊕) to 29–33% for the light planets (5–10 M⊕). Furthermore, regarding the improvement in the number of days, KOBEsim can be decisive even for the high-mass planets mentioned above since in this particular case we achieved an improvement of 38–61% (20–61 M⊕). Finally, the most impressive improvement is related to the number of days for low-mass planets, reducing the time span by 41–47% (5–10 M⊕). This could increase the speed of detection of rocky planets within the HZ of the parent star by nearly a factor of 2, provided the RV modulations due to stellar activity are well known.
Improvement achieved using KOBEsim beta (Kβ) in comparison with a monotonic cadence (MC) strategy for simulated datasets.
3.1.4 False detections
We test the behavior of KOBEsim when pursuing spurious periodicities caused by signals either behaving stochastically or not induced by Keplerian sources. If we have very few datapoints at the time of period selection, it may occur that the period pursued does not correspond to a planet signal. It is also possible that we select a periodicity resulting from stellar activity mimicking the wobble of the star when it has an orbiting planet (e.g., Queloz et al. 2001; Figueira et al. 2010; Santos et al. 2014). These possible scenarios raise the question of how KOBEsim behaves against a spurious period.
To test this, we now focus on a given periodicity that maximizes the GLS periodogram, Ppeak, and we base our strategy on it. However, there is a planet orbiting the star at a different period, Pplanet. To illustrate this scenario, we start by simulating the first ten datapoints as a signal with the spurious period (Ppeak), constraining it to be compatible within 1σ with the RV that would be induced by a planet at the true period (Pplanet). In this way we ensure that the preliminary GLS periodogram proposes Ppeak. The next observations are generated using the true period, thus the GLS periodogram will start showing Pplanet instead of Ppeak. We perform this test for four random periods and the corresponding planetary masses that induce the same RV semi-amplitude in all cases (K = 6 m s−1 in this example). In Fig. 5 we show the evolution of the Bayesian evidence. The solid lines indicate the cases in which KOBEsim is targeting the correct orbital period. Also in Fig. 5, we show a toy model for the active star case. We consider that after the first ten observations simulated with the spurious period Ppeak, the activity ceases, and thus the next datapoints follow a constant model (K = 0 case, corresponding to a RV= Vsys + Ej).
From this simulation, we find that when targeting false periods with KOBEsim, the Bayes factor can be reduced in contrast with a successful case (when targeting a correct period all the candidate dates increase the Bayes factor, or are at least compatible with no variation; see Sect. 3.1.2 and Fig. 3). Specifically, in the case where we test a signal produced by stellar activity that disappears (K = 0), it is quickly visible that the period is incorrect. Surprisingly, some spurious periods reach the planet detection according to the ln(B10) > 6 criterion. From the periodogram, we check that generally even selecting the optimum observing dates for a wrong period, the RV curve is well sampled and the GLS periodogram reveals the correct period (higher power for the true period than the targeted). Nonetheless, we find particular cases where this does not occur. As the semi-amplitude of this example is considerably high, the planet detection is reached too soon (with few datapoints) to sample the whole RV curve if Ppeak < Pplanet. To illustrate this situation, Fig. 6 shows the RV curves in phase for the case of Ppeak = 81.47 d and Pplanet = 107.57 d. In the top panel of Fig. 6 we show the correct RV phase-folded curve (i.e., phase-folded with the true periodicity). In view of this curve, there are not enough data to claim a detection since the orbital phase has not yet been covered. When looking at the periodogram shown in Fig. 7, we find that there is a whole family of periods.
In practice, this weak point can be easily circumvented by looking at the periodogram daily. KOBEsim is the strategy to decide when to observe, but in any case it can replace our analysis. The user must be responsible for testing all the periods appearing in the GLS periodogram to check which is most favorable (e.g., calculating the Bayes factor for those competing planet hypotheses at different periods instead of using the null hypothesis). For this reason, the period chosen to be targeted with our strategy is not immutable, instead it must be updated as we gather additional data, as we indicate in the workflow scheme in Fig. 1.
 |
Fig. 4 Prediction in the evolution of the logarithm of the Bayes factor for simulated planets of 5, 10, 20, and 60 M⊕ at P = 59 d. The period targeted with KOBEsim is Ppeak =57.54 d. The number of observations and the time it would take to detect the planet are compared using three different strategies: KOBEsim (K), KOBEsim beta (Kβ), and spacing the observations at a fixed cadence (MC) of 6 d. |
 |
Fig. 5 Prediction in the evolution of the logarithm of the Bayes factor when targeting with KOBEsim a period Ppeak (each chart), but the signal is induced by a planet at Pplanet (see legend for colors). All the cases induce a signal of semi-amplitude K = 6 m s−1. The solid lines are the cases in which KOBEsim is pursuing the correct period (Ppeak = Pplanet). The black line corresponds to the active-star case. After the first ten observations it is assumed that the signal is turned off (K = 0). |
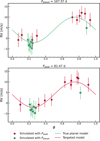 |
Fig. 6 Phase-folded RV curve of simulated data. Top: Assuming the true orbital period (Pplanet). In red are indicated the first observations, generated with Ppeak constrained to be compatible with the true signal within 1σ. Bottom: Assuming the incorrect period, the one used to perform KOBEsim, Ppeak. |
 |
Fig. 7 Periodogram for the studying case of Pplanet = 107.57 d and Ppeak = 81.47 d, with data gathered at the time of achieving the threshold ln(B10) > 6. |
3.2 Application to real data
3.2.1 KOBE target
We use the 21 first observed measurements from a particular KOBE target as a test bench. At this point a periodicity is visible inside the HZ (Ppeak = 94.13 d). By taking this periodicity as our prior knowledge to run KOBEsim (i.e., assuming the RV is induced by an orbiting planet at Ppeak), we infer the parameters Θ1 (see Eq. (4)). In Fig. 8, we show the RV time series (red dots), and the inferred model (solid line). With these inferred parameters, the lower limit for the planetary mass is mp sin i = (27.62 ± 8.05) M⊕.
We subsequently use these parameters to simulate the expected future RVs by making use of Eq. (2). In such a way, after the 21st observation we estimate the evolution of ln (B10) and we compare the prediction for the three different observing strategies that we consider in the efficiency test explained in Sect. 3.1.3 (i.e., K, Kβ, and MC). This can be seen in Fig. 9, where the ln (B10) obtained from the observed data is shown (magenta line).
Based on the results of this analysis, and as long as the same trend on the RV data continues, we can detect a planet within the HZ of this star in less than a year. The expected improvement in the case of purely following the Kβ instead of a MC is higher than 26% in terms of the number of observations, and around 41% in terms of time span. This improvement means, if this hypothetical planet actually exists in the system, that we could detect it a year earlier thanks to this approach.
3.2.2 HD 102365
We take the RV data measured by Tinney et al. (2011) to test the algorithm with a target from a different program and instrument. The goal is to evaluate the time that would have been saved if our strategy had been applied. We chose the system HD 102365 since it has a relatively low-mass (mp sin i = 16 M⊕) isolated planet at a large period (P = 122.1 d), inducing a RV semi-amplitude of ~ 3 m s−1 while orbiting a G-dwarf star. Thus, it required a vast number of observations over a long time span to be detected. Additionally, the star is known to be chromospherically inactive with a value of −4.99 for R′HK (Meunier et al. 2017; Boro Saikia et al. 2018), which corresponds to an induced RV semi-amplitude of ~41 cm s−1 (Suárez Mascareño et al. 2017) and has a very slow rotation velocity (v sin i = 0.7 km s−1), thus in this case activity does not play a relevant role. These observations were done with the UCLES échelle spectrograph (Diego et al. 1992) as part of the Anglo-Australian Planet Search (AAPS) program (Tinney et al. 2001; Wittenmyer et al. 2020).
We started testing the Kg strategy with the first ten real datapoints. The optimum date was chosen according to the algorithm, which simulates the RV at 20 sub-phases from the parameter inference of this reduced sample. In this case we considered that all the nights were available.
Once the date was decided, a new RV datapoint was added using the parameter inference from the whole sample (149 data-points). To this new observation, we applied a Gaussian noise of mean and standard deviation of the median and standard deviation of the residuals. We took the same associated RV uncertainty as the corresponding real datapoint for the sake of being more fair with the comparison. Then, the process was repeated until the planet was detected according to the Bayes factor. The target period, Ppeak, was updated at the beginning of each iteration by means of the GLS periodogram.
In the upper panel of Fig. 10 we show the evolution of the Bayes factor as a function of number of observations and time span, comparing our strategy with the real observations. We find that the number of measurements would be reduced by around 16% (from 105 to 88 observations), and the time span by ~41% (from 3318 to 1964 d). Since the exposure time varies from 200 to 400 s, 1–2 h of telescope time would be saved. In the lower panel of Fig. 10 we display the evolution of the maximum period in the GLS periodogram for both cases. It is remarkable that it converges more quickly toward the true period of the planet using Kβ.
 |
Fig. 8 RV observed data (red dots) vs. time. The inferred model is shown as a solid line, using as prior Ppeak = 94.13 d. The parameters resulting from the MCMC inference, as well as the corresponding mass lower limit, are collected in the bottom left box. The shaded region shows the confidence interval at 1σ (dark gray) and 2σ (light gray) for the hypothesis with a planet. |
 |
Fig. 9 Prediction in the evolution of the logarithm of the Bayes factor in a real case of the KOBE experiment, assuming a planet at Ppeak = 94.13 d. The number of observations and the time it takes to detect the planet are compared using three different strategies: KOBEsim (K), KOBEsim beta (Kβ), and spacing the observations in a fixed cadence (MC) of 6 d. Planet detection criterion: ln(B10) > 6. |
4 Conclusions
In this paper we present KOBEsim, an algorithm designed to improve the efficiency in the process of gathering new RV measurements in blind-search surveys. This new observational strategy is developed aspiring to maximize the chances of success of the KOBE experiment (Lillo-Box et al. 2022). It is a Bayesian approach using the Bayes factor as a metric to measure how well supported the planet hypothesis is at a given orbital period (H1) compared to the null hypothesis where there is no planet in the system (H0). Given the previous RV data and an orbital period to target, KOBEsim proposes a priority calendar to observe the star again according to the expected increase in this quantity. By weighting the increment in the Bayes factor with a beta distribution, we find a trade-off between number of measurements and time span necessary to claim a planet detection. We demonstrate its effectiveness in speeding up the planet detection when stellar activity is well characterized, being especially useful in lighter planets for which the improvement is nearly 50% in comparison with monotonic cadence strategies. This improvement can be decisive to detect rocky planets within the HZ in reasonable time spans.
These results show the importance of a continuous monitoring of the measurements in RV studies of planet searches and demonstrates that simple monotonic cadence strategies are not efficient, wasting more telescope time than required to confirm or characterize a given planet. It should be noted that, even though designed for blind-search surveys, it can also be highly useful in the follow-up of transiting candidates since the orbital period is clear. The approach described in this paper can be easily implemented for any instrument. High-resolution spectrographs able to detect planetary signals and installed in observatories offering service mode observations (e.g., ESO/Paranal or CAHA) should have the capability to adapt the observing strategy to improve their efficiency, which nowadays is difficult to achieve due to how observing time of the different programs is allocated. Offering the user the flexibility to adapt the cadence of the observations on a daily basis is a benefit to the community and to the observatories. In this regard, GTO programs can be highly benefited as they enjoy wider freedom in their schedules; it is an opportunity to save time and to favor the detection of the most elusive planets for the upcoming generation of instruments, such as HARPS3 (Thompson et al. 2016) or NIRPS (Wildi et al. 2017).
Throughout the manuscript we have mentioned some caveats to bear in mind when using KOBEsim. First of all, the user has to take care of the preprocessing of the data in order to mitigate any RV signal induced by activity. The RV time series should be corrected from activity before running KOBEsim, for instance subtracting linear and quadratic trends. The use of activity indicators such as line-bisector or the chromospheric contribution of the H and K Ca lines are also useful to disentangle the planetary and activity component in the signal (e.g., Queloz et al. 2001). Second, as concluded in Sect. 3.1.4, the period to be targeted must always be updated after a new observation is added to the dataset. Third, the implementation in the code of a multi-planetary system model (hypothesis Hn planets) is straightforward. We are conscious of the scientific value of this utility; KOBEsim is not only a tool to boost planet detection in single planet systems or in multi-planetary systems where no planets have been yet detected, but it can enable us to determine more quickly whether there is more than one planet inducing the signal. In the same regard, it would also be interesting not to always compare the evidence of the model with the null hypothesis, but with another planet hypothesis orbiting at other period to deal with aliasing. These implementations would make our algorithm more powerful, but are yet to be tested and are beyond the scope of the present work.
 |
Fig. 10 KOBEsim test with real HD 102365 RV data. Upper panel: Number of measurements (left) and time span (right) required to detect the planet comparing the real observations and the simulation for the KOBEsim beta strategy. Lower panel: Ppeak evolution for both strategies. |
Acknowledgements
We are grateful to Dr. Rodrigo Díaz for his useful suggestions as referee helping to improve the quality of the manuscript. O.B.-R., J.L.-B. and A.C.-G. acknowledge financial support received from “la Caixa” Foundation (ID 110000434) and from the European Unions Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 847648, with fellowship code LCF/BQ/PI20/11760023. This research has also been partly funded by the Spanish State Research Agency (AEI) Projects No.PID2019-107061GB-C61 and No. MDM-2017-0737 Unidad de Excelencia “María de Maeztu”- Centro de Astrobiología (INTA-CSIC). This work was supported by Fundação para a Ciência e a Tecnologia (FCT) and Fundo Europeu de Desenvolvimento Regional (FEDER) via COMPETE2020 – Programa Operacional Competitividade e Inter-nacionalização by these grants: UIDB/04434/2020; UIDP/04434/2020; PTDC/FIS-AST/32113/2017 & POCI-01-0145-FEDER-032113; PTDC/FIS-AST/28953/2017 & POCI-01-0145-FEDER-028953. A.M.S. acknowledges support from FCT through the Fellowship 2020.05387.BD. and POCH/FSE (EC). O.D.S.D. is supported in the form of work contract (DL 57/2016/CP1364/CT0004) funded by FCT. J.P.F. is supported in the form of a work contract funded by national funds through FCT with reference DL 57/2016/CP1364/CT0005. A.M.S. acknowledges financial support from the French Programme National de Planétologie (PNP, INSU).
Appendix A KOBEsim inputs and outputs
There are 12 fields accepted as input; they are all found in Table A.1. The observatory coordinates, the star name, and the file containing the RV time series are mandatory. As the orbital period is an input of the code, we highly recommend that the user perform a careful study of the period to be targeted, for instance using the ℓ1 periodogram (Hara et al. 2017) as a complementary method to the GLS periodogram.
As a result of running KOBEsim, a prioritized list of calendar dates is delivered in the form of an ascii file in csv format. Each row corresponds to a candidate future observing date ranked by preference: from highest to lowest weighted ∆ ln(B10). The columns from left to right are calendar date (format year-month-day), JD, the corresponding orbital phase, the expected ln(B10) and its associated uncertainty, and the increase in ∆ ln(B10) and its uncertainty. An example of this output file is shown in Table A.2 for the simulated case of Sect. 3.1.2. For a more illustrative inspection of the results, KOBEsim also returns a plot of ln (B10,n+1) versus the orbital phase. See Sect. 3.1.2 for details.
Inputs of the KOBEsim code: obs (or obs_n), star, and file are mandatory.
Output csv file of KOBEsim for the testing target with simulated data.
References
- Akeson, R. L., Chen, X., Ciardi, D., et al. 2013, PASP, 125, 989 [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., Hauser, H., & Shirts, P. 1997, ApJ, 474, L115 [Google Scholar]
- Cabona, L., Viana, P. T. P., Landoni, M., & Faria, J. P. 2021, MNRAS, 503, 5504 [NASA ADS] [CrossRef] [Google Scholar]
- Damasso, M., Sozzetti, A., Lovis, C., et al. 2020, A&A, 642, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demangeon, O. D. S., Zapatero Osorio, M. R., Alibert, Y., et al. 2021, A&A, 653, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Ségransan, D., Udry, S., et al. 2016, A&A, 585, A134 [Google Scholar]
- Diego, F., Crawford, I., Barlow, M., Fish, A., & Dryburgh, M. 1992, in European Southern Observatory Conference and Workshop Proceedings, Vol. 40, 267 [NASA ADS] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espada, D., Saito, M., Nyman, L.-Å., et al. 2014, SPIE Conf. Ser., 9149, 91491S [NASA ADS] [Google Scholar]
- Faria, J. P., Suárez Mascareño, A., Figueira, P., et al. 2022, A&A, 658, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figueira, P., Santos, N. C., Bonfils, X., et al. 2010, EAS Pub. Ser., 42, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B. 2008, AJ, 135, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Conley, A., Meierjurgen Farr, W., et al. 2013, Astrophysics Source Code Library [record ascl:1303.002] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Blunt, S., & Sinukoff, E. 2018, PASP, 130, 044504 [Google Scholar]
- Garcia-Piquer, A., Morales, J. C., Ribas, I., et al. 2017, A&A, 604, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Sipocz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Giuliano, M. E., Rager, R., & Ferdous, N. 2007, in Proceedings of The International Conference on Automated Planning and Scheduling (AAAI), 160 [Google Scholar]
- Hara, N. C., Boué, G., Laskar, J., & Correia, A. C. M. 2017, MNRAS, 464, 1220 [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability. 3rd Edition, (Oxford: Clarendon Press) [Google Scholar]
- Kopparapu, R. K., Ramirez, R. M., SchottelKotte, J., et al. 2014, ApJ, 787, L29 [Google Scholar]
- Lillo-Box, J., Figueira, P., Leleu, A., et al. 2020, A&A, 642, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Faria, J. P., Mascareño, A. S., et al. 2021, A&A, 654, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Santos, N. C., Santerne, A., et al. 2022, A&A, 667, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loredo, T. J. 2004, AIP Conf. Ser., 707, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Loredo, T. J., Berger, J. O., Chernoff, D. F., Clyde, M. A., & Liu, B. 2012, Stat. Methodol., 9, 101 [CrossRef] [Google Scholar]
- Mackay, D. J. C. 2003, Information Theory, Inference and Learning Algorithms (Cambridge: Cambridge University Press) [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Meunier, N., Mignon, L., & Lagrange, A. M. 2017, A&A, 607, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Zapatero Osorio, M. R., Malavolta, L., et al. 2020, MNRAS, 499, 5004 [Google Scholar]
- Oshagh, M., Santos, N. C., Figueira, P., et al. 2017, A&A, 606, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrakis, K., Ntzoufras, I., & Tsionas, E. G. 2014, Comput. Stat. Data Anal., 77, 54 [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., CARMENES Consortium, Amado, P. J., et al. 2020, SPIE Conf. Ser., 11447, 114473C [Google Scholar]
- Santos, N. C., Mortier, A., Faria, J. P., et al. 2014, A&A, 566, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2017, MNRAS, 468, 4772 [Google Scholar]
- Thompson, S. J., Queloz, D., Baraffe, I., et al. 2016, SPIE Conf. Ser., 9908, 99086F [Google Scholar]
- Thrane, E., & Talbot, C. 2019, PASA, 36, e010 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2001, ApJ, 551, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Butler, R. P., Jones, H. R. A., et al. 2011, ApJ, 727, 103 [Google Scholar]
- Wildi, F., Blind, N., Reshetov, V., et al. 2017, SPIE Conf. Ser., 10400, 1040018 [Google Scholar]
- Wittenmyer, R. A., Wang, S., Horner, J., et al. 2020, MNRAS, 492, 377 [NASA ADS] [CrossRef] [Google Scholar]
The code is publicly available at the following link: https://github.com/olgabalsa/KOBEsim
Both the number of walkers and steps can be customized by the user; see Table A.1.
The maximum days apart parameter can be set by the user; see Table A.1.
All Tables
Improvement achieved using KOBEsim beta (Kβ) in comparison with a monotonic cadence (MC) strategy for simulated datasets.
All Figures
 |
Fig. 1 KOBEsim workflow scheme. It starts by gathering RV data until it finds a dominant period (step 1), from which the KOBEsim algorithm provides the next optimum observing date (step 2). |
| In the text | |
 |
Fig. 2 Simulation of ten RV datapoints to test KOBEsim. Left: GLS periodogram showing an emerging period at Ppeak = 62.6 d nearly reaching a false alarm probability (FAP) of 0.1 (y-axis equal to 1). The lighter green region corresponds to the optimistic HZ, the darker region to the conservative HZ as defined in Kopparapu et al. (2014). Right: Fit of the simulated RV data. The solid black line is the fit for one-planet hypothesis (H1); the dash-dotted line is fit for the null hypothesis (H0); and the dotted line is the true model used to simulate the datapoints (in red). The shaded region shows the confidence interval at 1σ (dark gray) and 2σ (light gray) for the hypothesis with a planet. The lower panel shows the residuals for the one-planet hypothesis fit. |
| In the text | |
 |
Fig. 3 KOBEsim output figure. The y-axis shows the logarithm of the expected Bayes factor and the x-axis shows the orbital phase. The vertical dashed line gives the phase selected as the optimal option, and gives its corresponding date. The horizontal dashed lines indicate the initial ln(B10) (lower line) and the expected value at the selected phase (upper line). The increment is shown with a gray arrow. The color-coding shows the priority order for selecting the next observing date. |
| In the text | |
 |
Fig. 4 Prediction in the evolution of the logarithm of the Bayes factor for simulated planets of 5, 10, 20, and 60 M⊕ at P = 59 d. The period targeted with KOBEsim is Ppeak =57.54 d. The number of observations and the time it would take to detect the planet are compared using three different strategies: KOBEsim (K), KOBEsim beta (Kβ), and spacing the observations at a fixed cadence (MC) of 6 d. |
| In the text | |
 |
Fig. 5 Prediction in the evolution of the logarithm of the Bayes factor when targeting with KOBEsim a period Ppeak (each chart), but the signal is induced by a planet at Pplanet (see legend for colors). All the cases induce a signal of semi-amplitude K = 6 m s−1. The solid lines are the cases in which KOBEsim is pursuing the correct period (Ppeak = Pplanet). The black line corresponds to the active-star case. After the first ten observations it is assumed that the signal is turned off (K = 0). |
| In the text | |
 |
Fig. 6 Phase-folded RV curve of simulated data. Top: Assuming the true orbital period (Pplanet). In red are indicated the first observations, generated with Ppeak constrained to be compatible with the true signal within 1σ. Bottom: Assuming the incorrect period, the one used to perform KOBEsim, Ppeak. |
| In the text | |
 |
Fig. 7 Periodogram for the studying case of Pplanet = 107.57 d and Ppeak = 81.47 d, with data gathered at the time of achieving the threshold ln(B10) > 6. |
| In the text | |
 |
Fig. 8 RV observed data (red dots) vs. time. The inferred model is shown as a solid line, using as prior Ppeak = 94.13 d. The parameters resulting from the MCMC inference, as well as the corresponding mass lower limit, are collected in the bottom left box. The shaded region shows the confidence interval at 1σ (dark gray) and 2σ (light gray) for the hypothesis with a planet. |
| In the text | |
 |
Fig. 9 Prediction in the evolution of the logarithm of the Bayes factor in a real case of the KOBE experiment, assuming a planet at Ppeak = 94.13 d. The number of observations and the time it takes to detect the planet are compared using three different strategies: KOBEsim (K), KOBEsim beta (Kβ), and spacing the observations in a fixed cadence (MC) of 6 d. Planet detection criterion: ln(B10) > 6. |
| In the text | |
 |
Fig. 10 KOBEsim test with real HD 102365 RV data. Upper panel: Number of measurements (left) and time span (right) required to detect the planet comparing the real observations and the simulation for the KOBEsim beta strategy. Lower panel: Ppeak evolution for both strategies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


