| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 20 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202243306 | |
| Published online | 02 December 2022 | |
Revisiting fundamental properties of TiO2 nanoclusters as condensation seeds in astrophysical environments★
1
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz, Austria
e-mail: janphilip.sindel@oeaw.ac.at
2
Centre for Exoplanet Science, University of St Andrews,
North Haugh,
St Andrews,
KY16 9SS, UK
3
SUPA, School of Physics & Astronomy, University of St Andrews,
North Haugh,
St Andrews,
KY16 9SS, UK
4
Institute for Astronomy, KU Leuven,
Celestijnenlaan 200D,
3001
Leuven, Belgium
5
Department of Chemistry and Molecular Biology, University of Gothenburg,
Kemigárden 4,
412 96
Gothenburg, Sweden
6
TU Graz, Fakultät für Mathematik, Physik und Geodäsie,
Petersgasse 16,
8010
Graz, Austria
Received:
10
February
2022
Accepted:
24
June
2022
Context. The formation of inorganic cloud particles takes place in several atmospheric environments, including those of warm, hot, rocky, and gaseous exoplanets, brown dwarfs, and asymptotic giant branch stars. The cloud particle formation needs to be triggered by the in situ formation of condensation seeds since it cannot be reasonably assumed that such condensation seeds preexist in these chemically complex gas-phase environments.
Aims. We aim to develop a method for calculating the thermochemical properties of clusters as key inputs for modelling the formation of condensation nuclei in gases of changing chemical composition. TiO2 is used as benchmark species for cluster sizes N = 1–15.
Methods. We created a total of 90000 candidate (TiO2)N geometries for cluster sizes N = 3−15. We employed a hierarchical optimisation approach, consisting of a force-field description, density-functional based tight-binding, and all-electron density-functional theory (DFT) to obtain accurate zero-point energies and thermochemical properties for the clusters.
Results. In 129 combinations of functionals and basis sets, we find that B3LYP/cc-pVTZ, including Grimme’s empirical dispersion, performs most accurately with respect to experimentally derived thermochemical properties of the TiO2 molecule. We present a hitherto unreported global minimum candidate for size N = 13. The DFT-derived thermochemical cluster data are used to evaluate the nucleation rates for a given temperature-pressure profile of a model hot-Jupiter atmosphere. We find that with the updated and refined cluster data, nucleation becomes unfeasible at slightly lower temperatures, raising the lower boundary for seed formation in the atmosphere.
Conclusions. The approach presented in this paper allows finding stable isomers for small (TiO2)N clusters. The choice of the functional and basis set for the all-electron DFT calculations has a measurable impact on the resulting surface tension and nucleation rate, and the updated thermochemical data are recommended for future considerations.
Key words: molecular data / astrochemistry / planets and satellites: atmospheres / planets and satellites: gaseous planets / molecular processes
Tables E.1–E.123 and F.1–F.123 are only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/668/A35
© J. P. Sindel et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The quest for the first (or primary) astrophysical condensate that triggers the formation of cosmic dust is as old as the discovery of newly formed condensates in astrophysical environments (e.g. Blander & Katz 1967; Andriesse et al. 1978; Gail et al. 1986; Patzer et al. 1995; Sloan et al. 2009; Goumans & Bromley 2013). More recently, this quest was renewed by the need of understanding the formation of clouds in the chemically diverse atmospheres of extrasolar planets and brown dwarfs (e.g. Helling et al. 2008, 2016; Lee et al. 2018; Samra et al. 2020; Charnay et al. 2022; Min et al. 2020).
Cloud particles form when a supersaturated gas condenses on the surface of ultra-small particles. These nanosized particles are called cloud condensation nuclei (CCN) (Hudson 1993). The formation of CCN is a crucial step within cloud formation, but its formation rate needs to be determined from first principles, as attempts to derive it from models using the nucleation rate as a free parameter are unable to constrain it accurately (Ormel & Min 2019). Several efforts were undertaken to model the formation of CCN from a quantum-mechanical bottom-up approach including nucleating species such as titanates (Jeong et al. 2000; Plane et al. 2013; Patzer et al. 2014), SiO (Bromley et al. 2016), Fe- and Kr-bearing molecules (Chang et al. 2005, 2013) and alumina (Patzer et al. 2005), and Al2O3 (Lam et al. 2015; Gobrecht et al. 2022). Recently, Köhn et al. (2021) introduced a 3D Monte Carlo approach for the nucleation of TiO2 that agrees reasonably well with results from kinetic nucleation approaches. Comparison studies like this require knowledge of thermochemical cluster data of the most favourable isomers.
On cool rocky planets, CCN can be formed from external sources such as sulfites from volcanic activity (Andres & Kasgnoc 1998), sea salt from ocean spray, condensing meteoritic dust, and dust particles from sand storms. As these sources do not exist for gaseous planets and are not guaranteed to exist for hot rocky planets, CCN need to be produced by chemical reactions out of the gas phase within the atmosphere to allow cloud formation. The existence of clouds and hazes has been predicted by models and has been observed in hot Jupiters, for example HD189733b (Pont et al. 2013; Barstow et al. 2014), HAT-P-7b (Helling et al. 2019), or WASP-43b (Helling et al. 2020); warm Saturns (e.g. Nikolov et al. (2021); super-Earths Kreidberg et al. 2013); and brown dwarfs (Apai et al. 2013). The process that is considered to produce CCN in the atmospheres of gaseous planets is the formation of small clusters through nucleation. One of the species that has been considered for the formation of CCN in gas giant atmospheres is TiO2, in addition to less refractory species, for example SiO or KCl (Helling 2018). Different descriptions have been used to describe the formation of condensation seeds in exoplanet, brown dwarf, and asymptotic giant branch (AGB) star research: classical nucleation theory (Gail et al. 1986), modified classical nucleation theory (Gail & Sedlmayr 2013), kinetic nucleation networks (Patzer et al. 1998), and chemical-kinetic nucleation descriptions (Gobrecht et al. 2016; Boulangier et al. 2019). All rely at some point in the modelling process on thermochemical data of the species and their small nanosized clusters. Because experimental data often exist for condensed phases and simple gas-phase molecules only, quantum-chemical calculations provide the possibility of addressing the cluster size space in between. Each cluster size appears with different geometrical structures (i.e. its isomers), and it is not a priori known which of the isomers is the most favourable at each reaction step to eventually form a CCN. Experimental input would be required here. In lieu of this, we assume that the thermodynamically most favourable isomer takes this role of a key reactant. We therefore search for the isomer at the global minimum in potential energy for each cluster size because ideally, this will be the configuration that any cluster of that size will relax towards. Global minimum candidate isomers were found in previous studies on TiO2 clusters (Lamiel-Garcia et al. 2017; Berardo et al. 2014; Jeong et al. 2000) and in the analysis of their thermochemical properties (Lee et al. 2015). In this work, a hierarchical approach is applied that uses three different levels of complexity: force fields, density-functional based tight-binding (DFTB), and density-functional theory (DFT) calculations. This approach was developed to globally search for potential geometries of small (TiO2)N clusters (N = 3−15), and their thermochemical properties are analysed using quantum-chemical DFT calculations. In Sect. 2 we describe the methods we used to create possible (TiO2)N cluster structures and the approximations we used to describe their interatomic interactions when searching for a geometry that is energetically favourable, that is, is located at a potential minimum. This approach is tested against previous results for small TiO2 clusters N = 3−6. For the DFT calculations, 129 combinations of functionals and basis sets are benchmarked against experimental data, and we find that the B3LYP functional with the cc-pVTZ basis-set, including Grimme’s empirical dispersion, most accurately predicts the potential energies and thermochemical properties of the TiO2 molecule. In Sect. 3, we evaluate the results for the different steps in our multi-level approach. This section also evaluates the quality of the approach by comparing the cluster isomers we found with known isomers from the literature. Section 4 analyses the impact of the updated cluster potential energies and the related thermochemical data of nucleation rates for a model hot-Jupiter atmosphere. Finally, we discuss our results and possible further work in Sect. 5.
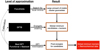 |
Fig. 1 Hierarchical approach to determine global minimum candidate structures for clusters. (1) The geometries and binding energies of small clusters and isomers are used to calibrate the accuracy of the force field and DFTB methods. (2) A force-field description of interatomic interactions is used to locally optimise the geometries of a large number of generated clusters for each size N towards a potential energy minimum. (3) The geometries of these locally and semi-classically optimised cluster candidates are then further refined in a third step, using DFTB methods. This step optimises the geometries of the cluster candidates for the lowest possible potential energy. This provides an energetic ordering of the candidate geometries. (4) The energetically most favourable candidate geometries are then used as inputs for DFT calculations, resulting in the final and most accurate geometries, binding energies, and vibrational and rotational frequencies for each cluster within this approach. |
2 Methods
The goal of this paper is to evaluate small clusters of titanium dioxide (TiO2)N, N = 1−15, with regard to their geometry, binding energy, and thermochemical properties and the impact of these parameters on cloud nucleation in exoplanet atmospheres. A search is conducted for the most favourable isomer of each size N that represents the global minimum of the potential energy surface (PES), which characterises the energy of the system. Additionally, other favourable isomers with potential energies close to the minimum are explored. In order to achieve this, the geometries of the clusters are varied and brought towards a geometry that is located at a potential minimum. A hierarchical method is employed that uses three different levels of complexity to describe the PES: force fields, DFTB, and DFT calculations (see Fig. 1). Because the DFTB approach takes Electron-electron interactions of the valence electrons into account compared to the purely ionic force-field description, it approximates the binding energies for the isomers better. This results in a more accurate energetic ordering of the candidate clusters for each size. For every cluster size N, candidate cluster isomers are created using different methods, and they are optimised towards a local minimum in potential energy using a basin-hopping algorithm. The energy evaluation in this optimisation procedure is based on a description of the inter-atomic interactions by the Coulomb-Buckingham force-field approximation. The resulting cluster geometries are then used as inputs for further geometry optimisation using the DFTB approach because it describes the PES and interatomic interactions more accurately than the force fields. The DFTB approach is used as a second step only as its higher accuracy comes at higher computational cost, making it more economical to only use pre-optimised clusters from the force-field description as inputs. Finally, the candidates at the lowest minima in the potential (which in turn have the highest binding energies) from this second step are used as inputs for all-electron DFT optimisations. With this approach, we aim to achieve highly accurate geometries and energies for the thermodynamically most stable isomers of each cluster size N.
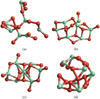 |
Fig. 2 Examples for initial un-optimised cluster geometries of size N = 7, generated (a) randomly, (b) from a known cluster with an additional monomer (marked with yellow circles), (c) from a mirrored cluster of size N = 3 with an additional monomer in the centre, and (d) from N = 7 monomers evenly distributed on a sphere. |
2.1 Construction of seed structures for cluster geometries
We applied the hierarchical approach to (TiO2)N cluster formation. This started with the creation of a broad range of different seed structures or cluster geometries. These seed structures are unoptimised cluster geometries for (TiO2)N, N = 3,…,15, which were then optimised towards potential energy minima. In the first optimisation step, these un-optimised cluster geometries were used as inputs with the force-field approach (Sect. 2.4.2 and the first box in Fig. 1). In order to minimise the chances of missing a particular stable cluster, a large number of seed structures that cover a wide range of structurally diverse geometries were generated. These candidate geometries ranged from closely packed and compact structures to larger and extended structures with void parts and included both symmetrical and asymmetrical structures for all sizes. Ideally, they are also easily optimisable, which means that the average distance between neighbouring atoms should not be much larger than their typical bond length. Four different approaches were used to create these seed clusters of size N:
Random: for a fully randomised seed structure creation, starting with a single TiO2 monomer unit, more units are iteratively attached. They are placed them at the end of a vector with a random orientation and a length of 1.6 Å, which corresponds to the typical Ti-O bond distance for nanosized TiO2 clusters (Fig. 2a).
Known+1: Known stable isomer structures from the literature (Lamiel-Garcia et al. 2017; Berardo et al. 2014) of size N – 1 are taken, and one monomer is randomly attached analogous to method 1 to obtain seed clusters for size N (Fig. 2b).
Both of these methods have a tendency to produce rather compact and highly asymmetric seed structures, especially for larger cluster sizes N. Therefore, two more approaches were introduced to create spatially extended clusters and symmetric clusters, respectively:
Mirror: For even cluster sizes N, a cluster of size
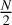 is taken and mirrored about a random axis. For uneven cluster sizes N, a cluster of size
is taken and mirrored about a random axis. For uneven cluster sizes N, a cluster of size 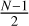 is taken and mirrored. Afterwards, a single monomer is added along the mirror axis to bring the total number of monomer units to N. All seed geometries created using this method fall within the C2 point group (Fig. 2c).
is taken and mirrored. Afterwards, a single monomer is added along the mirror axis to bring the total number of monomer units to N. All seed geometries created using this method fall within the C2 point group (Fig. 2c).Equidistant: Seed structures of size N are created by evenly distributing N monomers equidistant across a sphere of random radius, so that the distances between their centres of mass are between 1.6 and 3.2 Å. The resulting geometries resemble hollow spheres (Fig. 2d).
An example of a candidate geometry of size N = 7 produced by each of these approaches is depicted in Fig. 2. As the parameter space for possible cluster geometries grows with the cluster size N, a distinction between small (N = 3–7) and large (N = 8–15) clusters was made in order to save computational cost. For small clusters, 1000 clusters were created with method 1, 400 with method 2, 400 with method 3, and 200 with method 4, giving a total of 2000 cluster seed geometries for each size. For large clusters, the number of guessed geometries was multiplied by 5 to account for the larger parameter space. Ten thousand cluster seed geometries were created for each size, 5000 with method 1, 2000 with method 2, 2000 with method 3, and 1000 with method 4. Hence, 90 000 geometrical seed structures were tested in total. All seed geometries were then optimised towards potential minima using the force-field description of the PES that is presented at the end of Sect. 2.4.2.
2.2 Density functional theory
To accurately describe a cluster, a large number of interactions, including quantum-mechanical ones, need to be taken into account. We employed the DFT (see Appendix A.1) as a method for solving the Schrödinger equation approximately and for determining zero-point energies, vibrational frequencies, and rotational constants of our clusters. Density functional theory is parametrised through the choice of a functional and a basis set, which has a large impact on the resulting quantities. It is therefore essential to select an appropriate functional and basis set for our purpose.
2.3 Finding the ideal functional and basis set
For the calculations at the density functional level of theory (DFT), the Gaussian16 (Frisch et al. 2013) program was used. It is desirable to use a model parametrisation that agrees with measured data. In order to determine the DFT parametrisation in the form of a combination of functional and basis set that most closely resembles measured data, the results were compared to experimentally derived data for the zero-point energy (Malcolm 1998), vibrational frequencies (Malcolm 1998), and rotational frequencies (Brünken et al. 2008) for the TiO2 monomer molecule.
Approach for TiO2
The tested functionals include two GGA DFT functionals, 12 hybrid functionals that included Hartree-Fock exchange, and the three complete basis set (CBS) methods listed in Table 1. The functionals were selected to cover a broad range of theoretical approaches as well as with regard to their availability within Gaussian16. Although there are no interactions within our clusters that stem from non-bonded interactions, we found that empirical damping coefficients as described by Grimme et al. (2011) improve the overall accuracy of our calibration. The EmpiricalDispersion=GD3BJ keyword was therefore used if available. We note that the use of an empirical dispersion does not originate from a physical or chemical consideration. Employing a similar approach in the selection of basis sets, a total of 129 candidate combinations of functionals and basis sets was produced (Table 1). For each of the combinations, Gaussian16 was used to perform an optimisation of the TiO2 monomer and to calculate a zero-point energy for the titanium and oxygen atoms. The resulting energies for the individual functionals and basis sets were compared with the experimental data found in the JANAF-NIST tables. All 129 functional or basis set combinations were evaluated according to their binding energy for the TiO2 molecule calculated at a temperature of T = 0 K. The binding energy of the monomer (TiO2) was calculated according to
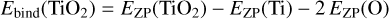 (1)
(1)
and can now be compared to experimental values (Table 2, Col. 4). EZP denotes the zero-point energy, that is, the energy of the system at rest in its ground electronic state.
Further values that are known from experiments are the vibrational frequencies v1, v2, and v3 (Malcolm 1998) and the rotational constants Arot, Brot, and Crot (Brünken et al. 2008) of the TiO2 monomer. These quantities are also a result of the DFT calculations, and the derived thermochemical properties depend on them (Eq. (C.6)). They were therefore used to further constrain which of the candidate combinations of functional and basis set was best suited for modelling TiO2 clusters. For the vibrational frequencies and the rotational constants, the quality of an individual candidate combination was assessed through a deviation parameter. Because the smallest deviation of the DFT results from the experimental data is desired, these deviation parameters were computed by taking the root sum squared of all relative deviations of the DFT results from the experimental data for the vibrational frequencies and the rotational constants (Table 2, Cols. 5 and 6). For the vibrational frequencies, this parameter (vibrational frequency deviation, VFD) was therefore calculated through
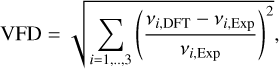 (2)
(2)
and equivalently, for the rotational constants (rotational constant deviation, RCD),
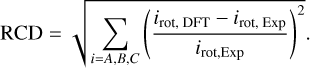 (3)
(3)
Using the Gaussian16 outputs for the zero-point energy of atomic oxygen, EZP(O) [kJ mol−1], atomic titanium, EZP(Ti) (kJ mol−1), and the titanium dioxide monomer, EZP(TiO2) (kJ mol−1), the binding energy of the monomer was calculated and compared to the literature value from the JANAF-NIST tables. Because the JANAF-NIST tables have an accuracy for the binding energy of 4 kJ mol−1 (Malcolm 1998), the selection was narrowed down to all candidate combinations that fall within this uncertainty. This decreased the number of candidate combinations of functionals and basis sets from 192 to 16 (Table 2). Lastly, the runtime for each monomer calculation on a single node (32 cores) was determined because computational speed and efficiency is desirable.
The thermochemical quantity of interest is the Gibbs free energy of formation ΔfG°(N), which is needed to compute nucleation rates (see Eqs. (9) and (17)). The molecular system properties that go into computing the Gibbs free energy are the zero-point energy, the vibrational frequencies, the rotational constants and spin multiplicities (Appendix C). The latter do not impact our results as we assumed closed-shell singlet clusters throughout our calculations.
The candidate combination of functional and basis set that has the smallest deviations from the experimentally known values for the zero-point energy, vibrational levels, and rotational constants was considered optimal. The B3LYP functional in combination with the cc-pVTZ basis set and empirical GD3BJ dispersion (Grimme et al. 2011) deviates least from the experimental values for the zero-point energy and the vibrational frequencies, and it has the second lowest value for the rotational constant deviation. Therefore, B3LYP/cc-pVTZ represents the most suitable choice for the calibration of approaches with a lower level of complexity (Sect. 2.4.1) and for the final optimisation of our candidate clusters (Sect. 2.5). Additionally, it is desirable to reduce computational cost. In order to achieve this, the fastest configuration that falls within the 4 kJ mol−1 threshold, the B3LYP functional in combination with the def2svp basis set, was chosen to pre-optimise candidate geometries. This allows the final optimisation with the cc-pVTZ basis set to be completed in fewer steps, leading to overall lower computational cost. The CCSD(T) method is known as the gold standard in computational quantum chemistry and has been the method of choice in quantum chemistry (Cížek 1969; Purvis & Bartlett 1998; Ramabhadran & Raghavachari 2013; Nagy & Kállay 2019). However, these calculations require many computational resources and are prohibitive for larger molecular systems such as nanosized clusters. Therefore, we performed CCSD(T)/6-311+G(2d,2p) single-point calculations for the GM candidates with the smallest cluster sizes of N = 1–4, and compared the 0K binding energies with our results from hybrid DFT ((B3LYP/cc-pVTZ with empirical dispersion). The CCSD(T) calculation results deviate from experimental results for the binding energy of the monomer by ≈90 kJ mol−1, which is not adequate for our calibration purposes. When the binding energy ratios are compared to the monomer, Ebind,N/Ebindi,1, the values for our DFT calculations do not differ by more than 2% from the CCSD(T) values. We therefore conclude that calibration of our method with the experimentally determined properties of the monomer is sufficient (Appendix B).
All Gaussian16 functionals (methods) and basis sets we considered when we searched for the closest representation of the JANAF-NIST experimental values.
Candidate combinations for functional and basis sets with a zero-point binding energy deviation ∣Ebind, JANAF – Ebind,DFT∣ < 4 kJ mol−1 sorted by deviation in the vibrational constant.
2.4 Calibration of force fields and DFTB
2.4.1 Calculation of known small clusters and isomers
After we selected the ideal combination of functional and basis set, judged by its ability to closely match the experimentally derived properties of TiO2, it was used to calculate the binding energies and geometries of the global minimum structures of the clusters of N = 2 … 6. The initial geometries for these calculations were taken from Berardo et al. (2014) and Lamiel-Garcia et al. (2017). Additionally, the binding energy and geometry for several energetically less favourable isomers for each size was calculated (Table 3). This was done so that the accurate depiction of the energetic ordering of isomers of the same size by force-field and DFTB+ models was ensured.
Number of isomers for each cluster size optimised at the DFT level that was used to calibrate force-field and DFTB models.
2.4.2 Force fields
In order to save computational time, it is beneficial to be as efficient as possible in the optimisation process towards local and global potential minima for candidate isomers. For example, a titanium-dioxide cluster of size N = 12 ((TiO2)12) has 36 atoms and accordingly, 3 × 36 = 108 degrees of freedom. The number of possible geometries is simply too large to be modelled at a feasible computational cost for a large number of clusters. Therefore, a modelling approach was employed that described the interactions between individual atoms through an interatomic Buckingham pair potential including the Coulomb potential (Appendix A.2). Several parametrisations for Ti-O systems are provided in previous studies, for instance Matsui & Akaogi (1991) or Lamiel-Garcia et al. (2017). However, we find that neither of them are well suited for our purposes as they do not accurately depict the B3LYP/cc-pVTZ energetic ordering within isomers of the same size N. To find a force-field prescription that reflects the experimental data available for TiO2 to the extent possible, a search was conducted for a set of Buckingham parameters that reproduce the binding energies and average bond distance of the smallest clusters calculated at the start of Sect. 2.4.1.
Approach to (TiO2)N
The program we used to calculate the energy as well as the bond distance is the general utility lattice program GULP (Gale & Rohl 2003). The optimise keyword was used in a constant pressure environment (conp) to optimise the DFT optimised clusters and determine their binding energies for each combination of parameters. The parameters that need to be determined in Eq. (A.1) are the charges of Ti and O, and the Buckingham pair parameters A, B, and C for each of the relevant interactions, Ti–Ti, O–O, and Ti–O. Because overall, charge neutrality needs to be conserved, the charge of Ti was directly coupled to the charge of O by a factor of −2, that is, there were two negatively charged oxygen anions for every positively charged titanium cation. For the TiO2 molecule, we found low formal charges. A Mulliken charge analysis of the smallest cluster sizes (N = 1 –4) revealed average Ti charges lower than +1e. The parametrisation therefore has ten free parameters, three from each of the interactions: Ti–Ti, O–O, and Ti–O, plus the charge. To determine the ideal parameter set, all interaction parameters as well as the charge were varied freely, and the scipy.optimise differential evolution algorithm (Storn & Price 1997) was used to determine the set of parameters that deviated the least from our calculated binding energies and average bond distances and that simultaneously reproduced the energetic ordering of isomers of the same size (Appendix D.1). With this physically consistent set of parameters, the potential energy of any Ti–O system, that is, any TiO2 cluster geometry, could now be predicted accurately and required little computational power. This approach of searching for candidate structures with the application of a Buckingham pair potential has been used before, for example in Gobrecht et al. (2018) for aluminium oxide, in Cuko et al. (2017) for hydroxylated silica clusters, and in Lamiel-Garcia et al. (2017) for titanium dioxide.
The seed structures were optimised using our re-parametrised force field as the first step in our hierarchical approach. To even further increase the structural complexity of our searches, a basin-hopping algorithm as described by Wales & Doye (1997) was employed. It was used in its implementation in the ase Python package (Hjorth Larsen et al. 2017) to optimise the geometries of all the seed structures. The potential energy calculation at each step of the optimisation was made through GULP with our parametrisation of the force field. After the force-field optimisation, the candidate geometries are analysed further in Sect. 2.4.3.
2.4.3 Density-functional based tight-binding method
From the geometry optimisation with the force-field approach (Sect. 2.4.2), 2000 candidate geometries at local potential minima for each small cluster size, N = 3–7, and 10 000 candidate geometries for each large cluster size, N = 8–15, were obtained. However, the Buckingham–Coulomb pair potential does not describe the interaction between electrons and their related orbitals. More precisely, only interactions between Ti cations, O anions, and themselves are taken into account. The interaction of (binding) electrons and the electron correlation is neglected. It still serves the purpose of optimising the candidate geometries on an approximate and simplified PES. The potential energies of the (TiO2)N cluster candidates are not accurate because among other reasons, the force-field approach considers single-point charges instead of a charge distribution of each ion in the cluster. It is therefore a reasonable assumption that the binding energies of these clusters and their energetic ordering can be improved by an intermediate optimisation step with a more accurate description accounting for electronic orbitals. This was done to obtain a more accurate energetic ordering of the candidate clusters. The best set of candidate clusters was chosen to be optimised with computationally expensive all-electron DFT calculations (see Sect. 2.5). For this intermediate step, the DFTB method (Appendix A.3) was chosen. The choice was made because in both complexity and computational cost, DFTB models fall in between the descriptions offered by force fields and all-electron DFT models (Hourahine et al. 2020). The parametrisation of the exchange-correlation functional is not included within the DFTB model and was performed through choosing an appropriate set of Slater–Koster files. These files relate to integrals and contain sets of functions that describe the exchange-correlation part of interactions between two atomic species (i.e. chemical elements). The database online1 hosts three different sets that describe the interaction of titanium and oxygen: matsci (Luschtinetz et al. 2009), a general-purpose material science set, trans3d (Zheng et al. 2007), a set describing transition metal elements in biological systems, and tiorg (Dolgonos et al. 2010), a set for describing Ti bulk, TiO2 bulk, TiO2 surfaces, and TiO2 with organic molecules. In order to determine the exchange-correlation parametrisation that best describes small TiO2 clusters, our test clusters calculated in Sect. 2.4.1 were used to test all three sets of Slater-Koster files.
Approach to (TiO2)N
The DFTB calculations were made using the DFTB+ program (Hourahine et al. 2020). For the calibration of the DFTB method, the energies calculated for geometries in Sect. 2.4.1 were used. For clusters of N = 3 … 6, equivalent to our approach in calibrating our force fields, DFTB+ was used to calculate the total energy for all the isomers with each of the three different sets of Slater–Koster files. Afterwards it was tested which of these reproduces the energetic ordering of the isomers found with all-electron DFT calculations. If two of the Slater–Koster files performed identically in this regard, we chose the file that better approximated the absolute values of the binding energies. The matsci (Luschtinetz et al. 2009) set of Slater–Koster files was found to perform best for the purpose of this paper (Appendix D.2). Subsequently, this set of Slater-Koster files was used to describe the exchange correlation in the further evaluation and optimisation of the seed structures from Sect. 2.4.2. To enable direct comparison to the results of DFTB+ optimised isomers, the potential energy for each of the candidate geometries was obtained by performing a single-point energy calculation with DFTB+. Next, an identical calculation for atomic Ti and atomic O was performed in order to obtain their respective potential energies. The binding energy of a (TiO2)N cluster can then be calculated by subtracting the individual contributions, analogously to Eq. (1),
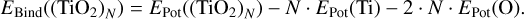 (4)
(4)
This calculation was performed for each of the candidate geometries obtained from Sect. 2.4.2. Each of the candidate geometries was then optimised using the ConjugateGradient method, making use of its implementation within DFTB+, and was again ordered according to their binding energies calculated with Eq. (4). Because the randomisation of seed structures is not ideal, there were duplicates among the optimised geometries. In order to filter them out, any two candidates with a binding-energy difference of ΔEBind ≤ 0.01eV were analysed with regard to their similarity. To do this, the mean of all inter-atomic distances within the cluster was calculated, giving a size parameter R. If the average inter-atomic distance of the two clusters was closer than ΔR ≤ 0.01 Å, the two clusters were found to be duplicates, and one was removed from the process. After the duplicate candidate geometries were removed, the lowest energy clusters for each size were used in our final step, optimisation with all-electron DFT. This is described in Sect. 2.5.
 |
Fig. 3 Binding energy per TiO2 monomer unit for small (N = 3–7, left) and large (N = 8–15, right) clusters for 90% of the most favourable clusters after optimisation with the force-field approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
2.5 Search for global minima with DFT
The energetically most favourable isomers found with DFTB (see Sect. 2.4.3) were further optimised using Gaussian16. In order to reduce the total computational time, a first optimisation was performed with the B3LYP/def2svp functional and basis set combination with empirical dispersion as described by Grimme et al. (2011). After this step, the final optimisation was made with the B3LYP/cc-pVTZ functional and basis set combination, also with empirical dispersion (Sect. 2.3). For all these isomers, a frequency analysis was carried out using the same functional and basis set, in order to ensure that the isomer was a true minimum and to exclude transition states. In addition, we calculated the final energies as well as rotational constants needed to determine the thermochemical properties we are interested in. The thermochemical properties entropy 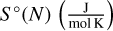 , change of enthalpy ddH (kJ mol−1) and Gibbs free energy of formation Δf G°(N)
, change of enthalpy ddH (kJ mol−1) and Gibbs free energy of formation Δf G°(N) 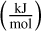 were calculated from the output of the DFT optimisations using the RRHO approximation as implemented within the thermo.pl (Irikura 2002) code.
were calculated from the output of the DFT optimisations using the RRHO approximation as implemented within the thermo.pl (Irikura 2002) code.
3 Results
3.1 Force-field optimised clusters
The new parametrisation (Table D.1) for the Buckingham-Coulomb force field was used to optimise the geometric seed structures (Sect. 2.1). The algorithm used for this search is the basin-hopping algorithm described by Wales & Doye (1997). The energy evaluation within this algorithm was made using GULP with the new set of parameters. At each step of the algorithm, a local energy minimisation using the FIRE algorithm (Bitzek et al. 2006) was performed. This algorithm was designed specifically for optimisation of atomistic systems towards their closest local minimum. A numerical temperature of T = 100 within the basin-hopping algorithm was chosen to allow for the exploration of nearby local minima in order to determine the deepest potential well in the vicinity. This temperature is not a physical temperature, but influences the rejection criterium within the algorithm. All seed structures created in Sect. 2.1 for each cluster size N = 3,…, 15 were optimised with this algorithm.
3.2 DFTB energy calculations and optimisation
A zero-point energy calculation was performed for all cluster geometries calculated in Sect. 3.1, and their binding energies were calculated according to Eq. (4) (Fig. 3). Then each of these cluster geometries was optimised, minimising their potential energy, with the DFTB description of interactions. The ConjugateGradient optimisation algorithm (Hestenes & Stiefel 1952) was used, and the binding energies of the optimised clusters were calculated again (Fig. 4). A comparison of Figs. 3 and 4 demonstrates the approximative character of the force-field approach, as a seemingly broad variety of local minima for small clusters disappears with the introduction of higher complexity in the form of DFTB. The energy levels become discrete, and many different cluster geometries from the force-field approach produce the same geometry after further optimisation. To find potentially new global minimum (GM) structures, all known literature GM clusters were optimised and their binding energies calculated with the DFTB approach for comparison. For each size, any unique cluster that had a higher binding energy than the known literature GM was categorised as a candidate for a new GM. Additionally, the ten isomers with binding energies closest to that of the literature GM were considered. These isomers (Table 4) were passed on to be optimised with all-electron DFT calculations.
3.3 Comparison of candidate creation approaches
In this section, the performance of the different methods for the creation of candidate geometries (see Sect. 2.1) is discussed. Additionally, the necessity for cluster geometries from the literature is assessed to establish whether the method is capable of operating without prior knowledge of particularly favourable cluster geometries. The parameter space that needs to be covered to find all possible geometric configurations increases dramatically with cluster size N. One metric to consider is the number of duplicate isomers. Table 5 lists the number of created candidates and resulting unique clusters for all cluster sizes N we considered. For the small clusters, many duplicates are found because the parameter space is small and many created geometries share a nearby potential minimum. As the size of the clusters grows, the number of identical geometries falls, creating more unique clusters per candidate. A plateau of unique clusters is reached from size 12, at which about 68% of the created clusters are unique. As larger clusters have a larger parameter space for possible geometric configurations, the trend of an increasing number of unique clusters is expected to continue. The resulting plateau therefore signals a limit of the current methods to fully explore the parameter space of clusters larger than N = 12.
Two out of the four approaches used in this work rely on known cluster geometries that are reported in the literature in order to produce cluster candidates (Known+1 and Mirror, methods 2 and 3 in Sect. 2.1, referred to as dependent methods), while the other two (Random and Equidistant, methods 1 and 4 in Sect. 2.1, referred to as independent methods) need only information about the monomer. Figure 5 and Table 6 show the 50 best candidates, that is, those with the highest binding energy, and their creation methods. For small clusters N = 3–6, the independent methods produce the majority of the 50 clusters with the highest binding energy. These independent methods also find the GM candidates reported in the literature for N = 3–6, which are needed for calibration. For larger clusters, the dependent methods perform better. The random generation method only produces one of the 50 energetically most favourable clusters for N > 10. This is because the PES is very large and complex at these sizes and cannot be sufficiently explored by a random walk. Therefore, the methods that contain prior information about stable configurations, such as the dependent methods, show an enhanced performance. The equidistant method is similar because it does not rely on previously reported favourable isomers either. For N > 10, the dependent methods therefore make up far more of the energetically most favourable clusters. More elaborate methods for creating first-guess cluster geometries are available through Gaussian process regression, for example (e.g., Meyer & Hauser 2020). For the present work, the choice was made to apply simple but fast methods, and comparisons to more complex approaches are desirable in future works.
 |
Fig. 4 Binding energy per TiO2 monomer unit for small (N = 3–7, left) and large (N = 8–15, right) clusters for the best 90% of clusters after optimisation with the DFTB approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
Number of GM candidates, i.e. cluster candidates with a higher binding energy than the literature GM, after DFTB optimisation, and number of isomers calculated with all-electron DFT calculations for each size.
Number of created candidate geometries, unique cluster geometries after DFTB optimisation, and percentage of unique clusters per created candidate for all sizes N.
 |
Fig. 5 Binding energy per monomer unit for small (N = 3−7, top) and large (N = 8−15, bottom) clusters for the best 50 clusters after optimisation with the DFTB approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
3.4 All-electron DFT calculations
All candidate geometries from Table 4, as well as all literature GM geometries from Berardo et al. (2014) and Lamiel-Garcia et al. (2017), were pre-optimised using Gaussianl6 with the B3LYP functional, def2svp basis set, and empirical dispersion. Afterwards, they were optimised and a frequency analysis was performed with the best-performing combination found in Sect. 2.3, B3LYP/cc-pVTZ with empirical dispersion. For all isomers, the binding energies were calculated according to Eq. (4), and their respective geometries can be found in electronic form at the CDS. For cluster sizes N = 3−10, the GM candidates predicted in the literature were found among the candidate geometries after DFTB optimisation. For cluster size N = 11, the predicted GM was found among the candidate geometries after DFT optimisation. For cluster sizes N = 12, 14, and 15, the predicted GM were not found among the candidate geometries, and no more favourable isomer, that is, with an even lower potential energy, was found either. The reason most likely is that the seed-creation approaches employed here are not well suited to cover the large parameter space for these large clusters within 10 000 candidates, as was mentioned in Sect. 3.3. For N = 13, we present a new global minimum candidate structure (Fig. 6), which was created through the mirror creation process (method 3 in Sect. 2.1). Its potential energy is 0.5 kJ mol−1 per monomer unit lower than the previous lowest-lying isomer reported by Lamiel-Garcia et al. (2017). This difference is lower than the typically assumed accuracy for DFT calculations of 4 kJ mol−1 per monomer unit. This supports the assumption that energetically similar isomers need to be studied for each cluster size because either could play a role in the nucleation process.
In thermochemical processes such as nucleation, the most relevant isomer for each cluster size is assumed to be the energetically most favourable one. Any less favourable, meta-stable isomer that forms relaxes into this global minimum, given sufficient time for the relaxation. To compare the thermochemical properties, the thermo.pl program was used to calculate the entropy S (J mol−1 K−1), change of enthalpy dΔH (kJ mol−1), and Gibbs free energy of formation ΔfG° (kJ mol−1) for three different sets of clusters:
The GM for each size, including cluster geometries reported in the literature, calculated with B3LYP/def2svp and empirical dispersion.
The GM for each size, including cluster geometries reported in the literature calculated with B3LYP/cc-pVTZ and empirical dispersion.
The GM for each size, only including cluster geometries that have been found in this work, calculated with B3LYP/cc-pVTZ and empirical dispersion.
This was done in order to compare the impact of the choice of functional and basis set on the zero-point energies and the thermochemical properties to the impact of the completeness of the GM search for the cluster geometries. The complete thermochemical tables for set 2 are only available in electronic form at the CDS.
Fifty lowest-energy clusters after DFTB optimisation for which the un-optimised geometry guess was created with four different procedures (random, mirror, known+1, equidistant).
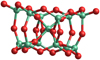 |
Fig. 6 New global minimum structure for (TiO2)13. The binding energy is Ebinding = −1782.96 kJ mol−1 per monomer unit. |
4 Astrophysically relevant (TiO2)N properties
In the previous sections, we have derived the fundamental quantities including the zero-point energy of TiO2 clusters. The thermochemical properties of interest for astrophysical studies are:
S(T), entropy (J mol−1 K−1)
dΔH(T), change in enthalpy (kJ mol−1)
ΔfG°(T), Gibbs free energy of formation (kJ mol−1).
The following sections present TiO2 in the context of the gas phase, TiO2 clusters as a promising precursors of TiO2 dust formation, and the derivation of their thermochemical properties, especially the size- and temperature-dependent Gibbs free energy of formation ΔfG°(N, T). These properties are relevant for cloud formation modelling in exoplanets and brown dwarfs and also for dust formation modelling in AGB stars and supernova ejecta.
4.1 Thermodynamical relevance of TiO2 in hot Jupiters
In order to assess the relevance of TiO2 for cloud formation in the atmospheres of hot Jupiters or for dust formation in an AGB envelope, it is necessary to know the thermodynamic quantity ranges in which TiO2 is the most abundant titanium-bearing molecule. To determine this, we applied the gas-phase equilibrium chemistry code GGChem from Woitke et al. (2018). TiO2 is the most abundant titanium-bearing molecule at a pressure of 10−3 bar in the low-temperature regime, that is, for T < 1200 K (Fig. 7). Less complex Ti-bearing species dominate the chemical Ti- content with increasing temperatures until Ti+ is the dominating Ti species at T > 3500 K. Figure 8 presents the GGChem model as a 2D (pgas, Tgas) plane. Four ID atmospheric pgas, Tgas profiles are superimposed. The profiles correspond to a model 3D atmosphere of a hot Jupiter with Teff = 1600 K and log(g) = 3, orbiting a G star with T* = 5650 K (Baeyens et al. 2021). This model was extrapolated to pressures of 10−14 bar. The 3D atmosphere model is plotted at four different locations on the planet: the substellar and anti-stellar point, and the morning and evening terminator for this hot Jupiter.
Only at the substellar point for the model atmosphere (Teff = 1600 K) is TiO2 not the most abundant Ti-bearing species at any pressure level, except in a thin layer of the atmosphere at 10−2 bar. For the anti-stellar point and morning terminator, TiO2 is the dominant Ti-bearing molecule in the upper atmosphere. Only in the lower atmosphere at around 10−1 bar are other molecules such as TiO and later atomic Ti dominant. For the evening terminator, TiO2 becomes less abundant than TiO at a pressure level of ~10−2 bar. Moreover, we note that the (TiO2)N cluster ionisation energies of 9.3−10.5 eV are too high to affect related abundances and the TiON nucleation in exoplanet atmospheres (Gobrecht et al. 2021b). This strengthens the argument that TiO2 is the most relevant Ti-bearing molecule in the upper atmosphere, which is cloud formation is expected to take place.
 |
Fig. 7 Concentrations of titanium containing molecules in gas-phase chemical equilibrium at 10−3 bar. Solar element abundance is assumed. TiO2 is the most abundant Ti-binding species up to 1200 K and the second most abundant species up to 1800 K. |
 |
Fig. 8 Most abundant gas-phase molecules containing titanium from a gas of solar composition using equilibrium chemistry. Pressure temperature profiles for a hot-Jupiter atmosphere with Teff = 1600 K included, probing the atmosphere at four distinct locations. |
4.2 Surface tension of TiO2
In classical and modified classical nucleation theory, the impact of the Gibbs free energy of formation ΔfG° on the nucleation process is modelled through the surface tension σ∞ of the bulk solid (Gail & Sedlmayr 2013). The surface tension is different for small clusters, due to significantly different geometries and properties than the bulk. This difference is neglected in classical approaches. It is possible, however, to determine a surface tension that is valid for small clusters if individual cluster data are available. Here the approach by Jeong et al. (2000) as applied by Lee et al. (2015) was followed, in which the dependence of the Gibbs free energy of formation on the cluster size is linked to the surface tension σ∞ through
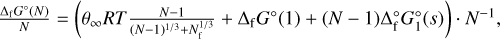 (5)
(5)
with cluster size N, the Gibbs free energy of formation of a cluster of size N, ΔfG°(N), the Gibbs free energy of the monomer ΔfG°(1), the Gibbs free energy of the bulk phase ΔfG°(s), a fitting factor Nf, and
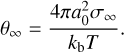 (6)
(6)
Here a0 is the theoretical monomer radius, which is derived from the bulk density of rutile and the molar mass through
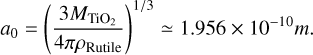 (7)
(7)
The fitting factor Nf is set to Nf = 0, analogously to Lee et al. (2015). The Gibbs free energies for the monomer and for the bulk are known from experiments (Malcolm 1998), as are the values necessary to derive a0. The Gibbs free energy of formation of the clusters was calculated from the thermochemical values derived from our all-electron DFT calculations and consistently compared to the thermochemical cluster data from the study by Lee et al. (2015).
This leaves σ∞ as the only free parameter, which was fit using Eq. (5). The left side of Fig. 9 compares the data from the two functional and basis set combinations used in this work to the results from Lee et al. (2015). It becomes apparent that the choice of the functional and basis set influences the resulting thermochemical properties and therefore the surface tension given by the fit. We obtain a different result for the surface tension than Lee et al. (2015) using their data. The result for the surface tension at T = 1000 K using all available GM data and the best-performing functional and basis set combination is σ∞ = 518 erg cm−2 (blue line in Fig. 9). In the right panel of Fig. 9, the comparison is made between the fits for σ∞ using all available GM data (blue) and only the best candidates that were produced from candidates in this work (red). Both the data and the results for σ∞ vary only slightly. Visible differences occur for N = 14 and N = 15, where this work did not produce candidates that were identical or energetically close to the literature GM. The best-fit value for σ∞ without using GM candidates found in the literature is σ∞ = 525 erg cm−2, which differs from the best-fit value by only 7 erg cm−2. This indicates that the choice of functional and basis set has a stronger impact on the resulting surface tension than finding the lowest-energy isomer for all sizes, given the extent of our searches.
Because the potential minimum geometries that were missed all have lower enthalpies and therefore presumably also lower Gibbs free energies, they can only lower the resulting surface tension. This approach therefore gives an upper limit for the surface tension σ∞.
The best-fit value for the surface tension is found to be dependent on the temperature. Figure 10 shows the best fit for a linear dependence of σ∞ on T for T = 500−2000 K,
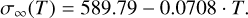 (8)
(8)
Studies have been conducted on the surface tension of bulk rutile at room temperature (Kubo et al. 2007), finding a value of σ∞(298.15 K) = 1001 erg cm−2 for the (011) lattice. The best fit for room temperature in this study gives a value of σ∞(298.15 K) = 575.72 erg cm−2 for small (TiO2)N molecular clusters. The factor of almost two in surface tension for small clusters versus the bulk phase of TiO2 makes it clear that the prior is recommended in all considerations regarding nucleation processes.
 |
Fig. 9 Gibbs free energy of formation per cluster size N as a function of cluster size N at a temperature of T = 1000 K. For each approach, a fit for σ∞ was calculated using Eq. (5). Left: comparison of the resulting surface tensions for different sources of cluster data. The sources are Lee et al. (2015) for the orange line, DFT calculations with the fast basis set def2svp for the green line, and DFT calculations with the accurate basis set cc-pVTZ for the blue line. Right: comparison of the impact of isomer completeness on resulting surface tension. Both lines use thermochemical data derived from the accurate cc-pVTZ basis set DFT calculations. For the blue line, the energetically most favoured isomer was chosen for all sizes, regardless of whether it was found by the approach in this paper. For the red line, only outputs from the approach described here were used. As the resulting difference is small, it becomes apparent that the choice of the basis set has a greater effect than the completeness of the cluster geometries. |
4.3 Nucleation rates of TiO2
To quantify the effect of the updated thermochemical cluster data on quantities relevant for cloud formation in exoplanet atmospheres, the nucleation rate for TiO2 was calculated along the temperature pressure profile of the morning terminator of a hot Jupiter with an effective temperature of Teff = 1600 K and a surface gravity of log g = 3 (blue lines in Fig. 8). The gas-phase composition was calculated with the equilibrium chemistry code GGChem.
 |
Fig. 10 Dependence of the best fit for σ∞ on the temperature T. A linear regression has been applied. |
4.3.1 Modified classical nucleation theory
In this work, the nucleation rates were computed analogously to Lee et al. (2015) to facilitate comparison. The stationary, homogeneous, homomolecular nucleation rate in classical nucleation theory is calculated by
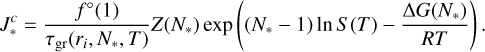 (9)
(9)
Here, S (T) and f°(1) are the supersaturation ratio and monomer number density of TiO2, respectively. τgr is the growth timescale, defined as
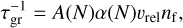 (10)
(10)
with 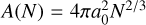 the effective cross-section of a spherical (TiO2)N cluster, nf the monomer number density (nf = f°(1)), the sticking factor α, which is assumed to be α = 1, and the relative velocity vrel, which is given for monomers with mass mx by the thermal velocity through
the effective cross-section of a spherical (TiO2)N cluster, nf the monomer number density (nf = f°(1)), the sticking factor α, which is assumed to be α = 1, and the relative velocity vrel, which is given for monomers with mass mx by the thermal velocity through
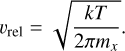 (11)
(11)
Z(N) is the Zeldovich factor, which accounts for the contribution to nucleation from Brownian motion,
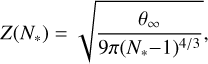 (12)
(12)
and in the final term, the Gibbs free energy ΔG(N) is approximated using modified classical nucleation theory, or MCNT, giving
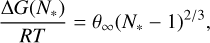 (13)
(13)
with θ∞ from Eq. (6). Equation (9) is evaluated at the critical cluster size N*, which is given by
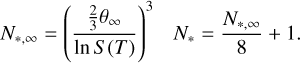 (14)
(14)
The critical cluster size is mainly influenced by the supersaturation of molecular TiO2 at various temperature and pressure points. When TiO2 is not supersaturated (In S (T) < 0), N* is negative (Eq. (14)), and consequently, Eq. (13) has no real solution, leading to the absence of nucleation for the modified classical case at these temperature pressure points. Using Eq. (9), we calculated the classical nucleation rate for the given (pgas,Tgas) profile using three different values for σ∞: the temperature-dependent σ∞ from this work, the temperature-dependent σ∞ from Lee et al. (2015), and a constant σ∞ = 797 erg cm−2, derived from the re-fit to Lee’s cluster data in this work. Results are shown in Fig. 11. Nucleation rates derived from updated cluster data are overall more efficient and extend to higher temperatures. The position of the peak nucleation rate within the atmosphere is very similar for the three different surface tensions. However, nucleation stays efficient up until slightly lower pressures for updated cluster data.
 |
Fig. 11 Classical nucleation rate for TiO2 for three different surface tensions σ∞. The temperature-pressure profile is equivalent to the solid blue line in Fig. 8. Top: nucleation rate at different temperatures. Bottom: position of the peak of the nucleation rate within the atmosphere. |
4.3.2 Non-classical nucleation theory
If detailed cluster data for all small sizes N are available, the nucleation rate can be computed using individual cluster growth rates. The non-classical nucleation rate is
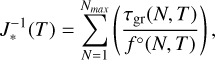 (15)
(15)
with τgr from Eq. (10) and f°(N) the number density of a cluster of size N. This can be computed from the partial pressure of the latter through
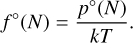 (16)
(16)
Applying the law of mass action to a cluster of size N gives its partial pressure as
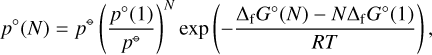 (17)
(17)
with p°(1) the partial pressure of the monomer and the reference pressure p⊖ = 1 bar. The results for the non-classical nucleation rates are shown in Fig. 12.
 |
Fig. 12 Nucleation rates J* for non-classical nucleation theory. The temperature–pressure profile is equivalent to the solid blue line in Fig. 8. Using individual cluster data from this work (B3LYP/cc-pVTZ) (blue), cluster data from Lee et al. (2015) (dashed orange), and the modified CNT approach from Sect. 4.3.1 (green). Top: dependence on temperature. Bottom: dependence on pressure. |
4.4 Results for TiO2 nucleation rates
For the modified classical nucleation approach, three values for the surface tension were compared. The shape of the nucleation rate in Fig. 11 is influenced by several factors. The reason that no nucleation occurs below a temperature of T ≈ 680 K lies in the pgas, Tgas profile that is used, which does not extend to lower temperatures (Fig. 8). At the upper temperature end, nucleation is limited because it depends on the supersaturation of the TiO2 monomer. Because supersaturation (S > 1) is required for nucleation and TiO2 is no longer super-saturated at these high temperatures, no nucleation occurs. For lower temperatures, the surface tension from this work results in a higher nucleation rate than the recomputed surface tension with cluster data from for Lee et al. (2015) by about one order of magnitude. The lower surface tension also causes nucleation to become inefficient at higher temperatures. Overall, the value for the surface tension from this work agrees well with the value derived in Lee et al. (2015). However, using their cluster data, we find a significantly higher surface tension (see Fig. 11).
Nucleation rates for non-classical nucleation (Fig. 12) are lower than for MCNT for T = 680−1600 K by about two orders of magnitude. This is the result of taking individual cluster data for all sizes into account instead of combining all the information into one quantity, the surface tension. Therefore, monomer growth processes from size N to size N + 1 are modelled more accurately. If one of the growth processes is less efficient than others, it will create a bottleneck for the overall nucleation rate. In this case, N + 1 is considered as the critical cluster size N*. At higher temperatures (T > 1600), cluster data from this work give lower nucleation rates than the cluster data from Lee et al. (2015) and MCNT. There is no strict upper temperature limit for non-classical nucleation, as clusters can grow as long as it is energetically favourable for them to do so and as long as nucleating material, that is, TiO2 monomers, are available (Eq. (17)). Because our updated cluster-data do predict that nucleation of TiO2 becomes inefficient at lower temperatures, the nucleation process starts at lower pressure levels, that is, higher up in the model atmosphere.
5 Conclusion
We have presented a method for determining and optimising the geometries, zero-point energies, and thermochemical properties for clusters. Emphasis was placed on exploring the parameter space of possible geometric configurations for these clusters and on deriving their potential energies and thermochemical properties accurately. This approach was tested for small (N = 3−15) (TiO2)N clusters. To ensure thermochemical accuracy, 129 combinations of DFT functionals and basis sets were tested with regard to their accuracy against known experimental data for the TiO2 monomer. The B3LYP functional with the cc-pVTZ basis set and GD3BJ empirical dispersion were found to closely approach the experimental data and were used for all final optimisation steps and frequency analysis. A new force-field parametrisation of the Buckingham-Coulomb pair potential was presented that more accurately reflects the cluster geometry (i.e. bond lengths) and energetic ordering for small TiO2 clusters than previous parametrisations. For the DFTB description of interactions, the matsci set of Slater–Koster integrals was found to best reflect the energetic ordering for small clusters and their isomers given by the all-electron DFT calculations. The hierarchical optimisation approach works as intended and produces a large number of energetically low-lying isomers for all sizes. For the smallest clusters N < 7, all global minimum candidates reported in the literature were found with methods that do not rely on using known cluster geometries. Because these are the same cluster sizes as were used to calibrate the less complex descriptions of inter-atomic potentials, this step of the approach is therefore independent of prior knowledge of cluster geometries. The Random approach of seed candidate creation is well suited to search small parameter spaces, such as N < 7. However, for any cluster sizes N > 10, the parameter space is too large to be searched with a fully randomised approach. For these larger cluster sizes, the Mirror and Known+1 approaches produce the largest number of energetically low-lying isomers. However, they require prior knowledge of favourable clusters of size N − 1 for Known+1 and of size N/2 for Mirror. This presents a constraint on the efficient search for clusters of these sizes, as without prior knowledge, the global minima in potential energy will have to be found iteratively, always growing from N to N + 1. The current implementation of the hierarchical approach was able to find all known global minima for N = 3−11, as well as a new global minimum candidate for N = 13 that lies 6 kJ mol−1 below the energy of the global minimum candidate structure reported by Lamiel-Garcia et al. (2017). For N = 12, the global minimum known from the literature could not be reproduced, the closest isomer produced lies 2.45 kJ mol−1 per monomer unit higher. For N = 14, this energetic distance between the lowest found isomer and the known global minimum is 5.71 kJ mol−1 per monomer unit, and for N = 15, it is 6.8 kJ mol−1 per monomer unit. This shows that the search method is still incomplete for larger clusters. Because only clusters up to size N = 6 had isomers that were used for calibration, the Mirror approach only had a single literature isomer to generate the clusters for N = 14 and N = 15, which drastically reduced the possible configurations explored by this approach.
To estimate the impact of the new thermochemical data on nucleation processes, the surface tension for small molecular clusters, as it is calculated in modified classical nucleation theory, was investigated. The findings of Lee et al. (2015) cannot be reproduced, raising the best-fit value for σ∞ for the test case at T = 1000 K to σ∞ = 797 erg cm−2. The fast basis set def2svp gives σ∞ = 325 erg cm−2, while the thermochemically more accurate basis set cc-pVTZ gives σ∞ = 518 erg cm−2. The spread between these values is a factor of two, and as the surface tension appears in the exponent of the modified nucleation rate (Eq. (9)), this spread is amplified. Because the B3LYP/cc-pVTZ functional and basis set was specifically chosen for its accuracy at modelling the thermochemical properties of small TiO2 molecular clusters, the updated value for the surface tension represents the currently best approximation. We find that for modified classical nucleation theory, the impact on the nucleation rates by the choice of the functional and basis set used to calculate the thermochemical properties is more important than finding a true global minimum as long as the structure that is used is one of the low-energy isomers. This is not true for non-classical nucleation description, which depends on accurate data for all sizes. The non-classical nucleation process described by the updated cluster data becomes inefficient at lower temperatures, which raises the atmospheric lower border for seed formation through that process. A limitation of this description is that it only allows for homogeneous and homomolecular nucleation, ignoring pathways through cluster-cluster collisions and through species other than TiO2.
We have shown that the updated cluster data affect the nucleation rates both in their classical and non-classical description. Providing cluster data for larger clusters N > 15 will allow a more detailed comparison with independent methods, for example with molecular dynamics methods as presented in Köhn et al. (2021). Additionally, the spectroscopic properties of small (TiO2)N clusters, in particular, the frequency-dependent opacities, are interesting because they can allow for dust coagulation processes to be constrained through observations (Köhler et al. 2012). The method will be improved by additional candidate creation methods and applied to other potentially CCN-forming species in the atmospheres of hot Jupiters.
Acknowledgements
The authors acknowledge computing time from the Kennedy HPC in St Andrews. J.P.S. acknowledges a St Leonard’s Global Doctoral Scholarship from the University of St Andrews and funding from the Austrian Academy of Science. Ch.H. and L.D. acknowledge funding from the European Union H2020-MSCA-ITN-2019 under Grant Agreement no. 860470 (CHAMELEON). R. Baeyens is thanked for providing the origial 3D GCM profiles, and D. Lewis for providing the extrapolated version. D.G. and L.D. acknowledge support from the ERC consolidator grant 646758 “AEROSOL”. D.G. acknowledges the Knut and Alice Wallenberg foundation for financial support.
Appendix A Theoretical approaches
Appendix A.1 Density functional theory
Density functional theory can be used to describe the interactions between atoms and electrons within a molecule. The behaviour of every electron is influenced by every other electron in the system, leading to a system of highly coupled differential equations, whose dimensionality cannot be reduced and which has to be solved simultaneously. Numerical approximations are required to do this. The Hartree-Fock method (Hartree 1928) approximates the many-electron wavefunction as a product of single-electron wavefunctions. The single-electron wavefunctions are chosen such that the many-body wavefunction built from them is anti-symmetric to obey the Pauli exclusion principle. The Hartree-Fock method is computationally still very expensive because one equation has to be solved for every electron in the system. A computationally more efficient solution is given by density functional theory (DFT) (Hohenberg & Kohn 1964; Kohn & Sham 1965; Kohn et al. 1996). In DFT, the multi-electron wavefunction is approximated by a function of the electron density. The electron density that minimises the total internal energy of a system is defined as its ground state. The interaction between electrons is then calculated through functionals of the electron density. The exact functionals are unknown. Many different approaches to describe and quantify these functionals have been investigated (Becke 2014). The first and simplest functionals use the local density approximation (LDA) (Hohenberg & Kohn 1964), where the functional is only dependent on the density at the exact coordinates where it is evaluated. This quickly leads to large inaccuracies as it assumes the homogeneity of the electron density, a variable that is highly non-homogeneous. More recent functionals use the gradient of the electron density as an additional qualifier. These functionals belong to the class of generalised gradient approximations (GGA; Langreth & Mehl 1983). Most currently used functionals do not rely on pure DFT, but also have a component in which the exchange energy is calculated from Hartree-Fock theory. These so-called hybrid functionals often combine high levels of accuracy with an acceptable computational cost, making them suitable for many purposes (Becke 1993a). In addition to choosing a functional, a basis set needs to be chosen for all DFT calculations. These basis sets represent a set of basis functions that can be combined linearly to express the electron orbitals in a computationally efficient way. These also exist at varying levels of complexity, mostly differing in the number of linear combinations that can be used to describe a single valence orbital. The choice of both the functional and basis set is crucial for the calculations in DFT. Section 2.3 is therefore dedicated to determine the functional and basis set that is best suited for our purpose, which is the optimisation of (TiO2)N clusters.
Appendix A.2 Buckingham-Coulomb potential
The Buckingham-Coulomb potential takes into account the interatomic van der Waals forces, the Pauli exclusion principle, and the electrostatic force, as opposed to the all-electron DFT calculations used later, which solve the Schrödinger equation to quantify the energy of a system. The general form of the Buckingham-Coulomb potential reads
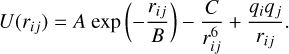 (A.1)
(A.1)
U(rij) is the potential energy of the interaction of two atoms i and j, in this case, O and Ti, O and O, or Ti and Ti. rij is the distance between these atoms, and qi and qj are their respective charges. A, B, and C are the Buckingham pair parameters. The first term in Eq. (A.1) represents the short-range repulsion according to the Pauli principle, with an increase in either parameter A or B leading to a increase in the potential barrier towards small distances. The second term describes the van der Waals force and its r−6 dependence on inter-atomic distance. An increase in its parameter C adds more attraction. The third and final term represents the Coulomb potential with its inverse proportionality to distance dominating the long-range interaction and implying alternating cation-anion ordering.
Appendix A.3 DFTB
We used DFTB methods as an intermediate step between a force-field description and all-electron DFT calculations. The basis of DFTB models is expanding the total energy functional given by Kohn-Sham (KS) DFT (Kohn & Sham 1965) in a Taylor series of up to third order (Hourahine et al. 2020). Several major approximations are made in each term of the Taylor series. Firstorder DFTB1 takes only the first-order expansion into account. A valence-only minimum basis set is used with a linear combination of atomic orbitals (LCAO) ansatz. This means that only electrons in the outer shells of the individual atoms, the valence electrons, and their interactions are described by this model. Additionally, a two-center approximation to the Hamiltonian operator is used, resulting in only interactions between neighbouring electronic orbitals being taken into account while distant overlapping orbitals are neglected. We used second-order DFTB, also known as DFTB2 or SCC-DFTB (self-consistent charge density functional tight-binding). In addition to the first term of the Taylor series, the second term in DFTB2 is also evaluated in order to calculate the energy of a system. Fluctuations in density, which become relevant in the second-order term, are approximated by a superposition of atomic contributions of all other atoms, each contributing an exponentially decaying spherically symmetric charge density.
Appendix B High level CCSD(T) calculations
Coupled cluster single-point calculations at the CCSD(T)/6-311+G(2d,2p) level of theory were run for the GM candidate clusters for N = 1−4. The value for the monomer binding energy differs from the experimental Janaf Nist value by ΔE ≈ 90kJ mol−1. This is far outside of the assumed error of DFT and Janaf-Nist values of ≈ 4kJ mol−1. To calibrate our methods on these high-level theoretical calculations, we would therefore have to ignore the experimental values. To quantify how closely our chosen B3LYP/cc-pVTZ empdisp method matches the higher-level results, the relative binding energies to the monomer were calculated for these clusters. As the deviation is < 2% for all sizes, we conclude that no information is lost by not using high-level CCSD(T) calculations to calibrate our methods.
Appendix C Calculating the Gibbs free energy of formation from the partition function
The Gibbs free energy of formation, ΔfG°, for a gas-phase cluster can be calculated using its enthalpy of formation ΔfH°, its entropy 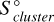 , and the entropy of the individual atoms comprised in the cluster
, and the entropy of the individual atoms comprised in the cluster 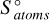 ,
,
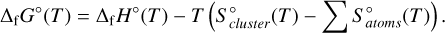 (C.1)
(C.1)
For a cluster of size N = 5, the last term is the sum of the entropies of five Ti atoms and ten oxygen atoms. Calculating the enthalpy of formation of the cluster requires information about the enthalpies of the elements that make up the cluster. The entropies and enthalpies for Ti and O used for these calculations are taken from the JANAF-NIST tables (Malcolm 1998). The enthalpy of formation of the cluster at temperature T is then calculated through
![$\matrix{ {{{\rm{\Delta }}_{\rm{f}}}{H^^\circ }\left( T \right) = {{\rm{\Delta }}_{\rm{f}}}{H^^\circ }\left( {{T^ \ominus }} \right) + {{\left[ {{H^^\circ }\left( T \right) - {H^^\circ }\left( {{T^ \ominus }} \right)} \right]}_{cluster}}} \hfill \cr {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad - \sum {{{\left[ {{H^^\circ }\left( T \right) - {H^^\circ }\left( {{T^ \ominus }} \right)} \right]}_{atoms}}} } \hfill \cr }$](/articles/aa/full_html/2022/12/aa43306-22/aa43306-22-eq27.png) (C.2)
(C.2)
with the reference temperature T⊖ = 0 K. The enthalpy of formation at the reference temperature Δf H○(T⊖) is the binding energy of the cluster, caluclated for a cluster of size N through
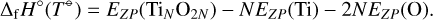 (C.3)
(C.3)
The entropy of the system 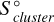 is calculated from the internal energy of the system,
is calculated from the internal energy of the system,
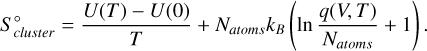 (C.4)
(C.4)
With the internal energy U(T) − U(0), the partition function q(V, T), and the number of atoms in the cluster Natoms. The internal energy is derived from the partition function q(V, T) through
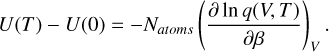 (C.5)
(C.5)
When the rigid-rotor harmonic-oscillator (RRHO) approximation for a polyatomic, non-linear molecule is used, its partition function is
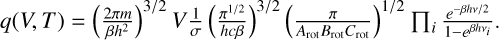 (C.6)
(C.6)
T is the temperature of the system, 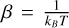 , with the Boltz-mann constant kB. h is the Planck constant, and c is the speed of light. σ is the symmetry number, correcting for the repeated count of indistinguishable configurations. The unknown inputs in Eq. (C.6) are the vibrational levels vi, the rotational constants Arot, Brot, and Crot, and V, the volume of the particle, which are all outputs of the DFT simulations. For further reading about the calculation of these thermochemical properties, we refer to Jeong (2000). The partition function used here omits the electronic partition function, qel,
, with the Boltz-mann constant kB. h is the Planck constant, and c is the speed of light. σ is the symmetry number, correcting for the repeated count of indistinguishable configurations. The unknown inputs in Eq. (C.6) are the vibrational levels vi, the rotational constants Arot, Brot, and Crot, and V, the volume of the particle, which are all outputs of the DFT simulations. For further reading about the calculation of these thermochemical properties, we refer to Jeong (2000). The partition function used here omits the electronic partition function, qel,
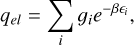 (C.7)
(C.7)
with the energy levels i, their energies ϵi and their respective degeneracies gi. This is because Gaussian16 assumes that the first electronic excitation energy is much greater than the thermal energy (ϵ1 ≫ kT) and that it is therefore inaccessible at any temperature, resulting in a value of qel = 1 for all clusters and temperatures. In addition, all clusters are assumed to be in a singlet state with gi =1 ∀ i.
Appendix D Calibrations of low-level methods
Appendix D.1 Recalibrated force field
Starting with a calculation of the potential energy of a (TiO2)5 cluster taken from Berardo et al. (2014), the ten individual parameters of the Buckingham-Coulomb force-field parametrisation are varied until they destabilise the potential, so that it does not have a stable minimum. For each of the parameters, the upper and lower value are taken as bounds for the following parameter search (See Table D.1). The quality of a set of parameters is determined by a comparison with the energies and geometries calculated with DFT in Sect. 2.4.1. Due to the differences in approximation between the DFT and the force-field calculations, it is difficult to directly compare their respective results. Since force-field calculations rely on a simplified representation of the PES, the absolute Buckingham-pair binding energy of the clusters is not realistic when compared to DFT calculations. However, the relative energies of isomers of the same size are portrayed accurately by the force field description and are therefore used as a point of comparison. The monomer and dimer are not addressed with the force-field approach because the impact of the electronic orbitals is not considered in the Buckingham pair potential. For any uni-directional force-field description, the monomer and dimer have linear and flat geometries that are known to not be accurate (Koch & Manzhos 2017). For increasing cluster sizes, the interactions described by the force field grow stronger than the quantum effects and therefore give a more accurate description of the clusters. For each isomer from Sect. 2.4.1, a conp optimisation is performed using GULP. The energies of all isomers are then compared to the energy of the global minimum cluster of their respective size to determine their relative energy given by the force-field approach 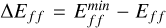 . This difference in binding energy is then compared to the corresponding difference in binding energy from the DFT calculations
. This difference in binding energy is then compared to the corresponding difference in binding energy from the DFT calculations 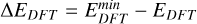 for the same cluster. The quality of a parameter set with regard to the energy Q(E) is then determined by the root sum squared of all relative deviations across all isomers (Eq. D.1),
for the same cluster. The quality of a parameter set with regard to the energy Q(E) is then determined by the root sum squared of all relative deviations across all isomers (Eq. D.1),
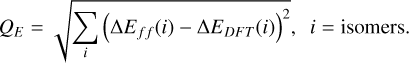 (D.1)
(D.1)
Additionally, the distance parameter  is introduced, which is calculated by taking the mean of all interatomic distances within a cluster. This is done to quantify the similarity of the geometries calculated by the force-field approach and the DFT calculations. This distance parameter is calculated for every isomer, for both the DFT optimised geometry and the force field optimised geometry. The quality of a set of parameters with regard to the geometry QGeom is then calculated analogously to the energy quality by the root sum squared of all deviations of
is introduced, which is calculated by taking the mean of all interatomic distances within a cluster. This is done to quantify the similarity of the geometries calculated by the force-field approach and the DFT calculations. This distance parameter is calculated for every isomer, for both the DFT optimised geometry and the force field optimised geometry. The quality of a set of parameters with regard to the geometry QGeom is then calculated analogously to the energy quality by the root sum squared of all deviations of 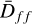 for the force-field geometries from
for the force-field geometries from 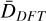 for the DFT geometries,
for the DFT geometries,
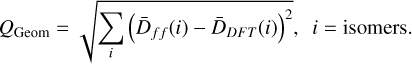 (D.2)
(D.2)
As optimisation for both quantities at the same time is crucial, a weight is introduced to normalise the values of QGeom and QE. Evaluation of typical values for QGeom and QE reveals a difference of one order of magnitude, giving a weight of 10 as a reasonable counter. The overall quality QTot of a parameter set is then given by the root sum squared of the energy quality Q(E) and the geometry quality QGeom with a weight of 10,
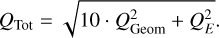 (D.3)
(D.3)
The quality parameter QTot is minimised in order to find the set of parameters for the Buckingham - Coulomb potential that best reproduces the results from DFT calculations. The minimisation is performed using the scipy.optimise.differential_evolution algorithm (Storn & Price 1997), with the bounds from Table D.1 as well as the bounds derived from the parameters of Lamiel-Garcia et al. (2017). This algorithm was chosen due to its capability to find a global minimum for a multidimensional, non-linear function, its convergence properties, and ease of parallelisation. Convergence is achieved after 415 iterations, giving a minimum quality parameter of QTot = 4.66, and it results in the parameter set listed in Table D.1. A comparison to the performance of this new parameter set is shown in Fig. D.1. In particular, results are plotted for the force-field parametrisation by Lamiel-Garcia et al. (2017) in Figs. D.1a and D.1b, for the values from Matsui & Akaogi (1991) in Figs. D.1c and D.1d, and for the results from this work in Figs. D.1e and D.1f. The left panels of these plots show the relative energies compared to the energy of the known global minimum geometry (which is set to zero), and their relative deviations are calculated with both the force-field description of interactions and all-electron DFT. The positions of the global minimum isomers for all sizes N overlap in the top right corner of each graph. The position on the x-axis, which represents the relative energy described by DFT calculations, is the same for all isomers of all sizes, representing the most realistic energetic ordering from right to left. Ideally, the relative energies calculated from the force field model reproduce the same energetic ordering on the y-axis from top to bottom, creating a linear function with a slope of 1. In order to aid visually, this line has been plotted in black. In the right panel of Fig. D.1, the same approach is followed for the average interatomic distance parameter 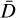 . In an ideal case, the interatomic distances from the force-field calculations match their DFT optimised counterparts and fall on the black line with slope 1. Significant deviations of individual clusters from that line can be explained by the fact that in some cases, the force-field approach produces a different local minimum geometry to the DFT approach from the same starting geometry. Finally, to ensure that the result is not a numerical artefact, the values for each parameter were rounded to the same accuracy as the parameters from the literature, and they still outperform them for our purpose (Table D.2).
. In an ideal case, the interatomic distances from the force-field calculations match their DFT optimised counterparts and fall on the black line with slope 1. Significant deviations of individual clusters from that line can be explained by the fact that in some cases, the force-field approach produces a different local minimum geometry to the DFT approach from the same starting geometry. Finally, to ensure that the result is not a numerical artefact, the values for each parameter were rounded to the same accuracy as the parameters from the literature, and they still outperform them for our purpose (Table D.2).
Appendix D.2 DFTB calibration
For the DFTB description of interactions, the energies and forces due to exchange-correlations between individual atoms are described by Slater-Koster integrals. These are constructed and pre-calculated for different purposes and collected in the form of Slater-Koster files on the website2. We evaluated all three available Slater-Koster files that describe the titanium-oxygen interaction to determine which of these three integrals reproduces the results of the all-electron DFT calculations most accurately. In order to do this, the three Slater-Koster files, matsci (Luschtinetz et al. 2009), trans3d (Zheng et al. 2007), and tiorg (Dolgonos et al. 2010), are used to calculate the binding energies for all clusters from Sect. 2.4.1 according to Eq. (4). These calculated energies for all isomers of each size (N = 3, .. , 6) are then compared to the energy of the global minimum isomer of that respective size to obtain the relative energy, equivalent to the approach for the force fields in Sect. D.1. These are again compared to the relative energies that result from the DFT calculations (Fig. D.2). Analogously to the left panel in Fig. D.1, the relative energy deviations from the global minimum are plotted for the DFT calculations. An ideal description matches the ordering in both directions and falls onto a slope of 1 (black line). If any clusters fall above the horizontal 0 eV line, the DFTB parametrisation shows a different isomer as the global minimum for this cluster size, which is not desirable. When the plots in Fig. D.2 are compared, it becomes apparent that for trans3d (Fig. D.2b) and tiorg (Fig. D.2c), there are several isomers for all cluster sizes N = 3−6 and N = 3, 5 that fall above the horizontal 0 eV line and therefore represent unlikely global minima candidates according to their DFTB description. For matsci (Fig. D.2a), this is not the case, and the lowest-energy isomer corresponds to the global minimum candidate derived from all-electron DFT calculations for each respective cluster size. Visual inspection also shows that the deviation of individual isomers from the linear function with slope 1 is the smallest for matsci, which means that it reproduces the energetic ordering of the DFT calculations best. In comparison, both trans3d and tiorg have large individual outliers for almost all cluster sizes. In order to quantify the quality of each of the Slater-Koster integral sets, the deviation of their relative energies as compared to the relative all-electron DFT energies is calculated. The sum of these residuals is equivalent to QE in Sec. D.1 and is given in the plots. The visual inspection is confirmed because the matsci set far outperforms the other two. Therefore, the matsci set of Slater-Koster integrals is used for all DFTB calculations in this work.
Comparison of quality parameters QTot, QGeom, and QE for parametrisations from the literature versus this work and this work rounded to the same precision as the literature.
 |
Fig. D.1 Calibration comparisons for the force-field approach. Left: Relative energy deviation to the global minimum cluster for the force-field approach vs the DFT approach for all clusters from Sect. 2.4.1. Ideally, if the force field approach exactly reproduced the results of the more accurate DFT approach, all points would be on the black line with slope 1. Right: Distance parameter DD for all clusters from the force-field paramterisation vs the DFT approach. In an ideal scenario, all clusters are exactly reproduced and therefore do not deviate from the black line with slope 1. Parameters in the top panel are from Lamiel-Garcia et al. (2017), in the middle panel from Matsui & Akaogi (1991), and in the bottom panel from this work. |
 |
Fig. D.2 Comparison of the DFT and DFTB energetic orderings for three different sets of Slater-Koster integrals. (a): Matsci Slater-Koster integrals. (b): Trans3d Slater-Koster integrals. (c): Tiorg Slater-Koster integrals. The positions of all isomers on the x-axis are consistent in all three panels. The energy level of the global minimum according to DFT is given by the horizontal blue lines. The relative energetic ordering from the DFT calculations is given by their order from right to left, and the DFTB ordering is given from top to bottom. |
References
- Adamo, C., & Barone, V. 1999, J. Chem. Phys., 110, 6158 [NASA ADS] [CrossRef] [Google Scholar]
- Andres, R. J., & Kasgnoc, A. D. 1998, J. Geophys. Res.: Atmos., 103, 25251 [NASA ADS] [CrossRef] [Google Scholar]
- Andriesse, C. D., Donn, B. D., & Viotti, R. 1978, MNRAS, 185, 771 [NASA ADS] [Google Scholar]
- Apai, D., Radigan, J., Buenzli, E., et al. 2013, ApJ, 768, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Austin, A., Petersson, G. A., Frisch, M. J., et al. 2012, J. Chem. Theory Comput., 8, 4989 [CrossRef] [Google Scholar]
- Baeyens, R., Decin, L., Carone, L., et al. 2021, MNRAS, 505, 5603 [NASA ADS] [CrossRef] [Google Scholar]
- Barstow, J. K., Aigrain, S., Irwin, P. G. J., et al. 2014, ApJ, 786 [Google Scholar]
- Becke, A. D. 1993a, J. Chem. Phys., 98, 1372 [Google Scholar]
- Becke, A. D. 1993b, J. Chem. Phys., 98, 5648 [Google Scholar]
- Becke, A. D. 2014, J. Chem. Phys., 140, 18 [Google Scholar]
- Berardo, E., Hu, H. S., Shevlin, S. A., et al. 2014, J. Chem. Theory Comput., 10, 1189 [CrossRef] [Google Scholar]
- Bitzek, E., Koskinen, P., Gähler, F., Moseler, M., & Gumbsch, P. 2006, Phys. Rev. Lett., 97, 170201 [NASA ADS] [CrossRef] [Google Scholar]
- Blander, M., & Katz, J. L. 1967, Geochim. Cosmochim. Acta, 31, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Boese, A. D., & Martin, J. M. 2004, J. Chem. Phys., 121, 3405 [NASA ADS] [CrossRef] [Google Scholar]
- Boulangier, J., Gobrecht, D., Decin, L., De Koter, A., & Yates, J. 2019, MNRAS, 489, 4890 [CrossRef] [Google Scholar]
- Bromley, S. T., Gómez Martín, J. C., Plane, J. M. C., et al. 2016, PCCP, 18, 26913 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Müller, H. S. P., Menten, K. M., McCarthy, M. C., & Thaddeus, P. 2008, ApJ, 676, 1367 [CrossRef] [Google Scholar]
- Chang, C., Patzer, A. B., Sedlmayr, E., & Sülzle, D. 2005, PhRvB, 72, 235402 [NASA ADS] [Google Scholar]
- Chang, C., Patzer, A. B., Kegel, W. H., & Chandra, S. 2013, Ap&SS, 347, 315 [CrossRef] [Google Scholar]
- Charnay, B., Mendonça, J. M., Kreidberg, L., et al. 2022, Exp. Astron., 53, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Cížek, J. 1969, in Advances in Chemical Physics (John Wiley & Sons, Ltd), 35 [Google Scholar]
- Cuko, A., Maciá, A., Calatayud, M., & Bromley, S. T. 2017, Comput. Theor. Chem., 1102, 38 [Google Scholar]
- Curtiss, L. A., McGrath, M. P., Blaudeau, J. P., et al. 1995, J. Chem. Phys., 103, 6104 [NASA ADS] [CrossRef] [Google Scholar]
- Dolgonos, G., Aradi, B., Moreira, N. H., & Frauenheim, T. 2010, J. Chem. Theory Comput., 6, 266 [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2013, Gaussian 09, Revision D.01 [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 2013, Physics and Chemistry of Circumstellar Dust Shells [CrossRef] [Google Scholar]
- Gail, H. P., Sedlmayr, E., Gail, H. P., & Sedlmayr, E. 1986, A&A, 166, 225 [NASA ADS] [Google Scholar]
- Gale, J. D., & Rohl, A. L. 2003, Mol. Simul., 29, 291 [CrossRef] [Google Scholar]
- Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gobrecht, D., Decin, L., Cristallo, S., & Bromley, S. T. 2018, Chem. Phys. Lett., 711, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Gobrecht, D., Sindel, J. P., Lecoq-Molinos, H., & Decin, L. 2021, Universe 2021, 7, 243 [NASA ADS] [Google Scholar]
- Gobrecht, D., Plane, J. M. C., Bromley, S. T., et al. 2022, A&A, 658, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goerigk, L. & Grimme, S. 2011, J. Chem. Theory Comput., 7, 291 [CrossRef] [Google Scholar]
- Goumans, T. P. M., & Bromley, S. T. 2013, RSPTA, 371, 20110580 [Google Scholar]
- Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comput. Chem., 32, 1456 [Google Scholar]
- Hartree, D. R. 1928, Math. Proc. Cambr. Philos. Soc., 24, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C. 2018, Annu. Rev. Earth Planet. Sci., 47, 1 [Google Scholar]
- Helling, C., Ackerman, A., Allard, F., et al. 2008, MNRAS, 391, 1854 [Google Scholar]
- Helling, C., Lee, G., Dobbs-Dixon, I., et al. 2016, MNRAS, 460, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Iro, N., Corrales, L., et al. 2019, A&A, 631, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helling, C., Kawashima, Y., Graham, V., et al. 2020, A&A, 641, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hestenes, M. R., & Stiefel, E. 1952, Methods of Conjugate Gradients for Solving Linear Systems 1, Tech. Rep. 6 [Google Scholar]
- Heyd, J., Scuseria, G. E., & Ernzerhof, M. 2003, J. Chem. Phys., 118, 8207 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth Larsen, A., JØrgen Mortensen, J., Blomqvist, J., et al. 2017, The atomic simulation environment - a Python library for working with atoms [Google Scholar]
- Hohenberg, P., & Kohn, W. 1964, Phys. Rev., 136, B864 [CrossRef] [Google Scholar]
- Hourahine, B., Aradi, B., Blum, V., et al. 2020, J. Chem. Phys., 152, 124101 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, J. G. 1993, J. Appl. Meteorol. Climatol., 32, 596 [CrossRef] [Google Scholar]
- Irikura, K. 2002, National Institute of Standards and Technology [Google Scholar]
- Jeong, K. S. 2000, PhD thesis, Technische Universität Berlin, Berlin, Germany [Google Scholar]
- Jeong, K. S., Chang, C., Sedlmayr, E., et al. 2000, JPhB, 33, 3417 [NASA ADS] [Google Scholar]
- Koch, D., & Manzhos, S. 2017, J. Phys. Chem. Lett., 8, 1593 [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohn, W., & Sham, L. J. 1965, Phys. Rev., 140, A1133 [CrossRef] [Google Scholar]
- Kohn, W., Becke, A. D., & Parr, R. G. 1996, J. Phys. Chem., 100, 12974 [Google Scholar]
- Köhn, C., Helling, C., Enghoff, M. B., et al. 2021, A&A, 654, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2013, Nature, 505, 69 [Google Scholar]
- Kubo, T., Orita, H., & Nozoye, H. 2007, J. Am. Chem. Soc., 129, 10474 [CrossRef] [Google Scholar]
- Lam, J., Amans, D., Dujardin, C., Ledoux, G., & Allouche, A.-R. 2015, J. Phys. Chem., 119, 8944 [NASA ADS] [CrossRef] [Google Scholar]
- Lamiel-Garcia, O., Cuko, A., Calatayud, M., Illas, F., & Bromley, S. T. 2017, Nanoscale, 9, 1049 [Google Scholar]
- Langreth, D. C., & Mehl, M. J. 1983, Phys. Rev. B, 28, 1809 [Google Scholar]
- Lee, E., Helling, C., Giles, H., & Bromley, S. T. 2015, A&A, 575, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, G. K., Blecic, J., & Helling, C. 2018, A&A, 614, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luschtinetz, R., Frenzel, J., Milek, T., & Seifert, G. 2009, J. Phys. Chem. C, 113, 5730 [NASA ADS] [CrossRef] [Google Scholar]
- Malcolm W., Chase, J. 1998, NIST-JANAF Thermochemical Tables, 4th edn. (Washington, DC: American Chemical Society; New York: American Institute of Physics for the National Institute of Standards and Technology) [Google Scholar]
- Matsui, M., & Akaogi, M. 1991, Mol. Simul., 6, 239 [CrossRef] [Google Scholar]
- Meyer, R., & Hauser, A. W. 2020, J. Chem. Phys., 152, 084112 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Ormel, C. W., Chubb, K., et al. 2020, A&A, 642, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, J. A., Frisch, M. J., Ochterski, J. W., & Petersson, G. A. 2000, J. Chem. Phys., 112, 6532 [NASA ADS] [CrossRef] [Google Scholar]
- Nagy, P. R., & Kállay, M. 2019, J. Chem. Theory Comput., 15, 5275 [CrossRef] [Google Scholar]
- Nikolov, N., Maciejewski, G., Constantinou, S., et al. 2021, AJ, 162, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Min, M. 2019, A&A, 622, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patzer, A. B. C., Köhler, T. M., Sedlmayr, E., et al. 1995, P&SS, 43, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Patzer, A. B. C., Gauger, A., & Sedlmayr, E. 1998, A&A, 337, 847 [Google Scholar]
- Patzer, A. B., Chang, C., Sedlmayr, E., & Sülzle, D. 2005, EPJD, 32, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patzer, A. B., Chang, C., & Sülzle, D. 2014, CPL, 612, 39 [NASA ADS] [Google Scholar]
- Peverati, R., & Truhlar, D. G. 2011, J. Phys. Chem. Lett., 2, 2810 [CrossRef] [Google Scholar]
- Peverati, R., & Truhlar, D. G. 2012, Phys. Chem. Chem. Phys., 14, 16187 [NASA ADS] [CrossRef] [Google Scholar]
- Plane, J. M. C., Plane, C. J. M. 2013, RSPTA, 371, 20120335 [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Purvis, G. D., & Bartlett, R. J. 1998, J. Chem. Phys., 76, 1910 [Google Scholar]
- Ramabhadran, R. O., & Raghavachari, K. 2013, J. Chem. Theory Comput., 9, 3986 [CrossRef] [Google Scholar]
- Samra, D., Helling, C., & Min, M. 2020, A&A, 639, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sloan, G. C., Matsuura, M., Zijlstra, A. A., et al. 2009, Science, 323, 353 [CrossRef] [Google Scholar]
- Storn, R., & Price, K. 1997, J. Global Optim., 11, 341 [Google Scholar]
- Tao, J., Perdew, J. P., Staroverov, V. N., & Scuseria, G. E. 2003, Phys. Rev. Lett., 91, 146401 [Google Scholar]
- Vydrov, O. A., & Scuseria, G. E. 2006, J. Chem. Phys., 125, 234109 [NASA ADS] [CrossRef] [Google Scholar]
- Wales, D. J., & Doye, J. P. 1997, J. Phys. Chem. A, 101, 5111 [CrossRef] [Google Scholar]
- Weigend, F. 2006, Phys. Chem. Chem. Phys., 8, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. K., Van Mourik, T., & Dunning, T. H. 1996, J. Mol. Struct.: Theochem, 388, 339 [CrossRef] [Google Scholar]
- Woitke, P., Helling, C., Hunter, G. H., et al. 2018, A&A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, G. P., Radom, L., Petersson, G. A., et al. 2006, J. Chem. Phys., 125, 094106 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., & Goddard, W. A. 2004, Proc. Natl. Acad. Sci. USA, 101, 2673 [Google Scholar]
- Yanai, T., Tew, D. P., & Handy, N. C. 2004, Chem. Phys. Lett., 393, 51 [NASA ADS] [Google Scholar]
- Zhao, Y., & Truhlar, D. G. 2008, Theor. Chem. Acc., 120, 215 [CrossRef] [Google Scholar]
- Zheng, G., Witek, H. A., Bobadova-Parvanova, P., et al. 2007, J. Chem. Theory Comput., 3, 1349 [CrossRef] [Google Scholar]
All Tables
All Gaussian16 functionals (methods) and basis sets we considered when we searched for the closest representation of the JANAF-NIST experimental values.
Candidate combinations for functional and basis sets with a zero-point binding energy deviation ∣Ebind, JANAF – Ebind,DFT∣ < 4 kJ mol−1 sorted by deviation in the vibrational constant.
Number of isomers for each cluster size optimised at the DFT level that was used to calibrate force-field and DFTB models.
Number of GM candidates, i.e. cluster candidates with a higher binding energy than the literature GM, after DFTB optimisation, and number of isomers calculated with all-electron DFT calculations for each size.
Number of created candidate geometries, unique cluster geometries after DFTB optimisation, and percentage of unique clusters per created candidate for all sizes N.
Fifty lowest-energy clusters after DFTB optimisation for which the un-optimised geometry guess was created with four different procedures (random, mirror, known+1, equidistant).
Comparison of quality parameters QTot, QGeom, and QE for parametrisations from the literature versus this work and this work rounded to the same precision as the literature.
All Figures
 |
Fig. 1 Hierarchical approach to determine global minimum candidate structures for clusters. (1) The geometries and binding energies of small clusters and isomers are used to calibrate the accuracy of the force field and DFTB methods. (2) A force-field description of interatomic interactions is used to locally optimise the geometries of a large number of generated clusters for each size N towards a potential energy minimum. (3) The geometries of these locally and semi-classically optimised cluster candidates are then further refined in a third step, using DFTB methods. This step optimises the geometries of the cluster candidates for the lowest possible potential energy. This provides an energetic ordering of the candidate geometries. (4) The energetically most favourable candidate geometries are then used as inputs for DFT calculations, resulting in the final and most accurate geometries, binding energies, and vibrational and rotational frequencies for each cluster within this approach. |
| In the text | |
 |
Fig. 2 Examples for initial un-optimised cluster geometries of size N = 7, generated (a) randomly, (b) from a known cluster with an additional monomer (marked with yellow circles), (c) from a mirrored cluster of size N = 3 with an additional monomer in the centre, and (d) from N = 7 monomers evenly distributed on a sphere. |
| In the text | |
 |
Fig. 3 Binding energy per TiO2 monomer unit for small (N = 3–7, left) and large (N = 8–15, right) clusters for 90% of the most favourable clusters after optimisation with the force-field approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
| In the text | |
 |
Fig. 4 Binding energy per TiO2 monomer unit for small (N = 3–7, left) and large (N = 8–15, right) clusters for the best 90% of clusters after optimisation with the DFTB approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
| In the text | |
 |
Fig. 5 Binding energy per monomer unit for small (N = 3−7, top) and large (N = 8−15, bottom) clusters for the best 50 clusters after optimisation with the DFTB approach. Individual clusters are colour-coded according to the method of creating the candidate cluster (Sect. 2.1). A random spread along the x-axis has been added to enable comparison between clusters at similar energies. |
| In the text | |
 |
Fig. 6 New global minimum structure for (TiO2)13. The binding energy is Ebinding = −1782.96 kJ mol−1 per monomer unit. |
| In the text | |
 |
Fig. 7 Concentrations of titanium containing molecules in gas-phase chemical equilibrium at 10−3 bar. Solar element abundance is assumed. TiO2 is the most abundant Ti-binding species up to 1200 K and the second most abundant species up to 1800 K. |
| In the text | |
 |
Fig. 8 Most abundant gas-phase molecules containing titanium from a gas of solar composition using equilibrium chemistry. Pressure temperature profiles for a hot-Jupiter atmosphere with Teff = 1600 K included, probing the atmosphere at four distinct locations. |
| In the text | |
 |
Fig. 9 Gibbs free energy of formation per cluster size N as a function of cluster size N at a temperature of T = 1000 K. For each approach, a fit for σ∞ was calculated using Eq. (5). Left: comparison of the resulting surface tensions for different sources of cluster data. The sources are Lee et al. (2015) for the orange line, DFT calculations with the fast basis set def2svp for the green line, and DFT calculations with the accurate basis set cc-pVTZ for the blue line. Right: comparison of the impact of isomer completeness on resulting surface tension. Both lines use thermochemical data derived from the accurate cc-pVTZ basis set DFT calculations. For the blue line, the energetically most favoured isomer was chosen for all sizes, regardless of whether it was found by the approach in this paper. For the red line, only outputs from the approach described here were used. As the resulting difference is small, it becomes apparent that the choice of the basis set has a greater effect than the completeness of the cluster geometries. |
| In the text | |
 |
Fig. 10 Dependence of the best fit for σ∞ on the temperature T. A linear regression has been applied. |
| In the text | |
 |
Fig. 11 Classical nucleation rate for TiO2 for three different surface tensions σ∞. The temperature-pressure profile is equivalent to the solid blue line in Fig. 8. Top: nucleation rate at different temperatures. Bottom: position of the peak of the nucleation rate within the atmosphere. |
| In the text | |
 |
Fig. 12 Nucleation rates J* for non-classical nucleation theory. The temperature–pressure profile is equivalent to the solid blue line in Fig. 8. Using individual cluster data from this work (B3LYP/cc-pVTZ) (blue), cluster data from Lee et al. (2015) (dashed orange), and the modified CNT approach from Sect. 4.3.1 (green). Top: dependence on temperature. Bottom: dependence on pressure. |
| In the text | |
 |
Fig. D.1 Calibration comparisons for the force-field approach. Left: Relative energy deviation to the global minimum cluster for the force-field approach vs the DFT approach for all clusters from Sect. 2.4.1. Ideally, if the force field approach exactly reproduced the results of the more accurate DFT approach, all points would be on the black line with slope 1. Right: Distance parameter DD for all clusters from the force-field paramterisation vs the DFT approach. In an ideal scenario, all clusters are exactly reproduced and therefore do not deviate from the black line with slope 1. Parameters in the top panel are from Lamiel-Garcia et al. (2017), in the middle panel from Matsui & Akaogi (1991), and in the bottom panel from this work. |
| In the text | |
 |
Fig. D.2 Comparison of the DFT and DFTB energetic orderings for three different sets of Slater-Koster integrals. (a): Matsci Slater-Koster integrals. (b): Trans3d Slater-Koster integrals. (c): Tiorg Slater-Koster integrals. The positions of all isomers on the x-axis are consistent in all three panels. The energy level of the global minimum according to DFT is given by the horizontal blue lines. The relative energetic ordering from the DFT calculations is given by their order from right to left, and the DFTB ordering is given from top to bottom. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


