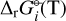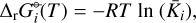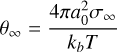EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A34 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A34
Number of page(s) 15
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202347693
Published online 26 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The presence of dust and clouds throughout the Universe has a strong impact on the physics and chemistry of various astrophysical environments (Henning 2010). Dust is known to form in the outflows of asymptotic giant branch (AGB) stars (Sedlmayr 1994; Ferrarotti & Gail 2002; Gail et al. 2013; Gobrecht et al. 2016; Khouri et al. 2016; Decin et al. 2017), supernovae ejecta (Patzer et al. 1998; Sarangi et al. 2018; Zhang et al. 2021), and protoplanetary disks (Liu & Ji 2020), whereas clouds are present in the atmospheres of brown dwarfs (Ackerman & Marley 2001; Woitke & Helling 2004; Helling & Woitke 2006; Suárez & Metchev 2023) and exoplanets (Charbonneau et al. 2002; Kreidberg et al. 2014; Lee et al. 2015; Sing et al. 2016; Gao et al. 2021; Helling et al. 2023; Samra et al. 2023; Feinstein et al. 2023). However, the formation processes of both clouds and dust grains remain unclear. In particular, the initial stages of the process, where gas-phase molecules recombine to form clusters, are not well understood.

In substellar atmospheres, these cluster particles provide the cloud condensation nuclei (CCN) necessary for the onset of cloud formation (Hudson 1993; Lee et al. 2018; Helling 2019; Sindel et al. 2022). On rocky planets, CCN are provided by processes that take place at the surface of the planet, such as volcanic activity or sandstorms. In gaseous exoplanets and brown dwarfs, the CCN formation process entails a transition from the gas-phase to the solid phase. From a microscopic perspective, the transition is initiated by reactions between molecules, atoms, and/or ions that lead to the formation of increasingly more complex species, such as nanometer-sized clusters. The clusters then continue to interact and grow until macroscopic solid particles are formed (Gail et al. 1984; Gail & Sedlmayr 2013; Lee et al. 2018; Boulangier et al. 2019) and provide a surface on which other gas-phase molecules can condense, forming a dust grain or a cloud particle. Clusters can therefore be considered as a bridge between the gas and the solid phase, filling the gap between small molecules and bulk materials (Johnston 2002). The formation of clusters is commonly referred to as the nucleation process.

There are two main approaches to modeling the nucleation process: top-down (Schoiswohl et al. 2006; Gail et al. 2013; De Jesus et al. 2018) and bottom up (Bromley et al. 2016; Gobrecht et al. 2022; Sindel et al. 2022). In the top-down approach, the macroscopic bulk properties are taken as a starting point and are extrapolated to nanoscale structures. However, the size reduction from macroscopic to nanometer length scales can lead to drastic changes in the material properties (e.g., atomic ordering in the lattice, stability of the material, melting temperatures; Viñes et al. 2017), because quantum and surface effects on the small clusters lead to noncrystalline structures, whose characteristics (geometry, energy, coordination, spectra) deviate significantly from those of the crystalline bulk material. In a bottom-up approach, the opposite direction is followed: we start with a single molecule or monomer and gradually increase in size towards the bulk limit. Clusters need to reach a certain size before the regular, periodic atomic ordering characteristic of the crystalline bulk material is thermodynamically favored. Therefore, the first steps of the nucleation process are more accurately described by a bottom-up approach, starting with the smallest molecules and using progressively larger clusters as building blocks.

Although there are different theories to describe the nucleation process, such as classical (CNT; Gail & Sedlmayr 1986), modified (MCNT; Gail et al. 1984; Draine & Salpeter 2008; Helling & Woitke 2006; Gail & Sedlmayr 2013) and non-classical nucleation theory (NCNT; Gail & Sedlmayr 2013; Helling & Fomins 2013; Lee et al. 2015), as well as kinetic nucleation networks (Patzer et al. 1998; Gobrecht et al. 2016; Boulangier et al. 2019; Gobrecht et al. 2022), all of them require thermochemical data for the nucleating species, in particular for their respective clusters. Experimental data are commonly available for the condensed species as well as for simple gas-phase molecules but become sparse for the nanocluster size regime. Nucleation has been studied experimentally (Li & Signorell 2021). However, such experiments are limited in the range of pressures and temperatures, and these ranges do not cover the conditions in substellar atmospheres. Therefore, these experiments cannot provide information regarding which materials are more likely to nucleate under substellar conditions. Metal-oxide cluster ions can be synthesized in cluster beam experiments (see e.g., Asmis & Sauer 2007; Fielicke & Rademann 2002; Mariñoso Guiu et al. 2022), but we aim to study neutral clusters. Quantum mechanical calculations provide a way to bridge the gap between the gas and the solid phase data. Global optimizations can be performed to determine the most favorable geometry for each cluster size, which is then assumed to take part in the nucleation process. Several studies have applied a quantummechanical bottom-up approach to the formation of CCN for a diverse range of chemical species, including Ti-bearing species, such as TiO2 (Sindel et al. 2022; Jeong et al. 2000), alumina (Gobrecht et al. 2022), SiO (Bromley et al. 2016), and Febearing species (Chang et al. 2013). Vanadium oxide compounds have been a common subject of study in materials science (Asmis et al. 2004; Asmis & Sauer 2007; Janssens et al. 2006; Archambault et al. 2021; Vyboishchikov & Sauer 2000) due to their various technological applications (Weckhuysen & Keller 2003; Whittingham 2004; Krusin-Elbaum et al. 2004) but their consideration as nucleation species in substellar atmospheres is unprecedented.

The vanadium monoxide molecule has been observed in the atmospheres of red giant stars (Alvarez & Plez 1998) and exoplanets (Evans et al. 2016; Pelletier et al. 2023), whereas solid vanadium oxide is found in pristine meteoric material (Rehder 2011). As refractory materials, vanadium oxides are alternative candidates to classical seed particle species, which include oxides of silicon (Gail et al. 2013; Bromley et al. 2016), titanium (Sindel et al. 2022; Jeong et al. 2000), and aluminum (Gobrecht et al. 2022; Patzer et al. 2005). Perhaps due to the comparatively low solar vanadium abundance, to our knowledge, no systematic study on the nucleation of vanadium oxides has been carried so far. Vanadium oxides exhibit relatively low vapor pressures and correspondingly high boiling temperatures (see e.g., Haynes 2016), which is also reflected in the high VO bond energy (~630 kJ mol−1 Balducci et al. 1983; Merriles et al. 2020). Furthermore, molecular VO is observed only in the hottest sub-stellar atmospheres, indicating that VO is incorporated into cloud particles in environments with lower temperatures. Therefore, vanadium oxides are promising nucleation (i.e., condensation seed) candidates at temperatures around ~1000 K, where dust nucleation occurs in astrophysical environments.

In this study, we aim to assess the viability of vanadium oxides as nucleation seeds in substellar atmospheres. In Sect. 2, we present the computational chemistry methods that we applied to obtain the most stable cluster for several vanadium oxide compounds ((VxOy)N, N = 1−10, x = 1,2, y = 1,2,5). The thermochemical characteristics of the lowest-energy isomers and the impact of the updated cluster data in chemical equilibrium calculations are presented in Sect. 3. In Sect. 4, we calculate the nucleation rates for a brown dwarf model atmosphere and present the vibrational spectra for each isomer. Finally, we summarize our findings and outline our proposed further work in Sect. 5.

2 Methods

The subjects of this paper are vanadium oxide clusters with different stoichiometries; namely (VxOy)N, N = 1−10, x = 1,2, y = 1,2,5. The selection of the clusters is based on our computational capabilities and the stability of the stoichiometric families in the gas-phase and as a solid. We investigate their geometries, binding energies, thermochemical properties, and equilibrium abundances.

We conducted a search for the most favorable isomers for each size and stoichiometry. The most favorable isomer for each cluster size represents the lowest minimum on the potential energy surface (PES) and we refer to it as the global minimum (GM) candidate. To find the GM candidate we use a large number of initial geometries of each considered cluster size and stoichiometry until we find the lowest energy configuration. The number of possible structural isomers increases rapidly with clusters size; that is, with the number of atoms in the cluster. Therefore, an exploration of the entire PES at the density functional theory (DFT) level of theory is computationally very demanding for clusters with tens of atoms. To minimize the computational effort, we employ a hierarchical global optimization technique using an interatomic potential as first step in our (VxOy)N cluster study (see Sect. 2.1). This procedure reduces the number of possible structural configurations significantly and generates low-energy candidate isomers. The lowest-energy candidate structures are subsequently refined by optimizations at the DFT level (see Sect. 2.2).

Table 1

Parametrizations of the Buckingham-Coulomb pair potential used for the first stage in the optimization process of each cluster.

2.1 Optimization with force fields

We first performed a global optimization search for low-energy isomers using the interatomic Buckingham-Coulomb pair potential. The optimizations were computed with the General Utility Lattice Program (GULP) (Gale 1997). The Buckingham– Coulomb pair potential (Buckingham & Lennard-Jones 1938) is commonly used for materials with an ionic character such as metal oxides, and has the form: 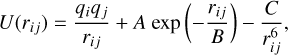U(rij)=qiqjrij+Aexp(−rijB)−Crij6,$U\left( {{r_{ij}}} \right) = {{{q_i}{q_j}} \over {{r_{ij}}}} + A\exp \left( { - {{{r_{ij}}} \over B}} \right) - {C \over {r_{ij}^6}},$(1)

where qi and qj are the charges of atoms i and j, rij is the distance between them, and A, B, and C are the Buckingham pair parameters. The first term in Eq. (1) describes electrostatic interactions between the ions. The second term accounts for the Pauli principle and represents the short range repulsion caused by the fact that ions occupy a certain volume in space. Lastly, the third term accounts for the attractive Van der Waals interaction. As opposed to the case for oxides of silicon, aluminum, and titanium, there are very few parameter sets for V–O systems available in the literature. Therefore, we used Buckingham pair parameters resembling those known for other metal oxides. We applied different parametrizations of the Buckingham–Coulomb pair potential to optimize the seed structure geometries. A summary of the different parameters sets used in this study can be found in Table 1. As initial seed geometries, we use a large number of polymorph structures reported for clusters of magnesium oxide (Chen et al. 2014), aluminium oxide (Gobrecht et al. 2018, and Gobrecht et al. 2022), silicon oxide (Bromley et al. 2016), titanium oxide (Sindel et al. 2022), and silicon carbide (Gobrecht et al. 2017).

As vanadium and oxygen have different electronegativities (3.44 and 1.63 on the Pauling scale Pauling 1932), we account for polarization effects in our calculations. For the vanadium monoxide isomers, we applied two different parameter sets. An initial set of calculations was performed with reduced electrostatic charges for both the cations and the anions, and with A, B, and C parameters for the V–O interactions from Lewis & Catlow (1985) and for the O–O interactions from Bush et al. (1994). A second set of calculations was performed using the core–shell model for each geometry. In the core–shell model (Dick & Overhauser 1958), the ion is divided into two closely lying coordinates connected by a spring with a spring constant k: a core that contains all the atomic mass, and a massless charged shell. For the second set of calculations, the electrostatic charges were not reduced, but distributed between the core and the shell and shell–shell values were used for both the V–O (estimated based on the values available in Lewis & Catlow 1985) and O–O (Bush et al. 1994) interactions. Both sets provide similar optimized geometries with slight differences in the bond lengths and the energetic ordering of the isomers. As the core set produces more candidates that result in global minima after the DFT calculations (sizes N = 2, 4, 5, 6, 9, 10), and – as mentioned above – interatomic potential parameters for the core–shell model are not available for many systems, we decided to use the reduced charges method for vanadium oxide clusters with stoichiometries different from 1:1.

2.2 Optimization with density functional theory

The candidate structures generated with the methods detailed in Sect. 2.1 are subsequently optimized at the quantum level of theory with the computational chemistry software package Gaussian16 (Frisch et al. 2016). We use the hybrid B3LYP density functional (Becke 1993) as a compromise between accuracy and computational cost; we discuss this choice further below. For our calculations, we used the correlation consistent polarized valence triple zeta basis set (cc-pVTZ, Wilson et al. 1996), whose basis functions are known to accurately describe electronic orbitals at an affordable computational cost. The accuracy of our choice was determined by comparing the computational results obtained from the DFT calculations with the experimental values published in the NIST-JANAF Thermochemical tables1 (Fig. 1).

Generally, the binding energies of the vanadium oxides for a temperature of T = 0 K are calculated as: 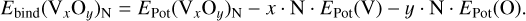Ebind(VxOy)N=EPot(VxOy)N−x⋅N⋅EPot(V)−y⋅N⋅EPot(O).${E_{{\rm{bind}}}}{\left( {{{\rm{V}}_x}{{\rm{O}}_y}} \right)_{\rm{N}}} = {E_{{\rm{Pot}}}}{\left( {{{\rm{V}}_x}{{\rm{O}}_y}} \right)_{\rm{N}}} - x \cdot {\rm{N}} \cdot {E_{{\rm{Pot}}}}({\rm{V}}) - y \cdot {\rm{N}} \cdot {E_{{\rm{Pot}}}}({\rm{O}}).$(2)

For coherence and consistency, the potential energies are calculated at the B3LYP/cc-pVTZ level of theory, and show very good agreement (~10 kJ mol−1) with the experimental values for VO and reasonable agreement (~22 kJ mol−1) for VO2. Moreover, this functional/basis set was found to accurately predict the binding energies of other transition metal oxides, such as TiO2 (Sindel et al. 2022). For each GM candidate, we also performed a frequency analysis with the same functional/basis set to determine whether or not the candidate is a true minimum and not a transition state and to calculate the relevant partition functions. The partition functions of the GM candidates are computed using the rigid rotor harmonic oscillator (RRHO) approximation, as implemented in the thermo.pl code (Irikura 2002). With the help of the partition functions, the temperaturedependent thermodynamic potentials such as the entropy S, the enthalpy of formation, ∆f H(T), and the Gibbs free energy of formation ∆f G(T) can be derived (see Sect. 3.2).

The choice of the B3LYP/cc-pVTZ method is based on the replication of the NIST-JANAF values for the VO molecule, which can be seen in Fig. 1. The calibration was done for the vanadium monoxide (VO) molecule because we aim to obtain accurate energies for the first steps of cloud formation using a bottom-up approach. We know that, when vanadium oxides are in their bulk solid phase and the atoms form a crystalline structure, the preferred oxidation state is V2 O5 (vanadium (V) oxide), which corresponds to the thermodynamically most stable form of solid vanadium oxide (Yan et al. 2009). Starting from atomic vanadium, we study the intermediate oxidation steps, with the smallest molecule being diatomic VO. Therefore, accurate values for the energy, vibration frequency, and rotational constant of VO are essential for modeling the vanadia nucleation starting from gas-phase molecules. In Fig. 1 we compare the Gibbs free energies of formation (∆f G(T)) for the vanadium-bearing gasphase molecules for which data are available in the NIST-JANAF Thermochemical tables. The excellent agreement between the DFT results and the JANAF values for VO confirms that our choice of functional and basis set (B3LYP/cc-pVTZ) accurately represents the behavior of VO for the entire temperature range that we are studying. The agreement between our data and the JANAF table for VN is reasonable at lower temperatures and starts to diverge above ~3000 K. The results for VO2 follow the same trend but show an offset of about 80-100 kJ mol−1 . This discrepancy likely arises because of an erroneous enthalpy estimation based on studies of Frantseva & Semenov (1969). Indeed, Balducci et al. (1983) revisited and re-evaluated the VO2 enthalpy in an experimental study and found significantly higher enthalpies of formation. A comparison of the binding energies published in JANAF, the results of Balducci et al. (1983), and the findings of this study can be found in Table 2. The VO bond energy derived from JANAF and B3LYP/cc-pVTZ calculations is within the confidence interval of the Balducci et al. (1983) values. This is not the case for VO2, but the results obtained with our calibrated DFT calculations are considerably closer to the results of Balducci et al. (1983) than those reported in the JANAF table. Owing to the open shell character of the vanadium atom with an electronic ground state of 4F3/2 and the VO molecule with a ground state of 4∑−, other V-bearing molecules and clusters can have spin quantum numbers larger than one (i.e., singlets). Therefore, we investigated several spin multiplicities for each of our vanadium cluster candidates.

thumbnail Fig. 1

Gibbs free energies of formation (in kJ mol−1) for VN, VO, and VO2 as a function of temperature. Dotted lines correspond to the values available in the JANAF database and full lines represent the data obtained from our DFT calculations at the B3LYP/cc-pVTZ level of theory using the RRHO partition function.
Table 2

VO and VO2 electronic binding energies from different sources.

2.3 Implementation of data for equilibrium chemistry calculations

In the following, we use the term abundance to refer to the species concentration relative to the total gas density. The thermodynamic ranges for which each vanadium-bearing species is the most abundant in a given substellar atmosphere can be determined with chemical equilibrium calculations. The abundances obtained from chemical equilibrium can later be used as a starting point to calculate reaction rates in a kinetic approach.

We applied the gas-phase equilibrium code GGChem from Woitke et al. (2018) to obtain the equilibrium abundances. GGChem applies the law of mass action derived by minimizing the Gibbs free energy of the total gas (∆fG°(T)) to calculate the number densities of each species at a given temperature and pressure. In order to implement the DFT data into the code, we first calculated the Gibbs free energies of the dissociation of each species 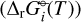(ΔrGi°(T))$\left( {{\Delta _{\rm{r}}}G_i^{\rlap{--} ^\circ }(T)} \right)$ following the approach used by Woitke et al. (2018) and Stock et al. (2018): ΔrGio(T)=ΔfGio(T)−∑j∈ϵ0vijΔfGjo(T),${{\rm{\Delta }}_{\rm{r}}}G_i^{}(T) = {{\rm{\Delta }}_{\rm{f}}}G_i^{}(T) - \mathop {\mathop \sum \nolimits^ }\limits_{j \in {_0}} {v_{ij}}{{\rm{\Delta }}_{\rm{f}}}G_j^{}(T),$(3)

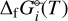where ΔfGi°(T)${{\Delta _{\rm{f}}}G_i^{\rlap{--} ^\circ }(T)}$ is the Gibbs free energy of formation of species i. The second term on the right hand side represents the sum over the Gibbs free energies of formation of each element in the species. є0 is the set of all the elements included in the code and vij the stoichiometric coefficients of the elements within species i. As the natural logarithm of the dimensionless equilibrium constant 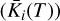(K¯i(T))$\left( {{{\bar K}_i}(T)} \right)$ of a certain species can be defined as 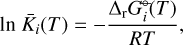lnK¯i(T)=−ΔrGio(T)RT,$\ln {\bar K_i}(T) = - {{{{\rm{\Delta }}_{\rm{r}}}G_i^{}(T)} \over {RT}},$(4)

we can express ΔrGi°(T)${{\Delta _{\rm{r}}}G_i^{\rlap{--} ^\circ }(T)}$ as ΔrGio(T)=−RTln(K¯i),${{\rm{\Delta }}_{\rm{r}}}G_i^{}(T) = - RT\ln \left( {{{\bar K}_i}} \right),$(5)

and fit the Gibbs free energies of dissociation from Eq. (3) with an expression in temperature with five coefficients (a0, a1, b0, b1, b2), which we use as input into GGChem: 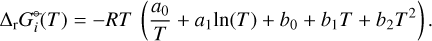ΔrGio(T)=−RT(a0T+a1ln(T)+b0+b1T+b2T2).${{\rm{\Delta }}_{\rm{r}}}G_i^{}(T) = - RT\left( {{{{a_0}} \over T} + {a_1}\ln (T) + {b_0} + {b_1}T + {b_2}{T^2}} \right).$(6)

All the calculations are performed under the assumption of local thermal equilibrium, and therefore the gas temperature and the cluster temperatures are the same. A summary of the fit coefficients for each cluster can be found in Appendix A.

3 Results

There are several thermochemical properties of interest for astrophysical studies, including the Gibbs free energies of formation, the entropy and the change in enthalpy. In the following sections, we present the geometries and derived thermochemical properties of all the vanadium oxide clusters covered in this study. We then show how we used the thermochemical properties to evaluate the impact of adding clusters on the gas-phase abundances of all vanadium-bearing species. The gas-phase abundances in chemical and thermal equilibrium can be used as a starting point in the modeling of atmosphere kinetics, which is needed in order to interpret observational data (e.g., from the James Webb Space Telescope (JWST)).

3.1 Lowest-energy cluster structures

For each considered vanadium oxide compound, the 10–100 lowest-energy candidate isomers found with the interatomic pair potential (see Sect. 2.1) were subsequently optimized at the B3LYP/cc-pVTZ level of theory with Gaussian16 (Frisch et al. 2016). The geometries of the GM candidates for each considered stoichiometry and cluster size are presented in Fig. 2.

In the following, the properties of the lowest-energy VxOy isomers listed in Table 3 are described in detail. We report the electronic binding energy of the GM clusters at T = 0 K as calculated with the B3LYP/cc-pVTZ method, the spin multiplicity Ms , the point symmetry group in the Schönflies notation, and the average V–O bond length in Å. Vanadium has atomic number 23 and therefore at least one unpaired electron. Its electronic ground state is a quartet. As a consequence, clusters containing an odd number of V cations show even spin multiplicities with values of Ms = 2,4,6, and so on, and vice versa, clusters with an even number of V atoms show an odd spin multiplicity.

The (VO)N clusters show high spin multiplicities, which is a consequence of different valencies of vanadium and oxygen. The lowest-energy state of the VO molecule (Fig. 2a) is a quartet state; that is, it has a spin multiplicity of 4. We find a bond dissociation energy of 636 kJ mol−1 which is close to the experimental value of 621 kJ mol−1 derived by Jakubikova et al. (2007). These authors find a bond length of 1.61 Å, which is about 0.03 Å longer than the optimized distance in our study. The lowest-energy V2O2 cluster structure (Fig. 2b) was extensively investigated by Hübner & Himmel (2017). The authors use multireference configuration interaction (MRCI) calculations and report a singlet electronic ground state and multiple vanadium–vanadium bonds, which is in contrast to previous findings (Jakubikova et al. 2007). With our single-reference B3LYP/cc-pVTZ calculations, we find a septet (Ms = 7) state and no V–V bond as the lowest-energy configuration, which is consistent with the results of Jakubikova et al. (2007). For the corresponding triplet state, we find an energy that is only 25 kJ mol−1 above the reported Ms = 7 state. High-level test calculations indeed indicate a multiconfigurational character of the V2O2 global minimum. However, owing to the high computational cost, an investigation with such post-Hartree-Fock methods is limited to relatively small systems and the cost is prohibitive for the larger cluster sizes considered in this study. The lowest-energy V3O3 isomer (Fig. 2c) is a closed-ring structure with nonuniform bond angles as reported in Kaur et al. (2019), which is similar to the GM candidates of Si3O3 studied by Bromley et al. (2016). The structures of larger (VO)N with N ≥ 4 were not investigated in previous studies and their respective GM candidates are reported for the first time in the present study. For sizes N = 4–9 (Figs. 2d–i), we find void cages with alternating V–O ordering as the most favorable isomers. For N = 4,5,6 (Figs. 2d–f) and 9 (Fig. 2i), the GM candidates are symmetric structures showing a mirror plane. (VO)10 (Fig. 2j) represents an outlier in this series of GM candidates as it exhibits several V–V bonds, is a singlet state, and is very compact, in contrast to smaller sized (VO)9.

Some of the (VO2)N GM candidates have geometries equivalent to those of the GM isomers of (TiO2)N reported in Lamiel-Garcia et al. (2017) and Sindel et al. (2022). These include N = 1,2,3,4, and 7 (Figs. 2k–n, p). Compared to the TiO2 monomer, the VO2 (Fig. 2k) molecule exhibits a similar geometry with slightly shorter bond lengths (1.61 Å) and a slightly larger bond angle (116°). The VO2 dimer (Fig. 2l), V2O4 , shows a trans configuration. In contrast to Jakubikova et al. (2007), we do not find a broken symmetry of this singlet GM candidate. To our knowledge, the GM candidate for V3O6 (Fig. 2m) is reported here for the first time. The planar V3O6 structure reported in Jakubikova et al. (2007) and Kaur et al. (2019) lies 178 kJ mol−1 above our GM candidate and corresponds to a transition state with an imaginary frequency. Also, the GM candidate of V4O8 (Fig. 2n) shows a similar geometry to the corresponding Ti4O8 GM candidate. For the isomer reported by Kaur et al. (2019), we find an energy of 55 kJ mol−1 above our GM candidate and two imaginary frequencies. The structures of the (VO2)N, N = 4–10 (Figs. 2n–t) GM candidates represent hitherto unreported structures. Apart from (VO2)10 (Fig. 2t), they are characterized by two singly coordinated terminal oxygen atoms with comparatively short bond lengths. Moreover, these favorable cluster isomers are not symmetric and belong to the C1 point group with the exception of (VO2 )6 (Fig. 2p).

The GM candidates of the (V2O5)N, N = 1–4 (Figs. 2u–x) cluster family show symmetric structures and are singlet states. As members of the vanadia stoichiometry, like solid V2O5 , these GM candidate clusters are well studied and were previously reported in, for example, Vyboishchikov & Sauer (2000) and Lasserus et al. (2019). Our search for low-energy (V2O5)N isomers confirms the results of these studies. The atomic coordinates of the reported GM cluster candidates are available in electronic form at the CDS.

3.2 Thermochemical properties

The spherical cluster approximation (Johnston 2002) was used to fit the potential energies of the GM candidates as a function of the cluster size N, allowing an extrapolation to cluster sizes that cannot be studied with DFT. Using the spherical cluster approximation, it can be shown that the surface area to “bulk” ratio of the cluster is proportional to N−1/3. This implies that many properties of the cluster, such as its dissociation energy or melting temperature, can be approximately fitted by the following scaling law: 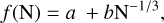f(N)=a+bN−1/3,$f({\rm{N}}) = a + b{{\rm{N}}^{ - 1/3}},$(7)

where a corresponds to the value of the property being studied but at the bulk phase of the material (Viñes et al. 2017). The results of fitting the GM candidates for (VO)N , (VO2 )N with N = 1–10, and (V2O5)N with N = 1–4 are shown in Fig. 3 and a summary of the fit parameters can be found in Table 4. For (VO)N and (VO2)N , we obtain acceptable agreement between the spherical cluster fit and our data for the smaller sizes, but for the larger clusters the normalized energies cease to decrease monotonically and can even follow an opposite trend. This is the case for cluster sizes N = 7–10 for (VO)N and (VO2 )N, indicating that our candidate might not correspond to the lowest energy configuration. However, with our extensive searches amongst a great diversity of structures, we hope to have minimized the probability of missing a particularly favorable isomer. The deviation from the fit may be due to the 1:1 and 1:2 stoichiometric ratios of V:O not being preferred as the clusters increase in size; this is because the preferred oxidation state in the bulk is V2O5.

From the partition functions that include vibrational contributions, we calculated the relevant thermochemical quantities as described in Sect. 2.2. We summarize our results for T = 1000 K in Table 5 and the complete tables (for the range 0 K ≤ T ≤ 5900 K) for each GM candidate are to be made available electronically as supplementary material at the CDS.

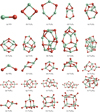thumbnail Fig. 2

Geometries of the global minima candidates for (VO)N and (VO2)N with N = 1–10 and (V2O5)N with N = 1–4. Vanadium and oxygen atoms are shown in green and red, respectively.
Table 3

Properties of the (VO)N, (VO2)N,N = 1–10, and(V2O5)N,N = 1–4 GM candidates listing (1) cluster size, (2) electronic binding energy Eb (in kJ mol−1 ), (3) electric binding energy normalized to cluster size Eb/N (in kJ mol−1 ), (4) spin multiplicity Ms , (5) point group symmetry in the Schönflies notation, and (6) average VO bond length 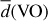d¯(VO)$\bar d\left( {{\rm{VO}}} \right)$ in Å.

Table 4

Summary of the fit parameters from Eq. (7) for VO, VO2 , and V2O5 atT = 0 K and T = 1000 K.

thumbnail Fig. 3

Dissociation free energy of each global (VO)N (top), (VO2)N (middle), and (V2O5 )N (bottom) GM candidate normalized by the cluster size at T = 0 K and T = 1000 K as a function of cluster size N and fitted to the spherical cluster approximation as described in Eq. (7).

3.3 Impact on abundances of vanadium-bearing species

As a first step, we determine the impact of implementing the revised and more accurate thermochemical data derived in this study for the vanadium-bearing species already present in GGChem. Our results for VO2 differ from the JANAF free energies2 presently used in GGchem as shown in Fig. 1 and therefore differences in the equilibrium abundances are expected.

As can be seen in Fig. 4, substituting the current ∆fG values for VO and VO2 with the updated energies obtained in this study has a strong impact at lower temperatures (T ≲ 2000 K) for VO and throughout the whole temperature range (100 K ≲ T ≲ 6000 K) for VO2 . Using the JANAF tables and a solar elemental composition, VO2 is the most abundant vanadium-bearing species for temperatures below ~1500 K. Between ~1500 K and ~2000 K, VO becomes the most abundant V-containing species and for higher temperatures the most abundant is then atomic vanadium. With the updated thermochemical data, the behavior of VO and VO2 is flipped for temperatures between ~300 K and ~1500 K. Due to the updated higher Gibbs free energies, the fractional abundance of VO2 has decreased throughout the entire temperature range. This behavior is consistent with observations. VO and atomic vanadium have both been detected in hot Jupiters (Pelletier et al. 2023), whereas the presence of VO2 has been predicted based on previous equilibrium chemistry calculations (Hoeijmakers et al. 2020) but not yet detected. Owing to element conservation, the abundances of other V-bearing species are also affected. This effect can be seen in the abundances of V and VN, for example.

As we aim to model CCN formation, it is necessary to study clusters with various V:O stoichiometries and larger sizes that go beyond the respective monomers and species currently included in GGchem. In Fig. 5, the chemical equilibrium abundances of the vanadium-bearing species are shown for a pressure of 1 bar and a gas temperature range between 100 and 2000 K. The top panel displays the abundances of vanadium-bearing molecules, including the (VO)N stoichiometric cluster family. The middle panel shows the (VO2)N clusters additionally included. The lower panel of Fig. 5 shows the abundances of V-containing species including all considered cluster families; that is, (VO)N, (VO2)N, and (V2O5)N. In a stepwise manner, each cluster was added individually in order of increasing size. We find that each newly added vanadium monoxide (VO)N cluster (Fig. 5 (top)) becomes the most abundant species below ~1000 K up to a size of N = 7. For N>7, this is no longer the case. Such behavior may be due to the higher stability of (VO)7 shown in Fig. 3 (top) and to the fact that the 1:1 ratio is not favored for bigger sizes. For the (VO2)N GM candidates (Fig. 5 (middle)), the situation is similar, as the heptamer (N = 7) also corresponds to the most abundant vanadium oxide cluster. The (V2O5 )N N = 1–4 cluster subset (Fig. 5 (bottom)) becomes the most abundant V-bearing species for temperatures below ~500 K, leaving (VO2)7 as the most abundant species between ~500 K and ~1000 K, and the vanadium monoxide monomer and atomic vanadium as predominant species for higher temperatures. As the latter case (Fig. 5 (bottom)) corresponds to the most extensive set of V-bearing species, we consider the resulting equilibrium abundances as most realistic. We note that vanadium monoxide is the only monomer more abundant than the clusters of its stoichiometric family, indicating it may remain detectable after the nucleation process has taken place. On the contrary, the spectral features of the VO2 and V2O5 monomers may be hidden by the spectral features of the most stable clusters in their respective stoichiometric families.

In order to account for the conditions of cloud formation in substellar atmospheres, we applied GGchem for a grid of gas pressures and gas temperatures in the ranges (700, 1 × 10−14) bar and (100, 4000) K, respectively. Figure 6 shows the pressure– temperature (Tgas, pgas) profiles of the hot Jupiter WASP-121 b (Helling et al. 2021; Parmentier et al. 2018; Mansfield et al. 2018) in black, a brown dwarf with log(𝑔)=5 (Dehn 2007; Helling et al. 2008; Witte et al. 2009, 2011) in green, and a T-Tauri proto-planetary disk (Kanwar et al. 2023) in blue over the pressure temperature grid results.

WASP-121 b is an ultrahot Jupiter (UHJ) with a global temperature of approximately 2700 K (Evans et al. 2016). Its evening terminator and substellar point are therefore too hot for the clusters to be abundant (Parmentier et al. 2018) and their chemistry to be relevant, which is in agreement with our equilibrium calculations. We believe the role of clusters in the formation of CCN will become more relevant for cooler objects, such as the brown dwarf shown in Fig. 6; the cooler regions toward the midplane of protoplanetary disks (the (Tgas, pgas) profile shown in Fig. 6 corresponds to a cut from the midplane outwards at a distance of 1 AU); and cooler exoplanets such as colder hot Jupiters or warm Saturns. We have chosen WASP-121 b as our example hot Jupiter because, together with TiO, VO has been considered as a possible driver for the temperature inversion in the atmosphere, even though their detection and their role as main drivers of the thermal inversion remain disputed (Evans et al. 2016; Ouyang et al. 2023; Mikal-Evans et al. 2020, 2019; Merritt et al. 2020). The related observed transmission spectra are constrained to optical and near-infrared wavelengths and do not probe transitions in VO with lower energies. Our findings predict VO as the most abundant vanadium-bearing species for a considerable extension of the atmosphere at the antistellar point (solid black line) and at the morning terminator (dotted black line) using chemical equilibrium and assuming that the atmosphere is cloud free. We therefore conclude that it is very likely that vanadium monoxide is present in the atmosphere of WASP-121 b.

Table 5

Summary of the thermochemical quantities (entropy S, heat capacity Cp, enthalpy change H(T) – H(0), enthalpy of formation dHf and Gibbs free energy of formation dGf) obtained for each of our GM candidates at T = 1000 K.

thumbnail Fig. 4

Comparison of the abundances of the vanadium-bearing species currently present in GGchem as a function of temperature. The dashed lines correspond to the data from previous studies already implemented in GGchem and the full lines correspond to the abundances obtained after implementing the ∆fG values obtained for VO and VO2 from our DFT calculations. The calculations were run at P = 1 bar and with solar elemental abundances from Asplund et al. (2009).
thumbnail Fig. 5

Abundances of all the vanadium-bearing species already present in GGchem and the clusters obtained from our DFT calculations as a function of temperature. Top: all (VO)N clusters included. Middle: all (VO)N and (VO2)N clusters included. Bottom: all (VO)N, (VO2)N, and (V2O5)N clusters included. The calculations were run again at P = 1 bar and with solar elemental abundances from Asplund et al. (2009).
thumbnail Fig. 6

Most abundant vanadium-bearing molecules in chemical equilibrium for a grid of gas pressures and temperatures. The model assumes solar elemental abundances from Asplund et al. (2009) as initial conditions. (Tgas, pgas) profiles of the hot Jupiter WASP-121b (Helling et al. 2021, Parmentier et al. 2018, Mansfield et al. 2018), a brown dwarf (Dehn 2007, Helling et al. 2008, Witte et al. 2009, 2011), and a T-Tauri protoplanetary disk (Kanwar et al. 2023) are over plotted.

4 Astrophysical relevance

In this section, we asses the viability of vanadium oxides as condensation seed candidates, as well as their possible observability. We apply different nucleation theories to determine the nucleation rate of the three considered vanadia stoichiometric families, taking into account the thermochemical data available for each of them. All the nucleation rates were calculated along the (Tgas , pgas) profile of the brown dwarf with log(𝑔)=5 from Fig. 6 (green line). The gas-phase composition was calculated with the equilibrium chemistry code GGchem, assuming that all the monomers (VO, VO2 and V2O5 ) and the additional vanadium-bearing species from Fig. 4 are present in the gasphase. Furthermore, we extracted the vibrational frequencies from our DFT calculations to generate vibrational spectra and determine the wavelength range at which the most intense emission peaks may appear. We find that all the emission peaks are within the JWST-MIRI detection range.

4.1 Nucleation rates of vanadium oxides

The difference in the free energies between the different vanadium oxide stoichiometries (i.e., oxidation states; Fig. 7) indicates that the formation pathways from atomic vanadium to a CCN consisting of hundreds to thousands of atoms is likely not through monomeric homomolecular addition. We provide a first step towards understanding vanadium nucleation by applying different nucleation theories for the three stoichiometric families considered in this study. Nucleation theories such as CNT and MCNT assume monomeric homomolecular addition and therefore give an incomplete image of vanadia nucleation, but they represent a first step towards a fully kinetic approach. As the thermodynamically most stable vanadium oxide stoichiometry in the solid phase is V2O5 , we applied CNT to this cluster family and calculate its surface tension and nucleation rate. We applied NCNT – which relies on the actual energies of the clusters – to (VO)N, (VO2)N, and (V2O5)N.

We followed the approach from Lee et al. (2015) and Sindel et al. (2022) to calculate the surface tension and the CNT nucleation rate. A detailed explanation, as well as the surface tension fit, can be found in Appendix B. As V2O5 undergoes a phase transition from crystalline to liquid at T = 943 K, we fitted the surface tension for the range T = 0 K to T = 900 K: 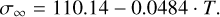σ∞=110.14−0.0484⋅T.${\sigma _\infty } = 110.14 - 0.0484 \cdot T.$(8)

Given the range of the surface tension, we are limited to calculating the CNT nucleation rate for objects cooler than 900 K. For comparison purposes, we chose to calculate all the nucleation rates for the brown dwarf (Tgas , pgas) profile from Fig. 6 and the results can be seen on Fig. 8.

(VO)N and (VO2)N are not the preferred oxidation state in the bulk phase and therefore the available solid phase data are less reliable. For this reason, we decided to calculate their nucleation rates applying only NCNT. We applied the Becker-Döring method (Gail & Sedlmayr 2013; Lee et al. 2015, Sindel et al. 2022) to obtain the summation: 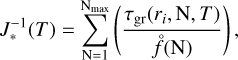J∗−1(T)=∑N=1Nmax(τgr(ri,N,T)f∘(N)),$J_ * ^{ - 1}(T) = \mathop {\mathop \sum \nolimits^ }\limits_{{{\rm{N}}_{\max }}}^{{\rm{N}} = 1} \left( {{{{\tau _{{\rm{gr}}}}\left( {{r_i},{\rm{N}},T} \right)} \over {\mathop f\limits^ \circ ({\rm{N}})}}} \right),$(9)

where τgr corresponds to Eq. (B.2) and the equilibrium number density of a cluster of size N can be calculated from the partial pressures, 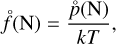f∘(N)=p∘(N)kT,$\mathop f\limits^ \circ ({\rm{N}}) = {{\mathop p\limits^ \circ ({\rm{N}})} \over {kT}},$(10)

which we obtain from applying the law of mass action to a cluster of size N: 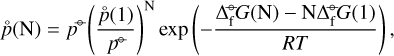p∘(N)=po(pp(1)po)Nexp(−ΔfoG(N)−NΔfoG(1)RT),$\mathop p\limits^ \circ ({\rm{N}}) = {p^{}}{\left( {{{\mathop p\limits^p (1)} \over {{p^{}}}}} \right)^{\rm{N}}}\exp \left( { - {{{\rm{\Delta }}_{\rm{f}}^{}G({\rm{N}}) - {\rm{N\Delta }}_{\rm{f}}^{}G(1)} \over {RT}}} \right),$(11)

where the 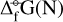Δf°G(N)${\Delta _{\rm{f}}^{\rlap{--} ^\circ }G({\rm{N}})}$ are derived from DFT calculations and the partial pressure of the monomer (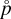po$\mathop p\limits^{\rm{o}} $ (1) [dyn cm−2]) is derived from our equilibrium data, assuming local thermodynamic equilibrium (LTE). The results are summarized in Fig. 8.

thumbnail Fig. 7

Comparison of the Gibbs free energies of formation normalized to the cluster size (∆fG(N)/N) for the clusters (VO)N and (VO2)N with N = 1–10, and for (V2O5)N with N = 1–4, as a function of the degree of oxidation for T = 0 K (full lines) and T = 1000 K (dashed lines).
thumbnail Fig. 8

Nucleation rates of the three vanadium oxide stoichiometries along the (Tgas, pgas) profile of a brown dwarf with log(𝑔) = 5 (black dotted line) and Teff = 1000 K. Full lines: NCNT nucleation rate (Eq. (9)) for VO, VO2, and V2O5 as a function of pressure. Dashed line: CNT nucleation rate (Eq. (B.1)) for V2O5.

4.2 Vibrational synthetic spectra

The VO molecule shows strong transitions between electronically excited A4II, B4II, and C4∑− states and the ground state C4∑−, which are located at 1055 nm, 790 nm, and 574 nm, respectively (Karlsson et al. 1997). In the present study, electronically excited states are not investigated, but internal vibrations and rotations are considered. A summary of the rotational constants of each cluster can be found in Appendix C. According to our calculations, VO exhibits an intense vibrational mode at 9.569 µm and has a rotational constant of 16 646.5 MHz. Related internal transitions of VO, if present, are potentially detectable in planetary atmospheres with state-of-the-art observing facilities, such as JWST.

The vibrational frequencies of the GM cluster candidates, which are required to calculate the partition functions and thermodynamic potentials, also provide us with a means to generate synthetic spectra. Figure 9 shows these spectra for the different cluster families and sizes considered in this study. Here, we assume Lorentzian line profiles with a full width at half maximum (FWHM) of 0.033 µm, which corresponds to a typical ALMA setup resolution. The line intensities are normalized to its maximum value for each cluster size. For (VO)N, N = 2–10, the most intense vibration modes occur in a wavelength range between 13 µm and 20 µm, whereas the VO monomer represents an exception. Overall, we do not find common spectral features for the different (VO)N sizes.

The (VO2)N, N = 1–3 GM candidates show their maximum emission below ~10 µm, while the larger clusters with N = 4– 10 emit most intensely between 12.0 µm and 13.2 µm. These larger clusters all show a common feature at around 9.1 µm that can be attributed to the stretching modes of the terminal, singly coordinated oxygen atom in these structures.

The four (V2O5)N clusters show only a few distinct peaks in the infrared spectra, as their symmetric lowest-energy structures have several vibrational modes with identical frequencies. Their maximum emission lies in the range of 9 to 12 µm. The crystalline V2O5 spectra from Abello et al. (1983) shows prominent emission at ~9.7 microns, similarly to our GM candidates. We note that the bulk spectral lines are broad and blurry in comparison with the discrete and narrow emission lines of the clusters.

Although an identification of a specific cluster in a real observed spectra might be challenging, the different cluster stoichiometric families show distinct spectral characteristics and could be distinguished from each other.

We also note that a number of approximations are used here, including the RRHO approximation at T = 0 K, a uniform line broadening, and a background noise that is independent of the planet or host star. We aim to address the spectral properties of the clusters in more detail in future kinetic study.

thumbnail Fig. 9

Normalized intensities of the vibration modes of the GM cluster candidates as a function of the wavelength (in µm) for (VO)N, N = 1–10 (top panel), (VO2)N, N = 1–10 (middle panel), and (V2O5)N, N = 1–4 (bottom panel).

5 Conclusions

The nucleation process is an important part of cloud formation in substellar atmospheres and in dust formation in several other astrophysical environments. Presently, the nature of the nucleation seeds, as well as their formation process, is not well understood.

This paper investigates the nucleation properties of vanadium oxides in substellar atmospheres, because both atomic vanadium and gaseous VO have been detected in substellar objects but have not previously been considered as nucleation species.

We used a hierarchical optimization approach to obtain hitherto unreported vanadium oxide cluster structures for the stoichiometries: (VO)N and (VO2)N with N = 1–10 and (V2O5)N with N = 1–4. We applied DFT at the B3LYP/cc-pVTZ level to obtain the final energies, thermochemical potentials, and vibrational frequencies.

The impact of revised and more accurate thermochemical potentials is studied in chemical equilibrium with the code GGchem. Our results suggest that even small changes in the Gibbs free energies of formation of the monomers can result in large changes in the abundances of vanadium bearing species at low temperatures (below ~1000 K). The consideration of larger cluster species also vastly modifies the equilibrium abundances, giving more realistic results and indicating thermodynamically viable cluster and dust formation routes. The updated abundances provide insights into which species could be observed by facilities such as the JWST.

Vanadium oxide clusters become predominant at temperatures around or below 1000 K, which makes them relevant for atmospheres of hot Jupiters as well as other astrophysical objects, such as brown dwarfs, AGB stars, and protoplanetary disks. We calculated the vibrational spectra of each cluster and found major emission peaks at wavelengths between 8 and 28 microns, which are within the JWST-MIRI detection range. We also calculated nucleation rates for a brown dwarf with log(𝑔) = 5. Due to the difference in the free energies of formation of the different vanadium stoichiometries, the nucleation process most likely does not follow monomeric homomolecular addition and therefore current theories such as CNT and MCNT do not provide an accurate description of the process. As V2O5 is the most stable oxidation state, solid bulk phase data are available and we were able to apply CNT to obtain a nucleation rate via the surface tension. The CNT nucleation rate is approximately 15 orders of magnitude lower than the NCNT nucleation rate for V2O5 . We were only able to obtain NCNT nucleation rates for VO and VO2 and those are comparable to the V2O5 NCNT rate. Our results suggest that, even though CNT is a useful tool for calculating nucleation rates when the thermochemical data for clusters are not available, taking such data into account can increase the nucleation rate of a given species by several orders of magnitude. A full chemical-kinetic approach is needed to explore the efficiency of vanadium oxides as heterogeneous nucleation candidates and compare them with the nucleation species used in other studies.

Acknowledgements

H.L.M., L.D. and Ch.H. acknowledge funding from the European Union H2020-MSCA-ITN-2019 under grant agreement no. 860470 (CHAMELEON). L.D. acknowledges support from the ERC consolidator grant 646758 AEROSOL and the KU Leuven IDN/19/028 grant Escher. D.G. was funded by the project grant ‘The Origin and Fate of Dust in Our Universe’ (research grant KAW 2020.0081) from the Knut and Alice Wallenberg Foundation. J.P.S. acknowledges a St Leonard’s Global Doctoral Scholarship from the University of St Andrews and funding from the Austrian Academy of Science. The computational results have been obtained using the Vienna Scientific Cluster and the St. Andrews HPC KENNEDY cluster. The computations involved the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant no. 2018-05973. We thank the referee for their insightful comments.

Appendix A GGchem fit parameters

Table A.1

Parameters a0, a1, b0, b1, and b2 implemented in GGchem to compute the global minimization.

Appendix B Surface tension calculations

In CNT, the stationary nucleation rate is calculated according to 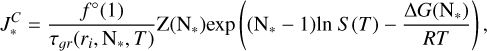J∗C=f∘(1)τgr(ri,N∗,T)Z(N∗)exp((N∗−1)lnS(T)−ΔG(N∗)RT),$J_ * ^C = {{{f^ \circ }(1)} \over {{\tau _{gr}}\left( {{r_i},{{\rm{N}}_ * },T} \right)}}{\rm{Z}}\left( {{{\rm{N}}_ * }} \right)\exp \left( {\left( {{{\rm{N}}_ * } - 1} \right)\ln S(T) - {{{\rm{\Delta }}G\left( {{{\rm{N}}_ * }} \right)} \over {RT}}} \right),$(B.1)

where S (T) is the supersaturation ratio, f °(1) is the monomer number density, τ𝑔r is the growth time scale, N* is the critical cluster size, and Z(N*) is the Zeldovich factor. We calculated the growth timescale according to 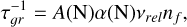τgr−1=A(N)α(N)vrelnf,$\tau _{gr}^{ - 1} = A({\rm{N}})\alpha ({\rm{N}}){v_{rel}}{n_f},$(B.2)

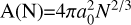where A(N)=4πa02N2/3${\rm{A}}({\rm{N}}) = 4\pi a_0^2{N^{2/3}}$ is the effective cross section of a spherical (VxOy)N cluster, α is the sticking coefficient (assumed to be 1), nf is the monomer number density, and νrel is the relative velocity defined as: 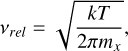vrel=kT2πmx,${v_{rel}} = \sqrt {{{kT} \over {2\pi {m_x}}}} ,$(B.3)

where mx is the mass of the monomer and k the Boltzmann constant. The Zeldovich factor accounts for the contribution from Brownian motion to the nucleation process and can be calculated as 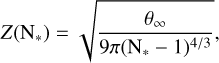Z(N∗)=θ∞9π(N∗−1)4/3,$Z\left( {{{\rm{N}}_ * }} \right) = \sqrt {{{{\theta _\infty }} \over {9\pi {{\left( {{{\rm{N}}_ * } - 1} \right)}^{4/3}}}}} ,$(B.4)

where θ∞ is defined as θ∞=4πa02σ∞kbT${\theta _\infty } = {{4\pi a_0^2{\sigma _\infty }} \over {{k_b}T}}$(B.5)

in CNT. Here, a0 is the theoretical monomer radius, which can be calculated from the bulk properties: 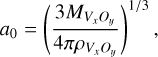a0=(3MVxoy4πρVxoy)1/3,${a_0} = {\left( {{{3{M_{{V_x}{o_y}}}} \over {4\pi {\rho _{{V_x}}}{o_y}}}} \right)^{1/3}},$(B.6)

and σ∞ is the surface tension, which is also dependent on the properties of the bulk solid. The final term of Eq. B.1 corresponds to the Gibbs free energies of formation of the critical cluster and we use the values from our DFT calculations. As the most stable vanadium oxide stoichiometry in the solid phase is V2O5 , we only apply CNT to the clusters from this stoichiometry. In order to eventually obtain a nucleation rate, we need to first compute the surface tension of the bulk solid σ∞, which is the quantity used to measure the impact of the Gibbs free energies of formation in the nucleation process. We follow the approach of Jeong et al. (2000) as done in Sindel et al. (2022) and Lee et al. (2015), where the nucleation is linked to the Gibbs free energies through: ΔfG∘(N)N=(θ∞RTN−1(N−1)1/3+Nf1/3+ΔfG∘(1)+(N−1)ΔfG∘(s))⋅N−1,${{{{\rm{\Delta }}_{\rm{f}}}{G^ \circ }({\rm{N}})} \over {\rm{N}}} = \left( {{\theta _\infty }RT{{{\rm{N}} - 1} \over {{{({\rm{N}} - 1)}^{1/3}} + {\rm{N}}_f^{1/3}}} + {{\rm{\Delta }}_{\rm{f}}}{G^ \circ }(1) + ({\rm{N}} - 1){{\rm{\Delta }}_{\rm{f}}}{G^ \circ }(s)} \right) \cdot {{\rm{N}}^{ - 1}},$(B.7)

and ∆fG°(N) is the Gibbs free energy of formation of cluster size N, ∆fG°(1) is the Gibbs free energy of formation of the monomer, 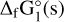ΔfG1°(s)${\Delta _{\rm{f}}}G_1^^\circ \left( {\rm{s}} \right)$ is the Gibbs free energy of the bulk phase, Nf is a fitting factor that we set to zero, and θ∞ is defined in Eq. B.5. We calculated a0 for the V2O5 monomer: 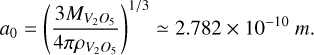a0=(3MV2O54πρV2O5)1/3≃2.782×10−10m.${a_0} = {\left( {{{3{M_{{V_2}{O_5}}}} \over {4\pi {\rho _{{V_2}}}{O_5}}}} \right)^{1/3}} \simeq 2.782 \times {10^{ - 10}}m.$(B.8)

This value approximately corresponds to half of the length between the most distant atomic centers in the V2O5 monomer; i.e., 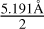5.191Å2${{5.191{\AA}} \over 2}$. We note that the V2O5 cluster is not spherical (Fig. 2(u)). We obtain a surface tension of 94.23 erg·cm−2 at T = 300 K. The value of σ∞ is dependent on pressure. For the range T = 0 K to T = 900 K, we obtain the following fit: 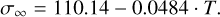σ∞=110.14−0.0484⋅T.${\sigma _\infty } = 110.14 - 0.0484 \cdot T.$(B.9)

thumbnail Fig. B.1

Gibbs free energies of formation for the clusters (V2O5)N with N = 1–4 at T = 1000 K. We calculated a fit for σ∞ according to Eq. (B.7).

The fitting range was chosen taking into account that V2O5 transitions from liquid to solid at T = 943 K. We used the surface tension to calculate the nucleation rate along the (Tgas , pgas) profile of the brown dwarf from Fig. 6 (green line) and the results are discussed in Sect. 4.1.

Appendix C Rotational constants

N Rotational constants (GHz)
(VO)N
1 16.646
2 9.199 2.972 2.246
3 1.971 1.517 0.857
4 1.659 0.660 0.517
5 0.850 0.558 0.463
6 0.410 0.367 0.340
7 0.360 0.282 0.225
8 0.342 0.212 0.204
9 0.293 0.138 0.125
10 0.268 0.166 0.139
(VO2)N
1 35.512 8.434 6.815
2 7.630 1.276 1.165
3 1.303 0.908 0.613
4 0.731 0.446 0.429
5 0.646 0.235 0.187
6 0.522 0.136 0.120
7 0.310 0.133 0.127
8 0.239 0.101 0.092
9 0.218 0.069 0.068
10 0.127 0.097 0.090
(V2O5)N
1 4.250 1.035 0.995
2 0.404 0.404 0.404
3 0.201 0.158 0.158
4 0.097 0.097 0.097

References

  1. Abello, L., Husson, E., Repelin, Y., & Lucazeau, G. 1983, Spectrochim. Acta A Mol. Biomol., 39, 641 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ackerman, A. S., & Marley, M. S. 2001, ApJ, 556, 872 [Google Scholar]
  3. Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
  4. Archambault, P., Wei, Y., & Peslherbe, G. H. 2021, Theor. Chem. Acc., 140, 127 [CrossRef] [Google Scholar]
  5. Asmis, K. R., & Sauer, J. 2007, Mass Spectrom. Rev., 26, 542 [NASA ADS] [CrossRef] [Google Scholar]
  6. Asmis, K. R., Meijer, G., Brümmer, M., et al. 2004, J. Chem. Phys., 120, 6461 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Balducci, G., Gigli, G., & Guido, M. 1983, J. Chem. Phys., 79, 5616 [NASA ADS] [CrossRef] [Google Scholar]
  9. Becke, A. D. 1993, J. Chem. Phys., 98, 1372 [Google Scholar]
  10. Boulangier, J., Gobrecht, D., Decin, L., de Koter, A., & Yates, J. 2019, MNRAS, 489, 4890 [CrossRef] [Google Scholar]
  11. Bromley, S. T., Gómez Martín, J. C., & Plane, J. M. C. 2016, Phys. Chem. Chem. Phys., 18, 26913 [NASA ADS] [CrossRef] [Google Scholar]
  12. Buckingham, R. A., & Lennard-Jones, J. E. 1938, Proc. R. Soc. A: Math. Phys. Eng., 168, 264 [Google Scholar]
  13. Bush, T. S., Gale, J. D., Catlow, C. R. A., & Battle, P. D. 1994, J. Mater. Chem., 4, 831 [Google Scholar]
  14. Chang, C., Patzer, A. B. C., Kegel, W. H., & Chandra, S. 2013, Astrophys. Space Sci., 347, 315 [NASA ADS] [CrossRef] [Google Scholar]
  15. Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [Google Scholar]
  16. Chase, M. W., 1998, NIST-JANAF Thermochemical Tables, 9 (Washington, DC: American Chemical Society) [Google Scholar]
  17. Chen, M., Felmy, A. R., & Dixon, D. A. 2014, J. Phys. Chem. A, 118, 3136 [NASA ADS] [CrossRef] [Google Scholar]
  18. Decin, L., Richards, A. M. S., Waters, L. B. F. M., et al. 2017, A&A, 608, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Dehn, M. 2007, PhD Thesis, Universität Hamburg, Hamburg, Germany [Google Scholar]
  20. De Jesus, L. R., Andrews, J. L., Parija, A., & Banerjee, S. 2018, ACS Energy Lett., 3, 915 [Google Scholar]
  21. Dick, B. G., & Overhauser, A. W. 1958, Phys. Rev., 112, 90 [NASA ADS] [CrossRef] [Google Scholar]
  22. Draine, B. T., & Salpeter, E. E. 2008, J. Chem. Phys., 67, 2230 [Google Scholar]
  23. Evans, T. M., Sing, D. K., Wakeford, H. R., et al. 2016, ApJ, 822, L4 [NASA ADS] [CrossRef] [Google Scholar]
  24. Feinstein, A. D., Radica, M., Welbanks, L., et al. 2023, Nature, 614, 670 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ferrarotti, A. S., & Gail, H.-P. 2002, A&A, 382, 256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Fielicke, A., & Rademann, K. 2002, Phys. Chem. Chem. Phys., 4, 2621 [NASA ADS] [CrossRef] [Google Scholar]
  27. Frantseva, K. E., & Semenov, G. A. 1969, High Temp. Engl. Transl., 7, 52 [Google Scholar]
  28. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian~16 Revision C.01, https://gaussian.com/citation/ [Google Scholar]
  29. Gail, H.-P., & Sedlmayr, E. 1986, A&A, 166, 225 [NASA ADS] [Google Scholar]
  30. Gail, H.-P., & Sedlmayr, E. 2013, in Physics and Chemistry of Circumstellar Dust Shells, Cambridge Astrophysics (CUP), 332 [CrossRef] [Google Scholar]
  31. Gail, H.-P., Keller, R., & Sedlmayr, E. 1984, A&A, 133, 320 [NASA ADS] [Google Scholar]
  32. Gail, H.-P., Wetzel, S., Pucci, A., & Tamanai, A. 2013, A&A, 555, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Gale, J. D. 1997, J. Chem. Soc. Faraday Trans., 93, 629 [CrossRef] [Google Scholar]
  34. Gao, P., Wakeford, H. R., Moran, S. E., & Parmentier, V. 2021, J. Geophys. Res. Planets, 126, e06655 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Gobrecht, D., Cristallo, S., Piersanti, L., & Bromley, S. T. 2017, ApJ, 840, 117 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gobrecht, D., Decin, L., Cristallo, S., & Bromley, S. T. 2018, Chem. Phys. Lett., 711, 138 [NASA ADS] [CrossRef] [Google Scholar]
  38. Gobrecht, D., Plane, J. M. C., Bromley, S. T., et al. 2022, A&A, 658, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Haynes, W. M. 2016, CRC Handbook of Chemistry and Physics (CRC Press) [Google Scholar]
  40. Helling, C. 2019, Annu. Rev. Earth Planet. Sci., 47, 583 [CrossRef] [Google Scholar]
  41. Helling, C., & Fomins, A. 2013, Philos. Trans. Ser. A Math. Phys. Eng. Sci., 371, 20110581 [NASA ADS] [Google Scholar]
  42. Helling, C., & Woitke, P. 2006, A&A, 455, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Helling, C., Woitke, P., & Thi, W.-F. 2008, A&A, 485, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Helling, C., Lewis, D., Samra, D., et al. 2021, A&A, 649, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Helling, C., Samra, D., Lewis, D., et al. 2023, A&A, 671, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Henning, T. 2010, Astromineralogy (Springer Science & Business Media) [CrossRef] [Google Scholar]
  47. Hoeijmakers, H. J., Seidel, J. V., Pino, L., et al. 2020, A&A, 641, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Hübner, O., & Himmel, H.-J. 2017, Angew. Chem. Int. Ed., 56, 12340 [CrossRef] [Google Scholar]
  49. Hudson, J. G. 1993, J. Appl. Meteor. Climatol., 32, 596 [Google Scholar]
  50. Irikura, K. K. 2002, THERMO.PL (National Institute of Standards and Technology) [Google Scholar]
  51. Jakubikova, E., Rappé, A. K., & Bernstein, E. R. 2007, J. Phys. Chem. A, 111, 12938 [NASA ADS] [CrossRef] [Google Scholar]
  52. Janssens, E., Santambrogio, G., Brümmer, M., et al. 2006, Phys. Rev. Lett., 96, 233401 [Google Scholar]
  53. Jeong, K. S., Chang, C., Sedlmayr, E., & Sülzle, D. 2000, J. Phys. B: At. Mol. Opt. Phys., 33, 3417 [NASA ADS] [CrossRef] [Google Scholar]
  54. Johnston, R. L. 2002, Atomic and Molecular Clusters (CRC Press) [Google Scholar]
  55. Kanwar, J., Kamp, I., Woitke, P., et al. 2024, A&A, 681, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Karlsson, L., Lindgren, B., Lundevall, C., & Sassenberg, U. 1997, J. Mol. Spectrosc., 181, 274 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kaur, N., Gupta, S., & Goel, N. 2019, J. Mol. Model, 25, 319 [CrossRef] [Google Scholar]
  58. Khouri, T., Maercker, M., Waters, L. B. F. M., et al. 2016, A&A, 591, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2014, Nature, 505, 69 [Google Scholar]
  60. Krusin-Elbaum, L., Newns, D. M., Zeng, H., et al. 2004, Nature, 431, 672 [NASA ADS] [CrossRef] [Google Scholar]
  61. Lamiel-Garcia, O., Cuko, A., Calatayud, M., Illas, F., & Bromley, S. T. 2017, Nanoscale, 9, 1049 [Google Scholar]
  62. Lasserus, M., Schnedlitz, M., Messner, R., et al. 2019, Chem. Sci., 10, 3473 [CrossRef] [Google Scholar]
  63. Lee, E. K. H., Helling, C., Giles, H., & Bromley, S. T. 2015, A&A, 575, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Lee, E. K. H., Blecic, J., & Helling, C. 2018, A&A, 614, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Lewis, G. V., & Catlow, C. R. A. 1985, J. Phys. C: Solid State Phys., 18, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  66. Li, C., & Signorell, R. 2021, J. Aerosol Sci., 153, 105676 [NASA ADS] [CrossRef] [Google Scholar]
  67. Liu, B., & Ji, J. 2020, Res. Astron. Astrophys., 20, 164 [Google Scholar]
  68. Mansfield, M., Bean, J. L., Line, M. R., et al. 2018, AJ, 156, 10 [NASA ADS] [CrossRef] [Google Scholar]
  69. Mariñoso Guiu, J., Ghejan, B.-A., Bernhardt, T. M., et al. 2022, ACS Earth Space Chem., 6, 2465 [CrossRef] [Google Scholar]
  70. Merriles, D. M., Sevy, A., Nielson, C., & Morse, M. D. 2020, J. Chem. Phys., 153, 024303 [NASA ADS] [CrossRef] [Google Scholar]
  71. Merritt, S. R., Gibson, N. P., Nugroho, S. K., et al. 2020, A&A, 636, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Mikal-Evans, T., Sing, D. K., Goyal, J. M., et al. 2019, MNRAS, 488, 2222 [Google Scholar]
  73. Mikal-Evans, T., Sing, D. K., Kataria, T., et al. 2020, MNRAS, 496, 1638 [Google Scholar]
  74. Ouyang, Q., Wang, W., Zhai, M., et al. 2023, Res. Astron. Astrophys., 23, 065010 [CrossRef] [Google Scholar]
  75. Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Patzer, A. B. C., Gauger, A., & Sedlmayr, E. 1998, A&A, 337, 847 [Google Scholar]
  77. Patzer, A. B., Chang, C., Sedlmayr, E., & Sülzle, D. 2005, Eur. Phys. J. D, 32, 329 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pauling, L. 1932, J. Am. Chem. Soc., 54, 3570 [Google Scholar]
  79. Pelletier, S., Benneke, B., Ali-Dib, M., et al. 2023, Nature, 619, 491 [NASA ADS] [CrossRef] [Google Scholar]
  80. Rehder, D. 2011, Coord. Chem. Rev., 255, 2227 [Google Scholar]
  81. Samra, D., Helling, C., Chubb, K. L., et al. 2023, A&A, 669, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Sarangi, A., Matsuura, M., & Micelotta, E. R. 2018, Space Sci. Rev., 214, 63 [NASA ADS] [CrossRef] [Google Scholar]
  83. Schoiswohl, J., Surnev, S., Netzer, F. P., & Kresse, G. 2006, J. Condens. Matter Phys., 18, R1 [NASA ADS] [CrossRef] [Google Scholar]
  84. Sedlmayr, E. 1994, in Molecules in the Stellar Environment, ed. U. G. Jørgensen, Lecture Notes in Physics (Berlin, Heidelberg: Springer), 163 [CrossRef] [Google Scholar]
  85. Sindel, J. P., Gobrecht, D., Helling, C., & Decin, L. 2022, A&A, 668, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Sing, D. K., Fortney, J. J., Nikolov, N., et al. 2016, AAS Meeting, 227, 306.03 [NASA ADS] [Google Scholar]
  87. Stock, J. W., Kitzmann, D., Patzer, A. B. C., & Sedlmayr, E. 2018, MNRAS, 479, 865 [NASA ADS] [Google Scholar]
  88. Suárez, G., & Metchev, S. 2023, MNRAS, 523, 4739 [CrossRef] [Google Scholar]
  89. Viñes, F., Lamiel-Garcia, O., Illas, F., & Bromley, S. T. 2017, Nanoscale, 9, 10067 [CrossRef] [Google Scholar]
  90. Vyboishchikov, S. F., & Sauer, J. 2000, J. Phys. Chem. A, 104, 10913 [NASA ADS] [CrossRef] [Google Scholar]
  91. Weckhuysen, B. M., & Keller, D. E. 2003, Catal. Today, 78, 25 [Google Scholar]
  92. Whittingham, M. S. 2004, Chem. Rev., 104, 4271 [Google Scholar]
  93. Wilson, A. K., van Mourik, T., & Dunning, T. H. 1996, J. Mol. Struct., 388, 339 [CrossRef] [Google Scholar]
  94. Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Witte, S., Helling, C., Barman, T., Heidrich, N., & Hauschildt, P. H. 2011, A&A, 529, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Woitke, P., & Helling, C. 2004, A&A, 414, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Woitke, P., Helling, C., Hunter, G. H., et al. 2018, A&A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Yan, B., Liao, L., You, Y., et al. 2009, Adv. Mater., 21, 2436 [NASA ADS] [CrossRef] [Google Scholar]
  99. Zhang, X., Wang, X., Sai, H., et al. 2021, MNRAS, 509, 2013 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Parametrizations of the Buckingham-Coulomb pair potential used for the first stage in the optimization process of each cluster.

In the text
Table 2

VO and VO2 electronic binding energies from different sources.

In the text
Table 3

Properties of the (VO)N, (VO2)N,N = 1–10, and(V2O5)N,N = 1–4 GM candidates listing (1) cluster size, (2) electronic binding energy Eb (in kJ mol−1 ), (3) electric binding energy normalized to cluster size Eb/N (in kJ mol−1 ), (4) spin multiplicity Ms , (5) point group symmetry in the Schönflies notation, and (6) average VO bond length 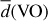d¯(VO)$\bar d\left( {{\rm{VO}}} \right)$ in Å.

In the text
Table 4

Summary of the fit parameters from Eq. (7) for VO, VO2 , and V2O5 atT = 0 K and T = 1000 K.

In the text
Table 5

Summary of the thermochemical quantities (entropy S, heat capacity Cp, enthalpy change H(T) – H(0), enthalpy of formation dHf and Gibbs free energy of formation dGf) obtained for each of our GM candidates at T = 1000 K.

In the text
Table A.1

Parameters a0, a1, b0, b1, and b2 implemented in GGchem to compute the global minimization.

In the text

All Figures

thumbnail Fig. 1

Gibbs free energies of formation (in kJ mol−1) for VN, VO, and VO2 as a function of temperature. Dotted lines correspond to the values available in the JANAF database and full lines represent the data obtained from our DFT calculations at the B3LYP/cc-pVTZ level of theory using the RRHO partition function.
In the text
thumbnail Fig. 2

Geometries of the global minima candidates for (VO)N and (VO2)N with N = 1–10 and (V2O5)N with N = 1–4. Vanadium and oxygen atoms are shown in green and red, respectively.
In the text
thumbnail Fig. 3

Dissociation free energy of each global (VO)N (top), (VO2)N (middle), and (V2O5 )N (bottom) GM candidate normalized by the cluster size at T = 0 K and T = 1000 K as a function of cluster size N and fitted to the spherical cluster approximation as described in Eq. (7).
In the text
thumbnail Fig. 4

Comparison of the abundances of the vanadium-bearing species currently present in GGchem as a function of temperature. The dashed lines correspond to the data from previous studies already implemented in GGchem and the full lines correspond to the abundances obtained after implementing the ∆fG values obtained for VO and VO2 from our DFT calculations. The calculations were run at P = 1 bar and with solar elemental abundances from Asplund et al. (2009).
In the text
thumbnail Fig. 5

Abundances of all the vanadium-bearing species already present in GGchem and the clusters obtained from our DFT calculations as a function of temperature. Top: all (VO)N clusters included. Middle: all (VO)N and (VO2)N clusters included. Bottom: all (VO)N, (VO2)N, and (V2O5)N clusters included. The calculations were run again at P = 1 bar and with solar elemental abundances from Asplund et al. (2009).
In the text
thumbnail Fig. 6

Most abundant vanadium-bearing molecules in chemical equilibrium for a grid of gas pressures and temperatures. The model assumes solar elemental abundances from Asplund et al. (2009) as initial conditions. (Tgas, pgas) profiles of the hot Jupiter WASP-121b (Helling et al. 2021, Parmentier et al. 2018, Mansfield et al. 2018), a brown dwarf (Dehn 2007, Helling et al. 2008, Witte et al. 2009, 2011), and a T-Tauri protoplanetary disk (Kanwar et al. 2023) are over plotted.
In the text
thumbnail Fig. 7

Comparison of the Gibbs free energies of formation normalized to the cluster size (∆fG(N)/N) for the clusters (VO)N and (VO2)N with N = 1–10, and for (V2O5)N with N = 1–4, as a function of the degree of oxidation for T = 0 K (full lines) and T = 1000 K (dashed lines).
In the text
thumbnail Fig. 8

Nucleation rates of the three vanadium oxide stoichiometries along the (Tgas, pgas) profile of a brown dwarf with log(𝑔) = 5 (black dotted line) and Teff = 1000 K. Full lines: NCNT nucleation rate (Eq. (9)) for VO, VO2, and V2O5 as a function of pressure. Dashed line: CNT nucleation rate (Eq. (B.1)) for V2O5.
In the text
thumbnail Fig. 9

Normalized intensities of the vibration modes of the GM cluster candidates as a function of the wavelength (in µm) for (VO)N, N = 1–10 (top panel), (VO2)N, N = 1–10 (middle panel), and (V2O5)N, N = 1–4 (bottom panel).
In the text
thumbnail Fig. B.1

Gibbs free energies of formation for the clusters (V2O5)N with N = 1–4 at T = 1000 K. We calculated a fit for σ∞ according to Eq. (B.7).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.