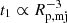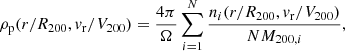| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202244338 | |
| Published online | 11 November 2022 | |
Anisotropy and characteristic scales in halo density gradient profiles
1
Key Laboratory for Research in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China, Hefei, Anhui 230026, PR China
e-mail: wambyybz@mail.ustc.edu.cn; whywang@ustc.edu.cn
2
School of Astronomy and Space Science, University of Science and Technology of China, Hefei 230026, PR China
3
Department of Astronomy, University of Massachusetts, Amherst, MA 01003-9305, USA
Received:
24
June
2022
Accepted:
7
September
2022
We use a large N-body simulation to study the characteristic scales in the density gradient profiles in and around halos with masses ranging from 1012 to 1015 M⊙. We investigate the profiles separately along the major (T1) and minor (T3) axes of the local tidal tensor and how the characteristic scales depend on halo mass, formation time, and environment. We find two prominent features in the gradient profiles: a deep “valley” and a prominent “peak.” We use the Gaussian process regression to fit the gradient profiles and identify the local extrema in order to determine the scales associated with these features. Around the valley, we identify three types of distinct local minima, corresponding to caustics of particles orbiting around halos. The appearance and depth of the three caustics depend on the direction defined by the local tidal field, formation time, and environment of halos. The first caustic is located at r > 0.8R200, corresponding to the splashback feature, and is dominated by particles at their first apocenter after infall. The second and third caustics, around 0.6R200 and 0.4R200, respectively, can be determined reliably only for old halos. The three caustics are consistent with the prediction of self-similar gravitational collapse. The first caustic is always the most prominent feature along T3, but may not be true along T1 or in azimuthally averaged profiles, suggesting that caution must be taken when using averaged profiles to investigate the splashback radius. We find that the splashback feature is approximately isotropic when proper separations are made between the first and the other caustics. We also identify a peak feature located at ∼2.5R200 in the density gradient profile. This feature is the most prominent along T1 and is produced by mass accumulations from the structure outside halos. We also discuss the origins of these features and their observational implications.
Key words: dark matter / large-scale structure of Universe / methods: statistical / methods: numerical
© X. Wang et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the standard cold-dark-matter paradigm of structure formation, dark matter halos are the building blocks of the cosmic web. Baryonic matter follows the collapse of dark matter and cools at the center of the halo to form galaxies (Rees & Ostriker 1977; White & Rees 1978; Fall & Efstathiou 1980; Mo et al. 2010). Understanding the properties and evolution of dark matter halos therefore not only forms the basis to model and characterize the large-scale structure of the Universe, but also to model and understand galaxy formation. One important first step in understanding the halo population is to discover salient properties related to their formation in the cosmic web.
In the simplest description, a dark matter halo is approximated by a sphere, within which the average mass density is a constant multiple (Δ) of some reference density, ρref. The halo mass, MΔ, is defined as the enclosed mass,
where RΔ is the radius of the sphere, also known as the halo radius. The reference density is generally taken as the critical or mean density of the Universe, and the multiplier is chosen to be 200, roughly the value predicted by the virial theorem applied to the collapse of a spherical top-hat perturbation in an expanding Universe (Gunn & Gott 1972; Gunn 1977; Peebles 1980; Mo et al. 2010). The halo radius is therefore also referred to as the virial radius of a halo. However, this approximate description cannot fully account for halo formation. For example, splashback substructures, which are physically associated with their host halo, are considered as isolated, independent halos in this description (e.g., Ludlow et al. 2009; Wang et al. 2009). In addition, small halos can start to lose their mass long before they fall into the virial radius of a massive halo (Behroozi et al. 2014; Peñarrubia & Fattahi 2017), suggesting that the zone of influence of a halo may be bigger than that given by the virial radius. All these indicate that the density field outside RΔ may also be physically connected to halos (see e.g., Prada et al. 2006; Hayashi & White 2008; Oguri & Hamana 2011; Diemer & Kravtsov 2014; Trevisan et al. 2017) and should be characterized. Another potential problem with the traditional definition is that the growth of a halo based on the definition may sometimes be unphysical. Indeed, based on the definition of Eq. (1), halos that have ceased mass accretion can still have their MΔ increase with time because of the increase in the halo boundary due to the decrease in ρref (Cuesta et al. 2008; Diemer et al. 2013; More et al. 2015).
Great amounts of effort have been made to investigate the density profile in and around halos, in the hope of discovering some characteristic features and scales that reflect physical processes underlying halo formation in the cosmic web. One of the most studied features is the so-called splashback radius, which was identified as the radius in the spherically averaged density where the gradient of the density profile is the most negative (e.g., Adhikari et al. 2014, 2016; Diemer & Kravtsov 2014; More et al. 2015, 2016). Subsequently, Mansfield et al. (2017) measured the density field along different directions around a single dark halo and identified a shell-like structure by connecting the steepest points of the gradient profile in different directions. The splashback radius for massive halos is found to decline with increasing halo mass (e.g., More et al. 2015; Diemer et al. 2017; O’Neil et al. 2022) and with increasing mass accretion rate (e.g., More et al. 2015; Diemer et al. 2017; Diemer 2020; Contigiani et al. 2021; O’Neil et al. 2021). More recently, attempts have also been made to use hydro-simulations to study whether or not baryonic physics affects this characteristic scale and whether or not baryons and stars follow the same trends as seen in dark matter (Deason et al. 2020; O’Neil et al. 2021; O’Neil et al. 2022).
By tracking particles as they approach a halo and recording the time and location of their subsequent motion, Diemer et al. (2017) and Diemer (2020) found that the splashback radius can roughly separate the infalling matter from the matter that orbits around the halo (see also Adhikari et al. 2014; Deason et al. 2020; Sugiura et al. 2020; Diemer 2022). This suggests that the splashback feature is the result of a caustic produced by particles at their first apocenter after infall (see e.g., Diemand & Kuhlen 2008; Vogelsberger et al. 2009, 2011; Diemer & Kravtsov 2014; Adhikari et al. 2014). Higher order caustics also seem to be present in simulated halos, although they are usually weak (see e.g., Diemand & Kuhlen 2008; Deason et al. 2020). Caustics are also studied in detail in the context of self-similar gravitational collapse (e.g., Fillmore & Goldreich 1984; Bertschinger 1985; Mohayaee & Shandarin 2006; Zukin & Bertschinger 2010).
There are also efforts to define the boundary of a halo based on other considerations. For example, Fong & Han (2021) defined a “characteristic depletion radius” using the position of the minimum of the halo bias parameter as a function of radius. Aung et al. (2021b) proposed an “edge radius” to define the halo boundary based on the phase-space structure around halos.
The presence of these characteristic scales in simulations have in turn inspired investigations to connect these scales with theoretical models and with observations. For example, Adhikari et al. (2018) and Contigiani et al. (2019b) used the splashback radius to distinguish models of modified gravity; Gavazzi et al. (2006) and Mohayaee & Salati (2008) suggested that the caustics can be used to detect dark matter; García et al. (2021) and Fong & Han (2021) considered the implications of these scales in halo models of the large-scale structure; the connection with galaxy evolution was investigated by Deason et al. (2020) and Dacunha et al. (2022); and the link to accretion shocks has been examined in many previous works (e.g., Anbajagane et al. 2022; Baxter et al. 2021; Aung et al. 2021a; Zhang et al. 2021). Using projected galaxy number density profiles around redMaPPER galaxy clusters, Rykoff et al. (2014) and More et al. (2016) measured splashback features associated with massive halos. These authors found a scale that is smaller than that expected from numerical simulations, possibly because of selection effects in the observational data (Zu et al. 2017; Busch & White 2017; Chang et al. 2018; Sunayama & More 2019; Murata et al. 2020). More recently, galaxy clusters selected via the Sunyaev–Zel’dovich effect (SZ, Sunyaev & Zeldovich 1972) were used in such analyses to minimize the risk of spurious correlations between the splashback radius and cluster selection (Shin et al. 2019; Zürcher & More 2019; Adhikari et al. 2021; Shin et al. 2021). Attempts have also been made using a small sample of X-ray-selected massive clusters (e.g., Umetsu & Diemer 2017; Contigiani et al. 2019a), spectroscopically confirmed galaxy members of massive clusters (e.g., Bianconi et al. 2021), and weak gravitational lensing (e.g., Umetsu & Diemer 2017; Chang et al. 2018; Contigiani et al. 2019a, 2021; Shin et al. 2019, 2021). The splashback radii obtained from these observational data are broadly consistent with simulations, although the uncertainties in current data are quite large. Fong et al. (2022) made a first attempt to measure the depletion radius using weak gravitational lensing data, and found that their results are consistent with those obtained from simulations.
There is growing evidence that the characteristic scales may be anisotropic. Mansfield et al. (2017) found a nonspherical splashback shell, the orientation of which is aligned with the mass distribution in the inner region of the halo. Contigiani et al. (2021) found that the depth of the splashback feature in a cluster correlates with the direction of the filament containing the cluster and with the orientation of the brightest cluster galaxy. Deason et al. (2020) found that the position of the splashback feature varies with the position angle relative to the neighboring structure. Such anisotropy is expected theoretically, as dark matter halos are found to be better described by ellipsoidal models (Jing & Suto 2002) and halo orientation is strongly aligned with the large-scale structure (e.g., Hahn et al. 2007; Wang et al. 2011; Tempel et al. 2013; Libeskind et al. 2013; Chen et al. 2016). However, a detailed analysis is still necessary to understand and characterize the anisotropy in the characteristic scales and its alignment with the large-scale structure.
Most of the investigations so far have been focused on massive halos or halos with a high accretion rate, and our knowledge about lower mass and old halos remains relatively poor (see e.g., Mansfield et al. 2017). There are indications that halos of lower masses may have characteristic scales that are different from those in massive halos. For example, Deason et al. (2020) found two caustic features in halos with masses similar to the Local Group (see also Diemer & Kravtsov 2014; Adhikari et al. 2014), Fong & Han (2021) found a transitional change in the ratio between the depletion radius and splashback radius as halo mass increases, and there is also evidence that the formation of caustic depends on halo assembly (e.g., Diemand & Kuhlen 2008). It is therefore important to use a halo sample covering a large range in both mass and assembly history to fully understand the dependence on halo properties.
In this paper, we use a large N-body simulation, the ELUCID (Wang et al. 2016), to investigate the characteristic scales of the density gradient profiles in different directions defined by the local tidal tensor, for halos with masses ranging from 1012 to 1015 M⊙. The rest of the paper is structured as follows. In Sect. 2, we briefly describe the ELUCID simulation, our halo catalog, the “halo tidal field,” and our method to calculate and fit the halo density and gradient profiles. In Sect. 3, we show the halo profiles and check the performance of our fitting procedure. We then identify the characteristic scales and study their anisotropy and dependence on halo mass, assembly history, and environment. We also use the phase space density to examine signatures of the characteristic scales in phase-space. We summarize our results in Sect. 4.
2. Data and methods of analysis
2.1. The simulation
Our analysis is based on the ELUCID simulation (Wang et al. 2014, 2016), which is a dark matter only, constrained simulation run with 30723 dark matter particles (each with a mass of 3.088 × 108 M⊙) in a cubic box of Lbox = 500 h−1 Mpc on each side. The simulation was run with L-GADGET, a memory-optimized version of GADGET2 (Springel 2005). The cosmological parameters adopted in the simulation are consistent with the WMAP5 (Dunkley et al. 2009) cosmology: density parameters in dark energy ΩΛ, 0 = 0.742, in matter Ωm, 0 = 0.258, and in baryons Ωb, 0 = 0.044; Hubble’s constant h = H0/100 km s−1 Mpc = 0.72; the amplitude of density fluctuations σ8 = 0.8; and the index of initial perturbation power spectrum ns = 0.96. The simulation is run from redshift z = 100 to z = 0. Outputs are made at 100 snapshots, from z = 18.4 to z = 0, equally spaced in the logarithm of the expansion factor.
2.2. Dark matter halos
In the ELUCID simulation, dark matter halos were identified using a friends-of-friends (FOF) algorithm with a linking length equal to 0.2 times the mean particle separation (Davis et al. 1985). Only halos containing at least 20 particles are identified. We used the SUBFIND algorithm (Springel et al. 2001) to identify subhalos in each FOF halo. This is a method to decompose a given FOF halo into a group of subhalos using the local overdensity and an unbinding algorithm. The largest substructure is called the main halo.
The halo mass, M200, for a main halo is defined using Eq. (1) with Δ = 200 and ρref equal to the cosmic mean density, and is therefore the mass contained in the spherical region of radius R200, centered on the most bound particle of the main halo, and within which the mean mass density is equal to 200 times the cosmic mean density. Diemer & Kravtsov (2014) found that R200 is a more natural choice, in order to scale the density profile at large radii than other definitions. These authors also found that the density slope profiles of halos of a given peak height, ν, at r ≳ R200 are remarkably similar at different redshifts when radii are scaled by R200. This suggests that R200 is suitable for describing the structure and evolution of the density profile in the outskirts of halos.
We then constructed the halo merger trees using the algorithm described in Springel et al. (2005). For a given halo “A” identified at a snapshot “i,” we track all particles of A in the next snapshot “i + 1” and give a certain weight to each particle according to its binding energy. We identify halo “B” as the descendant of halo A in snapshot i + 1 if it has the highest score among all halos containing these particles. It is therefore possible that one halo may have more than one progenitor, but a halo can only have one descendant. The branch that traces the main progenitor of a main halo back in time is referred to as the main trunk of the merger tree of the main halo. For a main halo at z = 0, we estimate its formation redshift, zf, the highest redshift when the main trunk reaches half of its final halo mass.
In order to obtain sufficiently accurate density profiles, each halo needs to contain a sufficiently large number of particles. We used halos with more than 3000 particles, corresponding to log(M200/M⊙)> 12.0. We only considered main halos because the density profiles of subhalos can be affected by the massive main halos. We divided the selected halo sample into five mass bins as shown in Fig. 1. The number of halos in each mass bin is indicated in the corresponding panel in Fig. 1.
 |
Fig. 1. Mean dark matter density (upper panels) and density gradient (lower panels) profiles for halos in five mass bins, shown by the data points. The solid lines represent the best-fitting profiles using the GPR method. The gray symbols and lines show the results averaged over all directions, red for results along T1 direction, and blue for T3 direction. Error bars are estimated using 1000 bootstrap samples. The halo mass ranges are shown in the upper panels. The number of halos in each mass bin is shown in the corresponding upper panel. Please see Sect. 2.4 for details. |
2.3. The large-scale tidal field
To explore the anisotropy in halo profiles, we adopt the “halo tidal field” proposed by Wang et al. (2011) to define the local reference frame for a halo. The tidal field is obtained from the distribution of halos above a certain mass threshold Mth, and can in principle be estimated from observations. As shown in Yang et al. (2005, 2007), galaxy groups and/or clusters properly selected from large galaxy redshift surveys can be used to represent the dark halo population, and halos with masses log(M200/M⊙)≳12 can be identified reliably in the low-z Universe. We therefore adopt log(Mth/M⊙)=12.
The tidal field tensor at the location of a halo, h, can be written as (Chen et al. 2016),
where ri is the distance from the ith halo with mass greater than Mth to halo “h,” and ri is the corresponding unit vector. Ri is the virial radius (R200) of halo i. We only use halos with ri < 100 h−1 Mpc to calculate the tidal tensor, and N is the number of halos used in the calculation.
We can obtain three eigenvalues, t1, t2, and t3, and the corresponding eigenvectors (T1, T2, T3) by diagonalizing the tidal field tensor. These three eigenvalues are defined so that t1 > t2 > t3, and by definition t1 + t2 + t3 = 0. The vectors T1, T2, and T3 represent the major, intermediate, and minor axes of the tidal field, respectively. Defined in this way, T1 corresponds to the direction of stretching of the external tidal force, while T3 corresponds to the direction of compression. Thus, nearby structures, such as filaments or massive halos, tend to reside along T1. In contrast, T3 tends to point toward low-density regions. As shown in our previous studies (e.g., Wang et al. 2011; Chen et al. 2016), the tidal force, t1, can be used to characterize the environment of halos. The tests presented in these studies showed that the principal axes of the halo tidal field are strongly aligned with those estimated from the mass density field (i.e., the method presented in Hahn et al. 2007) and our method is also valid at high redshift. We refer the readers to Wang et al. (2011) and Chen et al. (2016) for detailed tests of the halo tidal field.
2.4. Density-gradient profiles and the fitting method
We first sample the density profile of each halo in 25 logarithmically spaced bins between 0.1R200 and 10R200. We then derive the mean density profile for a given halo sample, and obtain the density gradient profile using the mean density profile. More specifically, the gradient at each radius bin is estimated using the densities in the two adjacent bins. The error bars of the density and gradient profiles are calculated using 1000 bootstrap samples. We take the 16–84 percentile range as the 1σ error on our measurements.
We consider two types of density and gradient profiles. The first is based on profiles averaged over all directions, as was adopted in many earlier studies. We refer to such a profile as the total profile. The second is based on the profiles along the major (T1) and minor (T3) principal axes of the local tidal tensor, respectively. These profiles are obtained by using dark matter particles within a cone around the corresponding principal axis with an opening angle of 30 deg. We also tested with other opening angles, and find that none of the results change significantly as long as the opening angle is below 30 deg. The profiles obtained this way are referred to as the T1 and T3 profiles, respectively.
In order to determine the location of an extremum in a profile to obtain a characteristic scale, most previous studies fitted the density and gradient profiles using a model proposed by Diemer & Kravtsov (2014, DK14). Here we use the Gaussian process regression (GPR) method as implemented in the PYTHON package SCIKIT-LEARN (Pedregosa et al. 2011) to fit the discrete data points. The GPR algorithm is one of the most widely used machine-learning algorithms in processing and analyzing data. Here we use GPR as a flexible, non-parametric method to fit profiles (see also Han et al. 2019). For more details about the method, we refer the reader to Rasmussen & Williams (2005).
More recently, O’Neil et al. (2022) fitted the density and gradient profiles with both the DK14 model and the GPR method. These authors found that both methods produce reliable results, and that the D14 method performed better for gradient profiles. We performed tests using both methods to fit the two types of profiles, and found that the uncertainties in the DK14 model are larger because of the complexity of the profiles. In contrast, all the profiles can be well fitted by the GPR method, with locations of all significant extrema identified reliably (see below). More importantly, we found that some small local minima and peak features, which are of interest to us, cannot be identified by the DK14 model. Because of these, we decided to adopt the GPR method.
To estimate the uncertainties in the characteristic scales, we chose to use two levels of bootstrap sampling technique. For any given halo sample, we first generated 100 level-one (L1) bootstrap samples. For each L1 sample, we generated 1000 level-2 (L2) bootstrap samples. For any L1 sample, we used the 1000 L2 samples to estimate the errors of the mean gradient profile. These errors are used in the GPR to fit the L1 gradient profile and to determine local extrema (and therefore characteristic scales; see next section) from the best-fitting curve. Finally, we estimated the errors of the characteristic scales using the 16–84 percentile of the 100 L1 samples. Similar techniques have been used in previous investigations (e.g., O’Neil et al. 2022).
3. Characteristic scales in halo profiles
In this section, we present a detailed study of a number of characteristic scales present in the density gradient profiles. In Sect. 3.1, we show the density and density gradient profiles for halos of different masses and along the two principal axes of the tidal tensor. We use the GPR method to fit these profiles and identify the characteristic scales. We investigate the dependence of the characteristic scales on halo mass, formation time, and environment in Sects. 3.2 and 3.3. In Sect. 3.4, we examine the particle distribution in phase space to understand how the characteristic scales in density profiles are linked to the dynamics of halo formation. In what follows, characteristic scales are usually expressed in terms of the halo virial radius.
3.1. Halo profiles and characteristic scales
Figure 1 shows the mean mass density and density gradient profiles for five halo mass bins at z = 0. These profiles are the averages over all directions. In general, halos of different masses have similar density profiles from the inner region to several virial radii. At r < R200, the density profiles can be well described by a universal formula, such as the Navarro–Frenk–White density profile (e.g., Navarro et al. 1997). At scales much larger than the virial radius, the density profile is usually dominated by the two-halo term. From the gradient profile, we can see that the density gradient decreases with r at r ≲ R200, and then increases rapidly up to r = 2 ∼ 3R200, remaining roughly at a constant value at larger r. In the transition region around r = R200, one can see a deep valley in the gradient profile, with a minimum (the steepest) gradient of about −3. This feature is often referred to as the “splashback feature,” and the corresponding position is referred to as the “splashback radius” (e.g., Adhikari et al. 2014; Diemer & Kravtsov 2014; More et al. 2015). We can see that the splashback feature becomes deeper as the halo mass increases. This is consistent with previous results showing that this feature becomes more pronounced as the peak height, ν, (equivalent to halo mass) increases (Diemer & Kravtsov 2014; Diemer 2022).
It is well known that both the density distribution and accretion around halos are anisotropic and both aligned with the large-scale tidal field (e.g., Hahn et al. 2007; Wang et al. 2011; Shi et al. 2015). It is therefore interesting to examine the density and gradient profiles along the major (T1) and minor (T3) principal axes of the tidal tensor (see Sect. 2.4 for details). For comparison, the T1 and T3 profiles are also presented in Fig. 1. As one can see, the density profiles change significantly with direction. Within R200, the density along T1 is usually higher than that along T3, and the difference becomes larger as halo mass increases. This is consistent with the fact that the halo orientation is aligned with the large-scale tidal field and the alignment becomes stronger with increasing halo mass (e.g., Hahn et al. 2007; Zhang et al. 2009; Wang et al. 2011; Tempel et al. 2013; Libeskind et al. 2013). At r ≥ R200, the difference becomes even more prominent. For example, at r ∼ 2R200, the density along T1 is about 100 times the cosmic mean density, while that along T3 is about ten times lower. This may be expected as the T1 vector is usually aligned with the large-scale filament containing the halo in question, and the T3 vector usually points to low-density regions. We note that the density profile along T1 at r ∼ 2R200 is quite flat.
In the density gradient profiles, we see two kinds of prominent features. The first one is a clear valley in both the T1 and T3 profiles, which is similar to the splashback feature in the total profiles. The splashback feature along T3 is deeper and narrower than that along T1 in all halo mass bins, and the difference becomes larger as the halo mass increases. The location of the valley varies with direction, and we quantify the location of the valley in Sect. 3.2. Recently, Contigiani et al. (2021) examined a sample of massive halos, and found that the splashback feature is more prominent along the direction toward voids than that along filaments. This is consistent with our result, given the correlation between the local tidal field and the large-scale mass distribution. The second prominent feature is a peak around 2R200. This feature shows up in the gradient profiles along T1, but is absent along the T3 direction and weak in the total profiles. Both the width and height of the peak decreases with increasing halo mass, and the peak gradient is around zero for low-mass halos.
In order to quantify the characteristic features and scales, we need to measure the locations of the local extrema. For this purpose, we fitted the discrete density gradient profiles using the GPR method as mentioned in Sect. 2.4. The best-fitting results are shown in the lower panels of Fig. 1 as smooth curves. As one can see, the fits reproduce the gradient profiles very well. To check the quality of the fitting, we calculated the coefficient of determination, R2, defined as
where y(r) represents the data points as a function of r, yGPR is the best-fitting curve, and ȳ is the value averaged over all radius bins (e.g., Di Bucchianico 2008; Chicco et al. 2021). The closer R2 is to 1, the better the fit. Our tests showed that all of the coefficients in our fitting are greater than 0.96, indicating that the GPR method is able to catch significant features in the profiles.
The gradient profiles can become much more complicated than those shown in Fig. 1 when samples are divided according to the halo formation time. In our analyses, we divided the halo sample in a given mass range into five equally sized subsamples according to their zf. Figure 2 shows the best-fitting curves for halos in the upper, middle, and lower 20% of the zf distribution. The T1, T3, and total profiles are all presented for comparison. For clarity, we do not show the data points. As one can see, the peak feature in the gradient profile along T1 is well defined in all cases, with its position showing some weak dependence on zf. The valley feature appears more complex and shows significant dependence on direction, halo mass, and formation time. A number of local minima can be seen around the valley region for subsamples of high zf. For example, one can see three local minima in the total profile of old halos with mass in the range between 1013 and 1013.5 M⊙. To check whether or not this owes to potential over-fitting by the GPR, we show the data points for the profiles where three local minima are detected by GPR in Fig. 3. These examples demonstrate clearly that the features are real and well captured by the GPR method. As discussed below, these features are likely caused by the caustics produced by particles at their (first or later) apocenter.
 |
Fig. 2. Best-fitting curves for gradient profiles. Different columns show the results of different halo mass, as indicated in each panel. The top, middle, and bottom sets of curves show the T1, total, and T3 profiles, respectively. The profiles are shifted up or down for the purpose of presentation. The red, green, and blue lines represent halos in the upper, middle, and lower 20% of the zf distribution in each mass bin. The vertical dotted lines indicate the splashback radii (the first caustic radii) determined from the T3 profiles (see texts for details). |
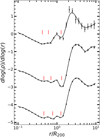 |
Fig. 3. Three gradient profiles that have three local minimums at 0.25R200 < r < 2R200. The points with error bars show the data and the solid lines show the best-fitting curves. The red vertical lines mark the locations of the measured local minimums. |
With the help of GPR, we obtain the locations of the local extrema in the gradient profiles, corresponding to the characteristic scales that we are interested in. The location of a peak feature is represented by a peak radius, Rp, and the location of a local minimum is denoted by a “caustic” radius, Rc. In order to distinguish radii measured from different profiles, we use subscripts “t,” “mj,” and “mn” to denote measurements from the total, T1, and T3 profiles, respectively. For example, Rc, mn is the caustic radius measured from a T3 profile while Rp, mj is the peak radius from a T1 profile. Table 1 lists all the measured radii and their definitions. As peak features in T3 profiles are weak or absent, we do not attempt to measure their locations.
Classification of caustic radius and peak radius.
As shown in Fig. 2, there are multiple local minima in the valley region. To better understand the relation between the splashback radius and the other caustic radii, we measure all the local minima in the valley region, over a radius range 0.25R200 < r < 2R200. We find that each region can have at most three local minima. As shown below, the three caustics can be well separated according to their positions in Rc − zf space. We refer to them here as the first, second, and third caustics in the order of decreasing radius. As mentioned above, these caustics may be produced by particles at their first, second, and third apocenters (see Sect. 3.2). This classification may therefore have some bearing on physical processes underlying the generation of the caustics. The definitions of these radii are also listed in Table 1.
3.2. Splashback, caustics, and their dependencies on halo properties
We first consider the dependence on halo mass. Figure 4 shows the caustic radius as a function of halo mass at z = 0. As shown in Fig. 1, there is only one local minimum in each gradient profile, and so only one caustic radius is measured for each profile. As we can see, both Rc, t and Rc, mn first rise and then fall with increasing halo mass over the mass range in consideration. There seems to be a peak at log(M200/M⊙)∼13, which is broadly consistent with the results shown in Fig. 5 in Diemer & Kravtsov (2014). Some previous investigations focused on relatively massive halos, and so their results can only show the monotonic decline with halo mass at the massive end (e.g., O’Neil et al. 2022). In contrast, Rc, mj is almost independent of halo mass, and its value, which is in the range of 0.6 ∼ 0.8R200, is less than that of Rc, mn, which ranges from 1 to 1.4R200. Previous studies also found anisotropy in the splashback and/or caustic radii measured with different methods (e.g., Mansfield et al. 2017; Deason et al. 2020). However, as we demonstrate in the following, the anisotropy can be explained by the difference between the first and second caustics, rather than the anisotropy in the splashback (first caustic).
 |
Fig. 4. Caustic radius as a function of halo mass. The black, red, and blue symbols show the results measured from total, T1, and T3 halo density gradient profiles, respectively. Error bars are calculated using the two-level (100 × 1000) bootstrap samples (see Sect. 2.4 for the details of the method). |
Now we study the caustic radius as a function of halo formation time. As shown in Fig. 2, there are multiple local minima in the valley regions of some gradient profiles. For each subsample of formation time, we measure all the caustic radii, and the results are presented in Fig. 5. The caustic radii appear to be in three distinct groups. To show this more clearly, we split each panel into three regions, each containing data points in one group. The first group has Rc, mj and Rc, mn larger than 0.8R200, with typical values of about 1.1R200. The caustic radius of the second group is around 0.6R200, and that of the third group is close to 0.4R200. The three groups are referred to as the first, second, and third caustics, and mentioned above. These three groups of caustics correspond to the three local minima shown in Fig. 2. We note that not all profiles have three measurable local minima, because some caustics are weak and contaminated by the presence of other nearby caustics. Indeed, a small fraction of measurements have large and asymmetric uncertainties, and some error bars are equal to the difference between two adjacent groups. We also note that classification into the first, second, and third caustics is different from that according to Rc, t, Rc, mj, and Rc, mn.
 |
Fig. 5. Caustic radii measured from total (black), T1 (red), and T3 (blue) profiles as functions of formation time in different halo mass bins, as indicated in each panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. We note that some profiles have multiple local minimums, and therefore multiple caustic radii. The shaded areas from light to dark indicate the regions where the first, second, and third caustics are located, respectively. |
The first caustic appears in all T3 profiles for all different zf, and these can all be measured accurately, with results shown in Fig. 5. In contrast, only very young halos with zf ≲ 0.6 have a measurable first caustic in their T1 profiles. For the total profiles of massive halos with log(M200/M⊙)> 13, the first caustic shows up for all zf bins, while it is only detectable in the total profiles of lower mass halos that have low zf. As long as the feature is significant and the corresponding caustic radius can be measured, Rc, mn, Rc, mj, and Rc, t all follow a similar trend. They all increase with zf at zf < 1 and decrease with zf at zf > 1. Previous studies (e.g., More et al. 2015; Diemer et al. 2017; Diemer 2020; Contigiani et al. 2021; O’Neil et al. 2021) found that the splashback radius decreases with increasing mass accretion rate for massive halos, which is consistent with the behavior seen here for the first caustic. The values of Rc, mj and Rc, mn for the first caustic are about the same for given zf and halo mass. In most cases, Rc, mn is only slightly larger than Rc, mj, suggesting that the first caustic is nearly isotropic.
It is interesting to investigate the appearance of the first caustic and whether it leaves any imprint in the T1 profiles where it cannot be determined reliably. In Fig. 2, we use vertical lines to mark the value of Rc, mn of the first caustic, corresponding to the steepest negative slope measured from the gradient profiles along T3. Here, we see that the first caustic (if exists) does not always correspond to the lowest gradient value in the total and T1 profiles. Interestingly, in the profiles where the corresponding local minimum does not exist, one still sees some signature of the first caustic around Rc, mn, which is usually either weak or strongly affected by nearby features. These results suggest that the first caustic actually exists along all directions for all halos, and that its location is quite independent of the direction defined by the tidal tensor.
Next let us examine the second group of caustics. This feature is located around 0.6R200, very close to the location of the “second caustic” reported in previous studies (e.g., Adhikari et al. 2014; Diemer & Kravtsov 2014; More et al. 2015; Deason et al. 2020; Xhakaj et al. 2020). This type of caustic tends to appear in relatively old halos, with zf > 0.5, and is visible in the total and T1 profiles but is totally absent from T3 profiles. As shown in Fig. 2, the second caustic is shallow in general and very close to the first one. In T3 profiles, this second caustic may be completely overwhelmed by the first, much deeper caustic, and is therefore difficult to measure. As shown in Fig. 2, the second caustic radius exhibits a modest increase with zf. The third caustic resides in the most inner region of a halo, with r ∼ 0.4R200. It is only visible in very old halos with zf > 0.9, and is likely produced by particles that have completed more than two apocentric passages. Interestingly, this feature is more visible in the T3 profiles than in the other two profiles (Fig. 2). In T3 profiles, the third caustic is quite far from the first one, meaning that contamination by this latter is reduced.
Bertschinger (1985) obtained an analytical solution for caustics by assuming spherical symmetry and self-similar collapse for collisionless matter in an Einstein-de Sitter Universe. These authors found that the radii of the first, second, and third caustics are 0.364, 0.236, and 0.179 times the turnaround radius (Rta), respectively (see also Mohayaee & Shandarin 2006). As shown in Sect. 3.4, Rta is anisotropic and has a weak dependence on halo mass. The mean Rta is about 2.5R200. Therefore, the radii of the three caustics of the analytic solution in Bertschinger (1985) correspond to 0.91, 0.59, and 0.45R200, respectively. These are in good agreement with our finding for the local minima, providing additional evidence that these minima correspond to caustics in gravitational collapse.
Figure 6 shows how the caustic radii depend on the strength of the tidal field, represented by the value of t1, the eigenvalue of the tidal tensor along T1. We divide the halo sample of a given mass bin into five equally sized subsamples in t1, and present the caustic radii as functions of the mean t1. There are sometimes multiple local minima in one profile, and we show the values for all the measurable radii. Consider first Rc, mj and Rc, mn. It is clear that there are two distinct groups of caustics. To guide the eye, we split each panel into two parts separated at r = 0.8R200. The caustics with radii larger than 0.8R200 correspond to the first caustic discussed above, and can be measured in all T3 profiles as well as in some T1 profiles in weak tidal fields. For halos of log(M200/ M⊙)> 13, the caustic radius is totally independent of t1. For low-mass halos, on the other hand, the radius decreases with increasing t1. Halos with very large t1 may reside in the splashback regions of nearby massive halos and their own splashback shells may have been affected severely by stripping effects. The first caustic is nearly isotropic, with Rc, mj ≈ Rc, mn when both can be measured.
 |
Fig. 6. Caustic radii measured from total (black), T1 (red), and T3 (blue) profiles as functions of tidal force t1 in different halo mass bins, as indicated in each panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. The shaded areas from light to dark indicate the regions where the first and second caustics are located, respectively. |
The other group has caustic radii around 0.6R200, and therefore corresponds to the second caustic. The second caustic can only be identified in T1 profiles, and its radius is almost independent of t1. We are not able to identify the third caustic reliably, as it only appears in very old halos (Fig. 5) and is likely diluted by young halos. In each of the total profiles, we can only identify one local minimum. At small t1, the location of the minimum follows that of the first caustic. At large t1, Rc, t lies between Rc, mj and Rc, mn, following the average between the first and second caustics. This indicates that the locations of the steepest slope in total profiles of halos with large t1 are actually a mixture of those of the first and second caustics.
Our analysis shows that the radius of the first caustic along T3 depends on both formation time and environment. Many factors, such as halo structure, halo merger, nearby structure (see following section), and velocity of the accreted material, can affect the first caustic and its measurement. These factors are related to both formation time and environment, and can therefore produce the dependencies we observe. This also suggests that the two dependencies may be related. As shown in Wang et al. (2011), t1 is positively correlated with zf for small halos. Therefore, the decrease in the first caustic radius with t1 may have the same origin as its decrease with zf at zf > 1.0 for small halos. At zf < 1.0, the increasing trend with zf may be caused by the fact that old halos are usually more compact than young ones.
The deep valley in T1 and total profiles is sometimes a mix of several features. As an example, we reanalyze the results presented in Fig. 4. We note that Rc, mn shown in the figure corresponds to the first caustic, as it is always the dominant feature in T3 profiles and its location depends only weakly on other properties. In contrast, the feature in T1 profiles varies dramatically with zf. The first caustic dominates at small zf, while the second one dominates at large zf (Figs. 2 and 5). Consequently, Rc, mj shown in Fig. 4, an average over all zf, is the result of the blending of the two caustics. Being in the range of 0.6 ∼ 0.8R200, the value of Rc, mj measured is closer to the second caustic. We therefore conclude that the anisotropy shown in Fig. 4 mainly reflects the difference between the first and second caustics rather than the anisotropy of the splashback feature. In particular, the caustic radius in total profiles of low-mass halos is the mean result of the first and second caustics. This is also true for the caustic radius obtained from the total profiles of halos with large t1 (Fig. 6).
The splashback radius studied in the literature corresponds to the first caustic, which is formed by particles at their first apocenter after infall (e.g., Diemer & Kravtsov 2014; Adhikari et al. 2014; More et al. 2015; Shi 2016). Our results demonstrate that the first caustic does not always correspond to the location of the steepest slope or even a local minimum. Therefore, using the lowest point in the gradient profile to represent the location of splashback may lead to significant bias, as discussed above. Moreover, using the DK14 model to fit the density and gradient profiles for small and old halos or along T1 may be inappropriate, as the profiles sometimes deviate significantly from the DK14 model (Fig. 2; see also More et al. 2015). As shown above, the first caustic in T3 profiles is prominent for both young and old halos over a large range in both halo mass and environment (represented by t1). Our results also show that the location of the first caustic is approximately isotropic relative to the local tidal tensor. Thus, the first caustic along T3 may provide a promising way to study the splashback radius and its dependence on halo properties. As shown in Wang et al. (2012), the tidal field in the local Universe can be reconstructed from galaxy groups (Yang et al. 2007). It is therefore possible to have an unbiased measurement of the splashback radius from observational data by studying the galaxy distribution in the frame defined by the local tidal field.
3.3. Gradient peak and its dependencies on halo properties
Compared to the splashback and caustic features discussed above, the gradient peak feature is simpler: it appears as a single peak in the T1 and total gradient profiles. We use the GPR method to fit the profiles and locate the local maxima to measure the peak radii. Figure 7 shows Rp, t and Rp, mj as functions of halo mass. Rp, t, ranging from 3.5 to 2.8R200, declines quickly with halo mass, while Rp, mj is around 2.5R200, almost independent of halo mass except at the massive end. In all cases, Rp, t is larger than Rp, mj. Examining the gradient profiles in Fig. 1, we can see that, around Rp, mj, the gradient in the T3 profiles is low but increases quickly with r, in contrast to the gradient in T1 profiles, which starts to drop quickly with r. The peak in the total profiles is a combined effect of both the T1 and T3 profiles, but does not indicate the existence of a particular structure. We note that the uncertainty in Rp, t is quite large, particularly for the most massive halos, because the peak is rather weak. In the following, we only present results for Rp, mj.
 |
Fig. 7. Peak radii measured from total (black) and T1 (red) profiles as functions of halo mass. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. |
The dependence of Rp, mj on halo formation time is shown in Fig. 8. We can see that the peak radius of halos with different masses follows almost the same trend with formation time, although the mean formation time (z̄f) depends strongly on halo mass. At zf < 0.6, the peak radius increases with increasing formation redshift, while the dependence disappears at zf > 0.6, with Rp, mj ∼ 2.5R200. This result clearly suggests that the weak mass dependence is the secondary effect of the zf-dependence combined with the M200−z̄f relation. This interesting correlation may be related to the assembly bias that indicates the dependence of halo assembly on environment (Gao et al. 2005; Wang et al. 2007).
 |
Fig. 8. Peak radius along T1 (Rp, mj) as a function of formation time in different halo mass bin as indicated in the panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. |
We also study the correlation of the peak radius with the tidal force (t1) by dividing halos of a given mass range into five equally sized subsamples in t1. Figure 9 shows the peak radius as a function of the mean tidal force. There is a strong dependence of Rp, mj on t1, with the peak radius deceasing rapidly with increasing tidal field strength. If the tidal force on a halo is dominated by another structure with distance r to the halo, the tidal force is proportional to r−3. As a reference, we show a curve of 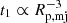 with an arbitrary amplitude. As one can see, the data points follow the t1 ∝ r−3 relation well, suggesting that the presence of a locally dominating structure (LDS) at r ∼ Rp, mj may be the main cause of the local tidal field of a halo. We do not find a peak within 10R200 for halos in the lowest t1 bins, suggesting that these halos reside in an environment without a LDS.
with an arbitrary amplitude. As one can see, the data points follow the t1 ∝ r−3 relation well, suggesting that the presence of a locally dominating structure (LDS) at r ∼ Rp, mj may be the main cause of the local tidal field of a halo. We do not find a peak within 10R200 for halos in the lowest t1 bins, suggesting that these halos reside in an environment without a LDS.
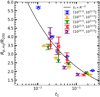 |
Fig. 9. Peak radius along T1 (Rp, mj) as a function of the strength of tidal field (t1) in different halo mass bin as indicated in the panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. The black curve shows |
Fong & Han (2021) defined a characteristic depletion radius, Rcd, using the location of the lowest point of the halo bias profile (defined as the ratio between the halo-mass cross-correlation function and the mass auto-correlation function). These authors found that the value of Rcd is about 2.5R200, similar to the value of Rp, mj we find here. They also found that Rcd – which scales with R200 – depends strongly on environment and only weakly on formation time and halo mass, similar to what we find for Rp, mj. This may not be surprising, as the halo-mass cross-correlation function is a measure of the mass density profile around halos. However, the bias function they used does not allow them to investigate any anisotropy in the mass distribution.
Anbajagane et al. (2022) studied the thermal SZ effect in and around observed, rich galaxy clusters, and found a clear flattening in the Compton-y profile and a prominent peak in the gradient profile at ∼2R200. The Compton y parameter is the integration of the electron pressure along the line of sight, and is therefore sensitive to both the gas density and gas temperature. In Fig. 10, we show the velocity dispersion of dark matter particles as a function of radius along both T1 and T3 directions. At 2.5R200, the velocity dispersion of particles distributed along T1 is much higher than that along T3. For galaxy clusters, the difference is a factor of ∼3, which suggests that the baryonic gas in the T1 direction is much hotter than that in the T3 direction. From the density profile in Fig. 1, one can also see that the mass density at ∼2.5R200 is about ten times higher in the T1 direction than in the T3 direction. Taken together, these findings suggest that the Compton y parameter measured at such a radius is dominated by the gas along the T1 direction. Our results also indicate that this property of the SZ effect should also exist for low-mass halos, such as poor clusters and galaxy groups. The thermal SZ effect therefore provides a promising probe of the peak feature in the mass distribution around halos.
 |
Fig. 10. Velocity dispersion, σ, of dark matter particles as a function of radius. The velocity dispersion and radius are scaled with V200 and R200, respectively. Line styles denote different halo masses, as indicated. Red lines show the results along T1 direction, and blue for T3 direction. |
Our results in Sects. 3.1 and 3.2 show that (i) the density gradient profiles at r < 2R200 and caustics along T1 are very different from those along T3 (Figs. 1–6); (ii) the first caustic along T1 only appears in halos in weak tidal field (Fig. 6); and (iii) the second caustic more likely appears along T1 rather than along T3 (Figs. 5 and 6). All these suggest that the peak feature, that is, the LDS, has a strong impact on the splashback and caustics. One possibility is that the gravitational field of the LDS can change the halo accretion history. Indeed, as found in Wang et al. (2021), the assembly history of a halo is correlated with the density field outside the corresponding proto-halo in the initial density field. Another possibility is that the existence of the LDS affects the determination of the first caustic radius using the location of the local minimum. As shown in Fig. 2, the peak feature can sometimes extend to the region where the first caustic is expected to appear, particularly for low-mass halos and halos in regions of high-t1 (see Figs. 5 and 6).
3.4. Signatures in phase space
To understand the origin of the characteristic features, we examine the dark matter particle distribution in phase space (r/R200, vr/V200). Here, r is the distance to the halo center and vr is the radial velocity relative to the halo. The phase space density is expressed as
where N is the halo number in the halo sample, M200, i is the mass of halo i, and ni(r/R200, vr/V200) is the number of dark matter particles associated with halo i in the corresponding r/R200 and vr/V200 bin. The phase space density is normalized by the halo mass to eliminate potential mass dependence. Results obtained using all particles in all directions, Ω = 4π, are marked as “total” in Figs. 11 and 12, while results along T1 and T3 use 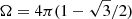 , corresponding to a solid angle with an opening angle of 30 deg. We note that the Hubble flow is included in the velocity, and a negative velocity indicates that the matter is falling onto the halo.
, corresponding to a solid angle with an opening angle of 30 deg. We note that the Hubble flow is included in the velocity, and a negative velocity indicates that the matter is falling onto the halo.
 |
Fig. 11. Phase space diagrams of dark matter particles in three halo mass bins. The left, middle, and right columns show the results averaged over all direction (labeled as “total”), along T1 and T3, respectively. The contour lines are color coded according to the phase space density (see Eq. (4)); red(blue) means high(low) phase space density. The green and red vertical lines indicate the caustic and peak radii, respectively. The dashed vertical lines indicate the caustic radii measured in the total or T1 profiles, while the solid vertical lines indicate the radii measured in the T3 profiles and are also shown in total and T1 panels. The black solid lines show the contour maxima of the accretion components. The red pentagram indicates the turnaround radius. |
 |
Fig. 12. Phase space diagrams of dark matter particles for halos with different zf and M200. The panels are split into three groups according to the halo mass. In each group, the upper (lower) panels show the results for the oldest (youngest) 20% halos, respectively. The left, middle, and right columns show the results averaged over all directions (labeled as “total”), along T1 and T3, respectively. The contour lines are color coded according to the phase space density (see Eq. (4)); red(blue) means high(low) density. The black dashed lines indicate the caustic radii measured from gradient profiles. |
Figure 11 shows the phase space density distribution averaged over all directions (left), along T1 (middle) and T3 (right) for three halo mass bins. The results for the other two mass bins are similar and not shown here. As one can see, there are two distinct components in the phase-space distribution. The first one has small r and a broad and symmetric distribution in vr, which is composed of particles that are orbiting around the halo. We refer to this component as the halo component. The halo component has an extended tail outside the virial radius with a small radial velocity. This is caused by splashback substructures together with diffuse mass (see e.g., Wang et al. 2009; Sugiura et al. 2020; Diemer 2022). The second component is mainly outside the virial radius, in which the mean radial velocity increases with distance. The inner part of this component penetrates into the halo component with an infall velocity, suggesting that halos are accreting material through this component. We refer to this component as the accretion component. Diemer (2022) separated particles according to orbital or infalling motions, and these two sets of particles are similar to the halo and accretion components defined here.
As shown by red vertical lines in Fig. 11, which mark the peak positions in the gradient profiles along T1, the peak feature in the T1 gradient profiles is associated with the accretion component. This component is much more prominent along T1 than along T3, as T1 tends to align with nearby filaments. The width of the velocity distribution for particles along T1 is also much broader than that along T3, and increases with decreasing halo mass, which is consistent with the velocity dispersion shown in Fig. 10. Although our analysis above suggests the existence of LDS around Rp, mj, we do not see any distinct structure in phase space. This is true even for analyses carried out on halos in regions of different t1. This suggests that the LDSs along T1 are mostly filamentary structures consisting of different halos.
The peak radius is close to the turnaround radius, Rta (marked by red stars in Fig. 11), defined as the location where the mean radial velocity (marked with black solid lines) is equal to zero. This suggests that the LDS responsible for the peak may be located at ∼Rta. As the mean velocity is close to zero at Rta, mass has the tendency to be deposited at this radius, forming the peak feature in the density gradient profile. However, along the T3 direction, one does not see any significant signal in the density gradient profile at ∼Rta, because not much material is available to be accreted in this direction. We have constructed the phase-space maps for halos in regions of different t1. Except for low-mass halos in the largest t1 bin, Rta along T1 is almost independent of t1, and is about 2 ∼ 2.5R200, which is very different from the strong t1-dependence of Rp, mj in this direction (see Fig. 9). This indicates that Rp, mj is a characteristic radius that is very different from Rta.
The green vertical lines mark the caustic radii defined using the gradient profiles. The values of Rc, t and Rc, mj are shown as the dashed lines only in their own panels, while for comparison, Rc, mn is drawn as the solid lines in all three panels (total, T1, and T3) for halos in a given mass bin. For the total sample, the halo and accretion components are well separated by both Rc, t and Rc, mn, as is expected from the similarity of the two radii (Fig. 4). For halos of the lowest mass, Rc, mn seems to perform better, even though it is defined from the T3 profiles. For particles along the T1 direction, Rc, mn performs better than Rc, mj in all three mass bins, which is consistent with the analysis in Sect. 3.2. We can see that the accretion component along T3 is very weak, indicating that the T3 profiles are dominated by the mass physically connected to halos, including mass both within the virial radius and the splashback mass outside the virial radius. Thus, Rc, mn may better represent the caustic formed by particles at their first apocenters. Along T1, the accretion component, in particular the peak feature, is prominent, making a significant contribution to the T1 profiles around Rc, mn and affecting the assessment of the splashback radius.
It is also interesting to check the phase space density for halos with different zf. Figure 12 shows the results for the 20% oldest and the 20% youngest halos in three mass bins. Here, we want to examine inner regions of halos, and so we only present particles within 2R200. For comparison, we mark the caustic radii determined above with vertical lines. For young halos, we can clearly see both the halo and accretion components in phase space, but no significant signal for the existence of subcomponents is seen within the halo component. This is consistent with the fact that only the splashback radii (first caustic) can be identified in the T1 and T3 profiles, as shown in Sect. 3.2. The splashback radius along T3 is slightly larger than that along T1. This may indicate that the accretion flow along T1 seen as the extension of the peak feature can affect the splashback radius. Alternatively, the accretion component along T3 may have larger infall velocities than that along T1, and can therefore reach a larger apocenter.
As opposed to young halos, old ones have clear subcomponents within their halo components, meaning that multiple caustic radii can be identified. There seems to be one significant subcomponent in the T3 phase-space density distribution, which is seen as a symmetric excess in ρp between the two caustic radii and has vr ∼ 0. This clump is very likely at its first apocenter, producing a prominent peak between the first and third caustics shown in the T3 profiles of old halos (Fig. 2). One can also see an excess at the similar place in the T1 phase-space density distribution. The corresponding contour has a configuration aligned with the accretion component, suggesting that this excess is contaminated by the accretion flow. As shown in Fig. 12, the caustic radii lie approximately between the two (sub)components, and characterize the boundaries of the (sub)structures in halos.
4. Summary
In this paper, we use the ELUCID N-body simulation to study the characteristic features on the density gradient profiles in and around halos with masses from 1012 to 1015.0 M⊙. We use the GPR method to fit the density gradient profiles and find the locations of these characteristic features, represented by their scales. We investigate the characteristic scales along the principal axes (the major axis T1 and minor axis T3) of the large-scale tidal field and their dependence on halo mass, halo formation redshift (zf), and environment (tidal field strength represented by t1). We also verify our results and investigate the origins of these features using the distribution of dark matter particles in phase space. Our main findings and conclusions are summarized below.
-
In the density gradient profiles, there are two types of dominant features: one is a deep “valley,” which corresponds to the caustic and splashback features formed by dark matter particles at their apocenters after infall. The other is a prominent “peak” along the T1 direction produced by the mass distribution surrounding halos.
-
The GPR method can fit the gradient profiles very well, and the performance is almost independent of the direction, halo mass, halo formation time, and environment; it is able to detect even weak structures in the gradient profiles.
-
The valley in the gradient profiles sometimes contains complicated subcomponents. We identified three groups of local minima, referred to as the first, second, and third caustics. Whether or not the three caustics appear depends on the direction relative to the local tidal field, halo formation time, and environment.
-
The first caustic radius corresponds to the steepest slope along the T3 direction, and ranges from 0.8 to 1.4R200. In gradient profiles along T1 for old halos and for halos in strong tidal fields, the first caustic appears either as a local minimum (sometimes the deepest one) or as a small but significant change in the gradient. The radius of the first caustic along T3 is slightly larger than that along T1. The first caustic radius corresponds to the splashback radius, and is produced by particles at their first apocenters after infall.
-
The second caustic, around 0.6R200, can be identified along T1 but not along T3, and it appears in relatively old halos (zf > 0.5). The third caustic, around 0.4R200, is clearly present in the T3 profiles, and only appears in very old halos of zf > 0.9. These two radii are produced by mass at the second and third apocenters.
-
The radii of the first, second, and third caustics are consistent with the prediction of self-similar gravitational collapse.
-
Our analyses show that using the gradient profiles averaged over all directions or along T1 may lead to a significant bias in estimating the splashback radius. Such an approach amplifies the anisotropy and may result in a biased estimation of the splashback radius. The splashback radius estimated from T3 direction, on the other hand, is reliable for both young and old halos and in both strong and weak tidal field. Correcting for such bias, we find that the splashback radius is approximately isotropic around a halo.
-
The peaks in gradient profiles are around 2.5R200, which correspond to a significant flattening in density profiles. The peak radius increases with zf at zf < 0.6 and becomes constant at zf > 0.6. At fixed zf, it is independent of halo mass.
-
Our results show that the peak feature is very likely produced by structures that dominate the tidal force. The dominating structures have significant impact on the caustics, as indicated by the difference in the caustic structure seen between the T1 and T3 profiles.
-
The caustic radii are found to separate different (sub)components of the particle distribution in phase space. The first caustic radius, that is, the splashback radius, obtained from the T3 direction performs the best in separating the accretion flow from particles that are orbiting around halos.
Our results show that the splashback radius can be determined in an unbiased way by measuring the gradient profile along the minor axis of the local large-scale structure. The measurement is reliable for both old and low-mass halos in various environments. The splashback radius obtained in this way can be used to study its correlations with halo properties and environments. We also investigated the connection between the caustics and the peak in gradient profiles and discuss how these two types of characteristic features are related to halo assembly in different environments. Our results show that the splashback feature along the T3 direction is prominent, and may be detected in observational data through the galaxy correlation function (e.g., More et al. 2016), weak lensing (e.g., Gavazzi et al. 2006), and dark matter annihilation (e.g., Mohayaee & Shandarin 2006). More tests are required to verify this. Our results also suggest that thermal SZ effects are expected from the peak feature around halos of various masses (see the SZ signal in Anbajagane et al. 2022), and in particular along the T1 direction. All these predictions, together with the information provided by accurate reconstructions of the cosmic web, such as the ELUCID, can be tested using observational data. We will come back to some of these in the future.
Acknowledgments
We thank the referee for a useful report. This work is supported by the National Key R&D Program of China (grant No. 2018YFA0404503), the National Natural Science Foundation of China (NSFC, Nos. 11733004, 12192224, 11890693, and 11421303), CAS Project for Young Scientists in Basic Research, Grant No. YSBR-062, and the Fundamental Research Funds for the Central Universities. The authors gratefully acknowledge the support of Cyrus Chun Ying Tang Foundations. We acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-A03. The work is also supported by the Supercomputer Center of University of Science and Technology of China.
References
- Adhikari, S., Dalal, N., & Chamberlain, R. T. 2014, JCAP, 2014, 019 [Google Scholar]
- Adhikari, S., Dalal, N., & Clampitt, J. 2016, JCAP, 2016, 022 [CrossRef] [Google Scholar]
- Adhikari, S., Sakstein, J., Jain, B., Dalal, N., & Li, B. 2018, JCAP, 2018, 033 [Google Scholar]
- Adhikari, S., Shin, T.-H., Jain, B., et al. 2021, ApJ, 923, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Anbajagane, D., Chang, C., Jain, B., et al. 2022, MNRAS, 514, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Aung, H., Nagai, D., & Lau, E. T. 2021a, MNRAS, 508, 2071 [NASA ADS] [CrossRef] [Google Scholar]
- Aung, H., Nagai, D., Rozo, E., & García, R. 2021b, MNRAS, 502, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Baxter, E. J., Adhikari, S., Vega-Ferrero, J., et al. 2021, MNRAS, 508, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., Lu, Y., et al. 2014, ApJ, 787, 156 [Google Scholar]
- Bertschinger, E. 1985, ApJS, 58, 39 [Google Scholar]
- Bianconi, M., Buscicchio, R., Smith, G. P., et al. 2021, ApJ, 911, 136 [Google Scholar]
- Busch, P., & White, S. D. M. 2017, MNRAS, 470, 4767 [CrossRef] [Google Scholar]
- Chang, C., Baxter, E., Jain, B., et al. 2018, ApJ, 864, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, S., Wang, H., Mo, H. J., & Shi, J. 2016, ApJ, 825, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Chicco, D., Warrens, J. M., & Jurman, G. 2021, PeerJ Comput. Sci., 7, e623 [CrossRef] [Google Scholar]
- Contigiani, O., Hoekstra, H., & Bahé, Y. M. 2019a, MNRAS, 485, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Contigiani, O., Vardanyan, V., & Silvestri, A. 2019b, Phys. Rev. D, 99, 064030 [NASA ADS] [CrossRef] [Google Scholar]
- Contigiani, O., Bahé, Y. M., & Hoekstra, H. 2021, MNRAS, 505, 2932 [NASA ADS] [CrossRef] [Google Scholar]
- Cuesta, A. J., Prada, F., Klypin, A., & Moles, M. 2008, MNRAS, 389, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Dacunha, T., Belyakov, M., Adhikari, S., et al. 2022, MNRAS, 512, 4378 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [Google Scholar]
- Deason, A. J., Fattahi, A., Frenk, C. S., et al. 2020, MNRAS, 496, 3929 [NASA ADS] [CrossRef] [Google Scholar]
- Di Bucchianico, A. 2008, Coefficient of Determination (R2) (New York: John Wiley& Sons, Ltd) [Google Scholar]
- Diemand, J., & Kuhlen, M. 2008, ApJ, 680, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B. 2020, ApJS, 251, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B. 2022, MNRAS, 513, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., & Kravtsov, A. V. 2014, ApJ, 789, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., More, S., & Kravtsov, A. V. 2013, ApJ, 766, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., Mansfield, P., Kravtsov, A. V., & More, S. 2017, ApJ, 843, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Fillmore, J. A., & Goldreich, P. 1984, ApJ, 281, 1 [Google Scholar]
- Fong, M., & Han, J. 2021, MNRAS, 503, 4250 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, M., Han, J., Zhang, J., et al. 2022, MNRAS, 513, 4754 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., Springel, V., & White, S. D. M. 2005, MNRAS, 363, L66 [NASA ADS] [CrossRef] [Google Scholar]
- García, R., Rozo, E., Becker, M. R., & More, S. 2021, MNRAS, 505, 1195 [CrossRef] [Google Scholar]
- Gavazzi, R., Mohayaee, R., & Fort, B. 2006, A&A, 445, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E. 1977, ApJ, 218, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, O., Porciani, C., Carollo, C. M., & Dekel, A. 2007, MNRAS, 375, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J., Li, Y., Jing, Y., et al. 2019, MNRAS, 482, 1900 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., & White, S. D. M. 2008, MNRAS, 388, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [Google Scholar]
- Libeskind, N. I., Hoffman, Y., Forero-Romero, J., et al. 2013, MNRAS, 428, 2489 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, A. D., Navarro, J. F., Springel, V., et al. 2009, ApJ, 692, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Mansfield, P., Kravtsov, A. V., & Diemer, B. 2017, ApJ, 841, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H., van den Bosch, F., & White, S. 2010, Galaxy Formation and Evolution (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Mohayaee, R., & Salati, P. 2008, MNRAS, 390, 1297 [NASA ADS] [Google Scholar]
- Mohayaee, R., & Shandarin, S. F. 2006, MNRAS, 366, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- More, S., Diemer, B., & Kravtsov, A. V. 2015, ApJ, 810, 36 [Google Scholar]
- More, S., Miyatake, H., Takada, M., et al. 2016, ApJ, 825, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Murata, R., Sunayama, T., Oguri, M., et al. 2020, PASJ, 72, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Oguri, M., & Hamana, T. 2011, MNRAS, 414, 1851 [NASA ADS] [CrossRef] [Google Scholar]
- O’Neil, S., Barnes, D. J., Vogelsberger, M., & Diemer, B. 2021, MNRAS, 504, 4649 [CrossRef] [Google Scholar]
- O’Neil, S., Borrow, J., Vogelsberger, M., & Diemer, B. 2022, MNRAS, 513, 835 [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton: Princeton University Press) [Google Scholar]
- Peñarrubia, J., & Fattahi, A. 2017, MNRAS, 468, 1300 [CrossRef] [Google Scholar]
- Prada, F., Klypin, A. A., Simonneau, E., et al. 2006, ApJ, 645, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. 2005, Gaussian Processes for Machine Learning (Cambridge: The MIT Press) [Google Scholar]
- Rees, M. J., & Ostriker, J. P. 1977, MNRAS, 179, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [Google Scholar]
- Shi, J., Wang, H., & Mo, H. J. 2015, ApJ, 807, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X. 2016, MNRAS, 459, 3711 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, T., Adhikari, S., Baxter, E. J., et al. 2019, MNRAS, 487, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, T., Jain, B., Adhikari, S., et al. 2021, MNRAS, 507, 5758 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [Google Scholar]
- Sugiura, H., Nishimichi, T., Rasera, Y., & Taruya, A. 2020, MNRAS, 493, 2765 [Google Scholar]
- Sunayama, T., & More, S. 2019, MNRAS, 490, 4945 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Tempel, E., Stoica, R. S., & Saar, E. 2013, MNRAS, 428, 1827 [NASA ADS] [CrossRef] [Google Scholar]
- Trevisan, M., Mamon, G. A., & Stalder, D. H. 2017, MNRAS, 471, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., & Diemer, B. 2017, ApJ, 836, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., White, S. D. M., Mohayaee, R., & Springel, V. 2009, MNRAS, 400, 2174 [Google Scholar]
- Vogelsberger, M., Mohayaee, R., & White, S. D. M. 2011, MNRAS, 414, 3044 [Google Scholar]
- Wang, H. Y., Mo, H. J., & Jing, Y. P. 2007, MNRAS, 375, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., & Jing, Y. P. 2009, MNRAS, 396, 2249 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Jing, Y. P., Yang, X., & Wang, Y. 2011, MNRAS, 413, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Yang, X., & van den Bosch, F. C. 2012, MNRAS, 420, 1809 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Yang, X., Jing, Y. P., & Lin, W. P. 2014, ApJ, 794, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Yang, X., et al. 2016, ApJ, 831, 164 [Google Scholar]
- Wang, X., Wang, H., Mo, H. J., Shi, J. J., & Jing, Y. 2021, A&A, 654, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [Google Scholar]
- Xhakaj, E., Diemer, B., Leauthaud, A., et al. 2020, MNRAS, 499, 3534 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., & Jing, Y. P. 2005, MNRAS, 356, 1293 [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [Google Scholar]
- Zhang, C., Zhuravleva, I., Kravtsov, A., & Churazov, E. 2021, MNRAS, 506, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Yang, X., Faltenbacher, A., et al. 2009, ApJ, 706, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., Mandelbaum, R., Simet, M., Rozo, E., & Rykoff, E. S. 2017, MNRAS, 470, 551 [CrossRef] [Google Scholar]
- Zukin, P., & Bertschinger, E. 2010, Phys. Rev. D, 82, 104044 [Google Scholar]
- Zürcher, D., & More, S. 2019, ApJ, 874, 184 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Mean dark matter density (upper panels) and density gradient (lower panels) profiles for halos in five mass bins, shown by the data points. The solid lines represent the best-fitting profiles using the GPR method. The gray symbols and lines show the results averaged over all directions, red for results along T1 direction, and blue for T3 direction. Error bars are estimated using 1000 bootstrap samples. The halo mass ranges are shown in the upper panels. The number of halos in each mass bin is shown in the corresponding upper panel. Please see Sect. 2.4 for details. |
| In the text | |
 |
Fig. 2. Best-fitting curves for gradient profiles. Different columns show the results of different halo mass, as indicated in each panel. The top, middle, and bottom sets of curves show the T1, total, and T3 profiles, respectively. The profiles are shifted up or down for the purpose of presentation. The red, green, and blue lines represent halos in the upper, middle, and lower 20% of the zf distribution in each mass bin. The vertical dotted lines indicate the splashback radii (the first caustic radii) determined from the T3 profiles (see texts for details). |
| In the text | |
 |
Fig. 3. Three gradient profiles that have three local minimums at 0.25R200 < r < 2R200. The points with error bars show the data and the solid lines show the best-fitting curves. The red vertical lines mark the locations of the measured local minimums. |
| In the text | |
 |
Fig. 4. Caustic radius as a function of halo mass. The black, red, and blue symbols show the results measured from total, T1, and T3 halo density gradient profiles, respectively. Error bars are calculated using the two-level (100 × 1000) bootstrap samples (see Sect. 2.4 for the details of the method). |
| In the text | |
 |
Fig. 5. Caustic radii measured from total (black), T1 (red), and T3 (blue) profiles as functions of formation time in different halo mass bins, as indicated in each panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. We note that some profiles have multiple local minimums, and therefore multiple caustic radii. The shaded areas from light to dark indicate the regions where the first, second, and third caustics are located, respectively. |
| In the text | |
 |
Fig. 6. Caustic radii measured from total (black), T1 (red), and T3 (blue) profiles as functions of tidal force t1 in different halo mass bins, as indicated in each panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. The shaded areas from light to dark indicate the regions where the first and second caustics are located, respectively. |
| In the text | |
 |
Fig. 7. Peak radii measured from total (black) and T1 (red) profiles as functions of halo mass. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. |
| In the text | |
 |
Fig. 8. Peak radius along T1 (Rp, mj) as a function of formation time in different halo mass bin as indicated in the panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. |
| In the text | |
 |
Fig. 9. Peak radius along T1 (Rp, mj) as a function of the strength of tidal field (t1) in different halo mass bin as indicated in the panel. Error bars are calculated using the two-level (100 × 1000) bootstrap samples. The black curve shows |
| In the text | |
 |
Fig. 10. Velocity dispersion, σ, of dark matter particles as a function of radius. The velocity dispersion and radius are scaled with V200 and R200, respectively. Line styles denote different halo masses, as indicated. Red lines show the results along T1 direction, and blue for T3 direction. |
| In the text | |
 |
Fig. 11. Phase space diagrams of dark matter particles in three halo mass bins. The left, middle, and right columns show the results averaged over all direction (labeled as “total”), along T1 and T3, respectively. The contour lines are color coded according to the phase space density (see Eq. (4)); red(blue) means high(low) phase space density. The green and red vertical lines indicate the caustic and peak radii, respectively. The dashed vertical lines indicate the caustic radii measured in the total or T1 profiles, while the solid vertical lines indicate the radii measured in the T3 profiles and are also shown in total and T1 panels. The black solid lines show the contour maxima of the accretion components. The red pentagram indicates the turnaround radius. |
| In the text | |
 |
Fig. 12. Phase space diagrams of dark matter particles for halos with different zf and M200. The panels are split into three groups according to the halo mass. In each group, the upper (lower) panels show the results for the oldest (youngest) 20% halos, respectively. The left, middle, and right columns show the results averaged over all directions (labeled as “total”), along T1 and T3, respectively. The contour lines are color coded according to the phase space density (see Eq. (4)); red(blue) means high(low) density. The black dashed lines indicate the caustic radii measured from gradient profiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



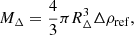
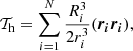
![$$ \begin{aligned} R^{2}=1-\frac{\sum _r[y(r)-y_{\rm GPR}(r)]^{2}}{\sum _r[y(r)-\bar{y}]^{2}}, \end{aligned} $$](/articles/aa/full_html/2022/11/aa44338-22/aa44338-22-eq3.gif)