| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142677 | |
| Published online | 04 August 2022 | |
Sub-surface stratification and dielectric permittivity distribution at the Chang’E-4 landing site revealed by the lunar penetrating radar
1
State Key Laboratory of Lunar and Planetary Sciences, Macau University of Science and Technology,
Macau, PR China
e-mail: yixu@must.edu.mo
2
College of Science, Guilin University of Technology,
Guilin, PR China
3
College of Geo-exploration Science and Technology, Jilin University,
Changchun, PR China
4
Earth Sciences, University College London,
London, UK
Received:
16
November
2021
Accepted:
19
March
2022
Context. In 2019, China’s Chang’E-4 (CE-4) probe landed on the far side of the Moon: a first in lunar exploration. The Lunar Penetrating Radar (LPR) mounted on the Yutu-2 rover allows the mapping of the near-surface structure and the dielectric permittivity of the landing area. The dielectric properties of the lunar soil affect the propagation of the LPR signals, which can be used to infer the depth of sub-surface boundaries and derive the composition of the component materials.
Aims. Our objectives are to estimate the fine-resolution spatial distribution of relative permittivity and to improve the interpretation of the geological processes combined with the radargram of the CE-4 landing area.
Methods. We used a modified method that combines the F-K migration and the minimum entropy of the ground penetrating radar (GPR) signals to estimate the velocity and permittivity values; this has the advantage of obtaining the appropriate velocity and permittivity, even with the incomplete or unnoticeable hyperbolic curves in the radar image
Results. The sub-surface stratification of the CE-4 landing area is seen in the first 31 lunar days of the LPR data. A fine-resolution dielectric permittivity profile ranging from ~2.3 to ~6.3 is obtained with our method, and the actual depths of the observed prominent sub-surface interfaces are determined, giving a maximum average depth of ~38 m. The thickness of the regolith layer is in the range of ~5.7–15.6 m, with an average of 11.8 m. The permittivity of the near-surface regolith (<30 cm) is ~2.78 ± 0.01, the bulk density is 1.57 ± 0.01 g cm−3, which is close to the results of ~1.61 g cm−3 at the Apollo 15 landing area. The permittivity map is consistent with the radargram; the regolith and the paleo-regolith layer have relatively low permittivity and low echo strengths, while the rock debris has high permittivity and shows strong echos in the radargram. Two buried craters of different diameters beneath the navigation sites 4–11 and 16–31 are revealed in the radar profile. The permittivity distribution map can show detailed variations of material properties both inside and outside craters.
Key words: Moon / planets and satellites: surfaces / techniques: radar astronomy
© ESO 2022
1 Introduction
Most of the lunar surface is covered by a shallow layer of regolith that potentially carries the record of billions of years of surface modifications. The electromagnetic properties of the components in the lunar regolith control the propagation of the electromagnetic (EM) waves in the lunar substrate: a better understanding of these properties is key to a more reliable interpretation of remote sensing data, which in turn improves our understanding of the evolution of the Moon. The complex dielectric permittivity of the sub-surface of the Moon is determined largely by its bulk density and, chemically, by titanium abundances (Olhoeft & Strangway 1975; Strangway et al. 1977). Consequently, a correct estimation of the complex dielectric permittivity can be used to estimate these two properties.
Our understanding of the dielectric properties of the lunar soil comes mostly from remote sensing measurements and analysis of the samples returned by the Apollo missions. The relative permittivity (the real part of the complex dielectric permittivity) of the Surveyor regolith samples ranges from 2.4 to 3.7 and for the Luna samples from 1.7 to 4.4 (Carrier et al. 1991).
Higher frequency electromagnetic radar and radiometry measurements of the lunar surface have been made from Earth (Dewitt & Stodola 1949; Evans & Pettengill 1963; Keihm & Langseth 1975; Pettengill 1978; Marpaung & Lu 2016), a lunar orbit (Tyler & Howard 1973; Peeples et al. 1978; Sharpton & Head III 1982; Ono et al. 2009), and directly at the surface (Fang et al. 2014). Given the high resolution of the Ground Penetrating Radar (GPR) on board the lunar rover compared to the remote sensing methods, this represents a unique opportunity to derive a detailed sub-surface profile. On January 3 2019, China’s Chang’E-4 (CE-4) probe touched down at 177.5991°E, 45.4446°S in the south of the Von Kármán crater (diameter = ~186 km; central coordinates as 176.2°E, 44.4°S) located inside the ancient South Pole-Aitken (SPA) basin (Li et al. 2020). Subsequently, the Yutu-2 rover was assigned to a scientific exploration mission. The lunar penetrating radar (LPR) on board the rover provides an unprecedented opportunity to investigate substructures and dielectric properties of the lunar regolith on the far side of the Moon, which is inaccessible from Earth-based investigations.
The topography, morphology, and geochemistry of the region around the landing site have been studied in detail (Huang et al. 2018; Qiao et al. 2019; Guo et al. 2021); it is relatively flat with a minimal slope and populated by secondary craters, which form chains and clusters, as seen from high-resolution Kaguya and Lunar Reconnaissance Orbiter (LRO) images (Huang et al. 2018; Qiao et al. 2019). In addition, clearly detectable texture and lineations arranged in the NE-SW direction suggest that they may be formed by ejecta from the Finsen crater (Guo et al. 2021). Kaguya MI-derived elemental maps show that the materials at the landing site are dominated by low-titanium basalts, a composition akin to the Apollo 15 pigeonite basalts (Qiao et al. 2019; Guo et al. 2021).
Based on the estimation of the iron-titanium abundances at the landing area, the penetrating depth of the low-frequency channel could reach ~300–450 m (Zhang et al. 2020, 2021a; Lai et al. 2020; Yuan et al. 2021), depending on the permittivity value used for time-depth conversion. Compared to the low-frequency channel, the CE-4 LPR’s high-frequency channel has a high range resolution, which is suited to deriving fine stratigraphic substructures in more detail at shallow depths (~45 m) (Lai et al. 2019; Li et al. 2020; Zhang et al. 2021b; Zhou et al. 2021). The high-frequency results so far show the lunar regolith layer to be relatively thick, about ~12 m, with the dominant source of materials probably consisting of Finsen ejecta (Gou et al. 2019; Lin et al. 2020).
Lai et al. (2019); Dong et al. (2020a, b); Li & Zhang (2021); Song et al. (2021); Giannakis et al. (2021); Wang et al. (2021) calculated the dielectric permittivity value or its depth profiles at the landing site to derive other attributes, including bulk density and mineralogical abundances. Most studies use the hyperbola fitting method due to its simplicity and computational efficiency (Dong et al. 2020a,b; Lai et al. 2019; Song et al. 2021). Giannakis et al. (2021) improved the method by considering the permittivity as varying with depth, while Li & Zhang (2021) used the migration method and separated the diffraction from reflections to estimate the permittivity.
Although the hyperbola fitting method is widely used, it has drawbacks such as a high dependence on the signal-to-noise ratio (S/N) of the LPR signals, and the distributions of scatters. It is difficult to identify the hyperbolic structure at a depth where the S/N is low (Daniels 2004); consequently, the inverted permittivity values can carry relatively large errors. The derivation of permittivity distribution along the horizontal direction is also limited by the absence of a hyperbola shaped signal. The permittivity map obtained by (Dong et al. 2020b; Li & Zhang 2021; Song et al. 2021) was produced by interpolation based on a couple of sparse points. The resolution is too coarse to reveal the finer details, which are necessary for a reliable mapping of the geological stratigraphy. The sectional permittivity map in Giannakis et al. (2021) shows additional sub-layers within approximately the first 10 m of the regolith layer, but it does not provide the permittivity variation at deeper depths and across the horizontal plane.
To minimise the shortcomings of the traditional hyperbola-fitting methods and obtain a high-resolution permittivity map, we applied a new method that combines the F-K migration and the minimum entropy of the GPR signals to estimate the appropriate electromagnetic velocity of lunar materials. Then, we calculated a relative permittivity distribution map along the exploration path of the Yutu-2 rover with the highest resolution so far using the high frequency LPR data during the first 31 lunar days (Fig. 1). Furthermore, the permittivity map was used to derive the actual thickness of the sub-surface layers and the density variations of materials, and to improve the geologic understanding of the sub-surface stratigraphy.
2 Data
The GPR on board the Yutu-2 rover is a dual-frequency, carrier-free, time-domain imaging radar. A pair of monopoles operating at 40–80 MHz with central frequency of 60 MHz are adopted into the low-frequency system with a vertical resolution of 3.75 m in vacuum for the purpose of detecting the upper, shallow crust terrain. Another set of identical bow-tie antennas with central frequency of 450 MHz and a bandwidth of 500 MHz are utilised as the high-frequency system with a high range resolution of 0.3 m in vacuum to detect the shallow substructure and the thickness of the lunar soil (Fang et al. 2014). When combined, these complementary data sets offer the opportunity to investigate the lunar substrata to build a reliable geological profile (Su et al. 2014). Radar data are collected and stored track by track. Each trace of data contains the relative amplitude intensity of the radar signal and its corresponding description information. Here, we employed the high-frequency channel (500 MHz) data to study the shallow substructures and their dielectric properties. At the time of writing, the Yutu-2 rover has already travelled ~690 m during the first 31 lunar days, as shown in Fig. 1.
We first performed signal processing on the CH-2 LPR data, mainly involving the removal of duplicated data, denoising, dielectric loss and geometric diffusion compensation, bandpass filtering, zero-time adjustment, and Kirchhoff migration. The redundant data were generated when the rover stopped to perform other experiments and were removed accordingly. The background noise was removed to eliminate ringing noises showing as horizontal and periodic events (Kim et al. 2007). Band-pass filtering was applied to reduce the lower and the higher frequency noises. Dielectric loss and geometric diffusion compensation (gain) was applied to compensate for the amplitudes of the LPR echoes at depth. The Kirchhoff migration method was applied to focus the received radar echoes into their correct locations. Because the receiving antenna is turned on 28.203 ns earlier than the transmitting antenna, the timing lag of each data track was compensated for.
3 Method
3.1 Velocity Inversion Method
Migration refers to the movement from the observed data to their true spatial positions. In a typical B-scan profile, any scatterer shows up as a hyperbola because of the different travel times of the EM wave propagating from the scatterer to the receiver at different locations, as the antenna is moving along the scanning direction. Therefore, the primary purpose for migration on GPR B-scan profiles is to produce a sharp and distinct peak at the location of the object and a little significant structure elsewhere. In fact, a library of migration algorithms (Yilmaz 2001) has been primarily developed from seismic images, including the Kirchhoff migration method (Schneider 1978), finite-difference migration (French 1974), Stolt F-K migration (Stolt 1978), and Gazdag phase-shift migration (Gazdag 1978). Those methods make use of the wave equations to back-propagate the surface data to the scattering sub-terrain based on the exploding source model (Claerbout 1985).
The F-K migration has proven to be an effective method in seismic signal processing (Peters et al. 1994), as well as in GPR signal processing (Özdemir et al. 2014). It is worth mentioning some assumptions for the F-K migration; for example, GPRs are located near to the ground, the signal being processed is free of noise and clutters, the material is homogeneous, and the ground surface is flat. However, those assumptions are probably unreasonable in the detection process of the GPR. Antennas are always located at some height (e.g. 0.3 m for the high frequency GPR of the Yutu-2 rover). The resulting noise and clutter usually distort the shape of the hyperbola. The rough ground surface may introduce some random time-delays to GPR signals. Despite these potential problems, the F-K migration has proven to work well in GPR applications. Besides, one key advantage of F-K migration is that the Fourier transformation used in this method converts the differential operations in the time domain into algebraic operations, which can be quickly computed.
Velocity estimation is critical for the F-K migration. If the correct velocity distribution is used, the energy will be condensed into a few pixels for a point-like target. The location of these buried targets can be clearly recognised. A lower estimation will cause under-migration, and a higher estimation will cause over-migration.
Entropy is a measure of the information content of a signal (Pun 1980). Calculating the entropy of the GPR B-scan profile is an efficient way to estimate the velocity as the input of the F-K migration. In contrast to maximum entropy, which is associated with randomness or uncertainty, minimum entropy is an expression of simplicity or certainty. In terms of GPR B-scan profiles, the migrated images with the sharp and distinct peak at the location of the object have small entropies (Flores-Tapia & Pistorius 2010; Marpaung & Lu 2016). Therefore, minimising the entropy could be a way to find the accurate velocity. The minimum entropy deconvolution approach is used to minimise the inverse of the varimax norm to approximate the entropy of the seismic signals (Wiggins 1978; Wu & Barba 1998). This approach is widely used in obtaining a simple structured signal and has proven very successful in the deconvolution of seismic signals. Subsequently, Xu & Miller (2001) and Xu et al. (2003) combined minimum entropy image restoration with the F-K migration approach to accurately locate shallow sub-surface objects in GPR profiles. They determine the characteristics of the ‘focus’ using an entropy-like criterion, namely, the inverse of the varimax norm (Wiggins 1978) because of its ease of computation.
Our approach is as follows: for a measured GPR wave field P of size M × N, we first divide it into a certain number of sub-wave fields Pi of size Mi × Ni, where i is ith of sub-wave field, and the sub-wave fields Pi are a subset of the full radargram P. As the entropy value depends on the pixel intensity, we divide the whole image based on the electric field strength. The varimax norm R, defined as the sum of the normalized squares of the variances of the amplitude of signals, is an approximation of the inverse of entropy (Wiggins 1978); we use the varimax norm R as the criterion for judging the degree of focus in practical computation. There are two key considerations for selecting subwave field in the real detection of GPR data: The first is that one computational sub-wave field is generally chosen to be of a relatively uniform electric field strength, and the whole GPR profile is divided both in the distance (x) and time (t) directions. The second is for some special cases. There may be many scatterers under the lunar surface, such as small rocks or fractured breccia lens, underground slope terrain, or other geological units, causing noticeable hyperbolas and oblique echoes, and so on. In such cases, the computational sub-wave fields are selected as regions, including the complete hyperbolas and oblique echoes.
The procedure to obtain the velocity in each sub-wave field Pi is as follows: (1) set a reasonable material velocity set; (2) perform regular F-K migration at each velocity υi on the preprocessed data; (3) calculate varimax norm of each migration data R(Pi):
![$ R\left( {{P_i}} \right) = {\left[ {{{\sum\nolimits_{M = 1}^{{M_i}} {\sum\nolimits_{n = 1}^{{N_i}} {P_i^4\left( {m,n} \right)} } } \over {{{\left[ {\sum\nolimits_{M = 1}^{{M_i}} {\sum\nolimits_{n = 1}^{{N_i}} {P_i^2\left( {m,n} \right)} } } \right]}^2}}}} \right]^{ - 1}}; $](/articles/aa/full_html/2022/08/aa42677-21/aa42677-21-eq1.png) (1)
(1)
(4) search the appropriate root-mean-square (RMS) velocity vRMS corresponding to the minimum value of R(Pi)mn; (5) transform υRMS to the local velocity υıocaı using the Dix equation (Dix 1955) by:
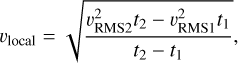 (2)
(2)
where υRMS(n) and t(n) are the RMS velocity and travel time of the nth sub-wave field.
After all sub-wave fields are processed following these steps, we obtain the whole local velocity distribution by interpolation.
The relative permittivity can then be calculated:
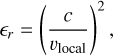 (3)
(3)
where c is the velocity in vacuum. The depth is calculated with the local velocity and corresponding propagation time. The depth di of the current sub-field Pi is determined by the local velocity υlocali, time interval ∆ti, and the depth di−1 of the previous sub-field Pi−1:
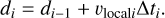 (4)
(4)
 |
Fig. 1 Routing path covered by the Yutu-2 rover on the Moon. (a) The base map is a Lunar Reconnaissance Orbiter (LRO) Narrow Angle Camera (NAC) image (File ID: M1314237625LR). (b) High-resolution NAC digital terrain model of CE-4 landing area. The red star marks the position of the CE-4 lander. The white line represents the traverse of the Yutu-2 rover, and the red points indicate the waypoints. The black circle outlines buried crater A, and the dashed circle shows buried crater B. |
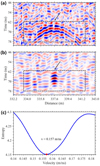 |
Fig. 2 Example with a hyperbola-shaped structure. (a) Classical hyperbola structure before migration. (b) Point-like structure after migration. (c) Variation of entropy with electromagnetic wave velocity in the material. |
3.2 Method Validation
We present an example of CH2 data with a classical hyperbola-shaped structure to verify the performance of our method, as shown in Fig. 2. This section of the echo is located at a shallow depth of ~46–81 ns in the vertical direction and ~332–343 m in the horizontal direction. A hyperbola with multiple reflections can be seen in the black box in Fig. 2a, whose vertices are pointed by a black arrow, illustrating the data before migration. This hyperbola echo was probably produced by a discrete scatterer (Daniels 2004). The hyperbola condenses into a series of point-like echo after migration processing, which is presented in Fig. 2b, indicating that the velocity calculated by our method is realistic. Figure 2c shows the variation of entropy with the electromagnetic wave velocities in the material. The minimum entropy is around 4.15, and its corresponding velocity is υ = 0.157 m ns−1; this velocity value will be used to calculate the local velocity and the actual depth.
Similarly, we use the same criterion to focus on other echoes with or without typical hyperbolic structures. Another example of waves without clear hyperbolic structures is shown in Fig. A.2, which is also used to illustrate the effectiveness of our method.
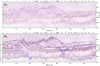 |
Fig. 3 Shallow sub-surface structure imaged by CH2 data during the first 31 lunar days. The colour bar represents the amplitude of the radar signals. The sites of 31 lunar days are indicated by the numbers at the top of the panel. (a) High-frequency LPR profile. (b) Interpreted stratification structure. Black dashed lines mark the boundary of the reflectors. The blue dashed lines indicate the fault plane, and the blue arrows represent the relative movement direction of the current layer. Black numbers represent the depth in metres varying with positions. On the left side of the figure, we show the division of the radar sub-surface structures: I, II, and III. |
4 Results
4.1 Stratigraphie Structure
The reflection intensity of the high-frequency GPR data after data processing including Kirchhoff migration is presented in Fig. 3, where the black dashed lines in Fig. 3b show the stratification, and the numbers indicate the depth value corresponding to the position of the dashed lines, which are generated using the proposed method. Two reflectors with the average depth of ~13.9 m and ~32.3 m are horizontally continuous through the routing path, and they can divide the sub-surface structure of the landing site into three geologic sub-layers: ~0–13.9 m (Layer I), ~13.9–32.3 m (Layer II), and ~32.3–38.1 m (Layer III), marked on the left side of Fig. 3b.
Reflections in the surface layer (the first layer within Layer I in Fig. 3) are relatively weak overall, with some slight fluctuations of stronger reflections. Surface materials have been pulverised into fine-grained particles by impacts (Melosh 2011) and space weathering processes (Pieters et al. 2000; Taylor et al. 2001), which may contain ejecta mostly from the neighbouring Finsen crater (Li et al. 2020; Huang et al. 2018; Hu et al. 2019; Gou et al. 2019). Moreover, some relatively strong signals with hyperbolic shape are probably produced by discrete scatterers (Daniels 2004). These scatterers were interpreted as ejecta rocks during the formation of Finsen crater, including an unknown fraction of local rocks. Another scenario is that these scatterers with relatively large permittivity in the regolith layer are probably broken pieces of glass-bearing breccia projectiles that were excavated from the consolidated bottom and walls of pre-existing small craters within the lunar regolith rather than from deeper hard igneous rocks (Lin et al. 2020). The thickness of the surface layer is ~5.7–15.6 m with an average depth of 11.8 m based on the permittivity value and the two-way time delay of the radar signals, our results are consistent with ~11.1 m from Wang et al. (2021).
The echoes become weaker at the bottom (~9–13 m) of this layer from the site that is 21st from the end, suggesting that the density of rocks and particle size in this local region are lower than those of the materials above. Between sites 16 and 22 in Fig. 3a, there is a well-defined and smooth down-slope reflection layer, which may represent a section of the crater wall of the buried impact crater. The Yutu-2 rover travelled close to a surface depression located to the southwest of the travel route, which is shown in the surface elevation map in Fig. 1b, the elevation values corresponding to each point are displayed in Fig. A.1. The reflector becomes flat between sites 22 and 31, where the Yutu-2 rover moved along the edge of the circular depression. This large depression southwest of the travel path is defined as Crater A, which is depicted as a solid black circle in Fig. 1b.
The first sub-surface reflector represents the lower interface of the fine-grained particles, which is located in the ~8–22 m range of the Finsen ejecta deposits, as estimated by ballistic sedimentation models (Huang et al. 2018; Xie et al. 2020; Xu et al. 2021). Beneath this fine-grained surface layer, there is a layer with stronger reflectance and upward slope from sites 1 to 16. The thickness of this coarse-grained layer varies widely from ~1.9 to ~7.3 m at different horizontal positions. The baseline of this reflector is also undulating; it stays generally unchanged at depths of ~17 m from C to D, fluctuates from ~12.8–16.1 m from D to E, and then goes up to the shallowest depth of ~5.7 m at F, and finally gradually falls down to the depth of ~13.8 m from G to the end (Fig. 3b). Point F might represent the rim of a buried crater. The materials with higher reflectivity in this layer are believed to be mostly a mixture of coarse-grained deposits both of Finsen primary ejecta and the ejecta of crater A (Fig. 1b). Since the surface layer and the underlying layer may have the same material source, we classify them as Layer I.
Layer II comprises at least four ejecta overlays and contains multiple reflectors from depths of ~13 to ~36 m. On the profile, these reflections’ layers are continuous overall, and the average thicknesses of each layer are ~5.89, ~2.33, ~2.36, ~8.41 m, and so on, respectively. Each deposited sub-layer is composed of two sub-stratigraphic regions. The upper part is relatively homogeneous and weak, because the surface material have undergone a longer period of weathering processes than the lower strata (Zhang et al. 2021b), while the lower part represents a larger reflectivity, since this part of material is distributed randomly and heterogeneously; it is thought to represent ejecta that are not completely weathered and that feature large rocks.
A small bowl-shaped crater below sites 4–11, named crater B, which was buried by the mixture of Finsen primary ejecta and local crater A ejecta deposits, disrupt the continuity of reflectors. The echoes inside the crater are chaotic and strong, while echoes outside are relatively weak. The crater A (~200 m in diameter) shown in Fig. 1b also disturbs the structure of the layered ejecta as seen in the right part of Fig. 3. For example, the upper two ejecta layers are mixed, and they blend into one as the rover moved from site 21 to the end. Impact-induced features such as faults and dislocations also appear under the crater wall. A V-shaped structure beneath sites 6–9, denoted by blue dashed lines in Fig. 3b, might represent a fault or fracture caused by the shockwave of the impact event. Similarly, there is another V-shaped structure below navigation points 20–22. We provide a zoomed-in picture of these two regional structures, as shown in Figs. 4 and 5, respectively.
We interpreted Layer II as the multiple deposited ejecta materials mixed with excavated local materials. These ejecta materials may come from several impact craters inside and outside Von Kármán crater, such as the Late Imbrian Maksutov and Early Imbrian Orientale Basin, and so on, and several unnamed local craters (Zhang et al. 2021b; Xu et al. 2021). Since the age of the neighbouring Alder crater is greater than the surface mare units (Lu et al. 2021), it might be excluded from the source. Also, the Copernican Zhinyu crater next to the CE-4 landing site (3.75 km in diameter) is too small to have formed a detectable ejecta layer at the CE-4 landing site.
Radar echoes in Layer III are weak and relatively homogeneous, and they are most likely caused by reflection or the scattering of grain particles, regarded as paleoregolith. The fine grain materials in this layer are probably subject to space weathering and frequent small impacts after mare filling events within Von Kármán. Below ~500 ns, no prominent radar features are detectable.
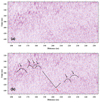 |
Fig. 4 ‘V’ structure at x ≈ 200 m. (a) Original radargram. (b) V structure and hyperbolas are marked by dashed lines and arrows. Red arrow points to the bottom of the V structure. |
 |
Fig. 5 ‘V’ structure at x ≈ 450 m. (a) Original radargram. (b) V structure and hyperbolas are depicted by dashed lines and arrows. The red arrow points to the bottom of the V structure. |
4.2 Dielectric Permittivity
The relative permittivity distribution estimated with the proposed method is illustrated in Fig. 6a, which is approximately in the 2.3–6.3 range. The resolution in the horizontal direction is in the range of ~10–50 m, and the one in the vertical direction is from 45 to 60 ns.
The relative permittivity of materials in the surface layer (the top layer within Layer I in Fig. 6) ranges from ~2.3 to ~3.7, indicating that the top surface materials have similar dielectric properties to the typical regolith (Carrier et al. 1991). The average permittivity in the shallow surface part (<30 cm) is ~2.78 ± 0.01, and the bulk density is ~1.57 ± 0.01 g cm−3, which is close to ~1.61 g cm−3 at the Apollo 15 landing area (Mitchell et al. 1972), supporting the observation that the surface materials are comparable with Apollo 15 basalts according to the elemental maps derived from MI data (Qiao et al. 2019). Based on the FeO and TiO2 abundances of 13.1 and 1.8 wt% (Guo et al. 2021), the rock density of the surface materials is estimated to be 2.78 g cm−3 (Huang & Wieczorek 2012), inferring a porosity of about 43.5% at the surface, a value somewhat smaller than the typical porosity of 45% (Fa & Wieczorek 2012). The layer with strong reflectivity beneath the regolith layer from site 1–21 exhibits a larger permittivity. Most of the values are approximately in the 2.9–4.6 range, but some are larger than ~5, or even reach up to ~5.6 inside the two white boxes b1 and b2, as shown in Fig. 6a.
Some irregular and abnormal scatterers are obviously observed at the regolith layer, the fine resolution permittivity map in Fig. 6a adds further detail compared to prior work. For instance, there are three regions of notably large values reaching ~3.5–3.7 indicated by three black arrows under the sites from 4 to 11, probably due to the buried scatterers. Although these abnormally large values also appear in Song et al. (2021), our results are in closer agreement with the positions of the scatterers.
The permittivity from site 21 to 31 of Layer I is lower than that in the upper regolith part, supporting the notion that the materials within Crater A are mainly composed of small particles (Rogers & Head 1961; Ogolo et al. 2015).
In Layer II, the unevenly distributed permittivity values have a wide range of fluctuations, varying from ~2.6 to ~6.3 along the route of the rover. Overall, the left (from site 1 to 5) and right parts (from site 12 to 31) are obviously larger than the middle part, as shown in Fig. 6a. These materials with higher permittivity values, similarly to the ones in the white box b3 in Fig. 6a, are local. The materials with small permittivity are considered to be paleoregolith or highly weathered ejecta with smaller particles, similarly to the ones in white box b4. Recurring regularly, each ejecta unit in Layer II is composed of two sub-layers: the weathering part overlying the coarse materials. For example, the permittivity in box b5 in Fig. 6a has a large value of ~5.8; this part of material is located in the lower part of the current deposits layer. A consistent value of ~5.6 in Dong et al. (2020b) is also shown in a similar region.
We collected four permittivity profiles varying with depths to highlight changes in the vertical direction, as shown in the white dashed lines P1–P4 in Fig. 6a. The horizontal positions of the profiles are at x = 60 m, x = 360 m, x = 450 m, and x = 600 m, respectively. The vertical distributions, shown in Figs. 6b–e, display a general trend with permittivity increasing with the depth and fitting well compared to Dong et al. (2020a) and Li & Zhang (2021) as show in Fig. 6b. In addition, the fine resolution distribution map also reveals obvious jitters in the depth profile caused by the multi-layered sub-surface structure.
At the bottom, the region where the permittivity values become smaller and more uniform than the upper layer is split into Layer III. Most of the values range from ~2.9 to ~4.6, and large values only appeared at boundary positions connected to the upper layer, which is influenced by ejecta materials. Due to the compaction of the material, the density of material in Layer III becomes greater than that in the regolith layer, with a relatively larger permittivity.
Our methodology has the advantage that the appropriate velocity can be efficiently obtained even if the hyperbolic curves are incomplete or unnoticeable. In a sub-field image with a hyperbolic structure, its tailing will converge to a point through migration in terms of the appropriate velocity, and thus the image has the smallest entropy. Similarly, after migration with the appropriate velocity, profiles without noticeable hyperbolic structures have minimum entropy. Thus, the whole permittivity profile obtained by our method offers greater detail and is useful for the interpretation of the radar profile.
 |
Fig. 6 Permittivity distribution determined by the CH2 data during the first 31 lunar days. The colour bar represents the relative permittivity values. The sites of 31 lunar days are indicated by the numbers at the top of the panel. (a) Permittivity distribution calculated by our method, where black dashed lines depict the boundary of the reflectors, and white dashed lines P1–P4 show the positions of permittivity profiles of the four vertical distribution in b−e. b−e Detailed permittivity varying with depths at a single horizontal position, located at x = 60, 360, 450, and 600 m, respectively. The grey horizontal dashed lines in b−e are the time values of the intersections between the four profiles (P1–P4) and reflector boundaries shown in a. The comparison of permittivity with Dong et al. (2020b) and Li & Zhang (2021) at x = 60 m, as shown in b. |
 |
Fig. 7 Radargram, relative permittivity, and absolute depths of the crater B. (a) Radar profile of crater B. The colour bar represents the amplitude of the radar signals. Black dashed lines show the outlines of layered structures and crater B, and discrete scatterers. Blue arrows point to a sharp reflection. (b) Permittivity varied with depth at x = 220 m. (c) Permittivity varied with horizontal distance at three time delays (blue, red and yellow line) in a; the time delays are at t = 210 ns, t = 240 ns, and t = 270 ns, respectively. (d) Absolute depths of the outline of crater B and its error bar (blue shaded area). |
5 Discussion
With the estimated fine-resolution permittivity map and the migrated radargram, detailed structures and variations of material properties of the two buried craters can be unveiled. The bowl-shaped degraded crater B is below the navigation sites from 4 to 11, and its rough boundaries are traced by dashed lines, as shown in Fig. 7a. The reflectance inside the crater is chaotic and greater than that in the regolith layer, while the reflectance outside the crater, especially on the right side, is relatively weaker. There are also some obvious hyperbolic structures inside the radar feature, marked by short dashed lines.
The permittivity in crater B and surrounding materials is shown in Fig. 6a. It ranges from ~3.4 to ~5.8 inside the crater and becomes smaller on its two sides, reaching maximum values in the middle of the crater. The changing trend of permittivity values with depth at the horizontal position of x = 220 m is illustrated in Fig. 7b, and these values are extracted from the permittivity map. The permittivity remains small between ~2.7 and 3.4 at first, and then it increases rapidly starting from ~150 ns and reaches the maximum value of ~5.6 at ~210 ns; finally, it quickly drops to a lower value of ~3–3.9 from ~210 ns to the end. Horizontally, the changing trend at different depths is shown in Fig. 7c. The two grey dashed lines are the horizontal positions of the intersections of the blue line and the crater wall in Fig. 7a. Correspondingly, inside the crater, the larger the permittivity values at the three depths (t = 210 ns, t = 240 ns, t = 270 ns), the greater the reflectance (Fig. 7a). Based on the permittivity, the depth of the boundary of crater B is shown in Fig. 7d. The blue line is the average depth of the boundary, and the shaded area indicates the error bar. The diameter of the crater seen in radar profile is D ~ 115 ± 5 m, and its bottom depth is d ~ 25.75 ± 0.95 m.
The materials inside crater B with strong reflectance and large permittivity are likely to contain sections of breccia lenses, which were formed by the impact process. After the formation of its transient crater, the brecciated and fractured walls of the cavity and the elevated rim area become highly unstable and collapse inward, partially infilling the crater with lenses of brecciated materials (Heiken et al. 1991). The depth of the crater is deeper than the ~19.55 ± 0.85 m predicted by applying a standard depth-to-diameter ratio of 0.17 for fresh small craters (Stopar et al. 2017). The difference (~6.0 m) between the bottom depth and the apparent depth is smaller than the theoretical range of thickness (~6.5–9.8 m) calculated using the same diameter, which is typically 1/2 to 1/3 of the apparent depth of a simple crater (Melosh 2011). Evidently, this part of the breccia lens represents only a sub-section of the entire structure. This is in accordance with the fact that the rover most probably did not cross its centre. A line of very sharp and obvious reflections is highlighted by a series of blue arrows in the left rim of this crater, as shown in Fig. 7a. The permittivity of this reflection is as high as 5.1, which may represent breccia or a melt formed by the impact.
The big depression in the right part of Fig. 3 (starting from the 16th day) is likely to represent an underground expression of crater profile A on the DEM map (Fig. 1b) (Lai et al. 2021). The downslope reflected layer from F to G in Fig. 3b may represent a section of the crater wall of the buried impact crater. Three continuous reflectors may depict the profile of this crater from G towards the end, which are denoted as L1, L2, and L3 in Fig. 3b, respectively. The correlation coefficient between the distance from the rover to the centre of crater A and the elevation of layer L1 is 0.68 between site 23 and 29, greater than layer L2 and L3 as shown in Fig. 3b, indicating that layer L1 may represent the cross-section of the impact crater A (Fig. 1b) and no other large-scale impact ejecta was deposited around the area between the formation of Finsen and this impact crater. At the same time, part of the ejecta materials from crater A would be deposited in the area, shown on the left in Fig. 6. They would be mixed with Finsen ejecta, and even add to the materials inside the small crater B. Hence, the materials inside the small crater B (Fig. 7a) are probably a mixture of a breccia lens and the ejecta deposits from Finsen and crater A.
Not only were the relative shallow echoes affected by the impact, the upper two layers merge together into one from site 21 to 31, encompassing the deeper echoes. A continuous horizontal echo line with strong reflection at deeper depths is highlighted by red arrows in Fig. 3b, and it may be caused by the squeezing of the shock waves generated during the formation of this impact. The materials in this location with high permittivity value of ~5.5 ± 0.5 may represent impact melts or a breccia lens produced by the impact. Along sites 30–31, the echoes grow slightly stronger as the rover moves farther away from the centre of crater A (Fig. 1b). These rising underground echoes may be affected by both this large crater and the irregular depression (width ≈ 300 m) in the northwest direction of the path, as from Fig. 1b. Therefore, in addition to autochthonous ejecta, the modification of the surface and topography of the Chang’E-4 landing area also includes this autochthonous ejecta, such as the deposits from this large crater or from the northwest depression.
6 Conclusions
The sub-surface stratification of the CE-4 landing area is seen in the first 31 lunar days of LPR data. To aid in the interpretation of geological processes, we applied an effective velocity estimation method to obtain a fine resolution permittivity profile of the shallow sub-surface structure. The method has the advantage that the appropriate velocity can be efficiently obtained whether the waves are with or without significant diffraction structures; further, the high-resolution dielectric permittivity map and actual depths can be calculated by the velocities.
The shallowest surface layer is represented by the regolith layer, with an average thickness of ~11.8 m and a dielectric constant between ~2.3 and 3.7. The top surface part (<30 cm) is ~2.78 on average, and the corresponding surface bulk density is ~1.57 g cm−3, indicating that the surface material is consistent with the Apollo 15 landing site. There are multiple horizontally continuous sub-layers with different thicknesses in Layer II, each ejecta unit comprising two sub-layers: a weathered part overlying coarser materials. This layering phenomenon is also shown in our fine permittivity map.
Two buried craters of different sizes beneath sites 4–11 (crater B) and 21–31 (crater A) have come to light through the radargram, with their permittivity values firstly calculated in our permittivity map. The relative permittivity inside crater B is as large as 3.4–5.8. We interpret the data as showing the materials inside crater B to include not only the breccia lens as it formed, in addition to Finsen ejecta, but also ejecta from local craters, such as those from the larger crater A. A segment of the radar profiles (L1) with an average depth of ~17 m may represent the cross-section of the impact crater A. As for the echoes climbing slightly as the rover moved farther away from the centre of crater A, the modification of the surface and topography of the Chang’E-4 landing area probably includes this autochthonous ejecta, such as the deposits from crater A or from the northwestern depression. The influence of the northwestern depression on the radar echoes is worth further study in future work.
Acknowledgements
The Chang’E-4 data used in this work is processed and produced by the Ground Research and Application System (GRAS) of China’s Lunar and Planetary Exploration Program can be downloaded from https://moon.bao.ac.cn/web/enmanager/home. This work is supported by the Science and Technology Development Fund of Macau (0089/2018/A3, 0042/2018/A2, 0049/2020/A1).
Appendix A Processing flow of high-frequency data of LPR
The main procedures of data processing of the high-frequency data are as follows.
The first step is to remove duplicated data. As the raw data of each lunar day are stored in PDS files in different segments separately, it is necessary to merge them to represent all 31 lunar day data as a B-scan profile. There are many redundant echoes reaching the LPR receivers at the same position when the rover stops moving, and needed to be removed.
The second step is Denoising. Ringing usually appears as horizontal and periodic events and is a common type of coherent noise in a GPR profile. In order to eliminate these ringing noises, we subtracted the horizontal average signal at each A-scan trace.
The third step is gain. The amplitude of electromagnetic waves will attenuate during the propagation in the materials, mainly due to the following reasons: dielectric loss and geometric diffusion. As the depth increases, the amplitude of the signals becomes smaller. Therefore, we need to highlight them by gain compensation to make them easier to analyse. It is worth noting that both signals and noise are amplified at the same time.
The fourth step is band-pass filtering. The bandwidth of transmitted signals of high frequency data is from 250 MHz to 750 MHz. However, the received signals have noise at other frequencies. Moreover, the actual bandwidth of the received signals is lower than the nominal parameters. Through spectrum analysis, we choose the band-pass filter with a frequency range of 150–650 MHz.
The fifth step is time-lag adjustment. The receiver is operated 28.203 ns earlier than the transmitter. Invalid data collected during this period should be removed.
The final step is Kirchhoff Migration. The migration method for imaging used in this paper is the Kirchhoff migration. We use the amplitudes of the electric field E(z = 0) of the received signals to calculate the depth of zA in Eq. (A.1):
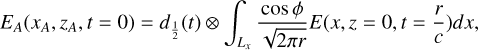 (A.1)
(A.1)
where ϕ is the view angle of the target, r is the distance from the antennas to the hyperbolic curves.
 |
Fig. A.1 Routing path of Yutu-2 rover and the surface elevation values for each site. (a) Path of Yutu-2 with elevation values at each site. (b) Elevation values profile read from LPR data. |
IDs of LPR CH-2 data.
 |
Fig. A.2 Example of waves without significant diffraction. (a) Area of fields with non-obvious diffraction but reflection. (b) Horizontal reflector after migration depicted by a set of black arrows in the black rectangle. (c) Variation of entropy with electromagnetic wave velocity in the material. |
References
- Carrier, W. D., Olhoeft, G. R., & Mendell, W. 1991, Lunar Sourcebook: A User’s Guide to the Moon (Cambridge: Cambridge University Press), 530 [Google Scholar]
- Claerbout, J. F. 1985, Imaging the Earth’s Interior (Hoboken: Blackwell scientific publications Oxford), 1 [Google Scholar]
- Daniels, D. J. 2004, Ground Penetrating Radar (London, UK: The Institution of Engineering and Technology) [CrossRef] [Google Scholar]
- Dewitt, J., & Stodola, E. 1949, Proceedings of the IRE, 37, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Dix, C. H. 1955, Geophysics, 20, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, Z., Fang, G., Zhao, D., et al. 2020a, Geophys. Res. Lett., 47, e2020GL089264 [NASA ADS] [Google Scholar]
- Dong, Z., Feng, X., Zhou, H., et al. 2020b, Remote Sens., 12, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, J. V., & Pettengill, G. H. 1963, J. Geophys. Res., 68, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Fa, W., & Wieczorek, M. A. 2012, Icarus, 218, 771 [CrossRef] [Google Scholar]
- Fang, G.-Y., Zhou, B., Ji, Y.-C., et al. 2014, Res. Astron. Astrophys., 14, 1607 [CrossRef] [Google Scholar]
- Flores-Tapia, D., & Pistorius, S. 2010, EURASIP J. Adv. Signal Process., 2010, 1 [CrossRef] [Google Scholar]
- French, W. S. 1974, Geophysics, 39, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Gazdag, J. 1978, Geophysics, 43, 1342 [NASA ADS] [CrossRef] [Google Scholar]
- Giannakis, I., Zhou, F., Warren, C., & Giannopoulos, A. 2021, Geophys. Res. Lett., 48, e2021GL092866 [CrossRef] [Google Scholar]
- Gou, S., Di, K., Yue, Z., et al. 2019, Earth Planet. Sci. Lett., 528, 115829 [CrossRef] [Google Scholar]
- Guo, D., Fa, W., Zeng, X., Du, J., & Liu, J. 2021, Icarus, 359, 114327 [CrossRef] [Google Scholar]
- Heiken, G. H., Vaniman, D. T., & French, B. M. 1991, Lunar Sourcebook, a User’s Guide to the Moon (Cambridge: Cambridge University Press) [Google Scholar]
- Hu, X., Ma, P., Yang, Y., et al. 2019, Geophys. Res. Lett., 46, 9439 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Q., & Wieczorek, M. A. 2012, J. Geophys. Res. Planets, 117, E05003 [CrossRef] [Google Scholar]
- Huang, J., Xiao, Z., Flahaut, J., et al. 2018, J. Geophys. Res. Planets, 123, 1684 [NASA ADS] [CrossRef] [Google Scholar]
- Keihm, S. J., & Langseth, M. G. 1975, Icarus, 24, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-H., Cho, S.-J., & Yi, M.-J. 2007, Geosci. J., 11, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, J., Xu, Y., Bugiolacchi, R., et al. 2020, Nat. Commun., 11, 1 [CrossRef] [Google Scholar]
- Lai, J., Xu, Y., Bugiolacchi, R., et al. 2021, Geophys. Res. Lett., 48, e2021GL095133 [Google Scholar]
- Lai, J., Xu, Y., Zhang, X., et al. 2019, Geophys. Res. Lett., 46, 12783 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., & Zhang, J. 2021, Remote Sens., 13, 4542 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Su, Y., Pettinelli, E., et al. 2020, Sci. Adv., 6, 6898 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H., Lin, Y., Yang, W., et al. 2020, Geophys. Res. Lett., 47, e2020GL087949 [Google Scholar]
- Lu, Y., Wu, Y., Michael, G. G., et al. 2021, Icarus, 354, 114086 [NASA ADS] [CrossRef] [Google Scholar]
- Marpaung, D. H. N., & Lu, Y. 2016, IEEE Geosci. Remote Sens. Lett., 13, 661 [CrossRef] [Google Scholar]
- Melosh, H. J. 2011, Planetary Surface Processes, (Cambridge: Cambridge University Press), 13 [Google Scholar]
- Mitchell, J., Houston, W., Scott, R., et al. 1972, Lunar Planet. Sci. Conf. Proc., 3, 3235 [Google Scholar]
- Ogolo, N. A., Akinboro, O. G., Inam, J. E., Akpokere, F. E., & Onyekonwu, M. O. 2015, in SPE Nigeria annual international conference and exhibition, OnePetro [Google Scholar]
- Olhoeft, G., & Strangway, D. 1975, Earth Planet. Sci. Lett., 24, 394 [CrossRef] [Google Scholar]
- Ono, T., Kumamoto, A., Nakagawa, H., et al. 2009, Science, 323, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Özdemir, C., Demirci, S., Yigit, E., & Yilmaz, B. 2014, Math. Problems Eng., 2014, 1 [Google Scholar]
- Peeples, W. J., Sill, W. R., May, T. W., et al. 1978, J. Geophys. Res. Solid Earth, 83, 3459 [CrossRef] [Google Scholar]
- Peters, L., Daniels, J., & Young, J. 1994, Proc. IEEE, 82, 1802 [CrossRef] [Google Scholar]
- Pettengill, G. H. 1978, Ann. Rev. Astron. Astrophys., 16, 265 [CrossRef] [Google Scholar]
- Pieters, C. M., Taylor, L. A., Noble, S. K., et al. 2000, Meteor. Planet. Sci., 35, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Pun, T. 1980, Signal Process., 2, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Qiao, L., Ling, Z., Fu, X., & Li, B. 2019, Icarus, 333, 37 [CrossRef] [Google Scholar]
- Rogers, J. J., & Head, W. B. 1961, J. Sediment. Res., 31, 467 [Google Scholar]
- Schneider, W. A. 1978, Geophysics, 43, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Sharpton, V. L., & Head, J. W. III 1982, J. Geophys. Res. Solid Earth, 87, 10983 [NASA ADS] [CrossRef] [Google Scholar]
- Song, H., Li, C., Zhang, J., et al. 2021, Remote Sens, 13 [Google Scholar]
- Stolt, R. H. 1978, Geophysics, 43, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Stopar, J. D., Robinson, M. S., Barnouin, O. S., et al. 2017, Icarus, 298, 34 [CrossRef] [Google Scholar]
- Strangway, D. W., Olhoeft, G. R., Massey, H. S. W., et al. 1977, Philos. Trans. R. Soc. London. Ser. A, Math. Phys. Sci., 285, 441 [Google Scholar]
- Su, Y., Fang, G.-Y., Feng, J.-Q., et al. 2014, Res. Astron. Astrophys., 14, 1623 [CrossRef] [Google Scholar]
- Taylor, L. A., Pieters, C. M., Keller, L. P., Morris, R. V., & McKay, D. S. 2001, J. Geophys. Res. Planets, 106, 27985 [NASA ADS] [CrossRef] [Google Scholar]
- Tyler, G. L., & Howard, H. T. 1973, J. Geophys. Res., 78, 4852 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, R., Su, Y., Ding, C., et al. 2021, Remote Sens., 13, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Wiggins, R. A. 1978, Geoexploration, 16, 21 [CrossRef] [Google Scholar]
- Wu, H.-S., & Barba, J. 1998, IEEE Trans. Syst. Man, Cybernetics, Part B, 28, 227 [CrossRef] [Google Scholar]
- Xie, M., Liu, T., & Xu, A. 2020, J. Geophys. Res. Planets, 125, e2019JE006113 [Google Scholar]
- Xu, X., & Miller, E. L. 2001, SPIE, 4394, 742 [NASA ADS] [Google Scholar]
- Xu, X., Miller, E., & Rappaport, C. 2003, IEEE Trans. Geosci. Remote Sens., 41, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L., Zhang, X., Qiao, L., & Jialong. 2021, AJ, 162, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yilmaz, Ö. 2001, Seismic data analysis: Processing, inversion, and interpretation of seismic data (Society of exploration geophysicists) [CrossRef] [Google Scholar]
- Yuan, Y., Zhu, P., Xiao, L., et al. 2021, Earth Planet. Sci. Lett., 569, 117062 [CrossRef] [Google Scholar]
- Zhang, L., Li, J., Zeng, Z., et al. 2020, Geophys. Res. Lett., 47, e2020GL088680 [Google Scholar]
- Zhang, J., Zhou, B., Lin, Y., et al. 2021a, Nat. Astron., 5, 25 [CrossRef] [Google Scholar]
- Zhang, L., Xu, Y., Bugiolacchi, R., et al. 2021b, Earth Planet. Sci. Lett., 564, 116912 [CrossRef] [Google Scholar]
- Zhou, H., Feng, X., Ding, C., et al. 2021, IEEE Trans. Geosci. Remote Sens., 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Routing path covered by the Yutu-2 rover on the Moon. (a) The base map is a Lunar Reconnaissance Orbiter (LRO) Narrow Angle Camera (NAC) image (File ID: M1314237625LR). (b) High-resolution NAC digital terrain model of CE-4 landing area. The red star marks the position of the CE-4 lander. The white line represents the traverse of the Yutu-2 rover, and the red points indicate the waypoints. The black circle outlines buried crater A, and the dashed circle shows buried crater B. |
| In the text | |
 |
Fig. 2 Example with a hyperbola-shaped structure. (a) Classical hyperbola structure before migration. (b) Point-like structure after migration. (c) Variation of entropy with electromagnetic wave velocity in the material. |
| In the text | |
 |
Fig. 3 Shallow sub-surface structure imaged by CH2 data during the first 31 lunar days. The colour bar represents the amplitude of the radar signals. The sites of 31 lunar days are indicated by the numbers at the top of the panel. (a) High-frequency LPR profile. (b) Interpreted stratification structure. Black dashed lines mark the boundary of the reflectors. The blue dashed lines indicate the fault plane, and the blue arrows represent the relative movement direction of the current layer. Black numbers represent the depth in metres varying with positions. On the left side of the figure, we show the division of the radar sub-surface structures: I, II, and III. |
| In the text | |
 |
Fig. 4 ‘V’ structure at x ≈ 200 m. (a) Original radargram. (b) V structure and hyperbolas are marked by dashed lines and arrows. Red arrow points to the bottom of the V structure. |
| In the text | |
 |
Fig. 5 ‘V’ structure at x ≈ 450 m. (a) Original radargram. (b) V structure and hyperbolas are depicted by dashed lines and arrows. The red arrow points to the bottom of the V structure. |
| In the text | |
 |
Fig. 6 Permittivity distribution determined by the CH2 data during the first 31 lunar days. The colour bar represents the relative permittivity values. The sites of 31 lunar days are indicated by the numbers at the top of the panel. (a) Permittivity distribution calculated by our method, where black dashed lines depict the boundary of the reflectors, and white dashed lines P1–P4 show the positions of permittivity profiles of the four vertical distribution in b−e. b−e Detailed permittivity varying with depths at a single horizontal position, located at x = 60, 360, 450, and 600 m, respectively. The grey horizontal dashed lines in b−e are the time values of the intersections between the four profiles (P1–P4) and reflector boundaries shown in a. The comparison of permittivity with Dong et al. (2020b) and Li & Zhang (2021) at x = 60 m, as shown in b. |
| In the text | |
 |
Fig. 7 Radargram, relative permittivity, and absolute depths of the crater B. (a) Radar profile of crater B. The colour bar represents the amplitude of the radar signals. Black dashed lines show the outlines of layered structures and crater B, and discrete scatterers. Blue arrows point to a sharp reflection. (b) Permittivity varied with depth at x = 220 m. (c) Permittivity varied with horizontal distance at three time delays (blue, red and yellow line) in a; the time delays are at t = 210 ns, t = 240 ns, and t = 270 ns, respectively. (d) Absolute depths of the outline of crater B and its error bar (blue shaded area). |
| In the text | |
 |
Fig. A.1 Routing path of Yutu-2 rover and the surface elevation values for each site. (a) Path of Yutu-2 with elevation values at each site. (b) Elevation values profile read from LPR data. |
| In the text | |
 |
Fig. A.2 Example of waves without significant diffraction. (a) Area of fields with non-obvious diffraction but reflection. (b) Horizontal reflector after migration depicted by a set of black arrows in the black rectangle. (c) Variation of entropy with electromagnetic wave velocity in the material. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


