| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202142715 | |
| Published online | 04 July 2022 | |
Fink: Early supernovae Ia classification using active learning
1
Université Paris-Saclay, CNRS/IN2P3, IJCLab,
91405
Orsay,
France
e-mail: leoni@lal.in2p3.fr
2
LPC, Université Clermont Auvergne, CNRS/IN2P3,
63000
Clermont-Ferrand,
France
e-mail: emille.ishida@clermont.in2p3.fr
3
Centre for Astrophysics and Supercomputing, Swinburne University of Technology,
Mail Number H29, PO Box 218,
31122
Hawthorn, VIC,
Australia
Received:
22
November
2021
Accepted:
14
April
2022
Context. The Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST) will produce a continuous stream of alerts made of varying sources in the sky. This data flow will be publicly advertised and distributed to scientists via broker systems such as FINK, whose task is to extract scientific information from the stream. Given the complexity and volume of the data to be generated, LSST is a prime target for machine learning (ML) techniques. One of the most challenging stages of this task is the construction of appropriate training samples which enable learning based on a limited number of spectroscopically confirmed objects.
Aims. We describe how the FINK broker early supernova Ia (SN Ia) classifier optimizes its ML classifications by employing an active learning (AL) strategy. We demonstrate the feasibility of implementing such strategies in the current Zwicky Transient Facility (ZTF) public alert data stream.
Methods. We compared the performance of two AL strategies: uncertainty sampling and random sampling. Our pipeline consists of three stages: feature extraction, classification, and learning strategy. Starting from an initial sample of ten alerts, including five SNe Ia and five non-Ia, we let the algorithm identify which alert should be added to the training sample. The system was allowed to evolve through 300 iterations.
Results. Our data set consists of 23 840 alerts from ZTF with a confirmed classification via a crossmatch with the SIMBAD database and the Transient Name Server (TNS), 1600 of which were SNe Ia (1021 unique objects). After the learning cycle was completed, the data configuration consisted of 310 alerts for training and 23 530 for testing. Averaging over 100 realizations, the classifier achieved ~89% purity and ~54% efficiency. From 01 November 2020 to 31 October 2021 FINK applied its early SN Ia module to the ZTF stream and communicated promising SN Ia candidates to the TNS. From the 535 spectroscopically classified FINK candidates, 459 (86%) were proven to be SNe Ia.
Conclusions. Our results confirm the effectiveness of AL strategies for guiding the construction of optimal training samples for astronomical classifiers. It demonstrates in real data that the performance of learning algorithms can be highly improved without the need of extra computational resources or overwhelmingly large training samples. This is, to our knowledge, the first application of AL to real alert data.
Key words: methods: data analysis / supernovae: general / methods: statistical
© M. Leoni et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Once large-scale photometric astronomical surveys successfully overcome the challenge of data acquisition, the next obstacle in the path for scientific exploration is to identify interesting candidates. This is especially important for researchers working on transient astronomy, where there is a window of opportunity when a potentially interesting target can be spectroscopically followed before becoming too dim to allow useful scrutiny. Depending on the specific astronomical target under investigation, this window can be as short as a few minutes.
Current surveys, such as the Zwicky Transient Facility1 (ZTF), publicly advertise detected candidates through an alert data stream distributed to community brokers, whose task is to filter and process as well as to redistribute interesting candidates with added values to the astronomical community. A similar protocol will also be adopted by the upcoming Vera C. Rubin Observatory Legacy Survey of Space and Time2 (LSST). However, due to the large data volume expected from LSST, only seven full copies of the stream will be distributed. The recently selected LSST brokers are ALERCE (Förster et al. 2021), AMPEL (Nordin et al. 2019), BABAMUL, ANTARES (Narayan et al. 2018), FINK3 (Möller et al. 2021), LASAIR (Smith et al. 2019), and PITT-GOOGLE.
The FINK broker is being developed by an international community of researchers with a large variety of scientific interests, including multimessenger astronomy, supernovae (SNe), solar system, anomaly detection, micro-lensing, gamma-ray bursts’ optical counterparts, among others. It is currently processing and classifying alerts from ZTF as a test bed for Rubin operations. In this work, we give a detailed description of the early SN Ia classifier currently operating within FINK.
The module uses an active learning (AL) strategy to select an optimum set of alerts which is subsequently used as a training sample for a random forest classifier. The basic idea of AL is to allow the algorithm to identify which alerts should be labeled and included in the training set, according to their potential at improving the classifier. This philosophy is at the core of many of the recommendation systems currently in place, from pharmaceutical studies (Spjuth et al. 2021) to urban planning (Abernethy et al. 2018). In astronomy, it has proven to be effective in a few different scenarios (e.g., Solorio et al. 2005; Richards et al. 2012; Vilalta et al. 2017; Walmsley et al. 2020), including the classification of astronomical transients (e.g., Ishida et al. 2019; Kennamer et al. 2020) and anomaly detection (Ishida et al. 2021).
The remaining sections of this paper are organized as follows: Sect. 2 describes the construction of our data set. Section 3 describes all of the stages of our methodology, including filtering (Sect. 3.1), feature extraction (Sect. 3.2), classifier (Sect. 3.3), learning strategy (Sect. 3.4), and evaluation metrics (Sect. 3.5). We show our results in Sect. 4 and discuss their implications and future plans for FINK in Sect. 6.
2 Data
Our starting point was a data set containing all public alerts from the ZTF survey from November 2019 to March 2020 with confirmed classifications available through the SIMBAD catalog (Wenger et al. 2000) or Transient Name Server4 (TNS) database. TNS classified objects are spectroscopically confirmed while SIMBAD contains highly curated labels from both spectroscopic and photometric surveys (Loup et al. 2019), with the majority of its classifications taking spectroscopic redshift measurements into account (CDS, private communication). Each alert contains the last 30 days of history of photometric measurements for a given point in the sky. From the SIMBAD data set, this amounts to 5 004 378 alerts corresponding to 1 313 3715 objects, with dominant classes being RRLyr (≈26%), eclipsing binaries (≈22%), and stars (≈19%). From the TNS data, there were 11 422 alerts corresponding to 11 329 objects, dominated by SNIa (52%) and SNII (19%).
From the TNS set, all alerts were used. Our experiments showed that including around five or six times the same number of alerts with a SIMBAD classification was enough to construct an informative training sample. Using a larger number of SIMBAD sources does not affect the main results of a binary classification study as the one presented here. In order to be conservative while not overusing computer resources, we randomly selected 75 000 alerts, corresponding to 41 076 objects6. In what follows, this combined set is referred to as raw data.
We used the photometric information contained in alerts, regarding ZTF broad-band filters [g, r], retrieved through the FINK API7. According to the FINK schema, these correspond to the alert id (candid), the time of observation in Julian dates (jd), the magnitude from PSF-fit photometry (magpsf), the error in magnitude (sigmapsf), and the ZTF filter (fid) as well as their TNS (TNS) and SIMBAD (cdsxmatch) associated classes. In order to avoid classification errors between the Ia and nonIa classes, we did not use SN from Simbad. Thus all SN used in this work are spectroscopically classified objects from TNS. The full raw data set consisted of 86 422 alerts, corresponding to 52 405 unique sources.
Table 1 shows the population of classes within this data set. Alerts possessing a SIMBAD crossmatch were divided into three categories (star, multiple_objects8, and AGN-like following SIMBAD’s classification scheme9,10. Those associated with SNe (not Ia) were allocated in the other_SN category, while all SN Ia are reported under the SNIa class (it comprises SN Ia, SN Ia-91T-like, SN Ia-91bg-like, SN Ia-CSM, SN Ia-pec, and SN Iax/02cx-like). Additional transients whose classification was provided via TNS were grouped under the other_TNS class, including cataclismic variable stars, TDEs, among others. We made this raw data set publicly available, along with the necessary code to reproduce the results in this paper, through Zenodo11.
Population types in our alert data set before and after feature extraction.
3 Methodology
We adapted the AL approach presented in Ishida et al. (2019) to optimize the construction of an effective training sample. Starting from their basic template pipeline of feature extraction, classification, and learning strategies, we performed a few adaptations to accommodate the higher complexity intrinsic to real data sets.
Since we are mostly interested in early classification (identifying SN Ia before they reach maximum brightness), we began by selecting only epochs corresponding to the rising part of the light curve (Sect. 3.1). Subsequently, we developed a feature extraction method based on a sigmoid function (Sect. 3.2) which requires at least three observed epochs per filter, which is less than the minimum of five observations needed to fit the parametric function used in Ishida et al. (2019). The numbers and percentages of each subclass surviving this preprocessing are shown in Table 1 and Fig. 1.
3.1 Filtering
In order to isolate the alerts depicting light curves on the rise, we treated each filter separately. An exponentially weighted moving average with a window of four points was performed, and its derivative (i.e., forward finite difference) was calculated. Epochs corresponding to a negative derivative were discarded. This process ensures that at least three points are on the rise, as one point will serve as the comparison baseline for the finite difference.
This procedure is successful in masking out the declining part of the light curve for transient events; however, it can fail to grasp details of periodic or oscillatory light curves (examples of outcomes from this filtering process are shown in Fig. 2 and the corresponding best-fit parameter values are shown in Appendix A). Nevertheless, it proved to be successful in filtering enough information to allow SN-like events to populate a specific area of the parameter space when combined with the feature extraction procedure described in Sect. 3.2.
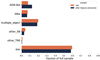 |
Fig. 1 Fraction of each class within the original data set before processing (orange) and the sample surviving feature extraction (blue). Numerical values are shown in Table 1. |
3.2 Feature extraction
All surviving epochs were converted from ZTF magnitudes m and magnitude error ∆m into SNANA12 (Kessler et al. 2009) flux units, f and its corresponding error ∆f derived by the chain rule,
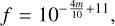 (1)
(1)
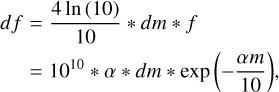 (2)
(2)
with α = 4 × ln 10 ~9.21034. Subsequently, observations in each filter were independently submitted to a sigmoid fit S at a given time ti,
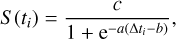 (3)
(3)
where ∆ti = ti – min(t) is the observation time of the ith data point since first detection. Employing a least square minimization routine and initialization values a0, b0, and c0 defined by
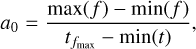 (4)
(4)
![${b_0} = {1 \over {{a_0}}}\log \left[{{{{c_0}} \over {\min \left(f \right) - 1}}} \right],$](/articles/aa/full_html/2022/07/aa42715-21/aa42715-21-eq5.png) (5)
(5)
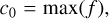 (6)
(6)
where N is the total number of points surviving the filtering for this alert and tfmax is the time of maximum flux for a given light curve, we obtained the three features for each alert and band from the best fit values of a, b, and c. The following three other features were extracted per band:
(i) the quality of the fit, represented by
 (7)
(7)
where Si is the flux estimate for the ith epoch using the best fit values for a, b, and c, and tilde quantities ( and
and 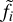 ) generalized as
) generalized as  are normalized values of Xi defined by
are normalized values of Xi defined by
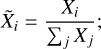 (8)
(8)
(ii) the mean signal-to-noise ratio (S/N),
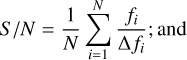 (9)
(9)
(iii) the total number of epochs used in the fit, N.
In summary, for each alert we have a total of six parameters, [a, b, c, ;χ2, S/N, N], per band. The input matrix was constructed by concatenating the parameters corresponding to [g, r] bands for the same alert in one line.
Figure 3 shows the two-dimensional representation of objects in this parameter space. Our final input matrix is composed of 23 775 lines (alerts) and 12 columns (features); this corresponds to 15 751 unique sky objects. The composition of this alert sample in classes is shown in Table 1. From this table, we noticed that although the feature extraction reduced the data volume considerably, it maintained the overall proportion between classes present in the original raw data.
3.3 Classifier
Following the framework outlined in Ishida et al. (2019), we used a random forest classifier (Breiman 2001). This is an ensemble method which uses a number of decision trees (Breiman et al. 1984), constructed from different subsamples of the training set. Once the forest is constructed, the estimated classes for the target sample are determined by majority voting considering all trees in the ensemble. The method proved to be effective in a variety of data scenarios in astronomy (e.g., Richards et al. 2012; Ishida & de Souza 2013; Lochner et al. 2016; Möller et al. 2016; Calderon & Berlind 2019; Nixon & Madhusudhan 2020; Kuhn et al. 2021; Nakazono et al. 2021).
Random forest has a number of advantages when faced with complex data sets. Since it is based on decision trees, the trained model is fully interpretable, which allows each decision to be scrutinized. Moreover, for the specific purpose of this project, its most important quality is the sensitivity to small changes in the training set. Decision trees divide the parameter space into small regions around each object in the training sample. Thus, in the small training data regime, it quickly adapts classification results when faced with a small number of new labels. This is a crucial feature for any classifier which needs to work within an AL framework (Sect. 3.4). All random forest models trained in this work were constructed using 1000 trees, so as to ensure good convergence in a reasonable time.
 |
Fig. 2 Alert data and sigmoid fit for alerts associated with a SNe Ia (objectId:ZTF20acqjmzk, candid: 1424192755315015009), a galaxy (AGN-like) (objectId:ZTFl8aarybyq, candid: 1452439215115010000), an eclipsing binary (objectId:ZTFl8aabtvle, candid: 1277247161915010000), and a RRLyr star (objectId:ZTFl8aaptrep, candid: 1385238050715015010). Points and error bars denote the observed values. Dashed lines show approximations obtained from the sigmoid fit (Sect. 3.2). The corresponding best-fit parameters are given in Appendix A. |
 |
Fig. 3 Distribution in feature space according to true alert classes. Each panel shows the same parameter in g and r bands (horizontal and vertical axis, respectively). The blue dots represent alerts from SN Ia sources, while the orange triangles represent all the other classes in our initial data set. We can observe that non-las occupy an overlapping and larger region of the parameter space than their Ia counterparts. |
3.4 Active learning
Active learning (Settles 2012) is a branch of machine learning methods whose goal is to optimize classification results when labeling is expensive and/or time-consuming. In its pool-based approach, at each iteration the algorithm identifies objects which can potentially increase the information content available in the training sample if labels were provided. This list is sent to an annotator (which can be a human or a machine) who is in charge of labeling the queried sample. Once labels are available, the queried sample is added to the training, the machine learning model is retrained and the process is repeated. The iterations continue until the labeling resources (budget) are exhausted.
In the context of astronomical transient classifications, we started with a small number of classified transients in available catalogs. Among all nonlabeled objects, the algorithm subsequently identified which of them would be more informative to the model if a classification (label) was provided. Once this queried object was identified and its classification was obtained, we added the new photometry and label to the training sample and retrained the learning model. Each iteration in this process is also called a “loop.” We highlight that, although here this exercise was performed in catalog data, our intent during LSST production was to obtain labels through spectroscopic follow-up.
Active learning strategies differ as to how the most informative objects are chosen (query strategy). In this work, we use uncertainty sampling (US, Sharma & Bilgic 2017), which identifies the objects closest to the decision boundary between classes at each iteration. We are focused on correctly identifying SNe Ia, thus, our experiment is designed as a binary classification problem (Ia versus non-Ia). At each iteration, the algorithm queries the object with the highest entropy (for a binary classifier, this corresponds to the object with a classification probability closest to 0.5. See, e.g., MacKay 2003).
We also performed experiments using a random sampling (RS) approach, where at each iteration objects were randomly selected from the target and added to the training sample. This allows us to better understand how much influence the decision process has on the final classification results.
3.5 Metrics
We evaluated our results using the classification metrics and nomenclature from the Supernova Photometric Classification Challenge (Kessler et al. 2010),
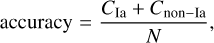 (10)
(10)
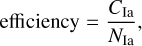 (11)
(11)
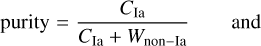 (12)
(12)
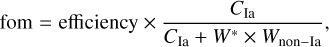 (13)
(13)
where fom stands for figure of merit, CIa is the number of correctly classified Ias, Cnon–Ia denotes the number of correctly classified non-Ias, N represents the total number of objects in the target sample, NIa is the total number of Ias in the target sample, Wnon–Ia is the number of wrongly classified non-Ias, and W* = 3 (Kessler et al. 2010) is a weight which penalizes false positives. We stress that for the purposes of this study, these metrics were used for diagnostic purposes only and they were not used in the decision-making process.
Mean and standard deviation results for the two query strategies investigated in this work.
4 Results
Starting from the initial data matrix described in Sect. 3, we repeated the same experiment 100 times. In each realization, we randomly selected ten objects (five SNe Ia and five non-Ia), to be used as the initial training sample, and evolved the system through 300 iterations. The final configuration consists of 310 alerts in the training sample and 23 425 in the test sample. This small number of iterations was enough to significantly improve the classification results while, at the same time, ensuring that the overall statistical properties of the target sample were maintained throughout the learning process13. The experiments were performed following RS and US query strategies. Figure 4 shows the evolution of classification metrics as a function of the learning loop. It begins with a very high efficiency (~0.80) and low purity (~0.05). This is a consequence of the small and equally balanced training sample and the large and highly unbalanced test sample. In this situation, random forest returns a high incidence of false positives (non-Ia classified as Ia). Nevertheless, since the number of non-Ias is very high, the initial accuracy is ≥0.60. As the system evolves and more information is added to the training sample, the model quickly improves. This first burning phase lasts for ~50 loops, with one object being added to the training set per loop. In this phase, results from the two strategies do not differ significantly (e.g., the efficiency decreases in both cases). Once general characteristics are learned, the model begins to grasp information about details of the class boundaries and results start to differ strongly (e.g., efficiency values start to improve for US and purity values grow apart for different query strategies). The system finally comes to a quasi-asymptotic behavior with US maintaining a much higher efficiency value, while both strategies present similar purity levels. This leads to US resulting in a figure of merit more than two times higher than the value achieved by RS (Table 2).
Qualitatively, these finds are in agreement with the full light curve results presented in Ishida et al. (2019, Fig. 6). However, we see a significant decrease in the effectiveness of the RS strategy when compared to the results archived by US. In Ishida et al. (2019), RS figure of merit results achieve between 70% and 80% of the levels reported by US, while Table 2 shows RS figures stabilizing in approximately 40% of US ones. Despite different feature extraction and data sets, this behavior is mostly driven by the composition of the target sample. The ideal binary classifier should be trained in an equally balanced data set. In Ishida et al. (2019), the sample available for query was composed of 22% SN Ia (Fig. 3 of that paper), while in our results they represent merely 7% of the objects available for query (Table 1). Thus, in that work, RS results in a training sample closer to the 50/50 fraction and consequently this leads to better classification results.
More details about the queried sample are shown in Table 3. The RS strategy, as expected, queries individual classes following their fraction in the original data (Table 1). On the other hand, US queries seven times more SNIa and more than five times as many the other_SN type. Figure 5 shows how the queried classes change as a function of the learning loop. In early stages the queries are basically random, thus only until loop 20 do we again see an agreement with the overall class population (larger fraction of classes star and AGN-like). Once information is gathered about the larger populations, learning is concentrated in the class of interest, with a larger fraction of SN Ia being queried in latter loops.
Almost half of the alerts queried by US in each full learning cycle (~135) were Ias. Thus, we can estimate that from the 23 425 alerts in the test sample, Ias correspond to ~1460. A detailed analysis of the photometrically classified set shows that, in over 100 realizations, RS identifies 443 ± 145 alerts as Ias, while US photometrically assigns 896 ± 33 alerts to the SNIa class. Given that both strategies report similar purity values, this means an almost double increase in the number of SNIa correctly classified when the training sample is constructed using the US query strategy. Figure 6 and Table 4 show the average composition of the final photometrically classified Ias.
Figure 7 illustrates how different query strategies produce different outcomes even when they start from the same initial state. The top panel shows the distribution of classification probabilities for SNIa (blue) and the remaining classes (orange) obtained from a training set with ten alerts (five SNIa and five randomly selected from other classes). We evolved this system through 300 loops following the two different strategies, thus resulting in two final training samples. The bottom left panel shows classification probabilities generated by the RS strategy and the bottom right panel shows the results from the US strategy. We can see that the probability distribution for non-Ias are very similar in both lower panels. However, the larger fraction of SNIa in the training sample gathered by the US strategy (Table 3) allows the classifier to better identify a subset of clear separable Ias, thus leading to the bimodal behavior seen in the bottom right panel.
 |
Fig. 4 Evolution of classification results as a function of the AL loop. In all panels the orange and blue lines show the results from random and uncertainty sampling, respectively. The dashed regions mark one standard deviation over 100 realizations. The initial training sample in all experiments consisted of ten alerts (five randomly selected from each class) and at each loop only one object was added to the training sample (batch = 1). |
Percentages of each class in the final queried sample.
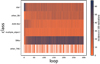 |
Fig. 5 Classes of the queried alerts as a function of the learning loop. The plot shows queries selected by the uncertainty sampling strategy over 100 realizations. |
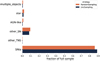 |
Fig. 6 Distribution of true classes among the alerts classified as SN Ia. The classifier was trained using the complete queried sample in addition to the initial training sample (after 300 learning loops) gathered by the random (orange) and uncertainty (blue) sampling strategies. The bar length shows the mean over 100 realizations. Numerical values are given in Table 4. |
Percentages of each true class in the final set of alerts photometrically classified as SNe Ia.
5 Deployment in Fink
The experiments described above resulted in a set of optimized training samples. We used the one that produced the best performing model (accuracy: 0.97, efficiency: 0.53, purity: 0.91, fom: 0.42) to train a random forest classifier, which was subsequently integrated into the broker. Since May 2020, FINK has been processing ZTF alerts using a previous version of this module and reporting candidates with an early SN Ia probability higher than 0.5 to TNS since November 2020. The user can access alerts and the light curves from their corresponding objects through the science portal14.
Following the procedure described in Sect. 3.2, in order for an alert to receive a score from this classifier, it is required for there to be at least three observed epochs in each filter. Thus the number of classifiable alerts is strongly influenced by the telescope observation strategy. In order to minimize the effect of this requirement, for the purpose of feature extraction, we also consider observed epochs which fail the broker’s quality cuts, but were included in individual alert history, thus allowing for alerts with at least one valid point, among the three required by the filtering process (Sect. 3.1), to be classified. In practice, we found that epochs that fail the broker’s quality cuts were due to a poor S/N rather than clear artifacts or pipeline errors (see Möller et al. 2021 for a discussion on the quality cuts). In order to tag an alert as an early SN Ia candidate, we have a set of six criteria15: (a) Ia probability larger than 50% from the early SN Ia module described in this work; (b) Ia probability larger than 50% from either of the deep learning classifiers based on SUPERNNOVA (Möller & de Boissière 2020) deployed in FINK; (c) no match with galactic objects from the SIMBAD database; (d) probability higher than 50% from the RealBogus algorithm (Mahabal et al. 2019; Duev et al. 2019); (e) star-galaxy classification score from SExtractor above 40% (Bertin & Arnouts 1996); and (f) the associated object holds no more than 20 photometric measurements.
Alerts fulfilling the above criteria were advertised to the community via publication in TNS. Over this period (01 November 2020 to 31 October 2021), 809 early SN Ia candidates were reported, from which 535 were spectroscopically confirmed. Among the confirmed set, 459 (86%) were confirmed as SNIa while the remaining ones were shown to belong to other SN types16.
The reported TNS numbers are in agreement with our results (Table 4). However, one should keep in mind that there is still a human screening involved in these numbers, which cannot be modeled. Every observer has the opportunity to inspect the alert candidate and make their own decision about moving forward with the spectroscopic follow-up. Nevertheless, the agreement between the reported numbers and the results presented in this paper are encouraging.
In order to allow the use of adaptive learning techniques “on the fly”, we developed an automated infrastructure which identifies alerts that can improve the classifier. This substream will be distributed to the community allowing further improvement to future classifications. We plan to extend this framework to enable the classifier to be automatically retrained as soon as target labels from spectroscopy are available in public repositories, such as TNS.
6 Conclusions
The impact of recent technological development and the rise of the era of “big data” has been known and widely discussed in a variety of research fields. This new paradigm is certainly also felt in astronomy; however, there are peculiar aspects of astronomical data which require special attention. Among them is the discrepancy between spectroscopic and photometric resources. If we aim to use real data for training as well as testing, we strongly recommend adopting automatic learning strategies which can work in the small data regime.
Active learning is a viable alternative when the number of spectroscopically classified objects is very limited. Working with cataloged transients observed in the ZTF alert stream as a case study, our final model achieves a purity of 89% and an efficiency of 54% while using merely 310 alerts for training – the cited results were obtained from a test sample of 23 465 alerts, ≈ 1463 of which were SN Ia. Such results, derived from a static database of alerts, were corroborated on real-time ZTF data. In the last year, we reported promising SNe Ia to the TNS service, from which 86% were found to be SNe Ia from spectroscopic follow-up observations. We stress that this does not correspond to a complete sample (not all candidates were spectroscopically followed) and that we cannot model the influence of human screening while selecting which candidates will be followed. Nevertheless, it is an encouraging result which can be further scrutinized in a purely automated environments, similar to the one proposed by Street et al. (2018).
Such fully automated pipelines would allow us to remove the current bias present in spectroscopic samples and enable the construction of small, optimized training samples according to the astronomical object of interest. Moreover, this has the potential to result in interesting classified objects benefiting from multiple communities. Among the queried alerts, ≈45% were SNIa, and others correspond to alerts which can be easily mistaken by SN Ias. The study of such objects may reveal details about their physical processes as well as their relationship with the Ia class.
This work represents the first step in the development of an AL environment which has been in the core design of FINK since its conception. Nevertheless, we can imagine similar classifiers being specifically design to target other classes of transients. This would allow us to expand our knowledge about the zoology of astronomical transient sources starting from the classes we know – thus enabling an optimal scientific exploitation of the large volumes of data expected from the next generation of large telescopes.
 |
Fig. 7 Distribution of classification probabilities in different stages of the learning loop. The top panel shows classification results from the classifier, trained with ten alerts (five SNIa and five randomly selected from other classes). This initial state was allowed to evolve through 300 iterations following different query strategies. Bottom left: results from a training sample built following a random sampling strategy. Bottom right: results from a training sample built following an uncertainty sampling strategy. The vertical dotted line in each panel denotes a 50% probability. |
Acknowledgements
We thank Johan Bregeon, Jean-Eric Campagne, Benoit Carry and Maria Pruzhinskaya for comments and discussions on the original draft. This work was developed within the Fink community and made use of the Fink community broker resources. Fink is supported by LSST-France and CNRS/IN2P3. E.E.O.I. receives financial support from CNRS International Emerging Actions under the project Real-time analysis of astronomical data for the Legacy Survey of Space and Time during 2021–2022. M.L. acknowledges financial support from the Paris Saclay University, DSI.
Appendix A Features’ values for Figure 2
Table A.1 shows the extracted features’ values for alerts shown in Figure 2.
References
- Abernethy, J., Chojnacki, A., Farahi, A., Schwartz, E., & Webb, J. 2018, in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD ’18 (New York, NY, USA: Association for Computing Machinery), 5 [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, Astron. Astrophys. Suppl. Ser., 117, 393 [CrossRef] [EDP Sciences] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [Google Scholar]
- Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. 1984, Classification and Regression Trees (Monterey, CA: Wadsworth and Brooks) [Google Scholar]
- Calderon, V. F., & Berlind, A. A. 2019, MNRAS, 490, 2367 [NASA ADS] [CrossRef] [Google Scholar]
- Duev, D. A., Mahabal, A., Masci, F. J., et al. 2019, MNRAS, 489, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Förster, F., Cabrera-Vives, G., Castillo-Navarrete, E., et al. 2021, AJ, 161, 242 [CrossRef] [Google Scholar]
- Ishida, E. E. O., & de Souza, R. S. 2013, MNRAS, 430, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Ishida, E. E. O., Beck, R., González-Gaitán, S., et al. 2019, MNRAS, 483, 2 [Google Scholar]
- Ishida, E. E. O., Kornilov, M. V., Malanchev, K. L., et al. 2021, A&A, 650, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennamer, N., Ishida, E. E. O., González-Gaitán, S., et al. 2020, in 2020 IEEE Symposium Series on Computational Intelligence (SSCI), 3115 [CrossRef] [Google Scholar]
- Kessler, R., Bernstein, J. P., Cinabro, D., et al. 2009, PASP, 121, 1028 [Google Scholar]
- Kessler, R., Bassett, B., Belov, P., et al. 2010, PASP, 122, 1415 [CrossRef] [Google Scholar]
- Kuhn, M. A., de Souza, R. S., Krone-Martins, A., et al. 2021, ApJS, 254, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lochner, M., McEwen, J. D., Peiris, H. V., Lahav, O., & Winter, M. K. 2016, ApJS, 225, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Loup, C., Oberto, A., Allen, M., et al. 2019, in Astronomical Society of the Pacific Conference Series, 521, Astronomical Data Analysis Software and Systems XXVI, eds. M. Molinaro, K. Shortridge, & F. Pasian, 50 [Google Scholar]
- MacKay, D. J. C. 2003, Information Theory, Inference, and Learning Algorithms (Cambridge University Press) [Google Scholar]
- Mahabal, A., Rebbapragada, U., Walters, R., et al. 2019, PASP, 131, 038002 [NASA ADS] [CrossRef] [Google Scholar]
- Möller, A., & de Boissière, T. 2020, MNRAS, 491, 4277 [CrossRef] [Google Scholar]
- Möller, A., Ruhlmann-Kleider, V., Leloup, C., et al. 2016, J. Cosmol. Astropart. Phys., 2016, 008 [CrossRef] [Google Scholar]
- Möller, A., Peloton, J., Ishida, E. E. O., et al. 2021, MNRAS, 501, 3272 [CrossRef] [Google Scholar]
- Nakazono, L., Mendes de Oliveira, C., Hirata, N.S.T., et al. 2021, MNRAS, 507, 5847 [CrossRef] [Google Scholar]
- Narayan, G., Zaidi, T., Soraisam, M. D., et al. 2018, ApJS, 236, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, M. C., & Madhusudhan, N. 2020, MNRAS, 496, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Nordin, J., Brinnel, V., van Santen, J., et al. 2019, A&A, 631, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, J. W., Homrighausen, D., Freeman, P. E., Schafer, C. M., & Poznanski, D. 2012, MNRAS, 419, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Settles, B. 2012, Active Learning (Morgan & Claypool) [Google Scholar]
- Sharma, M., & Bilgic, M. 2017, Data Mining Knowl. Discov., 31, 164 [CrossRef] [Google Scholar]
- Smith, K. W., Williams, R. D., Young, D. R., et al. 2019, Res. Note AAS, 3, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Solorio, T., Fuentes, O., Terlevich, R., & Terlevich, E. 2005, MNRAS, 363, 543 [Google Scholar]
- Spjuth, O., Frid, J., & Hellander, A. 2021, Expert Opin. Drug Discov., 0, 1 [Google Scholar]
- Street, R. A., Bowman, M., Saunders, E. S., & Boroson, T. 2018, in SPIE Conf. Ser., 10707, 1070711 [NASA ADS] [Google Scholar]
- Vilalta, R., Ishida, E. E. O., Beck, R., et al. 2017, in 2017 IEEE Symposium Series on Computational Intelligence (SSCI) [Google Scholar]
- Walmsley, M., Smith, L., Lintott, C., et al. 2020, MNRAS, 491, 1554 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
In data sets where such properties cannot be sustained through the system evolution, one should use an experiment design with separated pool and validation samples, as shown in Kennamer et al. (2020).
All Tables
Mean and standard deviation results for the two query strategies investigated in this work.
Percentages of each true class in the final set of alerts photometrically classified as SNe Ia.
All Figures
 |
Fig. 1 Fraction of each class within the original data set before processing (orange) and the sample surviving feature extraction (blue). Numerical values are shown in Table 1. |
| In the text | |
 |
Fig. 2 Alert data and sigmoid fit for alerts associated with a SNe Ia (objectId:ZTF20acqjmzk, candid: 1424192755315015009), a galaxy (AGN-like) (objectId:ZTFl8aarybyq, candid: 1452439215115010000), an eclipsing binary (objectId:ZTFl8aabtvle, candid: 1277247161915010000), and a RRLyr star (objectId:ZTFl8aaptrep, candid: 1385238050715015010). Points and error bars denote the observed values. Dashed lines show approximations obtained from the sigmoid fit (Sect. 3.2). The corresponding best-fit parameters are given in Appendix A. |
| In the text | |
 |
Fig. 3 Distribution in feature space according to true alert classes. Each panel shows the same parameter in g and r bands (horizontal and vertical axis, respectively). The blue dots represent alerts from SN Ia sources, while the orange triangles represent all the other classes in our initial data set. We can observe that non-las occupy an overlapping and larger region of the parameter space than their Ia counterparts. |
| In the text | |
 |
Fig. 4 Evolution of classification results as a function of the AL loop. In all panels the orange and blue lines show the results from random and uncertainty sampling, respectively. The dashed regions mark one standard deviation over 100 realizations. The initial training sample in all experiments consisted of ten alerts (five randomly selected from each class) and at each loop only one object was added to the training sample (batch = 1). |
| In the text | |
 |
Fig. 5 Classes of the queried alerts as a function of the learning loop. The plot shows queries selected by the uncertainty sampling strategy over 100 realizations. |
| In the text | |
 |
Fig. 6 Distribution of true classes among the alerts classified as SN Ia. The classifier was trained using the complete queried sample in addition to the initial training sample (after 300 learning loops) gathered by the random (orange) and uncertainty (blue) sampling strategies. The bar length shows the mean over 100 realizations. Numerical values are given in Table 4. |
| In the text | |
 |
Fig. 7 Distribution of classification probabilities in different stages of the learning loop. The top panel shows classification results from the classifier, trained with ten alerts (five SNIa and five randomly selected from other classes). This initial state was allowed to evolve through 300 iterations following different query strategies. Bottom left: results from a training sample built following a random sampling strategy. Bottom right: results from a training sample built following an uncertainty sampling strategy. The vertical dotted line in each panel denotes a 50% probability. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


