| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A181 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202450535 | |
| Published online | 11 November 2024 | |
ELEPHANT: ExtragaLactic alErt Pipeline for Hostless AstroNomical Transients
1
The Oskar Klein Centre, Department of Astronomy, Stockholm University,
AlbaNova 106 91,
Stockholm,
Sweden
2
Independent Researcher,
Ingolstadt,
Germany
3
Instituto de Astronomia, Geofísica e Ciências Atmosféricas da USP,
05508-900
São Paulo,
Brazil
4
Institute of Astronomy and Kavli Institute for Cosmology,
Madingley Road,
Cambridge
CB3 0HA,
UK
5
Astronomical Observatory, University of Warsaw,
Al. Ujazdowskie 4,
00-478
Warszawa,
Poland
6
Université Clermont Auvergne, CNRS/IN2P3, LPC,
63000
Clermont-Ferrand,
France
7
CENTRA, Universidade de Lisboa, FCUL,
Campo Grande, Edif. C8,
1749-016
Lisboa,
Portugal
8
Donald Bren School of Information and Computer Sciences, University of California,
Irvine,
CA
92697,
USA
9
Business School, University of Edinburgh,
29 Buccleuch Pl,
Edinburgh
EH8 9JS,
UK
10
Centre for Statistics, University of Edinburgh,
Peter Guthrie Tait Rd,
Edinburgh,
EH9 3FD,
UK
11
Centre for Astrophysics Research, University of Hertfordshire,
College Lane,
Hatfield
AL10 9AB,
UK
12
Independent Researcher,
Budapest,
Hungary
13
School of Mathematical and Physical Sciences, Macquarie University,
NSW
2109,
Australia
★ Corresponding author; priscila.pessi@astro.su.se
Received:
28
April
2024
Accepted:
9
September
2024
Context. Transient astronomical events that exhibit no discernible association with a host galaxy are commonly referred to as hostless. These rare phenomena can offer unique insights into the properties and evolution of stars and galaxies. However, the sheer number of transients captured by contemporary high-cadence astronomical surveys renders the manual identification of all potential hostless transients impractical. Therefore, creating a systematic identification tool is crucial for studying these elusive events.
Aims. We present the ExtragaLactic alErt Pipeline for Hostless AstroNomical Transients (ELEPHANT), a framework for filtering hostless transients in astronomical data streams. It was designed to process alerts from the Zwicky Transient Facility (ZTF) presented in the Fink broker; however, its underlying concept can be applied to other data sources.
Methods. We used Fink to access all the ZTF alerts produced between January 2022 and December 2023, selecting alerts associated with extragalactic transients reported in SIMBAD or TNS, as well as those classified as supernovae (SNe) or kilonovae (KNe) by the machine learning (ML) classifiers within the broker. We then processed the associated stamps using a sequence of image analysis techniques to retrieve hostless candidates.
Results. We find that ≲2% of all analyzed transients are potentially hostless. Among them, only ~10% have a spectroscopic class reported on TNS, with type Ia SNe being the most common class, followed by superluminous SNe. In particular, among the host-less candidates retrieved by our pipeline, there is SN 2018ibb, which has been proposed to be a pair instability SN candidate, and SN 2022ann, one of only five known SNe Icn. When no class is reported on TNS, the dominant classes are quasi-stellar object (QSO) and SN candidates, with the former obtained from SIMBAD and the latter inferred using the Fink ML classifier.
Conclusions. ELEPHANT represents an effective strategy to filter extragalactic events within large and complex astronomical alert streams. There are many applications for which this pipeline will be useful, ranging from transient selection for follow-up to studies of transient environments. The results presented here demonstrate the feasibility of developing specially crafted pipelines that enable a variety of scientific studies based on large-scale surveys.
Key words: methods: data analysis / methods: statistical / astronomical databases: miscellaneous / stars: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Contemporary wide-field, untargeted surveys that scan large portions of the sky on a regular basis, such as the All-Sky Automated Survey for Supernovae (ASAS-SN, Shappee et al. 2014), Gaia (Gaia Collaboration 2016), the Asteroid Terrestrial-impact Last Alert System (ATLAS, Tonry et al. 2018), and the Zwicky Transient Facility (ZTF; Bellm et al. 2019b), have significantly increased the number of transients discovered nightly over the past few decades1. Such projects have not only increased the number of confirmed transients of known classes but have also facilitated the discovery of new classes of events (e.g., Drout et al. 2014; Kankare et al. 2017). Thus, the past decade has witnessed a significant increase and diversification of the transient sky landscape, populated by a myriad of objects (e.g., Hambleton et al. 2023).
Extragalactic transients can be described as the observational consequence of energetic events taking place outside the Milky Way. This description implies a progenitor population of astrophysical sources that should, in principle, be associated with a host galaxy. Nevertheless, a small number of transients seem to not be associated with any host and are thus considered hostless, with the fraction of hostless events being ∼2% in a typical survey (e.g., Qin et al. 2022, 2024). In these cases, the host may remain undetected either because it is fainter than the survey’s limiting magnitude, which is likely the case for many low-surface-brightness galaxies (LSB, e.g., Zinn et al. 2012), or because the transient was produced by a progenitor that achieved hypervelocity, escaped its host galaxy (e.g., Martin 2006; Zinn et al. 2011), and became part of the intracluster stellar population (Graham et al. 2015). Hostless transients have been associated with superluminous supernovae (SLSNe; e.g., McCrum et al. 2015), gamma-ray burst (GRBs; e.g., Ho et al. 2020), fast X-ray transients (FXTs; e.g., Gillanders et al. 2024), and lensed transients (e.g., Ryczanowski et al. 2020), among others. Independently of the exact mechanism that rendered them hostless, such rare events represent an opportunity to further investigate peculiar astrophysical scenarios and may provide important clues regarding their local environment.
Given such scientific potential, whenever a hostless transient is discovered, it sparks the interest of the astronomical community focused on rare events. In the past, the moderate number of discovered transients allowed thorough investigation of each candidate together with their associated hosts (e.g., Filippenko 1997). Nowadays, untargeted searches are discovering transients in fainter and more distant host galaxies, substantially increasing their numbers and rendering it impossible to study all of them in detail. As an example, ZTF currently detects a few hundred thousand transient candidates per night, while the upcoming Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST) is expected to detect around 10 million per night over a period of 10 years (Bellm et al. 2019a). In this context, it became necessary to develop automated frameworks for mining large astronomical datasets.
In this work, we introduce the ExtragaLactic alErt Pipeline for Hostless Transients (ELEPHANT), whose goal is to enable automatic identification of confirmed or potential extragalactic events without an obvious host association. Although the final characterization of an event as truly hostless depends on analysis by an expert, ELEPHANTsignificantly reduces the number of candidates requiring visual inspection, allowing an optimal allocation of expert time and follow-up resources. It employs a range of established image processing techniques to analyze image stamps associated with each transient, assessing the likelihood of a host presence. We detail the components of our pipeline and discuss a number of noteworthy candidates identified during its development. We visually inspected candidates with an associated spectroscopic classification available on the Transient Name Server (TNS2) to confirm their hostless nature. This process also helped us define statistical thresholds to apply to the rest of the sample. We found that the most common classes of hostless candidates are quasi-stellar objects (QSOs), type Ia SNe, and SLSNe. Some hostless candidates identified by our pipeline, which present interesting features, had already been thoroughly discussed in the literature (see Section 4). Our results illustrate the potential of the pipeline if applied to more recent data. We are currently working in integrating it with the Fink broker (Möller et al. 2021), which will allow the ZTF alert stream to be processed in real time and increase the chances of identifying hostless transients while they are still bright enough for spectroscopic follow-up.
This paper is organized as follows. Section 2 outlines the data selected for this analysis. Section 3 describes the ELEPHANT workflow. Results are presented in Section 4 and conclusions in Section 5.
2 Data
We have used image data available within alerts distributed by ZTF. An alert package is produced when the difference imaging pipeline identifies a significant difference in brightness when comparing two images from the same point in the sky taken at different times. It includes photometric history, metadata, and three stamps: the original reference image – template, the new observation – science, and the difference image – difference (Bellm et al. 2019b; Masci et al. 2019). This information is distributed nightly to community brokers, whose task is to filter3, add value, and redistribute the alerts to domain experts. This work uses the alert stream information provided by the Fink broker (Möller et al. 2021); however, the pipeline is flexible enough to be used with other data sources4.
We retrieved all alerts processed by Fink between January 2022 and December 2023, including those alerts corresponding to events that were discovered before these dates. The dataset contained 70 176 557 alerts, which correspond to 17 683 691 objects. Approximately 50% of these have an associated classification. We only kept events associated with an extragalactic transient classification, including all classes of active galactic nuclei (AGN), SNe, and kilonova (KN) candidates, among others (the complete list of the classes considered for this work can be found in our repository5). The classifications provided by Fink were obtained via crossmatching with SIMBAD6 (Wenger et al. 2000), TNS, or produced by machine learning (ML) algorithms used by the broker (Möller & de Boissière 2020; Leoni et al. 2022; Biswas et al. 2023). If a cataloged classification was available, we considered it to be final. ML-based classifications were given per alert and not per each event’s light curve. Since one object can produce many alerts, this sometimes results in different classes associated with the same astrophysical source. When selecting sources for which only ML classification is available, the final class was chosen by majority vote, taking into account all alerts associated with the same object.
We excluded alerts with no associated classification or associated with galactic transients such as variable stars or objects present in the Minor Planet Center7. Since we are only interested in hostless events, we also considered crossmatching with the MANGROVE catalog (Ducoin et al. 2020) and removed any object within 1.5 arcsec of a known host, even if the host galaxy association is tentative. We kept only ∼3.5% of the original alerts by applying these conditions. To eliminate potentially bogus events, we only considered transients with two or more alerts, meaning that they have more than one associated set of stamps.
The stamps are typically 63 × 63 pixels, with the detected transient located at the center. Smaller stamps are produced in rare cases, normally related to detector edge effects or due to defects in the image acquisition process (Reyes-Jainaga et al. 2023). To guarantee a homogeneous sample, we removed any stamp whose size was smaller than the typical value. After applying these last conditions, we ended up with a total of 90 928 transients.
3 The ELEPHANT pipeline
The pipeline analyzes both the science and template stamps in parallel. Thus, a source is considered hostless if either its template or science stamps survives all filtering stages. In principle, the template image should suffice to detect the presence of a possible host; however, because of the template generation process (see Masci et al. 2019), some of them can suffer from transient contamination. In these cases, the transient would be detected as a source in the center of the template image, leading to the wrong detection of a host. Considering both the template and science stamps attenuates this issue. Below, we describe each step of the pipeline.
3.1 Stamp preprocessing
If a stamp contains pixels with missing or empty values, the pipeline estimates the probability density function (PDF) of the counts in the remaining pixels via Gaussian resampling using the scipy.stats.gaussian_kde Python method. The empty value is then replaced by randomly selected values from the resulting PDF, producing a homogenized sample where all images have the same number of valid pixels. Additionally, we used the full width at half maximum (FWHM) reported in the alert package corresponding to each stamp to estimate the image quality. In our sample, the FWHM can vary from FWHM < 1.0″ (a few cases) to FWHM > 3.0″, with a median value of FWHM ~ 2.0″. To select only the best available images representing each astrophysical source, all alerts associated with a given source were separated into three FWHM bins: FWHM < 1.0″, 1.0″ < FWHM < 2.0″, and FWHM > 2.0″. The pipeline only considers the stamps in the smallest available FWHM bin for each source, discarding all others.
All selected stamps for a given object are then stacked by adopting the median count value in each pixel of the 63 × 63 cutout. This stacking process aids to enhance the images’ signal- to-noise ratio (S/N), thereby improving the identification of potential hosts. Since the science stamps result from a single exposure, this process impacts them much more than their template counterparts. Nevertheless, this technique also serves to homogenize the effects of varying templates used throughout the lifespan of a given transient.
3.2 Segmentation masks
ELEPHANT uses sigma clipping to mask sources present in the stamps and uses those masks to detect the presence of a host galaxy. Sigma clipping is a typical method to detect outliers in astronomical images, usually used to remove the effect of defective pixels or cosmic rays by clipping out pixels above a given sigma threshold. The values of the clipped pixels can then be replaced with a mask or filled in with some characterization of the remaining image counts.
The ZTF alert package includes the aperture magnitude of the transient obtained from aperture photometry, calculated considering a 7-pixel radius aperture. We have used this size as a reference for the maximum size of any detected transient. ELEPHANT implements the astropy.stats.sigma_clip8 Python method considering σ = 3 as the median to compute the clipping center value, and a maximum of ten iterations. As a result, any pixels above the selected median threshold were clipped. The clipped segments of the stamp were considered as the mask. If a mask bigger than 5 continuous pixels was found at the center of the science stamp but not at the center of the corresponding template stamp, or vice versa, we flagged the transient as a potential hostless candidate.
ELEPHANT utilizes the obtained masks to identify the position of the pixel closest to the center that corresponds to a detected neighboring mask, considering any masked pixel within a 7-pixel square as indicative of a neighbor’s presence. Details on how the distance is computed can be found in Appendix A. Although we have not further used the distance information here, a future user could consider it to additionally assess the presence of a host. This could be useful when analyzing SNe, as they could occur on the outskirts of their hosts. In such a case, a mask will not be found at the center of the stamp but close to it. In this context, what is considered to be close should be defined by the user. Another popular image segmentation software in astronomy is SExtractor; we decided not to use it here as it requires more resources than sigma clipping, and it also requires the pipeline to use out-of-memory processing (for further discussion on the use of SExtractor, see Appendix B).
After applying sigma clipping, ELEPHANT retrieves 1669 hostless candidates. Figs. 1 and 2 show an example of a host detection and of the detection of a hostless candidate, respectively. Fig. 1 shows that the presence of a host galaxy at the center of the stamp is seen as a mask in the center of both the template and science stamps. On the other hand, Fig. 2 shows that a mask is present at the center of only one of the transient’s stamps; thus, it is flagged as a hostless candidate. Fig. 3 shows a spurious detection of a hostless candidate. In this case, the erroneous detection is driven by artifacts present on the template stamp.
 |
Fig. 1 Example of the template (left) and science (right) stamps for a transient associated with a host galaxy. The top row shows the original stamps and the bottom row shows the masks produced from sigma clipping. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
 |
Fig. 2 Example of the template (left) and science (right) stamps of a hostless transient candidate. The top row shows the original stamps, and the bottom row shows the masks produced by sigma clipping. We can see that the science stamp shows a mask at the center of the stamp that is absent in the template stamp. The absence of a mask is considered as the absence of a host. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
3.3 Host detection via Fourier power spectrum
To further examine the presence or absence of a host, if a transient is flagged as a hostless candidate by the sigma clipping method, ELEPHANT explores the Fourier space projections of the masked stamps. This strategy is reflective of methodologies previously applied to the classification of natural images across various landscapes (Kauppinen et al. 1995; van der Schaaf & van Hateren 1996; Balboa & Grzywacz 2003; Kuhn et al. 2021). By transforming the stamps into Fourier space, the pipeline is able to search for correlations in the background noise that can suggest the presence of a faint host, which would otherwise not be detected via the sigma clipping approach (see Appendix C for an example with pure noise and an example with an injected host). This process involves calculating the medianized onedimensional (1D) power spectrum from the two-dimensional Fourier transform of the images. The mathematical foundation of this method is laid out as follows: the Fourier transform, denoted by F(u, v), of an image, I(x, y), is calculated according to
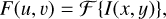 (1)
(1)
where (x, y) represents the pixel coordinates and (u, v) the frequency domain coordinates. From this, the power spectrum, P(u, v), is derived through the equation
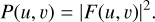 (2)
(2)
The median power, M(k), for each radial frequency  , is calculated by taking the median of the power values across all angular coordinates, θ, for a given power, k:
, is calculated by taking the median of the power values across all angular coordinates, θ, for a given power, k:
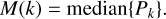 (3)
(3)
We assume that the power spectrum of an image containing even a faint host signal will distinguish itself from the power spectrum of another from which sources were removed and whose pixels have been randomly shuffled, and consequently does not contain any spatially coherent information to be extracted.
To explore this, we first carried out the power spectrum analysis on the stacked and clipped template and science stamps. After sigma clipping, these stamps arrive to the power spectrum analysis having been masked. We filled the masked sections of the stamps with random noise sampled from the pixel value distribution of the masked stamp itself. This process ensures a reliable estimate of the radially averaged 1D power spectrum. The stamps were then cropped to three distinct sizes: 7 × 7, 15 × 15, and 29 × 29 pixels, always with the center coinciding with the position of the transient. We computed the power spectrum for all three crops of the stamps. Afterward, we randomly shuffled the pixel positions and the power spectrum was recalculated for all three crops. This process was repeated 1000 times. For each of the three sizes that the stamps were cropped to, the radially averaged 1D power spectrum of the original template and science stamps was compared to that of each shuffled iteration. In this comparison, we used the Wasserstein distance (Kantorovich 1942, 2006), W(p, q):
 (4)
(4)
which measures a distance between the p and q distributions, or, more intuitively, the cost of transforming one distribution into the other (e.g., Villani 2003, 2016; Peyré & Cuturi 2019). The presence of a host, even if weak, is suggested if the distances from the original stamp’s power spectrum to those of the shuffled realizations are on average greater than the distances between the power spectra of some shuffled realizations to those of other shuffled realizations (see right panel of Fig. 4 for an example of distance distributions when a host is present, and Fig. 5 for an example of the distance distributions for a hostless candidate).
This process yields a sample of 1000 distances for comparisons between the original image’s power spectrum and the power spectra of the shuffled images for each cutout size. The final step involves estimating the Kolmogorov-Smirnov (K-S) statistic to quantify the similarity between these two distributions of distances. The K-S statistic was calculated using the following equation:
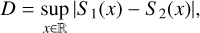 (5)
(5)
where D quantifies the maximum discrepancy between the cumulative distribution functions (CDFs) of two distinct samples. Here, S 1(x) represents the empirical cumulative distribution function (ECDF) for the first sample, which consists of the Wasserstein distances between the power spectrum of the original image and those derived from shuffled images. S2(x), on the other hand, corresponds to the ECDF of the second sample; namely, the distribution of distances among the shuffled images themselves. We used D as a proxy for identifying the presence of a faint host in all images that survived the sigma clipping selection.
 |
Fig. 3 Example of the template (left) and science (right) stamps of a spurious hostless candidate detection. The top row shows the original stamps and the bottom row shows the masks produced from sigma clipping. We can see that the erroneous detection is driven by artifacts present in the original template stamp. As a result, the sigma-clipped template in the bottom left panel shows no signal. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
 |
Fig. 4 Stages of the power spectrum analysis for a template (SN2017iuu / ZTF18aajwbhh) with a host previously identified by the sigma clipping method described in Sect. 3.2. From left to right, the panels show the template image, the mask, and the mask populated with noise. The right-most panel shows the distribution of Wasserstein distances between the original template and shuffled noised masks (gray) and between random pairs of shuffled noised masks (rose). The distributions were generated using 1000 different shuffles of the noised masks within the central patch of 7 × 7 pixels. |
 |
Fig. 5 Stages of the power spectrum analysis for a hostless template (SN2022knm/ZTF22aakkmri). Panel descriptions are equivalent to those described in Figure 4. |
4 Results
ELEPHANT combines two stages of filtering. All objects flagged as potential hostless candidates by the sigma clipping step (Section 3.2) were submitted to the power spectrum analysis (Section 3.3). This last stage attached to each object a K-S statistic value, D, which was constructed as a proxy indicating the presence of a faint host. We used a subset of visually inspected objects to define a selection cut threshold based on D (Section 4.1), and analyzed the results from imposing such a threshold on a subset of spectroscopically confirmed transients (Section 4.2).
 |
Fig. 6 Classified events. Central panel: Black dots indicate the comparison between the spectral classification reported on TNS (horizontal axis) and the classification reported by Fink obtained from other sources (vertical axis). The classes on the vertical axis will match those presented in the corresponding classifying source. In this case, the “SN*_candidate” class is assigned by SIMBAD, whereas the “SN candidate” class is assigned by Fink. Both indicate a possible SN. “GinCl” is also assigned by SIMBAD and indicates a galaxy toward a cluster of galaxies. The x and y axis side panels show the number of transients considered to be hostless by the sigma clipping method before applying the power spectrum analysis (orange), and the number of surviving hostless candidates after applying the power spectrum analysis (blue). |
4.1 D threshold for hostless candidates
After applying the segmentation mask module (see Section 3.2), ELEPHANT finds 1669 hostless candidates, 181 of which have an associated spectroscopic classification available on TNS. Fig. 6 compares the TNS classification (horizontal axis) against the classes found on SIMBAD (SN*_candidate, GinCl, SN and Unknown) or inferred via FINK classifiers (Microlensing candidate and SN candidate). We can see that most of these hostless candidates were classified as an SN candidate by the ML classifiers, which is consistent with the final spectroscopic classification available on TNS.
The stamps associated with the 181 hostless candidates with a TNS classification were visually inspected using the optical images available in the Aladin sky atlas9 (Bonnarel et al. 2000). We were not able to visually identify a host for 118 candidates, and thus we confirm them to be hostless candidates. The remaining 63 events are considered to be contaminants as a host was visually confirmed. Figure 7 shows the distribution of the K-S statistic, D, for the three considered cropped cutout sizes (see Section 3.3), for both classes, confirmed hostless candidates and contaminants with host. We used the distribution of the hostless candidates to empirically define a threshold that would enclose a minimum of 75% of the hostless events. Table 1 shows the 75th percentile for each image size. Aiming at a low contamination level with 75% completeness, we chose to use the 15 × 15 pixel images and imposed a threshold of the K-S statistic, D < 0.5. Thus, we have classified all objects with a K-S statistic below the threshold in either the template or the science image as hostless candidates. In most cases, the threshold condition is satisfied for both the template and science. However, ~9% of the hostless candidates with a TNS classification are considered hostless only based on the template and ~33% are considered hostless only based on the science. If we consider events without a TNS classification, ~5% of the candidates are considered hostless only based on the template and ~41% are considered hostless only based on the science cutouts. The last column of Table 1 shows the resulting contamination when the threshold is applied. We note that the output of ELEPHANT is the D value, and the user could employ a different threshold to select hostless candidates (see Section 4.3).
Kolmogorov–Smirnov threshold.
4.2 Hostless sources on TNS
After applying the K–S D statistic threshold to all the events flagged as hostless candidates by the image segmentation method, we find a total of 1563 ZTF events that match our criteria to be considered hostless candidates. We note that these events are flagged as hostless candidates because no extended source is found at the position of the transient at the center of the stamp. However, the transient could still be associated with a host that is either significantly off-center or that is dimmer than the limiting magnitude of the survey, which for ZTF is ~20.5 mag (Bellm et al. 2019b). To define an event as truly hostless, user inspection is required. The retrieved number of hostless candidates represents ≲2% of the analyzed extragalactic transients, which is consistent with the fraction of hostless candidates in other observed samples (see Qin et al. 2024); and ≲0.01% of the number of transients processed by Fink between January 2022 and December 2023.
Among the hostless candidates retrieved after applying the K-S statistic threshold (Section 4.1), 154 have an associated spectroscopic classification available on TNS. As the threshold was applied to the complete sample produced by the sigma clipping procedure (Section 3.2), including those events for which a host was spotted via visual inspection (see Section 4.1), 40 of the 154 hostless candidates with a TNS classification actually have a host that can be identified visually. In other words, the TNS classified hostless candidates present a contamination of ~26%, which is consistent with the value reported in Table ɪ. Table 2 lists the 154 events together with the reported classification. We can see that the most common class is type Ia SNe, encompassing ~67.5% of events (considering all type la subclasses). This is twice what was found by McCrum et al. (2015), but it is consistent with SNe Ia being predominant among hostless transients. The second most common class is SLSNe, which encompasses ~ 14% of the sample (considering both SLSNe I and SLSNe II). This is expected, since these are extremely bright objects that can be found in dwarf galaxies (Perley et al. 2016). These results are also consistent with the results of McCrum et al. (2015). In a few cases, a transient reported to TNS is associated with more than one ZTF identifier. Table 2 lists all of them, even if they are duplicated; this is because ELEPHANT only considers stamps associated with alerts, ignoring the associated coordinates. Inspecting the reasons for the duplicated ZTF identification is out of the scope of this paper.
The last column of Table 2 includes comments on some of the events. In particular, we see that a potential, usually faint, host has been reported on TNS for 11 events that we consider to be hostless. This is compatible with the contamination factor that we report above – further analysis is needed to confirm these associations. We also notice that eight of our hostless candidates were selected by the FLEET (“Finding Luminous and Exotic Extragalactic Transients” Gomez et al. 2020, 2023) pipeline as potentially luminous or exotic transients. In addition, five of our hostless candidates are part of the sample paper presented by Chen et al. (2023), which analyzes the characteristics of 78 SLSNe I. Moreover, three of the SNe reported in Table 2 were found in real time by different groups, followed up, and studied in great detail due to their rare or anomalous nature. Below, we provide further details on each of these events.
SLSN 2018ibb was identified by Schulze et al. (2024) as the best pair-instability supernova (PISNe) candidate to date. It has been proposed that PISNe occur when instabilities produced by pair production induce the thermonuclear explosion of the most massive stars (140 M⊙ < M < 260 M⊙). Thus, it has been proposed that PISNe mark the explosive death of population III stars, which could be indirectly studied through the characteristics of the observed explosion (e.g., Kasen et al. 2011; Gal-Yam 2012). Although SLSN 2018ibb is not hostless, it is associated with a faint (mR ~ 24.4 mag Schulze et al. 2024) dwarf host, detected by 4- and 8-m class telescopes. Thus, for the purposes of the ZTF alerts processed by our pipeline, the transient is expected to appear hostless. Figure 8 illustrates the interesting aspect that leads this object to be detected by our pipeline. It is a typical case of contaminated template, meaning that the template image was taken when the transient was bright, which results in a relatively lower central brightness in the science image. This result demonstrates the importance of considering both sets of stamps in parallel before a decision is made.
SN 2018bym was studied by Lunnan et al. (2020) alongside three other SLSNe discovered by ZTF to examine the origin and diversity of these events. The authors find that SN 2018bym can be considered a classical SLSN I, and that it is associated with a faint (mr ~ 22.4 mag) dwarf galaxy, for which they obtained deeper observations with the Canada–France–Hawaii Telescope (CFHT). This event is also a representative case of template contamination, in which the hostless stamp is the science one (Figure 9).
SN 2022ann was studied by Davis et al. (2023) as one of only five known SNe Icn. The early discovery of SN 2022ann enabled a detailed analysis of the progenitors of these rare objects. The authors find that SN 2022ann is associated with a faint dwarf host galaxy located at the lower end of the SN host galaxy luminosity distribution. Its stacked template and science stamps are shown in Figure 10.
The fact that ELEPHANT could identify such interesting sources while analyzing historical data demonstrates its potential in identifying similarly interesting objects when applied to more recent alerts. We are currently working on such an investigation and, in parallel, integrating ELEPHANT to Fink. Preliminary results are encouraging and will be reported in a subsequent work. We also anticipate that, among other applications, the pipeline can serve as a powerful tool to identify SNe potentially associated with dwarf host galaxies (e.g., Taggart & Perley 2021).
The classification distribution of the hostless candidates that do not have a class available on TNS is shown in Fig. 11. The classification associated with these events is mainly obtained from crossmatching with SIMBAD or inferred using a ML classifier. We find that ∼ 49% of these events are QSOs, which belong to the family of AGNs, and thus would be associated with a host by definition. However, hostless QSOs have been found before (e.g., Magain et al. 2005; Kemper et al. 2010). Although many of the QSOs in our sample of hostless candidates may be associated with a faint, undetected host, ELEPHANT can be used to perform systematic searches of hostless QSOs. The other dominant class in this sample is “SN candidate;” ∼48% of the sample is associated with this ML-based classification. As was mentioned above, ELEPHANT only considers ZTF stamps associated with individual alerts; however, some events seems to be associated with multiple ZTF identifiers, and when this occurs we consider all of the different identifications to be hostless candidates. An interesting case is that of AT 2024dum. This object was found to be a hostless candidate and is associated with three ZTF alerts: ZTF23aabtyzn, ZTF23aaiyhen, and ZTF23abkiray. AT 2024dum has been reported to be a fastmoving star (see report10 by Shumkov et al. 2024), which could explain the multiplicity of ZTF identifiers.
 |
Fig. 7 Distributions of the Kolmogorov-Smirnov statistic for the 181 objects with TNS classifications. The two categories, with a host (orange) and hostless (blue), were identified through visual inspection. The panels show the distributions obtained through the power spectrum analysis (Section 3.3) for different image sizes. |
Hostless candidates with associated spectroscopic classification in TNS.
 |
Fig. 8 Stacked template (left) and science (right) stamps for SLSN2018ibb (ZTF18acenqto, ZTF18adovhai). |
 |
Fig. 9 Stacked template (left) and science (right) stamps for SN2018bym (ZTF18aapgrxo). |
 |
Fig. 10 Stacked template (left) and science (right) stamps for SN2022ann (ZTF22aaaihet). |
 |
Fig. 11 Number of transients without a reported classification on TNS considered to be hostless by the sigma clipping method before applying the power spectrum analysis (orange), and the number of surviving hostless candidates after applying the power spectrum analysis (blue). |
4.3 Caveats to the presented method
The definition of an event as hostless is broad, as the origin of “hostless” events may be due to astrophysical causes, such as events that escaped their host galaxies, or due to observational limitations, such as events in low-surface-brightness host galaxies (see Section 1). In this work, we consider a hostless event to be any object that lacks a detected host within the alert cutouts region. This introduces some issues: first, events whose host occupies the whole cutout may be considered hostless as the power spectrum of the shuffled image will be similar to the power spectrum of the original image (see Section 3.3); second, events associated with hosts that are not contained within the alert cutout region will be considered to be hostless candidates for the same reason as before; third, hostless events in crowded fields will be missed because the power spectrum of the shuffled imaged will be different than the power spectrum of the original image (see Section 3.3). In addition, we consider events to be hostless candidates based on an empirical definition of an statistical threshold considering only a small subset of classified transients (see Section 4.1). Thus, our results are prone to bias toward characteristics defining transients in TNS. Consequently, visual inspection is needed to decide whether the candidates provided by ELEPHANT follow the hostless definition of the user. Still, ELEPHANT achieves the goal of lessening the burden on domain experts to visually classify hostless transients by providing a shortlist of likely hostless candidates. Furthermore, ELEPHANT returns statistical parameters associated with the analysis of the alert cutouts, rather than a single flag for being hostless. Therefore, the user can decide which thresholds for the associated statistics better select hostless events of interest to their science needs. By increasing the number of visually confirmed hostless events, the user can reassess the selection metrics and improve the efficiency of the pipeline for their science.
5 Conclusions
We developed the ELEPHANT pipeline, which processes stamps delivered by the ZTF alert stream and automatically detects hostless transient candidates. The pipeline (see Section 3) returns stacked science and template cutouts together with the number of stamps that were used to produce them, a Boolean that indicates whether the transient is a hostless candidate based on the segmentation mask analysis (see Section 3.2), the distance to the closest mask in pixels, and the associated K–S D statistic obtained from 7 × 7, 15 × 15 and 29 × 29 pixel square sub-cutouts (see Section 3.3).
In this work, we define a threshold on the K–S D statistic that is used to flag a transient as a hostless candidate (see Section 4). However, future users can use the output values to implement different selection cuts specific to their science case. The automatic detection of hostless transients has many potential applications that include but are not limited to:
Identification of transients associated with dwarf and/or dim galaxies to study their characteristics and environments;
Identification of AGNs associated with low-mass galaxies to study their impact on galaxy evolution;
Searching of sources that have been ejected from their host galaxies to study intra-cluster stellar populations;
Selection of SNe Ia and/or SLSNe, as they seem to be predominant among the hostless candidates that have a reported class on TNS;
Compilation of hostless candidates as training sets to improve ML classifiers.
ELEPHANT will be included in the Fink broker to allow the real-time detection of hostless candidates and also the retrieval of archival potentially hostless events. Recently, Qin et al. (2024) performed an statistical analysis of the environments of 161 hostless SNe reported to TNS since 2016. They find that their sample is dominated by SNe Ia and SLSNe, which is in agreement with our findings. ELEPHANT is a useful tool to gather hostless events for similar statistical environmental analyses of different types of SNe. In addition, it can be used to systematically select hostless candidates for classification to increase the number of spectroscopically classified hostless transients to be considered in future population analyses.
The methods we have used here are completely transferable to any dataset by scaling the sizes of the considered stamps. In particular, once the Fink broker starts ingesting LSST alerts, we could test and tune ELEPHANT as a tool for finding hostless candidates within the LSST alert stream. LSST is an 8-m class telescope that will have a limiting magnitude of ~25 mag in optical bands (LSST Science Collaboration 2009), which makes it much deeper than the current wide-field surveys. Thus, a big fraction of the events that we flag as hostless candidates here may have a visible host in the LSST stamps. Consequently, if an LSST stamp is flagged to be a hostless by ELEPHANT the chances are that the transient is either associated with an intergalactic progenitor or associated with hosts dimmer than any detected so far. We can only speculate that the hostless transients detected by LSST will be extraordinarily anomalous, providing unprecedented insights into the transient sky, with the study of their environments only being possible by using other 8-m class telescopes or by the next generation of large telescopes such as the Giant Magellan Telescope (Johns et al. 2012) and the Extremely Large Telescope (Gilmozzi & Spyromilio 2007). In this context, automatic pipelines tailored for specific science cases, such as ELEPHANT , will play a central role in the process of transient characterization and the optimization of follow-up resources.
Data availability
The data used here can be accessed via the FINK data transfer service: https://fink-portal.org/download. The ELEPHANT pipeline is publicly available on github: https://github.com/COINtoolbox/extragalactic_hostless. Full Tables 2 and D.1 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/691/A181
Acknowledgements
We thank Julien Peloton for assistance in retrieving data from FINK. We thank the referee for the valuable revision. P.J.P. acknowledges support from the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation program (grant agreement No. 10104229 – TransPIre). EEH is supported by a Gates Cambridge Scholarship (#OPP1144). This work is a result of the COIN Residence Program #711, held in Lisbon, Portugal, from 9 to 16 September 2023 and supported by the Portuguese Fundação para a Ciência e a Tecnologia (FCT) through the Strategic Programme UIDP/FIS/00099/2020 and UIDB/FIS/00099/2020 for CENTRA. The Cosmo-statistics Initiative (COIN, https://cosmostatistics-initiative.org/) is an international network of researchers whose goal is to foster interdisciplinarity inspired by astronomy. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work made use of the Fink community broker resources. Fink is supported by LSST-France and CNRS/IN2P3. This research has made use of “Aladin sky atlas” developed at CDS, Strasbourg Observatory, France. This work made use of Astropy (http://www.astropy.org) a community-developed core Python package and an ecosystem of tools and resources for astronomy (Astropy Collaboration 2013, 2018, 2022). The ELEPHANT icon was taken from https://icons8.com. The color palette used in this work was inspired by “The Temptation of St. Anthony” by Salvador Dali, 1946.
Appendix A Nearest neighbor
To compute the distance from the transient to the nearest mask, we assume an origin position at the center of the image from where to calculate the distance. Masked pixels have value 1, whereas background pixels have value 0. To find the nearest masked pixel to the transient, we compare pixel by pixel until a mask is found. First, we check all adjacent pixels (including diagonally adjacent ones) related to the central pixel, starting from left to right and top to bottom. This process is repeated for outer layers until a masked pixel is found or we reach the limits of the 7-pixel threshold. If the distance between the central pixel and the nearest neighbor is not within a 7-pixel radius, we keep that alert in our sample for further checks. The Euclidean distance between the nearest masked pixel and the central pixel is included for the user to assess whether a neighbor is close enough for it to be considered an associated host. The algorithm works as follows:
Appendix B Segmentation masks with SExtractor
A popular image segmentation tool in astronomy is SExtractor12 (Bertin & Arnouts 1996). This software is largely used for the detection of astronomical sources, background reduction, and photometry of astronomical images, being especially suitable for processing large field-of-view images. However, running SExtractor can be computationally expensive, especially compared to sigma clipping. We decided to compare the performance of both methods considering only those events that have a spectral classification available on the Transient Name Server (TNS)13. Applying the same methodology used for sigma-clipping (see Section 3.2), we find that SExtractor retrieves 149 hostless candidates while sigma clipping retrieves 181 hostless candidates. By visually inspecting each candidate in the search for the presence of a potential host, we find that the SExtractor method has a ~ 15% contamination while the sigma clipping method has a ~ 22% contamination. Thus, considering that running SExtractor involves writing and reading files on the disk, which is not ideal when working with large volumes of data; and that the performance of both methods is similar, we favor the simpler sigma clipping as an image segmentation method.
Appendix C Fourier power spectrum of a simulated host
Here, we demonstrate the method for evaluating whether a host is present using the Fourier power spectrum as described in Section 3.3 in simulated stamps. We expect a true hostless candidate to have a stamp that is purely instrumental noise, after sigma clipping as described in Section 3.2. Therefore, we first test that a simulated stamp with only noise is successfully detected as “hostless.” In the leftmost panel of the top row of Figure C.1, we show the simulated stamp which contains only Gaussian random noise drawn from a unit normal distribution. The power spectrum of the original image for the 7 × 7 cut-out, 15 × 15 cut-out, and 29 × 29 cut-out are shown next to the stamp from left to right, respectively. We also show the power spectrum for the shuffled images. In the case of a stamp with pure noise, it is difficult to distinguish the power spectrum of the original image from that of the shuffled copies. The KS statistic for the 15 × 15 cut-out is less than 0.5, so this simulated stamp would be considered “hostless,” as desired.
We additionally show that a simulated stamp with an artificial host injected into it would not be considered “hostless.” In the bottom row of Figure C.1, we again show a simulated stamp on the left, now with an injected host, with the power spectrum for each of the three cut-out sizes to the right of the stamp. We approximate the “host” as a multivariate Gaussian distribution centered in the stamp which has a peak amplitude of 2.3 units and an arbitrarily chosen covariance. Again, the background random noise in this stamp is simulated from a unit normal distribution. The power spectrum for the 15 × 15 and 29 × 29 cut-outs of the original stamp do deviate from the power spectrum of the shuffled copies of the stamp. In particular, these deviations are seen in the power spectrum on small scales. The simulated host is successfully identified by the power spectrum analysis, as indicated by the KS statistic for the 15 × 15 being greater than the threshold of 0.5.
 |
Fig. C.1 A simulated stamp is shown in the left panel. In the right three panels, the power spectrum for each of the three cut-out sizes are shown. The power spectrum of the original image is plotted with a blue solid line, while the average power spectrum for 200 shuffled versions of the stamp is plotted with an orange dashed line. The KS statistic for each cut-out size is shown in the bottom right hand side of each power spectrum panel. Top: A simulated stamp with pure Gaussian random noise. The stamp has a root mean square (RMS) of 1. The KS statistic for the 15x15 cut-out is less than 0.5, so this stamp would be considered a hostless candidate. Bottom: A simulated stamp with an injected host. The simulated host has a peak amplitude of 2.3 units and is injected into a background of Gaussian random noise with an RMS of 1. Because the KS statistic is greater than 0.5, the host is successfully detected. |
Appendix D Machine learning classified hostless candidates
Hostless candidates without a reported classification on TNS.
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Balboa, R. M., & Grzywacz, N. M. 2003, Vis. Res., 43, 2527 [CrossRef] [Google Scholar]
- Bellm, E., Blum, R., Graham, M., et al. 2019a, LDM-612, Plans and Policies for LSST Alert Distribution, https://ls.st/ldm-612 [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019b, PASP, 131, 018002 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biswas, B., Ishida, E. E. O., Peloton, J., et al. 2023, A&A, 677, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Z. H., Yan, L., Kangas, T., et al. 2023, ApJ, 943, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, K. W., Taggart, K., Tinyanont, S., et al. 2023, MNRAS, 523, 2530 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Chornock, R., Soderberg, A. M., et al. 2014, ApJ, 794, 23 [Google Scholar]
- Ducoin, J. G., Corre, D., Leroy, N., & Le Floch, E. 2020, MNRAS, 492, 4768 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Förster, F., Cabrera-Vives, G., Castillo-Navarrete, E., et al. 2021, AJ, 161, 242 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gal-Yam, A. 2012, in Death of Massive Stars: Supernovae and Gamma-Ray Bursts, 279, eds. P. Roming, N. Kawai, & E. Pian, 253 [NASA ADS] [Google Scholar]
- Gillanders, J. H., Rhodes, L., Srivastav, S., et al. 2024, ApJ, 969, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmozzi, R., & Spyromilio, J. 2007, The Messenger, 127, 11 [Google Scholar]
- Gomez, S., Berger, E., Blanchard, P. K., et al. 2020, ApJ, 904, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, S., Berger, E., Blanchard, P. K., et al. 2023, ApJ, 949, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. L., Sand, D. J., Zaritsky, D., & Pritchet, C. J. 2015, ApJ, 807, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hambleton, K. M., Bianco, F. B., Street, R., et al. 2023, PASP, 135, 105002 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, A. Y. Q., Perley, D. A., Beniamini, P., et al. 2020, ApJ, 905, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Johns, M., McCarthy, P., Raybould, K., et al. 2012, SPIE Conf. Ser., 8444, 84441H [NASA ADS] [Google Scholar]
- Kankare, E., Kotak, R., Mattila, S., et al. 2017, Nat. Astron., 1, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Kantorovich, L. V. 1942, Dokl. Akad. Nauk SSSR, 37, 227 [Google Scholar]
- Kantorovich, L. V. 2006, J. Math. Sci. (Engl. Transl.), 133, 1381 [CrossRef] [Google Scholar]
- Kasen, D., Woosley, S. E., & Heger, A. 2011, ApJ, 734, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kauppinen, H., Seppanen, T., & Pietikainen, M. 1995, IEEE Trans. Pattern Anal. Mach. Intell., 17, 201 [CrossRef] [Google Scholar]
- Kemper, F., Woods, P. M., Antoniou, V., et al. 2010, PASP, 122, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, M. A., de Souza, R. S., Krone-Martins, A., et al. 2021, ApJS, 254, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Leoni, M., Ishida, E. E. O., Peloton, J., & Möller, A. 2022, A&A, 663, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, arXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Lunnan, R., Yan, L., Perley, D. A., et al. 2020, ApJ, 901, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P., Letawe, G., Courbin, F., et al. 2005, Nature, 437, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, J. C. 2006, AJ, 131, 3047 [NASA ADS] [CrossRef] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [Google Scholar]
- Matheson, T., Stubens, C., Wolf, N., et al. 2021, AJ, 161, 107 [NASA ADS] [CrossRef] [Google Scholar]
- McCrum, M., Smartt, S. J., Rest, A., et al. 2015, MNRAS, 448, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Möller, A., & de Boissière, T. 2020, MNRAS, 491, 4277 [CrossRef] [Google Scholar]
- Möller, A., Peloton, J., Ishida, E. E. O., et al. 2021, MNRAS, 501, 3272 [CrossRef] [Google Scholar]
- Nordin, J., Brinnel, V., van Santen, J., et al. 2019, A&A, 631, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perley, D. A., Quimby, R. M., Yan, L., et al. 2016, ApJ, 830, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Peyré, G., & Cuturi, M. 2019, Found. Trends Mach. Learn., 51, 1 [Google Scholar]
- Qin, Y.-J., Zabludoff, A., Kisley, M., et al. 2022, ApJS, 259, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y.-J., Zabludoff, A., Arcavi, I., et al. 2024, MNRAS, 530, 4695 [NASA ADS] [CrossRef] [Google Scholar]
- Reyes-Jainaga, I., Förster, F., Muñoz Arancibia, A. M., et al. 2023, ApJ, 952, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Ryczanowski, D., Smith, G. P., Bianconi, M., et al. 2020, MNRAS, 495, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, S., Fransson, C., Kozyreva, A., et al. 2024, A&A, 683, A223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shappee, B., Prieto, J., Stanek, K. Z., et al. 2014, in American Astronomical Society Meeting Abstracts, 223, 236.03 [NASA ADS] [Google Scholar]
- Taggart, K., & Perley, D. A. 2021, MNRAS, 503, 3931 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505 [Google Scholar]
- van der Schaaf, A., & van Hateren, J. 1996, Vis. Res., 36, 2759 [CrossRef] [Google Scholar]
- Villani, C. 2003, Topics in Optimal Transportation, Graduate Studies in Mathematics Series (American Mathematical Society) [CrossRef] [Google Scholar]
- Villani, C. 2016, Optimal Transport: Old and New, Grundlehren der mathematis-chen Wissenschaften (Springer Berlin Heidelberg) [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, R. D., Francis, G. P., Lawrence, A., et al. 2024, RAS Techn. Instrum., 3, 362 [CrossRef] [Google Scholar]
- Yamaoka, H. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin, 29 [CrossRef] [Google Scholar]
- Zinn, P. C., Grunden, P., & Bomans, D. J. 2011, A&A, 536, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, P. C., Stritzinger, M., Braithwaite, J., et al. 2012, A&A, 538, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
See Yamaoka (2017) for numbers on the growth of discovered and classified supernovae (SNe) from 1991 to 2015. For statistics on transient discovery and classification from 2016 onward, refer to https://www.wis-tns.org/stats-maps
Other known community brokers include ALERCE (Förster et al. 2021), AMPEL (Nordin et al. 2019), ANTARES (Matheson et al. 2021), Babamul, LASAIR (Williams et al. 2024) and Pitt-Google.
TNS is the International Astronomical Union’s official mechanism for reporting new astronomical transients since 2016, https://www.wis-tns.org/.
All Tables
All Figures
 |
Fig. 1 Example of the template (left) and science (right) stamps for a transient associated with a host galaxy. The top row shows the original stamps and the bottom row shows the masks produced from sigma clipping. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
| In the text | |
 |
Fig. 2 Example of the template (left) and science (right) stamps of a hostless transient candidate. The top row shows the original stamps, and the bottom row shows the masks produced by sigma clipping. We can see that the science stamp shows a mask at the center of the stamp that is absent in the template stamp. The absence of a mask is considered as the absence of a host. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
| In the text | |
 |
Fig. 3 Example of the template (left) and science (right) stamps of a spurious hostless candidate detection. The top row shows the original stamps and the bottom row shows the masks produced from sigma clipping. We can see that the erroneous detection is driven by artifacts present in the original template stamp. As a result, the sigma-clipped template in the bottom left panel shows no signal. At the center of the stamps, we display a red circle of 7 pix radius that indicates the aperture radius of the associated photometry. |
| In the text | |
 |
Fig. 4 Stages of the power spectrum analysis for a template (SN2017iuu / ZTF18aajwbhh) with a host previously identified by the sigma clipping method described in Sect. 3.2. From left to right, the panels show the template image, the mask, and the mask populated with noise. The right-most panel shows the distribution of Wasserstein distances between the original template and shuffled noised masks (gray) and between random pairs of shuffled noised masks (rose). The distributions were generated using 1000 different shuffles of the noised masks within the central patch of 7 × 7 pixels. |
| In the text | |
 |
Fig. 5 Stages of the power spectrum analysis for a hostless template (SN2022knm/ZTF22aakkmri). Panel descriptions are equivalent to those described in Figure 4. |
| In the text | |
 |
Fig. 6 Classified events. Central panel: Black dots indicate the comparison between the spectral classification reported on TNS (horizontal axis) and the classification reported by Fink obtained from other sources (vertical axis). The classes on the vertical axis will match those presented in the corresponding classifying source. In this case, the “SN*_candidate” class is assigned by SIMBAD, whereas the “SN candidate” class is assigned by Fink. Both indicate a possible SN. “GinCl” is also assigned by SIMBAD and indicates a galaxy toward a cluster of galaxies. The x and y axis side panels show the number of transients considered to be hostless by the sigma clipping method before applying the power spectrum analysis (orange), and the number of surviving hostless candidates after applying the power spectrum analysis (blue). |
| In the text | |
 |
Fig. 7 Distributions of the Kolmogorov-Smirnov statistic for the 181 objects with TNS classifications. The two categories, with a host (orange) and hostless (blue), were identified through visual inspection. The panels show the distributions obtained through the power spectrum analysis (Section 3.3) for different image sizes. |
| In the text | |
 |
Fig. 8 Stacked template (left) and science (right) stamps for SLSN2018ibb (ZTF18acenqto, ZTF18adovhai). |
| In the text | |
 |
Fig. 9 Stacked template (left) and science (right) stamps for SN2018bym (ZTF18aapgrxo). |
| In the text | |
 |
Fig. 10 Stacked template (left) and science (right) stamps for SN2022ann (ZTF22aaaihet). |
| In the text | |
 |
Fig. 11 Number of transients without a reported classification on TNS considered to be hostless by the sigma clipping method before applying the power spectrum analysis (orange), and the number of surviving hostless candidates after applying the power spectrum analysis (blue). |
| In the text | |
 |
Fig. C.1 A simulated stamp is shown in the left panel. In the right three panels, the power spectrum for each of the three cut-out sizes are shown. The power spectrum of the original image is plotted with a blue solid line, while the average power spectrum for 200 shuffled versions of the stamp is plotted with an orange dashed line. The KS statistic for each cut-out size is shown in the bottom right hand side of each power spectrum panel. Top: A simulated stamp with pure Gaussian random noise. The stamp has a root mean square (RMS) of 1. The KS statistic for the 15x15 cut-out is less than 0.5, so this stamp would be considered a hostless candidate. Bottom: A simulated stamp with an injected host. The simulated host has a peak amplitude of 2.3 units and is injected into a background of Gaussian random noise with an RMS of 1. Because the KS statistic is greater than 0.5, the host is successfully detected. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



