EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 661 (May 2022) A&A, 661 (2022) A141 Full HTML
Free Access
Issue
A&A
Volume 661, May 2022
Article Number A141
Number of page(s) 8
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202142822
Published online 31 May 2022

© ESO 2022

1 Introduction

The most high-yielding technique for detecting exoplanets is the transit method, which is based on the fact that when a planet passes in front of a star, the flux received from that star decreases. It has been, is, and will be applied by several space missions such as CoRoT, Kepler/K2, TESS, and the upcoming PLATO mission, to try and detect planets in large areas of the sky. When a single planet orbits a single star, its orbit is periodic, which implies that the transit happens at a fixed time interval. This constraint is used to detect planets when their individual transits are too faint with respect to the noise of the data: using algorithms such as Boxed Least Squares (BLS, Kovács et al. 2002), the data- reduction pipelines of the transit survey missions fold each light curve over a large number of different periods and look for transits in the folded data (Jenkins et al. 2010, 2016). This folding of the light curve increases the number of observation per phase, and therefore also the signal-to-noise ratio (S/N) of the transit.

As soon as two or more planets orbit around the same star, their orbits cease to be strictly periodic. In some cases, the gravitational interaction of planets can generate relatively short-term transit timing variations (TTVs): transits no longer occur at a fixed period (Dobrovolskis & Borucki 1996; Agol et al. 2005). The amplitude, frequencies, and overall shape of these TTVs depend on the orbital parameters and masses of the planets involved (see e.g. Lithwick et al. 2012; Nesvorný & Vokrouhlický 2014; Agol & Deck 2016). As the planet-planet interactions that generate the TTVs typically occur on timescales that are longer than the orbital periods, space missions with longer baselines such as Kepler and PLATO are more likely to observe such effects. Over the last decade, several efforts have been made to estimate the TTVs of the Kepler objects of interest (KOIs, Mazeh et al. 2013; Rowe & Thompson 2015; Holczer et al. 2016; Kane et al. 2019).

TTVs are a gold mine for our understanding of planetary systems: they can constrain the existence of non-transiting planets, adding missing pieces to the architecture of the systems (Xie et al. 2014; Zhu et al. 2018), and allowing a better comparison with synthetic planetary-system population synthesis (see e.g. Mordasini et al. 2009; Alibert et al. 2013; Mordasini 2018; Coleman et al. 2019; Emsenhuber et al. 2020). TTVs can also be used to constrain the masses of the planets involved (see e.g. Nesvorný et al. 2013), and therefore their density, which ultimately provide constraints on their internal structure, as is the case for the Trappist-1 system (Grimm et al. 2018; Agol et al. 2021). Detection of individual dynamically active systems also provides valuable constraints on planetary system formation theory, as the current orbital state of a system can display markers of its evolution (see e.g. Batygin & Morbidelli 2013; Delisle 2017). Orbital interactions also impact the possible rotation state of the planets (Delisle et al. 2017), and therefore their atmosphere (Leconte et al. 2015).

However, TTVs can also be a bias that negatively affects the detection and characterisation of exoplanets. As previously stated, transit surveys rely on stacking the light curve over a constant period to extract the shallow transits from the noise. If TTVs of amplitude comparable to (or greater than) the duration of the transit occur on a timescale comparable to (or shorter than) the mission duration, there is not a unique period that will successfully stack the transits of the planet (García-Melendo & López-Morales 2011). This can lead to two problems: incorrect estimates of the planet parameters, and/or the absence of detection. To alleviate this bias, we developed the RIVERS method, which is based on the recognition of the tracks of planets in river diagrams using machine learning, and a photo-dynamic fit of the light curve. The method is described in detail in Leleu et al. (2021b).

In this paper, we apply the RIVERS method to KIC 4725681, which comprises three KOIs announced on the Kepler database1, the candidates KOI3184.01 and .03 with orbital periods of 7.54 and 4.02 days, respectively, and the false-positive KOI3184.02 at a period of 11.32 days, flagged as ‘Not transit-like’.

2 Detection of Kepler-1972

2.1 Application of the RIVERS.deep method

2.1.1 Preparation of the light curve

The raw PDCSAP flux was downloaded using the lightkurve2 package. We started by removing long-term trends of the flux using the flatten method of the lightkurve package using the default parameters. This method applies a Savitzky-Golay filter to the light curve. We then checked for gaps longer than 2.5 h. Such gaps were commonly produced by the monthly data downlinks. After repointing the spacecraft, there was usually a photometric offset produced due to thermal changes in the telescope. We therefore removed all data points until the average flux over 4 h was within one standard deviation of the median flux of the light curve. Finally, we removed points at more than four times the standard deviation from the median value of the light curve to remove outliers.

2.1.2 Application of RIVERS.deep

The RIVERS.deep method, introduced in detail in Leleu et al. (2021b), is based on the recognition of the track of a planet in a river diagram (Carter et al. 2012). An example of such a diagram is given in the top panel of Fig. 1. The RIVERS.deep algorithm takes this 2D array as input and produces two outputs: (1) A confidence matrix: an array of the same size as the input containing for each pixel the confidence that this pixel belongs to a transit. This task is performed by the ‘semantic segmentation’ (pixel-level vetting) subnetwork (Jégou et al. 2017). (2) A global prediction: a value between 0 and 1 which quantifies the model confidence that the output of the semantic segmentation module is due to the presence of a planet. This task is performed by the classification subnetwork.

An example confidence matrix is shown in the bottom panel of Fig. 1. The pixels recognised as belonging to a transit are highlighted in yellow. As described in Sect. 3.2.3 of Leleu et al. (2021b), a periodogram can be obtained by saving the output of the global prediction of the model over a series of river diagrams made for a grid of folding periods. The RIVERS.deep periodogram of KIC 4735826 is displayed in Fig. 2. This periodogram shows two strong peaks at 7.5 days and 11.3 days. One of the river diagrams belonging to the 7.5 days (11.3 days) peak is the top-left (top-right) diagram in Fig. 1. The transit timings proxy highlighted in the bottom panels of Fig. 1 are recovered and displayed as black data points in Fig. 3. We emphasise that the word ‘confidence’ used here refers to the output of a neural network, which is not a likelihood or probability. As such, the application of RIVERS.deep is only a preliminary step towards the photo dynamical fit of the light curve presented in the following section.

2.2 Planet detection

2.2.1 Stellar properties

The luminosity of KIC 4735826 is computed from the Gaia Early Data Release 3 parallax (Gaia Collaboration 2021) by taking into account the correction to the parallax from Lindegren et al. (2021). The K magnitude of the star is used together with the bolometric correction of Casagrande & VandenBerg (2014, 2018) and the extinction from the dust map of Green et al. (2018). We then obtain a luminosity L = 1.97 ± 0.07 L⨀ for KIC 4735826. The effective temperature and metallicity of KIC 4735826 are taken from the spectroscopic analysis of Brewer & Fischer (2018): Teff = 5818 ± 27 K and [M/H] = 0.23 ± 0.01 dex.

These observational constraints (L, Teff and [M/H]) are then used to determine the global parameters of KIC 4735826 from stellar models computed with the Geneva stellar evolution code (Eggenberger et al. 2008). For this determination, the adopted uncertainty on the effective temperature was increased to 50 K (instead of the small internal error of 27 K) to better account for possible uncertainties coming from different spectroscopic determinations. We then find that KIC 4735826 is a star at the end of its evolution on the main sequence with a mass of M = 1. 12 ± 0.03 M⨀, aradius of R = 1.384 ± 0.050 R⨀, and an age of 7.4 ± 1.2 Gyr. The stellar properties are summarised in Table 1.

2.2.2 Planetary solution

The fit of the light curve was performed with the same setup as the one presented in Leleu et al. (2021b). To highlight the effect of the TTVs on the recovered transit parameters, we performed two distinct fits of the light curve: a fit with Keplerian orbits (constant periods) for the three candidates at 4, 7.5, and 11.3 days, and a photodynamic fit where the transit timings of the two resonant planets where modelled using the TTVfast algorithm (Deck et al. 2014). The approximate initial conditions for the orbital elements and masses of these planets were obtained by a preliminary fit of the transit timings to the timing proxy shown in Fig. 3. In the photodynamic fit, the orbit of the 4d candidate is still considered as Keplerian since its interactions with the other two planets are negligible over the duration of the Kepler mission.

For both fits, we use the adaptive MCMC sampler samsam3 (see Delisle et al. 2018), which learns the covariance of the target distribution from previous samples in order to improve the subsequent sampling efficiency. The likelihood is defined as 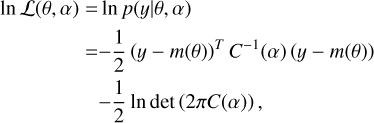lnL(θ,α)=lnp(y|θ,α)=−12(y−m(θ))TC−1(α)(y−m(θ))−12lndet(2πC(α)),$\matrix{{\ln {\cal L}\left({\theta ,\alpha} \right) = \ln p\left({\left. y \right|\theta ,\alpha} \right)} \cr {= - {1 \over 2}{{\left({y - m\left(\theta \right)} \right)}^T}{C^{- 1}}\left(\alpha \right)\left({y - m\left(\theta \right)} \right)} \cr {- {1 \over 2}\ln \det \left({2\pi C\left(\alpha \right)} \right),} \cr} $(1)

where y is the photometric data and θ is the vector of the fitted planetary parameters given in Table 2 as well as the limbdarkening coefficients and stellar density. The light curve model m(θ) was obtained by computing the transit timings for the chosen type of orbit (Keplerian ephemerides or n-body), and then modeling the transits of each planet with the batman package (Kreidberg 2015), with a supersampling parameter set to 29.42 min to account for the long exposure of the dataset. The effective temperature, log g, and metallicity of the star (Table 1) were used to compute the quadratic limb-darkening coefficients u1 and u2 and their error bars were adapted to the Kepler spacecraft using LDCU4. Based on the limb-darkening package (Espinoza & Jordán 2015), LDCU uses two libraries of stellar atmosphere models ATLAS9 (Kurucz 1979) and PHOENIX (Husser et al. 2013) to compute stellar intensity profiles for a given pass-band. Remaining long-term trends were modelled using the S+LEAF (Delisle et al. 2020). S+LEAF is a C library with Python wrappers that implements an optimised GP framework. While the computational cost of classical GP implementations typically scales as the cube of the dataset size, the cost of a S+LEAF GP scales linearly (Foreman-Mackey et al. 2017; Delisle et al. 2020, 2022). We used a Gaussian process framework with a Matérn 3/2 kernel whose timescale was forced to be above one day (uniform prior of the log of the timescale τGP set to U[0,3]) to avoid interfering with the modelled transits. A jitter term was also added to all photometric measurements. α is the vector of the noise parameters (jitter, σGP, τGP). C(α) is the corresponding covariance matrix.

The posteriors of the fits are summarised in Table 2, with the Keplerian model on the left and the n-body model on the right. The recovered stacked transits are shown in Fig. 4. The difference in the models for the two outer candidates did not significantly affect the fit of the inner candidate, for which the fit converged to a radius of 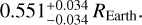0.551−0.034+0.034REarth$0.551_{- 0.034}^{+ 0.034}{R_{{\rm{Earth}}}}$ The difference is significant for the two resonant planets: the transits stacked along a Keplerian ephemerides yield a strong dispersion of points in and near the transit, which is responsible for the falsepositive flag attributed to KOI3184.02 by the Kepler pipeline. Stacking the transits along the TTV-corrected transit timings greatly reduces the in-transit scattering, as can be seen on the right-hand side of Fig. 4. The photodynamic fit yields radii of 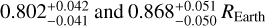4.020192−3.4e−05+3.5e−05$4.020192_{- 3.4e - 05}^{+ 3.5e - 05}$ for Kepler 1972 b and c, respectively, while the Keplerian model yields radii smaller by ~28% and ~35%, respectively. Finally, the photodynamic fit yields projected inclinations of 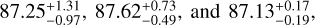87.25−0.97+1.31,87.62−0.49+0.73$\matrix{{87.25_{- 0.97}^{+ 1.31},} & {87.62_{- 0.49}^{+ 0.73}} \cr} $ which are consistent with a coplanar system.

The estimated amasses are of 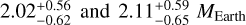4.02−1.31+1.44 and 3.33−1.07+1.17 ρEarth$4.02_{- 1.31}^{+ 1.44}\,{\rm{and}}\,3.33_{- 1.07}^{+ 1.17}\,{\rho_{{\rm{Earth}}}}$ for Kepler-1972 b and c, respectively, resulting in densities of 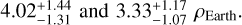m01/(m01+m02)=0.489−0.013+0.014${{{m_{01}}} \mathord{\left/ {\vphantom {{{m_{01}}} {\left({{m_{01}} + {m_{02}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({{m_{01}} + {m_{02}}} \right)}} = 0.489_{- 0.013}^{+ 0.014}$ Although the densities are poorly constrained, the planets appear to be denser than the Earth. The mass distribution between the two planets is well constrained 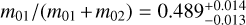(e12+c2e22Δϖ=ϖ2−ϖ1)$\left({\sqrt {e_1^2 + {c^2}e_2^2} \Delta \varpi = {\varpi_2} - {\varpi_1}} \right)$, while the total mass of the planets is not. This is due to the TTV signal dependency on the parameters: the mass distribution is linked to the relative amplitude of the TTVs between the two planets, while the total planetary mass is constrained by the TTV period (Agol et al. 2005; Nesvorný & Vokrouhlický 2016). The latter could not be properly estimated with the available baseline: as can be seen on the posterior of the TTVs shown in Fig. 3, there is a range of TTV periods that are consistent with the observed signal.

thumbnail Fig. 1

Top: river diagrams of KOI3184 at the period 7.5472d (left) and 11.3251d (right). The bottom row displays the first 7.5472 (resp. 11.3251) days of data for KOI3184, with the colour code representing the normalised flux. Each subsequent row displays a new set of 7.5472 (resp. 11.3251) days of data. The flux has been clipped at 3σ for visibility, and missing data have been replaced by a flux of 1. Bottom: corresponding RIVERS.deep confidence matrices, which show for each timing of the rivers diagram the ‘confidence’ for it to belong to the track of a planet. See Sect. 2.1.2 for more details about the confidence matrix.
thumbnail Fig. 2

RIVERS periodogram of KIC 4735826: for each period, we show the confidence of the RIVERS.deep classifier that the corresponding river diagram contains the track of a planet. As the false positive rate of the classifier is typically of a few percent, a photo dynamical fit of the data is required to confirm the planetary nature of the signals.
thumbnail Fig. 3

TTVs for Kepler-1972 b (top) and Kepler-1972 c (bottom). The black error bars represent the TTVs coming from the RIVERS.deep method which is the network’s highest confidence for the timing of each transit (highlighted pixels in Fig. 1). These timings are used as TTV proxies to initialise the photodynamical fit close to its final solution, but are not transit timings fitted to the data. Their error bars indicate the sensitivity of the method (30 min). We show 300 samples resulting from the photodynamic fit of the light curve in grey, and the solid coloured curves correspond to the best fit.
Table 1

Stellar global properties of Kepler-1972.

Table 2

Fitted and derived properties of the planets and candidate of the Kepler-1972 system.

thumbnail Fig. 4

Stacked transits of KOI3184.03 (top), Kepler-1972 b (middle), and Kepler-1972 c (bottom). The left panel results from the stacking along the Keplerian ephemeride, which is the left solution in Table 2. The right panel shows the result of stacking along the Keplerian ephemeride for the inner planet, and the n-body solution for Kepler-1972 b and c, which is the solution on the right-hand side of Table 2.

3 The resonant pair of Kepler-1972

In this section, we study a subpopulation of 2300 randomly chosen samples from the posteriors presented in Table 2. Figure 5 shows the projection of these samples in the 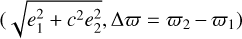g=(m2/m1)a2/a1$g = \left({{{{m_2}} \mathord{\left/ {\vphantom {{{m_2}} {{m_1}}}} \right. \kern-\nulldelimiterspace} {{m_1}}}} \right)\sqrt {{{{a_2}} \mathord{\left/ {\vphantom {{{a_2}} {{a_1}}}} \right. \kern-\nulldelimiterspace} {{a_1}}}} $ plane (c = –1. 22 for the 3:2 MMR and is discussed in Sect. 5.2 of Leleu et al. 2021b). The ej and ϖj represented here are the fitted initial conditions at the date 2454943.5394 BJD.

3.1 Stability

We verified the stability of the posteriors using the frequency analysis criterion (Laskar 1990, 1993), using the same implementation as in Leleu et al. (2021a,b). For this stability analysis, the resonant pair and the inner candidate at 4.02 days were considered. As only the radius of this inner candidate could be derived in our analysis, we assumed its density to be of 2.6 ρEarth, an arbitrary value which is consistent with the densities of the two outer planets. The top panel of Fig. 5 shows the resulting criterion for each initial condition, for n-body integration over 105 years. We find that the bulk of the low-eccentricity part of the posterior is stable for more than 106 years, which together correspond to more than 45 billion orbits of the resonant pair. On the other hand, a significant part of the posterior is unstable on a short timescale (red dots on the top panel of Fig. 5) for eccentricities typically higher than ~0.1.

thumbnail Fig. 5

Posterior of the solution shown in Table 2. The c = -1.22 parameter is discussed in (Leleu et al. 2021b). Top: stability of the posteriors, ranging from stable (blue) to unstable (red). Middle: value of the Hamiltonian parameter Γ′ over the posterior. Bottom: smallest amplitude between the two resonant angles. Grey dots indicate a circulation of both of them.
thumbnail Fig. 6

Surface of a section in the (Γ′,X) plane of the Hamiltonian (2). The black line shows the positions of the family of elliptic fixed points (the hyperbolic family exists for larger values of X and is not displayed here). The red line shows the intersection of the separatrix with the Y = 0 plane for each value of Γ′. The coloured dots show the intersection of the trajectories emanating from the initial conditions of the posterior summarised in Sect. 2 and the (Γ′, X) plane, for Kepler-1972 (this paper) and Kepler-1705 (Leleu et al. 2021b).

3.2 Dynamics and TTV degeneracy

3.2.1 Resonant state of the system

We consider the Hamiltonian formulation of the second fundamental model for resonance of (Henrard & Lemaitre 1983). Using the one-degree-of-freedom model of first-order resonances presented in Deck et al. (2013), the dynamics of a resonant system can be derived from the equations canonically associated with the conjugated variables X and Y of the Hamiltonian: H=12[12(X2+Y2)−Γ′]2−X.$H = {1 \over 2}{\left[{{1 \over 2}\left({{X^2} + {Y^2}} \right) - \Gamma \prime} \right]^2} - X.$(2)

The change of coordinates from the orbital elements and masses to the variables X and Y are given in Sect. 2 of Deck et al. (2013). For Γ′ < 1.5, the model has a single family of elliptic fixed points and no separatrix. At Γ′ = 1.5, a bifurcation occurs and for Γ′ > 1.5 there are two families of elliptic fix points and one family of hyperbolic fix points from which emanates a sep- aratrix. Systems are considered formally resonant when Γ′ > 1.5 and they lie inside the separatrix. As Y = 0 for all fixed points, and all trajectories of the Hamiltonian 2 cross the Y = 0 line, we show a surface of section of the Hamiltonian for Y = 0 in Fig. 6. This representation is equivalent to the one presented in Nesvorný & Vokrouhlický (2016) and Nesvorny et al. (2022). The blue dots represent the posterior of Kepler-1972, while the orange dots show the position of Kepler-1705 for comparison. Despite the large uncertainties on the orbital parameters and masses due to the observation baseline shorter than the resonant period, the whole posterior lies inside the 3:2 MMR.

3.2.2 TTV degeneracy

In Leleu et al. (2021b) we introduced the variables 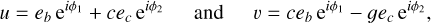u=ebeiϕ1+ceceiϕ2 and u=cebeiϕ1−geceiϕ2,$u = {e_b}{{\rm{e}}^{i{\phi_1}}} + c{e_c}{{\rm{e}}^{i{\phi_2}}}\quad {\rm{and}}\quad u = c{e_b}{{\rm{e}}^{i{\phi_1}}} - g{e_c}{{\rm{e}}^{i{\phi_2}}},$(3)

(Mardling, in prep.), where 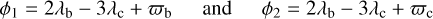ϕ1=2λb−3λc+ϖb and ϕ2=2λb−3λc+ϖc${\phi_1} = 2{\lambda_{\rm{b}}} - 3{\lambda_{\rm{c}}} + {\varpi_{\rm{b}}}\quad {\rm{and}}\quad {\phi_2} = 2{\lambda_{\rm{b}}} - 3{\lambda_{\rm{c}}} + {\varpi_{\rm{c}}}$(4)

are the resonant angles for the 3:2 resonance, c is a function of the Laplace coefficients whose value is−1.23 for the 3:2 commensurability, and 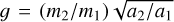Rb=0.802−0.042+0.042REarth${R_{\rm{b}}} = 0.802_{- 0.042}^{+ 0.042}{R_{{\rm{Earth}}}}$. For Kepler-1705 (the system discovered in Leleu et al. 2021b), a full resonant period is observed, and as a result Γ’ (and the corresponding range of values of u) is well determined and varies little across the posterior. In that case, we showed that the theoretical posterior of the variables ej and ϖj could be obtained by varying the real and imaginary parts of v in the range [–0.2, 0.2]; indeed, the TTV signal constrains the resonant part of the eccentricity u, but is blind to the free part v (Mardling, in prep.; Leleu et al. 2021b). However, in Kepler-1972, Γ’ (and u) is poorly constrained across the posterior, which parametrizes an additional degeneracy for the ej and ϖj variables; see the middle panel of Fig. 5.

4 Summary and conclusion

For planets that are too small to induce individually detectable transits, the shape of their transit is derived from light curves that are stacked along constant periods. In this case, TTVs can lead to erroneous estimations of the transit depth and duration, or even create a signal that is no longer recognised as a transit. We illustrate this on KOI-3184.02, which is flagged as “Not transit-like false positive” in the NASA Exoplanet Archive as of November 2021. Applying the RIVERS methods, we retrieved the track of KOI-3184.01 and KOI-3184.02 in the light curve. We show that both of these planets have anti-correlated TTVs of 6 hours of peak-to-peak amplitude, which are responsible for the apparent incoherence of the transit signature. We now name these planets Kepler-1972 b and c. As it was the case for Kepler-1705 (Leleu et al. 2021b), the recovered planets have individual transit S/Ns of ~ 1, showcasing the performance of the approach in recovering individual transits that would otherwise be lost in the noise.

Kepler-1972 b and c is a pair of Earth-sized planets with 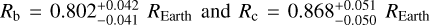Rc=0.868−0.050+0.051REarth${R_{\rm{c}}} = 0.868_{- 0.050}^{+ 0.051}{R_{{\rm{Earth}}}}$, with similar masses 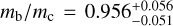I.03=87.25−0.97+1.31,Ib=87.62−0.49+0.73${I_{.03}} = 87.25_{- 0.97}^{+ 1.31},{I_{\rm{b}}} = 87.62_{- 0.49}^{+ 0.73}$. The observed TTV signal is enough to show that the pair is formally inside the 3:2 mean motion resonance (inside the separatrix). However, the baseline of the observation is not long enough to cover a full period of the TTV signal, leading to a somewhat imprecise estimation of the planet masses, putting an 1σ upper limit at Mb = 2.58 MEarth and Mc = 2.70 MEarth. 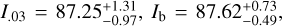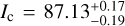Fitting the inner candidate (KOI-3184.03, P = 4.02[day]) at the same time as the resonant pair, we show that the three projected inclinations are 1σ compatible: Ic=87.13−0.19+0.17${I_{\rm{c}}} = 87.13_{- 0.19}^{+ 0.17}$ and Ic=87.13−0.19+0.17${I_{\rm{c}}} = 87.13_{- 0.19}^{+ 0.17}$ degrees. This is consistent with a co-planar three-planet system, which increases the probability that the 4.02d signal is also of planetary nature.

Recovering a planetary signal from a Kepler false positive shows that special care needs to be taken in the treatment of low-S/N planet candidates in transit surveys, as the stacking methods broadly used is not well suited when planet-planet interactions induce TTVs larger than the transit duration. This effect is especially relevant for the Kepler mission, TESS polar observations, and the upcoming PLATO mission.

Acknowledgements

This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation and benefited from the seed-funding program of the Technology Platform of PlanetS. The authors acknowledge the financial support of the SNSF.

References

  1. Agol, E., & Deck, K. 2016, ApJ, 818, 177 [Google Scholar]
  2. Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [Google Scholar]
  3. Agol, E., Dorn, C., Grimm, S. L., et al. 2021, Planet. Sci. J., 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
  4. Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Batygin, K., & Morbidelli, A. 2013, A&A, 556, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Brewer, J. M., & Fischer, D. A. 2018, ApJS, 237, 38 [NASA ADS] [CrossRef] [Google Scholar]
  7. Carter, J. A., Agol, E., Chaplin, W. J., et al. 2012, Science, 337, 556 [Google Scholar]
  8. Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [Google Scholar]
  9. Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 475, 5023 [Google Scholar]
  10. Coleman, G. A. L., Leleu, A., Alibert, Y., & Benz, W. 2019, A&A, 631, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Deck, K. M., Payne, M., & Holman, M. J. 2013, ApJ, 774, 129 [Google Scholar]
  12. Deck, K. M., Agol, E., Holman, M. J., & Nesvornÿ, D. 2014, ApJ, 787, 132 [CrossRef] [Google Scholar]
  13. Delisle, J. B. 2017, A&A, 605, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Delisle, J.-B., Correia, A. C. M., Leleu, A., & Robutel, P. 2017, A&A, 605, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Delisle, J. B., Ségransan, D., Dumusque, X., et al. 2018, A&A, 614, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Delisle, J. B., Hara, N., & Ségransan, D. 2020, A&A, 638, A95 [EDP Sciences] [Google Scholar]
  17. Delisle, J. B., Unger, N., Hara, N. C., & Ségransan, D. 2022, A&A, 659, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dobrovolskis, A. R., & Borucki, W. J. 1996, in BAAS, 28, 1112 [NASA ADS] [Google Scholar]
  19. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [Google Scholar]
  20. Emsenhuber, A., Mordasini, C., Burn, R., et al. 2022, A&A, 656, A69 [Google Scholar]
  21. Espinoza, N., & Jordan, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
  22. Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
  23. Gaia Collaboration (Brown, A.G.A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. García-Melendo, E., & López-Morales, M. 2011, MNRAS, 417, L16 [NASA ADS] [Google Scholar]
  25. Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [Google Scholar]
  26. Grimm, S. L., Demory, B.-O., Gillon, M., et al. 2018, A&A, 613, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Henrard, J., & Lemaitre, A. 1983, Celest. Mech., 30, 197 [Google Scholar]
  28. Holczer, T., Mazeh, T., Nachmani, G., et al. 2016, ApJS, 225, 9 [Google Scholar]
  29. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Jégou, S., Drozdzal, M., Vazquez, D., Romero, A., & Bengio, Y. 2017, in Proceedings of the IEEE conference on computer vision and pattern recognition workshops, 11 [Google Scholar]
  31. Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L87 [Google Scholar]
  32. Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
  33. Kane, M., Ragozzine, D., Flowers, X., et al. 2019, AJ, 157, 171 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [Google Scholar]
  35. Kreidberg, L. 2015, PASP, 127, 1161 [Google Scholar]
  36. Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  37. Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
  38. Laskar, J. 1993, Phys. D, 67, 257 [NASA ADS] [CrossRef] [Google Scholar]
  39. Leconte, J., Wu, H., Menou, K., & Murray, N. 2015, Science, 347, 632 [NASA ADS] [CrossRef] [Google Scholar]
  40. Leleu, A., Alibert, Y., Hara, N. C., et al. 2021a, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Leleu, A., Chatel, G., Udry, S., et al. 2021b, A&A, 655, A66 [CrossRef] [Google Scholar]
  42. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  43. Lithwick, Y., Xie, J., & Wu, Y. 2012, ApJ, 761, 122 [Google Scholar]
  44. Mazeh, T., Nachmani, G., Holczer, T., et al. 2013, ApJS, 208, 16 [Google Scholar]
  45. Mordasini, C. 2018, Planet. Popul. Synth., 143 [Google Scholar]
  46. Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Nesvorný, D., & Vokrouhlický, D. 2014, ApJ, 790, 58 [CrossRef] [Google Scholar]
  48. Nesvorný, D., & Vokrouhlický, D. 2016, ApJ, 823, 72 [Google Scholar]
  49. Nesvorný, D., Kipping, D., Terrell, D., et al. 2013, ApJ, 777, 3 [CrossRef] [Google Scholar]
  50. Nesvorny, D., Chrenko, O., & Flock, M. 2022, ApJ, 925, 38 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rowe, J. F., & Thompson, S. E. 2015, ArXiv e-prints, [arXiv:1504.00707] [Google Scholar]
  52. Xie, J.-W., Wu, Y., & Lithwick, Y. 2014, ApJ, 789, 165 [NASA ADS] [CrossRef] [Google Scholar]
  53. Zhu, W., Petrovich, C., Wu, Y., Dong, S., & Xie, J. 2018, ApJ, 860, 101 [Google Scholar]

All Tables

Table 1

Stellar global properties of Kepler-1972.

In the text
Table 2

Fitted and derived properties of the planets and candidate of the Kepler-1972 system.

In the text

All Figures

thumbnail Fig. 1

Top: river diagrams of KOI3184 at the period 7.5472d (left) and 11.3251d (right). The bottom row displays the first 7.5472 (resp. 11.3251) days of data for KOI3184, with the colour code representing the normalised flux. Each subsequent row displays a new set of 7.5472 (resp. 11.3251) days of data. The flux has been clipped at 3σ for visibility, and missing data have been replaced by a flux of 1. Bottom: corresponding RIVERS.deep confidence matrices, which show for each timing of the rivers diagram the ‘confidence’ for it to belong to the track of a planet. See Sect. 2.1.2 for more details about the confidence matrix.
In the text
thumbnail Fig. 2

RIVERS periodogram of KIC 4735826: for each period, we show the confidence of the RIVERS.deep classifier that the corresponding river diagram contains the track of a planet. As the false positive rate of the classifier is typically of a few percent, a photo dynamical fit of the data is required to confirm the planetary nature of the signals.
In the text
thumbnail Fig. 3

TTVs for Kepler-1972 b (top) and Kepler-1972 c (bottom). The black error bars represent the TTVs coming from the RIVERS.deep method which is the network’s highest confidence for the timing of each transit (highlighted pixels in Fig. 1). These timings are used as TTV proxies to initialise the photodynamical fit close to its final solution, but are not transit timings fitted to the data. Their error bars indicate the sensitivity of the method (30 min). We show 300 samples resulting from the photodynamic fit of the light curve in grey, and the solid coloured curves correspond to the best fit.
In the text
thumbnail Fig. 4

Stacked transits of KOI3184.03 (top), Kepler-1972 b (middle), and Kepler-1972 c (bottom). The left panel results from the stacking along the Keplerian ephemeride, which is the left solution in Table 2. The right panel shows the result of stacking along the Keplerian ephemeride for the inner planet, and the n-body solution for Kepler-1972 b and c, which is the solution on the right-hand side of Table 2.
In the text
thumbnail Fig. 5

Posterior of the solution shown in Table 2. The c = -1.22 parameter is discussed in (Leleu et al. 2021b). Top: stability of the posteriors, ranging from stable (blue) to unstable (red). Middle: value of the Hamiltonian parameter Γ′ over the posterior. Bottom: smallest amplitude between the two resonant angles. Grey dots indicate a circulation of both of them.
In the text
thumbnail Fig. 6

Surface of a section in the (Γ′,X) plane of the Hamiltonian (2). The black line shows the positions of the family of elliptic fixed points (the hyperbolic family exists for larger values of X and is not displayed here). The red line shows the intersection of the separatrix with the Y = 0 plane for each value of Γ′. The coloured dots show the intersection of the trajectories emanating from the initial conditions of the posterior summarised in Sect. 2 and the (Γ′, X) plane, for Kepler-1972 (this paper) and Kepler-1705 (Leleu et al. 2021b).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.