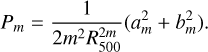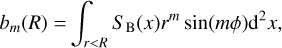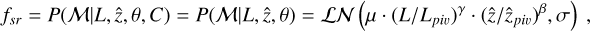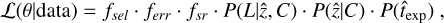| Issue |
A&A
Volume 661, May 2022
The Early Data Release of eROSITA and Mikhail Pavlinsky ART-XC on the SRG mission
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202141639 | |
| Published online | 18 May 2022 | |
The eROSITA Final Equatorial-Depth Survey (eFEDS)
Characterization of morphological properties of galaxy groups and clusters
1
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching,
Germany
e-mail: vittorio@mpe.mpg.de
2
IRAP, Université de Toulouse, CNRS, UPS, CNES,
Toulouse,
France
3
Argelander-Institut für Astronomie (AIfA), Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
4
Universitaets-Sternwarte Muenchen, Fakultaet fuer Physik, LMU Munich,
Scheinerstr. 1,
81679
Munich,
Germany
5
Hamburger Sternwarte, University of Hamburg,
Gojenbergsweg 112,
21029
Hamburg,
Germany
6
Faculty of Physics, Ludwig-Maximilians-Universität,
Scheinerstr. 1,
81679
Munich,
Germany
7
Department of Physics, Nara Women’s University, Kitauoyanishi-machi,
Nara
630–8506,
Japan
Received:
25
June
2021
Accepted:
11
November
2021
Context. Morphological parameters are the estimators for the dynamical state of clusters of galaxies. Surveys performed at different wavelengths through their selection effects may be biased toward, different populations of clusters. For example, X-ray surveys are biased to detecting cool-core clusters as opposed to Sunyaev-Zel’dovich (SZ) surveys being more biased toward non-cool-core systems. Understanding the underlying population of clusters of galaxies in surveys is of the utmost importance when these samples are to be used in astrophysical and cosmological studies.
Aims. We present an in-depth analysis of the X-ray morphological parameters of the galaxy clusters and groups detected in the eROSITA Final Equatorial-Depth Survey (eFEDS). The eFEDS, completed during the performance verification phase of the Spectrum-Roentgen-Gamma(SRG)/eROSITA telescope, is designed to provide the first eROSITA X-ray selected sample of galaxy clusters and groups.
Methods. We studied the eROSITA X-ray imaging data for a sample of 325 clusters and groups that were significantly detected in the eFEDS field. We characterized their dynamical properties by measuring a number of dynamical estimators: concentration, central density, cuspiness, centroid shift, ellipticity, power ratios, photon asymmetry, and the Gini coefficient. The galaxy clusters and groups detected in eFEDS cover a luminosity range of more than three orders of magnitude and a wide redshift range out to 1.2. They provide an ideal sample on which the redshift and luminosity evolution of the morphological parameters can be studied and the underlying dynamical state of the sample can be characterized. Based on these measurements, we constructed a new dynamical indicator, the relaxation score, for all the clusters in the sample.
Results. We find no evidence for a bimodality in the distribution of the morphological parameters of our clusters. We instead observe a smooth transition from the cool core to non-cool core and from relaxed to disturbed states, with a preference for skewed distributions or log-normal distributions. A significant evolution in redshift and luminosity is also observed in the morphological parameters we examined after taking the selection effects into account.
Conclusions. We determine that in contrast do ROSAT-based cluster samples, our eFEDS-selected cluster sample is not biased toward cool-core clusters, but contains a similar fraction of cool-cores as SZ surveys.
Key words: galaxies: clusters: intracluster medium / galaxies: clusters: general / X-rays: galaxies: clusters
© V. Ghirardini et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Clusters of galaxies are the most massive virialized systems in the Universe. They are located at the densest nodes of the cosmic web. Most of the cluster mass is in the form of a dark matter halo, whose mass ranges from ~1013 M⊙ (low-mass groups) to ~ 1015 M⊙ (high-mass clusters). The baryonic mass is dominated by the so-called intracluster medium (ICM), which is a diffuse gas that is heated up to tens of millions of degrees Kelvin (~keV scale) by the deep gravitational potential well, and therefore emits X-rays mainly through bremsstrahlung.
According to the hierarchical structure formation scenario, clusters form from and evolve through multiple accretion and merging processes that frequently take place during their lifetimes (see Kravtsov & Borgani 2012, for a review). These processes leave their imprints on the dynamical state of a cluster and often manifest themselves as a disturbed ICM morphology with observing features such as shocks (e.g., Markevitch et al. 2002, 2005; Russell et al. 2010), cold fronts (Vikhlinin et al. 2001; Markevitch & Vikhlinin 2007) and substructures or clumps (Eckert et al. 2015; Parekh et al. 2015; Ghirardini et al. 2018). These features have been observed and studied mostly in recent years, enabled by the growth in the volume and depth of X-ray cluster surveys and the good spatial resolution of focusing X-ray telescopes. In addition to these prominent features, the elongated shape of a relaxed cluster can simply serve as an immediate indication of past mergers. Therefore, ICM morphology and its evolution with cosmic time and cluster mass can be used as a tracer for the formation history of clusters, and consequently place constraints on the evolution of the large-scale structure (e.g., Evrard et al. 1993; Mohr et al. 1995; Suwa et al. 2003; Ho et al. 2006; Weißmann et al. 2013). On smaller scales, feedback activities of the central active galactic nuclei (AGN) can also affect the morphology of the ICM by producing X-ray cavities and regulating the core properties (Fabian 1994; McNamara & Nulsen 2007; Fabian 2012). Several morphological parameters, such as the concentration and central gas density, have been widely used as indicators for cool cores and non-cool cores (CCs and NCCs) (e.g., Hudson et al. 2010; Santos et al. 2008). Because the measurements of other thermodynamic observables rely on much more expensive X-ray spectroscopic data, cluster morphology is a practical and effective probe for tracing the evolution of cool cores up to high redshifts (see, e.g., Santos et al. 2008, 2010, 2012). It therefore provides important clues to reveal the cycle of baryons in the centers of galaxy clusters.
Many attempts have been made to study galaxy clusters morphologically by introducing various morphological parameters (see, e.g, Santos et al. 2008; Rasia et al. 2013; Lovisari et al. 2017; Yuan & Han 2020). However, because the X-ray emission of a cluster can extend up to several megaparsec, different morphological parameters evaluate the cluster dynamical state at different scales and reflect different physical properties. For example, concentration, central density, and cuspiness are most sensitive to core properties; ellipticity characterizes the distribution of the ICM at large scales and can be used to estimate how long it will take for the main halo to virialize; the power ratio and Gini coefficient reflect the fluctuation in the surface brightness distribution, related to the level of stochastic gas motions; symmetry or asymmetry and the separation between the X-ray center and the brightest central galaxy (BCG) mainly indicate the offset of the cluster core with respect to the center of the gravitational potential well, which is usually associated with features such as core-sloshing that is induced by off-center mergers.
Studies of morphological parameters that investigate how these parameters evolve with cluster mass and redshift, or whether these parameters follow a relaxed vs disturbed or cool-core vs non-cool-core bimodal distribution, are obviously dependent on selection effects of the cluster sample. Early studies based on X-ray selected cluster samples mainly focused their attention on the possible presence of two distinct cluster populations, cool cores and non-cool cores. While first results did indeed find that clusters can be divided into two populations (e.g., Sanderson et al. 2009; Cavagnolo et al. 2009; Hudson et al. 2010), following works did not observe this bimodal distinction (e.g., Santos et al. 2010; Pratt et al. 2010; Ghirardini et al. 2017; Yuan & Han 2020). In the past decade, the detection of the Sunyaev-Zel’dovich (SZ; Sunyaev & Zeldovich 1972) effect of galaxy clusters opened a new window for observing and studying the morphological properties of clusters. The signal is largely independent of redshift, therefore recent SZ surveys conducted by Planck (Planck Collaboration VIII 2011; Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2016), the South Pole Telescope (SPT; Bleem et al. 2020), and the Atacama Cosmology Telescope (ACT; Hilton et al. 2021) in particular have increased the volume of ICM-based cluster samples at high redshift. Because X-ray and SZ signals depend differently on cluster thermodynamic properties, X-ray and SZ samples may not represent the same underlying cluster population. In particular, X-ray surveys preferentially detect more relaxed clusters, while SZ surveys detect more disturbed clusters (see, e.g., Rossetti et al. 2016, 2017; Andrade-Santos et al. 2017; Lovisari et al. 2017). On the other hand, other works reported no significant difference between X-ray and SZ samples in their morphology distribution (Nurgaliev et al. 2013, 2017; Mantz et al. 2015; McDonald et al. 2017). The quantitative comparison of these results is not possible because the samples and morphological parameters used in these works differ from each other. Therefore, a coherent picture describing the morphological evolution of clusters is still lacking. The best approach to establish such a picture is through a more unified investigation of a more complete cluster sample that spans a wide range in mass and redshift.
Recently, the extended ROentgen Survey with an Imaging Telescope Array (eROSITA, Predehl et al. 2021) on board the Spectrum-Roentgen-Gamma (SRG) mission started its X-ray all-sky survey with unprecedented sensitivity (Sunyaev et al. 2021). eROSITA has been designed to provide unique survey science capabilities that will enable key cosmo logical studies with clusters of galaxies. With its large effective area (1365 cm2 at 1 keV), good spatial resolution (half-energy width of 26 arcsec averaged over the field of view at 1.49 keV), good spectral resolution (~ 80 eV full width at half maximum at 1 keV), and large field of view (1 deg diameter), it is able to quickly and efficiently scan large areas of the sky (Predehl et al. 2021).
The eROSITA Final Equatorial Depth Survey (eFEDS) is uniquely designed to test and demonstrate these survey capabilities. Covering an area of ~ 140 deg2, it has been observed during the performance verification (PV) phase at a depth of ~ 2.2 ks (non-vignetted), which is slightly deeper than the exposure of the final all-sky survey in equatorial fields. eFEDS will enable calibration of key mass scaling relations by combining X-ray properties with weak- lensing masses of detected groups and clusters that were obtained from the detailed analysis of Hyper-Suprime-Camera (HSC) data on the Subaru telescope (Chiu et al. 2022).
In this work, we study the morphological properties of the clusters and groups detected by eROSITA in the eFEDS field. We measure multiple morphological parameters using the eROSITA X-ray imaging data, we study the correlations in these parameters, and investigate their possible evolution with cosmic time and cluster luminosity after accounting for the selection effects of the sample. The paper is organized as follows. In Sect. 2 we briefly introduce our eFEDS cluster sample and eROSITA data analysis. In Sect. 3, we describe the morphological parameters that are studied in this work. In Sect. 4, we present our results regarding the dependence of the morphological parameters on redshift and luminosity, we introduce a new metric to measure morphological properties, and provide the comparison with previous literature results. Our conclusions are summarized and discussed in Sect. 5. Throughout this paper, we assume a concordance ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. Error bars correspond to the 1σ (68%) confidence level unless noted otherwise. In cases of an asymmetric error distribution, it corresponds to the difference between the median and the 16th and 84th percentiles of the distribution.
2 Data analysis
2.1 Source detection pipeline
The eROSITA Standard Analysis Software System (eSASS, Brunner et al. 2022) was used to process the eFEDS data. The eSASS (eSASSusers_201009) software consists of a pipeline whose end products are calibrated event lists for each eROSITA telescope module (TM). Pattern recognition and energy calibration are applied, good time intervals (GTI) and dead times are calibrated, and corrupted events, frames, and bad pixels are flagged. Celestial coordinates (i.e., equatorial RA and Dec) are assigned to each reconstructed event using star-tracker and gyro data. This allows us to project the photons onto the sky, and thus enables the production of images and exposure maps. In this work, we selected all valid pixel patterns, namely, single, double, triple, and quadruple events, and we removed events in the corners of the square CCDs. These events are detected with off-axis angles ≳30 arcmin, where the vignetting and point spread function (PSF) calibration is currently less accurate.
The source detection procedure is performed on the merged data from all seven eROSITA telescope modules. The detection is based on a sliding-cell method. In a first step, the algorithm scans the X-ray image with a local sliding window, which identifies enhancements above a certain threshold. The detected candidate objects are then excised from the images. The resulting source-free images are used to create background maps via adaptive filtering. The sliding window detection is then repeated, but this time using the background map that was created to search for signal excess with respect to this map. This produces another candidate source list. For each source candidate, a maximum likelihood PSF fitting algorithm determines the best-fit source parameters, detection, and extent likelihoods (Brunner et al. 2022). We applied this algorithm to the eFEDS data using images in the 0.2–2.3 keV energy band, an extent likelihood threshold of 6, a detection likelihood threshold of 5, and source extension threshold of 60 arcsec and detected 542 extended sources in total. For further details on the construction of the cluster catalog and some of the properties of the detected clusters from the eFEDS survey, we refer to Liu et al. (2022a).
In the full extent-selected catalog, our dedicated realistic simulations of the field, presented in Liu et al. (2022b), predict a contamination level of ~ 20%. To obtain a cleaner sample, we further applied selection criteria of extent likelihood and detection likelihood values higher than 12. This selection reduces the fraction of spurious clusters to ~ 14% in the eFEDS sample while decreasing the sample size to a total of 325 clusters. Figure 1 shows the luminosity (in the 0.5–2.0 keV energy band, see Bahar et al. 2022) versus redshift distribution of this sample. The luminosity covers a range from 9 × 1040 erg s−1 to 4 × 1044 erg s−1, and the redshift of the sample ranges from 0.017 out to 1.1 (Klein et al. 2022) using the recently developed code called Multi-Component Matched Filter (MCMF; Klein et al. 2018, 2019).
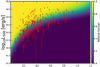 |
Fig. 1 Luminosity redshift distribution of the eFEDS clusters subsam-ple. As a background color reference, we show the eFEDS selection function with the same cuts according to extent and detection likelihoods. |
2.2 eROSITA imaging analysis
We applied the procedure presented in Ghirardini et al. (2021a) and Liu et al. (2022a) to all clusters in our sample in order to recover surface brightness and density profiles. While we refer to Ghirardini et al. (2021a) for details, we provide a short summary of the main steps of the analysis here. We start from the clean event files. We extracted images and exposure maps in the 0.5–2.0 keV energy band using the eSASS tasks evtool and expmap, respectively, with sizes as large as four times R5001 in arcmin (Chiu et al. 2022) around each cluster position. We directly fit the 2D distribution of the X-ray photons in the produced images of these clusters, allowing for multiple cluster fits at the same time (when more than one cluster is present in the image), to fit cluster centers and model detected point sources. As in our previous works, we modeled only bright point sources (with more than 0.1 counts per second) because modeling all of them would be too expensive computationally. These point sources were modeled as delta functions convolved with the PSF, that is, they take effects caused by PSF wings into account. Faint point sources were masked by removing a circular region around them with a radius large enough to ensure that the point source signal outside is consistent with the background level. The clusters were modeled in 2D using the Vikhlinin et al. (2006) model,
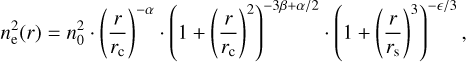 (1)
(1)
where the priors on our parameters are ϵ < 5 (as suggested by Vikhlinin et al. 2006), β > 1/3, and α > 0, and we froze rs = rc. When more clusters were present in the image, then this model was also used for these other clusters. The center of the clusters was not fixed, but was allowed to vary using a Gaussian prior centered on the detection location and σ of 20 arcsec. The resulting model cluster images were convolved with the PSF of eROSITA. The instrumental background model (particle-induced background and camera noise), see Freyberg et al. (2020), folded with the un-vignetted exposure map, and the sky background model (including the cosmic X-ray background and the soft background component from the galactic halo and local bubble) folded with the vignetted exposure map were added to the total model.
We then fit the image obtained from the eROSITA observations with the model image in 2D using the Monte Carlo Markov chain (MCMC) code emcee (Foreman-Mackey et al. 2013) to find the best-fit model parameters. We assumed a Poisson log-likelihood function 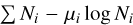 , where Ni are the model predicted counts, and μi are the observed counts in each pixel of the image.
, where Ni are the model predicted counts, and μi are the observed counts in each pixel of the image.
The fitting of the images can be interpreted as a true density when we consider the emissivity of the gas, which is determined, as in our previous works, by making use of the spectral information. Similarly as in Ghirardini et al. (2021a) and Liu et al. (2022a), we fit cluster spectra within R500 to obtain the conversion factor from count rate to emissivity. We determined the physical properties of the clusters in this way. We used only the products of imaging data, which are only density profiles, surface brightness profiles, and the luminosity within R500. The final luminosities we used in this work are provided in Bahar et al. (2022).
3 Description of the morphological parameters
In this section, we describe the different morphological parameters we used, which are the concentration parameter, central density, cuspiness, centroid shift, ellipticity, power ratios, photon asymmetry, and the Gini coefficient. We also provide details about how they were measured, and how instrumental factors affects these parameters. All these parameters were used in previous works to characterize the dynamical states of the underlying cluster samples in X-ray and SZ surveys (e.g., Santos et al. 2010; Rossetti et al. 2017; Nurgaliev et al. 2017; Lovisari et al. 2017).
For each of the computed parameters, we calculated the posterior distribution, from which we computed the median value and asymmetric errors using the 16th, 50th, and 84th percentiles of the distribution. We further point out that the entire distribution we calculated was used in both the fitting processes and the error propagation. When the parameter was computed directly from a previous MCMC, such as concentration, central density, ellipticity, and cuspiness, the distribution was computed directly by randomizing the choice of the parameter set in the second half of the chain. When parameters were computed directly from the images, however, such as the Gini coefficient, power ratios, centroid shift, and photon asymmetry, their distribution was computed by using a Monte Carlo process, by randomizing the pixel values of the observed cluster images.
We recall that some morphological parameters, such as power ratios (see Weißmann et al. 2013), are affected by low count statistics. However, we note that our main results are based on a number of different morphological parameters. To avoid being dominated by the core-properties, we retained the parameters that are more affected by low count statistics. Even though they add only a small weight, they account for the large-scale morphology of the detected clusters.
3.1 Central density
The central value of the gas density, n0, is another indicator of the relaxation state of clusters because relaxed systems are expected to have higher central densities (Hudson et al. 2010). We used the value of the electron density computed at 0.02 R500. This value is quite close to the center, and for the vast majority of eFEDS clusters, this is well within the field-of-view (FoV) averaged PSF value of eROSITA. However, as we also specified for the concentration parameter, the electron density profile was deconvolved by the eROSITA PSF, see Sect. 2.2. Therefore, the n0 we present is almost independent of PSF and can be used for a comparison with previous results. We did not consider the self-similar evolution of the density profile (McDonald et al. 2017; Ghirardini et al. 2021b) as a redshift correction for this morphological parameter because we modeled it separately in order to identify the actual evolution of the central density with redshift.
3.2 Concentration
The concentration parameter, cSB, has been introduced by Santos et al. (2008) as an indicator of a peaked X-ray surface brightness. This has been shown to correlate with the relaxation state of clusters. It is defined as the ratio of the integrated surface brightness in two different circular apertures. We used two definitions: the original definition introduced by Santos et al. (2008),
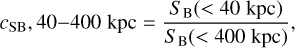 (2)
(2)
and a definition scaled with R500 (Maughan et al. 2012),
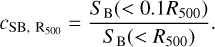 (3)
(3)
When we calculated the concentration parameter for our sample, the effects caused by the eROSITA PSF were fully taken into account. The concentration is not simply the count ratio in the two apertures, but comes from the 2D image fitting we described in Sect. 2.2, which produces PSF-deconvolved surface brightness profiles. This also means that the concentration we measure here, which is corrected for instrumental effects, can be directly compared with previous results with different instruments.
3.3 Centroid shift
The centroid shift parameter, defined as the variance of the centroid of the emission measured in increasing apertures,
![$w = {\left[{{1 \over {N - 1}}\sum\limits_{i = 1}^N {{{\left({{\Delta _i} - \bar \Delta} \right)}^2}}} \right]^{{1 \over 2}}}{1 \over {{R_{500}}}},$](/articles/aa/full_html/2022/05/aa41639-21/aa41639-21-eq5.png) (4)
(4)
has been studied many times in the literature (e.g., Mohr et al. 1993; Poole et al. 2006; Cassano et al. 2010; Lovisari et al. 2017). Disturbed systems are expected to have high centroid shift values. We recall that because centroid shift is computed directly on eROSITA images, this parameter is affected by instrumental PSF, which prevents a direct comparison with literature results.
3.4 Ellipticity
The ellipticity parameter, ϵ, is defined as the ratio of the minor and major axes. In contrast to several past studies, we did not compute the two axes using the second-order moments (variance) of the flux distribution in the cluster image because statistically, the variance is the width of the distribution only when the distribution is Gaussian. It is instead known that the photon distribution in cluster images is not Gaussian, but is similar to a β-model. Therefore, we measured the ellipticity by extending the analysis described in Sect. 2.2, allowing the density profile to be elliptical and rotated on the plane of the sky. This was accomplished by introducing a rotation angle and the ellipticity in the model construction of the image. In short, the 2D density profile along the x-axis was squeezed by changing the core radius as rc,x = ∈ x rc,y, and then it was rotated by an angle θ. The best-fitting parameter ∈ is the ellipticity we adopted in this work. We note that we placed a uniform prior between 0 and 1 on the ellipticity and a uniform prior between 0 and π on the rotation angle and not priors between 0 and 2π to avoid problems caused by the π rotational symmetry of the ellipse.
3.5 Cuspiness
The cuspiness parameter, α, introduced by Vikhlinin et al. (2007), measures the slope of the density profile at a specific radius. We used the value of the slope at 0.04 R500 as
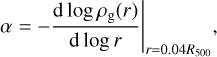 (5)
(5)
where ρg(r) is the gas-mass density profile. This particular radius has previously been used in the literature (e.g., Lovisari et al. 2017) because it is close enough to the core for cooling to play an important effect, and it is far enough away to avoid the flattening of the profile caused by the AGN outflows. By following the procedure highlighted in Sect. 2.2, we recovered the PSF-deconvolved value for this slope in this case as well. Its value can therefore be directly compared with results in the literature.
3.6 Power ratios
The power ratios Pm consist of a 2D decomposition of the surface brightness distribution within a specific aperture, of R500, and they account for radial fluctuations because the higher the order of the power ratio, the higher the sensitivity to smaller fluctuations. They were introduced by Buote & Tsai (1995) and are defined as Pm0 = Pm/P0, where
![${P_0} = {\left[{{a_0}\log \left({{R_{500}}} \right)} \right]^2},$](/articles/aa/full_html/2022/05/aa41639-21/aa41639-21-eq7.png) (6)
(6)
The values of am and bm are calculated as
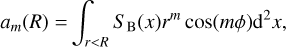 (8)
(8)
where the X-ray surface brightness SB(x) is calculated at the position expressed in polar coordinates x = (r, ϕ). In this work, we included only the power ratios up to order 4, that is, P10, P20, P30, and P40. We recall that power ratios can only be directly computed from the images, therefore it is not possible to corrected for the eROSITA PSF. Because the results will be affected by the PSF, a comparison with the literature will be challenging due to instrumental differences. For this reason, we did not compare our values with those of previous studies.
3.7 Photon asymmetry
Introduced by Nurgaliev et al. (2013), the photon asymmetry, Aphot, quantifies the degree of rotational symmetry in the emission of an object. Interestingly, Nurgaliev et al. (2013) investigated the evolution of the photon asymmetry when a cluster is moved to a different redshift. They reported that this parameter is insensitive (in the absence of instrumental effects) to the redshift of the cluster. It is therefore quite useful in determining the cluster morphology for cluster samples spanning a wide red-shift range. It has been introduced to study SPT-selected clusters, which span a wide redshift range, from 0.2 to 1.2, and therefore need a cluster morphological parameter that is independent of redshift. To compute it, we first used Watson’s test (Watson 1961), which compares two cumulative distributions (similarly to the Kolmogorov–Smirnov test) by evaluating the distance between the two:
![$U_N^2\left[{{F_N},G} \right] = N.\mathop {\min}\limits_{{\phi _0}} \int {{{\left({{F_N} - G} \right)}^2}{\rm{d}}G,} $](/articles/aa/full_html/2022/05/aa41639-21/aa41639-21-eq11.png) (10)
(10)
where N is the total counts in an annulus, FN is the observed cumulative distribution of the angle of all the photons located in a given annulus, G is the expected cumulative distribution assuming an axis-symmetric cluster, and ϕ0 is the starting angle for the cumulative distribution. In short, 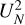 is the minimum value of the integrate squared difference between the observed and expected cumulative distribution over all possible starting points for the starting angles. If C is the number of cluster source counts in the annulus, then the distance between the two distribution is
is the minimum value of the integrate squared difference between the observed and expected cumulative distribution over all possible starting points for the starting angles. If C is the number of cluster source counts in the annulus, then the distance between the two distribution is
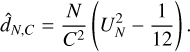 (11)
(11)
Finally, we can write the photon asymmetry as
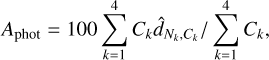 (12)
(12)
where the sum is performed over a set of annuli, which have edges of 0.05, 0.12, 0.2, 0.3, and 1 in units of R500. Because this parameter is calculated directly from the images, it is sensitive to the eROSITA PSF. It should therefore not be directly compared with previous works in the literature because the PSF might affect the redshift evolution.
3.8 Gini coefficient
The Gini coefficient is a standard measure of income inequality in economy. It was introduced in astronomy by Abraham et al. (2003). However, here we use the definition in Lotz et al. (2004) to measure the X-ray flux inhomogeneities in galaxy clusters,
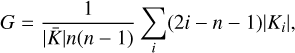 (13)
(13)
where Ki is the pixel value of the image in the ith pixel2, n is the total number of pixels, and 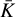 is the mean of the absolute values of all the pixels in the image. We point out that the Gini coefficient depends only little on surface brightness and does not require a precise center. Similarly, because it is calculated directly from images, it depends on the eROSITA PSF, and therefore cannot be compared directly with previous works.
is the mean of the absolute values of all the pixels in the image. We point out that the Gini coefficient depends only little on surface brightness and does not require a precise center. Similarly, because it is calculated directly from images, it depends on the eROSITA PSF, and therefore cannot be compared directly with previous works.
In Fig. 2, we show the parameter-parameter planes, and in Fig. 3 we show the correlation matrix between the parameters. As observed in previous works (e.g., Lovisari et al. 2017), the correlation between core-sensitive parameters such as central density and concentration and between core-insensitive parameters such as power ratios and photon asymmetry is strong.
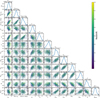 |
Fig. 2 Distribution of morphological parameters for the eFEDS clusters. |
4 Results
The eFEDS galaxy cluster and group sample covers the widest range in luminosity and redshift of the current X-ray and SZ selected samples and provides a unique opportunity to investigate the evolution of the several morphological parameters with redshift and luminosity. In this section, we provide the results of the evolution analysis and compare our result with similar studies in the literature that were based on different selections. However, these results must be compared with caution as the recently launched eROSITA detector properties, for example, PSF and effective area in particular, are quite different from those of the other instruments that were launched more than 20 yr ago, such as Chandra and XMM-Newton. A direct comparison with previous works on the morphological properties of clusters needs to be carefully interpreted, and a fair comparison is only possible for those parameters for which the instrumental effects have been corrected, namely concentration, central density, and cuspiness.
4.1 Analysis of the redshift and luminosity quartiles
In order to investigate the redshift dependence of the morphological parameters, we first divided our sample into four homogeneous sub samples. We selected the cluster population according to their quartile in the redshift distribution, z < 0.23, 0.23 < z < 0.35, 0.35 < z < 0.46, and z > 0.46, that is, with same number of clusters in each bin.
It must be noted that the detection (or non detection) of a significant redshift evolution of samples covering a wide redshift and luminosity span can be caused by the significant correlation between luminosity and redshift. Therefore, the redshift and luminosity evolution should be modeled simultaneously. Figure 1 shows that we observe a clear trend: at higher redshifts, we observe a larger number of luminous clusters because of the eROSITA selection function. Therefore, we further divided the samples based on their luminosity: L500 < 1.1 × 1043 erg s−1, 1.1 × 1043 erg s−1 < L500 < 2.6 × 1043 erg s−1, 2.6 × 1043 erg s−1 < L500 < 5.9 × 1043 erg s−1, and L500 > 5.9 × 1043 erg s−1. We used the quartile of the distribution in this case as well to have approximately the same number of clusters in each bin. The cumulative distributions of the morphological parameters for the sample of eFEDS clusters, split based on the above criteria, are shown in Figs. 4 and 5.
We performed the Kolmogorov-Smirnov statistical test (KS test) to check whether the morphological parameters in each redshift (and luminosity) bin are drawn from the same parent distribution as the unbinned cluster sample and whether there are clear indications for evolution with redshift. We compute the p-value from the KS test, which gives the probability for clusters in each redshift quartile to be indistinguishable from the unbinned cluster sample. Small value indicates that the morphological parameters in a specific redshift bin are clearly different than the unbinned distribution, while large values indicate they are indistinguishable. We find that the central density and the Gini coefficient have very small p-values, indicating that these two parameters might significantly evolve with redshift, while for the other parameters, with large p-values, such evidence is not present. On the other hand, all the morphological parameters, except for the cuspiness, centroid shift, ellipticity, and concentration, show a significant luminosity dependence. However, we recall that this dependence might be mimicked by or canceled out by the degeneracy between luminosity and redshift. A conclusive analysis of the redshift evolution or luminosity dependence can therefore only be derived when we model the two dependences simultaneously, considering the eROSITA selection function and luminosity function. In the next section, we provide the detailed analysis of this modeling.
 |
Fig. 3 Covariance between the morphological parameters in the eFEDS cluster sample. |
Best-tit values for the luminosity and redshift dependence.
4.2 Constraining the morphological parameters and their evolution with redshift and luminosity
The great survey capabilities of eROSITA allow us to reach luminosities as faint as 1041 erg s−1 (corresponding approximately to a group-scale mass of 1013 M⊙), which allows us to study high-redshift clusters up to z = 1.2. For the first time, we are able to constrain the evolution of luminosity and redshift of the morphological parameters simultaneously. To understand the underlying evolution in both redshift and luminosity simultaneously in morphological parameters, we modeled a power-law relation between each parameter ℳ, luminosity L500, and red-shift z. We took the selection function (probability of detecting a cluster with a given luminosity and redshift) and the luminosity function (the probability of detecting a cluster with a given luminosity and redshift at a fixed cosmology) into account, that is, we took the observed distribution in luminosity and redshift space of our clusters into account. We note that the scaling relation we used to connect intrinsic morphological parameters ℳ with luminosity and redshift is written as
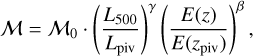 (14)
(14)
where Lpiv = 2.6 × 1043 erg s−1 and zPiV = 0.35 are the median luminosity and redshift, respectively, of the eFEDS sample. γ represents the luminosity-dependent slope, and β represents the slope of the redshift evolution. The likelihood derivation is provided in detail in Appendix B. The final likelihood for each cluster is written in Eq. (B.13). The best-fit values of all morphological parameters are given in Table 1. We show the morphological parameters as a function of luminosity and red-shift, while the best-fit models are shown in the gray shaded regions in Fig. 6. We highlight a few important results we obtained from our joint modeling below.
Central density (n0). The evolution of the central density with luminosity is slightly significant at a 4.5σ- level with a best-fit value of 0.17 ± 0.04. Overall, the central density evolves with redshift, in agreement with the self-similar evolution. The best-fit value of β is 1.5 ± 0.5. The expected value of the slope is 2 in the self-similar model. On the other hand, the significance of our measured evolution is only 3.2σ, therefore our result is marginally consistent with no redshift evolution.
The observed increase in central density values with luminosity can be easily explained: first we note that the gas density does not scale with mass according to the self-similar model. Results in the literature (Pratt et al. 2009; Lovisari et al. 2015) show, however, that the gas-mass fraction increases with cluster mass, and the only way to obtain a higher gas-mass fraction at a fixed scaled radius is by increasing the gas density profile, and therefore increasing the central density as well. On the other hand, McDonald et al. (2017) reported a lack of evolution in the distribution of the central density by combining the following three cluster samples: 49 low-z X-ray selected clusters (Vikhlinin et al. 2009), 90 SPT-selected clusters from z = 0.2 to z = 1.2 (McDonald et al. 2013), and the eight most massive clusters in the SPT cluster survey (Bleem et al. 2015) above z = 1.2. They interpreted this as lack of evolution in the core properties of clusters in the last ~lOGyr. A similar result was later reported in Ghirardini et al. (2021b), who compared the core properties of the same eight most massive clusters in SPT (Bleem et al. 2015) above z = 1.2, and a Planck -selected sample of 12 low-redshift (z < 0.1) clusters (X-COP, Eckert et al. 2017). In contrast, Sanders et al. (2018) analyzed a sample of 83 SPT-selected clusters from z = 0.2 to z = 1.2 and found no significant difference with respect to the self-similar evolution model. One important remark is that McDonald et al. (2017) selected clusters in order to satisfy evolutionary requirements, meaning that clusters at low redshift where chosen in a mass range expected from the evolutionary scenario (Fakhouri et al. 2010). They might therefore not be representative of the cluster population, but of how single clusters are expected to evolve.
Concentration parameter (cSB). Interestingly, concentration computed in terms of R500, cSB, R500 as defined in Maughan et al. (2012) is consistent with no evolution with both luminosity, with a slope of −0.04 ± 0.03), and redshift, with a slope of −0.2 ± 0.4. However, when we use the concentration defined with physical distances instead, cSB, 40−400 kpc as defined in Santos et al. (2008), we measure a significant luminosity dependence, (−0.23 ± 0.04), and no redshift evolution, (0.7 ± 0.5). This might be a selection effect, where at low luminosity we tend to detect mostly cool-core clusters that present a peaked surface brightness. However, we argue that because the same trend is not observed for the concentration computed using apertures with respect to R500, cSB, R500, this is not the case, and this trend is caused by the relative ratio of 400 kpc with R500. At low luminosity, R500 becomes smaller than 400 kpc, and this means that a larger fraction of cluster flux will be naturally concentrated within a fixed physical region. The concentration computed at a fixed physical radius will therefore increase significantly.
Centroid shift. This parameters shows a 3σ indication of a luminosity dependence and a 5.2σ significant redshift evolution. Interestingly, this parameter increases with redshift, which seems to indicate that at high redshift, clusters are more disturbed. However, we argue that at fixed luminosity, clusters at high red-shift have significantly fewer detected photons, and thus make centroid position vary strongly from one aperture to the next.
Ellipticity (∈) and cuspiness (α). Ellipticity does not show any significant dependence on luminosity (the slope is −0.012 ± 0.009) and redshift with a slope of 0.25 ± 0.09. The change in ellipticity in the sample with luminosity and red-shift is mild (~2σ). The cuspiness of the ICM changes with luminosity with a slope of 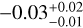 and evolves with red-shift with a slope of 0.5 ± 0.2. Similarly, the dependence of cuspiness on luminosity and redshift is moderate, <2σ and 2.6σ, respectively.
and evolves with red-shift with a slope of 0.5 ± 0.2. Similarly, the dependence of cuspiness on luminosity and redshift is moderate, <2σ and 2.6σ, respectively.
Power ratios (P10, P20, P30, and P40). All the power ratios indicate a significant luminosity and redshift dependence, which indicates that these parameters are difficult to interpret without a clear understanding of their evolution. We find that more luminous clusters have a lower power ratio and are therefore clusters that look more relaxed, and that clusters at higher redshift have higher power ratios and are therefore less relaxed-looking clusters.
Gini coefficient (G). The Gini coefficient shows a clear luminosity dependence with a formal significance of 21σ, where more luminous clusters have higher Gini values. Interestingly, we observe an anticorrelation of G with redshift at a 8σ confidence level, going in the direction of decreasing with increasing red-shift, which indicates the possible presence of more disturbed clusters at high redshift. This is particularly interesting because the eROSITA PSF is expected to produce smoother cluster images at higher redshift: they appear smaller on angular scales, and smoother images should result in higher Gini coefficients. This shows the great potential of eROSITA in understanding the larger fraction of more disturbed clusters at high redshift, as found in Santos et al. (2010). As a side note, we point out that at first glance, the Gini coefficient in Fig. 6 seems to increase with redshift, and the best-fit line shows the opposite trend. This is because we detect only the brightest clusters at high redshift, therefore the trend of an increase with redshift is only apparent, and at fixed luminosity, the Gini coefficient decreases. This is nicely captured by our best-fit line through the selection function.
Photon asymmetry (APhot). The photon asymmetry shows a clear dependence on luminosity with a slope of −0.53 ± 0.05, indicating that more luminous clusters tend to be more spherically symmetric. In other words, larger gravitational potential wells generate rounder objects. Furthermore, it shows a significant evolution with redshift with a slope of 4.3 ± 0.6. In particular, the plot shows that our analysis is able to disentangle an apparent redshift independence. Evolutions in redshift and luminosity conspire to produce an overall unevolving distribution, which starts to become clear when the color-coding is added to the figure.
Nurgaliev et al. (2017) compared a sample of 36 ROSAT-selected clusters (400 d, Burenin et al. 2007) in the redshift range 0.35 < z < 0.9 with a sample of 90 clusters selected from the SPT survey in the redshift range 0.25 < z < 1.2. Measuring the photon asymmetry, they reported no statistical difference between the morphological properties of their X-ray and SZ-selected cluster samples. Furthermore, they reported an absence of mass or redshift evolution in the photon asymmetry. They also studied a sample of 85 simulated clusters, applying X-ray and SZ selection. The measured X-ray morphology was indistinguishable, therefore they concluded that X-ray and SZ surveys probe the same cluster population. They interpreted this lack of evolution in the morphological properties as a lack of a direct correlation between the dynamical state of the clusters and these properties. Their results were confirmed by theoretical studies that found that substructure statistics can vary significantly on very short timescales during cluster mergers. The authors claimed that this absence of a difference between the X-ray and SZ cluster samples indicates that high-resolution (1 arcmin) SZ surveys are not biased toward selecting preferentially merging clusters, while other SZ instruments with lower resolution might still have a bias because it is more likely that multiple clusters along the line of sight contribute to the integrated signal.
In summary, it is difficult to properly quantify the effect of the PSF on the measured evolution with redshift for some parameters (Gini coefficient, photon asymmetry, and power ratios). The reduction in angular size of clusters at high redshift should imply that cluster images become smoother at higher redshift, and smoother images will result in larger Gini coefficients and lower photon asymmetry values. The fact that we observe the opposite trend implies that the underlying evolution of these parameters should be even stronger than the measured values. The same logic can then be applied to the power ratios because their evolution should in this case also be stronger than the measured ratios. The only parameter that would indicate the opposite trend, with more cool cores at high redshift, is the central density. However, in this case the expected evolution is not very significant, and is marginally consistent with no evolution at 3σ.
 |
Fig. 4 Cumulative distribution of the morphological parameters divided into four redshift bins. We indicate the p-value of the probability to be drawn from the same underlying distribution. |
 |
Fig. 6 In all four main panels, top left subpanel: distribution of morphological parameters vs. luminosity, color-coded with redshift. The black line shows the best-fitting line (see Sect. 4.2). In the bottom left subpanel, we show the distribution of morphological parameters vs. redshift, color-coded with luminosity. The black line again shows the best-fitting line. The gray shaded area represent the scatter around the best-fit line. The red data point shows (when a direct comparison can be made) the result value obtained by Lovisari et al. (2017), which can be directly compared with the blue data point, which shows our results when we restricted the luminosity and redshift range to the same range as in Lovisari et al. (2017). The orange data point represents the average morphological parameter values obtained in luminosity or redshift quintiles. We show parameters corrected for redshift and luminosity evolution against luminosity (in the top right subpanel) and redshift (in the bottom right subpanel). |
4.3 Redshift- and luminosity-independent morphological parameters
The fitting procedure we applied on our data to recovered the redshift evolution and luminosity dependence of our clusters, see Sect. 4.2. It can be also exploited to define new morphological parameters that are constructed from the original distributions after the luminosity and redshift dependence are factored out,
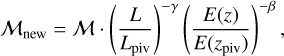 (15)
(15)
using γ and β from the corresponding row of Table 1. By construction, these newly defined parameters lack any redshift evolution or luminosity dependence and can therefore be used to properly and correctly investigate the presence or absence of bimodality in our parameter distribution. In Fig. 7, we show the changes in the distribution of the corrected morphological parameters when this correction is applied. Some correlations become tighter, while others become more loose. In particular the correlation between core properties, central density, both concentrations, and cuspiness become tighter, indicating that all these four parameters measure just the cluster core properties. Therefore, the connection among them is almost one to one. On the other hand, the correlation between parameters that are sensitive to large-scale fluctuations, power ratios, Gini coefficient, and photon asymmetry in particular, become much less significant, indicating that these parameters measure complementary properties of the large-scale emission of clusters.
4.4 New relaxation score
In the literature, morphological parameters are commonly used to characterize the physical state of the ICM, determining which clusters are relaxed and which are disturbed. Lovisari et al. (2017) used a morphological parameter that was previously introduced in Rasia et al. (2013). This parameter combines the concentration and centroid shift values and was then used to distinguish between the relaxed and disturbed systems. The authors measured the deviation from the mean value of concentration and centroid shift, adding these together, but changing the sign of the centroid shift deviation to take the anticorrelation between these two parameters into account. However, one important issue is that this parameter does not take the strength of the anticorre-lation into account, and because the correlation between these parameters is very strong, this parameter is likely affected by double-counting issues.
We here introduce a new parameter, the relaxation score, or Rscore. It contains the information that is stored in all the morphological parameters by taking the sign (positive or negative) of the correlations of the morphological parameters with respect to concentration and the strength of these correlations into account. The definition of Rscore is
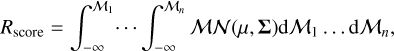 (16)
(16)
where ℳ(μ, Σ) is the multivariate normal PDF in n-dimensional space of our parameter distribution, where μ is an array containing the mean values for all the morphological parameters ℳ1 … ℳn, and Σ is the covariance matrix computed from our data. In other words, we computed the cumulative distribution function (CDF) in n-dimensional space. For the quantities that are anticorrelated with concentration, such as power ratios and photon asymmetry, we considered their reciprocal in the calculation of this quantity, Eq. (16), in order to build this parameter from quantities that are correlated, not from a mix of correlating and anticorrelating quantities. As noted before, to avoid being biased toward redshift and luminosity dependence in our parameters, we considered the corrected morphological parameters as introduced in Eq. (15) to compute the means and covariance matrix, and to compute the Rscore itself. By construction, the Rscore should be higher for objects with high concentration, central density, ellipticity, cuspiness, or Gini coefficient, and lower for objects with high photon asymmetry, high centroid shift, or high power ratios. This is reflected in Fig. 7.
We show the distribution of this newly introduced parameter in Fig. 8. At first glance, it looks unimodal, but we refer to the next section for an appropriate investigation of the best-fitting distribution for this new parameter. It is worth pointing out that this parameter was constructed with redshift- and luminosity-corrected morphological parameters. By construction, it therefore does not depend on redshift or luminosity.
Figure 9 shows the correlation between the concentration computed using the Maughan et al. (2012) definition with R500 and the relaxation score. The correlation between the two parameters is clear: the relaxation score increases with concentration. The correlation becomes insignificant above cSB, R500 = 0.27, which is the threshold adopted by Lovisari et al. (2017) to identify relaxed clusters. We interpret this as an indication that the concentration is a good indicator for probing the very central state of clusters, but it does not correlate well with the relaxation state. A relaxed cluster will generally have a cool core in its center, while the opposite may not be true: a merger along the line of sight (e.g., Dupke et al. 2007), or a merger in its initial stage might have a centrally peaked density profile. The mergers whose axis is along the line of sight might still not be visible from the cluster center prospective, while they are visible on a larger scale. Therefore we claim that clusters with a high concentration can still be disturbed clusters. This is supported by recent theoretical papers (e.g., Rasia et al. 2015; Biffi et al. 2016). On the other hand, by construction, the relaxation score is able to capture the ICM dynamics from small to large scales, and it can therefore be used to identify the cases in which a cool core is still existing in a disturbed cluster. Furthermore, Fig. 9 shows that the thresholds for disturbed clusters adopted by Lovisari et al. (2017) agree with the median of the log-normal best fit shown with the horizontal black line. This means that almost all the clusters to the left of the dashed line are also below the horizontal line. Therefore, we used this line to establish a threshold in terms of relaxation score: we define clusters as relaxed if Rscore > 0.0019, while they are defined as disturbed if the opposite holds.
This definition allows us to compute the fraction of relaxed clusters as a function of redshift by dividing the cluster sample into five redshift bins. In each bin, we counted the clusters based on their relaxation score. We had to add a further complication to this analysis: the relaxation score distribution for most clusters is wide and quite skewed, and computing the fraction using just the median values will therefore bias our results. We counted the number of clusters that satisfied our threshold by first randomizing the relaxation score values by using the MCMC obtained when estimating it. In other words, we performed 10 000 bootstrap iterations of the relaxation score for each cluster, and each time calculated the fraction of clusters that are relaxed.
The evolution of the fraction of objects that we classify as relaxed is shown in Fig. 10. The fraction of relaxed clusters is about 60-70% in the lowest redshift bin, and at the higher red-shift bins, it becomes about 40–50%. This is consistent with the cool-core fraction estimated in previous works (e.g., Rossetti et al. 2017; Sanders et al. 2018). We therefore find an indication (slightly more than 1σ) of a possible evolution with redshift of the fraction of relaxed clusters. We might argue, however, that the difference in the first bin might also not be a consequence of redshift evolution in the fraction of relaxed clusters, but might be caused by the incompleteness due to our source-finding and confirmation technique in the detection of very extended galaxy groups or clusters at low redshift with low surface brightness, similarly as was shown in a focused reanalysis of ROSAT observations (Xu et al. 2018).
For future works using this newly introduced parameter, we remark that the exact value obtained for the relaxation score is dependent upon the parameters and the instrument used. When a subset of the parameters used in this work is employed or an entirely different set of parameters, the resulting absolute values of the relaxation score will differ from the value we presented here. We suggest that future users compute this parameter using a large set of morphological properties that are sensitive in a variety of different scales, similar to the purpose of the parameter introduced by Rasia et al. (2013) that wa used by Lovisari et al. (2017). The instrument used changes both the number of photons used to determine some parameters. Weißmann et al. (2013) showed for the case of P40 that it can bias the resulting morphological parameters that are calculated, but the instrumental PSF also smooths the cluster images and biases some parameters toward relaxed clusters.
 |
Fig. 7 Morphological parameter distribution in eFEDS clusters after the redshift and luminosity correction were applied. We color-code the points according to their relaxation score to show the performance of the new parameter in identifying relaxed clusters. |
4.5 Investigating the bimodality
We investigated whether we observe an indication for bimodal-ity in the morphological parameter distribution in our eFEDS cluster subsample, and we studied this for the relaxation score as well. Our strategy consisted of fitting a normal, a log-normal, a double normal, a double log-normal, a skewed normal, and a skewed log-normal distribution to our data. For each distribution we estimated the Bayesian evidence. This quantity is widely used in Bayesian statistic to compare models, and thus it is a very good indicator in our specific case. In particular, we computed the Bayes factor, which was obtained as the difference between the Bayesian evidence of the compared models. This quantity directly relates to the relative odds of the two models that are compared by indicating the more likely model, and by determining the probability of this higher likelihood. We used the Jeffreys scale (Jeffreys 1961) to estimate the model preference and its relative odds. In particular, a model was strongly preferred if the Bayes factor was at least 5; it was weakly preferred if the Bayes factor was higher than 2.5 but lower than 5. These differences in Bayesian evidence correspond approximately to 3σ and 2σ significance level. We recall that because the Bayesian evidence, which is defined as the integral of the likelihood over the prior, by construction takes the size of the parameter space into account, the Bayes factor by definition penalizes a model with more parameters or with a larger parameter space.
However, we cannot apply this fitting to the observed morphological parameters because they are affected by redshift and luminosity dependence, as characterized in Sect. 4.2. We therefore first corrected these parameters for this evolution, and then characterized their best-fitting parent distribution. Additionally, we note that the low photon statistics in our data naturally cause large uncertainties in the measured morphological parameters. Therefore we need to consider these uncertainties when fitting the data distribution. We built a likelihood as
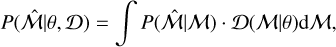 (17)
(17)
where 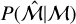 takes the uncertainties in the morphological parameter estimation into account, and
takes the uncertainties in the morphological parameter estimation into account, and 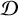 represents the distribution fitted to the data (normal, log-normal, double normal, double log-normal, skewed normal, or skewed log-normal) that depends on the parameters θ. As stated above, we are interested in the value of the Bayesian evidence E,
represents the distribution fitted to the data (normal, log-normal, double normal, double log-normal, skewed normal, or skewed log-normal) that depends on the parameters θ. As stated above, we are interested in the value of the Bayesian evidence E,
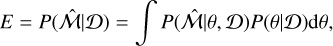 (18)
(18)
with which it is easy to derive the model posterior because it is linked to the previous equation by the Bayes theorem,
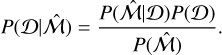 (19)
(19)
The fit of the model to the data and the evidence estimation were performed using the Bayesian nested sampling algorithm MultiNest (Feroz et al. 2009). We compare the values of the Bayes factor for the six fitted distributions against the best-fitting distribution in Table 2. Overall, a skewed distribution is always preferred by our data, except for concentration, cuspiness, and Pio, which favor a log-normal distribution.
We point out that a bimodal distribution, either double normal or double log-normal, is never the preferred model to our data. On the other hand, the Bayes factor difference with respect to the best-fitting model for a double log-normal is always smaller than 5, hence we cannot exclude the possibility that the observed preference for a single-peaked distribution is due to random fluctuation. Interestingly, for the concentration, we find that the best-fitting distribution is log-normal, as was found in a previous study using a Planck -selected sample (Rossetti et al. 2017). This analysis has been performed on the Rscore as well, and the best-fitting distribution is the skewed log-normal distribution.
It is worth pointing out that none of the morphological parameters we analyzed significantly prefers a skewed distribution (the Bayes factor of the best non-skewed distribution versus best skewed distribution is always smaller than 5). As an exercise, we removed the fit performed using a skewed distribution from our analysis, and compared single- versus double-peaked distributions in order to understand whether there would be a clear preference toward a double-peaked distribution. This is the case only for P30 and P40, and it is almost 3σ significant for the centroid shift parameter. This indicates that these parameters prefer a symmetric distribution. We can conclude our eFEDS cluster subsample shows no indication of bimodality in the distribution of our morphological parameters. Even for the Rscore, the parameter that should have separated the two cluster populations best, the best-fitting distribution is log-normal.
In past years, several studies have indicated that the observed cluster population can be split into two categories, cool-core and non-cool core clusters (e.g., Sanderson et al. 2009; Cavagnolo et al. 2009; Hudson et al. 2010; Liu et al. 2020). These studies reported that some morphological indicators have a characteristic bimodal distribution. They therefore concluded that clusters can be easily divided into two distinct populations, cool cores and non-cool cores, sometimes with an intermediate class, for instance, weak cool cores (Hudson et al. 2010). According to the particular trends in cluster research in the past two decades, clusters as observed by Chandra and XXMM-Newton typically tend to be extreme clusters and are not representative of the cluster population in the Universe. These clusters have been observed either to constrain AGN feedback, therefore the AGN contribution to ICM is quite strong, or they are clusters with a major merger with significant nonthermal pressure support. Therefore, it is clear that a selection like this would bias the cluster population toward the atypical clusters, and the observed bimodality can easily be explained by the sample selection. For instance, Cavagnolo et al. (2009) studied a cluster sample of 239 objects. Selection was based purely on the presence of clusters in the Chandra archive (ACCEPT; see Donahue et al. 2006), therefore they studied a large variety of clusters that spanned a very wide redshift and mass range. They reported that the distribution of the values of the central entropy is bimodal, and they interpreted the results by stating that this indicates a clear dichotomy between cool-core and non-cool core clusters. Sanderson et al. (2009) investigated a sample of 20 clusters at very low redshift (z < 0.1) selected from HIFLUGCS (Reiprich & Böhringer 2002). They studied the entropy slope distribution at fixed radius, which is a morphological parameter that is quite useful in understanding cooling in the cores of galaxy clusters. We cannot compute this parameter because it requires a higher data quality than eFEDS provides to compute the temperature profiles needed for entropy profile estimation. Sanderson et al. (2009) find a significant bimodal distribution, which they attributed to the presence of two distinct cluster populations, cool cores and non-cool cores. We argue that this sample was quite limited in the number of clusters involved, and therefore the bimodal distribution is not statistically significant, or that the cluster population studied is not the same as we studied here, given the high flux used in HIFLUGCS to select the cluster sample. Hudson et al. (2010) followed up Sanderson et al. (2009) by enlarging the cluster sample that they used for the analysis: they also selected clusters from the HIFLUGCS cluster sample, but more than tripled the number of studied clusters, reaching 64. They also doubled the redshift range, reaching up to z < 0.2, but only three clusters in the red-shift range between z = 0.1 and z = 0.2 were included in this study. They took advantage of 4.5 Ms clean Chandra data with good photon statistics to study several more morphological indicators, including central density, central entropy, cuspiness, and core temperature. They reported an indication of bimodality in several of these parameters. Similarly to Sanderson et al. (2009), this sample could either be affected by low numbers statistics, or, being based on clusters with very high fluxes, the authors selected an entirely different cluster population.
On the other hand, several other studies (e.g., Pratt et al. 2010; Santos et al. 2010; Ghirardini et al. 2017; Yuan & Han 2020) investigated similar morphological indicators, but did not find bimodality. This is consistent with our results. For instance, Santos et al. (2010) studied the distribution of the concentration parameter in three different cluster samples: a low- and an intermediate-redshift subsample of the 400 Square Degree ROSAT PSPC survey (Burenin et al. 2007) with a median red-shift of z = 0.08 (28 clusters) and z = 0.59 (20 clusters), 15 high-redshift clusters from the ROSAT Deep Cluster Survey (RDCS; Rosati et al. 1998), and the Wide Angle ROSAT Pointed Survey (WARPS; Jones et al. 1998) with a median redshift of z = 0.83 (15 clusters). Their cluster sample was one of the first on which cluster morphological parameters from low to high redshifts were studied. The authors found no indication of a bimodal distribution in the concentration parameter and therefore refuted claims of a bimodality of cool cores and non-cool cores. They concluded that a cluster population cannot be easily divided into two populations because the transition between cool cores and non-cool cores occurs smoothly: the observed distribution is unimodal. Nevertheless, they reported indications of an evolution of the concentration parameter, which similarly to our results, indicates that there are fewer cool cores at high red-shift than at low redshift. Pratt et al. (2010) studied the entropy in the REXCESS cluster sample (Böhringer et al. 2007), which is a local luminosity-limited cluster sample comprised of 33 clusters at z < 0.2 drawn from the REFLEX cluster sample (Böhringer et al. 2001). They observed two peaks in the distribution of the central entropy value and slope, but even though they estimated that a single Gaussian is the worst description of their data, they were unable to distinguish between a skewed normal distribution and a bimodal Gaussian distribution. Yuan & Han (2020) analyzed the entire Chandra archive, which contains 964 clusters up to z = 1.5. They studied the concentration distribution and P30, finding an absence of bimodality in the distribution of these morphological indicators. Ghirardini et al. (2017) investigated the population of clusters observed by Chandra at z > 0.4, selecting only clusters with at least 20 ks observing time. They found no indication for a preference for a bimodal distribution in the central entropy distribution.
Recently, great efforts have been made to characterize the role of the selection effects in determining the distribution of the objects using morphological parameters because it has become increasingly important to separate the selection bias from the measurements. In particular, it was proposed that X-ray cluster samples that select clusters according to their flux were affected by a cool-core bias (Hudson et al. 2010; Eckert et al. 2011; Mittal et al. 2011). Andrade-Santos et al. (2017) compared the fraction of cool-core clusters, estimated using a threshold in concentration, cuspiness, and central density, in the Planck ESZ cluster sample (Planck Collaboration VIII 2011) of 164 clusters, with a flux-limited X-ray selected sample (Voevodkin & Vikhlinin 2004) that is a subsample of the HIFLUGCS (Reiprich & Böhringer 2002) cluster sample. They reported that X-ray selected clusters contain a significantly larger fraction of cool-core clusters compared to the sample of SZ selected clusters. Rossetti et al. (2017) studied the evolution and mass dependence of the concentration parameter in the Planck cosmology sample (Planck Collaboration XXIX 2014), containing 189 clusters, and compared their results with same properties measured in ME-MACS X-ray selected sample (Mann & Ebeling 2012), containing 103 clusters. They investigated the cool-core fraction by dividing their sample into two different redshift bins and into two mass bins. They found a 1.5σ indication that low-mass systems have a smaller cool-core fraction, and they found no evolution with redshift. Furthermore, they investigated a possible bimodal distribution in the concentration parameter. Interestingly, they reported that Planck -selected clusters do not show any indication of a bimodal distribution, and the best-fitting distribution is a log-normal. However, the X-ray selected ME-MACS cluster sample is best fit by a bimodal distribution. Assuming that the Planck sample is a representative sample of the cluster population, they simulated the detection of a mock ME-MACS-like sample, and observed the appearance of a double-peaked distribution when the ME-MACS selection criteria were applied.
It is quite challenging to compare our results with the results of most of the studies mentioned above because the eFEDS cluster sample we used is different in luminosity, mass, and redshift with respect to these works. It is possible to extrapolate our best-fitting results, but this would ignore the possible real difference in the underlying cluster population between low- and high-luminosity clusters. The only study that provides an opportunity for a comparison is Lovisari et al. (2017). The authors studied a sample of 150 clusters selected from the Planck early cluster catalog (Planck Collaboration VIII 2011). These clusters extend in redshift up to z = 0.55 and have a median luminosity of 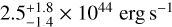 3. In comparison, the eFEDS sample involving 325 clusters extends out to redshifts of z = 1.2 with a median luminosity of
3. In comparison, the eFEDS sample involving 325 clusters extends out to redshifts of z = 1.2 with a median luminosity of 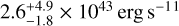 . It is clear that our redshift range is twice as wide and our median luminosity is factor 10 lower than in L17. They investigated the thresholds that yield the most complete and the most pure sample of relaxed and disturbed clusters. However, they used the visual inspection method with only a few astronomers to classify relaxed and unrelaxed clusters. This method might obviously be biased and is very difficult to reproduce or apply in our sample, where the photon statistic is low and the number of clusters is higher. They reported that it is generally better to use more than one single parameter to categorize clusters as relaxed and disturbed. In particular, they mentioned that the use of a new parameter obtained as a combination of concentration and centroid shift (Rasia et al. 2013) is very powerful in discriminating cool cores and non-cool cores, as we suggest in this work. They find that central density and Gini coefficient distribution are statistically different when they split their sample into two according to the luminosity, such that more luminous objects tend to be more concentrated, have a higher Gini coefficient, and have higher central gas densities, similarly to our results. In Fig. 6, we add the median value and the scatter observed in L17 for central density, concentration (the one defined with respect to R500), and cuspiness because for these parameters, a direct comparison can be made. We also calculated the median morphological parameters for the eFEDS clusters that fall within the L17 luminosity and redshift range. We note that for concentration and central density, the median value and the scatter of the parameters agree very well, indicating that eROSITA and Planck - selected clusters have similar morphological properties. For the cuspiness, we instead generally measure density profiles that are far steeper on average. However, we recall that cuspiness is a morphological parameter with a very large and skewed uncertainty in our work, therefore this difference is not very significant.
. It is clear that our redshift range is twice as wide and our median luminosity is factor 10 lower than in L17. They investigated the thresholds that yield the most complete and the most pure sample of relaxed and disturbed clusters. However, they used the visual inspection method with only a few astronomers to classify relaxed and unrelaxed clusters. This method might obviously be biased and is very difficult to reproduce or apply in our sample, where the photon statistic is low and the number of clusters is higher. They reported that it is generally better to use more than one single parameter to categorize clusters as relaxed and disturbed. In particular, they mentioned that the use of a new parameter obtained as a combination of concentration and centroid shift (Rasia et al. 2013) is very powerful in discriminating cool cores and non-cool cores, as we suggest in this work. They find that central density and Gini coefficient distribution are statistically different when they split their sample into two according to the luminosity, such that more luminous objects tend to be more concentrated, have a higher Gini coefficient, and have higher central gas densities, similarly to our results. In Fig. 6, we add the median value and the scatter observed in L17 for central density, concentration (the one defined with respect to R500), and cuspiness because for these parameters, a direct comparison can be made. We also calculated the median morphological parameters for the eFEDS clusters that fall within the L17 luminosity and redshift range. We note that for concentration and central density, the median value and the scatter of the parameters agree very well, indicating that eROSITA and Planck - selected clusters have similar morphological properties. For the cuspiness, we instead generally measure density profiles that are far steeper on average. However, we recall that cuspiness is a morphological parameter with a very large and skewed uncertainty in our work, therefore this difference is not very significant.
 |
Fig. 8 Distribution of the observed Rscore. |
 |
Fig. 9 Distribution of the observed Rscore vs concentration. The horizontal line represents the best-fitting value for the log-normal distribution best fit. The dashed and dotted vertical lines indicate the thresholds at which relaxed clusters are distinguished from disturbed clusters as suggested by Lovisari et al. (2017). Cool-core clusters lie right of the dotted lines, and non-cool core clusters lie left of the dashed line. |
 |
Fig. 10 Evolution of the fraction of cool-core clusters as a function of redshift. Each bin consists of 65 clusters. |
Bayes factor with respect to the best-fit model.
5 Conclusions
We have characterized the distribution of the morphological parameters in a sample of galaxy clusters and groups detected in the eROSITA Final Equatorial-Depth Survey (eFEDS). The great survey science capabilities of eROSITA enabled us to map these properties in a parameter space region that was previously unexplored, from low-mass and low-redshift groups to high-redshift clusters.
The eFEDS survey includes 542 candidate clusters and groups of galaxies, down to the flux limit of ~10−14 erg s−1 cm−2 in the soft band (0.5−2 keV) within 1’ (see Liu et al. 2022a). We applied a selection cut on the extent and detection likelihoods of 12 to reduce the total contamination in the sample. This selection reduces the contamination to 14%, and 325 clusters remain in the final sample. This sample covers a luminosity range from 9 × 1040 erg s−1 to 4 × 1044 erg s−1 and a redshift range from 0.017 out to 1.2. The conclusions we obtained from this analysis are summarized below.
Our work covers a wide range in luminosity and redshift. Our sample allows us to constrain the evolution of a morphological parameter with redshift and luminosity. The evolution in the central density is slightly significant for luminosity and redshift. Overall, the central density evolves with redshift in agreement with the self-similar model, and it is consistent with previous studies. Similarly, most morphological indicators, in particular the Gini coefficient, power ratios, and photon asymmetry, show significant evolution with redshift and luminosity.
The evolution we constrained in these parameters was then modeled to convert the evolution-independent morphological parameters into a new morphological parameter, the relaxation score. Using this new parameter, we searched for an indication of a bimodal distribution in our parameters, but we found that a skewed distribution, a single-peaked normal, or a log-normal distribution represent our observations better. By defining a threshold in relaxation score, we were able to determine whether a cluster is relaxed, and we found that the fraction of relaxed objects does not evolve with redshift. Based on the correlation between concentration and relaxation score, we defined a threshold to distinguish relaxed clusters from disturbed clusters by converting the concentration threshold used in Lovisari et al. (2017) into a threshold in relaxation score. Using this threshold on a redshift independent parameter, we find that at low red-shift, the fraction of relaxed clusters is about 50%. This fraction decreases to 30−35% at higher redshifts at z > 0.2. However, we argue that the high fraction of relaxed clusters at the lowest redshift bin could be explained by the incompleteness in the sample. Our detection strategy means that we are more sensitive to detecting relaxed groups and clusters with beta model profiles. The surface brightness distributions of disturbed clusters tend to be different than beta model profiles. They are flatter and more extended, and therefore the detection algorithm might miss these nearby objects. Another challenge is to confirm the redshifts of these groups and cluster using optical surveys. Disturbed clusters and groups at low redshifts (z < 0.2) are likely to be more extended than relaxed clusters and groups. As they appear to be so extended on the sky, algorithms based on the red sequence struggle to select the correct optical center and the correct member galaxies. Therefore, the optical incompleteness in the low-redshift regime might affect the disturbed clusters more than relaxed clusters. In our eFEDS cluster sample, however, we did not select our clusters based upon any optical properties, therefore this deficit of disturbed clusters is not caused by the optical cleaning of the sample.
This work bridges the gap between the characterization of cluster samples detected by previous flux-limited X-ray surveys and sets the stage for the upcoming eROSITA all-sky survey. Cluster surveys performed with ROSAT (Voges et al. 1999), REXCESS (Böhringer et al. 2007), HIFLUGCS (Reiprich & Böhringer 2002), and ME-MACS (Mann & Ebeling 2012) have successfully covered clusters with high luminosities > 5 × 1044 erg s−1 out to redshifts of 0.5. Ground-based SZ-selected cluster surveys with SPT (Bleem et al. 2020) and ACT (Hilton et al. 2021), on the other hand, which are sensitive to the most massive and highest-luminosity clusters, extended our knowledge of underlying cluster populations out to high redshifts of 1.7 (Nurgaliev et al. 2017). For instance, the highest luminosity we reach in the eFEDS sample is about 4 × 1044 erg s−1. The eRASS1 will explore the cluster samples with luminosities down to ~1040 erg s−1 and redshifts out to 1.5, probing a completely new cluster population with eROSITA that is complementary to previous flux-limited X-ray surveys and mass-limited SZ surveys.
Acknowledgements
We thank the anonymous referee, which helped us with useful comments at improving the quality of this manuscript. This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors, and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg and ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tubingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universitat Munich also participated in the science preparation for eROSITA. The eROSITA data shown here were processed using the eSASS software system developed by the German eROSITA consortium. E.B. acknowledges financial support from the European Research Council (ERC) Consolidator Grant under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 101002585). D.N.H. acknowledges support from the ERC through the grant ERC-Stg DRANOEL no. 714245. This work was supported in part by the Fund for the Promotion of Joint International Research, JSPS KAKENHI grant no. 16KK0101. Funded in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - 450861021.
Appendix A PSF profile
 |
Fig. A.1 eROSITA profile for the FoV-averaged PSF. |
Appendix B Likelihood derivation
The likelihood is the probability distribution of the data given the parameters in the model we used when seen as a function of the parameters,
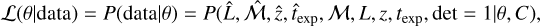 (B.1)
(B.1)
where  indicates the measured quantities, and x represents the intrinsic quantities. Here x can be the morphological parameter of interest ℳ, the luminosity L, the exposure time texp, or the redshift z. With det = 1, we indicate that the cluster is detected, θ indicates the scaling relation parameters: the normalization μ, the luminosity slope γ, the redshift dependence ß, and the intrinsic scatter σ. We further point out that our model depends on cosmology C, but a cosmology fit is not one of the goals of this paper, hence the cosmology is assumed to be fixed to a concordance cosmology with H0 = 70 km/s, Ωm = 0.3, and ΩΛ = 0.7.
indicates the measured quantities, and x represents the intrinsic quantities. Here x can be the morphological parameter of interest ℳ, the luminosity L, the exposure time texp, or the redshift z. With det = 1, we indicate that the cluster is detected, θ indicates the scaling relation parameters: the normalization μ, the luminosity slope γ, the redshift dependence ß, and the intrinsic scatter σ. We further point out that our model depends on cosmology C, but a cosmology fit is not one of the goals of this paper, hence the cosmology is assumed to be fixed to a concordance cosmology with H0 = 70 km/s, Ωm = 0.3, and ΩΛ = 0.7.
Furthermore, we assumed that the exposure time texp and the redshift z are perfect measurements, meaning that no uncertainty is associated with them (in principle, they have extremely small uncertainties, but including them in our fit will only slow down the computation without any significant improvement in the quality of the fit). This is mathematically expressed as
 (B.2)
(B.2)
where δx(y) is Dirac’s delta function. This means that we can marginalize over texp and z, thus our likelihood becomes the marginal likelihood as follows:
 (B.3)
(B.3)
Then we broke the likelihood into several pieces (selection function, errors on data, scaling relation, and cosmology dependence) by exploiting the Bayes theorem P(A, B) = P(A\B)P(B) = P(B\A)P(A)
 (B.4)
(B.4)
even further, where we note that the selection function is the only term that depends on exposure time, and the selection function was isolated from this equation. The selection function is written as
 (B.5)
(B.5)
In this equation we have assumed that the selection function is independent of the measured quantity  , but depends only on the corresponding intrinsic quantity L, and that morphological parameters do not enter the selection function directly. Next we split the errors on the data from the intrinsic quantities,
, but depends only on the corresponding intrinsic quantity L, and that morphological parameters do not enter the selection function directly. Next we split the errors on the data from the intrinsic quantities,
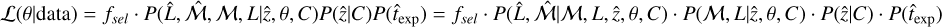 (B.6)
(B.6)
thus defining the modeling of our data as
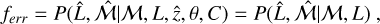 (B.7)
(B.7)
where in the last equation, we assume independence of the errors in our data from redshift, scaling relation parameters, and cosmology.
Then we isolate the dependent quantity M from the independent quantity in the scaling relation,
 (B.8)
(B.8)
where we have assumed that the intrinsic morphological parameters are cosmology independent, and we have explicitly written the scaling relation in terms of the parameters θ.
where we can assume a scaling relation between mass and luminosity, which allows us to compute  directly from the cluster mass function because
directly from the cluster mass function because
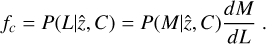 (B.11)
(B.11)
Therefore we can summarize our likelihood as
 (B.12)
(B.12)
We finally point out that the  and
and  terms are only a function of the data, and because we do not fit the cosmology, this is just a multiplicative factor in our likelihood. It can therefore be removed because the fit is insensitive to multiplicative factors that are independent of the model parameters.
terms are only a function of the data, and because we do not fit the cosmology, this is just a multiplicative factor in our likelihood. It can therefore be removed because the fit is insensitive to multiplicative factors that are independent of the model parameters.
As a last step, we can marginalize over the intrinsic properties L and ℳ because we are not interested in estimating them. Therefore
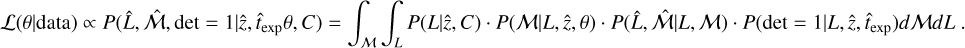 (B.13)
(B.13)
We point out that this is an improper likelihood because it is not normalized. We therefore have to normalize it by calculating the denominator D by integrating the previous equation over  and
and  . However, we immediately realize that such an integral applies only to the ferr term, which is built to be normalized,
. However, we immediately realize that such an integral applies only to the ferr term, which is built to be normalized,
 (B.14)
(B.14)
This simplification of the likelihood allows us to isolate in the denominator the integral over ℳ,
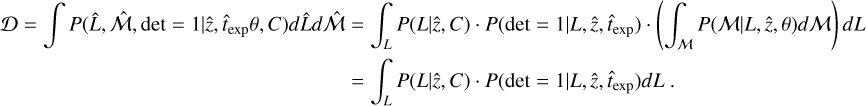 (B.15)
(B.15)
Therefore our denominator does not depend on the scaling relation parameters θ. This implies that we do not need to compute this because it would just be a multiplicative constant in the likelihood, to which our fit is insensitive.
To conclude, in the previous calculation, we have omitted the fact that this is the likelihood for a single cluster with observed quantities  , where i is a running index that goes through all detected clusters. Therefore the total likelihood is
, where i is a running index that goes through all detected clusters. Therefore the total likelihood is
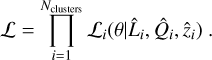 (B.16)
(B.16)
References
- Abraham, R. G., van den Bergh, S., & Nair, P. 2003, ApJ, 588, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Andrade-Santos, F., Jones, C., Forman, W. R., et al. 2017, ApJ, 843, 76 [Google Scholar]
- Bahar, Y. E., Bulbul, E., Clerc, N., et al. 2022, A&A, 661, A7 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biffi, V., Borgani, S., Murante, G., et al. 2016, ApJ, 827, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [Google Scholar]
- Bleem, L. E., Bocquet, S., Stalder, B., et al. 2020, ApJS, 247, 25 [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2001, A&A, 369, 826 [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunner, H., Liu, T., Lamer, G., et al. 2022, A&A, 661, A1 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [Google Scholar]
- Cassano, R., Ettori, S., Giacintucci, S., et al. 2010, ApJ, 721, L82 [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [Google Scholar]
- Chiu, I. N., Ghirardini, V., Liu, A., et al. 2022, A&A, 661, A11 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donahue, M., Horner, D. J., Cavagnolo, K. W., & Voit, G. M. 2006, ApJ, 643, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Dupke, R. A., Mirabal, N., Bregman, J. N., & Evrard, A. E. 2007, ApJ, 668, 781 [Google Scholar]
- Eckert, D., Molendi, S., & Paltani, S. 2011, A&A, 526, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Roncarelli, M., Ettori, S., et al. 2015, MNRASr, 447, 2198 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Pointecouteau, E., et al. 2017, Astron. Nachr., 338, 293 [Google Scholar]
- Evrard, A. E., Mohr, J. J., Fabricant, D. G., & Geller, M. J. 1993, ApJ, 419, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1994, ARA&A, 32, 277 [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Freyberg, M., Perinati, E., Pacaud, F., et al. 2020, SPIE Conf. Ser., 11444, 1144410 [Google Scholar]
- Ghirardini, V., Ettori, S., Amodeo, S., Capasso, R., & Sereno, M. 2017, A&A, 604, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirardini, V., Ettori, S., Eckert, D., et al. 2018, A&A, 614, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirardini, V., Bulbul, E., Hoang, D. N., et al. 2021a, A&A, 647, A4 [EDP Sciences] [Google Scholar]
- Ghirardini, V., Bulbul, E., Kraft, R., et al. 2021b, ApJ, 910, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Sifón, C., Naess, S., et al. 2021, ApJS, 253, 3 [Google Scholar]
- Ho, S., Bahcall, N., & Bode, P. 2006, ApJ, 647, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffreys, H. 1961, The Theory of Probability [Google Scholar]
- Jones, L. R., Scharf, C., Ebeling, H., et al. 1998, ApJ, 495, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, M., Mohr, J. J., Desai, S., et al. 2018, MNRAS, 474, 3324 [Google Scholar]
- Klein, M., Grandis, S., Mohr, J. J., et al. 2019, MNRAS, 488, 739 [Google Scholar]
- Klein, M., Oguri, M., Mohr, J. J., et al. 2022, A&A, 661, A4 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [Google Scholar]
- Liu, A., Tozzi, P., Ettori, S., et al. 2020, A&A, 637, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, A., Bulbul, E., Ghirardini, V., et al. 2022a, A&A, 661, A2 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, T., Merloni, A., Comparat, J., et al. 2022b, A&A, 661, A27 (eROSITA EDR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lovisari, L., Reiprich, T. H., & Schellenberger, G. 2015, A&A, 573, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovisari, L., Forman, W. R., Jones, C., et al. 2017, ApJ, 846, 51 [Google Scholar]
- Mann, A. W., & Ebeling, H. 2012, MNRAS, 420, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Allen, S. W., Morris, R. G., et al. 2015, MNRAS, 449, 199 [CrossRef] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, PhR, 443, 1 [NASA ADS] [Google Scholar]
- Markevitch, M., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, L27 [Google Scholar]
- Markevitch, M., Govoni, F., Brunetti, G., & Jerius, D. 2005, ApJ, 627, 733 [Google Scholar]
- Maughan, B. J., Giles, P. A., Randall, S. W., Jones, C., & Forman, W. R. 2012, MNRAS, 421, 1583 [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2013, ApJ, 774, 23 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Allen, S. W., Bayliss, M., et al. 2017, ApJ, 843, 28 [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Mittal, R., Hicks, A., Reiprich, T. H., & Jaritz, V. 2011, A&A, 532, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mhr, J. J., Fabricant, D. G., & Geller, M. J. 1993, ApJ, 413, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Mohr, J. J., Evrard, A. E., Fabricant, D. G., & Geller, M. J. 1995, ApJ, 447, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Nurgaliev, D., McDonald, M., Benson, B. A., et al. 2013, ApJ, 779, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Nurgaliev, D., McDonald, M., Benson, B. A., et al. 2017, ApJ, 841, 5 [Google Scholar]
- Parekh, V., van der Heyden, K., Ferrari, C., Angus, G., & Holwerda, B. 2015, A&A, 575, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Rasia, E., Meneghetti, M., & Ettori, S. 2013, Astron. Rev., 8, 40 [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [Google Scholar]
- Rosati, P., Della Ceca, R., Norman, C., & Giacconi, R. 1998, ApJ, 492, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, H. R., Sanders, J. S., Fabian, A. C., et al. 2010, MNRAS, 406, 1721 [Google Scholar]
- Rossetti, M., Gastaldello, F., Ferioli, G., et al. 2016, MNRAS, 457, 4515 [Google Scholar]
- Rossetti, M., Gastaldello, F., Eckert, D., et al. 2017, MNRAS, 468, 1917 [Google Scholar]
- Sanders, J. S., Fabian, A. C., Russell, H. R., & Walker, S. A. 2018, MNRAS, 474, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, A. J. R., O’Sullivan, E., & Ponman, T.J. 2009, MNRAS, 395, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, J. S., Rosati, P., Tozzi, P., et al. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., & Böhringer, H. 2010, A&A, 521, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., Nonino, M., & Giovannini, G. 2012, A&A, 539, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suwa, T., Habe, A., Yoshikawa, K., & Okamoto, T. 2003, ApJ, 588, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Markevitch, M., & Murray, S. S. 2001, ApJ, 551, 160 [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [Google Scholar]
- Vikhlinin, A., Burenin, R., Forman, W. R., et al. 2007, in Heating versus Cooling in Galaxies and Clusters of Galaxies, ed. H. Böhringer, G.W. Pratt, A. Finoguenov, & P. Schuecker, 48 [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [Google Scholar]
- Voevodkin, A., & Vikhlinin, A. 2004, ApJ, 601, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Watson, G. 1961, Biometrika, 48 [Google Scholar]
- Weißmann, A., Böhringer, H., & Chon, G. 2013, A&A, 555, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, W., Ramos-Ceja, M. E., Pacaud, F., Reiprich, T. H., & Erben, T. 2018, A&A, 619, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, Z. S., & Han, J. L. 2020, MNRAS, 497, 5485 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Luminosity redshift distribution of the eFEDS clusters subsam-ple. As a background color reference, we show the eFEDS selection function with the same cuts according to extent and detection likelihoods. |
| In the text | |
 |
Fig. 2 Distribution of morphological parameters for the eFEDS clusters. |
| In the text | |
 |
Fig. 3 Covariance between the morphological parameters in the eFEDS cluster sample. |
| In the text | |
 |
Fig. 4 Cumulative distribution of the morphological parameters divided into four redshift bins. We indicate the p-value of the probability to be drawn from the same underlying distribution. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but the cluster sample is divided into four luminosity bins. |
| In the text | |
 |
Fig. 6 In all four main panels, top left subpanel: distribution of morphological parameters vs. luminosity, color-coded with redshift. The black line shows the best-fitting line (see Sect. 4.2). In the bottom left subpanel, we show the distribution of morphological parameters vs. redshift, color-coded with luminosity. The black line again shows the best-fitting line. The gray shaded area represent the scatter around the best-fit line. The red data point shows (when a direct comparison can be made) the result value obtained by Lovisari et al. (2017), which can be directly compared with the blue data point, which shows our results when we restricted the luminosity and redshift range to the same range as in Lovisari et al. (2017). The orange data point represents the average morphological parameter values obtained in luminosity or redshift quintiles. We show parameters corrected for redshift and luminosity evolution against luminosity (in the top right subpanel) and redshift (in the bottom right subpanel). |
| In the text | |
 |
Fig. 7 Morphological parameter distribution in eFEDS clusters after the redshift and luminosity correction were applied. We color-code the points according to their relaxation score to show the performance of the new parameter in identifying relaxed clusters. |
| In the text | |
 |
Fig. 8 Distribution of the observed Rscore. |
| In the text | |
 |
Fig. 9 Distribution of the observed Rscore vs concentration. The horizontal line represents the best-fitting value for the log-normal distribution best fit. The dashed and dotted vertical lines indicate the thresholds at which relaxed clusters are distinguished from disturbed clusters as suggested by Lovisari et al. (2017). Cool-core clusters lie right of the dotted lines, and non-cool core clusters lie left of the dashed line. |
| In the text | |
 |
Fig. 10 Evolution of the fraction of cool-core clusters as a function of redshift. Each bin consists of 65 clusters. |
| In the text | |
 |
Fig. A.1 eROSITA profile for the FoV-averaged PSF. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.