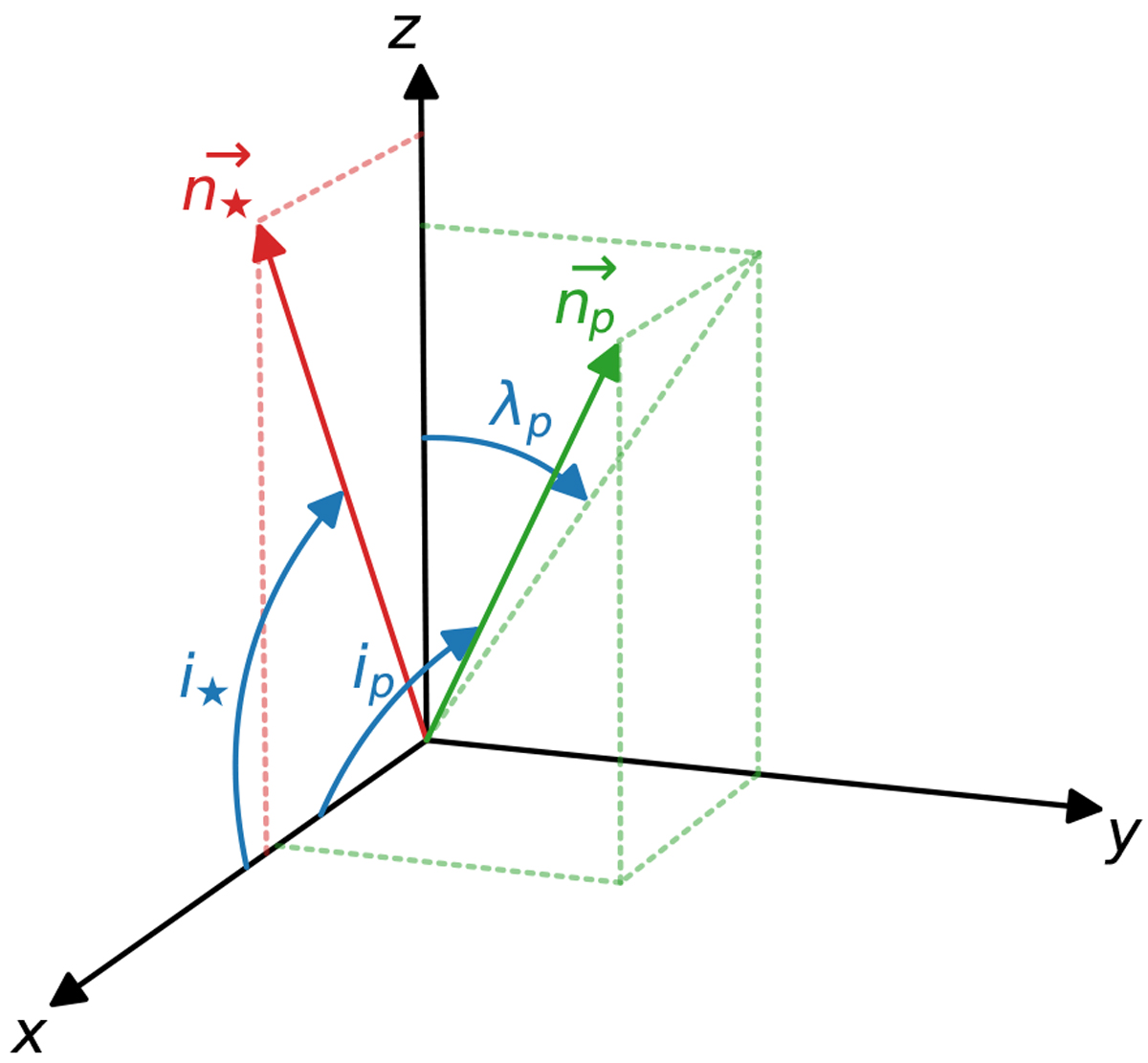
Geometry used to define the angular parameters of the GD model. The x-axis points towards the observer. The z-axis is defined so that the stellar spin axis is contained in the (x, z)-plane and its projection onto the plane of the sky is always along z ≥ 0. The y-axis completes the orthonormal basis. The orientation of the planetary orbit is defined by the orbital angular momentum unit vector that points perpendicularly to the orbital plane. The stellar inclination i_⋆ is the an- gle between the x-axis and the stellar spin axis . The inclination of the planetary orbit i_p is the angle between the x-axis and the orbital angular momentum unit vector . The projected orbital obliquity λ_p is the angle between the z-axis and the projection of onto the (y, z)-plane. Following the convention used in this work, the vector is always lo- cated in the half space where z ≥ 0, and we have λ_p > 0 when is in the half space where y < 0. Thus, the example displayed in the figure has i_⋆ > 0, i_p > 0 and λ_p < 0. The expression of the true orbital obliquity Ψ_p is obtained from the dot product of the two unit vectors: .