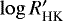EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 659 (March 2022) A&A, 659 (2022) A3 Full HTML
Free Access
Issue
A&A
Volume 659, March 2022
Article Number A3
Number of page(s) 20
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202141493
Published online 25 February 2022

© ESO 2022

1 Introduction

Differences in chemical composition between various regions of the solar corona and the photosphere were first documented by Pottasch (1963), who found significantly higher abundances for Si, Mg, and Fe in the corona compared with the photospheric abundances. These elements all exhibit first ionisation potentials (FIP) lower than 10 eV, and hence called low-FIP elements, while elements with FIP values higher than 10 eV (e.g. O, Ne, He) are called high-FIP elements. It has now become a well-known phenomenon that low-FIP element abundances are enhanced in the corona with respect to their photospheric values, while high-FIP elements show significantly lower enhancement, or even depletion (see, e.g. Meyer 1985; Feldman & Laming 2000; Feldman & Widing 2003).

After high-energy, space-borne observatories became available in the 1990s with the launch of the Extreme Ultraviolet Explorer (EUVE), similar abundance anomalies were discovered for several late-type stars (Laming et al. 1996; Drake et al. 1997; Laming & Drake 1999), and since then, the XMM-Newton and the Chandra X-ray observatories have further increased the sample of stars with known FIP effect (e.g. Wood & Linsky 2010; Wood & Laming 2013; Wood et al. 2018, etc.). Recently, Wood et al. (2018) pointed out that stars with effective temperatures similar to or higher than that of the Sun show similar abundance enhancements, while cooler stars tend to exhibit lower abundance enhancements. At Teff ≈ 4500 K, coronal abundances become equal to the photospheric values, and furthermore, even cooler stars seem to exhibit an inverse FIP effect (IFIP), where low-FIP elements are depleted rather than enhanced in the corona compared to the photosphere. Doschek et al. (2015) and Doschek & Warren (2016) also found signs of the IFIP effect on the Sun in flares, in small patches near sunspots, while Katsuda et al. (2020) observed IFIP effect in spatially unresolved segments of solar flare plasma.

The FIP and IFIP effects have been modelled by Laming (2004, 2009, 2012, 2015b, 2017), and more recently, by Laming et al. (2019), and it is explained by the effect of the ponderomotive force associated with Alfvén and fast mode waves, which separates ions from neutrals in the chromospheric regions. Most recently, it has been suggested that resonant Alfvén waves propagating along coronal loops can result in FIP effect (Laming 2015b, 2021), while originally upward propagating p-modes or magneto-acoustic waves, which are converted to fast modes and propagate into the β < 1 regions, can be a plausible explanation for the IFIP effect (Laming 2021; Baker et al. 2019, 2020). The competition between these two effects might be a deciding factor as to whether a star exhibits an overall FIP or IFIP effect.

To characterise the strength of the (I)FIP effect, the quantity known as the FIP bias is used, which is the mean coronal abundance of four high-FIP elements (C, N, O, and Ne) relative to the Fe abundance (the most easily observable low-FIP element) normalised to the photospheric abundance ratios. The abundance ratios (and hence the FIP-bias values) are given in logarithmic units. In the case of a solar-like FIP effect, the FIP bias is negative, while it is positive in the case of inverse-FIP effect. To measure the FIP bias, both the coronal abundances from X-ray spectra and photospheric abundances from optical spectra are needed. While it is hard to acquire high-quality X-ray observationseven for nearby stars, there is no straightforward way to measure photospheric abundances of certain elements at all (mainly N and Ne). Thus, it is common to use solar photospheric composition or empirical formulae instead.

On the original Teff −FIP bias diagram of main-sequence stars from Laming (2015a), updated from Wood & Linsky (2010), the stars form a tight sequence with Teff, but lack diversity in other parameters. In this work, we extend the diagram in two aspects: with a larger and more diverse stellar sample, and by involving other parameters; for example, surface gravity, metallicity, and age. We compiled the parameters from existing literature, prioritising homogeneity for stellar parameters, and transparency for the calculation of the FIP bias.

The structure of the paper is as follows. In Sect. 2, we describe the sample and the parameters of interest, and in Sect. 3 we describe the methods used to search for correlations within the dataset. In Sect. 4, we present the results, while their implications are discussed in Sect. 5.

2 Data

In order to extend the Teff −FIP-bias diagram, we collected all active stars regardless of spectral type and evolutionary stage for which coronal abundance values are available in the literature, and thus where it is possible to calculate the FIP bias. In our final sample, we selected a total of 59 stars, summarised in Table 1. From the 59 stars, only 18 (31%) are single. 41 are members of binaries or multiple systems, although 25 of them are effectively single, that is gravitationally bound wide binaries or long-period binaries that were formed together but do not interact, and the components evolve separately. Quite a few binaries are members of hierarchical multiple systems, but no interaction between the system members is observed.

The group of solar-type stars with 15 members contains six single stars, two close, and seven wide binaries. Among the nine flare stars, there are two close binaries: YY Gem (M1Ve+M1Ve) and AT Mic (M4Ve+M4Ve). With two equal components, both stars of the binaries are active, and the observed signals from the components are of a common origin. We have 13 K dwarfs in total, and three of those are well-known fast rotating, very active, and flaring stars. Most of the remaining ten K dwarfs are members of wide binaries, as in the case of the solar-type group. The vast majority of the wide binaries are from these groups, as part of the observing strategy (Chandra can observe the two components in the same frame, see e.g. Wood & Linsky 2006), besides the importance of having solar-like parameters and activity.

The sample of the evolved stars mostly consists of RS CVn type binaries. These are well-known magnetically active stars, and they are bright enough for coronal observations. Most of these 11 binaries are single-lined spectroscopic binaries (SB1); thus, most of the observed features can be attributed to the sub-giant or giant primary component. Double-lined binaries (SB2) are usually dominated by the primary as well, although the contribution of the secondary is not negligible. Spectral types of the binaries of evolved stars are from Eker et al. (2008).

The sample consists of dwarf stars from the main sequence (MS) and evolved stars from the red giant branch (RGB) of the Hertzsprung-Russell diagram. The MS stars of the sample start with the fully convective M dwarfs through K and G dwarfs to A-F stars, and in this sequence the depths of convective zones are continuously shrinking. Some stars are in an intermediate state: slightly before the MS or just after turning off it. The stars on the sub-giant and giant branches are inflated. These stars have thick convective envelopes and low surface gravities. All of the sample stars have magnetic activity in common, which is the basis of the observed element fractionation, and, through this, the FIP effect. The magnetic fields of the stars are thought to be generated by different types of dynamos. Sun-like stars with M ≲ M⊙ and usually showing (quasi-)cyclic magnetic variability, are believed to maintain solar-type αΩ dynamos, where differential rotation and large-scale convective flows play a crucial role. However, with vanishing differential rotation, such as in less massive stars with a fully convective interior, α2 dynamos are supposed to operate, driven rather by small-scale turbulent flows. The rotational rates of the stars are from about 0.5 days to over 200 days which have strong impact on the magnetic dynamo. Our sample is heterogeneous, and the task is to investigate how the FIP effect appears on stars of different masses and evolutionary status with different rotational velocities.

For the 59 stars with known coronal composition, we compiled several parameters from the literature, where available. We review these parameters here. Teff is the effective temperature, which is mostly derived from optical spectra. log g is the surface gravity fromoptical spectra. In a few cases when no literature data existed, it was calculated from mass and radius. [Fe/H] is the metallicity. 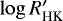logR′HK$\log R\prime_{\textrm{HK}}$ is the chromospheric contribution of the Ca H&K lines, excluding the photospheric component. It measures the chromospheric activity, but it varies strongly with activity level, rotational modulation of the activity features, and the incidental flares at the time of the observations. For the Sun it varies between −4.88 and −5.02 in the course of the activity cycle, and more active stars could exhibit bigger change. Thus, it is only a rough index for the strength of activity in a given star (see Ramírez et al. 2014 and their references). This parameter is missing for many objects, particularly for the evolved stars. Only three out of the 17 evolved stars have measured 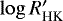logR′HK$\log R\prime_{\textrm{HK}}$. R is the stellar radius, log LX is the X-ray luminosity and log FX is the X-ray flux calculated from log LX and radius. t is the age. Ro = Prot∕τc represents the Rossby number, the ratio of rotational period, and the convective turnover time. The latter is not an observable parameter. It was calculated using the empirical relation from Noyes et al. (1984), with B − V values from the Simbad database. In the case of evolved stars, we used a different formula from Gondoin (2007) to calculate Ro directly from log FX and log g, without the use of τc. We note that while this empirical formula has a large scatter, Ro is itself strongly model-dependent through τc. Prot gives the photometric rotational period from the rotational modulation of the light curve. It was only used to calculate vrot and Ro. vrot is the rotational velocity at the surface, which is simply vrot = 2πR∕Prot. With regard to the literature FIP bias, these values were compiled from various sources and transformed to the same solar photospheric standard from Asplund et al. (2009) and Ne abundance from Drake & Testa (2005) ([Ne/O] = log100.41). Thus, we adopted the following abundance values with the normalisation of A(H) = 12: A(C) = 8.43, A(N) = 7.83, A(O) = 8.69, A(Ne) = 8.30. Where no photospheric abundance was available, solar composition was assumed. The FIP-bias values were corrected by + 0.084 according to Wood et al. (2018) to deal with atomic data changes. The individual abundances used for the calculation are listed in Table A.1. The KNN FIP bias is the same as the previous parameter, but recalculated with homogeneously predicted photospheric abundances with the k-nearest neighbour (KNN) algorithm from LAMOST data (Wang et al. 2020), and with the + 0.084 correction from Wood et al. (2018) to deal with atomic data changes. See Sect. 3.1 for details and Table A.2 for the individual abundances. Finally, the SME FIP bias was calculated using photospheric composition determined by spectral synthesis with the Spectroscopy Made Easy code (SME, Piskunov & Valenti 2017) to check the consistency of the previous methods. It is only available for a handful of stars, and only comes from C and O abundances (see Sect. 3.2 for details and Table B.1 for the abundances).

These parameters are summarized in Table 2, with their sources listed in Appendix C. The uncertainty of the FIP bias is taken as the standard deviation of [C/Fe], [N/Fe], [O/Fe], and [Ne/Fe]. We chose this method over propagating the individual error bars of the abundances, as those are not available in some cases, and they are not homogeneous.

We note that in the case of GJ 338 AB, the individual coronal abundance fractions are not available from emission measure analysis. Wood et al. (2012) estimated the FIP bias directly from FeXVII/OVIII. Thus, we cannot use the same methods to reproduce the results for this binary, and so we adopted the FIP-bias value from Wood et al. (2018).

Table 1

Representation of different types of stars in our sample.

Table 2

Compiled astrophysical parameters for the sample.

3 Methods

3.1 Photospheric abundances from LAMOST

Most of the time when the stellar FIP bias was calculated, there were no stellar photospheric abundances available, so the coronal abundances had to be compared to the solar photosphere. However, different stars can have significantly different chemical composition, which may affect the derived FIP-bias values. To take this into account, individual photospheric abundances are needed. Ideally, one would need a homogeneous survey of high resolution optical or near-infrared spectra with high signal-to-noise ratio, and observable transitions for each of the required elements. Given the absence of such data, to have an independentset of stellar photospheric abundances, as homogeneous as possible, we used the results of Wang et al. (2020), where a large set of abundances were predicted from medium resolution LAMOST spectra. They used deep learning with a training set compiled from APOGEE results for the common stars in the LAMOST and APOGEE sample. Instead of using individually measured equivalent widths, the full spectra were used in the prediction. Since the lines of some elements are weak or missing in the optical, the method inherently involves hidden correlations between abundances. Their cited precision is 0.06–0.12 dex for 11 elements, also including C, N, and O.

Since the LAMOST survey only extends to the northern hemisphere, roughly half of our sample is not covered by it. To circumvent this problem, we used a k-nearest-neighbours regressor (KNN, KNeighborsRegressor from sklearn.neighbors1) to predict the abundances of interest from Teff, log g, and [Fe/H]. This essentially means finding the nearest few stars in this three-dimensional parameter space, and obtaining their mean abundances as the result. For the prediction, we used k = 6 neighbours. The root-mean-square error of the method is 0.05 dex, using 10% of the whole LAMOST sample as a test set. The method gives the following abundances for the Sun: [C/Fe] = −0.09 ± 0.03, [N/Fe] = 0.06 ± 0.08, and [O/Fe] = 0.10 ± 0.03. A lower dimensional cut of this parameter space can be seen in Fig. 1. The tempting aspects of this method are the following: it is really accessible (only needs the three most fundamental parameters), it gives even N and O abundances, and since it practically involves interpolation, it cannot give too extreme results (which is a problem with spectral synthesis and non-local thermodynamic equilibrium (NLTE) correction, occasionally giving clearly unrealistic O abundances). But since the predictions are quite indirect, we only treat the results as a little better first approximation, after the initial zeroth approximation of solar composition.

3.2 Photospheric abundances from spectral synthesis

To derive homogeneous photospheric abundances for as many stars as possible from the sample, we used spectra from CFHT-ESpaDoNS (Donati 2003) and TBL-NARVAL (Aurière 2003). The high spectral resolution enables the use of spectral synthesis, where the whole line profiles are fitted with model spectra calculated from a model atmosphere with varying physical parameters. The results are used to validate the process described in the previous section.

After acquiring the optical echelle spectra, we began with a 99% percentile smoothing to locate the continuum and renormalised it where necessary. We used SME (Piskunov & Valenti 2017) for the spectral synthesis. During the synthesis, MARCS models were used (Gustafsson et al. 2008) with atomic parameters from VALD (Kupka et al. 1999) using a transition list typical for the approximate effective temperature of the star in question. Macroturbulence was computed with the following equation from Valenti & Fischer (2005): 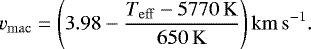vmac=(3.98−Teff−5770 K650 K) km s−1.\begin{equation*} v_{\mathrm{mac}}=\Bigg(3.98-\frac{T_{\mathrm{eff}}-5770 \mathrm{\,K}}{650 \mathrm{\,K}}\Bigg)\,\mathrm{km\,s}^{-1} .\end{equation*}(1)

Astrophysical parameters were determined by the following procedure. We first fit v sin i and microturbulence using rough astrophysical parameters and assuming solar abundances. Then we fit Teff, followed by metallicity and microturbulence. Microturbulence values can sometimes be unreliable and can alter the other astrophysical parameters slightly; thus, we fit it simultaneously with another parameter. In the next step, we fit log g for the Na doublet and the Mg triplet, or, in some cases, for a special line list only containing transitions with log gf > 0 (stronger lines tend to be more sensitive to changes in log g). We then refit Teff and metallicity, and finally we fit individual abundances (C, O, Ca, Mg, Si, Ti, Fe, Ni).

From the last step, only C, O, and Fe are of interest, the others were only added to help with line blends. Determining the Fe abundance is mostly straightforward, thanks to the multitude of Fe lines visible in practically any stellar spectra. The carbon abundance was fitted using several atomic and molecular lines, but most of them are really weak and blended. The oxygen abundance was fitted using only the O triplet at 7774 Å, since the 6300 Å line was not visible in any of the spectra. This is a highly NLTE-sensitive triplet, so we used an NLTE correction from Kovalev et al. (2018) with parameters from Sitnova et al. (2013) that resulted in slightly different values. This correction uses Teff, log g, [Fe/H], and microturbulence, and outputs separate correction factors for each line in the O triplet, which we averaged. As there are no N lines in the optical, the N abundance was estimated through proxies (i.e. we assumed the same relative N/O abundance as in the Sun). For Ne, we used the empirical relation from Drake & Testa (2005) ([Ne/O] = log100.41). We note, however, that the abundances of three out of four high-FIP elements depend on the NLTE-sensitive O triplet. Thus, we argue that in the case of the high-FIP elements, the photospheric abundances calculated with spectral synthesis are not much more reliable than the values from broader abundance trends or empirical correlations. The results of the spectral synthesis are listed in Table B.1.

thumbnail Fig. 1

Abundance trends based on data from Wang et al. (2020) for the LAMOST sample, for the three relevant high-FIP elements (there are no available Ne abundances).

3.3 Principal component analysis

In the space of physical parameters of the stars in the sample (Teff, log g, [Fe/H], age, radius R, vrot, Rossby number Ro, 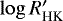logR′HK$\log R\prime_{\textrm{HK}}$, log LX, log FX, literature, and KNN FIP bias) there are several clear and not so clear correlations. To find these, we used the principal component analysis (PCA, Pearson 1901) with the PCA implementation of sklearn.decomposition. PCA is an algorithm that eliminates linear correlations by selecting directions in the parameter space with the highest variance, and defining new orthonormal basis vectors in those directions, thus creating a basis where a large portion of the variance can be described by only a few components. It is a powerful technique for dimensionality reduction and data compression, and it is often the first step when dealing with clustering problems (for a similar treatment, see e.g. Csörnyei et al. 2021). We used PCA to identify hidden correlations between parameters and to find the parameters that are not really useful. Before running the PCA on the full parameter set, we scaled the features to have zero mean and unit variance. In the case of missing parameters, we refilled them using the average value of the given parameter for the two nearest neighbours in the 12-dimensional parameter space. For parameters that change orders of magnitude (age, radius, vrot, and Rossby number), we used their base-ten logarithm.

3.4 Unsupervised clustering

To separate different groups of stars based on the available parameters, we used unsupervised k-means clustering (Macqueen 1967), with the KMeans implementation of sklearn.cluster. It identifies k different clusters, based on proximity in the parameter space, by minimising the variance within each cluster. The resulting clusters are basically Voronoi cells around k number of centres (cluster means), where k is defined a priori. Since some of the parameters in the original 12-dimensional dataset are correlated, they do not form an orthogonal basis, which can bias the clustering. Therefore, we ran the clustering after dimensionality reduction with PCA, only keeping four PCs.

3.5 Linear discriminant analysis

To find the main physical difference between the two emerging clusters on the Teff −FIP bias diagram, we carried out linear discriminant analysis (LDA, see Fisher 1936 for the original paper, McLachlan 2004 for a review of the method, or Rácz et al. 2018 for an application) using the LinearDiscriminantAnalysis implementation of sklearn.discriminant_analysis. It finds a linear combination of input features that maximises the separation between some pre-defined clusters, and then uses linear decision boundaries for classification. Interpreting the model given by LDA is relatively straightforward, as it is a simple linear combination of the scaled input parameters. The LDA method assumes that the input features follow a multivariate normal distribution, and are independent with no correlations between them. We note that in our case, none of these assumptions hold strictly. From the 12 input parameters 9 are independent measurements, while log FX follows from log LX and radius, vrot contains radius and rotational period, and the Rossby number for giants is derived from vrot and log g for the evolved sample. Also, there are deviations from normality. For the cluster labels, we used a simple linear boundary on the Teff −FIP bias diagram. Since the FIP bias was removed from the input features, LDA had to find a combination of the remaining ten parameters that separate the two clusters.

4 Results

Our first step was to plot a new Teff −FIP bias diagram with all stars in the extended sample using the already published and homogenised FIP-bias values and their error bars (see Sect. 3) in Fig. 2. The figure shows the names of the stars for easier identification, black points mark the stars from the original FIP-bias diagram of Laming (2015a), which was updated from Wood & Linsky (2010). Our important result, that the relation has now nearly parallel branches separated by about 0.5 in FIP bias, is seen clearly and is discussed later. The low-mass M dwarf stars (Teff < 4000 K) show a separate blob in the continuation of the original relation. A hint of a bimodal distribution of the FIP-bias values is found in Wood et al. (2018 see their Fig. 7a); all four stars lying above their diagram (τ Boo A, EK Dra, AB Dor A, and AU Mic) are included now in the parallel second branch of the relation (see Fig. 2).

4.1 Comparison with FIP-bias values derived with different methods

All stars from the sample have both literature and KNN FIP-bias values. No systematic difference is found between them except for the M dwarfs below Teff ~ 4200 K, as those stars are at the edge of the LAMOST Teff − log g−[Fe/H] parameter grid, and thus their predicted photospheric abundances are similar. There is generally a good agreement between the FIP-bias values calculated from the original photospheric composition and the newly derived one from spectral synthesis. Figure 3 shows a comparison between the literature and KNN FIP-bias values. The homogeneously predicted photospheric abundances from LAMOST slightly decrease the scatter, the Spearman correlation coefficient changes from −0.67 ± 0.07 for the literature values to −0.74 ± 0.05 for LAMOST KNN, with error bars calculated from bootstrap resampling.

The extended Teff −FIP bias diagram includes 59 stars, which seem to lie on two separate lines, shifted by a FIP-bias value of ~0.5. To show these trends in Fig. 3, we used a RANdom SAmple Consensus (RANSAC)2 regressor to fit two lines. We used this robust regression method to first identify the most prominent linear correlation (the Teff −FIP bias diagram of MS stars from Laming (2015a) shown in Fig. 2 with black points), and then we fitted the outlier points with another RANSAC line. To match visual inspection, the residual threshold parameter was set to 0.2 dex in FIP bias, it is the maximum residual to be classified as an inlier. The fitted lines seem to be similar for both the literature and KNN FIP biases (see the red and grey lines in Fig. 3). 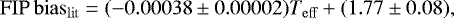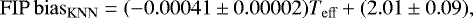For the lower branch, the fitted parameters are as follows: FIP biaslit=(−0.00038±0.00002)Teff+(1.77±0.08),\begin{equation*} \mathrm{FIP\,bias_{lit}} = (-0.00038 \pm 0.00002) T_{\mathrm{eff}} + (1.77 \pm 0.08) ,\end{equation*}(2) FIP biasKNN=(−0.00041±0.00002)Teff+(2.01±0.09),\begin{equation*} \mathrm{FIP\,bias_{KNN}} = (-0.00041 \pm 0.00002) T_{\mathrm{eff}} + (2.01 \pm 0.09) ,\end{equation*}(3)

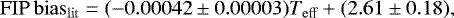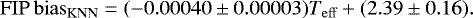and, for the upper branch: FIP biaslit=(−0.00042±0.00003)Teff+(2.61±0.18),\begin{equation*} \mathrm{FIP\,bias_{lit}} = (-0.00042 \pm 0.00003) T_{\mathrm{eff}} + (2.61 \pm 0.18) ,\end{equation*}(4) FIP biasKNN=(−0.00040±0.00003)Teff+(2.39±0.16).\begin{equation*} \mathrm{FIP\,bias_{KNN}} = (-0.00040 \pm 0.00003) T_{\mathrm{eff}} + (2.39 \pm 0.16) .\end{equation*}(5)

thumbnail Fig. 2

Literature FIP bias vs. Teff. Black dots indicate the stars from the original FIP-bias diagram of Laming (2015a), which is updated from Wood & Linsky (2010), forming a tight sequence with Teff.
thumbnail Fig. 3

Teff−FIP-bias diagram with recalculated FIP-bias values. For the Sun, orange points mark its activity minimum and maximum. Solid and dashed lines show two component linear fits with a RANSAC regressor, with grey and red corresponding to literature and the KNN FIP bias, respectively.

4.2 Contributions of the different stellar parameters to the structure of the Teff −FIP-bias diagram

To check the contribution of the different stellar parameters to the structure of the Teff −FIP-bias diagram, we plotted several relations with the data points weighted by a given parameter. In the following, we discuss which parameters have strong influence on the FIP-bias values of the sample, and ultimately shape the diagram, whereas other parameters have seemingly no direct relation to the FIP bias and its bimodal distribution.

In the left panels of Fig. 4 from top to bottom, data points in the Teff −FIP-bias diagram are indicated with increasingly dark shading as values of four stellar parameters increase: (a) the log g surface gravity, (b) the log LX X-ray luminosity, (c) the [Fe/H] metallicity, and (d) the log t age. The evolved stars seem to form a separate steep branch around Teff ~ 4500−5000 K, as seen from the points with light yellow hue accounting for their low log g values in Fig. 4a. The giant stars μ Vel, Capella, and β Cet, all around Teff ~ 5000 K with FIP bias slightly below zero, have low gravities and high X-ray luminosities as seen in Fig. 4b.

Metallicity is close to solar for almost all stars; see Fig. 4c. This parameter is uncertain anyway, and since all stars are close to the Sun in space, we cannot expect great differences. It looks that the observed age does not have an influence on the FIP bias at all (see Fig. 4d). However, we call attention to the uncertainty of the age determinations. The measured stellar parameters that are used for finding the age (such as effective temperature or rotation) are modified to different extents by stellar activity originating from magnetic fields of different strengths. Additionally, gyrochronology is valid on the MS only, since off the MS the internal structure of the stars changes quickly (Barnes 2007); therefore, it is not possible to use it for the whole sample.

The MS sample consists mostly of young stars with only a few exceptions. Among the solar-type stars, only the two components of the α Cen system are of a similar age to the Sun, and the third component, Proxima Cen, is among the M-type flare stars. From the 17 evolved stars, five are older than 5 Gyr and five are younger than 1.4 Gyr; the rest do not have derived ages. Finding the age of the ten close RS CVn systems in this group is problematic due to the non-trivial evolution of the close binaries with strong magnetic activity. If there is any age effect on the FIP-bias values, we cannot explore it on the basis of the available data.

In right panels of Fig. 4, from top top bottom, data points are represented with increasingly dark shading according to increasing values of e) the log vrot stellar rotational velocity, f) the log FX X-ray flux, g) the 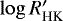logR′HK$\log R\prime_{\textrm{HK}}$ chromopheric activity index, and h) the logRo Rossby number. Fast rotating stars (with higher rotational velocity), regardless of spectral type and evolutionary state, have higher FIP-bias values by about 0.5 at the same Teff. The evolved stars with their high rotational velocity make up the majority of the stars on the upper branch of the diagram. Apart from the evolved stars the three fast-rotating K dwarfs (AB Dor, LO Peg and V471 Tau), all F-stars except Procyon, and a few fast-rotating G dwarfs are situated in the upper branch as well. From the evolved stars, Capella and β Cet are the slowest rotators with 104 and 205 days periods, respectively. For μ Vel, no rotational period is known; these stars lay on the original lower branch of the Teff −FIP bias diagram (see the black dots in Fig. 2).

Together with the higher rotational velocities, the X-ray fluxes are also higher in the parallel upper relation (Fig. 4f), as follows from the rotation-activity relation. We note that fast-rotating stars did not simply increase the scatter of the relation towards the higher FIP-bias values, but they appear on the new branch with a clear separation from the original one, which was implicitly suggested by Wood et al. (2018; see their Fig. 7a), depicting the Vaughan-Preston gap (Vaughan & Preston 1980). For the fast-rotating M-dwarf stars, the X-ray activity saturates (see, e.g. Magaudda et al. 2020). μ Vel, Capella, and β Cet have large radii, and these are three stars out of the four larger than 10 R⊙. The high X-ray luminosity of μ Vel, Capella, and β Cet (Fig. 4b) combined with their large radii result in lower X-ray fluxes which fit well in the lower original branch of the relation.

The important chromospheric activity parameter 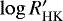logR′HK$\log R\prime_{\textrm{HK}}$ is missing for many stars, especially for the evolved stars. However, as a direct activity index, 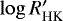logR′HK$\log R\prime_{\textrm{HK}}$ affects the FIP bias at least to some extent (see Fig. 4 g and the lower panel of Fig. 7 for more details). The Rossby numbers for the sample were calculated separately for MS (Noyes et al. 1984) and evolved stars (Gondoin 2007) with different empirical methods (see Sect. 2). From Fig. 4h, it seems that stars with lower Rossby numbers have higher FIP-bias values (M-type MS and evolved stars). However, due to the non-uniform calculation of the Rossby number this should be taken with caution. The visible trends would be the same with the dynamo number ND if we assume a power law ND(Ro) ~Roα with constant exponent. The role of the Rossby number in interpreting the magnetic dynamo inside the stars of the sample is further discussed in Sect. 5.

As a further insight into the importance of each parameter in the formation of the bimodality, the result of the LDA can be used. The upper panel of Fig. 5 shows the linear boundary we used to separate the two parallel sequences a priori. The FIP bias was removed from the input parameters, so the LDA only used ten scaled features to predict the membership to the lower or upper sequence. The absolute values of the LDA coefficients are plotted in the lower panel of Fig. 5. Since the input parameters were scaled to have zero mean and unit variance, these coefficients can be treated as a sort of feature importance. The thin lines show the result of bootstrap analysis, where all the input points were resampled with replacements in order to quantify the uncertainty of the method. It appears that the most important parameters separating the two sequences are the stellar radius and log LX. Naturally, these are correlated with log g, log FX, and log vrot. An interesting result is that the ratio of the coefficients corresponding to log R and log g is ~2, indicating that 2 log R+ log g ~ log M is a variable that separates the two branches, where M is the stellar mass. The dependence on metallicity, Rossby number, and age is negligible. The small contribution of 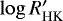logR′HK$\log R\prime_{\textrm{HK}}$ is due to the numerous missing values.

4.3 Correlations between the parameters of the stars in the Teff−FIP-bias diagram

As a start, we plotted the correlation matrix between the stellar parameters with Spearman correlation coefficients in Fig. 6, showing the most direct linear correlations. One can see, for example, that log LX is correlated with log vrot. The FIP bias shows the strongest correlation with Teff, but log FX also seems to be important.

Using all 12 parameters, we ran the PCA to represent the sample in a lower dimensional space, making it easier to look for emerging clusters. To find the optimal number of principal components (PCs) to keep, several heuristic methods can be used. Figure 7 shows the explained variance ratio for different number of PCs, that is the fraction of the sample variance that a given component can explain. An elbow point (abrupt change in the slope) appears around three or four components, hinting that the optimal number should be no greater, as adding more parameters does not cause such a steep increase in information content. Indeed, using the first four PCs can explain ~80% of the sample variance. It is interesting (although not surprising) that the elbow point is clearly at N = 3 for the MS stars, since there are parameters that do not change much if one excludes giants (e.g. log g). The Kaiser criterion (Kaiser 1960) states that one has to retain at least the PCs with eigenvalues larger than 1, which carry more information than an average single parameter from the original dataset (see the dashed line in Fig. 7). In our case, the eigenvalues drop below 1 after PC3. In the lower panel of Fig. 7, one can see how each of the PCs are made up. The following rough trends can be observed. PC1 contains parameters related to the corona, namely the FIP bias, log LX, log FX, and the Rossby number. PC2 contains Teff and parameters related to the size of the star, log g, and the radius. PC3 contains Teff and activity-related parameters vrot and 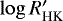logR′HK$\log R\prime_{\textrm{HK}}$. PC4 contains the otherwise unimportant metallicity.

Figure 8 shows two-dimensional projections in PC space. It is clearly seen from the colour gradient that the FIP bias plays an important role (red indicates positive FIP bias and blue indicates negative FIP bias).

thumbnail Fig. 4

Teff−FIP bias diagrams with data points coloured according to various parameters. Missing parameters are indicated with black crosses. See the text for the details.
thumbnail Fig. 5

Results of linear discriminant analysis (LDA). Upper panel: pre-defined boundary between the two clusters (red and blue points) is shown with dashed lines on the Teff −FIP-bias diagram. The larger circles indicate the clusters assigned by the LDA. The three misclassified stars are ι Hor, HR 7291, and AY Cet. Lower panel: absolute value of the LD components corresponding to the given parameters. Thin lines come from bootstrap resampling, and error bars indicate the region between the 16th and 84th percentiles.
thumbnail Fig. 6

Correlation matrix using Spearman correlation coefficients.
thumbnail Fig. 7

Results of the PCA. Upper panel: explained variance ratio of each principal component (PC). The dashed line denotes the Kaiser criterion (Kaiser 1960), and the red points show the elbow points. Lower panel: importance of each parameter to a given principal component, with darker colours indicating stronger contribution (in absolute values).

5 Discussion

5.1 On the bimodality of the Teff −FIP bias diagram

The Teff −FIP-bias plots (see Fig. 2 with the names of the stars indicated) show at least two distinct features: (i) the blob of data points splits into two linear correlations, and (ii) the part where M dwarfs are located seems to be separated. A question arises immediately, namely, is there a connection between the bimodal distribution of the FIP-bias values and the fact that as rotation increases, magnetic field increases and saturation can occur in the filling factor? Concerning the results of Saar (1996) and Reiners et al. (2009), it is possible that magnetic saturation occurs in the filling factor at higher rotation rates. According to Baker et al. (2019) and Laming (2021), a higher filling factor leads to less volume for expansion with increasing altitude for the magnetic field, and IFIP is more likely to occur in conditions with minimal field expansion. A higher photospheric filling factor may also lead to an increase in subsurface magnetic reconnection, which appears to be linked to transient solar IFIP coronal abundances (Baker et al. 2019, 2020). Figure 4e shows that stars with higher FIP bias exhibit higher rotational velocities. However, this feature alone cannot explain the separation of the two branches in the diagrams.

The bimodality of the FIP diagram probably depicts the Vaughan−Preston gap, originally defined as a discontinuity in the activity index ‘S’ for FGK main-sequence stars (Vaughan & Preston 1980), that is medium activity stars are missing. The origin of this discontinuity is still actively debated.

Stellar rotation periods show bimodality in open clusters: the speed of the evolution for stars of similar age depends only on the mass of the stars; this is addressed by Barnes (2010) depicting the rotational evolution of a star with age. The model finds a high-speed transition from fast to slow rotation, thereby creating a void at medium rotational periods depending on the colour (temperature) and mass of the stars. As a consequence of the discontinuity of rotational periods and concerning the existing activity−rotation relations (faster rotation results in higher activity level), the bimodality occurs in the activity levels of open cluster members regarding their age, and the transition is not continuous, as observed by Pace et al. (2009). However, this simple relation can be applied onlyto members of open clusters whose ages are known.

Unfortunately, we cannot use age as a parameter in finding the cause of the bimodality on the FIP bias diagrams. Deriving the age of active field stars is complicated, if not impossible. The existing age estimates are usually quite uncertain due to the effect of strong and variable magnetism, which is not taken into account in the stellar evolution models (for the evolved stars, see further discussion below). Thus, only the stellar rotation remains as the parameter when characterising the activity level through the known rotation−activity relations. In this work, we apply the rotational velocities as a parameter, and for this we need to know the stellar radii as well. We used X-ray flux (surface units) as coronal activity measure. The bimodal distribution of the FIP-bias values is clear between the high and low rotational velocities, in line with the X-ray flux, which is representative of the strength of magnetic activity (see Figs. 4e,f).

Brooks et al. (2017) showed that the FIP-bias value of the Sun as a star changes with the solar cycle by as much as 0.2. The magnetically active stars in the sample may have been at any point in their activity cycle at the time of the measurement of their coronal abundances, which may increase the scatter in the Teff −FIP-bias relation and may narrow the gap between the two branches.

Our sample contains 17 evolved stars, most of them are members of close binaries, and only four stars are single (see Table 1). From the evolved star sample, 11 are active RS CVn binaries that have more complicated rotational evolution due to the gravitational and magnetic effects, making it impossible to obtain reliable age estimates. The active binaries with sub-giant or giant primaries maintain fast rotation due to their binarity, and these stars make up the majority of the upper branch in the diagrams with fast rotating stars. The interested reader can find details about the theory of rotational evolution of low-mass stars in close binaries, also taking into account magnetic braking, in Fleming et al. (2019) and its references.

In Fig. 9, we present the result of a k-means clustering in the four-dimensional parameter space (keeping only 4 PCs), projected into two dimensions. Based on the elbow method and the average silhouette score (for an overview, see, e.g. Nanjundan et al. 2019), the optimal number of k-means clusters is k = 3, which resulted in physically interpretable groups. PC1 mostly reflects the contribution of the effects of the coronal parameters (FIP bias and X-ray flux), while PC2 depends mostly on the stellar parameters of radius and log g, as displayed in Fig. 7. Figure 9 shows that the first cluster is formed by flare stars from late-K to M type (light red background), the second one by MS stars from A to early-K type (light blue background), and the third cluster by evolved stars (light brown background). The upper branch on the Teff −FIP-bias diagram consists mainly of the stars from the third cluster, along with the three fast-rotating K dwarfs and the fastest rotating solar-type stars (cf. Tables 1 and 2), all of which are situated close to the evolved stars in Fig. 9. The three slowly rotating evolved stars (μ Vel, Capella and β Cet) show up in the second cluster and lie in the lower branch in all of the Teff −FIP-bias diagrams. To illustrate the three clusters, Fig. 10 shows the sample on the Gaia colour−magnitude diagram. We note that the same conclusion is reached with clustering in the original 12-dimensional parameter space.

thumbnail Fig. 8

First four PCs, coloured with the FIP bias (see Fig. 9 for the colour scale). The clear colour gradient shows the importance of the FIP bias parameter.

5.2 Clustering by different dynamo types

The three clusters found in our heterogeneous active star sample shown in Fig. 9 may reflect the differences of the dynamo working inside these stars. Magnetic activity signatures can manifest in different ways on different parts of the Hertzsprung-Russell diagram. On the Sun, active regions are mostly concentrated to a ± 30° latitude strip around the equator. On fast rotating solar-like stars, stellar spots tend to concentrate around the pole (e.g. V1358 Ori, Kriskovics et al. 2019). Using surface flux transport models, Işık et al. (2018) found that this can indeed happen on faster rotating, solar-like stars, due to the surface transport of emerging magnetic structures, which can be attributed to large scale surface flows (e.g. a strengthened meridional circulation) and the Coriolis-force and can deflect the rising flux towardsthe poles. On the other hand, fully convective M dwarfs can exhibit spot structures stable for a few thousand rotations (e.g. V374 Peg, Vida et al. 2016). Stars on the red giant branch can also have very different spot configurations; for example, from time to time, polar spot structures of varying contrast were observed on ζ And (Kővári et al. 2007, 2012; Roettenbacher et al. 2016). A similar RS CVn system, σ Gem also exhibitsintermittent polar structures (cf. Kővári et al. 2015; Korhonen et al. 2021). Since spots are the most easily observed proxies of dynamo action, this may also mean that on different types of stars, we observe the manifestations of different types of dynamos.

The depths of the convection zones on the MS vary from the total stellar interior (full convection, low-mass M dwarfs) through different sizes of convection zone decreasing from fully convective to a very thin layer going from M, K, and G dwarfs to F-type stars, all with log g values of around 4.5−5. Both the depth of the convective region and speed of rotation have a bearing on differential rotation, which is crucial for the Ω-effect; thus, this might point towards a more α-effect-dominated dynamo as the convective zone deepens. In the case of evolved stars, the convection zones are deep, but the surface gravity is much lower.

At first glance, one would expect the separation to be dependent on the Rossby number through activity, since it is connected to rotation, especially in light of the fact that log LX and log FX seem to play an important role here. However, it seems that the Rossby number does not. There could be a few reasons for that: the Rossby number was derived using different methods for MS and evolved stars using empirical relationships, and both rotation and the convective turnover time (e.g. through the depth of the convective envelope) can be drastically different on different parts of the Hertzsprung-Russell diagram.

For young and evolved stars, a common dynamo scaling was recently proposed by Lehtinen et al. (2020). Following their approach, using the chromospheric activity index 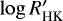logR′HK$\log R\prime_{\textrm{HK}}$ we plotted the coronal activity index log FX of the sample vs. stellar rotation+radius and Rossby number in Fig. 11. The result is very similar to that of Lehtinen et al. (2020): while there is a clear separation of log FX between MS and evolved stars in the function of rotation combined with radius (free from τc), the use of Rossby number results in one relation regardless of evolutionary state of the stars. This result shows that the strength of coronal activity depends on the underlying dynamo.

The clustering of the stars in our sample points towards the possibility to further check the dynamos at work in the stars within the clusters. We note, however, that the origin and working of the stellar dynamos have not been theoretically established to date, and it has a lot of unknown effects due to various physical parameters. A thorough and detailed review of dynamos in active stars (including the Sun) is given by Brun & Browning (2017), both from observational and theoretical points of view, and we direct the interested reader to consult this paper.

While the stars in the sample differ by dynamo type, the ways their coronae are heated could also be different (e.g. by waves, turbulence, braiding (nanoflares)) and helicity conservation (see Cranmer & Winebarger 2019), which could have implications for the FIP effect. Inverse FIP fractionation arises from upward propagating fast modes that are reflected or refracted back downwards (see e.g. Laming 2017). As this happens in the chromosphere, the fractionation itself does not tell us anything about how the corona is heated. Figure 12 shows that as the Rossby number decreases, the coronal X-ray flux (depending on the strength of the magnetic field) increases, which is similar to the results of Testa et al. (2015). Stars with increasing magnetic strength or X-ray flux show FIP effect, which gradually turns to inverse FIP effect. The magnetic field eventually saturates. Although the stellar dynamo generates magnetic field, it is destroyed by reconnection before it can rise to the corona, and the waves produced by this reconnection give the inverse FIP fractionation.

thumbnail Fig. 9

First two principal components, coloured (in the symbols’ centre) with FIP bias. Special stars (evolved, M dwarfs and A–F stars) are indicated separately with different symbols. The clusters found with k-means are shown with red, blue, and brown polygons.
thumbnail Fig. 10

Gaia EDR3 colour−magnitude diagram (within 100 pc) showing the clusters from the k-means analysis from Fig. 9, using the same colour coding for the three clusters. Gaiamagnitudes for stars brighter than G = 3m (e.g. the Sun) were estimated from V and IC magnitudes according to Riello et al. (2021). The nearly equal mass M-dwarf binaries YY Gem and AU Mic lie above the main sequence due to their binary nature. In the case of AU Mic, its youth also plays a role. The third star AT Mic is a PMS object, and this triple is a member of the β Pic moving group.
thumbnail Fig. 11

X-ray flux as a function of stellar rotation. Upper panel: log FX vs. combined rotation period and stellar radius Lower panel: log FX vs. Rossby number as in Figs. 3b and 2a in Lehtinen et al. (2020), but with log FX instead of logR′HK$\log R\prime_{\textrm{HK}}$. The colour bars in both panels indicate surface gravity.
thumbnail Fig. 12

X-ray flux vs. Rossby number, coloured with the FIP bias.

6 Summary and conclusions

We present FIP-bias values for 59 stars extending the sample with active MS and evolved stars for which no FIP-bias values were available to date. The literature FIP-bias values are recalculated, and as a second set, new FIP-bias values are presented for all stars in the sample using homogeneously derived photospheric abundances based on LAMOST data. For a few stars, we derived newphotospheric abundances via spectral synthesis with SME. The main results can be summarised as follows:

  • We did not find systematic difference among the FIP-bias values using the recalculated literature, KNN, or SME photospheric abundances, except for the KNN values of the coolest stars due to the lack of such stars in the LAMOST training set.

  • We find that the Teff−FIP bias diagram is not a simple relation, but it now has two branches separated by ~0.5 in FIP bias. The new (upper) branch consists of mostly evolved stars and additionally stars with high rotational velocity. The low-mass, flaring M dwarfs form a small blob in the continuation of the lower branch of the relation.

  • We suggest that the well-defined separation of the two branches in the Teff−FIP bias relation may be related to the bimodality in activity levels (the Vaughan-Preston gap), which in turn may be linked to a bimodality in rotation rates (periods) of stars of the same age but in different evolutionary stages due to different masses or binary evolution.

  • The separation of the two branches is observable through activity indicators such as vrot, log FX, Ro, and 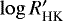logR′HK$\log R\prime_{\textrm{HK}}$ showing the importance of these parameters in the FIP bias of the stellar sample.

  • A statistical analysis of 12 stellar parameters reveals three clusters of stars in the sample. The evolved stars are well separated from the MS stars, which are roughly divided by the sign of the FIP-bias values. The distribution of stars in the diagrams showing the clusters by means of distances between the stellar parameters and the linear discriminant analysis suggest that the FIP bias relates to the depths and structures of the convection zones of the stars indicated by their measured parameters. The properties (or the lack) of the convection zones have a direct effect on the magnetic activity of the stars, and, through this, on the FIP-bias values.

The results presented in this paper through the investigation of the effects of different stellar parameters broaden our knowledge of the existing Teff −FIP-bias relation. The extension of the sample to evolved stars may help to generalise this relation for different kinds of magnetically active stars in different evolutionary stages.

Acknowledgements

We thank the referee for the useful suggestion concerning the connection between the (I)FIP and the heating of the stellar coronae. Konkoly Observatory, Budapest, Hungary hosted two workshops on Elemental Composition in Solar and Stellar Atmospheres (IFIPWS-1, 13-15 Feb, 2017 and IFIPWS-2, 27 Feb-1 Mar, 2018). The workshops have fostered collaboration by exploiting synergies in solar and stellar magnetic activity studies and exchanging experience and knowledge in both research fields. We thank G. Csörnyei for the useful discussions and enlightening ideas regarding statistical methods. This work was supported by the Hungarian National Research, Development and Innovation Office grants NKFIH (OTKA) K-131508, KH-130526, NN129075, K129249 and by the NKFIH grant 2019-2.1.11-TÉT-2019-00056. Authors acknowledge the financial support of the Austrian-Hungarian Action Foundation (101öu13, 104öu2). L.K. acknowledges the financial support of the Hungarian National Research, Development and Innovation Office grant NKFIH PD-134784. L.K. is a Bolyai János Research Fellow. J.M.L. was supported by the NASA Heliophysics Guest Investigator (80HQTR19T0029) and Supporting Research (80HQTR20T0076) programs, and by Basic Research FUnds of the Office of Naval Research. D.B. is funded under STFC consolidated grant number ST/S000240/1 and LvDG is partially funded under the same grant. Software: python (Van Rossum & Drake 2009), matplotlib (Hunter 2007), numpy (van der Walt et al. 2011), scipy (Virtanen et al. 2020), pandas (McKinney 2010), sklearn (Pedregosa et al. 2011).

Appendix A Tabulation of abundances for the FIP bias calculation

Table A.1

Data for the calculation of the literature FIP bias.

Table A.2

Data for the calculation of the KNN FIP bias.

Appendix B Results of the spectral synthesis

Table B.1

Results from the SME fit of CFHT-ESpaDoNS and TBL-NARVAL spectra.

Appendix C References for the individual stars listed in Table 2

M-type flare stars

AD Leo Teff, [Fe/H]: Rojas-Ayala et al. (2012), log g, R: Stassun et al. (2019), Prot: Morin et al. (2008), 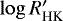logR′HK$\log R\prime_{\textrm{HK}}$: Astudillo-Defru et al. (2017), log LX: Wood et al. (2018, their Table 1), age (mean): Shkolnik et al. (2009)

CN Leo Teff: Shulyak et al. (2014), log g, R: Stassun et al. (2019), [Fe/H]: Rojas-Ayala et al. (2012), Prot: Newton et al. (2018), log LX: Schmitt & Liefke (2004), age (mean): Pavlenko et al. (2006)

EQ Peg A Teff: Yee et al. (2017), log g: calculated from mass, [Fe/H]: Yee et al. (2017), Prot: Morin et al. (2008), 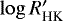logR′HK$\log R\prime_{\textrm{HK}}$: Gagné et al. (2016), R, log LX: Wood et al. (2018, their Table 6), mass: 0.36M⊙ from the Multiple Star Catalog (http://www.ctio.noao.edu/~atokovin/stars/stars.php), age: Zuckerman et al. (2013)

EQ Peg B Teff: Houdebine et al. (2019), log g: calculated from mass, [Fe/H] (as EQ Peg A): Yee et al. (2017), Prot: Morin et al. (2008), R, log LX: Wood et al. (2018, their Table 1), mass: 0.19M⊙ from the Multiple Star Catalog (http://www.ctio.noao.edu/~atokovin/stars/stars.php), age: Zuckerman et al. (2013)

Proxima Cen Teff, log g: Zhao et al. (2018), [Fe/H] (as α Cen A, B): Zhao et al. (2018), Prot: Klein et al. (2021), R: Zhao et al. (2018), 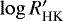logR′HK$\log R\prime_{\textrm{HK}}$: Astudillo-Defru et al. (2017), log LX: Wood et al. (2018, their Table 6), age (as α Cen A, B): Zhao et al. (2018)

EV Lac Teff, log g, [Fe/H]: Schweitzer et al. (2019), Prot: Contadakis (1995), R: Schweitzer et al. (2019), 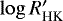logR′HK$\log R\prime_{\textrm{HK}}$: Gagné et al. (2016), log LX: Wood et al. (2018, their Table 6), age (mean): Shkolnik et al. (2009)

YY Gem Teff, log g (calculated from mass), R, mass: MacDonald & Mullan (2017), Prot: Kochukhov & Shulyak (2019), [Fe/H], log LX, age: MacDonald & Mullan (2014)

AU Mic Teff: Houdebine et al. (2019), log g: Cifuentes et al. (2020), [Fe/H]: Houdebine (2009), Prot: Messina et al. (2017), 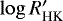logR′HK$\log R\prime_{\textrm{HK}}$: Ibañez Bustos et al. (2019), R, log LX: Wood et al. (2018, their Table 1), age: Gagné et al. (2018),

AT Mic Teff: Malo et al. (2014), log g: calculated from mass, [Fe/H]: Houdebine (2009), Prot, R: Messina et al. (2017), log LX: Pye et al. (2015), mass: 0.61M⊙ from the Multiple Star Catalog (http://www.ctio.noao.edu/~atokovin/stars/stars.php), age: Gagné et al. (2018),

Fast-rotating K dwarfs with flares

AB Dor Teff : Close et al. (2007), log g: calculated from mass, [Fe/H]: Cayrel de Strobel et al. (1997), Prot: Strassmeier (2009), R: Guirado et al. (2011), 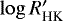logR′HK$\log R\prime_{\textrm{HK}}$: Boro Saikia et al. (2018), log LX: Wood et al. (2018, their Table 1), mass: 0.86M⊙ from Guirado et al. (2011), age: Gagné et al. (2018),

LO Peg Teff, log g: Folsom et al. (2016), [Fe/H]: Jeffries et al. (1994), Prot: Dal & Tas (2003), R: Folsom et al. (2016), 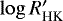logR′HK$\log R\prime_{\textrm{HK}}$: Plavchan et al. (2009), log LX: Lalitha et al. (2017), age: Gagné et al. (2018),

V471 Tau Teff, log g, [Fe/H], Prot, R, log LX, log FX: Kővári et al. (2021), age: Gagné et al. (2018)

K dwarfs

GJ 338 A Teff, log g [Fe/H], R: Schweitzer et al. (2019), Prot: González-Álvarez et al. (2020), 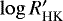logR′HK$\log R\prime_{\textrm{HK}}$: Gagné et al. (2016), log LX: Wood et al. (2018, their Table 6), age (upper limit, (B−V)SIMBAD$(B-V)_{\textrm{SIMBAD}}$=1.m41): Barnes (2007),

GJ 338 B Teff, log g [Fe/H], R: Schweitzer et al. (2019), Prot: González-Álvarez et al. (2020) 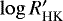logR′HK$\log R\prime_{\textrm{HK}}$: Gagné et al. (2016), log LX: Wood et al. (2018, their Table 6), age (upper limit, 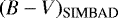(B−V)SIMBAD$(B-V)_{\textrm{SIMBAD}}$=1.m42): Barnes (2007),

36 Oph A Teff, log g: Luck (2017), [Fe/H]: Cayrel de Strobel et al. (1989), Prot, 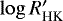logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

36 Oph B Teff, log g: Luck (2017), [Fe/H]: Cayrel de Strobel et al. (1989), Prot, 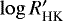logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

ξ Boo B Teff, log g, [Fe/H]: Aleo et al. (2017), Prot, 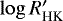logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

61 Cyg A Teff, log g: Heiter et al. (2015), [Fe/H]: Luck & Heiter (2005), Prot, 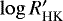logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

61 Cyg B Teff, log g: Heiter et al. (2015), [Fe/H]: Luck & Heiter (2005), Prot, 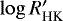logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

70 Oph A Teff, log g, [Fe/H]: from this paper, Prot, 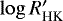logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

70 Oph B Teff, log g, [Fe/H]: from this paper, 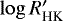logR′HK$\log R\prime_{\textrm{HK}}$ (as 70 Oph A), age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

ϵ Eri Teff, log g, [Fe/H]: from this paper, Prot, 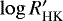logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

Solar-type stars

Sun α Cen A Teff, log g, [Fe/H]: Morel (2018), Prot: Angus et al. (2015), 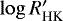logR′HK$\log R\prime_{\textrm{HK}}$: Mamajek & Hillenbrand (2008), R, log LX: Wood et al. (2018, their Table 1), age (mean): Zhao et al. (2018)

α Cen B Teff, log g, [Fe/H]: Morel (2018), Prot: Angus et al. (2015), 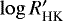logR′HK$\log R\prime_{\textrm{HK}}$: Mamajek & Hillenbrand (2008), R, log LX: Wood et al. (2018, their Table 1), age (mean): Zhao et al. (2018)

π1 UMa Teff, log g, [Fe/H]: from this paper, Prot, 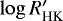logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

EK Dra Teff, log g, [Fe/H]: from this paper, Prot: Messina & Guinan (2002), 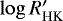logR′HK$\log R\prime_{\textrm{HK}}$: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1), age: Gagné et al. (2018),

ξ Boo A Teff, log g, [Fe/H]: from this paper, Prot, 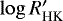logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 1)

χ1 Ori Teff, log g, [Fe/H]: from this paper, Prot, 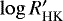logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 6)

κ Cet Teff, log g, [Fe/H]: from this paper, Prot, 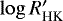logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 6)

β Com Teff, log g, [Fe/H]: from this paper, Prot, 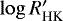logR′HK$\log R\prime_{\textrm{HK}}$, age: Barnes (2007), R, log LX: Wood et al. (2018, their Table 6)

47 Cas B Teff: Ness et al. (2004), [Fe/H]: Casagrande et al. (2011), Prot, log LX, age: Telleschi et al. (2005), R: Johnstone & Güdel (2015)

ι Hor Teff, log g, [Fe/H], R: Fuhrmann et al. (2017), Prot: Metcalfe et al. (2010), 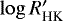logR′HK$\log R\prime_{\textrm{HK}}$: Boro Saikia et al. (2018), log LX: Peretz et al. (2015), age: Gagné et al. (2018),

11 LMi Teff: Yee et al. (2017), log g, [Fe/H], Prot, 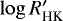logR′HK$\log R\prime_{\textrm{HK}}$: Olspert et al. (2018), R: Boyajian et al. (2013), log LX: Peretz et al. (2015), age: Montesinos et al. (2016)

HR 7291 Teff: Giribaldi et al. (2019, their Table 4), log g, [Fe/H], Prot, R: Fares et al. (2013), age: Takeda et al. (2007), 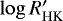logR′HK$\log R\prime_{\textrm{HK}}$: Wright et al. (2004), log LX: Peretz et al. (2015)

σ2 CrB Teff, R, [Fe/H], age: Raghavan et al. (2009), log g: Luck (2017), Prot: Strassmeier & Rice (2003), 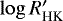logR′HK$\log R\prime_{\textrm{HK}}$: Gray et al. (2003), log LX: Pye et al. (2015)

ξ UMa B Teff, log g, [Fe/H]: Zhao et al. (2002), Prot (=Porb), R: Sanz-Forcada et al. (2003), log LX: Dempsey et al. (1993)

Evolved stars

HR 1099 Teff, log g, 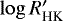logR′HK$\log R\prime_{\textrm{HK}}$: Sreejith et al. (2020), [Fe/H]: Luck (2017), Prot: Lanza et al. (2006), R: Fekel (1983), log LX: Huenemoerder et al. (2013)

UX Ari Teff, log g, [Fe/H], Prot, R, age: Hummel et al. (2017), log LX: Makarov (2003)

λ And Teff, log g, [Fe/H]: from this paper, Prot: Strassmeier et al. (1993), R, age: Montesinos et al. (2016), logR′HK$\log R\prime_{\textrm{HK}}$: Gray et al. (2003), log LX: Drake et al. (1992)

VY AriTeff, log g, [Fe/H]: Ottmann et al. (1998), Prot: Strassmeier et al. (1997), R: Gaia Collaboration (2018), log LX: Makarov (2003)

Capella Teff, log g, [Fe/H], Prot, R, age: Torres et al. (2015), log LX: Makarov (2003)

σ Gem Teff, log g, [Fe/H]: from this paper, Prot, R, age: Roettenbacher et al. (2015), log LX: Huenemoerder et al. (2013)

31 Com Teff, log g, [Fe/H], Prot, R, age: Strassmeier et al. (2010), log LX: García-Alvarez et al. (2006)

μ Vel Teff: Ayres et al. (2007), log g: calculated from mass, R: Mullan et al. (2006), log LX: Makarov (2003), mass: 3.3M⊙ from Mallik et al. (2003)

β Cet Teff, log g, [Fe/H]: from this paper, Prot: Tsvetkova et al. (2013), R: Berio et al. (2011), 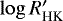logR′HK$\log R\prime_{\textrm{HK}}$: Rich et al. (2017), log LX: Makarov (2003), age: Stock et al. (2018)

FK Com Teff, log g, Prot: Korhonen et al. (2004), [Fe/H]: Anders et al. (2019), R: Gaia Collaboration (2018), log LX: Ayres et al. (2016)

YY Men Teff, log g: Randich et al. (1993), [Fe/H], Prot, R, log LX: Audard et al. (2004)

EI Eri Teff, log g, R, Prot, age: Washuettl et al. (2009), [Fe/H]: Ottmann et al. (1998), log LX: Osten et al. (2002)

V851 Cen Teff, log g, [Fe/H]: Katz et al. (2003), Prot: Kiraga (2012), R: Stawikowski & Glebocki (1994b), log LX: Dempsey et al. (1993)

AR PscTeff, log g, [Fe/H]: Shan et al. (2006), Prot: Matranga et al. (2010), R: Stawikowski & Glebocki (1994a), log LX: Dempsey et al. (1993), age: Fekel (1996)

AY CetTeff, log g, [Fe/H], age: Deka-Szymankiewicz et al. (2018), Prot: Strassmeier et al. (1990), R: Stawikowski & Glebocki (1994a), log LX: Sanz-Forcada et al. (2003)

II Peg Teff, log g, [Fe/H], R: Berdyugina et al. (1998), Prot: Strassmeier et al. (1990), log LX: Dempsey et al. (1993)

AR LacTeff, log g, Prot (=Porb): Lanza et al. (1998), [Fe/H]: Cayrel de Strobel et al. (1992), R: Zboril et al. (2005), log LX: Dempsey et al. (1993)

F stars, hotter than 6300K

η Lep Teff, log g, [Fe/H]: from this paper, 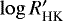logR′HK$\log R\prime_{\textrm{HK}}$: Boro Saikia et al. (2018), R, log LX: Wood et al. (2018, their Table 1), age: Casagrande et al. (2011)

π3 Ori Teff, log g, [Fe/H]: from this paper, 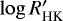logR′HK$\log R\prime_{\textrm{HK}}$: Wright et al. (2004), R, log LX: Wood et al. (2018, their Table 1), age: Wright et al. (2004)

τ Boo A Teff, log g, [Fe/H]: from this paper, Prot: Fares et al. (2009), 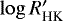logR′HK$\log R\prime_{\textrm{HK}}$, age: Mamajek & Hillenbrand (2008), R, log LX: Wood et al. (2018, their Table 1)

Procyon Teff, log g, [Fe/H]: Kervella et al. (2004), Prot: Ayres (1991), R: Aufdenberg et al. (2005), log LX: Ness et al. (2002), age: Liebert et al. (2013)

Altair Teff (mean), [Fe/H], R (mean): Monnier et al. (2007), log g: Malagnini & Morossi (1990), Prot: Peterson et al. (2006), log LX, age: Robrade & Schmitt (2009)

References

  1. Aleo, P. D., Sobotka, A. C., & Ramírez, I. 2017, ApJ, 846, 24 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allende Prieto, C., Barklem, P. S., Asplund, M., & Ruiz Cobo, B. 2001, ApJ, 558, 830 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allende Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Allende Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
  5. Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
  6. Anders, F., Khalatyan, A., Chiappini, C., et al. 2019, A&A, 628, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Angus, R., Aigrain, S., Foreman-Mackey, D., & McQuillan, A. 2015, MNRAS, 450, 1787 [Google Scholar]
  8. Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [Google Scholar]
  9. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  10. Astudillo-Defru, N., Delfosse, X., Bonfils, X., et al. 2017, A&A, 600, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Audard, M., Güdel, M., Sres, A., Raassen, A. J. J., & Mewe, R. 2003, A&A, 398, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Audard, M., Telleschi, A., Güdel, M., et al. 2004, ApJ, 617, 531 [NASA ADS] [CrossRef] [Google Scholar]
  13. Aufdenberg, J. P., Ludwig, H. G., & Kervella, P. 2005, ApJ, 633, 424 [Google Scholar]
  14. Aurière, M. 2003, EAS Pub. Ser., 9, 105 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Ayres, T. R. 1991, ApJ, 375, 704 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ayres, T. R., Hodges-Kluck, E., & Brown, A. 2007, ApJS, 171, 304 [NASA ADS] [CrossRef] [Google Scholar]
  17. Ayres, T. R., Kashyap, V., Saar, S., et al. 2016, ApJS, 223, 5 [NASA ADS] [CrossRef] [Google Scholar]
  18. Baker, D., van Driel-Gesztelyi, L., Brooks, D. H., et al. 2019, ApJ, 875, 35 [NASA ADS] [CrossRef] [Google Scholar]
  19. Baker, D., van Driel-Gesztelyi, L., Brooks, D. H., et al. 2020, ApJ, 894, 35 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ball, B., Drake, J. J., Lin, L., et al. 2005, ApJ, 634, 1336 [NASA ADS] [CrossRef] [Google Scholar]
  21. Barnes, S. A. 2007, ApJ, 669, 1167 [Google Scholar]
  22. Barnes, S. A. 2010, ApJ, 722, 222 [Google Scholar]
  23. Berdyugina, S. V., Jankov, S., Ilyin, I., Tuominen, I., & Fekel, F. C. 1998, A&A, 334, 863 [NASA ADS] [Google Scholar]
  24. Berio, P., Merle, T., Thévenin, F., et al. 2011, A&A, 535, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [Google Scholar]
  27. Brooks, D. H., Baker, D., van Driel-Gesztelyi, L., & Warren, H. P. 2017, Nat. Commun., 8, 183 [NASA ADS] [CrossRef] [Google Scholar]
  28. Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
  29. Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Cayrel de Strobel, G., Perrin, M. N., Cayrel, R., & Lebreton, Y. 1989, A&A, 225, 369 [NASA ADS] [Google Scholar]
  31. Cayrel de Strobel, G., Hauck, B., Francois, P., et al. 1992, A&AS, 95, 273 [NASA ADS] [Google Scholar]
  32. Cayrel de Strobel, G., Soubiran, C., Friel, E. D., Ralite, N., & Francois, P. 1997, A&AS, 124, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Cifuentes, C., Caballero, J. A., Cortés-Contreras, M., et al. 2020, A&A, 642, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Close, L. M., Thatte, N., Nielsen, E. L., et al. 2007, ApJ, 665, 736 [NASA ADS] [CrossRef] [Google Scholar]
  35. Contadakis, M. E. 1995, A&A, 300, 819 [NASA ADS] [Google Scholar]
  36. Cranmer, S. R., & Winebarger, A. R. 2019, ARA&A, 57, 157 [Google Scholar]
  37. Csörnyei, G., Dobos, L., & Csabai, I. 2021, MNRAS, 502, 5762 [CrossRef] [Google Scholar]
  38. Dal, H. A., & Tas, G. 2003, IBVS, 5390, 1 [NASA ADS] [Google Scholar]
  39. Deka-Szymankiewicz, B., Niedzielski, A., Adamczyk, M., et al. 2018, A&A, 615, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Dempsey, R. C., Linsky, J. L., Fleming, T. A., & Schmitt, J. H. M. M. 1993, ApJS, 86, 599 [NASA ADS] [CrossRef] [Google Scholar]
  41. Donati, J.-F. 2003, ASP Conf. Ser., 307, 41 [Google Scholar]
  42. Doschek, G. A., & Warren, H. P. 2016, ApJ, 825, 36 [NASA ADS] [CrossRef] [Google Scholar]
  43. Doschek, G. A., Warren, H. P., & Feldman, U. 2015, ApJ, 808, L7 [NASA ADS] [CrossRef] [Google Scholar]
  44. Drake, J. J., & Testa, P. 2005, Nature, 436, 525 [NASA ADS] [CrossRef] [Google Scholar]
  45. Drake, S. A., Simon, T., & Linsky, J. L. 1992, ApJS, 82, 311 [NASA ADS] [CrossRef] [Google Scholar]
  46. Drake, J. J., Laming, J. M., & Widing, K. G. 1997, ApJ, 478, 403 [NASA ADS] [CrossRef] [Google Scholar]
  47. Drake, J. J., Ratzlaff, P., Kashyap, V., et al. 2014, ApJ, 783, 2 [NASA ADS] [CrossRef] [Google Scholar]
  48. Eker, Z., Filiz-Ak, N., Bilir, S., et al. 2008, VizieR Online Data Catalog: V/128 [Google Scholar]
  49. Erspamer, D., & North, P. 2003, A&A, 398, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Fares, R., Donati, J. F., Moutou, C., et al. 2009, MNRAS, 398, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  51. Fares, R., Moutou, C., Donati, J. F., et al. 2013, MNRAS, 435, 1451 [NASA ADS] [CrossRef] [Google Scholar]
  52. Fekel, F. C., J. 1983, ApJ, 268, 274 [NASA ADS] [CrossRef] [Google Scholar]
  53. Fekel, F. C. 1996, AJ, 112, 269 [NASA ADS] [CrossRef] [Google Scholar]
  54. Feldman, U., & Laming, J. M. 2000, Phys. Scr, 61, 222 [CrossRef] [Google Scholar]
  55. Feldman, U., & Widing, K. G. 2003, Space Sci. Rev., 107, 665 [CrossRef] [Google Scholar]
  56. Fisher, R. A. 1936, Annals of Eugenics, 7, 179 [CrossRef] [Google Scholar]
  57. Fleming, D. P., Barnes, R., Davenport, J. R. A., & Luger, R. 2019, ApJ, 881, 88 [Google Scholar]
  58. Folsom, C. P., Petit, P., Bouvier, J., et al. 2016, MNRAS, 457, 580 [Google Scholar]
  59. Fuhrmann, K., Chini, R., Kaderhandt, L., & Chen, Z. 2017, ApJ, 836, 139 [Google Scholar]
  60. Fuhrmeister, B., Liefke, C., & Schmitt, J. H. M. M. 2007, A&A, 468, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Gagné, J., Plavchan, P., Gao, P., et al. 2016, ApJ, 822, 40 [Google Scholar]
  62. Gagné, J., Mamajek, E. E., Malo, L., et al. 2018, ApJ, 856, 23 [Google Scholar]
  63. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. García-Alvarez, D., Drake, J. J., Lin, L., Kashyap, V. L., & Ball, B. 2005, ApJ, 621, 1009 [Google Scholar]
  65. García-Alvarez, D., Drake, J. J., Ball, B., Lin, L., & Kashyap, V. L. 2006, ApJ, 638, 1028 [CrossRef] [Google Scholar]
  66. Giribaldi, R. E., Ubaldo-Melo, M. L., Porto de Mello, G. F., et al. 2019, A&A, 624, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Gondoin, P. 2007, A&A, 464, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Gondoin, P., Erd, C., & Lumb, D. 2002, A&A, 383, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Gonzalez, G., & Laws, C. 2007, MNRAS, 378, 1141 [NASA ADS] [CrossRef] [Google Scholar]
  70. González-Álvarez, E., Zapatero Osorio, M. R., Caballero, J. A., et al. 2020, A&A, 637, A93 [EDP Sciences] [Google Scholar]
  71. Gray, R. O., Corbally, C. J., Garrison, R. F., McFadden, M. T., & Robinson, P. E. 2003, AJ, 126, 2048 [Google Scholar]
  72. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
  73. Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348 [NASA ADS] [Google Scholar]
  74. Guirado, J. C., Marcaide, J. M., Martí-Vidal, I., et al. 2011, A&A, 533, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Houdebine, E. R. 2009, MNRAS, 397, 2133 [NASA ADS] [CrossRef] [Google Scholar]
  78. Houdebine, É. R., Mullan, D. J., Doyle, J. G., et al. 2019, AJ, 158, 56 [NASA ADS] [CrossRef] [Google Scholar]
  79. Huenemoerder, D. P., Canizares, C. R., & Schulz, N. S. 2001, ApJ, 559, 1135 [NASA ADS] [CrossRef] [Google Scholar]
  80. Huenemoerder, D. P., Canizares, C. R., Drake, J. J., & Sanz-Forcada, J. 2003, ApJ, 595, 1131 [NASA ADS] [CrossRef] [Google Scholar]
  81. Huenemoerder, D. P., Phillips, K. J. H., Sylwester, J., & Sylwester, B. 2013, ApJ, 768, 135 [NASA ADS] [CrossRef] [Google Scholar]
  82. Hummel, C. A., Monnier, J. D., Roettenbacher, R. M., et al. 2017, ApJ, 844, 115 [NASA ADS] [CrossRef] [Google Scholar]
  83. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  84. Ibañez Bustos, R. V., Buccino, A. P., Flores, M., et al. 2019, MNRAS, 483, 1159 [CrossRef] [Google Scholar]
  85. Işık, E., Solanki, S. K., Krivova, N. A., & Shapiro, A. I. 2018, A&A, 620, A177 [Google Scholar]
  86. Jeffries, R. D., Byrne, P. B., Doyle, J. G., et al. 1994, MNRAS, 270, 153 [NASA ADS] [CrossRef] [Google Scholar]
  87. Jofré, P., Heiter, U., Soubiran, C., et al. 2015, A&A, 582, A81 [Google Scholar]
  88. Johnstone, C. P., & Güdel, M. 2015, A&A, 578, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Kaiser, H. F. 1960, Educ. Psychol. Meas., 20, 141 [Google Scholar]
  90. Katsuda, S., Ohno, M., Mori, K., et al. 2020, ApJ, 891, 126 [NASA ADS] [CrossRef] [Google Scholar]
  91. Katz, D., Favata, F., Aigrain, S., & Micela, G. 2003, A&A, 397, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Kervella, P., Thévenin, F., Morel, P., et al. 2004, A&A, 413, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Kővári, Z s., Bartus, J., Strassmeier, K. G., et al. 2007, A&A, 463, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Kővári, Z s., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Kővári, Z s., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Kővári, Z., Kriskovics, L., Oláh, K., et al. 2021, A&A, 650, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Kiraga, M. 2012, Acta Astron., 62, 67 [NASA ADS] [Google Scholar]
  98. Klein, B., Donati, J.-F., Hébrard, É. M., et al. 2021, MNRAS, 500, 1844 [Google Scholar]
  99. Kochukhov, O., & Shulyak, D. 2019, ApJ, 873, 69 [Google Scholar]
  100. Korhonen, H., Berdyugina, S. V., & Tuominen, I. 2004, Astron. Nachr., 325, 402 [NASA ADS] [CrossRef] [Google Scholar]
  101. Korhonen, H., Roettenbacher, R. M., Gu, S., et al. 2021, A&A, 646, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Kovalev, M., Brinkmann, S., Bergemann, M., & MPIA IT-department. 2018, NLTE MPIA web server, [Online]. Available: http://nlte.mpia.de Max Planck Institute for Astronomy, Heidelberg. [Google Scholar]
  103. Kriskovics, L., Kővári, Zs., Vida, K., et al. 2019, A&A, 627, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Lalitha, S., Schmitt, J. H. M. M., & Singh, K. P. 2017, A&A, 602, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Laming, J. M. 2004, ApJ, 614, 1063 [Google Scholar]
  107. Laming, J. M. 2009, ApJ, 695, 954 [NASA ADS] [CrossRef] [Google Scholar]
  108. Laming, J. M. 2012, ApJ, 744, 115 [NASA ADS] [CrossRef] [Google Scholar]
  109. Laming, J. M. 2015a, Liv. Rev. Sol. Phys., 12, 2 [Google Scholar]
  110. Laming, J. M. 2015b, ApJ, 805, 102 [NASA ADS] [CrossRef] [Google Scholar]
  111. Laming, J. M. 2017, ApJ, 844, 153 [Google Scholar]
  112. Laming, J. M. 2021, ApJ, 909, 17 [NASA ADS] [CrossRef] [Google Scholar]
  113. Laming, J. M., & Drake, J. J. 1999, ApJ, 516, 324 [NASA ADS] [CrossRef] [Google Scholar]
  114. Laming, J. M., Drake, J. J., & Widing, K. G. 1996, ApJ, 462, 948 [NASA ADS] [CrossRef] [Google Scholar]
  115. Laming, J. M., Vourlidas, A., Korendyke, C., et al. 2019, ApJ, 879, 124 [Google Scholar]
  116. Lanza, A. F., Catalano, S., Cutispoto, G., Pagano, I., & Rodono, M. 1998, A&A, 332, 541 [NASA ADS] [Google Scholar]
  117. Lanza, A. F., Piluso, N., Rodonò, M., Messina, S., & Cutispoto, G. 2006, A&A, 455, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Lehtinen, J. J., Spada, F., Käpylä, M. J., Olspert, N., & Käpylä, P. J. 2020, Nat. Astron., 4, 658 [Google Scholar]
  119. Liebert, J., Fontaine, G., Young, P. A., Williams, K. A., & Arnett, D. 2013, ApJ, 769, 7 [NASA ADS] [CrossRef] [Google Scholar]
  120. Liefke, C., Ness, J. U., Schmitt, J. H. M. M., & Maggio, A. 2008, A&A, 491, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Luck, R. E. 2017, AJ, 153, 21 [Google Scholar]
  122. Luck, R. E., & Heiter, U. 2005, AJ, 129, 1063 [Google Scholar]
  123. MacDonald, J., & Mullan, D. J. 2014, ApJ, 787, 70 [NASA ADS] [CrossRef] [Google Scholar]
  124. MacDonald, J., & Mullan, D. J. 2017, ApJ, 850, 58 [NASA ADS] [CrossRef] [Google Scholar]
  125. Macqueen, J. 1967, in In 5-th Berkeley Symposium on Mathematical Statistics and Probability, 281–297 [Google Scholar]
  126. Magaudda, E., Stelzer, B., Covey, K. R., et al. 2020, A&A, 638, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Makarov, V. V. 2003, AJ, 126, 1996 [NASA ADS] [CrossRef] [Google Scholar]
  128. Malagnini, M. L., & Morossi, C. 1990, A&AS, 85, 1015 [NASA ADS] [Google Scholar]
  129. Mallik, S. V., Parthasarathy, M., & Pati, A. K. 2003, A&A, 409, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Malo, L., Doyon, R., Feiden, G. A., et al. 2014, ApJ, 792, 37 [NASA ADS] [CrossRef] [Google Scholar]
  131. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [Google Scholar]
  132. Matranga, M., Drake, J. J., Kashyap, V. L., Marengo, M., & Kuchner, M. J. 2010, ApJ, 720, L164 [NASA ADS] [CrossRef] [Google Scholar]
  133. McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. Stéfan van der Walt & Jarrod Millman, 56–61 [CrossRef] [Google Scholar]
  134. McLachlan, G. J. 2004, Discriminant Analysis and Statistical Pattern Recognition (Hoboken: John Wiley & Sons), 544 [Google Scholar]
  135. Messina, S., & Guinan, E. F. 2002, A&A, 393, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Messina, S., Millward, M., Buccino, A., et al. 2017, A&A, 600, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Metcalfe, T. S., Basu, S., Henry, T. J., et al. 2010, ApJ, 723, L213 [NASA ADS] [CrossRef] [Google Scholar]
  138. Meyer, J. P. 1985, ApJS, 57, 151 [CrossRef] [Google Scholar]
  139. Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [Google Scholar]
  140. Montesinos, B., Eiroa, C., Krivov, A. V., et al. 2016, A&A, 593, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  141. Morel, T. 2018, A&A, 615, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Morin, J., Donati, J. F., Petit, P., et al. 2008, MNRAS, 390, 567 [Google Scholar]
  143. Mullan, D. J., Mathioudakis, M., Bloomfield, D. S., & Christian, D. J. 2006, ApJS, 164, 173 [Google Scholar]
  144. Nanjundan, S., Sankaran, S., Arjun, C. R., & Paavai Anand, G. 2019, ArXiv e-prints [arXiv:1912.00643] [Google Scholar]
  145. Ness, J. U., Schmitt, J. H. M. M., Burwitz, V., et al. 2002, A&A, 394, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  146. Ness, J. U., Güdel, M., Schmitt, J. H. M. M., Audard, M., & Telleschi, A. 2004, A&A, 427, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  147. Newton, E. R., Mondrik, N., Irwin, J., Winters, J. G., & Charbonneau, D. 2018, AJ, 156, 217 [Google Scholar]
  148. Nordon, R., Behar, E., & Drake, S. A. 2013, A&A, 550, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  150. Olspert, N., Lehtinen, J. J., Käpylä, M. J., Pelt, J., & Grigorievskiy, A. 2018, A&A, 619, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Osten, R. A., Brown, A., Wood, B. E., & Brady, P. 2002, ApJS, 138, 99 [NASA ADS] [CrossRef] [Google Scholar]
  152. Osten, R. A., Ayres, T. R., Brown, A., Linsky, J. L., & Krishnamurthi, A. 2003, ApJ, 582, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  153. Ottmann, R., Pfeiffer, M. J., & Gehren, T. 1998, A&A, 338, 661 [NASA ADS] [Google Scholar]
  154. Pace, G., Melendez, J., Pasquini, L., et al. 2009, A&A, 499, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  155. Pavlenko, Y. V., Jones, H. R. A., Lyubchik, Y., Tennyson, J., & Pinfield, D. J. 2006, A&A, 447, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  156. Pearson, K. 1901, Philos. Mag. J. Sci., 2, 559 [CrossRef] [Google Scholar]
  157. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  158. Peretz, U., Behar, E., & Drake, S. A. 2015, A&A, 577, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006, ApJ, 636, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  160. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  161. Plavchan, P., Werner, M. W., Chen, C. H., et al. 2009, ApJ, 698, 1068 [Google Scholar]
  162. Pottasch, S. R. 1963, ApJ, 137, 945 [NASA ADS] [CrossRef] [Google Scholar]
  163. Pye, J. P., Rosen, S., Fyfe, D., & Schröder, A. C. 2015, A&A, 581, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  164. Raassen, A. J. J., Mewe, R., Audard, M., et al. 2002, A&A, 389, 228 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  165. Rácz, I. I., Balázs, L. G., Bagoly, Zs., Horváth, I., & Tóth, L. V. 2018, Astron. Nachr., 339, 352 [CrossRef] [Google Scholar]
  166. Raghavan, D., McAlister, H. A., Torres, G., et al. 2009, ApJ, 690, 394 [Google Scholar]
  167. Ramírez, I., Meléndez, J., Bean, J., et al. 2014, A&A, 572, A48 [Google Scholar]
  168. Randich, S., Gratton, R., & Pallavicini, R. 1993, A&A, 273, 194 [NASA ADS] [Google Scholar]
  169. Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
  170. Rich, E. A., Wisniewski, J. P., McElwain, M. W., et al. 2017, MNRAS, 472, 1736 [NASA ADS] [CrossRef] [Google Scholar]
  171. Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  172. Robrade, J., & Schmitt, J. H. M. M. 2005, A&A, 435, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  173. Robrade, J., & Schmitt, J. H. M. M. 2009, A&A, 497, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  174. Roettenbacher, R. M., Monnier, J. D., Henry, G. W., et al. 2015, ApJ, 807, 23 [NASA ADS] [CrossRef] [Google Scholar]
  175. Roettenbacher, R. M., Monnier, J. D., Korhonen, H., et al. 2016, Nature, 533, 217 [Google Scholar]
  176. Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [Google Scholar]
  177. Saar, S. H. 1996, in Stellar Surface Structure, eds. K. G. Strassmeier, & J. L. Linsky (Berlin: Springer), 176, 237 [NASA ADS] [Google Scholar]
  178. Sanz-Forcada, J., Brickhouse, N. S., & Dupree, A. K. 2003, ApJS, 145, 147 [Google Scholar]
  179. Sanz-Forcada, J., Favata, F., & Micela, G. 2004, A&A, 416, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  180. Sanz-Forcada, J., Affer, L., & Micela, G. 2009, A&A, 505, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  181. Sanz-Forcada, J., Stelzer, B., Coffaro, M., Raetz, S., & Alvarado-Gómez, J. D. 2019, A&A, 631, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  182. Schmitt, J. H. M. M., & Liefke, C. 2004, A&A, 417, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  183. Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  184. Shan, H., Liu, X., & Gu, S. 2006, New Astron., 11, 287 [NASA ADS] [CrossRef] [Google Scholar]
  185. Shkolnik, E., Liu, M. C., & Reid, I. N. 2009, ApJ, 699, 649 [CrossRef] [Google Scholar]
  186. Shulyak, D., Reiners, A., Seemann, U., Kochukhov, O., & Piskunov, N. 2014, A&A, 563, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  187. Sitnova, T. M., Mashonkina, L. I., & Ryabchikova, T. A. 2013, Astron. Lett., 39, 126 [Google Scholar]
  188. Sreejith, A. G., Fossati, L., Youngblood, A., France, K., & Ambily, S. 2020, A&A, 644, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  189. Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
  190. Stawikowski, A., & Glebocki, R. 1994a, Acta Astron., 44, 33 [NASA ADS] [Google Scholar]
  191. Stawikowski, A., & Glebocki, R. 1994b, Acta Astron., 44, 393 [NASA ADS] [Google Scholar]
  192. Stock, S., Reffert, S., & Quirrenbach, A. 2018, A&A, 616, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  193. Strassmeier, K. G. 2009, A&ARv, 17, 251 [Google Scholar]
  194. Strassmeier, K. G., & Rice, J. B. 2003, A&A, 399, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  195. Strassmeier, K. G., Fekel, F. C., Bopp, B. W., Dempsey, R. C., & Henry, G. W. 1990, ApJS, 72, 191 [NASA ADS] [CrossRef] [Google Scholar]
  196. Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&AS, 100, 173 [NASA ADS] [Google Scholar]
  197. Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodono, M. 1997, A&AS, 125, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  198. Strassmeier, K. G., Granzer, T., Kopf, M., et al. 2010, A&A, 520, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  199. Takeda, G., Ford, E. B., Sills, A., et al. 2007, ApJS, 168, 297 [Google Scholar]
  200. Telleschi, A., Güdel, M., Briggs, K., et al. 2005, ApJ, 622, 653 [Google Scholar]
  201. Testa, P., Saar, S. H., & Drake, J. J. 2015, Philos. Trans. R. Soc. London Ser. A, 373, 20140259 [NASA ADS] [Google Scholar]
  202. Torres, G., Claret, A., Pavlovski, K., & Dotter, A. 2015, ApJ, 807, 26 [NASA ADS] [CrossRef] [Google Scholar]
  203. Tsvetkova, S., Petit, P., Aurière, M., et al. 2013, A&A, 556, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  204. Valenti, J. A.,& Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
  205. van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
  206. Van Rossum, G., & Drake, F. L. 2009, Python 3 Reference Manual (Scotts Valley, CA: CreateSpace) [Google Scholar]
  207. Vaughan, A. H., & Preston, G. W. 1980, PASP, 92, 385 [Google Scholar]
  208. Vida, K., Kriskovics, L., Oláh, K., et al. 2016, A&A, 590, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  209. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  210. Wang, R., Luo, A. L., Chen, J.-J., et al. 2020, ApJ, 891, 23 [Google Scholar]
  211. Washuettl, A., Strassmeier, K. G., Granzer, T., Weber, M., & Oláh, K. 2009, Astron. Nachr., 330, 27 [NASA ADS] [CrossRef] [Google Scholar]
  212. Wood, B. E., & Laming, J. M. 2013, ApJ, 768, 122 [NASA ADS] [CrossRef] [Google Scholar]
  213. Wood, B. E., & Linsky, J. L. 2006, ApJ, 643, 444 [NASA ADS] [CrossRef] [Google Scholar]
  214. Wood, B. E., & Linsky, J. L. 2010, ApJ, 717, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  215. Wood, B. E., Laming, J. M., & Karovska, M. 2012, ApJ, 753, 76 [NASA ADS] [CrossRef] [Google Scholar]
  216. Wood, B. E., Laming, J. M., Warren, H. P., & Poppenhaeger, K. 2018, ApJ, 862, 66 [Google Scholar]
  217. Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [Google Scholar]
  218. Yee, S. W., Petigura, E. A., & von Braun, K. 2017, ApJ, 836, 77 [Google Scholar]
  219. Yüce, K., Adelman, S. J., Gulliver, A. F., & Hill, G. 2011, Astron. Nachr., 332, 681 [CrossRef] [Google Scholar]
  220. Zboril, M., Oliveira, J. M., Messina, S., Djuraševič, G., & Amado, P. J. 2005, Contrib. Astron. Observ. Skalnate Pleso, 35, 23 [NASA ADS] [Google Scholar]
  221. Zhao, G., Chen, Y. Q., Qiu, H. M., & Li, Z. W. 2002, AJ, 124, 2224 [NASA ADS] [CrossRef] [Google Scholar]
  222. Zhao, L., Fischer, D. A., Brewer, J., Giguere, M., & Rojas-Ayala, B. 2018, AJ, 155, 24 [Google Scholar]
  223. Zuckerman, B., Vican, L., Song, I., & Schneider, A. 2013, ApJ, 778, 5 [Google Scholar]
2

The RANSAC algorithm selects a subset of the original data points and splits it to inlier and outlier points after fitting them by a model. By iterating these steps a final set of outliers is created where the outliers will have no influence on the final fit. We used RANSACRegressor from sklearn.linear_model.

All Tables

Table 1

Representation of different types of stars in our sample.

In the text
Table 2

Compiled astrophysical parameters for the sample.

In the text
Table A.1

Data for the calculation of the literature FIP bias.

In the text
Table A.2

Data for the calculation of the KNN FIP bias.

In the text
Table B.1

Results from the SME fit of CFHT-ESpaDoNS and TBL-NARVAL spectra.

In the text

All Figures

thumbnail Fig. 1

Abundance trends based on data from Wang et al. (2020) for the LAMOST sample, for the three relevant high-FIP elements (there are no available Ne abundances).
In the text
thumbnail Fig. 2

Literature FIP bias vs. Teff. Black dots indicate the stars from the original FIP-bias diagram of Laming (2015a), which is updated from Wood & Linsky (2010), forming a tight sequence with Teff.
In the text
thumbnail Fig. 3

Teff−FIP-bias diagram with recalculated FIP-bias values. For the Sun, orange points mark its activity minimum and maximum. Solid and dashed lines show two component linear fits with a RANSAC regressor, with grey and red corresponding to literature and the KNN FIP bias, respectively.
In the text
thumbnail Fig. 4

Teff−FIP bias diagrams with data points coloured according to various parameters. Missing parameters are indicated with black crosses. See the text for the details.
In the text
thumbnail Fig. 5

Results of linear discriminant analysis (LDA). Upper panel: pre-defined boundary between the two clusters (red and blue points) is shown with dashed lines on the Teff −FIP-bias diagram. The larger circles indicate the clusters assigned by the LDA. The three misclassified stars are ι Hor, HR 7291, and AY Cet. Lower panel: absolute value of the LD components corresponding to the given parameters. Thin lines come from bootstrap resampling, and error bars indicate the region between the 16th and 84th percentiles.
In the text
thumbnail Fig. 6

Correlation matrix using Spearman correlation coefficients.
In the text
thumbnail Fig. 7

Results of the PCA. Upper panel: explained variance ratio of each principal component (PC). The dashed line denotes the Kaiser criterion (Kaiser 1960), and the red points show the elbow points. Lower panel: importance of each parameter to a given principal component, with darker colours indicating stronger contribution (in absolute values).
In the text
thumbnail Fig. 8

First four PCs, coloured with the FIP bias (see Fig. 9 for the colour scale). The clear colour gradient shows the importance of the FIP bias parameter.
In the text
thumbnail Fig. 9

First two principal components, coloured (in the symbols’ centre) with FIP bias. Special stars (evolved, M dwarfs and A–F stars) are indicated separately with different symbols. The clusters found with k-means are shown with red, blue, and brown polygons.
In the text
thumbnail Fig. 10

Gaia EDR3 colour−magnitude diagram (within 100 pc) showing the clusters from the k-means analysis from Fig. 9, using the same colour coding for the three clusters. Gaiamagnitudes for stars brighter than G = 3m (e.g. the Sun) were estimated from V and IC magnitudes according to Riello et al. (2021). The nearly equal mass M-dwarf binaries YY Gem and AU Mic lie above the main sequence due to their binary nature. In the case of AU Mic, its youth also plays a role. The third star AT Mic is a PMS object, and this triple is a member of the β Pic moving group.
In the text
thumbnail Fig. 11

X-ray flux as a function of stellar rotation. Upper panel: log FX vs. combined rotation period and stellar radius Lower panel: log FX vs. Rossby number as in Figs. 3b and 2a in Lehtinen et al. (2020), but with log FX instead of logR′HK$\log R\prime_{\textrm{HK}}$. The colour bars in both panels indicate surface gravity.
In the text
thumbnail Fig. 12

X-ray flux vs. Rossby number, coloured with the FIP bias.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.