| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141872 | |
| Published online | 19 January 2022 | |
The Fornax Cluster VLT Spectroscopic Survey
IV. Cold kinematical substructures in the Fornax core from COSTA
1
School of Physics and Astronomy, Sun Yat-sen University Zhuhai Campus, 2 Daxue Road, Tangjia, Zhuhai, Guangdong 519082, PR China
e-mail: napolitano@mail.sysu.edu.cn
2
CSST Science Center for Guangdong-Hong Kong-Macau Great Bay Area, 519082 Zhuhai, PR China
3
INAF, Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Naples, Italy
4
Department of Physics E. Pancini, University Federico II, Via Cinthia 6, 80126 Naples, Italy
5
Sub-Department of Astrophysics, Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
6
INAF Osservatorio Astr. di Teramo, Via Maggini, 64100 Teramo, Italy
7
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
8
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, 02138 Cambridge, MA, USA
9
INFN, Sez. di Napoli, Via Cintia, 80126 Napoli, Italy
10
Kapteyn Astronomical Institute, University of Groningen, PO Box 72, 9700 AV Groningen, The Netherlands
11
Astronomy Research Unit, University of Oulu, Pentti Kaiteran katu 1, 90014 Oulu, Finland
Received:
24
July
2021
Accepted:
17
September
2021
Context. Substructures in stellar haloes are a strong prediction of galaxy formation models in ΛCDM. Cold streams such as those from small satellite galaxies are extremely difficult to detect and kinematically characterize. The COld STream finder Algorithm (COSTA) is a novel algorithm able to find streams in the phase space of planetary nebulae (PNe) and globular cluster (GC) populations. COSTA isolates groups of (N) particles with small velocity dispersion (between 10 km s−1 and ∼120 km s−1) using an iterative (n) sigma-clipping over a defined number of (k) neighbor particles.
Aims. We applied COSTA to a catalog of PNe and GCs from the Fornax Cluster VLT Spectroscopic Survey (FVSS) within ∼200 kpc from the cluster core in order to detect cold substructures and characterize their kinematics (mean velocity and velocity dispersion).
Methods. We selected more than 2000 PNe and GCs from the FVSS catalogs and adopted a series of optimized setups of the COSTA parameters based on Montecarlo simulations of the PN and GC populations to search for realistic stream candidates. We find 13 cold substructures with velocity dispersion ranging from ∼20 to ∼100 km s−1, which are likely associated either to large galaxies or to ultra-compact dwarf (UCD) galaxies in the Fornax core.
Results. The luminosities of these streams show a clear correlation with internal velocity dispersion, and their surface brightness correlates with their size and distance from the cluster center, which is compatible with the dissipative processes producing them. However, we cannot exclude that some of these substructures formed by violent relaxation of massive satellites that finally merged into the central galaxy. Among these substructures we have: (1) a stream connecting NGC 1387 to the central galaxy, NGC 1399, previously reported in the literature; (2) a new giant stream produced by the interaction of NGC 1382 with NGC 1380 and (possibly) NGC 1381; (3) a series of streams kinematically connected to nearby UCDs; and (4) clumps of tracers with no clear kinematical association to close cluster members.
Conclusions. We show evidence for a variety of cold substructures predicted in simulations. Most of the streams are kinematically connected to UCDs, supporting the scenario that they can be remnants of disrupted dwarf systems. However, we also show the presence of long coherent substructures connecting cluster members and isolated clumps of tracers possibly left behind by their parent systems before these merged into the central galaxy. Unfortunately, the estimated low-surface brightness of these streams does not allow us to find their signatures in the current imaging data and deeper observations are needed to confirm them.
Key words: intergalactic medium / galaxies: interactions / galaxies: formation / galaxies: kinematics and dynamics
© ESO 2022
1. Introduction
In the context of the hierarchical structure-formation scenario, galaxy clusters formed through highly nonlinear growth (e.g., Blumenthal et al. 1986). During their assembly, a variety of physical processes take place, such as tidal interactions, ram pressure stripping, and gas accretion, all contributing to shaping the luminous and dark matter component of galaxies in their cores (e.g., Genel et al. 2014; Vogelsberger et al. 2014; Schaye et al. 2015). These physical mechanisms are expected to leave signatures in the kinematics of the galaxy components, from their stellar haloes (Duc et al. 2011; Amorisco 2019), out to the intracluster regions (Napolitano et al. 2003; Murante et al. 2007), for example in the form of cold substructures which survive after stripping events due to the long dynamical times in the outskirts of galaxies. Semi-analytic models combined with cosmological N-body simulations and hydrodynamical simulations have shown that the number of substructures in stellar haloes, their stellar populations, and their dynamics directly probe fundamental aspects of galaxy formation in ΛCDM. In particular, such signposts can provide information as to the hierarchical assembly of massive galaxies; for example, the mix between their in situ and accreted components (Cooper et al. 2013, 2015a,b; Pillepich et al. 2015; Pulsoni et al. 2020, 2021). One of the classical approaches to looking for such substructures in galaxy halos is to use deep photometric observations (Mihos et al. 2005; Martínez-Delgado et al. 2010; Montes & Trujillo 2019; Iodice et al. 2017, 2019; Spavone et al. 2017, 2018, 2020). However, this approach is challenging because of the faint surface brightness of the tidal streams and remnants, which is typically below μ ∼ 27 mag arcsec−2, and only the brightest substructures are generally detected. Furthermore, most of the accreted mass provided by the fainter tidal substructures, which have surface brightnesses of the order of 30 mag arcsec−2 or below in the V-band (Cooper et al. 2010, 2015a), remain hidden in the central galaxy background. To go beyond the purely photometric studies, in the last few years, deep spectroscopy programs have provided kinematic information on the tidal debris around galaxies and allowed us look into the phase space (projected positions and line-of-sight velocities) to search for the typical signatures expected for galaxy interactions (e.g., Johnston et al. 1998; Romanowsky et al. 2012; Longobardi et al. 2015; Hartke et al. 2018). However, the use of kinematic tracers like planetary nebulae (PNe) or globular clusters (GCs), which are observable out to large distances from the galaxy centers (Durrell et al. 2003; Merrett et al. 2003; Shih & Méndez 2010; Cortesi et al. 2011; Richtler et al. 2011), is often a viable alternative to the standard kinematical measurements based on the integrated stellar light in the faint galaxy haloes (PNe; Napolitano et al. 2002, 2009; Romanowsky et al. 2003; Douglas et al. 2007; De Lorenzi et al. 2009; Coccato et al. 2009; Pota et al. 2013; Longobardi et al. 2015; Hartke et al. 2018; Pulsoni et al. 2018 – GCs; Côté et al. 2003; Romanowsky et al. 2009, 2012; Schuberth et al. 2010; Woodley & Harris 2011; Richtler et al. 2011; Forbes et al. 2011; Foster et al. 2014; Veljanoski & Helmi 2016; Longobardi et al. 2018). These discrete tracers allow us to probe the dynamics and the kinematics further out in galaxy clusters, where the potential of the cluster begins to dominate over that of individual galaxies (e.g., Spiniello et al. 2018; Pota et al. 2018). The first attempts to use GCs and PNe to find signatures of substructures from minor merger or accretion events led to a substantial number of claims based on the assumption that shells and tidal streams are located in chevron-like substructures in the position–velocity diagram (but see also Coccato et al. 2013). This could be explained in terms of a near radial infall of objects with almost the same initial potential energy (Côté et al. 2003; Romanowsky et al. 2009, 2012; McNeil et al. 2010; Shih & Méndez 2010; Schuberth et al. 2010; Woodley & Harris 2011; Foster et al. 2014; Longobardi et al. 2015). However, these patterns do not represent low-dispersion streams made by a handful of particles and originated from dwarf galaxies in a recent encounter with a massive galaxy.
Recently, we developed an optimized stream-finding algorithm named COld STream finder Algorithm (COSTA Gatto et al. 2020, G+20 hereafter) that is able to spot tidal debris in the phase space by detecting cold kinematics substructures moving in a warm/hot environment background of relaxed particles. COSTA is the first algorithm of its kind, although a similar concept was proposed to detect large substructures in the phase space of galaxies in rich clusters (Dressler & Shectman 1988).
In particular, COSTA relies on a deep friend-of-friend procedure that, through an iterative sigma clipping, detaches groups of neighbor particles with cold kinematics (tens of km s−1). This procedure allows the user to find small samples of tens of low-velocity-dispersion particles, as expected for low-surface-brightness streams originated by the disruption of dwarf galaxies orbiting in the diffuse stellar halos of giant galaxies or cluster-dominant (cD) galaxies. In G+20, COSTA was fully tested on hydrodynamical simulations of galaxy encounters and Montecarlo simulations of realistic cluster-like velocity fields. COSTA can efficiently work on samples of a few hundred to thousands of discrete tracers in cluster cores, like the one we have collected in the multi-instrument observational program Fornax Cluster VLT Spectroscopic Survey (FVSS, see Sect. 2). Within this program we have assembled catalogs of ∼1200 GCs (Pota et al. 2018, P+18 hereafter) and ∼1200 PNe (Spiniello et al. 2018, S+18 hereafter) out to ∼200 kpc from the cluster center. The velocity dispersion (σ) radial profiles from both PNe and GCs reveal a clear signature of an intracluster population with a sharp σ increase from ∼200 km s−1 to ∼350 km s−1 at a radius of ∼10 arcmin (60 kpc) from the center of NGC 1399 (see also Napolitano et al. 2002). In P+18 and S+18, we noted that this rise in velocity dispersion is compatible with the scenario where both PN and GC populations at this distance start to feel the cluster potential rather than that of the central galaxy. This scenario was recently confirmed with updated FVSS measurements of the PN and GC populations (Chaturvedi et al. 2022). An alternative scenario, whereby a mix of populations produce an inflated profile, as observed in Hydra cluster (Hilker et al. 2018), cannot be excluded in Fornax, although does not seem to be supported by dynamical arguments (see S+18 and P+18). In these regions, the dynamical timescales are long enough to preserve kinematical substructures for a longer time (Napolitano et al. 2003; Arnaboldi et al. 2004, 2012; Bullock & Johnston 2005; Coccato et al. 2013; Longobardi et al. 2015), and therefore the FVSS represents the ideal dataset with which to use COSTA to look for stream candidates. The Fornax cluster is the most massive galaxy overdensity after the Virgo cluster within 20 Mpc and, as such, is an ideal target to search for cold substructures produced by the interaction of the large population of dwarf galaxies (see e.g., Munoz et al. 2015; Venhola et al. 2017, 2019; Ordenes-Briceño et al. 2018) with the cluster environment and to investigate the assembly of the diffuse halo and the intracluster component in its core (Arnaboldi et al. 1996; Napolitano et al. 2002; Iodice et al. 2016; Spavone et al. 2020). Despite its regular appearance, recent investigations have found that the assembly of Fornax is ongoing, as shown by deep photometry with the ESO/VST, which found signatures of stellar and GC tidal streams (e.g., Iodice et al. 2016, I+16 hereafter; Iodice et al. 2017; D’Abrusco et al. 2016, DA+16; Cantiello et al. 2020, C+20; see also Chaturvedi et al. 2022). Due to its proximity, Fornax provides a unique opportunity to kinematically map the complexity of its core out to at least 200 kpc using discrete kinematical tracers (e.g., GCs and PNe) and finally connect the “hot” large-scale kinematics down to the “cold” scale of dwarf satellite galaxies, which are expected to produce most of the kinematical substructure in Fornax.
In this paper, we apply COSTA to the full sample of PN and GC radial velocities. In Sect. 2 we present the available discrete tracer populations (PNe and GCs) and demonstrate that their velocity and spatial distributions are statistically consistent with belonging to the same parent population of tracers on cluster scale, meaning that they can be combined to look for substructures. In Sect. 3 we briefly introduce COSTA and describe the parameter setup adopted when looking for streams. In Sect. 4, we present the stream candidates and discuss their reliability and general properties. We also identify correlations among their observed parameters and discuss possible physical mechanisms behind them. In Sect. 5 we discuss the results and give further details on the stream candidates. In Sect. 6 we finally draw some conclusions and perspectives. In this paper, we assume a distance modulus of m − M = 31.51 for the Fornax Cluster (Blakeslee et al. 2009).
2. Datasets
2.1. The Fornax Cluster VLT Spectroscopic Survey
The dataset used in this work is based on the first catalog of GCs and PNe produced within the Fornax Cluster VLT Spectroscopic Survey (FVSS; Pota et al. 2018). This program is designed to collect multi-instrument observations of the Fornax Cluster using the VLT at ESO telescopes. In particular, in FVSS I, we collected multi-object spectroscopy of 387 new GC and ultra-compact dwarf (UCD) systems with VIMOS at VLT (Pota et al. 2018). This sample, added to archival data for a further 746 GCs (Bergond et al. 2007; Schuberth et al. 2010), makes a final catalog of 1183 GCs/UCDs (Pota et al. 2018). In FVSS II, we obtained dispersed imaging with FORS2 (VLT), with which we detected and measured the radial velocities of ∼1268 PNe (Spiniello et al. 2018). Together with 184 PNe previously observed by McNeil et al. (2010), this gives a total of 1452 kinematical tracers. Recently in Chaturvedi et al. (2022, FVSS III), we refined the data-reduction of the GC sample and pushed the measurement of GC radial velocities to lower signal-to-noise ratios (S/N ∼ 5). This increased the number of GCs measured in the VIMOS data to 777 and the total GC velocities to 2341, after including other unpublished data. Hence, within FVSS, we have collected the most extended velocity field from GCs and PNe ever measured in a cluster (out to ∼300 kpc).
In this paper, we use, for the first time, a combination of GCs and PNe to reveal cold substructures in the core of the Fornax cluster. The main reason for combining radial velocities from different tracers is to maximize the number of test particles populating the streams, thus augmenting the probability of detecting small substructures. The total size (> 2000 test particles) and velocity errors of the two datasets (ΔV ≃ 37 km s−1 for GCs, P+18, and between 30 and 45 km s−1 for PNe, S+18; we adopt an average error of 37.5 km s−1 in the following) are suitable for the detection and characterization of stream candidates in hot environments like the stellar halo in cluster cores (see G+20). For the GC population, we decided to use the P+18 catalog because this is based on a sample with higher S/N, which allows us to keep the statistical errors (37 km s−1) below those of the new catalog (70−100 km s−1, see Chaturvedi et al. 2022) and similar to those for the PNe1.
There are differences between the GC and PN observing strategies, which impact their spatial coverage of the Fornax core area. We refer the interested reader to the original papers for a detailed description of the observation techniques, data analysis, and sample characterizations. Below, we report only the information that is of significant interest for the analysis performed in this paper and the strategies used to resolve the spatial nonuniformity of the observed samples.
2.2. The GC sample
P+18 presented a new catalog of GCs observed in an area of about 1 deg2 around the NGC 1399, the bright galaxy in the center of the Fornax cluster, which corresponds to a galactocentric radius of ∼175 kpc. Observations consisted of a mosaic of 25 VIMOS pointings where about 2400 slits were allocated over a photometrically selected sample of GC candidates. This sample was defined using VST/OmegaCAM photometry in the de-reddened g and i bands from the Fornax Deep Survey (FDS) (D’Abrusco et al. 2016; Iodice et al. 2016) and preliminary VISTA/VIRCAM photometry in the Ks band from the Next Generation Fornax Survey (NGFS; see Munoz et al. 2015). The observed sample had i-mag in the range 17.0 ≤ i ≤ 23.0 mag. This restriction has been used in order to avoid contamination by foreground stars at bright magnitudes and too low signal-to-noise spectra at faint magnitudes.
Spectra have been analysed with iraf/fxcor and the derived radial velocities (or GC redshift) showed typical errors of the order of 37 km s−1. We combined the new catalog with the literature catalogs from Schuberth et al. (2010), including sources within 18 arcmin of NGC 1399, and Bergond et al. (2007) covering a strip of about 1.5° in right ascension (RA) and 0.5° in declination (Dec). The final sample includes 1183 GCs in total, with a systemic velocity of 1452 ± 9 km s−1 (i.e., fully consistent with the one of NGC 1399).
Figure 1 shows the position in RA and Dec of the objects and a reduced phase space made by the radial velocity of GCs (top panels) versus cluster-centric radius (i.e., the distance from the center of NGC 1399). In the reduced phase space, we report (as black lines) the mean velocities and the 1σ and 2.5σ contours of the velocities versus radius. These were calculated by dividing the sample in distance bins, such that the number of GCs is about the same in each bin (∼150).
 |
Fig. 1. Relative distances of the GCs (top left) and PNe (bottom left) from NGC 1399, and reduced phase-space (top right: GCs; bottom right: PNe). Overplotted on the phase-space are the mean velocity of the particles (solid line), the 1σ (dotted lines), and the 2.5σ (dash-dotted lines). Black triangles are the main galaxies in the field. The dashed horizontal line in the phase space is the systemic velocity of NGC 1399 (1425 km s−1). |
2.3. The PN sample
S+18 assembled a kinematic catalog of PNe out to 200 kpc in the Fornax cluster core using a counter-dispersed slitless spectroscopic technique (CDI, Douglas & Taylor 1999). They obtained the final PN dataset observing 20 new pointings (for a total of 5 h exposure time) with FORS2, and also supplemented these new data with 180 central PN velocities presented in McNeil et al. (2010). The covered total final area is ∼50′ × 33′, centered around α = 3 : 37 : 51.8 and δ = −35 : 26 : 13.6.
The CDI technique has been shown to be very successful for the analysis of PNe because it allows both the detection of PNe and the measurement of their Doppler shift within a single observation. CDI uses two counter dispersed frames with the position angle of the field rotated by 180 deg and with an [OIII] filter (specifically the [OIII]/3000, 51 Å wide) to select the light. In this way, all the oxygen emission-line objects (among which PNe) appear as point-like sources, while sources emitting continuum (e.g., stars and background galaxies) show up as strikes or star trails. PN candidates therefore appear in the two images (at the two rotated angles) at the same y-position, but shifted by a δx proportional to their line-of-sight velocity. These line-of-sight velocity measurements were then calibrated using the PNe in common with McNeil et al. (2010), which were calibrated against the measurements of Arnaboldi et al. (1994) obtained with NTT multi-object-spectroscopy.
The final sample of PNe with measured velocities comprises 1452 objects, and has a mean velocity of 1433 km s−1 with a standard deviation of 312 km s−1, which were calculated after applying heliocentric correction to each field separately. However, for the purpose of this paper, and our aims to detect streams possibly distributed over large areas, we have strictly excluded the tracers around NGC 1379 (i.e., 150 PNe in Field 1 from Fig. 1 of S+18), because this latter is isolated and not extended enough to probe the intracluster region. Furthermore, according to Gatto et al. (2020), the number of tracers might be too small to detect cold substructures, if any exist. Figure 1 (bottom panels) shows the position in RA and Dec of the objects and the reduced phase space of PNe as done for GCs (upper panels).
2.4. Spatial homogeneity of the PN and GC samples
Looking at the 2D distribution of GCs in Fig. 1 (top left), we see that this is rather spherically uniform, with the number density of objects increasing towards the center of the cluster. This homogeneity comes from a relative uniformity in the GC selection for the slit allocation of the VLT observations, both in spatial and luminosity distribution. Spatially, the VLT allocation was meant to collect a complementary dataset to previous existing observations, which allowed us to obtain uniform radial coverage of the spectroscopic sample finally collected by FVSS. In terms of luminosity, the FVSS strategy was designed to emulate the depth of previous datasets in order to minimize the inhomogeneity of the luminosity function among the different datasets. In particular, we used the Schuberth et al. (2010) as a reference sample as it is the most largest. Looking at the globular cluster luminosity function (GCLF) in three radial shells (see Sect. 2.5.1 and Table 1 for their definition) from the cluster center in Fig. 2, the net result is that the GC sample becomes incomplete at a magnitude of magg ∼ 23.4 in all bins.
 |
Fig. 2. GCLF evaluated in the three different radial bins, along with their fitted Gaussian function whose parameters are described in the text. |
Parameters and p-values of the Kolmogorov–Smirnov test.
To quantify this, we first fitted the bright half of the GCLF with a Gaussian distribution (Brodie & Strader 2006, and references therein): we obtained a mean equal to ⟨magg⟩ = 22.5 for all the bins, a variance of σ(magg) = 0.88, 0.87, 0.79, and a normalization factor of A = 300, 168, and 114 for the three bins, respectively. We then derived the magnitude where the observed interpolated histogram deviates from the best-fit by 50% of the counts (mag50 in short) and found these to be mag50 ∼ 23.5, 23.6, 23.2, with a mean of 24.4 and a scatter of 0.2. Therefore, only the most external radial bin shows a slightly brighter limiting magnitude but reasonably within the tentative variance of these measurements. Due to the high-S/N selection in P+18, there are only a few GCs in the magnitude bin fainter than magg ∼ 23.4, and only in the more external bin. In light of the overall regularities discussed above, we decided to keep the full GC sample for the analysis.
On the other hand, PNe have a smaller spatial extension than GCs, namely ∼25 arcmin versus ∼50 arcmin, respectively (see Fig. 1, bottom left), but more importantly they have, overall, an inhomogeneous distribution. This is due to the tiling of the FORS2 observations, which produces a patchy sky coverage around the cluster center (see Fig. 1 in S+18). Moreover, as the fields were observed under different observational conditions (seeing), and sometimes with different final integration times, each of them has a different intrinsic depth and consequently also a different limiting magnitude for the PNe detection (e.g., the luminosity at which almost half of the real PNe are detected). Hence, the number of identified PNe in each pointing varies not only because of the intrinsic local differences in the density of PNe but also because of our inability to find them down to the same magnitude limit. This aspect as not relevant for S+18, where the authors were not interested in using the spatial information of PNe for their analysis. In our study, instead, the spatial incompleteness can affect the stream detection because artificial overdensities generated by a different observation depth have a higher chance of mimicking a stream. To correct for differences in the field-to-field depth, we need to select PNe within the same limiting magnitude –taken as the mean magnitude where half of the PNe are missed (assuming all PNe are at the same distance)– with respect to their intrinsic luminosity function, as done for GCs. We first build the planetary nebula luminosity function (PNLF) in each pointing and best fit a standard empirical formula to interpolate it. Then, assuming that the sample is complete in the brightest bins, we compute the magnitude where the fraction of observed PNe is 50% of the expected number of PNe from the best-fitted PNLF (see below).
We derived the photometry of the PNe detected in the FORS2 data where the [OIII] filter was used to isolate the [OIII] emission from PNe. This gives the so-called [OIII] magnitude, which is generally used to construct the PNLF (Ciardullo et al. 1998). In particular, we use the software SExtractor (Bertin & Arnouts 1996) and retrieve the output parameter MAGAUTO which has often been found to provide the best estimates of PNe [OIII] magnitudes (see also Arnaboldi et al. 2003, for a discussion).
As we are not interested in absolute photometry, but only in the relative photometry of the observed PNe, we did not calibrate the PN fluxes, but arbitrarily assumed mzero = 25 as the zeropoint. Therefore, the numerical values of MAGAUTO correspond to instrumental magnitudes, maginstr.
SExtractor was able to measure fluxes of 99% for all sources detected by eye in S+18, allowing us to derive the PNLF in all the S+18 fields, as shown in Fig. 3. These measured PNLFs were best fitted using the fitting formula of Aguerri et al. (2005):
 |
Fig. 3. Planetary nebulae luminosity function in all the S+18 fields. The best fit of Eq. (1) is shown as a continuous line. We have excluded from the fit the bins with one single ultra-luminous object, generally brighter than ∼17 mag. See discussion in the text. |
where c is a positive normalization constant and m* represents the apparent magnitude of the bright cutoff. The best fits are also shown in Fig. 3 as a continuous line in each field. We note that in most of the fields (i.e., F1, F2, F4, F5, F6, F10, F15, F16, F17, F20) there are some ultra-luminous [OIII] emitters. These are typically found in surveys of intracluster PNe and have been associated to either PNe located in the closer side of the cluster (e.g., Aguerri et al. 2005) or to other kinds of contaminants like [OII]-emitting galaxies at z ∼ 0.35 or Lymanα galaxies at z ∼ 3.14 (e.g., Castro-Rodríguez et al. 2003). As discussed in S+18, these authors minimized the presence of the high-z outliers, however we cannot exclude some residual contamination. We removed these ultra-luminous “outliers” in the PNLF fitting procedure by excluding all bright bins with only one count. However, we did not exclude these ultra-luminous objects from the PN sample because (1) there are very few of them and (2) we cannot securely classify them as noncluster members. Finally, the limiting magnitude was obtained by comparing a simple interpolating function of the data to the fitted PNLF to find the magnitude at which the interpolated counts fall to 50% of the fitted PNLF (mag50 as for the GCs). From the distribution of the limiting magnitude from Fig. 3 we find an average mag50 = 19.3 ± 0.1: therefore all PNe with measured MAGAUTO > 19.3 were excluded from the final sample, which finally contains 887 PNe.
2.5. The combined GC+PN sample
In this section, we discuss the phase space properties of the GC and PN populations to show that they can be combined to increase the statistics of the stream tracers. If we assume that PNe and GCs both respond in the same way to the encounters and have initially no statistically significant differences in their kinematics, they will keep sharing the same phase space properties when captured in the streams. This is a reasonable assumption if their kinematics is (almost) indistinguishable in their parent galaxy; generally, this is not true, and in fact the two families (GCs and PNe) are often considered dynamically disconnected, with PNe and red, metal-rich GCs often sharing spatial and velocity distributions (e.g., Napolitano et al. 2014). However, as discussed in P+18 and S+18, there are clear similarities between the GC and PN populations in the Fornax core.
In particular, their velocity dispersion profiles show clear and spatially similar signatures of a superposition of the bright central galaxy, which dominates the inner regions up to ∼25 kpc (4.3′), and the cluster potential, which becomes dominant outside ∼100 kpc (17.2′).
Most of the kinematical differences are due to the different spatial distribution (i.e., their number density profiles) and intrinsic anisotropy of the two populations (see Eqs. (3) and (4) in Napolitano et al. 2014). Given the typical values of these parameters, in massive galaxies the difference between their projected velocity dispersions can be of the order of 10%–20% (see Napolitano et al. 2014), which is within the typical errors of individual dispersion values obtained for PNe and GCs.
In principle, if we had information on the number density profile and anisotropy of the tracers in dwarf galaxies (as done for massive systems) we would be able to predict the difference in projected velocity dispersion one should expect between PNe and GCs. Unfortunately, we know little about the detailed slope of these populations in low-mass systems, while we have sparse information on the metal-rich and metal-poor stellar populations in the Local Group, which might be used as a reference because PNe and GCs could be tracers of the former and the latter populations, respectively. For instance, Walker & Peñarrubia (2011) discuss the dispersion predictions of different metal-rich and metal-poor subpopulations assuming realistic profile slopes and anisotropy parameters. These authors show (see e.g., their Fig. 3) that the velocity dispersion difference becomes very small (of the order of 10% or smaller) outside 1−2 Re. If we assume that the PNe and GCs follow the kinematics of these subcomponents, then we can reasonably expect the two populations to show differences in their velocity dispersion profiles of the same order of magnitude, again within the typical statistical errors. Assuming that all these arguments are valid, we use a total of 2070 objects in our analysis, where GCs represent 57% of the whole catalog and the PNe 43%.
2.5.1. The GC versus PN phase-space properties
In order to further support the assumption that PNe and GCs are a single family of tracers, in order to facilitate our search for streams, here we look in more details at their phase-space properties. As already mentioned, Fig. 1 shows the position in RA and Dec of the objects and a reduced phase-space made by the radial velocity (of GCs top panels, in yellow and PNe, bottom panels, in green) versus cluster-centric radius (i.e., the distance from the center of NGC 1399).
The first evident feature is the different spatial extension of PNe and GCs mentioned above, which implies that within 25 arcmin we must rely on the combined sample with a higher tracer density and higher statistics, while outside 25 arcmin the chance of finding streams is considerably reduced because of the smaller statistics. Also, we can see that NGC 1387 has an exceptionally high density of PNe, while the GC coverage is limited (possibly because of the incomplete slit allocation of the GC observations with VIMOS). In the phase space, this large overdensity does not seem to be aligned to the galaxy systemic velocity (a discrepancy that has not been solved in S+18). Finally, another visible difference between the two phase-space diagrams is found very close to the center, i.e., R < 5′, where the PN sample is numerically smaller and shows a smaller overall scatter in the radial velocity. This is due to two main factors: first, a large spatial incompleteness of the PNe caused by the bright NGC 1399 diffuse halo, and second, a shallower and lower resolution dataset from FORS1 observations from McNeil et al. (2010) covering this area. However, for the purpose of the present paper we exclude regions too close to the galaxy center, and therefore the differences inside a 5′ radius will not affect any of the final results.
In Fig. 4 we show how the GC and PN samples (plotted with different gray scales) combine. Looking at the phase space, we see that, besides some residual inhomogeneities in the PN distribution (left panel), after having cleaned the PN catalog from incompleteness, the two samples show (in the right panel) a smaller dispersion in the center and an increasing dispersion going toward larger radii. Overall the two samples do not show large differences in terms of mean velocity or velocity dispersion (continuous and dotted lines respectively in the bottom of Fig. 4). We discuss this in a more quantitative way in the following section.
 |
Fig. 4. Left: image of the whole sample of GCs (dark gray) and 887 bright PNe (light gray) in RA vs. Dec with the galaxies overplotted as black triangles. Right: GCs (dark gray) and PNe (light gray) in the phase space. The lines correspond to the mean velocity of the particles (solid line, dark red for the GCs and light red for the PNe), to the velocity dispersion at 1σ (dotted line), and to the velocity dispersion at 2.5σ (point-dotted line). |
To further quantify the differences in the spatial distributions of PNe and GCs, in Fig. 5 we plot the distribution of the cluster-centric radii of the two subpopulations. In the top panel we plot number counts as a function of the radius for the separated populations of GCs (yellow) and PNe (green) and the total population (gray). The different populations show some distinctive features, some of them mirroring the differences in the phase space: (1) PNe extend out to a distance of about 25′ from NGC 1399 because no observations were performed outside this radius, while GCs are distributed out to ∼45′. (2) Inside ∼7′, PNe show a clear incompleteness (i.e., their normalized counts are systematically lower than those of GCs), while outside 7′ they nicely align with GC number densities, decreasing with a similar slope (e.g., in the range 7′−17′). (3) There is a PN density peak at about 20′ around NGC 1387, where we observe a mild but visible dip in the GC density which is due to the selection effect in the GC spectroscopic sample mentioned above. In the bottom panel of the same figure, we have converted the number counts per radial bin into a surface density (N/arcmin2), where the area is that of the circular annulus enclosing any bin and finally arbitrarily re-scaled along the vertical axis to match the surface brightness distribution of the central galaxy from I+16. The latter plot shows a strong similarity between the PNe+GC tracers and the galaxy light, except in the areas where there is a clear effect of the spatial incompleteness (i.e., the center below 5′ and around NGC 1387). Looking at the individual density distributions, PNe and GCs also show appreciable consistency in most of the radial bins, confirming that these two populations of tracers are fairly representative of the total stellar light in the cluster.
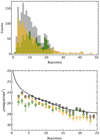 |
Fig. 5. Top: number counts as a function of the radius of GCs (in yellow), PNe (in green), and the total population (in gray). The overdensity of PNe around NGC 1387 is clearly seen at R ∼ 20″ (see text). Bottom: radial density distribution of GCs (yellow open dots), PNe (green), and the total population (black), arbitrarily re-scaled to match the surface brightness of the Fornax core from I+16 (gray tick line). Error bars represent Poissonian errors on the tracer counts. |
2.5.2. Kolmogorov–Smirnov test
To check whether the two tracers are statistically representative of a single kinematical population, we performed a Kolmogorov–Smirnov (K-S) test. We defined three shells at different radial distances from NGC 1399 (see Table 1) and performed a K-S test on the GC and PN velocity dispersion distribution separately in each shell. We excluded from this non parametric test the inner region of the cluster (R ≤ 5 arcmin) and the galactocentric distances where NGC 1387 and NGC 1404 are located because these regions are excluded in our search for cold substructures (see Sect. 3.3).
The inner and outer radii of each shell were selected in order to have about the same number of GCs and PNe, except for the inner shell, which has a larger number of GCs (298 vs. 208 PNe) because of the higher number of GCs in the inner regions of the cluster (see also the top of the Fig. 5). Because the PNe are selected out to a maximum distance of about ∼25 arcmin, no shells beyond this radius are considered.
Table 1 shows the results of the K-S test in each shell. Figure 6 shows the histograms of the density of GCs (yellow) and PNe (green) per velocity interval for the three shells and their equivalent Gaussian distribution. The results obtained from the K-S test are consistent with the null hypothesis that both GCs and PNe follow the same distribution. Indeed, the p-values for all the shells shown in Table 1 are well above the significance level of 5%. Moreover, it is also evident from Fig. 6 that the two distributions are very similar, as also shown by the Gaussian fit to their velocity histograms. In Appendix A we discuss the further case where we separate blue and red GCs and find that their velocity distributions remain statistically consistent and are also consistent with that of the PNe.
 |
Fig. 6. Histograms of the density of GCs (yellow) and of the PNe (green) per velocity interval in the three shells at different radial distances. Overlapped on these histograms are the distributions of the two samples. |
Having presented several arguments supporting the assumption that GCs and PNe have similar spatial and velocity profiles, from now on we consider them as a single family of test particles, which allows us to increase the statistics and, consequently, the chances of finding cold substructures.
3. The COSTA algorithm
In this section, we briefly summarize the features and assess the reliability of the COSTA algorithm. This has been fully tested on hydrodynamical simulations of galaxy encounters and Monte Carlo simulations of realistic cluster-like velocity fields. These latter consist of realizations of the phase space distribution of tracer particles created by random sampling from a smooth model of the observed tracer density profile in equilibrium with an analytic model of the Fornax potential (see G+20 for details). Here we report the most relevant properties and definitions used throughout the paper.
3.1. COSTA steps
The algorithm looks for coherent structures in both the RA/Dec position space and in the reduced phase space (radial velocity vs. cluster-centric radius), with the additional necessary condition of low velocity dispersion. Indeed, we are particularly interested in dwarf galaxy disruption as a major mechanism, which is still active in the local Universe and contributes to the intracluster stellar population and the assembly of large stellar halos around galaxies. Therefore, we introduce a velocity dispersion threshold to define a “cold” substucture, σcut, to vary in the range of [10−120] km s−1, according to typical dwarf dispersion values found in the Coma cluster (Kourkchi et al. 2012)2.
The main steps performed by COSTA are summarized below (see G+20 for a more detailed description):
-
(i)
For each particle, COSTA finds the first k nearest neighbors in the position space;
-
(ii)
It estimates the mean velocity and velocity dispersion of these k tracers;
-
(iii)
It performs an iterated sigma clipping by removing all tracers beyond n standard deviations from the mean velocity of the group. During each iteration, it recalculates the average velocity and the velocity dispersion, until no more outliers are found;
-
(iv)
It retains all structures with a number of particles greater than Nmin and with a velocity dispersion lower than σcut.
Finally, as the search for closer neighbors is based on a projected circular distance, while streams tend to lie on elongated structures, COSTA performs a further step:
-
(v)
If there are groups with some particles in common, these are considered as belonging to a single stream if their mean velocity and velocity dispersion values are consistent with each other within uncertainties.
Ultimately, COSTA depends on four free parameters: the three friend-of-friend parameters (k, n, Nmin) and σcut, which need to be properly chosen to maximize the number of genuine cold substructures (completeness) and minimize the number of spurious detections (purity) caused by the intrinsic stochastic nature of the velocity field of hot systems.
In G+20, we showed how we obtained a list of parameter combinations that produce an acceptable probability of finding “false positives”, that is, spurious cold substructures based on Monte Carlo simulations. This is done by assigning a maximum reliability to the combination of parameters for which no streams are detected on Monte Carlo simulations of the Fornax core where all test particles are in equilibrium with the “warm” cluster potential (where no cold streams are added; see G+20). Vice versa, a lower reliability is assigned to the parameter combinations that find an increasing number of (false) detections in the same simulations (see following section).
3.2. Reliability map from Monte Carlo simulations of the Fornax cluster core
Following G+20, the first step to perform before running COSTA on a given dataset is to derive the reliability map. This is obtained by producing Monte Carlo simulations of the dataset to which COSTA will be applied (we refer to the original Napolitano et al. 2001 paper for more details). In G+20 we obtained such Monte Carlo simulations for a Fornax-like cluster, including the presence of the major galaxies in the Fornax core (see G+20 for details). We also showed that COSTA is able to retrieve a series of artificial streams with different physical sizes and particle numbers corresponding to the expected surface brightness for streams produced by the interaction of dwarf galaxies with the cluster environment (i.e., of the order of 28−29 mag arcsec−2).
Here we briefly summarize the main concepts of the simulated sample and how this is used to define the reliability map. We start by simulating random discrete radial velocity fields of particles:
-
We consider only the region covered by our objects, i.e., 1.8 deg2 around the cD, NGC 1399, where there are two other bright, approximately spherical, early-type galaxies: NGC 1404, located at ∼9 arcmin southeast of the cD, and NGC 1387, ∼19 arcmin west of NGC 1399;
-
Following Napolitano et al. (2001), we consider GCs and PNe at the equilibrium in the gravitational potential of these three galaxies, where we assume a total mass of about 1014 solar masses for the cluster and a Hernquist (Hernquist 1990) density distribution of the stellar-like tracers;
-
We consider a dark matter halo following a Navarro-Frenk-White profile (NFW); hence, the potential of the system at equilibrium is given by the total mass:
where Ml and Mdm are the total luminous and dark mass, respectively;
-
We assume an isotropic velocity dispersion tensor, and solve the radial Jeans equation to derive the 3D velocity dispersion σ2 along the three directions in the velocity space, and generate a full 3D phase space;
-
We simulate an observed phase space first, by projecting the tracer distribution on the sky plane. We then derive the line-of-sight velocity of the individual particles by randomly extracting the observed velocities from a Gaussian distribution centered at the true value with a standard deviation equal to the velocity errors. We assume these latter to be 37 km s−1, i.e., approximately equal to the average errors of real GCs and PNe (see P+18 and S+18).
We carefully verified that the mock catalogs of positions and radial velocities closely resemble the real one, and also that the simulated cluster is consistent with the mean observable quantities of the galaxies in the area (see Table 2 in G+20). Finally, we created a “white noise sample” (WNS) as described in G+20 by randomly drawing 100 realizations of the mock catalog –with no substructures– from the model described above. COSTA is run on the WNS using a grid of different parameters to check which combinations produce a (false) detection due to randomly connected particles.
The parameters have been uniformly taken in the following ranges:
-
10 ≤ k ≤ 50;
-
1.3 ≤ n ≤ 3;
-
5 ≤ Nmin ≤ k;
-
10 ≤ σcut ≤ 120 km s−1.
This choice allowed us to search both for small substructures, that we expect to find with low k, low Nmin, and a low velocity dispersion value, and for larger and spatially extended groups with greater values of both k and Nmin and rather hot velocity dispersion, e.g., of the kind expected from moderate-luminosity galaxies like NGC 1387 (see e.g.; Iodice et al. 2016).
For a given parameter combination, the reliability is defined as the fraction of detections over the 100 realizations in the WNS, i.e., 100 − Ndet/100% (with Ndet expected to be zero by definition in the WNS). In G+20 we discussed the impact of threshold on the completeness of the candidates and checked that a good compromise between the completeness and the contamination is obtained with a threshold of 70% in reliability. However, for this first test on Fornax, we decided to apply a less conservative threshold of 50%, which can return more candidates at the cost of a higher probability of spurious detections. In case this brings all genuine streams, then the completeness can increase as much as 20% (see G+20). In case the extra candidates are all false positive, then the contamination can rise to ∼58%, which is a risk we decided to accept. In Fig. 7 we show the reliability distribution in the 4D parameter space. The 2D projection plots are color-coded by the fraction of configurations (FN) with reliability ≥50%. Yellow regions are those with the highest density of configurations with minimal or no false detections. Histograms in the same figure show the fraction of times where the reliability passes the 50% threshold for each value of the four free parameters of COSTA.
 |
Fig. 7. Reliability map in the 4D parameter space for the simulated Fornax cluster. The 2D projected plots for each pair of parameters are color-coded according to the fraction of configurations (FN) with reliability ≥50% according to the legend. Histograms show the fraction of times the reliability passes the 50% threshold for each value of the four free parameters of COSTA. |
3.3. Running COSTA on the combined GC+PN sample
Once the reliability map has been drawn from the WNS, we run COSTA on the detection sample (DS; see G+20), which is made of the real positions and the radial velocities of the combined GC+PN sample discussed in Sect. 2.5. This produces a series of detections consisting of a number of candidates that recur in multiple setups, each time with a slightly different number of particles but with a common bulk of members, as demonstrated in G+20. To define these “representative” particles, which correspond to a given substructure, we decided to select the ones corresponding to the median parameters among all the allowed configurations, marginalizing over all the other parameters in the 4D parameter space (see e.g., Fig. 7). Similarly, we can obtain all physical properties characterizing the stream as the median values among all configurations that select the representative particles. For instance, some properties can be directly derived from the region of the parameter space with the highest density of detections, in particular in the space defined by Nmin − σ (as discussed in G+20, their Sect. 4 and Fig. 11).
Finally, to increase the detection significance, we perturb the PN+GN velocity field. We obtain ten additional random realizations (i.e., 11 velocity fields in total) of the radial velocity field, each time assuming a Gaussian centered in the individual particle Vrad and with a mean velocity error of 37 km s−1. We use these random artificial velocity fields to check, for each stream detected in the unperturbed dataset, whether or not the additional detection configurations are allowed by the randomized data, and finally obtain the distribution of these configurations in the parameter space. This is shown in detail in Appendix B where we report all configurations for the detected streams in the parameter space (see Fig. B.1). The detected streams derived with the above procedure are presented in the following section.
We note here that we excluded the inner regions of the three galaxies from our search, as GCs and PNe catalogs are generally highly incomplete there because of the bright galaxy background. In particular, we excluded the regions inside 5′ from the NGC 1399 center and inside two effective radii from the other galaxies, i.e., 49″ for NGC 1404 and 84″ for NGC 1387. Furthermore, we also excluded all selected groups of particles that have one or more members overlapping these excluded areas.
4. Results
In this section, we present the candidate streams found in the GC+PN combined catalog. We detected 13 stream candidates in total for which a detailed illustration of the COSTA parameters is given in Appendix B, where we show the different projections of the parameter space as compared with the reliability map.
As anticipated in Sect. 3.3, to visualize the most significant setup configurations, we focus on a particular projection of the parameter space, the Nmin − σcut, that we have proven to be representative of the stream physical quantities. Hence, we define the “median” configuration as the median of the parameters in the Nmin − σcut projected space, reported in Fig. 8, where we clearly see that setups generally concentrate in narrow regions in the projection space.
 |
Fig. 8. Density plot of the σcut as a function of Nmin for each stream, color-coded by the number of times COSTA detected the stream with a given σcut − Nmin pair. Data were smoothed using a Gaussian kernel with a bandwidth equal to 3. |
4.1. A catalog of cold substructures
The stream candidates are reported in Table 2, where we list the stream ID, coordinates of the centroid of the stream, number of particles belonging to the stream (divided in GCs and PNe), their mean velocity, velocity dispersion, size (defined as the maximum distance among the particles) and distance from the cluster center. In the same table, we also report the luminosity associated to the stream, based on the PN specific number density and the related surface brightness. More details about the definition of each of these parameters are given in the following sections.
Statistics of the streams.
Finally, in Table 2 we also report the median and maximum reliability among all configurations in which COSTA detected the stream and the occurrence of the stream detection over the Monte Carlo re-samplings of the GC+PN velocity field. The reliability exceeds 70% for nine streams, and in particular two streams have a reliability of greater than 85%. The total number of particles ranges from 9 to 22, while their sizes are spread out over a relatively large interval, which goes from 1.8 arcmin up to ∼20 arcmin. Most of the streams have a comparable number of GCs and PNe, while FVSS-S6 is around NGC 1380 where there is no spatial coverage of PNe (see Fig. 1).
The positions of the particles composing each stream are plotted in different colors in Fig. 9 superposed on the deep g-band image of the core of Fornax cluster from FDS. To visualize the stream particles, we choose the closest configuration to the median parameter setup of each stream as representative of the “average stream”. In the same figure, we also report dwarf galaxies from the literature (Munoz et al. 2015; Eigenthaler et al. 2018) that are in the vicinity of the streams and can be associated to them with confidence (see details in Sect. 5.1). These are plotted as orange diamonds or squares (depending whether they have velocity measurements or not, respectively) and their sizes are proportional to the i-band total magnitude taken from Cantiello et al. (2020). From this figure, we see that streams are either very close to some of the detected dwarf galaxies (e.g., FVSS-S1, FVSS-S2, FVSS-S5, FVSS-S7, FVSS-S12) or live in the halo or are associated to larger galaxies in the Fornax core (e.g., FVSS-S3, FVSS-S4, FVSS-S6, FVSS-S8, FVSS-S13). In addition, there are candidate streams that are particularly compact (e.g., S4, S12, S13) or rather diffuse (e.g., S8) or stretched (e.g., S6). A detailed discussion about the stream association with the galaxy population in the core of Fornax is reported in Sect. 5.
 |
Fig. 9. Image of the Fornax cluster core region. We show representative particles of each cold substructure found by COSTA in the closest configuration to the median setups; these are colored according to the associated stream. Orange squares and diamonds indicate galaxies listed in Tables 3 and 4 respectively, with symbol size proportional to their i-band luminosities. Orange crosses represent galaxies listed in the tables with no luminosity measurement. |
In Fig. 10 we show the candidate streams in the phase space of all GCs and PNe in the Fornax core. The locations of the major galaxies in the area are also reported in the same figure. Also here we can see notable differences in the stream typologies: (1) compact streams with small extensions (i.e., along the x-axis) and small dispersion, that is, a compact distribution in radial velocity (y-axis), for instance FVSS-S4, FVSS-S11, FVSS-S12, and FVSS-S13; (2) streams that are clearly related to individual large galaxies, for example S13 around NGC 1404 and FVSS-S8 with NGC 1387; (3) extended streams that seem to connect different large galaxies, for example S6 connecting NGC 1380, NGC 1381, and NGC 1382; and (4) other streams still rather compact in velocity but more diffuse in radius, for example FVSS-S1, FVSS-S2, FVSS-S3, FVSS-S5, and FVSS-S10.
 |
Fig. 10. Left: particles of each cold substructure in the phase space, with the same colors as in Fig. 9, superposed on all particles used in this work (light gray). Right: Gaussians with mean = 1425 km s−1, i.e., the NGC 1399 systemic velocity, and standard deviation of 300 km s−1 (blue solid lines) and 374 km s−1 (red solid lines), namely the velocity dispersion of the Fornax cluster and of the Fornax members analyzed by Drinkwater et al. (2001). |
Based on visual inspection, there seem to be likely associations between the stream candidates and the positions of galaxies of different size and/or luminosity (not only dwarf systems). In Sect. 5, we investigate these possible associations in close detail according to their vicinity and kinematical similarities. Here we estimate the important global physical properties of these candidate streams and search for signatures that suggest they are likely genuine; although we are aware that the final confirmation should come from direct observations with deep photometry to find evidence of stellar tails.
4.2. Stream luminosity and surface brightness
For the streams including PNe, we can use some empirical formula to estimate the luminosity of the associated stellar population. In particular, as discussed in G+20, we can estimate the total light associated to the PN population using their specific number density within 2.5 mag from the cut-off magnitude of the luminosity function α2.5 = 50 × 10−9 PN/L⊙ (Feldmeier et al. 2004), which corresponds, on average, to the completeness limit of our sample (see Fig. 3). The total bolometric luminosity is obtained as Lbol = NPN/α2.5. This can be converted into a g-band luminosity to compare the stream luminosity with the photometry from the Fornax core galaxies (e.g., I+16). We estimate that using a combination of F, G, and K stars; this amounts to about one-third of the flux in the optical range. Finally, considering an average 75% completeness in the fraction of true recovered particles (see Fig. 14 of G+20) we can also correct the final luminosity by this factor. The final corrected g-band luminosities are listed in Table 2, together with the corresponding surface brightness (SB), which is computed assuming a squared area of side length equal to the size given in the same table.
The SB values we obtain, which are always > 28 mag arcsec−2, agree with typical predictions from cluster simulations: Cooper et al. (2015a) (C15 hereafter) found streams produced by disrupted galaxies covering a broad range in galaxy luminosity function, including major galaxies. However, typical surface mass densities of obvious features are in the range 105 − 106 M⊙ kpc−2, which corresponds to ∼27.5 − 30 mag arcsec−2 for the assumed mass-to-light ratios. Such faint structures are hard to see even in very deep images. Indeed, careful visual inspection of the deep images from FDS (e.g., Venhola et al. 2017) and the Next Generation Fornax Survey (e.g., Munoz et al. 2015) reveals no clear counterparts for our candidate streams, except in one case, namely FVSS-S8 (NGC 1387 stream hereafter), which we have independently found with COSTA but which was previously claimed in I+16. As we discuss later, this is the first kinematical confirmation of a photometric stream candidate.
4.3. Stream radial velocities as compared to other populations of the intracluster medium
Mean stream velocity and velocity dispersion values of all setups from different stream occurrences are computed respectively using the following standard definition (see also P+18):
where we use σI to indicate the intrinsic velocity dispersion, having subtracted the measurement errors Δv = 37 km s−1 in quadrature. The final median values of radial velocity and velocity dispersion are reported in Table 2. In this section, we concentrate on the mean velocity estimates, while in the following section we discuss the stream intrinsic velocity dispersion values.
The distribution of the radial velocities of stream candidates is relatively sparse and in principle can give insights into the global kinematics of streams as member populations of the cluster. The mean velocity value of all the stream candidates is 1501 ± 59 km s−1, which is consistent with the systemic velocity of NGC 1399 (1425 km s−1), while their standard deviation is 213 ± 42 km s−1. This value is smaller than the kinematics of other intracluster objects, which generally have a larger velocity dispersion; see for example cluster galaxies (σ = 374 km s−1, from Drinkwater et al. 2001), intracluster PNe (σ = 285 km s−1, from S+18), and GCs (σ = 285 and σ = 304 km s−1 for red and blue ones respectively from P+18), at R ∼ 20′3. This indicates that, if all of these streams are genuine, streams possibly have a decoupled dynamics from other virialized populations. This would be the case if they have a peculiar density or orbital distribution. One possibility is that these streams are produced by satellites that are preferentially placed on high eccentric orbits, hence possessing a strong radial anisotropy, different from those of other cluster member families. In this case, streams should form in the pericenter of their trajectory around the central galaxy (see e.g., simple models from Longobardi et al. 2018) and therefore also have a more centrally concentrated distribution with respect to other satellite systems (e.g., galaxies and intracluster GCs and PNe).
Alternatively, the low velocity dispersion may indicate that some stream candidates might simply be a random extraction of the hot intracluster populations of tracers. In Appendix C, we demonstrate that, if streams are a population of cluster members whose overall velocity dispersion should be comparable to that of other dynamical members (i.e., of the order of 300 km s−1), the maximum number of spurious streams that might produce a “dilution” of their measured σ down to 213 km s−1 is Nspur ∼ 6. In this worst case, more than half of the stream candidates (i.e., 7 out of 13) are real, although in Appendix C we discuss why the fraction of real streams is very likely higher than that.
4.4. Stream internal-velocity dispersion
We focus here on the stream internal kinematics. The velocity dispersion values show a wide distribution ranging from 35 km s−1 (FVSS-S13) to 100 km s−1 (FVSS-S2), while the mean value is 74 km s−1. As seen in G+20, the accuracy of these estimates is hard to assess, as both incompleteness and contamination can alter the final estimated velocity dispersion value. However, the estimates shown in Fig. 8 indeed take into account the statistical fluctuations considering that they come from stream detections from a large variety of setup configurations (see Sect. 4). In G+20, we also demonstrated that, even in the case of significant contamination, the bias on the final stream dispersion estimates is confined within the statistical fluctuation. This is because COSTA tends to collect only the particles that have a small scatter with respect to the intrinsic bulk kinematics of the stream (if the number of stream particles is dominant). Also, the lowest velocity dispersion values are simply nominal, as they are smaller than our measurement errors and were obtained after subtracting the measurement errors in quadrature. Hence, for these ones we assume 37 km s−1 as an upper limit in the discussion hereafter.
In order to evaluate the dynamical range of the velocities of the streams and compare their internal kinematical structure with respect to their local cluster environment, in Fig. 10 we plot the stream particles as reported in Fig. 9 over the total projected phase space of the GC+PN system of the Fornax core. First, stream particles show a velocity range that is colder (lower dispersion) than the underlying radial velocity distribution of the total PN+GC sample at the same radius. Also, their mean velocities are confined well within the dynamical range allowed by the cluster potential. This is shown in the histogram reported in Fig. 10, where we also mark the systemic velocities of the large galaxies in the area and the velocity range corresponding to the maximum velocity dispersion measured by galaxies (red line) and the ICL (blue line), assuming a Gaussian distribution normalized to the number of streams. Some streams show a clear association to some of the giant galaxies (e.g., NGC 1404 and NGC 1387); in all other cases they are likely to have some other association (see Sect. 5.1).
We also do not see any chevron features, as one would expect from nearly shell-like orbits (see e.g., Romanowsky et al. 2012; Longobardi et al. 2015), but rather short substructures, such as those detected in recent stripping events seen in hydrodynamical simulations (G+20). Overall, the kinematics of the streams shows that these structures are decoupled from the local potential (i.e., streams have a lower velocity dispersion than the particles at the same distance from the center), even though their mean velocities are well inside the dynamical range allowed by the cluster potential. This is compatible with the assumption that these candidate streams are tracing the kinematics of the interaction of parent dwarf galaxies and the overall cluster plus central galaxy potential, although they might not be in dynamical equilibrium in such a potential (see Sect. 4.3).
4.5. Correlations among stream properties
Before describing the properties of the individual streams in more detail and looking into their association with the dwarf population of the Fornax cluster, here we discuss the correlations among some of the parameters reported in Table 2. In particular, in the left panel of Fig. 11 we show the correlation between the stream luminosities and the inferred velocity dispersion. The (logarithm of the) velocity dispersion clearly increases with the stream (log) luminosity, as also measured by the linear regression of the two correlations shown as a solid line in the figure, for which we found a slope of 0.40 ± 0.12, which is compatible with a nonzero correlation at > 3σ level, despite the large error bars. This is confirmed by a high Spearman’s rank correlation coefficient of ρ = 0.76, which corresponds to a significance of more than 99%. We find no significant correlation between the stream surface brightness or the size, and its velocity dispersion. Similarly, we do not find a significant correlation between the stream luminosity and surface brightness and between luminosity and the distance from the cluster center. On the other hand, we find a significant correlation between the clustercentric distance and both the stream surface brightness and stream size, as shown in the middle and right panels of Fig. 11, respectively. Here we also overplot the linear fit in log-log space for which we obtain a slope of 3.09 ± 1.19 and 1.10 ± 0.20 respectively, that is, both consistent with nonzero correlation at > 2.5σ significance. We note that the correlation with the surface brightness seems weaker because of the presence of a larger scatter at small radii, especially because of stream 9. This latter stream has μg = 30.3 mag arcsec−2 which is estimated on the basis of only two PNe, making its value relatively insecure (we return on this stream later). The Spearman’s rank correlation coefficient for the correlation between surface brightness and clustercentric distance is ρ = 0.48 and a significance > 90%; instead, if we remove stream 9, the correlation coefficient increases to ρ = 0.73, which corresponds to a significance of > 99%. For the correlation between stream size and clustercentric distance, ρ = 0.74 and it is significant at > 99%.
 |
Fig. 11. Correlation of the stream luminosity inferred by the PN specific number density with the estimated velocity dispersion (left) and the stream surface brightness (center), and the correlation between stream size (right) and distance from the cluster center. |
These correlations, although based on stream candidates, suggest the presence of physical connections among the stream parameters. However, we cannot a priori exclude that they are the result of some selection effects. For instance, the correlations between surface brightness and size with the distance from the cluster center could be the consequence of the decreasing density of tracers (see Fig. 5). In particular, one might expect streams of fewer particles to be more easily identified at larger distances from the center because of the lower density of the overall ICL population of tracers. This might explain the anti-correlation between SB and radius. However, this cannot explain why, at larger distances, we do not find streams with larger particle numbers and smaller sizes, that is, with higher SB, which would be even easier to find in a lower density environment. This means that if no smaller sized, high-brightness streams are located in the bottom-right sides of both SB versus radius and size versus radius panels in Fig. 11, it is likely that they do not exist.
Another possible selection effect that could mimic a trend in the stream properties is the “tracer completeness”. Due to the higher density of particles in the center, COSTA could collect a large number of contaminants there than at larger distances. This might produce overall brighter streams in the centers (i.e., more contaminants per unit of real stream particle), eventually with a higher SB than the ones at larger distances, which is compatible with what we see in the SB versus radius relation in Fig. 11. For a more quantitative analysis, in G+20 (Fig. 14) we conducted a series of tests to estimate, for simulated streams of different shapes and sizes, the “observed” and “true” completeness (OC and TC respectively). The former is defined as the ratio of true stream members (Nmemb) to the total number of particles selected as stream (Ntot = Nmemb + Ncont) – including contaminant particles, Ncont – and the latter is defined as the ratio of true selected members (Nmemb) to total true members (Nstr). With simple algebra one can easily relate the total numbers of particles recovered by COSTA, Ntot, to the OC and TC by Ntot = TC/OC × Nstr. From Fig. 14 in G+20 we can see that TC/OC is strongly varying as a function of the parameter and the distance from the cluster center, but for Nmin = 15 − 25, which are typical values for most of the real streams (see Fig. 8), the TC/OC goes from 0.9/0.7 in the inner bin, to 0.9/0.85 in the outermost bin. This implies that the TC/OC in the inner bin is ∼1.2 factor higher of the outer bin, meaning Ntot decreasing by the same factor. This means that (1) streams are detected at all distances, although (2) the number of the associate members can indeed change from the center to the outskirts (mainly due to a different contamination; see Fig. 13 of G+20). However the overall variation does not exceed a factor of 1.2, considering the Nmin involved (but can reach 1.6 if a wider Nmin range is allowed). This is not sufficient to justify the 2 mag arcsec−2 variation in SB seen in the middle panel of Fig. 11, where one would expect a factor > 6 in numbers if the overall size of streams is not increased significantly by the contaminants.
According to the arguments above, we conclude that the correlations in Fig. 11 are likely real. If so, we need to understand the physics behind them, and in particular whether these correlations are compatible with being produced in the interaction between dwarf and intermediate galaxy systems and the environment (either larger galaxies or the cluster potential). For instance, in regard to the luminosity–velocity dispersion correlation, one can expect that the more massive a dwarf galaxy is, the more light is stripped during an interaction and the larger the velocity dispersion of the particles that possibly still hold the memory of the dwarf internal kinematics. We note that this effect would be less efficient for more massive galaxies, which tend to loose less stellar mass by tidal stripping than dwarf-like systems (see Rudick et al. 2009).
On the other hand, the correlation of the surface brightness with the distance from the cluster center can be interpreted as the effect of dynamical friction. We can qualitatively understand that the higher the density of the medium, the higher the dynamical friction experienced by a satellite. This can be illustrated using a simplified formula for the dynamical drag: 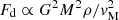 (Carroll & Ostlie 1996). Here G is the gravitational constant, M is the mass of the satellite, ρ is the density of the stellar medium the satellite is entering, and vM is the velocity of the satellite. This equation shows that a higher ρ produces a stronger dynamical pull behind the intruder. This would produce more compact streams from satellites closer to the cluster center than satellites of the same mass but further away, hence impacting both the size and surface brightness of the candidate streams. Fd also depends on vM, which is larger for systems falling toward the centers, while it can be small at the pericenter, where Fd ∼ 0, hence generating more diffuse tails. For this reason, we should expect some scatter added to the correlation by the proximity of the stream to the pericenter of the dwarf orbits, which might be larger toward the center because of the intrinsic higher compactness of the streams. As there is no clear variation of the luminosity function of dwarf galaxies as a function of the distance from the Fornax center (see e.g., Venhola et al. 2018), then we can expect the correlation between stream size and distance to directly reflect the statistical effect of the dynamical friction as a function of the clustercentric radius.
(Carroll & Ostlie 1996). Here G is the gravitational constant, M is the mass of the satellite, ρ is the density of the stellar medium the satellite is entering, and vM is the velocity of the satellite. This equation shows that a higher ρ produces a stronger dynamical pull behind the intruder. This would produce more compact streams from satellites closer to the cluster center than satellites of the same mass but further away, hence impacting both the size and surface brightness of the candidate streams. Fd also depends on vM, which is larger for systems falling toward the centers, while it can be small at the pericenter, where Fd ∼ 0, hence generating more diffuse tails. For this reason, we should expect some scatter added to the correlation by the proximity of the stream to the pericenter of the dwarf orbits, which might be larger toward the center because of the intrinsic higher compactness of the streams. As there is no clear variation of the luminosity function of dwarf galaxies as a function of the distance from the Fornax center (see e.g., Venhola et al. 2018), then we can expect the correlation between stream size and distance to directly reflect the statistical effect of the dynamical friction as a function of the clustercentric radius.
Is there some other physical mechanism based on which we can make similar predictions? In addition to standard tidally stripped streams, C15 discussed the clumpy 2D distribution of stars associated with ‘subresolution’ haloes that survive in the semi-analytic part of their simulations but not in the N-body part (their Fig. 2 panel 6). These latter possibly represent the remnants of disrupted galaxies that cannot be resolved with low-resolution dark-matter particles. These fragments, similar to the patchy distribution of some candidates we see in Fig. 9, are likely the product of the violent relaxation that might have involved progenitors of the bright central cluster galaxy (BCG). According to C15, these progenitors can have any mass, but are more likely associated to low-mass dark haloes that are easily stripped below a total mass of 20 particles, corresponding to ∼2 × 108 M⊙. Unfortunately, in C15 there is no radial velocity information, nor internal velocity dispersion for these clumps to check against the correlations we show in Fig. 11. From Fig. 2 of C15 (panel 6), we notice that the densest knots are present at R > 100 kpc from the center, possibly suggesting an anti-correlation between SB and radius. However, given the “semi-analytic” nature of their stellar particles we do not to want to over-interpret the projected distribution of these orphan stars. In fact, according to C15, the most conservative interpretation is that they have to belong to the BCG halo component, with no detailed information of their actual geometry or properties.
To conclude, we cannot exclude that some of our streams are the product of a violent relaxation involving massive progenitors of the BCG (see also Sect. 5), although we should probably expect for these streams to show a larger velocity dispersion than the dwarf-like galaxies we are intrinsically selecting with COSTA (< 120 km s−1). Therefore in order to finally test this scenario, we need more detailed predictions about the size, internal kinematics, morphology, and frequency of these surviving structures, possibly from simulations more closely reproducing Fornax (e.g., the clusters in C15 are all about ten times richer or more).
5. Discussion
In this section we discuss the stream properties in more detail and investigate whether a connection exists between these properties and those of the galaxy population in their vicinity, and in particular the dwarf-like systems. This may provide further insight into the mechanisms contributing to the build-up of the intracluster stellar population in the Fornax cluster, as a prototype of a rather evolved galaxy cluster system with ongoing galaxy transformation (see e.g., Raj et al. 2019, 2020).
Especially in its core, recent observations have revealed signatures of interactions between the cD, NGC 1399, and other bright galaxies; for example overdensities in the photometrically selected GCs, D’Abrusco et al. (2016), C+20, Chaturvedi et al. (2022), and faint μr ∼ 28 − 29 mag arcsec−2 and diffuse intracluster patches of light (Iodice et al. 2017), which were predicted in earlier dynamical studies (Napolitano et al. 2002) and mirrored by asymmetries in the X-ray halo emission of NGC 1399 (Paolillo et al. 2002; Su et al. 2017).
Tidal stripping of stars (including PNe) and GCs from the outskirts of galaxies in close passages through the cluster core is indeed predicted from N-body simulations (Rudick et al. 2009) to provide the main mechanism for the origin of the ICL in Fornax. However, evidence of the tidal stripping origin of the ICL is all indirect and circumstantial. For example, (1) the similarity between the fraction of the luminosity in the ICL with respect to the total light of cD (∼5%) and the fraction of blue GCs in the total population of GCs (∼4 − 6%) in the same region of the ICL, which seems to suggest that blue GCs are an intracluster population in the Fornax core (Iodice et al. 2017 but see also Bassino et al. 2003 for further evidence of ICL in Fornax). Another example is (2) the lower GC specific frequency (SN ∼ 2) with respect to typical values for cluster massive ellipticals (SN ∼ 5) for the GC population of NGC 1404, which supports the scenario of tidal stripping of GCs in a close passage to the cD (e.g., Bekki et al. 2003). Evidence of such interactions was found by Napolitano et al. (2002) using the velocity structure of PNe as kinematical tracers.
A third example is (3) the presence of an extended structure found especially in the GC population (DA+16, C+20, but see also Spiniello et al. 2018 for evidence of a cold structure in the PN population). These are some examples of indirect evidence supporting the idea that the ICL was formed by tidal stripping, but “smocking gun” proof remains to be found.
Correlating the stream candidates found by COSTA with the parent galaxies from which they might have formed would provide both direct evidence of tidal stripping and proof that this is still ongoing and producing streams in the Fornax cluster. To this end, we take advantage of new collections of Fornax dwarf candidates (Munoz et al. 2015; Venhola et al. 2017; Eigenthaler et al. 2018), and a recent spectroscopic compilation of objects (including normal galaxies, dwarf galaxies and UCDs) in the Fornax cluster from Maddox et al. (2019). This latter includes previous literature from Ferguson (1989), Hilker et al. (1999), Drinkwater et al. (2000, 2001), Mieske et al. (2004), Bergond et al. (2007), Firth et al. (2007, 2008), Gregg et al. (2009), Schuberth et al. (2010), Huchra et al. (2012). We finally crossmatch the catalog of new UCDs already classified in P+18 with the catalog from Saifollahi et al. (2021) as a further check of the correct classification of the former. Associating the candidate streams to the properties of the dwarf galaxies is important: (i) because this is part of the validation of the stream candidates, as we have assumed that the COSTA algorithm can detect tails of stream particles recently lost by their parent dwarf systems, (ii) because we expect that these recently stripped systems provide a record of the kinematical properties of the parent galaxy (see e.g., Gatto et al. 2020) and therefore tell us something about their internal dynamics4, and (iii) because we can understand both the origin of the streams and the fate of the stripped (parent) systems.
5.1. Close inspection of the stream candidates
We start by taking a closer look at the individual streams that are overplotted on the Fornax core image in Fig. 9 and try to relate them to the properties of the known galaxies around them. As mentioned above, our aim is to check whether there is a realistic association between the candidate streams and dwarf galaxies or any other galaxy sample in the Fornax core in order to validate our working hypothesis.
FVSS-S1. This is the most recurrent stream (found with 542 setups) and has also a relatively high median reliability (76%), with some setups even reaching 100%. FVSS-S1 is made of 19 particles (i.e., by averaging the number of particles over all setups), 14 of which are PNe. This is also among the most luminous streams (log L/L⊙ = 8.1, g-band) but with a relatively low SB (∼30 mag arcsec−2) due to its large size (6.7′). FVSS-S1 is placed at about 20′ east from NGC 1399, in a region where Ordenes-Briceño et al. (2018) identified a dwarf galaxy overdensity. From the cross-match with Maddox et al. (2019), we find a UCD (ID = F11747, with absolute magnitude in i-band, Mi = −11.81; see Table 4) 4.4′ away, with a systemic velocity of 1448 km s−1, within ∼2σ of the mean stream radial velocity (1500 km s−1). It is also closer (2.8′) to a slightly fainter dwarf system (NGFS 034003–352754 from Munoz et al. 2015, Mi = −11.57; see Table 3), which has an effective radius of 9.6″ but no systemic velocity measurement from the literature to confirm the association. Both galaxies are located along the direction of the maximum elongation of the stream, suggesting that this could be the tail of one of the galaxies moving southward on the sky plane. From Fig. 9, the candidate stream seems to lie on a region of light excess, although this is at the detection limit of the FDS images.
Distance between candidate streams and their closest dwarfs taken from Munoz et al. (2015) and Eigenthaler et al. (2018).
FVSS-S2. This structure is located southwest of NGC 1399. It has an average median reliability of 74%, with a maximum reliability of 100%. It is made of approximately 20 particles, 7 of which are PNe, corresponding to a luminosity of log L/L⊙ = 7.79. It has a relatively high velocity dispersion (100 km s−1), while its radial velocity is more than 100 km s−1 higher than that of the BCG. An object classified as a bright (Mi = −11.66) GC from the Maddox et al. (2019) catalog (see Table 4), located at less than 3′, has a systemic velocity (1490 km s−1) within ∼2σ of its mean velocity (1563 km s−1). This structure is also classified as a UCD in Fornax in Gregg et al. (2009). If the stream is associated to this galaxy, the morphology seen in Fig. 9 is consistent with a stream stretched from a dwarf galaxy slowly falling toward the cluster center and seems to coincide with one of the overdensities found by Cantiello et al. (2020). We also see from Table 4 and Fig. 9 that two GCs from the P+18 sample are also classified as UCDs, although they are close to the lower limit separating them from bright GCs. FVSS-SS2 has also two bright dwarfs at less than 5′ (see Table 3) away, NGFS 033819–353151 with Mi = −14.79 and NGFS 033842–353308 with Mi = −12.23, but the former has a cz = 1725 km s−1, taken from the Simbad database5, which makes it inconsistent with S2. We therefore keep NGFS 033842–353308 as a possible association in Table 3.
Cross-match with Maddox et al. (2019), Pota et al. (2018), and Saifollahi et al. (2021).
FVSS-S3. This stream is the most recurrent after FVSS-S1, and has a median reliability of 75% with its maximum at 100%. It is composed of 20 particles, 8 of which are PNe, giving it a luminosity of log L/L⊙ = 7.85 and a SB of ∼30 mag arcsec−2. The low SB does not make it possible to observe any counterpart in the deep imaging of the Fornax core. It is located very close to NGC 1404, but because of its mean radial velocity we exclude the possibility that it is associated to it (1392 km s−1 vs. 1947 km s−1). FVSS-S3 has two dwarfs within ∼5′ of its median centroid (see Table 3), but none of them has a measured systemic velocity, and both look too displaced to be a convincing association. Other more likely associations are two UCDs from P+18 and one from S+21 within 4′ of the stream centroid, and having radial velocities within 100 km s−1 of the stream mean velocity. Among these, one is rather bright (I = 13.66 mag, see Table 4) and represents a convincing association. Figure 12 (top panel) displays a zoom onto the surrounding area of FVSS-S3 overlapped also with nearby dwarf galaxies listed in Tables 3 and 4 (yellow squares). The brightest UCD is directly above NGC 1404 and is clearly visible in the image. This is the first UCD ever discovered (Hilker et al. 1999; Drinkwater et al. 2000), and is still the most massive confirmed UCD of the Fornax cluster (Hilker et al. 2007). It has a small stellar envelope of 100 pc in size (Evstigneeva et al. 2008) and very likely has a SMBH (Afanasiev et al. 2018).
 |
Fig. 12. Zoom images of each cold substructure. Green circles indicate particles of the streams, whereas blue squares and circles represent all galaxies listed in Tables 3 and 4, respectively. |
FVSS-S4. This structure has the highest median reliability, together with S6, and is also very recurrent. Moreover, it is the closest structure to NGC 1399 and is very compact, resulting in a SB of 27.7 mag arcsec−2. Despite this, it is the candidate with the greatest SB, but its vicinity to NGC 1399 and NGC 1396 means that its luminous counterpart is undetected in the g-band image where the SB profile of the BGC has been subtracted. The only possible association we find is a faint UCD (i-mag = 20.4, Table 3) from P+18 with radial velocity of ∼1544 km s−1, which is consistent within 2σ with the mean velocity of the stream.
FVSS-S5. This candidate stream occurs 80 times and has a median reliability of 68% and a maximum reliability of 98%. It is located close to NGFS 033750–353302 (Munoz et al. 2015), which has a measured effective radius of Re = 3.2″, and a total magnitude of Mi = −9.75, but no measured systemic velocity in the literature (Table 3). It has another dwarf placed at 2.5′ (NGFS 033754–353429), but no information about the size or luminosity (see also Table 3). Another possible association is a UCD from P+18 at 2.6′ distance from the stream centroid, with Mi = −11.3 and a radial velocity of 1319 km s−1 (Table 4), very close to that of the stream (1351 km s−1).
FVSS-S6. Discovery of a giant, undetected stream connecting NGC 1380, NGC 1381, and NGC 1382. This is a very recurrent structure and has the highest median reliability, namely of 85%. It is made up entirely of GCs because there is no coverage of PN observations, and shows a semi-ellipsoidal shape connecting NGC 1380 with NGC 1382 on one side, and possibly with NGC 1381 on the opposite side, suggesting that this stream might originate from one of these galaxies. Indeed, its mean radial velocity (1795 km s−1) is considerably higher than that of NGC 1399 (i.e., 1425 km s−1) and very similar to the radial velocities of the three connected galaxies (1877 km s−1, 1724 km s−1 and 1740 km s−1, respectively for NGC 1380, NGC 1381 and NGC 1382, Vanderbeke et al. 2011; Drinkwater et al. 2001; D’Onofrio et al. 1995). Because some of the GCs appear to still be “attached” to the halo of NGC 1382, we argue this might be the progenitor. This is possibly supported by the fact that the stream has a velocity dispersion of 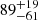 km s−1, which is fully compatible with that of this galaxy (i.e., 77 km s−1, Wegner et al. 2003). We finally note that the GCs on the west side of the stream (connecting NGC 1382 and NGC 1380) have a mean velocity of ∼1748 km s−1 (i.e., consistent with the systemic velocity of NGC 1382), while those on the east side have a mean velocity of ∼1849 km s−1. Finally, the stream GCs around NGC 1380 have a mean velocity of ∼1786 km s−1, showing a clear gradient compatible with a hyperbolic trajectory with the pericenter being located somewhere around NGC 1380 itself.
km s−1, which is fully compatible with that of this galaxy (i.e., 77 km s−1, Wegner et al. 2003). We finally note that the GCs on the west side of the stream (connecting NGC 1382 and NGC 1380) have a mean velocity of ∼1748 km s−1 (i.e., consistent with the systemic velocity of NGC 1382), while those on the east side have a mean velocity of ∼1849 km s−1. Finally, the stream GCs around NGC 1380 have a mean velocity of ∼1786 km s−1, showing a clear gradient compatible with a hyperbolic trajectory with the pericenter being located somewhere around NGC 1380 itself.
In the same region, there are other dwarf galaxies that have a systemic velocity within 3σ of the mean velocity of the stream (F08831, F08944, F16830, F16832, F15915, see Table 3), meaning that this region is highly populated by systems with a significant velocity offset with respect to the cluster barycenter. However, the association with these systems is not as significant as the association with NGC 1382.
FVSS-S7. This structure is located northwest of NGC 1399 and recurs 146 times. As for S1, this stream also seems to lie in a region with light excess with respect to the surrounding regions. It has five dwarfs from the Munoz et al. (2015) sample at less than 5′ from its center; the closest one is about 1′ away and has a low magnitude in the I-band = −10.48; see Table 3. There are two systems with a comparable systemic velocity from the Maddox et al. (2019) catalog. The closest of these two (F15141) has been re-observed in S+21, while the other one (F10101) was classified as a UCD by Gregg et al. (2009) and is also brighter (I-mag = −12.24); see Table 4.
FVSS-S8. Kinematical confirmation of a photometric stream candidate. This stream has a low occurrence (27) and a median reliability of 70%, but it overlaps with the photometric stream previously reported by D’Abrusco et al. (2016) and Iodice et al. (2016). Therefore, this independent finding from COSTA represents the first kinematical confirmation of one of the newly found substructures in the deep photometry of the Fornax cluster by the FDS survey. From the PNe luminosity function, we estimate a luminosity of log L/L⊙ = 7.9 and a SB of ∼29.7 mag arcsec−2, which is fully compatible with the estimates from deep FDS photometry (29 ≤ μg ≤ 31 mag arcsec−2, Iodice et al. 2016). Kinematically, the measurement of the mean stream velocity, 1319 km s−1, is comparable with the systemic velocity of NGC 1387 (1302 km s−1). However, the measured velocity dispersion is 84 km s−1, which is about half the central value found for NGC 1387 (σ = 170 km s−1, Wegner et al. 2003). A possible explanation would be a steeply decreasing velocity dispersion profile towards the outskirts of the galaxy due to a low-concentration dark-matter halo (see e.g., Napolitano et al. 2009). However, we cannot exclude that the stream originates from a different dwarf-like system. Indeed, there are two cataloged systems in Munoz et al. (2015) within 5′, three matches with the Maddox et al. (2019) catalog within 6′, and four UCDs from P+18 with compatible radial velocities (see Table 4). This could indeed explain the inconsistency in terms of stream color with NGC 1399 and NGC 1387, both redder than the average g − i ∼ 0.9 measured along the stream (FDS, Iodice et al. 2016). Two of the UCDs in the area have instead g − i ∼ 0.9. If these latter have interacted with the halo of NGC 1387, then the stream color from the FDS images could be a mix of the stripped stars from NGC 1387 and the two UCDs.
FVSS-S9. This structure is one of the closest to NGC 1399. It is relatively compact and is found to have 14 members on average, almost all of which are GCs (11 on average). FVSS-S9 has a low velocity dispersion (46 km s−1), making it one of the coldest stream candidates of the COSTA catalog. There is one object from Munoz et al. (2015) at about 3′ with a relative low absolute luminosity, namely Mi = −9.99, and classified as a LSB galaxy, but with no systemic velocity measurement. FVSS-S9 is also in the proximity of the largest of the dwarf galaxies, NGC 1396, in the halo of NGC 1399, which however has a much smaller systemic velocity (∼808 km s−1, Drinkwater et al. 2001) than the one estimated for FVSS-S9 (∼1388 km s−1), making an association unlikely. The mean velocity of this stream candidate, compatible with NGC 1399, and the vicinity to the central galaxy both suggest that this candidate stream might be produced by some yet undetected dwarf galaxy falling toward the cluster center (similarly to what is seen for FVSS-S4). Its very low surface brightness (∼30.3 mag arcsec−2) makes this diffuse stream hard to detect in the deep images of the halo of NGC 1399.
FVSS-S10. This stream has the lowest median reliability (61%) and occurs only 45 times. It is made up of about 20 particles, of which 75% are PNe. FVSS-S10 has a mean estimated velocity higher than that of NGC 1399 (i.e., 1488 km s−1) and its velocity dispersion is about 100 km s−1. There is one cataloged dwarf at about 3′ (see Table 3) with no information about its systemic velocity. The associations to this is rather insecure and visual inspection of the FDS images shows no evident counterpart because of the faint intrinsic SB of the stream (∼29.9 mag arcsec−2, see Table 2) and the presence of bright stars to the west. On the other hand, there are two convincing associations to the Maddox et al. (2019) catalog (Table 4) with compatible velocities within 2σ, and located on opposite sides of the stream. One of the two (F11747) is classified as a UCD, while the other is a bright GC (I-mag = −12.48, likely a misclassified UCD).
FVSS-S11. This is another stream inhabiting the halo regions of NGC 1399, but occurring only a few times (23). Like other similar substructures close to the cluster center (e.g., S4 and S9), it is very compact. FVSS-S11 has an average radial velocity of about 200 km s−1 lower than that of NGC 1399. It has two compact objects with a systemic velocity within 2σ (Table 4), of which the most convincing one has no luminosity information, and a further dwarf at about 3′ with no velocity and no luminosity information (Table 3). Like the other compact structures in the strict halo of the central galaxy, these streams possibly form a family whose progenitors have gone through a more dramatic transformation, perhaps caught in the final passages before being fully merged in the BCG.
The possible association with UCD systems of this stream, and other ones of the same kind, is rather interesting. This suggests that these could be the last phase of the disruption of former dwarf galaxies before only their compact core (i.e. the observed UCD) is left surviving (see Sect. 5.2.2).
FVSS-S12. This candidate stream is spatially very close to NGC 1404; it is very compact (2.2′) and relatively cold (55 km s−1). FVSS-S12 is made up of 14 particles almost equally split between GCs (8) and PNe (6), and has a median reliability of 69%. As the mean radial velocity of its particles is about 400 km s−1 lower than the systemic velocity of NGC 1404, and is instead close to that of NGC 1399, FVSS-S12 is more likely associated to this latter. In light of its compactness and position, this stream seems to join the family of halo streams containing S4, S9, and S11, but has no clear associations. We finally note that this stream is very close in position and radial velocity to FVSS-S12, with which for some parameter combinations it has a few particles in common. This suggests a possible connection between the two substructures that COSTA did not find to be significant (in the step-v described in Sect. 3.1).
FVSS-S13. This is the most compact stream, and is found to the west of NGC 1404, but only occurs 27 times. The systemic velocity suggests a connection with NGC 1404 (2046 km s−1 vs. 1947 km s−1). No dwarfs have been discovered in its proximity. However, there is a UCD from P+18 (confirmed by S+21) at a distance of 1.4′ with a similarly high radial velocity (2000 km s−1), which is possibly interacting with the NGC 1404 halo and being stripped of material.
5.2. Summary of the stream–galaxy associations
We conclude this section by summarizing our results for the stream–galaxy associations. As mentioned above, the difficulty in finding clear luminous counterparts for the stream candidates found by COSTA in the Fornax core makes the stream catalog in Table 2 insecure. On the other hand, convincing indications that streams have associations with progenitor candidates allow us to make a step forward in understanding their origin. These can also trigger further investigations and new observations (e.g., dedicated deeper photometry) to look for the integrated light signature of these streams. In terms of the origin of the streams and the connection with the Fornax systems we have found, in the previous section, a series of evidence that we summarize in the following subsections. However, we stress that a more physical interpretation of these associations is beyond the scope of this paper and will be addressed in a forthcoming work (Napolitano et al., in prep.).
5.2.1. Streams associated to normal galaxies
FVSS-S6 is likely connected to NGC 1382 while FVSS-S8 is connected to NGC 1387. In particular, FVSS-S6 appears similar to the coherent streams of tidally stripped material from large galaxies found in C15 (Fig. 2 panel 5). For the first time, we bring evidence of a kinematical link between these streams and their parent galaxies based on similarities between the mean velocities of the stream tracers and those of their associated systems. However, while the velocity dispersion of FVSS-S6 (σ = 89 km s−1) is fully compatible with that of NGC 1382 from stellar spectroscopy (77 km s−1, average from Simbad database), for FVSS-S8, the stream velocity dispersion value, σ = 84 km s−1, is much smaller that that of the internal galaxy kinematics (σ* = 167 km s−1). We also discuss in Sect. 5.1 that, as the g − i colour (= 0.9) of the stream is bluer than the NGC 1387 outskirts, there is a chance that the stream GC+PN population contains a mixture of particles coming from NGC 1387 and the bluer UCD (F09174 and F09244 in Table 4) found in the proximity of the stream.
We conclude this section by noting that, in general, the velocity dispersion values estimated for the streams in Table 2, which are of the order of 70 − 90 km s−1 (after the subtraction of the measurement errors), are typical of galaxies with absolute magnitudes of the order of V = −19.5, and total luminosities of LT ∼ 5 × 109 L⊙, V according to the Faber–Jackson relation (FJR; e.g., Falcón-Barroso et al. 2011). Looking at the typical luminosities of the streams also reported in Table 2, we see that these latter would correspond on average to ∼3−10% of the LT expected by the FJR. In other words, most of the streams would be compatible with the stripping of a minimal amount of stars from these intermediate-luminosity systems (e.g., Rudick et al. 2009; Cooper et al. 2015a). However, we were able to find these associations for most of the streams above, not even at reasonably large distances. This leaves us with the possibility that these streams might still be produced by dwarf-like systems with intermediate velocity dispersions, but that these have been significantly transformed and have not survived as recognizable dwarf systems (see also Sect. 5.2.3).
5.2.2. Streams associated to ultra-compact dwarfs
Streams FVSS-S1, FVSS-S2, FVSS-S3, FVSS-S4, FVSS-S5, FVSS-S7, FVSS-S10, FVSS-S11, and FVSS-S13 have, instead, a kinematical link (i.e., radial velocity within ∼2σ) to systems classified as compact objects or UCDs (see Table 4). For all these streams (except S11), the estimated velocity dispersion of ∼70 − 90 km s−1 is higher than that expected considering a typical FJR of UCDs (see e.g., Mieske et al. 2008; Penny et al. 2014). However, the error bars on the velocity dispersions calculated here are so large that all of them are consistent within 1σ with the typical velocity dispersions of UCDs on the FJR (∼40 km s−1 at Mi = −12).
5.2.3. Streams with no clear associations
There are two remaining streams that lack a clear kinematical association, namely FVSS-S9 and FVSS-S12 (see Table 4). As such, these streams remain dubious and are listed among the possible spurious streams outlined in Sect. 4.3. However, as discussed in Sect. 4.5, clumps of stripped stars apparently dissociated from visible stellar systems are predicted from simulations (C15) as a result of violent relaxation due to the interaction of galaxies merging in the halo region of the BCG. Among the stellar streams in Table 2, the two streams with no clear associations are the most likely candidates to belong to this family. This does not exclude that some other streams associated to UCDs may be remnants of disrupted galaxies of different mass. For instance, FVSS-S10, which is not particularly close to its tentative UCD association (see Fig. 12), or FVSS-S13 in the halo of NGC 1404 could be good examples. The former has a velocity dispersion of ∼90 km s−1, after subtraction of measurement errors, while the latter has a velocity dispersion of 35 km s−1, likely produced by the disruption of a rather bright galaxy, V ∼ −19.5, and a faint dwarf, V ∼ −16.0, respectively.
6. Conclusions
The census of streams around the brightest cluster galaxies is a key diagnostic with which to understand the origin and assembly of the large galaxy haloes around galaxies in dense environments and the construction of the intracluster stellar population. Streams have been predicted in simulations and lately also directly detected in the nearby Universe (Napolitano et al. 2003; Cooper et al. 2010; Romanowsky et al. 2012; Foster et al. 2014; Longobardi et al. 2015). However, without kinematical information it is hard to connect the streams with the galaxy formation mechanisms and, ultimately, fully confirm predictions about their evolution. For instance, one firm prediction of the galaxy formation scenario is that dwarf galaxies orbiting around cluster centers experience tidal interactions with the potential of the cluster and the galaxies orbiting in it. After many passages, these dwarf galaxies lose most of their stellar mass, which is accreted in the intracluster medium to form a diffuse component (Rudick et al. 2009). Remnants of these disruption processes could be at the origin of some of the families of galaxy populations observed in the cluster cores, such as UCDs, which have recently been recognized as an abundant population in the cluster cores (see e.g., Janssens et al. 2019). Therefore, streams carry a wealth of information about the transformation of the dwarf systems and the extent to which their baryoninc material can be fully disrupted, which leads to differences in the luminosity function of cluster cores with respect to the lower density environments.
In order to explore all these avenues, the first step is to find a robust approach to detecting such substructures. Due to their low SB (of the order of 29 mag arcsec−2), streams are hard to be detected with deep photometry (Cooper et al. 2010), although bright streams have been seen in imaging surveys (see e.g., Mihos et al. 2005; Martínez-Delgado et al. 2010; Iodice et al. 2017; Montes & Trujillo 2019). The next step should be their kinematical characterization. There have been a few works able to kinematically characterize faint streams (e.g., Merrett et al. 2003), including some preliminary experiments making use of GCs (Romanowsky et al. 2012) and PNe (Longobardi et al. 2015) in galaxy haloes.
In this study, we used a sample of about 2000 objects accurately selected from the FVSS from Pota et al. (2018) and Spiniello et al. (2018) in order to have a comparable sample in terms of number density and depth from the two types of tracers. We also verified that their velocities and spatial distributions were statistically similar (at more than 5% significance; see Sect. 2) so that they could be used together to extract candidate streams with our new COld STream finding Algorithm (COSTA, Gatto et al. 2020).
We tested the algorithm on a simulated reduced phase space of the Fornax core where there is the major contribution of at least three large galaxies, NGC 1399, NGC 1387, and NGC 1404, which, with their local velocity field, complicate the overall phase-space structure. We obtained the first catalog of 13 stellar stream candidates, selected in the intracluster regions of the Fornax cluster (Table 2). For these streams, we provide mean centroid position (RA and Dec), the number of PN and GC particles forming them, reliability, radial velocity (i.e., mean velocity of the PN+GC particles composing them), velocity dispersion (as the standard deviation of the PN+GC particles composing them), size, total luminosity (as derived by the number of PNe multiplied by an average plausible PN specific number density; see Sect. 4.2), and SB. Based on statistical arguments (see Sect. 4.3), we predict that more than half of these are likely to be real. This is the main result of the study, which is designed to provide a first attempt to select cold substructures in a cluster environment. The main conclusions we draw from this catalog are as follows.
-
Streams are detected at different distances from the cluster center, with a radial velocity distribution that follows that of other cluster members (e.g., galaxies and IC PNe and GCs) but with a smaller velocity dispersion. This has been explained either with the possible presence of spurious streams or with a disequilibrium of the stream population within the cluster.
-
The estimates of SB for the streams vary between ∼28 and ∼30 mag arcsec−1, which is too faint to be deblended from the diffuse light distribution in the core of the Fornax cluster with current imaging data. Deeper, more targeted observations are needed to obtain photometric confirmation.
-
The internal velocity dispersion values for the streams vary between ∼35 km s−1 and ∼100 km s−1, in line with typical velocity dispersions of dwarf-like galaxies, which are very likely their main progenitor systems.
-
Based on the correlations between their luminosity and velocity dispersion, and between their size and SB as a function of their distance from the cluster center, we conclude that streams show signatures of dynamical friction, that is, they are produced, as expected, by tidal stripping. However, we are not able to exclude that other physical mechanisms are also involved in the formation of (a part of) the observed streams. For instance, violent relaxation of galaxies up to intermediate luminosity that have merged into the halo of the central galaxy (see e.g., C15).
-
We have discovered a new giant stream (FVSS-S6) likely connecting NGC 1380 and NGC 1382. In particular, we suggest that this stream is produced by the galaxy NGC 1382 (with which it shares a compatible velocity dispersion) having performed a hyperbolic orbit around NGC 1380.
-
We independently detected the stream FVSS-S8, photometrically observed in Iodice et al. (2016) and associated to NGC 1387, and estimated its velocity dispersion which is about half of that of the galaxy. Due to the compatibility of the radial velocity of this stream with two blue (g − i ∼ 0.9) UCDs in the proximity of NGC 1387, we suggest that this stream might be formed by a mixture of particles stripped by both NGC 1387 and the two satellite systems.
-
We demonstrate kinematical links of most of the streams with UCDs inhabiting the Fornax cluster core. Within the large uncertainties on their velocity dispersion estimates, most of the streams are compatible with the velocity dispersion values expected for the UCDs they are seemingly connected with. However, part of the excess on the velocity dispersion can be reconciled with a dwarf-like FJR if we assume that these UCDs are the remnants of more luminous galaxies that have lost a significant fraction of their initial luminous mass and have therefore moved away from the original FJR. This would be compatible with the formation scenario of the UCD galaxies as remnants of nucleated dwarf spheroidal galaxies (see e.g., Pfeffer & Baumgardt 2013). More evidence of a connection between the physical mechanism (the tidal stripping) and the transient effect (the stream) producing the transformation of the dwarf galaxies into UCDs will be discussed in a forthcoming paper (Napolitano et al., in prep.).
-
Two stream candidates are lacking a clear close physical connection (either in position or velocity) with dwarf-like systems. As such, they may either be spurious detections or, more interestingly, could represent a class of streams from disrupted progenitors merged in the halo of the central galaxies. These are expected to produce orphan clumps of stellar tracers with no clear parent systems, very similar to examples observed as part of the present study (e.g., FVSS-S9 and FVSS-S12). However, more accurate predictions on the morphology, photometry, and kinematics of this family of streams are needed to draw clear comparisons with our observational findings. In this respect, higher resolution N-body+tagging particles or hydrodynamical simulations would be very desirable in order to better resolve and characterize these substructures.
In a forthcoming analysis, we plan to further explore the last two families of streams described above. In particular, we will carry out a detailed investigation of the FJR of the streams for which we have a clear galaxy association with UCDs and draw more quantitative conclusions about their origin. Furthermore, we plan to search for more of the candidate “orphan clumps” predicted in C15. If some of these clumps come from large galaxies and follow the FJR, they might have a larger velocity dispersion than the upper limit we have imposed for dwarf-like systems (i.e., 120 km s−1) but possibly not too large to be detected as “cold substructures” by COSTA.
We do not exclude the UCD candidates of P+18 from the PN+GC catalog because they are a minor fraction of the total sample (< 0.1%) and because if they are part of a stream, they are likely to be the nuclear core of that stream (see Sect. 5).
Even if most of the dwarf galaxies in Coma from Kourkchi et al. (2012) have σ < 100 km s−1, we decided to use a slightly larger range of σcut to avoid border effects. These could happen, e.g., when taking larger N neighbor particles, as this could increase the chance of measuring a larger velocity dispersion for a group of particles, hence producing a clustering of parameters toward higher σcut.
If we compare the velocity dispersion of the stream candidate population at their mean distance from the center, 13′±1.9′, with the ones of the PNe and red and blue GCs at the same distance from S+18 and P+18, which are 312 km s−1, 312 km s−1, and 361 km s−1 respectively, we find the stream kinematics to be even more discrepant from the other intracluster populations.
Acknowledgments
We thank the referee, Dr. A. Cooper, for the careful review of the paper that allowed us to improve the interpretation and discussion of the paper results. N.R.N. acknowledges financial support from the “One hundred top talent program of Sun Yat-sen University” grant N. 71000-18841229, and from the European Union Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement n. 721463 to the SUNDIAL ITN network. C.S. is supported by an ‘Hintze Fellow’ at the Oxford Centre for Astrophysical Surveys, which is funded through generous support from the Hintze Family Charitable Foundation.
References
- Afanasiev, A. V., Chilingarian, I. V., Mieske, S., et al. 2018, MNRAS, 477, 4856 [Google Scholar]
- Aguerri, J. A. L., Gerhard, O. E., Arnaboldi, M., et al. 2005, AJ, 129, 2585 [CrossRef] [Google Scholar]
- Amorisco, N. C. 2019, MNRAS, 482, 2978 [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Hui, X., Capaccioli, M., & Ford, H. 1994, The Messenger, 76, 40 [NASA ADS] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Mendez, R. H., et al. 1996, ApJ, 472, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Okamura, S., et al. 2003, AJ, 125, 514 [Google Scholar]
- Arnaboldi, M., Gerhard, O., Aguerri, J. A. L., et al. 2004, ApJ, 614, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Ventimiglia, G., Iodice, E., Gerhard, O., & Coccato, L. 2012, A&A, 545, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bassino, L. P., Cellone, S. A., Forte, J. C., & Dirsch, B. 2003, A&A, 399, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bekki, K., Forbes, D. A., Beasley, M. A., & Couch, W. J. 2003, MNRAS, 344, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Bergond, G., Athanassoula, E., Leon, S., et al. 2007, A&A, 464, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, ApJ, 694, 556 [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Flores, R., & Primack, J. R. 1986, ApJ, 301, 27 [Google Scholar]
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [Google Scholar]
- Cantiello, M., Venhola, A., Grado, A., et al. 2020, A&A, 639, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, B. W., & Ostlie, D. A. 1996, An Introduction to Modern Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Castro-Rodríguez, N., Aguerri, J. A. L., Arnaboldi, M., et al. 2003, A&A, 405, 803 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaturvedi, A., Hilker, M., Cantiello, M., et al. 2022, A&A, 657, A93 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Feldmeier, J. J., & Bartlett, R. E. 1998, ApJ, 492, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [Google Scholar]
- Coccato, L., Arnaboldi, M., & Gerhard, O. 2013, MNRAS, 436, 1322 [Google Scholar]
- Cooper, A., Cole, S., Frenk, C., et al. 2010, MNRAS, 406, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [Google Scholar]
- Cooper, A. P., Gao, L., Guo, Q., et al. 2015a, MNRAS, 451, 2703 [Google Scholar]
- Cooper, A. P., Parry, O. H., Lowing, B., Cole, S., & Frenk, C. 2015b, MNRAS, 454, 3185 [Google Scholar]
- Cortesi, A., Merrifield, M. R., Arnaboldi, M., et al. 2011, MNRAS, 414, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, P., McLaughlin, D. E., Cohen, J. G., & Blakeslee, J. P. 2003, ApJ, 591, 850 [CrossRef] [Google Scholar]
- D’Abrusco, R., Cantiello, M., Paolillo, M., et al. 2016, ApJ, 819, L31 [CrossRef] [Google Scholar]
- De Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onofrio, M., Zaggia, S. R., Longo, G., Caon, N., & Capaccioli, M. 1995, A&A, 296, 319 [NASA ADS] [Google Scholar]
- Douglas, N. G., & Taylor, K. 1999, MNRAS, 307, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [Google Scholar]
- Drinkwater, M. J., Phillipps, S., Jones, J. B., et al. 2000, A&A, 355, 900 [NASA ADS] [Google Scholar]
- Drinkwater, M., Gregg, M., Holman, B., & Brown, M. 2001, MNRAS, 326, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., Serra, P., et al. 2011, MNRAS, 417, 863 [Google Scholar]
- Durrell, P. R., Mihos, J. C., Feldmeier, J. J., Jacoby, G. H., & Ciardullo, R. 2003, ApJ, 582, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Eigenthaler, P., Puzia, T. H., Taylor, M. A., et al. 2018, ApJ, 855, 142 [Google Scholar]
- Evstigneeva, E. A., Drinkwater, M. J., Peng, C. Y., et al. 2008, AJ, 136, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., van de Ven, G., Peletier, R. F., et al. 2011, MNRAS, 417, 1787 [Google Scholar]
- Feldmeier, J. J., Ciardullo, R., Jacoby, G. H., & Durrell, P. R. 2004, ApJ, 615, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C. 1989, AJ, 98, 367 [Google Scholar]
- Firth, P., Drinkwater, M. J., Evstigneeva, E. A., et al. 2007, MNRAS, 382, 1342 [NASA ADS] [CrossRef] [Google Scholar]
- Firth, P., Drinkwater, M. J., & Karick, A. M. 2008, MNRAS, 389, 1539 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Spitler, L. R., Strader, J., et al. 2011, MNRAS, 413, 2943 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, C., Lux, H., Romanowsky, A. J., et al. 2014, MNRAS, 442, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Gatto, M., Napolitano, N. R., Spiniello, C., Longo, G., & Paolillo, M. 2020, A&A, 644, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genel, S., Vogelsberger, M., Springel, V., et al. 2014, MNRAS, 445, 175 [Google Scholar]
- Gregg, M. D., Drinkwater, M. J., Evstigneeva, E., et al. 2009, AJ, 137, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Hartke, J., Arnaboldi, M., Gerhard, O., et al. 2018, A&A, 616, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [Google Scholar]
- Hilker, M., Infante, L., Vieira, G., Kissler-Patig, M., & Richtler, T. 1999, A&AS, 134, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Baumgardt, H., Infante, L., et al. 2007, A&A, 463, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hilker, M., Richtler, T., Barbosa, C. E., et al. 2018, A&A, 619, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [Google Scholar]
- Iodice, E., Capaccioli, M., Grado, A., et al. 2016, ApJ, 820, 42 [Google Scholar]
- Iodice, E., Spavone, M., Cantiello, M., et al. 2017, ApJ, 851, 75 [Google Scholar]
- Iodice, E., Spavone, M., Capaccioli, M., et al. 2019, A&A, 623, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janssens, S. R., Abraham, R., Brodie, J., Forbes, D. A., & Romanowsky, A. J. 2019, ApJ, 887, 92 [Google Scholar]
- Johnston, K. V., Zhao, H. S., Spergel, D. N., & Hernquist, L. 1998, BAAS, 30, 1378 [NASA ADS] [Google Scholar]
- Kourkchi, E., Khosroshahi, H. G., Carter, D., et al. 2012, MNRAS, 420, 2819 [NASA ADS] [CrossRef] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., & Mihos, J. C. 2015, A&A, 579, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., Pulsoni, C., & Söldner-Rembold, I. 2018, A&A, 620, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maddox, N., Serra, P., Venhola, A., et al. 2019, MNRAS, 490, 1666 [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [Google Scholar]
- McNeil, E., Arnaboldi, M., Gerhard, O., et al. 2010, Highlights Astron., 15, 66 [NASA ADS] [Google Scholar]
- Merrett, H. R., Kuijken, K., Merrifield, M. R., et al. 2003, MNRAS, 346, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Mieske, S., Hilker, M., & Infante, L. 2004, A&A, 418, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mieske, S., Hilker, M., Infante, L., & Mendes de Oliveira, C. 2007, A&A, 463, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mieske, S., Hilker, M., Jordán, A., et al. 2008, A&A, 487, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [Google Scholar]
- Montes, M., & Trujillo, I. 2019, MNRAS, 482, 2838 [Google Scholar]
- Munoz, R. P., Eigenthaler, P., Puzia, T. H., et al. 2015, ApJ, 813, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Murante, G., Giovalli, M., Gerhard, O., et al. 2007, MNRAS, 377, 2 [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., Freeman, K. C., & Capaccioli, M. 2001, A&A, 377, 784 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., & Capaccioli, M. 2002, A&A, 383, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Pannella, M., Arnaboldi, M., et al. 2003, ApJ, 594, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2009, MNRAS, 393, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Pota, V., Romanowsky, A. J., et al. 2014, MNRAS, 439, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Ordenes-Briceño, Y., Eigenthaler, P., Taylor, M. A., et al. 2018, ApJ, 859, 52 [Google Scholar]
- Paolillo, M., Fabbiano, G., Peres, G., & Kim, D. W. 2002, ApJ, 565, 883 [Google Scholar]
- Penny, S. J., Forbes, D. A., Strader, J., et al. 2014, MNRAS, 439, 3808 [NASA ADS] [CrossRef] [Google Scholar]
- Pfeffer, J., & Baumgardt, H. 2013, MNRAS, 433, 1997 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Madau, P., & Mayer, L. 2015, ApJ, 799, 184 [Google Scholar]
- Pota, V., Forbes, D. A., Romanowsky, A. J., et al. 2013, MNRAS, 428, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Pota, V., Napolitano, N. R., Hilker, M., et al. 2018, MNRAS, 481, 1744 [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2018, A&A, 618, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2020, A&A, 641, A60 [EDP Sciences] [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2021, A&A, 647, A95 [EDP Sciences] [Google Scholar]
- Raj, M. A., Iodice, E., Napolitano, N. R., et al. 2019, A&A, 628, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raj, M. A., Iodice, E., Napolitano, N. R., et al. 2020, A&A, 640, A137 [EDP Sciences] [Google Scholar]
- Richtler, T., Salinas, R., Misgeld, I., et al. 2011, A&A, 531, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Strader, J., Spitler, L. R., et al. 2009, AJ, 137, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Strader, J., Brodie, J. P., et al. 2012, ApJ, 748, 29 [Google Scholar]
- Rudick, C. S., Mihos, J. C., Frey, L. H., & McBride, C. K. 2009, ApJ, 699, 1518 [Google Scholar]
- Saifollahi, T., Janz, J., Peletier, R. F., et al. 2021, MNRAS, 504, 3580 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shih, H.-Y., & Méndez, R. H. 2010, ApJ, 725, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Spavone, M., Capaccioli, M., Napolitano, N. R., et al. 2017, A&A, 603, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spavone, M., Iodice, E., Capaccioli, M., et al. 2018, ApJ, 864, 149 [Google Scholar]
- Spavone, M., Iodice, E., van de Ven, G., et al. 2020, A&A, 639, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiniello, C., Napolitano, N. R., Arnaboldi, M., et al. 2018, MNRAS, 477, 1880 [Google Scholar]
- Su, Y., Nulsen, P. E. J., Kraft, R. P., et al. 2017, ApJ, 851, 69 [Google Scholar]
- Vanderbeke, J., Baes, M., Romanowsky, A. J., & Schmidtobreick, L. 2011, MNRAS, 412, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Veljanoski, J., & Helmi, A. 2016, A&A, 592, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2017, A&A, 608, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2018, A&A, 620, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2019, A&A, 625, A143 [EDP Sciences] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [Google Scholar]
- Walker, M. G., & Peñarrubia, J. 2011, ApJ, 742, 20 [CrossRef] [Google Scholar]
- Wegner, G., Bernardi, M., Willmer, C. N. A., et al. 2003, AJ, 126, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Woodley, K. A., & Harris, W. E. 2011, AJ, 141, 27 [CrossRef] [Google Scholar]
Appendix A: K-S test for red and blue GCs versus PNe
In this section, we test the kinematical consistency of the PNe with the separated population of red and blue GCs. In §2.5 we mention that the PNe and GCs are generally dynamically decoupled, but that PNe and red GCs usually more closely follow the properties of the old stellar population of galaxies. The use of the GC population as a whole can therefore produce some bias if the kinematical properties are significantly different. For this reason, we have adopted the same color value used by P+18, namely g − i = 0.85 mag, to separate blue and red GCs, In Fig. A.1 we display the K-S test performed on the three populations paired in turn: blue GCs and PNe (top panels), red GCs and PNe (middle panels), and finally with blue and red GCs (bottom panels), for each of the three shells defined in Table 1. The results for all cases are reported in Table A.1. Overall, the p-values are higher than the significance level of 5%, with the exception of one case, i.e., red GCs and PNe in the Shell 2. However, in all other cases, the derived p−values are even larger that the ones obtained for the GC as a single population. In particular, we do not find statistical differences between the blue GC population and either the red GCs or PNe, which was our primary concern. We therefore conclude that due to the general agreement found in all other shells, we can reasonably assume that the three populations do not show difference across the cluster that can introduce biases. On the contrary, stressing the diversity of tracers could introduce a selection bias in the search for streams, which we wanted to prevent because this is the first time cold streams are tentatively isolated and our understanding of these objects has just begun to take form.
 |
Fig. A.1. Outcomes of the K-S test in the three shells at different radial distances. Top: Blue GCs and PNe. Middle: Red GCs and PNe. Bottom: Red GCs and PNe. |
Parameters and p-values of the Kolmogorov-Smirnov test.
Appendix B: Stream reliability maps
In Fig B.1 we display, for each of the 13 cold substructures found with COSTA, the reliability maps of the Fornax cluster core obtained using only the WNS as described in §3.2, overlapped with the setups in which COSTA detected the streams.
 |
Fig. B.1. Reliability map for the Fornax cluster obtained with a reliability threshold of 50%. For every stream detected by COSTA, we mark the setups where COSTA revealed them as red points. |
 |
Fig. B.1. continued. |
Appendix C: Spuriousness of streams candidates
In §4.3 we mention the possibility that some candidate streams may simply be a random extraction of “cold tails” of a generally hotter population of tracers. In order to investigate this latter possibility, we follow a very simple statistical argument and suppose that the stream particles are randomly extracted by a population being in equilibrium with the cluster potential. We can then assume that they have a normal velocity distribution with mean equal to the velocity of NGC 1399 and standard deviation σ ∼ 300 kms−1. Then the mean of these groups of particles should have a standard deviation equal to 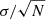 where N is the number of streams, i.e., typically 300/
where N is the number of streams, i.e., typically 300/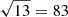 kms−1.
kms−1.
To confirm this, we can use the Monte Carlo simulations above, with no added artificial streams. We select 13 groups of 20 random particles (i.e., the typical number size of one of the detected streams) in each simulation and compute their mean velocity (the mean group velocities). We then use these to determine the average velocity and the standard deviation, finding that the mean was compatible with the systemic velocity assumed for the cluster and the standard deviation of the random groups was 80 ± 17 kms−1 over the 100 simulations, smaller than the one we measure from the mean velocities of the streams in Table 2. This suggests that the overall kinematics of the stream candidates is incompatible with random particles extracted from an equilibrium population. However, this begs the question of why they do not share the kinematics of other intracluster objects (i.e., galaxies, PNe, and GCs). It is also unclear as to whether or not they posses a decoupled dynamics from other equilibrium populations and it remains possible that some of the candidate streams are spurious. If spurious, we have seen that they should contribute to the overall velocity dispersion of the “real stream” with a low velocity dispersion (of the order of ∼80 kms−1, as discussed immediately above) which would reduce the intrinsic velocity dispersion of the stream population.
Under the assumption that streams were recently stripped by the parent galaxy, it is fair to believe that they should still record the kinematics of the parent galaxy in the cluster potential. If this is the case, some pseudo-equilibrium should still hold and the mean velocities of real streams should follow the dynamics of the cluster as their parent galaxies do. This, in turn, allows us to estimate what fraction of spurious streams would produce the observed factor of ∼213/300 between the scatter of the stream radial velocities and the typical cluster velocity dispersion value in the area, by simply assuming that all spurious streams have contributed σspur ∼ 83 kms−1 (see above). Hence we can write 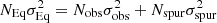 , where Nobs and σobs (= 213 kms−1) are the number of stream candidates and the measured dispersion for them respectively, Nspur and σspur are the possible spurious streams and their individual velocity dispersion (see above), and NEq and σEq (= 300 kms−1) are the true number of streams and the equilibrium velocity dispersion. As, by definition, NEq = Nobs − Nspur, with a little algebra, we obtain
, where Nobs and σobs (= 213 kms−1) are the number of stream candidates and the measured dispersion for them respectively, Nspur and σspur are the possible spurious streams and their individual velocity dispersion (see above), and NEq and σEq (= 300 kms−1) are the true number of streams and the equilibrium velocity dispersion. As, by definition, NEq = Nobs − Nspur, with a little algebra, we obtain 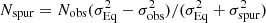 , which returns Nspur ∼ 6. Thus, in the case where streams are a population of dynamical components in equilibrium with the cluster potential, we expect that our catalog might contain up to six spurious detections. This simple estimate does not take into account the density slope of the streams or the anisotropy of their orbital distribution, which are fully unknown and can both affect the expected velocity dispersion of them as an equilibrium population. On the other hand, it is likely that the streams are not a canonical equilibrium population and the Nspur ∼ 6 has to be taken as an upper limit.
, which returns Nspur ∼ 6. Thus, in the case where streams are a population of dynamical components in equilibrium with the cluster potential, we expect that our catalog might contain up to six spurious detections. This simple estimate does not take into account the density slope of the streams or the anisotropy of their orbital distribution, which are fully unknown and can both affect the expected velocity dispersion of them as an equilibrium population. On the other hand, it is likely that the streams are not a canonical equilibrium population and the Nspur ∼ 6 has to be taken as an upper limit.
Indeed, as we see in §4.5, the stream population shows signatures of dynamical friction, which suggests the presence of ongoing dissipative processes. This would reasonably drive the loss of kinetic energy and consequently cause a reduction in the velocity dispersion of the streams as an intracluster population, making the actual Nspur smaller than that estimated above. In summary, we can conclude that, even in the worst case (Nspur ∼ 6), at least half of the stream candidates (i.e., 7 over 13) are real.
Appendix D: The connection between FVSS-S2 and FVSS-S12
In §5.1 we mention that FVSS-S2 and FVSS-S12 are, among all streams in Table 2, those with the most similar radial velocity that are simultaneously close in position. This might indicate a link between the two substructures that has either been missed or considered not significant by COSTA. This latter possibility cannot be excluded if the size of a stream is particularly large (as discussed in Sect. 3.4.2 of G+20). We a posteriori checked the presence of overlapping particles among the different parameter combinations, e.g., the ones shown in Fig. 8 and Fig. B.1. Indeed, we found a few particles in common for some parameter setups which favor the detection of large streams (large k, Nmin and σcut). However, in the majority of the parameter combinations, COSTA does detect them as two separate structures with velocity dispersion values that are only marginally compatible (within 2σ, see Table 2, but with a very large error on the FVSS-S12 velocity dispersion value). Looking at the σ − Nmin diagrams in Fig. 8, we see that the parameter spaces of the two streams barely overlap, demonstrating that the numbers of configurations that return common particles is rather small. On the other hand, if joined together, the parameter spaces of the two streams would cover a very large volume, much wider than a medium-sized cold substructure (see e.g., G20 Fig. 12).
We tried to mimic the presence of a much larger structure by adding a large artificial stream (10′ × 5′) made of 40 particles with an intrinsic velocity dispersion of 90 km s−1 to the combined GC+PN sample of the Fornax core, and then applying COSTA to recover it (following the procedure adopted for real streams described in §3.3). This simulated stream should reasonably reproduce the properties of the FVSS-S2 and S12 combined, assuming that FVSS-S2 is a fragment of a bigger stream with higher velocity dispersion, whose upper limit is given by the σ estimated for FVSS-S12 (see Table 2). In particular, we derived the σ − Nmin diagram, which is reported in Fig. D.1. This shows two main features. First, the parameter space covered by the allowed configurations is distributed along a banana-shaped region revealing a parameter degeneracy. This could be the consequence of an increasing fraction of contaminants in larger Nmin, producing larger velocity dispersion configurations. Second, the distribution of parameters is multi-variate with three peaks at (σ; Nmin)≃(10, 10),(20, 80), and (25, 110). These might correspond to some subgroups that, if not continuously connected, could be selected as independent units.
 |
Fig. D.1. Density plot of the σcut as a function of Nmin for a simulated stream of stream 40 particles, 10′×5′ size, with an intrinsic velocity dispersion of 90 km s−1, mimicking a large stream as expected if FVSS-S2 and FVSS-S12 are part of a single substructure. Color code and smoothing are defined as in the real streams in Fig. 8. |
This test shows that it is possible that FVSS-S2 and -S12 are part of a larger stream whose main body is formed by the latter. This would possibly support the origin suggested for FVSS-S12 in §5.1, namely the remnant of a larger galaxy disrupted via violent relaxation, being similar to the clumpy remnants found in C15.
All Tables
Distance between candidate streams and their closest dwarfs taken from Munoz et al. (2015) and Eigenthaler et al. (2018).
Cross-match with Maddox et al. (2019), Pota et al. (2018), and Saifollahi et al. (2021).
All Figures
 |
Fig. 1. Relative distances of the GCs (top left) and PNe (bottom left) from NGC 1399, and reduced phase-space (top right: GCs; bottom right: PNe). Overplotted on the phase-space are the mean velocity of the particles (solid line), the 1σ (dotted lines), and the 2.5σ (dash-dotted lines). Black triangles are the main galaxies in the field. The dashed horizontal line in the phase space is the systemic velocity of NGC 1399 (1425 km s−1). |
| In the text | |
 |
Fig. 2. GCLF evaluated in the three different radial bins, along with their fitted Gaussian function whose parameters are described in the text. |
| In the text | |
 |
Fig. 3. Planetary nebulae luminosity function in all the S+18 fields. The best fit of Eq. (1) is shown as a continuous line. We have excluded from the fit the bins with one single ultra-luminous object, generally brighter than ∼17 mag. See discussion in the text. |
| In the text | |
 |
Fig. 4. Left: image of the whole sample of GCs (dark gray) and 887 bright PNe (light gray) in RA vs. Dec with the galaxies overplotted as black triangles. Right: GCs (dark gray) and PNe (light gray) in the phase space. The lines correspond to the mean velocity of the particles (solid line, dark red for the GCs and light red for the PNe), to the velocity dispersion at 1σ (dotted line), and to the velocity dispersion at 2.5σ (point-dotted line). |
| In the text | |
 |
Fig. 5. Top: number counts as a function of the radius of GCs (in yellow), PNe (in green), and the total population (in gray). The overdensity of PNe around NGC 1387 is clearly seen at R ∼ 20″ (see text). Bottom: radial density distribution of GCs (yellow open dots), PNe (green), and the total population (black), arbitrarily re-scaled to match the surface brightness of the Fornax core from I+16 (gray tick line). Error bars represent Poissonian errors on the tracer counts. |
| In the text | |
 |
Fig. 6. Histograms of the density of GCs (yellow) and of the PNe (green) per velocity interval in the three shells at different radial distances. Overlapped on these histograms are the distributions of the two samples. |
| In the text | |
 |
Fig. 7. Reliability map in the 4D parameter space for the simulated Fornax cluster. The 2D projected plots for each pair of parameters are color-coded according to the fraction of configurations (FN) with reliability ≥50% according to the legend. Histograms show the fraction of times the reliability passes the 50% threshold for each value of the four free parameters of COSTA. |
| In the text | |
 |
Fig. 8. Density plot of the σcut as a function of Nmin for each stream, color-coded by the number of times COSTA detected the stream with a given σcut − Nmin pair. Data were smoothed using a Gaussian kernel with a bandwidth equal to 3. |
| In the text | |
 |
Fig. 9. Image of the Fornax cluster core region. We show representative particles of each cold substructure found by COSTA in the closest configuration to the median setups; these are colored according to the associated stream. Orange squares and diamonds indicate galaxies listed in Tables 3 and 4 respectively, with symbol size proportional to their i-band luminosities. Orange crosses represent galaxies listed in the tables with no luminosity measurement. |
| In the text | |
 |
Fig. 10. Left: particles of each cold substructure in the phase space, with the same colors as in Fig. 9, superposed on all particles used in this work (light gray). Right: Gaussians with mean = 1425 km s−1, i.e., the NGC 1399 systemic velocity, and standard deviation of 300 km s−1 (blue solid lines) and 374 km s−1 (red solid lines), namely the velocity dispersion of the Fornax cluster and of the Fornax members analyzed by Drinkwater et al. (2001). |
| In the text | |
 |
Fig. 11. Correlation of the stream luminosity inferred by the PN specific number density with the estimated velocity dispersion (left) and the stream surface brightness (center), and the correlation between stream size (right) and distance from the cluster center. |
| In the text | |
 |
Fig. 12. Zoom images of each cold substructure. Green circles indicate particles of the streams, whereas blue squares and circles represent all galaxies listed in Tables 3 and 4, respectively. |
| In the text | |
 |
Fig. A.1. Outcomes of the K-S test in the three shells at different radial distances. Top: Blue GCs and PNe. Middle: Red GCs and PNe. Bottom: Red GCs and PNe. |
| In the text | |
 |
Fig. B.1. Reliability map for the Fornax cluster obtained with a reliability threshold of 50%. For every stream detected by COSTA, we mark the setups where COSTA revealed them as red points. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. D.1. Density plot of the σcut as a function of Nmin for a simulated stream of stream 40 particles, 10′×5′ size, with an intrinsic velocity dispersion of 90 km s−1, mimicking a large stream as expected if FVSS-S2 and FVSS-S12 are part of a single substructure. Color code and smoothing are defined as in the real streams in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} N(m) = ce^{0.307m}[1 - e^{3(m^*-m)}], \end{aligned} $$](/articles/aa/full_html/2022/01/aa41872-21/aa41872-21-eq1.gif)