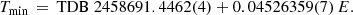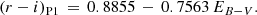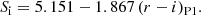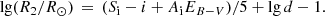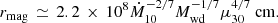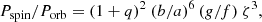| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202141585 | |
| Published online | 19 January 2022 | |
J1832.4-1627, the first eclipsing stream-fed intermediate polar
1
Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
e-mail: beuermann@astro.physik.uni-goettingen.de
2
Pascal Gymnasium, Uppenkampstiege 17, 48147 Münster, Astronomy and Internet in Münster (AiM), Dorotheenstr. 17, 48145 Münster, Germany
e-mail: p-breitenstein@online.de
3
GSI Helmholtzzentrum für Schwerionenforschung GmbH, Planckstr. 1, 64291 Darmstadt, Germany
e-mail: e.schwab@gsi.de
4
Volunteer for ESA/ESOC, Robert-Bosch Str. 5, 64293 Darmstadt, Germany
Received:
18
June
2021
Accepted:
21
October
2021
We present a photometric study of the newly discovered eclipsing intermediate polar J183221.56-162724.25 (in short J1832) with an orbital period of 8.87 h. The system features a box-like deep eclipse with a full width at 50% depth of 1970 ± 2 s and a large-amplitude coherent pulsation with Pobs = 65.18 min, which represents either the synodic (beat) period or the spin period of the white dwarf (WD). The period ratio is either Pspin/Porb = 0.1091 or 0.1225, respectively. The eclipsed light originates almost entirely from the two accretion spots and columns on the WD, with characteristics indicative of pole flipping. There is no evidence for an accretion disk, and we identify J1832 as the first deeply eclipsing stream-fed intermediate polar. Our grizy photometry in eclipse yielded an i-band AB magnitude of the Roche-lobe-filling secondary star of 18.98(3), an extinction EB − V = 0.54 ± 0.17, and a spectral type ∼K6. Dynamic models, fitting the photometry, limit the distance to between 1270 and 2500 pc for masses of the secondary star, M2, between 0.16 and 1.0 M⊙, well within the Gaia EDR3 confidence limits. Employing a luminosity selection inspired by binary population studies yields a mean M2 = 0.32 M⊙ with a 2σ upper limit of 0.60 M⊙ and a mean distance d = 1596 pc with a 2σ upper limit of 1980 pc. The secondary star is located in its Hertzsprung-Russell diagram at a mean Teff, 2 = 4120 K and log(L2/L⊙) = − 0.92, from where the binary can evolve into either a polar or an ultracompact binary with a highly magnetic primary. The system displays a variable accretion rate, lapses repeatedly into short-lived low states of negligible accretion, and currently displays an orbital period that decreases on a timescale of τ ∼ 3 × 105 yr. X-ray observations, optical spectroscopy, and spectropolarimetry have a high potential for studies of the properties of J1832 as an individual object and of stream-fed accretion in general.
Key words: binaries: eclipsing / novae, cataclysmic variables / binaries: close / stars: individual: J1832.4-1627
© ESO 2022
1. Introduction
Magnetic cataclysmic variables (CVs) contain an accreting white dwarf (WD) with a surface field strength in the MG regime fed by a low-mass secondary star. They come in two flavors, the synchronized polars (or AM Herculis stars) and the non-synchronized intermediate polars (IPs). Polars lack an accretion disk, and the WD accretes via a quasi-stationary stream that guides the matter from the inner Lagrangian point, L1, more or less directly to the WD. In most IPs, on the other hand, the WD accretes via the intermediary of an accretion disk with an inner bound defined by the equality of viscous and magnetic stresses at the radius of the WD’s magnetosphere. The difference reflects the typically larger orbital periods and system dimensions of IPs and, perhaps, the typically lower magnetic moments of their primary stars. An intriguing, yet controversial, idea suggested an evolutionary link between the two, identifying IPs as the progenitors of polars (e.g., King et al. 1985; Hameury et al. 1986; Wickramasinghe et al. 1991; King & Lasota 1991; Patterson 1994; Norton et al. 2004, 2008; Southworth et al. 2007). The proposition postulates the existence of non-synchronized counterparts to polars, which synchronize and appear as polars in their further evolution toward shorter orbital periods. An IP, approaching such a scenario, might have a freely spinning WD with a sufficiently strong magnetic moment to avoid the formation of a disk and accrete instead from a stream that alternately feeds its two poles, a situation referred to as pole flipping. Unfortunately, no such IP has yet been found. The process of synchronization has been studied, however, in asynchronously rotating polars that were already synchronized and had temporarily lost synchronism by some event, such as a nova outburst, and are currently re-synchronizing. They display spin and orbital periods that differ by only ∼1%, which corresponds to the situation in an IP just preceding synchronization. Well-studied cases include V1500 Cyg = Nova Cyg 1975, which seems to have acquired synchronism again after 40 years (Harrison & Campbell 2016), and the still asynchronous systems BY Cam (Honeycutt & Kafka 2005), V1432 Aql (Littlefield et al. 2015), and CD Ind (Littlefield et al. 2019). Because of the near equality of spin and orbital periods, the synodic (beat) periods are long, between 7 and about 62 days. As a consequence, the phenomenology of asynchronous polars is generally rather complex, more complex, in fact, than expected for a stream-fed IP that is still far from synchronism.
Despite intense searches, only one secure candidate of a stream-fed IP has so far been discovered, V2400 Oph, which, unfortunately, is not particularly well suited for studying the conjectured IP-polar connection. It is seen at an inclination of only ∼10°, and consequently its system parameters are not well known (Buckley et al. 1995, 1997; Hellier & Beardmore 2002; Joshi et al. 2019). Other IPs display a mixture of disk-fed and stream-fed accretion, showing pulsations at both the spin and the synodic period that are produced by the phenomenon of stream overflow. Part of the stream that impacts on the outer disk manages to flow over the disk and carry its angular momentum directly into the WD’s magnetosphere (Lubow 1989). Still others, such as TX Col, usually dominated by disk-fed accretion, show stream-fed intervals after losing and before reestablishing the disk (Littlefield et al. 2021), which is of interest in itself as it allows the process of disk formation to be observed.
Eclipsing systems offer obvious advantages for in-depth studies of the system parameters. They permit reliable measurements of the component masses, allow the usually faint secondary star to be detected in eclipse, and provide insight into the structure of the accretion region because practically the entire surface of the WD comes into view as it rotates. Unfortunately, the number of eclipsing IPs is exceedingly small. Of the 117 IPs and IP candidatesv in the last version of the Ritter & Kolb (2003) catalog (final online version 7.24, 2016), only four show a deep eclipse. These are, with one addition, the classical systems DQ Her (Nova Her 1934) and XY Ari, V902 Mon=IPHAS J0627 (Aungwerojwit et al. 2012), V597 Pup, the now faint Nova Puppis 2007 (Warner & Woudt 2009), and Nova Sco 1437 (Potter & Buckley 2018, and references therein). Alas, all five contain luminous accretion disks.
A feature shared by some IPs and many polars are irregular long-term brightness variations, including states of vanishing accretion, referred to as low states. In the usual high states, the accretion luminosity outshines the stellar components, and, in many systems, the WD becomes detectable only in a low state. By no means do all IPs provide this opportunity. The well-studied 13 mag disk-fed system EX Hya, for example, exhibits rare outbursts but has not lost its bright disk since observations started more than 60 yr ago (see the AAVSO long-term light curve1). As a consequence, the properties of both stellar components are still not well known (Eisenbart et al. 2002; Belle et al. 2003; Hoogerwerf et al. 2004; Beuermann & Reinsch 2008, 2013).
In this paper we present a photometric study of J183221.56-162724.25 (henceforth J1832), the first deeply eclipsing stream-fed IP that has it all: (i) Its orbital period of 8.87 h and a coherent large-amplitude 65-minute pulsation qualify it as an IP; (ii) it showed no evidence for an accretion disk in three consecutive observing seasons, suggesting that this is a long-lasting feature; (iii) the emitted light, apart from that of the secondary star, originates from the immediate vicinity of the WD, probably the tall accretion columns at both poles; (iv) the entire central region suffers a deep eclipse by the secondary star; (v) ingress and egress are fast and unresolved at our time resolution of about 30 s; (vi) the evidence for pole flipping supports its identification as a stream-fed IP; and (vii) it lapsed repeatedly into low states, offering the prospect for orbital phase-resolved studies of the secondary star and the WD in spectral regions where either one dominates. No object similar to short is currently known.
The new IP was discovered on 26 July 2019 by E. Schwab as a side product of the search for the lost comet P/2012 K3 (Gibbs) using the 80 cm Schmidt telescope of the German-Spanish Astronomical Center at Calar Alto (CA), Spain, and described by Schwab & Breitenstein (2019). It received the AAVSO2 Unique Identifier 000-BNG-512. It was previously (and incorrectly) automatically classified in the Pan-STARRS 3π survey (Sesar et al. 2017) as an RR Lyr star. It carries the Gaia Data Release 2 (DR2) identifier 4102856333775127296 and is located at RA, Dec (2000) 18 32 21.56, −16 27 24.2 ( ) in the Milky Way (Fig. 1). The Gaia Early Data Release 3 (EDR3) lower and upper confidence limits for the geometric distance are 1254 and 2847 pc, respectively (Bailer-Jones et al. 2021)3. We present a photometric study of the object, including an analysis of phase-resolved light curves taken in white light (WL) and multicolor grizy light curves taken through the eclipse. The extinction as measured by us is EB − V = 0.54 ± 0.17. Measurements of the brightness and spectral type of the secondary star allowed us to restrict the system parameters.
) in the Milky Way (Fig. 1). The Gaia Early Data Release 3 (EDR3) lower and upper confidence limits for the geometric distance are 1254 and 2847 pc, respectively (Bailer-Jones et al. 2021)3. We present a photometric study of the object, including an analysis of phase-resolved light curves taken in white light (WL) and multicolor grizy light curves taken through the eclipse. The extinction as measured by us is EB − V = 0.54 ± 0.17. Measurements of the brightness and spectral type of the secondary star allowed us to restrict the system parameters.
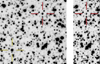 |
Fig. 1. Finding chart for J183221.56-162724.25. The r-band images were taken on 12 May 2021 with MuSCAT3 on the FTN. N is up, E to the left, and sizes are 80″ × 80″ and 30″ × 80″. The target and the comparison star are indicated by the red and yellow crosses, respectively. The right panel shows the target in the eclipse. |
2. Observations
A total of 3551 WL images were taken on 32 nights in 2019, 2020, and 2021 with the 80 cm Schmidt telescope at the CA Observatory, Spain, equipped in 2019 with an SBIG ST 10-XME charge-coupled device camera and in 2020 and 2021 with a Proline PL23042 camera. The 2019 data were described by Schwab & Breitenstein (2019). Here, we summarize the combined results of the 2019, 2020, and 2021 campaigns and report updated ephemerides for the orbital motion and the rotation of the WD. All CA data were taken with a clear filter in WL and exposed for 60 s. Additional long runs in WL were performed with the MONET/South telescope at the Sutherland site of the South African Astronomical Observatory (SAAO). Shorter observations that covered preferentially the eclipse were performed with telescopes of the Las Cumbres Observatory (LCO), namely the 2-meter Faulkes Telescope South (FTS) and the 1-meter telescope at Siding Spring, Australia, the 2-meter Faulkes Telescope North (FTN) at the Haleakala Observatory, Hawaii, and the 1-meter telescope at the McDonald Observatory, Texas, USA. These runs were taken in the grizy filters on the Pan-STARRS1 (P1) system (Tonry et al. 2012) or in WL with exposure times mostly of 40 s. Table 1 provides a log of the observations.
All images were corrected for dark current and flat-fielded in the usual way. We performed photometry relative to the comparison star C3, which is located at RA, Dec (2000) 18 32 24.118, −16 28 08.13, or 57.2″ SE of the target (Fig. 1). It has AB magnitudes on the P1 system g = 16.933(3),r = 16.357(10),i = 16.107(8),z = 15.931(7), and y = 15.897(7). All times were measured in UTC and converted to Barycentric Dynamical Time (TDB), using the tool provided by Eastman et al. (2010)4, which accounts also for the leap seconds. As described in Beuermann et al. (2017), the WL measurements at the MONET/S telescope were tied into the standard griz system. For most incident spectra, the WL AB magnitude w is within 0.1 mag of the r-band magnitude. We assumed this calibration to be approximately valid also for the CA WL measurements, which is supported by the similar calibration of the P1 w-band (Tonry et al. 2012).
The experimental setups of the CA observations were tailored to comet and asteroid searches and not optimized for studies of faint CVs in a dense star field. In particular, the 2020 and 2021 setups with their comparatively large plate scale (Table 1) led to spillover of flux from the near neighbors visible in Fig. 1. The cameras at the MONET/S and the two Faulkes telescopes had more favorable plate scales and for these runs, a spillover problem from the near neighbors at ∼5″ did not exist. They were still disturbed, however, by at least three faint companions at ∼1″ separation to the N, E, and S of the target, which required a special effort in the photometric analysis. The southern one is listed in the Gaia EDR3 (Gaia Collaboration 2021) with G = 20.82 at a separation of 1 29. In the Gaia high-state measurement, our target had G = 18.55 and the influence of the near neighbors was negligible, but in the eclipse they may add noticeably to the measured flux, particularly in the g-band, where the secondary star becomes faint. A special effort is, therefore, required for reliable measurements of the eclipse fluxes. Our method makes use of the variability of the target: the difference image of equal exposures outside and inside eclipse lacks all constant sources and contains a clean image of the target in the selected filter. Its relative flux fdif was measured with respect to comparison star C3, which has the physical flux FC3. We subtracted a fraction fecl of the difference image from the eclipse image, such that the result was as best as possible devoid of the target. The target flux in eclipse is then fecl fdif FC3 and its error is estimated from the uncertainty in establishing fecl. The method yielded background images in g, r, i, z, and y that contained the near neighbors and illustrated the complexity of the background at this position in the Milky Way.
29. In the Gaia high-state measurement, our target had G = 18.55 and the influence of the near neighbors was negligible, but in the eclipse they may add noticeably to the measured flux, particularly in the g-band, where the secondary star becomes faint. A special effort is, therefore, required for reliable measurements of the eclipse fluxes. Our method makes use of the variability of the target: the difference image of equal exposures outside and inside eclipse lacks all constant sources and contains a clean image of the target in the selected filter. Its relative flux fdif was measured with respect to comparison star C3, which has the physical flux FC3. We subtracted a fraction fecl of the difference image from the eclipse image, such that the result was as best as possible devoid of the target. The target flux in eclipse is then fecl fdif FC3 and its error is estimated from the uncertainty in establishing fecl. The method yielded background images in g, r, i, z, and y that contained the near neighbors and illustrated the complexity of the background at this position in the Milky Way.
3. Temporal analysis
3.1. Light curves
The largest body of light curves was taken with the CA Schmidt telescope in WL (Table 1). The source displayed substantial long-term variability as shown in Fig. 2, where the average relative WL fluxes are displayed versus time, supplemented by g-band fluxes of July 2021. The “error” bars represent the standard deviations of all individual flux measurements of a given run. The peak-to-peak variations are another factor of about two larger. Most of the time, the source was found at an average WL flux of around 0.30 relative to the comparison star, which we take to represent the high state of the source. In all three observing seasons, the system lapsed into short-lived low or intermediate states of accretion. It was found in a low state on 3 − 5 August 2019 (JD 2458700), in an intermediate state between 20 and 27 June 2020 (JD 2459020-9028), and it oscillated between low and intermediate states between 17 July and at least 9 August 2021. Since the source is accreting, we associate these fluctuations with variations in the accretion rate, though not necessarily the mass loss rate from the secondary star.
 |
Fig. 2. Long-term light curve, showing nightly averages of the WL fluxes relative to comparison star C3 (green dots). The g-band fluxes of July 2021 (crosses) are adjusted to approximately match the WL fluxes. |
The two panels of Fig. 3 show the WL measurements of 2019 and 2020 phased on the 8.87 h orbital period and on the 65-minute pulse period of Eqs. (1) and (6), respectively. All individual flux measurements are displayed as green dots and individual light curves are emphasized by other colors. In the upper parts of both panels, we show the average light curves collected into 32 phase bins. All light curves are characterized by the deep eclipses of the WD by the secondary star and large-amplitude pulsations that we relate to the WD rotation. Examples of the eclipse light curves are shown in Fig. 4. The left panel presents WL light curves at three different accretion levels (note that the zero levels of the ordinate are displaced with respect to each other) and the right one simultaneous high-state griz light curves. The remnant flux at the center of the eclipse is independent of the accretion level and reaches down to that of the secondary star at the center of the eclipse (Sects. 4.1 and 5.5). We can, therefore, exclude a grazing or partial eclipse as in EX Hya (Beuermann & Osborne 1988; Rosen et al. 1988; Allan et al. 1998). The WD itself is faint compared with the accretion spots and columns, as evidenced by the light curve of 4 August 2019, when the system was caught in a state, when accretion had dropped to a trickle and the eclipse had practically vanished (Figs. 3 and 4, blue dots, and Sect. 4.2). Examples of the large-amplitude pulsations are shown in Fig. 3. The light curve in the left panel (black dots) was pieced together from four individual runs to illustrate the magnitude of the effect.
 |
Fig. 3. Bottom panels: light curves in WL folded on the orbital period of Eq. (1) (left) and on the pulse period of Eq. (6) (right). All individual relative WL fluxes are shown as green dots, and selected individual light curves are emphasized in black, red, and blue (see text). Top panels: mean light curves collected into 32 orbital bins (left) and pulse bins (right). |
The rotational light curves in Fig. 3 show that the pulse maxima are more or less double-peaked and the mean rotational light curve in the upper right-hand panel suggests that this is a permanent feature of J1832. Transient double peaks were observed in the photometric light curves of V2400 Oph and V1062 Tau as well (Buckley et al. 1995; Lipkin et al. 2004). Permanent double peaks are naturally produced in pole-flipping stream-fed accretors, as demonstrated by the model calculations of Ferrario & Wickramasinghe (1999, their Fig. 3).
3.2. Is there an accretion disk?
The mean orbital light curve in the left panel of Fig. 3 is essentially flat, with the remnant modulation related to individual 65-minute pulsations. In particular, it lacks the orbital hump expected if there were a viscous disk with a locally puffed-up bulge. Furthermore, the eclipse profile in Fig. 4 lacks disk characteristics as the wide rounded-off component observed in IPHAS J0627 (Aungwerojwit et al. 2012) or the V-shaped eclipse of KIC 5608384 (Yu et al. 2019). Any disk component is, furthermore, limited to stay below the minima of the spin modulation. At our moderate temporal resolution, the transitions into and out of eclipse stay largely unresolved. For the large body of CA WL observations with exposure times of 60 s, the formal average of the fitted transition times between the contact points is tine = 80 ± 56 s. For the best-resolved of our observations with 20 s exposure and 9 s readout, the transition still occurs within one or two time bin. This corresponds to a lateral extent in the orbital plane of 2π a tine/Porb ≲ 109 cm. While this is entirely consistent with the extent of the accretion columns discussed in Sect. 3.3, even a minimal disk is more than ten times larger. Its diameter would exceed two times the corotation radius where q = M2/M1 ∼ 0.5 was used for the mass ratio, Porb is the orbital period, and we used the observed pulse period in lieu of the spin period Pspin. Hence, a luminous disk cannot hide in the rapid transitions in J1832.
 |
Fig. 4. Left: eclipse light curves in WL, taken with the CA Schmidt telescope, shifted vertically by the indicated amounts. Right: simultaneous eclipse light curves in the griz filters, taken with the MuSCAT3 photometer on the FTN. The dotted lines indicate the length and flux level of the totality. |
We now consider the sagging flux profile in the eclipses displayed in Fig. 4. The decreasing flux in the first third and the increasing flux in the last third of the eclipse indicate that an extended source exists that suffers a delayed or incomplete eclipse. In the WL light curve of 16 September 2019, 92% of the eclipsed flux at ingress disappear within a minute and the remaining 8% (until eclipse center) within the next 15 min. In the r-band light curve of 12 May 2021, 3% of the eclipsed flux reappear between eclipse center and the end of totality and the remaining 97% within the final minute. Hence, in WL or r, a few percent of the total high-state flux are contributed by the extended source. The MuSCAT3 simultaneous griz-observations in the right panel of Fig. 4 suggest that this component is rather blue. Our nonsimultaneous observations show that it is highly variable, in particular in the g-band. It seems plausible to assign this emission to the outer part of the magnetically guided and likely optically thin accretion stream or to the ballistic stream between L1 and its impact on the magnetosphere, which are both prone to a partial eclipse. For the quoted corotation radius, the stream rises to ∼1.5 × 1010 cm above the orbital plane, sufficient for a time-dependent fraction of the stream to escape eclipse (see also Sect. 5.5). Such a component was seen in other magnetic CVs as well: the long-period IP V902 Mon showed Hα emission that did not completely disappear in eclipse (Worpel et al. 2018), and so did the long-period CV KIC 5608384 (Yu et al. 2019), and the polar HY Eri (Beuermann et al. 2017). Hence, emission from the accretion stream far away from the WD is a natural candidate for the variable flux of J1832 in eclipse. Alternatively, we cannot exclude that a minimal faint disk or a ring of matter, circulating the WD near rco (King 1993; King & Wynn 1999; Norton et al. 2008), contributes a few percent to the optical flux.
A final argument against the presence of a viscous accretion disk follows from the low-state observation of 3 − 5 August 2019. On 4 August (blue light curve in the left panel of Fig. 4) a viscous disk was absent. Had it been present on 1 August 2019, when the source was still bright, it would have had to have disappeared within 2 days, which is hard to reconcile with the viscous timescale tvisc ∼ R2/(αHcs) ≳ 20 d for R > rco, a relative disk height H/R ≲ 0.02, a sound speed of 10 km s−1, and a Shakura-Sunyaev parameter α < 1. In summary, we conclude that J1832 lacks a viscous accretion disk.
3.3. Orbital period and ephemeris
We fitted the ingress into or the egress from eclipse by an analytical model of the occultation of a circular disk of uniform surface brightness by an opaque secondary star. For a given individual exposure, the model value was represented by a Simpson integral of the time-dependent model flux over the finite exposure time, which provides an optimal description of the poorly resolved transitions. The fit parameters for either ingress or egress were (i) the flux before the transition, (ii) the flux after the transition, (iii) the time, at which 50% of the depth is reached, (iv) the duration of the transition between the contact points, (v) the slopes of the time-dependent flux before the transition, and (vi) the slope after the transition. Additional parameters account, as far as possible, for a systematic variation in the atmospheric conditions, for example, an air-mass-dependent transmission. The mid-eclipse time was calculated as the mean of the two times that mark the 50% points at egress and ingress, and the full width at half maximum (FWHM) or duration of the eclipse as their difference. The light curves in Fig. 3 show that the steps in flux and the slopes may differ substantially between ingress and egress, depending on the respective phase in the 65-minute pulsation. It also illustrates the need to include the slopes of the time-dependent fluxes into the fit. The derived mid-eclipse times and the O–C values relative to a linear ephemeris are listed in Table 2 and the O–C values are shown in the top panel of Fig. 5. The alias-free linear ephemeris for all data is
 |
Fig. 5. Top: O–C diagram of the mid-eclipse times relative to the linear ephemeris of Eq. (1). The difference between the quadratic and linear ephemerides of Eqs. (2) and (1) is shown as the dashed curve. Second from top: FWHM of the eclipse vs. pulse phase from Eq. (6). Center: O–C values of the mid-eclipse times relative to the quadratic ephemeris vs. pulse phase. The model curve is from Eq. (4) (see text). Second from bottom: O–C diagram for the minimum times of the 65-minute pulsations relative to the linear ephemeris of Eq. (6). Bottom: O–C values of the previous graph vs. orbital phase (see text). |
with χ2 = 387.8 for 25 d.o.f. (degrees of freedom) and 1σ errors in the last digits quoted in brackets. Fitting a quadratic ephemeris to all data gives
with χ2 = 97.2 for 24 d.o.f., which is still not good. The difference between the two fits of Eqs. (2) and (1), Tecl, 2 − Tecl, 1, is shown as the dashed curve in the top panel of Fig. 5. From Eq. (2), the period derivative is Ṗorb = −3.5 × 10−9 s s−1. Taken at face value, this implies a current period decrease of 0.11 s per year and a timescale of the variation of 3 × 105 yr, about two orders of magnitude faster than that predicted by nuclear evolution (e.g., Kalomeni et al. 2016).
3.4. Evidence for pole flipping
Accounting for a period change improves the fit to the mid-eclipse times, but with 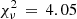 , Eq. (2) still fails to represent the eclipse times well. We searched for a further dependence and found that the mid-eclipse times varied quasi-sinusoidally with the 65-minute pulse phase ϕ65, c measured at the center of the eclipse (Fig. 5, center panel). A sine fit, Δ Tecl = A sin(φc − φ0)−γ, gave an amplitude A = 13.6 ± 1.6 s, a zero-crossing at ϕ0 = 0.03 ± 0.02, and γ = − 0.5 ± 1.1 s, with χ2 = 25.9 for 24 d.o.f. For brevity, we use here the phase angle φc at the center of eclipse instead of 2πϕ65, c. The final model of Eq. (4) below, depicted in the center panel Fig. 5 center, provided a small improvement over the sine fit with χ2 = 24.0 for 23 d.o.f. No modulation similar to that of the mid-eclipse times is seen in the FWHM or duration of the eclipse (Fig. 5, second panel from top). The weighted mean FWHM of 17 completely covered eclipses is 1970 s with a standard deviation of the distribution of 2 s. The pulsations are discussed in Sect. 3.5, their ephemeris is provided in Eq. (6), and its zero point is defined as the pulse minimum.
, Eq. (2) still fails to represent the eclipse times well. We searched for a further dependence and found that the mid-eclipse times varied quasi-sinusoidally with the 65-minute pulse phase ϕ65, c measured at the center of the eclipse (Fig. 5, center panel). A sine fit, Δ Tecl = A sin(φc − φ0)−γ, gave an amplitude A = 13.6 ± 1.6 s, a zero-crossing at ϕ0 = 0.03 ± 0.02, and γ = − 0.5 ± 1.1 s, with χ2 = 25.9 for 24 d.o.f. For brevity, we use here the phase angle φc at the center of eclipse instead of 2πϕ65, c. The final model of Eq. (4) below, depicted in the center panel Fig. 5 center, provided a small improvement over the sine fit with χ2 = 24.0 for 23 d.o.f. No modulation similar to that of the mid-eclipse times is seen in the FWHM or duration of the eclipse (Fig. 5, second panel from top). The weighted mean FWHM of 17 completely covered eclipses is 1970 s with a standard deviation of the distribution of 2 s. The pulsations are discussed in Sect. 3.5, their ephemeris is provided in Eq. (6), and its zero point is defined as the pulse minimum.
The shifts of the mid-eclipse times follow naturally in an IP model with pole flipping that features two accretion columns with brightness varying in antiphase. For simplicity, we adopted sinusoidal variations and represented the columns as point sources that are located at the centroid of the emission at a radial distance ρ > Rwd and an angular offset β from the rotational axis (Fig. 6). They are eclipsed by the limb of the secondary star that is modeled as a straight edge inclined by an angle α against the vertical (the preferred dynamic models in Sect. 5 have α = 47° or 53°). Special about J1832 is the near equality of the FWHM of the eclipse (1970 s) with one half of the observed 65-minute pulse period (1955 s), implying that the phase angles at ingress and egress are related by φi ≃ φc − π/2 and φe ≃ φc + π/2, respectively. We assumed that the brightness of the sources near both poles varied as f1 = 1 + a1 cos φ for the upper pole and f2 = 1 − a2 cos φ for the lower one. With a2 > a1, the pulse maximum occurs at φ = π or ϕ65 = 0.5 and is dominated by the lower pole. The phasing is as observed (Fig. 3 and Eq. (6)) and the preference of the lower pole is adapted from the accretion geometry of EX Hya (Beuermann & Osborne 1988; Rosen et al. 1988; Allan et al. 1998). Both poles display their maximal brightness difference at ingress and egress for central phases of 0.25 and 0.75 (Fig. 6, green = maximum, yellow = intermediate, open = minimum). For central phases ϕ65, c = 0 or 0.50, on the other hand, ingress and egress occur at ϕ65 = 0.25 or 0.75 with both poles at intermediate brightness. The dotted lines in Fig. 6 denote the displacements from the limb and the time shifts of ingress and egress relative to that experienced by the center of the WD. The time shifts at both poles are formally the same and differ only by their sign,
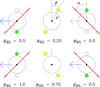 |
Fig. 6. Schematic sketch of the two-pole accreting WD passing the limb of the secondary star, inclined by an angle α to the vertical (red line). The emission regions are located at radial distance ρ and displaced by an angle β from the rotational axis. They are indicated by circles, color-coded for their relative brightness: maximal (green), intermediate (yellow), and minimal (open). The projected views are shown for pulse phase at the center of the eclipse, ϕ65, c = 0.25 (top) and 0.75 (bottom). The pictures refer to the ingress (right), mid-eclipse (center), and egress (left). The transit takes almost exactly one half of the observed pulse period. The blue arrows indicate the motion of the WD. |
with φ the current phase angle and υ the orbital speed of the WD relative to the secondary star. We estimated the combined effect Δ Tecl on the mid-eclipse time by averaging the four contributions flux-weighted with f1 and f2. Similarly, we estimated the FWHM as the difference of the weighted mean contributions at egress and ingress. Our simple model predicts that the FWHM does not vary with φc, but that substantial shifts of the mid-eclipse times occur,
with an amplitude A = (a1 + a2)ρ/2υ. The observed dependence of ΔTecl on φc (or ϕ65) in the center panel of Fig. 5 is only moderately skewed, suggesting that the first term in Eq. (4) dominates. We fitted this model to the observed time shifts and obtained β = 21 ± 10°, an amplitude A = (a1 + a2)ρ/2υ = (12.2 ± 1.4) s for α = 50° and χ2 = 24.0 for 23 d.o.f., as quoted already above. With these parameters, Eq. (4) becomes
with an amplitude of 14 s and φc = 2πϕ65, c defined by Eq. (6), below. For β > 40°, the model curve becomes excessively skewed and develops double humps. The amplitudes a1 ≃ 0.2 and a2 ≃ 0.8 fit the observed mean 65-min light curve in Fig. 3. The orbital speed is υ ≃ 3.1 × 107 cm s−1 for a binary separation a ≃ 1.6 × 1011 cm (Sect. 5) and the characteristic size of the columns is a plausible ρ ≃ 109 cm, similar to the value estimated by Siegel et al. (1989) for EX Hya. Correcting the original mid-eclipse times for the shifts defined by Eq. (4), linear ephemerides for the individual years gave period differences for 2019 and 2021 relative to 2020 of +(94 ± 39) ms and −(95 ± 52) ms, respectively. A complete orbital ephemeris, given by the addition of Eqs. (2) and (5), requires knowledge of the pulse phase.
The subsequent eclipses of both poles are expected to lead to a phase-dependent structure of the ingress and egress light curves that stayed unresolved in our data, but may provide insight into the accretion geometry, if measured with higher time resolution. We emphasize that such a study was not previously possible, because no deeply eclipsing stream-fed IP was known.
Our simple model of Eq. (4) does not account for more complex geometrical effects and radiative transfer in the emission regions. Consequently, it does not account for variations in the pulse profile as a function of orbital phase. Such variations are predicted, however, in the more elaborate model of Ferrario & Wickramasinghe (1999) for a stream-fed IP accreting alternately at two opposite poles. The model light curves presented in their Fig. 4, feature double-peaked pulses of the line emission and the optical continuum from the extended accretion columns, while the X-ray pulses are single-peaked, because of the two accretion spots on the WD only one is visible at any given instant. The optical pulses display phase shifts over the orbital period and a variation in the separation of the double peaks, including a short single-peaked interval. We measured the minimum times of the continuum flux from Fig. 4 in Ferrario & Wickramasinghe (1999) and found that they display a quasi-sinusoidal variation over the orbit. Such a variation is also observed in our data and shown in the bottom panel of Fig. 5. The amplitude of a fitted sinusoid is −1.5 ± 0.5 min (where we have excluded the three outlying minimum times of 2020 in the second panel from the bottom, which show no phase preference). We searched for an orbital variation in the pulse shape in our WL data by sorting all individual WL measurements into an image of 15 × 15 orbital and pulsational phase bins (not shown). In that image, the shifting pulse minimum is even more clearly visible than in the bottom panel of Fig. 5. In addition, there is an indication that the separation of the two peaks varies over the orbit including what may be a short interval with a central single peak near orbital phase ϕ = 0.5. Given improved observations, dedicated modeling may be rewarding. Presently, our findings strongly suggest that pole-flipping occurs in J1832, supporting its classification as a stream-fed IP.
Finally, we caution against prematurely identifying the O–C variation in the top panel of Fig. 5 and the quoted period differences between the individual years as real variations in the orbital period before the dynamics of the system is fully understood. Orbital period changes in close binaries, mostly detached ones, are ubiquitous and not well understood. Neither the concept of a third body in the system nor varieties of the Applegate mechanism (Applegate 1992; Völschow et al. 2018; Lanza 2020) have so far led to a generally accepted explanation of the observed variations.
3.5. Pulse period and ephemeris
We employed two methods to determine the period of the pulsation: (i) calculating a Lomb-Scargle power spectrum in the MIDAS-TSA context5 and (ii) subjecting the minimum times of the pulsations to a period search. The former uses the entire information from the rather complex pulse profile, the latter only the reduced information of a well-defined feature with a lower internal scatter. The times of the minima were determined graphically by the bisected-chord technique, marking the center between descent into and ascent from minimum at different flux levels and extrapolating these times to the flux at the minimum. The standard deviation of the distribution of the O–C values of the 47 minima of Table 3 around a linear fit is 2.9 min. For comparison, locating an individual maximum may prove complicated and the uncertainty may exceed 10 min or more. Consequently, the Lomb-Scargle periodogram is expected to be less efficient in measuring the pulse period, but is free of the necessarily somewhat subjective procedure of defining the minima.
The Lomb-Scargle power spectrum for the 2019–2021 high- and intermediate-state observations outside the eclipse, is displayed in the lower left panel of Fig. 7, normalized to a peak value of unity. Maximum power is attained at an observed frequency of the pulsation ωo = 22.09 day−1, closely followed by the 1-day alias at 21.09 day−1. The center bottom panel shows that at higher resolution power appears also at the 1-year alias frequencies separated from the best value by 0.003 day−1, reflecting the separation of the 2019 and 2020 observing periods by about 320 days. The two right-hand panels demonstrate that there is no power at the side bands ωo ± Ω, where Ω = 2.70644(1) day−1 is the orbital frequency. The same holds for the side band at ωo − 2Ω (Warner 1986) and is true also for the corresponding side bands that belong to the alias at ωo = 21.09 day−1. Not surprisingly, in view of the double peaks, there is significant power at the second harmonics of observed pulse frequency ωo and its alias frequencies (not shown). Gratifyingly, the periodogram yields the same frequencies as the Lomb-Scargle power spectrum, but more clearly prefers ωo = 22.09 day−1 with a nominal reduced 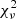 of unity over 21.09 day−1 with
of unity over 21.09 day−1 with 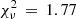 . Again, no signal is detected at any of the side bands of ωo. Its best value is ωo = 22.09281(4) day−1. In case of the 1-day alias, the fit selects also a different of the 1-year alias frequencies and the best value would become ω = 21.090 day−1. We consider ωo = 22.09281 day−1 as the most probable choice. The analysis of the 47 minimum times in Table 3 yielded the linear ephemeris
. Again, no signal is detected at any of the side bands of ωo. Its best value is ωo = 22.09281(4) day−1. In case of the 1-day alias, the fit selects also a different of the 1-year alias frequencies and the best value would become ω = 21.090 day−1. We consider ωo = 22.09281 day−1 as the most probable choice. The analysis of the 47 minimum times in Table 3 yielded the linear ephemeris
 |
Fig. 7. Top: periodograms for the minimum times of the 65-minute pulsations. The scale on the left also applies to the center panels. Bottom: lomb-Scargle power spectra for the high- and intermediate-state pulsations outside the eclipse, normalized to a peak value of unity. |
The best period is Po = 3910.774(6) s = 65.1796(1) min and the O-C diagram is shown in the second panel from below in Fig. 5. Fitting the minimum times of 2019 and 2020 individually gave periods of 65.1798(10) min and 65.1806(14) min, respectively. There is no evidence for a period variation so far and we accept the pulsation in J1832 as a stable coherent signal. We cannot presently identify the observed period uniquely with either the spin period or the synodic (beat) period of the WD. For the two cases, the spin period is either Pspin = 3910.775(7) s or 3483.976(7) s and the ratio of spin versus orbital periods is Pspin/Porb = 0.1225 or 0.1091, respectively.
4. Multicolor spectral energy distribution
4.1. Secondary star
In this section we consider the grizy eclipse measurements of J1832 performed with the Faulkes North and South telescopes and derive the spectral energy distribution (SED) of the secondary star. We measured the spectral fluxes of the target in the central part of the eclipse, using the method described in the last paragraph of Sect. 2. These fluxes varied by about 10% in rizy and more in g. We adopted generally the lowest of the photometrically well defined fluxes as representative of the SED of the secondary star, list these in Table 4, and show them as black solid circles in the left panel of Fig. 8.
 |
Fig. 8. Left: observed SED of J1832. Black dots refer to the minimum fluxes in the eclipse and represent our best estimate of the SED of the secondary star. Green and yellow squares indicate the SED outside eclipse measured simultaneously with the MuSCAT3 photometer and the FTN on 9 May and 15 April 2021, respectively. Colored dots indicate nonsimultaneous out-of-eclipse fluxes (see text). Center: de-reddened SED based on the best-fit EB − V = 0.54. Right:Δχ2 vs. EB − V (plus signs, left scale) and the associated (r − i)P1 (green dots, right scale). |
Fitting the observed SED of the secondary star requires de-reddening it. The reddening at the position of J1832 was studied by Lallement et al. (2018) within the framework of their 3D-model of the galactic extinction and is in the range of EB − V = 0.3–0.7 for distances between 900 and 2100 pc. The geometric distances d quoted in the Gaia data releases DR2 and EDR3 have lower and upper error bounds of 941 − 2696 pc and 1254 − 2847 pc, respectively (Bailer-Jones et al. 2018, 2021). Models of J1832 that include EB − V and the distance d as independent parameters are presented in Sect. 5. Here, we vary EB − V, fitting the de-reddened relative rizy fluxes with a stellar SED (Tonry et al. 2012; Covey et al. 2007; Pecaut & Mamajek 2013) to obtain the best-fit color r − i for a given EB − V and thereby the spectral type. For consistency with the observations, all colors were transformed into the Pan-STARRS P1 system. Since the g-band flux exceeded the predicted stellar flux slightly, but systematically (see Sect. 3.2 and Fig. 4), we restricted the fit to the rizy bands. The fit gave an overall χ2 minimum for EB − V = 0.54 and (r − i)P1 = 0.48, with 1σ ranges (Δχ2 = + 1) of the two quantities of 0.37 − 0.71 and 0.35 − 0.61, respectively. The errors are rather large because the reddening path in the color-color diagram runs more or less parallel to the stellar locus. The green dots in the right panel of Fig. 8 show the relation between (r − i)P1 and EB − V,
The derived range of EB − V agrees with the above quoted result of Lallement et al. (2018) at the position of J1832 for distances between 1 and 2 kpc. The SED of the secondary star of J1832 de-reddened with EB − V = 0.54 is displayed in the center panel of Fig. 8 (black solid circles). The implied spectral type of the secondary star depends on the employed algorithm. Covey et al. (2007), for instance, used “the Hammer” (Kesseli et al. 2020), which relates (r − i)P1 = 0.48 and its confidence range to K6.0 and K3.9 to K7.5. The spectral types assigned to the same (r − i)P1 in the system of Pecaut & Mamajek (2013)6 are about half a subclass later.
4.2. Limit on the photospheric flux of the WD
The minute excess of the out-of-eclipse flux over the eclipse flux in the low-state observation of 4 August 2019 (left panel of Fig. 4, blue dots) allowed us to set an upper limit on the WL photospheric flux of the WD. The excess of the flux at orbital phases ϕorb = − 0.065 to −0.032 and ϕorb = 0.032 to 0.038 over the eclipse flux between ϕorb = − 0.0295 and +0.0295 corresponds to a WL AB magnitude of w = 21.84 ± 0.20, which qualifies approximately also as an r magnitude (see Sect. 2). A 2σ upper limit to the WD is r > 21.44. On 17, 20, and 27 July 2021, J1832 was found in a low state again and observed in the g-band through the eclipse. In all three nights, the flux difference between outside and inside the eclipse was consistent with zero and a combined 2σ upper limit for the WD is g > 21.69.
4.3. Overall spectral energy distribution of J1832
In the left panel of Fig. 8 we provide an overview of the SED of J1832 outside eclipse as well, based on a mixture of simultaneous and nonsimultaneous flux measurements of our own and from public catalogs accessed mainly via the Vizier SED tool7. The external sources included the NOMAD catalog (Zacharias et al. 2005), the SkyMapper catalog (Wolf et al. 2019), the Pan-STARRS catalog (Chambers et al. 2017), and the Gaia catalog (Gaia Collaboration 2021). No entry was found in the GALEX catalog bianchietal17. The object is too faint for 2MASS (Skrutskie et al. 2006), but is listed in the UKIRT Galactic plane survey (Lucas et al. 2008). The dynamic range of the observed fluxes increases toward short wavelengths. We take the upper envelope to the observed spectral flux Fν as representative of the high state of the system and obtain the accretion-induced spectral flux by correcting it for the secondary star. The optical component of the accretion-induced flux is obtained by de-reddening it with the selected EB − V and integrating it from the Balmer edge into the infrared. The center panel shows that the spectral flux de-reddened with the same EB − V = 0.54 as the eclipse fluxes is slowly rising toward short wavelengths. For this choice of EB − V, the optical component of the accretion-induced flux is Fopt = 7.4 × 10−12 erg cm−2s−1. In the models of Sect. 5, we use Fopt de-reddened with the free parameter EB − V. Well studied IPs, as EX Hya (Eisenbart et al. 2002, their Fig. 3) or V1223 Sgr (Beuermann et al. 2004, their Fig. 2) have SEDs that extend to the Lyman edge, with an integrated de-reddened ultraviolet flux that exceeds the optical flux by a factor of about two to three and considering the X-ray regime, the total accretion induced flux can exceed the optical flux by a still higher factor. J1832 was not detected in the few days of coverage in the ROSAT All Sky Survey (Boller et al. 2016), which does not argue against J1832 being an X-ray source, considering its frequent low states, the sizable extinction, and the fact that there is no pointed ROSAT observation of the region. J1832 is not an INTEGRAL hard X-ray source (Krivonos et al. 2017)8 and searching the NASA HEASARC archive9 at the position of J1832, gave no entry for any earlier X-ray mission. It is not an obvious bright source in the preliminary eROSITA All Sky Map (Predehl et al. 2021)10 with its 15′×15′ pixels. It may still have been detected in the survey, of which a source list is not yet available. We return to the overall SED in the context of estimating the accretion rate (Sect. 5.4).
5. System parameters
5.1. Photometric limit on M2
In the absence of spectroscopy, the information on the system parameters is limited. Some important information, however, can be drawn from the measured i-band magnitude of the secondary star. In particular, it allows M2 to be calculated as a function of the distance, d, with a minor dependence on EB − V. The quantities are related by the surface brightness Si = Mi + 5 lg(R2/R⊙), where Mi is the absolute magnitude in the i-band and R2 the stellar radius. Using Mamajek’s table of the stellar locus (footnote 5) with colors transformed to the Pan-STARRS 1 (P1) system, we expressed the surface brightness for the restricted range of (r − i)P1 = 0.3 - 0.8 as
With i − Mi = 5 lg d − 5 and d in pc, R2 in solar units becomes
Since J1832 is accreting, the secondary star must fill its Roche lobe and is necessarily bloated if of low mass. We adopted the model radii of Baraffe et al. (2015) for main-sequence stars of solar composition at an age of 5 Gyr and approximated them by a power law RBHAC/R⊙ = a(M2/M⊙)b with a = 0.93 and b = 0.96 for the mass range of 0.15 − 0.8 M⊙. Secondary stars in normal CVs are known to exceed these radii by a few percent (Knigge et al. 2011, see also Beuermann et al. 2017). We expressed the stellar radii in our models as R2 = f1f2f3RBHAC, with f1 = 1.020 and f2 = 1.045 accounting for starspots and the effect of rotation and Roche geometry, respectively (Knigge et al. 2011). The factor f3 describes any additional bloating required to make the secondary star fill its lobe. We used Paczynski’s approximation R2, R = 0.462(q/(1 + q)1/3a for the mean volume filling Roche radius, which has the advantage that with the binary separation a eliminated with help of Kepler’s third law, one obtains an expression that is independent of q and M1
Replacing R2/R⊙ with Eqs. (9), (8), and (7), M2 can be calculated for given d and EB − V. For instance, for a distance of 1600 pc and the best-fitting extinction of 0.54 mag, M2 = 0.29 M⊙. To fill its Roche-lobe, this star would be bloated by a factor f3 = 2.27 over its main-sequence radius. An unevolved secondary star of 1.0 M⊙ as expected for a standard CV at P ≃ 9 h would require a distance of 2500 pc, near the upper end of the confidence range of the Gaia EDR3, d = 1254 − 2847 pc (Bailer-Jones et al. 2021).
5.2. Grid of photometrically accepted models
We computed a grid of dynamical models of J1832 that extended over d = 1200 − 2900 pc and EB − V = 0.37 − 0.71 with step widths of 10 pc and 0.01, respectively. Each bin is characterized by the single value of M2(d, EB − V) that matches the observed i = 18.98 (Table 4) and contains models for M1 between 0.40 and 1.30 M⊙ with a step width of 0.01 M⊙. As side conditions we required q < 0.85, which ensures stable mass transfer, and M2 > 0.16 M⊙, which accounts for the strict lower limit to M2 in evolving CVs with 9 h orbital period in the binary population study (BPS) of Kalomeni et al. (2016), as defined by their Eq. (12). For each individual model, we calculated a wide range of system parameters. Results are provided in Cols. 3 − 5 of Table 5. A coarser version of the grid with steps of 0.04 in EB − V and 100 pc in d was used for Fig. 9. The left panel shows all photometrically accepted models in the d − EB − V plane as dots or circled dots. They cover a distance range that stays well within the Gaia EDR3 confidence limits (Bailer-Jones et al. 2021): There are no accepted models at d < 1270 pc, because M2 would fall below 0.16 M⊙, and none at d > 2500 pc, because q > 0.85 or M1 > 1.3 M⊙ would be required. The M2 values quoted in the figure are the averages of M2(d, EB − V) over EB − V for the selected distance. The quoted spectral types are obtained from EB − V via (r − i)P1 and do not depend explicitly on d. The center panel shows the accepted models in the Teff, 2−log(L2/L⊙) plane, the Hertzsprung-Russell (HR) diagram of the secondary star. The right panel shows the theoretical results on the q dependence of the period ratio Pspin/Porb together with the observed level in J1832(green lines). These results are now discussed in turn.
 |
Fig. 9. Left: confidence range for models of the secondary star permitted by the photometric SED in the eclipse of J1832 (dots and encircled dots). All models have distances within the error bounds of Gaia EDR3 (footnote 3). The red curve represents the best estimate of the extinction along the line of sight to J1832 (Lallement et al. 2018). Center: position of the secondary star of J1832 in its HR diagram. The dots indicate all photometrically accepted models. The encircled dots denote here and in the left panel the subsample with luminosity L2 not exceeding the limit set by the BPS of Kalomeni et al. (2016) (red curve). No model should be found above and to the right of the red curve (see text). The yellow-filled square in both panels marks the mean position of this subsample. The dashed blue curves from Kalomeni et al. (2016) indicate two evolutionary tracks along which J1832 may evolve. Also shown are the position of the 9 h binary KIC 5608384 of Yu et al. (2019) (magenta dot) and its suggested evolutionary track that leads to the graveyard of ultracompact binaries (magenta dashed curve). Right: period ratio Pspin/Porb vs. mass ratio q. The horizontal green lines indicate the observed period ratio of J1832. The open and filled circles denote the theoretical period ratios from the analytical theory of K93 and the numerical calculations of WK95. |
Mean values and ranges of parameters of all photometrically accepted models (Cols. 3–5) and those in spin equilibrium with Pspin = 3484 s (Cols. 6–8; see text for explanation).
5.3. J1832 in the Hertzsprung-Russell diagram
Using the stellar-locus tables of Mamajek (Pecaut & Mamajek 2013, see footnote 5) and Mann et al. (2015), we constructed the color dependence of the effective temperature Teff, 2 of the secondary star as a function of (r − i)P1. Each of our models is tagged by a value of (r − i)P1 and a value of Teff, 2. Combined with R2 from Eq. (9), we calculated log(L2/L⊙) for all models and thereby their position in the HR diagram of the secondary star. The center and left panels of Fig. 9 show the same photometrically accepted models as small black dots. The center panel includes, in addition, results of the BPS of Kalomeni et al. (2016). The red curve indicates the strict upper limit to the luminosity L2 of the secondary star as a function of Teff, 2, taken from their Fig. 20. Our photometrically accepted models are distributed across this line and for about 50% of them the secondary star is too bright by up to a factor of 2.6. The encircled dots indicate the luminosity-restricted sample of models that are consistent with the Kalomeni et al. (2016) BPS calculations, allowing for a 10% uncertainty and spillover in L2. We list the mean values and standard deviations of all parameters of the luminosity-restricted sample in Cols. 6 and 7 of Table 5. The centroid of this restricted sample is indicated by the yellow squares and given by d = 1596 ± 208 pc, EB − V = 0.58 ± 0.09, M2 = 0.32 ± 0.14 M⊙, Teff, 2 = 4185 ± 136 K, and log(L2/L⊙) = − 0.92 ± 0.15, where the quoted errors represent the standard deviations of the distributions and we consider all models a priori as equally probable. The strongly skewed M2 distribution of the luminosity-restricted sample still contains M2 values up to 1.0 M⊙, but all models with secondary masses M2 more than 2 σ above the mean, or M2 > 0.60 M⊙, lie in the extended tail of the distribution at d > 1980 pc in the left panel and at log(L2/L⊙) > − 0.68 in the center panel of Fig. 9. This tail contains 5% of the models. We consider them correspondingly unlikely and take this as an indication of a low-mass secondary star in J1832, with M2 lower than expected for a normal CV of 9 h orbital period.
The two dashed blue curves in the center panel of Fig. 9 show two selected evolutionary tracks of CVs from the BPS calculations of Kalomeni et al. (2016, their Figs. 20 and 1), a normal one with a secondary near the main sequence that evolves close to the red line and a binary with an evolved secondary of lower mass that departs from that track and heads for the lower left of the diagram into the general region occupied by ultracompact binaries. They represent possible evolutionary scenarios for J1832. In the former case, J1832 would probably evolve into a polar, and in the latter, it might follow the 9 h binary KIC 5608384 of Yu et al. (2019) (magenta dot and magenta dashed curve) to become an ultracompact binary, with the decisive difference of one component being highly magnetic.
5.4. Accretion rate and WD temperature
We have no good handle yet on the accretion rate of J1832, but it is useful to obtain at least an estimate. Assuming isotropic emission, the accretion luminosity is Lacc ≃ 4πd2Facc and the accretion rate is estimated as Ṁ ≃ LaccR1/GM1. So far, only the optical part Fopt of the accretion-induced high-state flux Facc, is available. We identify it with the upper envelope to the observed (reddened) fluxes in the left panel of Fig. 8. Integrated from the Balmer edge into the infrared they give Fopt, red = 2.5 × 10−12 erg cm−2s−1. For each model, we obtained the individually de-reddened value of Fopt and estimated Facc = (1 + fuvx) Fopt with a correction factor fuvx that accounts for the still missing UV and X-ray fluxes. We considered two cases, of which case A with fuvx = 0 or Facc ≡ Fopt represents the absolute minimum. Guided by the well-studied IPs EX Hya and V1223 Sgr (Eisenbart et al. 2002; Beuermann et al. 2004), we adopted case B with fuvx = 2.0 or Facc = 3.0 × Fopt, accounting for an ultraviolet flux as in other IPs and a moderate X-ray flux. In what follows we use case B in the attempt to obtain an overview of the system parameters. The range of case-B accretion rates is listed in line 19 of Table 5.
The secular mean accretion rate ⟨Ṁ⟩10 of systems with a sufficiently old WD averaged over its Kelvin-Helmholtz timescale determines its effective temperature by compressional heating,
(Townsley & Gänsicke 2009), where ⟨Ṁ⟩10 is in units of 10−10 M⊙ yr−1M1 in solar units. We estimated the current WD temperature by replacing ⟨Ṁ⟩10 in Eq. (11) with the case-B accretion rate for each model. The resulting mean temperature of all photometrically accepted models is 27 kK (line 15 of Table 5). The corresponding reddened WD AB magnitudes are r = 22.56 − 25.16 and g = 22.57 − 25.39, which are all at least 1 mag fainter than our observed 2σ upper limits of 21.44 and 21.69, respectively (Sect. 4.2). The faintest WDs are found in the most distant models with a primary mass of 1.3 M⊙.
5.5. Orbital inclination
We estimated the inclination of J1832, using the Roche lobe parameters x1 = b/a, x4, y4, z6, and 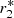 in the notation of Kopal (1959)11, expressed as functions of the mass ratio q. For a given duration of the eclipse in phase units, the orbital inclination is a function of q (e.g., Horne 1985). For J1832, the inclination is 87
in the notation of Kopal (1959)11, expressed as functions of the mass ratio q. For a given duration of the eclipse in phase units, the orbital inclination is a function of q (e.g., Horne 1985). For J1832, the inclination is 87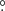 6, 81
6, 81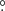 8, 77
8, 77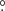 4, or 73
4, or 73 3 for q = 0.1, 0.2, 0.4, or 0.8, respectively. The path of the WD across the shadow of the secondary star defines an arced section with a chord length ρ and a height σ, which are also functions of q. For the luminosity-selected sample in Fig. 9 (encircled dots), the mean inclination is 78
3 for q = 0.1, 0.2, 0.4, or 0.8, respectively. The path of the WD across the shadow of the secondary star defines an arced section with a chord length ρ and a height σ, which are also functions of q. For the luminosity-selected sample in Fig. 9 (encircled dots), the mean inclination is 78 4 and the full range is
4 and the full range is 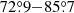 (Table 5). At eclipse center, the WD has dived into the shadow of the secondary star to a mean depth σ = 20.6Rwd (full range 6.2 − 58.2Rwd). The magnetically guided part of the accretion stream reaches a similar height above the orbital plane and, depending on the details of the accretion geometry, only a small part of the stream emission escapes eclipse. Hence, the system qualifies as deeply eclipsing.
(Table 5). At eclipse center, the WD has dived into the shadow of the secondary star to a mean depth σ = 20.6Rwd (full range 6.2 − 58.2Rwd). The magnetically guided part of the accretion stream reaches a similar height above the orbital plane and, depending on the details of the accretion geometry, only a small part of the stream emission escapes eclipse. Hence, the system qualifies as deeply eclipsing.
5.6. The magnetic moment of the WD
In an IP, matter accretes to the magnetic field of the WD near the magnetospheric radius, rmag, which is usually quoted as a fraction of the Alfvén radius, ralf. The latter is obtained by equating the ram pressure of the infalling matter for isotropic accretion with the magnetic pressure of a dipolar field. The rapid drop of the magnetic pressure with increasing radius as r−6 implies that the usual estimate of rmag ≃ 0.5 ralf cannot be severely wrong. The factor 0.5 accounts for the difference between spherical and equatorial accretion (Frank et al. 1975), and results in
For each of our models of J1832, we obtained an estimate of the magnetic moment μ30 of the WD in units of 1030 G cm3 by using the case-B accretion rate in units of 10−10 M⊙ yr−1, the WD mass in solar units, and equating rmag with the corotation radius 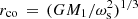 . For the sample of models restricted by the photometry and luminosity of the secondary star (encircled dots in Fig. 9), we found a mean magnetic moment μ = (1.6 ± 0.3) × 1034 G cm3 (Table 5, line 24), which is at the upper limit of the range discussed for IPs (Norton et al. 2004) and is more characteristic of a polar. The implied field strength would be typical of or exceed that of a polar as well.
. For the sample of models restricted by the photometry and luminosity of the secondary star (encircled dots in Fig. 9), we found a mean magnetic moment μ = (1.6 ± 0.3) × 1034 G cm3 (Table 5, line 24), which is at the upper limit of the range discussed for IPs (Norton et al. 2004) and is more characteristic of a polar. The implied field strength would be typical of or exceed that of a polar as well.
5.7. Spin equilibrium
Most IPs are expected to accrete in spin equilibrium (Ṗspin = 0), because a mismatch between the velocities of matter and field at the accretion radius racc leads to rapid spin-up or spin-down of the WD, ensuring rmag ≃ racc ≃ rco most of the time. Matter leaving L1 with a specific angular momentum jL1 = b2Ωo will settle into a Keplerian orbit at the circularization radius rci with jci = (GM1rci)1/2 = jL1ζ, giving rci = (1 + q)(b/a)4ζ2. Here, b is the separation between the WD and L1, Ωo = [GM1(1 + q)/a3]1/2 is the orbital frequency, and ζ(q) ≃ 0.84 − 0.89 for q = 1.0 − 0.1, respectively, is the fraction of the angular momentum at L1 that is preserved at rci, when the pull of the secondary star or the non-sphericity of the problem is accounted for (Flannery 1975; Lubow & Shu 1975). For rmag ≃ rco ≳ rci, a viscous disk cannot form and the WD accretes from the stream, either directly or after circularization. This is obviously the case in J1832: the entire sample of our dynamical models that match the photometry of J1832 (dots and circled dots in Fig. 9) have rco > rci (Table 5, lines 13 to 17).
King & Lasota (1991) argued that the accretion of jci = jL1ζ in spin equilibrium implies rco ≃ rci as well, leading to
where b/a ≃ 0.500 − 0.227log q (Plavec & Kratochvil 1964). They identified the preferred occurrence of IPs near Pspin/Porb = 0.10 with stream-fed accretion in spin equilibrium. A period ratio of 0.10, however, or larger as in J1832, requires q ≲ 0.15, which is much lower than the typical q ≈ 0.6 for nine IPs above the period gap that have measured component masses (Ritter & Kolb 2003). The likely cause is that rco and rci do not agree as closely as assumed. As a consequence, a reliable value of q for J1832 cannot be obtained from Eq. (13).
The relation between rco and rci in spin equilibrium is determined by the exchange of angular momentum between matter and field inside and outside rco, which may take place over a substantial radial interval. An example is the accretion from a viscous disk. Another is the accretion of a stream of diamagnetic blobs of matter studied analytically by King (1993) (henceforth K93) and numerically by Wynn & King (1995) (henceforth WK95). Such blobs plunge deep into the magnetosphere on quasi-ballistic orbits, experience a drag by the excitation of Alfvén waves, when they move across field lines and “pluck them like violin strings” (Drell et al. 1965), until they are broken up by Kelvin-Helmholtz instabilities, invaded by the field, and accreted (Arons & Lea 1980). K93 made the problem analytically tractable by treating the blobs as test particles, disregarding changes in their internal state, neglecting viscous collisions between them, assuming spherical symmetry (ζ = 1), selecting a simple parameterization of the drag, and describing the blob orbits as Kepler ellipses that slowly change under the influence of the drag. He described the drag as F = − k0 r−nυ, where, υ is the velocity of the blob relative to the field and the integer n ≥ 0 regulates the radial dependence of the drag. The azimuthal motion of a blob is typically accelerated near apastron and decelerated near periastron, which circularizes the orbit. K93 expressed the equilibrium period ultimately as a function of n and q (his Eq. (38) ff). The relation between the characteristic radii becomes rci = (f/g)2/3 rco, with functions f(q) and g(q) for a given parameter n. This relation bears a formal similarity to 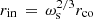 for disked systems (Wang 1995), with ωs the fastness parameter (not to be mixed up with the spin angular velocity). In both cases a competition exists between orbits that accelerate the magnetosphere inside rco and decelerate it outside rco. The decisive dissimilarity is the absence of viscous inter-blob interactions in the model of K93 and WK95, which holds as long as the blobs do not accumulate and form a nascent disk. Consequently, the radial transport of angular momentum, characteristic of an accretion disk, is absent in the model of K93 and leads to a relation between Pspin/Porb and q (his Eq. (37)),
for disked systems (Wang 1995), with ωs the fastness parameter (not to be mixed up with the spin angular velocity). In both cases a competition exists between orbits that accelerate the magnetosphere inside rco and decelerate it outside rco. The decisive dissimilarity is the absence of viscous inter-blob interactions in the model of K93 and WK95, which holds as long as the blobs do not accumulate and form a nascent disk. Consequently, the radial transport of angular momentum, characteristic of an accretion disk, is absent in the model of K93 and leads to a relation between Pspin/Porb and q (his Eq. (37)),
where we have added the factor ζ3 to correct approximately for the neglect of the gravitational pull of the secondary star. The functions f(q) and g(q) are given by K93 and WK95 for n = 0, 2, and 3. For n = 1, g/f = 1. The numerical study of WK95, treating the particle orbits correctly in the nonspherical geometry, gave period ratios that consistently exceeded the analytical results, less so for n = 0 than for positive n. Unfortunately, only two sets of results for Pspin/Porb versus q were published.
In the right panel of Fig. 9, we compare the q dependence of Pspin/Porb obtained from the analytical and numerical calculations of K93 and WK95 for n = 0–2 with the level of the observed Pspin/Porb of J1832 (green lines). As noted in Eq. (14), the correction ζ(q) from Lubow & Shu (1975) has been applied to the analytical period ratios, while the numerical ones correctly account for the non-sphericity of the gravitational field. We note that the numerical values of ζ displayed in Fig. 1 of King et al. (1990) show the opposite trend from those of Lubow & Shu (1975), which leads to a period ratio in WK95 that varies little with q. The numerical results exceed the analytical ones by about 30% for n = 0 and by more for n = 2. The analytical n = 0 model and the numerical n = 0 and n = 2 models best match the observed period ratio of J1832. Hence, the K93 and WK95 models support the nature of J1832 as a stream-fed IP in spin equilibrium, but they are not sufficiently accurate to allow a determination of q from Pspin/Porb.
6. Discussion
J1832.4-1627 is the first deeply eclipsing stream-fed IP. It is disk-less in the sense that it lacks a viscous (i.e., luminous) accretion disk. It combines two properties that are extremely rare within the class. There are only five IPs that display deep eclipses of the central accretion region surrounding the WD, the two long-known systems DQ Her and XY Ari, V902 Mon=IPHAS J0627 (Aungwerojwit et al. 2012), Nova Sco 1437 (Potter & Buckley 2018, and references therein), and V597 Pup, the now faint remnant of Nova Puppis 2007 Warner & Woudt (2009), and all of them accrete via disks. Stream-fed systems are even less common and none of the candidates is eclipsing. The identification of a stream-fed system may be ambiguous because of the phenomenon of stream overflow that occurs also in disked systems (Lubow 1989). The best and so far only example of a stream-fed IP is V2400 Oph (Buckley et al. 1995, 1997; Hellier & Beardmore 2002; Joshi et al. 2019), which, however, is seen at an inclination of only i ∼ 10°, preventing a measurement of its component masses. The combination of a deep eclipse and a stream-fed and seemingly disk-less accretion geometry in J1832 is unique with important prospects for follow-up studies.
Our Fourier and periodogram analyses gave a clear signal at a single period Pobs = 3911 s. Our data contain no hint for identifying it with either the spin or the synodic period. If a stream of tenuous matter impinges on the magnetosphere, is instantaneously permeated by the field, and accreted on the spot, the resulting signal will be pulsed at the synodic (beat) period. Such matter is generally hold responsible for the emission of hard X-rays. Denser blobs of matter, on the other hand, continue on ballistic orbits in the magnetosphere and are carried around by the field until threaded. They lose the memory of the orbital phase of impact and the resulting emission is likely pulsed on the spin period. For a structured stream, covering a wide range of densities, a mixture of spin and synodic periods and their side bands may be expected (Warner 1986), and a prediction for an individual wavelength band is not easily made. In the stream-fed IP V2400 Oph, the X-ray flux is pulsed at the synodic and the spin period (Buckley et al. 1997; Joshi et al. 2019), the optical circularly polarized flux appears at the spin period (Buckley et al. 1995), and the optical continuum preferentially at the synodic period (Hellier & Beardmore 2002). Performing a hard X-ray study and optical circular spectropolarimetry are, therefore, the most obvious next steps for further study of J1832.
There is preliminary, and certainly incomplete, evidence that J1832 may not be a strong X-ray source (Sect. 4.3). With an interstellar atomic hydrogen column density NH ≃ 5 × 1021 H-atoms cm−2, based on EB − V ≃ 0.54 (Nguyen et al. 2018), X-rays with E < 1 keV would be absorbed. A strong soft X-ray component was observed in some IPs (e.g., PQ Gem, V405 Aur, and UU Col), and such a source would not be detectable in J1832. The spectroscopic detection of He IIλ4686 line emission would, however, demonstrate the presence of such a source. Other IPs emit hard X-rays, possibly reflecting differences in the accretion geometry and in the density structure of the accreted matter. For example, Nova Sco 1437 and XY Ari are strong hard X-ray sources, while IPHAS J0627 is faint. Aungwerojwit et al. (2012) argued that the X-ray emission region in IPHAS J0627 may be obscured by the inner edge of the disk, but this may not be the whole story.
The lack of a luminous disk and the observed stream flipping in J1832 are not short-lived transitory phenomena. The evidence for the stream flipping is based on the pulse phase dependence of the eclipse centers and the orbital phase dependence of the pulse minima observed in all three observing seasons (Sect. 3.4). These results strongly suggest that J1832 is stream-fed, a conclusion that is supported also by the fact that all of our photometrically accepted models have rco > rci and, hence, lack a classical viscous disk. The accretion process is regulated by the hierarchy between three characteristic timescales, the dynamical (Kepler) timescale tkep, the threading timescale tmag, and the viscous timescale tvis. On-the-spot accretion takes place for tmag ≪ tkep, while the matter is circularized before being accreted for tmag ≫ tkep, assuming in both cases that tvis is much longer. A theory for the former case that allows for a structured stream is not available. A theory for the latter, assuming the accretion of dense diamagnetic blobs of matter, was devised by K93 and WK95 and discussed in Sect. 5.7. In their model, the matter is circularized by the drag it experiences when crossing field lines. It does not spread into a disk as long as tmag stays sufficiently short and the blobs do not accumulate and get viscously into contact. Because of the similarities with disk theory, K93 insisted on calling his accretion mode stream-fed and not disk-less. A relation of the form of Eq. (14) exists for stream-fed, but not for disk-fed systems. It is, however, burdened by the factor g/f in the theory of K93 or a corresponding factor in any alternative theory.
The factual absence of viscous interaction would render any ring-like structure cool. On the other hand, if it is irradiated and heated by a central X-ray source, it may be difficult to hide it at optical wavelengths. In any case, the presence of Balmer and helium line emission may help to trace the geometry of the magnetically guided stream and the potential presence of an accretion ring. K93 estimated that individual blobs may survive in the vicinity of rco for up to ten orbits around the WD, before they lose their identity, are invaded by the field, and accreted. We estimated the times scales tdrag of Drell et al. (1965) and K93 and tevap of Arons & Lea (1980) for the parameters of J1832 and obtained smaller numbers comparable to one pulse period of the WD, which is not enough to establish a ring, but sufficient for the matter to lose the memory of the impact point. Whether a well developed ring exists in J1832 and whether the synodic or spin period is preferred for the optical continuum emission are, therefore, open questions.
Of the stellar components, we have a secure photometric detection of the secondary star at the center of the eclipse, with a Pan-STARRS i-band AB magnitude of 18.98(3) and a spectral type ∼K6. The mean M2 of the models that fit the photometry (Table 5, Col. 7) is 0.32 M⊙ and the 2σ range is 0.16 − 0.60 M⊙. The secondary star is bloated over a main sequence star by a factor f3 = 1.4 − 3.3 (Table 5). This finding suggests that J1832 may have previously passed through a phase of thermal timescale mass transfer, which would determine its future evolution as well. From its present position in the HR diagram of the secondary star (Fig. 9, center panel), the system may either still evolve into a polar or end up as an ultracompact binary, as predicted also for the nonmagnetic CV KIC 5608384 (Yu et al. 2019), but in the present case one of the final degenerate components would be strongly magnetic.
Detecting the WD in J1832 will not be a trivial task, given the 2σ upper limits to its reddened (observed) magnitude of g > 21.69 and r > 21.44 (Sect. 4.2). Our dynamical models suggest probable magnitude ranges of g = 23.8 ± 0.6 and r = 23.7 ± 0.6, but the WD may reach 25 mag in both colors if the WD mass is as high as 1.3 M⊙. The quoted magnitudes are based on the radii of WDs with a thick hydrogen envelope (Althaus & Benvenuto 1998; Renedo et al. 2010) and effective temperatures computed from Eq. (11) with the long-term accretion rate replaced by the current case-B rate (Sect. 5.4). They disregard accretion-heated hot polar caps and can only be approximate. The dK6 secondary star with r = 18.98 can be traced spectroscopically by its photospheric absorption lines or by emission lines from its face heated by the WD. Given the frequent low states, a phase-resolved study appears feasible. Tracing the motion of the WD will be more challenging. The predicted velocity amplitudes K1 and K2 of primary and secondary star are quoted in Table 5.
The estimated magnetic moment of the WD in J1832 of μ ≃ 1.6 × 1034 G cm3 suggests a surface field strength typical of polars (Norton et al. 2004). Hence, studying the magnetic field structure by means of spectropolarimetry and cyclotron spectroscopy seems a realistic prospect. Besides the high magnetic moment, the comparatively low accretion rate in the high state, assuming case-B to be valid, is reminiscent of long-period polars (Townsley & Gänsicke 2009). While low in comparison with nonmagnetic CVs, the case-B accretion rate substantially exceeds that expected from gravitational radiation.
7. Outlook
We have presented a detailed photometric study of the first deeply eclipsing stream-fed IP that demonstrably lacks a viscous accretion disk. The grizy photometry through the total eclipse yielded the magnitude and spectral type of the moderately evolved secondary star, while the WD has so far remained undetected. The Milky Way object is tolerably absorbed at a distance of about 1.6 kpc and is observable from both hemispheres. Key follow-up observations include: (i) a hard X-ray study and optical circular polarimetry to identify the spin period; (ii) phase-resolved optical spectroscopy to measure the velocity structure of the stream and the HeIIλ4686 emission line flux; (iii) high-cadence high-state blue photometry through the eclipse to obtain information on the accretion geometry; (iv) the same in a deep low state to measure the diameter and mass of the WD; (v) high-resolution spectroscopy of the K star in a low state; and (vi) circular spectropolarimetry to measure the strength and structure of the magnetic field of the WD. A dedicated theoretical study is needed to understand its past and future evolution.
http://www.pas.rochester.edu/~emamajek/EEM_dwarf_UBVIJHK_colors_Teff.txt, version 2019.3.22.
Provided by the Centre de Données astronomiques de Strasbourg http://vizier.unistra.fr/vizier/sed/
With the WD at the origin and the x axis connecting the two stars, x1 measures the distance to the L1 point, x4 ≃ 1 locates the position along the x axis of maximum excursion of the lobe, y4 is the lobe position in the orbital plane and z6 in the direction of the rotational axis, and  is the equivalent volume-filling radius of the secondary star.
is the equivalent volume-filling radius of the secondary star.
Acknowledgments
We thank the anonymous referee for a very helpful report that improved the paper. We thank Axel Schwope for reading an earlier version of the paper and providing useful comments, Tim-Oliver Husser for essential help with using the MONET/S telescope for this project, and Boris Gaensicke for help in accessing the UKIRT archive. We thank the European Space Agency (ESA) for supporting our project within the Near-Earth Segment of the Space Situational Awareness Program of ESA under contract number 4000116155/15/D/AH (P2-NEO-VIII), by assigning observation time at the Calar Alto Schmidt telescope. We thank the Faulkes Telescope Project, Cardiff/UK, as partner of the Las Cumbres Observatory (LCO) for providing telescope time without much bureaucracy on sometimes very short notice. We also thank the LCO for Director’s Discretion Time for using MuSCAT3 at the Faulkes Telescope North on Maui, HI, an instrument that was developed by the Astrobiology Center under financial supports by JSPS KAKENHI (JP18H05439) and JST PRESTO (JPMJPR1775). Part of the photometric data were collected with the MONET/S telescope funded by the Alfried Krupp von Bohlen und Halbach Foundation, Essen, and operated by the Georg-August-Universität Göttingen and the South African Astronomical Observatory. We made use of the PanSTARRS data base, the UKIRT Galactic Plane Survey, and further sources accessed via the VizieR Photometric viewer operated at CDS, Strasbourg, France.
References
- Allan, A., Hellier, C., & Beardmore, A. 1998, MNRAS, 295, 167 [CrossRef] [Google Scholar]
- Althaus, L. G., & Benvenuto, O. G. 1998, MNRAS, 296, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [Google Scholar]
- Arons, J., & Lea, S. M. 1980, ApJ, 235, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Aungwerojwit, A., Gänsicke, B. T., Wheatley, P. J., et al. 2012, ApJ, 758, 79 [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., et al. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., et al. 2021, AJ, 161, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577 [Google Scholar]
- Belle, K. E., Howell, S. B., Sion, E. M., et al. 2003, ApJ, 587, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., & Osborne, J. P. 1988, A&A, 189, 128 [NASA ADS] [Google Scholar]
- Beuermann, K., & Reinsch, K. 2008, A&A, 480, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., & Reinsch, K. 2013, A&A, 555, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Harrison, T. E., McArthur, B. E., et al. 2004, A&A, 419, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Burwitz, V., Reinsch, K., et al. 2017, A&A, 603, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buckley, D. A. H., Sekiguchi, K., Motch, C., et al. 1995, MNRAS, 275, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Buckley, D. A. H., Haberl, F., Motch, C., et al. 1997, MNRAS, 287, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2017, VizieR Online Data Catalog: II/349 [Google Scholar]
- Covey, K. R., Ivezić, Ž., Schlegel, D., et al. 2007, AJ, 134, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Drell, S. D., Foley, H. M., & Ruderman, M. A. 1965, Phys. Rev. Lett., 14, 171 and J. Geophys. Res., 70, 3131 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [Google Scholar]
- Eisenbart, S., Beuermann, K., Reinsch, K., et al. 2002, A&A, 382, 984 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrario, L., & Wickramasinghe, D. T. 1999, MNRAS, 309, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Flannery, B. P. 1975, ApJ, 201, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. Accretion Power in Astrophysics, 3rd edn. (Cambridge University Press), 2002 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J.-M., King, A. R., & Lasota, J.-P. 1986, MNRAS, 218, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, T. E., & Campbell, R. K. 2016, MNRAS, 459, 4161 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., & Beardmore, A. P. 2002, MNRAS, 331, 407 [CrossRef] [Google Scholar]
- Honeycutt, R. K., & Kafka, S. 2005, MNRAS, 364, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Hoogerwerf, R., Brickhouse, N. S., & Mauche, C. W. 2004, ApJ, 610, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1985, MNRAS, 213, 129 [NASA ADS] [Google Scholar]
- Joshi, A., Pandey, J. C., & Singh, H. P. 2019, AJ, 158, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Kalomeni, B., Nelson, L., Rappaport, S., et al. 2016, ApJ, 833, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kesseli, A., West, A., Veyette, M., et al. 2020, Astrophysics Source Code Library [record ascl:2002.011] [Google Scholar]
- King, A. R. 1993, MNRAS, 261, 144 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., & Lasota, J.-P. 1991, ApJ, 378, 674 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., & Wynn, G. A. 1999, MNRAS, 310, 203 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Frank, J., & Ritter, H. 1985, MNRAS, 213, 181 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Frank, J., & Whitehurst, R. 1990, MNRAS, 244, 731 [NASA ADS] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [Google Scholar]
- Kopal, Z. 1959, Close binary systems, 135 [Google Scholar]
- Krivonos, R. A., Tsygankov, S. S., Mereminskiy, I. A., et al. 2017, MNRAS, 470, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F. 2020, MNRAS, 491, 1820 [NASA ADS] [Google Scholar]
- Lipkin, Y. M., Leibowitz, E. M., & Orio, M. 2004, MNRAS, 349, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefield, C., Mukai, K., Mumme, R., et al. 2015, MNRAS, 449, 3107 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefield, C., Garnavich, P., Mukai, K., et al. 2019, ApJ, 881, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefield, C., Scaringi, S., Garnavich, P., et al. 2021, AJ, 162, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H. 1989, ApJ, 340, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, P. W., Hoare, M. G., Longmore, A., et al. 2008, MNRAS, 391, 136 [Google Scholar]
- Mann, A. W., Feiden, G. A., Gaidos, E., et al. 2015, ApJ, 804, 64 [CrossRef] [Google Scholar]
- Nguyen, H., Dawson, J. R., Miville-Deschênes, M.-A., et al. 2018, ApJ, 862, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. J., Wynn, G. A., & Somerscales, R. V. 2004, ApJ, 614, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. J., Butters, O. W., Parker, T. L., et al. 2008, ApJ, 672, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. 1994, PASP, 106, 209 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Plavec, M., & Kratochvil, P. 1964, Bull. Astron. Inst. Czechoslovakia, 15, 165 [NASA ADS] [Google Scholar]
- Potter, S. B., & Buckley, D. A. H. 2018, MNRAS, 473, 4692 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [Google Scholar]
- Ritter, H., & Kolb, U. 2003, A&A, 404, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosen, S. R., Mason, K. O., & Cordova, F. A. 1988, MNRAS, 231, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, E., & Breitenstein, P. 2019, BAV-Rundbrief, 68, 187 [Google Scholar]
- Sesar, B., Hernitschek, N., Mitrović, S., et al. 2017, AJ, 153, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, N., Reinsch, K., Beuermann, K., et al. 1989, A&A, 225, 97 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Gänsicke, B. T., Marsh, T. R., et al. 2007, MNRAS, 378, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [Google Scholar]
- Townsley, D. M., & Gänsicke, B. T. 2009, ApJ, 693, 1007 [Google Scholar]
- Völschow, M., Schleicher, D. R. G., Banerjee, R., & Schmitt, J. H. M. M. 2018, A&A, 620, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y.-M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
- Warner, B. 1986, MNRAS, 219, 347 [NASA ADS] [Google Scholar]
- Warner, B., & Woudt, P. A. 2009, MNRAS, 397, 979 [Google Scholar]
- Wickramasinghe, D. T., Wu, K., & Ferrario, L. 1991, MNRAS, 249, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Onken, C. A., Luvaul, L. C., et al. 2019, VizieR Online Data Catalog: II/358 [Google Scholar]
- Worpel, H., Schwope, A. D., Traulsen, I., et al. 2018, A&A, 617, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wynn, G. A., & King, A. R. 1995, MNRAS, 275, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Z., Thorstensen, J. R., Rappaport, S., et al. 2019, MNRAS, 489, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, VizieR Online Data Catalog: I/297 [Google Scholar]
All Tables
Mean values and ranges of parameters of all photometrically accepted models (Cols. 3–5) and those in spin equilibrium with Pspin = 3484 s (Cols. 6–8; see text for explanation).
All Figures
 |
Fig. 1. Finding chart for J183221.56-162724.25. The r-band images were taken on 12 May 2021 with MuSCAT3 on the FTN. N is up, E to the left, and sizes are 80″ × 80″ and 30″ × 80″. The target and the comparison star are indicated by the red and yellow crosses, respectively. The right panel shows the target in the eclipse. |
| In the text | |
 |
Fig. 2. Long-term light curve, showing nightly averages of the WL fluxes relative to comparison star C3 (green dots). The g-band fluxes of July 2021 (crosses) are adjusted to approximately match the WL fluxes. |
| In the text | |
 |
Fig. 3. Bottom panels: light curves in WL folded on the orbital period of Eq. (1) (left) and on the pulse period of Eq. (6) (right). All individual relative WL fluxes are shown as green dots, and selected individual light curves are emphasized in black, red, and blue (see text). Top panels: mean light curves collected into 32 orbital bins (left) and pulse bins (right). |
| In the text | |
 |
Fig. 4. Left: eclipse light curves in WL, taken with the CA Schmidt telescope, shifted vertically by the indicated amounts. Right: simultaneous eclipse light curves in the griz filters, taken with the MuSCAT3 photometer on the FTN. The dotted lines indicate the length and flux level of the totality. |
| In the text | |
 |
Fig. 5. Top: O–C diagram of the mid-eclipse times relative to the linear ephemeris of Eq. (1). The difference between the quadratic and linear ephemerides of Eqs. (2) and (1) is shown as the dashed curve. Second from top: FWHM of the eclipse vs. pulse phase from Eq. (6). Center: O–C values of the mid-eclipse times relative to the quadratic ephemeris vs. pulse phase. The model curve is from Eq. (4) (see text). Second from bottom: O–C diagram for the minimum times of the 65-minute pulsations relative to the linear ephemeris of Eq. (6). Bottom: O–C values of the previous graph vs. orbital phase (see text). |
| In the text | |
 |
Fig. 6. Schematic sketch of the two-pole accreting WD passing the limb of the secondary star, inclined by an angle α to the vertical (red line). The emission regions are located at radial distance ρ and displaced by an angle β from the rotational axis. They are indicated by circles, color-coded for their relative brightness: maximal (green), intermediate (yellow), and minimal (open). The projected views are shown for pulse phase at the center of the eclipse, ϕ65, c = 0.25 (top) and 0.75 (bottom). The pictures refer to the ingress (right), mid-eclipse (center), and egress (left). The transit takes almost exactly one half of the observed pulse period. The blue arrows indicate the motion of the WD. |
| In the text | |
 |
Fig. 7. Top: periodograms for the minimum times of the 65-minute pulsations. The scale on the left also applies to the center panels. Bottom: lomb-Scargle power spectra for the high- and intermediate-state pulsations outside the eclipse, normalized to a peak value of unity. |
| In the text | |
 |
Fig. 8. Left: observed SED of J1832. Black dots refer to the minimum fluxes in the eclipse and represent our best estimate of the SED of the secondary star. Green and yellow squares indicate the SED outside eclipse measured simultaneously with the MuSCAT3 photometer and the FTN on 9 May and 15 April 2021, respectively. Colored dots indicate nonsimultaneous out-of-eclipse fluxes (see text). Center: de-reddened SED based on the best-fit EB − V = 0.54. Right:Δχ2 vs. EB − V (plus signs, left scale) and the associated (r − i)P1 (green dots, right scale). |
| In the text | |
 |
Fig. 9. Left: confidence range for models of the secondary star permitted by the photometric SED in the eclipse of J1832 (dots and encircled dots). All models have distances within the error bounds of Gaia EDR3 (footnote 3). The red curve represents the best estimate of the extinction along the line of sight to J1832 (Lallement et al. 2018). Center: position of the secondary star of J1832 in its HR diagram. The dots indicate all photometrically accepted models. The encircled dots denote here and in the left panel the subsample with luminosity L2 not exceeding the limit set by the BPS of Kalomeni et al. (2016) (red curve). No model should be found above and to the right of the red curve (see text). The yellow-filled square in both panels marks the mean position of this subsample. The dashed blue curves from Kalomeni et al. (2016) indicate two evolutionary tracks along which J1832 may evolve. Also shown are the position of the 9 h binary KIC 5608384 of Yu et al. (2019) (magenta dot) and its suggested evolutionary track that leads to the graveyard of ultracompact binaries (magenta dashed curve). Right: period ratio Pspin/Porb vs. mass ratio q. The horizontal green lines indicate the observed period ratio of J1832. The open and filled circles denote the theoretical period ratios from the analytical theory of K93 and the numerical calculations of WK95. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



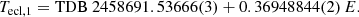
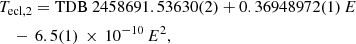
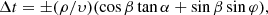
![$$ \begin{aligned} \Delta \,T_\mathrm{ecl} =A\,[\mathrm{cos} \,\beta \,\mathrm{tan} \,\alpha \,\mathrm{sin} \varphi _\mathrm{c} - (1/2)\mathrm{sin} \,\beta \,\mathrm{sin} (2\varphi _\mathrm{c} )], \\ \end{aligned} $$](/articles/aa/full_html/2022/01/aa41585-21/aa41585-21-eq7.gif)
![$$ \begin{aligned} \Delta \,T_\mathrm{ecl} =0\overset{\text{d}}{.}00016(2)\,[\mathrm{sin} \varphi _\mathrm{c} - 0.16\,\mathrm{sin} (2\varphi _\mathrm{c} )], \\ \end{aligned} $$](/articles/aa/full_html/2022/01/aa41585-21/aa41585-21-eq8.gif)