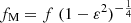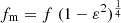| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202140946 | |
| Published online | 14 December 2021 | |
Imaging from STIX visibility amplitudes
1
MIDA, Dipartimento di Matematica, Università degli Studi di Genova, Via Dodecaneso 35, 16146 Genova, Italy
e-mail: piana@dima.unige.it
2
CNR-SPIN, Via Dodecaneso 33, 16146 Genova, Italy
3
Space Sciences Laboratory, University of California, 7 Gauss Way, 94720 Berkeley, USA
4
University of Applied Sciences and Arts Northwestern Switzerland, Bahnhofstrasse 6, 5210 Windisch, Switzerland
5
Swiss Federal Institute of Technology in Zurich (ETHZ), Rämistrasse 101, 8039 Zurich, Switzerland
Received:
31
March
2021
Accepted:
9
August
2021
Aims. This study is aimed at providing the first demonstration of STIX Fourier-transform X-ray imaging using semi-calibrated (amplitude-only) visibility data acquired during Solar Orbiter’s cruise phase.
Methods. We used a parametric imaging approach whereby STIX visibility amplitudes are fitted by means of two non-linear optimization methods: a fast meta-heuristic technique inspired by social behavior and a Bayesian Monte Carlo sampling method that, although slower, provides a better way of quantifying the uncertainties.
Results. When applied to a set of solar flare visibility amplitudes recorded by STIX on November 18, 2020, the two parametric methods provide very coherent results. The analysis also demonstrates the ability of STIX to reconstruct data at a high time resolution and, from a spectral viewpoint, it shows the reliability of a double-source scenario that is consistent with a thermal versus nonthermal interpretation.
Conclusions. In this preliminary analysis of STIX imaging based only on visibility amplitudes, we formulate the imaging problem as a non-linear parametric issue addressed by means of two high-performance optimization techniques that both show the ability to sample the parametric space in an effective fashion, thus avoiding any local minima.
Key words: Sun: flares / techniques: image processing / methods: data analysis
© ESO 2021
1. Introduction
The solar corona is permanently heated to temperatures of several million degrees – well above the moderately hot solar surface that is around 6000 K. While the source of the energy that heats the corona was previously identified as the solar magnetic field, the detailed process(es) of how the energy release is triggered and how energy is eventually dissipated into heat has been an ongoing research topic spanning many decades. The recently launched missions Parker Solar Probe and Solar Orbiter open new windows for unraveling this mystery. Hard X-ray observations provide strong diagnostics of the hottest solar plasma and nonthermal electrons through the bremsstrahlung process; therefore, they play a key role in investigating the impulsive magnetic energy release in the corona during solar flares. While hard X-ray focusing optics has made great progress in the past years (e.g., Krucker et al. 2013), indirect imaging systems in hard X-rays have had great success with instruments such as the Hard X-ray Telescope on-board Yohkoh (Kosugi et al. 1992) and the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI; Lin et al. 2002).
The Spectrometer/Telescope for Imaging X-rays (STIX; Krucker et al. 2020) is a hard X-ray imaging-spectrometer onboard the Solar Orbiter spacecraft. STIX imaging uses an indirect Fourier technique in which the native form of the data is a set of angular Fourier components. Imaging-spectroscopy is based on the choice of the energy of the photons used as the input to the imaging process. The hardware includes a set of 30 independent subcollimators, each consisting of a coarsely-pixelated photon detector with good energy resolution located behind a pair of widely separated grids whose joint transmission creates a large-scale Moiré pattern. Each Moiré pattern can be interpreted to measure a Fourier component of the incoming flux, called “visibility”, whose amplitude corresponds to the difference between the maximum and the minimum of the Moiré pattern and whose phase corresponds to the location of the peak of the Moiré pattern (Giordano et al. 2015; Massa et al. 2019). The angular frequency, which corresponds to each such visibility, is fixed by the choice of orientation and pitch of the corresponding grids. The choices can be divided into ten groups, each of which corresponds to one of ten logarithmically-spaced angular resolutions in the range 7.1 to 180 arcseconds as measured at three different orientations.
For a fully calibrated instrument, the image reconstruction problem for STIX is therefore the linear Fourier inversion problem from limited data that can be addressed by means of regularization methods, such as interpolation and extrapolation (Perracchione et al. 2021), maximum entropy (Massa et al. 2020), or compressed sensing (Duval-Poo et al. 2018).
However, while the current calibration of the STIX imaging system is reliable for visibility amplitudes, the more complex phase calibration is not yet available (at the writing of this paper, the calibration and validation process for STIX visibilities remains in progress and is expected to be finalized well in advance of the beginning of the nominal phase of the mission in September 2021). Therefore, the current image reconstruction problem is the one of determining (partial) information on the flaring source from measurements of the visibility amplitudes only. Such a reconstruction problem carries two main difficulties: (1) it is non–linear; and (2) no information on the source location can be retrieved from the amplitude of the Fourier transform alone. We point out that this situation is analogous to amplitude-only imaging in the early days of very long baseline radio interferometry (Pearson & Readhead 1984) and other fields.
This study describes an approach to the solution of the STIX image reconstruction problem from visibility amplitudes, in which the flaring source is modeled by means of a limited number of simple but flare-appropriate parametric shapes (Dennis & Pernak 2009). We address the problem of source parameter estimation with two alternative methods. The first one is based on a stochastic optimization technique (Eberhart & Kennedy 1995) for solving the forward–fitting problem. It also relies on a confidence strip approach (Piana 1994) for computing parameter uncertainties, which has the advantage of being fast, but comes at the price of having to perturb the input data multiple times, often resulting in misinterpretations. The second one is a Bayesian technique (Sciacchitano et al. 2019), which produces full probabilistic description of the source parameters in a mathematically sound way, typically producing smaller uncertainties, but with a higher computational cost. We point out that forward-fitting techniques have been already used within the framework of Fourier imager missions. Indeed, a forward-fitting algorithm based on deterministic optimization is in the Solar Software (SSW) tree of the RHESSI mission (Aschwanden et al. 2003) and the Bayesian technique illustrated in Sciacchitano et al. (2018) has been validated against fully-calibrated RHESSI visibilities.
We illustrate the two parametric methods using STIX visibility amplitudes associated with a flaring event of the Sun in November 2020. The images provided by this example should not be considered to be science products. However, this analysis may represent a timely demonstration of STIX imaging capabilities in terms of temporal and spectral resolution.
The plan of the paper is as follows. Section 2 introduces the visibility amplitude imaging problem. Section 3 describes the computational approach to its solution and Sect. 4 contains the results of the application of such an approach to a set of experimental STIX observations. Our conclusions are presented in Sect. 5.
2. Visibility amplitude imaging problem
When a stable and calibrated imaging pipeline becomes available, the STIX imaging problem will be described by:
where φ = φ(x) is the incoming photon flux emitted from location x = (x, y) on the solar disk, V is the set of N visibilities measured by the telescope in correspondence of the N points 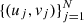 on the (u, v)-plane made of all angular frequencies, and F is the imaging operator that maps the functions representing the flaring source into samples of their Fourier transform, namely:
on the (u, v)-plane made of all angular frequencies, and F is the imaging operator that maps the functions representing the flaring source into samples of their Fourier transform, namely:
The 30 STIX subcollimators will provide N = 30 visibilities. We note that the STIX imaging problem, namely, that of reconstructing the photon flux from N visibilities, is linear, but it does not have a unique solution.
Unfortunately, the calibration of the imaging system that is currently available is limited to the visibility amplitudes, given that the phase calibration is more complex and, therefore, still under construction. The formal consequence of this limitation is that the STIX imaging operator at this stage is represented by:
and, therefore, the imaging problem addressed in the present study is:
where A = |V| and | ⋅ | should be intended as component-wise. This imaging problem is more challenging to solve than Eq. (1) for two key reasons: (1) it is non-linear; and (2) visibility amplitudes do not encode any information on the position of the flaring source. To overcome these limitations, we implemented forward–fitting procedures to estimate the parameters of three different parametric shapes of very simple architecture. Specifically, we considered:
-
A Gaussian circular source:
where ϕ is the total flux of the source,
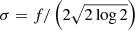 and f is the Full Width at Half Maximum (FWHM). The set of parameters for this source is θC = (ϕ, f).
and f is the Full Width at Half Maximum (FWHM). The set of parameters for this source is θC = (ϕ, f). -
A Gaussian elliptical source:
where ϕ is the total flux of the source,
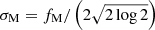 ,
, 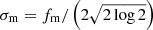 , fM is the major FWHM and fm is the minor FWHM. Moreover,
, fM is the major FWHM and fm is the minor FWHM. Moreover,where α is the angle between the semi-major and the x-axis measured counterclockwise. The set of parameters for the elliptical source is θE = (ϕ, fM, fm, α)1.
-
A double Gaussian circular source:
where ϕj is the total flux,
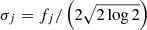 , fj is the FWHM (j = 1, 2) and (x0, y0) are the coordinates of the center of one source (the other is symmetric with respect to the origin). The set of parameters for the double circular source is θD = (x0, y0, ϕ1, f1, ϕ2, f2).
, fj is the FWHM (j = 1, 2) and (x0, y0) are the coordinates of the center of one source (the other is symmetric with respect to the origin). The set of parameters for the double circular source is θD = (x0, y0, ϕ1, f1, ϕ2, f2).
The shapes of the three parametric sources are illustrated in Fig. 1. In the next section, we present the two computational methods for estimating the set of source parameters; without loss of generality, we denote such a set as θ, which is intended to be either θC, θD, or θE, according to the estimated shape.
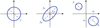 |
Fig. 1. Gaussian shapes considered in the parametric imaging process. |
3. The approach to image reconstruction
The multivariate optimization problem in hard X-ray solar imaging is typically represented by the minimum problem:
where 𝒟 is the so-called feasibility region for the imaging parameter θ and χ2(θ) measures the square of the discrepancy between the experimental visibility amplitudes and those predicted by computing the Fourier transform of the source shape parameterized by θ. The solution of this problem usually relies on the RHESSI legacy (Lin et al. 2002) and, specifically, on the vis_fwdfit routine that computes the imaging parameters by means of a simplex approach. However, the number of visibilities provided by STIX is significantly smaller than the one provided by RHESSI and, at this stage of the calibration process, the information contained in STIX observations is even more limited. This is the reason why, in this first and preliminary study devoted to STIX imaging, we have implemented two more sophisticated approaches that have been explicitly designed in order to avoid local minima in the optimization process.
3.1. Particle swarm optimization
Particle swarm optimization (PSO, Eberhart & Kennedy 1995; Qasem & Shamsuddin 2011) does not require any strong assumptions on the issue defined in Eq. (10) and takes advantage of being usually more robust than deterministic strategies (see e.g., Nocedal & Wright 1999) in the presence of multiple local minima. To briefly review it, let us consider a group of particles or birds, represented as points in the space 𝒟. The goal of swarm intelligence is to model the trajectories of each single particle. Indeed, the target of a flock is to look for the maximum availability of food, namely, the minimum of the objective function χ2. The trajectory of each single bird is updated at each step of the algorithm by taking into account both its “selfish” and its “social behavior”. More precisely, supposing that a particle visits some local minima then the other birds can either:
-
Move away from the flock towards the local minimum (selfish behavior)
-
Stay close to the flock (social behavior).
Assuming that the two behaviors are well-balanced, then the flock gradually changes its position until the global minimum is reached.
The IDL implementation was designed following the guidelines given by Mezura-Montes & Coello Coello (2011) and MATLAB (2019). Specifically, given a first random initialization, at the jth iteration, each ith bird position 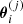 is defined via its velocity
is defined via its velocity 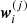 and its best local position
and its best local position 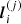 . Letting g(j) the global best position, the position of each particle is updated as
. Letting g(j) the global best position, the position of each particle is updated as
where
for i = 1, …, M, where 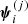 ,
, 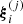 are randomly fixed and ⊙ denotes the component-wise product. The parameters η and ρ are the acceleration coefficients and ω(j) is the inertia weight that is adaptively updated in our implementation (Mezura-Montes & Coello Coello 2011).
are randomly fixed and ⊙ denotes the component-wise product. The parameters η and ρ are the acceleration coefficients and ω(j) is the inertia weight that is adaptively updated in our implementation (Mezura-Montes & Coello Coello 2011).
Uncertainty quantification with PSO is determined by means of a confidence strip approach: several realizations of the input data are computed by randomly perturbing the experimental set of visibility amplitudes with Gaussian noise whose standard deviation is set equal to the errors on the measurements. Then, for each realization, the PSO is applied and, finally, the standard deviation of each optimized source parameter is computed.
3.2. Sequential Monte Carlo
The second approach to image reconstruction from STIX visibility amplitudes is based on a Bayesian source identification method (Sciacchitano et al. 2019) that has been proven capable of assessing, using RHESSI data (Sciacchitano et al. 2018): (1) the likely number of sources in the image; (2) the parameters characterizing each source; and (3) the associated uncertainties.
Given the current restriction on the calibration of the imaging system and the consequent loss of information on the position of the flaring source, here we restrict the usage of the Sequential Monte Carlo (SMC) method to the identification of one single shape per image, which is one of the three described in Sect. 2 (Fig. 1). The resulting method is an alternative approach to the one outlined in Eq. (10), as we are interested in providing “probabilistic estimates” of the set of source-related parameters θ. In a Bayesian setting2, we need to describe the posterior distribution for the flare source parameters conditioned on the set of observed visibility amplitudes p(θ|A), which takes the following form:
Here, p(A|θ) is the likelihood function, expressing the probability that the observed visibility amplitudes A are produced by an image with parameters θ; in addition, p(θ) is the prior probability on the set of parameters; and p(A) is a normalisation factor.
The likelihood function is assumed to be (Hurford et al. 2002):
where the standard deviations are known. Statistical errors in the visibility data are directly inferred from photon statistics in the corresponding detectors. An additional allowance of 5% is added in quadrature to account for systematic errors.
The choice for the prior distributions on the parameters is done according to Sciacchitano et al. (2018):
where FOV indicates the field of view of the map.
As a consequence of these choices for prior and likelihood, the posterior probability density results to be an analytically intractable function on a high-dimensional space. Therefore, to compute it, we use the SMC method (Sciacchitano et al. 2018), which produces a sample set that is approximately distributed according to the posterior and can be used to make inference on the values of the various parameters. Once the algorithm converges, the parameters of the reconstructed map are computed by using the mean values of the posterior distributions (for the different parameters). The notable advantage of this algorithm is that it is capable of realizing the uncertainty quantification in a very elegant way. In fact, the availability of the posterior distribution allows for a straightforward computation of the variance as the second moment associated with each source parameter, hence, with no need to perturb the input visibility amplitude bag. With respect to what was done by Sciacchitano et al. (2018), in the present study, we fixed the number and the type of sources. This is the reason why we used the mean values of the posterior distribution without conditioning it on these two random variables.
4. Flaring event on November 18, 2020
On November 18, 2020, during its cruise phase, STIX observed a series of flaring events with main peak of the lightcurve at around 05:50 UT (see Fig. 2).
 |
Fig. 2. STIX light curves from November 18, 2020, 05:38 UT to November 18, 2020, 06:20 UT with different energy channels. |
We used the PSO and SMC to analyze the visibility amplitudes associated with this flare with the main aim to give a first and very preliminary assessment of STIX imaging performances. Therefore, the results illustrated in the next figures should be intended not as science products, but as the first hints toward what STIX will permit with regard to the investigation of hard X-ray flare physics when the instrument calibration process is complete.
4.1. 05:45:30 UT–05:46:15 UT time window
Focusing on the impulsive phase of the flare (05:45:30 UT – 05:46:15 UT), we applied the PSO and SMC to the set of visibility amplitudes corresponding to six energy channels. Each bag was made of 24 visibilities, with 6 visibilities having been discarded as not well-calibrated yet (the discarded visibilities correspond to detectors with smallest pitch). The reconstruction results are presented in Fig. 3, the corresponding fits in Fig. 4 and the parameter estimates in Fig. 5. The six energy channels have been selected by keeping the upper limit fixed at 70 keV and gradually decreasing the lower limit of the channels. Precisely, we have taken E1: 36–70 keV, E2: 32–70 keV, E3: 28–70 keV, E4: 25–70 keV, E5: 22–70 keV and E6: 20–70 keV, which correspond to the weighted mean energies of 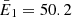 keV,
keV, 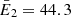 keV,
keV, 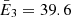 keV,
keV, 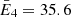 keV,
keV, 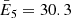 keV and
keV and 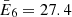 keV, respectively. From the spectral analysis, the interval 36–7 keV should mainly contain the nonthermal emission and the corresponding reconstruction presents two distinguished rather compact sources, one at the bottom-right position (first source, henceforth) and the other one at the up-left position (second source, henceforth). While decreasing the lower limit of the energy channel, the flux associated with the first source significantly increases, while the flux and dimension of the second source remain quite stable. This holds true for the reconstructions provided by both methods and, correspondingly, the small χ2 values confirm a notable statistical reliability of the results. A possible interpretation of this behavior is that the first source might be associated with the thermal emission with a nonthermal tail, while the second one reflects a nonthermal bremsstrahlung process. In any case, the interpretation of the physical nature of the different sources is not the goal of this paper, and the interpretation of the hard X-ray sources in this flare is left for when the full calibration of the STIX imaging system is available.
keV, respectively. From the spectral analysis, the interval 36–7 keV should mainly contain the nonthermal emission and the corresponding reconstruction presents two distinguished rather compact sources, one at the bottom-right position (first source, henceforth) and the other one at the up-left position (second source, henceforth). While decreasing the lower limit of the energy channel, the flux associated with the first source significantly increases, while the flux and dimension of the second source remain quite stable. This holds true for the reconstructions provided by both methods and, correspondingly, the small χ2 values confirm a notable statistical reliability of the results. A possible interpretation of this behavior is that the first source might be associated with the thermal emission with a nonthermal tail, while the second one reflects a nonthermal bremsstrahlung process. In any case, the interpretation of the physical nature of the different sources is not the goal of this paper, and the interpretation of the hard X-ray sources in this flare is left for when the full calibration of the STIX imaging system is available.
 |
Fig. 3. Reconstructions computed via PSO (first box) and SMC (second box) from the visibility amplitudes observed by STIX at 05:45:30 UT–05:46:15 UT on November 18, 2020. For each box, from top to bottom, left to right: reconstructions corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. The SMC reconstructions use the conditional mean. |
 |
Fig. 4. Amplitude fits computed via PSO (first box) and SMC (second box) from the visibility amplitudes observed by STIX at 05:45:30 UT–05:46:15 UT on November 18, 2020. For each box, from top to bottom, left to right: amplitude fits corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. |
 |
Fig. 5. Parameter values and related uncertainties reconstructed by PSO (left column) and SMC (right column) from the visibility amplitudes measured on November 18, 2020 from 05:45:30 to 05:46:15 UT in the energy channels E1, E2, E3, E4, E5, and E6, which are identified in the abscissa by their weighted mean energies. From top to bottom: total flux and FWHM of the two sources and x and y coordinates of the center of the first source (the other one is symmetric with respect to the origin). |
We note that in the PSO analysis, uncertainty quantification has been performed by means of the confidence strip method, namely, repeatedly perturbing the input data, re-running the algorithm for each data realization, and computing the standard deviations over the set of reconstructed parameters. On the contrary, the SMC method returns the estimated probability distributions of the parameters (via the histograms in Fig. 6), and based on these, the means and standard deviations can be easily computed. This approach, which does not require the perturbation of the data, usually provides smaller uncertainties with respect to the ones provided by the confidence strip approach. The drawback of this method is an higher computational burden with respect to PSO. Indeed, each reconstruction took approximately 5 min with SMC, while it took 1.5 min with the PSO combined with confidence strip. We point out that reconstruction with PSO alone (i.e., not producing uncertainty estimation) is even faster, with ∼5 s of computational time.
 |
Fig. 6. Parameter histograms returned by the SMC reconstruction from the visibility amplitudes observed by STIX at 05:45:30 UT – 05:46:15 UT on November 18, 2020. From top to bottom: each box contains the histograms corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. Each of the six boxes contains the probability distributions of the sources locations and associated FWHM and fluxes. In red, we show the estimated means (used to provide the reconstructed maps) and standard deviations. |
Another interesting aspect concerning the SMC histograms in Fig. 6 is that the width parameters, particularly the ones associated with the second source, are rather narrow. This is rather surprising, given that the six visibilities discarded from the analysis are the ones associated with the smallest angular resolution (smaller than 15″). However, this super-resolution effect (which is present also in the case of the reconstructions provided by PSO) is a reasonable intrinsic consequence of the application of forward-fitting approaches: indeed, the use of predefined source shapes imposes strong constraints on the solution that may lead to an enhancement of the angular resolution of the reconstruction. This behavior has been noticed also in the case of RHESSI visibilities, when a deterministic forward-fitting approach is applied for parameter estimation (see point (5) in the conclusions section of Aschwanden et al. 2002).
Finally, some of the histograms in Fig. 6 present a shape that is far from Gaussian-like and is sometimes even close to a bi-modal one. This is most likely due to the fact that we are addressing a very ambiguous problem, in which two configurations characterized by interchanged sources provide the same χ2 value. Indeed, visibility amplitudes are not sensitive to parity transformations.
4.2. Time resolution analysis
We considered the STIX observation at 05:46:30 UT of the November 18, 2020, with a time integration of one second, in the energy range from 7 to 12 keV, in order to verify whether the count statistic, determined by the count rate recorded by the detectors and measured in counts keV−1 s−1, was sufficient to allow for the realization of reliable reconstructions. Figure 7 shows that the count statistic is rather stable across detectors and that even at such a short integration time the statistical error is dominated by the 5% systematic component.
 |
Fig. 7. STIX observation for one second integration time, starting from 05:46:30 UT, in the energy channel 7–12 keV. Left panel: count statistic per detector. Middle panel: signal-to-noise ratio on visibility amplitudes. Right panel: contributions of the statistical and systematic errors on visibility amplitudes. |
The application of SMC to the corresponding visibility amplitude bag produced the visualization and fitting that is shown in Fig. 8 (top row) that correspond to an input configuration made of two Gaussian sources. We refer to the “first source” as the most energetic one and the “second source” as the least energetic one. The histograms for the FWHM and flux parameters in the bottom row of that same figure show that the parameters for both sources are computed with sound uncertainty quantification. The values of such parameters are illustrated in Table 1, where we also reported the results of the analysis performed by means of PSO.
 |
Fig. 8. SMC reconstruction from the visibility amplitudes observed by STIX at 05:46:30 UT on November 18, 2020, with one second integration time in the energy channel 7–12 keV. Top left: flaring source modeled by means of a double-Gaussian input configuration. Top right: corresponding data fit. Bottom: histograms for the FWHM and flux probability distributions for the two sources. In red, we show the mean and standard deviations of the posterior distributions (used to give point estimates). |
Estimated parameters and associated uncertainties computed by SMC and PSO for the visibility amplitudes recorded by STIX at 05:46:30 UT on the November 18, 2020, with one second integration time in the energy channel 7–12 keV.
We note here that the integration time of the November 18, 2020 observation was set to 1 s. This time interval is currently considered as the maximal time resolution achievable by STIX, although tests at faster time cadences (down to 0.1 s) will be carried out later in 2021. Considering our initial results at 1 second cadence, we are confident that sub-second time resolution imaging will be possible at least in the thermal range.
5. Comments and conclusions
This study represents a preliminary attempt to reconstruct hard X-ray images of solar flares from data collected by STIX during its cruise phase. As a consequence, these results should be considered with caution, first of all because the current calibration stage of the instrument does not allow for the exploitation of the visibility phases, so that the non–linear image reconstruction problem of determining the flaring source from the visibility amplitudes is highly ambiguous. It follows that the only approaches we could implement were those based on the forward fitting of very simple parametric source shapes and the only information we could try and determine were related to the flux and dimensions of such shapes and, in the case of a configuration made of two Gaussian sources, their relative position.
However, even with these limitations, some hints can be deduced from the results of this analysis. For example, STIX appears to allow for a high temporal resolution analysis, providing data with significantly high signal-to-noise ratio even in the case of very short integration times. Furthermore, a simple spectral analysis provided us with results that are consistent with a scenario in which a nonthermal footpoint persists at higher energies, while a (probably coronal) thermal component becomes more evident when lower energies are included in the processing.
Finally, the two parametric imaging approaches considered in this work provide rather similar reconstructions. However, from a methodological viewpoint, the two methods exhibit a key difference: PSO realizes uncertainty quantification through the confidence strip method, which is fast but does not leave the measurements untouched, possibly leading to suboptimal results. On the other hand, SMC provides a full probabilistic description of the reconstructed shape and, therefore, a more robust uncertainty estimation, but at the cost of an higher computational burden. We point out that both methods can be easily extended for use with fully calibrated visibilities (i.e., when even the visibility phases are calibrated) and that they will be included in the STIX data analysis software of the mission.
In a Bayesian setting, all the variables of the problem are considered as random variables, with information on their values encoded as their probability distributions. In the following we will use lower-case letters to indicate both the random variables and their specific values in a given instance.
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The STIX instrument is an international collaboration between Switzerland, Poland, France, Czech Republic, Germany, Austria, Ireland, and Italy. AFB is supported by the Swiss National Science Foundation Grant 200021L_189180 for STIX. PM, EP, FB and MP acknowledge the financial contribution from the agreement ASI-INAF n.2018-16-HH.0. SG acknowledges the financial support from the “Accordo ASI/INAF Solar Orbiter: Supporto scientifico per la realizzazione degli strumenti Metis, SWA/DPU e STIX nelle Fasi D-E”.
References
- Aschwanden, M. J., Schmahl, E., & RHESSI Team 2002, Sol. Phys., 210, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Schmahl, E., & RHESSI Team 2003, in The Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI) (Springer), 193 [CrossRef] [Google Scholar]
- Dennis, B. R., & Pernak, R. L. 2009, ApJ, 698, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Duval-Poo, M. A., Piana, M., & Massone, A. M. 2018, A&A, 615, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eberhart, R., & Kennedy, J. 1995. IEEE Int. Conf. Neural Netw., 4, 1942 [Google Scholar]
- Giordano, S., Pinamonti, N., Piana, M., & Massone, A. M. 2015, SIAM J. Imaging Sci., 8, 1315 [Google Scholar]
- Hurford, G., Schmahl, E., Schwartz, R., et al. 2002, Sol. Phys., 210, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Sakao, T., Masuda, S., et al. 1992, PASJ, 44, L45 [NASA ADS] [Google Scholar]
- Krucker, S., Christe, S., Glesener, L., et al. 2013, in Solar Physics and Space Weather Instrumentation V, eds. S. Fineschi, & J. Fennelly, SPIE Conf. Ser., 8862, 88620R [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Hurford, G. J., Grimm, O., et al. 2020, A&A, 642, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Massa, P., Piana, M., Massone, A. M., & Benvenuto, F. 2019, A&A, 624, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massa, P., Schwartz, R., Tolbert, A., et al. 2020, ApJ, 894, 46 [NASA ADS] [CrossRef] [Google Scholar]
- MATLAB 2019, Global Optimization Toolbox (Natick, Massfachusetts: The Mathworks Inc.) [Google Scholar]
- Mezura-Montes, E., & Coello Coello, C. A. 2011, SWEVO, 1, 173 [Google Scholar]
- Nocedal, J., & Wright, S. 1999, Numerical Optimization (New York: Springer-Verlag) [CrossRef] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [Google Scholar]
- Perracchione, E., Massa, P., Massone, A. M., & Piana, M. 2021, ApJ, 919, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Piana, M. 1994, A&A, 288, 949 [NASA ADS] [Google Scholar]
- Qasem, S. N., & Shamsuddin, S. M. 2011, Appl. Soft Comput., 11, 1427 [CrossRef] [Google Scholar]
- Sciacchitano, F., Sorrentino, A., Emslie, A. G., Massone, A., & Piana, M. 2018, ApJ, 862, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sciacchitano, F., Lugaro, S., & Sorrentino, A. 2019, SIAM J. Imaging Sci., 12, 319 [Google Scholar]
All Tables
Estimated parameters and associated uncertainties computed by SMC and PSO for the visibility amplitudes recorded by STIX at 05:46:30 UT on the November 18, 2020, with one second integration time in the energy channel 7–12 keV.
All Figures
 |
Fig. 1. Gaussian shapes considered in the parametric imaging process. |
| In the text | |
 |
Fig. 2. STIX light curves from November 18, 2020, 05:38 UT to November 18, 2020, 06:20 UT with different energy channels. |
| In the text | |
 |
Fig. 3. Reconstructions computed via PSO (first box) and SMC (second box) from the visibility amplitudes observed by STIX at 05:45:30 UT–05:46:15 UT on November 18, 2020. For each box, from top to bottom, left to right: reconstructions corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. The SMC reconstructions use the conditional mean. |
| In the text | |
 |
Fig. 4. Amplitude fits computed via PSO (first box) and SMC (second box) from the visibility amplitudes observed by STIX at 05:45:30 UT–05:46:15 UT on November 18, 2020. For each box, from top to bottom, left to right: amplitude fits corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. |
| In the text | |
 |
Fig. 5. Parameter values and related uncertainties reconstructed by PSO (left column) and SMC (right column) from the visibility amplitudes measured on November 18, 2020 from 05:45:30 to 05:46:15 UT in the energy channels E1, E2, E3, E4, E5, and E6, which are identified in the abscissa by their weighted mean energies. From top to bottom: total flux and FWHM of the two sources and x and y coordinates of the center of the first source (the other one is symmetric with respect to the origin). |
| In the text | |
 |
Fig. 6. Parameter histograms returned by the SMC reconstruction from the visibility amplitudes observed by STIX at 05:45:30 UT – 05:46:15 UT on November 18, 2020. From top to bottom: each box contains the histograms corresponding to the energy channels E1, E2, E3, E4, E5, and E6, respectively. Each of the six boxes contains the probability distributions of the sources locations and associated FWHM and fluxes. In red, we show the estimated means (used to provide the reconstructed maps) and standard deviations. |
| In the text | |
 |
Fig. 7. STIX observation for one second integration time, starting from 05:46:30 UT, in the energy channel 7–12 keV. Left panel: count statistic per detector. Middle panel: signal-to-noise ratio on visibility amplitudes. Right panel: contributions of the statistical and systematic errors on visibility amplitudes. |
| In the text | |
 |
Fig. 8. SMC reconstruction from the visibility amplitudes observed by STIX at 05:46:30 UT on November 18, 2020, with one second integration time in the energy channel 7–12 keV. Top left: flaring source modeled by means of a double-Gaussian input configuration. Top right: corresponding data fit. Bottom: histograms for the FWHM and flux probability distributions for the two sources. In red, we show the mean and standard deviations of the posterior distributions (used to give point estimates). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



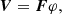
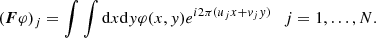
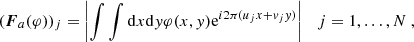
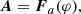
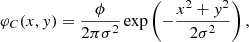
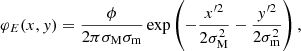
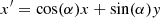
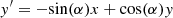
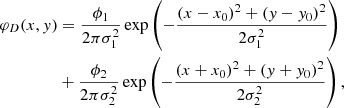
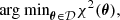
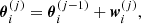
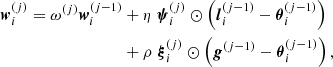
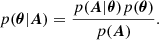
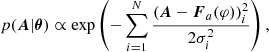
![$$ \begin{aligned} f&\sim \mathcal{U} \left(\left[0, \frac{2}{3}FOV\right]\right)\end{aligned} $$](/articles/aa/full_html/2021/12/aa40946-21/aa40946-21-eq25.gif)
![$$ \begin{aligned} \phi&\sim \mathcal{U} \left(\left[0, \max \boldsymbol{A}\right]\right)\end{aligned} $$](/articles/aa/full_html/2021/12/aa40946-21/aa40946-21-eq26.gif)
![$$ \begin{aligned} (x_0, { y}_0)&\sim \mathcal{U} \left(\left[ - \frac{FOV}{2}, \frac{FOV}{2}\right], \left[ - \frac{FOV}{2}, \frac{FOV}{2}\right]\right)\end{aligned} $$](/articles/aa/full_html/2021/12/aa40946-21/aa40946-21-eq27.gif)
![$$ \begin{aligned} \alpha&\sim \mathcal{U} \big (\left[0, 180^{\circ }\right]\big )\end{aligned} $$](/articles/aa/full_html/2021/12/aa40946-21/aa40946-21-eq28.gif)
![$$ \begin{aligned} \varepsilon&\sim \mathcal{U} \left(\left[0, 1\right]\right), \end{aligned} $$](/articles/aa/full_html/2021/12/aa40946-21/aa40946-21-eq29.gif)