| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 18 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140932 | |
| Published online | 14 December 2021 | |
Observations of whistler mode waves by Solar Orbiter’s RPW Low Frequency Receiver (LFR): In-flight performance and first results
1
LPP, CNRS, Ecole Polytechnique, Sorbonne Université, Observatoire de Paris, Université Paris-Saclay, Palaiseau, Paris, France
e-mail: thomas.chust@lpp.polytechnique.fr
2
LPC2E, CNRS, University of Orléans, 3A avenue de la recherche scientifique, Orléans, France
3
Swedish Institute of Space Physics (IRF), Uppsala, Sweden
4
Department of Space and Plasma Physics, School of Electrical Engineering and Computer Science, Royal Institute of Technology, Stockholm, Sweden
5
Department of Space Physics, Institute of Atmospheric Physics of the Czech Academy of Sciences, Prague, Czech Republic
6
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
7
CNES, 18 avenue Edouard Belin, 31400 Toulouse, France
8
Technische Universität Dresden, Würzburger Str. 35, 01187 Dresden, Germany
9
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
10
Astronomical Institute of the Czech Academy of Sciences, Prague, Czech Republic
11
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, Meudon, France
12
Radboud Radio Lab, Department of Astrophysics, Radboud University, Nijmegen, The Netherlands
13
Space Sciences Laboratory, University of California, Berkeley, CA, USA
14
Physics Department, University of California, Berkeley, CA, USA
15
Stellar Scientific, Berkeley, CA, USA
16
Department of Physics, Imperial College, SW7 2AZ London, UK
Received:
30
March
2021
Accepted:
20
June
2021
Context. The Radio and Plasma Waves (RPW) instrument is one of the four in situ instruments of the ESA/NASA Solar Orbiter mission, which was successfully launched on February 10, 2020. The Low Frequency Receiver (LFR) is one of its subsystems, designed to characterize the low frequency electric (quasi-DC – 10 kHz) and magnetic (∼1 Hz–10 kHz) fields that develop, propagate, interact, and dissipate in the solar wind plasma. Combined with observations of the particles and the DC magnetic field, LFR measurements will help to improve the understanding of the heating and acceleration processes at work during solar wind expansion.
Aims. The capability of LFR to observe and analyze a variety of low frequency plasma waves can be demontrated by taking advantage of whistler mode wave observations made just after the near-Earth commissioning phase of Solar Orbiter. In particular, this is related to its capability of measuring the wave normal vector, the phase velocity, and the Poynting vector for determining the propagation characteristics of the waves.
Methods. Several case studies of whistler mode waves are presented, using all possible LFR onboard digital processing products, waveforms, spectral matrices, and basic wave parameters.
Results. Here, we show that whistler mode waves can be very properly identified and characterized, along with their Doppler-shifted frequency, based on the waveform capture as well as on the LFR onboard spectral analysis.
Conclusions. Despite the fact that calibrations of the electric and magnetic data still require some improvement, these first whistler observations show a good overall consistency between the RPW LFR data, indicating that many science results on these waves, as well as on other plasma waves, can be obtained by Solar Orbiter in the solar wind.
Key words: solar wind / waves / plasmas / instrumentation: miscellaneous
© T. Chust et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
As part of the Radio and Plasma Waves (RPW) instrument (Maksimovic et al. 2020) on the Solar Orbiter mission (Müller et al. 2020), the Low Frequency Receiver (LFR) is designed to digitize and process the signals from a triaxal coplanar electric antenna system (ANT), its associated biasing unit (BIAS), and a triaxal search-coil magnetometer (SCM, Jannet et al. 2021) over a frequency range of quasi DC to 10 kHz. With the aim to study the electromagnetic and electrostatic activity in the extended corona and the near-Sun solar wind, this frequency range of observation covers the electron gyrofrequency as well as most of the Doppler frequency shifts of the low frequency and small scale plasma waves, structures, and turbulence (e.g., kinetic or inertial Alfvén waves, ion cyclotron waves, ion acoustic waves, magnetosonic or whistler mode waves, electron cyclotron waves, and Bernstein’s waves). For example, Sahraoui et al. (2009) emphasized the importance of taking into account the Doppler-shifted protons and electrons gyroscales to correctly interpret the observed breakpoints in the solar wind magnetic spectrum. As the first outcomes of the RPW instrument suite in the LFR frequency range, Khotyaintsev et al. (2021) were able to accurately identify proton-band electromagnetic ion cyclotron waves from the measurement of their polarization properties, including the density fluctuation and the Doppler effect. At higher frequencies, Graham et al. (2021), established a statistical study of the ion-acoustic waves observed in the solar wind at 0.5 AU. The characterization and the determination of the respective role of such low frequency and small-scale fluctuations in heating and accelerating the solar wind, during its expansion, as well as their relationship to solar wind disturbances (e.g., interplanetary shocks, current sheets) are the main scientific issues addressed by the LFR.
The observation of whistler mode waves in the solar wind reveals an important scientific question. As noted and discussed by Kretzschmar et al. (2021), these waves are most likely an important factor in the dynamics of the solar wind expansion as a result of their effects on the electron population. First, this is because there is substantial observational evidence of their presence at all distances from the Sun observed so far, up to at least 1 AU (Lacombe et al. 2014; Tong et al. 2019b; Jagarlamudi et al. 2020, 2021; Agapitov et al. 2020). Secondly, this is because they are expected to be able to efficiently scatter suprathermal electrons. In particular, they are good candidates for the diffusion of electrons from the strahl population to the halo population, as well as for the regulation of the heat flux carried by the bulk flow of halo electrons (Gary et al. 1999). However, the exact mechanisms by which these whistler mode waves are generated and the way they dissipate the free energy of the solar wind are still under debate. For example, the heat flux instability often appears to be the most likely source of whistler mode waves propagating antisunward at small angles to the background magnetic field (Lacombe et al. 2014; Stansby et al. 2016; Tong et al. 2019a). However, since the frequency range of the whistler mode waves is lower than the electron gyrofrequency, the resonant wave-particle interaction experienced by antisunward-propagating whistler mode waves can only affect suprathermal electrons that are counterstreaming in the plasma rest frame – which, thus, are not strahl electrons (Stansby et al. 2016; Vasko et al. 2020; Behar et al. 2020).
This brief review of the question around whistler mode waves and their possible role in the regulation of the solar wind heat flux shows the importance of adequately characterizing the properties of the waves. In particular, the experimental determination of their propagation direction, antisunward or sunward (in other words, parallel or antiparallel to the electron heat flux) is of crucial relevance to obtaining a prediction of which part of the electron distribution function is affected by the wave-particle interaction. The LFR’s nominal inputs consist of eight low-frequency (LF) analog voltage signals which are continuously digitized and routinely processed. Three arrive directly from the SCM LF windings and five arrive indirectly from the ANT LF preamplifiers. More specifically, the signals, which are measured by the three RPW electric monopole antennas, are conditioned and transformed by the BIAS unit into five signals before entering the LFR: one is dedicated to single-ended electric potential measurements and two pairs are dedicated to DC- and AC-coupled differential electric field measurements, respectively. The LFR signal processing, based on a FPGA (Field-Programmable Gate Array), provides basically three kind of data products, namely: waveforms, spectral matrices, and basic wave parameters, at different time and frequency resolutions. In order to cover the entire frequency range from quasi DC to 10 kHz, the strategy chosen has been to digitally decimate the input signals several times in cascade, thus simultaneously providing four waveform data streams sampled at F0 = 24576 Hz, F1 = 4096 Hz, F2 = 256 Hz, and F3 = 16 Hz, respectively. More details can be found in the RPW instrument description in Maksimovic et al. (2020).
In this article we illustrate the proper functioning of the LFR through some examples of observations of whistler mode waves not very far from the first Solar Orbiter perihelion on June 15, 2020 at 0.515 AU. In order to properly characterize these waves, some context parameters are needed. For this purpose, we used the DC magnetic field vector provided by the MAG instrument (Horbury et al. 2020). Unfortunately at this early stage of the mission the particle data from the SWA instrument (Owen et al. 2020) are not yet systematically available. However, it is possible to use an estimate of the plasma density derived from the continuous measurement of the spacecraft floating potential, a product provided by LFR/BIAS at the same time as its measurement of two components of the quasi-DC electric field of the solar wind (Khotyaintsev et al. 2021; Steinvall et al. 2021). In order to calibrate this electron plasma density obtained from the spacecraft potential, a more direct but sporadic estimation was also made by detecting the emission peak at the local plasma frequency using the RPW Thermal Noise and High Frequency Receiver (TNR-HFR) subsystem (Maksimovic et al. 2020).
The article is organized as follows. We begin by establishing the results obtained with the richest but rarest set of the LFR data products, namely, the waveforms. Then we show how to retrieve these results from the spectral data products, which are continuously calculated on board and systematically transmitted to the ground.
2. Observations from the waveform data
Whatever the operation mode and the targeted sampling frequency, the waveforms produced by LFR always consist of: three vector components of the fluctuating magnetic field, one potential measurement by an electric monopole antenna, and two components of the electric field. By design, in terms of the data acquisition and signal processing, these six waveforms are time-series collected simultaneously for a given sampling frequency.
The electric field measurements are carried out in a plane parallel to the heat shield that is normal to the Solar Orbiter-Sun axis. This plane corresponds to the YZ-plane of the spacecraft reference frame (SRF), defined such that 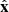 points toward the Sun,
points toward the Sun, 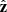 is along the electric antenna ANT1 of RPW (thus approximately normal to the ecliptic plane for small heliographic latitude of Solar Orbiter) and
is along the electric antenna ANT1 of RPW (thus approximately normal to the ecliptic plane for small heliographic latitude of Solar Orbiter) and 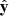 completes the direct coordinate system. The other two electric antennas, ANT2 and ANT3 of RPW, are arranged symmetrically with respect to the spacecraft, creating an angle of 125° with the antenna ANT1 (Steinvall et al. 2021; Maksimovic et al. 2020).
completes the direct coordinate system. The other two electric antennas, ANT2 and ANT3 of RPW, are arranged symmetrically with respect to the spacecraft, creating an angle of 125° with the antenna ANT1 (Steinvall et al. 2021; Maksimovic et al. 2020).
The LFR waveform data can be either of two kinds: (1) recorded continuously for a long time, from few minutes to one full day, and are referred to as continuous waveforms (CWF); or (2) segments of time series collected periodically, referred to as snapshots of waveform or waveform snapshots (SWF). All the SWF have the same size and consist of 2048 data points. The SWF produced with the sampling frequency F0, F1, and F2 are centered with respect of each other, and recorded, for the RPW baseline NORMAL mode, every 300 s. Below, we begin with a wave event observed in BURST mode, namely, when continuous waveforms have been recorded with a sampling frequency equal to F2.
2.1. Continuous waveforms sampled at 256 Hz
On July 11, 2020, the RPW instrument was operating two hours in BURST mode from 6:30 to 8:30 UTC. Between 6:50 and 7:40 a succession of electromagnetic wave emissions was clearly detected. Figure 1 shows the corresponding spectrograms of the power spectral densities (PSD) of the perturbed electric and magnetic field components, expressed in the SRF, which are typical of what we have observed up to now as whistler mode wave emissions in the solar wind. The PSD have been computed from the continuous waveforms sampled at F2 with a time and frequency resolution of 2 s and 2 Hz, respectively. To do this, we performed, for each field component, a moving average without overlap of four power spectra, using a 128-point fast Fourier transform (FFT). Beforehand, a Hanning window was applied to each 128-point segment to smooth out edge discontinuities and, in a correlative way, the mean value was also subtracted to reduce the low-frequency disturbance due to this apodization. In order to correct for the windowing bias effect on the determination of the wave amplitudes, the PSD were multiplied by a factor of 4. However, we did not multiply by a factor of 2 so that we did not include negative frequencies.
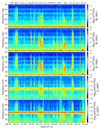 |
Fig. 1. Case study of July 11, 2020: Spectrograms of the electric and magnetic PSD computed on the ground from the continuous waveforms. The line visible at 24 Hz on the electric field components is a spurious interference line. Although weaker, other stray horizontal lines are also visible in the background of the magnetic field components. They are produced at 8 Hz and its harmonics, and originate from the spacecraft (AOCS Synchronization Pulse). |
The data calibration and their expression in the SRF call for several comments by way of explanation. The magnetic field data were calibrated by the SCM team, taking into account the overall signal processing chain, that is, the transfer functions of SCM and LFR (Kretzschmar et al., in prep.). These are originally expressed in the SCM axis coordinate system. We rotated them in the SRF using the orientations of the SCM axes, as indicated in Maksimovic et al. (2020). For electric field data, this is made more difficult because the calibration of the electric sensor, ANT, depends on the plasma conditions of the solar wind and it was for this reason that it was not possible on the ground. Indeed, at this early stage of the mission, the electric field data were calibrated by the BIAS team, taking into account only the BIAS and LFR transfer functions, thus providing us with data in units of V and leaving open the question of the effective lengths and orientations of the antennas. In order to obtain, in units of V/m, two electric field components measured in the SRF YZ-plane, it is therefore necessary to apply an effective ANT transfer matrix. At the time of writing, due to the geometry of the electric measurement performed by the ANT/BIAS instrument, it has become common to use the following transformation:
with LY and LZ the effective antenna lengths along the Y- and Z-coordinates, respectively, and where V12 = V1 − V2 and V23 = V2 − V3 are the original electric field data calibrated by the BIAS team, with V1, V2, and V3 denoting, respectively, the single-ended signals from the three electric antennas of RPW. A first estimation of LY and LZ can be deduced by considering the half-distances between the antennas from tip to tip, which yields LY ≈ LZ ≈ 7 m (Maksimovic et al. 2020; Steinvall et al. 2021). However, Steinvall et al. (2021) and Kretzschmar et al. (2021), who addressed the question of the effective antenna length in parallel with the development of this article, showed that it depends significantly on the local Debye length (λD) and thus on the electron plasma density of the solar wind (n0). Although their preliminary results are obtained statistically and show important fluctuations in the determination of the effective antenna length, a clear trend can be observed: for λD ≥ 12 m, LY ≈ 4 m, while for λD ≤ 3 m, LY ≈ 10 − 14 m. The greater the density of the plasma, the greater the effective length of the antenna. The upper limit of ≈14 m for LY is obtained by Kretzschmar et al. (2021), using a calibration method based on the observation of whistler mode waves, as in this article. A smaller upper limit of ≈10 m for LY is observed by Steinvall et al. (2021), using a deHoffmann-Teller analysis, thus based on the comparison of the DC electric field measurements to ion convection measured by PAS. Throughout this article, unless otherwise indicated, we use LY = LZ = 9.1 m, a value that appears relevant as a first approximation. Henceforth, this value may be re-evaluated on a case by case basis, so that the observation is consistent with the theoretical model. As we see later in this work, our results are in agreement with the general trend reported by the two authors mentioned above, although the fluctuations in the determination of the effective antenna length are still not well understood. Since this article focuses on the performance of the LFR, and not on the calibration of the electric field, the question of a more precise determination of the effective length of the electric antennas is left for a later work, although this discussion already stands as a contribution to the subject.
Figure 2 shows the DC magnetic field (B0) and the electron plasma density (n0) estimated from the spacecraft potential. The magnetic field is frequently reduced to relatively small values, which is associated with decreases in the radial magnetic field component (B0X). These magnetic field dips are likely signatures of current sheets. At the end of the interval, around 07:40 UTC (July 11, 2020), the B0X component even shows a reversal, which might correspond to the spacecraft crossing of the heliospheric current sheet region (Lavraud et al. 2020; Szabo et al. 2020). The detailed study of the relationship between the magnetic dips and the observed wave emissions is of great interest and will be addressed in our further studies.
 |
Fig. 2. Components and amplitude of the DC magnetic field (B0) measured by the MAG instrument (Horbury et al. 2020), and the electron plasma density (n0) as estimated by the RPW instrument suite from the spacecraft potential measurement (Khotyaintsev et al. 2021) for the same time interval as in Fig. 1. |
Figure 3 displays another set of more elaborate wave parameters that are useful for analysing the wave properties. Their calculation involves computing a 5 × 5 electromagnetic spectral matrix (SM) that consists of the auto- and cross-power spectra of the three magnetic and the two electric perturbed field components, which are time-averaged (i.e., the average of a number of successive realizations):
 |
Fig. 3. Case study of July 11, 2020: Spectrograms of several wave parameters computed on the ground from the continuous waveforms, for the same time interval and frequency range as in Fig. 1. From top to bottom: total power of magnetic (PB) and electric (PE) field fluctuations measured, degree of polarization (DOP), wave ellipticity (ellip), wave normal vector components (nX, nY, nZ) in SRF, angle between the wave normal vector (n), and the DC magnetic field vector (B0), radial SRF X-component of the Poynting vector (SX) as the real part of the complex Poynting flux |
where 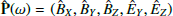 is the FFT of the wave electromagnetic field vector P(t) = (BX, BY, BZ, EY, EZ) expressed in the SRF, Δf is the frequency resolution of the FFT, the superscript symbol * denotes the complex conjugate, and ⟨.⟩t corresponds to the time-averaging operator. For computing the 15 independent SM components we did the same kind of moving average and FFT calculations, including apodization, as done for computing the PSD shown in Fig. 1. Since we also used the same parameters that determine the time and frequency resolution (2 s and 2 Hz) here, the SM diagonal components are nothing else than the PSD already shown. For completeness regarding data calibration, since the definition of the SM components does not include negative frequencies, their magnitude is 1/2 of the (auto- or cross-) mean power of the corresponding fluctuating field components. Let us call SMB and SME the magnetic and electric spectral matrices, respectively, defined as the magnetic and electric parts of the SM matrix.
is the FFT of the wave electromagnetic field vector P(t) = (BX, BY, BZ, EY, EZ) expressed in the SRF, Δf is the frequency resolution of the FFT, the superscript symbol * denotes the complex conjugate, and ⟨.⟩t corresponds to the time-averaging operator. For computing the 15 independent SM components we did the same kind of moving average and FFT calculations, including apodization, as done for computing the PSD shown in Fig. 1. Since we also used the same parameters that determine the time and frequency resolution (2 s and 2 Hz) here, the SM diagonal components are nothing else than the PSD already shown. For completeness regarding data calibration, since the definition of the SM components does not include negative frequencies, their magnitude is 1/2 of the (auto- or cross-) mean power of the corresponding fluctuating field components. Let us call SMB and SME the magnetic and electric spectral matrices, respectively, defined as the magnetic and electric parts of the SM matrix.
The two top panels of Fig. 3 show the total measured PSD of the magnetic (PB) and electric (PE) field fluctuations: PB and PE are computed as the trace of SMB and SME, respectively. The third panel gives a measure of the degree of polarization of the wave (DOP) based on Samson’s formula (Samson 1973; Samson & Olson 1980), which we applied to the three-dimensional (3D) wave magnetic field vector:
with n = 3, and the symbol tr the trace operator. This DOP, within the framework of linear physics, is an estimator of the validity of the assumption of the presence of a single plane wave, for a given frequency. It allows to detect a pure state wave, that is, a wave with a single polarization state. A value close to 1 indicates a pure state wave while a lower value indicates a non pure state wave (with the presence of noise, two or more plane waves, ...). In that case, the value also depends on the number of averaged spectral matrices (Taubenschuss & Santolík 2019). For our setup, values above 0.6–0.7 indicate a pure state wave. An interesting review of such an estimator and comparisons with others for the purpose of evaluating the consistency of the magnetic field components with a single polarization state can be found in Pinçon et al. (1992) and Santolík et al. (2006).
The next five panels display the polarization properties of the wave magnetic field in terms of the ellipticity (ellip) and the normal vector (n), which we computed from the Means method (Means 1972):
with 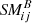 the ij-component of the magnetic spectral matrix, and the symbol ℑ the imaginary part operator. As this study is based on the analysis of the pure plane waves, only cases matching DOP ≥ 0.9 are plotted.
the ij-component of the magnetic spectral matrix, and the symbol ℑ the imaginary part operator. As this study is based on the analysis of the pure plane waves, only cases matching DOP ≥ 0.9 are plotted.
The wave ellipticity parameter as given by Eq. (5) is an estimator of
where a and b are the magnitudes of the major and minor axes of the polarization ellipse. It thus indicates a purely circularly polarized wave when it is 1, and a purely linearly polarized wave when it is 0.
The wave normal vector n (Eqs. (6)–(8)) is determined as the unit vector perpendicular to the plane of polarization of the wave and oriented in such a way that the rotation of the fluctuating magnetic field within that plane is observed right-handed (RH) with respect to it (i.e., rotate counter-clockwise or in the direct direction about it). We note that n is, thus, not exactly the wave vector k just normalized. In fact, we find the following relationship:
where K is a signed wave number whose sign is determined by the direction of the wave propagation along n.
In a first analysis, the electromagnetic wave emissions that we observe here are all very circularly polarized (ellip ≃ 1) and propagating approximately radially (nX ≃ −1), parallel (or anti-parallel) to the ambient magnetic field (θn, B0 ≤ 15°). As n ⋅ B0 is positive, this corresponds to a RH polarization of the wave magnetic field with respect to B0.
In order now to know the direction of wave propagation, we need to correlate the electric and magnetic field fluctuations. The last four panels of Fig. 3 address precisely this question, in two different ways. Firstly we are interested in the measurement of the Poynting flux along the radial direction (X in SRF):
with ℜ the real part operator and
similar to Eq. (12) of Santolík et al. (2010). Secondly we propose a first way of measuring the signed phase velocity 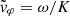 , based on the Maxwell-Faraday equation and the measurement of two electric field components:
, based on the Maxwell-Faraday equation and the measurement of two electric field components:
where
and
with ρij the spectral correlation coefficient between components i and j, as given by Eq. (A.7). A derivation of this formula is given in Appendix A.
During this case study and for all frequencies, a negative SRF X-component of the Poynting vector is observed (SX < 0), indicating that the electromagnetic wave energy flows in the antisunward direction. This is consistent with the positive phase velocities which are measured (sign(K1) > 0), indicating that the waves propagate along n. Indeed, in that case, nX < 0 and thus n is oriented in the antisunward direction.
As indicated in Appendix A, for a pure plane wave, 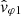 (as given by Eq. (15)) should, in principle, be a purely real number and its complex argument be either 0° or 180°. As shown in the last panel of Fig. 3, this is not the case, with
(as given by Eq. (15)) should, in principle, be a purely real number and its complex argument be either 0° or 180°. As shown in the last panel of Fig. 3, this is not the case, with 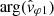 varying roughly between 20° and 60°. In fact, in this case study, as well as in all the other whistler mode wave events we have studied so far, a systematic phase deviation of this order from 0° or 180° is observed. The origin of this relative phase shift issue between the ANT/BIAS/LFR and SCM/LFR data is still not understood. In the present work, we propose a way to deal with this question. Two hypotheses are possible: either (i) the phase deviation does not imply any error in the sign of K1 given by Eq. (14), we call this hypothesis the “weak phase deviation” hypothesis; or, inversely, (ii) it implies a change of sign, a hypothesis we denote as the “strong phase deviation” hypothesis. Let us now interpret the observed values for
varying roughly between 20° and 60°. In fact, in this case study, as well as in all the other whistler mode wave events we have studied so far, a systematic phase deviation of this order from 0° or 180° is observed. The origin of this relative phase shift issue between the ANT/BIAS/LFR and SCM/LFR data is still not understood. In the present work, we propose a way to deal with this question. Two hypotheses are possible: either (i) the phase deviation does not imply any error in the sign of K1 given by Eq. (14), we call this hypothesis the “weak phase deviation” hypothesis; or, inversely, (ii) it implies a change of sign, a hypothesis we denote as the “strong phase deviation” hypothesis. Let us now interpret the observed values for 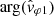 in the present case study. Under the first hypothesis, as
in the present case study. Under the first hypothesis, as 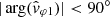 , they simply represent the values of the relative phase shift, which therefore varies roughly in the range of 20° to 60°. Under the second hypothesis, on the other hand,
, they simply represent the values of the relative phase shift, which therefore varies roughly in the range of 20° to 60°. Under the second hypothesis, on the other hand, 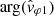 corresponds to 180° plus the relative phase shift, which then varies in the range of −160° to −120°. To be exact, these angular gap ranges are defined as modulo 360°. Thus the determination of the direction of wave propagation given by Eq. (14) is only valid if the “weak phase deviation” hypothesis is correct. We go on to see that this hypothesis is very likely to be the most consistent with all of our observations.
corresponds to 180° plus the relative phase shift, which then varies in the range of −160° to −120°. To be exact, these angular gap ranges are defined as modulo 360°. Thus the determination of the direction of wave propagation given by Eq. (14) is only valid if the “weak phase deviation” hypothesis is correct. We go on to see that this hypothesis is very likely to be the most consistent with all of our observations.
First of all we have to go back to the Poynting flux measurement, which also involves a relative phase shift test between the electric and magnetic field data. As a matter of fact, the complex Poynting flux 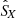 , as given by Eq. (12), exhibits approximately the same phase shift variations (with respect to 180°) as observed with
, as given by Eq. (12), exhibits approximately the same phase shift variations (with respect to 180°) as observed with 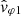 (with respect to 0°). This is clearly visible when comparing in Fig. 3 those panels displaying
(with respect to 0°). This is clearly visible when comparing in Fig. 3 those panels displaying 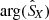 and
and 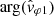 , respectively. Of course, Eq. (11), which determines the average Poynting flux over the wave period, is an exact equation and
, respectively. Of course, Eq. (11), which determines the average Poynting flux over the wave period, is an exact equation and 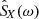 may have a finite imaginary part under the circumstance of a finite longitudinal component of the wave electric field (the longitudinal direction is defined with respect to k). But the waves discussed here propagate almost parallel to B0 (or anti-parallel if the “weak phase deviation” hypothesis is wrong) and have their frequencies of the order of a fraction of the electron gyrofrequency (0.05fce < f < 0.25fce), with the latter much smaller than the plasma frequency (fce ≪ fpe). Their magnetic field-aligned electric field component is thus negligible in comparison to their perpendicular one (E∥ ≪ E⊥) and it must also be the same for its longitudinal electric field component in comparison to their transverse one (El ≪ Et), since El ∼ E∥ and Et ∼ E⊥ when the propagation is almost parallel or anti-parallel. Therefore,
may have a finite imaginary part under the circumstance of a finite longitudinal component of the wave electric field (the longitudinal direction is defined with respect to k). But the waves discussed here propagate almost parallel to B0 (or anti-parallel if the “weak phase deviation” hypothesis is wrong) and have their frequencies of the order of a fraction of the electron gyrofrequency (0.05fce < f < 0.25fce), with the latter much smaller than the plasma frequency (fce ≪ fpe). Their magnetic field-aligned electric field component is thus negligible in comparison to their perpendicular one (E∥ ≪ E⊥) and it must also be the same for its longitudinal electric field component in comparison to their transverse one (El ≪ Et), since El ∼ E∥ and Et ∼ E⊥ when the propagation is almost parallel or anti-parallel. Therefore, 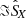 should in this case be negligible compared to
should in this case be negligible compared to 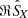 . In conclusion, we thus observe with
. In conclusion, we thus observe with 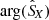 the same systematic relative phase shift problem as with
the same systematic relative phase shift problem as with 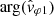 . Under the “weak phase deviation” hypothesis, the sign of SX from Eq. (11) gives a correct idea for the direction of wave energy flow along the radial direction X. However, the magnitude of SX is systematically underestimated because of the spurious phase shift which introduces an attenuation factor of the order of cos(60° ) in the worst case here. Also, as indicated in Appendix A, a more subtle amplitude correction could be performed by dividing the cross-product terms by the corresponding spectral correlation coefficients, as we did for the derivation of Eq. (15).
. Under the “weak phase deviation” hypothesis, the sign of SX from Eq. (11) gives a correct idea for the direction of wave energy flow along the radial direction X. However, the magnitude of SX is systematically underestimated because of the spurious phase shift which introduces an attenuation factor of the order of cos(60° ) in the worst case here. Also, as indicated in Appendix A, a more subtle amplitude correction could be performed by dividing the cross-product terms by the corresponding spectral correlation coefficients, as we did for the derivation of Eq. (15).
From a qualitative point of view, the wave emissions that we presented in Figs. 1 and 3 seem to be satisfactorily measured, and are a priori associated with waves emitted on the whistler mode. A quantitative comparison with the dispersion relation of the whistler mode is necessary to go further. Figures 4 and 5 are precisely devoted to this question. As we will see, in the current state of the art of electric field calibration, we find that the measurement of the V12 component is not as good as the measurement of the V23 component. In reality, the measurement of the electric field V23 is expected to be the best possible because the antennas ANT2 and ANT3 are arranged symmetrically to the spacecraft and the Sun (Khotyaintsev et al. 2021; Steinvall et al. 2021). This is why we established a second method to measure the signed phase velocity 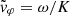 , using only one component of the electric field, namely, the EY component:
, using only one component of the electric field, namely, the EY component:
 |
Fig. 4. Case study of July 11, 2020: Spectra extracted from the spectrograms displayed in Fig. 3 and corresponding to 07:11:12 UTC, plus a second estimate of the phase velocity and a comparison with a theoretical whistler mode phase velocity model. From top to bottom: magnetic (PB) and electric (PE) trace power spectra of the measured field fluctuations; degree of polarization (DOP) and wave ellipticity (ellip); wave normal vector components (nX, nY, nZ) in SRF; angle between n and B0; observed phase velocities |
where
and
with b0 = B0/B0, the unit vector parallel to the ambient magnetic field. A derivation of this formula is given in Appendix B. Admittedly, this second method assumes that the parallel component of the electric field is negligible, whereas the first method indicated by Eq. (13) is valid in general. Nevertheless, this condition on E∥ is not a strong restriction because, as we can see above, in this case study, it should be properly verified in principle as well as a priori in many other situations.
Figure 4 is partly a cut at 07:11:12 UTC (July 11, 2020) of Fig. 3, done by extracting some spectra. From top to bottom, the first five panels show some of the wave parameters already described: the magnetic (PB) and electric (PE) trace power spectra; the degree of polarization and wave ellipticity (DOP, ellip); the wave normal vector components (nX, nY, nZ); and the angle it makes with B0 (θn, B0). We also slightly broadened the criterion to plot the points considered sufficiently polarized to cases corresponding to DOP ≥ 0.75. The last two panels display modules and arguments, respectively, of the complex numbers 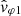 and
and 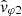 , from which the signed phase velocities ω/K1 and ω/K2 are computed as given by Eqs. (13) and (16), respectively. For comparison, the theoretical phase velocity of the whistler mode has been plotted with the measured phase velocities (green curve in the second-to-last panel). It was computed for a cold electron-proton magnetoplasma (Stix 1962), with n0 = 13.4 cm−3, B0 = 5.6 nT and θk, B0 = 7°. The plasma parameters used are those measured locally and shown in Fig. 2, while the wave propagation angle retained is a rough estimation as given by this wave analysis. As a matter of fact, the two empirical determinations of the phase velocity (blue and orange curves) exhibit a discrepancy with the theoretical whistler mode phase velocity (green curve). The
, from which the signed phase velocities ω/K1 and ω/K2 are computed as given by Eqs. (13) and (16), respectively. For comparison, the theoretical phase velocity of the whistler mode has been plotted with the measured phase velocities (green curve in the second-to-last panel). It was computed for a cold electron-proton magnetoplasma (Stix 1962), with n0 = 13.4 cm−3, B0 = 5.6 nT and θk, B0 = 7°. The plasma parameters used are those measured locally and shown in Fig. 2, while the wave propagation angle retained is a rough estimation as given by this wave analysis. As a matter of fact, the two empirical determinations of the phase velocity (blue and orange curves) exhibit a discrepancy with the theoretical whistler mode phase velocity (green curve). The 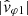 (blue curve) shows however a much larger variance than
(blue curve) shows however a much larger variance than 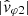 (orange curve), which follows in an almost parallel fashion the smooth variation of the theoretical prediction ω′/k (green curve), with a gap of the order of 200 km s−1. Concerning the complex argument of
(orange curve), which follows in an almost parallel fashion the smooth variation of the theoretical prediction ω′/k (green curve), with a gap of the order of 200 km s−1. Concerning the complex argument of 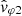 , which as explained in Appendix B should also be either 0° or 180° as for
, which as explained in Appendix B should also be either 0° or 180° as for 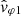 , there is a slightly lower deviation over the frequency range. The second method of measuring phase velocity is therefore better than the first, although there is still a measurement bias to be understood.
, there is a slightly lower deviation over the frequency range. The second method of measuring phase velocity is therefore better than the first, although there is still a measurement bias to be understood.
The last problem raised is not serious, ultimately, and it seems to have been come about through a lack of accounting for the Doppler frequency shift. Indeed, the green curve of Fig. 4, showing the theoretical phase velocity of the whistler mode, has been determined in the frame of the plasma, which is of course the solar wind (SW) plasma, and not in the frame of the Solar Orbiter (SO) spacecraft. Moreover, the observed phase velocity deviation is of the order of the solar wind velocity, which is consistent with the magnitude of the expected Doppler frequency shift. Indeed, the relationship between the pulsations ω and ω′ observed, respectively, in the SO and SW frames, is as follows :
with VSW the solar wind velocity relative to the spacecraft. Hence, the relationship between the phase velocities vφ = ω/k and 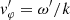 observed, respectively, in the SO and SW frames can be written as follows:
observed, respectively, in the SO and SW frames can be written as follows:
We note that when using the latter equation to evaluate vφ to ω, also 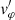 must be evaluated to ω′, as indicated by Eq. (19). In the present study, this inverse problem could be solved numerically, without any approximation of the Stix parameters used to express the theoretical dispersion relation of the cold magnetoplasma (Stix 1962). For the low-frequency range considered (f ≤ 0.2fce) and standard solar wind plasma conditions, the theoretical whistler dispersion relation is not greatly affected by finite temperature effects, which are therefore not considered here in this first approximation. A more detailed analysis should certainly consider a finite electron beta in its theoretical dispersion relation (Stansby et al. 2016).
must be evaluated to ω′, as indicated by Eq. (19). In the present study, this inverse problem could be solved numerically, without any approximation of the Stix parameters used to express the theoretical dispersion relation of the cold magnetoplasma (Stix 1962). For the low-frequency range considered (f ≤ 0.2fce) and standard solar wind plasma conditions, the theoretical whistler dispersion relation is not greatly affected by finite temperature effects, which are therefore not considered here in this first approximation. A more detailed analysis should certainly consider a finite electron beta in its theoretical dispersion relation (Stansby et al. 2016).
Figure 5 is aimed at measuring the Doppler effect for the case presented in Fig. 4. The theoretical prediction neglecting the Doppler effect (green curve) and the phase velocities measured by both methods (blue and orange curves) are reproduced. The purple and red curves shows the results obtained when taking into account the Doppler effect, for the two possible directions of wave propagation, respectively, −k and +k, as given from the measurement of n. Since we had for this time no solar wind velocity estimation, we used the standard slow wind velocity value of 300 km s−1. The direction of the wave vector +k was deduced from the wave analysis under the “weak phase deviation” hypothesis. The observation is clear, the orange curve aligns well with the red curve, while the purple curve is far from it. This observation leads to several conclusions. First of all, for relatively low frequencies (f ∼ 0.1 − 0.2fce) and a small Alfvén velocity (vA ≤ 0.1VSW), the Doppler effect has an important effect that must be taken into account when trying to observe the dispersion relation of the whistler mode (Huang & Sahraoui 2019). Secondly, it confirms that the direction of wave propagation in this case study is indeed antisunward, and therefore that the “weak phase deviation” hypothesis is shown to be correct. And, finally, it confirms that the second method of phase velocity measurement, based on the measurement of the electric field component V23 alone, is more accurate than the first method, based on the measurement of both components, V23 and V12.
 |
Fig. 5. Case study of July 11, 2020: Phase velocity spectra corresponding to 07:11:12 UTC, and comparison with theoretical models. Blue and orange curves: observed phase velocity spectra with DOP > 0.75, as already shown in Fig. 4, and still with LY = LZ = 9.1 m. Green curve: cold plasma model of the phase velocity of the whistler mode, calculated in the plasma frame, i.e., in the solar wind (SW) frame, at frequencies observed in the Solar Orbiter (SO) frame. Purple and red curves: same calculation as for the green curve but performed in the SO frame, thus taking into account the Doppler frequency shift, for the two directions of wave propagation, −k and +k, respectively. See text for more details. |
2.2. Waveform snapshots sampled at 256 Hz
The day of June 25, 2020 provides a typical example of observing a series of whistler mode wave emissions over a long period of time, from 8:00 to 23:50 UTC, when the RPW instrument operates in NORMAL mode and collects waveform snapshots of 2048 data points every 300 s. The same wave analysis performed in Sect. 2.1 on the CWF data can be applied to the present SWF data. Figure 6 displays the corresponding electromagnetic wave power spectrograms, where the calculation of the PSD, as well as the calibration and rotation in the SRF of the data, were performed in the same way as we did for the July 11, 2020 case study, except that the moving average applied to each field component was performed over 16 power spectra here; so, we get one PSD per waveform snapshot. The time resolution and time separation of the colored rectangular points in Fig. 6 are, thus, respectively, 8 s and 300 s, their frequency resolution being the same as in Fig. 1 (i.e., 2 Hz). Qualitatively, we can observe two different regions: before ∼18:00, the observed narrowband wave emissions are relatively sporadic in time and frequency; whereas after this time, they are observed with less variability at lower frequencies.
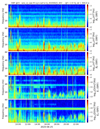 |
Fig. 6. Case study of June 25, 2020: Spectrograms of the electric and magnetic PSD computed on the ground from the snapshots of waveform. The line visible at 38 Hz on the electric field components is a spurious interference line. The weaker horizontal lines visible in the background of the magnetic field components are also stray lines, the same as we have already seen in Fig. 1. Strong parasitic vertical lines are also observed on the magnetic field components: they are caused by the activation of the SCM survival heater. |
Figure 7 shows the DC magnetic field and the electron plasma density for this period of time. A similar qualitative observation can be made. Before ∼18:00, the solar wind magnetic field exhibits strong fluctuations, as well as large scale dips associated with decreases in the X-component of the magnetic field, as in the case shown in Fig. 2. After ∼18:00, we observe a much more stable solar wind with an almost purely radial magnetic field.
 |
Fig. 7. Components and amplitude of the DC magnetic field measured by the MAG instrument for the same time interval as in Fig. 6, along with the electron plasma density obtained from the RPW instrument suite in two different ways : (1) via the measurement of the spacecraft potential (Khotyaintsev et al. 2021); and (2) by the detection of the plasma frequency peak (Maksimovic et al. 2020). blue Although we obtain slightly different density evaluations with these two methods, the general trend is the same. We also recall that the calibration of the first method relies on the possibility to measure the electron plasma density by the second method. |
Figure 8 shows the spectrograms obtained for the same set of wave parameters defined and computed for the July 11, 2020 case study, and displayed in Fig. 3, except for the last two panels for which 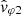 was calculated instead of
was calculated instead of 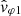 . At first glance, the overall conclusion is the same: all observed electromagnetic waves (DOP ≥ 0.9, except spurious points) show a very circularly RH polarization (ellip ≃ 1 and n ⋅ B0 > 0), and propagate approximately parallel to the ambient magnetic field (θn, B0 ≤ 15° and
. At first glance, the overall conclusion is the same: all observed electromagnetic waves (DOP ≥ 0.9, except spurious points) show a very circularly RH polarization (ellip ≃ 1 and n ⋅ B0 > 0), and propagate approximately parallel to the ambient magnetic field (θn, B0 ≤ 15° and 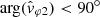 ). Consistently with our first remark, after ∼18:00 the observed waves propagate almost radially (nX ≃ −1), whereas prior to this, there were many more varied wave propagation angles observed. In all cases, an antisunward direction of wave propagation is observed (SX < 0, or B0X < 0 with a near field-aligned propagation). Conclusions on the direction of propagation are of course made under the “weak phase deviation” hypothesis.
). Consistently with our first remark, after ∼18:00 the observed waves propagate almost radially (nX ≃ −1), whereas prior to this, there were many more varied wave propagation angles observed. In all cases, an antisunward direction of wave propagation is observed (SX < 0, or B0X < 0 with a near field-aligned propagation). Conclusions on the direction of propagation are of course made under the “weak phase deviation” hypothesis.
 |
Fig. 8. Case study of June 25, 2020: Spectrograms of the wave parameters calculated on the ground from the snapshots of waveform, for the same time interval and frequency range as in Fig. 6, and with the same format as in Fig. 3, except for the last two panels where the second method of phase velocity measurement (as given by Eq. (16)) is used instead of the first one, as given by Eq. (13). Again, only cases matching DOP ≥ 0.9 are displayed. The strong spurious vertical lines already observed in the magnetic power spectrograms of Fig. 6 are still visible here in the top panel (PB), as well as in all others, as spurious coherent vertical lines. |
The same fact, observed in Fig. 3 between 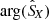 and
and 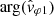 , is also observed in Fig. 8 between
, is also observed in Fig. 8 between 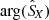 and
and 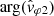 : the phase shift variations of
: the phase shift variations of 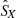 (with respect to 180°) are approximately the same as the phase shift variations of
(with respect to 180°) are approximately the same as the phase shift variations of 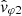 (with respect to 0°). Under the “weak phase deviation” hypothesis, these relative phase shifts vary approximately in the range of 40° to 80°. Although this range of angular deviation is slightly closer to 90°, this does not seem to be a problem because it is still possible to proceed with the “weak phase deviation” hypothesis or the opposite hypothesis. In any case, as we will check again now, the measurement of phase velocities that takes into account the Doppler effect often allows us to decide between the two hypotheses.
(with respect to 0°). Under the “weak phase deviation” hypothesis, these relative phase shifts vary approximately in the range of 40° to 80°. Although this range of angular deviation is slightly closer to 90°, this does not seem to be a problem because it is still possible to proceed with the “weak phase deviation” hypothesis or the opposite hypothesis. In any case, as we will check again now, the measurement of phase velocities that takes into account the Doppler effect often allows us to decide between the two hypotheses.
Figures 9 and 10 have been etablished in the same way as Figs. 4 and 5, the same analysis carried out for the July 11, 2020 case study on the Doppler effect being applied here. Figure 9 shows the spectra extracted at 08:25:16 UTC (June 25, 2020) from the spectrograms displayed in Fig. 8. The wave parameters are well defined and stable whenever DOP ≥ 0.75. The empirical phase velocities 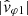 and
and 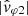 (blue and orange curves, respectively) are approximately parallel to the cold plasma prediction for the whistler mode wave, ω′/k (green curve), as determined in the SW frame with the observed parameters, n0 = 20.9 cm−3, B0 = 11.4 nT, and θn, B0 = 5°. The deviation observed with
(blue and orange curves, respectively) are approximately parallel to the cold plasma prediction for the whistler mode wave, ω′/k (green curve), as determined in the SW frame with the observed parameters, n0 = 20.9 cm−3, B0 = 11.4 nT, and θn, B0 = 5°. The deviation observed with 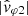 (the best estimate) is about 650 km s−1, which is significant compared to the standard slow solar wind velocity value of 300 km s−1. Indeed, as we will see, this observation makes the use of a constant effective antenna length to calibrate electric field data questionable. Up to now we have used LY = LZ = 9.1 m in order to get a correct order of magnitude most of the time. But, as described in Sect. 2.1 when introducing the method for calibrating electric field data, the response of the electric antenna system is expected to be sensitive to specific plasma parameters, such as the Debye length, and turns out to be quite variable (Kretzschmar et al. 2021; Steinvall et al. 2021). Figure 10 shows how the theoretical phase velocity estimated by neglecting the Doppler effect (green curve) is shifted upward (red curve) or downward (purple curve), when the Doppler frequency shift is taken into account, in the two possible cases of wave vector directions, either antisunward (+k, red curve) or sunward (−k, purple curve).
(the best estimate) is about 650 km s−1, which is significant compared to the standard slow solar wind velocity value of 300 km s−1. Indeed, as we will see, this observation makes the use of a constant effective antenna length to calibrate electric field data questionable. Up to now we have used LY = LZ = 9.1 m in order to get a correct order of magnitude most of the time. But, as described in Sect. 2.1 when introducing the method for calibrating electric field data, the response of the electric antenna system is expected to be sensitive to specific plasma parameters, such as the Debye length, and turns out to be quite variable (Kretzschmar et al. 2021; Steinvall et al. 2021). Figure 10 shows how the theoretical phase velocity estimated by neglecting the Doppler effect (green curve) is shifted upward (red curve) or downward (purple curve), when the Doppler frequency shift is taken into account, in the two possible cases of wave vector directions, either antisunward (+k, red curve) or sunward (−k, purple curve).
 |
Fig. 9. Case study of June 25, 2020: Wave parameter spectra extracted from the spectrograms displayed in Fig. 8 and corresponding to 08:25:15.7 UTC, in the same format as in Fig. 4. See text for more details. |
 |
Fig. 10. Case study of June 25, 2020: Theoretical model versus observed phase velocities for the event shown in Fig. 9 and occuring at 08:25:15.7 UTC, with LY = LZ = 14.6 m. In the same format as in Fig. 5. |
Here, we have taken k/k ≃ [ − 0.63, 0.43, 0.64] as observed in Figs. 9 or 8, considering the “weak phase deviation” hypothesis as correct. Since, again, we had for this time no solar wind velocity estimation, we used the standard slow wind value of 300 km s−1. Finally, for the orange curve (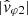 ) to be best aligned with the red curve (ω/k with +k), we had to take LY = LZ = 14.6 m. This large value deduced for the effective antenna lengths is actually of the order of their tip-to-tip length. A much greater increase in the effective antenna length is necessary if we want to align
) to be best aligned with the red curve (ω/k with +k), we had to take LY = LZ = 14.6 m. This large value deduced for the effective antenna lengths is actually of the order of their tip-to-tip length. A much greater increase in the effective antenna length is necessary if we want to align 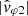 with the purple curve (ω/k with −k): LY = LZ = 19.7 m, which makes the hypothesis of whistler mode waves propagating sunward very unlikely in this case. We note that considering higher solar wind velocities would lead us to the same conclusion: the Doppler frequency shift would be increased (red curve correlatively shifted upward, purple curve downward), which would make the adequacy with waves propagating antisunward easier (LY = LZ < 14.6 m), and conversely, the hypothesis of waves propagating sunward even more implausible (LY = LZ > 19.7 m).
with the purple curve (ω/k with −k): LY = LZ = 19.7 m, which makes the hypothesis of whistler mode waves propagating sunward very unlikely in this case. We note that considering higher solar wind velocities would lead us to the same conclusion: the Doppler frequency shift would be increased (red curve correlatively shifted upward, purple curve downward), which would make the adequacy with waves propagating antisunward easier (LY = LZ < 14.6 m), and conversely, the hypothesis of waves propagating sunward even more implausible (LY = LZ > 19.7 m).
The contents of Fig. 11 are similar to Fig. 10, but related to the whistler event occuring at 20:55:16 UTC (June 25, 2020); thus, in the region where the solar wind appears more quiet. At this time, the plasma parameters measured locally, as shown in Fig. 7, are n0 = 29.4 cm−3 and B0 = 5.8 nT; and the wave parameters observed under the “weak phase deviation” hypothesis, as shown in Fig. 8, are k/k ≃ [ − 0.99, 0.03, 0.11] and θk, B0 ∼ 6°. We again considered a solar wind velocity value of 300 km s−1 and compared for different values of the effective antenna length, the observed phase velocity 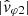 (orange curve) and the theoretical model, which includes the Doppler frequency shift (red and purple curves). A good agreement is found for the antisunward propagation (red curve), with LY = LZ = 12.3 m. We note that here, due to a particularly low value of Alfvén velocity (VA ≃ 23.4 km s−1), the Doppler effect has proportionally a very strong impact, even more important than for the case presented in Fig. 5.
(orange curve) and the theoretical model, which includes the Doppler frequency shift (red and purple curves). A good agreement is found for the antisunward propagation (red curve), with LY = LZ = 12.3 m. We note that here, due to a particularly low value of Alfvén velocity (VA ≃ 23.4 km s−1), the Doppler effect has proportionally a very strong impact, even more important than for the case presented in Fig. 5.
 |
Fig. 11. Case study of June 25, 2020: Same comparison between model and observation as in Fig. 10 but for the spectra measured at 20:55:15.7 UTC and with LY = LZ = 12.3 m. |
The 8 s time resolution used in the present spectral analysis of the SWF data may deserve some commentary. It is a fact that the whistler mode wave emissions we are studying demonstrate an intermittent nature, which is clearly visible when zooming in on the data, and already perceptible in the power spectrograms presented in Fig. 1, in the form of fine structures. However, using for example a time resolution of 2 s, as we did for the CWF data, and thus calculating four spectra per waveform snapshot, we actually obtain similar results with the most intense spectra among the four, with slightly less smooth curves. As a result, the average of the spectral data over the whole waveform snapshot does not seem to have distorted the wave analysis presented in this section. A more in-depth analysis of the individual wavepackets of the whistler mode waves is, of course, still necessary in order to characterize their intermittency or to observe cases of very short life span. The statistical method developed by Kretzschmar et al. (2021) to characterize whistler mode waves as a function of distance from the Sun and solar wind parameters is a first step toward such a fine analysis of individual wave packets.
To conclude this part of the study, devoted to the analysis of whistler mode waves from LFR waveforms, we can assert that both types of waveforms, whether CWF or SWF, make it possible to observe their polarization, their direction of propagation, and their dispersion relation, and thus to clearly identify and characterize them. The two one-day case studies presented here, as well as most of the cases observed so far, give the same results: the bursts of narrowband electromagnetic waves observed with frequencies between 0.05fce and 0.25fce are RH quasicircularly polarized, propagating away from the Sun in a direction that is almost parallel or antiparallel to the mean magnetic field, and having a phase velocity dependence with the frequency corresponding well to the dispersion relation of the whistler mode. A statistical work conducted in parallel by Kretzschmar et al. (2021) strongly confirms these results obtained on the basis of some case studies. They are also consistent with previous studies and results established in the free solar wind at 1 AU (Zhang et al. 1998; Lacombe et al. 2014; Stansby et al. 2016).
3. Observations from the spectral data
Given the limitations of Solar Orbiter’s telemetry, in order to be able to transmit the maximum amount of scientific information from the recorded waveforms, a strategy of onboard spectral calculations was implemented on the LFR. Basically, three types of spectral data are produced for each of the waveform data streams sampled at F0, F1, and F2. First, time-averaged spectral matrices (ASM), as given by Eq. (3), are computed routinely but with different computation parameters than those used in this paper. Regardless of the sampling rate of the data stream, the FFT used is always 256 points, and the non-overlapping moving average is performed over the same duration, nominally over 4 s. In order to save onboard calculation resources, no mean value was subtracted before applying the Hanning window for each 256-point segment. Indeed, this choice should not have consequences on the quality of the spectra because the first and last FFT frequency bins are dropped due to the frequency overlaps between the F0, F1, F2, and F3 frequency ranges. Thus, for the ASM calculated from the F2 data stream, only 96 frequency bins are retained, covering the frequency range from 7 Hz to 102 Hz with a resolution of 1 Hz. For completeness, we note that the onboard FFT computation has been implemented in the LFR FPGA with entire numbers having the same number of bits as the waveform data (i.e., 16 bits), therefore bringing on a disadvantage for weak signals: results lower than 1 are rounded to 0. As we show later in this work, the spectral products computed on board have a numerical noise level that is clearly higher than that observed for spectral products computed on the ground from waveforms.
Second, since the output of all these ASM nominally exceeds the telemetry allowed for RPW, two sets of basic wave parameters, BP2 and BP1, are calculated from them. Beforehand, the frequency resolutions of the ASM were reduced by averaging over packets of nominally eight consecutive frequency bins. The BP2 data are just a compression of these frequency-averaged ASM. The BP1 data consist of most of the wave parameters shown in Figs. 3 and 8. Nominally, BP1 data are transmitted to the ground every 4 s, thus without loss of temporal coverage; BP2 data every 20 s, and ASM every 1 h. ASM are the best LFR spectral data products, but they are nominally transmitted for data control and therefore generally too rarely for science.
In the following, we continue our analysis of whistler events with the BP2 dataset recorded on June 25, 2020.
3.1. Basic parameters set 2 of the 256 Hz data stream
Figure 12 shows, for the same period and format as in Fig. 6, the power spectrograms of electric and magnetic field fluctuations obtained from the BP2 dataset, which were computed on board from the F2 data stream. As indicated above for the nominal NORMAL mode, the temporal resolution and temporal separation of the BP2 power spectra are, respectively, 4 s and 20 s; and their frequency resolution is 8 Hz, namely, eight times lower than the frequency resolution of the onboard FFT calculation on which they are based.
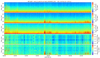 |
Fig. 12. Case study of June 25, 2020: Same time interval and format as in Fig. 6 but where the electric and magnetic field fluctuation power spectrograms are obtained from the BP2 dataset rotated in the SRF. See text for more details. |
As for the waveform data, the calibration of the BP2 data and their expression in the SRF calls for several comments. When decompressed, BP2 are nothing more than 5 × 5 electromagnetic spectral matrices (SMBP2) and must be calibrated and transformed in the SRF as such. As spectral data products combining electric and magnetic field data, their calibration was the responsibility of the LFR team. Standard matrix transformations were used based on the following tensorial relationship between the L1 (count unit, sensor frame) and L2 (physical unit, SRF) BP2 data:
where the prescript T denotes the transpose, the superscript −1 marks the inverse, and
with MSCM and MANT the global transfer matrices of the magnetic and electric antennas, respectively, which take into account the processing of the whole signal chain (i.e., the LFR/SCM, and LFR/BIAS/ANT transfer functions, respectively) including the sensor frame-specific geometric transformations to the SRF. In principle, the same transformations and transfer functions involved in the calibration of the waveform data that are presented in Sect. 2 have been implemented here. In particular, the same transformation given by Eqs. (1)–(2) for the calibration of the electric field fluctuation measurement was used again.
A comparison of Figs. 12 and 6 shows that the BP2 power spectrograms qualitatively recover the same observations made from the SWF power spectrograms. Even with a reduced frequency resolution of 8 Hz but with a better temporal resolution of 20 s (when zooming in, this is even clearer), we can notice that before ∼18:00 the observed narrowband wave emissions are quite sporadic in terms of time and frequency, while after this point, they are observed with less variability at lower frequencies. As indicated above, the background level observed on BP2 power spectrograms is higher than that observed on the corresponding SWF power spectrograms.
By taking advantage of the complete spectral matrix SMBP2, we can calculate the same set of wave parameters as the one elaborated in Sect. 2. Figure 13 shows the spectrograms of the wave parameters calculed from these BP2 spectral matrices, for the same period and format as in Fig. 8, except that we set here DOP > 0.75. At first glance, they are well consistent with those calculated with the corresponding waveform snapshots.
 |
Fig. 13. Case study of June 25, 2020: Same time interval and format as in Fig. 8, but here the wave parameters have been computed on the ground from the BP2 dataset. See text for more details. |
In order to quantify a little more the comparison between Figs. 13 and 8, we can, for example, compare the wave parameter spectra obtained from the waveform snapshots with those obtained from the BP2 spectral matrices, when temporal overlaps occur. The timestamp of an LFR data product is always the time of the first sample in the time series on which the data product is based. Figure 14 plots the BP2 spectra corresponding to 08:25:15.6 UTC (June 25, 2020), and can thus be compared with the SWF spectra plotted in Fig. 9. The theoretical phase velocity of the whistler mode wave as determined in the SW frame (ω′/k, green curve in the second-to-last panel) was calculated with n0 = 20.9 cm−3, B0 = 11.5 nT, and θn, B0 = 7°. The SWF and BP2 wave parameter spectra are qualitatively consistent with each other, with only small quantitative differences. The latter could be explained by the different time resolution used: BP2 spectra matrices (SMBP2) are averaged over 4 s while the SWF spectral matrices (SMSWF) here are averaged over 8 s. However, as we see later on with the BP1 dataset (Fig. 19), most of the wave power measured during the 8 s of the waveform snapshots occurs in the first 4 s. The quantitative differences are therefore mainly due to (i) the lower frequency resolution and (ii) the higher background level, which characterize the onboard calculation of BP2 data. These lower performance levels of BP2 data products mean some effects of frequency dispersion and digital noise when evaluating wave properties. This explain why the DOP measured from the SMBP2 are systematically lower than those measured from the SMSWF. It is the reason for which we have reduced the DOP threshold value to 0.75 for the display of Fig. 13. This is also the reason why it is important to take into account the finite spectral correlation coefficients in Eqs. (A.8) and (B.3) to estimate phase velocities. Indeed, it was a condition to find with the BP2 data the same agreement between the observations and the theoretical model as the one observed with the SWF data.
 |
Fig. 14. Case study of June 25, 2020: Same format and approximately the same time (08:25:15.6 UTC) as in Fig. 9, with the wave parameter spectra extracted from the BP2 spectrograms displayed in Fig. 13. See text for more details. |
In Fig. 15, as in Figs. 5 and 10, but for the BP2 wave parameter spectra shown in Fig. 14, we plot the theoretical phase velocity predictions, computed for the two possible wave propagation directions, against the observed phase velocity estimates. This figure can thus be compared with Fig. 10, which was computed for the SWF wave parameter spectra observed approximately at the same time and presented in Fig. 9. Again, we see a very good agreement between the measurement of the phase velocities of the observed waves, in particular, the 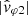 estimate (orange curve), and their theoretical calculation for whistler mode waves propagating antisunward (red curve). We note that almost the same effective antenna length of 14.6 m as in Fig. 10 was used. In the same vein, Fig. 16, which was computed for the BP2 wave parameter spectra observed at 20:55:15.2 UTC (June 25, 2020), can be compared to Fig. 11; however, due to a much smaller bandwidth of the wave emission, only one point with DOP > 0.71 is observed with the BP2 spectra. And this single point seems quite consistent. Therefore, most of the isolated colored bars shown in Fig. 13 are surprisingly relevant from a scientific point of view.
estimate (orange curve), and their theoretical calculation for whistler mode waves propagating antisunward (red curve). We note that almost the same effective antenna length of 14.6 m as in Fig. 10 was used. In the same vein, Fig. 16, which was computed for the BP2 wave parameter spectra observed at 20:55:15.2 UTC (June 25, 2020), can be compared to Fig. 11; however, due to a much smaller bandwidth of the wave emission, only one point with DOP > 0.71 is observed with the BP2 spectra. And this single point seems quite consistent. Therefore, most of the isolated colored bars shown in Fig. 13 are surprisingly relevant from a scientific point of view.
 |
Fig. 15. Case study of June 25, 2020: Same format and approximately the same time (08:25:15.6 UTC) as in Fig. 10, along with a comparison between the theoretical model and the observed phase velocities, obtained with the BP2 spectra shown in Fig. 14, with LY = LZ = 14.1 m. |
 |
Fig. 16. Case study of June 25, 2020: Same comparison between the model and observation as in Fig. 15, but for the BP2 spectra measured at 20:55:15.2 UTC, and with LY = LZ = 12.7 m. |
To conclude this part of the paper, we can assert that the observations made with the BP2 spectral dataset are as reliable as those made with the CWF and SWF datasets.
3.2. Basic parameters set 1 of the 256 Hz data stream
Although BP2 data provide better temporal coverage than SWF data, full statistical characterization of solar wind electromagnetic wave emissions, particularly with regard to their intermittent nature, requires complete coverage. The BP1 dataset is specifically designed to meet this requirement. As with BP2 data, BP1 data are calculated on board from the frequency-averaged ASM, except that all of them are used here, so that BP1 data are produced at the same rate as the ASM, that is, nominally every 4s.
All wave parameters shown in Figs. 3, 8, and 13, which only involve SCM measurements of magnetic field fluctuations, were computed on board without difficulties: the magnetic trace power spectra (PB), the degree of polarization (DOP), the wave ellipticity (ellip), and the wave normal vector (n). The reason is that, as a first approximation, the three SCM antennas (i) have identical transfer functions and (ii) are perpendicular to each other. Indeed, the computations of DOP and ellip by Eqs. (4) and (5), respectively, are independent of any orthonormal transformation of the magnetic spectral matrices. The same applies to the calculation of PB by tr SMB, which must only be calibrated on the ground with one factor, as well as to the form of Eqs. (6)–(8) to determine the components of the unit vector n. These can, therefore, simply be expressed within the frame of measurement of the magnetic field fluctuations (i.e., in the SCM axis system).
The calculation of the radial X-component of the Poynting vector, as well as the phase velocity estimator, requires cross-calibration of the electric and magnetic field data and their transformation in the SRF. The onboard calculation of SX, as given by Eq. (11), has been successfully implemented by updating specific coefficients in the LFR flight software, called k-coefficients, from the ground. They actually integrate all the transfer functions and geometric transformations required, as summarized in Eq. (21). Appendix C gives some details on how these k-coefficients were determined. In the same vein, the calculation of a phase velocity similar to 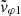 , as given by Eq. (13), was programmed but could not be completed. In particular, an update of the LFR flight software is in progress for this purpose.
, as given by Eq. (13), was programmed but could not be completed. In particular, an update of the LFR flight software is in progress for this purpose.
The onboard calculation of PE from the two electric field components measured with non-orthogonal antennas of different lengths also requires a transformation and cross-calibration of the components to an orthonormal frame (e.g., the SRF). Other k-coefficients are implemented by LFR for that purpose. See Appendix C for more details. However, as a first approximation, the two electric field antennas can be considered to be of the same effective length and orthogonal to each other.
To illustrate the proper operation of the LFR onboard calculation of BP1 data, Fig. 17 shows for comparison these data for the same time interval and format as the wave parameters calculated from BP2 data and displayed on the first eight panels of Fig. 13. The Poynting flux SX is indeed not shown because the correct update of the k-coefficients, took place only on July 6, 2020, which is later than the recording of these data. To deepen the comparison, Fig. 18 traces the spectra extracted from Fig. 17 and corresponding to 08:25:15.6 UTC (June 25, 2020), which should, in principle, be identical to Fig. 14 calculated from BP2 data (except for the phase velocity panels). Small differences are due to the compression of BP1 data prior to transmission, especially the DOP and ellip wave parameters, which are encoded with three and four bits, respectively. The slight difference observable on PE is due to the fact that the onboard calculations were still performed with the default k-coefficients, that is, without rotating the electric field components in the SRF, as was done here with the BP2 data.
 |
Fig. 17. Case study of June 25, 2020: Same time interval and format as in the first eight upper panels of Fig. 13, but here the wave parameters (magnetic and electric trace power spectra, PE and PB, degree of polarization, DOP, ellipticity, ellip, and wave normal vector, n) were computed on board (BP1 dataset). See text for more details. |
 |
Fig. 18. Case study of June 25, 2020: Same format and the same time (08:25:15.6 UTC) as in Fig. 14, with wave parameter spectra extracted from the BP1 spectrograms shown in Fig. 17. |
Figure 19 is a zoom of Fig. 17 between 08:24:00 and 08:28:00 UTC (June 25, 2020), which is aimed at making the intermittency perceptible. For instance, it shows that the intense wave emission observed at 08:25:15.6 UTC (June 25, 2020) with the snapshots of waveform (see Figs. 8 and 9) is, in fact, an isolated event of 4 s (which, moreover, is not the most intense).
Figures 20 and 21 briefly present the last case study in this article. Zooming in on a few minutes of August 27, 2020, these again illustrate the intermittency of the whistler mode waves and the correct calculation of BP1 data, but this time including the Poynting flux SX, showing that the update of the k-coefficients worked very well. For example, the spectrum of SX measured at 04:26:44 UTC (August 27, 2020) with BP2 data (Fig. 20) corresponds to a very good accuracy to that observed with BP1 data at the same time (Fig. 21).
 |
Fig. 20. Case study of August 27, 2020: Spectrograms of the wave parameters computed from the BP2 dataset, as in Fig. 13, between 04:23:15 and 04:30:50 UTC. |
 |
Fig. 21. Case study of August 27, 2020: Same time interval as in Fig. 20, with the spectrograms of the wave parameters computed on board (BP1 dataset) as in Figs. 17 and 19, but with the addition of the radial X-component of the Poynting flux (last panel). |
4. Discussion and conclusion
In this article, we strive to characterize the properties of the whistler mode waves we have observed, in particular their propagation direction, and to remove some of the instrumental ambiguities that arise from this problem. In practice, the measurement of the Poynting flux (SX) and that of a signed phase velocity (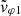 or
or 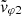 ) have indeed raised the problem of a recurrent phase shift between the measurements of the electric and magnetic field components of the fluctuations. The origin of this phase shift is still unknown and it seems relatively constant for given solar wind conditions. Kretzschmar et al. (2021) gives some statistics on this subject. Although there is always a possible ambiguity, we demonstrate, via the several case studies presented here, that the observed phase shifts (with respect to the theoretical predictions) can generally be neglected when determining the sign of SX or the direction of the wave propagation. We called this condition the “weak phase deviation” hypothesis, as opposed to the “strong phase deviation” hypothesis.
) have indeed raised the problem of a recurrent phase shift between the measurements of the electric and magnetic field components of the fluctuations. The origin of this phase shift is still unknown and it seems relatively constant for given solar wind conditions. Kretzschmar et al. (2021) gives some statistics on this subject. Although there is always a possible ambiguity, we demonstrate, via the several case studies presented here, that the observed phase shifts (with respect to the theoretical predictions) can generally be neglected when determining the sign of SX or the direction of the wave propagation. We called this condition the “weak phase deviation” hypothesis, as opposed to the “strong phase deviation” hypothesis.
In favor of this “weak phase deviation” hypothesis, there are cases where a large Doppler frequency shift is theoretically expected and give strong constraints on the data interpretation. In particular, if the opposite hypothesis had been assumed, that is, a “strong phase deviation” and, thus, a reversal of the direction of wave propagation, this would have implied effective antenna lengths far in excess of the physical tip-to-tip size of the electric antennas (14 m).
This leads us to another instrumental problem, namely, the absolute calibration of the electric field measurement, which is shown to be dependent of the solar wind condition (Steinvall et al. 2021; Kretzschmar et al. 2021). At the time of writing, there is still no clear understanding of the factors that accurately determine the effective electric antenna lengths. While there is a clear general trend correlated with the Debye length, other possible effects may need further investigation.
Assuming a slow SW speed of 300 km s−1 to model the Doppler frequency shifts, Fig. 10 (and correlatively Fig. 15) reveals a good consistency between the theoretical model and the observations by adjusting the LY and LZ antenna lengths to 14.6 m. Given the absence of direct plasma measurements and the electric calibration issue, one can consider this value as marginally acceptable. Moreover, following the deHoffmann-Teller analysis performed by Steinvall et al. (2021) that consist in minimizing the function:
with E0Y the Y-component of the SW convection electric field, as measured by the RPW instrument suite and provided as L3 data (Khotyaintsev et al. 2021), we could (i) validate the hypothesis of a slow solar wind, and (ii) observe a positive Z-component of the SW speed on the order of 50 % of its X-component. As in this case study, we observe kZ/k ≈ +0.66, a significant additional positive contribution in the Doppler frequency shift is expected. A value as large as 14.6 m invoked for the effective length of the antennas is, thus, no longer necessary, allowing for greater consistency in our results.
Regardless of their scientific interest, as whistler mode waves are widely observed in the slow solar wind, their observation was a natural reference to demonstrate the proper working of the LFR. All the results obtained from the waveform data products, CWF and SWF, could be obtained again from the spectral data products, BP2 and BP1. Nevetheless, given the reduced frequency resolution and higher background noise of the spectral datasets, the comparison is not always feasible. Where possible, comparisons between all LFR data products show a very good consistency. We note, on the other hand, that if the comparison was not always possible it was also for a very good reason: the spectral data products computed on board were designed to provide full temporal coverage of wave emissions, which is not the case for SWF data. For example, the question of the sporadic occurence of whistler mode waves in the solar wind, as pointed out and discussed by Lacombe et al. (2014) and Tong et al. (2019a), could be addressed statistically with the BP1 dataset in more depth than has been done to date.
For completness, we should mention that the case studies and validations presented in this article have been limited to electromagnetic wave events observed in the F2 frequency range. At this early stage of the Solar Orbiter mission, wave events observed at much higher frequencies are very few. For example, a remarkable case occurred during the first Solar Orbiter Venus flyby on December 27, 2020. An overview of the observations made by the RPW instrument suite during this event is presented by Hadid et al. (2021). The RPW instrument operated in BURST mode so that the LFR F2 frequency range was covered by the CWF data, while the upper F1 and F0 frequency ranges were covered by the BP2 and BP1 datasets. It was thus possible to carry out observations without any loss of time coverage, just at and downstream of the shock crossing, of very intense electrostatic waves over the entire frequency range of the LFR, as well as strong whistler mode waves up to the F1 frequency range. These advantages illustrate the flexibility of the LFR in these respects.
Acknowledgments
We thank the Centre National d’Etudes Spatiales (CNES), the Centre National de la Recherche Scientifique (CNRS) and all the institutes involved for their funding and support. The RPW instrument has been designed and funded by CNES, CNRS, the Paris Observatory, the Swedish National Space Agency, ESA-PRODEX and all the participating institutes. Solar Orbiter magnetometer operations are funded by the UK Space Agency (grant ST/T001062/1). Tim Horbury is supported by STFC grant ST/S000364/1. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA.
References
- Agapitov, O. V., Dudok de Wit, T., Mozer, F. S., et al. 2020, ApJ, 891, L20 [Google Scholar]
- Behar, E., Sahraoui, S., & Berčič, L. 2020, J. Geophys. Res., 125, 10 [Google Scholar]
- Gary, S. P., Skoug, R. M., & Daughton, W. 1999, Phys. Plasmas, 6, 2607 [Google Scholar]
- Graham, D. B., Khotyaintsev, Yu. V., Vaivads, A., et al. 2021, A&A, 656, A23 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadid, L. Z., Edberg, N. J. T., Chust, T., et al. 2021, A&A, 656, A18 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 (Solar Orbiter SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, S. Y., & Sahraoui, F. 2019, ApJ, 876, 138 [Google Scholar]
- Jagarlamudi, V. K., Alexandrova, O., Berčič, L., et al. 2020, ApJ, 897, 118 [Google Scholar]
- Jagarlamudi, V. K., Dudok de Wit, T., Froment, C., et al. 2021, A&A, 650, A9 (Parker Solar Probe SI) [EDP Sciences] [Google Scholar]
- Jannet, G., Dudok de Wit, T., Krasnoselskikh, V., et al. 2021, J. Geophys. Res., 126, e2020JA028543 [Google Scholar]
- Khotyaintsev, Yu. V., Graham, D. B., Vaivads, A., et al. 2021, A&A, 656, A19 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretzschmar, M., Chust, T., Krasnoselskikh, V., et al. 2021, A&A, 656, A24 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacombe, C., Alexandrova, O., Matteini, L., et al. 2014, ApJ, 796, 5 [Google Scholar]
- Lavraud, B., Fargette, N., Reville, V., et al. 2020, ApJ, 894, L19 [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 (Solar Orbiter SI) [EDP Sciences] [Google Scholar]
- Means, J. D. 1972, J. Geophys. Res., 77, 5551 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 (Solar Orbiter SI) [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 (Solar Orbiter SI) [EDP Sciences] [Google Scholar]
- Pinçon, J. L., Marouan, Y., & Lefeuvre, F. 1992, Ann. Geophys., 10, 82 [Google Scholar]
- Sahraoui, F., Goldstein, M. L., Robert, P., et al. 2009, Phys. Rev. Lett., 102 [CrossRef] [Google Scholar]
- Samson, J. C. 1973, Geophys. J. R. Astron. Soc., 34, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, J. C., & Olson, J. V. 1980, Geophys. J. Int., 61, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Santolík, O., Nĕmec, F., Parrot, M., et al. 2006, Planet Space Sci., 54, 512 [CrossRef] [Google Scholar]
- Santolík, O., Pickett, J. S., Gurnett, D. A., et al. 2010, J. Geophys. Res., 115, A00F13 [Google Scholar]
- Stansby, D., Horbury, T. S., Chen, C. H. K., et al. 2016, ApJ, 829, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Steinvall, K., Khotyaintsev, Yu. V., Cozzani, G., et al. 2021, A&A, 656, A9 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stix, T. H. 1962, The Theory of Plasma Waves (McGraw-Hill: New York) [Google Scholar]
- Szabo, A., Larson, D., Whittlesey, P., et al. 2020, ApJS, 246, 47 [Google Scholar]
- Taubenschuss, U., & Santolík, O. 2019, Surv. Geophys., 40, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Tong, Y., Vasko, I. Y., Pulupa, M., et al. 2019a, ApJ, 870, L6 [Google Scholar]
- Tong, Y., Vasko, I. Y., Artemyev, A. V., et al. 2019b, ApJ, 878, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Vasko, I. Y., Kuzichev, I. V., Artemyev, A. V., et al. 2020, Phys. of Plasmas, 27 [Google Scholar]
- Zhang, Y., Matsumoto, H., & Kojima, H. 1998, J. Geophys. Res., 103, 20529 [CrossRef] [Google Scholar]
Appendix A: Phase velocity formula using both electric field components
In the the presence of a single plane wave at a given frequency, ω/2π, with a wave vector, k, all wave field vectors, for instance, E or B, as a function of time, t, and position, r, can be written as:
where  represents the complex amplitude vector of the wave field vector A. Substituting this general form of electric and magnetic field fluctuations in the Maxwell-Faraday equation, and using Eq. (10), gives a straightforward expression:
represents the complex amplitude vector of the wave field vector A. Substituting this general form of electric and magnetic field fluctuations in the Maxwell-Faraday equation, and using Eq. (10), gives a straightforward expression:
Then the projection of this equation on the X-axis yields:
The question now is to develop an experimental estimate of this theoretical relationship. Taking advantage of the calculation of the SM components as given by Eq. (3), we propose to evaluate the absolute value of a theoretical wave field component 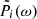 using the following approximation based on the measured spectral autocorrelation :
using the following approximation based on the measured spectral autocorrelation :
In order to evaluate its complex argument, only a relative determination is, in fact, necessary, for example, related to another wave field component 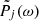 . Based on the measured spectral crosscorrelation, we propose the following estimate for the relative phase between two components :
. Based on the measured spectral crosscorrelation, we propose the following estimate for the relative phase between two components :
Combining Eq. (A.4) and Eq. (A.5), any theoretical spectral cross-product term can thus be approximated as:
with
as the spectral correlation coefficient between components i and j.
By multiplying the numerator and denominator in Eq. (A.3) by 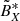 , and substituting for the theoretical terms their experimental measure as proposed by Eq. (A.6), we finally obtain :
, and substituting for the theoretical terms their experimental measure as proposed by Eq. (A.6), we finally obtain :
The following comments describe this result more fully. From the derivation above, it is known that in the pure plane wave hypothesis, the imaginary part of 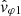 should be null. In practice, first of all because a wave is never a pure plane wave, but also due to instrumental biases, a deviation from the real axis of this number can be observed. This is why we have written the Eq. (13) such that we can evaluate the deviation from the ideal situation. As shown throughout the present article, we are facing a slight but evident phase shift issue between the electric and magnetic field fluctuation measurements. It should also be noted that the inclusion of correlation coefficients in this calculation may seem paradoxical. Indeed, assuming a pure plane wave, all field components should perfectly be correlated and these coefficients should constantly be equal to 1. However, for the same reason of non-ideal measurement conditions, as well as due to the mixing of several plane waves over a finite frequency range, it sometimes seems important, when estimating the amplitude of the spectral cross-product terms, to take these attenuation coefficients into account. The same amplitude correction could be applied when estimating the complex Poynting flux
should be null. In practice, first of all because a wave is never a pure plane wave, but also due to instrumental biases, a deviation from the real axis of this number can be observed. This is why we have written the Eq. (13) such that we can evaluate the deviation from the ideal situation. As shown throughout the present article, we are facing a slight but evident phase shift issue between the electric and magnetic field fluctuation measurements. It should also be noted that the inclusion of correlation coefficients in this calculation may seem paradoxical. Indeed, assuming a pure plane wave, all field components should perfectly be correlated and these coefficients should constantly be equal to 1. However, for the same reason of non-ideal measurement conditions, as well as due to the mixing of several plane waves over a finite frequency range, it sometimes seems important, when estimating the amplitude of the spectral cross-product terms, to take these attenuation coefficients into account. The same amplitude correction could be applied when estimating the complex Poynting flux 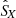 , as given by Eq. (12). As we do not seek to compare quantitatively this measurement with a theoretical model as we do for the measurement of the phase velocity with the cold plasma dispersion relation, it has been omitted as a first approximation.
, as given by Eq. (12). As we do not seek to compare quantitatively this measurement with a theoretical model as we do for the measurement of the phase velocity with the cold plasma dispersion relation, it has been omitted as a first approximation.
Appendix B: Phase velocity formula using a single electric field component
By carrying out the vector product of B0 with both sides of Eq. (A.2) from the left, and by making 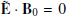 in the result, we directly obtain :
in the result, we directly obtain :
This equation is a general expression of electric field fluctuations entirely determined by the knowledge of magnetic field fluctuations, when the field-aligned component of the electric field (E∥) is negligible. As we wish to use only the EY component, we just have to take the projection on the Y-axis of this equation, which leads after multiplication by 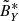 to:
to:
By making the same approximations as in the appendix A, namely, using Eq. (A.6), we finally obtain :
The derivation of this result is done in exactly the same spirit as in Appendix A. For the same reason as for 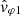 , the imaginary part of
, the imaginary part of 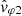 should also ideally be zero. The formula (16) was therefore written in the same way as Eq. (13), which allows us to deal with the deviation from the ideal situation.
should also ideally be zero. The formula (16) was therefore written in the same way as Eq. (13), which allows us to deal with the deviation from the ideal situation.
The choice to multiply by 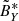 to get Eq. (B.2) deserves a last comment. It is indeed somewhat arbitrary and any other variable well correlated with the components of the electromagnetic field is also possible. In the particular case where
to get Eq. (B.2) deserves a last comment. It is indeed somewhat arbitrary and any other variable well correlated with the components of the electromagnetic field is also possible. In the particular case where 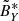 becomes too small, for example when the waves propagate perpendicularly to the plane ZX, it is preferable to multiply by
becomes too small, for example when the waves propagate perpendicularly to the plane ZX, it is preferable to multiply by 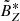 or
or 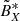 to obtain another formula, which in this case, provides a better level of precision for the computation. The same remark can be made for the case of obtaining Eq. (A.8).
to obtain another formula, which in this case, provides a better level of precision for the computation. The same remark can be made for the case of obtaining Eq. (A.8).
Appendix C: Onboard transformation and calibration using k-coefficients
Let D(ω) = [DY, DZ]SRF be the 2D-electric field vector in physical unit (V/m) that the electric antenna system feels (i.e., the ANT input), and VANT(ω) = [V12, V23]ANT be the corresponding ANT output in engineering unit (V). The relationship between these two vectors defines the transfer matrix of ANT:
where the indices 1, 2 refer to the two directions of measurement of the electric field. In general, the inverse of Eq. (C.1) reads:
For A1Y = + 3.5 m, A1Z = − 7. m, A2Y = − 7. m, and A2Z = 0. m, Eq. (C.2) is equivalent to Eqs. (1)-(2) with LY = LZ = 7 m.
The electrical signals V12(ω), V23(ω) are then injected into the BIAS unit and finally sampled by the LFR. Let ELFR(ω) = [E1, E2]LFR be the corresponding LFR output in count unit, which is simply related to VANT(ω) by a factor equal to the BIAS/LFR transfer function:
In the following, for simplicity, this transfer function factor will be dropped in the notations and implicitly incorporated into the ANT transfer matrix components.
After straightforward calculations, the electric trace power spectrum PE can be expressed as follows:
where the factor
is a calibration factor to be aplied on the ground, and
are the k-coefficients transmitted by telecommand and dedicated to the onboard computation of the term in brackets in the right part of Eq. (C.4).
Similarly, let H(ω) = [HX, HY, HZ]SRF be the 3D-magnetic field vector in physical unit (nT) that the search-coil magnetometer feels (i.e., the SCM input), and JSCM(ω) = [J1, J2, J3]SCM be the corresponding SCM output in engineering unit (V). The relationship between these two vectors defines the transfer matrix of SCM:
where
is the transfer matrix expressed in its own magnetic coil axis system, and MSCM − SRF is the transformation matrix from the SRF to this SCM B1-B2-B3 axis system. The inverse of Eq. (C.8) can be written in the following form:
The electrical signals J1(ω), J2(ω), J3(ω) are then injected into the LFR for digitization. Let BLFR(ω) = [B1, B2, B3]LFR be the corresponding LFR output in count unit, which is simply related to JSCM(ω) by a factor equal to the LFR transfer function:
In the following, as above for the ANT signals, this transfer function factor will be dropped in the notations and implicitly incorporated into the SCM transfer matrix components.
After some calculations in the same vein as above, the radial X-component of the Poynting flux 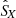 can be expressed as follows:
can be expressed as follows:
where the factor
is a calibration factor to be aplied on the ground, and
with
are the k-coefficients transmitted by telecommand and dedicated to the onboard computation of the term in brackets in the right part of Eq. (C.12).
All Figures
 |
Fig. 1. Case study of July 11, 2020: Spectrograms of the electric and magnetic PSD computed on the ground from the continuous waveforms. The line visible at 24 Hz on the electric field components is a spurious interference line. Although weaker, other stray horizontal lines are also visible in the background of the magnetic field components. They are produced at 8 Hz and its harmonics, and originate from the spacecraft (AOCS Synchronization Pulse). |
| In the text | |
 |
Fig. 2. Components and amplitude of the DC magnetic field (B0) measured by the MAG instrument (Horbury et al. 2020), and the electron plasma density (n0) as estimated by the RPW instrument suite from the spacecraft potential measurement (Khotyaintsev et al. 2021) for the same time interval as in Fig. 1. |
| In the text | |
 |
Fig. 3. Case study of July 11, 2020: Spectrograms of several wave parameters computed on the ground from the continuous waveforms, for the same time interval and frequency range as in Fig. 1. From top to bottom: total power of magnetic (PB) and electric (PE) field fluctuations measured, degree of polarization (DOP), wave ellipticity (ellip), wave normal vector components (nX, nY, nZ) in SRF, angle between the wave normal vector (n), and the DC magnetic field vector (B0), radial SRF X-component of the Poynting vector (SX) as the real part of the complex Poynting flux |
| In the text | |
 |
Fig. 4. Case study of July 11, 2020: Spectra extracted from the spectrograms displayed in Fig. 3 and corresponding to 07:11:12 UTC, plus a second estimate of the phase velocity and a comparison with a theoretical whistler mode phase velocity model. From top to bottom: magnetic (PB) and electric (PE) trace power spectra of the measured field fluctuations; degree of polarization (DOP) and wave ellipticity (ellip); wave normal vector components (nX, nY, nZ) in SRF; angle between n and B0; observed phase velocities |
| In the text | |
 |
Fig. 5. Case study of July 11, 2020: Phase velocity spectra corresponding to 07:11:12 UTC, and comparison with theoretical models. Blue and orange curves: observed phase velocity spectra with DOP > 0.75, as already shown in Fig. 4, and still with LY = LZ = 9.1 m. Green curve: cold plasma model of the phase velocity of the whistler mode, calculated in the plasma frame, i.e., in the solar wind (SW) frame, at frequencies observed in the Solar Orbiter (SO) frame. Purple and red curves: same calculation as for the green curve but performed in the SO frame, thus taking into account the Doppler frequency shift, for the two directions of wave propagation, −k and +k, respectively. See text for more details. |
| In the text | |
 |
Fig. 6. Case study of June 25, 2020: Spectrograms of the electric and magnetic PSD computed on the ground from the snapshots of waveform. The line visible at 38 Hz on the electric field components is a spurious interference line. The weaker horizontal lines visible in the background of the magnetic field components are also stray lines, the same as we have already seen in Fig. 1. Strong parasitic vertical lines are also observed on the magnetic field components: they are caused by the activation of the SCM survival heater. |
| In the text | |
 |
Fig. 7. Components and amplitude of the DC magnetic field measured by the MAG instrument for the same time interval as in Fig. 6, along with the electron plasma density obtained from the RPW instrument suite in two different ways : (1) via the measurement of the spacecraft potential (Khotyaintsev et al. 2021); and (2) by the detection of the plasma frequency peak (Maksimovic et al. 2020). blue Although we obtain slightly different density evaluations with these two methods, the general trend is the same. We also recall that the calibration of the first method relies on the possibility to measure the electron plasma density by the second method. |
| In the text | |
 |
Fig. 8. Case study of June 25, 2020: Spectrograms of the wave parameters calculated on the ground from the snapshots of waveform, for the same time interval and frequency range as in Fig. 6, and with the same format as in Fig. 3, except for the last two panels where the second method of phase velocity measurement (as given by Eq. (16)) is used instead of the first one, as given by Eq. (13). Again, only cases matching DOP ≥ 0.9 are displayed. The strong spurious vertical lines already observed in the magnetic power spectrograms of Fig. 6 are still visible here in the top panel (PB), as well as in all others, as spurious coherent vertical lines. |
| In the text | |
 |
Fig. 9. Case study of June 25, 2020: Wave parameter spectra extracted from the spectrograms displayed in Fig. 8 and corresponding to 08:25:15.7 UTC, in the same format as in Fig. 4. See text for more details. |
| In the text | |
 |
Fig. 10. Case study of June 25, 2020: Theoretical model versus observed phase velocities for the event shown in Fig. 9 and occuring at 08:25:15.7 UTC, with LY = LZ = 14.6 m. In the same format as in Fig. 5. |
| In the text | |
 |
Fig. 11. Case study of June 25, 2020: Same comparison between model and observation as in Fig. 10 but for the spectra measured at 20:55:15.7 UTC and with LY = LZ = 12.3 m. |
| In the text | |
 |
Fig. 12. Case study of June 25, 2020: Same time interval and format as in Fig. 6 but where the electric and magnetic field fluctuation power spectrograms are obtained from the BP2 dataset rotated in the SRF. See text for more details. |
| In the text | |
 |
Fig. 13. Case study of June 25, 2020: Same time interval and format as in Fig. 8, but here the wave parameters have been computed on the ground from the BP2 dataset. See text for more details. |
| In the text | |
 |
Fig. 14. Case study of June 25, 2020: Same format and approximately the same time (08:25:15.6 UTC) as in Fig. 9, with the wave parameter spectra extracted from the BP2 spectrograms displayed in Fig. 13. See text for more details. |
| In the text | |
 |
Fig. 15. Case study of June 25, 2020: Same format and approximately the same time (08:25:15.6 UTC) as in Fig. 10, along with a comparison between the theoretical model and the observed phase velocities, obtained with the BP2 spectra shown in Fig. 14, with LY = LZ = 14.1 m. |
| In the text | |
 |
Fig. 16. Case study of June 25, 2020: Same comparison between the model and observation as in Fig. 15, but for the BP2 spectra measured at 20:55:15.2 UTC, and with LY = LZ = 12.7 m. |
| In the text | |
 |
Fig. 17. Case study of June 25, 2020: Same time interval and format as in the first eight upper panels of Fig. 13, but here the wave parameters (magnetic and electric trace power spectra, PE and PB, degree of polarization, DOP, ellipticity, ellip, and wave normal vector, n) were computed on board (BP1 dataset). See text for more details. |
| In the text | |
 |
Fig. 18. Case study of June 25, 2020: Same format and the same time (08:25:15.6 UTC) as in Fig. 14, with wave parameter spectra extracted from the BP1 spectrograms shown in Fig. 17. |
| In the text | |
 |
Fig. 19. Case study of June 25, 2020: Zoom of Fig. 17 between 08:24:00 and 08:28:00 UTC. |
| In the text | |
 |
Fig. 20. Case study of August 27, 2020: Spectrograms of the wave parameters computed from the BP2 dataset, as in Fig. 13, between 04:23:15 and 04:30:50 UTC. |
| In the text | |
 |
Fig. 21. Case study of August 27, 2020: Same time interval as in Fig. 20, with the spectrograms of the wave parameters computed on board (BP1 dataset) as in Figs. 17 and 19, but with the addition of the radial X-component of the Poynting flux (last panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



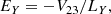
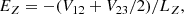
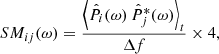
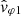
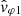
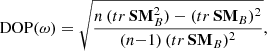
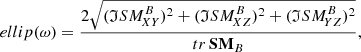
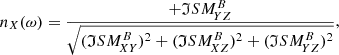
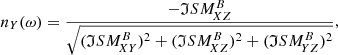
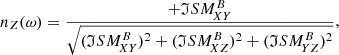
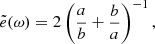
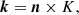
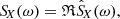
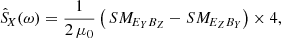
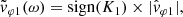
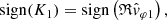
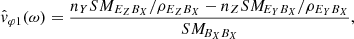
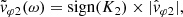
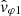
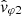
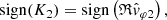
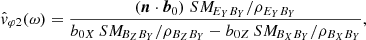
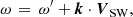
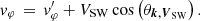
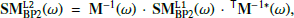
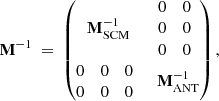
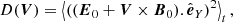
![$$ \begin{aligned} \mathbf A (t, \mathbf r ) = \mathfrak{R} \left[\tilde{\mathbf{A }}(\omega , \mathbf k ) \exp \left(i\omega t{-}i\mathbf k \cdot \mathbf r \right) \right], \end{aligned} $$](/articles/aa/full_html/2021/12/aa40932-21/aa40932-21-eq80.gif)
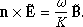
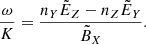
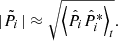
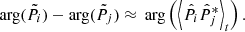
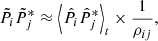
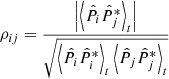
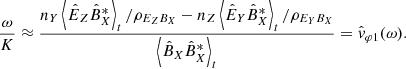
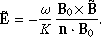
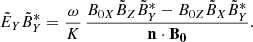
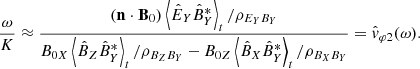
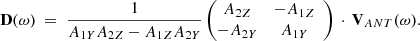
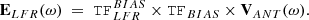
![$$ \begin{aligned} \begin{array}{ll}&\left\langle \hat{E}_Y \hat{E}_Y^{*}\right\rangle _t + \left\langle \hat{E}_Z \hat{E}_Z^{*}\right\rangle _t = \alpha _ {PE} \left(\ \left\langle \hat{E}_1 \hat{E}_1^{*}\right\rangle _t + k_{55}^{PE} \left\langle \hat{E}_2 \hat{E}_2^{*}\right\rangle _t + \right.\\&\quad \left. \mathfrak{R} \left[k_{45}^{PE} \left\langle \hat{E}_1 \hat{E}_2^{*}\right\rangle _t\right] \ \right), \end{array} \end{aligned} $$](/articles/aa/full_html/2021/12/aa40932-21/aa40932-21-eq108.gif)
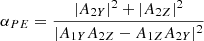
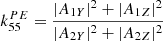
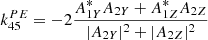
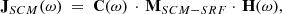
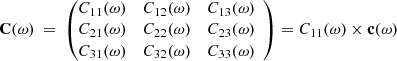
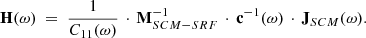
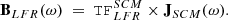
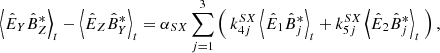
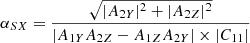
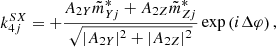
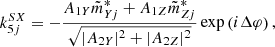
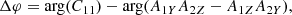
![$$ \begin{aligned} \tilde{m}_{ij} \ =\ \left[\mathbf M _{SCM-SRF} ^{-1} \,\cdot \, \mathbf c ^{-1}\right]_{ij} \ \ (i\!=\!Y, Z, \ j\!=\!1, 2, 3), \end{aligned} $$](/articles/aa/full_html/2021/12/aa40932-21/aa40932-21-eq122.gif)