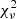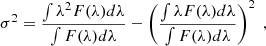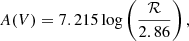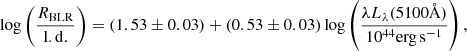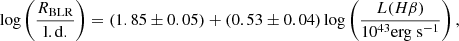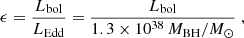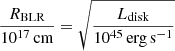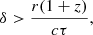| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141409 | |
| Published online | 21 October 2021 | |
Hunting for the nature of the enigmatic narrow-line Seyfert 1 galaxy PKS 2004-447
1
Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Vesilinnantie 5, 20014 University of Turku, Finland
e-mail: marco.berton@utu.fi
2
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
3
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
4
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
5
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6
INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, LC, Italy
7
Department of Physics, Technion 32000, Haifa 32000, Israel
8
Departamento de Astronomía, Universidad de Chile, Camino del Observatorio 1515, Las Condes, Santiago, Chile
9
Department of Astronomy and Physics, Saint Mary’s University, 923 Robie Street, Halifax, NS B3H 3C3, Canada
10
Aalto University Department of Electronics and Nanoengineering, 15500, 00076 Aalto, Finland
11
Las Campanas Observatory, Carnegie Observatories, Colina El Pino, Casilla 601, La Serena, Chile
12
European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
13
Dr. Karl Remeis Observatory, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
14
Lehrstuhl fur Astronomie, Universität Würzburg, Campus Hubland Nord, Emil-Fischer-Strasse 31, 97074 Würzburg, Germany
15
European Southern Observatory, Alonso de Cordova 3107, Casilla 19, Santiago 19001, Chile
16
Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Department of Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA
Received:
28
May
2021
Accepted:
30
June
2021
Narrow-line Seyfert 1 (NLS1) galaxies are a class of active galactic nuclei (AGN) that, in some cases, can harbor powerful relativistic jets. One of them, PKS 2004-447, shows γ-ray emission, and underwent its first recorded multifrequency flare in 2019. However, past studies revealed that in radio this source can be classified as a compact steep-spectrum source (CSS), suggesting that, unlike other γ-ray sources, the relativistic jets of PKS 2004-447 have a large inclination with respect to the line of sight. We present here a set of spectroscopic observations of this object, aimed at carefully measuring its black hole mass and Eddington ratio, determining the properties of its emission lines, and characterizing its long term variability. We find that the black hole mass is (1.5 ± 0.2)×107 M⊙, and the Eddington ratio is 0.08. Both values are within the typical range of NLS1s. The spectra also suggest that the 2019 flare was caused mainly by the relativistic jet, while the accretion disk played a minor role during the event. In conclusion, we confirm that PKS 2004-447 is one of the rare examples of γ-ray emitting CSS/NLS1s hybrid, and that these two classes of objects are likely connected in the framework of AGN evolution.
Key words: galaxies: active / galaxies: jets / quasars: supermassive black holes
© ESO 2021
1. Introduction
Since the launch of the Fermi Satellite, narrow-line Seyfert 1 galaxies (NLS1s) have been identified as the third class of active galactic nuclei (AGN) that can harbor powerful beamed relativistic jets and produce γ-ray emission in addition to the two well-known classes of blazars, BL Lacertae objects (BL Lacs) and flat-spectrum radio quasars (FSRQs, Abdo et al. 2009a,b,c; Fermi/Lat Collaboration 2010). NLS1s are characterized by a relatively low full width at half maximum (FWHM) of Hβ, which by definition must be lower than 2000 km s−1, by a flux ratio [O III]/Hβ < 3, and by two bumps of Fe II multiplets, which indicate that these objects are type 1 AGN with an unobscured view of their central engine (Osterbrock & Pogge 1985; Goodrich 1989).
The narrowness of the permitted lines observed in NLS1s is typically interpreted as a sign of low rotational velocity around a relatively low-mass black hole (106 − 108 M⊙, Boller et al. 1996; Peterson et al. 2000; Peterson 2011; Cracco et al. 2016; Rakshit et al. 2017; Chen et al. 2018). The black hole accretes close to or above the Eddington limit (Boroson & Green 1992; Sulentic et al. 2000), especially in the strongest Fe II emitters (Du et al. 2016). Non-jetted NLS1s are typically hosted by a spiral galaxy with a pseudobulge (Crenshaw et al. 2003; Deo et al. 2006; Orban de Xivry et al. 2011; Mathur et al. 2012). This ensemble of properties has led several authors to hypothesize that these NLS1s may represent an early evolutionary stage in the life of AGN, that will eventually grow into classical broad-line Seyfert 1 galaxies (Grupe 2000; Mathur 2000; Sulentic et al. 2000; Komossa et al. 2006; Fraix-Burnet et al. 2017). Jetted NLS1s appear to behave like their non-jetted counterparts. They are the low-mass tail of the FSRQ distribution (Abdo et al. 2009a,c; Foschini et al. 2015; Berton et al. 2015b), which in turn suggests that they may be the progenitors of FSRQs (Berton et al. 2016b). NLS1s with misaligned relativistic jets may eventually evolve to form the parent population of FSRQs, that is, high-excitation radio galaxies (HERG, Berton et al. 2016b, 2017; Foschini 2017). Several authors pointed out that a possible link between jetted NLS1s and other classes of young radio galaxies (see O’Dea & Saikia 2021, for a review), such as compact steep-spectrum sources (CSS) and gigahertz-peaked sources (GPS), may exist (Oshlack et al. 2001; Gallo et al. 2006; Komossa et al. 2006; Yuan et al. 2008; Wu 2009; Caccianiga et al. 2014, 2017; Schulz et al. 2016; Gu et al. 2015; Sulentic et al. 2015; Liao & Gu 2020; Zhang et al. 2020; O’Dea & Saikia 2021; Yao & Komossa 2021). It is also worth noting that there is even evidence in X-rays that the corona in some non-jetted NLS1s exhibit jet-like properties such as collimation and outflow. This behavior is remarkable, because it might indicate potential jet-like behavior even in non-jetted AGN (see Gallo 2018, for a review).
The NLS1s are located on the horizontal branch of the so-called quasar main sequence (MS, Sulentic & Marziani 2015; Marziani et al. 2018a). The MS is the locus on the plane defined by the flux ratio between the Fe II multiplets and Hβ, known as R4570, and the FWHM(Hβ), where all type 1 AGN lie. This sequence was originally identified by means of a principal component analysis (Boroson & Green 1992). The MS can be roughly divided into two distinct populations of sources, called population A and B. Population A forms a horizontal branch in the MS because its sources have different values of R4570, but they all have FWHM ≤4000 km s−1. Population A can be binned into four groups from A1 to A4: the values of R4570 increase by 0.5 from one group to the next. Population B instead forms a vertical branch because all AGN have R4570 < 0.5, but FWHM > 4000 km s−1 (Sulentic et al. 2000). By definition, all NLS1s belong to population A.
The main driver of the MS may be an Eddington ratio that decreases from population A to B (Boroson & Green 1992). Some authors even hypothesized that the MS might be an evolutionary path for AGN (Fraix-Burnet et al. 2017). However, some other factors also appear to play a role in the MS, such as metallicity and inclination with respect to the line of sight (Shen & Ho 2014; Panda et al. 2019; Śniegowska et al. 2021). This last parameter can be particularly confusing because in the presence of a flattened broad-line region (BLR) that is observed pole-on, a low inclination can produce narrow permitted lines even in the presence of high black hole masses due to the lack of Doppler broadening (Decarli et al. 2008). Some authors suggested that this may be the case for jetted NLS1s (e.g., Calderone et al. 2013; Baldi et al. 2016; D’Ammando 2019). However, recent observations dedicated to the host galaxies of these objects showed that jetted NLS1s are typically hosted in disk galaxies, similar to their non-jetted counterparts, and confirmed that their black hole mass is lower than that of FSRQs (Antón et al. 2008; Orban de Xivry et al. 2011; Mathur et al. 2012; León Tavares et al. 2014; Kotilainen et al. 2016; Olguín-Iglesias et al. 2017, 2020; Järvelä et al. 2018; Berton et al. 2019c; Hamilton et al. 2021, but see D’Ammando et al. 2017, 2018).
The number of currently known γ-ray emitting NLS1s is rather limited; approximately 20 sources are classified to date (e.g., Romano et al. 2018; Paliya 2019; Järvelä et al. 2020; Rakshit et al. 2021, see the review by Komossa 2018). Because of their relatively high redshift (all but 3 have z > 0.2), γ-NLS1s are rather faint in optical bands, and very few studies have been dedicated specifically to their optical spectra (e.g., Komossa et al. 2018; Kynoch et al. 2018, 2019; Yao & Komossa 2021). Here we present new spectroscopic data for the southernmost (to date) γ-NLS1, PKS 2004-447. This NLS1 was identified as a γ-ray source soon after the launch of the Fermi Satellite (Abdo et al. 2009c), and at the end of 2019, it underwent its first ever recorded γ-ray flare (Gokus 2019; Gokus et al. 2021). The goal of this work is to study its long-term behavior and the nature of this flare by means of optical spectroscopy. We also accurately measure some of its most important physical parameters such as the black hole mass, the Eddington ratio, and the emission line properties, and we determine its role in the family of γ-ray emitting NLS1s. In Sect. 2 we provide a brief review of the target, in Sect. 3 we describe the process of data reduction, in Sect. 4 we analyze the profiles of the most prominent emission lines, in Sect. 5 we determine its black hole mass, in Sect. 6 we study its time variability, and in Sect. 7 finally we provide a summary of our results. Although we are aware of the tension in the value of the Hubble constant (Riess et al. 2019), which would require the use of H0 ∼ 74 km s−1 Mpc−1 for the sources in the nearby Universe, we adopt a standard ΛCDM cosmology throughout, with a Hubble constant H0 = 70 km s−1 Mpc−1, and ΩΛ = 0.73 (Komatsu et al. 2011) to facilitate comparison with previous works.
2. PKS 2004-447
The target of this study is the γ-ray emitting NLS1 PKS 2004-447 (R.A. 20 h 07 m 55 s, Dec. –44 d 34 m 44 s, z = 0.240). Like most NLS1s, it is hosted in a spiral galaxy with a pseudobulge (Kotilainen et al. 2016). The source was noticed early on due to its prominent radio emission, and it was originally included in the Parkes Half-Jansky Flat-Spectrum Sample because its radio spectrum1 between 2.7 and 5.0 GHz is flat (F2.7 GHz = 0.81 Jy, αν = 0.36, with Fν ∝ ν−α, Drinkwater et al. 1997). However, this radio spectral measurement was carried out on nonsimultaneous data. Later observations instead revealed a steep spectral index of αν = 0.67, which suggests a radio classification as a CSS (Oshlack et al. 2001; Gallo et al. 2006). This result was confirmed more recently with new high-resolution observations in radio that additionally found a core-jet morphology and a flattening in the spectrum below 2 GHz (Schulz et al. 2016). This may be interpreted as a turnover, which is a defining property of CSS and GPS sources (O’Dea 1998). The linear projected jet size of ∼2 kpc, derived from the turnover frequency, is also consistent with CSS sources (Schulz et al. 2016). Its radio luminosity at 5 GHz is ∼3.8 × 1042 erg s−1 (7.4 × 1025 W Hz−1, Schulz et al. 2016), which lies at the lower end of the CSS/GPS luminosity distribution (O’Dea 1998), but within the typical range of jetted NLS1s (Berton et al. 2018a).
The history of its optical classification has been somewhat troubled. The source was originally included in the NLS1 class by Oshlack et al. (2001), who estimated the black hole mass for the first time as 5.4 × 106 M⊙ 2. However, the spectrum they analyzed was derived from Drinkwater et al. (1997), and it unfortunately showed an issue in the y-axis of their Fig. 2, where the flux was underestimated by a factor 200 with respect to the original paper. This error propagated throughout their work and in the subsequent literature based on it. The low signal-to-noise ratio of the spectrum furthermore hampered a fully reliable classification of the source as an NLS1. Because of its seemingly weak Fe II emission, PKS 2004-447 was considered to be a possible narrow-line radio galaxy (NLRG) or a type 2 AGN (Zhou et al. 2003; Sulentic et al. 2003; Komossa et al. 2006), although Gallo et al. (2006) noted that strong Fe II multiplets are not always included in the definition of NLS1. They therefore preferred an NLS1 classification. More recently, a new estimate of the black hole mass from optical spectroscopy is 7 × 107 M⊙ (see Foschini et al. 2015), close to the value 9 × 107 M⊙ derived from the K-band bulge luminosity (Kotilainen et al. 2016). A significantly higher value, 6 × 108 M⊙, was instead derived using optical spectropolarimetry (Baldi et al. 2016).
PKS 2004-447 was eventually included in the NLS1 class due to its multiwavelength properties, which are similar to those of other γ-ray NLS1s. Its X-ray spectrum, in particular, is well described by a single power law, likely due to the nonthermal emission of the relativistic jet (Kreikenbohm et al. 2016). A soft X-ray excess was detected in XMM-Newton observations (Gallo et al. 2006; Foschini et al. 2009), although its presence is not confirmed in all observations and is correlated to a high flux level (Kreikenbohm et al. 2016; Gokus et al. 2021). It seems to be the high-energy tail of the synchrotron emission (Foschini et al. 2009; Foschini 2020). It is worth noting that unlike what is seen in other γ-NLS1s (e.g., see PMN J0948+0022, Foschini 2012b), PKS 2004-447 has a less prominent variability in X-rays and in radio (Schulz et al. 2016; Kreikenbohm et al. 2016).
3. Observations and data reduction
The calibrated spectrum observed with the Anglo-Australian Telescope (AAT) on 1984-05-02 was extracted from Drinkwater et al. (1997). The spectra from the FOcal Reducer and low dispersion Spectrograph 2 (FORS2) mounted on the Very Large Telescope (VLT) were originally acquired to obtain a reliable optical classification of the source, and study its optical variability (program ESO/096.B-0256, P.I. Kreikenbohm). The data from the Las Campanas Observatory (Clay and Dupont telescopes) were collected to monitor the low state of the source and its γ-ray flare. Finally, the spectrum in the flaring state was observed in the framework of a larger NLS1 study carried out with the ESO Faint Object Spectrograph and Camera 2 (EFOSC2) at the New Technology Telescope (NTT, program ESO/0104.B-0587, P.I. Berton). The technical details of each spectrum are reported in Table 1. For all these new observations, we carried out the standard data reduction with IRAF, with bias and flat-field correction, and wavelength and flux calibration.
Observational details for the spectra.
In all cases, we corrected the spectrum for Galactic absorption using A(V)=0.091 (Schlafly & Finkbeiner 2011) and assuming a reddening law with Rv = 3.1 (Cardelli et al. 1989). After this step, we corrected the spectrum for redshift, z = 0.240, and subtracted the AGN continuum by fitting it with a power law. We did not try to model the host galaxy contribution, because no absorption lines from the host are visible in the spectra. Furthermore, at the relatively high redshift of PKS 2004-447, the host contribution is expected to be negligible (Letawe et al. 2007).
To account for the different observing facilities and conditions of our spectra, we decided to use the total flux of the [O III]λ5007 line as a reference to rescale the spectra. Because this line originates in the narrow-line region (NLR), which is significantly larger than the BLR and much farther away from the nucleus, its flux is expected to remain constant over several years (Peterson et al. 2004). Because the VLT spectra have the highest signal-to-noise ratio (S/N), we decided to use their median [O III] flux as a reference, excluding the noisiest spectra. The first (2015-10-17) and the fifth observing nights (2016-03-29) were indeed likely affected by some passing clouds, so they were not used. The reference flux we adopted is 4.84 × 10−15 erg s−1 cm−2, based on fitting the line profile with a double Gaussian. The exact measurement procedures are described in Sect. 4.2 and in Sect. 6.
4. Line profiles
To carry out an analysis of the line profiles, it is crucial to have a spectrum with a high S/N. This parameter is crucial to examine the wings of profiles in detail and to obtain an accurate decomposition (e.g., Järvelä et al. 2020). Therefore, we combined all the spectra obtained by the VLT. We reached an S/N ∼ 90 in the continuum around 5100Å. Although we may lose some information about the variability in the continuum and permitted lines over the six months of observations, this operation is necessary to ensure a good quality spectrum that can be studied in detail. The combined spectrum is shown in Fig. 1. All of the fitting procedures that follow were performed with our own Python code (Harris et al. 2020). An analysis of the variability is instead carried out in Sect. 6. In our line profile analysis, we focused on the most prominent lines: Hβ, [O III]λλ4959, 5007, the [S II]λλ6716, 6731 doublet, and the Hα+[N II]λλ6548, 6584 complex.
 |
Fig. 1. Redshift-corrected optical spectrum of PKS 2004-447, observed by FORS2. The most prominent emission lines are identified. The telluric absorptions are marked with the crossed circle. |
4.1. Fe II multiplets
The Hβ+[O III] region of NLS1s, between 4000 and 5500Å, is typically characterized by the presence of Fe II multiplets. These lines lie very close to the other emission features, and they are often blended with them. In particular, they can significantly affect the red wings of the [O III]λ5007 line and of the Hβ line. To reproduce the multiplets, we used the templates based on photoionization models provided by Marziani et al. (2009), adopting an FWHM for the Fe II of ∼1500 km s−1 (comparable to that of Hβ broad, see Sect. 4.3) and rescaling it to match the observed spectrum. The best fit is shown in Fig. 2. The typical errors produced by Fe II subtraction were already estimated by Cracco et al. (2016), and they are about 10% of the flux. The template we used yields a flux of Fe II on the blue side of Hβ of (3.1 ± 0.3)×10−15 erg s−1 cm−2. This value is used below to calculate the R4570 parameter.
 |
Fig. 2. Fit of the Fe II multiplets in the Hβ region. The original spectrum, redshift corrected and continuum subtracted, is represented by the solid black line. The Fe II multiplets from Marziani et al. (2009) are the dashed red line. The spectrum was cut off for visual purposes. |
4.2. [O III] lines
After subtracting the Fe II multiplets, we modeled the [O III]λλ4959, 5007 lines. These lines usually show two separate components. The first is a narrow core component, which is associated with the gas of the NLR and typically has the same redshift as the host galaxy. The second component is a broad wing that is usually interpreted as a sign of outflowing gas. Therefore, the two lines should be modeled with four Gaussian functions. To reduce the number of free parameters, we introduced some constraints on the λ4959 line. The flux ratio of the components was fixed to the theoretical value of 1/3 (Dimitrijević et al. 2007), the FWHM of the core and the wing were forced to be the same in both lines, and the relative shift between the two components was also fixed to be the same in both lines. The measurements were performed by using a Monte Carlo method. We repeated the fit one thousand times while adding a different Gaussian noise proportional to the noise in the continuum every time to the line profiles. The Gaussian noise was also used to estimate the 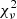 . We finally used the median value for each parameter and its standard deviation. The result of the fit is shown in Fig. 3, where the
. We finally used the median value for each parameter and its standard deviation. The result of the fit is shown in Fig. 3, where the 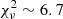 is also reported. The total flux we obtained for the two lines is 6.45 × 10−15 erg s−1 cm−2, with one quarter of the flux in the λ4959 line and the rest in the λ5007 line. The fit indicates that the core component is unresolved. This result may not be real, but only a product of the limited spectral resolution. Therefore no robust conclusion can be obtained on the [O III] line components.
is also reported. The total flux we obtained for the two lines is 6.45 × 10−15 erg s−1 cm−2, with one quarter of the flux in the λ4959 line and the rest in the λ5007 line. The fit indicates that the core component is unresolved. This result may not be real, but only a product of the limited spectral resolution. Therefore no robust conclusion can be obtained on the [O III] line components.
 |
Fig. 3. Fit of the [O III] lines after continuum and Fe II subtraction. The spectrum is represented by the solid black line. The two Gaussian components represent the line core (dashed orange line) and wing (dashed green line). The best fit is represented by the dot-dashed red line, the residuals by the solid blue line, and the horizontal dashed line represents the zero level of the continuum. The rest-frame wavelength of the two lines is indicated by the vertical dashed lines. Due to the low spectral resolution, the core component is unresolved. |
We also tried to reproduce the [O III] lines by modeling them with a skewed Gaussian function. The function can be expressed as
where λ0 represents the central wavelength, σs represents the width of the skewed Gaussian, α is the skewness parameter, and A0 is a constant. Physically, this model appears to indicate that the ionized gas producing the [O III] lines is distributed in a bipolar outflow, and one of the outflows is partially obscured by an intervening medium (i.e., the central engine). We fixed the parameters of the λ4959 line as described for the previous model. This new function provides a slightly worse representation of the line profile than the double Gaussian (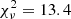 ,
, 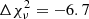 ). However, it is worth noting that the skewness parameter is α = −1.07 ± 0.07, suggesting a slight asymmetry on the blue side. This may indicate that the receding outflow could be partially obscured, as we would expect in a system that is observed not too far from its symmetry axis, such as a type 1 AGN.
). However, it is worth noting that the skewness parameter is α = −1.07 ± 0.07, suggesting a slight asymmetry on the blue side. This may indicate that the receding outflow could be partially obscured, as we would expect in a system that is observed not too far from its symmetry axis, such as a type 1 AGN.
4.3. Hβ line
The modeling of Hβ, shown in Fig. 4, was carried out after the subtraction of the Fe II multiplets. At first we attempted simple fits with a single Gaussian profile or a single Lorentzian profile. The single Gaussian profile is the worst fit (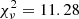 ) because it cannot correctly reproduce the core or the wings of the line. A single Lorentzian provides a slight improvement (
) because it cannot correctly reproduce the core or the wings of the line. A single Lorentzian provides a slight improvement (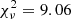 ), but it shows that the line profile is not perfectly symmetric, because the Lorentzian function fits the red side of the line well, but fails to reproduce the blue side and the peak.
), but it shows that the line profile is not perfectly symmetric, because the Lorentzian function fits the red side of the line well, but fails to reproduce the blue side and the peak.
Because neither function is good enough to fully reproduce the whole profile, we first added a single Gaussian to the Lorentzian function to represent the narrow component of Hβ (LG model). Its flux was fixed at 1/10 of the total flux of the [O III]λ5007 line, that is, 4.8 × 10−15 erg s−1 cm−2, because this ratio is often observed in type 1 AGN (Véron-Cetty et al. 2001). Its FWHM was instead fixed to that of the [O II]λ3727 line (14.4Å ∼1158 km s−1, 936 km s−1 when corrected for instrumental resolution), and its central wavelength was left free to vary. We did not use the FWHM of [O III] as reference because high-ionization lines are significantly more perturbed than low-ionization lines such as [O II] (Komossa et al. 2008). The [O I]λ6300 line would also be a good indicator, but as Fig. 1 shows, it is weaker than [O II] and therefore less suitable for this. Nevertheless, it is worth noting that its FWHM∼830 km s−1 (corrected for instrumental resolution) is similar to that of [O II]. The addition of the narrow component leads to a significant statistical improvement of the fit (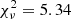 ). However, the blue side of Hβ is still not perfectly reproduced, and the same is true for the peak of the line. We therefore tried to reproduce the line using three Gaussians (3G model), two representing the broad component and one the narrow component. The last component had the same characteristics as before, while all the parameters of the two broad Gaussians were left free to vary. Statistically, this produces the best fit for the line (
). However, the blue side of Hβ is still not perfectly reproduced, and the same is true for the peak of the line. We therefore tried to reproduce the line using three Gaussians (3G model), two representing the broad component and one the narrow component. The last component had the same characteristics as before, while all the parameters of the two broad Gaussians were left free to vary. Statistically, this produces the best fit for the line (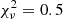 ) because it can reproduce the asymmetry of the profile by shifting the center of the very broad component. It is worth noting that this shift is consistent with the outflowing component that may be present in [O III]. Using this model, we can derive the fundamental parameters of Hβ, that is FWHM(Hβ)=1617 ± 8 km s−1, and total integrated flux F = (3.17 ± 0.01)×10−15 erg s−1 cm−2.
) because it can reproduce the asymmetry of the profile by shifting the center of the very broad component. It is worth noting that this shift is consistent with the outflowing component that may be present in [O III]. Using this model, we can derive the fundamental parameters of Hβ, that is FWHM(Hβ)=1617 ± 8 km s−1, and total integrated flux F = (3.17 ± 0.01)×10−15 erg s−1 cm−2.
 |
Fig. 4. Fit of the Hβ line with different functions. The original spectrum is the solid black line, the residuals of the model subtractions are the solid blue line, the horizontal dashed black line represents the zero level of continuum, and the vertical dashed line represents the rest-frame wavelength of Hβ. The values of |
Using the LG model, we find that the width of the Hβ broad component is FWHM(Hβb)=1577 ± 10 km s−1, and the 3G model provides an FWHM(Hβb)=1804 ± 62 km s−1, while the second-order moment of the line, defined as
is σ(Hβb)=1007 ± 20 km s−1. The σ of the LG model cannot be estimated because the second-order moment of a Lorentzian function by construction is infinite. The total flux of the broad component of the line estimated with the LG model is (2.76 ± 0.01)×10−15 erg s−1 cm−2, and the 3G model provides (2.67 ± 0.02)×10−15 erg s−1 cm−2. Using the mean of these two values, we calculated R4570 = F (Fe II) / F (Hβb)=1.14 ± 0.14. According to the classification by Marziani et al. (2018b), PKS 2004-477 therefore belongs to population A3 of the quasar MS.
4.4. Hα region
We modeled the Hα profile by fixing it to the Hβ parameters. Specifically, we fixed the flux ratio of the different components in the LG and 3G model, the velocity shifts between the components, and the velocity associated with the FWHM of each component. This essentially leaves only one free parameter to be determined, which is the height of the narrow component. Finally, we added two more Gaussians to reproduce the [N II]λλ6548, 6584 lines, which are blended with Hα due to its width and to the low resolution. Their FWHM was identical in both lines, but was free to vary, their flux ratio was fixed to the theoretical value of 2.95, and their positions were fixed to rest frame. Therefore this leaves two free parameters.
This lead to the results shown in Fig. 5. Neither of the two fits is perfect because the Hβ profile used as reference appears to have a more prominent red wing that is not observed in Hα. The adoption of the double Gaussian instead of the Lorentzian to reproduce the broad component leads to a very significant improvement in the 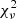 , with
, with 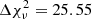 (
(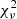 values are reported in Fig. 5). This appears to indicate that the double Gaussian is better suited to reproduce the broad component of both Hα and Hβ. The reason for the asymmetry observed in Hβ but not in Hα might be some residual Fe II in the former that the template was unable to account for, or a real physical difference due to a different kinematics of the emitting gas. Only better data will allow us to distinguish between these two possibilities.
values are reported in Fig. 5). This appears to indicate that the double Gaussian is better suited to reproduce the broad component of both Hα and Hβ. The reason for the asymmetry observed in Hβ but not in Hα might be some residual Fe II in the former that the template was unable to account for, or a real physical difference due to a different kinematics of the emitting gas. Only better data will allow us to distinguish between these two possibilities.
 |
Fig. 5. Fitting of the Hα+[N II] complex. The original spectrum is the solid black line, the residuals of the model subtractions are the solid blue line, the horizontal dashed black line represents the zero level of the continuum, and the vertical dashed line represent the rest-frame wavelength of Hα. Two Gaussians reproduce the two [N II] lines, represented by the solid cyan line, and one Gaussian reproduces the Hα narrow component, indicated by the dashed orange line. The solid yellow line is the actual Hα profile, while the best fit is indicated by the dot-dashed red line. Left panel: broad component of Hα is reproduced with one Lorentzian function, reproduced by the dashed green line. Right panel: broad component of Hα is reproduced with two Gaussians, indicated by the dashed green and purple lines. |
After fitting Hα, we estimated the internal reddening due to the dust by studying the Balmer decrement. We calculated the ratio ℛ between the flux of the narrow component of Hα and Hβ, which is ℛ ∼ 4.86. Assuming a theoretical ratio of 2.86, and following Cardelli et al. (1989)
we found an internal extinction A(V) = 1.66 mag. This result agrees with what was found by Gallo et al. (2006), who derived A(V) = 1.9 ± 1.5 from the AAT spectrum3. As they already pointed out, this extinction is significantly higher than what can be estimated from the X-ray spectra, which instead show negligible absorption, as confirmed by more recent observations (Kreikenbohm et al. 2016; Berton et al. 2019a; Gokus et al. 2021). They also suggested that a possible explanation for this is a very different gas-to-dust ratio than what is seen in the Milky Way, and the jet may play a role in this by transferring material from the nucleus into the NLR. However, given the significant uncertainty on the A(V) value, we decided not to apply an additional correction for internal extinction in the calculations presented below.
4.5. Electron density and temperature
To derive the physical parameters of the NLR, we reproduced the [S II]λλ6716, 6731 doublet in order to measure the electron density. The lines are only partially resolved, therefore we fit them with two Gaussians with the same width as [O II] (in velocity), with fluxes and positions free to vary. The flux ratio we obtained is F(6716)/F(6731) ∼1.03.
Furthermore, we measured the flux of the [O III]λ4363 line, which is detected blended with Hγ in our spectrum. Because both lines are rather faint, we adopted a simple model to fit them, using one Gaussian function for Hγ and one for [O III]. This yields a flux of 0.29 × 10−15 erg s−1 cm−2, and a ratio [F(4959) + F(5007)]/F(4363)∼23.0.
Using these ratios, we can provide an estimate of the electron density and temperature. We used the temden task of IRAF, which is based on the five-level atomic model described by De Robertis et al. (1987). The observed line ratios are reproduced if the electron density is ne = 7.6 × 102 cm−3, and the electron temperature is Te = 3.1 × 104 K. While the density value we derived is rather typical for AGN (Congiu et al. 2017b), it is worth noting that, if some internal absorption is present, as was tentatively suggested in the previous section, the temperature value we obtained should be treated as a lower limit.
5. Black hole mass
To estimate the black hole mass, we used different techniques. All of them are based on the assumption that the gas orbiting the black hole is virialized. In this case, the black hole mass can be calculated using the virial theorem,
where RBLR is the radius of the BLR, v is the rotational velocity of the gas, G is the gravitational constant, and finally f is the so-called scaling factor. The weight of this factor is still largely unknown, therefore we fixed f = 1 for now and discuss the results under different assumptions below.
5.1. Dependence on line width and velocity
The two key parameters that are to be determined are the radius of the BLR and the rotational velocity. To obtain the first, we used two relations calibrated in the literature. Both of them are based on the assumption of photoionization equilibrium. The accretion disk radiation causes the formation of BLR lines and pushes the clouds away due to radiation pressure. If the ionizing continuum from the disk is strong, the BLR will have a large radius. A relation appears to connect the BLR radius that is measured with the reverberation mapping technique and the luminosity of the continuum at λ5100Å. The coefficients were estimated by Bentz et al. (2013),
where the BLR radius is expressed in light days. However, as pointed out before, the ionizing continuum produced by the accretion disk is also responsible for the formation of the emission lines. Therefore the intensity of the lines is also proportional to the accretion disk luminosity, and the BLR radius depends on the luminosity. The relation between these quantities was derived by Greene et al. (2010),
where L(Hβ) is the integrated luminosity of the line. In principle, this second method should be less contaminated by the jet contribution, which is a non-negligible factor in the λ5100 luminosity (Berton et al. 2015a).
To derive the gas velocity, we used the Hβ line decomposition described above. The best results were obtained when the broad component was fit either by two Gaussians or a Lorentzian function. For both profiles, we adopted the FWHM of the broad component as a proxy of the rotational velocity of the gas. In the case of the double Gaussian, we also estimated the second-order moment σ of the broad component, defined in Eq. (2). The use of σ instead of FWHM generally provides better results, especially in low-contrast lines, and it is less affected by inclination effects and BLR geometry (Peterson et al. 2004; Peterson 2011; Peterson & Dalla Bontà 2018). We did not use this method for the Lorentzian profile because the σ of a Lorentzian function by definition is infinite.
In conclusion, we had six different combinations to use for the calculation of this virial product. The results are shown in Table 2. The estimate of the errors on the mass was performed in two ways. The first error source is in the fitting procedure, and we evaluated it using a Monte Carlo technique. We calculated the virial product one thousand times by varying the Hβ profile adding a Gaussian noise proportional to the root mean square measured in the λ5100 continuum. This error source is relatively small, typically about 0.03 dex, likely because of the high S/N of our spectrum. Another error source are the uncertainties on Eqs. (5) and (6). We estimated the BLR radius in both ways one thousand times by applying a Gaussian noise proportional to the errors of the coefficients, and used these different values in the final calculation. Finally, we applied the normal propagation of errors to the virial theorem of Eq. (4). We calculated the weighted average of all the estimates obtained in Table 2, and the resulting product is (6.0 ± 0.4)×106 M⊙. In conclusion, Table 2 shows that different methods can lead to statistically significant differences in the black hole mass calculation. Because of the high S/N of the spectrum we used for the fitting procedure, the main error source is not the fit itself, but instead the propagation of the errors on all the uncertain quantities such as the BLR radius.
Product Rv2/G calculated with different techniques.
5.2. Dependence on the f factor
We neglected the scaling factor f that appears in Eq. (4), so far. This is another major source of uncertainty in the black hole mass estimate. The scaling factor accounts for the difference between the mass obtained with the product RBLRv2/G and the actual black hole mass. This difference strongly depends on the geometry and inclination of the BLR. If the BLR has a flattened geometry, it is clear that when observed pole-on, there would be no velocity component parallel to the line of sight, thus causing a severe underestimate of the gas rotational velocity, and as a consequence, of the black hole mass (e.g., Decarli et al. 2008). In case of a more sphere-like geometry, this effect would be less evident. Our knowledge of the structure of the BLR is still relatively limited. While it is clear that Keplerian motion of the clouds is present (Peterson & Wandel 1999; Gravity Collaboration 2018), there may be some additional components such as turbulent vertical motion, possibly originating in a disk wind, that can significantly affect the value of f (Gaskell 2009; Kollatschny & Zetzl 2013a). A perfectly thin BLR is indeed clearly unphysical. The BLR clouds must be illuminated by the ionizing photons coming from the central engine. If the clouds were distributed on a thin disk, the outer clouds would not be reached by the disk radiation (Collin et al. 2006). Shen & Ho (2014) suggested that f is inversely proportional to the FWHM(Hβ), with higher values, up to ∼100, corresponding to small FWHMs. However, a lower FWHM(Hβ) typically corresponds to different line profiles, because type 1 AGN with narrow lines (e.g., NLS1s) tend to show Lorentzian profiles instead of Gaussian ones (Sulentic et al. 2000; Marziani et al. 2001; Komossa 2008; Cracco et al. 2016). Because Lorentzian profiles might be associated with the presence of a significant vertical structure in the BLR (Kollatschny & Zetzl 2011, 2013b), the effect of inclination may not be so prominent in NLS1s and population A objects (Vietri et al. 2018; Berton et al. 2020).
Several estimates of the f factor, both fσ and fFWHM, exist in the literature, and they are mostly based on reverberation mapping observations. Typical values can span between ∼0.8–5.0 (Mandal et al. 2021). In the case of PKS 2004-447 this means that its black hole mass, using the weighted average estimated above, ranges between (4.8–30.0) ×106 M⊙, within the typical range of NLS1s (Peterson 2011). A weak dependence on the FWHM(Hβ) and also on the ratio of the FWHM of the line and its dispersion appears to be present. Collin et al. (2006) calculated different values of f depending on how the rotational velocity is estimated (FWHM, σ), on the ratio of FWHM and σ, and on the FWHM(Hβ) itself. In the case of PKS 2004-447, we decided to use their values, which are fσ = 3.93 for σ-based measurements, and fFWHM = 2.12 for FWHM-based measurements. By applying these values to the virial products calculated in Table 2 and taking the weighted average, we obtained a mass value of (1.5 ± 0.2) ×107 M⊙. In the following, we use this value for our calculations.
6. Time variability
6.1. Lines and continuum
Our goal is to study the long-term variability of the PKS 2004-447 spectra. As previously mentioned, we accounted for the variability induced by different observing conditions by rescaling our spectra using the [O III]λ5007 as a reference. The measurement of the [O III] flux density was carried out after redshift correction, continuum subtraction, and Fe II multiplet modeling and subtraction. The exceptions to this are the spectra in which, because of the low S/N, we could not model the Fe II multiplets. They are 1984-05-02, 2015-10-17, 2016-03-29, and 2019-10-31. All the spectra were rescaled to the value derived in Sect. 4.2, that is 4.84 × 10−15 erg s−1 cm−2. The two parameters we measured are the continuum flux at 5100Å, and the Hβ total flux. The errors on the line fluxes were estimated as previously described, while the uncertainty on the continuum at 1 σ confidence level is provided by the standard deviation of a spectral region dominated by continuum emission with no (or very little) contamination by strong emission lines between 5075 and 5125 Å. The results are shown in Fig. 6.
 |
Fig. 6. Variability measured in the continuum flux density and in the Hβ line flux. The blue circles represent the [O III]λ5007 flux, which was forced to be the same in all spectra. The black squares represent the flux of Hβ, and the red circles in the bottom panel represent the continuum flux. |
The most apparent result is the major flux increase that was observed in the continuum on 2019-10-31, which is remarkably followed by the highest measured Hβ flux one month later (2019-11-29). This is due to the flaring activity of PKS 2004-447 measured in these days. The flare was detected in γ-rays by the Fermi Satellite on 2019-10-25 (Gokus 2019) and by AGILE until 2019-10-27 (Verrecchia et al. 2019), and enhanced activity was measured at other frequencies as well (D’Ammando et al. 2019; Berton et al. 2019b; Blaufuss 2019). Even if PKS 2004-447 has been included in the γ-ray catalogs since its very first detection soon after the launch of Fermi (Abdo et al. 2009c), this was its first recorded major flare (Gokus 2019). Our long-term spectroscopy indeed shows that the continuum flux has been remarkably constant during the last 30 years. The values we measured at each epoch are reported in Table 3. In addition to the flare, the continuum has varied between minimum and maximum values (5.3 ± 2.4) and (9.1 ± 0.6) ×10−17 erg s−1 cm−2 Å−1, recorded on 2016-03-29 and 2016-03-18, respectively. The Hβ flux is instead more variable. A local maximum is seen in the 1984-05-02 spectrum. The Hβ flux also appears to also be increased in the three spectra following the maximum continuum value measured on 2016-03-18. Furthermore, we investigated the presence of a correlation between the continuum flux and the equivalent width of Hβ (which we define as positive in emission lines). The result is shown in Fig. 7. A strong anticorrelation was found, with a Pearson coefficient of –0.81 and a p-value of 0.008. This effect is well known to depend on the jet activity (the higher the jet flux, the lower the equivalent width), and has been observed in other sources (Corbett et al. 2000; Foschini 2012a). In particular, it is interesting to compare what we observed with what was seen during a flare of the FSRQ 3C 345, in which the emission lines reacted to a significant flux increase in the continuum (Berton et al. 2018b). In this case, the source was deviating from the best-fit relation between the continuum flux and the equivalent width, and this was interpreted as a sign of prominent disk contribution to the typically jet-dominated continuum. In this case, we do not observe any significant deviation during the flare. Therefore, the jet emission appears to dominate the disk at all epochs.
Spectral measurements at different epochs.
 |
Fig. 7. Anticorrelation of the continuum flux at 5100Å and the equivalent width of the Hβ emission line. The dashed red line indicates the best linear fit. |
The flux of Hβ may be responding to the continuum variation. The two spectra showing the maximum continuum flux and Hβ flux were observed 29 days apart. As reported in Table 4, the BLR size is ∼15.2 light days. Assuming that this distance is similar to the light-crossing time from the central engine to the BLR clouds, it is reasonable to assume that the enhanced Hβ flux we observe in the last spectrum is the echo of the enhanced continuum produced in the nucleus during the flare. However, while the continuum increased by a factor of ∼4, the line flux did so only by a factor of ∼1.3. Because of the sparse sampling of our observations, neither of these measurements probably reflect the behavior of the source during the flare, but they can still provide some insights. Cracco et al. (2016) found in a large sample of NLS1s that the continuum and Hβ luminosity are related as L(Hβ) ∝ λL(5100)1.203. If this relation applies to our source as well, the ionizing continuum should have increased only by a factor of 1.24 to account for the observed variation in Hβ, which is much lower than what we actually observe. This may indicate that the vast majority of the flux increase was due to an enhanced activity of the relativistic jet, while the accretion disk, which produces most of the ionizing photons and later affects Hβ, played a significantly smaller, although non-negligible, role. This may reflect what is seen in the X-ray spectrum of this source, which is dominated by a power-law component coming from the relativistic jet, while the thermal Comptonization model coming from the disk corona accounts for only 2% of the total flux (Gallo et al. 2006; Kreikenbohm et al. 2016; Berton et al. 2019a). It is worth mentioning that Gokus et al. (2021) did not detect any component associated with the accretion disk in their analysis of the PKS 2004-447 X-ray spectrum observed after the flare, and this agrees well with our conclusions. If the jet flux is strongly enhanced, while the corona contribution does not change significantly, the latter will likely become too weak to be detected. In contrast, as the soft X-ray excess is associated with a high X-ray flux, hence with high jet activity, it is likely to be the high-energy tail of the synchrotron emission, as was found for low-frequency peaked BL Lac objects (Foschini et al. 2009; Foschini 2020).
6.2. Eddington ratio
The Eddington ratio is defined as
that is the ratio between the bolometric luminosity Lbol and the Eddington luminosity LEdd. This parameter is often thought to be the driver of the quasar MS. Sources with a high Eddington ratio show the most prominent Fe II multiplets and the narrowest Hβ, while low Eddington sources are characterized by large FWHM(Hβ) and little or no Fe II. In NLS1s, the Eddington ratio is typically between 0.1 and 1 (Boroson & Green 1992; Williams et al. 2002, 2004; Grupe et al. 2010; Xu et al. 2012), but even super-Eddington accretion can be observed in a handful of sources (Chen et al. 2018). The bolometric luminosity is usually roughly estimated by adopting a simple linear relation that connects it to the continuum luminosity at 5100Å, Lbol = 9λLλ(5100 Å) (Kaspi et al. 2000). However, in the light of what was shown in Sect. 6.1, this approach can be misleading in jetted sources, especially in those like PKS 2004-447 where the jet component dominates the continuum emission. An alternative way is using the emission lines luminosity instead as a proxy for the disk luminosity. As shown in Eq. (6), the Hβ luminosity has a linear relation in the log-log plane with the BLR radius. Assuming a photoionization regime, the latter directly depends on the disk luminosityas
(Koratkar & Gaskell 1991; Ghisellini & Tavecchio 2009). The median disk luminosity we obtain from this relation is 2.0 × 1044 erg s−1. Under the reasonable hypothesis that the disk luminosity is comparable to the bolometric luminosity without the jet emission, we can use it to estimate the Eddington ratio.
The results of both techniques are shown in Fig. 8. On the y-axis, a logarithmic scale was adopted to enhance the visibility of the variations. Regardless of the method we used, the Eddington ratio lies within the typical range of NLS1s, with median values 0.29 and 0.09 for continuum- and Hβ-based estimate, respectively. While the continuum-based estimate varies from 0.22 on 2015-10-22 to 1.23 during the 2019 flare, the Hβ-based estimate has a more limited range that extends from 0.07 on 2015-10-17 to 0.11 in the last spectrum. It is worth noting that the estimate based on the Hβ luminosity allows us to measure the Eddington ratio as it was 15.2 days ago, that is, the BLR light-crossing time, before the observation date. Considering this, both estimates agree that the Eddington ratio increased during the flare. This may suggest a possible connection between the accretion disk and the jet, as seen in other AGN flares (e.g., Grandi & Palumbo 2004).
 |
Fig. 8. Evolution of the Eddington ratio estimated by using the continuum (red squares) and the Hβ line luminosity (black circles). |
6.3. The 2019 flare
By using the lines and continuum luminosities of Fig. 1, we tried to derive the scales involved in the inner structure of PKS 2004-447. The results are reported in Table 4. The BLR radius was derived using Eq. (6) and the disk luminosity following Eq. (8). For the dust sublimation radius and the outer radius of the torus, we used the scaling relations between these quantities and the disk luminosity (Elitzur 2008). To estimate the maximum extension of the NLR, we used its correlation with the [O III] luminosity (Fischer et al. 2018). All the values we found are comparable to those derived in the other γ-ray emitting NLS1 1H 0323+342 (Foschini et al. 2019), suggesting that their inner structure is rather similar.
These values can provide an idea of the region in which the γ-ray photons were produced during the 2019 flare. It is known that the minimum Doppler factor needed to account for a source variability is
where r is the radius of the emitting region and τ is the observed timescale. Using the 6-hour binned γ-ray light curve derived by Gokus et al. (2021), the variability between adjacent points indicated that the doubling time is ∼2−4 hours, consistent with the values observed at hard X-rays by Berton et al. (2019a). If we assume that the jet structure is self-similar, and that its semi-opening angle is 0.1 radians, the size of the emitting region depends on the distance of the dissipation region from the central source. If the production of γ-rays is located relatively close to the jet base at ∼103rg (Ghisellini et al. 2010), the minimum Doppler factor therefore is δ ≥ 0.6−1.3, which is a rather weak constraint that can also be achieved with a large viewing angle (Schulz et al. 2016 estimated θ < 50°). This is consistent with what is typically observed in high-energy emitting radio galaxies (e.g., NGC 6251, θ < 47°, δ ∼ 3.2, or Cen A, θ < 80°, δ ∼ 1.2, see Chiaberge et al. 2001, 2003; Foschini et al. 2005). Furthermore, the γ-ray spectrum they measured is rather steep. If the production of γ-rays had occurred close to the black hole, we would indeed expect to see a rather steep spectrum because of absorption of the most energetic photons due to the BLR gas (e.g., Romano et al. 2020). Gokus et al. (2021) argued that the dissipation region is instead close to the molecular torus, but to calculate its radius, they assumed a disk luminosity that is one order of magnitude lower than what we derived from Hβ. Using our estimate for the torus inner radius, that is, the dust sublimation radius, which is based on the observed disk luminosity, the minimum Doppler factor required would be δ > 177−354, which is clearly unrealistic. We therefore suggest that a dissipation region closer to the central source, in this case, is more likely.
7. Discussion
7.1. Optical classification
Our new high-quality spectral data can finally confirm with certainty the classification of PKS 2004-447 as an NLS1 because its spectrum meets all the fundamental criteria. As calculated in 4.3, the FWHM(Hβ)=1617 km s−1, which is lower than the 2000 km s−1 threshold. The ratio R5007 = F([O III])/F(Hβ) = 1.53, also meets the R5007< 3 limit. Finally, Fe II multiplets are definitely present and rather strong. Specifically, the value of R4570 = 1.14 ± 0.14 we found is above the median value of 0.49 found for NLS1s (Cracco et al. 2016), but agrees well with what is often observed in these objects and, in general, in population A sources. We remark here that the 2000 km s−1 threshold is an artificially imposed value that does not reflect any physical difference between sources above and below it. As long as they can be classified as type 1 AGN, all sources within population A roughly share the same physical properties (Marziani et al. 2018a).
The Hβ profile of PKS 2004-447, when reproduced with a single function, is better described by a Lorentzian profile. However, the best fit is obtained with three Gaussian functions, one representing the narrow component, and two reproducing the broad component. This result supports the view that the BLR is not homogeneous, but rather stratified depending on its chemical composition (Peterson & Wandel 1999; Kovačević et al. 2010). This double-Gaussian approach to modeling the BLR can also reproduce the Hα profile better than a Lorentzian profile, possibly indicating that the structure of the region in which the Balmer lines are produced is similar. As we already pointed out, Hβ may have a slightly redward asymmetry that is not seen in Hα, but only better data will allow us to determine whether this difference is real or just a residual left after the Fe II multiplet subtraction.
Another noteworthy fact that can be derived from the optical spectrum is the remarkable width of the forbidden lines. All of them have an FWHM of about 900 km s−1 after correcting for instrumental resolution, which is significantly broader than what is typically seen in AGN (Peterson 1997). Assuming that, as hypothesized by Nelson & Whittle (1996), there is a correlation between the forbidden lines width and the stellar velocity dispersion σ*, we can derive σ* ∼ 330 km s−1, using its scaling relation with the FWHM([O II]) derived by Greene & Ho (2005). This value would be high even for a large elliptical galaxy (Forbes & Ponman 1999), but the host galaxy of PKS 2004-447 is a spiral galaxy with a pseudobulge (Kotilainen et al. 2016). This suggests that at least in our source, the forbidden line width does not obviously correlate with the stellar velocity dispersion. A possible alternative origin for the observed large width may instead be interaction through shocks between the NLR gas and the relativistic jet. Shocks can indeed produce turbulent motion in the gas, which in turn causes the lines to become broader (e.g., Whittle 1985; Nesvadba et al. 2008; Morganti 2017). The presence of jet/NLR interaction may also explain the rather high temperature we have derived in Sect. 4.5, which is higher than the typical value observed in AGN (Osterbrock & Ferland 2006). Further investigation, especially by means of integral-field spectroscopy, can clarify this aspect.
7.2. High mass or low mass?
We have verified that the black hole mass of PKS 2004-447 derived from the optical spectrum is well within the typical range of NLS1s (Peterson 2011). However, it is interesting to compare our value with other results in the literature. In particular, we tried to verify how the f factor changes when we use mass indicators that are independent of the inclination. For instance, Kotilainen et al. (2016) used the bulge infrared magnitude to estimate a black hole mass of 9 × 107 M⊙, which is higher than the value we derived. If we assume that this host-based value is correct, and using the weighted average of all our σ- and FWHM-based measurements, we obtain fσ = 24.7 and fFWHM = 8.5. Both these values are higher than the average correction needed for type 1 AGN, and it might suggest that inclination and BLR geometry do play a significant role in this source.
Another value that can be found in the literature is derived from spectropolarimetric observations of PKS 2004-447 (Baldi et al. 2016). These observations are based on the concept that spectropolarimetry can offer a periscopic view of the nucleus, which in this case should be seen edge-on in polarized light. The mass obtained by Baldi et al. (2016) is much higher than both our estimate and that derived from the host galaxy, 6 × 108 M⊙. In this case, the scaling factors should be fσ = 165.0 and fFWHM = 56.7, which are both extremely high. It is worth noting, however, that similar observations of other sources revealed that PKS 2004-447 seems to be a unique case among type 1 AGN (Capetti et al. 2021). Even among Capetti et al. (2021) sources, PKS 2004-447 is the only source that would require an unrealistically high value for the scaling factor. This might indicate that the polarization results obtained for PKS 2004-447 are not fully reliable, likely because of the insufficient statistics. More observing time is required to confirm or to reject these hypotheses.
Multiple powerful physics-based arguments against these high-mass values in the class of jetted NLS1s abound. First, as argued by Komossa et al. (2006), if NLS1s as a class had the highest inclination correction factors and therefore much higher black hole masses, they should show a much higher fraction of beamed systems than comparison samples of broad-line Seyfert 1s (BLS1s). However, the opposite is the case: beaming and radio loudness is systematically less frequent in NLS1s as a class than in BLS1s. A second argument was given by Foschini (2017). According to the theory of the blazar sequence (Fossati et al. 1998; Ghisellini et al. 1998; Ghisellini 2016), both classical blazar classes FSRQs and BL Lacs have a double-humped spectral energy distribution (SED). The first hump originates from synchrotron radiation and the second from inverse Compton. Essentially, the blazar sequence can be interpreted in terms of electron cooling and nuclear environments. FSRQs have a photon- and gas-rich environment, and the electron-cooling process occurs efficiently through inverse Compton, in particular external Compton, where the seed photons come from the accretion disk, the torus, or the interstellar medium. BL Lacs instead are the opposite. Their environment is photon-starved, and the only cooling mechanism is synchrotron self-Compton. The SED shape of γ-NLS1s is very similar to that of FSRQs, but the total emitted power is much lower (cf. Fig. 1 in Fermi/Lat Collaboration (2010). This is also the case for PKS 2004-447 (see Paliya et al. 2013, their Fig. 5, left panel). This agrees with the findings of Foschini et al. (2015), who calculated the jet power of NLS1s, FSRQs, and BL Lacs. They found that jetted NLS1s have a systematically lower jet power than FSRQs, but it is comparable to the jet power of BL Lacs. This can be interpreted in terms of mass difference because as predicted theoretically by Heinz & Sunyaev (2003), the jet power scales nonlinearly with the black hole mass. The physics behind jetted NLS1s and FSRQs is exactly the same, hence the similar SED, but NLS1s are scaled-down versions of FSRQs because of their lower black hole mass. This result is confirmed by the observations of their radio luminosity function, which clearly showed that jetted NLS1s are the low-luminosity tail of FSRQs (Berton et al. 2016a). Vice versa, in BL Lacs, the mass is similar to that of FSRQs, but the cooling mechanism is different because of the different environment, and this translates into the lower jet power and the different SED. It is worth noting that, if NLS1s had high-mass black holes, they would have a low jet power in a high-density environment. This would indicate that the relativistic electrons of their jets are not cooling despite the photon-rich environment, and this is clearly unphysical (Foschini 2017). Therefore the only reasonable explanation for the different jet power in FSRQs and NLS1s is the black hole mass, and NLS1s do not fit in the classical blazar sequence because their behavior is not regulated by electron cooling alone. The blazar sequence is missing an ingredient, which is the black hole mass, or if NLS1s are the progenitors of FSRQs, the evolution of AGN (Berton et al. 2017).
7.3. A rare γ-ray NLS1/CSS hybrid
We confirmed that the optical spectrum of PKS 2004-447 is definitely that of a rather typical NLS1s. The SED of PKS 2004-447, along with its γ-ray emission, confirm its blazar-like nature (Foschini et al. 2009; Abdo et al. 2009c; Paliya et al. 2013). The one-sided morphology of the relativistic jets and the high brightness temperature also show that relativistic beaming in this source is not negligible (Schulz et al. 2016). Its radio properties, however, clearly indicate that the source is also a CSS of relatively low luminosity, with a turnover below 1 GHz (Schulz et al. 2016). This result is not new because historically, PKS 2004-447 was the first source that was identified as a potential link between NLS1s and CSS (Oshlack et al. 2001; Gallo et al. 2006). The detection of γ-ray emission from a CSS is instead quite rare: only five objects with this classification have been included in the 4FGL catalog, along with six more that were classified as young radio galaxies (Abdollahi et al. 2020).
In the case of PKS 2004-447, possible emission from a counter-jet has been found in VLBA observations at 1.5 GHz (Schulz et al. 2016). If this is the case, the jet of PKS 2004-447 may have a non-negligible inclination with respect to the line of sight (θ < 50°). The minimum Doppler factor we have estimated from the observed variability at X- and γ rays (Berton et al. 2019b; Gokus et al. 2021) (see Sect. 6.3), requires that the dissipation occurs close to the black hole. This is also consistent with what is observed in some γ-ray emitting radio galaxies (Foschini et al. 2005).
An alternative option is that the source of γ-ray emission is not located close to the black hole, but farther away from it. In their VLBA map at 1.5 GHz, Schulz et al. (2016) found signs of coherent emission coming from a hotspot ∼45 mas away from the nucleus (projected size ∼170 pc), which corresponds to a change in the jet position angle. This potentially indicates ongoing interaction of the relativistic jet plasma and the interstellar medium. However, according to the jet model by Blandford & Königl (1979), ultrarelativistic speed and small viewing angle are required for a dominant contribution from curvature. This is not verified in the present case, as is clearly shown by radio maps.
Another interesting possibility is that the inclination of the relativistic jet in the core is different from than at larger scales. If the jet axis has changed its position with time, it is possible that it had a high inclination with the line of sight in the past, but today it is closely aligned with it. An episode of jet realignment from radio galaxy to blazar has already been observed directly (Hernández-García et al. 2017), and precession of the jet axis was also invoked to explain the properties of the jetted NLS1 Mrk 783 (Congiu et al. 2017a, 2020).
PKS 2004-447 is not the only example of CSS/NLS1 with γ-ray emission, because the strong radio source 3C 286 can also be classified as an NLS1 (Berton et al. 2017; Liao & Gu 2020; Yao & Komossa 2021), and it is included in the Fermi catalog (Abdollahi et al. 2020). For 3C 286, radio observations were able to obtain a rather high inclination value of ∼48°, and alternative mechanisms to produce its γ-ray emission such as interaction of the jet with the interstellar medium have been suggested (An et al. 2017). However, a number of jetted NLS1s do show a compact morphology at the kiloparsec scale and a steep radio spectrum (Berton et al. 2018a). Most of them, however, show lower luminosities than typical CSS, and they mostly belong to the class of low-luminosity compact sources (Kunert-Bajraszewska et al. 2010). Because of all these similarities between NLS1s and CSS, it has been suggested that some CSS, especially those of relatively low luminosity and with high-excitation emission lines, may represent the parent population of γ-ray NLS1s (Berton et al. 2016a). In other words, some of them may be the exact same type of source, but seen at different angles. This tentative unification has not been fully confirmed yet, but the existence of hybrid sources such as PKS 2004-447 may be an indication that this idea is at least in part correct (see also Sect. 7.1.3 of O’Dea & Saikia 2021).
It is also worth noting that at least a fraction of luminous CSS are also characterized by moderate to high Eddington ratios typical of population A sources (Wu 2009). For instance, the high R4570 and other properties of 3C 57 suggest that this luminous CSS source is optically young (or more likely rejuvenated) in addition to being radio young, as CSS have been suggested to be (e.g., Fanti et al. 2011). Considering that luminous CSS have relatively high mass black holes, it seems at least conceivable that they include already massive black holes and are rather evolved sources, rejuvenated by a new accretion episode yielding a moderate-to-high Eddington ratio. Conversely, low-luminosity CSS may be their younger counterparts at their first accretion episodes, and could be directly linked to NLS1s.
8. Summary
We analyzed a set of optical spectra of the γ-ray emitting source PKS 2004-447. Based on our new data, we can confirm its classification as an NLS1 galaxy, that belongs to population A3 of the quasar main sequence. From a detailed spectral analysis, we found that the source probably has some absorption along the line of sight, although this result is not consistent with past X-ray observations. The temperature and density values we derived, along with the width of the narrow lines, may suggest that some interaction between the NLR gas and the relativistic jet is present. The black hole mass we derived from the optical spectrum using the Hβ line is (1.5 ± 0.2)×107 M⊙. Despite the uncertainties related to this estimate, several arguments allow us to rule out that PKS 2004-447, and NLS1s in general, are powered by black holes with very high mass.
The long-term variability of the spectra indicates that the source continuum emission is rather stable, with the noteworthy exception of the flare, which was also observed in γ- and X-rays, in October 2019. We do not know how and if the Hβ line has been responding to the flare because the reverberation time is shorter than the gap between our observations, but we can speculate that most of the continuum variation is produced by the relativistic jet and not by the accretion disk. The Eddington ratio is within the typical range of NLS1s (0.09–0.29, depending on how it is measured), and we found a significant increase during the 2019 flare.
We finally discussed the role of PKS 2004-447 as a link between NLS1s and CSS. The radio properties of our source clearly suggest that it belongs to both classes, and that its relativistic jet may have a relatively high inclination with respect to the line of sight, given the possible detection of its counterjet in previous radio observations. PKS 2004-447 is then the second hybrid CSS/NLS1 with γ-ray emission after 3C 286. Continuous multiwavelength monitoring of this object, particularly by means of optical spectroscopy, may help us to finally solve the puzzle of NLS1s and determine their link with CSS and other young radio galaxies.
Because this estimate involves a line ratio, the issue with the y-axis in Oshlack et al. (2001) is not important as it affects all lines with a multiplicative factor.
Acknowledgments
The authors are grateful to the anonymous referee for the constructive comments. M.B, S.C., and L.F. acknowledge the financial support from the visitor and mobility program of the Finnish Centre for Astronomy with ESO (FINCA), funded by the Academy of Finland grant nr. 306531. E.C. acknowledges support from ANID project Basal AFB-170002. J.K. acknowledges financial support from the Academy of Finland, grant 311438. I.B. acknowledges Kulttuurirahasto for their continuing support. Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programmes ID 096.B-0256 and 0104.B-0587. This paper includes data gathered with the 2.5 meter Dupont Telescope located at Las Campanas Observatory, Chile. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 699, 976 [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 707, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, ApJ, 707, L142 [NASA ADS] [CrossRef] [Google Scholar]
- Abdollahi, S., Acero, F., Ackermann, M., et al. 2020, ApJS, 247, 33 [Google Scholar]
- An, T., Lao, B.-Q., Zhao, W., et al. 2017, MNRAS, 466, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Antón, S., Browne, I. W. A., & Marchã, M. J. 2008, A&A, 490, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Capetti, A., Robinson, A., Laor, A., & Behar, E. 2016, MNRAS, 458, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [Google Scholar]
- Berton, M., Foschini, L., Ciroi, S., et al. 2015a, A&A, 578, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Foschini, L., Caccianiga, A., et al. 2015b, Proc. “The many facets of extragalactic radio surveys: towards new scientific challenges” (EXTRA-RADSUR2015). 20-23 October 2015, Bologna, Italy, http://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=267, 75 [Google Scholar]
- Berton, M., Caccianiga, A., Foschini, L., et al. 2016a, A&A, 591, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Foschini, L., Ciroi, S., et al. 2016b, A&A, 591, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Foschini, L., Caccianiga, A., et al. 2017, Front. Astron. Space Sci., 4, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Berton, M., Congiu, E., Järvelä, E., et al. 2018a, A&A, 614, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Liao, N. H., La Mura, G., et al. 2018b, A&A, 614, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Braito, V., Mathur, S., et al. 2019a, A&A, 632, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berton, M., Ciroi, S., Congiu, E., et al. 2019b, ATel, 13259, 1 [NASA ADS] [Google Scholar]
- Berton, M., Congiu, E., Ciroi, S., et al. 2019c, AJ, 157, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Berton, M., Björklund, I., Lähteenmäki, A., et al. 2020, Contributions of the Astronomical Observatory Skalnate Pleso, 50, 270 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [Google Scholar]
- Blaufuss, E. 2019, ATel, 13249, 1 [NASA ADS] [Google Scholar]
- Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53 [NASA ADS] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
- Caccianiga, A., Antón, S., Ballo, L., et al. 2014, MNRAS, 441, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Caccianiga, A., Dallacasa, D., Antón, S., et al. 2017, MNRAS, 464, 1474 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Laor, A., Baldi, R. D., Robinson, A., & Marconi, A. 2021, MNRAS, 502, 5086 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Chen, S., Berton, M., La Mura, G., et al. 2018, A&A, 615, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 2001, MNRAS, 324, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Gilli, R., Capetti, A., & Macchetto, F. D. 2003, ApJ, 597, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Congiu, E., Berton, M., Giroletti, M., et al. 2017a, A&A, 603, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Congiu, E., Contini, M., Ciroi, S., et al. 2017b, Front. Astron. Space Sci., 4, 27 [CrossRef] [Google Scholar]
- Congiu, E., Kharb, P., Tarchi, A., et al. 2020, MNRAS, 499, 3149 [NASA ADS] [CrossRef] [Google Scholar]
- Corbett, E. A., Robinson, A., Axon, D. J., & Hough, J. H. 2000, MNRAS, 311, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cracco, V., Ciroi, S., Berton, M., et al. 2016, MNRAS, 462, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., & Gabel, J. R. 2003, AJ, 126, 1690 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F. 2019, Galaxies, 7, 87 [Google Scholar]
- D’Ammando, F., Acosta-Pulido, J. A., Capetti, A., et al. 2017, MNRAS, 469, L11 [CrossRef] [Google Scholar]
- D’Ammando, F., Acosta-Pulido, J. A., Capetti, A., et al. 2018, MNRAS, 478, L66 [NASA ADS] [Google Scholar]
- D’Ammando, F., Gokus, A., Kadler, M., & Ojha, R. 2019, ATel, 13233, 1 [Google Scholar]
- Decarli, R., Dotti, M., Fontana, M., & Haardt, F. 2008, MNRAS, 386, L15 [NASA ADS] [Google Scholar]
- Deo, R. P., Crenshaw, D. M., & Kraemer, S. B. 2006, AJ, 132, 321 [NASA ADS] [CrossRef] [Google Scholar]
- De Robertis, M. M., Dufour, R. J., & Hunt, R. W. 1987, JRASC, 81, 195 [NASA ADS] [Google Scholar]
- Dimitrijević, M. S., Popović, L. Č., Kovačević, J., Dačić, M., & Ilić, D. 2007, MNRAS, 374, 1181 [CrossRef] [Google Scholar]
- Drinkwater, M. J., Webster, R. L., Francis, P. J., et al. 1997, MNRAS, 284, 85 [NASA ADS] [Google Scholar]
- Du, P., Wang, J.-M., Hu, C., et al. 2016, ApJ, 818, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2008, New Astron. Rev., 52, 274 [CrossRef] [Google Scholar]
- Fanti, C., Fanti, R., Zanichelli, A., Dallacasa, D., & Stanghellini, C. 2011, A&A, 528, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fermi/Lat Collaboration (Foschini, L., et al.) 2010, in Accretion and Ejection in AGN: a Global View, eds. L. Maraschi, G. Ghisellini, R. Della Ceca, F. Tavecchio, et al., ASP Conf. Ser., 427, 243 [NASA ADS] [Google Scholar]
- Fischer, T. C., Kraemer, S. B., Schmitt, H. R., et al. 2018, ApJ, 856, 102 [Google Scholar]
- Forbes, D. A., & Ponman, T. J. 1999, MNRAS, 309, 623 [CrossRef] [Google Scholar]
- Foschini, L. 2012a, Res. Astron. Astrophys., 12, 359 [Google Scholar]
- Foschini, L. 2012b, in Proceedings of Nuclei of Seyfert galaxies and QSOs – Central engine& conditions of star formation, Proc. Sci., 10 [Google Scholar]
- Foschini, L. 2017, Front. Astron. Space Sci., 4, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L. 2020, Universe, 6, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Chiaberge, M., Grandi, P., et al. 2005, A&A, 433, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Maraschi, L., Tavecchio, F., et al. 2009, Adv. Space Res., 43, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Berton, M., Caccianiga, A., et al. 2015, A&A, 575, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Ciroi, S., Berton, M., et al. 2019, Universe, 5, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [Google Scholar]
- Fraix-Burnet, D., D’Onofrio, M., & Marziani, P. 2017, Front. Astron. Space Sci., 4, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Gallo, L. 2018, in Revisiting narrow-line Seyfert 1 galaxies and their place in the Universe, Proc. Sci., 34 [Google Scholar]
- Gallo, L. C., Edwards, P. G., Ferrero, E., et al. 2006, MNRAS, 370, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 2009, New Astron. Rev., 53, 140 [Google Scholar]
- Ghisellini, G. 2016, Galaxies, 4, 36 [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [Google Scholar]
- Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [Google Scholar]
- Gokus, A. 2019, ATel, 13229, 1 [NASA ADS] [Google Scholar]
- Gokus, A., Paliya, V. S., Wagner, S. M., et al. 2021, A&A, 649, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodrich, R. W. 1989, ApJ, 342, 224 [Google Scholar]
- Grandi, P., & Palumbo, G. G. C. 2004, Science, 306, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Gravity Collaboration (Sturm, E., et al.) 2018, Nature, 563, 657 [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 627, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Hood, C. E., Barth, A. J., et al. 2010, ApJ, 723, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D. 2000, New Astron. Rev., 44, 455 [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M., Chen, Y., Komossa, S., et al. 2015, ApJS, 221, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, T. S., Berton, M., Antón, S., et al. 2021, MNRAS, 504, 5188 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Heinz, S., & Sunyaev, R. A. 2003, MNRAS, 343, L59 [Google Scholar]
- Hernández-García, L., Panessa, F., Giroletti, M., et al. 2017, A&A, 603, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Järvelä, E., Lähteenmäki, A., & Berton, M. 2018, A&A, 619, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Järvelä, E., Berton, M., Ciroi, S., et al. 2020, A&A, 636, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2011, Nature, 470, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2013a, A&A, 549, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollatschny, W., & Zetzl, M. 2013b, A&A, 558, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [Google Scholar]
- Komossa, S. 2008, Rev. Mex. Asron. Astrofis., 32, 86 [NASA ADS] [Google Scholar]
- Komossa, S. 2018, in Revisiting narrow-line Seyfert 1 galaxies and their place in the Universe, Proc. Sci., 15 [Google Scholar]
- Komossa, S., Voges, W., Xu, D., et al. 2006, AJ, 132, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Xu, D., Zhou, H., Storchi-Bergmann, T., & Binette, L. 2008, ApJ, 680, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Xu, D. W., & Wagner, A. Y. 2018, MNRAS, 477, 5115 [CrossRef] [Google Scholar]
- Koratkar, A. P., & Gaskell, C. M. 1991, ApJ, 370, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Kotilainen, J. K., León-Tavares, J., Olguín-Iglesias, A., et al. 2016, ApJ, 832, 157 [CrossRef] [Google Scholar]
- Kovačević, J., Popović, L. Č., & Dimitrijević, M. S. 2010, ApJS, 189, 15 [Google Scholar]
- Kreikenbohm, A., Schulz, R., Kadler, M., et al. 2016, A&A, 585, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunert-Bajraszewska, M., Gawroński, M. P., Labiano, A., & Siemiginowska, A. 2010, MNRAS, 408, 2261 [NASA ADS] [CrossRef] [Google Scholar]
- Kynoch, D., Landt, H., Ward, M. J., et al. 2018, MNRAS, 475, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Kynoch, D., Landt, H., Ward, M. J., et al. 2019, MNRAS, 487, 181 [NASA ADS] [CrossRef] [Google Scholar]
- León Tavares, J., Kotilainen, J., Chavushyan, V., et al. 2014, ApJ, 795, 58 [Google Scholar]
- Letawe, G., Magain, P., Courbin, F., et al. 2007, MNRAS, 378, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, M., & Gu, M. 2020, MNRAS, 491, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Mandal, A. K., Rakshit, S., Stalin, C. S., et al. 2021, MNRAS, 502, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2001, ApJ, 558, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Stirpe, G. M., Zamfir, S., & Calvani, M. 2009, A&A, 495, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marziani, P., del Olmo, A., D’Onofrio, M., et al. 2018a, in Revisiting narrow-line Seyfert 1 galaxies and their place in the Universe, Proc. Sci., 2 [Google Scholar]
- Marziani, P., Dultzin, D., Sulentic, J. W., et al. 2018b, Front. Astron. Space Sci., 5, 6 [CrossRef] [Google Scholar]
- Mathur, S. 2000, MNRAS, 314, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Fields, D., Peterson, B. M., & Grupe, D. 2012, ApJ, 754, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R. 2017, Front. Astron. Space Sci., 4, 42 [CrossRef] [Google Scholar]
- Nelson, C. H., & Whittle, M. 1996, ApJ, 465, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A. M., & van Breugel, W. 2008, A&A, 491, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [Google Scholar]
- O’Dea, C. P., & Saikia, D. J. 2021, A&ARv, 29, 3 [Google Scholar]
- Olguín-Iglesias, A., Kotilainen, J. K., León Tavares, J., Chavushyan, V., & Añorve, C. 2017, MNRAS, 467, 3712 [NASA ADS] [Google Scholar]
- Olguín-Iglesias, A., Kotilainen, J., & Chavushyan, V. 2020, MNRAS, 492, 1450 [Google Scholar]
- Orban de Xivry, G., Davies, R., Schartmann, M., et al. 2011, MNRAS, 417, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Oshlack, A. Y. K. N., Webster, R. L., & Whiting, M. T. 2001, ApJ, 558, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei [Google Scholar]
- Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [Google Scholar]
- Paliya, V. S. 2019, A&A, 40, 39 [Google Scholar]
- Paliya, V. S., Stalin, C. S., Shukla, A., & Sahayanathan, S. 2013, ApJ, 768, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Panda, S., Marziani, P., & Czerny, B. 2019, ApJ, 882, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1997, An Introduction to Active Galactic Nuclei [Google Scholar]
- Peterson, B. M. 2011, Narrow-Line Seyfert 1 Galaxies and theirPlace in the Universe, 32 [Google Scholar]
- Peterson, B., & Dalla Bontà, E. 2018, in Revisiting narrow-line Seyfert 1 galaxies and their place in the Universe, Proc. Sci., 8 [Google Scholar]
- Peterson, B. M., & Wandel, A. 1999, ApJ, 521, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., McHardy, I. M., Wilkes, B. J., et al. 2000, ApJ, 542, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [Google Scholar]
- Rakshit, S., Stalin, C. S., Chand, H., & Zhang, X.-G. 2017, ApJS, 229, 39 [Google Scholar]
- Rakshit, S., Schramm, M., Stalin, C.S., et al. 2021, MNRAS, 504, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [Google Scholar]
- Romano, P., Vercellone, S., Foschini, L., et al. 2018, MNRAS, 481, 5046 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Böttcher, M., Foschini, L., et al. 2020, MNRAS, 494, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schulz, R., Kreikenbohm, A., Kadler, M., et al. 2016, A&A, 588, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- \’{S}niegowska, M., Marziani, P., Czerny, B., et al. 2021, ApJ, 910, 115 [CrossRef] [Google Scholar]
- Sulentic, J., & Marziani, P. 2015, Front. Astron. Space Sci., 2, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000, ApJ, 536, L5 [Google Scholar]
- Sulentic, J. W., Zamfir, S., Marziani, P., et al. 2003, ApJ, 597, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Martínez-Carballo, M. A., Marziani, P., et al. 2015, MNRAS, 450, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., Véron, P., & Gonçalves, A. C. 2001, A&A, 372, 730 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verrecchia, F., Piano, G., Tavani, M., et al. 2019, ATel, 13244, 1 [NASA ADS] [Google Scholar]
- Vietri, A.,Berton, M.& Ciroi, S. 2018, in Revisiting narrow-line Seyfert 1 galaxies and theirplace in the Universe, Proc.Sci., 47 [Google Scholar]
- Whittle, M. 1985, MNRAS, 213, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Pogge, R. W., & Mathur, S. 2002, AJ, 124, 3042 [CrossRef] [Google Scholar]
- Williams, R. J., Mathur, S., & Pogge, R. W. 2004, ApJ, 610, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Q. 2009, MNRAS, 398, 1905 [CrossRef] [Google Scholar]
- Xu, D., Komossa, S., Zhou, H., et al. 2012, AJ, 143, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, S., & Komossa, S. 2021, MNRAS, 501, 1384 [Google Scholar]
- Yuan, W., Zhou, H. Y., Komossa, S., et al. 2008, ApJ, 685, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Zhang, H.-M., Gan, Y.-Y., et al. 2020, ApJ, 899, 2 [CrossRef] [Google Scholar]
- Zhou, H.-Y., Wang, T.-G., Dong, X.-B., Zhou, Y.-Y., & Li, C. 2003, ApJ, 584, 147 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Redshift-corrected optical spectrum of PKS 2004-447, observed by FORS2. The most prominent emission lines are identified. The telluric absorptions are marked with the crossed circle. |
| In the text | |
 |
Fig. 2. Fit of the Fe II multiplets in the Hβ region. The original spectrum, redshift corrected and continuum subtracted, is represented by the solid black line. The Fe II multiplets from Marziani et al. (2009) are the dashed red line. The spectrum was cut off for visual purposes. |
| In the text | |
 |
Fig. 3. Fit of the [O III] lines after continuum and Fe II subtraction. The spectrum is represented by the solid black line. The two Gaussian components represent the line core (dashed orange line) and wing (dashed green line). The best fit is represented by the dot-dashed red line, the residuals by the solid blue line, and the horizontal dashed line represents the zero level of the continuum. The rest-frame wavelength of the two lines is indicated by the vertical dashed lines. Due to the low spectral resolution, the core component is unresolved. |
| In the text | |
 |
Fig. 4. Fit of the Hβ line with different functions. The original spectrum is the solid black line, the residuals of the model subtractions are the solid blue line, the horizontal dashed black line represents the zero level of continuum, and the vertical dashed line represents the rest-frame wavelength of Hβ. The values of |
| In the text | |
 |
Fig. 5. Fitting of the Hα+[N II] complex. The original spectrum is the solid black line, the residuals of the model subtractions are the solid blue line, the horizontal dashed black line represents the zero level of the continuum, and the vertical dashed line represent the rest-frame wavelength of Hα. Two Gaussians reproduce the two [N II] lines, represented by the solid cyan line, and one Gaussian reproduces the Hα narrow component, indicated by the dashed orange line. The solid yellow line is the actual Hα profile, while the best fit is indicated by the dot-dashed red line. Left panel: broad component of Hα is reproduced with one Lorentzian function, reproduced by the dashed green line. Right panel: broad component of Hα is reproduced with two Gaussians, indicated by the dashed green and purple lines. |
| In the text | |
 |
Fig. 6. Variability measured in the continuum flux density and in the Hβ line flux. The blue circles represent the [O III]λ5007 flux, which was forced to be the same in all spectra. The black squares represent the flux of Hβ, and the red circles in the bottom panel represent the continuum flux. |
| In the text | |
 |
Fig. 7. Anticorrelation of the continuum flux at 5100Å and the equivalent width of the Hβ emission line. The dashed red line indicates the best linear fit. |
| In the text | |
 |
Fig. 8. Evolution of the Eddington ratio estimated by using the continuum (red squares) and the Hβ line luminosity (black circles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} f(\lambda ) = \frac{A_0}{\sigma _s \sqrt{2\pi }} \exp {\left[-\frac{(\lambda - \lambda _0)^2}{2\sigma _s^2}\right]} \left[ 1 + \mathrm{erf} \left( \frac{\alpha }{\sqrt{2}} \frac{(\lambda - \lambda _0)}{\sigma _s}\right) \right], \end{aligned} $$](/articles/aa/full_html/2021/10/aa41409-21/aa41409-21-eq3.gif)