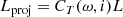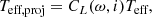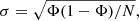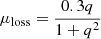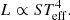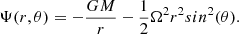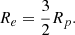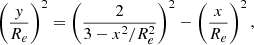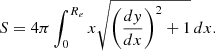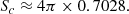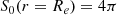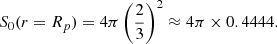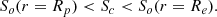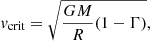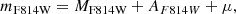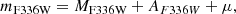| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202141269 | |
| Published online | 24 September 2021 | |
Stringent upper limit on Be star fractions produced by binary interaction
1
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: bhastings@astro.uni-bonn.de
2
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3
Dipartimento di Fisica e Astronomia “Galileo Galilei” Univ. di Padova, Vicolo dell’Osservatorio 3, Padova 35122, Italy
Received:
7
May
2021
Accepted:
17
June
2021
Context. Binary evolution can result in fast-rotating stars through accretion of angular momentum during mass-transfer phases. These fast-rotating stars are predicted to be observable as Be stars. Current models struggle to produce a satisfactory description of Be star populations, even though numerous pieces of observational evidence indicate that the accretion process might be the dominant Be formation channel.
Aims. Given the distinct uncertainties in detailed binary evolution calculations, we investigate a rigorous and model-independent upper limit for the production of Be stars through binary interaction and aim to confront this limit with observations of Be stars in young star clusters.
Methods. Using extreme assumptions, we calculate the number ratio of post-interaction to pre-interaction binary systems in a coeval population. This ratio describes an upper limit to Be star formation through mass transfer. A detailed comparison is made between our derived upper limit and relevant observations of Be stars, which allows us to probe several aspects of binary star physics.
Results. We find that in coeval populations, binary interaction can at most account for one-third of all main-sequence stars being Be stars. Near the cluster turn-off region, this limit appears to be realised in the clusters studied. Away from the turn-off, a good fit to the observed Be fraction as a function of mass is obtained by applying simple assumptions about which systems undergo unstable mass-transfer produces.
Conclusions. We find that assuming distinct physics, binary evolution alone can in principle match the high numbers of Be stars that are observed in open clusters. Whether the required binary physics is realised in nature remains to be investigated.
Key words: stars: emission-line, Be / binaries: general / stars: evolution / stars: massive / stars: rotation
© ESO 2021
1. Introduction
Be stars are massive main-sequence stars that display emission features in their spectra. Since their discovery more than 150 years ago (Secchi 1866), we have advanced our understanding to explain the emission as a result of a decretion-disc, which is being ionised by the central star (Struve 1931), but it is still unclear how a Be star gains its disc. Observations conclusively show that Be stars rotate significantly faster than their B counterparts (Struve 1931; Porter 1996; Huang et al. 2010; Zorec et al. 2016), such that the centripetal force potentially matches the gravitational force at the equator (Collins & Truax 1995; Townsend et al. 2004). However, the fundamental origin of this fast rotation is still unknown with both single and binary star channels having been proposed to play a role.
One way to achieve such rotation is for a star to be spun up by mass transfer in a binary system (Kriz & Harmanec 1975; Pols et al. 1991; Liu et al. 2006; Langer 2012). When a star accretes material, it also accretes angular momentum, which in the absence of tidal forces can lead to critical rotation of the accreting star, allowing material to become unbound and form a disc. The accretion of angular momentum is an efficient process, with a star needing to accrete typically a few percent of its own mass to rotate critically (Packet 1981).
In wide systems that initiate mass-transfer after the primary has exhausted hydrogen in the core (so-called Case B mass transfer), tidal forces are generally weak for the accretor star, and it can be spun up to near-critical velocities. Furthermore, rapid rotators can also originate from close systems that undergo mass transfer while the donor is still core hydrogen-burning(so-called Case A mass transfer). Although tides inhibit the spin-up of the accretor during the initial mass-transfer phases, these phases cause a widening of the binary (Petrovic et al. 2005) so that when the donor expands to become a giant star (initiating Case AB mass transfer), many systems are wide enough to render tides ineffective, allowing the mass gainer to rotate super-synchronously (Sen et al., in prep.). Therefore rapidly rotating mass gainers can originate from both short- and long-period systems. What is common between these cases is that the spun-up star is usually produced after the initially more massive star in the system has exhausted its central supply of hydrogen.
In binary systems that produce a Be star and in which the primary star is not massive enough to undergo a supernova explosion, a short-lived helium star or long-lived white dwarf would be the companion to the Be star. Despite the difficulty of detection, both of these types of systems have been observed (Li et al. 2012; Schootemeijer et al. 2018; Shenar et al. 2020; Coe et al. 2020). Furthermore, studies of Be star discs have found that many are truncated, suggesting that they are acted upon by unseen companions (Klement et al. 2017, 2019).
When the mass donor does explode as a supernova, the majority of systems are expected to become unbound(due to a supernova kick) (Brandt & Podsiadlowski 1995) and the Be star will probably have no companion. The fact that this does not occur in every case is evidenced by large numbers of Be-Xray binaries (Raguzova & Popov 2005), which consist of a neutron star in an eccentric orbit around a Be star such that Xrays are produced when the Be disc and neutron star interact. When the binary is disrupted, the Be star would likely be a runaway star. Boubert & Evans (2018) and Dorigo Jones et al. (2020) both found the peculiar space velocities of Be stars in the Gaia catalogue to be consistent with a binary origin of Be stars.
Observations show the Be phenomenon to be more common at lower metallicities (Maeder et al. 1999; Martayan et al. 2010; Iqbal & Keller 2013), in good agreement with predictions of single star models whereby metal-rich stars suffer stronger angular momentum losses through winds, thus making fast-rotators rarer at higher metallicities (Hastings et al. 2020). Naively, this trend is difficult to explain in the binary framework. However, further observational characteristics of Be stars have been uncovered that are difficult to explain with a single-star formation channel. Initially fast-rotating single stars are expected to exhibit enhanced surface nitrogen abundances, as rotational mixing dredges up CNO-processed material to the photosphere. However, there appears to be an incompatibility between models of rotating single stars and measurements of nitrogen abundances in Be stars, with many Be stars showing much lower nitrogen abundances than expected (Lennon et al. 2005; Dunstall et al. 2011; Ahmed & Sigut 2017; Hastings et al. 2020). On the other hand, spun-up mass gainers might not be rich in surface nitrogen. Although the physics governing the details of mass transfer remains uncertain, accretion may be limited by the angular momentum content of the gainer, such that accretion becomes non-conservative once critical rotation is achieved (Wang et al. 2020; Langer et al. 2020). Another factor is the strong mean molecular weight barrier established from hydrogen burning, which prevents efficient rotational mixing in the critically rotating mass gainer (Kippenhahn et al. 1974; Pinsonneault et al. 1989).
As demonstrated by Ekström et al. (2008) and Hastings et al. (2020), single stars may achieve near-critical rotation during the late stages of hydrogen burning, in contrast to observations showing that Be stars have a range of fractional main-sequence ages (Zorec et al. 2005; McSwain & Gies 2005; Milone et al. 2018). If Be stars are mostly single, we would expect pre-interaction binaries to host Be primaries because regardless of which proposed single-star mechanism causes the Be phenomenon, it should work for stars in a pre-interaction binary just as well as for single stars. It is thus telling that almost no Be stars with a main-sequence companion have been detected (Bodensteiner et al. 2020b).
Despite the numerous pieces of evidence that support the dominance of a binary formation channel, several uncertainties in binary evolution prevent a solid and accurate theoretical description of Be star populations. Proof of the difficulty of modelling the production of Be stars is given by the contrasting results of previous authors. It has been concluded that binaries are responsible for either all (Shao & Li 2014), half (Pols et al. 1991) or only a small minority (van Bever & Vanbeveren 1997) of galactic Be stars. This difference is mostly due to different assumptions on mass-transfer efficiency and the stability of mass transfer.
In light of these uncertainties, we find it useful to determine a model-free upper limit to Be star production from mass transfer in binary systems. Assessment of this limit can provide insight into whether it is at all possible for Be stars to be formed exclusively in binaries, and to which extent other formation mechanisms must be invoked. Under the assumption that binary evolution dominates the production of Be stars, we can also probe uncertain binary physics. We use recent high-quality observations of Be stars in open clusters (Milone et al. 2018) to rigorously test our simple picture.
In Sect. 2 we explain the procedure with which we calculated an upper limit to Be star production from mass transfer in binary systems. The results of this endeavour are presented in Sect. 3. In Sect. 4 we compare our results to the numbers of Be stars observed in young open clusters. We infer the conditions for stable mass transfer that are required for our prescription to reproduce the Be fractions along the main sequences of young open clusters in Sect. 5. Uncertainties and the implications of the upper limit are discussed in Sect. 6. Concluding remarks are given in Sect. 7.
2. Method
2.1. Hypothetical population of interacting binary stars
In order to calculate an upper limit to the numbers of Be stars that may be produced, we take extreme assumptions. The of which is that the initial binary fraction in the population is 1; that is, every star is born as a member of a binary. Nextly, as the hydrogen-burning episode of a massive star comprises about 90% of the total lifetime of a star, we then assumed that as soon as a primary star leaves the main sequence, stable mass transfer occurs on a very short timescale, instantly producing a Be star. In our model, a Be star is produced regardless of the initial period, primary mass, or mass ratio of the system, so that every secondary star will at some point during its lifetime become a Be star. In this framework, the orbital period distribution becomes irrelevant. Furthermore, we shall assume that once a Be star is formed, it remains so for the rest of its lifetime.
For simplicity, we ignore the effects of mass loss through stellar winds, such that every system remains at its initial mass ratio, q, until mass transfer occurs (which may be either conservative or non-conservative). Moreover, because the stellar mass-luminosity relation is very steep, we define each binary system by its most luminous component, so that each binary can be assigned an equivalent single-star mass. To facilitate comparison with open cluster observations, our synthetic population is assumed to be coeval.
Other properties of our population are not designed to maximise the efficiency of Be star formation, and are more or less standard in binary evolution calculations. We denote the initial masses of the initially more massive star as M1 and the initial mass of the initially less massive star as M2, i and define the initial mass ratio, q, as
such that
We considered a population of binary stars in which the distribution of initial primary mass follows a power law like
and the distribution of initial mass ratios is described similarly as
where ξ0 and f0 are normalising constants to ensure that the integral over the whole parameter space is unity (as befitting a probability-density function). For example, the value of f0 is easily computed as
where qmin is the minimum mass-ratio in our population and is nominally set to qmin = 0.1 to match the observing campaigns of Sana et al. (2012, 2013). It is assumed that systems born with mass ratios lower than this value are likely to be unstable and merge either during their formation or early in their evolution and hence are not considered.
Mass gain of the accretor shall be parametrised by assuming that a total mass of ΔM is accreted, giving the relation between final and initial masses of the accretor as
with ΔM/M2, i being a free parameter.
Our assumptions on the population are summarised in the list below.
-
initial binary fraction is 1
-
every system will undergo stable Case B mass transfer and form a Be star, regardless of period or mass ratio
-
once a primary star leaves the main sequence, a Be star is immediately formed
-
once a Be star is formed, it remains so for the rest of its lifetime
-
the accretor star gains mass ΔM, with the relative mass gain ΔM/M2, i being a free parameter.
-
the effects of wind mass loss are ignored so that a system remains at its initial mass ratio until mass transfer occurs.
-
the distribution of initial primary masses follows a power law,
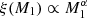
-
the distribution of initial mass ratios follows a power law, f(q) ∝ qκ
-
only considered are binaries with a mass ratio greater than qmin, which is set to 0.1.
-
when both stars are burning hydrogen, the luminosity of a binary system is given by that of the primary. When the primary has evolved off the main sequence, the luminosity of the system is naturally that of the secondary.
According to our assumptions, every secondary star with a post-main-sequence companion is a Be star, meaning that the number of Be stars with a given mass M is
where MTO is the turn-off mass of our coeval population. In our model the number of non-Be stars is given by the number of primaries at a given mass. The Be fraction, ϕBe(M) is defined as the number fraction of Be stars to all stars at a given mass. In a coeval population, this becomes
In our model, the mass of a Be star is related to its initial mass, M2, i, and the relative mass gain, ΔM/M2, i via Eq. (6), such that the expression above becomes
With the aid of Eqs. (1) and (6), the condition
can be rewritten as
leading to
This results in
To study coeval populations, a more convenient approach is to find the Be fraction as a function of the fractional main-sequence turn-off mass, M/MTO. This produces the expression
which shall be our basis for exploring the Be fraction in coeval populations.
To evaluate the Be fraction, it is necessary to determine the relative numbers of primary stars to the number of secondary stars at a given mass. We may write that the number of primary stars with a given mass, n(M1), is the integral of the primary mass distribution across an infinitesimally small mass range, dM1, multiplied by the total number of stars in the population, ntot, as
To tackle the number of secondary stars at a given mass is sightly more involved as we do not have directly the distribution of secondary masses, instead it is inferred from the primary mass and mass-ratio distributions. First consider a population in which there exists only a single mass-ratio, q0, i.e. the mass-ratio distribution is a delta-Dirac function. If one is interested in the number of secondary stars with initial mass M2, i, one must count the number of primaries with mass M2, i/q0, so we have
with  representing an infinitesimally small change in
representing an infinitesimally small change in 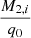 .
.
Any distribution may be expressed as an infinite sum of appropriately weighted delta-Dirac distributions, with the weighting coming from the probability-density function. For the general case, we therefore have
It is then clear that the limits of the integral above place constraints on the initial mass ratios counted. The number of systems with a given initial secondary mass M2, i and initial mass ratios between qmin and qmax can thus be written as
The differential 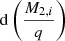 in Eq. (19) is quite cumbersome, therefore we chose to let
in Eq. (19) is quite cumbersome, therefore we chose to let
We may now write
We have
thus
As we are interested in the number of secondary stars at a fixed mass, dM2, i = 0,
Differentiating r gives
Combining Eqs. (24) and (25) results in
Inserting this into our expression for n(M2, i & qmin < q < qmax) (Eq. (21)) gives
We now divide Eq. (16) by Eq. (27), leaving
When the distributions for initial primary mass and mass ratio, Eqs. (3) and (4), are inserted, Eq. (28) simplifies further to
This result may be readily checked against Monte Carlo sampling of the primary mass and mass-ratio distributions.
Equation (29) can be used to directly determine the Be fraction (Eq. (15)) by setting M1 = M/MTO, 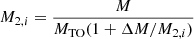 and
and 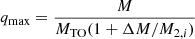 . This leaves
. This leaves
where the integral has a simple analytic solution. Equation (30) describes the Be star fraction as a function of the fractional turn-off mass, M/MTO, for our model open cluster. As the mass dependence in Eq. (30) is expressed by the fractional turn-off mass, is not necessary to specify the turn-off mass.
2.2. Limits for the remaining parameters
All that remains is to explore Eq. (30) in a suitable parameter space. The parameters we have are α, κ, and ΔM/M2, i, which are the primary mass distribution exponent, the initial mass-ratio distribution exponent, and the relative accretor mass gain, respectively.
The canonical value for the exponent of the initial mass function (IMF), α, is given by the Salpeter IMF, α = −2.35 (Salpeter 1955). However, recent observations of young stars in the 30 Doradus starburst region instead suggest 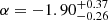 (Schneider et al. 2018). Similarly, in the R136 star-forming region, an exponent of α = −2.0 ± 0.3 was found (Bestenlehner et al. 2020). On the other hand, it has also been proposed that the IMF follows an even steeper law with α = −2.7 (Scalo 1986). Therefore we consider the range −1.9 < α < −2.7.
(Schneider et al. 2018). Similarly, in the R136 star-forming region, an exponent of α = −2.0 ± 0.3 was found (Bestenlehner et al. 2020). On the other hand, it has also been proposed that the IMF follows an even steeper law with α = −2.7 (Scalo 1986). Therefore we consider the range −1.9 < α < −2.7.
Observations of Galactic O-type stars show that the mass-ratio distribution follows a power law with exponent κ = −0.1 ± 0.6 (Sana et al. 2012) for 0.1 < q < 1. In the Large Magellanic Cloud, the mass ratios of massive binaries appear to be distributed differently, with κ = −1.0 ± 0.4 again in the range 0.1 < q < 1 (Sana et al. 2013). There are many claims that mass ratios of binaries favour either low values (Trimble 1990; Tout 1991; Hogeveen 1991) or follow a uniform distribution (Kobulnicky & Fryer 2007; Kouwenhoven et al. 2007). In light of these findings, we consider κ values in the range −1 < κ < 0.
Estimates of the accretor mass gain, ΔM/M2, i, obtained by demanding that mass transfer stops when the mass gainer reaches critical rotation, tell us that ΔM/M2, i is 0.1 at most and in most cases is about 0.02, depending on the angular momentum content and physical structure of the mass gainer before accretion (Packet 1981; Petrovic et al. 2005; Wang et al. 2020). It has been found that around 70% of the mass leaving the donor must be ejected from the system to explain the observed distributions of Be star masses in Be X-ray binaries (Vinciguerra et al. 2020). However, it must be noted that because it is expected that up to 90% of massive binary systems are broken apart by a supernova kick (Brandt & Podsiadlowski 1995), Be X-ray binaries represent a small fraction of the population and may therefore well contain strong biases. Furthermore, it is thought that mass transfer must be highly non-conservative to explain the observed populations of Wolf-Rayet O-star binaries (Petrovic et al. 2005; Shao & Li 2016). On the other hand, several systems show evidence that near-conservative mass transfer has taken place (de Mink et al. 2007; Schootemeijer et al. 2018; Brož et al. 2021). To fully explore the effects of mass-transfer efficiency on Be star populations, we consider the full range 0 < ΔM/M2, i < 1.
3. Results
The results of Eq. (30) are plotted in Fig. 1 for the extremal parameters outlined in Sect. 2.2. The primary mass distribution affects the absolute numbers of Be stars because for a shallower distribution (α closer to 0), there is an abundance of massive binaries, such that many systems contain post-main-sequence primaries, and therefore the number of Be stars increases. Conversely, when α ≪ 0, the population contains fewer primaries of mass greater than the turn-off mass, and the Be count decreases.
 |
Fig. 1. Maximum Be fraction, ΦBe, in a coeval population as defined by Eq. (30) plotted as a function of fractional main-sequence turn-off mass, M/MTO, for varying parameters. Left and right panels: ΔM/M2, i = 0 and 1, respectively. The colour of the lines represents differing κ values. Red is κ = 0 and blue is κ = −1. Dashed lines show α = −1.9 and solid lines show α = −2.7, as indicated by the annotations. |
The effect of the mass-ratio distribution can be understood by considering a population with a high value of κ such that secondary stars have a similar mass to their companion. In this case, when the primary leaves the main sequence, the secondary will be rather evolved, and hence most Be stars will be found near the turn-off. On the other hand, in a population with a low κ, the opposite is true; the secondary stars will have lower masses compared to the turn-off mass, and Be stars will be more evenly distributed along the main sequence, as shown in Fig. 1.
Figure 1 shows how a varying mass gain changes the Be count, with accretors that gain more mass producing fewer Be stars. This can be understood by considering a Be star of mass 0.9MTO that is produced by inefficient mass transfer. For the primary to exceed the turn-off mass, the initial mass ratio of the system must be lower than 0.9. If this star had gained 0.1MTO, the initial mass would be 0.8MTO and the initial mass ratio must be lower than 0.8. This shows that mass gain restricts the number of systems that are able to produce Be stars of a given mass, and a low mass-transfer efficiency leads to higher numbers of Be stars being produced at a given mass.
Figure 1 shows that the largest Be fractions are produced when mass transfer is inefficient (ΔM/M2, i = 0) and the IMF is shallow. The mass-ratio distribution then tunes the distribution of Be stars along the main sequence. Therefore it is judged that most Be stars are produced with the parameters ΔM/M2, i = 0, α = −1.9 and −1 < κ < 0. Depending on the chosen parameters, the maximum Be fraction is in the range 0.2–0.35 near the main-sequence turn-off.
4. Comparison to observations
To contextualise to our results, we attempt here a comparison with observations using high-quality Hubble Space Telescope photometry of young Small and Large Magellanic Cloud open clusters in which Be stars are revealed as bright objects in a narrow-band filter centred on Hα (Milone et al. 2018). Photometry was performed with Hubble wide-band filters F814W and F336W and the narrow-band F656N filter, allowing colour-magnitude diagrams in which Be stars are identified from Hα photometry to be produced.
As many spectroscopically confirmed Be stars in NGC 330 are bright in Hα (Bodensteiner et al. 2020a), we judge Hα emission to be a good proxy for Be stars. It is possible for the accretion discs of Algol-type binaries to exhibit Hα emission (Peters 1989), but these systems are expected to make up only about 3% of the total population (de Mink et al. 2014; Sen et al., in prep.). Furthermore, some field stars may be Hα emitters. Milone et al. (2018) noted that no more than one-tenth of the stars in the cluster field are suspected field stars. Field stars will also contaminate the population of stars that do not emit in Hα, therefore their presence is not expected to significantly alter the relative fractions of Hα emitters and non-emitters.
Be star fractions have previously been measured as a function of magnitude (Keller et al. 1999; Milone et al. 2018; Bodensteiner et al. 2020a). We find it worthwhile to repeat this exercise, including several factors that were previously overlooked.
Our goal is to measure the observed Be fraction as a function of mass along the main sequence of an open cluster. To do this, we must note the two major differences between a Be star and a “normal” B star: fast rotation, and the presence of a decretion disc. The effect of the centrifugal force means that a fast-rotating star has a reduced effective gravity at the equator. According to the von Zeipel theorem (von Zeipel 1924), this results in a lower effective temperature. Therefore fast-rotating stars are cooler and redder than their non-rotating counterparts. Furthermore, light from a Be star consists of radiation from the star itself and also of light from the decretion disc. Typically, the average temperature of the disc is about 70% of the effective temperature of the star itself (Sigut et al. 2009), and so the disc is expected to emit mostly in visible and infrared wavelengths.
In a colour-magnitude diagram, the magnitude in a red filter is plotted on the y-axis, and a colour defined by the blue and red filter (B–R) on the x-axis. When a star becomes brighter in the red filter, it therefore moves to the right and upwards in the colour-magnitude diagram. This effect means that to count the Be stars as a function of mass, we must do so in bins that are sloped with respect to the x-axis. The gradient of this slope depends on how much redder a near-critically rotating star is than a slow rotator at the same mass, and on how much light the decretion disc radiates.
As no reliable numerical models exist of stars rotating at the critical velocity, we shall adopt a simple model to relate the luminosity and temperature of a critical rotator to an equivalent non-rotating star. After having been spun up, a star will change its shape, becoming oblate. At the same time, we do not expect a great difference in luminosity between a star before and after the spin-up. This is because stars are generally very centrally condensed, such that the centrifugal force is small compared to gravity in the regions where nuclear burning occurs, meaning that (excluding the effects of rotational mixing) central temperatures and thus luminosities are not very sensitive to rotation, in agreement with models (Brott et al. 2011; Paxton et al. 2019). Following the Stefan-Boltzmann law, because of the increased surface area of a critical rotator, the effective temperature decreases. Using the Roche model (see Appendix A), one can show that a critically rotating star has a surface area of approximately 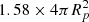 , with Rp being the polar radius. This corresponds to a decrease in effective temperature by a factor of
, with Rp being the polar radius. This corresponds to a decrease in effective temperature by a factor of 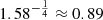 . Knowing this, we can construct isochrones describing the intrinsic properties of critically rotating stars from non-rotating isochrones.
. Knowing this, we can construct isochrones describing the intrinsic properties of critically rotating stars from non-rotating isochrones.
A further complication that is brought about by gravity darkening is that a fast-rotating star appears cooler and dimmer when viewed equator-on as compared to pole-on. Assuming a random orientation of the inclination axis, the mean value of the sine of the inclination angle is π/4, corresponding to a mean inclination angle of 51.8°. To take the mean effect of gravity darkening into account, we employed the model of Espinosa Lara & Rieutord (2011) as implemented in MESA (Paxton et al. 2019). Here, the projected luminosity and effective temperature, Lproj, Teff, proj are related to the intrinsic luminosity and effective temperature, L, Teff by
with CT and CL depending on the fraction of critical velocity, ω, and inclination angle i.
The temperatures and luminosities of critically rotating stars are found by using the coefficients CT(ω = 1, i = 51.8°) = 1.02 and CL(ω = 1, i = 51.8°) = 1.22. It is a rather curious feature of the gravity darkening model that at the mean inclination, the coefficients exceed unity, meaning the average effect of gravity darkening is not darkening at all, but brightening. Finally, by interpolating tables of synthetic stellar spectra (Choi et al. 2016) to produce magnitudes in Hubble filters, we are able to produce an isochrone of critical rotators, as shown in Fig. 2.
 |
Fig. 2. Colour-magnitude diagram of NGC 330 focused on the turn-off region. Hα emitters are marked in red. An isochrone of non-rotating stars is plotted in blue (see Appendix B for model details). Green and red isochrones depict critically rotating stars viewed pole-on and equator-on, respectively, as derived from a simple model of critical rotators (see Appendix A). The solid purple isochrone represents critically rotating stars viewed at the mean inclination angle when the rotation axis is randomly oriented (51.8°), and for the dotted purple isochrone, 0.25mF814W has been added to simulate the decretion disc. The isochrone age is 30 Myr, the distance modulus is μ = 18.8 mag, and the reddening of E(B–V) = 0.1 mag. Data are from Milone et al. (2018). |
The contribution of a Be star’s disc to its total flux is more difficult to assess. It has been noted that a loss of spectral emission features in certain Be stars coincides with a dimming of about 0.3–0.5 magnitudes in the R and V filters (Carciofi et al. 2012; Labadie-Bartz et al. 2017; Rímulo et al. 2018). If the loss of emission features is interpreted as the disappearance of the disc, one can take this change in brightness to equal the flux contribution of the disc. By comparing the colour of our isochrones with the colours of Be stars in NGC 330, we can assess how much the Be disc shines, as in Fig. 2. After assuming that the disc shines in the F814W filter but not in the F336W filter, we find a reasonable fit to the Hα emitters when a disc brightness of 0.25mF814W is adopted, as shown by the solid and dashed purple lines in Fig. 2.
For NGC 330, we find that in the regions of the colour-magnitude diagram containing Be stars, stars of equal mass on the non-rotating and Be star isochrones are connected by lines of gradient 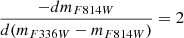 . For NGC 2164, again assuming a constant disc magnitude of 0.25mF814W, the gradient is found to be 1.8. These differing values are caused by the ways in which stellar spectra, and hence magnitude in a given filter, vary with luminosity and effective temperature.
. For NGC 2164, again assuming a constant disc magnitude of 0.25mF814W, the gradient is found to be 1.8. These differing values are caused by the ways in which stellar spectra, and hence magnitude in a given filter, vary with luminosity and effective temperature.
Figure 3 shows the colour-magnitude diagrams of NGC 330 and NGC 2164 with the Be fraction as counted in slanted bins with gradients of 2.0 and 1.8, respectively. It is noted that as compared to counting the Be fraction in bins of constant mF814W magnitude (i.e. horizontal bins), the values measured here are lower. This is because due to the effects described above, the sequence of Be stars is brighter than the sequence of B stars with the same mass. Therefore a horizontal bin contains relatively massive B stars and relatively low mass Be stars. According to the initial mass function, higher-mass stars are less populous, and hence the Be fraction is higher when horizontal bins are used solely because fewer B stars are counted.
 |
Fig. 3. Colour-magnitude diagrams with isochrone fits and Be star counts for the Small Magellanic Cloud cluster NGC 330 (left) and Large Magellanic Cloud cluster NGC 2164 (right). Hα emitters are marked in red. Bottom panels: Be fraction counted in bins as defined in the top panels. The errors are given by the binomial counting error. The bins have a gradient of 2.0 and 1.8 for NGC 330 and NGC 2164, respectively. Mass values associated with the bins are provided by the isochrone fit. For both clusters, the isochrone depicts stars with initial rotation equal to 0.6vrot/vcrit. For NGC 330, the isochrone age is 30 Myr, the distance modulus μ = 18.8 mag, and the reddening is E(B–V) = 0.1 mag. For NGC 2164, the age is 80 Myr, μ = 18.3 mag, and E(B–V) = 0.12 mag. Data are from Milone et al. (2018). |
We used isochrones of rotating single stars based on an extended model grid of Schootemeijer et al. (2019) (see Appendix B for a thorough description) with an initial rotation rate of vrot/vcrit = 0.6 to assign mass ranges to each bin, so that the Be fraction can be evaluated as a function of mass. The bins were placed so that the outer edge of the last bin was at the point at which hydrogen has been exhausted in the stellar core. We chose a value of vrot/vcrit = 0.6, as suggested by Gossage et al. (2019) and Wang et al. (in prep.). This produced equatorial rotation velocities that broadly agree with spectroscopic observations (Dufton et al. 2013; Marino et al. 2018; Sun et al. 2019; Kamann et al. 2020). The reddening and distance modulus values were tailored to give the best fit to the cluster and agree well with previous isochrone fittings for these clusters (Milone et al. 2018). The isochrone fits are shown in Fig. 3.
The isochrones allowed us to measure the turn-off mass and the masses associated with each bin. This enables a direct comparison between the theory presented in Sect. 3 and observations. Figure 4 shows this comparison. Uncertainties on the Be fraction are given by the standard error, σ, assuming a binomial distribution as
 |
Fig. 4. Comparison of theory and observations. Be fraction as a function of fractional main-sequence turn-off mass in NGC 330 and NGC 2164, as shown in Fig. 3. Dashed lines show the theoretical upper limit given by Eq. (30) with α = −1.9, ΔM/M2, i = 0, and κ = −1.0, 0 (see Fig. 1), as given by the legend. |
with Φ being the measured Be fraction and N the total number of stars in a given bin.
We find that although the two clusters have different metallicities and ages, they appear to have similar Be fractions as a function of relative turn-off mass. This may be an indication that the dominant Be production channel is universal, regardless of its nature.
In both clusters the Be fraction steadily increases from zero to about 0.4 in the range 60–80% of the turn-off mass. Near the turn-off, the Be fraction is found to be approximately 0.4, with a significant counting uncertainty because relatively few stars occupy this region. When these uncertainties are taken into account, our upper limit can describe the numbers of Be stars in the upper part of the main-sequence. It is important to note that because it is difficult to perform an isochrone fit, the Be fractions near the turn-off are particularly uncertain. A small change in the isochrone fit results in a large change in the measured Be fraction (see Sect. 6.1 for a quantitative discussion). Even though the measured Be fraction in NGC 330 at times exceeds our upper limit, it is therefore reasonable to conclude that the upper limit does provide a reasonable fit to the Be star numbers near the turn-off. However, it fails to explain the lack of Be stars below M/MTO ≈ 0.7. The reason may be that certain systems do not form Be stars but merge instead, as we discuss in the next section.
5. Inferring the initial conditions for stable mass transfer
The observations presented in Sect. 4 show that our upper limit can approximately describe the numbers of Be stars near the turn off, but fails to reproduce the sharp cut-off in the Be star sequence We investigate the change required in our prescription to reproduce this feature.
In reality, not every binary system undergoes stable mass transfer to form a Be star. For the specific case when the donor is in the Hertzsprung gap, as for Case AB or Case B mass transfer, the mass transfer proceeds at the Kelvin-Helmholtz (or thermal) timescale (Tout et al. 1997; Wellstein et al. 2001), meaning that if there is a large discrepancy in the Kelvin-Helmholtz timescales of the donor and accretor, the mass transfer will become unstable and a common-envelope situation will ensue, most likely leading to a stellar merger.
To model the occurrence of mergers, it is often assumed in simplified binary evolution calculations (Pols et al. 1991; Hurley et al. 2002; Schneider et al. 2015) that systems below a certain mass ratio will merge. This simple criterion is unsuitable to reproduce the observations shown in Fig. 3, however. Equation (30) gives the Be star fraction as an integral quantity, such that the Be star fraction at the main-sequence turn-off is the accumulation of systems with mass ratios from qmin to 1. This may be understood intuitively by noting that a Be star of mass near the main-sequence turn-off mass can originate from either an extreme mass-ratio system with a very massive primary or from a system with mass ratio close to unity. When we demand that all systems below a given mass-ratio merge, we therefore naturally decrease the Be fraction at the turn-off, which we must avoid to retrieve high numbers of Be stars at the turn-off.
To keep the Be fraction near the turn-off high and produce a sharp break in the Be fraction at M/MTO ≈ 0.7, more sophisticated criteria are needed, namely that depend on primary mass and mass ratio. We propose that the systems most likely to suffer unstable mass transfer are those with an extreme mass-ratio and low primary mass because the components of these systems have the largest difference in Kelvin-Helmholtz timescales. This can be visualised in a grid of primary mass against mass ratio, in which the bottom corner consists of systems that merge. In this grid, systems with a fixed secondary mass are represented by parabolae, as depicted in Fig. 5a. If the parabola representing a secondary with the turn-off mass can avoid the region containing merger progenitors, the Be fraction at the turn-off will remain close to the maximum theoretical prediction. Then as the secondary mass decreases, the parabolae will move into the corner with low mass ratio and low primary mass, and consequently, the Be fraction will decrease.
 |
Fig. 5. (a) Adopted region of stable mass transfer in the primary mass-mass ratio plane. Regions coloured red experience unstable mass transfer and merge. For green regions, mass transfer is stable, and a Be star is formed. The black and orange lines show systems with secondary masses of 9 and 6 M⊙, respectively. (b) Results of a Monte Carlo simulation showing the Be fraction, ΦBe, when the stable mass-transfer region in (a) is applied. Binary systems have a flat mass-ratio distribution (κ = 0), a primary mass distribution ξ(M1) ∝ M−1.9, and we have assumed inefficient accretion (ΔM/M2, i = 0). The black line shows a simulation with a turn-off mass of 9 M⊙, and the orange line a turn-off mass of 6 M⊙. The dashed grey line shows the theoretical upper limit, as given by Eq. (30). Measured Be fractions of NGC 330 and NGC 2164 according to Fig. 3 are plotted as black and orange crosses, respectively. |
To test our hypothesis, we performed a Monte Carlo simulation in which systems were selected randomly from given distributions of initial primary mass and initial mass ratio. As before, we assumed that mass transfer is completely non-conservative (ΔM/M2, i = 0). By choosing a turn-off mass, we can calculate the masses of Be stars in the simulation and thus assess the Be fraction. The occurrence of mergers is decided using the stable mass-transfer region depicted in Fig. 5a. The motivation for selecting this region is explained next. Analysis of mass transfer from giant donors (Pavlovskii & Ivanova 2015) has indicated that mass transfer from Hertzsprung-gap stars is stable at mass ratios greater than around 0.6. We therefore assumed that all systems with initial mass ratios greater than 0.6 undergo stable mass transfer. The stability of mass transfer is determined by the donor’s reaction to mass loss, where stars with radiative envelopes generally tend to contract as the envelope is being stripped (Hjellming & Webbink 1987). This is reversed for convective-envelope stars, which typically expand in response to mass loss (Hjellming & Webbink 1987). Stellar structure calculations suggest that stars with a mass greater than around 60 M⊙ spend very little time as red giants, meaning that they mostly have radiative envelopes (Schootemeijer et al. 2019; Klencki et al. 2021) such that mass-transfer is much more likely to occur when the donor has a radiative envelope. We therefore propose that mass transfer is stable for all systems with a primary mass exceeding 60 M⊙. The region of instability is then defined by a linear interpolation between systems with M1 = 60 M⊙, q = 0.1 and M1 = 5 M⊙, q = 0.6, as depicted in Fig. 5a. We again assumed that the orbital period plays no role in determining the stability of mass transfer, which allows us to avoid specifying an orbital period distribution.
Merger products change the distribution of masses in a population and thus affect the Be fraction as a function of mass. We assumed that Be stars are not merger products for two reasons. Firstly, it is thought that although merger products are initially fast-rotators, while thermal equilibrium is returned, internal angular momentum redistribution causes a rapid spin-down (Schneider et al. 2019). What is more, stellar mergers may produce strongly magnetised stars (Ferrario et al. 2009; Wickramasinghe et al. 2014; Schneider et al. 2019) that would further spin down due to magnetic braking. Secondly, a merger of a star with a helium core and a main-sequence object does not produce a hydrogen-burning star owing to the higher mean molecular weight and lower entropy of the helium-core star (Langer 2012; Justham et al. 2014). As observations (Milone et al. 2018) show Be stars to be concentrated on the main sequence, we assumed that Be stars are unlikely to be produced from the merging of two stars. For mergers, we assumed that the fraction of mass lost during the merging process to the total binary mass is equal to
(Glebbeek & Pols 2008), which equates to between 2 and 15% over the range 0.1 < q < 1. As the mass lost during the merging process is assumed to be low, mergers always have a mass exceeding the turn-off mass and do not affect the Be fractions on the main sequence.
Figure 5b shows the results of the simulation for clusters with turn-off masses of 9 and 6 M⊙, which roughly correspond to NGC 330 and NGC 2164, respectively. The chosen criteria have maintained a high Be fraction near the turn-off and also produced a sudden end to the Be-sequence. They provide a reasonable fit to the measured Be fractions in NGC 330 and NGC 2164. It is remarkable that these simple, although physically motivated, stable mass-transfer criteria can successfully reproduce the numbers of Be stars in the open clusters studied here. Our empirical mass-transfer stability criteria could be tested in the next generation of detailed binary evolution models.
6. Discussion
6.1. Uncertainties
The largest uncertainty in our procedure comes from the isochrone fits. Most if not all open clusters display an extended main-sequence turn-off, making the choice of a suitable isochrone age difficult. This is illustrated in Fig. 6, where isochrones of two different ages are fitted to NGC 330 and the Be fractions are evaluated. A small variation in the adopted age can cause the Be count in some bins to vary by up to 0.2. The end of the Be sequence is particularly affected. A similar sensitivity is also found for small differences in the distance modulus, reddening, and isochrone rotation rates. Based on Fig. 6, we judge that the uncertainty on the measured Be fractions is approximately 0.1 without the counting error.
 |
Fig. 6. Colour-magnitude diagram of NGC 330 with Hα emitters marked in red (left). Isochrone fits with ages 30 and 36 Myr are plotted in purple and green, respectively. Both isochrones have an initial rotation of vrot/vcrit = 0.6, a distance modulus of 18.8 mag, and a reddening of E(B–V) = 0.1 mag. Be fraction as a function of fractional turn-off mass as measured by the 30 Myr isochrone (in purple) and the 36 Myr isochrone (in green; right). Dashed lines show theoretical upper limit given by Eq. (30) with α = −1.9, ΔM/M2, i = 0, and κ = −1.0, 0, as given by the legend. |
To measure the observed Be fraction as a function of mass, we must use slanted bins. In calculating the gradient of these bins, we have assumed that the Be star disc always adds 0.25mF814W to the magnitude of the star. This may be an over-simplification, with Be stars of differing mass or evolutionary status hosting relatively brighter or dimmer discs. Unfortunately, this effect is difficult to observe and characterise and is also compounded by the fact that Be stars can display spectral and photometric variability (Porter & Rivinius 2003). Sigut et al. (2009) reported that the ratios of stellar effective temperature to mean disc temperature and infrared excess are indeed functions of spectral type.
Far older clusters, such as the 300 Myr old NGC 1856, have much lower Be fractions than their younger counterparts (see Milone et al. 2018, Fig. 17). Our simple model and mass-transfer stability criteria predict that the Be fraction does not vary strongly with turn-off mass and therefore is unable to explain the turn-off Be fraction in NGC 1856 of about 0.2. However, this discrepancy may be partly explained by a changing binary fraction with mass because it is known that more massive stars display a stronger preference for binary companionship (Köhler et al. 2006; Kouwenhoven et al. 2009). Older clusters that contain fewer binaries therefore naturally have fewer Be stars produced from binary interaction. Another aspect behind the emission line phenomenon is the ionising power of the star. To produce an emission line, the central Be star must ionise its decretion disc. Without sufficient ionising power, no emission line will be observable even if a disc is present, and hence the star will seem ordinary. The ionising photon emission rate is known to be strongly dependent on effective temperature (Sternberg et al. 2003). At some limiting mass, we therefore expect the central star to be unable to ionise a disc. This effect may play a role in lowering the Be fraction in older clusters and causing a dearth of Be stars at low magnitudes in the colour-magnitude diagram. The two clusters studied here have several stars that are very red, even though they are not marked as Hα emitters. They might be such “dormant Be stars”.
Lastly, we note that we assumed that the properties of binary systems are distributed according to very simple laws. In reality, however, the distributions may well be complex functions of one another, for example the mass-ratio distribution might be a function of the primary mass. The nature of these distributions is set by poorly understood binary star formation mechanisms, as outlined by Tokovinin & Moe (2020).
6.2. Mass-transfer efficiency
To construct our prediction of Be star fractions, we assumed that no mass is accreted during mass transfer. This scenario fits the observations reasonably well. It has been demonstrated that for efficient mass transfer, the Be star fraction decreases, meaning that the theoretical framework presented here would not fit observations if mass transfer were efficient. This leads us to propose that if the binary Be formation channel is the dominant one, mass transfer is far from conservative on average.
Binary models with conservative mass transfer predict Be stars to be blue stragglers after having gained a lot of mass (van Bever & Vanbeveren 1997). The observations presented in Fig. 3 contradict this prediction. The vast majority of Be stars lie either on the main sequence or are slightly redder than it. This strengthens our conclusion that mass transfer is highly non-conservative.
6.3. Initial binary fraction
To obtain our results, we assumed an initial binary fraction of 1, which might be thought too extreme. We have demonstrated that in a coeval population of binary systems, 30% of the systems at most are post-interaction binaries (see Sect. 3). Pre-interaction systems would therefore comprise not less than 70% of this population. Dedicated models show that under the assumption of a constant star formation rate, 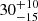 % of the massive stars are the products of binary interaction (de Mink et al. 2014), in broad agreement with this work.
% of the massive stars are the products of binary interaction (de Mink et al. 2014), in broad agreement with this work.
Post-interaction binaries are either merger products, contain a relatively low-mass post-main-sequence object (helium star, black hole, neutron star, or white dwarf) with a main-sequence (possibly emission-line) star or form a runaway star ejected from the binary orbit after a supernova. These objects manifest themselves either as single stars or would be difficult to detect as binaries (de Mink et al. 2011b,a). Even in a population whose initial binary fraction is 1, apparently single stars are therefore present in the proportions described above.
By examining radial velocity variations of very massive stars, we may only measure the pre-interaction binary fraction (as supernova kicks are believed to disrupt almost all binary systems (Brandt & Podsiadlowski 1995)), which has been observed to be about 0.7 for O-type stars (Sana et al. 2012). We therefore argue that the initial binary fraction is certainly greater than the observed pre-interaction binary fraction. At this stage, we therefore must remain open to the possibility that an initial binary fraction very close to one is indeed realised in nature.
7. Conclusions
In light of various uncertainties plaguing binary evolution calculations, we have investigated whether binary evolution can possibly reflect the large numbers of Be stars observed in open clusters. Starting from the premise that any binary system, regardless of primary mass, orbital period, or mass-ratio, will undergo stable mass transfer to form a Be star, we have calculated a rigorous upper limit to the formation of Be stars through this channel. It has been demonstrated that this binary evolution does not allow more than about 30% of stars to have been spun up through binary interaction and become emission-line objects.
After using isochrone fits to assign stars in the colour-magnitude diagram masses, a count of the Hα emitters in two open clusters revealed that for objects near the turn-off, our upper limit provides a reasonable description of the numbers of Be stars, especially when uncertainties arising from the counting method are taken into account. The upper limit, however fails to describe the sudden decrease in Be fraction that both clusters exhibit at a mass approximately 70–80% of the turn-off mass.
This problem can be rectified by assuming that systems with a low mass ratio and low primary mass merge. By adopting simple, although physically justified, stable mass-transfer criteria, we have shown that a good fit to the observational data is produced by this postulate.
It has been demonstrated in a qualitative way that in coeval populations, a larger mass gain of the donor results in a smaller Be fraction at a given mass. Because the observed Be fractions are very close to our upper limit when totally inefficient mass transfer is assumed, it follows that to be able to explain such high Be fractions, mass transfer must be non-conservative.
We have highlighted the distinction between the initial binary fraction and the binary fraction that can be observed, and we argued that these two quantities are not equal. This is so because a population of binary stars will always contain post-interaction systems that will appear to be single stars. The calculations outlined in this work provide rough constraints on this discrepancy, suggesting that the initial binary fraction is much higher than previously thought.
In conclusion, our theoretical argument serves to reinforce numerous observational arguments that suggest binary interactions to be responsible for Be stars. We conclude that observations of Be stars in young open clusters (Milone et al. 2018; Bodensteiner et al. 2020a) do not contradict the hypothesis that Be stars originate exclusively from mass transfer in binary systems. We have shown that if all Be stars are binary interaction products, somewhat extreme assumptions must be realised, such as an initial binary fraction very close to unity, a shallow initial mass function, and very non-conservative mass transfer. Whether these conditions can be met by the stars in the sky remains to be determined.
Acknowledgments
The authors extend gratitude to an anonymous referee for useful comments on an earlier version of this manuscript.
References
- Ahmed, A., & Sigut, T. A. A. 2017, MNRAS, 471, 3398 [Google Scholar]
- Bestenlehner, J. M., Crowther, P. A., Caballero-Nieves, S. M., et al. 2020, MNRAS, 499, 1918 [Google Scholar]
- Bodensteiner, J., Sana, H., Mahy, L., et al. 2020a, A&A, 634, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodensteiner, J., Shenar, T., & Sana, H. 2020b, A&A, 641, A42 [CrossRef] [EDP Sciences] [Google Scholar]
- Boubert, D., & Evans, N. W. 2018, MNRAS, 477, 5261 [Google Scholar]
- Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brož, M., Mourard, D., Budaj, J., et al. 2021, A&A, 645, A51 [EDP Sciences] [Google Scholar]
- Carciofi, A. C., Bjorkman, J. E., Otero, S. A., et al. 2012, ApJ, 744, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
- Claret, A., & Torres, G. 2016, A&A, 592, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coe, M. J., Kennea, J. A., Evans, P. A., & Udalski, A. 2020, MNRAS, 497, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G. W., II, & Truax, R. J. 1995, ApJ, 439, 860 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., & Izzard, R. G. 2011a, Bull. de la Soc. Royale des Sci. de Liege, 80, 543 [NASA ADS] [Google Scholar]
- de Mink, S. E., Langer, N., & Izzard, R. G. 2011b, in Active OB Stars: Structure, Evolution, Mass Loss, and Critical Limits, eds. C. Neiner, G. Wade, G. Meynet, G. Peters, 272, 531 [NASA ADS] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2014, ApJ, 782, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Dorigo Jones, J., Oey, M. S., Paggeot, K., Castro, N., & Moe, M. 2020, ApJ, 903, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Langer, N., Dunstall, P. R., et al. 2013, A&A, 550, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunstall, P. R., Brott, I., Dufton, P. L., et al. 2011, A&A, 536, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrario, L., Pringle, J. E., Tout, C. A., & Wickramasinghe, D. T. 2009, MNRAS, 400, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Glebbeek, E., & Pols, O. R. 2008, A&A, 488, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gossage, S., Conroy, C., Dotter, A., et al. 2019, ApJ, 887, 199 [CrossRef] [Google Scholar]
- Hastings, B., Wang, C., & Langer, N. 2020, A&A, 633, A165 [CrossRef] [EDP Sciences] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Hogeveen, S. J. 1991, The mass-ratio distribution of binary stars, PhD Thesis [Google Scholar]
- Huang, W., Gies, D. R., & McSwain, M. V. 2010, ApJ, 722, 605 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iqbal, S., & Keller, S. C. 2013, MNRAS, 435, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Podsiadlowski, P., & Vink, J. S. 2014, ApJ, 796, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kamann, S., Bastian, N., Gossage, S., et al. 2020, MNRAS, 492, 2177 [Google Scholar]
- Keller, S. C., Wood, P. R., & Bessell, M. S. 1999, A&AS, 134, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kippenhahn, R. 1974, in Late Stages of Stellar Evolution, eds. R. J. Tayler, & J. E. Hesser, 66, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Klement, R., Carciofi, A. C., Rivinius, T., et al. 2017, A&A, 601, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klement, R., Carciofi, A. C., Rivinius, T., et al. 2019, ApJ, 885, 147 [Google Scholar]
- Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, R., Petr-Gotzens, M. G., McCaughrean, M. J., et al. 2006, A&A, 458, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Goodwin, S. P., Portegies Zwart, S. F., & Kaper, L. 2009, A&A, 493, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kriz, S., & Harmanec, P. 1975, Bull. Astr. Inst. Czechosl., 26, 65 [NASA ADS] [Google Scholar]
- Labadie-Bartz, J., Pepper, J., McSwain, M. V., et al. 2017, AJ, 153, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [CrossRef] [EDP Sciences] [Google Scholar]
- Lennon, D. J., Lee, J. K., Dufton, P. L., & Ryans, R. S. I. 2005, A&A, 438, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, K. L., Kong, A. K. H., Charles, P. A., et al. 2012, ApJ, 761, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2006, A&A, 455, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Grebel, E. K., & Mermilliod, J.-C. 1999, A&A, 346, 459 [NASA ADS] [Google Scholar]
- Marino, A. F., Przybilla, N., Milone, A. P., et al. 2018, AJ, 156, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Martayan, C., Baade, D., & Fabregat, J. 2010, A&A, 511, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McSwain, M. V., & Gies, D. R. 2005, ApJS, 161, 118 [Google Scholar]
- Milone, A. P., Marino, A. F., Di Criscienzo, M., et al. 2018, MNRAS, 477, 2640 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Peters, G. J. 1989, Space Sci. Rev., 50, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Langer, N., & van der Hucht, K. A. 2005, A&A, 435, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Cote, J., Waters, L. B. F. M., & Heise, J. 1991, A&A, 241, 419 [NASA ADS] [Google Scholar]
- Porter, J. M. 1996, MNRAS, 280, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, J. M., & Rivinius, T. 2003, PASP, 115, 1153 [Google Scholar]
- Raguzova, N. V., & Popov, S. B. 2005, Astron. Astrophys. Trans., 24, 151 [Google Scholar]
- Rímulo, L. R., Carciofi, A. C., Vieira, R. G., et al. 2018, MNRAS, 476, 3555 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scalo, J. M. 1986, Fund. Cosmic Phys., 11, 1 [NASA ADS] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Izzard, R. G., Langer, N., & de Mink, S. E. 2015, ApJ, 805, 20 [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, F. R. N., Ohlmann, S. T., Podsiadlowski, P., et al. 2019, Nature, 574, 211 [Google Scholar]
- Schootemeijer, A., Götberg, Y., de Mink, S. E., Gies, D., & Zapartas, E. 2018, A&A, 615, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Secchi, A. 1866, Astron. Nachr., 68, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, Y., & Li, X.-D. 2014, ApJ, 796, 37 [Google Scholar]
- Shao, Y., & Li, X.-D. 2016, ApJ, 833, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Bodensteiner, J., Abdul-Masih, M., et al. 2020, A&A, 639, L6 [EDP Sciences] [Google Scholar]
- Sigut, T. A. A., McGill, M. A., & Jones, C. E. 2009, ApJ, 699, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Hoffmann, T. L., & Pauldrach, A. W. A. 2003, ApJ, 599, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Struve, O. 1931, ApJ, 73, 94 [Google Scholar]
- Sun, W., de Grijs, R., Deng, L., & Albrow, M. D. 2019, ApJ, 876, 113 [CrossRef] [Google Scholar]
- Tokovinin, A., & Moe, M. 2020, MNRAS, 491, 5158 [CrossRef] [Google Scholar]
- Tout, C. A. 1991, MNRAS, 250, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., Aarseth, S. J., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 291, 732 [NASA ADS] [Google Scholar]
- Townsend, R. H. D., Owocki, S. P., & Howarth, I. D. 2004, MNRAS, 350, 189 [Google Scholar]
- Trimble, V. 1990, MNRAS, 242, 79 [NASA ADS] [Google Scholar]
- van Bever, J., & Vanbeveren, D. 1997, A&A, 322, 116 [NASA ADS] [Google Scholar]
- Vinciguerra, S., Neijssel, C. J., Vigna-Gómez, A., et al. 2020, MNRAS, 498, 4705 [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., Langer, N., Schootemeijer, A., et al. 2020, ApJ, 888, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wickramasinghe, D. T., Tout, C. A., & Ferrario, L. 2014, MNRAS, 437, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P., Ranc, C., & Morel, P. 2010, A&A, 517, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., Domiciano de Souza, A., et al. 2016, A&A, 595, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., & Cidale, L. 2005, A&A, 441, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Stars at the critical velocity
Here we investigate how critically rotating and slowly rotating stars vary in terms of their effective temperatures and luminosities. Because stable and reliable numerical models of very fast rotating stars are difficult to produce, we employ a simple analytic model.
The luminosity of a main-sequence star is generated from nuclear reactions in the central region. As stars are centrally condensed, when a given star is spun up to the critical velocity, the centripetal forces acting in the central regions are much weaker than the force of gravity, meaning the structure of the core is largely unchanged. Hence, the intrinsic luminosity is constant to first order.
When a star is spun up, the outer structure changes, however. The equatorial radius increases, and therefore so does the surface area of the star, S. This then causes the effective temperature to decrease, as evidenced by the Stefan-Boltzmann law,
To characterise this change in effective temperature, we used the Roche model, which describes a star in which all mass is concentrated at the centre, and that rotates with constant angular velocity Ω. In this framework, the effective potential with respect to the radial coordinate r and latitude θ is
At the critical angular velocity, the polar radius, Rp, is equal to the radius of an equivalent non-rotating star of the same mass, whereas the equatorial radius, Re, is given by
Taking the x − y plane to be parallel to the axis of rotation, where y represents the distance along the rotation axis and x the perpendicular distance from the rotation axis, the surface of a critically rotating star is described by
(Zahn et al. 2010). The surface area of a star is (see Paxton et al. 2019, Appendix B) in general
After choosing units such that Re = 1, Eqs. (A.4) and (A.5) can be solved numerically to give the surface area of a critical rotator, Sc, as
Compare this to the surface areas of non-rotating stars with radii Re and Rp,
and
As expected, we have
The surface area of a critically rotating star is about 1.58 times larger than that of its non-rotating counterpart.
According to Eq. (A.1), the temperature of a star after it is spun up to critical therefore decreases by a factor of 0.89.
Appendix B: Stellar isochrones
As our model predictions give the Be fraction as a function of mass, we must extract masses from stars in the colour-magnitude diagram to make an effective comparison with observations. To this end, we employed isochrones of single rotating stars to assign mass ranges to different areas of the colour-magnitude diagram.
We used the grid of Schootemeijer et al. (2019), which was extended to masses between 2 and 20 M⊙ with slight changes to internal mixing (see below). The code used was MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019). Models were computed at initial rotation rates between 0 and 80% of the critical velocity in steps of 10%. As is standard in MESA, the critical velocity is defined as
where Γ is the ratio of the luminosity to the Eddington luminosity, and is negligible for the models presented here. At early times, the models undergo a relaxation period, during which the critical velocity fraction can oscillate wildly. To circumvent this, we defined the initial critical velocity fraction at the point when the model has burnt 3% of its initial hydrogen content by mass.
The physics employed in the models is mostly identical to that of Brott et al. (2011), except for the treatment of two mixing processes. Stepped convective overshooting was adopted, which extends the convective zone by αOV times the local pressure scale height. A dependence of αOV on mass accounts for observational trends (Castro et al. 2014; Claret & Torres 2016; Schootemeijer et al. 2019), whereby αOV increases linearly from 0.1 at 1.66 M⊙Claret & Torres (2016) to 0.3 at 20 M⊙Brott et al. (2011). Furthermore, time smoothing in rotational mixing was turned off to avoid unrealistically strong mixing.
Isochrones were generated through a series of linear interpolations and were split up into two equivalent evolutionary phases (EEPs). The first phase lasts until core-hydrogen depletion, and the second phase lasts from core-hydrogen depletion until core-helium depletion. To compute the parameters of a star in the first EEP with initial mass Mi and initial critical velocity fraction vi at time t, we first determined the time at which this star would experience core-hydrogen exhaustion, TMS. Four models were used for the interpolation: two models with initial masses M1 and initial critical velocity fractions v1, a and v1, b, and similarly, two models with initial masses M2 and initial critical velocity fractions v2, a and v2, b. The models were selected such that M1 < Mi < M2 and v1, a < vi < v1, b and similarly for v2, a, v2, b. For M1 and M2, we interpolated the lifetime when initial vrot/vcrit = vi from these models, as shown in Fig. B.1a. The hydrogen-burning lifetime was then computed as an interpolation in mass between the values of M1 and M2, as depicted in Fig. B.1 b. For this step, the most accurate results are obtained when the logarithm of the hydrogen-burning lifetime is interpolated against the logarithm of initial mass. Using the interpolated lifetime, Ti, of this star with initial mass Mi and initial critical velocity fraction vi, we defined its fractional lifetime as t/Ti. This fractional lifetime is the value at which all further interpolations were carried out. Next, a given quantity (for the purposes of making isochrones, the quantities of interest are effective temperature and luminosity), Q, was interpolated at a fractional lifetime of t/Ti for the four selected models, as in B.1 c. The penultimate step was to calculate the quantities QM1, QM2, which represent the values of Q of a star with mass M1, M2, initial critical velocity fraction vi, and fractional lifetime t/Ti by interpolating across the initial critical velocity fraction like in Fig. B.1 d. Finally, an interpolation in initial mass between the quantities QM1 and QM2 was made to produce the value of the chosen parameter for a star of given mass, initial rotation rate, and age.
 |
Fig. B.1. Schematic representation of the interpolation procedure employed to produce isochrones. See text for a thorough explanation. |
To generate the second EEP, the same procedure was used, but only with a different fractional lifetime, namely the fractional helium-burning lifetime, t/THe, such that at core-hydrogen exhaustion t/THe = 0 and at core helium exhaustion t/THe = 1.
Absolute magnitudes in Hubble Space Telescope filters were computed by interpolating tables of synthetic stellar spectra provided by the MIST project of Choi et al. (2016). Apparent magnitudes were then calculated as
with μ being the distance modulus, and absorption coefficients AF814W = 2.04E(B − V) and AF336W = 5.16E(B − V) (Milone et al. 2018).
All Figures
 |
Fig. 1. Maximum Be fraction, ΦBe, in a coeval population as defined by Eq. (30) plotted as a function of fractional main-sequence turn-off mass, M/MTO, for varying parameters. Left and right panels: ΔM/M2, i = 0 and 1, respectively. The colour of the lines represents differing κ values. Red is κ = 0 and blue is κ = −1. Dashed lines show α = −1.9 and solid lines show α = −2.7, as indicated by the annotations. |
| In the text | |
 |
Fig. 2. Colour-magnitude diagram of NGC 330 focused on the turn-off region. Hα emitters are marked in red. An isochrone of non-rotating stars is plotted in blue (see Appendix B for model details). Green and red isochrones depict critically rotating stars viewed pole-on and equator-on, respectively, as derived from a simple model of critical rotators (see Appendix A). The solid purple isochrone represents critically rotating stars viewed at the mean inclination angle when the rotation axis is randomly oriented (51.8°), and for the dotted purple isochrone, 0.25mF814W has been added to simulate the decretion disc. The isochrone age is 30 Myr, the distance modulus is μ = 18.8 mag, and the reddening of E(B–V) = 0.1 mag. Data are from Milone et al. (2018). |
| In the text | |
 |
Fig. 3. Colour-magnitude diagrams with isochrone fits and Be star counts for the Small Magellanic Cloud cluster NGC 330 (left) and Large Magellanic Cloud cluster NGC 2164 (right). Hα emitters are marked in red. Bottom panels: Be fraction counted in bins as defined in the top panels. The errors are given by the binomial counting error. The bins have a gradient of 2.0 and 1.8 for NGC 330 and NGC 2164, respectively. Mass values associated with the bins are provided by the isochrone fit. For both clusters, the isochrone depicts stars with initial rotation equal to 0.6vrot/vcrit. For NGC 330, the isochrone age is 30 Myr, the distance modulus μ = 18.8 mag, and the reddening is E(B–V) = 0.1 mag. For NGC 2164, the age is 80 Myr, μ = 18.3 mag, and E(B–V) = 0.12 mag. Data are from Milone et al. (2018). |
| In the text | |
 |
Fig. 4. Comparison of theory and observations. Be fraction as a function of fractional main-sequence turn-off mass in NGC 330 and NGC 2164, as shown in Fig. 3. Dashed lines show the theoretical upper limit given by Eq. (30) with α = −1.9, ΔM/M2, i = 0, and κ = −1.0, 0 (see Fig. 1), as given by the legend. |
| In the text | |
 |
Fig. 5. (a) Adopted region of stable mass transfer in the primary mass-mass ratio plane. Regions coloured red experience unstable mass transfer and merge. For green regions, mass transfer is stable, and a Be star is formed. The black and orange lines show systems with secondary masses of 9 and 6 M⊙, respectively. (b) Results of a Monte Carlo simulation showing the Be fraction, ΦBe, when the stable mass-transfer region in (a) is applied. Binary systems have a flat mass-ratio distribution (κ = 0), a primary mass distribution ξ(M1) ∝ M−1.9, and we have assumed inefficient accretion (ΔM/M2, i = 0). The black line shows a simulation with a turn-off mass of 9 M⊙, and the orange line a turn-off mass of 6 M⊙. The dashed grey line shows the theoretical upper limit, as given by Eq. (30). Measured Be fractions of NGC 330 and NGC 2164 according to Fig. 3 are plotted as black and orange crosses, respectively. |
| In the text | |
 |
Fig. 6. Colour-magnitude diagram of NGC 330 with Hα emitters marked in red (left). Isochrone fits with ages 30 and 36 Myr are plotted in purple and green, respectively. Both isochrones have an initial rotation of vrot/vcrit = 0.6, a distance modulus of 18.8 mag, and a reddening of E(B–V) = 0.1 mag. Be fraction as a function of fractional turn-off mass as measured by the 30 Myr isochrone (in purple) and the 36 Myr isochrone (in green; right). Dashed lines show theoretical upper limit given by Eq. (30) with α = −1.9, ΔM/M2, i = 0, and κ = −1.0, 0, as given by the legend. |
| In the text | |
 |
Fig. B.1. Schematic representation of the interpolation procedure employed to produce isochrones. See text for a thorough explanation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



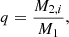
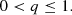
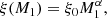
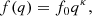
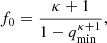
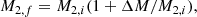
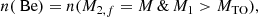
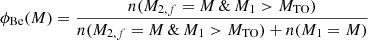
![$$ \begin{aligned} &= \left[ 1+ \frac{n(M_1=M)}{n(M_{2,f}=M \, \& \, M_1 >M_{\rm TO}) }\right] ^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41269-21/aa41269-21-eq10.gif)
![$$ \begin{aligned} \phi _{\text{Be}}(M) = \left[ 1+ \frac{n(M_1=M)}{n(M_{2,i}=\frac{M}{1+\Delta M/M_{2,i}} \, \& \, M_1 >M_{\rm TO}) }\right] ^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41269-21/aa41269-21-eq11.gif)
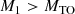
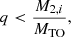
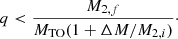
![$$ \begin{aligned} \phi _{\text{Be}}(M)\!=\! \left[ 1+ \frac{n(M_1=M)}{n(M_{2,i}\!=\!\frac{M}{1+\Delta M/M_{2,i}} \, \& \,q< \frac{M}{M_{\rm TO}(1+\Delta M/M_{2,i})}) }\right] ^{-1}\cdot \end{aligned} $$](/articles/aa/full_html/2021/09/aa41269-21/aa41269-21-eq15.gif)
![$$ \begin{aligned}&\phi _{\mathrm{Be}}(M/M_{\rm TO})\nonumber \\&\quad = \bigg [ 1+ \frac{n(M_1=M/M_{\rm TO})}{n(M_{2,i}=\frac{M}{M_{\rm TO}(1+\Delta M/M_{2,i})} \, \& \,q< \frac{M}{M_{\rm TO}(1+\Delta M/M_{2,i})}) }\bigg ] ^{-1}, \end{aligned} $$](/articles/aa/full_html/2021/09/aa41269-21/aa41269-21-eq16.gif)
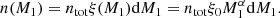
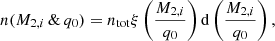
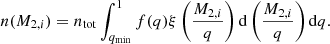
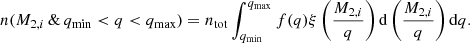
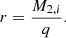
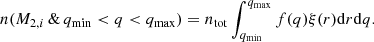
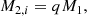
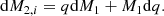

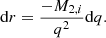
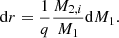
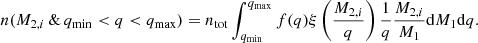
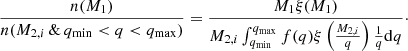
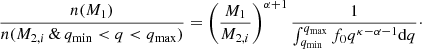
![$$ \begin{aligned} \phi _{\rm Be}(M/M_{\rm TO}) = \left[ 1+ \frac{( 1+ \Delta M /M_{2,i})^{(\alpha +1)} }{ \int _{q_{\rm min}} ^ {\frac{M}{( 1+ \Delta M/M_{2,i})M_{\rm TO}}} f_0 q^{\kappa - \alpha -1 } \mathrm{d}q}\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2021/09/aa41269-21/aa41269-21-eq36.gif)