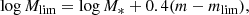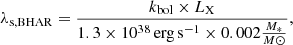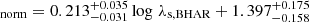| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140630 | |
| Published online | 10 September 2021 | |
The role of AGN and obscuration in the position of the host galaxy relative to the main sequence⋆
1
Instituto de Fisica de Cantabria (CSIC-Universidad de Cantabria), Avenida de los Castros, 39005 Santander, Spain
e-mail: gmountrichas@gmail.com
2
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
e-mail: veronique.buat@lam.fr
3
Institut Universitaire de France (IUF), Paris, France
4
Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
5
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, College Station, TX 77843-4242, USA
6
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
7
National Centre for Nuclear Research, ul. Hoza 69, 00-681 Warszawa, Poland
8
Astronomy Centre, Department of Physics & Astronomy, University of Southampton, Southampton SO17 1BJ, UK
9
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
Received:
22
February
2021
Accepted:
19
June
2021
We use X-ray active galactic nuclei (AGN) observed by the Chandra X-ray Observatory within the 9.3 deg2 Boötes field of the NDWFS to study whether there is a correlation between X-ray luminosity (LX) and star formation rate (SFR) of the host galaxy, at 0.5 < z < 2.0, with respect to the position of the galaxy to the main sequence (SFRnorm). About half of the sources in the X-ray sample have spectroscopic redshifts. We also construct a reference galaxy catalogue. For both datasets we use photometric data from the optical to the far-infrared compiled by the HELP project, and apply spectral energy distribution fitting, using the X-CIGALE code. We exclude quiescent sources from both the X-ray and the reference samples. We also account for the mass completeness of our dataset, in different redshifts bins. Our analysis highlights the importance of studying the SFR–LX relation in a uniform manner, taking into account systematics and selection effects. Our results suggest, in less massive galaxies (log [M*(M⊙)] ∼ 11), that an AGN enhances the SFR of the host galaxy by ∼50% compared to non-AGN systems. A flat relation is observed for the most massive galaxies. The SFRnorm does not evolve with redshift. The results, although tentative, are consistent with a scenario where, in less massive systems, both AGN and star formation are fed by cold gas supplied by a merger event. In more massive galaxies the flat relation could be explained by a different supermasssive black hole fuelling mechanism that is decoupled from the star formation of the host galaxy (e.g., hot diffuse gas). Finally, we compare the host galaxy properties of X-ray absorbed and unabsorbed sources. Our results show no difference, which suggests that X-ray absorption is not linked with the properties of the galaxy.
Key words: X-rays: general / X-rays: galaxies / galaxies: star formation / quasars: supermassive black holes / galaxies: active
Tables with the X-ray and host galaxy properties used in the analysis are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/653/A74
© ESO 2021
1. Introduction
In recent years we have witnessed significant progress in our understanding of how supermassive black holes (SMBHs) form and grow over cosmic time. It is also widely accepted and well established that there is a correlation between the mass of a SMBH and the properties of the galactic bulge (e.g., Magorrian et al. 1998; Ferrarese & Merritt 2000). However, it is still not clear what physical mechanisms drive the black hole (BH) growth and if there is a connection between the properties of a BH, such as accretion luminosity, and those of the host galaxy, for example star formation rate (SFR) and stellar mass.
Black holes grow through accretion of cold gas onto the accretion disc. This gas originates on scales that are least nine orders of magnitude larger, either from the host galaxy or the extragalactic environment. Various mechanisms have been suggested that drive the gas from kiloparsec to sub-parsec scales (for a review see Alexander & Hickox 2012). The SMBH becomes active when material is accreted onto it, and then the galaxy is called an active galactic nucleus (AGN). Star formation is also driven by cold gas. Moreover, AGN activity and star formation peak at the same cosmic time (z ∼ 2; e.g., Boyle & Terlevich 1998; Boyle et al. 2000; Sobral et al. 2013). These advocate for a connection between the BH activity and galaxy growth. However, the nature of the connection, if any, is still a matter of debate.
Hydrodynamical simulations and semi-analytic models require negative AGN feedback to suppress the formation of stars and avoid the production of too many massive galaxies. Cooling outflows generated by strong winds, which are produced by the AGN (e.g., DeBuhr et al. 2012), remove or heat the star-forming gas. At high accretion rates this feedback is radiation-based (quasar mode), whereas at lower accretion rates AGN feedback is provided mechanically by the kinetic energy of jets (Scheuer 1974; Blandford & Rees 1974). Nevertheless, AGN feedback can work both ways (e.g., Zinn et al. 2013). In the late gas-poor phase AGN feedback may quench star formation. In the gas-rich phase, however, AGN outflows can provide positive feedback to their hosts by overcompressing cold gas (e.g., Zubovas et al. 2013).
Observationally, a popular method to examine whether and how an AGN affects the evolution of its host galaxy is to examine whether there is a link between the SFR of the galaxy and the X-ray luminosity of the AGN. The former is an indicator of the galaxy growth, while the latter is a proxy of the AGN power. Results from the first studies that examined these two properties had controversial results (e.g., Lutz et al. 2010; Page et al. 2012). These discrepancies were attributed to selection effects and low number statistics, for example, as a result of the small sample sizes available (e.g., Harrison et al. 2012; Rosario et al. 2012). Different conclusions can also be drawn depending on the binned parameter (Hickox et al. 2014; Lanzuisi et al. 2017; Brown et al. 2019; Masoura et al. 2021). This was attributed to AGN variability that is significantly shorter compared to the average timescales of star formation (e.g., Hickox et al. 2014).
It is well known that star-forming galaxies follow a tight correlation between their SFR and stellar mass, known as the main sequence (MS) of star formation (e.g., Noeske et al. 2007; Elbaz et al. 2007; Pannella et al. 2009). Therefore, more recent studies started to explore the link between SFR and LX relative to the MS. This allows the study of the two properties taking into account the stellar mass and redshift of the host galaxy (i.e. the position of the host galaxy with respect to the MS). The parameter used for this purpose was the SFRnorm, defined as the ratio of the SFR of X-ray AGN to the SFR of star-forming MS galaxies. The first results following this more refined approach showed that AGN and star-forming galaxies have similar mean SFRnorm values, although the SFR distributions of the two populations are different. They also found no evolution of the SFRnorm with redshift (Mullaney et al. 2015). Later works found that the distribution of SFRnorm of higher LX AGN is narrower and closer to that of MS galaxies than that of lower LX (Bernhard et al. 2019). However, the results of these studies were limited by the small sample sizes (Mullaney et al. 2015) or the narrow redshift range, and thus X-ray luminosity baselines spanned by the datasets (Bernhard et al. 2019). Deploying a significantly larger sample with more than 3000 X-ray sources revealed a non-flat relation between the SFR of the host galaxy and the AGN power (Masoura et al. 2018) and a hint of evolution of SFRnorm with redshift (Masoura et al. 2021). Nevertheless, a downside of these studies is that they did not define their own reference (non-AGN) galaxy sample to estimate SFRnorm. Instead, they used relations from the literature to estimate the star formation of MS galaxies (e.g., Eq. (9) in Schreiber et al. 2015) with which they compare the SFR of X-ray AGN. This approach hints at a number of systematics. For example, different methods are utilised to estimate galaxy properties, there is no exact definition of the MS, and different selection criteria are applied on X-ray and non-X-ray galaxy samples in different studies.
Shimizu et al. (2015) compared the SFRs of X-ray AGN in the local universe (z < 0.1) with that of MS galaxies, by constructing their own MS galaxy sample and using the same methods to measure the SFRs and stellar masses of the sources in both datasets. They used different datasets to estimate galaxy properties for AGN and non-AGN systems. Based on their results, X-ray luminous AGN have decreased SFRs compared to non-AGN systems. Santini et al. (2012) compared the average SFR of X-ray AGN with inactive galaxies of similar mass. Their analysis showed that lower luminosity AGN (LX ≤ 1043.5 erg s−1) have enhanced star formation (by ∼0.26 dex) compared to non-AGN systems, while for higher luminosity AGN the enhancement is more evident (∼0.56 dex). Rosario et al. (2013) found that the mean SFR of broad-line AGN are consistent with those of normal massive star-forming galaxies. Recently, Florez et al. (2020) used X-ray selected AGN in the Stripe 82 field and compared their SFRs with non-X-ray galaxies, in a wide range of redshifts and luminosities. They estimated SFRs for both samples in a consistent way by applying spectral energy distribution (SED) fitting on both datasets. Their analysis showed that X-ray AGN have on average SFRs that are three to ten times higher than their control galaxy sample, at the same stellar mass and redshift.
Another aspect of the AGN-galaxy co-evolution is whether the absorption of the system is linked with the host galaxy properties. According to the simple unification model (e.g., Antonucci 1993) the classification of AGN into absorbed (type 2) and unabsorbed (type 1) is only a geometrical effect. Type 1 refers to face-on AGN and type 2 to edge-on. This simplified picture has been updated in more complex scenarios within the unification framework. However, the inclination determines the classification even in these updated unified pictures of the AGN structure (e.g., Ogawa et al. 2021). On the other hand, according to the evolutionary model (e.g., Ciotti & Ostriker 1997; Hopkins et al. 2006) AGN growth coincides with host galaxy activity, during which the AGN appears absorbed. At later stages, as the AGN becomes more powerful it blows away the star formation material, and thus star formation is quenched. Therefore, comparison of host galaxy properties between the two AGN types could favour one over the other model (e.g., Merloni et al. 2014; Chen et al. 2015; Zou et al. 2019; Masoura et al. 2021). However, these efforts are hindered by the fact that absorption may occur, not only close to the accretion disc, but also on galactic scales (e.g., Maiolino & Rieke 1995; Circosta et al. 2019; Malizia et al. 2020). Furthermore, classification criteria based on different wavelengths (e.g., X-ray criteria, optical spectra, optical–mid-IR colours) are sensitive to different levels of absorption, and this may lead to a different characterisation of a source (e.g., Li et al. 2019; Masoura et al. 2020; Ogawa et al. 2021).
In this paper we revisit the SFR–LX relation using X-ray sources from the 9.3 deg2 Boötes field. In Sect. 2 we describe the datasets and the available photometry. The SED fitting analysis, the mass completeness of our samples, and the reliability of the host galaxy measurements are presented in Sect. 3. In Sect. 4 we describe how we identify and exclude quiescent systems from our datasets, and present the systematics introduced by different definitions of the star-forming MS. The relation between SFRnorm and LX is studied in Sect. 5. In the last section we compare host galaxy properties of X-ray absorbed and unabsorbed sources. The classification is parametrised using the hydrogen column density, NH.
Throughout this work, we assume a flat ΛCDM cosmology with H0 = 69.3 Km s−1 Mpc−1 and ΩM = 0.286.
2. Data
In this work we use X-ray AGN observed by the Chandra X-ray Observatory within the 9.3 deg2 Boötes field of the NOAO Deep Wide-Field Survey (NDWFS). The catalogue is compiled and fully described in Masini et al. (2020). It consists of 6891 X-ray point sources with an exposure time of about 10 ks per XMM pointing and a limiting flux of 4.7 × 10−16, 1.5 × 10−16, and 9 × 10−16 erg cm−2 s−1 in the 0.5−7 keV, 0.5−2 keV, and 2−7 keV energy bands, respectively. Of the 6891 X-ray sources in this catalogue, 2346 (∼33%) have available spectroscopic redshifts (specz). Specz values are obtained by cross-matching the I band data of the NDWFS catalogue and the AGES catalogue (Kochanek et al. 2012), using a matching radius of 0.5 arcsec. We use these specz sources to optimise the spectral energy distribution (SED) grid used in our analysis (see Sect. 3). For the remaining sources, we use hybrid photometric redshifts (photoz; Duncan et al. 2018a,b, 2019) that are available in the Masini et al. (2020) catalogue. A Gaussian process redshift code, GPz, is combined with template photoz estimates through hierarchical Bayesian combination and produce a hybrid estimate that significantly improves the individual methods. The normalised median absolute deviation of the photoz is σNMAD = 0.054, and the fraction of outliers, defined as |photoz − specz|/(1 + specz) > 0.15, is 13.23%. The X-ray absorption of each X-ray AGN is available and is parametrised with NH, which has been calculated from hardness ratio (HR) estimations measured using the Bayesian Estimator for Hardness Ratio (BEHR; Park et al. 2006). A fixed Galactic absorption of NH, Gal = 1.04 × 1020 cm−2 is assumed. The average uncertainty on the NH values is ∼17%.
The X-ray catalogue is cross-matched with the Boötes photometric catalogue produced by the HELP1 Collaboration. HELP provides homogeneous and calibrated multiwavelength data over the Herschel Multitiered Extragalactic Survey (HerMES, Oliver et al. 2012) and the H-ATLAS survey (Eales et al. 2010) from the ultraviolet (UV) to near-infrared (NIR). The position of NIR and IRAC sources are then used as prior information to extract sources in the Herschel maps. IRAC1 positions are used for the Boötes field (Shirley et al. 2019), where IRAC1 is the [3.6] μm bands of Spitzer. The XID+ tool (Hurley et al. 2017) developed for this purpose uses a Bayesian probabilistic framework and works with prior positions. Fluxes are measured for the Spitzer MIPS/24 microns, and Herschel PACS and SPIRE bands. In this work only the MIPS and SPIRE fluxes are considered, given the much lower sensitivity of the PACS observations for this field (Oliver et al. 2012).
The cross-match of the X-ray sample with the HELP dataset was done using 1″ radius and the I-band coordinates provided in the X-ray catalogue. This process resulted in 5887 matches. In our analysis we need to accurately measure the host galaxy properties via SED fitting; thus, we require the best possible photometric coverage for the sources, and at the same time we need to keep the size of the dataset large. For this reason we restricted the X-ray sample to those sources that have been detected in the following photometric bands: u, g or B, R, I, z, H or Ks, IRAC1, IRAC2, and MIPS/24, where IRAC2 is the [4.5] μm band of Spitzer. This reduces the number of X-ray sources to 2778. Since our dataset does not have UV data, which can directly trace the young stellar population, we restricted our sample to sources that lie at redshifts higher than 0.5. At z > 0.5 the u band is redshifted to rest-frame wavelength < 2000 Å, allowing observation of the emitted radiation from young stars. This further reduces the X-ray sources to 2338. Nearly half of the sources have available Herschel photometry (see Sect. 3.5).
In the first part of our analysis we compared the SFR of X-ray AGN with the SFR of normal (i.e. non-AGN) star-forming systems. For this purpose we applied the same SED fitting analysis to both the X-ray catalogue and to a comparison galaxy sample (hereafter the reference galaxy catalogue). This enabled us to make a fully consistent comparison between the SFR of X-ray AGN with that of non-X-ray systems. The reference galaxy catalogue was provided by the HELP project. The same photometric criteria were applied for homogeneity with the X-ray catalogue. We also excluded from the reference galaxy catalogue sources with X-ray emission (i.e. sources in the X-ray sample). This resulted in 56 627 sources at z > 0.5. Next, we re-estimated SFRnorm using expression (9) in Schreiber et al. (2015) that parametrises the SFR of MS galaxies. This allowed us to facilitate a fair comparison with previous X-ray AGN studies that used the same expression (e.g., Mullaney et al. 2015; Masoura et al. 2018; Bernhard et al. 2019). More importantly, it allowed us to examine how the systematics and selection effects of the latter methodology affect the correlation of SFRnorm with LX.
3. Analysis
In this section we describe the SED fitting analysis we performed to measure the galaxy properties. We define the mass completeness of the data in different redshift ranges and describe the final selection criteria we applied on the datasets. Finally, we examine the reliability of the SED fitting measurements.
3.1. X-CIGALE
To measure the properties of our selected galaxies, we performed SED fitting using the X-CIGALE code (Yang et al. 2020). X-CIGALE is a new branch of the CIGALE fitting algorithm (Boquien et al. 2019) that adds the ability to model the X-ray emission of galaxies and the presence of polar dust. The dust accounts for the extinction of the UV and optical emission at the poles of AGN. The re-emitted radiation is considered isotropic, thus it contributes to the infrared (IR) emission of type 1 and 2 AGN. The improvements that these new features add in the results of the fitting process are described in Yang et al. (2020) and Mountrichas et al. (2021).
The galaxy component was built using a delayed star formation history (SFH) with the functional form SFR ∝ t × exp(−t/τ). A star formation burst was also included and modelled as a constant ongoing star formation no longer than 50 Myr. The burst was superimposed to the delayed SFH (Buat et al. 2019). Stellar emission was modelled using the Bruzual & Charlot (2003) single stellar populations template. The initial mass function (IMF) of Chabrier (2003) was adopted with metallicity equal to the solar value (0.02). Stellar emission was attenuated following Charlot & Fall (2000). The IR SED of the dust heated by stars was implemented with the Dale et al. (2014) model. In this model the star-forming component is parametrised by a single parameter α defined as dMd(U) ∝ U−αdU, with Md being the dust mass and U the radiation field intensity. AGN emission was modelled using the SKIRTOR templates (Stalevski et al. 2012, 2016). A detailed description of the SKIRTOR implementation in (X-) CIGALE is given in Yang et al. (2020). The AGN fraction, fracAGN, is defined as the ratio of the AGN IR emission to the total IR emission of the galaxy. A polar dust component (EB − V) was added and modelled as a dust screen absorption and a grey-body emission. The extinction curve of the Small Magellanic Cloud (SMC; Prevot et al. 1984) was adopted. Re-emitted grey-body dust was parametrised with a temperature of 100 K and emissivity index of 1.6.
The same modules and parametric space were used for the X-ray catalogue and for the reference galaxy catalogue. The AGN module was included in the SED fitting of the reference catalogue to identify sources with a strong AGN component (see Sect. 3.4). All free parameters used in the SED fitting process and their input values are presented in Table 1. The grid has been optimised using only sources with spectroscopic redshift to avoid uncertainties and scatter introduced by the photoz measurements.
Models and values of their free parameters used by X-CIGALE for the SED fitting of our galaxy sample.
X-CIGALE requires intrinsic (X-ray absorption corrected) X-ray fluxes. We used the fluxes in the hard energy band (2−7 keV) and the correction factor, defined as the ratio of the observed to the unabsorbed fluxes, provided in the Masini et al. (2020) catalogue, to estimate the intrinsic hard X-ray flux and included it in the fitting process. The photon index, Γ, was fixed to 1.8. A maximum value of |Δαox|max = 0.2 was adopted for the dispersion of the αox − L2500 Å (Risaliti & Lusso 2017), which corresponds to ≈2σ scatter in the αox − L2500 Å relation (Just et al. 2007).
We verified that our results are robust and independent, for example of adding more values for the slope, α, of the Galactic dust emission in the Dale et al. (2014) model and the exact choice of the age of the stellar mass populations in the star-forming history module. More importantly, in our analysis we used the SFRnorm parameter to compare the SFR of X-ray sources with the SFR of non-X-ray galaxies. Since the SFRs for the two populations were calculated by X-CIGALE, by using the same parameter space we expect any biases and systematics introduced by the grid to be alleviated.
3.2. Exclusion of sources with bad fits
X-CIGALE provides two estimates for each of the measured galaxy properties, one that is evaluated from the best-fit model and one that weights all models allowed by the parametric grid, with the best-fit model having the heaviest weight (Boquien et al. 2019). This weight is based on the likelihood, exp(−χ2/2), associated with each model. A large difference between these two values indicates that the probability density function (PDF) is asymmetric and a simple model (e.g., Gaussian) for the errors is not valid. To exclude from our datasets such cases that result in unreliable SFRs and stellar mass estimations, from the X-ray and the reference galaxy catalogues we only keep the systems with 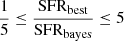 and
and 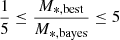 , where SFRbest and M*, best are the best-fit values of SFR and M*, respectively, and SFRbayes and M*, bayes are the Bayesian values, estimated by X-CIGALE. These reduce the number of available X-ray AGN to 1989 (from 2338) and the number of sources in the reference galaxy catalogue to 52 531 (from 56 627). Varying the boundaries of the criterion within a range of 0.1−0.33 for the lower limit and 3−10 for the upper limit changes the size of our samples by up to ±0.05%, and therefore does not affect the results of our analysis. Figure 1 presents the X-ray luminosity as a function of redshift. Specz sources (red circles) have, on average, slightly higher X-ray luminosities (median LX, 2−10 keV ∼ 1044.5 erg s−1) compared to photoz sources (median LX, 2−10 keV ∼ 1044 erg s−1), while both populations lie at similar redshifts.
, where SFRbest and M*, best are the best-fit values of SFR and M*, respectively, and SFRbayes and M*, bayes are the Bayesian values, estimated by X-CIGALE. These reduce the number of available X-ray AGN to 1989 (from 2338) and the number of sources in the reference galaxy catalogue to 52 531 (from 56 627). Varying the boundaries of the criterion within a range of 0.1−0.33 for the lower limit and 3−10 for the upper limit changes the size of our samples by up to ±0.05%, and therefore does not affect the results of our analysis. Figure 1 presents the X-ray luminosity as a function of redshift. Specz sources (red circles) have, on average, slightly higher X-ray luminosities (median LX, 2−10 keV ∼ 1044.5 erg s−1) compared to photoz sources (median LX, 2−10 keV ∼ 1044 erg s−1), while both populations lie at similar redshifts.
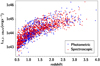 |
Fig. 1. X-ray hard instrinsic luminosity as a function of redshift for the 1989 X-ray AGN in our sample. There are 1020 sources with spectroscopic redshifts (red circles) and 969 with photometric redshifts (blue circles). |
3.3. Mass completeness
In our analysis we split the sources into four redshift bins, from 0.5 to 2.5, with a bin size of 0.5. This allowed us to study separately the possible dependence of the SFR of X-ray AGN with redshift and X-ray luminosity. To avoid any biases introduced by mass incompleteness of our samples, we estimated the mass completeness of the X-ray and reference galaxy catalogues at each redshift bin. For that purpose, we used the method described in Pozzetti et al. (2010). We estimated the limiting stellar mass (Mlim) of each galaxy at each redshift, which is the mass the galaxy would have if its apparent magnitude were equal to the limiting magnitude of the survey for a specific photometric band. The value of Mlim is calculated by the expression
where m is the AB magnitude of the source and mlim is the AB magnitude limit of the survey. The result is a distribution of log Mlim that reflects the distribution of stellar mass-to-light ratio (M/L) at each redshift. To obtain a representative mass limit of our dataset, we used the log Mlim of the 20% faintest galaxies at four redshift bins. This effectively removes galaxies with the highest M/L that do not significantly contribute close to the magnitude limit of the survey. Then, the minimum stellar mass at each redshift interval for which our sample is complete is the 95th percentile of log Mlim, of the 20% faintest galaxies in each redshift bin. The Ks band is the limiting band of our sample, and was chosen to define the mass completeness of our dataset (20% of the sources in the parent HELP catalogue have detection in this band). Moreover, the Ks band is shallow enough that essentially all galaxies with a detection in this band are also detected in bluer bands.
Following this procedure, and using the Ks band2 with mlim = 21.35 mag, we find that the stellar mass completeness for our galaxy sample is defined at log [M*, 95%lim(M⊙)] = 10.73, 11.19, 11.52, 11.43 at 0.5 < z < 1.0, 1.0 < z < 1.5, 1.5 < z < 2.0, and 2.0 < z < 2.5, respectively. Using a different photometric band that traces the stellar mass at high redshift, for instance the IRAC1 or IRAC2 bands, changes the mass completeness limits by < 0.15 dex. Finally, we note that these stellar mass limits are quite high. Equation (9) in Schreiber et al. (2015), which is used to estimate SFRnorm in Sect. 5.2, was calibrated for sources up to log [M*(M⊙)] = 11.5.
3.4. Final samples
In Sect. 5.2 we estimate SFRnorm applying the Schreiber et al. equation. For this we used the X-ray sample defined in Sect. 3.2 (i.e. the 1989 X-ray selected AGN). This allowed us to perform a fair comparison with previous studies that used the same equation and did not apply any mass completeness criteria on their X-ray sources. This is also the X-ray sample used in Sect. 6, where we study the host galaxy properties of X-ray absorbed and unabsorbed AGN. However, in Sect. 5.1, where we examine the relation of the AGN with the SFR of the host galaxy, we apply the mass completeness limits we estimated in the previous section, on both the X-ray and reference galaxy catalogues (in addition to the cuts described below).
As already noted, most previous X-ray studies used the Schreiber et al. (2015) equation to calculate the SFRs of star-forming MS galaxies and explore the SFRs of X-ray AGN relative to MS star-forming galaxies. In Schreiber et al. they do not explicitly exclude AGN from their star-forming galaxy sample. Since there is no AGN template in their fitting analysis, most AGN systems will be badly fitted. Thus, they reject sources for which the SED fits have large χ2 values (χ2 > 10). In our analysis we included an AGN template when we fitted the X-ray and the reference galaxy catalogues (see Sect. 3.1). This enabled us to identify systems with an AGN component and quantify it. We used the fracAGN parameter to exclude such systems from the reference galaxy catalogue. Specifically, we rejected sources with fracAGN > 0.2. These systems account for ≈14% of the total reference galaxy sample. The percentage ranges from ∼14% at z < 1.5, up to ∼50% at higher redshifts. This is qualitatively and quantitatively consistent with observational studies that found higher AGN duty cycles at earlier epochs and for more massive galaxies (e.g., Genzel et al. 2014; Georgakakis et al. 2017).
Application of the mass completeness criteria in both the X-ray and the reference galaxy catalogues and the exclusion of systems with a (strong) AGN component from the reference sample results in 1020 X-ray AGN and 18 248 sources in the reference galaxy catalogue. The number of available sources in the two datasets are presented in Table 2.
Number of X-ray AGN and sources in the reference galaxy catalogue.
3.5. Reliability of galaxy properties measurements
From the 1989 X-ray AGN, 935 (∼47%) were detected by Herschel. In the analysis the 100 and 160 μm PACS bands and the SPIRE 500 μm band were not considered, given their lower sensitivity for this field (Oliver et al. 2012). For these sources, we performed SED analysis with and without Herschel bands, using the same parameter space in the fitting process. The comparison of the SFR measurements is presented in Fig. 2. To examine whether photoz introduce (additional) scatter to the comparison of the SFR calculations, we plot sources with specz in red and those with photoz in blue. We find a very good agreement of the SFR values between the two measurements (SFRno Herschel = (1.02 ± 0.01) SFRHerschel − 0.07 ± 0.01). We also note that sources with photoz do not present larger dispersion compared to spectroscopic sources. This result shows that the SFR calculations of those sources without far-IR photometry in our dataset are reliable.
 |
Fig. 2. Comparison of SFR measurements with and without Herschel photometry for 935 sources that have far-IR coverage and satisfy our selection criteria (see text for details). X-ray AGN with spectroscopic redshifts (490) are shown in red, while sources with photometric redshift estimations (445) are presented in blue. The blue solid line presents the 1:1 relation. The results show an excellent agreement between the two measurements. The mean offset and the standard deviation, of the SFR difference (Herschel − no Herschel) are shown in the legend. |
We then examined the accuracy and reliability of the SFR and M* measurement of X-CIGALE. We quantify the accuracy using the sigma parameter (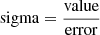 ). For the X-ray catalogue, the average sigma is ∼3.7 and ∼4.5, for the SFR and M* measurements, respectively. For the reference galaxy catalogue, sigma is ∼4.2 and ∼5.8, for the SFR and M* measurements, respectively. Stellar mass and SFR calculations of sources in the reference galaxy catalogue are more robust than those for X-ray AGN. This is due to the AGN emission that can outshine the optical emission of the host galaxy, thus rendering measurements less accurate for AGN, in particular for unobscured or type 1 AGN.
). For the X-ray catalogue, the average sigma is ∼3.7 and ∼4.5, for the SFR and M* measurements, respectively. For the reference galaxy catalogue, sigma is ∼4.2 and ∼5.8, for the SFR and M* measurements, respectively. Stellar mass and SFR calculations of sources in the reference galaxy catalogue are more robust than those for X-ray AGN. This is due to the AGN emission that can outshine the optical emission of the host galaxy, thus rendering measurements less accurate for AGN, in particular for unobscured or type 1 AGN.
X-CIGALE offers the option to create and analyse mock catalogues based on the best-fit model of each source of the dataset. When this option is chosen, the code uses the best fit of each source and creates a mock sample. Each best flux is modified by injecting noise extracted from a Gaussian distribution with the same standard deviation as the observed flux. Then the mock data are analysed in the same way as the observed data. The precision of each estimated parameter can be tested by comparing the input and output values (ground truth versus estimated value). We used these mock catalogues to examine the reliability of SFR and M* results. In Fig. 3 (left panel) we plot the comparison of the Bayesian values of SFR obtained from the fit of the mock catalogue with the true SFR values from the best fit of the X-ray sample. The right panel shows the results of the stellar mass measurements. Figure 4 shows the comparison for the reference galaxy sample. The scatter in the stellar mass measurements is larger for X-ray AGN compared to the reference sample. As mentioned earlier, this is due to the AGN component. In both cases X-CIGALE successfully recovers the true SFR and M* values of the mock sources.
 |
Fig. 3. Comparison of the SFR and M* measurements (left and right panel, respectively) for the mock sources (estimated) with the true values (data), using the X-ray sample. X-CIGALE accurately recovers the true SFR and M* values of the mock sources. |
 |
Fig. 4. Comparison of the SFR and M* measurements (left and right panel, respectively) for the mock sources (estimated) with the true values (data), using the reference galaxy sample. X-CIGALE accurately recovers the true SFR and M* values of the mock sources. |
In the analysis presented in Sect. 5, we take into account the uncertainties of the SFR and M*, estimated by X-CIGALE. Specifically, in the analysis based on SFRnorm, each source is weighted by the sigmaSFR × sigmaM*, while for the analysis based on λs, BHAR, each source is weighted using the value of sigmaM*.
4. Definition of the main sequence: Systematics and selection effects
The goal of this work is to examine whether there is a correlation between the AGN power and the SFR of the host galaxy. The SFR of X-ray AGN evolves with stellar mass and redshift in a way that is qualitatively similar to the SFR evolution of star-forming galaxies (Masoura et al. 2018). To account for this evolution, previous studies estimated the SFRnorm parameter, which is defined as the ratio of the SFR of X-ray AGN to the SFR of star-forming MS galaxies, SFR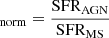 (Mullaney et al. 2015; Masoura et al. 2018, 2021; Bernhard et al. 2019; Aird et al. 2019; Grimmett et al. 2020). For that purpose, nearly all of them used the analytical expression (9) of Schreiber et al. (2015) to parametrise the SFR of MS galaxies. However, this method hints at a number of systematics and uncertainties. X-ray and non-X-ray galaxy samples are defined differently, and different methods are applied to estimate galaxy properties and specifically SFRs and stellar masses, which are used to define the MS.
(Mullaney et al. 2015; Masoura et al. 2018, 2021; Bernhard et al. 2019; Aird et al. 2019; Grimmett et al. 2020). For that purpose, nearly all of them used the analytical expression (9) of Schreiber et al. (2015) to parametrise the SFR of MS galaxies. However, this method hints at a number of systematics and uncertainties. X-ray and non-X-ray galaxy samples are defined differently, and different methods are applied to estimate galaxy properties and specifically SFRs and stellar masses, which are used to define the MS.
To acquire better control of these systematics, in our analysis of both the X-ray and the galaxy reference samples we applied the same photometric criteria. Furthermore, the SFR (and M*) values of both datasets were measured using the same SED fitting method by applying the same parametric grid. We also defined our own MS for star-forming galaxies using our data. To this end, we identified and excluded quiescent galaxies from our datasets. Our goal was not to make a strict definition of star-forming MS galaxies, but mainly to exclude in a uniform manner (most) of the quiescent systems from both the X-ray and the reference galaxy catalogues, by applying the same selection criteria in the two samples. For this purpose, we estimated the sSFR, defined as the 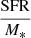 of each source that is above the mass completeness limit at the corresponding redshift (Sect. 3.3). We used only the galaxy reference sample to define sSFR criteria at different redshift bins and to exclude quiescent galaxies, due to its significantly large size compared to the X-ray sample. These sSFR criteria were then used to exclude quiescent systems from the X-ray sample as well.
of each source that is above the mass completeness limit at the corresponding redshift (Sect. 3.3). We used only the galaxy reference sample to define sSFR criteria at different redshift bins and to exclude quiescent galaxies, due to its significantly large size compared to the X-ray sample. These sSFR criteria were then used to exclude quiescent systems from the X-ray sample as well.
The sSFR distributions are presented in Fig. 5. Up to z < 2 a tail and a second smaller peak is present. The quiescent population of the galaxy sample is defined by applying a sSFR cut at the location of this second peak of each distribution. At the highest redshift bin the sSFR distribution does not appear Gaussian, probably due to the small number of sources, and the definition of the sSFR cut is not obvious. In the rest of our analysis we do not include sources from that redshift bin. The above sSFR cuts exclude ∼35% of the sources as quiescent galaxies (Table 2). Most of them lie at z < 1.5 (∼40% at 0.5 < z < 1.0 and ∼25% at 1.0 < z < 1.5), while ∼10% of the galaxies in the reference catalogue are classified as quiescent systems at z > 1.5. This is consistent with studies that examine the evolution of quiescent and star-forming galaxies (e.g., Bezanson et al. 2012).
 |
Fig. 5. sSFR distribution in four redshift intervals. The blue lines present the full distributions. The green areas are the sSFR distributions after applying the sSFR cut, which is defined based on the location of the second lowest peak of each distribution. At the highest redshift bin (2.0 < z < 2.5), the sSFR distribution does not have a Gaussian shape, most likely due to the small number of sources (see Table 2) and the sSFR cut cannot be defined as described above. |
Figure 6 illustrates the systematic difference between the SFR calculations of X-CIGALE for star-forming galaxies defined from our galaxy sample, as described above, and the SFR measuremments using the expression of Schreiber et al. for star-forming MS galaxies. At z < 1.5 SFR values from X-CIGALE are ∼0.25 dex lower compared to those using Schreiber et al., whereas at z > 1.5 the two SFRs are similar (Table 3). We also compare these values with the MS definition of Whitaker et al. (2014) (their Eq. (3)). There is a small systematic offset at z > 1. At this redshift interval, SFR measurements of X-CIGALE are lower by ∼0.15 dex compared to SFR values using the expression of Whitaker et al. (right panel of Fig. 6). At z < 1 the two SFR estimations are similar (distribution peaks at zero). We conclude that the small offset we observe between X-CIGALE SFR measurements and those using the Schreiber et al. formula, is not a systematic miscalculation of the SED fitting algorithm, but is most likely related to the lack of a rigorous definition of the MS due to the uncertainties and different analysis in the estimations of galaxy properties among the various studies.
 |
Fig. 6. Comparison of different SFR estimates. Left: difference between the SFR calculations of X-CIGALE for star-forming galaxies defined from our galaxy sample (see text for more details) and the SFR measurements using the expression of Schreiber et al. for star-forming MS galaxies. At z < 1.5 the SFR values from X-CIGALE are ∼0.25 dex lower than those using Schreiber et al., whereas at higher redshift the two estimates are consistent. Right: difference between the SFR calculations of X-CIGALE for star-forming galaxies defined from our galaxy sample (see text for more details) and the SFR measurements using the expression of Whitaker et al. (2014) for star-forming MS galaxies. At z < 1.0 the SFR values from X-CIGALE are similar (distribution peaks at zero) to those using the Whitaker et al. formula, whereas at 1 < z < 2, SFRX-CIGALE are lower by ∼0.15 dex (see also Table 3). |
Mean (μ) and standard deviation (σ) of the difference in the calculations of SFR (Δlog SFR), using X-CIGALE and the expressions derived in Schreiber et al. (2015) and Whitaker et al. (2014), for MS star-forming galaxies (see also Fig. 6).
In the next section we study the SFRnorm − LX relation, when the same methodology (i.e. SED fitting and using the same parametric grid) is applied to measure the SFR and M* of both X-ray and non-X-ray systems and using our own definition of the star-forming MS. We also examine how this relation changes when the systematics and selection effects, presented in this section, are not taken into account.
5. Results I: AGN power and SFR
In this section, we study the relation between SFRnorm and LX. For that purpose, we first estimate SFRnorm using SFR calculations from X-CIGALE both for the X-ray and the galaxy reference sample. In the second part of the section, we follow recent studies and measure SFRnorm using Eq. (9) of Schreiber et al. (2015). The latter facilitates a direct comparison with previous works.
5.1. SFR of X-ray AGN relative to our non-X-ray galaxy sample
5.1.1. SFRnorm measurements using quiescent and star-forming galaxies
We use the 18 248 galaxies from our reference galaxy catalogue (see Sect. 3.4), to estimate SFRnorm values for the 1020 X-ray sources that are above the mass completeness limit (Table 2). The SFR of each X-ray AGN is divided by the SFR of galaxies from the reference catalogue that are within ±0.1 dex in M* and ±0.075 × (1 + z) in redshift. This flexible criterion allows us to increase the number of sources from the reference sample used at high redshifts, thus making our SFRnorm calculations more robust. As mentioned, each source is weighted based on the uncertainty on the SFR and M* parameters (see Sect. 3.5). Then, the median values of these ratios is used as the SFRnorm of the X-ray source. Only X-ray sources for which their SFRnorm has been estimated using at least 30 galaxies from the reference catalogue are used in our measurements. This limit is lowered to at least five galaxies for the highest redshift bin, due to the smaller number of available sources. Our measurements are not sensitive to the choice of the box size around the AGN. Changing the above boundaries to 0.05−0.2 does not change the observed trends, but affects the errors of the calculations.
The top panel of Fig. 7 presents the results of our calculations. Measurements are the median values of SFRnorm, grouped in LX bins of size 0.5 dex. Errors are calculated using bootstrap resampling (e.g., Loh 2008), by performing 100 resamplings with replacement at each bin. As shown in Table 2, the highest redshift bin includes a small number of sources, and thus these measurements should be taken with caution. The SFRnorm values using the reference galaxy catalogue present only a mild increase, if any, with X-ray luminosity. The transition point is at LX, 2−10 keV ∼ 1044 erg s−1. SFRnorm − LX appears flat at higher LX and redshifts. Rosario et al. (2012) used X-ray selected AGN from the GOODS-South, GOODS-North, and COSMOS fields and found similar results (see their Fig. 4). Specifically, their analysis showed that when mean values are used the SFRs (L60) of AGN increase with the AGN luminosity at low redshifts with a turning point at LX, 2−10 keV ∼ 1044 erg s−1, while at z > 1.5 they observed a flattening of the relationship of the two parameters for luminous sources.
 |
Fig. 7. SFRnorm vs. X-ray luminosity. SFRnorm and LX are the median values of our binned measurements, in bins of LX, with 0.5 dex width. Errors are calculated using bootstrap resampling by performing 100 resamplings with replacement at each bin. Results are colour-coded based on the redshift interval. Top: SFRnorm estimated using our reference galaxy catalogue with SFR measurements from X-CIGALE. Middle: results when excluding quiescent galaxies from the reference catalogue. Bottom: measurements when excluding quiescent systems from the X-ray and the reference galaxy catalogues (see text for more details). |
Filled circles present the weighted average SFRnorm, in bins of LX, over the total redshift range (also shown with green points in Fig. 8). The mean values are weighted based on the number of sources included in each LX bin, shown by the coloured circles. This allows us to downweight measurements from bins with small numbers of sources (e.g., at 2.0 < z < 2.5). The errors present the standard deviation of the measurements. The SFR of X-ray AGN appears enhanced compared to that of the galaxy sample, by ∼20%. Although this difference is not constant, but appears lower at LX < 1044 erg s−1 (∼10%) and higher at LX > 1044 erg s−1 (∼30%), it is systematic across all LX spanned by our dataset. This can also be seen by the individual points presented in the top panel of Fig. 7. Florez et al. (2020) used 898 X-ray AGN with LX > 1044 erg s−1 selected in the Stripe 82 field, and compared their SFRs with a sample of ∼320 000 non-X-ray galaxies. The two samples were selected in a similar way, and their galaxy properties were measured consistently using the same code (CIGALE). The authors found that X-ray AGN have on average 3−10× higher SFRs than their control galaxy sample, at fixed stellar mass and redshift. However, their calculations are based on mean SFR values. If we consider mean instead of median SFRnorm values for the coloured bins, and then estimate their weighted average, the SFR of X-ray AGN host galaxies is enhanced by ∼40%. This is still lower than what Florez et al. claim.
 |
Fig. 8. SFRnorm vs. X-ray luminosity. SFRnorm and LX are the mean values of the measurements presented in Figs. 7 and 9, grouped in LX bins of 0.5 dex, at all redshfits combined, and weighted based on the number of sources in each bin shown in Fig. 7. The errors represent the standard deviation of SFRnorm and LX in each bin. |
5.1.2. SFRnorm measurements excluding quiescent systems
In this section we re-calculate the SFRnorm of each X-ray AGN, using our own star-forming galaxy sample. For this purpose we use the analysis described in Sect. 4 (see also Fig. 5) to identify and exclude quiescent galaxies. The results are presented in the middle panel of Fig. 7. SFRnorm values appear to be lower compared to those presented in the previous section (top panel of Fig. 7). This is expected since we have now excluded quiescent systems from the reference sample. In agreement with our previous calculations, the results show no evolution of SFRnorm with redshift. Regarding the dependence of the SFRnorm on LX, we confirm our previous findings of a mild dependence. This is also illustrated by the average SFRnorm values across all redshifts spanned by our dataset (black circles in Figs. 7 and 8).
Next, we exclude quiescent systems from both the X-ray and the reference galaxy catalogues. Based on our definition of quiescent systems, ∼25% of X-ray AGN are found in quiescent galaxies. The percentage is higher at z < 1 (∼35%) and drops to ∼7% at z > 1.5. These percentages are similar to those found for the galaxies in the reference sample in Sect. 4. In the bottom panel of Fig. 7 we present the SFRnorm values as a function of X-ray luminosity. The filled circles show the weighted average SFRnorm values estimated in LX bins of width 0.5 dex, and the open circles show those weighted based on the number of sources in the bins. As expected, SFRnorm values are higher compared to those when we exclude quiescent systems only from the reference sample; however, they follow the same trends with our previous measurements. Specifically, we do not find a dependence of SFRnorm on redshift, although there is a mild increase (∼30%) of SFRnorm with LX, only at LX, 2−10 keV < 1044.5 erg s−1.
5.2. SFR of X-ray AGN relative to main sequence galaxies, defined in previous studies
Recent studies that examined the correlation of SFRnorm with LX, used Eq. (9) of Schreiber et al. to calculate SFRnorm. In this section we follow their approach. Our goal is to compare our findings following this methodology with their results and most importantly with our measurements presented in the previous section.
In Fig. 9 we plot the SFRnorm, estimated using Eq. (9) in Schreiber et al., as a function of X-ray luminosity, in four redshift bins. For these measurements we used the total X-ray sample (i.e. without excluding sources below the mass completeness limit; see Sect. 3.3). This allows a direct comparison with previous studies that followed the same approach. The measurements are the median values of SFRnorm, grouped in LX bins of size 0.5 dex. The errors are calculated using bootstrap resampling. Each source is weighted based on the uncertainty on the SFR and M* parameters (see Sect. 3.5). The SFRnorm increases with LX at all redshift intervals, up to X-ray luminosities LX, 2−10 keV < 1045 erg s−1. At higher luminosities, SFRnorm values appear lower. However, the two bins at the highest LX regime spanned by our sample include a very small number of X-ray sources (< 30 sources). We do not detect evolution of SFRnorm with redshift. Filled circles present the mean SFRnorm in bins of LX over the total redshift range studied in this work (0.5 < z < 2.5). The width of each bin is 0.5 dex. The mean values are weighted based on the number of sources included in each LX bin shown by the coloured circles. The errors present the standard deviation of the measurements. Based on these results, SFRnorm presents a strong evolution with LX. Specifically, SFRnorm increases by a factor of ≈2 up to LX, 2−10 keV < 1045 erg s−1.
 |
Fig. 9. SFRnorm vs. X-ray luminosity. SFRnorm values are estimated using the expression of Schreiber et al. (2015) to measure the SFRs of star-forming MS galaxies. SFRnorm and LX are the median values of our binned measurements, in bins of LX, with 0.5 dex width. The errors are calculated using bootstrap resampling by performing 100 resamplings with replacement at each bin. The results are colour-coded based on the redshift interval. |
5.2.1. Comparison with previous studies
Mullaney et al. (2015) used 110 AGN at 0.5 < z < 1.5 selected from Chandra Deep Field North (CDFN) and South (CDFS) and 49 AGN at 1.5 < z < 4.0 from CDFS. They compare the SFRs of their AGN sample with the SFRs of MS galaxies, using for the latter the equation of Schreiber et al. They found that the SFR distributions of their AGN and MS galaxy samples differ. However, AGN have mean SFRnorm ∼ 1. They attributed the apparent contradiction between the SFR distributions and SFRnorm values to bright outliers that skew their mean SFRnorm calculation to higher values. They also found no evolution of the SFRnorm between their low and high redshift AGN samples. Using mean values for our calculations instead of median does not practically affect the LX values of each bin, although it increases the SFRnorm values by 0.25−0.50. We also find no evolution of SFRnorm with redshift, in agreement with Mullaney et al.
Bernhard et al. (2019) used 541 AGN in the COSMOS field, within 0.8 < z < 1.2 and found that the SFRnorm of higher LX AGN (LX, 2−10 keV > 2 × 1043 erg s−1) is narrower and closer to that of the MS galaxies than that of lower LX AGN. Although their sample spans significantly lower X-ray luminosities and lacks high LX compared to the X-ray sample used in this study (see their Fig. 1 and our Fig. 1), our results are in broad agreement. As shown in Fig. 9, our lowest LX bin lies below the dashed line (i.e. the SFRs of low LX AGN are lower than those of MS galaxies), while at LX, 2−10 keV ∼ 1044 erg s−1 the SFRs of AGN are consistent with those of MS galaxies (SFRnorm ∼ 1).
The LX and redshift distributions of our sample is closer to that used in Masoura et al. (2018, 2021). In the latter work they used 3213 X-ray AGN in the XMM-XXL, and found evolution of the SFRnorm parameter with X-ray luminosity. Our results are in agreement with their measurements. However, Masoura et al. (2021) find higher SFRnorm values for sources at z > 1.2 compared to those at z < 1.2 (see their Fig. 8). As already mentioned, we do not find evolution of SFRnorm with redshift. We note that in Masoura et al. the low redshift bin also includes sources at z < 0.5. Such sources have been excluded from our analysis (and Mullaney et al.) for the reasons mentioned in Sect. 2. Perhaps the redshift evolution of SFRnorm found in Masoura et al. is driven by sources at z < 0.5, and this could be the reason why we (and Mullaney et al.) do not detect it in our samples.
5.2.2. Effect of systematics and selection effects on the SFRnorm−LX relation
The blue triangles in Fig. 8 present the weighted mean values of SFRnorm when we are using the Schreiber et al. equation and are compared with the results following our analysis, as presented in Sect. 5.1. We note that SFRnorm values are higher using our definition of MS galaxies at low redshift and X-ray luminosities (z < 1, LX, 2−10 keV < 1044 erg−1), and decrease at higher redshift and luminosities compared to SFRnorm calculations using the Schreiber et al. formula. Part of this difference can be attributed to two main factors. First, the X-ray sample used when SFRnorm is estimated with the Schreiber formula includes sources below the mass completeness limit that have been excluded from the measurements presented in the bottom panel of the figure. Furthermore, there are small but systematic offsets of the SFR calculations using X-CIGALE compared to the SFR measurements using the Schreiber et al. (2015) analytic formula, as shown in the left panel of Fig. 6 and in Table 3. Moreover, at z < 1.5 the SFRnorm values using the reference galaxy catalogue are higher than those using the Schreiber et al. analytical form (top panel of Fig. 7). This is expected since our reference galaxy catalogue includes a mix of star-forming and quiescent galaxies. The Schreiber et al. formula estimates the SFRs of galaxies in the locus of the MS.
We conclude that following the same methodology with recent studies to calculate the SFRnorm parameter and to study its dependence on LX and redshift gives results that are generally in agreement with those reported in previous works. However, the results presented in Fig. 8 highlight the importance of studying the SFRnorm − LX relation in a uniform manner, taking into account the systematics and selection effects. Inconsistencies among the different methodologies may lead to incorrect conclusions regarding the SFRnorm − LX relation.
5.3. Discussion
The analysis using our definition of MS galaxies showed only a mild increase in SFRnorm with LX, with a transition luminosity at LX, 2−10 keV ∼ 1044 erg s−1 (Sect. 5.1). Here we check whether this result holds when we account for the stellar mass of the examined systems.
5.3.1. The effect of stellar mass
To examine whether the SFRnorm − LX relation differs with stellar mass, we use the specific black hole accretion rate parameter (λs, BHAR; Aird et al. 2012, 2018), which is the rate of accretion onto the supermassive black hole relative to the stellar mass of the host galaxy. Instead, using the specific X-ray luminosity (Yang et al. 2018) does not change the observed trends and our conclusions. For the estimation of λs, BHAR we use the mathematical expression (2) of Aird et al. (2018),
where kbol is a bolometric correction factor. We adopt the same value as in Aird et al. (2018): kbol = 25. Each source is weighted based on the uncertainty of M* (see Sect. 3.5). The results are shown in Fig. 10. For these measurements we used SFRnorm values calculated after excluding quiescent systems from the X-ray and reference galaxy catalogues. The black circles present the average measurements over the total redshift range, in bins of λs, BHAR, weighted by the number of sources in each bin, shown by the coloured open circles. Based on our results, the SFRnorm increases with the specific accretion rate of the supermassive black hole by a factor of ∼1.3.
 |
Fig. 10. SFRnorm vs. specific black hole accretion rate (λs, BHAR). The SFRnorm has been estimated after excluding quiescent systems from both the X-ray and the reference galaxy catalogues (see text for more details). The results are colour-coded based on the redshift interval. The measurements are grouped in λs, BHAR bins, with 0.5 dex width. Median values are presented and the errors are calculated using bootstrap resampling. The average SFRnorm values (black squares) are weighted based on the number of sources in each bin (coloured circles), across all redshift intervals. The errors on the average values correspond to the standard deviation within each λs, BHAR bin. The solid line presents the best fit of the average values: SFR |
5.3.2. Are AGN accretion and star formation linked?
Our analysis shows enhancement of SFRnorm with λs, BHAR at all redshifts and specific black hole accretion rates, spanned by our sample. However, the SFRnorm − LX relation does not present a consistent trend. In Table 4, we present the weighted median values of LX, M*, and redshift for each LX and λs, BHAR bins, presented in the bottom panel of Figs. 7 and 10. The weight is based on the accuracy of the SFR and M* calculation of X-CIGALE for each source. LX and λs, BHAR are binned the in the same way across the redshift range spanned by our dataset. Additionally, our previous results showed no evolution of SFRnorm with redshift. Therefore, redshift is not a differentiating factor. We note that λs, BHAR bins of low value tend to include, on average, the most massive and least luminous systems. On the other hand, when SFRnorm is grouped in LX bins the most massive systems are included in the highest LX bins. In Fig. 11 we repeat the measurements presented in the bottom panel of Fig. 7, but at each redshift range the results are also grouped in stellar mass bins and in LX bins. The results are colour-coded based on the redshift range (black for 0.5 < z < 1.0, blue for 1.0 < z < 1.5, and green for 1.5 < z < 2.0). The different symbols refer to different stellar mass intervals. We note that for the less massive sources (log [M*(M⊙)] ∼ 11−11.5) SFRnorm increases, with a turning point at LX, 2−10 keV ∼ 1044 erg−1, by a factor of up to ∼1.5. These results, in conjunction with those presented in Fig. 10 and the numbers shown in Table 4, may indicate that in less massive systems (log [M*(M⊙)] < 11.5), SFRnorm increases with the AGN power for luminosities up to a few times 1044 erg s−1, while at higher LX the samples are dominated by massive systems in which the SFRnorm − LX relation appears flat. We note, however, that a strong conclusion cannot be drawn as the trend is based on bins that include a small number of AGN (∼120). Furthermore, data from deeper surveys that will provide us with AGN at lower luminosities are needed to provide corroborating evidence.
 |
Fig. 11. SFRnorm vs. X-ray luminosity. The SFRnorm was estimated after excluding quiescent systems from both the X-ray and the reference galaxy catalogues (see text for more details). The results are grouped in LX bins of 0.5 dex width and stellar mass bins. The results are colour-coded based on the redshift range (black for 0.5 < z < 1.0, blue for 1.0 < z < 1.5, and green for 1.5 < z < 2.0). Different symbols refer to different stellar mass intervals, as indicated in the legend. M* values are in log [M*(M⊙)]. Median SFRnorm values are presented and the errors are calculated using bootstrap resampling. The number of sources included in each bin are shown next to each symbol. |
Although the results appear marginally significant, it is interesting to consider their plausible interpretations if we assume that there is a correlation between the SMBH accretion and galaxy star formation, and that this correlation exists only in lower mass systems (log [M*(M⊙)] < 11.5). Instantaneous AGN accretion does not appear to track star formation in the most massive galaxies (log [M*(M⊙)] > 11.5) and at high accretion rates (LX, 2−10 keV > 1044.5 erg−1). A scenario that could explain this hypothesis is that different physical mechanisms fuel AGN at these two mass regimes. AGN constitute a diverse population and previous works, both observational (e.g., Allevato et al. 2011; Mountrichas et al. 2013, 2016) and theoretical (e.g., Fanidakis et al. 2012, 2013), find that different AGN triggering processes may be dominant depending on redshift, X-ray luminosity, and mass of the source, for example.
A plausible process that may link star formation with AGN activity are galaxy mergers in gas-rich galactic discs (e.g., Hopkins et al. 2008). This AGN fuelling mechanism is associated with star formation events, and assumes that a fraction of the cold gas in galaxies that is available for star formation accretes onto the SMBH (e.g., Bower et al. 2006; Fanidakis et al. 2012). In higher mass systems other mechanisms, which are decoupled from the star formation of the host galaxy, may fuel the SMBH. For example, the SMBH may be activated when diffuse hot gas in quasi-hydrostatic equilibrium accretes onto the SMBH without first being cooled onto the galactic disc. Based on semi-analytic models, this mechanism becomes dominant at very massive systems (e.g., Fanidakis et al. 2013). The above scenario implies that if the correlation between AGN activity and SFR exists, it is the result of a common mechanism that affects both properties. In other words, there is not an actual connection between the two parameters.
Our results may suggest that the SFRs of luminous X-ray AGN are enhanced compared to the SFRs of star-forming galaxies in less massive systems (log [M*(M⊙)] ∼ 11). However, our results are only tentative and further investigation is required before strong conclusions can be made. Additional data that would be mass-complete to lower masses could provide stronger evidence.
6. Results II: The role of absorption in host galaxy properties
In this section we examine whether absorbed X-ray AGN present different host galaxy properties compared to their unabsorbed counterparts. Specifically, we compare the stellar masses, SFRs, and SFRnorm of the two populations. In this part of our analysis we use the full X-ray catalogue (i.e. the 1989 X-ray AGN; see Sect. 3.4).
We use the NH parameter to classify sources into X-ray absorbed and unabsorbed, using a cut at NH = 1021.5 cm−2. We chose this threshold as it provides a good agreement between X-ray and optical classification of type 1 and 2 AGN (e.g., Merloni et al. 2014). Using a higher NH cut (NH = 1022 cm−2) does not change our results and conclusions. There are 374 (550) X-ray unabsorbed and 965 (778) absorbed AGN, using NH = 1021.5 cm−2 (= 1022 cm−2). NH measurements become less accurate for sources with a small number of counts (photons). Moreover, NH values, derived by HR measurements, are less secure as we move to higher redshifts because the absorption redshifts out of the soft X-ray band in the observed frame. Restricting our sample to sources with 50 or more net counts and at z < 1 does not change our conclusions.
Figure 12 presents the redshift and X-ray luminosity distributions of the two populations. The distributions of absorbed and unabsorbed sources are similar. Nevertheless, we account for the small differences. For this purpose we combine the redshift distributions of the two populations (and similarly the LX distributions) and normalise them to the total number of sources in each redshift (LX) bin. This gives us the PDF in this 2D (z, LX) parameter space. Then, each source is weighted, based on its redshift and X-ray luminosity, according to the estimated PDF (Mendez et al. 2016; Mountrichas et al. 2016).
 |
Fig. 12. Redshift (left panel) and X-ray luminosity (right panel) distributions of X-ray absorbed (red histograms) and unabsorbed (blue histograms) AGN. Both histograms have been normalised to the total number of sources. |
The top panel of Fig. 13 presents the M* distributions of X-ray absorbed and unabsorbed X-ray AGN in bins of 0.2 dex. The two distributions are similar, as confirmed by the two-sample Kolmogorov-Smirnov test (KS test, p-value = 0.12). Our results are in agreement with most studies that used X-ray criteria for the classification of X-ray AGN (Merloni et al. 2014; Masoura et al. 2021). However, Lanzuisi et al. (2017) found that NH and M* show a clear positive correlation using NH = 1022 cm−2 to classify their sources. Adopting the same NH threshold does not change our results. Zou et al. (2019) used optical spectra, morphology, and variability to classify 2463 X-ray selected AGN in the COSMOS field. Their analysis showed that type 1 AGN tend to have lower M* than type 2. The disagreement with our results could be attributed to the different classification criteria.
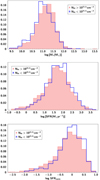 |
Fig. 13. Distributions of host galaxy properties of X-ray absorbed (red shaded histograms) and unabsorbed (blue line histograms) AGN. From top to bottom: stellar mass, SFR, and SFRnorm distributions. The two populations have similar host galaxy properties. |
In the middle panel of Fig. 13 we present the SFR distributions of the two X-ray populations in bins of 0.2 dex. There is no significant difference between the SFR of X-ray absorbed and unabsorbed sources (p-value = 0.33 from KS−test). Our results are in agreement with previous X-ray studies (Rosario et al. 2012; Merloni et al. 2014; Lanzuisi et al. 2017; Zou et al. 2019; Masoura et al. 2021).
The bottom panel of Fig. 13 presents the SFRnorm distributions of X-ray absorbed and unabsorbed AGN in bins of 0.2 dex. The SFRnorm distributions of the two AGN populations are similar (p-value = 0.27 from KS test). Our findings are in agreement with those of Masoura et al. (2021).
Based on our results X-ray absorbed and unabsorbed AGN reside in galaxies with similar properties.
7. Summary and conclusions
In this work we used X-ray sources observed by the Chandra X-ray Observatory within the 9.3 deg2 Boötes field of the NDWFS catalogue (Masini et al. 2020) to study whether there is a link between AGN power and star formation of the host galaxy at 0.5 < z < 2.0. After applying our selection criteria (e.g., photometry, mass completeness; Sect. 3.4), the X-ray sample consisted of 711 sources (Table 2). About half of these sources have spectroscopic redshifts; a similar fraction has been observed by Herschel. Furthermore, a reference galaxy catalogue was constructed with which the SFR of the X-ray sources are compared. The same selection criteria were applied in the reference sample. Additionally, sources with X-ray emission and a strong AGN component were excluded from the latter dataset. The reference catalogue includes 11 639 galaxies.
For both datasets we used photometric data compiled by the HELP project and applied SED fitting using the X-CIGALE code. This enabled us to measure the properties of the sources (e.g., SFR, stellar mass). In the fitting process we included the X-ray flux that is available in the X-ray catalogue, and accounted for the possible presence of a polar dust component.
We studied the SFR–LX relation with respect to the position of the galaxy to the MS. For that purpose, we estimated the SFRnorm parameter. We used SFR measurements from X-CIGALE, for the X-ray and the reference galaxy catalogues. Quiescent systems were excluded from both datasets. From the galaxy reference catalogue, we also rejected sources with a strong AGN component (fracAGN > 0.2). We detect only a mild correlation between SFRnorm and LX. Specifically, SFRnorm increases by 20−30% up to LX, 2−10 keV ∼ 1044.5 erg s−1.
The values of SFRnorm were also estimated using the SFR measurements of X-CIGALE for the X-ray sources, while for the SFR of star-forming galaxies we used Eq. (9) from Schreiber et al. (2015). This allowed us to compare our measurements with those from the literature that used the same approach. In this case, SFRnorm increases by a factor of 2, within an order of magnitude in LX. We do not detect evolution of SFRnorm with redshift, within 0.5 < z < 2.5.
These results highlight the importance of performing a uniform and consistent analysis when studying the correlation between the SFR of a galaxy with the X-ray luminosity. Systematics that are inserted in the analysis due to the different methodologies used in the estimation of SFR of AGN and non-AGN systems among different studies, the different definitions of the star-forming MS among them, and not accounting for the mass incompleteness of the samples at different redshift may greatly affect the measurements and lead to incorrect conclusions.
Using our SFR measurements for both X-ray and star-forming galaxies, we studied the dependence of SFRnorm on the specific accretion rate. SFRnorm increases by ∼20% within the λs, BHAR range spanned by the dataset. Prompted by this result, we split our samples into stellar mass bins and revisited the SFRnorm − LX relation. Our analysis suggests that in less massive systems (log [M*(M⊙)] ∼ 11) the SFR of X-ray AGN is enhanced by ∼50% compared to that of non-X-ray AGN galaxies. In the most massive galaxies a flat relation is detected. Our results, although tentative, are consistent with a scenario in which mergers trigger the AGN activity and the star formation of the host galaxy by increasing the available cold gas, while in the most massive systems (log [M*(M⊙)] > 11.5) other mechanisms that are decoupled from the star formation fuel the SMBH (e.g., diffuse hot gas).
Finally, we split the X-ray sample into X-ray obscured and unobscured AGN by applying a cut at NH = 1021.5 cm−2 and examined whether the host galaxy properties of the two populations differ. Our analysis showed that both AGN types have similar SFRs, stellar masses, and SFRnorm distributions. This suggests that X-ray absorption is not linked with the properties of the host galaxy.
Our analysis and results highlight the fact that AGN constitute a diverse population of galaxies with, for example, a wide range of SMBH fuelling mechanisms, luminosities, stellar masses, SFRs, and across large cosmological epochs. Therefore, to accurately measure the effect of one parameter on another we need first to disentangle all the other parameters from the analysis. This is extremely challenging given the number of available X-ray sources and the selection biases that affect the datasets and thus the final results. Ongoing and future X-ray surveys (eROSITA, Athena) will provide us with large samples of X-ray sources that are orders of magnitude larger than current datasets. Along with consistent methodologies and improved machinery these X-ray surveys will enable us to shed light on galaxy evolution and the interplay between SMBH and their host galaxies.
The Herschel Extragalactic Legacy Project (HELP, http://herschel.sussex.ac.uk/) is a European funded project to analyse all the cosmological fields observed with the Herschel satellite. All the HELP data products can be accessed on HeDaM (http://hedam.lam.fr/HELP/).
Acknowledgments
The authors thank the anonymous referee for their detailed report that improved the quality of the paper. GM acknowledges support by the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu, ref. MDM-2017-0765. MB acknowledges FONDECYT regular grant 1170618. The project has received funding from Excellence Initiative of Aix-Marseille University – AMIDEX, a French ‘Investissements d’Avenir’ programme. KM has been supported by the National Science Centre (UMO-2018/30/E/ST9/00082).
References
- Aird, J., Coil, A. L., Moustakas, J., et al. 2012, ApJ, 746, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Aird, J., Coil, A. L., & Georgakakis, A. 2018, MNRAS, 474, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Aird, J., Coil, A. L., & Georgakakis, A. 2019, MNRAS, 484, 4360 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., & Hickox, R. C. 2012, New Astron. Rev., 56, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Allevato, V., Finoguenov, A., Cappelluti, N., et al. 2011, ApJ, 736, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Bernhard, E., Grimmett, L. P., Mullaney, J. R., et al. 2019, MNRAS, 483, L52 [CrossRef] [Google Scholar]
- Bezanson, R., van Dokkum, P., & Franx, M. 2012, ApJ, 760, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., & Terlevich, R. J. 1998, MNRAS, 293, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, B. J., Shanks, T., Croom, S. M., et al. 2000, MNRAS, 317, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A., Nayyeri, H., Cooray, A., et al. 2019, ApJ, 871, 87 [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Ciesla, L., Boquien, M., Małek, K., & Burgarella, D. 2019, A&A, 632, A79 [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Chen, C.-T. J., Hickox, R. C., Alberts, S., et al. 2015, ApJ, 802, 50 [Google Scholar]
- Ciotti, L., & Ostriker, J. P. 1997, ApJ, 487, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Circosta, C., Vignali, C., Gilli, R., et al. 2019, A&A, 623, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [NASA ADS] [CrossRef] [Google Scholar]
- DeBuhr, J., Quataert, E., & Ma, C.-P. 2012, MNRAS, 420, 2221 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K. J., Brown, M. J. I., Williams, W. L., et al. 2018a, MNRAS, 473, 2655 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K. J., Jarvis, M. J., Brown, M. J. I., & Röttgering, H. J. A. 2018b, MNRAS, 477, 5177 [Google Scholar]
- Duncan, K. J., Sabater, J., Röttgering, H. J. A., et al. 2019, A&A, 622, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Borgne, D. L., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanidakis, N., Baugh, C. M., Benson, A. J., et al. 2012, MNRAS, 419, 2797 [NASA ADS] [CrossRef] [Google Scholar]
- Fanidakis, N., Georgakakis, A., Mountrichas, G., et al. 2013, MNRAS, 435, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Florez, J., Jogee, S., Sherman, S., et al. 2020, MNRAS, 497, 3273 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Schreiber, N. M. F., Rosario, D., et al. 2014, ApJ, 796, 7 [Google Scholar]
- Georgakakis, A., Aird, J., Schulze, A., et al. 2017, MNRAS, 471, 1976 [NASA ADS] [CrossRef] [Google Scholar]
- Grimmett, L. P., Mullaney, J. R., Bernhard, E. P., et al. 2020, MNRAS, 495, 1392 [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Mullaney, J. R., et al. 2012, ApJ, 760, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C., Mullaney, J. R., Alexander, D. M., et al. 2014, ApJ, 782, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Keres, D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, P. D., Oliver, S., Betancourt, M., et al. 2017, MNRAS, 464, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 685, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Eisenstein, D. J., Cool, R. J., et al. 2012, ApJS, 200, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzuisi, G., Delvecchio, I., Berta, S., et al. 2017, A&A, 602, 13 [Google Scholar]
- Li, J., Xue, Y., Sun, M., et al. 2019, ApJ, 877, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Loh, J. M. 2008, ApJ, 681, 726 [CrossRef] [Google Scholar]
- Lutz, D., Mainieri, V., Rafferty, D., et al. 2010, ApJ, 712, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [Google Scholar]
- Maiolino, R., & Rieke, G. H. 1995, ApJ, 454, 95 [Google Scholar]
- Malizia, A., Bassani, L., Stephen, J. B., Bazzano, A., & Ubertini, P. 2020, A&A, 639, A5 [CrossRef] [EDP Sciences] [Google Scholar]
- Masini, A., Hickox, R. C., Carroll, C. M., et al. 2020, ApJS, 251, 2 [Google Scholar]
- Masoura, V. A., Mountrichas, G., Georgantopoulos, I., et al. 2018, A&A, 618, 31 [Google Scholar]
- Masoura, V. A., Georgantopoulos, I., Mountrichas, G., et al. 2020, A&A, 638, A45 [CrossRef] [EDP Sciences] [Google Scholar]
- Masoura, V. A., Mountrichas, G., Georgantopoulos, I., & Plionis, M. 2021, A&A, 646, A167 [EDP Sciences] [Google Scholar]
- Mendez, A. J., Coil, A. L., Aird, J., et al. 2016, ApJ, 821, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Bongiorno, A., Brusa, M., et al. 2014, MNRAS, 437, 3550 [NASA ADS] [CrossRef] [Google Scholar]
- Mountrichas, G., Georgakakis, A., Finoguenov, A., et al. 2013, MNRAS, 430, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Mountrichas, G., Georgakakis, A., Menzel, M. L., et al. 2016, MNRAS, 457, 4195 [NASA ADS] [CrossRef] [Google Scholar]
- Mountrichas, G., Buat, V., Yang, G., et al. 2021, A&A, 646, A29 [EDP Sciences] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Aird, J., et al. 2015, MNRAS, 453, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Ogawa, S., Ueda, Y., Tanimoto, A., & Yamada, S. 2021, ApJ, 906, 84 [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, M. J., Symeonidis, M., Vieira, J. D., et al. 2012, Nature, 485, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009, ApJ, 698, L116 [Google Scholar]
- Park, T., Kashyap, V. L., Siemiginowska, A., et al. 2006, ApJ, 652, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, 23 [Google Scholar]
- Prevot, M., Lequeux, J., Maurice, E., Prevot, L., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [Google Scholar]
- Risaliti, G., & Lusso, E. 2017, Astron. Nachr., 338, 329 [CrossRef] [Google Scholar]
- Rosario, D. J., Santini, P., Lutz, D., et al. 2012, A&A, 545, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosario, D. J., Trakhtenbrot, B., Lutz, D., et al. 2013, A&A, 560, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Rosario, D. J., Shao, L., et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, 29 [Google Scholar]
- Shimizu, T. T., Mushotzky, R. F., Meléndez, M., Koss, M., & Rosario, D. J. 2015, MNRAS, 452, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, R., Roehlly, Y., Hurley, P. D., et al. 2019, MNRAS, 490, 634 [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Fritz, J., Baes, M., Nakos, T., & Popović, L. Č. 2012, MNRAS, 420, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Ricci, C., Ueda, Y., et al. 2016, MNRAS, 458, 2288 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Yang, G., Brandt, W. N., Vito, F., et al. 2018, MNRAS, 475, 1887 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Boquien, M., Buat, V., et al. 2020, MNRAS, 491, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, P.-C., Middelberg, E., Norris, R. P., & Dettmar, R.-J. 2013, ApJ, 774, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Zou, F., Yang, G., Brandt, W. N., & Xue, Y. 2019, ApJ, 878, 11 [Google Scholar]
- Zubovas, K., Nayakshin, S., King, A., & Wilkinson, M. 2013, MNRAS, 433, 3079 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Models and values of their free parameters used by X-CIGALE for the SED fitting of our galaxy sample.
Mean (μ) and standard deviation (σ) of the difference in the calculations of SFR (Δlog SFR), using X-CIGALE and the expressions derived in Schreiber et al. (2015) and Whitaker et al. (2014), for MS star-forming galaxies (see also Fig. 6).
All Figures
 |
Fig. 1. X-ray hard instrinsic luminosity as a function of redshift for the 1989 X-ray AGN in our sample. There are 1020 sources with spectroscopic redshifts (red circles) and 969 with photometric redshifts (blue circles). |
| In the text | |
 |
Fig. 2. Comparison of SFR measurements with and without Herschel photometry for 935 sources that have far-IR coverage and satisfy our selection criteria (see text for details). X-ray AGN with spectroscopic redshifts (490) are shown in red, while sources with photometric redshift estimations (445) are presented in blue. The blue solid line presents the 1:1 relation. The results show an excellent agreement between the two measurements. The mean offset and the standard deviation, of the SFR difference (Herschel − no Herschel) are shown in the legend. |
| In the text | |
 |
Fig. 3. Comparison of the SFR and M* measurements (left and right panel, respectively) for the mock sources (estimated) with the true values (data), using the X-ray sample. X-CIGALE accurately recovers the true SFR and M* values of the mock sources. |
| In the text | |
 |
Fig. 4. Comparison of the SFR and M* measurements (left and right panel, respectively) for the mock sources (estimated) with the true values (data), using the reference galaxy sample. X-CIGALE accurately recovers the true SFR and M* values of the mock sources. |
| In the text | |
 |
Fig. 5. sSFR distribution in four redshift intervals. The blue lines present the full distributions. The green areas are the sSFR distributions after applying the sSFR cut, which is defined based on the location of the second lowest peak of each distribution. At the highest redshift bin (2.0 < z < 2.5), the sSFR distribution does not have a Gaussian shape, most likely due to the small number of sources (see Table 2) and the sSFR cut cannot be defined as described above. |
| In the text | |
 |
Fig. 6. Comparison of different SFR estimates. Left: difference between the SFR calculations of X-CIGALE for star-forming galaxies defined from our galaxy sample (see text for more details) and the SFR measurements using the expression of Schreiber et al. for star-forming MS galaxies. At z < 1.5 the SFR values from X-CIGALE are ∼0.25 dex lower than those using Schreiber et al., whereas at higher redshift the two estimates are consistent. Right: difference between the SFR calculations of X-CIGALE for star-forming galaxies defined from our galaxy sample (see text for more details) and the SFR measurements using the expression of Whitaker et al. (2014) for star-forming MS galaxies. At z < 1.0 the SFR values from X-CIGALE are similar (distribution peaks at zero) to those using the Whitaker et al. formula, whereas at 1 < z < 2, SFRX-CIGALE are lower by ∼0.15 dex (see also Table 3). |
| In the text | |
 |
Fig. 7. SFRnorm vs. X-ray luminosity. SFRnorm and LX are the median values of our binned measurements, in bins of LX, with 0.5 dex width. Errors are calculated using bootstrap resampling by performing 100 resamplings with replacement at each bin. Results are colour-coded based on the redshift interval. Top: SFRnorm estimated using our reference galaxy catalogue with SFR measurements from X-CIGALE. Middle: results when excluding quiescent galaxies from the reference catalogue. Bottom: measurements when excluding quiescent systems from the X-ray and the reference galaxy catalogues (see text for more details). |
| In the text | |
 |
Fig. 8. SFRnorm vs. X-ray luminosity. SFRnorm and LX are the mean values of the measurements presented in Figs. 7 and 9, grouped in LX bins of 0.5 dex, at all redshfits combined, and weighted based on the number of sources in each bin shown in Fig. 7. The errors represent the standard deviation of SFRnorm and LX in each bin. |
| In the text | |
 |
Fig. 9. SFRnorm vs. X-ray luminosity. SFRnorm values are estimated using the expression of Schreiber et al. (2015) to measure the SFRs of star-forming MS galaxies. SFRnorm and LX are the median values of our binned measurements, in bins of LX, with 0.5 dex width. The errors are calculated using bootstrap resampling by performing 100 resamplings with replacement at each bin. The results are colour-coded based on the redshift interval. |
| In the text | |
 |
Fig. 10. SFRnorm vs. specific black hole accretion rate (λs, BHAR). The SFRnorm has been estimated after excluding quiescent systems from both the X-ray and the reference galaxy catalogues (see text for more details). The results are colour-coded based on the redshift interval. The measurements are grouped in λs, BHAR bins, with 0.5 dex width. Median values are presented and the errors are calculated using bootstrap resampling. The average SFRnorm values (black squares) are weighted based on the number of sources in each bin (coloured circles), across all redshift intervals. The errors on the average values correspond to the standard deviation within each λs, BHAR bin. The solid line presents the best fit of the average values: SFR |
| In the text | |
 |
Fig. 11. SFRnorm vs. X-ray luminosity. The SFRnorm was estimated after excluding quiescent systems from both the X-ray and the reference galaxy catalogues (see text for more details). The results are grouped in LX bins of 0.5 dex width and stellar mass bins. The results are colour-coded based on the redshift range (black for 0.5 < z < 1.0, blue for 1.0 < z < 1.5, and green for 1.5 < z < 2.0). Different symbols refer to different stellar mass intervals, as indicated in the legend. M* values are in log [M*(M⊙)]. Median SFRnorm values are presented and the errors are calculated using bootstrap resampling. The number of sources included in each bin are shown next to each symbol. |
| In the text | |
 |
Fig. 12. Redshift (left panel) and X-ray luminosity (right panel) distributions of X-ray absorbed (red histograms) and unabsorbed (blue histograms) AGN. Both histograms have been normalised to the total number of sources. |
| In the text | |
 |
Fig. 13. Distributions of host galaxy properties of X-ray absorbed (red shaded histograms) and unabsorbed (blue line histograms) AGN. From top to bottom: stellar mass, SFR, and SFRnorm distributions. The two populations have similar host galaxy properties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.