EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 652 (August 2021) A&A, 652 (2021) L4 Full HTML
Free Access
Issue
A&A
Volume 652, August 2021
Article Number L4
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202141456
Published online 04 August 2021

© ESO 2021

1. Introduction

The solar chromosphere serves as an important conduit for mass and energy between the dense, 6000 K photosphere and the tenuous, million degree corona. The solar chromosphere has a complex magnetic structure, where the plasma beta changes dramatically (Gary 2001). Determining the processes that maintain the thermal structure of the solar atmosphere is one of the fundamental problems in solar physics (Narain & Ulmschneider 1996).

The energy transfer in the chromosphere can be attributed to a number of mechanisms, such as Alfen waves (Osterbrock 1961; Stein 1981; van Ballegooijen et al. 2011; Shelyag et al. 2016; Grant et al. 2018; Sakaue & Shibata 2020), spicules (Beckers 1968; Pneuman & Kopp 1978; Athay & Holzer 1982; De Pontieu et al. 2009; Beck et al. 2016), nanoflares (Priest et al. 2018; Syntelis & Priest 2020), and magneto-acoustic shocks (De Pontieu et al. 2015). Some authors have suggested that the heating of the chromosphere is due to the dissipation of acoustic waves (Ulmschneider et al. 1978; Kalkofen 2007), although this has been questioned by Athay & Holzer (1982) and Beck et al. (2009, 2012).

Another candidate for heating the solar chromosphere is resistive Ohmic dissipation (Parker 1983; Tritschler et al. 2008). The occurrence of dynamic phenomena in the chromosphere and transition region has been attributed to plasma heating by the formation of current sheets when a discontinuity in the three-dimensional (3D) magnetic field arises (Solanki et al. 2003; Bahauddin et al. 2021). Such currents are often seen in sunspot light bridges (LBs) and δ spots (Jurčák et al. 2006; Shimizu et al. 2009; Balthasar et al. 2014; Toriumi et al. 2015a; Robustini et al. 2018). However, estimates of the current density are typically confined to the solar photosphere and only provide the vertical component of the current Jz, while Socas-Navarro (2005) found only a weak correlation between currents and chromospheric heating. In this article, we combine non-force-free field (NFFF) extrapolations with thermal inversions to study intense electric currents and strong chromospheric temperature enhancements over a sunspot, which occur as a result of large-scale magnetic flux emergence in an LB.

2. Observations

We analyzed observations of the leading sunspot in NOAA AR 12002 (Fig. 1a) on 2014 March 13 from 20:44 to 21:00 UT, combining data from the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) and the Interferometric BI-dimensional Spectrometer (IBIS; Cavallini 2006) at the Dunn Solar Telescope (DST). The SDO data comprise two Spaceweather HMI Active Region Patch (SHARP) maps of the vector magnetic field at 20:48 UT and 21:00 UT. IBIS acquired spectral scans in the Ca II IR line at 854 nm with a spatial sampling of 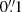0 . ″ 1 $ 0{{\overset{\prime\prime}{.}}}1 $ px−1 across a 90″ circular field of view (FOV). Only the two scans at 20:44 UT and 20:55 UT were used here. The DST setup and data are described in detail in Louis et al. (2020), hereafter LBC20.

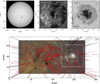thumbnail Fig. 1.

HMI and IBIS observations of the leading sunspot in NOAA AR 12002. Top: full-disk HMI continuum image (left) at 21:00 UT on 2014 March 13, IBIS Ca II IR line-core image (middle), and speckle-reconstructed IBIS broadband image (right). The square and dashed rectangle in panel a indicate the IBIS and HMI SHARP FOV, respectively. Bottom: field lines derived from the NFFF extrapolation overlaid on a composite image of the vertical component of the magnetic field and the AIA 171 Å image for the SHARP FOV. The solid and dashed white squares correspond to the IBIS FOV and the smaller FOV shown in Fig. 2, respectively.

3. Data analysis

To infer the magnetic connectivity, we used the NFFF extrapolation technique (Hu & Dasgupta 2008; Hu et al. 2008, 2010), where the magnetic field is described by the double-curl Beltrami equation derived from a variational principle of the minimum energy dissipation rate (Bhattacharyya et al. 2007). This method is well suited to the high plasma-β photospheric boundary (Gary 2001) and has been successfully used in many recent studies (Nayak et al. 2019; Liu et al. 2020; Yalim et al. 2020; Prasad et al. 2020). The extrapolation provides the magnetic field vector B(x, y, z), from which we derived the total (|J|), vertical (Jz), and horizontal (Jhor) current densities. The mean values of Bx, By, and Bz in the LB and their errors, as derived from the HMI SHARP maps, were 525 ± 45 G, 890 ± 50 G, and 850 ± 55 G, respectively. The uncertainty in the current density was determined by using the deviation between the extrapolated and observed horizontal magnetic field, which yielded a mean error of 1.6 × 10−2 A m−2, 1.5 × 10−2 A m−2, and 5.0 × 10−3 A m−2 in Jx, Jy, and Jz, respectively, within the LB. These values translate into relative errors of 33%, 27%, and 16%, respectively, and pertain to the HMI sampling of 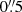0 . ″ 5 $ 0{{\overset{\prime\prime}{.}}}5 $. The frictional Joule heating profile was calculated from the dissipation of currents perpendicular to the magnetic field through the Cowling resistivity ηC (Yalim et al. 2020), where ηC is a function of the magnetic field B, plasma bulk density ρ, and temperature T as well as the ion and electron number densities ni and ne in the chromosphere. All values of physical quantities, apart from B, were taken from the tabulated data of the Maltby-M umbral core model (Maltby et al. 1986). We discarded the Coulomb resistivity because it is two to three orders of magnitude smaller than ηC (see Fig. 3 of Yalim et al. 2020) and only retained the Cowling heating: 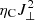η C J ⊥ 2 $ \eta_{\rm C}J^2_{\bot} $, where J⊥ is the component of the current perpendicular to the magnetic field. The relative error in the Joule heating was about 34%, corresponding to about 0.06 W m−3 in the LB.

The IBIS spectra were inverted with both the local thermodynamic equilibrium (LTE) and non-LTE (NLTE) version of the CAlcium Inversion based on a Spectral ARchive (CAISAR; Beck et al. 2015, 2019) code. Individual spectra are inverted on a pixel-by-pixel basis. The model atmospheres in the archives are in hydrostatic equilibrium. The resulting temperature stratifications were converted from optical depth to geometrical height based on the Harvard Smithsonian reference atmosphere (Gingerich et al. 1971) without considering lateral pressure equilibrium. The temperature maps were then spatially de-projected to the local reference frame to match the HMI SHARP magnetic field in x and y. The LTE and NLTE temperature excess, estimated with respect to the mean umbral temperature, were subsequently converted to the increase in internal energy as in Eq. (1) of Beck et al. (2013), see also Rezaei & Beck (2015), their Sect. 4.7. For a partially ionized gas, this value serves as the lower limit since the product of the ionization fraction and the ionization potential per unit mass is an additional term in the internal energy. The error in temperature is 20−100 K for −5 < log τ < −2, with nearly identical temperatures in LTE and NLTE for log τ > −2 (LBC20, Sect. 3.3).

4. Results

4.1. Global topology of NOAA AR 12002

Figure 1b shows the sunspot in the chromospheric Ca II spectral line, with a strong brightness enhancement all along the LB. The LB formed as a result of large-scale magnetic flux emergence in the sunspot over a duration of 13 h, which was seen as strong blueshifts of about 1 km s−1 all along the body of the LB (LBC20). The LB comprised weak and highly inclined magnetic fields, with a mean field strength and inclination of about 1.5 kG and 55°, respectively, while in the southern part of the structure the values are about 1.2 kG and 85°, respectively. The LB has a pronounced curvature that connects the southern and northwestern penumbral sections (panel c). Figure 1d shows the coronal magnetic field from the NFFF extrapolation overlaid on a composite of the Atmospheric Imaging Assembly (AIA, Lemen et al. 2012) 171 Å image and Bz. Prominent loops connect the sunspot to the opposite polarity to the east, while the field lines in the western part of the sunspot are mostly open. No loops were found to follow the LB structure, but a few field lines directly neighboring the LB showed a small dent away from the LB for z < 1 Mm.

4.2. Electric current density and temperature

Figure 2 shows that both the current density and temperature are larger over the LB than anywhere else in the sunspot at 21:00 UT. At the bottom boundary the total current |J| reaches a maximum value of 0.3 A m−2 with a mean value of 0.11 A m−2. The total current is dominated by Jhor, which is three times stronger than Jz. At z = 0.36 Mm, the maximum values of Jz and Jhor reduce to 0.05 A m−2 and 0.13 A m−2, respectively. At the same height, the entire length of the LB is hotter than the surroundings, with LTE and NLTE temperatures of 4700 K and 4900 K, respectively. At the southern end of the LB, the temperature reaches 5270 K and 6775 K in LTE and NLTE, respectively. The LB is nearly 600−800 K hotter than the neighboring umbra. Panels 3 and 4 of Fig. 2 show that the components of the currents parallel (J||) and perpendicular (J⊥) to the magnetic field are about 0.04 A m−2 in the LB at a height of 0.36 Mm and reduce by about 60% at 0.72 Mm. The ηC increases by a factor of five from 0.36 Mm to 0.72 Mm, although it is weaker in the LB relative to the umbra, by a factor of about 1.7, owing to its B2 dependence on the magnetic field strength. The Joule heating due to ηC is about 1 W m−3 at 0.72 Mm.

thumbnail Fig. 2.

Electric currents, temperature enhancements, and Joule heating in the sunspot LB. Panels 1a–1d: spatial distribution of the vertical current density Jz and horizontal current density Jhor at z = 0.36 Mm (top) and z = 0.72 Mm (bottom). The horizontal lines in panel 1b indicate the locations of the 2D cuts shown in Fig. 4. The white horizontal line marks cut No. 5 used in Figs. 4g and h. Panels 2a–2b: spatial distribution of the vertical (top) and horizontal (bottom) component of the magnetic field at z = 0.36 Mm. Panels 2c–2d: spatial distribution of the NLTE temperature at z = 0.36 Mm (top) and z = 0.72 Mm (bottom). The white rectangle in panel 2c is a smaller FOV centered on the LB shown in Fig. 3. Panels 3a–3d and 4a–4d: spatial distribution of J||, J⊥, Cowling resistivity ηC, and its associated Joule heating. The color bar in panels 4 comprises two scales, where the top and bottom numbers correspond to 0.36 Mm and 0.72 Mm, respectively.

Figure 3 shows that the temperature enhancement along the spine of the LB is flanked by intense currents that have opposite signs in Jz. The Jhor, depicted with arrows, is parallel to the LB spine, with opposite directions on either side. Nearly identical properties were found for the second data set at 20:48 UT.

thumbnail Fig. 3.

Distribution of electric currents around the temperature enhancements in the LB. Left: horizontal current vectors overlaid on the NLTE temperature map at 0.36 Mm for the FOV depicted with the white rectangle in Fig. 2 (panel 1a). Arrows have been drawn for every pixel where |Jz| is greater than 0.01 A m−2. Right: horizontal current vectors overlaid on Jz at 0 Mm.

Panels a–e of Fig. 4 show 2D x − z plots of different physical parameters along the cuts across the LB indicated in panel 2b of Fig. 2. The bottom and top panels (i.e., 1a and 13a) correspond to the cut at the southern and northern end, respectively. Both current and temperature enhancements follow the location of the spine of the LB along its extent. As already seen in Figs. 2 and 3, the LB is hottest at its southern end (panels 1–4), with temperature decreasing towards its northern end. The temperature enhancement is seen in both LTE and NLTE, although in NLTE the enhancement is much hotter and narrower, confined to a height between 0.2 and 0.6 Mm (panels 1d–5d and 1e–5e in Fig. 4). The Joule heating (panel c) also exhibits the same spatial variation along the spine of the LB. However, the heating is confined to a narrow height range at about 0.7 Mm (panels 3c–9c) because of the vertical stratification of ηC.

thumbnail Fig. 4.

Vertical variation in physical parameters at different positions on the spine of the LB. Columns a–e: 2D slices of the currents Jz and Jhor, Joule heating by Cowling resistivity, LTE temperature T, and NLTE temperature T (left to right) for the horizontal cuts across the LB (panel 2b in Fig. 2). Panel f: vertical distribution of parameters at the center of the LB at the white horizontal cut shown in Fig. 2b. The heating term has been scaled down by a factor of five. Panel g: horizontal variation in parameters along the same cut after temperature, current, and heating were averaged in height. The heating term has been reduced by a factor of two. Panel h: same as above but for J⊥, ηC, and the Joule heating. J⊥ has been scaled up by a factor of three.

The height extent of the different quantities is better seen in Fig. 4f, which shows the stratification of T, |J|, and heating for cut No. 5. The NLTE temperature has a sharp peak of up to 2000 K of 0.4 Mm width at a height of 0.42 Mm, while the LTE temperature shows a broader, lower enhancement of 800 K over a larger height range. The current drops monotonically with height, while the heating shows a sharp peak, similar to the NLTE temperature but at a slightly higher altitude of 0.72 Mm.

Figure 4g, with height-averaged T, |J|, and heating values for the same cut, confirms once more that the largest currents flank the LB spine, while the temperature enhancements are co-spatial with the Joule heating at the center of the LB. The temperature, current, and heating were averaged in height between 0.18−0.6 Mm, 0−0.36 Mm, and 0−0.72 Mm, respectively. Figure 4h shows the heating to be highest at the LB as J⊥ has a maximum value due to the large field inclination in the LB even if ηC decreases slightly. The 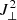J ⊥ 2 $ J_{\bot}^2 $ dependence of the Joule heating renders it a factor of six higher in the LB than the adjacent umbra. Similar currents and heating were already present at 20:36 UT, about 10 min prior to the DST observations.

4.3. Ohmic dissipation in the LB

While Figs. 2 and 3 demonstrate the spatial association of the currents and Joule heating with temperature, Fig. 5 shows the scatter plots of currents, heating, and temperature. The scatter plots were constructed by taking a 13-pixel-wide horizontal cut, centered on the location of maximum temperature on the LB spine, and then averaging temperature, the total current, and the Joule heating over height as described in the previous section. To cover the spatial extent of the LB, we moved the location of these cuts in steps of one pixel from south to north. The left panel of Fig. 5 reveals that the total current |J| is strongly positively correlated with the temperature, exhibiting a Spearman coefficient of 0.75 and 0.73 for the LTE and NLTE case, respectively. The scatter plots between the increase in internal energy over the neighboring umbra and the Joule heating (right panel of Fig. 5) also exhibit a high correlation, with values of 0.75 and 0.7 for the LTE and NLTE case, respectively.

thumbnail Fig. 5.

Correlation between currents and temperature enhancements as well as Joule heating and increase in internal energy in the LB. Left: scatter plots of |J| and temperature. The pluses and open circles correspond to the LTE and NLTE case, respectively. The red and black colors correspond to the data set at 20:48 UT and 21:00 UT, respectively. The solid black line and the grey line are a linear fit to the scatter in the NLTE and LTE case, respectively. The Spearman correlation coefficient for the NLTE case is shown in the lower right corner, while the LTE value is enclosed in parentheses. The dotted and dashed lines correspond to the average umbral and quiet Sun temperature, respectively. Right: scatter plots of Joule heating and internal energy. The mean error associated with the different parameters in the LB is shown in the top right corner of each panel.

The ratio of the increase in internal energy and the Joule heating provides the timescale over which the currents must dissipate in order to produce the observed temperature enhancements. The dissipative timescale is about 10 min, with both the LTE and NLTE cases having a nearly identical slope in the linear fit. This is consistent with the lifetime of the currents that are permanently present from 20:36 UT to 21:00 UT. The excess emission in the Ca II IR line core in the LB relative to the quiet Sun amounted to only about 6 × 10−3 W m−3 at a characteristic heating rate of 0.2 W m−3. Radiative losses should thus have no strong impact on the timescale.

5. Discussion

We find that the LB is hotter than the rest of the sunspot, both spatially and vertically. The temperature enhancement is driven by intense electric currents, with the horizontal component dominating the vertical current. The maximum value of Jz at z = 0 Mm is about 0.1 A m−2, which is consistent with Toriumi et al. (2015a). These values are about a factor of two smaller than those reported by Jurčák et al. (2006), Balthasar (2006), and Shimizu et al. (2009), which could be due to the HMI spatial resolution in our case being insufficient to resolve current sheets. The true currents are expected to be larger than the values derived. The |J| had maximum and mean values of 0.2 and 0.14 A m−2, respectively, in the penumbra in Puschmann et al. (2010). The large values of 0.3 A m−2 estimated in the LB arise from the emergence of a relatively weak, nearly horizontal magnetic structure in the sunspot over a duration of at least 13 h (LBC20). As a consequence of the sustained emergence of horizontal magnetic fields, one would expect the corresponding temperature enhancements to likely be present over a similar timescale. The value of the current density in the rest of the sunspot is consistent with the results of Socas-Navarro (2005) and Puschmann et al. (2010). Flux emergence thus seems to be a good indicator for locations, with a strong correlation between currents and temperature enhancements. While the strong correlation between currents and increased temperature is seen for most of the LB spine, the strongest temperature enhancements at the southern end of the LB are associated with weaker currents (Figs. 2 and 3). This suggests that the heating mechanism in the LB could be more intricate than just a strongly localized current dissipation with an instant temperature rise. The complex structure of the LB and its emerging magnetic flux (which is not fully resolved in the HMI data), the magnetic field extrapolation, directed mass flows, heat conduction, and possible time lags between heating and temperature could lead to spatio-temporal displacements between currents and enhanced temperatures.

The LTE and NLTE temperature maps reveal that the thermal enhancements are confined to a comparably narrow slab in the vertical direction, especially in the NLTE inversion. The height resolution of the spectra is limited to a few hundred kilometers by the thermal broadening (Beck et al. 2012, 2013), which smears out current sheets with heights of only a few kilometers. Toriumi et al. (2015b) reported a shift in the log τ = 1 layer by a few hundred kilometers in height between an LB and the umbra. This is still within a single pixel in height in the extrapolation results that employ the HMI sampling of about 360 km in the vertical axis as well. Our approach of averaging over height reduces the impact of all effects related to the specific geometrical heights attributed to the different quantities.

The currents are strongest at the bottom boundary and decrease monotonically with height. However, the Joule heating term, which is dominated by the Cowling resistivity, tends to have strong peaks at two heights, 0.72 Mm and 1.8 Mm (Yalim et al. 2020), and only the lower one is inside the Ca II IR formation height. The height of the temperature enhancements is close to the lower peak, where Joule heating is prevalent (Fig. 4), well within the uncertainties associated with the geometrical height scale provided by the spectral inversions or the tabulated Maltby umbral model. We note that in the cool Maltby model the simplified calculation with a hydrogen-only atmosphere and an approximate estimate of the ionization degree in the derivation of ηC (Yalim et al. 2020) can cause additional errors in the strength and location in height of the Joule heating.

We find a strong, overall spatial association and a high correlation between Ohmic dissipation and the increase in internal energy, which would also be important in the context of how small-scale flux emergence (Louis et al. 2015) or magnetic inhomogeneities in sunspots (Louis et al. 2009; Louis 2015) heat the chromosphere. Along with the estimated dissipative timescale that matches the duration of the increased temperatures, the above results are direct evidence of chromospheric heating by Ohmic dissipation, which, to the best of our knowledge, has not been demonstrated in previous investigations. This process could thus be a valid heating source not only in the solar chromosphere but also in lab plasmas and other magnetically active stars wherever appropriate magnetic field strengths and densities exist.

6. Conclusions

The large chromospheric temperature enhancement in the sunspot at the location of the LB arises from strong electric currents that are caused by the magnetic configuration of the LB, where relatively weak and highly inclined magnetic fields emerge over a duration of about 13 h. The temperature excess due to the dissipation of the currents is located in the lower chromosphere between 0.4 and 0.7 Mm and is possibly sustained over the whole passage of flux emergence. The characteristic timescale for the heating is about 10 min. Our study provides direct evidence of lower chromospheric heating by the Ohmic dissipation of electric currents in a sunspot.

Acknowledgments

The Dunn Solar Telescope at Sacramento Peak/NM was operated by the National Solar Observatory (NSO). NSO is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under cooperative agreement with the National Science Foundation (NSF). HMI data are courtesy of NASA/SDO and the HMI science team. They are provided by the Joint Science Operations Center – Science Data Processing at Stanford University. IBIS has been designed and constructed by the INAF/Osservatorio Astrofisico di Arcetri with contributions from the Università di Firenze, the Universitàdi Roma Tor Vergata, and upgraded with further contributions from NSO and Queens University Belfast. This work was supported through NSF grant AGS-1413686. M.S.Y. and A.P. acknowledge partial support from NSF award AGS-2020703. M.S.Y. also acknowledges partial support from NASA LWS grant 80NSSC19K0075 and the NSF EPSCoR RII-Track-1 Cooperative Agreement OIA-1655280. We would like to thank the referee for reviewing our article and for providing insightful comments.

References

  1. Athay, R. G., & Holzer, T. E. 1982, ApJ, 255, 743 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bahauddin, S. M., Bradshaw, S. J., & Winebarger, A. R. 2021, Nat. Astron., 5, 237 [CrossRef] [Google Scholar]
  3. Balthasar, H. 2006, A&A, 449, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Balthasar, H., Beck, C., Louis, R. E., Verma, M., & Denker, C. 2014, A&A, 562, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Beck, C., Rezaei, R., & Puschmann, K. G. 2012, A&A, 544, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Beck, C., Rezaei, R., & Puschmann, K. G. 2013, A&A, 553, A73 [NASA ADS] [EDP Sciences] [Google Scholar]
  8. Beck, C., Choudhary, D. P., Rezaei, R., & Louis, R. E. 2015, ApJ, 798, 100 [NASA ADS] [CrossRef] [Google Scholar]
  9. Beck, C., Rezaei, R., Puschmann, K. G., & Fabbian, D. 2016, Sol. Phys., 291, 2281 [CrossRef] [Google Scholar]
  10. Beck, C., Gosain, S., & Kiessner, C. 2019, ApJ, 878, 60 [NASA ADS] [CrossRef] [Google Scholar]
  11. Beckers, J. M. 1968, Sol. Phys., 3, 367 [NASA ADS] [Google Scholar]
  12. Bhattacharyya, R., Janaki, M. S., Dasgupta, B., & Zank, G. P. 2007, Sol. Phys., 240, 63 [CrossRef] [Google Scholar]
  13. Cavallini, F. 2006, Sol. Phys., 236, 415 [NASA ADS] [CrossRef] [Google Scholar]
  14. De Pontieu, B., McIntosh, S. W., Hansteen, V. H., & Schrijver, C. J. 2009, ApJ, 701, L1 [NASA ADS] [CrossRef] [Google Scholar]
  15. De Pontieu, B., McIntosh, S., Martinez-Sykora, J., Peter, H., & Pereira, T. M. D. 2015, ApJ, 799, L12 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [Google Scholar]
  18. Grant, S. D. T., Jess, D. B., Zaqarashvili, T. V., et al. 2018, Nat. Phys., 14, 480 [CrossRef] [Google Scholar]
  19. Hu, Q., & Dasgupta, B. 2008, Sol. Phys., 247, 87 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hu, Q., Dasgupta, B., Choudhary, D. P., & Büchner, J. 2008, ApJ, 679, 848 [Google Scholar]
  21. Hu, Q., Dasgupta, B., Derosa, M. L., Büchner, J., & Gary, G. A. 2010, J. Atmos. Solar-Terr. Phys., 72, 219 [Google Scholar]
  22. Jurčák, J., Martínez Pillet, V., & Sobotka, M. 2006, A&A, 453, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kalkofen, W. 2007, ApJ, 671, 2154 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  25. Liu, C., Prasad, A., Lee, J., & Wang, H. 2020, ApJ, 899, 34 [CrossRef] [Google Scholar]
  26. Louis, R. E. 2015, Adv. Space Res., 56, 2305 [NASA ADS] [CrossRef] [Google Scholar]
  27. Louis, R. E., Bellot Rubio, L. R., Mathew, S. K., & Venkatakrishnan, P. 2009, ApJ, 704, L29 [NASA ADS] [CrossRef] [Google Scholar]
  28. Louis, R. E., Bellot Rubio, L. R., de la Cruz Rodríguez, J., Socas-Navarro, H., & Ortiz, A. 2015, A&A, 584, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Louis, R. E., Beck, C., & Choudhary, D. P. 2020, ApJ, 905, 153 [CrossRef] [Google Scholar]
  30. Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
  31. Narain, U., & Ulmschneider, P. 1996, Space Sci. Rev., 75, 453 [NASA ADS] [CrossRef] [Google Scholar]
  32. Nayak, S. S., Bhattacharyya, R., Prasad, A., et al. 2019, ApJ, 875, 10 [Google Scholar]
  33. Osterbrock, D. E. 1961, ApJ, 134, 347 [NASA ADS] [CrossRef] [Google Scholar]
  34. Parker, E. N. 1983, ApJ, 264, 635 [NASA ADS] [CrossRef] [Google Scholar]
  35. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  36. Pneuman, G. W., & Kopp, R. A. 1978, Sol. Phys., 57, 49 [NASA ADS] [CrossRef] [Google Scholar]
  37. Prasad, A., Dissauer, K., Hu, Q., et al. 2020, ApJ, 903, 129 [Google Scholar]
  38. Priest, E. R., Chitta, L. P., & Syntelis, P. 2018, ApJ, 862, L24 [Google Scholar]
  39. Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010, ApJ, 721, L58 [NASA ADS] [CrossRef] [Google Scholar]
  40. Rezaei, R., & Beck, C. 2015, A&A, 582, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Robustini, C., Leenaarts, J., & de la Cruz Rodríguez, J. 2018, A&A, 609, A14 [CrossRef] [EDP Sciences] [Google Scholar]
  42. Sakaue, T., & Shibata, K. 2020, ApJ, 900, 120 [Google Scholar]
  43. Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
  44. Shelyag, S., Khomenko, E., de Vicente, A., & Przybylski, D. 2016, ApJ, 819, L11 [NASA ADS] [CrossRef] [Google Scholar]
  45. Shimizu, T., Katsukawa, Y., Kubo, M., et al. 2009, ApJ, 696, L66 [NASA ADS] [CrossRef] [Google Scholar]
  46. Socas-Navarro, H. 2005, ApJ, 633, L57 [NASA ADS] [CrossRef] [Google Scholar]
  47. Solanki, S. K., Lagg, A., Woch, J., Krupp, N., & Collados, M. 2003, Nature, 425, 692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Stein, R. F. 1981, ApJ, 246, 966 [Google Scholar]
  49. Syntelis, P., & Priest, E. R. 2020, ApJ, 891, 52 [NASA ADS] [CrossRef] [Google Scholar]
  50. Toriumi, S., Katsukawa, Y., & Cheung, M. C. M. 2015a, ApJ, 811, 137 [NASA ADS] [CrossRef] [Google Scholar]
  51. Toriumi, S., Cheung, M. C. M., & Katsukawa, Y. 2015b, ApJ, 811, 138 [NASA ADS] [CrossRef] [Google Scholar]
  52. Tritschler, A., Uitenbroek, H., & Reardon, K. 2008, ApJ, 686, L45 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ulmschneider, R., Schmitz, F., Kalkofen, W., & Bohn, H. U. 1978, A&A, 70, 487 [Google Scholar]
  54. van Ballegooijen, A. A., Asgari-Targhi, M., Cranmer, S. R., & DeLuca, E. E. 2011, ApJ, 736, 3 [Google Scholar]
  55. Yalim, M. S., Prasad, A., Pogorelov, N. V., Zank, G. P., & Hu, Q. 2020, ApJ, 899, L4 [Google Scholar]

All Figures

thumbnail Fig. 1.

HMI and IBIS observations of the leading sunspot in NOAA AR 12002. Top: full-disk HMI continuum image (left) at 21:00 UT on 2014 March 13, IBIS Ca II IR line-core image (middle), and speckle-reconstructed IBIS broadband image (right). The square and dashed rectangle in panel a indicate the IBIS and HMI SHARP FOV, respectively. Bottom: field lines derived from the NFFF extrapolation overlaid on a composite image of the vertical component of the magnetic field and the AIA 171 Å image for the SHARP FOV. The solid and dashed white squares correspond to the IBIS FOV and the smaller FOV shown in Fig. 2, respectively.
In the text
thumbnail Fig. 2.

Electric currents, temperature enhancements, and Joule heating in the sunspot LB. Panels 1a–1d: spatial distribution of the vertical current density Jz and horizontal current density Jhor at z = 0.36 Mm (top) and z = 0.72 Mm (bottom). The horizontal lines in panel 1b indicate the locations of the 2D cuts shown in Fig. 4. The white horizontal line marks cut No. 5 used in Figs. 4g and h. Panels 2a–2b: spatial distribution of the vertical (top) and horizontal (bottom) component of the magnetic field at z = 0.36 Mm. Panels 2c–2d: spatial distribution of the NLTE temperature at z = 0.36 Mm (top) and z = 0.72 Mm (bottom). The white rectangle in panel 2c is a smaller FOV centered on the LB shown in Fig. 3. Panels 3a–3d and 4a–4d: spatial distribution of J||, J⊥, Cowling resistivity ηC, and its associated Joule heating. The color bar in panels 4 comprises two scales, where the top and bottom numbers correspond to 0.36 Mm and 0.72 Mm, respectively.
In the text
thumbnail Fig. 3.

Distribution of electric currents around the temperature enhancements in the LB. Left: horizontal current vectors overlaid on the NLTE temperature map at 0.36 Mm for the FOV depicted with the white rectangle in Fig. 2 (panel 1a). Arrows have been drawn for every pixel where |Jz| is greater than 0.01 A m−2. Right: horizontal current vectors overlaid on Jz at 0 Mm.
In the text
thumbnail Fig. 4.

Vertical variation in physical parameters at different positions on the spine of the LB. Columns a–e: 2D slices of the currents Jz and Jhor, Joule heating by Cowling resistivity, LTE temperature T, and NLTE temperature T (left to right) for the horizontal cuts across the LB (panel 2b in Fig. 2). Panel f: vertical distribution of parameters at the center of the LB at the white horizontal cut shown in Fig. 2b. The heating term has been scaled down by a factor of five. Panel g: horizontal variation in parameters along the same cut after temperature, current, and heating were averaged in height. The heating term has been reduced by a factor of two. Panel h: same as above but for J⊥, ηC, and the Joule heating. J⊥ has been scaled up by a factor of three.
In the text
thumbnail Fig. 5.

Correlation between currents and temperature enhancements as well as Joule heating and increase in internal energy in the LB. Left: scatter plots of |J| and temperature. The pluses and open circles correspond to the LTE and NLTE case, respectively. The red and black colors correspond to the data set at 20:48 UT and 21:00 UT, respectively. The solid black line and the grey line are a linear fit to the scatter in the NLTE and LTE case, respectively. The Spearman correlation coefficient for the NLTE case is shown in the lower right corner, while the LTE value is enclosed in parentheses. The dotted and dashed lines correspond to the average umbral and quiet Sun temperature, respectively. Right: scatter plots of Joule heating and internal energy. The mean error associated with the different parameters in the LB is shown in the top right corner of each panel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.