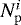| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202140699 | |
| Published online | 13 July 2021 | |
Quantifying the similarity of planetary system architectures
Porter School of the Environment and Earth Sciences, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University,
Tel Aviv,
6997801,
Israel
e-mail: dolevbas@mail.tau.ac.il, shayz@tauex.tau.ac.il
Received:
2
March
2021
Accepted:
31
May
2021
The planetary systems detected so far exhibit a wide diversity of architectures, and various methods have been proposed to quantitatively study this diversity. Straightforward ways to quantify the difference between two systems, and more generally two sets of multi-planetary systems, are helpful for studying this diversity. In this work we present a novel approach, using a weighted extension of the energy distance (WED) metric, to quantify the difference between planetary systems on the logarithmic period-radius plane. We demonstrate the use of this metric and its relation to previously introduced descriptive measures to characterise the arrangements of Kepler planetary systems. By applying exploratory machine-learning tools, we attempt to find whether there is some order that can be ascribed to the set of multi-planet Kepler system architectures. Based on the WED, the ‘Sequencer’, which is such an automatic tool, identifies a progression from small and compact planetary systems to systems with distant giant planets. It is reassuring to see that a WED-based tool does indeed identify this progression. Next, we extend the WED to define the inter-catalogue energy distance – a distance metric between sets of multi-planetary systems. We have made the specific implementation presented in the paper available to the community through a public repository. We suggest using these metrics as complementary tools in attempts to compare different architectures of planetary systems and, in general, different catalogues of planetary systems.
Key words: planets and satellites: general / planets and satellites: fundamental parameters / methods: statistical / methods: data analysis / catalogs
© ESO 2021
1 Introduction
One of the most prominent results of the Kepler mission (Borucki et al. 2010) was the detection of hundreds of multi-planet systems. Analysis of the architectures of these systems has revealed the ubiquity of close-in sub-Neptune, super-Earth, and Earth-like planets and led to important insights about the statistical relations among planets within such systems (Lissauer et al. 2011; Fabrycky et al. 2014; Weiss et al. 2018). One example is the ‘peas in a pod’ pattern, first noted by Millholland et al. (2017) and Weiss et al. (2018) and further discussed in Kipping (2018), Weiss & Petigura (2020), Mulders et al. (2020), and He et al. (2020). In systems that exhibit this pattern, planets orbiting the same host tend to be similar in size and have regular orbital spacing. At present, it is not completely clear whether this pattern is indeed of astrophysical origin or a selection effect due to observational biases (Zhu 2020; Murchikova & Tremaine 2020); nonetheless, the evidence seems to support the case that the pattern is of astrophysical origin (Weiss & Petigura 2020; Gilbert & Fabrycky 2020; He et al. 2020).
There are currently two main approaches in the literature to quantitatively analyse the architectures of planetary systems. The first approach uses various attributes of the system architecture that are easy to identify and quantify. Some authors have used information theory in order to identify such attributes. Thus, Kipping (2018) proposed a model to define the entropy of the planet size ordering within a planetary system. Using this model, he argued that the observed multi-planet Kepler systems displayed a highly significant deficit in entropy compared to a randomly generated population. Gilbert & Fabrycky (2020, hereafter GF20), in an attempt to assess system-level trends, have recently suggested using several descriptive measures in order to characterise the arrangements of planetary masses, periods, and mutual inclinations within exoplanetary systems.
In the second approach one quantifies the difference between system architectures using some distance metric. Alibert (2019) introduced such a metric, based on planet properties, and then used it to infer the similarity of the protoplanetary disks in which the planetary systems had formed. The metric introduced by Alibert involves representing the planets of the two systems as points on the logarithmic radius-period plane, spreading the points with a Gaussian kernel whose weights are determined by the planet masses, and integrating the squared difference between the two functions.
In this work we pursue the second approach and introduce a new metric to quantify the difference between planetary systems based on the ‘energy distance’. Originally, the energy distance was introduced as a statistical distance between probability distributions defined on vector spaces (Székely 2002). We propose to consider the distribution of mass among the planets in the examined parameter space (e.g. mass and period) as a discrete probability density function and introduce a weighted extension of the energy distance (WED).
Expanding upon our newly introduced method to quantify the difference between two planetary system architectures, we also propose a method to compare between sets and catalogues of planetary systems that is based on the WED. We call this extension the inter-catalogue energy distance (ICED). Such a method can be useful in the context of forward models for population synthesis of planetary systems, such as SysSim (He et al. 2019), EPOS (Mulders et al. 2018), or NGPPS (Emsenhuber et al. 2020; Schlecker et al. 2020). Quantifying the similarity of catalogues or simulated sets of planetary systems is usually done (e.g. Mulders et al. 2018; He et al. 2019, 2020; Emsenhuber et al. 2020) via the Kolmogorov-Smirnov test statistic (Kolmogorov 1933; Smirnov 1948) and the Anderson-Darling test statistic (Anderson & Darling 1952) to compare between the distributions of planet properties and with a Pearson χ2 test or Cressie-Read power divergence (CRPD; Cressie & Read 1984) to compare the distribution of planet multiplicity numbers (Mulders et al. 2018; He et al. 2019). In this work we propose using the ICED as a tool for quantifying the similarity between two catalogues of planetary systems.
In Sect. 2 we introduce the detailed computation of the WED metric and present a few examples. In Sect. 3 we calculate a WED matrix for a sample of multi-planetary Kepler systems and examine it in the context of the descriptive quantities suggested by GF20. Next, we apply machine-learning exploratory tools to the Kepler dataset with the WED metric, looking for suggestive trends in the data. In Sect. 4 we use the WED to define the ICED as a unique summary statistic that can be used to compare between catalogues of multi-planet systems. Finally, in Sect. 5 we discuss our approach and its applicability.
2 Weighted energy distance
The concept of statistical distance is a central theme in statistics. Statistical distances quantify the difference between two statistical objects, which can be random variables, sample distributions, population distributions, etc. A statistical distance may or may not obey all the metric properties, that is, positive definiteness, symmetry, and the triangle inequality. Metrics induce certain topological properties on the space on which they are defined, and thus it is usually preferred that statistical distances be proper metrics. However, the well-known Kullback-Leibler divergence (Kullback & Leibler 1951), also known as relative entropy, is acounter example of a statistical distance that is not a metric since it violates the requirement of symmetry.
In 2002 the statistician Gábor Székely introduced a novel statistical distance, which he dubbed energy distance (Székely 2002). Energy distance does obey the metric axioms, and it can be applied as a statistical distance between samples or populations defined on any metric space, for example high-dimensional Euclidean spaces. Since its introduction, the energy distance hasserved as the basis for a new class of methods to quantify various statistical concepts ranging from goodness of fit to cluster analysis (Székely & Rizzo 2017).
Let f and g be the probability density functions of the two independent random variables X and Y, defined on the d-dimensional Euclidean space (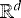 ). The squared energy distance between the distributions f and g is defined by:
). The squared energy distance between the distributions f and g is defined by:
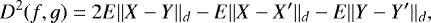 (1)
(1)
where E denotes the expected value and a primed random variable X′ denotes an independent and identically distributed (i.i.d.) copy of X; in other words, X and X′ are i.i.d. and, similarly, Y and Y′ are i.i.d. (Székely & Rizzo 2017).
This description is somewhat abstract since it relates to the population properties of the random variables X and Y. Estimating the energy distance from sample data is straightforward. Let the data consist of two sets of samples in a certain Euclidean space: 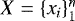 and
and 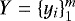 . The energy distance between the two distributions from which the two sets are drawn is estimated by:
. The energy distance between the two distributions from which the two sets are drawn is estimated by:
![\begin{equation*}\begin{split}D^2(X,Y) =\;& \frac{2}{n m} \sum_{i=1}^n \sum_{j=1}^m \Vert x_i-y_j \Vert - \frac{1}{n^2}\sum_{i=1}^n \sum_{j=1}^n \Vert x_i-x_j \Vert \\[3pt]& - \frac{1}{m^2}\sum_{i=1}^m \sum_{j=1}^m \Vert y_i-y_j {\Vert}.\end{split}\end{equation*}](/articles/aa/full_html/2021/07/aa40699-21/aa40699-21-eq5.png) (2)
(2)
The first term in this expression is actually proportional to the average of all pairwise distances between samples in X and samples in Y. Besides reflecting the distance between the two samples, this average is also undesirably inflated by the variances of the two samples, and the subtraction of the second and third terms removes this unwanted contribution. As Székely & Rizzo show, this definition amounts to a proper metric under very broad conditions.
Székely & Rizzo also show that for random one-dimensional variables the energy distance between distributions is closely related to the Cramér-von Mises-Kolmogorov distance (e.g. Darling 1957) (in astronomy another very similar distance is commonly applied: the Kolmogorov-Smirnov distance). However, Cramér-type distances (including the Kolmogorov-Smirnov distance) all rely on using the cumulative probability function, which in general Euclidean spaces becomes difficult to define and requires various arbitrary assumptions. The energy distance, on the other hand, is straightforward to calculate and is easily applicable to any kind of metric space.
Having established that the energy distance is an easily applicable distance between distributions, we can now, based on the above definition, quantify the distance between two planetary systems, X and Y, consisting of n and m planets, respectively. As most currently known multi-planetary systems have been detected by the Kepler mission and the transit method, their two most robustly observable properties are the orbital period, P, and planet radius, Rp. We therefore represented every planetary system as a set of points on the logarithmic period-radius plane, such that each point corresponds to a planet. We also assigned a weight corresponding to the planet mass, Mp, to each point using a mass-radius relation (e.g. Bashi et al. 2017). The need for a weight that represents the planetary mass, as also suggested by Alibert (2019), can be demonstrated by a hypothetical case of two systems of giant planets that are identical except for the existence of an additional very small planet in one of them. The weight function guarantees that the two systems are still considered close according to the WED.
Based on the above, we can now define the energy distance between two planetary architectures as follows:
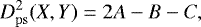 (3)
(3)
where in ourcase A, B, and C are weighted averages of pairwise distances:
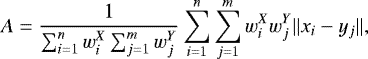 (4)
(4)
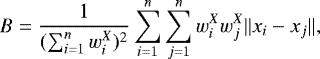 (5)
(5)
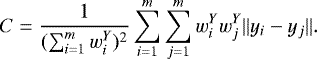 (6)
(6)
We calculated the WED (Dps) between planetary systems on the log P– logRp plane, using planetary masses (approximated by a simple mass-radius relation) as the weights wi in order to assign higher weights to more massive planets.
We show several of the tests we performed in order to demonstrate the capability of the WED to quantify the difference between planetary systems. We selected the two four-planet systems Kepler-107 (Rowe et al. 2014) and Kepler-65 (Chaplin et al. 2013)as the starting points of our tests (Fig. 1). We chose Kepler-107 as an example of a tightly packed system, with four planets of similar radii and masses (except for Kepler-107d, which is smaller). Kepler-65 represents another type of multi-planetary system: one that includes a distant giant planet, in this case Kepler-65e (Mills et al. 2019). In each test we calculated the WED between a certain planetary system and each of a set of 10000 simulated systems that differed from the original system in a certain random but controlled way. The resulting sets of WED values are shown as histograms in Fig. 2 and can be used as a sanity check to show that the values behave as expected.
In the first test we compiled the 10 000 random architectures by randomly varying the logP and logRp of all four planets using a Gaussian distribution with a standard deviation σ = 0.1. The WED values of this test are shown in the figure as the blue histogram. In the second test we followed thesame procedure but increased the standard deviation we used in the random simulation to σ = 0.3. The results of this second test are presented as the orange histogram. As expected, in both the Kepler-107 and Kepler-65 tests the WED values are typically larger and exhibit a wider spread than those in the first test.
In the third test we changed the architecture to a three-planet architecture by excluding one randomly chosen planet and randomly varying the properties of the remaining three planets in the same way as in the first test. The result is shown as the green histogram. In the Kepler-107 system, interestingly, this histogram seems to be bimodal. This is expected when we recall that one of the planets (Kepler-107d) is significantly smaller than the other three, and excluding it leaves a system that is not very different from a similar four-planet system. This explains the left peak of the histogram, which overlaps somewhat with the blue histogram. The right peak is caused by excluding one of the three more ‘influential’ planets. Similarly, in the Kepler-65 test, the clear bimodality is related to the inclusion or exclusion of the dominant giant planet Kepler-65e in the random generation of each simulated system.
In the fourth test the difference from the original system was already drastic – we changed the system to a single-planet system by randomly drawing this planet out of the four original ones and varying its properties in the same way as in the first and third tests. The set of resulting WED values is represented by the red histogram. The WED values are now typically much larger than those of the other tests, again, as expected.
 |
Fig. 1 Planet properties of the systems Kepler-107 and Kepler-65, which serve as the starting points of the tests presented in the text. The circle size represents the planet radius in logarithmic scale, while colour represents planet mass. In all cases, mass estimates were based on an empirical mass-radius relation (Bashi et al. 2017), except for the planet Kepler-65e (large yellow point), for which we used the mass estimates of Mills et al. (2019). |
3 Multi-planet Kepler systems
Now that we have formalised the WED as a method for quantifying the difference between architectures of planetary systems, we can apply the WED to the set of multi-planet Kepler systems. The sample we use here is the sample of all high-multiplicity (Np ≥ 3) Kepler systems (GF20), which is based on the California Kepler Survey (CKS) catalogue (Johnson et al. 2017; Weiss et al. 2018) and comprises N = 129 systems. We therefore started by calculating the 129 × 129 matrix of WED distances of system pairs:
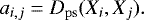 (7)
(7)
3.1 Comparison with complexity measures
As mentioned above, GF20 introduced a set of descriptive measures, which they dubbed ‘complexity measures’, to describe the details of planetary system architectures. We tested whether the information encapsulated by those measures is also contained in the WED distance matrix. We examined the six measures suggested by GF201. We did not include the GF20 flatness measure in our analysis since our current simple definition of the WED does not include the inclination. The six measures are: (i) the dynamical mass (μ), which describes the overall mass scale of the system; (ii) the mass partitioning (Q), which captures the variance in masses; (iii) the monotonicity (M), which quantifies the size ordering of the planets; (iv) the characteristic spacing (S), which is theaverage separation between planets in units of mutual Hill radii; (v) the gap complexity (C), which summarises the relationships between orbital periods of adjacent planets; and (vi) the multiplicity (Np), which is the number of observed planets in a system.
GF20 have already tested the dependence among the various complexity measures using the distance correlation dependence (dCor) metric (Székely et al. 2007; Székely & Rizzo 2017). Unlike the Pearson correlation coefficient, which tests for linear relationships between two variables, the dCor can be used to quantify non-linear associations (dependence) between variables in arbitrary metric spaces. The dCor vanishes if and only if the random variables are statistically independent, and it only assumes the value 1 for a strict linear relation (either positive or negative). The usefulness of the dCor has already been demonstrated in some recent astrophysical works (Martínez-Gómez et al. 2014; Zucker 2018; GF20).
In our case, the metric space we focus on is the space of planetary system architectures, which is endowed with the metric defined by the WED. Estimating the dCor requires first calculating a distance matrix for the two variables in question, which we have already calculated for the 129 high-multiplicity systems, ai,j. The distance matrix for each of the six complexity measures is calculated using the simple absolute difference:
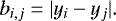 (8)
(8)
The next step in the dCor calculation is ‘double centring’ the matrices a and b:
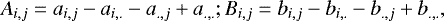 (9)
(9)
where ai,. is the ith row mean, a.,j is the jth column mean, and a.,. is the grand mean of the matrix a. Similar definitions apply for the matrix b.
We thus calculated six dCor values as measures of dependence between the metric space of architectures with the WED and each complexity measure using the expression:
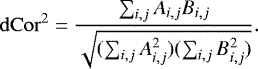 (10)
(10)
In order to assess the significance of these six dCor values, we repeatedly calculated them with 10 000 random shufflings of the corresponding complexity measures. We then counted how many of the dCor values were higher than those of the original ordering. We present in Fig. 3 the distribution of the dCor values between the sample of 129 architectures and the random shuffles of the GF20 complexity measures. The red line represents the value obtained for the original ordering.
In all cases, except for the multiplicity, we found that all 10 000 random shufflings resulted in very low dCor values as compared to the original ordering. We therefore could only estimate an upper limit on their p values of 10−4 (putting aside the monotonicity p value of 8 × 10−4). Table 1 shows the dCor values for all six complexity measures. We therefore conclude that the WED metric effectively contains the combined information encoded by the complexity measures (except for the multiplicity), and maybe even additional information.
 |
Fig. 2 Histograms of WED values for the four tests described in the main text. Each histogram represents 10 000 simulated architectures that deviate in some way from the original four-planet system of Kepler-107 (left panel) and Kepler-65 (right panel). The blue and orange histograms show the properties of all four planets drawn from a log-normal distribution around the original values, with a standard deviation of 0.1 and 0.3, respectively. The green histogram represents the same as the blue, but with only three of the four original planets, where the excluded planet is chosen randomly. The red shows the case where only one of the original planets is retained, chosen at random, with its properties again drawn from a log-normal distribution with a standard deviation of 0.1. |
3.2 Exploratory tools
Next we further explored the WED matrix of the high-multiplicity Kepler systems using exploratory machine-learning tools.
We began by applying the t-distributed stochastic neighbour embedding (t-SNE; Van der Maaten & Hinton 2008) method. The t-SNE method is a tool for visualising high-dimensional data. It converts similarities between data points to joint probabilitiesand then minimises the Kullback-Leibler divergence (Kullback & Leibler 1951) between the joint probabilitiesof the low-dimensional embedding and the high-dimensional data (in our case, however, the data are not high-dimensional but are rather in a metric space with no clearly defined dimensionality). Alibert (2019) applied a similar approach in order to relate the similarity between planetary systems with the similarity of the protoplanetary disks in which they formed. In our case we used t-SNE to search for patterns in the set of high-multiplicity Kepler systems by trying to identify possible clusters or trends with other properties using colour coding. In the left panel of Fig. 4, we present the result of performing t-SNE using the default hyper-parameters of the scikit-learn python library (Pedregosa et al. 2011) on our sample, colour-coded based on the dynamical mass (μ)2. A clear trend is evident, as expected from our dependence tests. Furthermore, the plot may suggest the emergence of a pattern of two clusters. GF20 already suggested the emergence of such two patterns in their attempt to apply robust path-based spectral clustering (R-PBSC; Chang & Yeung 2008).
Next, we employed an exploratory tool called the Sequencer, recently introduced by Baron & Ménard (2020). The Sequencer is an algorithm that searches for trends in a dataset. Baron & Ménard showed how the Sequencer can identify the stellar main sequence in a set of stellar spectra based only on the pairwise differences between the spectra and without using any stellar parameter, such as the temperature. In order to perform its task, the algorithm uses the shape of graphs, which describes the multi-scale similarities (e.g. in our case using the WED matrix) in the data. In particular, it uses the fact that continuous trends (sequences) in a dataset lead to more elongated graphs. We applied the Sequencer to the same set of 129 high-multiplicity Kepler systems, with the WED metric as a measure of dissimilarity, to see whether any order emerged. We applied the algorithm using a breadth-first search (BFS) walk (i.e. along the longest branch of the graph and scanning each branch along the way). We present the result in the right panel of Fig. 4. Each circle represents a planet, and its radius is proportionalto the planet radius. All planets in the same system share a row, which is also colour-coded based on the dynamical mass (μ). The main obvious feature in the preferred sequence seems to be a progression in terms of the dynamical mass as well as in terms of the typical period. This may also be related to the fact that the dynamical mass and the characteristic spacing are the quantities that show the strongest distance correlation in Table 1.
 |
Fig. 3 Distribution of distance correlation values (dCor) between high-multiplicity Kepler systems with WED and 10 000 random shuffles of the six GF20 measures. The vertical red line marks the dCor value of the original ordering. (a) Dynamical mass (μ); (b) mass partitioning (Q); (c) monotonicity (M); (d) characteristic spacing (S); (e) gap complexity (C); (f) multiplicity (Np). |
 |
Fig. 4 Results of using the WED in the context of machine-learning exploratory tools: t-SNE (left) and the Sequencer (right). In both cases, it seems there is a clear trend with the order of systems based on dynamical mas (μ). It is important to note that each point on the t-SNE plot represents a single planetary system, while on the Sequencer plot each row of points represents a single planetary system. |
4 Distance between catalogues
The WED, as a measure of similarity between planetary systems, can now be used as the basis for a method to compare catalogues or samples of planetary systems: the ICED.
Suppose that 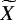 and
and 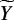 are two independent sets consisting of N and M planetary systems, respectively. In the same way that we defined the WED based on weighted Euclidean distance, we can now define
are two independent sets consisting of N and M planetary systems, respectively. In the same way that we defined the WED based on weighted Euclidean distance, we can now define 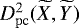 based on the WED between architectures of planetary systems in
based on the WED between architectures of planetary systems in 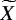 and
and 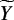 :
:
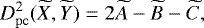 (11)
(11)
where 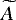 ,
, 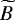 , and
, and 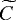 are simply the pairwise WEDs:
are simply the pairwise WEDs:
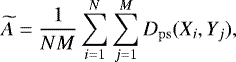 (12)
(12)
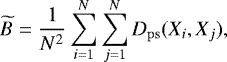 (13)
(13)
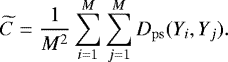 (14)
(14)
We demonstrate the ability of the ICED to quantify the difference between sets of planetary systems via a test similar to the one we used in Sect. 2 for the WED. We used the sample of 129 high-multiplicity (Np ≥ 3) Kepler systems (Sect. 3) as a reference sample. In each test we calculated the ICED between our reference sample and each one of a set of 1000 simulated catalogues, which differed from the original one in a certain random but controlled way. The results of these tests are shown as histograms in Fig. 5.
In the first test we compiled the 1000 random catalogues by randomly varying the logP and logRp of all planets in each system, using a Gaussian distribution with a standard deviation σ = 0.1. The ICED values of this test are shown in the figure as the blue histogram. In the second test we followed thesame procedure but increased the standard deviation we used in the random simulation to σ = 0.3. The results of this second test are presented as the orange histogram. As expected, the ICED values are typically larger and exhibit a wider spread than those in the first test. Both tests preserved the multiplicity of the systems included in the reference sample.
Next, we tested how the ICED values differed as we changed the system multiplicities. In the third test (green histogram) we randomly changed the multiplicity by drawing the number of planets in each system from a uniform distribution of between zero planets (effectively excluding this system as it no longer hosted planets) and the actual number of planets detected in the system. We then randomly chose the remaining planets and varied their properties in the same way as in the first test. We can clearly see that in this case, where we allowed the multiplicity to attain lower values (i.e. a higher discrepancy from the original sample), the ICED values again tended to be higher compared to the first test. However, it seems that the ICED in this case is generally lower than that obtained in the case in which we preserved the multiplicity but significantly varied (σ = 0.3) the planet properties (second test). Thus, we conclude that the WED, as a tool for quantifying the similarity of two sets of multi-planetary systems, is affected more by the properties of the planets and less by the number of planets in each system (i.e. multiplicity).
5 Discussion
We have introduced the WED as a novel metric based on energy distance to quantify the difference between architectures of planetary systems3. We have shown that the information conveyed by the WED includes the information conveyed by previous descriptive measures used to characterise the arrangements of planetary systems (GF20). Nonetheless, it is important to note that while the WED is an exploratory tool that can be applied to discover interesting and previously unknown trends between architectures of planetary systems, thecomplexity measures of GF20 are still very valuable as they provide a clear and explicit description of the system properties, which are conveniently and intuitively interpretable.
Our aim was to suggest a way to quantify dependences between the architectures and other characteristics of the planetary system without restricting the analysis to any specific feature of the architecture. In that sense the dCor with the WED is an integrative way to find such relations and is agnostic of any predisposition we might have regarding planetary system architectures. Once we detect such a relation, the next step would be to check whether any of the more intuitive quantities, such as the GF20 measures, can explain this finding or perhaps dig deeper and come up with new insights.
In this context it is important to address our finding that the multiplicity did not exhibit any significant dependence on the WED (as manifested in the dCor). At first glance this seems to be a drawback of the WED, but this may not actually be such a big surprise.As an example, the WED will be small for two systems with two similar giant planets that differ only in the number of the other small planets. This can be justified since the physical formation processes that formed these two systems were probably similar as both formed two similar dominant planets. Alternatively, two systems with an otherwise identical setof planets except that one is terrestrial and one is giant will rightfully be considered very different. The WED will reflect those trends, showing its value in quantifying the difference between architectures in a physically meaningful way. The fact that small planets in wide orbits might easily evade detection, dramatically affecting the value of the multiplicity, also casts doubts regarding the physical significance of the multiplicity measure.
We took the WED concept one step further and introduced the ICED to quantify the difference between samples of planetary systems. Wedemonstrated how the ICED can be used as a summary statistic to compare between catalogues or samples of planetary systems. An easily estimated distance function between architectures of planetary systems can complement forward modelling as a tool for comparing between observed and simulated samples of planetary systems. Previous works (He et al. 2019; Mulders et al. 2018) used some linear combinations of statistical distances between the separate distributions of the planetary parameters (Kolmogorov-Smirnov test, Anderson-Darling statistics, Cressie-Read statistics, or a simple Euclidean distance). Very similar to the WED, the ICED suggests an integrative approach that can also be useful in comparing observed catalogues with planetary population-synthesis models of planet formation and evolution (e.g. Chambers 2018; Mulders et al. 2019; Emsenhuber et al. 2020), comparing sub-populations from the model that was recently used by Schlecker et al. (2020), and comparing populations produced by varying the details of a model (Ndugu et al. 2019).
Our choice to characterise planetary systems in a two-dimensional period-radius space (weighted according to planet mass) is not an exclusive choice. Depending on the scientific question at hand and the relevant properties of the architecture or of the catalogue, more dimensions and properties can be added to the definitions of the WED and the ICED, such as the orbital eccentricity, mutual inclination, or the norm of the angular momentum (Laskar & Petit 2017). For example, if one is interested in exploring systems that host habitable planets, a change in weights based on planet effective temperatures may be better suited to quantify the similarity of such systems.
As mentioned above, Alibert (2019) also presented a metric that used the period and radius quantities. It is therefore instructive to compare the metric of Alibert and the WED. Alibert also converted the locations of the planets on the logarithmic period-radius plane to an analogous probability distribution. However, he effectively used a Gaussian kernel estimation of the probability distribution and ‘smeared’ the delta functions into Gaussians, with widths that were determined somewhat arbitrarily. Next, he calculated the distance between the two distributions by integrating them on the plane. This involved numerical integration, and, furthermore, the boundaries of integration had to be values that were considered effectively infinite. Thus, his metric was sensitive to the arbitrary choice of the Gaussian widths and the involved approximation of the integral and was somewhat computationally demanding due to the numeric integration. The WED, on the other hand, is quite simple to calculate, and it involves no arbitrary choice of parameters as its definition (Eqs. (3)–(6)) involves only the simplest algebraic operations.
The tools presented in this work are not limited to any specific detection method; they can be generalised to a population of planets detected by any method. In fact, our method is not limited to planets – it is also applicable for comparison between binary and multiple star systems.
In this work we defined the WED between planetary systems by using a simple Euclidean distance to measure the distance between planets. This can also be generalised by instead using the Mahalanobis distance (Mahalanobis 1936) in order to account for uncertainties in planet properties, assigning different weights for each property and even accounting for correlated uncertainties.
As we show in Sect. 3.1, presenting the set of possible configurations as a metric space enables the use of the distance correlation. We used this in order to show, as a kind of sanity check, the dependence between the architectures and the complexity measures introduced by GF20. This opens the way to exploring the possible dependence of the planetary system architectures on various stellar properties, such metallicity, kinematics, and age. Consequently, using dCor with the WED (while accounting for selection effects and detection biases) will allow us to explore whether the current properties of planetary systems correlate with their host properties or, otherwise, whether the planetary system dynamical evolution erased the information about the primordial conditions in the protoplanetary disks where they formed (Kipping 2018; Zhu 2020). Thus, instead of testing for such a dependence separately for each of the GF20 complexity measures, using dCor with the WED we will potentially get initial hints about complex relations, which might not be easily detectable through the individual explicit complexity measures.
 |
Fig. 5 Histograms of ICED values for the three tests described in the main text. Each histogram represents 1000 simulated catalogues that deviate in some way from the original set of 129 high-multiplicity (Np ≥ 3) Kepler systems. The blue and orange histograms show the properties of all planets drawn from alog-normal distribution around the original values, with a standard deviation of 0.1 and 0.3, respectively. The green histogram is the same as the blue histogram except that it includes the possibility of changing each system’s planet multiplicity by drawing the number of planets per system from a uniform distribution between zero planets and the actual number of planets detected around that system,
|
Acknowledgements
We thank the anonymous referee for the constructive report whose comments helped to improve this manuscript. We are grateful to Dalya Baron for helping us run the Sequencer and further commenting on an early version of the manuscript and to Gábor Sékely and Russell Lyons for very insightful discussions about the energy distance and the distance correlation. This research was supported by the Israel Science Foundation (grant No. 848/16). We also acknowledge partial support by the Ministry of Science, Technology and Space, Israel.
References
- Alibert, Y. 2019, A&A, 624, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson T. W., & Darling D. A. 1952, Ann. Math. Stat., 23, 193 [CrossRef] [Google Scholar]
- Baron, D., & Ménard, B. 2020, ArXiv e-prints [arXiv:2006.13948] [Google Scholar]
- Bashi, D., Helled, R., Zucker, S., & Mordasini, C. 2017, A&A, 604, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chambers, J. E. 2018, ApJ, 865, 30 [Google Scholar]
- Chang, H., & Yeung, D.-Y. 2008, Pattern Recogn., 41, 191 [CrossRef] [Google Scholar]
- Chaplin, W. J., Sanchis-Ojeda, R., Campante, T. L., et al. 2013, ApJ, 766, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Cressie N., & Read T. R. C. 1984, J. R. Stat. Soc. B, 46, 440 [Google Scholar]
- Darling, D. A. 1957, Ann. Math. Stati., 28, 823 [CrossRef] [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2020, A&A, submitted [arXiv:2007.05561] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [Google Scholar]
- Gilbert, G. J., & Fabrycky, D. C. 2020, AJ, 159, 281 [Google Scholar]
- He, M. Y., Ford, E. B., & Ragozzine, D. 2019, MNRAS, 490, 4575 [CrossRef] [Google Scholar]
- He, M. Y., Ford, E. B., Ragozzine, D., & Carrera, D. 2020, AJ, 160, 276 [Google Scholar]
- Johnson, J. A., Petigura, E. A., Fulton, B. J., et al. 2017, AJ, 154, 108 [Google Scholar]
- Kipping, D. 2018, MNRAS, 473, 784 [CrossRef] [Google Scholar]
- Kolmogorov A. N. 1933, G. Ist. Ital. Attuar., 4, 83 [Google Scholar]
- Kullback, S., & Leibler, R. A. 1951, Ann. Math. Stat., 22, 79 [CrossRef] [Google Scholar]
- Laskar, J., & Petit, A. C. 2017, A&A, 605, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [Google Scholar]
- Mahalanobis, P. C. 1936, Proc. Natl. Inst. Sci. India, 2, 49 [Google Scholar]
- Martínez-Gómez, E., Richards, M. T., & Richards, D. St. P. 2014, ApJ, 781, 39 [CrossRef] [Google Scholar]
- Millholland, S., Wang, S., & Laughlin, G. 2017, ApJ, 849, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, S. M., Howard, A. W., Weiss, L. M., et al. 2019, AJ, 157, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Murchikova, L, & Tremaine, S. 2020, AJ, 160, 4 [CrossRef] [Google Scholar]
- Mulders, G. D., Pascucci, I., Apai, D., & Ciesla, F. J. 2018, AJ, 156, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., Mordasini, C., Pascucci, I., et al. 2019, ApJ, 887, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., O’Brien, D. P., Ciesla, F. J., et al. 2020, ApJ, 897, 72 [CrossRef] [Google Scholar]
- Ndugu N., Bitsch B., & Jurua E., 2019, MNRAS, 488, 3625 [CrossRef] [Google Scholar]
- Pedregosa. F., Varoquaux. G., Gramfort. A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Rowe, J. F., Bryson, S. T., Marcy, G. W., et al. 2014, ApJ, 784, 45 [Google Scholar]
- Schlecker, M., Mordasini, C., Emsenhuber, A., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202038554 [Google Scholar]
- Smirnov, N. 1948, Ann. Math. Stat., 19, 279 [CrossRef] [Google Scholar]
- Székely, G. J. 2002, E-statistics: Energy of Statistical Samples, Bowling Green State University, Department of Mathematics and Statistics Technical Report No. 03–05 [Google Scholar]
- Székely, G. J., & Rizzo, M. L. 2017, Ann. Rev. Stat. Appl., 4, 447 [CrossRef] [Google Scholar]
- Székely, G. J., Rizzo, M. L., & Bakirov, N. K. 2007, Ann. Stat., 35, 2769 [CrossRef] [Google Scholar]
- Van der Maaten, L., & Hinton, G. 2008, J. Mach. Learn. Res., 9, 2579 [Google Scholar]
- Weiss, L. M., & Petigura, E. A. 2020, ApJ, 893, L1 [Google Scholar]
- Weiss, L. M., Marcy, G. W., Petigura, E. A., et al. 2018, AJ, 155, 48 [Google Scholar]
- Zhu, W. 2020, AJ, 159, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S. 2018, MNRAS, 474, L86 [CrossRef] [Google Scholar]
See Sect. 3 of GF20 for further details.
We provide a public Python package (PASSta: Planetary Architecture System Statistics) with the implementation of the tools presented in this work at: https://github.com/dolevbas/PASSta
All Tables
All Figures
 |
Fig. 1 Planet properties of the systems Kepler-107 and Kepler-65, which serve as the starting points of the tests presented in the text. The circle size represents the planet radius in logarithmic scale, while colour represents planet mass. In all cases, mass estimates were based on an empirical mass-radius relation (Bashi et al. 2017), except for the planet Kepler-65e (large yellow point), for which we used the mass estimates of Mills et al. (2019). |
| In the text | |
 |
Fig. 2 Histograms of WED values for the four tests described in the main text. Each histogram represents 10 000 simulated architectures that deviate in some way from the original four-planet system of Kepler-107 (left panel) and Kepler-65 (right panel). The blue and orange histograms show the properties of all four planets drawn from a log-normal distribution around the original values, with a standard deviation of 0.1 and 0.3, respectively. The green histogram represents the same as the blue, but with only three of the four original planets, where the excluded planet is chosen randomly. The red shows the case where only one of the original planets is retained, chosen at random, with its properties again drawn from a log-normal distribution with a standard deviation of 0.1. |
| In the text | |
 |
Fig. 3 Distribution of distance correlation values (dCor) between high-multiplicity Kepler systems with WED and 10 000 random shuffles of the six GF20 measures. The vertical red line marks the dCor value of the original ordering. (a) Dynamical mass (μ); (b) mass partitioning (Q); (c) monotonicity (M); (d) characteristic spacing (S); (e) gap complexity (C); (f) multiplicity (Np). |
| In the text | |
 |
Fig. 4 Results of using the WED in the context of machine-learning exploratory tools: t-SNE (left) and the Sequencer (right). In both cases, it seems there is a clear trend with the order of systems based on dynamical mas (μ). It is important to note that each point on the t-SNE plot represents a single planetary system, while on the Sequencer plot each row of points represents a single planetary system. |
| In the text | |
 |
Fig. 5 Histograms of ICED values for the three tests described in the main text. Each histogram represents 1000 simulated catalogues that deviate in some way from the original set of 129 high-multiplicity (Np ≥ 3) Kepler systems. The blue and orange histograms show the properties of all planets drawn from alog-normal distribution around the original values, with a standard deviation of 0.1 and 0.3, respectively. The green histogram is the same as the blue histogram except that it includes the possibility of changing each system’s planet multiplicity by drawing the number of planets per system from a uniform distribution between zero planets and the actual number of planets detected around that system,
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.