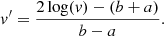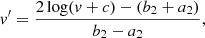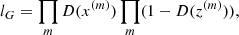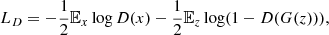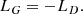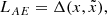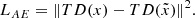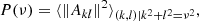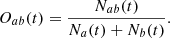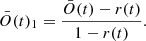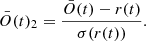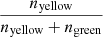| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202039866 | |
| Published online | 12 July 2021 | |
Encoding large-scale cosmological structure with generative adversarial networks
1
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, Bâtiment 121 Campus Paris-Sud, 91405 Orsay, France
e-mail: marion.ullmo@ias.u-psud.fr
2
Université Paris-Saclay, CNRS, TAU team INRIA Saclay, Laboratoire de recherche en informatique, 91190 Gif-sur-Yvette, France
3
Departamento de Física Téorica I, Universidad Complutense, 28040 Madrid, Spain
Received:
6
November
2020
Accepted:
24
April
2021
Recently, a type of neural networks called generative adversarial networks (GANs) has been proposed as a solution for the fast generation of simulation-like datasets in an attempt to avoid intensive computations and running cosmological simulations that are expensive in terms of time and computing power. We built and trained a GAN to determine the strengths and limitations of such an approach in more detail. We then show how we made use of the trained GAN to construct an autoencoder (AE) that can conserve the statistical properties of the data. The GAN and AE were trained on images and cubes issued from two types of N-body simulations, namely 2D and 3D simulations. We find that the GAN successfully generates new images and cubes that are statistically consistent with the data on which it was trained. We then show that the AE can efficiently extract information from simulation data and satisfactorily infers the latent encoding of the GAN to generate data with similar large-scale structures.
Key words: methods: data analysis / methods: numerical / methods: statistical
© M. Ullmo et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The standard cosmological model provides a description of the Universe as a whole: its content, evolution, and dynamics. In this model, the structures observed today (galaxies and clusters of galaxies) have evolved from tiny fluctuations of density imprinted during the very early stages of the Universe (Bond et al. 1996; Coles & Chiang 2000; Forero-Romero et al. 2009). Matter has accreted over time from this homogeneous distribution to form what today is a complex network of structures known as the cosmic web (Bond et al. 1996). This hierarchical assembly of matter was tested with increasingly large numerical simulations such as the Millennium (Springel et al. 2005) and Illustris (Vogelsberger et al. 2014) simulations, and was confirmed with actual observations of the large-scale matter distribution in galaxy surveys such as the Sloan Digital Sky Survey (SDSS; Tempel et al. 2014).
However, the large and detailed simulations that included detailed baryonic physics, such as Horizon-AGN (Dubois et al. 2016), BAHAMAS (McCarthy et al. 2016), or IllustrisTNG (Pillepich et al. 2018), which are needed to compare theory with observations, are computationally expensive. Faster fully analytical approaches (Shandarin & Zeldovich 1989; Kitaura & Heß 2013) and semianalytical simulations (Monaco et al. 2002; Tassev et al. 2013) relying on first- or second-order perturbation theory exist, but they cannot address the highly nonlinear stages of the structure formation.
The recent advances in computer technology and in machine learning have prompted an increasing interest from the astronomical community in proposing machine learning as an interesting alternative for the fast generation of mock simulations and mock data, or for image processing. The ever larger quantities and quality of astronomical data call for systematic approaches to properly interpret and extract the information that can be based on machine-learning techniques such as in Villaescusa-Navarro et al. (2020), Schawinski et al. (2018), or Bonjean (2020). Machine learning can also be used to produce density maps from large N-body simulations of dark matter (DM; Rodríguez et al. 2018; Feder et al. 2020) in a computationally cheaper manner, to predict the effects of DM annihilation feedback on gas densities (List et al. 2019), or to infer a mapping between the N-body and the hydrodynamical simulations without resorting to full simulations (Tröster et al. 2019; Zamudio-Fernandez et al. 2019).
In this context, certain types of neural networks, called convolutional neural networks (CNN; LeCun et al. 1990), excel in the general field of image processing through their automatic pattern detection property (for a comprehensive review, see Ntampaka et al. 2019). Generative models among CNN, such as generative adversarial networks (or GANs; Goodfellow et al. 2014), have shown promising results in computer science and physics (Casert et al. 2020; de Oliveira et al. 2017; Ahdida et al. 2019). These networks aim to learn a probability distribution as close as possible to that of a considered dataset in order to later generate new instances that follow the same statistics. GANs have proven to be very promising tools in terms of media generation (Donahue et al. 2018; Clark et al. 2019). In astronomy, they have recently been used in several cases, and more specifically, by Rodríguez et al. (2018) and Feder et al. (2020), to provide a fast and easy alternative to simulations and images. Wasserstein GANs (or WGANs) have also been used to detect anomalies in astronomical images (Margalef-Bentabol et al. 2020; Storey-Fisher et al. 2020).
In the present work, we first further explore the use of GANs in generating simulation-like data. We built networks and conducted statistical tests for two types of data: images built from 2D simulations and cubes from 3D simulations. This is a way to test the applicability of the networks on two data types that are of interest for further work. The 2D simulations provide a simplified best-case scenario, and have potential applications on observational projected probes such as lensing (Kaiser et al. 1995) and Sunyaev-Zeldovich (SZ) effects (Birkinshaw 1999), and the 3D simulations are used for direct application in studying simulations of the density field. In this respect, this part of our work is an independent confirmation of the studies of Feder et al. (2020) on GANs, but introduces simpler and more effective image preprocessing techniques than were used previously.
We also present how we can build on a trained GAN to construct an autoencoder (AE; Hinton & Salakhutdinov 2006) that is able to preserve the statistics of a dataset. This network, made up of an encoder and a decoder, takes in data of a certain dimension (typically an image), learns a representation with a reduced size of the data (typically a vector) in a latent space, and provides the means, through the encoder and decoder, to translate data from one space into the other. Developing a meaningful latent encoding space for data can have several applications, such as semisupervised classification, disentangling style and content of images, unsupervised clustering, and dimensionality reduction (Hinton & Salakhutdinov 2006), as can be seen, for example, in the case of variational autoencoders (Makhzani et al. 2015) and adversarial autoencoders (Kingma & Welling 2013). In the case of astrophysics or cosmology, AEs could be used to help remove instrumental or astrophysical signal contamination (e.g., point sources, beam, andinstrumental noise; Vojtekova et al. 2021) or for inpainting masked areas while preserving the statistics of the data (Sadr & Farsian 2021; Puglisi & Bai 2020).
In Sect. 2 we describe the data we used to train the neural networks, from the simulations from which they are extracted to the way in which we construct the training sets. In Sect. 3 we present the two types of networks that we used in our analysis in detail, and in Sect. 4 we present the results we obtained with the two network types for both datasets. Finally, we draw conclusions from our findings.
2. Data
Our work rests on the use of convolutional networks that are applied on 2D and 3D arrays that we refer to as images and cubes, respectively.
2.1. Simulations
The images were produced from a publicly available 2D particle-mesh N-body simulation code1 to simulate 1000 2D snapshots of size (100 Mpc h−1)2 with 5122 particles using the standard ΛCDM cosmology. In detail, the evolution of matter distribution along cosmic time was described by a Hamiltonian system of equations that were solved using the leap-frog method. Moreover, the gravitational potential was computed by solving the Poisson equation in Fourier space from the 2D grid density field.
The 3D data used for this analysis are snapshots from numerical simulations of large-scale structures produced with the publicly available code GADGET2 (Springel et al. 2001; Springel 2005). These are DM only simulations, referred to as N-body simulations. GADGET2 follows the evolution of self-gravitating collisionless particles. This is a good description of DM dynamics in accordance with the cosmological model because DM gravitationally only interacts with itself as well as with baryons. In practice, the GADGET2 code computes gravitational forces with a hierarchical tree algorithm to reduce computing time and to avoid having to compute the gravitational effect of N particles on each particle (which would mean N2 computations at each time step). The algorithm divides space using a grid. To compute the gravitational forces exerted on an individual particle, GADGET2 then groups particles increasingly coarsely according to their distance and computes the gravitational pull of groups rather than that of individual particles.
The simulation started at redshift z = 99 with a 3D box of 100 Mpc3 size (chosen to contain representative large-scale structures) with a quasi-homogeneous distribution in space of 5123 DM particles, with Gaussian-distributed very low-amplitude inhomogeneities, and an initial velocity associated with each particle. The inhomogeneities stand for the initial density perturbations produced in the early Universe that eventually evolve into galaxies, clusters, and filaments. The system was then evolved, and the particles were subject to gravity alone. Cosmic expansion was also taken into account, and we used the cosmological parameters Ωm: 0.31, ΩΛ: 0.69 and H0: 0.68 from Planck 2018 (Aghanim et al. 2020). The simulation was run up to the present epoch (z = 0). At any time step, we were able to retrieve the individual particle positions and velocities in the 3D box. These data, describing the dynamical state of the system at a particular time, are referred to as a snapshot. To build our dataset, we only retained the positions. They were used as input for the network.
2.2. Construction of the sample
2.2.1. Pre-augmentation data
For the images, we first used a set of 1000 2D simulations. From these we obtained 1000 independent discrete 256 × 256 density maps by estimating local densities from 2D snapshots with the help of a Delaunay tessellation field estimator (Aragon-Calvo 2020). We used this as a basis to construct the images.
For the cubes, we built a 3D discrete density field from one 3D (z = 0) snapshot by computing the histogram of particles over a 768 × 768 × 768 grid. After we applied a log-like transformation (see Eq. (2)), the grid was smoothed with a Gaussian filter with a standard deviation of the size of three pixels with a stride of three pixels. This choice yielded cubes with smooth structures while preserving the fine low-density structures. It therefore resulted in significantly better results than standard stride-less Gaussian smoothing when used with the different networks in our study. This left us with a cube of side 256 pixels and 100 Mpc.
2.2.2. Data augmentation
From the initial 1000 2D images and the 3D cube (both of side 256 pixels, corresponding to 100 Mpc), we extracted and augmented the final smaller training images and cubes (128 pixels and 50 Mpc side for the 2D cube, and 64 pixels and 25 Mpc side for the 3D cube). This is commonly done by dividing the larger arrays into smaller arrays that do not overlap (e.g., one 256 × 256 array yields four 128 × 128 arrays). However, we considered that for the sake of variety and continuity within our training sets, we instead extracted all possible subarrays (by the periodic boundary conditions of our larger arrays, this corresponds to one n × n array that yields n × n possible subarrays, regardless of their size). This quickly led to a dataset that was too large to load or store (1000 × 2562 images and 2563 cubes before rotations). We therefore elected to load the larger arrays and randomly extracted the smaller arrays on a need basis to create training batches or a subset.
We thus generated batches by choosing a set of random positions within the images or cube. Then we extracted a set of squares of side 128 pixels or cubes of side 64 pixels for the 2D or 3D case, respectively, centered on random positions. In addition, we rotated or flipped these images or cubes by randomly inverting and permuting the axes (d!×2d possibilities for an array of dimension d, i.e., 8 for the images and 48 for the cubes). These transformations augmented the dataset to yield a total of 5 × 108 different possible training images for the 2D case and 8 × 108 training cubes for the 3D case. However, we expect the networks to capture the key features of the original datasets long before all of the possible images or cubes were encountered. We therefore did not define an epoch as the network having encountered all these possibilities, but instead arbitrarily defined an epoch as the network having encountered 40 000 images/cubes. This approximately corresponds to the size of the 2D dataset if we use subarrays that do not overlap (32 000) and ten times that of the 3D dataset (≈3000). We therefore expect the network to have on average encountered all possible structures at every angle by the time it has encountered this number of data.
2.2.3. Data transformation
The GANs operate by using a set of filters (Sect. 3.1) to recognize and learn patterns at different size scales in an image. Therefore we need to work with images with clearly apparent patterns such that the GAN can easily detect the set of salient features. However, linear density maps of the cosmic web show a poor array of shapes, with images appearing mostly uniformly dark, with occasional bright pixels corresponding to dense halo centers. On the other hand, a log representation of the same density maps makes the cosmic web filaments apparent, providing shapes and texture that the GAN can more readily detect and reproduce. Finally, our GAN was built to take in and output images with pixel values ∈[−1, 1]. We thus needed to map the original pixel distribution into this interval.
We hence applied a log-like transformation to the image pixel values (1). For the 2D images, the pixel value v′ in the transformed images reads
 |
Fig. 1. Example of a simulation image (upper left) or cube slice of thickness ≈0.4 Mpc (lower left), histogram of the pixel values before and after log-like transformation (middle), and pixel value transformation function (right) for the images (top) and cubes (bottom). In the middle column, gray represents the pixel value histogram in linear scale, and blue shows the pixel value histogram after log-like transformation (Eq. (1) at the top and Eq. (2) at the bottom) of the images. For both cases, the GAN has been trained using the log-transformed sets of images. |
v is the original pixel value, and a and b are chosen such that a ≲ min(log(v)) and b ≳ max(log(v)) so as to have v′∈]−1, 1[ compatible with the network outputs. We used these strict inequalities to give the network freedom to exceed the boundaries of its training set when it generates images with pixel values ∈[−1, 1]. We thus set a = log(0.01) and b = log(600).
The cubes from the 3D simulation have a significantly wider range of values than the 2D cubes, with values up to 2000 particles per pixel as well as zero values. For these cubes, we adapted the transformation described above to better suit the pixel range of the images and 0 values. We recall that this transformation was applied before the smoothing with a Gaussian filter. The obtained pixel value v′ reads
where b2 was chosen such that b ≳ max(log(v)), c was chosen such that c > 0, but 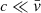 to increase the contrast, while allowing for a log transform, and a2 = log(c). We set b2 = log(2632), c = 0.001, and a2 = log(0.001).
to increase the contrast, while allowing for a log transform, and a2 = log(c). We set b2 = log(2632), c = 0.001, and a2 = log(0.001).
While adding the constant c allows for a log-like transformation, linear values smaller than c become difficult to distinguish from one another after transformation. This can be observed in the lower right panel of Fig. 1, which represents the transformation function given by Eq. (2). We clearly see a saturation effect for values below c = 10−3. We therefore do not expect our networks to correctly recover the pixel PDF for values below c.
3. Unsupervised neural networks
In the following, we use two types of neural networks that we describe in more detail below. First, we train a GAN to recover the underlying distribution of our data and generate new data hailing from this distribution. Second, after learning a meaningful and continuous representation in latent space of our datasets with the GAN’s generator, we build upon it to construct an AE that can recover the latent encoding of any given datum within this representation. Concretely, this will create a tool that can extract any image or the essential information of a data cube in the form of a vector of small size (100 elements for 2D and 200 for 3D) and recover the same image or data cube with this information.
The two networks are more specifically CNNs. A neural network can be described as a differentiable function N with parameters (or weights) θN, input(s) x, and output(s) N(x). As with other machine-learning models, it is trained to complete a specific task by minimizing a loss function LN(θN, x) by gradually modifying the parameters to reduce the loss over multiple iterations with different x. A CNN builds or extracts information from images through a series of convolutions between these images and filters that act as feature detectors. Training of the network rests on learning a set of filters that optimally detect or recover the defining shapes and structures of a set.
3.1. GAN
Given a dataset on which to train, GANs extract the underlying modes of its distribution and can then generate new data that share the same distribution and thereby are similar to the training dataset. Trained correctly, GANs can hence be used to produce an infinite number of new images given a large but finite number of input images (i.e., training dataset).
The GAN consists of two competing neural networks. The first, a generator, takes a random vector as input from which it produces data (an image or cube in our cases). The second network, a discriminator, distinguishes these generated data from true data from the training set. As both networks start out with no information about the data, the tasks of generator and discriminator start out as simple: the generator easily misleads the discriminator, and the discriminator has to distinguish very dissimilar images. However, as each of the two networks becomes more efficient, one at generating convincing images and the other at distinguishing them from the true set, the task is made harder for the other network. Through this competition, the two networks train each other by gradually increasing the difficulty of the other’s task while simultaneously improving themselves.
In practice, the networks work in the following way. The generator takes a random Gaussian-distributed vector (z) as input and from this builds a datum (G(z)) through a series of deconvolutions and activations, as described in Appendix A. The discriminator takes in a datum, either from the training set (x) or from the set produced by the generator (G(z)), and through a series of convolutions and activations further described in Appendix A, produces a single number D(x/G(z)) ∈ [0; 1] that can be interpreted as the probability that the input datum is drawn from the training set.
The training procedure can therefore be described as follows. First, the generator will generate a batch of images or cubes (in our case, 50 for 2D and 100 for 3D), and the same number of images or cubes will be drawn from the training set. Then, the parameters θD of the discriminator are adjusted such that the probability given by the discriminator that the generated data are true decreases, while at the same time, the same probability computed on the training set increases. Denoting m = 0, …, 50/100 the indices of the generated images or cubes z(m) and the training set of images or cubes x(m) in the batch, we wish to maximize the following loss:
which is equivalent to minimizing the following log-loss:
where 𝔼x represents the average over the dataset and 𝔼z the average over the random vector z. To minimize this expression, the discriminator should yield a prediction near to one for the data of the training dataset and near to zero for the data produced by the generator. Conversely, the generator should aim at producing images or cubes that look like true images or cubes, and so for the discriminator to yield predictions close to one when assessing its generated data. Therefore the generator’s loss is simply defined as
At the end of the training stage, the two networks should converge to an equilibrium wherein the discriminator is unable to distinguish between the two sets of data and the generator is outputting data sampled from the true underlying distribution of the training set.
In practice, most GANs, including ours, never perfectly reach this equilibrium and instead reach a point at which the quality and diversity of the generated images fluctuates with training. Instead of stopping training and collecting the resulting networks at a specific point, we therefore elected to regularly save the weights of our networks during training and chose the best set of weights by comparing the quality of images they generated and their statistical properties. When this was done, we were equipped with a functioning generator and discriminator that we further used in the construction and training of an AE.
3.2. Autoencoder
An AE is a neural network that learns a representation (encoding) for a set of data in an unsupervised manner. It is built and trained in the following way: A first network e, called encoder, takes as input a datum x and outputs a vector of reduced size z = e(x). A second network d, the decoder, takes as input z and outputs a recovered datum 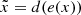 . The AE is trained by imposing that the resulting
. The AE is trained by imposing that the resulting 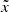 is as close as possible to the initial x. This is typically (but not systematically) done by using a cross-entropy loss, or by making ∥x − d(e(x))∥2 as small as possible.
is as close as possible to the initial x. This is typically (but not systematically) done by using a cross-entropy loss, or by making ∥x − d(e(x))∥2 as small as possible.
Incidentally, we can also consider and use the GAN’s generator as a readily trained decoder from a reduced space (R100 for 2D and R200 for 3D) to our target space (z = 0 simulation images or cubes). The generator has learned a representation of the simulated data. Taking in an input z of reduced size, the generator is to output any image 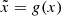 from the simulations. Furthermore, given the ability of the generator to generate images or cubes that are statistically consistent with those of the simulations, using it in the AE would constrain the outputs to share the same statistical properties. Thus, we would avoid the common AE pitfall to output blurry images (Dosovitskiy & Brox 2016). To create a functioning AE, we therefore need only build and train a functioning encoder that works as an inverse function of the generator, such that
from the simulations. Furthermore, given the ability of the generator to generate images or cubes that are statistically consistent with those of the simulations, using it in the AE would constrain the outputs to share the same statistical properties. Thus, we would avoid the common AE pitfall to output blurry images (Dosovitskiy & Brox 2016). To create a functioning AE, we therefore need only build and train a functioning encoder that works as an inverse function of the generator, such that 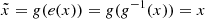 .
.
In a classical autoencoder, the encoder and decoder are trained alongside each other. In our approach, the decoder was first trained separately in an effort to constrain it to output data that are statistically sound (i.e., that hail from the underlying distribution of the simulation). These constraints might imply a loss of accuracy in our recovery of structures in individual images. It is therefore important to consider both global and pairwise statistics to determine how the AE fares in both regards, as we show in Sect. 4.
The different layers of the encoder are based on the discriminator architecture because the latter is especially developed to extract essential information from simulated data. However, because the goal of the network differs from that of the discriminator, we only retain the architecture and not the weights. Further details about the architectures of the networks can be found in Appendix A.
We can now build the AE by setting the two networks (encoder and decoder) end to end. This can be described as the following function: a(x) = d(e(x)). We fixed the weights of the decoder and updated the weights of the encoder to decrease the loss function described above: ∥x − a(x)∥2. However, instead of using the ℓ2 loss in the space of the image or cube, comparing pixels at the same location on the true and inferred images or cubes, which accounts poorly for well-recovered but slightly shifted structures, we instead used the discriminator2. It is expected that the discriminator learns a latent representation of our datasets during the training of the GAN. This representation is given by the penultimate layer, where its elements are used to estimate the probability for a datum to be a true image or cube. This representation in the latent space of the discriminator is semantically meaningful (Bang et al. 2020) because it accounts for the presence of specific structures or shapes, and tends to place visually similar images or cubes at a small distance in this space, where they would otherwise be more distant in the space of the images or cubes.
Therefore we define the AE loss as:
where Δ is the ℓ2 difference in the latent space of the discriminator. Alternatively, calling TD the truncated discriminator with its final layer removed,
We then trained the AE by updating its weights to minimize this loss. Training was stopped when the loss measured on a separate validation set reached a minimum. From now on, we refer to the images or cubes 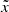 reconstructed by the AE as inferred images or cubes. We assess their quality in Sect. 4.
reconstructed by the AE as inferred images or cubes. We assess their quality in Sect. 4.
4. Results
In this section, we use a set of statistical estimators to evaluate the performances of both the GAN and the AE in emulating or reproducing the input data from 2D or 3D simulations, which are considered here as the ground truth. Because we ultimately wish to reproduce ground truth linear density maps, we applied an inverse-log transformation to revert to linear density. This density, corresponding to the pixel values, is expressed in particles per pixel (hereafter noted ppp) and is referred to as ρ.
We compared datasets on the basis of their pixel PDFs, the distribution of their mean density, their power spectra, and their peak counts. Additionally, as we expect that the AE-inferred images or cubes reproduce their input images or cubes, we performed a pairwise measure described in Sect. 4.1.4 to quantify how well the individual images or cubes are recovered.
4.1. Statistical estimators
4.1.1. Pixel PDF and distribution of the mean density
A first basic test is to compare the distributions of the pixel values, which correspond to a density measure in ppp in both sets of data. We also computed the mean particle density, μ, of each image or cube and compared their PDF over the simulated (truth) sets and generated and inferred sets from the GAN and AE. Whereas the pixel PDF is informative of the density distribution of a datum on average, and therefore ensures that two sets of images or cubes are similar on average, the mean density serves as a simple one-dimensional visualization of the distribution of images or cubes over a set. This type of information is important to ensure that we recover the underlying distribution of both datasets and recover different cosmic regions and different halo densities in the correct proportions. Furthermore, GANs can often experience so-called mode collapse (Thanh-Tung & Tran 2018). In this situation, the generated images or cubes are indistinguishable from the original set, but show little to no diversity. Although visual inspection of the images can help to detect mode collapse, a visualization of the overall distribution through the mean density provides additional information to confirm its absence.
4.1.2. Peak counts
We computed the average peak counts over the generated or simulated dataset. A peak is a local maximum (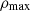 ), defined as a pixel whose contiguous neighbors (8 for images and 26 for cubes) have lower values. For each image or cube, we computed the number of peaks for a given value of ρmax and averaged this number over the whole dataset. In the simulated data, the higher peaks, which are dense local maxima, are expected to correspond to halo centers, whereas smaller near-zero peaks are more likely to be the result of noise from the simulation or the image-making process. Therefore we are more interested in the higher peaks, which give us an indication as to our recovery of the halo distribution.
), defined as a pixel whose contiguous neighbors (8 for images and 26 for cubes) have lower values. For each image or cube, we computed the number of peaks for a given value of ρmax and averaged this number over the whole dataset. In the simulated data, the higher peaks, which are dense local maxima, are expected to correspond to halo centers, whereas smaller near-zero peaks are more likely to be the result of noise from the simulation or the image-making process. Therefore we are more interested in the higher peaks, which give us an indication as to our recovery of the halo distribution.
4.1.3. Power spectrum
We computed the 2D and 3D power spectrum of each image or cube from the different sets (input, generated, and inferred). For a frequency ν, it is given by
where Ak, l are the discrete Fourier transform elements of the image.
4.1.4. Sørensen-Dice coefficient
As stated above, we need an additional test to quantify how well the AE infers individual images or cubes. Therefore we need a pairwise comparison of input images or cubes from the simulations and their inferred counterparts from the AE. Taking a simulation or inferred pair, we tested how well the structures overlap by thresholding the images or cubes at different values and counting the fraction of pixels or voxels above the threshold that overlap.
For a pair of images or cubes a and b, the overlap is expressed in the following way:
Here Naorb(t) is the number of pixels or voxels whose value is above the threshold t in a or b, and Nab(t) is the number of pixels or voxels whose value is above t for both a and b in a given position in an image or cube. To gauge the overall quality of the encoded images or cubes, we plotted the dice coefficient averaged over a set of simulated-inferred pairs: 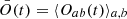 . For clarity, the overlap Oab(t) was plotted against the top percentage, associated with a given threshold, rather than the threshold itself (Figs. 10 and 13). The thresholds were independently defined for the simulated and inferred sets.
. For clarity, the overlap Oab(t) was plotted against the top percentage, associated with a given threshold, rather than the threshold itself (Figs. 10 and 13). The thresholds were independently defined for the simulated and inferred sets.
A random pair of true and inferred images or cubes on average provides a nonzero overlap. Two images or cubes with n% thresholded pixels or voxels are expected to overlap by n% on average. To better gauge the entire performance or recovery of the inferred set, we thus computed a random overlap, defined as an overlap measured over a random set of simulation pairs. We plotted this along with our overlap averaged on simulation or inferred pairs. From this random overlap measure, we proceeded to build an unbiased estimator of the feature recovery by subtracting it from the overlap measured for simulated or inferred pairs. This difference is not informative by itself, therefore we studied it relative to relevant values.
First we observed it relative to its maximum possible score (1 − r(t)), r(t) being the average random overlap for a given threshold t. This provided a completion score between 0 and 1, in which 1 corresponds to a perfect overlap and 0 to a completely random overlap,
We refer to this as the normalized sd coefficient.
Next we observed it relative to the standard deviation of the random overlap to ensure that the inferred images or cubes, if imperfect, were well beyond the random range. This corresponds to a signal-to-noise ratio,
We refer to this as the sd coefficient significance.
These measures allowed us to determine whether the structures are well recovered, and at which scale they are best recovered.
4.2. Results from GANs
4.2.1. 2D images
We first present the results of the GAN trained on images from 2D simulations. The network consistently outputs sets of verisimilar images as early as 30 epochs, but we trained the GAN for 85 epochs for the best results. We expect the relative simplicity of the images of our training set to result in a faster convergence than a GAN trained on natural images. We also note that our chosen number of epochs, consisting of 40 000 images each, corresponds to longer training than that of Rodríguez et al. (2018; 20 epochs for a dataset of 15 000 projected cubes). In addition, training the GAN for too long (e.g., > 100 epochs) eventually results in mode collapse, whereas the quality of the generated data stops to improve long before that point is reached.
Two sets of 50 images taken at random from the simulations and from the GAN-generated images in Fig. 2 show the ability of the GAN to generate images of convincing similarity. Visually, we observe that the large-scale structure is well recovered. This is most notably the case for the filaments, which are reproduced in all their diversity of length, thickness, and frequency. It is also the case for high-density regions, or halos, in terms of their occurrence, brightness (or density), and positions within the structures.
 |
Fig. 2. Two subsets of 50 images taken at random from a set of 2D simulation images (left) and a set of images generated by the GAN (right). Every image represents a 128 × 128 log density map of side 50 Mpc. They are virtually indistinguishable by eye. |
This observation is further corroborated by the statistical estimators, as shown in Fig. 3. The pixel PDFs (lower left panel of Fig. 2) show an almost perfect overlap for the majority of the pixel density values, with a very slight under-representation in the generated images of the densest values. This agreement shows that the density distribution of the images is very well recovered by the GAN.
 |
Fig. 3. Statistics of the 2D simulation images compared to their GAN-generated counterparts. The upper left panel shows the pixel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median power spectrum as well as the median absolute deviation (mad) layer, and the lower right panel shows the average peak count per image. The curves overlap almost perfectly. |
The mean particle density distribution of the generated set (displayed in the upper right panel of Fig. 2) shows an almost perfect agreement with the simulation set. The overall agreement indicates that the diversity of the original set is globally well represented in the generated set. The median power spectra and their median absolute deviation (mad) layer (Fig. 3 upper left panel) for the simulated and generated sets show a satisfactory overlap, indicating a good recovery of the correlations at various distances and thus a good representation of the different scales in the images. Finally, we show the peak counts in the lower right panel of Fig. 2. The very good agreement between the true simulated images and the generated images confirms that the dense regions are well represented. In particular, not only a similar average number of peaks is observed, but also a similar average distribution of the peak values in both sets, with a slight under-representation of the densest peaks and a more notable over-representation of low-density peaks. However, the peaks at low density are due to simulation noise and are not physical, so this is not an issue.
4.2.2. 3D cubes
We now turn to the results obtained by the GAN trained on the 3D cubes. The GAN again progressed in a stable manner and consistently produced very similar cubes after about 30 epochs of training. For the best results, we trained it for 50 epochs. We find that this agrees with the training time of Feder et al. (2020; 150 epochs for a dataset of 16 000 cubes). As for the 2D GAN, training for too long results in mode collapse, but not before the quality of the generated cubes stabilizes.
First, we focus on two subsets taken at random from the original set of simulated cubes and from the set of generated cubes (Fig. 4). Our visual inspection again shows that the diversity of the simulated cubes is well recovered by the GAN in terms of distribution in size, frequency of filaments, and number and brightness of high-density regions. A closer look at the statistical properties of the images as seen in Fig. 5 further confirms this.
 |
Fig. 4. Two subsets of cube slices (of thickness Δz ≈ 0.4 Mpc) taken at random from a set of 3D simulation cubes (left) and a set of cubes generated by the GAN (right). Every cube represents a 64 × 64 × 64 log density map of side 25 Mpc. They are virtually indistinguishable by eye. |
 |
Fig. 5. Statistics of the 3D simulation cubes (red) compared to their GAN-generated counterparts (blue). The upper left panel shows the voxel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median 3D power spectrum as well as the mad layer, and the lower right panel shows the average peak count per cube. The curves overlap almost perfectly. |
Notably, the voxel PDFs (Fig. 5 upper left panel) show an almost perfect overlap, confirming the good recovery of the density distribution on the average cubes. However, the lower tail of the distribution is poorly represented for voxel values < 10−4 ppp. The generated cubes show a deficit compared to the simulations. This can be explained by the saturation effect related to the constant c in Eq. (2).
Meanwhile, the mean density PDF (Fig. 5 upper right panel) seems to be well recovered, confirming the good recovery of the cube diversity. The median 3D power spectra and their mad regions (Fig. 5 lower left panel) yield an almost perfect overlap, with a slight over-representation of higher frequencies in the generated cubes. We plot the peak counts in the lower right panel of Fig. 5. True simulated cubes and generated cubes again show an almost perfect agreement, confirming that the high-density region centers are well represented in terms of their numbers as well as their distribution. However, we observe a slight misrepresentation of the lower tail of the distribution, similarly to the voxel PDF, for similar reasons.
We find that the mean density distributions of the simulated and generated sets are somewhat distinguishable but overlap very well, and that the power spectra overlap satisfactorily in both their medians and their mad regions. We note that our results appear to agree with those of Feder et al. (2020), who encountered similar saturation issues as we did at low densities for similar reasons. Because Rodríguez et al. (2018) studied projected 3D simulations whereas we present results for actual 3D cubes, a proper comparison is not possible.
4.3. Results from the AE
4.3.1. 2D images
We now focus on the outcome of the AE for the set of images. For this dataset, the AE was trained over 195 epochs. To determine the best point at which to stop training, we considered the evolution of the loss function of our model when it was tested on a validation set. We expect it to decrease up to a point at which our model should start overfitting, that is to say, it becomes too fine-tuned for its training set and starts to perform poorly on new sets, after which the validation loss should start to increase. In practice, we never observed an overfitting during our training of the AE on the images. The loss on the validation set instead converged almost monotonously toward a constant.
We studied how the AE fares with images that it had never encountered during its training because our goal is to be able to apply it on new datasets. All the images shown and used to measure the different statistical properties in the results were therefore part of or were inferred from a separate set than those used for training. We call this a test set. This was the case for the 2D images and 3D cubes.
We first illustrate the results in terms of the AE’s performance and recovery of features with a set of ten simulated images taken at random from the test set (Fig. 6, first column from left to right) and their inferred counterparts (Fig. 6, second column from left to right). We note that the inferred images visually look similar to the simulated images, but the larger and denser structures tend to be recovered better than the smaller diffuse structures.
 |
Fig. 6. Ten images taken at random from the 2D simulations (top row) and their AE-inferred counterparts (bottom row). Every image represents a 128 × 128 log density map of side 50 Mpc. The larger dense structures are better recovered than the finer diffuse structures. |
We recall that while the decoder, which has the exact same structure and weights as the GAN’s generator, is expected to infer images that are statistically similar to that of the GAN, it nevertheless infers images from a different prior. While the GAN’s inputs were selected randomly from a Gaussian distribution, the decoder’s inputs were all constructed in a deliberate fashion by the AE’s encoder and are not expected to follow quite the same distribution. A change in statistics is therefore expected. As a sanity check, we additionally trained an isolated encoder directly on images that were randomly generated by the 2D GAN, constraining it to output an encoded vector z = E(G(x)) similar to the input vector x of the generated images, with a simple l2 loss LE = ∥z − x∥2. The ensuing images inferred by the AE when tested on new GAN-generated images give very satisfactory results with all estimators (almost perfect overlap of all estimators, dice coefficient> 0.7 even for the top 1% pixels). However, this did not translate well when we tested the AE thus trained on real simulation images. This test suggests that much of the AE’s limitations might be due to a certain dissimilarity between GAN-generated images and true images, and thus due to the GAN’s limitations themselves. An identical check for the 3D cubes yielded the same results, from which we can draw the same conclusions.
A closer inspection of the statistical properties of the images (Fig. 7) shows a very satisfactory agreement of the sets of inferred and simulated images. The pixel PDFs (Fig. 7 upper left panel) show a satisfactory overlap for the two sets, presenting a very slight under-representation of high-density pixels in the inferred images. The mean particle density distributions (Fig. 7 upper right panel) show a satisfactory agreement. The inferred images exhibit a slight skewness toward higher mean densities. In the lower left panel of Fig. 7, the power spectra overlap satisfactorily. Finally, the peak counts (Fig. 7 lower right panel) show an almost perfect overlap, with a slight over-representation of lower peak values in the inferred images. Overall, while slightly less so than the GAN-generated images, the images are recovered with almost perfect statistical quality.
 |
Fig. 7. Statistics of the 2D simulation images compared to their encoded counterparts. Upper left shows the pixel PDF, upper right shows mean density distribution, lower left shows median power spectrum as well as mad (median absolute deviation) layer, and lower right shows average peak count per image. As for the GAN the curves overlap quite satisfyingly, with only the MPDD showing a slight flattening. |
We now focus on the Sørensen-Dice coefficient, which computes the overlap fraction of two thresholded images. Visual inspection (Figs. 8 and 9) of the thresholded simulated or inferred image pairs and how they overlap suggests that dense structures are strikingly well recovered. The AE favors the retrieval of thick, contrasted features to the detriment of finer ones. This is again expected because of the predisposition of the CNN to detect and construct well-defined shapes.
 |
Fig. 8. Examples of 2D simulation or inferred image pairs (Cols. 1–2) and their thresholded equivalents as used to compute the overlap function. The first column in each pair represents images from the simulations, and the second column lists their inferred counterparts. Here they are thresholded for top 20% (Cols. 3–4), 40% (Cols. 5–6), 60% (Cols. 7–8), and 80% (Cols. 9–10). |
 |
Fig. 9. Examples of the overlap of thresholded structures for 2D simulation or inferred image pairs. Yellow pixels indicate where the structures overlap, and green pixels show where they do not. The dark background represents pixels below the threshold. The Dice coefficient is simply measured as |
An inspection of the Dice coefficient (Fig. 10, left) corroborates this finding. Despite some slight shifts in structures and the loss of finer structures, we note that the high-density regions overlap satisfactorily and apparently well beyond the random region for up to the top 60% pixels. The normalized Dice coefficient (Fig. 10, right, blue) lets us assess the density threshold at which the AE captures structures best. Here, it peaks for the top 20% pixels.
 |
Fig. 10. Left: dice coefficient (as defined by Eq. (9)) of the top n% pixels between 2D simulation images and their inferred counterparts in increments of 5% (yellow). The inner dark yellow layer represents measure uncertainty, and the outer yellow layer represents the standard deviation over the set. The random overlap is represented in black. Right, red: dice coefficient significance (see Eq. (11)). Blue: Normalized Dice coefficient (see Eq. (10)); both are represented with their standard deviation layers. |
4.3.2. 3D cubes
We now consider the AE’s performance when trained on cubes from the 3D simulation. For these cubes, the AE was trained for 55 epochs, after which the loss measured on the validation set showed that the network started to overfit.
To illustrate our results, we first show a random set of ten cubes from the 3D simulations test set and their inferred counterparts (Fig. 11). We again observe that the densest structures appear to be better recovered than the more diffuse structures. We concentrate on the statistical properties of the cubes (Fig. 12) to better assess the AE’s performance.
 |
Fig. 11. Ten cube slices from the 3D simulations (top row) and their ten AE-inferred counterparts (bottom row). Every image represents a slice from a 64 × 64 × 64 log density map of side 25 Mpc. As for the 2D case, the larger dense structures are better recovered than the finer diffuse structures. |
 |
Fig. 12. Statistics for the 3D simulation cubes (red) and their AE-inferred counterparts (blue). The upper left panel shows the voxel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median 3D power spectrum as well as mad layer, and the lower right panel shows the average peak count per cube. In the same way as for the GAN, the curves overlap quite satisfactorily. |
First, the voxel PDFs (Fig. 12 upper left panel), as for the GAN’s case, overlap well up to the lower tail of the distribution, with an over-representation of lower densities in the inferred cubes. The mean density distribution, as we show in the upper right panel of Fig. 12, is well recovered, as is the 3D power spectrum (Fig. 12 lower left), although it again shows a slight under-representation of higher frequencies in the inferred cubes. The peak counts (Fig. 12 lower right panel) show, similarly to the voxel PDF, a slight over-representation in the high-density regime.
An inspection of the Dice coefficient (Fig. 13, left) shows an overall satisfactory recovery of the cubes that significantly differ from random cubes. We further note that the retrieval of high-density structures is good for the top 60% voxels in a majority of cubes, as shown by the Dice coefficient significance (Fig. 13, right, red). The normalized Dice coefficient (Fig. 13, right, blue) suggests that structures associated with the top 10% voxels are captured best by the AE.
 |
Fig. 13. Left: dice coefficient (as defined by Eq. (9)) of the top n% voxels between the 3D simulation cubes and their inferred counterparts in increments of 5% (yellow). The inner dark yellow layer represents the measure uncertainty, and the outer yellow layer represents the standard deviation over the set. The random overlap is represented in black. Right, red: dice coefficient significance (see Eq. (11)). Blue: Normalized Dice coefficient (see Eq. (10)). The coefficients are represented with their standard deviation layers. |
5. Conclusion
We trained a GAN on two types of simulations to produce statistically consistent data. The first set was built from 2D N-body simulations using a Delaunay tessellation field estimator, and the second set was built from 3D simulations using a smoothed-histogram field estimation method.
Using an ensemble of estimators (pixel PDF, mean density distribution, power spectrum, and peak counts), we confirmed the ability of the GAN to extract the underlying statistical distribution of data built from the simulations and generate new data hailing from this distribution. We showed that this was the case for both data types. They were indeed emulated with striking similarity to the true original data, as we showed visually and with the almost perfect overlap of the different statistical estimators. Additionally, the training proved stable. The networks consistently generated images of increasing quality with training up to a stable point after which the generated images were visually indistinguishable from the true ones. We note that despite the success of GANs to reproduce a desired input with high fidelity, it is important to be careful when these black-box models are used.
As we noted when we tried to train an AE on GAN-generated data alone and noted its poor generalization to simulation data, a visual inspection is not sufficient to guarantee that the generated dataset is statistically equivalent to the targeted set. Because the generated data cannot be distinguished visually from the simulation data, it is thus very important to design a series of quantitative tests ensuring in which range they can be exploited. In other words, neural networks are very appealing tools to be explored and exploited, but at the cost of devising precise tests of their domains of validity and their generalization capability.
Building on the GAN’s properties, we used the trained network to devise an AE that reduced images or cubes, and related information, to encoded vectors of smaller size that were then decoded with as little loss as possible, while satisfactorily conserving the statistical properties of the data. A visual appraisal of the data inferred by the AE suggested that large dense structures were very well reproduced for both data types (images and cubes), while for the smaller fine structures, the degree of reproduction was not satisfactory at all. Furthermore, the inferred data appeared to be visually realistic. Statistical estimators showed a quite satisfactory overlap, but suggested a slight overall decrease in statistical similarity with the original sets when compared with the results from the GAN. This is to be expected. Although the decoder is constrained to output realistic data when given a Gaussian-distributed input and the encoder is constrained to translate data into a meaningful way in the latent space of the decoder, we cannot expect the data to perfectly follow a Gaussian distribution when they are translated into the latent space. Finally, the fact that the AE can successfully reproduce the contrasted features of the input data on a test set indicates that the GAN did capture meaningful features of the dataset, and is far from overfitting it by only reproducing the training set with small perturbations.
Acknowledgments
The authors thank an anonymous referee for comments and suggestions. They thank M. Aragon-Calvo for providing 2D simulations, H. Tanimura for providing the 3D simulations, and the whole ByoPiC team for useful discussions. This project was funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme grant agreement ERC-2015-AdG 695561. A.D. was supported by the Comunidad de Madrid and the Complutense University of Madrid (Spain) through the Atraccián de Talento program (Ref. 2019-T1/TIC-13298).
References
- Aghanim, N., Akrami, Y., Ashdown, M., et al. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahdida, C., Albanese, R., Alexandrov, A., et al. 2019, J. Instrum., 14, P11028 [CrossRef] [Google Scholar]
- Aragon-Calvo, M. A. 2020, MNRAS, 503, 557 [CrossRef] [Google Scholar]
- Bang, D., Kang, S., & Shim, H. 2020, Int. J. Comput. Vision, 1 [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [Google Scholar]
- Bond, J. R., Kofman, L., & Pogosyan, D. 1996, Nature, 380, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Bonjean, V. 2020, A&A, 634, A81 [CrossRef] [EDP Sciences] [Google Scholar]
- Casert, C., Mills, K., Vieijra, T., Ryckebusch, J., & Tamblyn, I. 2020, ArXiv e-prints [arXiv:2002.07055] [Google Scholar]
- Clark, A., Donahue, J., & Simonyan, K. 2019, ArXiv e-prints [arXiv:1907.06571] [Google Scholar]
- Coles, P., & Chiang, L.-Y. 2000, Nature, 406, 376 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Oliveira, L., Paganini, M., & Nachman, B. 2017, Comput. Software Big Sci., 1, 4 [CrossRef] [Google Scholar]
- Donahue, C., McAuley, J., & Puckette, M. 2018, Adversarial Audio Synthesis [arXiv: 1802.04208] [Google Scholar]
- Dosovitskiy, A., & Brox, T. 2016, Generating Images with Perceptual Similarity Metrics based on Deep Networks [arXiv: 1602.02644] [Google Scholar]
- Dubois, Y., Peirani, S., Pichon, C., et al. 2016, MNRAS, 463, 3948 [Google Scholar]
- Feder, R. M., Berger, P., & Stein, G. 2020, Phys. Rev. D, 102, 103504 [Google Scholar]
- Forero-Romero, J. E., Hoffman, Y., Gottlöber, S., Klypin, A., & Yepes, G. 2009, MNRAS, 396, 1815 [NASA ADS] [CrossRef] [Google Scholar]
- Goodfellow, I., Pouget-Abadie, J., Mirza, M., et al. 2014, in Advances in Neural Information Processing Systems, 2672 [Google Scholar]
- Hinton, G. E., & Salakhutdinov, R. R. 2006, Science, 313, 504 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kingma, D. P., & Welling, M. 2013, ArXiv e-prints [arXiv:1312.6114] [Google Scholar]
- Kitaura, F.-S., & Heß, S. 2013, MNRAS, 435, L78 [Google Scholar]
- LeCun, Y., Boser, B. E., Denker, J. S., et al. 1990, in Advances in Neural Information Processing Systems, 396 [Google Scholar]
- List, F., Bhat, I., & Lewis, G. F. 2019, MNRAS, 490, 3134 [Google Scholar]
- Makhzani, A., Shlens, J., Jaitly, N., Goodfellow, I., & Frey, B. 2015, ArXiv e-prints [arXiv:1511.05644] [Google Scholar]
- Margalef-Bentabol, B., Huertas-Company, M., Charnock, T., et al. 2020, MNRAS, 496, 2346 [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2016, MNRAS, stw2792 [Google Scholar]
- Monaco, P., Theuns, T., & Taffoni, G. 2002, MNRAS, 331, 587 [Google Scholar]
- Ntampaka, M., Avestruz, C., Boada, S., et al. 2019, The Role of Machine Learning in the Next Decade of Cosmology, BAAS, 51, 14 [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018, MNRAS, 473, 4077 [Google Scholar]
- Puglisi, G., & Bai, X. 2020, ApJ, 905, 143 [Google Scholar]
- Rodríguez, A. C., Kacprzak, T., Lucchi, A., et al. 2018, Comput. Astrophys. Cosmol., 5, 4 [Google Scholar]
- Sadr, A. V., & Farsian, F. 2021, JCAP, 2021, 012 [Google Scholar]
- Schawinski, K., Turp, M. D., & Zhang, C. 2018, A&A, 616, L16 [EDP Sciences] [Google Scholar]
- Shandarin, S. F., & Zeldovich, Y. B. 1989, Rev. Mod. Phys., 61, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Springel, V., White, S. D., Jenkins, A., et al. 2005, Nature, 435, 629 [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. 2001, New Astron., 6, 79 [Google Scholar]
- Storey-Fisher, K., Huertas-Company, M., Ramachandra, N., et al. 2020, ArXiv e-prints [arXiv:2012.08082] [Google Scholar]
- Tassev, S., Zaldarriaga, M., & Eisenstein, D. J. 2013, JCAP, 2013, 036 [Google Scholar]
- Tempel, E., Stoica, R., Martinez, V. J., et al. 2014, MNRAS, 438, 3465 [Google Scholar]
- Thanh-Tung, H., & Tran, T. 2018, ArXiv e-prints [arXiv:1807.04015] [Google Scholar]
- Tröster, T., Ferguson, C., Harnois-Déraps, J., & McCarthy, I. G. 2019, MNRAS, 487, L24 [Google Scholar]
- Villaescusa-Navarro, F., Anglés-Alcázar, D., Genel, S., et al. 2020, ArXiv e-prints [arXiv:2010.00619] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Vojtekova, A., Lieu, M., Valtchanov, I., et al. 2021, MNRAS, 503, 3204 [Google Scholar]
- Zamudio-Fernandez, J., Okan, A., Villaescusa-Navarro, F., et al. 2019, ArXiv e-prints [arXiv:1904.12846] [Google Scholar]
Appendix A: Network specifications
A.1. GAN
The generator and discriminator are based on the structure described by Tiago Freitas3 and built following the structure detailed in Table A.1. They are trained using the Adam optimizer with parameters (lr = 0.0002, β1 = 0.5) and minimize the loss given in Eq. (4), wherein a small noisy component that labels the images incorrectly is added. This imperfect loss avoids the common pitfall of GANs wherein one of the competing parties, usually the discriminator, becomes too efficient compared to the other, which stops the competition and thus the training well before quality images can be generated.
Architecture specifications for each layer of the 2D GAN generator network (G) and discriminator network (D) as well as the 2D AE’s encoder (E) and decoder(De).
Architecture specifications for each layer of the 3D GAN generator network (G) and discriminator network (D) as well as the 3D AE’s encoder (E) and decoder(De).
A.2. AE
We recall that the AE is built by appending a second network, the decoder, to a first network, the encoder. In our case, as explained in Sect. 3.2, we took the trained generator of a GAN as a readily built decoder. Similarly, we based the encoder architecture on that of the discriminator, and only changed the final (8192 → 1 for 2D and 4096 → 1 for 3D) dense layer to a (8192/4096 → 100/200) dense layer with no activation, such that the output was of the correct size and limitations. The general structures of the encoder and decoder are also defined in Table A.1. With the weights of the decoder fixed, the AE was trained by varying the weights of the encoder to reduce the loss given in Eq. (7) using the Adam optimizer with the same parameters as above (lr = 0.0002, β1 = 0.5).
All Tables
Architecture specifications for each layer of the 2D GAN generator network (G) and discriminator network (D) as well as the 2D AE’s encoder (E) and decoder(De).
Architecture specifications for each layer of the 3D GAN generator network (G) and discriminator network (D) as well as the 3D AE’s encoder (E) and decoder(De).
All Figures
 |
Fig. 1. Example of a simulation image (upper left) or cube slice of thickness ≈0.4 Mpc (lower left), histogram of the pixel values before and after log-like transformation (middle), and pixel value transformation function (right) for the images (top) and cubes (bottom). In the middle column, gray represents the pixel value histogram in linear scale, and blue shows the pixel value histogram after log-like transformation (Eq. (1) at the top and Eq. (2) at the bottom) of the images. For both cases, the GAN has been trained using the log-transformed sets of images. |
| In the text | |
 |
Fig. 2. Two subsets of 50 images taken at random from a set of 2D simulation images (left) and a set of images generated by the GAN (right). Every image represents a 128 × 128 log density map of side 50 Mpc. They are virtually indistinguishable by eye. |
| In the text | |
 |
Fig. 3. Statistics of the 2D simulation images compared to their GAN-generated counterparts. The upper left panel shows the pixel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median power spectrum as well as the median absolute deviation (mad) layer, and the lower right panel shows the average peak count per image. The curves overlap almost perfectly. |
| In the text | |
 |
Fig. 4. Two subsets of cube slices (of thickness Δz ≈ 0.4 Mpc) taken at random from a set of 3D simulation cubes (left) and a set of cubes generated by the GAN (right). Every cube represents a 64 × 64 × 64 log density map of side 25 Mpc. They are virtually indistinguishable by eye. |
| In the text | |
 |
Fig. 5. Statistics of the 3D simulation cubes (red) compared to their GAN-generated counterparts (blue). The upper left panel shows the voxel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median 3D power spectrum as well as the mad layer, and the lower right panel shows the average peak count per cube. The curves overlap almost perfectly. |
| In the text | |
 |
Fig. 6. Ten images taken at random from the 2D simulations (top row) and their AE-inferred counterparts (bottom row). Every image represents a 128 × 128 log density map of side 50 Mpc. The larger dense structures are better recovered than the finer diffuse structures. |
| In the text | |
 |
Fig. 7. Statistics of the 2D simulation images compared to their encoded counterparts. Upper left shows the pixel PDF, upper right shows mean density distribution, lower left shows median power spectrum as well as mad (median absolute deviation) layer, and lower right shows average peak count per image. As for the GAN the curves overlap quite satisfyingly, with only the MPDD showing a slight flattening. |
| In the text | |
 |
Fig. 8. Examples of 2D simulation or inferred image pairs (Cols. 1–2) and their thresholded equivalents as used to compute the overlap function. The first column in each pair represents images from the simulations, and the second column lists their inferred counterparts. Here they are thresholded for top 20% (Cols. 3–4), 40% (Cols. 5–6), 60% (Cols. 7–8), and 80% (Cols. 9–10). |
| In the text | |
 |
Fig. 9. Examples of the overlap of thresholded structures for 2D simulation or inferred image pairs. Yellow pixels indicate where the structures overlap, and green pixels show where they do not. The dark background represents pixels below the threshold. The Dice coefficient is simply measured as |
| In the text | |
 |
Fig. 10. Left: dice coefficient (as defined by Eq. (9)) of the top n% pixels between 2D simulation images and their inferred counterparts in increments of 5% (yellow). The inner dark yellow layer represents measure uncertainty, and the outer yellow layer represents the standard deviation over the set. The random overlap is represented in black. Right, red: dice coefficient significance (see Eq. (11)). Blue: Normalized Dice coefficient (see Eq. (10)); both are represented with their standard deviation layers. |
| In the text | |
 |
Fig. 11. Ten cube slices from the 3D simulations (top row) and their ten AE-inferred counterparts (bottom row). Every image represents a slice from a 64 × 64 × 64 log density map of side 25 Mpc. As for the 2D case, the larger dense structures are better recovered than the finer diffuse structures. |
| In the text | |
 |
Fig. 12. Statistics for the 3D simulation cubes (red) and their AE-inferred counterparts (blue). The upper left panel shows the voxel PDF, the upper right panel shows the mean density distribution, the lower left panel shows the median 3D power spectrum as well as mad layer, and the lower right panel shows the average peak count per cube. In the same way as for the GAN, the curves overlap quite satisfactorily. |
| In the text | |
 |
Fig. 13. Left: dice coefficient (as defined by Eq. (9)) of the top n% voxels between the 3D simulation cubes and their inferred counterparts in increments of 5% (yellow). The inner dark yellow layer represents the measure uncertainty, and the outer yellow layer represents the standard deviation over the set. The random overlap is represented in black. Right, red: dice coefficient significance (see Eq. (11)). Blue: Normalized Dice coefficient (see Eq. (10)). The coefficients are represented with their standard deviation layers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.