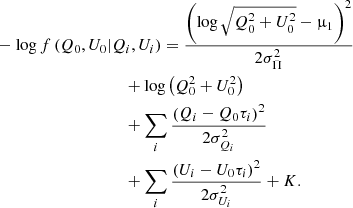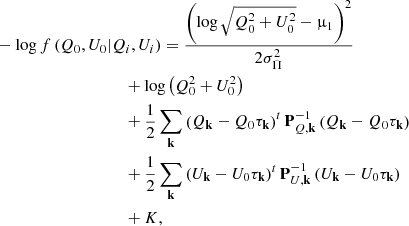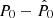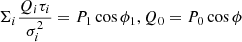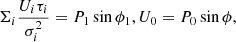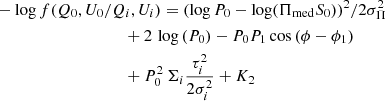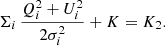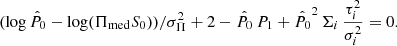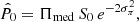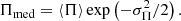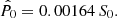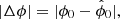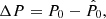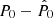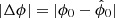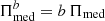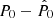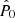| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 13 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202039741 | |
| Published online | 06 July 2021 | |
A Bayesian method for point source polarisation estimation
1
Instituto de Física de Cantabria, CSIC-UC, Av. de Los Castros s/n, 39005 Santander, Spain
e-mail: herranz@ifca.unican.es
2
Departamento de Matemáticas, Universidad de Oviedo, C. Federico García Lorca 18, 33007 Oviedo, Spain
3
Departamento de Física, Universidad de Oviedo, C. Federico García Lorca 18, 33007 Oviedo, Spain
4
Instituto Universitario de Ciencias y Tecnologías Espaciales de Asturias (ICTEA), Escuela de Ingeniería de Minas, Materiales y Energía de Oviedo, C. Independencia 13, 33004 Oviedo, Spain
5
Departamento de Física Moderna, Universidad de Cantabria, 39005 Santander, Spain
6
ESAC, Camino Bajo del Castillo s/n, 28692 Villafranca del Castillo, Madrid, Spain
Received:
22
October
2020
Accepted:
2
March
2021
The estimation of the polarisation P of extragalactic compact sources in cosmic microwave background (CMB) images is a very important task in order to clean these images for cosmological purposes –for example, to constrain the tensor-to-scalar ratio of primordial fluctuations during inflation– and also to obtain relevant astrophysical information about the compact sources themselves in a frequency range, ν ∼ 10–200 GHz, where observations have only very recently started to become available. In this paper, we propose a Bayesian maximum a posteriori approach estimation scheme which incorporates prior information about the distribution of the polarisation fraction of extragalactic compact sources between 1 and 100 GHz. We apply this Bayesian scheme to white noise simulations and to more realistic simulations that include CMB intensity, Galactic foregrounds, and instrumental noise with the characteristics of the QUIJOTE (Q U I JOint TEnerife) experiment wide survey at 11 GHz. Using these simulations, we also compare our Bayesian method with the frequentist filtered fusion method that has been already used in the Wilkinson Microwave Anisotropy Probe data and in the Planck mission. We find that the Bayesian method allows us to decrease the threshold for a feasible estimation of P to levels below ∼100 mJy (as compared to ∼500 mJy which was the equivalent threshold for the frequentist filtered fusion). We compare the bias introduced by the Bayesian method and find it to be small in absolute terms. Finally, we test the robustness of the Bayesian estimator against uncertainties in the prior and in the flux density of the sources. We find that the Bayesian estimator is robust against moderate changes in the parameters of the prior and almost insensitive to realistic errors in the estimated photometry of the sources.
Key words: methods: data analysis / techniques: image processing / polarization / cosmic background radiation / radio continuum: galaxies
© ESO 2021
1. Introduction
The polarisation properties of extragalactic radio sources (ERS) –that is to say radio galaxies, radio loud quasars, blazars, etc.– are not well constrained even at centimetre wavelengths, given that the total linear polarisation of ERS, P, in general constitutes a small fraction of their total flux density, S. The observed value of P being typically a few per cent, with only very few ERS showing a total polarisation fraction, Π = P/S, as high as ∼10 per cent of the total flux density (e.g., Sajina et al. 2011; Tucci & Toffolatti 2012). Moreover, at shorter wavelengths, that is at λ ≤ 1 cm, these properties are still poorly known due to the difficulty of properly calibrating in the radio to millimetre regime that afflicted the polarisation experiments until a few years ago. However, the knowledge of the total and polarisation fraction of ERS is rapidly improving at high radio frequencies thanks to large samples of sources mainly observed by the Australia Telescope Compact Array (ATCA) and by the Very Large Array (VLA; Sadler et al. 2006; López-Caniego et al. 2009; Massardi et al. 2008, 2011, 2013; Murphy et al. 2010; Jackson et al. 2010; Galluzzi et al. 2017, 2018). More recently, and thanks to the very high sensitivity of the new detectors of the Atacama Large Millimetre Array (ALMA), Galluzzi et al. (2019) could extend the analysis of polarisation properties of ERS performed by Galluzzi et al. (2018) up to 97.5 GHz, by polarimetric observations of a complete sample of 32 extragalactic radio sources. Their findings show that the distribution of the observed Π fractions is, again, well fitted by a log-normal distribution, thus confirming previous outcomes at lower frequencies (Massardi et al. 2013; Galluzzi et al. 2018) and also the predictions of Tucci & Toffolatti (2012). The analysis of Galluzzi et al. (2019) also confirms the absence of any statistically significant trend of polarisation properties of ERS with the frequency or the flux density.
Recent analyses of the ERS present in the full sky cosmic microwave background (CMB) anisotropy maps in polarisation provided by the European Space Agency (ESA) Planck mission (Planck Collaboration I 2016; Planck Collaboration XXVI 2016) also indicate typical median polarisation fractions of ERS of 2−3% at frequencies as high as 300 GHz (Bonavera et al. 2017a,b; Trombetti et al. 2018). Therefore, an accurate characterisation of polarisation properties of ERS as well as their efficient detection and subtraction from CMB maps is especially crucial for measuring the primordial CMB B-mode polarisation down to values of the tensor to scalar ratios r ∼ 0.001, which could be achievable by future space probes (i.e. LiteBird: Sekimoto et al. 2018; COrE: Delabrouille et al. 2018). We remind readers that the simulations by Remazeilles et al. (2018) have shown that at these low values of r, unresolved polarised ERS can probably be the dominant foreground at multipoles ℓ > 50 in the power spectrum of the CMB anisotropy. These results have been confirmed by Puglisi et al. (2018) by exploiting the state-of-the-art data sets on polarised point sources over the 1.4–217 GHz frequency range.
In addition to the essential information that the polarisation of ERS provides about the structure and evolution of extragalactic baryonic matter at low to intermediate redshifts, the study of this polarised radiation is paramount for cosmology, and in particular for CMB science. ERS detection and subtraction is a fundamental part of the component separation process necessary to achieve the science goals set for the next generation of CMB experiments. In particular, ERS would significantly affect the estimation of the CMB polarisation angular power spectra and, therefore, limit the ability of CMB experiments to constrain cosmological parameters such as the tensor-to-scalar ratio r of primordial perturbations during inflation. ERS could become an important obstacle for the detection of the primordial gravitational wave background (PGWB) for low values of r (Tucci et al. 2005; Puglisi et al. 2018; Trombetti et al. 2018) due to both the additional noise they constitute in themselves and the reduction in delensing power they cause by degrading lensing potential reconstructions (see, e.g., Sailer et al. 2020). Therefore, during recent years, the interest in the development of signal processing techniques specifically tailored for the detection and characterisation of ERS in CMB images has grown in the literature.
Signal processing techniques for the detection of polarised ERS must take the spinorial nature of electromagnetic waves into account. The signal can not only be described by one but as many as four independent components, one for the total intensity of the radiation field and three for its polarisation state. It is convenient to use the Stokes’ parameters S, Q, U, and V (S for total intensity1 in terms of flux density, see, e.g., Galluzzi et al. (2019), Q and U for linear polarisation, and V for circular polarisation), but other representations are also possible. The Stokes’ V parameter is not usually considered since Thomson scattering does not induce circular polarisation in the CMB. Circular polarisation mechanisms in active galaxies have been described in the literature (see for example Rayner et al. 2000), but they are nonetheless considered to be sub-dominant in comparison to linear polarisation mechanisms. Therefore, in this paper we consider, as it is customary2, V = 0. Then the signal processing of polarised ERS must deal with three independent quantities, two of them having the mathematical structure of a spinor field.
The S, Q, and U signals (or, alternatively, S, E, and B, or any other set of three quantities obtained from the Stokes’ parameters) can be treated separately as independent images to which any of the standard compact component separation techniques could be applied. The main difference with respect to the classical setting is that, unlike the total flux density S, which is always non-negative, Q and U can be either positive, negative, or zero. From a physical point of view, however, it makes more sense to process the polarisation data jointly (see Herranz et al. 2012, for a review on the topic). In particular, the total polarisation of a source 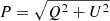 and its polarisation fraction Π = P/S are directly related to the physical processes occurring along the path of photons from the ERS to Earth, while Q and U are frame-dependent quantities lacking in physical meaning on themselves.
and its polarisation fraction Π = P/S are directly related to the physical processes occurring along the path of photons from the ERS to Earth, while Q and U are frame-dependent quantities lacking in physical meaning on themselves.
The two main problems arising when dealing with P are the typically low signal-to-noise ratio of the polarisation signal coming from ERS and the non-Gaussian distribution of its noise statistics. Regarding the former, as mentioned above, the typical polarisation fractions of ERS at frequencies below ∼10 GHz are at most 10%. This means that only a few ERS are bright enough to be detected in polarisation with present-day technology. A standard procedure to avoid false detections in polarisation is to detect sources in total intensity and then to try to estimate their polarisation properties in a non-blind way3. We follow this approach in this paper. Regarding the latter problem, assuming that the Q and U noises are Gaussian-distributed, P would have a non-Gaussian Rice distribution (Rice 1945). Rician distribution has strictly non-negative support and heavy tails, which firstly biases the estimation of the polarisation of the sources and secondly disrupts the intuitive interpretation of signal-to-noise in terms of σ thresholds which is used virtually everywhere else in radio astronomy. Simmons & Stewart (1985) discussed four estimators which attempted to correct for biasing in the degree of linear polarisation in the presence of low signal-to-noise ratios. More recently, Argüeso et al. (2009) studied the problem in the context of CMB astronomy and developed two methods for the detection and estimation of ERS in polarisation data: one that applies the Neyman-Pearson lemma to the Rice distribution, the Neyman-Pearson filter (NPF), and another based on pre-filtering before fusion of Q and U to obtain P, the filtered fusion (FF) method. That work found that under typical CMB-experiment settings, the FF outperforms the NPF both in terms of computational simplicity and accuracy, especially for low fluxes. López-Caniego et al. (2009) applied the FF to the Wilkinson Microwave Anisotropy Probe (WMAP) five-year data. The same method has been used to study the polarisation of the Planck Second Catalogue of Compact Sources (PCCS2, Planck Collaboration XXVI 2016) and of the QUIJOTE experiment wide survey source catalogue (Herranz et al. 2021). Alternatively, a novel method for the estimation of the polarisation intensity and angle of compact sources in the E and B modes of polarisation based on steerable wavelets has been recently proposed by Diego-Palazuelos et al. (2021).
All the previously mentioned methods attempt to estimate the ERS polarisation by minimising, as much as possible, the impact of noise and Galactic and extragalactic foregrounds on the observed signal. The expected value of the polarisation does not intervene in the estimation process. In other words, no a priori information is used in the estimation. Until very recently, this had been the most sensible choice as the polarisation properties of extragalactic sources were virtually unknown at microwave frequencies. However, as recent experiments and facilities such as the ALMA, Planck, and the upgraded versions of ATCA and VLA start shedding light on the λ ≤ 1 cm polarised sky, the possibility of adding physical priors to our signal processing techniques is gradually opening. In this paper, we propose a Bayesian maximum a posteriori (MAP) method for the estimation of the polarisation properties of point sources.
The structure of this paper is as follows. In Sect. 2 we review the current observational evidence to construct physical priors on the polarisation fraction of ERS and incorporate that information into two possible MAP estimators of the polarisation of a compact source of known flux density S. These MAP estimators take a form analogous to the Neyman-Pearson filter and FF by Argüeso et al. (2009), respectively, plus additional terms that contain the a priori physical information on the probability distribution function of P for ERS. We call these two methods Bayesian Rice and Bayesian filtered fusion (BFF), respectively. The BFF is easily applicable for both white and colour noise. For this reason, and because in Argüeso et al. (2009) it was shown that the FF outperforms the NPF, we focus on the BFF in the rest of the paper. In Sect. 3 we describe the simulations we used to test the BFF method. We first made simplistic simulations containing just white noise in Q and U and then we upgraded to realistic simulations with polarised Galactic foregrounds and CMB emissions. In both cases, we used angular resolution, pixel scale, and noise levels similar to the upcoming QUIJOTE experiment wide survey data at 11 GHz (Rubino et al. 2021). The results of applying the BFF to our simulations are discussed in Sect. 4, where we also provide a brief discussion about the robustness of the method against uncertainties on the priors and the determination of the total flux density of the sources. Finally, we draw our conclusions in Sect. 5.
2. Method
When we try to detect or estimate the polarisation P0 of a compact source embedded in Gaussian noise, which can be a good approximation when dealing with sources present in CMB maps, and when we consider the measured polarisation 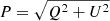 with similar Gaussian noise dispersions in Q and U, that is σQ = σU = σ, the distribution of P given P0 follows the Rice distribution
with similar Gaussian noise dispersions in Q and U, that is σQ = σU = σ, the distribution of P given P0 follows the Rice distribution
This is the conditional probability distribution of P, the measured polarisation, the given P0, and the source polarisation, with I0 being the modified Bessel function of zero order (Rice 1945). This distribution has been used to obtain suitable estimators of P0 (Simmons & Stewart 1985; Argüeso et al. 2009; López-Caniego et al. 2009; Herranz et al. 2012). However, no previous knowledge about P0 is assumed in these papers and this information, if available, could be very useful after being incorporated in a Bayesian scheme. Recently, relevant data about the distribution of the polarisation fraction at different frequencies, Π = P0/S0, with S0 being the source flux density, have been presented (Massardi et al. 2013; Galluzzi et al. 2017, 2019). According to these authors, this distribution can be represented by a log-normal probability density function (pdf)
where μ = log Πmed –with Πmed being the median polarisation fraction– and σΠ are easily obtained from ⟨Π⟩ and ⟨Π2⟩ (Crow & Shimizu 1988). Since P0 = ΠS0, if we assume that the value of S0 is known, then the distribution of P0 is readily calculated
with μ1 = μ + log(S0) = log(S0Πmed). This assumption is safe, since estimating S0 is much simpler than estimating P0 and point sources for which the polarised emission is detectable tend to have high flux densities. Therefore, we work, in general, with non-blind detection in polarisation. The knowledge of S0 allowed us to write the joint probability distribution of P and P0, h(P, P0) = f(P|P0)g(P0), and by using Bayesâ theorem
with g(P) = ∫h(P,P0)dP0. Finally, by substituting Eqs. (1) and (3) in Eq. (4), we obtain
The integral in the denominator is just a normalisation. We have found the distribution of P0 given P, the posterior distribution, simply by assuming Gaussian noise in Q and U with the same dispersion and a log-normal pdf for Π (prior distribution). Everything has been calculated for a source located at a central pixel and without taking into account any information about the beam and the data in a certain patch around the source. If we consider a polarised source at the central pixel of an n-pixel patch, a beam with a spatial profile τ(x), and values of Pi for the polarisation measured at each pixel i = 1, …, n, we can write the following expression for the conditional pdf of P0 given the Pi values at the different pixels:
Here Πi is the product symbol, τi is the profile at each pixel, and σi is the noise dispersion (it could be different from pixel to pixel). We took the natural logarithm from the right-hand side and changed sign, this is minus the log-posterior of the distribution, save constant terms. In this way, we obtained a simplified expression which we later minimised to find the estimator that makes the posterior distribution maximum
with
and
and where K is a constant term that encloses the proportionality terms not directly included in Eq. (7). If we differentiate with respect to P and equate to zero, the estimator 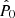 satisfies
satisfies
with I1 being the modified Bessel function of order one. On the other hand, in Argüeso et al. (2009), the FF method was shown to perform better than the one derived from the Rice distribution. The FF calculates the square root of the sum of the squares of the maps in Q and U to which a matched filter has been previously applied. This method is just a maximisation of the conditional probability of the data Qi, Ui given the source polarisation Q0, U0, assuming that the noise is Gaussian with zero mean and independent for each pixel
If we also assume that P0 follows a log-normal pdf and the polarisation angle distribution is uniform, we can combine the previous formula with the prior distribution of Q0, U0 and write, by applying Bayes’ theorem, minus the log-posterior of Q0, U0 given the data Qi, Ui
This expression could be very easily generalised, allowing even the treatment of correlations between the noise in different pixels. In that case, Eq. (12) can be written as
where the subindex k refers to the Fourier wave vector (or, for the case of spherical data, the appropriate spherical harmonic) and Px, k is the power spectrum (or angular power spectrum) of the noise for the Stokes parameter x. This formula is expressed in Fourier space for the sake of computational efficiency, but it could also be expressed in real space by means of the correlation matrix of the noise. In Eq. (13), it is clear that the third and fourth terms on the right side of the equation are analogous to the matched filter on the Q and U maps, which in turn are the solution of a maximum likelihood estimator (MLE). The first term adds the prior information, whereas the second term acts as a penalty for large values of the estimated polarisation, and finally the last term is a constant that is irrelevant for the solution.
Now we can obtain the estimators 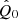 and
and 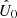 that minimise the previous expression. Finally, we find
that minimise the previous expression. Finally, we find
as our estimator of P0. In all of these formulas, we have not considered the effect of the circular polarisation, V. As mentioned in the introduction, this effect is very small and can be neglected in general. At any rate, the generalisation of the Rice and FF methods to include circular polarisation has been presented in Argüeso et al. (2011). However, in order to extend our Bayesian methods to this case, we would have to use a prior distribution for V which is not known yet.
To sum up the previous paragraphs: We have presented four possible estimators of P0, the old ones are the Rice method and the FF (Argüeso et al. 2009; López-Caniego et al. 2009; Herranz et al. 2012; Planck Collaboration XXVI 2016), and the new ones, obtained by minimising the right-hand sides of Eqs. (7) and (12) or (13), which we call the Bayesian Rice method and the Bayesian FF method, respectively. These new methods incorporate, in a natural way, our information about the source polarisation distribution. The FF and Rice methods are implemented by minimising Eqs. (7) and (12)–(13) without the first two terms, which come from the Bayesian prior.
3. Simulations
3.1. White noise
As a first test bed to assess the performance of the Bayesian techniques, we ran 10 000 simulations using only white noise as background for simulated sources. Table 1 shows the simulation parameters for these simulations; the pixel size, beam full width half maximum (FWHM), and white noise root mean square (rms) emulate those of the QUIJOTE (Rubiño-Martín et al. 2010, 2012; Génova-Santos et al. 2015; López-Caniego 2016) experiment wide survey at 11 GHz (Rubino et al. 2021). We used the same simulation parameters for the full sky simulations, which are discussed in Sect. 3.2.
Simulation parameters used for this work.
For these white noise simulations, we directly created flat images with uncorrelated Gaussian noise and at the centre we injected a point source with the FWHM listed in Table 1, a given flux density S0, and polarisation fraction Π randomly drawn from the log-normal distribution Eq. (2) with the mean and standard deviation values ⟨Π⟩ and σΠ described in Table 1. We simulated the intensities of S0 in ten logarithmically spaced values between 0.1 and 100 Jy. In this way, we obtained a sample of sources from moderately faint to extra bright (and, since the polarisation fraction follows distribution Eq. (2) with average ⟨Π⟩ = 0.02, values of P from below 1 mJy to a few tens of Janskys).
3.2. Full sky simulations
In order to assess the performance of our Bayesian techniques under realistic conditions, we used realistic simulations of the QUIJOTE experiment wide survey (Rubino et al. 2021). The QUIJOTE wide survey is observing approximately half the sky at 11, 13, 17, and 19 GHz. These simulations have been produced thanks to the EU RADIOFOREGROUNDS project4, but they are not yet available publicly. The simulations make use of the Planck Sky Model (PSM, Delabrouille et al. 2013), a global representation of the multi-component sky at frequencies ranging from 1 GHz to 1 THz that summarises, in a synthetic way, as much of our present knowledge of the gigahertz sky as possible. The PSM is a public code5 developed mostly by members of the Planck collaboration as a simulation tool for Planck activities and it makes it possible to simulate the sky in total intensity and the Q, U Stokes parameters for any experimental configuration in the gigahertz range. For this work, we chose to simulate the QUIJOTE wide survey at 11 GHz. Figures 1 and 2 show the full Q Stokes wide survey simulated at 11 GHz and the simulated QUIJOTE instrumental noise for the same Stokes parameter, area, and frequency. Table 1 indicates the main parameters used for this simulation.
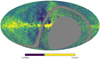 |
Fig. 1. Q-Stokes simulated QUIJOTE wide survey sky at 11 GHz. The false colour bar is expressed in Janskys. |
 |
Fig. 2. Q-Stokes simulated QUIJOTE wide survey instrumental noise at 11 GHz. The false colour bar is expressed in Janskys. The non-uniformity of the noise reflects the non-uniform sky scanning strategy of the telescope. |
Formula (13) could be applied to the whole sky, but since the statistical properties of the foregrounds vary strongly with Galactic latitude, we preferred to apply the Bayesian estimator locally. In order to test the method, we computed Eq. (13) on flat sky patches, projecting the HEALPix6 simulations described above on 64 × 64 pixel (that is, a 14.658 × 14.658 square degrees area) planar images.
We ran the estimator on 2000 flat patches as described above. In order to study the effect of the level Galactic contamination, we divided the sky in two areas: 10 000 simulations within a ‘Galactic’ band with a Galactic latitude of |b|≤10° and 10 000 within an external region with |b|> 10°. The centre sky coordinate of each patch was chosen randomly, according to these latitude intervals and inside the simulated wide survey observed area (see Figs. 1 and 2). For each patch, at the centre, we injected a point source with the FWHM listed in Table 1, a given flux density S0, and polarisation fraction Π randomly drawn from the log-normal distribution Eq. (2) with the mean and standard deviation values ⟨Π⟩ and σΠ described in Table 1. It is important to note that the PSM simulations already contain resolved and unresolved polarised point sources apart from the synthetic test sources we are injecting at the central position of each simulated patch. Figure 3 shows the Q and U Stokes parameters for one of our simulations. We simulated intensities of S0 in ten logarithmically spaced values between 0.1 and 100 Jy (that is, 200 sources–100 of them in the band, 100 of them outside it– with S0 = 0.1 Jy, 200 with S0 = 0.2154 Jy, and so on). In this way, we obtained a sample of sources from moderately faint to extra bright (and, since the polarisation fraction follows distribution Eq. (2) with average ⟨Π⟩ = 0.02, values of P from below 1 mJy to a few tens of Janskys).
 |
Fig. 3. Projected sky patches for one of our simulations. Map units are expressed in Janskys. (a) Stokes Q. (b) Stokes U. |
4. Results
4.1. White noise
In all the cases analysed with the white noise simulations, the performance of the Bayesian FF at estimating the source polarisation is better than that of the Bayesian Rice method. This was also the case for their non-Bayesian counterparts (Argüeso et al. 2009, etc.). Due to this and in also taking into account that the generalisation of the Bayesian Rice method to full-sky simulations is far from trivial7, from now on, we only compare the Bayesian FF and the FF techniques.
The left panel of Fig. 4 shows the estimation of the polarised flux density for the 10 000 white noise simulations. The results have been binned into eleven logarithmically spaced intervals in input P0. In blue, we show the results from the Bayesian estimator Eq. (13). The error bars show the 68.27% intervals of the corresponding empirical distributions. The filled circles indicate the median value of the distribution of results; the dots indicate the average value of the distribution. For comparison, the results of a MLE, which correspond to the third and fourth terms of Eq. (13), are shown in orange. The red dotted line shows the P = P0 line. The MLE is equivalent to the FF technique (Argüeso et al. 2009; López-Caniego et al. 2009; Herranz et al. 2012). Both the Bayesian FF and the MLE estimator work well for highly polarised sources (P0 ≳ 0.5 Jy). For input polarisation levels below ∼0.2 Jy (which is approximately the rms of the filtered noise of the simulations), however, the MLE reaches a plateau: It is naturally limited by the level filtered noise. The Bayesian estimator, on the contrary, uses the a priori information on the Π distribution and the knowledge of the source flux density S to predict lower P values. As a matter of fact, the Bayesian FF tends to overcompensate and predict, for the lower end of values of the input P0, polarised fluxes Pest ∼ 0.2P0. To see why this happens, we carried out a short theoretical calculation based on Eq. (12). The first part of Eq. (12) as a function of P0 is written below:
 |
Fig. 4. Left: binned estimates of the polarised flux density as a function of binned input P0, in Janskys, for the set of 10 000 simulated white noise patches. Right: error in the estimation |
If we define
and
the previous formula can be expressed in terms of P0, P1 and the polarisation angles
with
Taking the partial derivatives of Eq. (18) with respect to P0 and ϕ and equating them to zero, we obtain the estimators 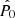 and
and 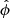 that minimise minus the log-posterior. It can be easily seen that
that minimise minus the log-posterior. It can be easily seen that 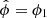 and
and 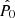 is the solution of the following equation:
is the solution of the following equation:
This equation is very interesting: If we assume that 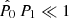 and
and 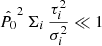 , that is, the source polarisation is much lower than the noise, the estimation is dominated by the Bayesian prior and in neglecting the last two terms in Eq. (20), we find a constant value for the estimator, independently of the data,
, that is, the source polarisation is much lower than the noise, the estimation is dominated by the Bayesian prior and in neglecting the last two terms in Eq. (20), we find a constant value for the estimator, independently of the data,
for a lognormal distribution and
Taking into account the values of ⟨Π⟩ and σΠ given in Table 1, Πmed = 0.012 and we obtain
In order to check these theoretical results, we carried out 10 000 simulations with S0 = 1 Jy. In this case, the noise, σ = 0.386 Jy, is much higher than the source polarisation. We find, for all our simulations, the estimated value 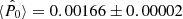 , which is compatible with the calculation above. Though the estimator is constant in this case, this value is closer to the real value than that obtained by using the matched filter, which is completely dominated by the noise.
, which is compatible with the calculation above. Though the estimator is constant in this case, this value is closer to the real value than that obtained by using the matched filter, which is completely dominated by the noise.
For higher values of S0, for example S0 = 10 Jy, there are around 5000 simulations, corresponding to the lower polarisations, that produce an estimator close to the default value 0.016−0.020 Jy. For higher values of the real polarisation, there is a combination of the prior and the matched filter terms in the solution of (20). At any rate, the performance of the Bayesian FF is better than that of the plain FF.
The right panel of Fig. 4 shows the polarised flux estimation error8 as a function of the input flux density (temperature) of the source S0. For low flux densities, the figure shows both the systematic overestimation of the MLE, due to the noise limit, and the underestimation of the Bayesian FF estimator due to the reasons discussed above. In absolute terms, the statistical error of the MLE is much larger than that of the Bayesian FF estimator in the low flux density regime. There is an interesting interval at intermediate flux densities (∼10 Jy) at which the errors of the MLE and Bayesian FF estimator are of the same order, but in opposite directions. The Bayesian estimator seems to reach a plateau (i.e. is noise-limited) around P0 ∼ 10 mJy, a, order of magnitude below in polarised flux than the MLE.
Figure 5 shows the absolute polarisation angle error,
 |
Fig. 5. Binned estimates of |
where ϕ0 and  are the input and estimated polarisation angles (in degrees), as a function of the input polarisation of the source P0. The figure shows that there is little difference between the Galactic and extragalactic areas, and between the Bayesian estimator and the MLE. This is not a surprise, since the priors in Eq. (13) are constant with respect to ϕ0, that is, the Bayesian estimator and the MLE should perform similarly, as is the case.
are the input and estimated polarisation angles (in degrees), as a function of the input polarisation of the source P0. The figure shows that there is little difference between the Galactic and extragalactic areas, and between the Bayesian estimator and the MLE. This is not a surprise, since the priors in Eq. (13) are constant with respect to ϕ0, that is, the Bayesian estimator and the MLE should perform similarly, as is the case.
4.2. Full sky simulations
Figure 6 shows the estimation of the polarised flux density for firstly the 10 000 ‘Galactic’ sky patches (|b|≤10°) and secondly the 10 000 ‘extragalactic’ (|b|> 10°) simulated QUIJOTE sky patches. The results have been binned into eleven logarithmically spaced intervals in input P0. In blue, we show the results from the Bayesian estimator Eq. (13). The error bars show the 68.27% intervals of the corresponding empirical distributions. For comparison, the results of a MLE, which correspond to the third and fourths terms of Eq. (13), are shown in orange. The MLE is equivalent to the FF technique (Argüeso et al. 2009; López-Caniego et al. 2009; Herranz et al. 2012). As it happened in the case of the white noise simulations (Sect. 4.1), for low flux density sources the MLE estimator reaches a plateau dominated by the noise level (higher for Galactic than for extragalactic sources). The Bayesian estimator reaches a similar plateau at much lower polarised fluxes, again in the ∼10 mJy regime instead of the ∼100 mJy regime of the MLE. Please note, however, that the distribution of the estimated  by means of the Bayesian estimator becomes more and more skewed as P0 decreases9.
by means of the Bayesian estimator becomes more and more skewed as P0 decreases9.
 |
Fig. 6. Binned estimates of the polarised flux density as a function of binned input P0, in Janskys, for the set of 10 000 simulated QUIJOTE sky patches with |b|≤10° (left) and the set of 10 000 simulated QUIJOTE sky patches with |b|> 10° (right) at 11 GHz. Bayesian estimations appear in blue, whereas maximum likelihood estimations are shown with an orange colour. Error bars show the 68.27% interval of the distribution of results in each case. Filled circles indicate the median of the distribution; the diamonds (for the MLE) and crosses (for the Bayesian estimator) indicate the average value of the distribution. |
Figure 7 shows the error of the estimation of P as a function of the input flux density of the sources (in Janskys). As in the case of white noise, the MLE estimator tends to overestimate the polarised flux of faint sources, whereas the Bayesian FF tends to underestimate it. This error is a systematic bias that tends to a constant value in relative terms, but decreases to zero Janskys in absolute terms for S0 → 0. Error bars are smaller for extragalactic sources than for Galactic sources, which are embedded in more intense foreground emission. Figures 8 and 9 show the normalised histograms of the difference ΔP between the input polarisation P0 and the estimated polarisation P,
 |
Fig. 7. Error in the estimation |
for eleven different values of the total (Stokes I) flux density S0. ‘Galactic’ sources are shown in Fig. 8 and ‘extragalactic’ sources are shown in Fig. 9. The estimation  has been obtained with the BFF method introduced in this paper (in blue) and the MLE (in red). For bright sources (S0 > 10 Jy), the histograms are approximately symmetric and centred around ΔP = 0, but for fainter sources the MLE histograms are skewed to the left, showing the same kind of overestimation already observed in Fig. 6. The histograms for the Bayesian estimator, however, are skewed to the right but much narrower than the MLE histograms, which indicates that the Bayesian estimator predicts the polarisation of a source with a smaller margin of error. Both types of error, MLE-overestimation and Bayesian FF-underestimation, must be dealt with in CMB polarisation experiments, but the amount of bias is significantly smaller for the Bayesian FF estimator.
has been obtained with the BFF method introduced in this paper (in blue) and the MLE (in red). For bright sources (S0 > 10 Jy), the histograms are approximately symmetric and centred around ΔP = 0, but for fainter sources the MLE histograms are skewed to the left, showing the same kind of overestimation already observed in Fig. 6. The histograms for the Bayesian estimator, however, are skewed to the right but much narrower than the MLE histograms, which indicates that the Bayesian estimator predicts the polarisation of a source with a smaller margin of error. Both types of error, MLE-overestimation and Bayesian FF-underestimation, must be dealt with in CMB polarisation experiments, but the amount of bias is significantly smaller for the Bayesian FF estimator.
 |
Fig. 8. Normalised histogram of the difference ΔP between the input polarisation P0 and the estimated polarisation for the Bayesian estimator (blue, /) and the MLE (red, \) for sources located within the Galactic band |b|≤10°, and for nine different values of the input total flux density S0. |
 |
Fig. 9. Normalised histogram of the difference ΔP between the input polarisation P0 and the estimated polarisation for the Bayesian estimator (blue, /) and the MLE (red, \) for sources located outside the Galactic band |b|> 10°, and for nine different values of the input total flux density S0. |
Finally, Fig. 10 shows the absolute polarisation angle error as a function of the input polarisation P0. The figure shows that there is little difference between the Galactic and extragalactic areas and between the Bayesian estimator and the MLE. This is not a surprise since the priors in Eq. (13) are constant with respect to ϕ0, that is, the Bayesian estimator and the MLE should perform similarly, as is the case.
 |
Fig. 10. Binned estimates of |
4.3. A note on the robustness of the Bayesian estimator
Every time some prior information is used in the Bayesian framework, one inevitably questions the effect a wrong guess has on the prior in the estimation. In order to shed some light on this, we re-analysed the one hundred simulations of ‘extragalactic’ sources with a flux density of S0 = 10 Jy10. Instead of using the correct value of the median polarisation fraction Πmed in Eq. (13), we used a biased parameter 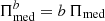 with b = [0.5, 0.6, …, 2.0], that is, we tested what happens if our guess for the median polarisation fraction is wrong by a factor from 50% to 200%. Figure 11 shows the average estimation error
with b = [0.5, 0.6, …, 2.0], that is, we tested what happens if our guess for the median polarisation fraction is wrong by a factor from 50% to 200%. Figure 11 shows the average estimation error 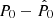 as a function of the bias factor b. Error bars show the 68.27% intervals of the corresponding empirical distributions. The figure shows that the average error of the Bayesian estimator varies smoothly with the bias in the prior. For comparison, for the same simulations, the MLE produces a (bias independent, as the maximum likelihood estimator does not use prior information) value for the error
as a function of the bias factor b. Error bars show the 68.27% intervals of the corresponding empirical distributions. The figure shows that the average error of the Bayesian estimator varies smoothly with the bias in the prior. For comparison, for the same simulations, the MLE produces a (bias independent, as the maximum likelihood estimator does not use prior information) value for the error 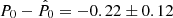 , which is larger than the Bayesian estimation (for this particular value of S0) even when the prior is wrong by a factor of two.
, which is larger than the Bayesian estimation (for this particular value of S0) even when the prior is wrong by a factor of two.
 |
Fig. 11. Error in the estimation of the total polarisation of a test source with S0 = 10 Jy as a function of the bias factor b (defined as |
Another potential source of bias is the uncertainty on the true flux density of the source. The estimators in Eqs. (12) and (13) depend implicitly on an a priori knowledge of the source flux density S0 through the factor μ1 = μ + log(S0). In the previous tests, we have assumed that S0 is known with arbitrary precision, but in practice this is not the case. In a real experiment, one expects to know some reasonable estimation of 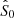 of the true flux density of the source. In a typical CMB experiment setting, the difference between S0 and
of the true flux density of the source. In a typical CMB experiment setting, the difference between S0 and 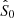 is relatively small (at least in comparison with the relative difference between P0 and
is relatively small (at least in comparison with the relative difference between P0 and 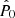 ), but not zero. The uncertainty on the source flux density can bias the estimators Eqs. (12) and (13) even if the distribution of
), but not zero. The uncertainty on the source flux density can bias the estimators Eqs. (12) and (13) even if the distribution of 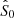 is symmetric around S0, as S0 enters the estimators in a non-linear fashion. Moreover, one expects the uncertainty in S to increase the statistical error of the estimators.
is symmetric around S0, as S0 enters the estimators in a non-linear fashion. Moreover, one expects the uncertainty in S to increase the statistical error of the estimators.
In order to test the effect of the uncertainty on S on our Bayesian estimator, we conducted a new batch of 10 000 simulations in the same fashion as described in Sect. 4.2. The analysis followed the same pipeline as described above, but every time we computed the estimator Eq. (13), we introduced a random photometric error in S0. These photometric errors follow a Gaussian distribution of standard deviation σ = 0.3 Jy, which is a little smaller than the QUIJOTE simulation noise rms level11.
Figure 12 shows the average error of the estimation of the polarisation of our simulated sources comparing the two cases: if the source flux density S0 is perfectly known in advance (blue dots and error bars) or if a 0.3 Jy photometric uncertainty is present in the analysis (orange dots and bars, slightly displaced to the right for the sake of clarity). Galactic and extragalactic cases (as defined above) are shown in the left and right panels, respectively. The effect of a ∼0.3 Jy photometric error on the flux density of the sources is negligible in our simulated experimental setting. This does not come as a surprise since a ∼0.3 Jy variation in S0 produces only a ∼10% change in the μ1 term that appears in Eqs. (12) and (13) in the worst case (1 Jy sources)12. This discrepancy quickly decreases as S0 grows. Moreover, the rms around the mean ⟨μ1⟩ also decreases very quickly with S0. Therefore, we conclude that our Bayesian estimator is robust against moderate uncertainties on the prior and the flux density of the sources.
 |
Fig. 12. Error in the estimation P − P0 (Jy), as a function of binned input S0 (Jy), for the set of 10 000 simulated QUIJOTE sky patches with |b|≤10° (left) and the set of 10 000 simulated QUIJOTE sky patches with |b|> 10° (right) at 11 GHz. Bayesian estimations for a perfect photometry of the source total flux density S0 appear in blue, whereas Bayesian estimations including a 0.3 Jy uncertainty in S0 are shown in orange. Error bars show the 68.27% interval of the distribution of results in each case. Filled circles indicate the median of the distribution, and dots indicate the average value of the distribution. Orange points and lines have been slightly displaced to the right in order to make the figure more readable. |
5. Conclusions
The estimation of the polarimetric properties of extragalactic compact sources at microwave wavelengths will be very relevant in the upcoming years. In this work, we have introduced a Bayesian approach for the estimation of the polarised flux density P of these kinds of sources. Following the recent works by Massardi et al. (2013) and Galluzzi et al. (2017, 2019), among others, we have proposed an analytical prior for the polarisation fraction of extragalactic radio sources, which takes the form of a log-normal distribution whose parameters (median, average, and variance values of the polarisation fraction) can be constrained by the latest observational data. Using this prior, we have proposed two MAP estimators of the polarisation of a given source given observations of its Q and U Stokes parameters. The first method works directly on the quadratic combination P2 = Q2 + U2, whereas the second method produces individual estimators of the ground-truth values Q0 and U0 that are then quadratically added to give an estimator of the ground-truth polarisation P0 of the source. We have called these methods Bayesian Rice and BFF, respectively. Both can be considered as natural Bayesian extensions of the frequentist Neyman-Pearson and standard FF methods introduced by Argüeso et al. (2009). The standard FF is shown to be equal to the MLE for P, whereas the BFF adds a number of additional terms to the MLE, including the a priori information on the distribution of the polarisation fraction. The BFF method can be easily accommodated to non-white noise and foregrounds. For this reason, we have focused on this method in most of our paper. We have tested the performance of the BFF method and compared it to that of FF using two sets of simulations: polarised sources embedded in Q and U white noise, and more realistic simulations that also include polarised CMB and Galactic foreground emission. In both cases, we have used the pixel and beam scales plus the noise levels and sky coverage of the QUIJOTE experiment wide survey (Rubino et al. 2021; Herranz et al. 2021) at 11 GHz. For the BFF, we assumed that the flux density S0 of the sources is perfectly known. For highly polarised sources, the two methods yield the same results, but for medium to low polarisations (P0 ≤ 400 mJy in our simulations) the BFF gets more accurate estimations of the polarisation of the sources. The FF gets noise-limited around a polarisation flux P0 ∼ 500 mJy, whereas the BFF allows us to reach polarised fluxes well below P0 ∼ 100 mJy before becoming noise-limited itself. Both estimators are biased for low polarisation (i.e. P0 ≲ 500 mJy) sources: The BFF tends to underestimate the polarisation, whereas the standard FF overestimates the polarisation of these sources. In the case of the FF, the bias is due to noise boosting of the signal (akin to Eddington bias). In the case of the BFF, the bias is originated by the extra terms in the estimator formula that come from the physical prior. However, the absolute value of bias is significantly smaller for the BFF than for the FF, especially for faint sources.
In the above discussion, we have assumed that the prior describes the real distribution of polarisation of the sources adequately and that the total flux density S0 of each source is perfectly known. However, information about the polarisation properties of extragalactic sources at microwave frequencies above ≃10 GHz is still scarce. Moreover, for any given source, S0 is known with a certain degree of uncertainty due to instrumental noise, less-than-perfect modelling of the spectral energy distribution of the source, and variability, among other possible causes. Towards the end of this work, we have tested the robustness of the BFF estimator against moderate changes in the prior parameters and realistic uncertainties in the flux density of the sources. Our simulations indicate that assuming the wrong prior has a mild effect on the Bayesian estimator. For example, for a S0 = 10 Jy source, a change by a factor of two in the assumed median polarisation fraction of the sources introduces errors or the order of ≲100 mJy in the estimation of P. Regarding uncertainties in the flux density of the sources, we find that non-catastrophic photometric error bars have a minimal impact on the estimation of P.
We therefore conclude that the Bayesian approach can significantly improve the estimation of the polarisation of extragalactic radio sources in current and upcoming CMB polarisation experiments. In an upcoming work, we will explore the extension of the Bayesian framework to the multi-frequency case.
The usual notation for this Stokes parameter is I. However, in this work we have changed the notation in order to avoid confusion between the intrinsic intensity of a source, which we refer to as S0 later in this paper, and the modified Bessel function of zero order, I0, that appears in several equations in Sect. 2.
Foregrounds can produce circular polarisation under some circumstances, and it has been observed in a few extragalactic sources. The value of V is typically much lower than the other Stokes’ parameters. As it is explained in Sect. 2, the existence of sources with non-zero circular polarisation would not affect our estimations of the Q and U Stokes parameters. Of course, if there was a significant V term, neglecting it would lead us to miss a part of the polarisation P. However, our method can be easily adapted to work with a third component in the form of an additional image –corresponding to the V Stokes’ parameter– if necessary.
The RADIOFOREGROUNDS project aims to combine two unique datasets, the nine Planck all-sky (30–857 GHz) maps and the four QUIJOTE Northern sky (10–20 GHz) maps, to provide the best possible characterisation of the physical properties of polarised emissions in the microwave domain, together with an unprecedentedly thorough description of the intensity signal. This legacy information will be essential for future sub-orbital or satellite experiments. See more information in http://www.radioforegrounds.eu/
Hierarchical Equal Area isoLatitude Pixelation of a sphere, http://healpix.sf.net.
We chose this particular flux density value because according to Fig. 9 it marks the flux density for which the Bayesian estimator begins to outperform the MLE.
We assume that the rms of the photometric errors has been lowered by means of some filtering scheme, such as a matched filter or a Mexican hat wavelet, or any other suitable signal processing technique. Then the ∼0.3 Jy uncertainty becomes a more realistic approximation of error in the determination the flux density of compact sources in the QUIJOTE wide survey.
Moreover, the estimation of the polarisation is not given directly by Eqs. (12) and (13), but by the minimisation of these functions. A small variation in one of the terms of the functions does not necessarily mean that the position of the minimum of the function changes in a noticeable way. The non-linear way in which S0 appears in these equations makes it difficult to find an analytical expression of how an uncertainty in S0 affects the minimisation. This question is better answered by simulations, just as we have done in this section.
Acknowledgments
We thank the Spanish MINECO and the Spanish Ministerio de Ciencia, Innovación y Universidades for partial financial support under projects AYA2015-64508-P and PGC2018-101814-B-I00, respectively. D. H. also acknowledges funding from the European Union’s Horizon 2020 research and innovation programme (COMPET-05-2015) under grant agreement number 687312 (RADIOFOREGROUNDS). Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) and healpy (Zonca et al. 2019) packages. This research made use of astropy, (http://www.astropy.org) a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018), matplotlib, a Python library for publication quality graphics (Hunter 2007), and SciPy, a Python-based ecosystem of open-source software for mathematics, science, and engineering (Virtanen et al. 2020). We acknowledge Santander Supercomputacion support group at the University of Cantabria (UC) who provided access to the supercomputer Altamira Supercomputer at the Institute of Physics of Cantabria (IFCA-UC-CSIC), member of the Spanish Supercomputing Network (https://www.res.es/en/about), for performing simulations/analyses.
References
- Argüeso, F., Sanz, J. L., Herranz, D., López-Caniego, M., & González-Nuevo, J. 2009, MNRAS, 395, 649 [Google Scholar]
- Argüeso, F., Luis Sanz, J., & Herranz, D. 2011, Signal Process., 91, 1527 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bonavera, L., González-Nuevo, J., Argüeso, F., & Toffolatti, L. 2017a, MNRAS, 469, 2401 [Google Scholar]
- Bonavera, L., González-Nuevo, J., De Marco, B., Argüeso, F., & Toffolatti, L. 2017b, MNRAS, 472, 628 [Google Scholar]
- Crow, E., & Shimizu, K. 1988, Lognormal Distributions: Theory and Applications (New York: M. Dekker) [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delabrouille, J., de Bernardis, P., Bouchet, F. R., et al. 2018, JCAP, 2018, 014 [Google Scholar]
- Diego-Palazuelos, P., Vielva, P., & Herranz, D. 2021, JCAP, 03, 048 [Google Scholar]
- Galluzzi, V., Massardi, M., Bonaldi, A., et al. 2017, MNRAS, 465, 4085 [Google Scholar]
- Galluzzi, V., Massardi, M., Bonaldi, A., et al. 2018, MNRAS, 475, 1306 [Google Scholar]
- Galluzzi, V., Puglisi, G., Burkutean, S., et al. 2019, MNRAS, 489, 470 [Google Scholar]
- Génova-Santos, R., Rubiño-Martín, J. A., Rebolo, R., et al. 2015, in Highlights of Spanish Astrophysics VIII, eds. A. J. Cenarro, F. Figueras, C. Hernández-Monteagudo, J. Trujillo Bueno, L. Valdivielso, et al., 207 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Herranz, D., Argüeso, F., & Carvalho, P. 2012, Adv. Astron., 2012, 410965 [Google Scholar]
- Herranz, D., López-Caniego, M., Génova-Santos, R., et al. 2021, A&A, submitted [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, N., Browne, I. W. A., Battye, R. A., Gabuzda, D., & Taylor, A. C. 2010, MNRAS, 401, 1388 [Google Scholar]
- López-Caniego, M. 2016, IAU Focus Meeting, 29, 54 [Google Scholar]
- López-Caniego, M., Massardi, M., González-Nuevo, J., et al. 2009, ApJ, 705, 868 [Google Scholar]
- Massardi, M., Ekers, R. D., Murphy, T., et al. 2008, MNRAS, 384, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Bonaldi, A., Bonavera, L., et al. 2011, MNRAS, 415, 1597 [Google Scholar]
- Massardi, M., Burke-Spolaor, S. G., Murphy, T., et al. 2013, MNRAS, 436, 2915 [Google Scholar]
- Murphy, T., Sadler, E. M., Ekers, R. D., et al. 2010, MNRAS, 402, 2403 [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puglisi, G., Galluzzi, V., Bonavera, L., et al. 2018, ApJ, 858, 85 [Google Scholar]
- Rayner, D. P., Norris, R. P., & Sault, R. J. 2000, MNRAS, 319, 484 [Google Scholar]
- Remazeilles, M., Banday, A. J., Baccigalupi, C., et al. 2018, JCAP, 2018, 023 [Google Scholar]
- Rice, S. O. 1945, Bell Syst. Tech. J., 24, 46 [Google Scholar]
- Rubiño-Martín, J. A., Rebolo, R., Tucci, M., et al. 2010, Astrophys. Space Sci. Proc., 14, 127 [Google Scholar]
- Rubiño-Martín, J. A., Rebolo, R., Aguiar, M., et al. 2012, in Ground-based and Airborne Telescopes IV, Proc. SPIE, 8444, 84442Y [Google Scholar]
- Rubino, M., Pizzella, A., Morelli, L., et al. 2021, A&A, submitted [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2006, MNRAS, 371, 898 [Google Scholar]
- Sailer, N., Schaan, E., & Ferraro, S. 2020, Phys. Rev. D, 102, 63517 [Google Scholar]
- Sajina, A., Partridge, B., Evans, T., et al. 2011, ApJ, 732, 45 [Google Scholar]
- Sekimoto, Y., Ade, P., Arnold, K., et al. 2018, in Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave, eds. M. Lystrup, H. A. MacEwen, G. G. Fazio, N. Batalha, et al., Int. Soc. Opt. Photonics (SPIE), 10698, 613 [Google Scholar]
- Simmons, J. F. L., & Stewart, B. G. 1985, A&A, 142, 100 [NASA ADS] [Google Scholar]
- Trombetti, T., Burigana, C., De Zotti, G., Galluzzi, V., & Massardi, M. 2018, A&A, 618, A29 [CrossRef] [EDP Sciences] [Google Scholar]
- Tucci, M., & Toffolatti, L. 2012, Adv. Astron., 2012, 624987 [Google Scholar]
- Tucci, M., Martínez-González, E., Vielva, P., & Delabrouille, J. 2005, MNRAS, 360, 935 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Zonca, A., Singer, L., Lenz, D., et al. 2019, J. Open Source Software, 4, 1298 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Q-Stokes simulated QUIJOTE wide survey sky at 11 GHz. The false colour bar is expressed in Janskys. |
| In the text | |
 |
Fig. 2. Q-Stokes simulated QUIJOTE wide survey instrumental noise at 11 GHz. The false colour bar is expressed in Janskys. The non-uniformity of the noise reflects the non-uniform sky scanning strategy of the telescope. |
| In the text | |
 |
Fig. 3. Projected sky patches for one of our simulations. Map units are expressed in Janskys. (a) Stokes Q. (b) Stokes U. |
| In the text | |
 |
Fig. 4. Left: binned estimates of the polarised flux density as a function of binned input P0, in Janskys, for the set of 10 000 simulated white noise patches. Right: error in the estimation |
| In the text | |
 |
Fig. 5. Binned estimates of |
| In the text | |
 |
Fig. 6. Binned estimates of the polarised flux density as a function of binned input P0, in Janskys, for the set of 10 000 simulated QUIJOTE sky patches with |b|≤10° (left) and the set of 10 000 simulated QUIJOTE sky patches with |b|> 10° (right) at 11 GHz. Bayesian estimations appear in blue, whereas maximum likelihood estimations are shown with an orange colour. Error bars show the 68.27% interval of the distribution of results in each case. Filled circles indicate the median of the distribution; the diamonds (for the MLE) and crosses (for the Bayesian estimator) indicate the average value of the distribution. |
| In the text | |
 |
Fig. 7. Error in the estimation |
| In the text | |
 |
Fig. 8. Normalised histogram of the difference ΔP between the input polarisation P0 and the estimated polarisation for the Bayesian estimator (blue, /) and the MLE (red, \) for sources located within the Galactic band |b|≤10°, and for nine different values of the input total flux density S0. |
| In the text | |
 |
Fig. 9. Normalised histogram of the difference ΔP between the input polarisation P0 and the estimated polarisation for the Bayesian estimator (blue, /) and the MLE (red, \) for sources located outside the Galactic band |b|> 10°, and for nine different values of the input total flux density S0. |
| In the text | |
 |
Fig. 10. Binned estimates of |
| In the text | |
 |
Fig. 11. Error in the estimation of the total polarisation of a test source with S0 = 10 Jy as a function of the bias factor b (defined as |
| In the text | |
 |
Fig. 12. Error in the estimation P − P0 (Jy), as a function of binned input S0 (Jy), for the set of 10 000 simulated QUIJOTE sky patches with |b|≤10° (left) and the set of 10 000 simulated QUIJOTE sky patches with |b|> 10° (right) at 11 GHz. Bayesian estimations for a perfect photometry of the source total flux density S0 appear in blue, whereas Bayesian estimations including a 0.3 Jy uncertainty in S0 are shown in orange. Error bars show the 68.27% interval of the distribution of results in each case. Filled circles indicate the median of the distribution, and dots indicate the average value of the distribution. Orange points and lines have been slightly displaced to the right in order to make the figure more readable. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} f \left( P | P_{ 0 } \right) = P / \sigma ^ { 2 } \exp \left[ - \left( P ^ { 2 } + P_{ 0 }^{ 2 } \right) / 2 \sigma ^ { 2 } \right] I_{ 0 } \left( P P_{ 0 } / \sigma ^ { 2 } \right) .\end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq3.gif)
![$$ \begin{aligned} { g} ( \Pi ) = \frac{ 1 }{ \sqrt{ 2 \pi } \sigma _{ \Pi } \Pi } \exp \left[ - ( \log ( \Pi ) - \upmu )^{ 2 } / 2 \sigma _{ \Pi }^{ 2 } \right] ,\end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq4.gif)
![$$ \begin{aligned} { g} \left( P_{ 0 } \right) = \frac{ 1 }{ \sqrt{ 2 \pi } \sigma _{ \Pi } P_{ 0 } } \exp \left[ - \left( \log P_{ 0 } - \upmu _{ 1 } \right)^{ 2 } / 2 \sigma _{ \Pi }^{ 2 } \right] \end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq5.gif)
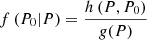
![$$ \begin{aligned} f \left( P_{ 0 } | P \right) = \frac{ e^{ - P_{ 0 }^{ 2 } / 2 \sigma ^ { 2 }} I_{ 0 } \left[\frac{ P P_{ 0 }}{ \sigma ^ { 2 }} \right] \exp \left[ - \frac{\left( \log P_{ 0 } - \upmu _{ 1 } \right)^2 }{ 2 \sigma _{\Pi } ^2} \right] \frac{ 1 }{P_0} }{ \int { e^{ - P_{ 0 }^{ 2 } / 2 \sigma ^ { 2 }} I_{ 0 } \left[\frac{ P P_{ 0 }}{ \sigma ^ { 2 }} \right] \exp \left[ - \frac{\left( \log P_{ 0 } - \upmu _{ 1 } \right)^2 }{ 2 \sigma _{\Pi } ^2} \right] \frac{ d P_0 }{P_0}} } . \end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq7.gif)
![$$ \begin{aligned}&f \left( P_{ 0 } | P_{ i } \right) \propto \exp \left[ - \frac{\left( \log P_{ 0 } - \upmu _{ 1 } \right)^{ 2 } }{ 2 \sigma _{ \Pi }^{ 2 }} \right] \frac{ 1 }{ P_{ 0 } } \nonumber \\&\qquad \qquad \times \prod _ { i } \exp \left[ - P_{ 0 }^{ 2 } \frac{ \tau _{ i }^{ 2 } }{ 2 \sigma _{ i }^{ 2 } } \right] I_{ 0 } \left[ P_{ 0 } \frac{ P_{ i } \tau _{ i } }{ \sigma _{ i }^{ 2 } } \right] .\end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq8.gif)
![$$ \begin{aligned}&- \log f \left( P_{ 0 } | P_{ i } \right) = \frac{\left( \log P_{ 0 } - \upmu _{ 1 } \right)^{ 2 } }{ 2 \sigma _{ \Pi }^{ 2 }} + \log \left( P_{ 0 } \right) + P_{ 0 }^{ 2 } z \nonumber \\&\qquad \qquad \qquad \qquad - \sum _{ i } \log I_{ 0 } \left[ P_{ 0 } \, { y}_{ i } \right] + K \end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq9.gif)
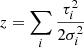
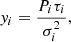
![$$ \begin{aligned} \frac{ \log \hat{ P }_{ 0 } - \upmu _{ 1 } }{ \hat{ P }_{ 0 } \sigma _{ \Pi }^{ 2 }} + \frac{ 1 }{ \hat{ P }_{ 0 } } + 2 \hat{ P }_{ 0 } z - \sum _{ i } \frac{ I_{ 1 } \left[ \hat{ P }_{ 0 } { y}_{ i } \right] }{ I_{ 0 } \left[ \hat{ P }_{ 0 } { y}_{ i } \right] } \, { y}_{ i } = 0 ,\end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq13.gif)
![$$ \begin{aligned} f(Q_i,U_i|Q_0,U_0)\!=\!\prod _ { i } \! \exp \left[ \frac{ \left( Q_{ i } - Q_{ 0 } \tau _{ i } \right)^{ 2 } }{ 2 \sigma _{Q_ i }^{ 2 } } +\, \frac{ \left( U_{ i } - U_{ 0 } \tau _{ i } \right)^{ 2 } }{ 2 \sigma _{U_ i }^{ 2 } } \right] .\end{aligned} $$](/articles/aa/full_html/2021/07/aa39741-20/aa39741-20-eq14.gif)