EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 651 (July 2021) A&A, 651 (2021) A53 Full HTML
Free Access
Issue
A&A
Volume 651, July 2021
Article Number A53
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201936385
Published online 12 July 2021

© ESO 2021

1 Introduction

Methanol is the most abundant alcohol in the Universe. It is commonly accepted that the molecule is the end product of successive hydrogenation of CO onto dust grains (Tielens & Whittet 1997; Watanabe et al. 2004). In the vicinity of young protostars, icy mantles of the grains are warmed up and release the molecules back into the gas phase (e.g., Garrod & Herbst 2006). Methanol is excited in the warm envelopes and outflows around protostars (Flower et al. 2010) and creates a dense forest of emission lines that almost covers the whole continuum emission at submillimeter (submm) to millimeter (mm) wavelengths (e.g., Bergin et al. 2010).

The challenge to the current understanding of the interstellar chemistry is the presence of methanol and other complex organic molecules in cold clouds and starless cores found in submm/mm observations (Cernicharo et al. 2012; Bacmann et al. 2012; Jiménez-Serra et al. 2016; Taquet et al. 2017; Punanova et al. 2018). A starless core is a compact, dense region of a molecular cloud, with a typical radius of about 0.1 pc (see Bergin & Tafalla 2007, for review). Visual extinctions at the central regions range from AV ~ 20 mag for less developed cores to >100 mag for the densest ones. With no heating sources nearby or embedded within them, the gas and dust in these cores are cold, with typical temperatures ~10 K or lower (Crapsi et al. 2007; Harju et al. 2008; Hocuk et al. 2017). As a result, CO and other heavy molecules containing oxygen and carbon are frozen onto dust grains toward the center of these cores, possibly leaving only molecular hydrogen and nitrogen-bearing volatile species such as NH3, N2H+, and HCN in the gas phase (Walmsley et al. 2004).

Methanol and other large organics have been found in starless cores near the edges of the CO depletion zones (Tafalla et al. 2006; Bizzocchi et al. 2014; Vastel et al. 2014; Jiménez-Serra et al. 2016; Chacón-Tanarro et al. 2019a). This is inexplicable for two reasons. First, as no energetic sources are in cold starless cores, it is hard to eject methanol and other molecules formed on the grain surface to the gas phase. Second, radical-radical reactions on the grain surface are assumed to play a key role in the formation of complex organic molecules in the interstellar medium (Garrod & Herbst 2006; Garrod et al. 2008). For the surface reactions between radicals, the dust temperatures should be 30–40 K (e.g., Tielens & Hagen 1982), so that the grains are not too hot to evaporate the molecules, but also not too cold to hinder the surface diffusion and to allow surface atomic hydrogen to saturate radicals. Although methanol itself can form because atomic hydrogen remains mobile at low temperatures, most of the precursors of complex organic molecules would be fixed on their binding sites at temperatures near 10 K.

Vasyunin et al. (2017) further developed the scenario proposed in Vasyunin & Herbst (2013), and explained the presence of methanol and of large organics in starless cores with two new mechanisms: efficient chemical (i.e., reactive) desorption from CO-rich ice surface (Minissale et al. 2016a) as opposed to water-ice surface, and a class of OH radical reactions that proceed fast at low temperatures in the gas phase (Shannon et al. 2013; Balucani et al. 2015; Antiñolo et al. 2016). The formation of methanol and complex organic molecules proceeds as follows: (i) CO starts to freeze out catastrophically at distances of thousands of AU from the cloud center (e.g., Caselli et al. 1999). The grain surfaces are covered by CO-rich ice, where CO molecules are efficiently transformed into CH3OH through hydrogenation reactions. (ii) A fraction of the CH3OH molecules formed on CO-rich ice desorbs from the surface using the additional energy made available upon formation (e.g., Garrod et al. 2006; Minissale et al. 2016a). (iii) When it is in the gas phase, methanol and other radicals such as CH3O and HCO initiate a series of reactions in the gas phase that lead to oxygen-bearing organic molecules. Neutral-neutral reactions involving OH are particularly important because they proceed fast at low temperatures, as the lifetimes of the hydrogen-bonded intermediate complexes become longer, and quantum tunneling allows reactions to proceed. The new model not only explains how methanol and complex organic molecules could be present in cold starless cores, but also why they are found near the edges of the CO depletion zones (Tafalla et al. 2006; Bizzocchi et al. 2014). Models invoking nondiffuse grain surface chemical processes have recently been proposed (Jin & Garrod 2020). However, the abundances of complex organics predicted by these models fall short by at least one order of magnitude with respect to those measured toward the L 1544 starless core.

The chemical model of Vasyunin et al. (2017) is based on the radial profiles of the density, temperatures, and AV computed for the starless core L 1544 by Keto & Caselli (2010). CO is heavily depleted in L 1544, showing a cavity of C17O emission with a radius of ≃6500 AU (Caselli et al. 1999). Bizzocchi et al. (2014) found that methanol emission peaks about 4000 AU away from the dust emission peak, close to the rim of the CO freeze-out zone (see also Punanova et al. 2018). Other organics such as dimethyl ether and methyl formate were also found near the methanol peak (Jiménez-Serra et al. 2016). Vasyunin et al. (2017) predicted that the local fractional abundance of methanol ice to water ice could be as high as 50% at the edge of the CO depletion zone. The goal of the present study is to measure the abundances of methanol and water ice toward L 1544 through 3 μm spectroscopy and compare them to the model predictions by Vasyunin et al. (2017). The paper is organized as follows. The observations are described in Sect. 2, the results are presented in Sect. 3, and the comparison between the observations and the model is discussed in Sect. 4.

thumbnail Fig. 1

Background stars observed toward L 1544 in the present study. First panel from the left: DSS color image of L 1544 to delineate the dark patch of the starless core. Second panel: extinction map based on the Herschel/SPIRE far-infrared imaging. Third panel: close-up view of the central part of L 1544, enclosed within the orange rectangle on the second panel. The positions of the 2MASS/WISE sources are marked with crosses. Fourth panel: dust color temperature based on Herschel/SPIRE imaging. The methanol peak observed by Bizzocchi et al. (2014) is shown with orange contours. The half-transparent circle roughly denotes the region where CO is frozen out (Caselli et al. 1999).

2 Observations

2.1 Target selection

The gas-phase methanol peak in L 1544 is located about half an arcminute northeast of the sub-mm/mm dust emission peak (RA = 05:04:17.21, Dec = +25:10:42.8; J2000 Ward-Thompson et al. 1994, 1999). In order to perform spectroscopy through the cloud, we needed suitable background stars. We selected all stars within 5′ of the continuum peak from the WISE1 and 2MASS2 catalogues. The archival images by Herschel/SPIRE (Griffin et al. 2010) are used to construct the extinction map on L 1544 that we compare with the locations of the potential targets. Five sources are visible in the seven near-mid infrared bands from 1.2 to 22 μm (Fig. 1). To avoid the sources on the foreground, the infrared photometry of the sources was compared to the stellar photospheric models of Bressan et al. (2012) after applying the interstellar extinction law derived by Boogert et al. (2011). All five sources are consistent with being G - to M-type stars on the background. The three brightest sources in WISE W1 band (3.4 μm), 3, 5, and 1 in Fig. 1, are observed in the present study. The summary of the targets is listed in Table 1.

2.2 Spex at IRTF

The spectroscopic observations were carried out with the SpeX spectrograph (Rayner et al. 2003) at the IRTF on Maunakea in the nights of 20 and 21 November 2018 UT. The instrument was remotely operated from Munich in Germany. The sky was clear on both nights, and the seeing was 0.″ 5–0.″6 at K band. The secondary mirror of the IRTF was fresh from recoating, which helped to suppress the telescope emissivity during the observation.

The instrument optics was set to LXD short configuration with 0.″5 × 15″ slit to deliver a spectral resolution R = 1200. The full coverage of the wavelength in LXD short is 1.67–4.22 μm. The targets were continuously guided in the slit during the integration in the guiding camera of SpeX at K band. The position angle of the slit was set roughly along the parallactic angle at the time of the observation to minimize the flux loss by the atmosphericrefraction. The telescope was nodded along the slit every other exposure to remove the background emission of the sky. The total on-source integration times are summarized in Table 1. The spectroscopic standard star HR 1791 (B7 III, R = 1.66 mag) was observed each night at a similar airmass as the science targets. The spectrograms of the flat-field illumination and the arc lamp were obtained after the science and the standard star observations without changing the telescope pointing to prevent the wavelength mapping from moving on the detector by the instrument flexure. In addition to the calibrations at each pointing positions, additional flat field frames were obtained in the daytime after the observations with the telescope in the stow position.

Table 1

Column densities of water and methanol ice.

2.3 Data reduction

The raw data were reduced by the software suite xSpextool coded by Cushing et al. (2004). xSpextool3 produces flat-field images to normalize the pixel-by-pixel fluctuation of the detector response and sets up the wavelength mapping on the detector array referring to the arc-lamp images. After calibrating the flux and the wavelength, xSpextool removes the sky and telescope emissions by pair subtraction, combines the spectrograms obtained for one target, and extracts one-dimensional spectra from the fully calibrated spectrogram images.

The spectra of the science targets are divided by the spectrum of the standard star to remove the telluric lines. The blackbody radiation spectrum of the temperature equal to the effective temperature of the standard star is multiplied to restore the continuum shape of the science targets. The spectral strips of the different diffraction orders are stitched together so that the overlapping intervals appear to be smooth. All these additional tasks after the aperture extraction are handled by the programs that come with the xSpextool suite.

The prominent H I lines of the photosphere of the standard stars (e.g., Br γ and Pf γ) were removed by subtracting Lorentzian profiles that fit the line shape. The H I lines that are blended with the telluric lines (e.g., Pf δ) were removed from the science spectrum after the telluric lines were corrected for the standard star spectrum.

The sources we observed are background field stars of late spectral types. In order to measure the ice optical depth, the intrinsic photospheric features had to be removed. The water vapor absorption at 2.5–2.7 μm is particularly troublesome as it lies on top of the water ice absorption at 3.0 μm. The photospheric lines were removed by comparing the science spectra to the template spectra of the IRTF spectral library (Rayner et al. 2009) after the templates were reddened by the interstellar extinction law. Best-matching templates were sought for manually by inspecting how good they reproduced the overall continuum shape and the CO overtone band at 2.3 μm. The optical depths of the ice were calculated with the template spectrum as a reference of the null absorption. The details of the data reduction can be found in Goto et al. (2018). The reduced optical depth spectra are reported in Fig. 2. The spectra look flat for the wavelength range between ~2 and 2.5 μm as well as toward the end of the long-wavelength wing of the water absorption feature centered at 3 μm, which is anindication of the goodness of the continuum fit in the observed spectra.

3 Result

3.1 Methanol ice at 3.54 μm

The prime goal of the observation is to detect the ν3 stretching band of methanol ice at 3.53–3.54 μm. Of the three stars we observed, only source 3 shows significant absorption at 3.54 μm over the noise level (top row in Fig. 3). To measure the methanol to water-ice ratio quantitatively, the laboratory transmission spectra of water ice with different degrees of methanol inclusions (Hudgins et al. 1993) were compared to the spectrum of source 3. The interstellar weak mix of Hudgins et al. (1993) is a blend of ice with the mixing ratio H2O:CH3OH:CO:NH3 = 100:10:1:1. The interstellar strong mix only differs in containing more methanol ice following the ratio H2O:CH3OH:CO:NH3 = 100:50:1:1 (see the left panels in Fig. 3). Pure water ice does not contain methanol or other molecules. The laboratory data are taken for low-temperature measurements at 10 K.

The use of a H2O:CH3OH:CO:NH3 chemical mixture is justified by the chemical models of the L 1544 starless core (Vasyunin et al. 2017). In these models, the formation of CH3OH from CO ice hydrogenation takes place while O and N atoms (still present in the gas phase) also adsorb onto the grain surface. This leads to the production of H2O and NH3 ice on the surface at the same time as CH3OH in such a way that the presence of H2O and NH3 ice on CO-rich mantles is expected (see Müller et al. 2020). In addition, we note that the red wing of the water absorption feature at 3 μm can be contaminated by NH3 hydrates (Dartois & d’Hendecourt 2001).

We employed the laboratory data from Hudgins et al. (1993) because they are easily available from the most common databases and because they present the advantage of allowing a straightforward comparison with ice mixtures with two significant H2O:CH3OH ratios (100:10 and 100:50). In particular, the data from Hudgins et al. (1993) are the only ones available for a H2O:CH3OH ratio of 100:10, which is required to explain our observations (see below).

The transmission spectra were converted into optical depths and then scaled so that the peak optical depth of water ice matched what is observed toward source 3 at 3.0 μm (left panel in the top row of Fig. 3; the middle panel is a close-up view at 3.54 μm). Polynomial functions were fit to the local continua near 3.54 μm, and subtracted from the laboratory and astronomical data (right panel). An excess absorption is found at 3.54 μm in the spectrum of source 3, with a corresponding optical depth of τ ~ 0.03. This is taken as a positive detection of methanol ice. When we linearly scale the laboratory spectrum of the interstellar weak mix to the astronomical spectrum, the methanol over water-ice ratio is 10.6 ± 0.7%. This ratio is consistent with those measured toward other starless cores such as L 429 and L 694 (of ~12–14%; see Boogert et al. 2011; Chu et al. 2020), also using the 3.54 μm methanol absorption feature.

There is a small offset (0.01 μm) in the peak absorption wavelengths toward longer wavelengths between the laboratory and the astronomical spectra (right panel in the top row of Fig. 3). The nature of the offset is not clear. The size of the shift is too large to be considered an uncertainty of the wavelength calibration in the SpeX spectra.The water-ice absorptions at 3.0 μm have a similar shift between the laboratory and the astronomical spectra. This shift could be produced by scattering effects caused by different grain shapes and sizes (see, e.g., Pontoppidan et al. 2003; Thi et al. 2006; Noble et al. 2013). However, given the low signal-to-noise ratio (S/N) of the methanol absorption feature, these effects are probably not noticeable. The observed shift is more likely associated with variations in the chemical composition of the ices (W.-F. Thi, priv. comm.). This will be explored in a separate paper (Müller et al. 2020).

We point out that a comparison with spectra from the Sackler Laboratory Ice Database (Fraser & van Dishoeck 2004) has also been attempted for CH3OH:CO 1:1 ice mixtures and layers. The laboratory methanol feature at 3.54 μm, however, does not show a significant shift when co-deposited with CO as compared to the layered deposition, at least for the ratio probed in these experiments. In any case, the comparison with the data from Hudgins et al. (1993) provides a better match to the CH3OH ice absorption spectra observed toward star 3 in the L 1544 starless core.

The same analysis as used for star 3 was applied to sources 1 and 5, and is shown in Fig. 3. Source 1 is the closest to the methanol peak, and is expected to show the highest methanol-ice abundance among the three sources we observed. However, the source is faint, and we could only set the upper limit on the methanol-ice abundance at 12.0% for 3σ significance. The upper limit of the methanol-ice abundance in source 5 is 59%.

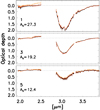thumbnail Fig. 2

Optical depth spectra of three sources behind L 1544 shown in the order of visual extinction. The optical depth is measured with respect to the matching template spectra chosen from the IRTF spectral library (Rayner et al. 2009). The spectra reduced with three best-matching templates are shown (black, orange, and yellow traces in the order of goodness of matching). The identification of the sources is the same as in Fig. 1. The atmospheric transmission is low at the wavelengths 2.50–2.85 μm and 3.29–3.31 μm because of the telluric water and methane absorption, respectively. The data in these intervals are removed from the presentation.

3.2 Water ice at 3.0 μm

The water ice is positively detected in all three sources in L 1544. The peak optical depths were measured by fitting a Gaussian profile to the spectra, and they are shown in Table 1. To measure the column density of the water ice quantitatively, first the optical-depth spectrum of pure water ice from the laboratory (Hudgins et al. 1993) was scaled so that the maximum optical depth τ3.0 was unity. The normalized optical depth spectrum was integrated over the whole band to the equivalent width. The column density of the water ice in the laboratory was then calculated from the equivalent width by multiplying the integrated band strength of Gerakines et al. (1996). In this way, we know that the unit peak optical depth at 3.0 μm amounts to a column density of 1.68 × 1018 cm−2. The column density of the water ice was calculated by multiplying this factor with the observed τ3.0 of each source.

We note that the laboratory pure water-ice spectrum does not reproduce the red wing observed for the water absorption features measured at 3 μm toward the three stars. This is caused by a possible mixture with NH3 ice and scattering by larger grains (see Sect. 3.1 and Dartois & d’Hendecourt 2001; Pontoppidan et al. 2003; Thi et al. 2006; Noble et al. 2013). The Gaussian profile, however, nicely fits the water feature between ~2.9 and 3.15 μm, which is sufficient to accurately determine the peak optical depths (see, e.g., Chu et al. 2020).

thumbnail Fig. 3

Optical depth spectra obtained toward the three stars located behind L 1544, shown in order of visual extinction. The optical depth is measured with respect to the matching template spectra chosen from the IRTF spectral library (Rayner et al. 2009). Source labels are the same as in Fig. 1. The atmospheric transmission is low at the wavelengths between 2.50–2.85 μm and 3.29–3.31 μm because of the telluric water and methane absorption, respectively. The data in these intervals are removed from the presentation. Left panel in the top row: spectrum of star 3 (black) compared to the laboratory ice spectra from Hudgins et al. (1993). The pure water ice spectrum is shown in yellow, the interstellar weak mix (H2O:CH3OH:CO:NH3 = 100:10:1:1) in orange, and the interstellar strong mix, 100:50:1:1, in red. Middle panel: zoomed view of the left panelwithin the gray rectangle. Right panel: comparison of astronomical (black) and laboratory (red) spectra after the local continua were subtracted. The laboratory spectrum of methanol ice is scaled so that the absorption peak matches the observation. The thick red trace is shifted by 0.01 μm from the laboratory measurement (thin trace). Middle and bottom rows: same as the top row, but for sources 1 and 5, respectively.The methanol ice absorption feature is not detected.

4 Discussion

4.1 Assessment of AV

We discuss first how the visual extinction was measured in the three sources. In our study, AV was estimated in four different ways. (i) We used the thermal emission of dust grains in the far-infrared observed by SPIRE on the Herschel telescope at 250, 350, and 500 μm. The mass absorption coefficient used was κν ∝ νβ, where β = 2.0, and was normalized to κ0 = 0.1 cm2 g−1 at 250 μm (Hildebrand 1983). (ii) We calculated AV with the color-extinction method developed by Lombardi (2009; NICEST algorithm) extended for six near-infrared bands [J, H, K, IRAC 1 (3.55 μm), IRAC 2 (4.49 μm), IRAC 3 (5.73 μm), and IRAC 4 (7.87 μm)]. The J, H, and K images were obtained with the OMEGA 2000 camera at the 3.5 m telescope in the Calar Alto Observatory. The IRAC/Spitzer data are from the Taurus Legacy Project4. The extinction map was constructed using the extinction law of Roman-Zuniga et al. (2007). (iii) We compared the infrared spectral energy distributions (SEDs) of the science targets taken from the 2MASS and WISE catalogs (1.2–22 μm) to the stellar photospheric model of Bressan et al. (2012) to simultaneously assess the spectral types of the stars and the extinction on the line of sights. The empirical extinction curve of Boogert et al. (2011) was used. (iv) We used the IRTF spectral library (Rayner et al. 2009) as the null absorption reference to measure the ice optical depth. AV was measured simultaneously in the same way as (iii). The empirical extinction curve of Boogert et al. (2011) was used.

The visual extinctions on the three sources measured by the techniques above are listed in Table 1. They should ideally all match on each source, which evidently is not the case. Instead of trying to reconcile the AV s, we would like to underscore the following points. (1) AV on a single line of sight measured in different ways may have a range nearly 100%, that is, if AV is 10 mag, the full interval of the scatter could be ±5 mag. (2) When solid-phase chemistry in the interstellar medium is tested, AV may not be a reliable reference of the mass in front of a target. It is preferred to have more than one species of molecules in ice observed on a single line of sight so that 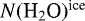N(H2O)ice$N({\textrm{H}_2\textrm{O}})^{\textrm{ice}}$ may serve as a reference of the solid matter, for instance. The complications in using AV as a reference of mass on the line of sight in the context of ice study has been discussed in Chiar et al. (2011), Boogert et al. (2013), and Whittet et al. (2013).

Here we present a nonexhaustive list of the problems in measuring AV, and introduce one issue special to the present case. A cloud may have a particular geometry, such as local minima and maxima, or an additional extinction on foreground and background. All are potential sources of an unexpected tweak in AV on a particular line of sight. The theoretical models of stellar photospheres used in technique (iii) require numbers of inputs that are not well known for an individual target, such as the age, the metallicity, or the presence of circumstellar dust. The uncertainty in the photospheric reference propagates to the uncertainty in AV. The color-dependent extinction technique (ii) requires the intrinsic color of stars as the null reference of the extinction. The intrinsic color is often sampled in a nearby control field. The fidelity of the intrinsic color systematically affects the finally measured extinction. The interstellar extinction law is not universal, but depends on the optical property of the dust grains on the line of sight, such as grain size and chemical composition. Dust optical properties also affect the wavelength dependence of the mass absorption coefficient κν and therefore the total mass of the dust grains deduced from the far-infrared dust emission.

Another issue is the astrometric accuracy. Techniques (i) and (ii) do not use photometry or spectroscopy of the science targets directly, but read AV from the extinction map at the position of the targets. The accuracy of the extinction relies on the accuracy with which the astrometry of the extinction map matches the coordinate system of the targets. The angular resolutions of the extinction map produced by techniques (i) and (ii) are 10″ to 1′ in most cases, while a typical starless core (~0.1 pc) spans 2′ at 140 pc away. Astrometric mismatch may result in serious offsets in AV when a cloud has a small-scale structure and a target is located close to it.

The wide range of possible AV toward our science targets makes it difficult to compare the water-ice optical depth to the existing observations in the Taurus Molecular Cloud (Fig. 4; Whittet et al. 1988; Smith et al. 1993; Murakawa et al. 2000). The peak optical depths of water ice τ3.0 in L 1544 are either consistent with Taurus when compared with the AV measured by SPIRE/Herschel and an SED analysis, or they are smaller, when compared with the AV measured using IRTF templates and the color-dependent extinction technique.

4.2 Comparison with the model

We now compare the measured methanol abundance to the chemical model calculated by Vasyunin et al. (2017). There are two modifications from the published model of L 1544. First, the gas density profile was updated. Vasyunin et al. (2017) used the radial profile of the gas density calculated by Keto & Caselli (2010). This density profile was found to be marginally inconsistent with the far-infrared/mm emission of dust grains (Chacón-Tanarro et al. 2019b). The chemical model was recalculated using the density profile proposed by Chacón-Tanarro et al. (2019b). The radial profiles of the abundances of molecules in gas and ice are affected little.

Second, the oxygen abundance was reduced. Figure 4 shows the comparison of τ3.0 -AV correlations between the observations and the model. The curve computed with the standard low metal oxygen abundance (1.8 × 10−4; the initial gas phase abundance at the start of the cloud collapse) predicts a slope that is too steep (light gray) to match the observations. We had to reduce the oxygen abundance by 23% (1.4 × 10−4). This is a known problem called oxygen crisis (Ayres 2008). The crisis here implies not a shortage of oxygen, but that the solar abundance of oxygen is significantly higher than the total sum of the element observationally identified in the interstellar medium (Whittet 2010; Jenkins 2009, 2019). It is also interesting to note that Hincelin et al. (2011) found that a similar elemental abundance of oxygen was needed in their models to reproduce the observed concentration of molecular oxygen in molecular dark clouds. Oxygen is present in the interstellar medium in atomic and molecular form. It is also incorporated in larger molecules, silicates, and oxides in dust grains, including ice mantles. In a dense cloud, observable oxygen in ice, dust, and gas accounts for only 65% (Whittet et al. 2007) of the solar abundance of oxygen [O]/[H] = 4.57 × 10−4 (Asplund et al. 2009). The reduced [O]/[H] abundance decreases τ3.0 with respectto AV, so that the model results match the canonical slope observed in the Taurus Molecular Cloud better (dark gray trace). The deficit of τ3.0 at the low AV could stem from the chemical youth of L 1544 compared to other star-forming clouds in Taurus. The abundances of methanoland other large organics in the gas phase observed by Jiménez-Serra et al. (2016) are still reproduced within an order of magnitude by the model with the reduced oxygen abundance, and with the peak in the abundance radial distribution matching the radial distance of the observed methanol peak properly, see Bizzocchi et al. (2014). The local fractional abundance of methanol ice with respect to nH is affected little.

The local fractional abundances of ice were converted into column densities through the cloud in the same way as in Jiménez-Serra et al. (2016). The model abundance of methanol ice with respect to water ice is shown in Fig. 5 as a function of AV (gray trace). The predicted abundance of methanol ice reaches 50% at AV = 18 mag and becomes flat toward AV = 40–50 mag with 30–40%. Neither of the observed methanol-ice fraction toward source 3 nor the upper limit on source 1 comes close to the high predicted abundances, regardless of the large uncertainty in the visual extinction on the different lines of sight.

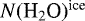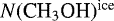Figure 6 compares the observed ice column densities, N(H2O)ice$N({\textrm{H}_2\textrm{O}})^{\textrm{ice}}$ and N(CH3OH)ice$N({\textrm{CH}_3\textrm{OH}})^{\textrm{ice}}$, to the model. The column density of the water ice on source 3 is 2.03 × 1018 cm−2. The column density of the methanol ice predicted by the model is then 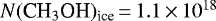N(CH3OH)ice = 1.1 × 1018$N(\textrm{CH}_3\textrm{OH})_{\textrm{ice}} \,{=}\, 1.1\,{\times}\, 10^{18}$ cm−2, which is five times larger than what is actually observed (2.2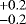−0.2+0.2$^{+0.2}_{-0.2}$ × 1017 cm−2; Table 1). The column density of methanol in the gas phase toward L 1544 is ~ few × 1013 cm−2 (see, e.g., Bizzocchi et al. 2014). This means that the absolute majority of CH3OH in L 1544 is in the solid phase. In the model by Vasyunin et al. (2017), methanol exhibits a similar behavior.

It is not clear why the observed and predicted methanol-ice abundances differ that much. One technical issue is that it is not straightforward to convert the abundances of ice given in a model into the optical-depth spectra that are the observable. An ice mantle is a three-dimensional structure on the surface of a grain that works as a substrate. The optical constants of a single grain should in principle be calculated with a realistic geometry of the mantle on the grain with the vertical profile of the molecular abundances given in the model. The visibility of the molecules may change depending on the depth in the ice mantle. On the other hand, an observation assumes that every molecule in the ice mantle contributes equally to the ice opacity, regardless of the depths of their presence or the size of the grains that they cover.

Vasyunin et al. (2017) indeed distinguished the surface and the bulk molecules in the ice mantle, in the sense that molecules in the bulk, below a few layers of the ice mantle, do not participate in the surface chemistry, but only contribute to the chemistry by slow diffusions through the ice matrix. As a consequence, the chemical compositions of ice are substantially different in bulk and surface. We used the bulk composition to compare it with the observations because it is a conservative choice, as the methanol to water-ice ratio is even higher on the surface at the AV in question. An invisible population of methanol below the thick ice mantle therefore would not account for the deficit of the methanol ice in the present case.

We recall, however, that a chemical model is built on numerous parameters that we do not yet understand well. Rate coefficients of gas-phase reactions (Wakelam et al. 2005, 2006a; Vasyunin et al. 2004, 2008), binding energies of molecules to the grain surface (Wakelam et al. 2017), or diffusion efficiencies on the surface (Iqbal et al. 2018) are known poorly, let alone the physical conditions of the cloud in question (Wakelam et al. 2006a,b, 2010). As a result, the uncertainties in the output chemical abundances may exceed an order of magnitude. Finally, although it is commonly accepted that methanol in dense molecular clouds is formed efficiently only through surface hydrogenation of CO molecules (Watanabe & Kouchi 2002; Fuchs et al. 2009), the processes that may affect the methanol production rate are not fully understood yet (see, e.g., Minissale et al. 2016b).

thumbnail Fig. 4

Peak optical depth of water ice at 3.0 μm in L 1544 plotted against the visual extinction (AV) toward the sources. AV was measured in four different ways: by comparing the object spectrum with the IRTF spectral library (dark red circles), from the extinction map constructed by the colors of reddened background stars (red circles), by comparing the object SEDs with the stellar photospheric model (orange circles), and from the dust column density calculated based on the far-infrared thermal emission of dust observed by Herschel/SPIRE (yellow circles). The optical depths of water ice on the sources in the Taurus Molecular Cloud are shown for comparison (red symbols). The references are Whittet et al. (1988), Smith et al. (1993), and Murakawa et al. (2000). The dashed line denotes the AV – τ3.0 relation known in Taurus (Whittet et al. 2001). The range of AV for each science source measured in different techniques is 50–100%. The peak optical depths of water ice in L 1544 are in the range between being consistent with and smaller than those in Taurus. The gray lines represent the model calculation by Vasyunin et al. (2017) with standard low-metal abundance of oxygen ([O]/[H] = 1.8 × 10−4; light gray) and a reduced oxygen abundance (1.4 × 10−4; dark gray).
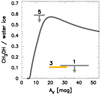thumbnail Fig. 5

Fraction of methanol-ice with respect to water-ice column density plotted as a function of the visual extinction AV along the line of sight through the cloud. The gray curve shows the model calculations by Vasyunin et al. (2017) with an updated radial density profile and a reduced initial oxygen abundance (see text for details). The methanol to water-ice ratio observed on source 3 is marked by a horizontal yellow line, which denotes the full range of AV measured by the different methods. The upper limits on the methanol-ice abundance are shown with downward arrows in light grayfor sources 1 and 5. The fraction of methanol ice detected toward star 3 is 4.5 times smaller than predicted by the models.
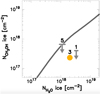thumbnail Fig. 6

Column density of methanol ice plotted against that of water ice. The gray curve represents the model calculated by Vasyunin et al. (2017) with the updated radial density profile and the reduced initial oxygen abundance (see details in the text). The methanol-ice column density on source 3 is shown with a yellow circle. Theuncertainty in the column densities is smaller than the size of the symbol. The upper limits on sources 1 and 5 are shown by downward arrows. The extent of the horizontal bars denotes the uncertainty in N(H2O)ice$N(\textrm{H}_2\textrm{O})^{\textrm{ice}}$. The methanol ice detected on source 3 and the upper limit set on source 1 are smaller than the values predicted by the model by factors of 5.0 and 4.1, respectively.

5 Conclusions

We performed 3 μm medium resolution spectroscopy toward three field stars behind the starless core L 1544 to constrain the methanol-ice abundance with respect to the water ice. One of the stars shows a methanol-ice abundance of 11% with respect to water ice. This is consistent with the value measured toward other starless cores such as L 429 and L 694 (of ~12–14%; Boogert et al. 2011; Chu et al. 2020), but it is still far too low compared to the chemical model computed by Vasyunin et al. (2017). The comparison of the observations with the model reveals that the initial abundance of atomic oxygen at the start of the chemical evolution of the dense cloud in the model has to be reduced by 23% to match the optical depth of water ice as a function of visual extinction toward L 1544.

Acknowledgements

M.G. thanks all the staff and crew of the IRTF, in particular, Mike Connelley, Brian Cabreira, Dave Griep, Miranda Hawarden-Ogata and Bobby Bus who kindly helped conducting the observation from Munich. We would like to thank the hospitality of the Hawaiian community that made the research presented here possible. My sincere appreciation goes to Jorma Harju and Viktor Zivkov who gave me thorough instructions how to construct dust emission / color temperature maps, and a color extinction map, respectively. We thank Wing-Fai Thi for the fruitful discussion about the influence of dust grain size on the shape of methanol ice absorption feature. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The optical spectra of the ice was taken from Sackler Laboratory Ice Database. This research has made use of NASA’s Astrophysics Data System. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. M.G. is supported by the German Research Foundation (DFG) grant GO 1927/6-1. The work of A.I.V. is supported by the Russian Ministry of Science and Higher Education via the State Assignment project FEUZ-2020-0038. A.I.V. is a head of the Max Planck Partner Group at the Ural Federal University. I.J.-S. has received partial support from the Spanish FEDER (ESP2017-86582-C4-1-R) and the State Research Agency (AEI; PID2019-105552RB-C41). C.R.-Z. acknowledges support from program UNAM-DGAPA IN112620, Mexico. The authors thank the anonymous referee for the valuable suggestions that have significantly improved the manuscript.

References

  1. Antiñolo, M., Agúndez, M., Jiménez, E., et al. 2016, ApJ, 823, 25 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ayres, T. R. 2008, ApJ, 686, 731 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Balucani, N., Ceccarelli, C., & Taquet, V. 2015, MNRAS, 449, L16 [Google Scholar]
  6. Bergin, E. A.,& Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
  7. Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bizzocchi, L., Caselli, P., Spezzano, S., & Leonardo, E. 2014, A&A, 569, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Boogert, A. C. A., Huard, T. L., Cook, A. M., et al. 2011, ApJ, 729, 92 [NASA ADS] [CrossRef] [Google Scholar]
  10. Boogert, A. C. A., Chiar, J. E., Knez, C., et al. 2013, ApJ, 777, 73 [Google Scholar]
  11. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  12. Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [Google Scholar]
  13. Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chacón-Tanarro, A., Caselli, P., Bizzocchi, L., et al. 2019a, A&A, 622, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Chacón-Tanarro, A., Pineda, J. E., Caselli, P., et al. 2019b, A&A, 623, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Chiar, J. E., Pendleton, Y. J., Allamandola, L. J., et al. 2011, ApJ, 731, 9 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chu, L. E. U., Hodapp, K. W., & Boogert, A. C. A. 2020, ApJ, 904, 86 [CrossRef] [Google Scholar]
  18. Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Cushing, M. C., Vacca, W. D., & Rayner, J. T. 2004, PASP, 116, 362 [Google Scholar]
  20. Dartois, E., & d’Hendecourt, L. 2001, A&A, 365, 144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Flower, D. R., Pineau Des Forets, G., & Rabli, D. 2010, MNRAS, 409, 29 [Google Scholar]
  22. Fraser, H., & van Dishoeck, E. 2004, Adv. Space Res., 33, 14 [Google Scholar]
  23. Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Chem. Evol. Universe, 133, 51 [Google Scholar]
  26. Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
  28. Goto, M., Bailey, J. D., Hocuk, S., et al. 2018, A&A, 610, A9 [EDP Sciences] [Google Scholar]
  29. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [EDP Sciences] [Google Scholar]
  30. Harju, J., Juvela, M., Schlemmer, S., et al. 2008, A&A, 482, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
  32. Hincelin, U., Wakelam, V., Hersant, F., et al. 2011, A&A, 530, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Hocuk, S., Szucs, L., Caselli, P., et al. 2017, A&A, 604, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
  35. Iqbal, W., Wakelam, V., & Gratier, P. 2018, A&A, 620, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
  37. Jenkins, E. B. 2019, ApJ, 872, 55 [Google Scholar]
  38. Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
  39. Jin, M., & Garrod, R. T. 2020, ApJS, 249, 26 [Google Scholar]
  40. Keto, E., & Caselli, P. 2010, MNRAS, 402, 1625 [Google Scholar]
  41. Lombardi, M. 2009, A&A, 493, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Minissale, M., Congiu, E., & Dulieu, F. 2016a, A&A, 585, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Minissale, M., Moudens, A., Baouche, S., Chaabouni, H., & Dulieu, F. 2016b, MNRAS, 458, 2953 [Google Scholar]
  44. Müller, B., Giuliano, B. M., Goto, M., & Caselli, P. 2020, A&A, submitted [Google Scholar]
  45. Murakawa, K., Tamura, M., & Nagata, T. 2000, ApJS, 128, 603 [Google Scholar]
  46. Noble, J. A., Fraser, H. J., Aikawa, Y., Pontoppidan, K. M., & Sakon, I. 2013, ApJ, 775, 85 [NASA ADS] [CrossRef] [Google Scholar]
  47. Pontoppidan, K. M., Dartois, E., van Dishoeck, E. F., Thi, W.-F., & d’Hendecourt, L. 2003, A&A, 404, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Punanova, A., Caselli, P., Feng, S., et al. 2018, ApJ, 855, 0 [Google Scholar]
  49. Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
  50. Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [Google Scholar]
  51. Roman-Zuniga, C. G., Lada, C. J., Muench, A., & Alves, J. F. 2007, ApJ, 664, 357 [NASA ADS] [CrossRef] [Google Scholar]
  52. Shannon, R. J., Blitz, M. A., Goddard, A., & Heard, D. E. 2013, Nat. Chem., 5, 745 [Google Scholar]
  53. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  54. Smith, R. G., Sellgren, K., & Brooke, T. Y. 1993, MNRAS, 263, 749 [NASA ADS] [CrossRef] [Google Scholar]
  55. Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, A&A, 455, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Taquet, V., Wirström, E. S., Charnley, S. B., et al. 2017, A&A, 607, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Thi, W.-F., van Dishoeck, E. F., Dartois, E., et al. 2006, A&A, 449, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
  59. Tielens, A. G. G. M., & Whittet, D. C. B. 1997, IAU Symp., 178, 45 [Google Scholar]
  60. Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
  61. Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
  62. Vasyunin, A. I., Sobolev, A. M., Wiebe, D. S., & Semenov, D. A. 2004, Astron. Lett., 30, 566 [Google Scholar]
  63. Vasyunin, A. I., Semenov, D., Henning, T., et al. 2008, ApJ, 672, 629 [Google Scholar]
  64. Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, ApJ, 842, 33 [Google Scholar]
  65. Wakelam, V., Selsis, F., Herbst, E., & Caselli, P. 2005, A&A, 444, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Wakelam, V., Herbst, E., & Selsis, F. 2006a, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Wakelam, V., Herbst, E., Selsis, F., & Massacrier, G. 2006b, A&A, 459, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Wakelam, V., Herbst, E., Le Bourlot, J., et al. 2010, A&A, 517, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Wakelam, V., Loison, J. C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Ward-Thompson, D., Scott, P. F., Hills, R. E., & Andre, P. 1994, MNRAS, 268, 276 [Google Scholar]
  72. Ward-Thompson, D., Motte, F., & Andre, P. 1999, MNRAS, 305, 143 [Google Scholar]
  73. Watanabe, N.,& Kouchi, A. 2002, ApJ, 571, L173 [Google Scholar]
  74. Watanabe, N., Nagaoka, A., Shiraki, T., & Kouchi, A. 2004, ApJ, 616, 638 [Google Scholar]
  75. Whittet, D. C. B. 2010, ApJ, 710, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  76. Whittet, D. C. B., Bode, M. F., Longmore, A. J., et al. 1988, MNRAS, 233, 321 [NASA ADS] [CrossRef] [Google Scholar]
  77. Whittet, D. C. B., Gerakines, P. A., Hough, J. H., & Shenoy, S. S. 2001, ApJ, 547, 872 [NASA ADS] [CrossRef] [Google Scholar]
  78. Whittet, D. C. B., Shenoy, S. S., Bergin, E. A., et al. 2007, ApJ, 655, 332 [Google Scholar]
  79. Whittet, D. C. B., Poteet, C. A., Chiar, J. E., et al. 2013, ApJ, 774, 102 [Google Scholar]
  80. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
1

The Wide-field Infrared Survey Explore (Wright et al. 2010).

2

The Two Micron All Sky Survey (Skrutskie et al. 2006).

All Tables

Table 1

Column densities of water and methanol ice.

In the text

All Figures

thumbnail Fig. 1

Background stars observed toward L 1544 in the present study. First panel from the left: DSS color image of L 1544 to delineate the dark patch of the starless core. Second panel: extinction map based on the Herschel/SPIRE far-infrared imaging. Third panel: close-up view of the central part of L 1544, enclosed within the orange rectangle on the second panel. The positions of the 2MASS/WISE sources are marked with crosses. Fourth panel: dust color temperature based on Herschel/SPIRE imaging. The methanol peak observed by Bizzocchi et al. (2014) is shown with orange contours. The half-transparent circle roughly denotes the region where CO is frozen out (Caselli et al. 1999).
In the text
thumbnail Fig. 2

Optical depth spectra of three sources behind L 1544 shown in the order of visual extinction. The optical depth is measured with respect to the matching template spectra chosen from the IRTF spectral library (Rayner et al. 2009). The spectra reduced with three best-matching templates are shown (black, orange, and yellow traces in the order of goodness of matching). The identification of the sources is the same as in Fig. 1. The atmospheric transmission is low at the wavelengths 2.50–2.85 μm and 3.29–3.31 μm because of the telluric water and methane absorption, respectively. The data in these intervals are removed from the presentation.
In the text
thumbnail Fig. 3

Optical depth spectra obtained toward the three stars located behind L 1544, shown in order of visual extinction. The optical depth is measured with respect to the matching template spectra chosen from the IRTF spectral library (Rayner et al. 2009). Source labels are the same as in Fig. 1. The atmospheric transmission is low at the wavelengths between 2.50–2.85 μm and 3.29–3.31 μm because of the telluric water and methane absorption, respectively. The data in these intervals are removed from the presentation. Left panel in the top row: spectrum of star 3 (black) compared to the laboratory ice spectra from Hudgins et al. (1993). The pure water ice spectrum is shown in yellow, the interstellar weak mix (H2O:CH3OH:CO:NH3 = 100:10:1:1) in orange, and the interstellar strong mix, 100:50:1:1, in red. Middle panel: zoomed view of the left panelwithin the gray rectangle. Right panel: comparison of astronomical (black) and laboratory (red) spectra after the local continua were subtracted. The laboratory spectrum of methanol ice is scaled so that the absorption peak matches the observation. The thick red trace is shifted by 0.01 μm from the laboratory measurement (thin trace). Middle and bottom rows: same as the top row, but for sources 1 and 5, respectively.The methanol ice absorption feature is not detected.
In the text
thumbnail Fig. 4

Peak optical depth of water ice at 3.0 μm in L 1544 plotted against the visual extinction (AV) toward the sources. AV was measured in four different ways: by comparing the object spectrum with the IRTF spectral library (dark red circles), from the extinction map constructed by the colors of reddened background stars (red circles), by comparing the object SEDs with the stellar photospheric model (orange circles), and from the dust column density calculated based on the far-infrared thermal emission of dust observed by Herschel/SPIRE (yellow circles). The optical depths of water ice on the sources in the Taurus Molecular Cloud are shown for comparison (red symbols). The references are Whittet et al. (1988), Smith et al. (1993), and Murakawa et al. (2000). The dashed line denotes the AV – τ3.0 relation known in Taurus (Whittet et al. 2001). The range of AV for each science source measured in different techniques is 50–100%. The peak optical depths of water ice in L 1544 are in the range between being consistent with and smaller than those in Taurus. The gray lines represent the model calculation by Vasyunin et al. (2017) with standard low-metal abundance of oxygen ([O]/[H] = 1.8 × 10−4; light gray) and a reduced oxygen abundance (1.4 × 10−4; dark gray).
In the text
thumbnail Fig. 5

Fraction of methanol-ice with respect to water-ice column density plotted as a function of the visual extinction AV along the line of sight through the cloud. The gray curve shows the model calculations by Vasyunin et al. (2017) with an updated radial density profile and a reduced initial oxygen abundance (see text for details). The methanol to water-ice ratio observed on source 3 is marked by a horizontal yellow line, which denotes the full range of AV measured by the different methods. The upper limits on the methanol-ice abundance are shown with downward arrows in light grayfor sources 1 and 5. The fraction of methanol ice detected toward star 3 is 4.5 times smaller than predicted by the models.
In the text
thumbnail Fig. 6

Column density of methanol ice plotted against that of water ice. The gray curve represents the model calculated by Vasyunin et al. (2017) with the updated radial density profile and the reduced initial oxygen abundance (see details in the text). The methanol-ice column density on source 3 is shown with a yellow circle. Theuncertainty in the column densities is smaller than the size of the symbol. The upper limits on sources 1 and 5 are shown by downward arrows. The extent of the horizontal bars denotes the uncertainty in N(H2O)ice$N(\textrm{H}_2\textrm{O})^{\textrm{ice}}$. The methanol ice detected on source 3 and the upper limit set on source 1 are smaller than the values predicted by the model by factors of 5.0 and 4.1, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.