| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A203 | |
| Number of page(s) | 26 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202039842 | |
| Published online | 29 June 2021 | |
The effects of the initial mass function on Galactic chemical enrichment⋆
1
SISSA, Via Bonomea 265, 34136 Trieste, Italy
e-mail: sgoswami@sissa.it, alessandro.bressan@sissa.it
2
CNR-IFN Padova, Via Trasea 7, 35131 Padova, Italy
3
Dipartimento di Fisica e Astronomia, Università degli studi di Padova, Vicolo Osservatorio 3, Padova, Italy
e-mail: paola.marigo@unipd.it
4
INAF-OAPD, Vicolo dell’osservatorio 5, Padova, Italy
5
INAF-OATs, Via G. B. Tiepolo 11, 34143 Trieste, Italy
6
IFPU – Institute for fundamental physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
7
INFN, Sezione di Padova, Via Marzolo 8, 35131 Padova, Italy
8
Center for Interdisciplinary Exploration & Research in Astrophysics (CIERA) and Department of Physics & Astronomy, Northwestern University, Evanston, IL 60208, USA
9
INFN-Sezione di Trieste, Via Valerio 2, 34127 Trieste, Italy
Received:
4
November
2020
Accepted:
7
April
2021
Context. We have been seeing mounting evidence that the stellar initial mass function (IMF) might extend far beyond the canonical Mi ∼ 100 M⊙ limit, but the impact of such a hypothesis on the chemical enrichment of galaxies is yet to be clarified.
Aims. We aim to address this question by analysing the observed abundances of thin- and thick-disc stars in the Milky Way with chemical evolution models that account for the contribution of very massive stars dying as pair instability supernovae.
Methods. We built new sets of chemical yields from massive and very massive stars up to Mi ∼ 350 M⊙ by combining the wind ejecta extracted from our hydrostatic stellar evolution models with explosion ejecta from the literature. Using a simple chemical evolution code, we analysed the effects of adopting different yield tables by comparing predictions against observations of stars in the solar vicinity.
Results. After several tests, we set our focus on the [O/Fe] ratio that best separates the chemical patterns of the two Milky Way components. We find that with a standard IMF, truncated at Mi ∼ 100 M⊙, we can reproduce various observational constraints for thin-disc stars; however, the same IMF fails to account for the [O/Fe] ratios of thick-disc stars. The best results are obtained by extending the IMF up to Mi = 350 M⊙, while including the chemical ejecta of very massive stars in the form of winds and pair instability supernova (PISN) explosions.
Conclusions. Our study indicates that PISN may have played a significant role in shaping the chemical evolution of the thick disc of the Milky Way. Including their chemical yields makes it easier to reproduce not only the level of the α-enhancement, but also the observed slope of thick-disc stars in the [O/Fe] vs. [Fe/H] diagram. The bottom line is that the contribution of very massive stars to the chemical enrichment of galaxies is potentially quite important and should not be neglected in models of chemical evolution.
Key words: stars: abundances / stars: massive / Galaxy: abundances / Galaxy: disk / solar neighborhood / Galaxy: evolution
The tables described in Appendix A are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/650/A203
© ESO 2021
1. Introduction
The chemical evolution of the Milky Way is one of the most important astrophysical topics because it provides direct hints on the more general question of how galaxies formed and evolved. It is also an anchor for galaxy models because of the possibility of studying their properties thanks to the analysis of individual stars. This field of research is indeed continuously growing, as it provides, on the one side, an increasing amount of observational abundance data that contribute to enlarging and sharpening the whole picture (Gilmore et al. 2012; Bensby et al. 2014; Majewski et al. 2017; de Laverny et al. 2013). On the other hand, a growing number of interpretative tools that go from simple chemical evolutionary models to more complex chemo-hydrodynamical models (e.g., Valentini et al. 2019). A key ingredient for interface model predictions with the observations are the stellar chemical yields which describe the contribution of stars of different types to the metal enrichment of the galaxies. Other physical processes, of course, play an important role in the chemical evolution of the galaxies, such as the functional forms adopted to describe the stellar birthrate function, the gas inflows and outflows, the mixing of newly ejected elements with the surrounding medium, the relative displacement of individual stars from their original positions, etc. However, the role of stellar yields continues to gain attention because as they result from the evolution of stars, they may provide a tight link between stellar and galactic timescales. The contribution of individual stars to metal enrichment has been the subject of many studies in the past (e.g., Matteucci 2014). The chemical enrichment from stars takes place when elements newly produced by nuclear reactions in the deep stellar interiors are ejected into the interstellar medium, via stellar winds or supernova explosions.
Low- and intermediate-mass stars, Mi ≃ 0.8 M⊙ − 6 M⊙, never reach the carbon ignition temperature and enrich the interstellar medium (ISM) mainly during the red giant branch (RGB) and asymptotic giant branch (AGB) phases (Marigo 2001; Cristallo et al. 2009, 2011, 2015; Karakas 2010; Karakas & Lugaro 2016; Karakas et al. 2018; Ventura et al. 2013, 2017, 2018; Pignatari et al. 2016; Slemer et al. 2017; Ritter et al. 2018).
Stars in a narrow mass interval, Mi ≃ 6 M⊙ − 10 M⊙, are able to burn carbon in their non- or mildly degenerate cores and experience the so-called super-AGB phase (Ritossa et al. 1996; García-Berro et al. 1997; Iben et al. 1997). Depending on the efficiency of stellar winds and the growth of the core mass, the final fate of Super-AGB stars splits into two channels that lead to either the formation of an O–Ne–Mg white dwarf (7 ≲ Mi/M⊙ ≲ 9) or to an electron capture supernova (9 ≲ Mi/M⊙ ≲ 10; Hurley et al. 2000; Siess 2007; Poelarends et al. 2008).
Massive stars (Mi ≃ 10−120 M⊙) experience more advanced nuclear burnings (Ne, O, Si) up to the formation of an iron core, which eventually implodes, producing either a successful core-collapse supernova (CCSN) explosion. There is also the possibility of a direct collapse into a black hole as a failed CCSN (Woosley & Weaver 1995; Fryer 1999; Chieffi & Limongi 2004; Limongi & Chieffi 2006, 2018; Nomoto et al. 2006; Fryer et al. 2006, 2012; Fryer & Kalogera 2001; Heger & Woosley 2002; Heger et al. 2003; Janka 2012; Ugliano et al. 2012; Ertl et al. 2016; Pignatari et al. 2016; Ritter et al. 2018). On rare occasions that depend on the characteristics of the progenitor and the details of the explosion, stars in this mass range may give rise to powerful hypernovae (Izzo et al. 2019). Very massive objects (VMOs), 100 ≲ Mi/M⊙ ≲ 300 M⊙, enter the pair instability regime during central oxygen burning, which may trigger their final thermonuclear explosion (Heger & Woosley 2002; Umeda & Nomoto 2002; Kozyreva et al. 2014a; Woosley & Heger 2015; Woosley 2017).
The chemical ejecta contributed by all stars of different initial masses and evolutionary stages are the key ingredients of galactic chemical evolution studies. In most cases, the adopted stellar IMF is truncated at around Mi ≃ 100 M⊙, which implies that no chemical contribution from VMOs is taken into account. This common assumption is due to the fact that very few evolutionary models exist for stars with Mi > 100 M⊙. With the exception of zero-metallicity stars (e.g., Haemmerlé et al. 2018; Yoon et al. 2012; Ohkubo et al. 2009, 2006; Lawlor et al. 2008; Marigo et al. 2003, 2001), the lack of systematic evolutionary studies of VMOs has effectively limited the exploration area of chemical evolution models, which has limited their focus to the role of population III stars only (e.g., Cherchneff & Dwek 2010, 2009; Rollinde et al. 2009; Ballero et al. 2006; Matteucci & Pipino 2005; Ricotti & Ostriker 2004). In fact, the occurrence of VMOs and their final fates were thought to apply only to primordial population III stellar populations (Bond et al. 1982, 1984; Heger & Woosley 2002; Nomoto et al. 2013).
In recent years, our understanding of the evolution of massive and very massive stars has dramatically changed as a result of important discoveries. We can now rely on studies focussed on young super star clusters (Evans et al. 2010; Walborn et al. 2014; Schneider et al. 2018; Crowther 2019; Crowther et al. 2016) and on the identification of massive stellar black holes hosted in binary systems (Abbott et al. 2016, 2020; Spera & Mapelli 2017; Spera et al. 2015). All this evidence points to an IMF that extends up to VMO that is characterised either as a genuine top-heavy IMF or one that results from an early efficient merging in binary systems (Senchyna et al. 2021). Further support for a top-heavy IMF in certain environmental conditions also comes from recent findings suggesting that the low observed 16O/18O isotopic ratios in starburst galaxies can be reproduced only by models that assume an excess of massive stars (Romano et al. 2017). However, while there is strong evidence supporting the existence of stars with initial mass up to Mi ≃ 350 M⊙, other evidence exists in favour of the opposite scenario, that is, that the IMF is bottom-heavy, as in the case of observations of the gravity-sensitive narrow-band integrated indices in local ellipticals (van Dokkum & Conroy 2012; van Dokkum et al. 2017). These latter observations are quite challenging from the chemical evolution point of view because massive elliptical galaxies are among the most metal-rich stellar systems known thus far and it is difficult to explain their chemical pattern with such a bottom-heavy IMF (Bressan et al. 1994; Matteucci 1994; Thomas et al. 2005). In parallel, it has also been suggested that the IMF may be a self regulating process leading to a variation of its form in different environmental conditions. Early models based on an IMF varying with time and with galactic environment (Padoan et al. 1997) could better explain many of the observed properties of elliptical and low surface brightness galaxies, such as α-enhancement, downsizing, fundamental plane, etc. (Chiosi et al. 1998; Jimenez et al. 1998). Since then, more evidence of a dependence of the IMF on the environment has been acquired, leading to the definition of galaxy-wide IMF (gwIMF) and time-integrated gwIMF (IGIMF) that may deviate from a canonical IMF, depending on metallicity and star-formation activity (Kroupa & Weidner 2003; Weidner & Kroupa 2005; Kroupa 2008; Recchi et al. 2009; Marks et al. 2012; Jeřábková et al. 2018; Hosek et al. 2019).
Motivated by these studies, our group recently carried out the first systematic analysis of stellar models for massive stars and VMOs, extending up to Mi = 350 M⊙, for a broad grid of initial metallicity, from Zi = 0.0001 to Zi = 0.06 (Tang et al. 2014; Chen et al. 2015; Costa et al. 2021). These models, computed with the PARSEC code, are based on updated input physics and, above all, they rely on the most recent advances in the theory of stellar winds, which critically affect the evolution of massive stars and VMO.
In this work, we used the same PARSEC models of massive stars and VMO to derive their stellar wind ejecta, which were then incorporated in a chemical evolution model to analyse the impact of varying the slope of the IMF and its upper mass limit. Additionally, we tested different sets of chemical ejecta and check their ability to reproduce the chemical characteristics of the thin and thick-disc stars.
For this purpose, we first collected from the literature various sets of ejecta, which cover the contributions from low-, intermediate-mass and massive stars, with the latter usually provided up to Mi ≃ 100 M⊙. Then, we constructed new tables of chemical ejecta, extending the initial mass range to include the contribution of VMOs, up to Mi = 350 M⊙. The new set of chemical yields of massive stars and the VMOs contains the stellar wind ejecta, based on the PARSEC models, suitably tailored to explosive yields for CCSN, pulsational pair instability SN (PPISN), and of pair instability SN (PISN) taken from the recent literature.
The structure of the paper is as follows. Basic stellar classification and relevant mass limits are recalled in Sect. 2. In Sect. 3, we introduce our new set of chemical ejecta for massive and very massive stars. Following an outline of our PARSEC code, we describe the method adopted to combine PARSEC stellar evolution models of massive stars with explosive models available in the literature. Then we discuss the resulting ejecta due to both stellar winds and explosions (CCSN, PPISN, and PISN). The full content of the ejecta tables, which have been made publicly available, is detailed in Appendix A. Section 4 summarises the main characteristics of the AGB yields obtained with our COLIBRI code. Section 5 introduces and compares various sets of chemical ejecta of AGB and massive stars taken from the recent literature. Section 6 briefly describes the observational sample of thin- and thick-disc stars in the solar vicinity and the adopted chemical evolution code used for the interpretation of their abundances. In Sect. 7, we analyse the predictions of chemical evolution models calculated adopting different sets of chemical ejecta. Their performance is tested through the use of various diagnostics, with particular focus on the observed [O/Fe] vs. [Fe/H] diagram populated by thin- and thick-disc stars. Finally, Sect. 8 recaps our study and our main conclusions.
2. Stellar classes and mass limits
The final fate of stars depends primarily on their initial mass, Mi, and metallicity, Zi. To characterise the chemical contributions of stars it is convenient to group them in classes as a function of Mi according to their evolutionary paths and final fates. Let us introduce a few relevant limiting masses that define each stellar family. Mass limits and other relevant quantities used throughout the paper are also defined in Table 1.
Description of the main quantities used in this work.
It should be noted that the mass ranges specified below should not be considered as strict, but rather approximate limits, since they significantly depend on the efficiency of processes such as convective mixing and stellar winds and, especially for massive stars, also on the initial chemical composition.
We define, with MAGB ≃ 6 M⊙, the maximum initial mass for a star to build a highly electron-degenerate C–O core after the end of the He-burning phase. This class comprises low- and intermediate-mass stars, which then proceed through the AGB phase leaving a C–O WD as compact remnant.
Stars with Mi > MAGB are able to burn carbon in mildly degenerate or non-degenerate conditions. Those stars that build an electron-degenerate O–Ne–Mg core are predicted to enter the Super-AGB phase, undergoing recurrent He-shell flashes and powerful mass loss, similarly to the canonical AGB phase. If stellar winds are able to strip off the entire H-rich envelope while the core mass is still lower than ≃1.38 M⊙, then the evolution will end as an O–Ne–Mg WD (Nomoto 1984; Iben et al. 1997). We denote the upper mass limit of this class of stars with MSAGB (Herwig 2005; Siess 2006, 2007; Doherty et al. 2014).
Stars with Mi > MSAGB and having an electron-degenerate O–Ne–Mg core that is able to grow in mass up to the critical value of ≃1.38 M⊙, are expected to explode as electron capture supernovae with MSAGB ≃ 7 M⊙ (ECSN; Nomoto 1984; Poelarends et al. 2008; Leung et al. 2020).
We set Mmas as the minimum initial mass for a star to avoid electron degeneracy in the core after carbon burning. We note that following this definition, the progenitors of electron capture SN cover the range of MSAGB < Mi < Mmas.
Stars with Mmas ≤ Mi < MVMO ≃ 100 M⊙ are capable of proceeding through all hydrostatic nuclear stages up to Si-burning, with the formation of a Fe core that eventually undergoes a dynamical collapse triggered by electron-captures and photodisintegrations (Woosley & Weaver 1995; Thielemann et al. 2011).
Very massive stars with Mi ≥ MVMO may experience electron-positron pair creation instabilities before and during oxygen burning, with a final fate that is mainly controlled by the mass of the helium core, MHe (Heger & Woosley 2002; Heger et al. 2003; Nomoto et al. 2013; Kozyreva et al. 2014a; Woosley 2017; Leung et al. 2019), resulting in a successful or a failed CCSN or thermonuclear explosion. For further details, we refer to Sect. 3.6.
3. Chemical ejecta of massive and very massive stars using PARSEC models
In this work, our reference set of evolutionary tracks for massive and very massive stars is taken from the large database of Padova and TRieste Stellar Evolution Code (PARSEC)12. The PARSEC code is extensively described elsewhere (Bressan et al. 2012; Costa et al. 2019a,b) and here we provide only a synthetic description of the relevant input physics.
3.1. Evolutionary models
The PARSEC database includes stellar models with initial masses from 8 M⊙ to 350 M⊙ and metallicity values of Zi = 0.0001, 0.0005, 0.001, 0.004, 0.006, 0.008, 0.017, 0.02, 0.03 (Chen et al. 2015; Tang et al. 2014). The adopted reference solar abundances are taken from Caffau et al. (2011), with a present-day solar metallicity Z⊙ = 0.01524. We note that the latter value does not correspond to the initial metallicity of the Sun, which instead is predicted to be ZprotoSUN = 0.017 (see Sect. 7.1). For all metallicities, the initial chemical composition of the models is assumed to be scaled-solar. The isotopes included in the code are: H, D, 3He, 4He, 7Li, 7Be, 12, 13C,14, 15N, 16, 17, 18O, 19F, 20, 21, 22Ne,23Na 24, 25, 26Mg, 26, 27Al, 28Si. Opacity tables are from Opacity Project At Livermore (OPAL)3 team (Iglesias & Rogers 1996, and references therein) for 4.2 ≤ log(T/K) ≤ 8.7, and from the ÆSOPUS tool4 (Marigo & Aringer 2009), for 3.2 ≤ log(T/K) ≤ 4.1. Conductive opacities are included following Itoh et al. (2008). Neutrino energy losses by electron neutrinos are taken from Munakata et al. (1985), Itoh & Kohyama (1983), and Haft et al. (1994). The equation of state is from FREEEOS5 code version 2.2.1 by Alan W. Irwin.
The mass loss prescriptions employed in PARSEC are the law of de Jager et al. (1988) for red super giants (RSG; Teff ≤ 12 000 K), the Vink et al. (2000) relations for blue super giants (BSG; Teff > 12 000 K), and Gräfener (2008) and Vink et al. (2011) during the transition phase from O-type to Luminous Blue Variables (LBV) and RSG, and finally to Wolf Rayet (WR) stars.
3.2. Calculation of the chemical ejecta
With the adopted version of the PARSEC code, models of massive and very massive stars are evolved until central carbon exhaustion; thus, we combine our evolutionary tracks with extant explosive models covering a range of initial masses that corresponds to different final fates (CCSN, failed SN, PPISN, and PISN). Following the work by Slemer (2016), for each stellar model of given initial mass Mi, we first compute the amount of ejected mass of the element j due to the stellar winds, 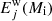 , and then the contributions of the associated supernova channels,
, and then the contributions of the associated supernova channels, 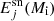 , as detailed in Sect. 3.5. The total ejecta Ej(Mi) are given by
, as detailed in Sect. 3.5. The total ejecta Ej(Mi) are given by
The complete tables of wind and explosion ejecta for massive and very massive stars (8 ≤ Mi/M⊙ ≤ 350) and four values of the initial metallicity (0.0001 ≤ Zi ≤ 0.02) are described in Appendix A. They are available at the CDS.
We consider the most important chemical species and their isotopes from H to Zn. The species explicitly included in PARSEC nuclear networks are all the isotopes from 1H to 28Si. Heavier elements are present in the initial chemical composition, according to the adopted scaled-solar mixture (see Sect. 3), and are not affected by the nuclear reactions and mixing events during the hydrostatic H- and He-burning phases.
In the following, we detail how we calculate the wind and explosion ejecta, 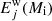 and
and 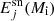 , that appear in Eq. (1).
, that appear in Eq. (1).
3.3. Wind ejecta
The wind ejecta of a species j contributed by a star of initial mass, Mi, is computed with the following equation:
where the integral is performed over the stellar lifetime, from the zero age main sequence (ZAMS) up to the stage of carbon ignition, τC. For a given Mi the quantities Ṁ(Mi,t) and 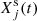 denote, respectively, the mass-loss rate and surface abundance (in mass fraction) of the species j, at the current time t.
denote, respectively, the mass-loss rate and surface abundance (in mass fraction) of the species j, at the current time t.
The total amount of mass lost by a star during its hydrostatic evolution, Mi − Mfin, can be appreciated from Fig. 1, which shows the pre-SN mass (Mfin) as a function of Mi, for a few selected values of the initial metallicity.
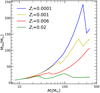 |
Fig. 1. Pre-SN mass Mfin as function of initial Mi for different values of the initial metallicity Zi, as indicated. Stellar tracks are taken from PARSEC VI.1 models. |
Figure B.1, in the appendix, illustrates the fractional wind ejecta, 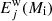 /Mi, of the main chemical species considered in the PARSEC models, as a function of Mi and Zi. For Mi ≤ 100 M⊙ the wind ejecta generally increase with initial mass and metallicity, which is explained by the strengthening of stellar winds at higher luminosities and larger abundances of metals. This applies to H, He, N, Ne, Na, Mg, Al, and Si.
/Mi, of the main chemical species considered in the PARSEC models, as a function of Mi and Zi. For Mi ≤ 100 M⊙ the wind ejecta generally increase with initial mass and metallicity, which is explained by the strengthening of stellar winds at higher luminosities and larger abundances of metals. This applies to H, He, N, Ne, Na, Mg, Al, and Si.
The metallicity trends for C and O reverse in the case of VMO. Compared to the predictions for Zi = 0.02, at low metallicities and high initial masses, Zi ≤ 0.006 and Mi > 100−200 M⊙, the wind ejecta may be larger by even one order of magnitude for C and up to two orders of magnitude for O. This result is explained when considering the stage at which stars of different Mi and Zi enter the WC and WO phases, which are characterised by powerful winds enriched in C and O.
At Zi = 0.02 all VMO experience high mass-loss before entering in the WC regime, which is attained close to the end of the He-burning phase. We note that these models are not expected to go through the WO regime. As a consequence, their ejecta are characterised by low amounts of primary C and O. Conversely, at lower metallicities, Zi = 0.0001 and 0.004, due to the relatively weak stellar winds during the early evolutionary stages, VMOs reach the WC and WO regimes with a much larger mass, hence producing higher ejecta of C and O.
3.4. Explosion ejecta of electron capture supernovae
To account for the ECSN channel, we may take advantage of the recent revision of the PARSEC code (Costa et al. 2021), which extended the sequence of hydrostatic nuclear burnings up to oxygen. In this way, we can check which models develop a degenerate O–Ne–Mg core after the carbon-burning phase. As mentioned in Sect. 4, we did not follow the super-AGB phase and the corresponding yields are taken from Ritter et al. (2018) using the models with Mi = 6 M⊙ and 7 M⊙.
As to the ECSN channel we proceed as follows. Given the severe uncertainties that affect the definition of the mass range for the occurrence of ECSN (e.g., Doherty et al. 2017; Poelarends et al. 2008) and the modest chemical contribution expected from the explosive nucleosynthesis (e.g., Wanajo et al. 2009), we adopt a simple approach. For each value of Zi, we look over the mass range of 8 ≤ Mi/M⊙ ≤ 10, and assign the ECSN channel to the PARSEC models that (after the carbon-burning phase) develops a degenerate core with mass close to the critical value of 1.38 M⊙. In the metallicity range under consideration (0.0001 ≤ Zi ≤ 0.02), this condition is met by PARSEC models with 8 ≤ Mi/M⊙ ≤ 9.
The ECSN explosion ejecta are taken from the work of Wanajo et al. (2009, along with their Table 2) and using the FP3 model, as suggested by the authors. The nucleosynthesis results derive from a neutrino-driven explosion of a collapsing O–Ne–Mg core of mass = 1.38 M⊙, with a stellar progenitor of Mi = 8.8 M⊙ (Nomoto 1984). According to this model, the total mass ejected by the explosion is quite low, ≃ 1.39 × 10−2 M⊙. This fact, together with the neutron-richness of the ejecta, lead to a modest production of radioactive 56Ni and hence of stable 56Fe (≈0.002−0.004 M⊙). In addition, the ECSN yields are characterised by a minor production of α-elements (e.g., O and Mg), and an appreciable synthesis of heavier species like 64Zn and some light p-nuclei (e.g., 74Se, 78Kr, 84Sr, and 92Mo). Assuming no fall-back during the explosion, the ECSN event is expected to produce a neutron star with mass Mrem = 1.366 M⊙. Finally, we add the ejecta of the layers above Mrem with the chemical composition predicted by the corresponding PARSEC model.
The specific ECSN model adopted for each Zi serves as a bridge between AGB and massive stars, to avoid a coarse mass-interpolation of the ejecta in the transition region MAGB < Mi/M⊙ < Mmas (see Table 1). We note that with a canonical IMF extending up to 350 M⊙, the weight of the MAGB − Mmas range should be not that large and only a few elements would be affected, that are not the focus of the present paper. A more careful consideration of this mass interval is planned for a future study.
3.5. Explosion ejecta of core collapse supernovae
Stars in this class have Mmas < Mi < MVMO. The upper limit, MVMO, corresponds to a star that reaches MHe ∼ 32 M⊙ after central He burning and enters the pair-instability regime during O-burning (Woosley 2017), thus avoiding the standard evolutionary path to the silicon burning stage (see Sect. 3.6). At solar composition, this mass limit is typically MVMO ∼ 100 M⊙ but it is expected to vary with metallicity, as it is affected by mass loss during the early evolutionary phases.
One aspect that is of particular relevance for this mass range is the determination of the explodability of a model, in other words, the conditions that lead to a successful SN or to a failed SN. In recent years, there have been many attempts to explore the dependence of the outcome of the supernova collapse on the input physics, with the final goal to possibly determine a relation between the explodability and the main stellar parameters, in particular, the initial or pre-supernova mass of the star (Fryer 1999; Fryer et al. 2006, 2012; Fryer & Kalogera 2001; Heger & Woosley 2002; Heger et al. 2003; O’Connor & Ott 2011; Janka 2012; Ugliano et al. 2012; Ertl et al. 2016).
We briefly recall that Fryer et al. (2012) provided simple relations of the explodability with the final C–O core mass (MCO), O’Connor & Ott (2011) introduced the compactness criterion as a threshold for the explodability and Ertl et al. (2016) introduced a two-parameter explodability criterion. The models of Fryer et al depend only on the C–O core mass after carbon burning and on the pre-supernova mass of the star. Conversely, the other models predict a non-monotonic behaviour of the explodability with the core mass, with the existence of islands of explodability intermixed with islands of failures. A related issue concerns the material that may fall back onto the surface of the proto-neutron star after the explosion, eventually leading to the formation of a black hole and possibly also to a failed SN (Fryer et al. 2012).
It is clear that the present theoretical scenario is heterogeneous and there is no unanimous consensus of different authors on the explodability of a massive star following the collapse of its Fe core. This is mainly due to the fact that when the models are near the critical conditions for explosion, they become critically sensitive to slight variations in the input micro-physics and numerical treatments (Burrows et al. 2018).
All these facts make it difficult to unambiguously set a threshold mass between successful and failed explosions. However, since indications exist that a reasonable limit could be in the range of 25 M⊙ ≲ Mi ≲ 30 M⊙ (e.g., O’Connor & Ott 2011; Sukhbold et al. 2016), we assume that massive stars with Mi ≥ 30 M⊙ will fail to explode.
The other important parameter needed to obtain the ejecta is the remnant mass, Mrem. To derive this quantity one could use the observed relation between the ejecta of 56Ni and the pre-supernova mass of CCSN (Umeda & Nomoto 2008; Utrobin & Chugai 2009; Utrobin et al. 2010). We note that also this relation is affected by some uncertainty, in particular on the determination of the pre-supernova mass Mfin. For this reason, as the calibrating value for the models, we prefer to use the estimated value of the 56Ni mass ejected by SN1987A, 56Ni ∼ 0.07 M⊙ (Nomoto et al. 2013; Prantzos et al. 2018).
Given the explodability criterion and the ejected mass of 56Ni, we adopted suitable explosion models to derive the corresponding ejecta. For this purpose, we use the CCSN models by Limongi & Chieffi (2003) and Chieffi & Limongi (2004, hereafter CL04) because they tabulate the explosion isotopes as a function of the internal mass coordinate.
Each stellar model of the PARSEC grid is characterised by four known parameters, namely: Mi, Zi, and MCO. We use the mass of the C–O core, MCO, to match the PARSEC models to CL04 ones for Zi = 0.0001, 0.001, 0.006, 0.02. These are the only values of Zi in common between CL04 and PARSEC. Once identified, the CL04 explosion model that corresponds to a given MCO can be integrated in a straightforward way from the external layers inward until the desired ejecta of 56Ni is reached. The corresponding mass coordinate of the inner layer provides the mass cut, Mcut and, hence, the explosion ejecta.
This scheme needs to be made a bit more articulated to take into account that for the same Mi, the PARSEC and CL04 models do not predict exactly the same MCO. Therefore, we applied simple interpolations for our purposes.
We proceeded as follows. For each PARSEC model of metallicity Zi we identified, in the corresponding CL04 grid, the two explosive models that bracket the mass of the core, MCO1 < MCO < MCO2, with pre-explosive masses Mfin1 and Mfin2, respectively. Using the 56Ni criterion we derive the corresponding mass cuts, Mcut(MCO1) and Mcut(MCO2), and the explosive ejecta, integrating from Mcut(MCO1, 2) to Mfin1, 2. Finally, we use MCO of the PARSEC model as interpolating variable to obtain Mcut(Mi, Zi, MCO) and the explosion ejecta 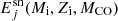 for all chemical species under consideration.
for all chemical species under consideration.
To estimate the mass of the remnant, Mrem, we assume that in successful CCSN the efficiency of fall-back is negligible, as shown by recent hydrodynamical simulations (Ertl et al. 2016). It follows that Mrem = Mcut for successful CCSN and Mrem = Mfin for failed SN. As to the nature of the compact remnant, we assign a neutron star for Mrem < 2.9 M⊙, or a black hole otherwise (Tews & Schwenk 2020; Kalogera & Baym 1996).
Before closing this section, a few remarks are worth making. The first applies to the matching parameter MCO. Figure 2 compares the PARSEC values of MHe and MCO with those derived from CL04 models, as a function of Mi. We note that the values of MHe and MCO of our PARSEC models are slightly larger than predicted by CL04. This is due to the fact that in PARSEC, we adopt a slightly more efficient core overshooting. An implication of this difference will be discussed later (Sect. 5).
 |
Fig. 2. MHe (left panel) and MCO (right panel) as a function of Mi, for different values of Zi. Lines show the data extracted from PARSEC stellar evolution models, while crosses represent the models of Chieffi & Limongi (2004). |
The second is that we assume that differences in the internal configurations between PARSEC models and pre-explosive models with the same MCO do not impact the final nucleosynthesis outcome. Differences are in fact expected because the two evolutionary models adopt different mass-loss rates, mixing schemes and distribution of heavy elements.
The latter difference is considered when computing the yields of newly produced elements by properly accounting for the initial composition. As to the differences in input physics, we note the following: the stellar models of the CL04 grid were computed at constant mass, while our PARSEC tracks include mass loss by stellar winds for Mi ≥ 14 M⊙. However, this difference should not affect our results because, besides the fact that we match the models using MCO (which somewhat alleviates the problem of the different mixing scheme), mass loss is not as important for the progenitors of successful CCSN with Mi ≤ 25 M⊙, and especially not for Zi ≤ 0.006. Powerful stellar winds affect the pre-supernova evolution of more massive stars, but in this case, the matching with CCSN explosive models is not required, as these stars fail to explode and only their wind ejecta are considered. We conclude this section in noting that, for example, differences between the new yields of massive stars obtained in this work and those of Limongi & Chieffi (2018, hereafter LC18) for zero rotational velocity are generally less than those between LC18 models with different rotational velocities, as discussed in Sect. 5.
3.6. Explosion ejecta of pulsational pair instability and pair instability supernovae
Very massive stars that develop a final helium core mass in the range between ∼32 M⊙ and ∼64 M⊙ are expected to enter the domain of pulsational pair-instability supernovae (PPISN) before ending their life with a successful or failed CCSN (Woosley et al. 2002; Chen et al. 2014; Yoshida et al. 2016; Woosley 2017). During the pair-instability phase, several strong pulses may eject a significant fraction of the star’s residual envelope and, possibly, a small fraction of the core mass. In contrast, the thermonuclear ignition of oxygen in stars with helium core masses between ∼64 M⊙ and ∼135 M⊙ leads to a pair-instability supernova (PISN), assimilated to a single strong pulse that disrupts the entire star, leaving no remnant behind (Heger & Woosley 2002; Heger et al. 2003).
Typically, PISN have been associated to the first, extremely metal-poor stellar generations (e.g., Karlsson et al. 2008). However, recent stellar evolution models have suggested that PISN could occur also for stars with initial metallicity Zi ≈ Z⊙/3, which implies that they are potentially observable even in the local universe (Yusof et al. 2013; Kozyreva et al. 2014a). For these reasons, PPISN and PISN may play a key role to understand the chemical evolution of the Galaxy.
While the physical mechanisms behind PPISN and PISN are quite well understood, severe uncertainties affect the range of helium (or, equivalently, carbon–oxygen) core masses that drive stars to enter the pair-instability regime (e.g., Leung et al. 2019; Farmer et al. 2019; Marchant & Moriya 2020; Renzo et al. 2020; Costa et al. 2021). In this work, we adopt the indications from Woosley (2017), who suggests 32 ≲ MHe/M⊙ ≲ 64 for PPISN and 64 ≲ MHe/M⊙ ≲ 135 for PISN.
We modelled PPISN as a super-wind phase that ejects the surface layers, without any appreciable synthesis of new elements, until the star collapses to a BH. For each PARSEC model with a given helium core mass, the corresponding Mrem is obtained by interpolation in MHe, between the values tabulated by Woosley (2017). Then, the total PPISN ejecta are estimated by integrating in mass the PARSEC structures from Mrem to Mfin. Finally, we add the PARSEC wind ejecta.
For PISN, we calculate the explosion ejecta from the zero-metallicity pure-helium stellar models provided by Heger & Woosley (2002), as a function of the mass MHe-star. Similarly to the case of PPISN, the helium core mass, MHe, of our PARSEC tracks is taken as interpolating variable to perform the match with the explosion models and derive the ejecta. Finally, we add the PARSEC contributions of all layers from MHe to Mfin and the wind ejecta.
We used the models of Heger & Woosley (2002), computed at Zi = 0, to derive the PISN ejecta for VMO with Zi > 0. This assumption is reasonable since the total ejected mass of metals6, Mmetals, comprises most of the PISN ejecta, with a fractional contribution, Mmetals/MHe-star, that is generally larger than 97% for all tabulated models.
It is worth noting that stars with Mi ≥ 90 M⊙ enter the PPISN and PISN regimes already at Zi = 0.006 (see Fig. 3). Our models agree with earlier theoretical findings (e.g., Kozyreva et al. 2014a) and support the hypothesis that some superluminous supernovae recently observed at metallicity ≈Z⊙/3, may be explained through the pair-instability mechanism, provided the IMF extends to VMOs (Woosley et al. 2007; Kozyreva et al. 2014b). In this respect, we note that according to IGIMF analysis by Jeřábková et al. (2018), galaxies with metallicity [Fe/H] < 0 dex and SFR > 1 M⊙ yr−1 are characterised by a top-heavy and bottom-light IGIMF, as compared to the canonical one. Using the IGIMF grid provided by Jeřábková et al. (2018) and assuming, for example, a metallicity [Fe/H] = −1 dex and a SFR ∼2 M⊙ yr−1, the slope in the high mass tail would be x ∼ −2.1. Extrapolating this slope up to 200 M⊙ instead of 150 M⊙, the value adopted in the grid, this will allow about 66 700 stars with 10 M⊙ ≤ Mi ≤ 120 M⊙ and 2000 stars with 120 M⊙ ≤ Mi ≤ 200 M⊙, to be born every three Myr (the lifetime of the most massive stars).
 |
Fig. 3. Final fate of massive and very massive stars as a function of Mi and Zi. Green dot is a successful SN, from ECSN if the background is light green or CCSN if it is yellow; red dot is a BH from a failed CCSN; red dot in a black box is a BH from PPISN; yellow star is a thermonuclear explosion from PISN and black dot is a DBH. |
3.7. Ejecta of very massive stars that directly collapse to black holes
If a star is massive enough to build a helium core with MHe > 135 M⊙, no material will be capable of avoiding the direct collapse into a black hole (DBH) induced by the pair creation instability. Under these conditions, no explosive ejecta are produced (Fryer & Kalogera 2001; Heger & Woosley 2002; Nomoto et al. 2013) and the only chemical contribution comes from wind ejecta. With the adopted mass-loss rates in PARSEC, these objects appear only at a low metallicity, Zi = 0.0001, and initial masses Mi > 200 M⊙. Conversely, at larger metallicities stars with Mi > 200 M⊙ avoid the DBH channel, since mass loss is efficient enough to drive their He-core masses into the regimes of PISN or failed CCSN.
4. Ejecta of AGB stars
We complemented the ejecta of massive stars with those of AGB stars computed with the COLIBRI code (Marigo et al. 2013), in the mass range of 0.7 ≲ Mi/M⊙ ≲ 6 and for the same values of the PARSEC metallicities, already mentioned in Sect. 3.1. These models follow the whole thermally pulsing phase (TP-AGB) up to the ejection of the entire envelope by stellar winds. The initial conditions are taken from the PARSEC grid of stellar models at the first thermal pulse or at an earlier stage on the Early-AGB. COLIBRI and PARSEC share the same input physics (e.g., opacity, equation of state, nuclear reaction rates, mixing-length parameter) and the numerical treatment to solve the structures of the atmosphere and the convective envelope. For these reasons, the PARSEC+COLIBRI combination provides a dense, homogeneous and complete grid of models for low- and intermediate-mass stars (roughly ≃70 values of Mi for each metallicity value).
In COLIBRI models, the parameters describing the main processes that affect the TP-AGB phase, such as the mass-loss rates and the efficiency of the third dredge-up, have been thoroughly calibrated with observations of AGB stars in the Galaxy, Magellanic Clouds, and low-metallicity nearby galaxies (Girardi et al. 2010; Rosenfield et al. 2014, 2016; Marigo et al. 2017, 2020; Lebzelter et al. 2018; Pastorelli et al. 2019, 2020). The COLIBRI yields account for the chemical changes due to the first, second, third dredge-up episodes and hot-bottom burning in the most massive AGB stars (Mi ≳ 3−4 M⊙), and include the same chemical species as in PARSEC, from 1H to 28Si (see Sect. 3.1).
Finally, super-AGB stars are not explicitly treated here and their ejecta are taken from Ritter et al. (2018), for stars with Mi = 6, 7 M⊙ and Zi = 0.0001, 0.001, 0.006, 0.027. The chemical composition of the ejecta is the result of third dredge-up episodes and hot-bottom burning. An overshoot scheme is applied to the borders of convective regions, including the bottom of the pulse-driven convection zone. As a consequence, the intershell composition is enriched with primary 16O (≈15%) in Ritter et al. (2018) computations, much more than in standard models without overshoot (16O ≈ 1−2%), like in Karakas (2010).
5. Chemical ejecta from other studies
Here, we present various combinations of chemical ejecta taken from the literature and compare the main trends as a function of Mi and Zi. The results are summarised in Table 2. The different sets of ejecta are then incorporated in our chemical evolution model of the Milky Way (see Sect. 6.2).
Sets of chemical ejecta adopted in the chemical evolution models.
As to the yields from AGB stars, we consider three sets, namely: M20 (from the COLIBRI code, Sect. 4), K10 (Karakas 2010) and R18 (Ritter et al. 2018). K10 provides the ejecta of AGB stars in the mass range 1 ≲ Mi/M⊙ ≲ 6 for four metallicities (Zi = 0.0001, 0.004, 0.008, 0.02). To obtain the yields at Zi = 0.001 and Zi = 0.006, we interpolate in metallicity between their original tables. R18 provide the ejecta of AGB and super-AGB stars in the mass range 1 ≤ Mi/M⊙ ≤ 7 for five metallicities (Zi = 0.0001, 0.001, 0.006, 0.01, 0.02).
As to the yields of massive stars, including both wind and explosion contributions, we consider three sets, namely: R18 (Ritter et al. 2018), L18 (Limongi & Chieffi 2018) with and without rotation, and TW that refers to the new ejecta from this work (see Sect. 3). Nomoto et al. (2013) also published yields for massive stars, which however do not include the wind contributions, and therefore we did not consider them in our analysis. R18 computed the ejecta of massive stars in the mass range 12 ≤ Mi/M⊙ ≤ 25, for the same initial metallicities as their AGB models, that is, Zi = 0.0001, 0.001, 0.006, 0.01, 0.02, and for two models of explosion conditions, rapid (Rr) or delayed (Rd), respectively (Fryer et al. 2006).
LC18 calculated the ejecta in the mass range 13 ≤ Mi/M⊙ ≤ 120 for three different rotational velocities (Vrot = 0, 150, 300 km s−1), and four metallicities ([Fe/H] = 0, −1, −2, −3 dex). Here, we use the version of their ejecta for Zi = 0.0001, 0.004, 0.008, 0.02 publicly available on the Github NuPyCEE repository8. Both R18 and LC18 sets have the noticeable property that wind and explosion ejecta derive from homogeneous stellar evolution models.
The distinguishing feature of our TW ejecta is that they range in mass beyond the classical limit of Mi ≃ 100 M⊙, extending up to Mi = 350 M⊙, thus opening up the possibility for investigating the chemical role of VMOs in terms of stellar winds, PPISN and PISN explosions, and the DBH channel.
To make a meaningful comparison among the different sets of ejecta, we opted to use a dimensionless quantity, defined as the ratio between the newly produced yield of a given species j and the stellar initial mass, Pj(Mi):
where the total ejecta Ej(Mi) is defined by Eq. (1), and Xj, 0 is the initial stellar abundance (in mass fraction) of the element j.
The different sets are compared in Figs. B.2–B.6 as a function of Mi and a few values of the initial metallicity, Zi = 0.0001, 0.001, 0.006, 0.02 respectively. We note that, for comparison purposes only, the LC18 yields for Zi = 0.006 are obtained through a metallicity interpolation. The various panels show the ejecta of 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ar, Ca, Ti, and Fe.
The AGB ejecta of 4He, 12C, 14N exhibit significant differences among different sets. At Zi = 0.0001 the K10 ejecta are much larger than those of R18 and M20. In general, the production of 12C and 14N predicted by K10 is much higher than M20, reaching a factor of ten for 14N at Zi = 0.006. At increasing metallicity the differences become less pronounced. At Zi = 0.02 the trend reverses with K10 predicting the lowest yields, but for the most massive AGB stars with hot-bottom burning. These discrepancies are mainly the result of different input physics (e.g., molecular opacities, mixing length parameter), mass-loss prescriptions, as well as differences in the efficiency of the third dredge-up.
In the domain of massive stars, our TW ejecta agree fairly well with non-rotating LC18 at both Zi = 0.0001 and Zi = 0.006, while the comparison slightly worsens at Zi = 0.02, likely because the effect of mass loss becomes important at higher metallicity. We note that our TW set produces slightly larger fractions of 16O, 20Ne and 24Mg than non-rotating LC18 at any Zi.
At Zi = 0.0001, the rotating LC18 models yield a much larger fraction of 14N and, to a much less extent, 16O and 12C, compared to the non-rotating set. This trend remains at increasing metallicity (Zi = 0.006 and Zi = 0.02) but the over-production of 14N appears less pronounced. Conversely, species such as 20Ne and 24Mg are produced less by stars with rotation.
The comparison between TW and R18 shows that at Zi = 0.0001, there is a fairly good agreement for 14N, 16O, 28Si, S, Ar and Ca. At the same time, our TW ejecta produce less 12C, more 20Ne and 24Mg than R18. At Zi = 0.006 the TW predictions for 12C, which agree well with non-rotating LC18, are about twice the R18 ejecta. We note that at this metallicity R18 presents a notable Fe production, higher by more than a factor of three compared to TW and LC18. A less pronounced, but still large Fe yield is predicted by R18 also at lower metallicity (Zi = 0.0001). Possible consequences of such Fe over-production will be discussed later in the sections devoted to chemical evolution models.
We note that none of the stellar models in the LC18 grid reach a value of MHe that is high enough to enter the pair-instability regime. Recalling that stars with Mi > 30 M⊙ fail to explode and collapse to a BH, it follows that in the mass range, 30 ≤ Mi/M⊙ ≤ 120, LC18 ejecta are only due to stellar winds and become null for Mi > 120 M⊙. Since the maximum mass in the R18 grid is Mi = 25 M⊙, beyond this limit all R18 ejecta are zero. It follows that we can analyse the total ejecta of VMO, Mi ≳ 100 M⊙, by only referring to our MTW set.
At Zi = 0.02, the most important contributions from VMO correspond to 4He, 12C and 14N. For all the other elements there is no significant production because, due to the large mass-loss rates at this metallicity, our models do not enter the PISN channel. The large production of 14N is due to the large convective cores of the high mass stars, which mix the CNO products into the external regions, subsequently exposed to the ISM by mass-loss. We note that for Mi ≤ 30 M⊙, the 14N production in our models is only slightly larger than that of LC18 models with zero rotational velocity and so significantly less than that of their models with high rotational velocities. However, at Mi ≳ 30 M⊙, our models have a 14N wind production that is almost identical to that of LC18 models with high rotational velocities. Since the latter is about 60% larger than that of their zero rotation models at the same Mi, we identify the reason for this difference in the larger mass-loss rates and consequent more rapid pealing and faster core mass decrease in the LC18 models. At the level of Zi = 0.006, VMOs are expected to eject appreciable amounts of newly produced 4He and 12C, while the yield of 14N decreases considerably. At the same time, other species provide notable contributions, such as 16O, 24Mg, 28Si, S, Ar, Ca, Ti, and Fe. The yields of these nuclides increase at higher Mi. This is a clear effect of the occurrence of PPISN and PISN, which is favoured at lower metallicities. At Zi = 0.001 and Zi = 0.0001 the ejecta of all models with Mi > 100 M⊙ have typical signatures of these explosive events. We note that at these metallicities the yields of 56Fe may reach extremely high values, up to 20 M⊙ and 40 M⊙, respectively.
6. Chemical evolution of the Milky Way: Thin and thick discs
We aim to investigate how the adoption of different chemical ejecta affect our interpretation of the observed abundances in Milky Way (MW) thin- and thick-disc stars.
6.1. Observed abundance data
The large volume of data collected over the years for stars in the solar vicinity led to the definition of different Galactic components, namely: the thin and thick discs, the halo and the α-enhanced metal-rich population (Allende Prieto et al. 2008; Gilmore et al. 2012; Zucker et al. 2012; de Laverny et al. 2013). The populations of the MW disc can be distinguished in various ways. For example, by adopting kinematic parameters, Jurić et al. (2008) pointed out that the stellar number density distribution of the MW could be well reproduced with two components with different scale heights above the Galactic plane: the thick disc, with a scale height of ≃900 pc and the thin disc, with a scale height ≃300 pc.
At the same time, chemical abundances reveal the existence of clearly separate sequences of α-elements as a function of [Fe/H], with thick-disc stars generally belonging to a high [α/Fe] (α-enhanced) sequence, while thin-disc stars exhibiting a lower [α/Fe] ratio at the same [Fe/H] (e.g., Plevne et al. 2020; Grisoni et al. 2017; Kawata & Chiappini 2016; Bekki & Tsujimoto 2011; Feltzing et al. 2003; Prochaska et al. 2000).
The classification based on kinematical properties and the one based on abundance measurements provide somewhat different results so that it is not clear which is the best way to group these stars (Boeche et al. 2013). In this respect, it has often been pointed out that chemical evolution leaves a persistent imprint that hardly changes, while kinematic properties are more likely to vary as they may be affected by dynamical interactions (Schönrich & Aumer 2017; Vera-Ciro et al. 2016).
In recent years, the ages of individual stars have been measured with sufficient accuracy to be used as robust population indicators, as in the case of star clusters (Fuhrmann 2011). We emphasise that age cannot be taken as a proxy for metallicity, rather, it is a complementary independent parameter that concurs to define the full population box, that is, the distribution of stars in age and abundances which, together with spatial and kinematic parameters, gives the information necessary to reconstruct the star formation history in a galaxy.
In this work, we use the homogeneous set of data of disc stars provided by Bensby et al. (2014), who conducted a high-resolution and high signal-to-noise spectroscopic analysis of 714 F and G dwarf and subgiant stars in the solar neighbourhood. This study is particularly suited for our purpose because, based on the analysis of the kinematical properties by Casagrande et al. (2011), each star in the sample is assigned a relative membership probability, TD/D defined as the ratio between the thick-disc and thin-disc probability, and TD/H defined as the ratio between the thick-disc and halo probability.
Bensby et al. (2014) classified stars with TD/D > 2 as having a probability of belonging to the thick disc that is at least twice that of belonging to the thin disc as potential thick-disc stars, while those with TD/D < 0.5 are in relation to potential thin-disc stars. Some of the thick disc stars were then assigned to the halo population following the TD/H < 0.5 kinematical criterion.
Adopting the same kinematical criteria, we counted 387 thin disc stars, 203 thick disc stars, and 36 halo stars. We discard 88 stars with 0.5 < TD/D < 2. The existence of at least two distinct disc sequences is clearly visible in the abundance patterns that define the so-called α-enhancement, as illustrated in the [O/Fe], [Mg/Fe], [Si/Fe] and [Ca/Fe] vs. [Fe/H] diagrams of Fig. 6. Interestingly, the [O/Fe] vs. [Fe/H] diagram clearly shows not only that the two disc populations draw separate sequences, but also that the slopes of two branches are different at increasing [Fe/H]. Interpreting the different slopes with chemical evolution models is quite challenging, as already noted by Kubryk et al. (2015).
6.2. Chemical evolution models
To analyse the evolution of the thin and thick disc populations, we used the chemical evolution model CHE-EVO (Silva et al. 1998), a one-zone open chemical evolution code that follows the time evolution of the gas abundances of the elements, including infall of primordial gas. It has been used in several contexts to provide the input star formation and metallicity histories to interpret the spectro-photometric evolution of both normal and starburst galaxies (e.g., Vega et al. 2008; Silva et al. 2011; Fontanot et al. 2009; Lo Faro et al. 2013, 2015; Hunt et al. 2019). The equation describing the evolution of the gas masses reads:
where, for the specie j, 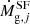 represents the rate of gas consumption by star formation,
represents the rate of gas consumption by star formation, 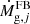 is the rate of gas return to ISM by dying stars and
is the rate of gas return to ISM by dying stars and 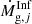 refers to the infall rate of pristine material. For the star formation rate (SFR), we adopt a modified Kennicutt–Schmidt law (Schmidt 1959; Kennicutt 1998):
refers to the infall rate of pristine material. For the star formation rate (SFR), we adopt a modified Kennicutt–Schmidt law (Schmidt 1959; Kennicutt 1998):
where ν is the efficiency of star formation, Mg is the mass of the gas and k is the exponent of the star formation law. The quantity 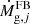 is calculated from the yields tables described in Sect. 5, integrating the contributions of dying stars at any time-step. The gas infall is assumed exponential, with an e-folding time scale τinf and a chemical composition equal to the primordial one (e.g., Grisoni et al. 2017).
is calculated from the yields tables described in Sect. 5, integrating the contributions of dying stars at any time-step. The gas infall is assumed exponential, with an e-folding time scale τinf and a chemical composition equal to the primordial one (e.g., Grisoni et al. 2017).
Type Ia supernovae are also taken into account, according to the single degenerate scenario and computed following the standard formalism first introduced by Matteucci & Greggio (1986). The contribution of these sources to the chemical enrichment is regulated by the parameter ASNIa which sets the fraction of the number of binary systems with total mass in the 3 M⊙ − 16 M⊙ range, effectively contributing to the SNIa rate. Our adopted ejecta for SNIa are taken from Iwamoto et al. (1999). As to AGB, massive, and very massive stars, we adopt the ejecta described in Sects. 3–5, and reported in Table 2. In addition to the evolution of elemental gas masses, metallicity, and the gas fraction, the code provides also the evolution of SNII and SNIa rates, and total mass in stars (Ms).
A fundamental assumption of chemical evolution models is the IMF:
We use a Kroupa-like three-slope power law IMF with x = 0.3 for 0.1 ≤ Mi/M⊙ ≤ 0.5, x = 1.3 for 0.5 ≤ Mi/M⊙ ≤ 1, while we vary the slope for Mi > 1 M⊙, as well as the upper mass limit of the IMF, MUP, to search for best-fitting models with different ejecta combinations. We consider IMF slopes between x = 1.7 (Kroupa et al. 1993) and x = 1.3 (Kroupa 2001; Chabrier 2003).
6.3. Previous analyses of the MW thin and thick discs
In the past, as well as in the more recent literature, there have been many attempts to explain the different chemical evolutionary paths of different MW components, particular those of the thin and thick discs. The outcome of these studies is that the observed different chemical evolutionary paths are related to differences in the main physical processes that drive galaxy evolution, the most significant of which are the gas accretion time-scale and the star formation efficiency and, possibly, radial migration (Larson 1972; Lynden-Bell 1975; Pagel & Edmunds 1981; Matteucci & Greggio 1986; Matteucci & Brocato 1990; Ferrini et al. 1994; Prantzos & Aubert 1995; Chiappini et al. 1997, 2001; Portinari & Chiosi 1999; Bekki & Tsujimoto 2011; Micali et al. 2013; Sahijpal 2014; Snaith et al. 2014; Grisoni et al. 2017; Grand et al. 2018; Spitoni et al. 2021). A good agreement between observations and theoretical predictions for the Galaxy is obtained by models that are based on the assumption that the disc formed via the infalling of gas (Chiosi 1980; Matteucci & Francois 1989; Chiappini et al. 1997). The formation of the different components is associated with distinct sequential main episodes of gas accretion (infall phases) that, at first, rapidly accumulates in the central regions and then, more slowly, in the more external ones, according to the so-called ‘inside-out scenario’ (Chiappini et al. 2001). In particular, the three-infall model, devised by Micali et al. (2013), is capable of reproducing the abundance patterns of the MW halo, thick and thin disc at once. In this model, the halo forms in a first gas infall episode of short timescale (0.2 Gyr) and mild star formation efficiency, ν = 2 Gyr−1, lasting for about 0.4 Gyr. It is immediately followed by the thick disc formation, characterised by a somewhat longer infall timescale (1.2 Gyr), a longer duration (about 2 Gyr) and a higher star formation efficiency (ν = 10 Gyr−1). Finally, star formation continues in the thin disc with a longer infall timescale (6 Gyr in the solar vicinity) and is still continuing to this day, with a star-formation efficiency of ν = 1 Gyr−1. The [O/Fe] vs. [Fe/H] path is thus continuous across the regions populated by halo, thick, and thin disc stars. While Micali et al. (2013) described the chemical enrichment as continuous across the three different infall stages, Grisoni et al. (2017) used also an alternative scheme where the thin and thick disc components evolve separately, in a parallel approach (see also Chiappini 2009). In such a parallel approach, the disc populations are assumed to form in parallel but to proceed at different rates. The gas infall exponentially decreases with a timescale that is 0.1 Gyr and 7 Gyr, for the thick and thin disc, respectively. This alternative approach better reproduces the presence of the metal-rich α-enhanced stars in the [Mg/Fe] vs. [Fe/H] diagram obtained with the recent AMBRE data (Mikolaitis et al. 2017).
In our analysis, we assume that the thin and thick disc populations evolve separately, as in the parallel model approach adopted by Grisoni et al. (2017). This is clearly an oversimplification since these stellar components occupy the same volume in the solar neighbourhood but, nevertheless, this allows us to at least check our models against individually well-separated populations. Alternatively, we could have considered the two populations together and tried to obtain a model that recovers a sort of average path, as has been done several times in the past. However, the evidence that the two populations are different is so strong that reproducing their ‘averaged’ properties is even less meaningful.
7. Analysis of stellar abundances in the solar vicinity
7.1. Model constraints for the thin disc
For each combination of ejecta in Table 2, we built a large library of chemical evolution models by varying the following parameters: the star-formation rate efficiency (0.2 ≤ ν ≤ 2.0) the normalisation factor for the SNIa (0.02 ≤ AIa ≤ 0.1), and the infall timescale (0.1 ≤ τinf ≤ 10). For simplicity, we set k = 1 for all models. With this choice for parameter ranges, the chemical evolution models are able to bracket a few basic observational constraints for the thin disc, namely:
-
The current SFR of the MW – To a large degree it corresponds to that the thin disc, and is estimated as SFR = 0.65 − 3.0 M⊙ yr−1 (Robitaille & Whitney 2010).
-
The current gas fraction – It is assumed to be Mg/(Mg + Ms) ∼ 0.2 (Kubryk et al. 2015).
-
The current SNII rate – We set RSNII = 2 ± 1 SNII events per century (Prantzos et al. 2011).
-
The current SNIa rate – We set RSNIa = 0.4 ± 0.2 SNIa events per century (Prantzos et al. 2018).
-
The protosolar metallicity ZprotoSUN – Although there are contrasting opinions in the literature concerning the significance of the differences between Sun’s abundances and those of solar twin stars (e.g., Bensby et al. 2014; Botelho et al. 2020), we take the protosolar metallicity as representative of that of other disc stars with similar [Fe/H] and, thus, as a constraint for disc chemical evolution models. The protosolar metallicity represents the bulk metallicity of the molecular cloud out of which the Sun was born. It does not coincide with the current photospheric solar metallicity, Z⊙ ≃ 0.0134−0.0152, from Asplund et al. (2009) and Caffau et al. (2011), respectively, as a result of chemical sedimentation effects over a time of about 4.6 Gyr (the present Sun’s age). Here, we adopt ZprotoSUN = 0.017, which is the initial metallicity of the PARSEC 1 M⊙ model that best reproduces the currently observed Sun’s properties when using the Caffau et al. (2011) solar mixture (Bressan et al. 2012). Assuming an age of 13 Gyr for the formation of the Galaxy (e.g., Savino et al. 2020), it follows that the Galactic age at the birth of the proto-Sun is tprotoSUN = 8.4 Gyr. At this epoch, the metallicity in the solar vicinity is ZprotoSUN.
In addition to the constraints just mentioned above, we also require the models to reproduce the observed ([Fe/H]) metallicity distribution function (MDF) of thin-disc stars derived from the Bensby et al. (2014) data.
In summary, we built a database of about 1300 models for each combination of yields. Then, after identifying the group of models that satisfy all the constraints within the uncertainty bars, for each set of yields we found the best model that fits the observed path in the [O/Fe] vs. [Fe/H] plane (Bensby et al. 2014), with the aid of a χ-square minimisation technique. Finally, we performed a fine tuning and group the best models so as to minimise the change of the parameters obtained with different yield sets, without worsening the fits. This allows us to better isolate and analyze the effects produced by changing either the yields or the IMF.
The evolution of the SFR, the gas mass fraction, the SNII and SNIa rates and the gas metallicity (Z) of the selected models are shown in Fig. 4. The predicted thin-disc MDF of our reference model, MTW, is compared with the observed one in Fig. 5. In the same figure we also plot the observed MDF of the thick-disc MDF, for sake of comparison. The vertical bars in the figure mark the location of the median values of the distributions. Let us now analyse the results obtained with the various yield combinations. The adopted parameters of the selected models are summarised in Table 3.
 |
Fig. 4. Evolution of SFR, gas fraction, SNII and SNIa rates, and total gas metallicity. Different lines correspond to the best chemical evolution models obtained with different sets of yields, as indicated. Vertical bars at an age of 13 Gyr show their present-day estimated values. In the bottom-right panel the solid triangle at the age of 8.4 Gyr marks the protosolar metallicity, ZprotoSUN = 0.017, resulting from the PARSEC calibration. The parameters of the chemical evolution models are listed in Table 3. |
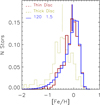 |
Fig. 5. Observed [Fe/H] distributions of thin-disc stars (solid brown) and thick-disc stars (dotted yellow). Predicted thin-dick MDF, obtained with the MTW set (solid blue), are superimposed. All histograms are self-normalised. Vertical lines mark the median values of the distributions. |
MTW yields. The MTW model that adopt the yields determined in this work is our reference model. It is shown in dark yellow in Fig. 4. This model reproduces all the constraints fairly well, but for the gas fraction that approaches the observed lower limit. The predicted MDF of the MTW model is very similar to the observed one, with a median value in very close agreement to that of the observed one. The thin disc MDF is significantly different from that of the thick disc. The IMF used to reproduce the observed constraints has a slope of x = 1.5 in the high-mass range (Kroupa et al. 1993), and MUP = 120 M⊙.
KTW yields. The KTW model is shown in blue dashed in Fig. 4. The IMF used in this case is the same as in the MTW model. Likewise, this model reproduces all the constraints satisfactorily, including the observed MDF, which is not shown here for sake of clarity. We note that the metallicity of the KTW model increases with time a bit faster than the MTW model. At ages of 2 Gyr and 8 Gyr the metallicity Z in the KTW model is about 4% and 6% higher, respectively, than predicted with MTW. This small difference is due mainly to the larger AGB yields of 12C and 14N in K10 than in M20.
Rrand Rdyields. The Rr and Rd models are shown in green in Fig. 4. Both provide similarly good fits as the other sets, but the model parameters are quite different from the other cases, as shown in Table 3. First, the mass limit is set to MUP = 25 M⊙, in agreement with their yield tables. Second, since the Fe production by CCSN in some of these models is significantly higher than predicted by other authors, in order to reproduce the observed [Fe/H] distribution and ZprotoSUN at the Galaxy age, we need to decrease the SNIa efficiency factor to ASNIa = 0.025 and to adopt a flatter IMF in the high-mass regime.
MLr yields. The MLr model is shown in cyan in Fig. 4. This model also aptly reproduces the above observational constraints without the need to change the chemical evolution parameters.
In general, we conclude that with all yield combinations it is possible to find chemical evolution models able to nicely reproduce the observed constraints for thin-disc component in the solar vicinity. As to the metallicity distribution traced by [Fe/H], models generally tend to slightly under-populate the central bins at lower metallicities, at the same time extending a bit beyond the maximum observed [Fe/H]. Being of opposite signs, the two deviations roughly compensate each other, allowing for a good reproduction of the observed median value. In principle, the agreement could be improved even more through a fine-tuning of the chemical evolution parameters. However, we note the discrepancies between the predicted and observed thin-disc MDFs are much lower than the intrinsic differences between the thin- and thick-disc observed distributions. Therefore, we may reasonably consider our results as fair models for the thin disc and proceed with the analysis of the predicted abundance ratios.
7.2. Chemical evolution of the thin disc
For each set of chemical yields, we compared the elemental abundances predicted by the corresponding best model with observations of thin-disc, thick-disc, and halo low-metallicity stars (Fig. 6). The four diagrams show the trends of a few selected species, O, Mg, Si and Ca, as a function of [Fe/H]. We recall that all the data are normalised according to the scaled-solar abundances given by Caffau et al. (2011), which sets the reference solar mixture in PARSEC.
 |
Fig. 6. Comparison of predicted abundances, derived with our best chemical evolution models (see Fig. 4) with observations of thin-disc stars (blue points) and thick-disc stars (magenta points) and halo stars (cyan triangles) in the solar neighbourhood from Bensby et al. (2014). Plotted in the figure are also the sample of metal-poor (black dots) and very metal-poor (gray dots) stars from Nissen et al. (2002) and Cayrel et al. (2004), respectively. We note that the MTW and KTW models overlap almost completely. |
MTW yields. This model is able to reproduce fairly well the observed trend in the [O/Fe] diagram, with a modest over-production at the highest [Fe/H]. Such small discrepancy should be attributed to the chemical yields from massive stars. In fact, in the COLIBRI models used here (M20 yields), TP-AGB stars produce a negligible amount of primary oxygen, as the chemical composition of the intershell is the standard one and it contains no more than 1%−2% of 16O (see, e.g., Herwig 2000, models without overshooting).
Taking the MTW model as representative of the main thin-disc branch, we see that at decreasing [Fe/H] the difference in [O/Fe] between thin and thick-disc stars increases. At [Fe/H] ≤ −1 the thin-disc branch disappears, and the MTW model approaches the lower boundary of the halo population.
Following the probability TD/D-criterion (Bensby et al. 2014), we note that a second, less populated, thin-disc branch overlaps with the sequence of thick-disc stars in the same abundance diagram. Clearly, The MTW model is not able to reproduce this secondary branch.
Concerning the [Mg/Fe] ratio, the MTW model runs through the lower border of the data, showing a well-known difficulty likely related with the 24Mg yields (Romano et al. 2010). The [Si/Fe] ratio is fairly well recovered by this model, while the [Ca/Fe] is under-produced.
KTW yields. This model behaves similarly to the MTW model for all the four abundance ratios. We recall that KTW and MTW models only differ for the AGB yields in use. Small differences appear at the lowest [Fe/H] values where the increase of KTW metallicity with time takes place somewhat faster than predicted by the MTW model (see Fig. 4 and the discussion in Sect. 7.1). Since MTW and KTW models share the same chemical evolution parameters and massive star yields, differences in the trends of chemical species should be likely ascribed to their reaching somewhat different metallicities at the same evolutionary time.
Rrand Rdyields. While successfully reproducing basic constraints of the MW thin disc, these models fail to recover the evolution of the selected abundance ratios (see Fig. 6). Even adopting a low SNIa efficiency parameter, models exhibit a substantial deficit in 16O, 24Mg, 28Si and Ca relative to Fe. In the attempt to solve the discrepancy we explored a wide range of chemical evolution parameters, but we were unable to find better models than those shown in Figs. 4 and 6. The results worsen for the rapid case and, since the ratios [α/Fe] run much flatter than observed, we argue that the issue may be linked to the iron yields of CCSN. In fact, we find that at Zi < 0.02, iron production by CCSNs predicted by R18 is significantly higher than in L18 explosive models (used in MTW, KTW and MLr), by a factor from two to four.
MLr yields. The MLr model reproduces fairly well the [O/Fe] data of the thin disc. The abundance of Mg is clearly under-predicted as already found by Prantzos et al. (2018), while predictions for Si and Ca are able to populate the regions of both thin- and thick-disc components. We note the MLr model shows a general tendency to produce abundance ratios running with slightly steeper slopes than observed.
From all the tests carried out with different combinations of chemical yields, we may draw a several key conclusions. First, the chemical species discussed here are marginally dependent on the chemical yields of AGB stars and, therefore, they cannot be considered useful diagnostics for testing the goodness of low- and intermediate-mass evolutionary models. This is not surprising since we do not expect that AGB stars synthesise Fe and Ca, whereas they may indeed be contributors of Mg isotopes, which are present both in the dredged material and involved in the Mg–Al cycle when hot-bottom burning is active in AGB stars with Mi > 3−4 M⊙ (Slemer et al. 2017; Marigo et al. 2013; Ventura & D’Antona 2009). As discussed above, the production of some primary oxygen by AGB stars depends on the inclusion of convective overshoot at the boundaries of the pulse-driven convective zone (Herwig 2000), which applies to R18, but not to M20 and K10 yields. In the context of this work, the role of AGB stars as oxygen producers is not critical irrespective of the selected yield set. This reinforces the conclusion that we need to consider other more suitable elements, such as carbon and nitrogen, to compare and check different sets of AGB yields. An in-depth analysis of AGB yields is postponed to a dedicated future work.
It follows that the abundance trends investigated in this work are critically dependent on the chemical yields from massive stars and VMO. Therefore, the reader should keep in mind that even when not explicitly stated, the discussion that follows mainly deals with the effects produced by chemical yields of stars with Mi > 8 M⊙.
Once the chemical evolution models are calibrated on a few basic observables of thin-disc stars, it is possible to reproduce fairly well the enrichment paths of [O/Fe] and [Si/Fe] with most of the yield sets. As to the [Mg/Fe] ratio, we meet the long-lasting problem of underproduction (e.g., Prantzos et al. 2018), which appears somewhat less pronounced with the MTW yields. As to the [Ca/Fe], the observations are better reproduced by massive star models with rotation. Using the R18 yields, none of the elemental ratios is well reproduced. The discrepancy is likely due to the high Fe yields in some of the Ritter et al. (2018) explosion models, which makes it hard to recover the observed [α/Fe] ratios at a given [Fe/H].
7.3. Chemical evolution of the thick disc
We turn now our attention to the chemical evolution of thick-disc stars. The diversity between thin (blue) and thick (magenta) disc stars is clearly visible in the [O/Fe] vs. [Fe/H] diagram of Fig. 6. The models adopted for the thin-disc stars are clearly not able to account for the [O/Fe] enrichment history of thick-disc stars. Furthermore, stellar age determinations indicate that thick-disc stars are, on average, older than thin-disc stars.
The origin of this marked difference may be linked to different star formation histories, similarly to other components of the MW, such as the Galactic Bulge, whose stars are even more metal-rich than thick-disc stars (Bensby et al. 2017). Some chemo-dynamical models suggest that thick-disc stars may have originated in the inner regions of the MW, characterised by an earlier and faster enrichment so that they had the time to migrate into the solar vicinity and become kinematically hotter. Under this hypothesis, these stars would be naturally characterised by certain chemical compositions and, in particular, levels of α-enhancement different from the native stellar populations of the solar neighbourhood (e.g., Aumer et al. 2017; Schönrich & Aumer 2017). More recently, an analysis of Gaia data (Gaia Collaboration 2018) provided evidence that the peculiar chemical composition of the thick disc could have originated in an early merger of the MW with a satellite galaxy, the Gaia Enceladus Sausage galaxy (Belokurov et al. 2018; Helmi et al. 2018; Haywood et al. 2018).
Contrary to the case of a thin disc, where we can constrain the chemical evolution models based on a range of observational data, such as the current SFR, gas fraction etc., for the thick disc, the most robust constraint is the MDF. The model that best reproduces the observed thick disc MDF – while keeping the IMF parameters identical to our model MTW for the thin disc, MUP = 120 and x = 1.5 and the same chemical evolution parameters k = 1 and ASNIa = 0.04 – is obtained by using τinf = 0.5 Gyr and ν = 1.4 Gyr−1. The resulting theoretical thick disc MDF (blue histogram) is compared with the observed one (yellow histogram) in Fig. 7. The parameters of this model, named TD1 are listed in Table 4. In order to fit the high [Fe/H] tail of the observed MDF, we need to include a galactic wind at an epoch of tGW = 2.5 Gyr in order to expel the residual gas (about 10% of the total mass) and stop the SF. While this assumption is introduced to cope with the simplicity of our chemical evolution code, we note that the adopted tGW corresponds to the epoch of the end of the second infall episode in the Micali et al. (2013) model. We note that models with shorter τinf show a clear star number excess below [Fe/H] ∼ −1, with respect to the observed one while, models with a larger τinf show an excess in the high metallicity tail of the MDF. The [O/Fe] vs. [Fe/H] abundance patterns obtained with model TD1, are shown in Fig. 8. This model is able to fit the observed region occupied by thick disc stars but the slope is different from the observed one. In the [O/Fe] vs. [Fe/H] diagram, it underestimates the high [O/Fe] values at low [Fe/H] and, it overestimates the low [O/Fe] values at high [Fe/H]. This model is, however, able to reproduce the region occupied by the most metal-poor stars, likely belonging to the halo population. We discuss this aspect later in the paper.
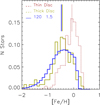 |
Fig. 7. Observed thick-disc MDF (yellow thick solid line Bensby et al. 2014) compared with the predictions of model TD1 (Table 4). The thin-disc MDF is also plotted for comparison. Vertical lines are the median values of the corresponding distributions. |
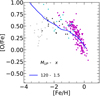 |
Fig. 8. Comparison of the observed [O/Fe] vs. [Fe/H] ratios of the thick disc (magenta dots) with those predicted by model TD1 discussed in the text (see Table 4). |
IMF parameters of the chemical evolution models for the thick disc.
7.3.1. Models with stellar rotation
An improvement of the fit of the model TD1 in the [O/Fe] vs. [Fe/H] diagram could be obtained adopting yields that account for rotational mixing in massive stars, as recently suggested by Romano et al. (2019, 2020). In support of this indication, we recall that, only yields including stellar rotation, for instance, model MLr, are actually able to produce slopes similar to the ones observed for the thick-disc stars (except for Mg; see Fig. 6). For this purpose, we calculated new models based on the chemical evolution parameters of model TD1, but using the Limongi & Chieffi (2018) yields for different initial rotational velocities, Vrot = 0, Vrot = 150, Vrot = 300 km s−1 and with the averaged rotation yields, already discussed in model MLr. The [O/Fe] vs. [Fe/H] diagram obtained with the new models is shown in Fig. 9. Using yields from stars with higher rotational velocity, we obtain higher [O/Fe] ratios. This simply reflects the fact that massive stars produce larger amount of oxygen at increasing Vrot (see Figs. B.2–B.4), while levels of iron, being mainly contributed by SNIa, barely change. Figure 9 shows that enhancing the fraction of stars with high rotational velocity may help explaining the observed [O/Fe], especially at metallicities [Fe/H] ≲ −1. Looking at Fig. 9, we may see that the non-rotating model computed with Limongi & Chieffi (2018) yields fits the lower envelope of the thin disc stars, of some thick disc outliers at [Fe/H] ≃ −2 and of the few halo stars with [Fe/H] < −2. By increasing the rotational velocity the models shifts toward higher [Fe/H] values. In particular, using the model computed adopting the averaged yields obtained from the three different rotational velocity values (cyan line, Prantzos et al. 2018), our model fits the border between thin and thick disc stars. Then, by further increasing the rotational velocity, all the thick disc stars can be fitted. These models are also able to reproduce the observed [O/Fe] values of the halo stars.
 |
Fig. 9. [O/Fe] vs. [Fe/H] abundances predicted by massive star models without and with rotation. The blue, orange and green lines refer to Limongi & Chieffi (2018) yields for initial rotational velocities Vrot = 0, Vrot = 150 and Vrot = 300 km s−1, respectively. The cyan line represents the MLr model with rotation-averaged yields. |
7.3.2. Effects due to IMF variations and VMO
Another possible explanation for the different [O/Fe] evolution of thin- and thick-disc stars could be linked to the different IMFs of the two populations. As already discussed in Sect. 3.6, the IGIMF predicts that at low metallicity and high star-formation rates, the IMF may become steeper at low masses and flatter at high masses than the canonical one (Marks et al. 2012; Jeřábková et al. 2018). This suggests that in the early phases of the thick disc evolution, the IMF could be well populated up to MUP. To investigate this aspect, we make use of our new MTW set of yields, which includes also the chemical contributions of VMO (winds, PPISN-PISN explosions, and DBH). This gives us the possibility to investigate the effects of changing both the IMF exponent x (for Mi > 1 M⊙), and the upper mass limit MUP, which can be pushed up to 350 M⊙.
Starting from the chemical evolution parameters calibrated to reproduce the MDF shown in Fig. 7, we vary the IMF parameters (x and MUP), shifting the upper mass limit into the range (120 ≤ MUP/M⊙ ≤ 350). The adopted values, listed in Table 4, are meant to test slopes typically found in the literature (1.3 ≤ x ≤ 1.7 for Mi > 1 M⊙; see Sect. 6.2), and to obtain models that are able to bracket the observed thick disc data shown in Fig. 8. The theoretical thick-disc MDFs somewhat change with the IMF variation (Fig. 10), however, the impact is not dramatic within the explored ranges of the IMF parameters, and the corresponding models actually bracket the median [Fe/H] of the observed distribution.
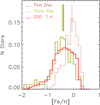 |
Fig. 10. Observed thick-disc MDF (yellow thick solid line Bensby et al. 2014) compared with the predictions of model TD4 (Table 4). |
The abundance patterns of thick disc stars predicted by these new models are compared with observations in the [O/Fe] and [Mg/Fe] vs. [Fe/H] diagrams shown in Fig. 11. We note that, in the diagram displaying [O/Fe] vs. [Fe/H], model TD2, with x = 1.7, runs almost parallel and below model TD1, and is eventually able to reproduce the branch with low [O/Fe] ratios at [Fe/H] = 0. Models TD1 and TD2 are also able to reproduce the lower envelope of observed halo stars with [Fe/H] ≥ −3. However, while below this metallicity, the data show a plateau or even a decreasing branch, the [O/Fe] values of the above two models continue to increase. We recall that the majority of these halo stars are sub-giant or giant stars from Cayrel et al. (2004) and their [O/Fe] values have been corrected for 3D effects, as suggested in Nissen et al. (2002).
 |
Fig. 11. Comparison of the observed [O/Fe] vs. [Fe/H] (left panel) and [Mg/Fe] vs. [Fe/H] (right panel) ratios of the thick disc stars, with the predictions of models with different IMF parameters as listed in Table 4. We see that increasing MUP, so as to include the contributions of VMO (winds, PPISN and PISN), thick-disc stars can be reproduced pretty well. Moreover, changing both the IMF slope and MUP, different populations can be recovered. |
The behaviour of the models change significantly if they include the ejecta from VMO. In Table 4, we report also the expected number of stars per 106 M⊙ of gas converted into stars, that are born with 10 M⊙ ≤ Mi ≤ 120 M⊙ and with 120 M⊙ ≤ Mi ≤ MUP, resulting from the corresponding IMF parameters. It is easy to see from Table 4 that the fractional contribution of VMOs to the total number of massive stars progressively increase as we move from model TD3 to model TD4 and TD5. We first note that even a small fraction of stars born as VMO is enough to change the initial evolution of the [O/Fe] ratios (model TD3). This is due to the fact that low metallicity VMOs are able to produce enough Fe to decrease the [O/Fe] ratio. Then, as the fractional number of VMOs increases, the models are able to reach lower and lower [O/Fe] ratios. Models TD3, TD4, and TD5 are successful in reproducing the distribution of halo stars with [Fe/H] ≤ −2.
When the metallicity rises above Zi ∼ 0.0001, there is a jump in the 16O production with respect to that of Fe. Indeed, while 16O is copiously produced in almost all PISN models, for Fe this is true only for the more massive ones, with Ej(Fe) ∼ 20 M⊙ for MHe ∼ 115 M⊙ and Ej(Fe) ∼ 0.5 M⊙ or MHe ∼ 85 M⊙ (Heger & Woosley 2002). This alternative behaviour of 16O and Fe production by PISNe at decreasing MHe, gives rise to a rapid jump in the [O/Fe] ratio at [Fe/H] ∼ −2. After the jump, the [O/Fe] ratio reaches a peak well within the observed thick disc data, and then decreases following the observed slope of the data. At [Fe/H] ≥ −2, models TD3 and TD4 bracket the majority of the thick disc, data leaving outside only a few objects with high [O/Fe] ratios. Model TD5 can be considered as an extreme case, that is able to reproduce the lower and upper envelopes of the [O/Fe] ratios, at the lower and higher metallicities, respectively.
A similar evolution can be seen also in the case of the [Mg/Fe] vs. [Fe/H] ratios, as shown in the right panel of Fig. 11. We note that models without VMOs, TD1 and TD2, are not able to reproduce the [Mg/Fe] ratios observed at very low metallicity [Fe/H] ≤ −2. On the contrary, models TD3, TD4 and TD5 run across the observed metal-poor halo stars, well reproducing the growing [Mg/Fe] ratio at increasing [Fe/H]. Thus, in the very early stages of the thick disc chemical evolution, the models with VMOs are able to reproduce the observed α-poor (Mg) stars, for instance, those with [Mg/Fe] ∼ 0.0 at [Fe/H] ≲ −1. For [Fe/H] > −2, models TD3, TD4, and TD5 jump inside the thick disc observations, providing an overall good fit to the evolution of halo and thick disc stars.
In summary, while no single TD model is able to reproduce the [O/Fe] and [Mg/Fe] observations of the halo and thick disc stars at once, a combination of TD models with varying IMF, in line with the predictions of the IGIMF already discussed, is able to reproduce the location and the dispersion observed among halo stars and the thick disc chemical evolution pattern. Finally, we note that the inclusion of PISNe may also help in solving the issue of Mg under-prediction that is present in most of the previously published yield tables (Timmes et al. 1995; Portinari et al. 1998; Prantzos et al. 2018).
In conclusion, our analysis shows that IMF variations, in terms of slope but more importantly in terms of MUP, may significantly affect the predictions of chemical evolution models. In turn, this may impact on our understanding of the observed MW populations.
8. Summary and concluding remarks
In this work, we investigate the impact of the ejecta of massive and very massive stars on the predictions of chemical evolution models. We constructed different sets of chemical yields that include both winds and explosion contributions. To this aim, we collected various explosion yields available in the literature and combined them with the wind ejecta computed with our code PARSEC or other authors. A novelty of this work is that we investigate the effect of increasing the IMF upper mass limit up to MUP = 350 M⊙, which is well beyond the standard value of MUP ∼ 100 M⊙, typically used in most studies. This allows us to explore the impact of VMOs, which are expected to eject significant amounts of newly produced elements through both powerful stellar winds and PPISN-PISN explosions. For completeness, we also include the chemical yields of AGB stars computed with our COLIBRI (Marigo et al. 2013) and from other studies. We note that the impact of AGB stars on the chemical species considered in this work (Fe, O, Mg, Si, Ca) is minor. An analysis aimed at highlighting the role of the chemical yields from low- and intermediate-mass stars is postponed to a dedicated future work.
The different sets of chemical yields are then incorporated in our chemical evolution code CHE-EVO (Silva et al. 1998) to analyse the chemical evolution of thin- and thick-disc stars in the solar vicinity, for which we can rely on accurate abundance measurements and kinematical classifications (Bensby et al. 2014).
For each set of chemical yields, we ran grids of chemical evolution models to single out the parameters that best fit the main observational constraints of the MW thin disc, namely: the present-day star formation rate and gas fraction, the rates of CCSN and SNIa, the metallicity of the Sun at its birth epoch ≃4.6 Gyr ago, and the observed MDF. For all sets of chemical yields, we were able to find suitable combinations of input parameters that match all the constraints reasonably well (see Table 2). In the best-fit models the Schmidt star-formation law exhibits a typical efficiency in the range 0.4 < ν < 0.8 and an exponent k = 1. The gas infall time-scale generally varies in the range 3 < τ/Gyr < 6.
Once the chemical evolution model is calibrated for each set of yields, we move to test them against the observations. We focus on the trends of the abundance ratios for a few α-elements ([O/Fe], [Mg/Fe], [Si/Fe], [Ca/Fe]) as a function of the metallicity, traced by [Fe/H]. A general agreement is found for [O/Fe] and [Si/Fe], while the predictions for [Mg/Fe] and [Ca/Fe] run below the observed data. The best results are obtained when including the yields from rotating massive stars (Limongi & Chieffi 2018) and those based on our PARSEC models for the hydrostatic phases. With the Ritter et al. (2018) yields, all abundance ratios are significantly below the observed values, despite the fact that the corresponding calibrated chemical evolution model reproduces the thin-disc constraints. After carefully examining the problem, we conclude that a possible cause is the large iron production of these sets of yields.
Most best-fit models are able to recover reasonably well the slope of the bulk of the thin-disc stars. With our MTW set of yields, the calibrated IMF exponent is x = 1.5, which is intermediate between the results of Kroupa et al. (1993, x = 1.7) and the top-heavier IMFs of Kroupa (2001, x = 1.3) and Chabrier (2003, x = 1.3).
In this study we did not find evidence that the IMF exponent is degenerate with other chemical evolution parameters, such as ν or k, but we cannot exclude the possibility that more complex chemical evolution models may provide a different indication. Recently Valentini et al. (2019) pointed out that hydrodynamical models support either of the Kroupa IMF slopes, depending on the set of observational data adopted for comparison. In this respect, we note that a steeper slope of the IMF is more suitable to reproduce thin-disc stars, as suggested by various other investigations (Matteucci & Francois 1989; Matteucci 2001; Grisoni et al. 2018; Matteucci et al. 2019, 2020).
Thick-disc stars exhibit a [O/Fe] vs. [Fe/H] pattern that is different from that of the thin-disc stars, characterised by a steeper slope and a larger degree of α-enhancement, with higher [O/Fe] ratios. This feature is much less evident in the [Mg/Fe] diagram. In this respect, we note that there are stars that likely belong to the thin disc according to the kinematical classification, but which have higher [O/Fe] values and fall in the region populated by the thick-disc stars. Our thin-disc models do not reproduce such stars. Possible explanations of this anomalous behaviour are that either they have formed in different environmental conditions that are more compatible with a top-heavier IMF (e.g., in the IGIMF scenario for a low metallicity or high SFR, or both) or, rather, the kinematical parameters of these stars varied in such a way that they are now classified as thin-disc members.
None of the chemical evolution models calibrated on the thin disc are able to reproduce the [O/Fe] trend of the thick disc. To reproduce the higher values of the α-enhancement seen in thick disc stars, it is necessary to change the chemical evolution parameters, in particular, to reduce the infall time-scale to τinf = 0.5 Gyr and increase the star formation efficiency to ν = 1.4 Gyr−1, in agreement with the literature (Grisoni et al. 2019, 2020a,b). The MDF of thick disc stars is well reproduced with these parameters but, in order to better fit its fast decreasing tail at the higher metallicity with our simple chemical evolution model, we need to impose a galactic wind at an age of 2.5 Gyr. Although the MDF is well reproduced, the tuning on the [O/Fe] vs. [Fe/H] diagram is not satisfactory. The model enters the region populated by thick disc stars but with a slope that is flatter than that of the trend of the data. In particular, the model cannot reproduce the high α-enhanced thick disc stars at low metallicities. The model cannot reproduce also the pattern of halo stars, which have been included here to check its early chemical evolution.
Since it has been recently suggested that a higher α-enhancement could be obtained by considering yields from fast-rotating stars (Limongi & Chieffi 2018; Romano et al. 2019), we calculated new models changing only the yields and using those that include effects of rotation (Limongi & Chieffi 2018; Prantzos et al. 2018). Our analysis shows that we can well reproduce the [O/Fe] vs. [Fe/H] diagram of thick disc by increasing only the fraction of rotating stars. The LC18 models without rotation run along the lower envelope of thick disc while those with intermediate and high rotational velocity reproduce its upper envelope as shown in Fig. 9. This, in fact, may give rise to a degeneracy between chemical evolution parameters (τinf and ν) and stellar rotational velocities. The low metallicity halo stars in this diagram cannot be reproduced by our model.
An alternative way to reproduce the observations of the thick disc has been offered by the recent growing evidence for a significant dependence of the IMF on the environment (Marks et al. 2012; Jeřábková et al. 2018). In the IGIMF theory, the IMF may become top heavier at decreasing metallicity and increasing star-formation rate. If this is true, the different MDFs of the thin and thick discs could be not only the result but also one of the reasons of the different chemical evolution patterns of the two MW components. In particular, in the early phases of the thick disc evolution, the IMF could be well populated up to an MUP that is able to switch on the chemical contribution from PISNe. Motivated by the above reasons, we used our MTW yields to analyse the effects of varying both the slope and MUP. Using the same chemical evolution parameters of model TD1, we computed other models to check the effects of such IMF variations. Among the calculated new models we have selected four representative cases that are able to match the properties of thick disc stars. One with a steeper IMF (x = 1.7) and canonical MUP = 120 which defines the lower boundary of the thick disc in the [O/Fe] vs. [Fe/H] diagram, other two with MUP = 200 and x = 1.7 and 1.4, respectively, and a final one with MUP = 350 and x = 1.2.
The latter three models, characterised by a MUP that falls within the VMOs, are able to bracket the thick disc observations in both the [O/Fe] vs. [Fe/H] and the [Mg/Fe] vs. [Fe/H] diagrams. At the same time, while with canonical MUP we are not able to reproduce the properties of metal-poor halo stars in neither of the above diagrams, this is possible with the models that include the contribution of PISNe. Halo stars, in the [O/Fe] and [Mg/Fe] vs. [Fe/H] diagrams, show a constant or even decreasing trend of the α-enhancement at decreasing [Fe/H]. This trend can be reproduced if the models include enough Fe contribution coming from PISNe at lower metallicities ([Fe/H] ≤ −2). While there is a dispute concerning the reality of this decreasing branch in the [O/Fe] diagram (Nissen et al. 2002; Cayrel et al. 2004; Micali et al. 2013) this constant or even decreasing trend is seen also in the [Mg/Fe] diagram. In any case, a recent analysis of O and Fe measurements in disc and halo stars by Amarsi et al. (2019) has indicated that the [O/Fe] ratio reaches a constant plateau of [O/Fe] ∼ 0.6 below [Fe/H] ∼ −1 and it is thus not compatible with the constant growth, at decreasing [Fe/H], indicated by our models with canonical MUP. It is worthwhile noting that the models that include the effects of rotation are facing the same problem. Instead, an increasing fraction of VMOs (eventually in line with the prediction of the IGIMF theory) will produce models that progressively show lower [α/Fe] ratios, thus naturally explaining the halo star dispersion and, at the same time, matching the high [α/Fe] ratios of thick-disc stars.
In conclusion, our study provides a clear indication that PISN may have played a significant role in shaping the chemical evolution path of halo and thick-disc stars. Especially in view of the possible flattening of the IMF at low metallicity and high SFR, their contribution should not be neglected in chemical evolution models. In the light of these results, we may reasonably expect that similar data, which actually exist for nearby extremely metal-poor star bursting galaxies (Kojima et al. 2020), might host the chemical signature of very massive stars, and that would witness their key role in the early phases of galaxy evolution. The complete TW sets of chemical ejecta for massive and very massive stars, described in Appendix A, have been made publicly available9.
Acknowledgments
We thank F. Matteucci, D. Romano and the anonymous referee for useful suggestions that helped to improve the manuscript. PM and AS acknowledge the support from the ERC Consolidator Grant funding scheme (project STARKEY, grant agreement n. 615604). AB and LS acknowledge PRIN MIUR 2017 – 20173ML3WW_001. MS acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie-Skłodowska-Curie grant agreement No. 794393. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018) and matplotlib, a Python library for publication quality graphics (Hunter 2007). This work has been partially supported by PRIN MIUR 2017 prot. 20173ML3WW 002, ‘Opening the ALMA window on the cosmic evolution of gas, stars and supermassive black holes’. AL acknowledges the MIUR grant ‘Finanziamento annuale individuale attivita base di ricerca’ and the EU H2020-MSCA-ITN-2019 Project 860744 ‘BiD4BEST: Big Data applications for Black hole Evolution STudies’. VG acknowledges financial support at SISSA from the European Social Fund operational Programme 2014/2020 of the autonomous region Friuli Venezia Giulia.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [CrossRef] [Google Scholar]
- Allende Prieto, C., Majewski, S. R., Schiavon, R., et al. 2008, Astron. Nach., 329, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Amarsi, A. M., Nissen, P. E., & Skúladóttir, Á. 2019, A&A, 630, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Aumer, M., Binney, J., & Schönrich, R. 2017, MNRAS, 470, 3685 [NASA ADS] [CrossRef] [Google Scholar]
- Ballero, S. K., Matteucci, F., & Chiappini, C. 2006, New Astron., 11, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Tsujimoto, T. 2011, ApJ, 738, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Gould, A., et al. 2017, A&A, 605, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boeche, C., Chiappini, C., Minchev, I., et al. 2013, A&A, 553, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, J. R., Arnett, W. D., & Carr, B. J. 1982, in NATO Advanced Science Institutes (ASI) Series C, eds. M. J. Rees, & R. J. Stoneham, 90, 303 [Google Scholar]
- Bond, J. R., Arnett, W. D., & Carr, B. J. 1984, ApJ, 280, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Botelho, R. B., Milone, A. D. C., Meléndez, J., et al. 2020, MNRAS, 499, 2196 [CrossRef] [Google Scholar]
- Bressan, A., Chiosi, C., & Fagotto, F. 1994, ApJS, 94, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Vartanyan, D., Dolence, J. C., Skinner, M. A., & Radice, D. 2018, Space Sci. Rev., 214, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chen, K.-J., Woosley, S., Heger, A., Almgren, A., & Whalen, D. J. 2014, ApJ, 792, 28 [CrossRef] [Google Scholar]
- Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I., & Dwek, E. 2009, ApJ, 703, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I., & Dwek, E. 2010, ApJ, 713, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C. 2009, in The Galaxy Disk in Cosmological Context, eds. J. Andersen, B. Nordströara, & J. Bland-Hawthorn, IAU Symp., 254, 191 [NASA ADS] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [Google Scholar]
- Chieffi, A., & Limongi, M. 2004, ApJ, 608, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C. 1980, A&A, 83, 206 [NASA ADS] [Google Scholar]
- Chiosi, C., Bressan, A., Portinari, L., & Tantalo, R. 1998, A&A, 339, 355 [NASA ADS] [Google Scholar]
- Costa, G., Girardi, L., Bressan, A., et al. 2019a, A&A, 631, A128 [CrossRef] [EDP Sciences] [Google Scholar]
- Costa, G., Girardi, L., Bressan, A., et al. 2019b, MNRAS, 485, 4641 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, G., Bressan, A., Mapelli, M., et al. 2021, MNRAS, 501, 4514 [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
- Crowther, P. A. 2019, Galaxies, 7, 88 [CrossRef] [Google Scholar]
- Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- de Laverny, P., Recio-Blanco, A., Worley, C. C., et al. 2013, The Messenger, 153, 18 [NASA ADS] [Google Scholar]
- Doherty, C. L., Gil-Pons, P., Lau, H. H. B., Lattanzio, J. C., & Siess, L. 2014, MNRAS, 437, 195 [Google Scholar]
- Doherty, C. L., Gil-Pons, P., Siess, L., & Lattanzio, J. C. 2017, PASA, 34, e056 [NASA ADS] [CrossRef] [Google Scholar]
- Ertl, T., Janka, H.-T., Woosley, S. E., Sukhbold, T., & Ugliano, M. 2016, ApJ, 818, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Walborn, N. R., Crowther, P. A., et al. 2010, ApJ, 715, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [CrossRef] [Google Scholar]
- Feltzing, S., Bensby, T., & Lundström, I. 2003, A&A, 397, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrini, F., Molla, M., Pardi, M. C., & Diaz, A. I. 1994, ApJ, 427, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Somerville, R. S., Silva, L., Monaco, P., & Skibba, R. 2009, MNRAS, 392, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Kalogera, V. 2001, ApJ, 554, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Young, P. A., & Hungerford, A. L. 2006, ApJ, 650, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2011, MNRAS, 414, 2893 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Berro, E., Ritossa, C., & Iben, I., Jr 1997, ApJ, 485, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Girardi, L., Williams, B. F., Gilbert, K. M., et al. 2010, ApJ, 724, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G. 2008, in Clumping in Hot-Star Winds, eds. W. R. Hamann, A. Feldmeier, & L. M. Oskinova, 103 [Google Scholar]
- Grand, R. J. J., Bustamante, S., Gómez, F. A., et al. 2018, MNRAS, 474, 3629 [NASA ADS] [CrossRef] [Google Scholar]
- Grisoni, V., Spitoni, E., Matteucci, F., et al. 2017, MNRAS, 472, 3637 [Google Scholar]
- Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
- Grisoni, V., Matteucci, F., Romano, D., & Fu, X. 2019, MNRAS, 489, 3539 [NASA ADS] [CrossRef] [Google Scholar]
- Grisoni, V., Cescutti, G., Matteucci, F., et al. 2020a, MNRAS, 492, 2828 [NASA ADS] [CrossRef] [Google Scholar]
- Grisoni, V., Romano, D., Spitoni, E., et al. 2020b, MNRAS, 498, 1252 [CrossRef] [Google Scholar]
- Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018, MNRAS, 474, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., et al. 2018, ApJ, 863, 113 [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hosek, M. W., Jr., Lu, J. R., Anderson, J., et al. 2019, ApJ, 870, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr, Ritossa, C., & García-Berro, E. 1997, ApJ, 489, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., & Kohyama, Y. 1983, ApJ, 275, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Uchida, S., Sakamoto, Y., Kohyama, Y., & Nozawa, S. 2008, ApJ, 677, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Izzo, L., de Ugarte Postigo, A., Maeda, K., et al. 2019, Nature, 565, 324 [Google Scholar]
- Janka, H.-T. 2012, Ann. Rev. Nucl. Part. Sci., 62, 407 [Google Scholar]
- Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jimenez, R., Padoan, P., Matteucci, F., & Heavens, A. F. 1998, MNRAS, 299, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kalogera, V., & Baym, G. 1996, ApJ, 470, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lugaro, M., Carlos, M., et al. 2018, MNRAS, 477, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Karlsson, T., Johnson, J. L., & Bromm, V. 2008, ApJ, 679, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Kawata, D., & Chiappini, C. 2016, Astron. Nachr., 337, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kojima, T., Ouchi, M., Rauch, M., et al. 2020, ApJ, 913, 22 [CrossRef] [Google Scholar]
- Kozyreva, A., Yoon, S.-C., & Langer, N. 2014a, A&A, 566, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozyreva, A., Blinnikov, S., Langer, N., & Yoon, S.-C. 2014b, A&A, 565, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 3 [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1972, Nature, 236, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lawlor, T. M., Young, T. R., Johnson, T. A., & MacDonald, J. 2008, MNRAS, 384, 1533 [CrossRef] [Google Scholar]
- Lebzelter, T., Mowlavi, N., Marigo, P., et al. 2018, A&A, 616, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leung, S.-C., Nomoto, K., & Blinnikov, S. 2019, ApJ, 887, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, S.-C., Nomoto, K., & Suzuki, T. 2020, ApJ, 889, 34 [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2018 ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Franceschini, A., Vaccari, M., et al. 2013, ApJ, 762, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Silva, L., Franceschini, A., Miller, N., & Efstathiou, A. 2015, MNRAS, 447, 3442 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1975, Vistas Astron., 19, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., & Moriya, T. J. 2020, A&A, 640, L18 [EDP Sciences] [Google Scholar]
- Marigo, P. 2001, A&A, 370, 194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., & Aringer, B. 2009, A&A, 508, 1539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Chiosi, C., & Wood, P. R. 2001, A&A, 371, 152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Chiosi, C., & Kudritzki, R. P. 2003, A&A, 399, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Bressan, A., Nanni, A., Girardi, L., & Pumo, M. L. 2013, MNRAS, 434, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Cummings, J. D., Curtis, J. L., et al. 2020, Nat. Astron., 4, 1102 [CrossRef] [Google Scholar]
- Marks, M., Kroupa, P., Dabringhausen, J., & Pawlowski, M. S. 2012, MNRAS, 422, 2246 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 1994, A&A, 288, 57 [NASA ADS] [Google Scholar]
- Matteucci, F. 2001, The Chemical Evolution of the Galaxy (Berlin: Springer-Verlag) [Google Scholar]
- Matteucci, F. 2014, Saas-Fee Advanced Course, 37, 145 [CrossRef] [Google Scholar]
- Matteucci, F., & Brocato, E. 1990, ApJ, 365, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- Matteucci, F., & Pipino, A. 2005, MNRAS, 357, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., Grisoni, V., Spitoni, E., et al. 2019, MNRAS, 487, 5363 [Google Scholar]
- Matteucci, F., Vasini, A., Grisoni, V., & Schultheis, M. 2020, MNRAS, 494, 5534 [Google Scholar]
- Micali, A., Matteucci, F., & Romano, D. 2013, MNRAS, 436, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Mikolaitis, Š., de Laverny, P., Recio-Blanco, A., et al. 2017, A&A, 600, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munakata, H., Kohyama, Y., & Itoh, N. 1985, ApJ, 296, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., Primas, F., Asplund, M., & Lambert, D. L. 2002, A&A, 390, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [Google Scholar]
- O’Connor, E., & Ott, C. D. 2011, ApJ, 730, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ohkubo, T., Umeda, H., Maeda, K., et al. 2006, ApJ, 645, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Ohkubo, T., Nomoto, K., Umeda, H., Yoshida, N., & Tsuruta, S. 2009, ApJ, 706, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Nordlund, A., & Jones, B. J. T. 1997, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., & Edmunds, M. G. 1981, ARA&A, 19, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [Google Scholar]
- Pastorelli, G., Marigo, P., Girardi, L., et al. 2020, MNRAS, 498, 3283 [Google Scholar]
- Pignatari, M., Herwig, F., Hirschi, R., et al. 2016, ApJS, 225, 24 [CrossRef] [Google Scholar]
- Plevne, O., Önal Tas, Ö., Bilir, S., & Seabroke, G. M. 2020, ApJ, 893, 108 [CrossRef] [Google Scholar]
- Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [Google Scholar]
- Portinari, L., & Chiosi, C. 1999, A&A, 350, 827 [NASA ADS] [Google Scholar]
- Portinari, L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505 [NASA ADS] [Google Scholar]
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69 [NASA ADS] [Google Scholar]
- Prantzos, N., Boehm, C., Bykov, A. M., et al. 2011, Rev. Mod. Phys., 83, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [Google Scholar]
- Prochaska, J. X., Naumov, S. O., Carney, B. W., McWilliam, A., & Wolfe, A. M. 2000, AJ, 120, 2513 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Calura, F., & Kroupa, P. 2009, A&A, 499, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzo, M., Farmer, R. J., Justham, S., et al. 2020, MNRAS, 493, 4333 [CrossRef] [Google Scholar]
- Ricotti, M., & Ostriker, J. P. 2004, MNRAS, 350, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Ritossa, C., Garcia-Berro, E., & Iben, I., Jr 1996, ApJ, 460, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, C., Herwig, F., Jones, S., et al. 2018, MNRAS, 480, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Rollinde, E., Vangioni, E., Maurin, D., et al. 2009, MNRAS, 398, 1782 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z. Y., Papadopoulos, P. P., & Ivison, R. J. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., Ivison, R. J., & Ventura, P. 2019, MNRAS, 490, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Franchini, M., Grisoni, V., et al. 2020, A&A, 639, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenfield, P., Marigo, P., Girardi, L., et al. 2014, ApJ, 790, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfield, P., Marigo, P., Girardi, L., et al. 2016, ApJ, 822, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Sahijpal, S. 2014, Int. J. Astron. Astrophys., 4, 491 [CrossRef] [Google Scholar]
- Savino, A., Koch, A., Prudil, Z., Kunder, A., & Smolec, R. 2020, A&A, 641, A96 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [Google Scholar]
- Schönrich, R., & Aumer, M. 2017, MNRAS, 472, 3979 [NASA ADS] [CrossRef] [Google Scholar]
- Senchyna, P., Stark, D. P., Charlot, S., et al. 2021, MNRAS, 503, 6112 [CrossRef] [Google Scholar]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, L., Schurer, A., Granato, G. L., et al. 2011, MNRAS, 410, 2043 [NASA ADS] [Google Scholar]
- Slemer, A. 2016, PhD Thesis, Padova University, Italy [Google Scholar]
- Slemer, A., Marigo, P., Piatti, D., et al. 2017, MNRAS, 465, 4817 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Spera, M., & Mapelli, M. 2017, MNRAS, 470, 4739 [Google Scholar]
- Spera, M., Mapelli, M., & Bressan, A. 2015, MNRAS, 451, 4086 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H. T. 2016, ApJ, 821, 38 [Google Scholar]
- Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]
- Tews, I., & Schwenk, A. 2020, ApJ, 892, 14 [CrossRef] [Google Scholar]
- Thielemann, F. K., Hirschi, R., Liebendörfer, M., & Diehl, R. 2011, in Lecture Notes in Physics, eds. R. Diehl, D. H. Hartmann, & N. Prantzos (Berlin: Springer Verlag), 812, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Ugliano, M., Janka, H.-T., Marek, A., & Arcones, A. 2012, ApJ, 757, 69 [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, ApJ, 565, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2008, ApJ, 673, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P., & Chugai, N. N. 2009, A&A, 506, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., Chugai, N. N., & Botticella, M. T. 2010, ApJ, 723, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Valentini, M., Borgani, S., Bressan, A., et al. 2019, MNRAS, 485, 1384 [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2012, ApJ, 760, 70 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P., Conroy, C., Villaume, A., Brodie, J., & Romanowsky, A. J. 2017, ApJ, 841, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Vega, O., Clemens, M. S., Bressan, A., et al. 2008, A&A, 484, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., & D’Antona, F. 2009, A&A, 499, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., Di Criscienzo, M., Carini, R., & D’Antona, F. 2013, MNRAS, 431, 3642 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Stanghellini, L., Dell’Agli, F., & García-Hernández, D. A. 2017, MNRAS, 471, 4648 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Karakas, A., Dell’Agli, F., García-Hernández, D. A., & Guzman-Ramirez, L. 2018, MNRAS, 475, 2282 [NASA ADS] [Google Scholar]
- Vera-Ciro, C., D’Onghia, E., & Navarro, J. F. 2016, ApJ, 833, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R., Sana, H., Simón-Díaz, S., et al. 2014, A&A, 564, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wanajo, S., Nomoto, K., Janka, H. T., Kitaura, F. S., & Müller, B. 2009, ApJ, 695, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2005, Astron. Nachr., 326, 605 [Google Scholar]
- Woosley, S. E. 2017, ApJ, 836, 244 [Google Scholar]
- Woosley, S. E., & Heger, A. 2015, in Very Massive Stars in the Local Universe, ed. J. S. Vink, Astrophys. Space Sci. Lib., 412, 199 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yoon, S. C., Dierks, A., & Langer, N. 2012, A&A, 542, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoshida, T., Umeda, H., Maeda, K., & Ishii, T. 2016, MNRAS, 457, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Yusof, N., Hirschi, R., Meynet, G., et al. 2013, MNRAS, 433, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, D. B., de Silva, G., Freeman, K., Bland-Hawthorn, J., & Hermes Team 2012, in Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, eds. W. Aoki, M. I. Ishigaki, T. Suda, T. Tsujimoto, & N. Arimoto, ASP Conf. Ser., 458, 421 [Google Scholar]
Appendix A: Tables of chemical ejecta
Here, we present the ejecta tables (set TW) for massive and very massive stars used in this work that will be available at the CDS, for 4 values of the initial metallicity (Zi = 0.0001, 0.001, 0.006, 0.02) and 30 values of the initial mass (8 ≤ Mi/M⊙ ≤ 350). Each table corresponds to one selected value of Zi. The row labelled Xj, 0 gives the initial abundances (in mass fraction) corresponding to a scaled-solar composition for elements heavier than He (Caffau et al. 2011). The initial abundances of H and He as a function of Zi are derived from the enrichment law calibrated with PARSEC models (Bressan et al. 2012). The complete ejecta tables include the following chemical species: 1H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, 21Ne, 22Ne, 23Na, 24Mg, 25Mg, 26Mg, 26Al, 27Al, 28Si, 29Si, P, S, Cl, Ar, K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn. For elements without the indication of the atomic mass, we give the sum of the ejecta of their stable isotopes.
We recall that mass loss in the PARSEC code is applied only to stars with Mi ≥ 14 M⊙. It follows that the wind ejecta for stars with Mi < 14 M⊙ are set to zero. It is worthwhile specifying that the ejecta of the VMO that avoid the explosion and directly collapse to black holes (DBH, for MHe > 130 M⊙) are included in the wind tables. The explosion ejecta tables contain the chemical contribution of all layers that extend from Mcut to Mfin. This applies to both successful CCSN, PPISN and PISN. We recall that in the case of a failed core-collapse supernova we have Mcut = Mrem = Mfin and the explosion ejecta are zero for all species. With regard to PISN, we set Mcut = 0, as the associated thermonuclear explosion leaves no remnant.
Other relevant stellar parameters are tabulated (in units of M⊙), namely: the pre-SN mass (Mfin), the mass of He core (MHe), the mass of the C–O core (MCO), and remnant mass (Mrem). We also provide the pre-SN phase (see also Sect. 3):
-
RSG: red supergiant
-
BSG: blue supergiant
-
WC: Wolf-Rayet stars enriched in carbon
-
WN: Wolf-Rayet stars enriched in nitrogen
-
WO: Wolf-Rayet stars enriched in oxygen
-
LBV: luminous blue variables
and the final fate:
-
ECSN: electron capture SN
-
sCCSN: successful core collapse SN
-
fCCSN: failed core collapse SN
-
PPISN: pulsation-pair instability SN
-
PISN: pair instability SN
-
DBH: stars that direct collapse into black hole without explosion
As an example, a reduced version of an ejecta table containing a smaller number of elements is presented in Table A.1.
Example table containing the total ejecta, 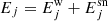 (in M⊙, see Sect. 3.2), of massive and very massive stars used in this work (extracted from the set MTW), for Zi = 0.02 and a few selected chemical species.
(in M⊙, see Sect. 3.2), of massive and very massive stars used in this work (extracted from the set MTW), for Zi = 0.02 and a few selected chemical species.
Appendix B: Comparison of the ejecta from various authors
To compare the wind ejecta over a very large range of initial masses, it is convenient to define the quantity:
which corresponds to the fraction of Mi lost through stellar winds in the form of the species j. Figure B.1 shows Wj(Mi) derived from PARSEC models at varying Mi and Zi, for a few relevant species: 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ca, Ar, Ti, Fe.
 |
Fig. B.1. Fractional wind ejecta, Wj, derived from PARSEC stellar models, as a function of Mi and Zi. The chemical species shown are 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ar, Ca, Ti, Fe. |
Similarly, the newly synthesised total ejecta (winds plus explosion) can be suitably analysed with the aid of the calculation:
which represents the fraction of the initial stellar mass that is ejected in the form of the species j. From the definition it follows that Pj(Mi) > 0 corresponds to a net production of the species j, while Pj(Mi) < 0 means that the species j is effectively destroyed compared to its initial content. Figures B.2–B.6 show Pj(Mi) as a function of Mi and Zi for the same chemical species as Fig. B.1, and compare the predictions obtained with the various sets of yields discussed in this work.
 |
Fig. B.2. Fractional total ejecta (winds and explosion) of new production, Pj, for Zi = 0.0001 as a function of Mi. Our MTW ejecta are compared with those of other literature works. The chemical species shown are 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ar, Ca, Ti, Fe. |
 |
Fig. B.3. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.001. Same description as in Fig. B.2. |
 |
Fig. B.4. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.006. Same description as in Fig. B.2. We note that LC18 ejecta are taken from their closest lower metallicity, Zi = 0.004. |
 |
Fig. B.5. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.006. We note that LC18 ejecta are taken from their closest larger metallicity, Zi = 0.008. Same description as in Fig. B.2. |
 |
Fig. B.6. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.02. Same description as in Fig. B.2. |
All Tables
Example table containing the total ejecta, 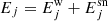 (in M⊙, see Sect. 3.2), of massive and very massive stars used in this work (extracted from the set MTW), for Zi = 0.02 and a few selected chemical species.
(in M⊙, see Sect. 3.2), of massive and very massive stars used in this work (extracted from the set MTW), for Zi = 0.02 and a few selected chemical species.
All Figures
 |
Fig. 1. Pre-SN mass Mfin as function of initial Mi for different values of the initial metallicity Zi, as indicated. Stellar tracks are taken from PARSEC VI.1 models. |
| In the text | |
 |
Fig. 2. MHe (left panel) and MCO (right panel) as a function of Mi, for different values of Zi. Lines show the data extracted from PARSEC stellar evolution models, while crosses represent the models of Chieffi & Limongi (2004). |
| In the text | |
 |
Fig. 3. Final fate of massive and very massive stars as a function of Mi and Zi. Green dot is a successful SN, from ECSN if the background is light green or CCSN if it is yellow; red dot is a BH from a failed CCSN; red dot in a black box is a BH from PPISN; yellow star is a thermonuclear explosion from PISN and black dot is a DBH. |
| In the text | |
 |
Fig. 4. Evolution of SFR, gas fraction, SNII and SNIa rates, and total gas metallicity. Different lines correspond to the best chemical evolution models obtained with different sets of yields, as indicated. Vertical bars at an age of 13 Gyr show their present-day estimated values. In the bottom-right panel the solid triangle at the age of 8.4 Gyr marks the protosolar metallicity, ZprotoSUN = 0.017, resulting from the PARSEC calibration. The parameters of the chemical evolution models are listed in Table 3. |
| In the text | |
 |
Fig. 5. Observed [Fe/H] distributions of thin-disc stars (solid brown) and thick-disc stars (dotted yellow). Predicted thin-dick MDF, obtained with the MTW set (solid blue), are superimposed. All histograms are self-normalised. Vertical lines mark the median values of the distributions. |
| In the text | |
 |
Fig. 6. Comparison of predicted abundances, derived with our best chemical evolution models (see Fig. 4) with observations of thin-disc stars (blue points) and thick-disc stars (magenta points) and halo stars (cyan triangles) in the solar neighbourhood from Bensby et al. (2014). Plotted in the figure are also the sample of metal-poor (black dots) and very metal-poor (gray dots) stars from Nissen et al. (2002) and Cayrel et al. (2004), respectively. We note that the MTW and KTW models overlap almost completely. |
| In the text | |
 |
Fig. 7. Observed thick-disc MDF (yellow thick solid line Bensby et al. 2014) compared with the predictions of model TD1 (Table 4). The thin-disc MDF is also plotted for comparison. Vertical lines are the median values of the corresponding distributions. |
| In the text | |
 |
Fig. 8. Comparison of the observed [O/Fe] vs. [Fe/H] ratios of the thick disc (magenta dots) with those predicted by model TD1 discussed in the text (see Table 4). |
| In the text | |
 |
Fig. 9. [O/Fe] vs. [Fe/H] abundances predicted by massive star models without and with rotation. The blue, orange and green lines refer to Limongi & Chieffi (2018) yields for initial rotational velocities Vrot = 0, Vrot = 150 and Vrot = 300 km s−1, respectively. The cyan line represents the MLr model with rotation-averaged yields. |
| In the text | |
 |
Fig. 10. Observed thick-disc MDF (yellow thick solid line Bensby et al. 2014) compared with the predictions of model TD4 (Table 4). |
| In the text | |
 |
Fig. 11. Comparison of the observed [O/Fe] vs. [Fe/H] (left panel) and [Mg/Fe] vs. [Fe/H] (right panel) ratios of the thick disc stars, with the predictions of models with different IMF parameters as listed in Table 4. We see that increasing MUP, so as to include the contributions of VMO (winds, PPISN and PISN), thick-disc stars can be reproduced pretty well. Moreover, changing both the IMF slope and MUP, different populations can be recovered. |
| In the text | |
 |
Fig. B.1. Fractional wind ejecta, Wj, derived from PARSEC stellar models, as a function of Mi and Zi. The chemical species shown are 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ar, Ca, Ti, Fe. |
| In the text | |
 |
Fig. B.2. Fractional total ejecta (winds and explosion) of new production, Pj, for Zi = 0.0001 as a function of Mi. Our MTW ejecta are compared with those of other literature works. The chemical species shown are 4He, 12C, 14N, 16O, 20Ne, 24Mg, 28Si, S, Ar, Ca, Ti, Fe. |
| In the text | |
 |
Fig. B.3. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.001. Same description as in Fig. B.2. |
| In the text | |
 |
Fig. B.4. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.006. Same description as in Fig. B.2. We note that LC18 ejecta are taken from their closest lower metallicity, Zi = 0.004. |
| In the text | |
 |
Fig. B.5. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.006. We note that LC18 ejecta are taken from their closest larger metallicity, Zi = 0.008. Same description as in Fig. B.2. |
| In the text | |
 |
Fig. B.6. Fractional total ejecta (winds and explosion) of new production, Pj, but for Zi = 0.02. Same description as in Fig. B.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



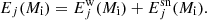
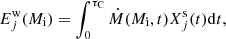
![$$ \begin{aligned} P_j(M_{\rm i}) = \left[E_j(M_{\rm i}) - (M_{\rm i} - {M}_{\rm rem})\,X_{j,0}\right]/M_{\rm i}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa39842-20/aa39842-20-eq10.gif)
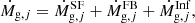
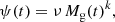
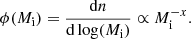
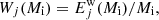
![$$ \begin{aligned} P_j(M_{\rm i}) = \left[(E_j^\mathrm{w} + E_j^\mathrm{sn}) - (M_{\rm i}-{M}_{\rm rem})X_{j,0}\right]/M_{\rm i}, \end{aligned} $$](/articles/aa/full_html/2021/06/aa39842-20/aa39842-20-eq22.gif)