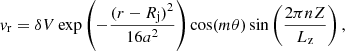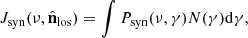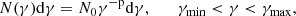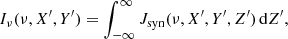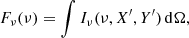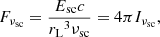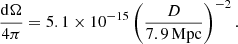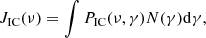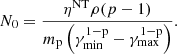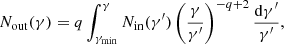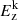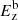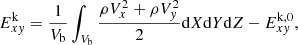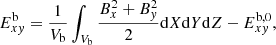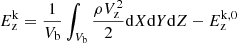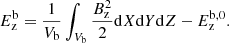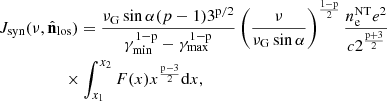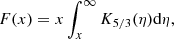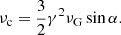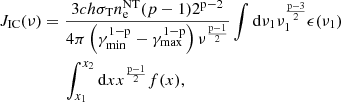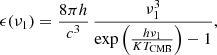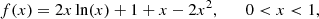| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202140440 | |
| Published online | 01 June 2021 | |
Numerical study of the Kelvin-Helmholtz instability and its effect on synthetic emission from magnetized jets
1
Discipline of Astronomy Astrophysics and Space Engineering, Indian Institute of Technology Indore, Khandwa Road, Simrol, Indore, 453552, India
e-mail: nb29100@gmail.com
2
Inter-University Centre for Astronomy and Astrophysics, Post Bag 4, Pune, 411007, India
3
INAF/Osservatorio Astrofisico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy
4
Dipartimento di Fisica Generale, Universita degli Studi di Torino, Via Pietro Giuria 1, 10125 Torino, Italy
Received:
28
January
2021
Accepted:
11
March
2021
Context. Nonthermal emission from active galactic nucleus (AGN) jets extends up to large scales, even though they are prone to many magnetohydrodynamic instabilities.
Aims. The main focus of this study is to understand the effect of magnetohydrodynamic instabilities on the nonthermal emission from large-scale AGN jets.
Methods. We performed high-resolution three-dimensional numerical magnetohydrodynamic simulations of a plasma column to investigate the dynamical and emission properties of jet configurations at kiloparsec scales with different magnetic field profiles, jet speeds, and density contrast. We also obtained synthetic nonthermal emission signatures for different viewing angles using an approach that assumes static particle spectra and that is obtained by evolving the particle spectra using Lagrangian macroparticles incorporating the effects of shock acceleration and radiative losses.
Results. We find that shocks due to the Kelvin-Helmholtz (KH) instability in the axial magnetic field configurations can strongly affect the jet dynamics. Additionally, we also find weak biconical shocks in the underdense jet columns. The helical magnetic field hinders the vortex growth at the shear surface and thereby stabilizes the jet column. With the evolving particle spectra approach, the synthetic spectral energy distributions obtained for cases with strong KH instability show multiple humps ranging from the radio to the TeV gamma-ray band.
Conclusions. We conclude that high-energy electrons that are accelerated in the vicinity of freshly formed shocks due to KH instability result in high X-ray emission.
Key words: galaxies: jets / methods: numerical / magnetohydrodynamics (MHD) / plasmas / shock waves / instabilities
© ESO 2021
1. Introduction
Jets from AGN represent channels through which energy is transported from the central black hole region, where they are formed and accelerated, toward the extended regions up to scales that can reach megaparsecs, where the jet terminates. Along their way, part of their energy can be dissipated and transferred to a relativistic electron population, giving rise to the observed nonthermal radiation, which can cover the complete electromagnetic spectrum, that is, from radio up to γ-rays. In this process, jet instabilities play a fundamental role because they initiate the dynamical processes that lead to energy dissipation. Two types of instabilities are mainly considered in this context: Kelvin-Helmholtz (KH) instabilities, driven by the velocity shear between the jet and the ambient medium, and current-driven instabilities (CDI) that develop in the presence of a helical magnetic field. The KH leads to the formation of shocks and turbulence through which the energy is dissipated. Instead, dissipation in CDI mainly occurs through the formation of current sheets and magnetic reconnection.
Much literature has focused on understanding the characteristics of these instabilities in magnetohydrodynamic jets, determining the physical parameters that control their growth. KH instabilities have been extensively studied in several different configurations, both in Newtonian and in relativistic jets and with or without a magnetic field, both performing a linear analysis (see, e.g., Bodo et al. 1989, 1996; Birkinshaw 1991; Hardee & Clarke 1992; Kersalé et al. 2000; Urpin 2002; Perucho et al. 2004, 2010; Hardee 2006; Mizuno et al. 2007) and following the nonlinear evolution through numerical simulations (Frank et al. 1996; Malagoli et al. 1996; Ryu et al. 2000). The main parameters that control the behavior of the instability are the Mach number, the density ratio between the jet and ambient medium, and the plasma β in the presence of a magnetic field. The magnetic field configuration also has a strong effect on the instability evolution; a longitudinal field may have a stabilizing effect, while a toroidal field may introduce the other class of instabilities discussed above, that is, CDIs. A linear analysis of the CDI has been performed both in the Newtonian and in the relativistic cases by performing a linear analysis (see, e.g., Appl & Camenzind 1992; Istomin & Pariev 1994, 1996; Kim et al. 2015, 2016, 2017; Kim et al. 2018; Bodo et al. 2013, 2016, 2019) and following the evolution by numerical simulations. When both instabilities are possible, Appl & Camenzind (1992) showed that KH instabilities are stabilized, and this result was confirmed by Baty & Keppens (2002) through three-dimensional numerical simulations. Rossi et al. (2008) and Mukherjee et al. (2020) showed that instabilities might have also a strong effect on the large-scale morphological properties of jets, leading either to the transition to an FRI type morphology (see also Massaglia et al. 2016) or in higher power jets, to strongly different properties of the cocoon.
Here we are interested in another effect of instabilities. As discussed above, the instability evolution leads to energy dissipation and consequently to the formation of a nonthermal electron population and the observed emission. Connecting all these processes is a formidable challenge since they involve a huge range of physical scales, where emission processes occur at the microscale, while the dynamics occur at the macroscale. For this reason, studies of jets have concentrated either on the dynamics, sometimes providing emission properties by using very simplified recipes, or on the radiation, employing very simplified dynamical structures. Few studies have tried more sophisticated approaches, in which the evolution of a nonthermal electron population subject to energy losses and gains is followed together with the dynamics of the thermal fluid (Micono et al. 1999; Tregillis et al. 2001; Mimica et al. 2013; Vaidya et al. 2018; Fromm et al. 2019; Winner et al. 2019; Huber et al. 2021), under the assumption that nonthermal particles are advected with the fluid velocity and have no back-reaction on the fluid. In particular, energy gains at shocks are treated in a subgrid manner by employing more or less sophisticated recipes for determining the properties of the nonthermal particle distribution function depending on the shock characteristics. In particular, we have adopted the treatment for the particle acceleration process at shocks developed within the hybrid particle framework for the PLUTO code (Vaidya et al. 2018).
The main goal of this work is to analyze the possible imprint of the KH instabilities on the jet radiation properties, as was done in Micono et al. (1999), and because our focus is on the instability evolution, we adopted an idealized approach in which we considered a small section of a jet, assuming that in the nearby regions all jet sections behave in the same way. With this approach, we can employ an adequate numerical resolution to accurately follow the evolution of the KH instability. Our focus is on the jet properties on a scale of tens of kiloparsec (kpc); at these distances, the jet has most likely slowed down from the highly relativistic regime at its base, reaching non-relativistic or mildly relativistic velocities. For this reason, our simulations are performed using nonrelativistic magnetohydrodynamic equations.
The paper is organized as follows. Section 2 describes the required numerical method and initial conditions for dynamical modeling. In Sect. 3, different emission modeling approaches are presented. Section 4 describes the results obtained from dynamical analysis and emission modeling with the effects of orientation. The effect of shock formation, particle acceleration, and instabilities on the emission signatures are explained in Sect. 5. Finally, Section 6 lists the important findings of this work.
2. Numerical setup
2.1. Equations and numerical method
Three-dimensional simulations of cylindrical plasma columns were carried out by solving the following set of ideal time-dependent magnetohydrodynamic equations in the Cartesian coordinate system (X, Y, Z),
where ρ, P, B, and v are the density, isotropic gas pressure, magnetic field, and velocity, respectively. A factor 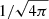 was reabsorbed in the definition of B. The energy density is the sum of thermal, kinetic, and magnetic energy densities, respectively. It is given by the following expression:
was reabsorbed in the definition of B. The energy density is the sum of thermal, kinetic, and magnetic energy densities, respectively. It is given by the following expression:
where the internal energy is governed by the ideal gas equation, and the ratio of specific heats, Γ is 5/3. Furthermore, we employed a scalar tracer field τ to distinguish between the jet and the ambient fluid. Its value was set to unity for the region r < Rj, where 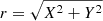 is the cylindrical radius and Rj is the jet radius.
is the cylindrical radius and Rj is the jet radius.
The numerical simulations were carried out employing the magnetohydrodynamic module of the astrophysical fluid dynamics code PLUTO (Mignone et al. 2007). A linear reconstruction shock-capturing method employing the hllc solver was used.
2.2. Initial conditions
We simulated a portion of an AGN jet at kpc scales assuming that the jet has become nonrelativistic (Laing & Bridle 2014). For this purpose, a three-dimensional cylindrical plasma column is initialized in a Cartesian box of size 4Rj × 4Rj × Lz. Here, Rj is the radius of the plasma column, which was set to unity, and Lz is the axial size of the box following an aspect ratio Lz/Rj = 2. The resolution of the grid was set to 200 × 200 × 100 zones, which translates into ΔX = ΔY = ΔZ = 0.02Rj. We refer to this three-dimensional plasma column as a jet, but it should be noted that we only modeled a representative section of the large-scale kpc jet because similar dynamical features are likely to also occur in other regions in this portion of the jet. The simulation runs were typically performed using nondimensional quantities and were expressed in code units (c.u.). To scale them in physical units, we chose three scales: the jet radius (Rj = 100 pc), a reference velocity (Vsc = 5000 km s−1), and the external density (ρout = 1.004 × 10−26 g cm−3) relevant for our study. As a consequence, the unit for the magnetic field is 177 μG.
The density in the jet was set using a parameter η = ρout/ρ0 that represents the density contrast between the ambient value (ρout = 1 ) and that on the jet axis ρ(r = 0)=ρ0. We modeled jets with a density equal to ambient (η = 1) and also those that were underdense (η > 1). The density profile is
The flow velocity was set along the axial direction ẑ and sheared radially with a hyperbolic tangent profile. The initial radial distribution of the velocity field is given as (Baty & Keppens 2002)
where V is the amplitude of the velocity shear, Rj is the jet radius, a is the width of the shear layer, and r is the radius in the cylindrical coordinate system. The values of these initial model parameters are Rj = 1, a = 0.1, and the on-axis pressure P(r = 0)=P0 = 1. The sonic speed on the jet axis is given by cs = (ΓP0/ρ0)1/2. For the jet models with a density equal to ambient (η = 1), the value of the sound speed is cs = 1.29, which in physical units is 6450 kms−1, corresponding to a thermal temperature of ∼3 × 109 K at the axis of the jet. The flow regime by Mach number can be found by calculating the Mach number along the axis using Ms = V/cs, where V is the speed of the jet at the axis.
The radial profile of the magnetic field structure can be expressed in the following general form given by Baty & Keppens (2002):
where the parameters B0 and B1 control the magnetic field strength and the radial pitch profile, and rc is the characteristic column radius.
For positive values of the parameter B1, the current density has its maxima on the jet axis. The initial radial profiles of the azimuthal magnetic field Bϕ are shown in Fig. 1. For the system to be in a state of magnetohydrodynamic equilibrium initially, which is essentially a balance between gas pressure and magnetic pressure forces, the gas pressure distribution must follow the radial component of the momentum conservation equation, which is given by
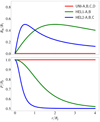 |
Fig. 1. Initial radial profiles of the azimuthal magnetic field Bϕ (top), and gas pressure P (bottom) for all the jet models given in Table 1. |
The radial profile of the gas pressure distribution can then be derived analytically from the radial component of the above expression to yield the form
and is shown in Fig. 1 for all configurations. We further define the radial pitch profile as follows:
where the choice of rc governs the position of the maximum of the pitch Π.
Summary of the parameters in the initial configuration of the jet.
A periodic boundary condition was used along the axial direction, which restricts the wavelength of the perturbations to values that fit within the length Lz, which is the size of the computational domain along the axial direction. The boundary condition on the side walls was chosen as reflective to have a helical field structure in the jet.
The magnetohydrodynamic equilibrium is perturbed only using the m = ±1 modes. The mathematical form of the velocity perturbations applied to the three cases is given by
where δV = 0.01 is the amplitude of the applied velocity perturbation, and 4a = 0.2 is its width along the radial direction. The axial and azimuthal numbers were set to n = 1 and m = 1 to excite the Fourier modes that may play a role in destabilizing the jet. These perturbations can trigger Kelvin-Helmholtz modes on the surface and kink modes in the presence of nonzero current density because there is a small but finite displacement of the jet localized at the boundary or the jet radius Rj.
We studied a total of nine models with varying sonic Mach number Ms, density contrast η, characteristic column radius rc, and magnitude of the axial and azimuthal component of the magnetic field strength. A summary of the detailed model parameters for all the cases is given in Table 1. The initial conditions for the jet models with Ms = 1.26 (i.e., the A cases) follow that of Baty & Keppens (2002). The A cases are primarily for validation purposes. Based on the magnetic field structure, the jet models are classified as the UNI, HEL1, and HEL2 cases and are described as follows.
The UNI cases have a uniform axial magnetic field. Model UNI-B is our reference case. In addition to UNI-B, we investigated the dynamical evolution of model UNI-A for validation and underdense jets UNI-C and UNI-D for comparison. The UNI-B, C, and D cases have an axial sonic Mach number Ms = 5.0, while the UNI-A case has Ms = 1.26. The UNI-C and D cases are underdense jets that vary smoothly along the radial direction. The UNI-D configuration has the highest density contrast η.
The HEL1 cases are current-carrying magnetized jets with an initial helical magnetic field with a pitch profile with a characteristic column radius rc = 2.0 (see Eq. (12)). The HEL1-B case is for comparison with the reference case UNI-B, and the HEL1-A case is for validation. The HEL1-A and B cases have the same axial sonic Mach numbers of Ms = 1.26 and Ms = 5.0, respectively, as their UNI counterparts.
The HEL2 cases are identical to the HEL1 cases, but they differ in their pitch profile as rc is set to 0.5 for the HEL2 cases as opposed to rc = 2.0 for the HEL1 cases. The HEL2-B and C cases are for comparison with the reference case UNI-B, whereas the HEL2-A case is for validation. The axial sonic Mach numbers corresponding to the HEL2-A, B, and C cases are Ms = 1.26, 5.0, and 10.0, respectively.
The values of the parameters B1 and B0 are 1 and 0.25, respectively, and were kept the same for all models with helical magnetic fields (see Eq. (9)). With the choice of physical scales we used, the value of Bz at the axis corresponds to 44 μG, and the value of the azimuthal component of the magnetic field is Bϕ = 71 μG at r = Rj for the HEL1 and HEL2 cases. We defined the parameter β = 2P/B2 to characterize the magnetic field strength for the simulation runs. For all the runs, we initially set β = 32 corresponding to the values of gas pressure (P0) and total magnetic field (B0) on the jet axis. This initial value of β defined at the axis was the same for UNI cases within the plasma column, but the HEL1 and HEL2 cases had a radial dependence on β. The initial value of β at the jet radius Rj was β(r = Rj)=7.37 for the HEL1 cases and β(r = Rj)=4.67 for the HEL2 cases. The UNI cases were subject to purely hydrodynamical KH instability at the jet boundary, while the HEL2 cases had a helical magnetic field, which can hinder the KH modes on the jet surface.
Time is in units of the radial Alfvén crossing time, which is defined as 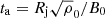 . When the jet density is equal to that of the ambient (η = 1), the radial Alfvén crossing time ta corresponds to ≈78.3 kyr for the chosen set of physical scales. We ran the simulation for A cases up to 3.75 ta, while the jet models UNI-B, HEL1-B, and HEL2-B were ran up to 4.75 ta because the instabilities develop slightly later for high sonic Mach number flows because the growth rate of KH instabilties depends inversely on the sonic Mach number (Hardee 2008). The UNI-C and UNI-D cases had the same sonic Mach number (Ms = 5.0) as the B cases, but higher jet-speed on-axis because of the low-density ρ0 that results in a higher sound speed cs. Consequently, these two cases were ran up to 7.25 ta and 15.0 ta because it takes a long time for the instabilities to develop because the jet speeds on-axis are higher.
. When the jet density is equal to that of the ambient (η = 1), the radial Alfvén crossing time ta corresponds to ≈78.3 kyr for the chosen set of physical scales. We ran the simulation for A cases up to 3.75 ta, while the jet models UNI-B, HEL1-B, and HEL2-B were ran up to 4.75 ta because the instabilities develop slightly later for high sonic Mach number flows because the growth rate of KH instabilties depends inversely on the sonic Mach number (Hardee 2008). The UNI-C and UNI-D cases had the same sonic Mach number (Ms = 5.0) as the B cases, but higher jet-speed on-axis because of the low-density ρ0 that results in a higher sound speed cs. Consequently, these two cases were ran up to 7.25 ta and 15.0 ta because it takes a long time for the instabilities to develop because the jet speeds on-axis are higher.
3. Emission modeling
Synchrotron and inverse-Compton (IC) are the two most primary radiation mechanisms responsible for the observed double-humped spectral energy distribution (SED) in the jets. To study the effects of magnetohydrodynamic instabilities on the continuum emission spectra of jets at large scales, we considered two different approaches to model the nonthermal emission. For the first approach, we developed a post-processing tool that considers static particle spectra, that is, the spectra did not evolve with time. For the second approach, we used the hybrid macroparticle-based framework in the PLUTO code developed by Vaidya et al. (2018), where the particle spectra evolve with time depending on local fluid quantities. The history was also preserved when they were updated. In the following subsection, we describe the methods involved to calculate the synchrotron (Sect. 3.1.1) and IC (Sect. 3.1.2) emissivity for the first approach with the static particle spectra along with the associated intensity and flux.
3.1. Static particle spectra
In this approach, each grid cell of the computational domain is treated as a single emitting blob for which the emissivity is modeled. This considers a nonuniform distribution of the mass density and magnetic fields and assumes a homogeneous energy distribution of the emitting ultra-relativistic particles for the calculation of grid distribution of emissivities. The inputs are the fluid variables obtained from the simulations performed using the PLUTO code and the viewing angle. Additionally, the parameters that prescribe the static particle spectrum are also provided as inputs. For static power-law spectra (Eq. (15)), input parameters are the lower and upper energy bounds, γmin and γmax, respectively, the power-law index p, and the ratio of the number density of the nonthermal electrons to fluid number density ηNT = 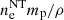 , where
, where 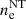 is the number density of nonthermal electrons. The outputs are the intensity maps and flux (see Eqs. (16) and (17)). The validation of this approach is given in Appendix A.
is the number density of nonthermal electrons. The outputs are the intensity maps and flux (see Eqs. (16) and (17)). The validation of this approach is given in Appendix A.
3.1.1. Synchrotron emission
The synchrotron emission from the jets may have either leptonic or hadronic or leptohadronic origin. We assumed that the synchrotron emitting particles are mainly electrons and their energy distribution is a power law with spectral index p.
Given the synchrotron power radiated by a single electron Psyn(ν, γ), the total synchrotron emissivity due to an ensemble of ultra-relativistic electrons is computed using the following expression (Longair 2011):
where N(γ)dγ is the total number of electrons per unit volume having a Lorentz factor in the range γ to γ + dγ with power-law spectral index p, and it is given by
where γmin and γmax are the limits of the electron energies and N0 is the normalization constant.
We used the fundamental radiative transfer equation in the optically thin limit (Rybicki & Lightman 1986) to calculate the specific intensity. For this, the emissivity Jsyn(ν,n̂los) (see Eq. (A.1)) obtained at each grid cell (i.e., X′, Y′, and Z′) is integrated for a given line of sight along the direction n̂los defined by the spherical coordinates θ and ϕ (i.e., n̂los = [sin θ cos ϕ, sin θ sin ϕ, cos θ]) using
where we chose a Cartesian coordinate system with the Z′-axis along the line of sight of the observer, while the other two axes are in the sky plane.
Then the flux density at a particular frequency ν can be estimated by integrating the specific intensity distribution over the solid angle subtended at the observer’s position by the projection of the emitting region in the jet on the sky plane. This is given by
where the solid angle is given by dΩ = (dX′×dY′)/D2.
The total integrated flux density Fν(ν) can then be used to plot the continuum emission spectra. The flux density is scaled with Fνsc,
where Esc = γscmec2 is the energy scale where γsc = 1, and the frequency is scaled in units of Larmor frequency νsc = νG ≈ 122 Hz, which is estimated using the initial magnetic field strength, defined at the axis of the plasma column (i.e., Bz(t = 0)). Furthermore, rL is the Larmor radius for highly relativistic electrons, with the Lorentz factor γmax, and is obtained using the same initial axial field strength. For the chosen set of physical scales, the value of the flux scale in physical units is 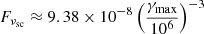 ergs s−1 cm−2 Hz−1. We estimated the synthetic emission assuming a reference distance D = 7.9 Mpc between the source and the observer. As a result, considering the length scale (Rj) and the grid resolution, we obtained the solid angle as
ergs s−1 cm−2 Hz−1. We estimated the synthetic emission assuming a reference distance D = 7.9 Mpc between the source and the observer. As a result, considering the length scale (Rj) and the grid resolution, we obtained the solid angle as
3.1.2. IC emission
Inverse-Compton scattering involves two types: synchrotron self-Compton (SSC) and external Compton (EC). As the focus is on studying the portion of the jet that is far away from the central black hole, the seed photons for the inverse-Compton scattering are typically from the cosmic microwave background (CMB). We assumed an isotropic seed photon distribution and the bulk-flow of the jet at kpc scales to be in the nonrelativistic limit. The total IC emissivity at a particular frequency due to this ensemble of ultra-relativistic electrons can be computed using the form given in Petruk (2009),
where PIC(ν, γ) is the IC power radiated by a single electron. The IC intensity maps and flux density were calculated using the same methods as explained in Sect. 3.1.1, and using the expression of emissivity from Eq. (A.4) at each grid cell in the numerical domain.
3.2. Evolving particle spectra
One of the limitations of our first approach that makes it a rather simplistic prescription for emission modeling is the assumption of a static power-law distribution of relativistic electrons (i.e., a constant value of the power-law index p). In order to relax this constraint and take the effects of microphysical processes (e.g., particle acceleration due to shocks) on the distribution function of emitting particles and subsequently on emissivities into account that in general depend on the grid position Jsyn(ν,n̂los, X′, Y′, Z′) and JIC(ν,n̂los, X′, Y′, Z′), we used another approach in which the energy spectra of the emitting particles evolve with time.
This approach follows a Lagrangian macroparticle-based approach in which each of these macroparticles is essentially an ensemble of nonthermal particles (e.g., electrons in this case). The outputs of the hybrid model are the synchrotron and IC emissivities that are generated by evolving the particle spectra for a user-defined observing frequency value. These emissivities are provided as inputs to the post-processing tool to obtain the intensity maps and flux using Eqs. (16) and (17). The detailed method of this approach and the equations considered to calculate the emissivities are given in Vaidya et al. (2018). We initialized all the runs listed in Table 1 using the hybrid framework in the PLUTO code with 6 × 105 Lagrangian macroparticles that were randomly distributed in space following Gaussian deviates that depend on the cylindrical radius. This allowed a complete sampling of the plasma column as more particles are initialized close to the axis. The initial electron distribution was chosen as a power law given by Eq. (15), in which the normalization constant is
The electron distribution within each macroparticle was evolved depending on the physical grid quantities interpolated at the macroparticle position. In particular, for each macroparticle, the Fokker-Planck equation was solved, accounting for the radiative losses due to adiabatic expansion, synchrotron, and IC-CMB emission. At kpc scales in jets, stochastic acceleration of particles due to turbulence may also contribute to the evolution of the particle spectra and the diffuse emission at high energies (H. E. S. S. Collaboration 2020). However, we did not account for the diffusion of particles in momentum space (Fermi second-order process). Additionally, the spatial diffusion of electrons was neglected. When these diffusion terms are neglected, the adopted approach ensures that the total number of electrons remains constant within a single macroparticle.
To account for particle acceleration at shocks, the spectral distribution of any macroparticle experiencing the shock was updated based on the compression ratio of the shock. To estimate the compression ratio, the shocked regions were flagged using conditions on the pressure gradient threshold and a negative value of the velocity divergence. Furthermore, the macroparticles entering these shocked regions quantify the pre-shock and post-shock conditions from interpolated fluid values. These conditions were then used to compute the orientation of the shock normal and thereafter the shock speed using the coplanarity theorem (Schwartz 1998). Finally, the compression ratio s was estimated as the ratio of upstream and downstream velocities in the shock rest frame. It should be noted that we only considered shocks as a possible reacceleration mechanism and did not distinguish quasi-parallel or quasi-perpendicular shocks. As the shocks encountered are nonrelativistic, the standard diffusive shock acceleration (DSA) approach that assumes isotropic particle distribution was adopted, whereby the spectral slope flattens to a momentum index given as q = 3s/(s − 1) (e.g., Blandford & Ostriker 1978; Drury 1983; Kirk et al. 2000; Achterberg et al. 2001). Additionally, the maximum energy of the updated spectra was estimated by equating the acceleration timescale with the radiative cooling timescale, which depends on the strength of the magnetic field B. It can be expressed as follows:
Using the maximum energy of the updated spectra and the compression ratio, the particle distribution is updated by following (e.g., Jones et al. 1994; Micono et al. 1999; Winner et al. 2019; Mukherjee et. al., in prep.)
where γ ∈ [γmin, γmax], and Nout is the updated spectrum in the post-shock region, which is dependent on the incoming (pre-shock) particle spectra Nin. Such an update of the particle spectrum allowed preserving the history of the particle distribution as it traverses the shock.
At any given time, the instantaneous distribution of electrons for each macroparticle was convolved with the single electron power to estimate the emissivity associated with that macroparticle. Finally, the emissivity value for each macroparticle was interpolated back onto the grid. When we obtained the grid distribution of the emissivities Jsyn(ν,n̂los, X′, Y′, Z′) and JIC(ν,n̂los, X′, Y′, Z′), we integrated them along a line of sight to generate the intensity maps and emission spectra using the same method as described in Sect. 3.1.1.
4. Results
The methods of dynamical and emission modeling of magnetohydrodynamic instabilities in jets are described in Sects. 2 and 3, respectively. This section comprises the results obtained from the dynamical modeling and emission modeling. We discuss our major findings in detail. Sections 4.2–4.4 describe the effects of the magnetohydrodynamic instabilities on the observed jet emission based on different scenarios.
4.1. Dynamical modeling results
We modeled the jets to study the effects of magnetohydrodynamic instabilities on the jet dynamics and energetics. By solving the ideal magnetohydrodynamic equations, we studied the temporal evolution of three-dimensional scalar and vector fields such as mass density ρ, gas pressure P, magnetic field B, and velocity field v. Three-dimensional snapshots of the jet density structure for the models UNI-A, UNI-B, HEL2-A, and HEL2-B at t/ta = 3.75 are shown in Fig. 2 for a direction lying in the X − Z plane (i.e., n̂los = [sin θ, 0 ,cos θ]) along a line of sight inclined at θ = 20° with the jet axis. In the uniform magnetic field configurations, that is, UNI-A and UNI-B, where only the Kelvin-Helmholtz instability is present, the jet dynamics are greatly altered by t/ta = 3.75 as compared to the helical configurations HEL2-A and HEL2-B, in which the jet remains relatively stable as the jet boundary is clearly distinguishable.
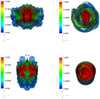 |
Fig. 2. Three-dimensional isosurface density contours of the model UNI-A (top left), HEL2-A (top right), UNI-B (bottom left), and HEL2-B (bottom right) at t/ta = 3.75 for a direction along a line of sight inclined at 20° with the jet axis. The color bars represent the jet density ρ/ρ0. While the UNI cases have a turbulent flow structure as they only experience the KH instability, the HEL2 cases have a clearly identifiable jet boundary as they are relatively stable. |
Figure 3 shows the two-dimensional cuts of pressure and vorticity distribution in the Y − Z plane for the UNI-B case at t/ta = 3.75, for the UNI-C case at t/ta = 5.59, and for the UNI-D case at t/ta = 10.61. In the UNI-B case, the KH instability in the shear layer at the jet boundary results in the formation of strong shocks. Such shocked structures are also seen at the jet boundary in the UNI-C and UNI-D cases. Additionally, for these cases, there are regions at high pressure on the jet axis due to the formation of biconical shocks that are relatively weaker than those formed at the jet boundary. A detailed discussion of the underdense jets UNI-C and UNI-D is presented in Sect. 4.4.2.
 |
Fig. 3. Left panels: distribution of jet pressure P/P0 in the Y − Z plane of the models UNI-B at t/ta = 3.75 (top), UNI-C at t/ta = 5.59 (middle), and UNI-D at t/ta = 10.61 (bottom). Right panels: distribution of the vorticity along the normal to the Y − Z plane (∇×v)x for the corresponding cases at the same times. The color bars in the left and right panels represent the corresponding pressure and vorticity in code units, respectively. The tracer contours at level 0.8 are overplotted as black lines to demarcate the jet boundary in all three cases. The tracer levels close to the jet axis are greater than 0.8 and are not shown here. |
In all three cases, the vortical structures are present at the jet boundary because they can only form in regions with velocity shear. The vorticity is highest in the UNI-D case because there is a strong velocity shear due to the high axial velocity inside the jet (Vz = 0.7c). The strong shocks resulting from the high-velocity shear affect the emission properties of magnetohydrodynamic jets. This is discussed in Sect. 4.3.
4.1.1. Jet energetics and validation of dynamical jet models
In order to validate our dynamical jet models, we set up our A cases with initial conditions identical to those given for the three configurations in Baty & Keppens (2002). For comparison, we plot the time evolution of the volume-averaged energies defined below (see Fig. 4).
 |
Fig. 4. Left panels: time evolution of the volume-averaged perturbed (a) kinetic energy in the X − Y plane |
The volume-averaged perturbed kinetic energy confined to the X − Y plane 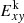 is given by
is given by
and the volume-averaged perturbed magnetic energy confined to the X − Y plane 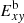 is
is
where 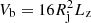 is the volume of the simulation box, and
is the volume of the simulation box, and 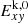 and
and 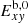 are the initial kinetic and magnetic energies obtained from the equilibrium conditions. As
are the initial kinetic and magnetic energies obtained from the equilibrium conditions. As 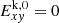 , the volume-averaged perturbed kinetic energy confined to the X − Y plane
, the volume-averaged perturbed kinetic energy confined to the X − Y plane 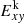 is the same as the volume-averaged kinetic energy. The volume-averaged perturbed axial kinetic and magnetic energies are given by
is the same as the volume-averaged kinetic energy. The volume-averaged perturbed axial kinetic and magnetic energies are given by
and
We extend this analysis to the jet configurations with a higher sonic Mach number (Ms = 5) (i.e., B cases). The results for the UNI-A and HEL2-A cases (Ms = 1.26) shown in the left panels of Fig. 4 agree with those obtained by Baty & Keppens (2002). The results for the corresponding B cases are shown in the right panels of Fig. 4. In the jet configuration UNI-A where only the Kelvin-Helmholtz instability is present, vortex growth occurs at the jet boundary (Baty & Keppens 2002). The magnetic field lines concentrate around the edges of these vortices, and the build-up of magnetic and kinetic energy 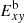 and
and 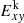 in the transverse direction disrupts the flow (see panels a and b in Fig. 4). In contrast, the vortex growth is suppressed by the azimuthal magnetic field Bϕ, which stabilizes the jet in the HEL2-A configuration. In the B cases with Ms = 5, the beginning of the instability is marked by a deviation of the axial kinetic energy from its initial value, which occurs at t/ta ≈ 3.375 in the UNI-B case (see panel g in Fig. 4). In the UNI-B case, the Kelvin-Helmholtz instability makes the flow turbulent at small scales, resulting in freshly formed shocks that disrupt the flow. As a result, the kinetic and magnetic energies in the transverse direction
in the transverse direction disrupts the flow (see panels a and b in Fig. 4). In contrast, the vortex growth is suppressed by the azimuthal magnetic field Bϕ, which stabilizes the jet in the HEL2-A configuration. In the B cases with Ms = 5, the beginning of the instability is marked by a deviation of the axial kinetic energy from its initial value, which occurs at t/ta ≈ 3.375 in the UNI-B case (see panel g in Fig. 4). In the UNI-B case, the Kelvin-Helmholtz instability makes the flow turbulent at small scales, resulting in freshly formed shocks that disrupt the flow. As a result, the kinetic and magnetic energies in the transverse direction 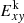 and
and 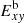 increase from t/ta ≈ 3.375 (see the top two panels in the right column of Fig. 4). In the HEL2-B case, small deviations are seen in the transverse and axial magnetic energies
increase from t/ta ≈ 3.375 (see the top two panels in the right column of Fig. 4). In the HEL2-B case, small deviations are seen in the transverse and axial magnetic energies 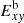 and
and 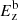 as the presence of a helical magnetic field suppresses the steepening of any turbulent features, thereby curbing any shock formation.
as the presence of a helical magnetic field suppresses the steepening of any turbulent features, thereby curbing any shock formation.
4.2. Emission modeling: No-shocks case
To model the emission, we adopted two different mechanisms: static and evolving particle spectra. Modeling emission with evolving particle spectra helps to incorporate the additional physics due to radiative losses.
Figure 5 shows the synchrotron emission maps for the UNI-A case obtained at t/ta = 2.25 using the static particle spectra (top panels of Fig. 5) and evolving particle spectra (bottom panels of Fig. 5). In the A cases, we assumed for both approaches that the energy distribution of the ultra-relativistic emitting electrons is a power law with spectral index p = 3 and energy limits γmin = 100 and γmax = 106. The ratio of the number density of the nonthermal electrons to fluid number density was taken to be ηNT = 10−3. As the initial distribution of nonthermal particles is a power law for both approaches, the number of emitting electrons drops with increasing energy, which leads to a dimming effect in the intensity maps. The two bright features resembling a figure of eight that appear in these emission maps can be attributed to the magnetic field structure at t/ta = 2.25. The Kelvin-Helmholtz instability in the UNI-A case leads to vortex formation at the jet boundary. The magnetic field lines concentrate at the edges of the vortices due to a local increase in jet density, which results in increased emission from these regions. An enhanced dimming is seen in the intensity maps obtained with evolving particle spectra (bottom panels of Fig. 5) at higher frequencies as the bright features completely vanish in the emission map obtained at ν/νsc = 3.5 × 108. This difference is purely caused by radiative losses due to the synchrotron process that is not accounted for in the static particle spectra approach. Furthermore, the UNI-A case, which has a relatively lower initial axial sonic Mach number, does not show any shock feature to energize particles undergoing radiative losses. Therefore the nonthermal electrons lose energy with time due to the synchrotron cooling effect, which results in the enhanced dimming of the jet emission at higher energies as cooling becomes more efficient at higher energies due to the shorter cooling time. In the evolving particle spectra, no shocks were captured in any of the A cases. To study the effect of shocks, we increased the initial sonic Mach number to Ms = 5 along the jet axis for all three configurations to study its effects on the jet emission.
 |
Fig. 5. Synchrotron emission maps produced using the static particle spectra (top panels) and evolving particle spectra (bottom panels) with an initial power-law index p = 3 for case UNI-A at t/ta = 2.25 projected on the sky plane X′–Y′. These maps are obtained for a direction along a line of sight inclined at 20° with the jet axis at three different observing frequencies normalized to the frequency scale νsc = 122 Hz. The color bar represents the magnitude of specific intensity Iν normalized to the specific intensity scale Iνsc = 7.46 × 10−9 ergs s−1 cm−2 Hz−1 str−1. |
4.3. Emission modeling: Cases with shocks
Initially, the reference case UNI-B with axial sonic Mach number Ms = 5 had a uniform density, pressure, and axial magnetic field. The growth of the KH instability led to a highly turbulent flow structure, as shown in Fig. 2. Vortex formation occurred near the shear layer due to the turbulence (see the top right panel in Fig. 3). This led to the formation of shocks near the shear layer.
Using evolving particle spectra, we chose a spectral index p = 6 in the reference case as opposed to the A cases, for which we set a spectral index p = 3 for the initial power-law distribution of nonthermal particles with initial energy bounds as γmin = 100 and γmax = 108 distributed equally in log-space using 512 bins. The ratio of the number density of the nonthermal electrons to fluid number density was kept the same as in the A cases (i.e., ηNT = 10−3). We used the evolving particle spectra to obtain both synchrotron and inverse-Compton emission maps at three different energies for the B cases at t/ta = 3.75 for a direction along a line of sight inclined at θ = 20° with the jet axis in the X − Z plane. The observing frequencies for the synchrotron emission maps in scaled units are ν/νsc = 8.2 × [104, 106, 108], which correspond to radio for νsc ∼ 122 Hz. The energies for the inverse-Compton emission maps in scaled units range from E/hνsc = 7.9 × [1016, 1018, 1020] and correspond to emission in γ-rays. The three-dimensional distributions of pressure and density are integrated along the same line of sight. The resulting pressure and density maps along with the emission maps for the reference case UNI-B are shown in Fig. 6. A complex network of shocks evolves due to the turbulence during the nonlinear phase of the KH instability. As the macroparticles encounter multiple shocks, the nonthermal electrons are reaccelerated to higher energies depending on the strength of the shocks. Consequently, the particle spectra flatten, and we see bright emission features in the intensity maps at all three energies coinciding with regions at high pressure and density (see the bottom panels in Fig. 6). In particular, the synchrotron emission maps for higher frequency values (middle and right panels of the top row) show bright emission structures consistent with the density and pressure maps. In contrast, the synchrotron intensity map at the lowest frequency ν1/νsc = 8.2 × 104 is rather more diffused, as expected, and also shows bright emission in the center. Similar diffused emission is also seen for the lowest IC emission energy (left middle panel), although the general features of the emission map are consistent with the shocked regions depicted in the pressure map. Furthermore, at the high energy E3/hνsc = 7.9 × 1020, the emission map shows scattered bright spots. These findings are consistent with the results obtained by Micono et al. (1999) for the spectral index as the particles encounter multiple shocks in a two-dimensional slab jet experiencing KH instability.
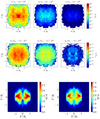 |
Fig. 6. Top panels: synchrotron emission maps obtained using the evolving particle spectra with an initial power-law index p = 6 for the UNI-B case at t/ta = 3.75 projected on the sky plane X′–Y′. These maps are produced for a direction along a line of sight inclined at 20° with the jet axis at observing frequencies of ν/νsc≈ 8.2 × 104, 8.2 × 106, and 8.2 × 108, where νsc = 122 Hz is the frequency scale. Middle panels: corresponding inverse-Compton emission maps at observing energies of E/hνsc≈ 7.9 × 1016, 7.9 × 1018, and 7.9 × 1018, where h is the Planck constant and the other model parameters are the same. The specific intensity is normalized to Iνsc = 7.46 × 10−15 ergs s−1 cm−2 Hz−1 str−1, corresponding to γmax = 108. Bottom panels: density ρ/ρ0 (left panel) and pressure P/P0 (right panel) maps integrated along the same line of sight. |
Furthermore, we also examined the effects of the boundary on the qualitative behavior of the synthetic SED. In particular, we increased the domain size to 8Rj × 8Rj × Lz to study the effect of side boundaries on the jet dynamics and radiative properties. We found that the jet dynamics are slightly altered, whereas the radiative properties remain the same, qualitatively showing spectral hardening. In addition to the intensity maps, the SEDs for the B cases with two different inclination angles with static particle spectra are also discussed in Appendix A.
A histogram of the probability density distribution function of the macroparticles with a compression ratio s is shown in Fig. 7 for the reference case UNI-B (blue bars) at t/ta = 3.75. The area below the histogram in each bin is the probability of a macroparticle having a compression ratio between s to s + Δs, where Δs = 0.2 is the bin width. We have about 5.5% particles in the reference case UNI-B with a compression ratio s > 4. They typically arise when the shocks begin to steepen and cover only one or two grids zones in the transverse direction. These particles were neglected in Fig. 7 and were not accounted for in the calculations. The blue histogram for the reference case UNI-B shown in Fig. 7 peaks at s = 2.2, which lies in the range 2.19 < s < 2.49.
 |
Fig. 7. Histogram showing the probability density distribution of the number of shocked macroparticles with the compression ratio for the UNI-B and HEL2-C cases at t/ta = 3.75. The dark red color is due to the overlapping of the blue and red bars. |
Additionally, the effect of shocks on the jet emission can be understood by studying the temporal evolution of the SED. The time-evolving SEDs for the reference case UNI-B are shown in Fig. 8. The left panel of Fig. 8 shows the evolving synchrotron SED, whereas the right panel shows the corresponding IC emission. The initial SED is a straight line given the power-law distribution of nonthermal electrons and is shown using a black line for both the synchrotron and inverse-Compton components. This is steeper than the SED in Fig. A.2 as the spectral index of the particle distribution has been increased to p = 6. For the synchrotron emission, the total integrated fluxes first drop until t/ta ≈ 2.875 as a result of the synchrotron cooling of the nonthermal electrons. A sudden flattening of the SED occurs at t/ta ≈ 2.875 as the turbulence results in freshly formed shocks that are captured using the evolving particle spectra. The interaction of multiple shocks accelerates the nonthermal particles to higher energies as the particle distribution spectra flatten. When the hybrid framework in the PLUTO code is used, a second population of nonthermal electrons with Lorentz factors γ ≥ 107 is seen. The emergence of this second population of electrons occurs in the vicinity of freshly formed shocks and is demonstrated using synchrotron emissivity contours at ν/νsc ≈ 1015 shown as black lines in Fig. 9. The maximum Lorentz factor for the spectrum associated with macroparticles in the vicinity of newly formed shocks is γ ≈ 109 and the typical magnetic field strength of B = 100 μG. This amounts to a gyro-frequency νG = 280 Hz, which implies that the critical frequency of synchrotron emission given by νc ≈ 1.5γ2νG is estimated to be about 1021 Hz. This is consistent with the fact that the peak of the bump in X-rays and γ-rays lies at ν/νsc ≈ 1019. However, the shape of the SED evolves as it is a transient phenomenon. The particle acceleration due to shocks is more efficient at higher energies. However, flatter spectra occur at lower energies as the nonthermal electrons at higher energies cool down and populate the low energy levels.
 |
Fig. 8. Time evolution of the SED for model UNI-B produced using the evolving particle spectra with an initial power-law index, p = 6 when observed from a direction inclined at 20° with the jet axis. The colors of the lines indicate the time normalized to Alfvén time. Lines with t/ta = 0.0, 2.62, 3.00, 3.12, 3.37, 3.5, 3.62, 3.75, 3.87, and 4.37 are shown in the left panel for the synchrotron emission, and the corresponding IC emission is shown in the right panel. The total integrated flux νFν is normalized with νscFνsc, where νsc = 122 Hz is the frequency scale and Fνsc = 9.38 × 10−14 ergs s−1 cm−2 Hz−1 is the flux scale corresponding to γmax = 108. |
 |
Fig. 9. Distribution of jet pressure P/P0 of the reference case UNI-B in the X − Z plane at t/ta = 3.75. The contours representing 1% of the peak value of normalized synchrotron emissivity at ν/νsc ≈ 8.2 × 1014 are overplotted as black lines, where νsc = 122 Hz is the frequency scale. The black lines indicate regions of X-ray spots resulting from the second population of nonthermal electrons generated in the vicinity of newly formed shocks due to shear. |
Because of the contribution from the second synchrotron component, the slope of the SED at t/ta = 3.5 directly evolves as 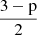 and equals 0.10 between the scaled frequencies ν/νsc = 109 and 1013 and 0.03 between the scaled frequencies ν/νsc = 1013 and 1015. These slopes drop to −0.26 and −0.01 at t/ta = 3.75 for the same frequency ranges, respectively, as a result of synchrotron cooling of the newly emerged second population of nonthermal electrons. The spectral indices corresponding to these slopes at t/ta = 3.75 are p = 3.51 and p = 3.02, while the compression ratios obtained using the standard diffusive shock acceleration theory p = 3s/(s − 1)−2 are s = 2.19 and s = 2.49, respectively, indicating that the shocks are moderately strong.
and equals 0.10 between the scaled frequencies ν/νsc = 109 and 1013 and 0.03 between the scaled frequencies ν/νsc = 1013 and 1015. These slopes drop to −0.26 and −0.01 at t/ta = 3.75 for the same frequency ranges, respectively, as a result of synchrotron cooling of the newly emerged second population of nonthermal electrons. The spectral indices corresponding to these slopes at t/ta = 3.75 are p = 3.51 and p = 3.02, while the compression ratios obtained using the standard diffusive shock acceleration theory p = 3s/(s − 1)−2 are s = 2.19 and s = 2.49, respectively, indicating that the shocks are moderately strong.
The inverse-Compton emission follows a similar trend of temporal evolution as it results from CMB photons scattering off the same nonthermal electron population that is responsible for the synchrotron emission. Kobak & Ostrowski (2000) studied particle acceleration due to shocks using Monte Carlo simulations. Stawarz & Ostrowski (2002) derived the emission spectra for such a distribution of nonthermal electrons and found an increased emission at higher energies, similar to the results shown in Fig. 8.
4.4. Comparison with other runs
4.4.1. Comparison with helical jets
To investigate the role of instabilities in magnetohydrodynamic jets using radiative signatures, we compared the emission spectra of the uniform magnetic field configuration UNI-B with the helical magnetic field configurations HEL2-C obtained using the evolving particle spectra. The synchrotron and IC SED for HEL2-C case at t/ta = 3.0, 3.75, and 4.5 are shown in Fig. 10. In the UNI-B case, the synchrotron component of the SED flattens as a result of particle acceleration because of the freshly formed shocks. This gives rise to the second population of nonthermal electrons at high energies. As mentioned in Sect. 4.3, the flattening of the spectra occurs after t/ta ≈ 2.875, when freshly formed shocks appear first. The number of shocked Lagrangian macroparticles grows rapidly with time. The probability distribution of these shocked particles represented by the blue histogram shown in Fig. 7 peaks at a compression ratio s = 2.2, indicating moderately strong shocks.
 |
Fig. 10. Time evolution of the SED for model HEL2-C produced using the evolving particle spectra with an initial power-law index p = 6 when observed from a direction inclined at 20° with the jet axis. Lines with t/ta = 3.0, 3.75, and 4.5 are shown in the left panel for the synchrotron emission, and the corresponding IC emission is shown in the right panel. The frequency, flux, and time have the same normalization as in Fig. 8. |
The jet boundary is clearly identifiable in the HEL2-B case (see Fig. 2) as the helical magnetic field suppresses vortex formation. As a result, no shock formation occurs in the HEL2-B case. In the HEL2-C case, the perturbations do not steepen enough due to the helical magnetic field to form strong shocks even though the initial sonic Mach number increases. Consequently, the HEL2-C case shows weak shocks that are represented by the probability density distribution function in the red histogram in Fig. 7. As most of the weakly shocked particles in the HEL2-C case have a compression ratio s = 1.3, we obtain p = 3s/(s − 1)−2 = 11 for these particles, making the spectrum steep (see Fig. 10). The total integrated fluxes at high energies drop as a result of synchrotron cooling. Furthermore, the HEL2 cases also have higher magnetic field strengths at the interface than the UNI-B case. This also enhances the radiative cooling observed in these runs. Negligible emission is seen beyond a scaled frequency ν/νsc > 1010 as the particle acceleration is inefficient because shocks are either absent or weaker in the helical jet configurations. The corresponding inverse-Compton components of the spectra have similar shapes because the same electron population is responsible for the synchrotron and IC-CMB emission. The shapes of the spectra appear to be like discontinuous curves with sharp edges as a result of an artificial effect because the SEDs have a limited resolution in the frequency domain.
In conclusion, in the jet configuration with the Kelvin-Helmholtz instability alone, a disruptive flow causes shock formation. This results in a flatter emission spectrum. In contrast, the helical jet configuration is relatively stable, with weaker shocks leading to a steeper emission spectrum.
4.4.2. Comparison with underdense jets
In the reference case UNI-B, no biconical shocks form near the jet axis as the density and pressure are initially uniform. For comparison, we modeled the jet configurations UNI-C and UNI-D, which are underdense as compared to the surroundings (see Eq. (7)). The ambient-jet density contrast η leads to the formation of weak biconical shocks in the UNI-D case, which coincide with regions at high pressure on the jet axis. This is shown in the bottom left panel in Fig. 3.
We expect biconical shocks to affect the emission spectra. However, the emission spectra of these underdense jets are similar to the spectrum in the reference case UNI-B. In the underdense jet UNI-D, it takes a longer time for the shocks to form due to the higher jet speed. The spectral features for model UNI-D are similar to those in the reference case UNI-B (figure not shown). We infer that the particle acceleration due to the weak biconical shocks is not as efficient as the shocks formed at the shear surface. The minor difference in SED that arises between the UNI-B and UNI-D case particularly at low energies can be attributed to the gradual steepening of weak biconical shocks.
In order to quantify the strength of biconical shocks at t/ta = 13.25, we considered the shocked macroparticles in the cylindrical region 0 < r < a and the cylindrical shell Rj − a < r < Rj + a, where a = 0.1 is the shear layer width and Rj = 1.0 is the jet radius. As the biconical shocks are weak, the number of shocked particles in the cylindrical region around the axis is smaller (< 100), and the majority of them have a compression ratio in the range 1.5 < s < 2.0. The biconical shocks are weak as the density contrast η is not high enough. In contrast, the stronger shocks at the jet boundary result in a large number (> 104) of shocked particles in the cylindrical shell, and most of them have a compression ratio in the range 2.0 < s < 2.5. The formation of strong shocks at the jet boundary is similar to what occurs in the reference case UNI-B. This is consistent with our understanding that the emission spectra in the underdense jet UNI-D are similar to that in the reference case with a minor deviation in the low-energy part.
5. Discussion
We have investigated the effects of magnetohydrodynamic instabilities on the dynamics of the plasma column and their effect on synthetic nonthermal emission. In particular, we carried out three-dimensional simulations of a plasma column with different magnetic field configurations and shear velocity between the column and the ambient medium.
From the dynamical evolution of the plasma column, the configuration with a dominant axial magnetic field (UNI-A) is unstable due to the KH mode. However, the presence of an azimuthal magnetic field suppresses the growth of instability and stabilizes the jet (HEL1-A and HEL2-A). We also carried out simulation runs with varying shear flow velocities that are supersonic. The evolution of the plasma column with initial axial sonic Mach number Ms = 5.0 and dominant axial magnetic fields (UNI-B case) depicted a complex network of shocks due to KH instabilities. These shocks are typically seen near the interface between the plasma column and the surroundings. In addition to these shocks, we also find weak biconical shocks for underdense cases (UNI-C and UNI-D).
This complex network of shocks produced in the shear layer of the plasma column due to KH instabilities accelerates the particles. From our evolving spectra analysis, we observe a local reacceleration of electrons within the vicinity of these shocks (see Fig. 9). The evolution of the resulting synthetic spectra is shown in Figs. 8 and 10 for the cases UNI-B and HEL2-C. At a certain evolutionary stage, the spectra show typical features corresponding to particle acceleration as multiple humps and radiative cooling as sharp cutoffs, respectively.
To quantify the amount of flux received in different frequency bands from radio to γ-rays, the normalized values must be expressed in terms of physical units. For the reference case UNI-B, we have B0 = 44 μG at the axis at t = 0, which corresponds to νsc = 122 Hz. Furthermore, the flux scale is Fνsc = 9.38 × 10−14 ergs s−1 cm2 Hz for γmax = 108, which is the maximum Lorentz factor set for the initial power-law spectra. With these scales, the synthetic multiwavelength synchrotron spectrum for the UNI-B case becomes flat in the optical to X-ray band (i.e., between ν = 1015 to 1019 Hz) at t/ta ≈ 3.37 due to the formation of shocks as the result of KH instabilities (see the left panel of Fig. 8). The generation of shocks in localized regions results in the reacceleration of electrons that have a flat spectral slope, consistent with the evolution of the spectral index using two-dimesional magnetohydrodynamic runs, as discussed in Micono et al. (1999). These electrons are accelerated up to a maximum energy γ = 109, forming a secondary population of energetic electrons. This exhibits a unique signature of a secondary hump in the synchrotron spectra peaking at ν = 1021 Hz with a corresponding flux density νFν ≈ 10−16 ergs s−1 cm−2. Additionally, such a population of a few dozen to hundreds of TeV energies gives rise to TeV γ-rays (ν ∼ 1025 − 1028 Hz) due to the upscattering of CMB photons (Meyer et al. 2015; Breiding et al. 2017).
On the other hand, because of the weak shocks we obtained for the HEL2-C case (see Fig. 7), the secondary population of such high-energy electrons is not formed. This results in the absence of a secondary hump in the synchrotron spectra for the HEL2-C case. Instead, we observe sharp cutoffs due to effective synchrotron cooling around ν/νsc ≈ 1010 (see Fig. 10). A similar evolution of the SED is also seen for the IC emission in the HEL2-C case.
The origin of X-ray emission in the multiwavelength SED of kiloparsec scale AGN jets is still an open question. Breiding et al. (2017) have proposed two possible models to explain this: synchrotron emission produced by a secondary population of higher energy electrons, and hadronic emission processes such as proton synchrotron emission or the synchrotron emission produced by a secondary population of electrons arising from photohadronic interactions. Our findings discussed in Sect. 4.3 indicate that the first of these models, synchrotron emission from a second electron population, is a viable explanation for the high X-ray emission in the multiwavelength SED of kiloparsec-scale AGN jets.
It should be noted that the synthetic SED obtained from this work is from a rather idealized simulation where the focus was on the portion of a jet at kpc scale and not the whole jet. Therefore the synthetic SEDs that are generated demonstrate the effects due to dynamical features that occur locally. Although these effects occur in localized regions, they are likely to occur in other regions of the jet and can be thought of as representative of a portion of the jet. Therefore the synthetic SEDs we generated can only be qualitatively compared with observations.
6. Summary and outlook
We have carried out three-dimensional simulations of a plasma column that represents a section of a jet at kiloparsec scales. This study was conducted with the aim to understand the effects of magnetohydrodynamic instabilities on jet dynamics and energetics, which have implications for stability and emission signatures.
Dynamical analyses of simulation runs for A cases were validated with those of Baty & Keppens (2002). In particular, for uniform density cases with sonic Mach number Ms = 1.26, we find that the case with an axial magnetic field (UNI-A) is unstable because of the KH mode and results in a disrupted and turbulent jet. When the azimuthal field is incorporated, the jet column achieves stability as the growth of vortices at the shear surface is damped by a helical field (HEL1-A and HEL2-A) (see Fig. 2).
Cases with higher shear flow velocity and/or high-density contrast (cases B, C, and D) show a generation of more vorticity at the shear surface and also shocks in comparison to the A cases (see Fig. 3). Additionally, the underdense jet columns (cases C and D) show weak biconical shocks.
The onset of instability in these cases occurs at a later Alfvén time than in cases A. The jet column with axial magnetic fields and high sonic Mach number is prone to KH mode instability and shows more and stronger shocks than the cases with a helical field structure that have the same sonic Mach number.
The effect of instabilities on emission signatures has been demonstrated by generating synthetic emission maps and SEDs using static power-law spectra. We find differences in SEDs for UNI cases in comparison to cases with helical magnetic fields. These differences become more acute with a smaller viewing angle because the synchrotron emissivity depends on |B × n̂los| = |B|sin α (see Fig. A.2).
In order to capture localized physical effects such as particle acceleration due to shocks and radiative losses, we produced emission signatures using a more accurate model that uses evolving particle spectra. A significant difference in terms of multiband intensity maps appeared in comparing the static and evolving spectrum models (see Fig. 5) for the UNI-A case. This difference is purely caused by synchrotron cooling of the nonthermal electrons as the UNI-A case with a lower axial sonic Mach number Ms = 1.26 does not show any shocks. Similar features of enhanced emission at the shear surface due to compressing magnetic fields are seen in both the emission models, especially at low frequencies.
Using the evolving particle spectra for the uniform magnetic field configuration UNI-B, we see a flattening of the SED due to localized physical effects such as particle acceleration caused by the steepening of perturbations resulting in freshly formed shocks at small scales due to the KH instability. In the helical magnetic field configurations, HEL2-B and HEL2-C, the SED is relatively steeper at higher energies as the changes in jet density occur at large scales and localized shocks are either absent or weaker.
The main finding from this study is the demonstration of spectral hardening resulting in multipeaked synthetic SED generated using the hybrid model of evolving particle spectra. The onset of KH instabilities gives rise to strong shocks at the shear surface, thereby accelerating particles nearby strong shocks and generating a localized second population of high-energy particles. For our reference run, we find that the particles can be accelerated up to γmax ∼ 109, and in the presence of moderate magnetic field strengths of ∼100 μG, they result in a transient peak at 1021 Hz (∼4 MeV) due to the synchrotron process. This can potentially explain the bright X-ray emission seen at kpc scale AGN jets. Another consequence of the second population of electrons is that they can produce TeV γ-rays as a result of the IC-CMB process (Meyer et al. 2015; Breiding et al. 2017).
For cases with an underdense jet column, we find that the bulk of the emission arises from strong shocks formed at the shear surface, whereas the biconical shocks formed near the jet axis are relatively weaker and do not contribute significantly to the hardening of spectra for the cases considered here.
To summarize, the presence of Kelvin-Helmholtz instability alone disrupts the flow, causing shock formation. This results in a flatter emission spectrum. The inclusion of a helical magnetic field, in contrast, hinders the growth of Kelvin-Helmholtz instability and has a stabilizing effect on the jet. It causes the emission spectra to steepen due to the absence of strong shocks. The spectral hardening due to the production of a shock-accelerated localized second population of high-energy electrons can provide a qualitative explanation of the bright X-ray spots typically observed in AGN jets at kiloparsec scales. Another observable that can constrain the properties of AGN jets at kiloparsec scales is the polarization. By studying the polarization properties of the jet emission, we can probe the magnetic field structure of the jet (Avachat et al. 2016). The magnetic field structure can reveal important clues about how shocks may form and lead to particle acceleration in large-scale jets. We aim to study the polarization properties of the jet emission in future work.
Acknowledgments
The authors would like to thank the referee for providing valuable comments and helping to improve the manuscript significantly. B. V. acknowledges the financial support from the Max Planck Partner Group Award. The computations presented in this work are carried out using the facilities provided at IIT Indore and the Max Planck Institute for Astronomy Supercomputing Cluster. The data underlying this article will be shared on reasonable request to the corresponding author.
References
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Kelner, S. R., & Prosekin, A. Y. 2010, Phys. Rev. D, 82, 043002 [Google Scholar]
- Appl, S., & Camenzind, M. 1992, A&A, 256, 354 [Google Scholar]
- Avachat, S. S., Perlman, E. S., Adams, S. C., et al. 2016, ApJ, 832, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Baty, H., & Keppens, R. 2002, ApJ, 580, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M. 1991, MNRAS, 252, 505 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Bodo, G., Rosner, R., Ferrari, A., & Knobloch, E. 1989, ApJ, 341, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Rosner, R., Ferrari, A., & Knobloch, E. 1996, ApJ, 470, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Mamatsashvili, G., Rossi, P., & Mignone, A. 2013, MNRAS, 434, 3030 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Mamatsashvili, G., Rossi, P., & Mignone, A. 2016, MNRAS, 462, 3031 [Google Scholar]
- Bodo, G., Mamatsashvili, G., Rossi, P., & Mignone, A. 2019, MNRAS, 485, 2909 [Google Scholar]
- Breiding, P., Meyer, E. T., Georganopoulos, M., et al. 2017, ApJ, 849, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., Jones, T. W., Ryu, D., & Gaalaas, J. B. 1996, ApJ, 460, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Fromm, C. M., Younsi, Z., Baczko, A., et al. 2019, A&A, 629, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H. E. S. S. Collaboration (Abdalla, H., et al.) 2020, Nature, 582, 356 [Google Scholar]
- Hardee, P. E. 2006, in Relativistic Jets: The Common Physics of AGN, Microquasars, and Gamma-Ray Bursts, eds. P. A. Hughes, & J. N. Bregman, Am. Inst. Phys. Conf. Ser., 856, 57 [Google Scholar]
- Hardee, P. 2008, J. Phys.: Conf. Ser., 131, 012052 [Google Scholar]
- Hardee, P. E., & Clarke, D. A. 1992, ApJ, 400, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Kissmann, R., Reimer, A., & Reimer, O. 2021, A&A, 646, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Istomin, Y. N., & Pariev, V. I. 1994, MNRAS, 267, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Istomin, Y. N., & Pariev, V. I. 1996, MNRAS, 281, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. W., Kang, H., & Tregillis, I. L. 1994, ApJ, 432, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Kersalé, E., Longaretti, P. Y., & Pelletier, G. 2000, A&A, 363, 1166 [Google Scholar]
- Khangulyan, D., Aharonian, F. A., & Kelner, S. R. 2014, ApJ, 783, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J., Balsara, D. S., Lyutikov, M., et al. 2015, MNRAS, 450, 982 [Google Scholar]
- Kim, J., Balsara, D. S., Lyutikov, M., & Komissarov, S. S. 2016, MNRAS, 461, 728 [Google Scholar]
- Kim, J., Balsara, D. S., Lyutikov, M., & Komissarov, S. S. 2017, MNRAS, 467, 4647 [Google Scholar]
- Kim, J., Balsara, D. S., Lyutikov, M., & Komissarov, S. S. 2018, MNRAS, 474, 3954 [Google Scholar]
- Kirk, J. G., Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ, 542, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Kobak, T., & Ostrowski, M. 2000, MNRAS, 317, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., & Bridle, A. H. 2014, MNRAS, 437, 3405 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 2011, High Energy Astrophysics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Malagoli, A., Bodo, G., & Rosner, R. 1996, ApJ, 456, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Massaglia, S., Bodo, G., Rossi, P., Capetti, S., & Mignone, A. 2016, A&A, 596, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, E. T., Georganopoulos, M., Sparks, W. B., et al. 2015, Nature, 521, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Micono, M., Zurlo, N., Massaglia, S., Ferrari, A., & Melrose, D. B. 1999, A&A, 349, 323 [NASA ADS] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mimica, P., Aloy, M. A., Rueda-Becerril, J. M., Tabik, S., & Aloy, C. 2013, in Journal of Physics Conference Series, J. Phys. Conf. Ser., 454, 012001 [Google Scholar]
- Mizuno, Y., Hardee, P., & Nishikawa, K.-I. 2007, ApJ, 662, 835 [Google Scholar]
- Mukherjee, D., Bodo, G., Mignone, A., Rossi, P., & Vaidya, B. 2020, MNRAS, 499, 681 [Google Scholar]
- Pandya, A., Zhang, Z., Chandra, M., & Gammie, C. F. 2016, ApJ, 822, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Hanasz, M., Martí, J. M., & Sol, H. 2004, A&A, 427, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Martí, J. M., Cela, J. M., et al. 2010, A&A, 519, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petruk, O. 2009, A&A, 499, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossi, P., Mignone, A., Bodo, G., Massaglia, S., & Ferrari, A. 2008, A&A, 488, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Ryu, D., Jones, T. W., & Frank, A. 2000, ApJ, 545, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Ruppel, J. 2010, New J. Phys., 12, 033044 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, S. J. 1998, ISSI Sci. Rep. Ser., 1, 249 [Google Scholar]
- Stawarz, Ł., & Ostrowski, M. 2002, ApJ, 578, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Tregillis, I. L., Jones, T. W., & Ryu, D. 2001, ApJ, 557, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V. 2002, A&A, 385, 14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., Rossi, P., & Massaglia, S. 2018, ApJ, 865, 144 [Google Scholar]
- Winner, G., Pfrommer, C., Girichidis, P., & Pakmor, R. 2019, MNRAS, 488, 2235 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V. 2015, in 34th International Cosmic Ray Conference (ICRC2015), Int. Cosmic Ray Conf., 34, 922 [Google Scholar]
Appendix A: Static particle spectra approach: Formulations and validation
In this section, we describe the formulations we used for the static particle spectra approach in detail (see Sect. 3.1) and validate them. Furthermore, we also discuss the effect of the line-of-sight variation on the shape of the spectral distribution obtained with fixed particle spectra.
The synchrotron emissivity (14) can be expressed in the form given by Pandya et al. (2016),
where α is the angle between the line-of-sight vector n̂los and the magnetic field vector B, and νG = eB/2πmec is the gyrofrequency of an electron (Longair 2011). The function F(x) is the modified Bessel function integral of the order 5/3,
where 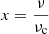 and νc is the critical frequency of synchrotron emission for a single electron given by
and νc is the critical frequency of synchrotron emission for a single electron given by
Emissivity due to inverse-Compton scattering from the CMB can be expressed in the form given by Rybicki & Lightman (1986),
where σT is the Thomson-scattering cross section, and ϵ(ν1) is the blackbody distribution of the seed photons from the CMB given by the expression
and the function f(x) is given by
where  . For low-energy electrons with Lorentz factor γ ≪ γk, IC losses are in the Thomson limit, but for high-energy electrons with γ ≫ γk, the IC losses occur in the extreme Klein-Nishina limit where
. For low-energy electrons with Lorentz factor γ ≪ γk, IC losses are in the Thomson limit, but for high-energy electrons with γ ≫ γk, the IC losses occur in the extreme Klein-Nishina limit where  is the critical Klein-Nishina Lorentz factor for a CMB photon with T = TCMB = 2.73K (Schlickeiser & Ruppel 2010; Petruk 2009).
is the critical Klein-Nishina Lorentz factor for a CMB photon with T = TCMB = 2.73K (Schlickeiser & Ruppel 2010; Petruk 2009).
We validated the above formulations used in our post-processing tool with static particle spectra for a single grid-cell with the open-source one-zone model NAIMA (Zabalza 2015). We assigned a particular set of free parameters to model the synchrotron and IC emission from the jet at kpc scales. The parameters are a minimum electron energy E0 = 1 TeV, power-law index p = 5, the distance between the blob and observer D = 1.5 kpc, magnetic field strength B = 100 μG, and the ratio of the number density of nonthermal electrons to fluid number density ηNT = 0.01. The same set of parameters were input to the NAIMA code to obtain the SED. A comparison of the SED obtained using the static particle spectra for a single grid-cell with those produced using the NAIMA code is shown in Fig. A.1. The SEDs from both these codes match well across the electromagnetic spectrum ranging from frequencies between 1 MHz in radio to 1 YHz in γ-rays. This clearly validates the equations adopted for the static particle spectra approach. While the NAIMA code uses analytical approximations to compute both the synchrotron (Aharonian et al. 2010) and IC (Khangulyan et al. 2014) emissivities, our approach computes the exact integrals in Eqs. (A.1) and (A.4) numerically for more accurate results.
 |
Fig. A.1. Comparison of the SED of synchrotron and inverse-Compton emission with a power-law index p = 5 obtained using the static particle spectra for a single grid-cell and the one-zone model NAIMA. All other parameters were kept the same. The flux is normalized with νscFνsc, where νsc = 122 Hz is the frequency scale and Fνsc = 9.38 × 10−8 ergs s−1 cm−2 Hz−1 is the flux scale corresponding to γmax = 106. |
We also studied the direction dependence of the static particle spectra approach. To understand this, we obtained the SEDs for the B cases with two different inclination angles. The input parameters for the static particle spectra are the same as considered for the intensity maps (as given in Sect. 4.2). The sharp cutoffs at both ends of the spectrum arise because of the energy limits of the emitting electrons, whereas the slope of the flat portion of the SED is zero for our chosen value of the spectral index, p = 3 as it evolves as (3 − p)/2. For a direction along a line of sight that is close to the axial direction with θ = 20°, the total integrated flux in the UNI-B case normalized to νscFνsc is about 10−11 which is nearly two orders of magnitude lower than the normalized flux values in the HEL1-B and HEL2-B cases, which are about 10−9. The fluxes for all the B cases are on the same order for a direction along a line of sight that is highly inclined with the jet axis (θ = 50°) in the X − Z plane. The increased synchrotron emission for the UNI-B case at higher inclination angles of the line of sight with the jet axis can be attributed to the orientation of the line-of-sight vector n̂los with the magnetic field vector B.
The synchrotron emissivity given by Eq. (A.1) evolves directly as |B × n̂los| ∝ |B|sin α, where α is the angle between the line-of-sight vector n̂los and the magnetic field vector B. In the UNI-B case, as the axial magnetic field dominates the transverse magnetic field in most of the grid zones, we obtain θ ≈ α. For a line of sight close to the jet axis (θ = 20°), the contribution to the total integrated flux from most of the grid zones will be less as sinα has lower values for small α. However, in the HEL1-B and HEL2-B cases, the azimuthal magnetic field Bϕ , which is nearly perpendicular to a line of sight close to the jet axis, contributes significantly to the synchrotron emission as sinα → 1 for α → 90°. This explains the higher total integrated flux levels in the HEL1-B and HEL2-B cases for θ = 20°. For θ = 50°, on the other hand, the axial magnetic field in the UNI-B case will now have a component that is perpendicular to the line of sight, which contributes to the synchrotron emission of the jet. This results in fluxes of roughly the same order for the B cases, as shown in the right panel of Fig. A.2.
 |
Fig. A.2. SED of the synchrotron emission produced using static particle spectra with a power-law index p = 3 for the B cases with Ms = 5.00 at t/ta = 2.25 when seen from a direction inclined at 20° (left panel) and 50° (right panel) with the jet axis. The frequency and flux have the same normalization as in Fig. A.1. |
All Tables
All Figures
 |
Fig. 1. Initial radial profiles of the azimuthal magnetic field Bϕ (top), and gas pressure P (bottom) for all the jet models given in Table 1. |
| In the text | |
 |
Fig. 2. Three-dimensional isosurface density contours of the model UNI-A (top left), HEL2-A (top right), UNI-B (bottom left), and HEL2-B (bottom right) at t/ta = 3.75 for a direction along a line of sight inclined at 20° with the jet axis. The color bars represent the jet density ρ/ρ0. While the UNI cases have a turbulent flow structure as they only experience the KH instability, the HEL2 cases have a clearly identifiable jet boundary as they are relatively stable. |
| In the text | |
 |
Fig. 3. Left panels: distribution of jet pressure P/P0 in the Y − Z plane of the models UNI-B at t/ta = 3.75 (top), UNI-C at t/ta = 5.59 (middle), and UNI-D at t/ta = 10.61 (bottom). Right panels: distribution of the vorticity along the normal to the Y − Z plane (∇×v)x for the corresponding cases at the same times. The color bars in the left and right panels represent the corresponding pressure and vorticity in code units, respectively. The tracer contours at level 0.8 are overplotted as black lines to demarcate the jet boundary in all three cases. The tracer levels close to the jet axis are greater than 0.8 and are not shown here. |
| In the text | |
 |
Fig. 4. Left panels: time evolution of the volume-averaged perturbed (a) kinetic energy in the X − Y plane |
| In the text | |
 |
Fig. 5. Synchrotron emission maps produced using the static particle spectra (top panels) and evolving particle spectra (bottom panels) with an initial power-law index p = 3 for case UNI-A at t/ta = 2.25 projected on the sky plane X′–Y′. These maps are obtained for a direction along a line of sight inclined at 20° with the jet axis at three different observing frequencies normalized to the frequency scale νsc = 122 Hz. The color bar represents the magnitude of specific intensity Iν normalized to the specific intensity scale Iνsc = 7.46 × 10−9 ergs s−1 cm−2 Hz−1 str−1. |
| In the text | |
 |
Fig. 6. Top panels: synchrotron emission maps obtained using the evolving particle spectra with an initial power-law index p = 6 for the UNI-B case at t/ta = 3.75 projected on the sky plane X′–Y′. These maps are produced for a direction along a line of sight inclined at 20° with the jet axis at observing frequencies of ν/νsc≈ 8.2 × 104, 8.2 × 106, and 8.2 × 108, where νsc = 122 Hz is the frequency scale. Middle panels: corresponding inverse-Compton emission maps at observing energies of E/hνsc≈ 7.9 × 1016, 7.9 × 1018, and 7.9 × 1018, where h is the Planck constant and the other model parameters are the same. The specific intensity is normalized to Iνsc = 7.46 × 10−15 ergs s−1 cm−2 Hz−1 str−1, corresponding to γmax = 108. Bottom panels: density ρ/ρ0 (left panel) and pressure P/P0 (right panel) maps integrated along the same line of sight. |
| In the text | |
 |
Fig. 7. Histogram showing the probability density distribution of the number of shocked macroparticles with the compression ratio for the UNI-B and HEL2-C cases at t/ta = 3.75. The dark red color is due to the overlapping of the blue and red bars. |
| In the text | |
 |
Fig. 8. Time evolution of the SED for model UNI-B produced using the evolving particle spectra with an initial power-law index, p = 6 when observed from a direction inclined at 20° with the jet axis. The colors of the lines indicate the time normalized to Alfvén time. Lines with t/ta = 0.0, 2.62, 3.00, 3.12, 3.37, 3.5, 3.62, 3.75, 3.87, and 4.37 are shown in the left panel for the synchrotron emission, and the corresponding IC emission is shown in the right panel. The total integrated flux νFν is normalized with νscFνsc, where νsc = 122 Hz is the frequency scale and Fνsc = 9.38 × 10−14 ergs s−1 cm−2 Hz−1 is the flux scale corresponding to γmax = 108. |
| In the text | |
 |
Fig. 9. Distribution of jet pressure P/P0 of the reference case UNI-B in the X − Z plane at t/ta = 3.75. The contours representing 1% of the peak value of normalized synchrotron emissivity at ν/νsc ≈ 8.2 × 1014 are overplotted as black lines, where νsc = 122 Hz is the frequency scale. The black lines indicate regions of X-ray spots resulting from the second population of nonthermal electrons generated in the vicinity of newly formed shocks due to shear. |
| In the text | |
 |
Fig. 10. Time evolution of the SED for model HEL2-C produced using the evolving particle spectra with an initial power-law index p = 6 when observed from a direction inclined at 20° with the jet axis. Lines with t/ta = 3.0, 3.75, and 4.5 are shown in the left panel for the synchrotron emission, and the corresponding IC emission is shown in the right panel. The frequency, flux, and time have the same normalization as in Fig. 8. |
| In the text | |
 |
Fig. A.1. Comparison of the SED of synchrotron and inverse-Compton emission with a power-law index p = 5 obtained using the static particle spectra for a single grid-cell and the one-zone model NAIMA. All other parameters were kept the same. The flux is normalized with νscFνsc, where νsc = 122 Hz is the frequency scale and Fνsc = 9.38 × 10−8 ergs s−1 cm−2 Hz−1 is the flux scale corresponding to γmax = 106. |
| In the text | |
 |
Fig. A.2. SED of the synchrotron emission produced using static particle spectra with a power-law index p = 3 for the B cases with Ms = 5.00 at t/ta = 2.25 when seen from a direction inclined at 20° (left panel) and 50° (right panel) with the jet axis. The frequency and flux have the same normalization as in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



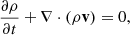
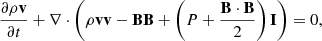
![$$ \begin{aligned} \frac{\partial E}{\partial t} + \nabla \cdot \left[\left(P + E + \frac{B^{2}}{2} \right)\mathbf{v } -\mathbf{B }(\mathbf{v } \cdot \mathbf{B }) \right] = 0, \end{aligned} $$](/articles/aa/full_html/2021/05/aa40440-21/aa40440-21-eq3.gif)
![$$ \begin{aligned} \frac{\partial \mathbf{B }}{\partial t} + \nabla \cdot [ \mathbf{v } \mathbf{B } - \mathbf{B } \mathbf{v } ] = 0, \end{aligned} $$](/articles/aa/full_html/2021/05/aa40440-21/aa40440-21-eq4.gif)
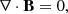
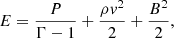
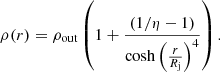
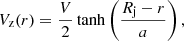
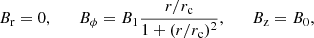
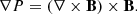
![$$ \begin{aligned} P = P_{\rm 0} - \frac{{B_{\rm 1}}^{2}}{2 \rho _{\rm 0}} \left( 1 - \frac{1}{[1 + (r/r_{\rm c})^{2}]^{2}} \right), \end{aligned} $$](/articles/aa/full_html/2021/05/aa40440-21/aa40440-21-eq13.gif)
![$$ \begin{aligned} \Pi (r)= \frac{r B_{\rm z}}{B_{\rm \phi }} = \frac{r_{\rm c} B_{\rm 0}}{B_{\rm 1}} \left[1 + \left(\frac{r}{r_{\rm c}} \right)^{2} \right], \end{aligned} $$](/articles/aa/full_html/2021/05/aa40440-21/aa40440-21-eq14.gif)